Modeling Fractals in the Setting of Graphical Fuzzy Cone Metric Spaces

Abstract

This study introduces a new metric structure called the Graphical Fuzzy Cone Metric Space (GFCMS) and explores its essential properties in detail. We examine its topological aspects in detail and introduce the notion of Hausdorff distance within this setting—an advancement not previously explored in any graphical structure. Furthermore, a fixed-point result is proven within the framework of GFCMS, accompanied by examples that demonstrate the applicability of the theoretical results. As a significant application, we construct fractals within GFCMS, marking the first instance of fractal generation in a graphical structure. This pioneering work opens new avenues for research in graph theory, fuzzy metric spaces, topology, and fractal geometry, with promising implications for diverse scientific and computational domains.

1. Introduction

Graph theory (GT) has attracted increasing attention because of its wide range of practical applications and importance in both mathematics and the practical sciences. A graph with $\mathfrak{V}\left(\mathfrak{G}\right)$ as the set of vertices and $\mathfrak{Z}\left(\mathfrak{G}\right)$ as the set of edges that reflect the connections between these vertices is called an ordered pair. The size of the edge set, $\left|\mathfrak{Z}\right(\mathfrak{G}\left)\right|$, indicates the number of edges, and the order of the vertex set, $\left|\mathfrak{V}\right(\mathfrak{G}\left)\right|$, determines the order of the graph.

GT can be generically classified into two groups. The first focuses on undirected graphs, which allow for unrestricted movement between connected vertices since connections between them do not have direction. The second category includes directed graphs, where each edge is assigned a particular direction. Whereas edges in undirected graphs are regarded as unordered pairs, edges in directed graphs are represented as ordered pairs.

Leonhard Euler became renowned as the Father of GT in 1736 after solving the famous Konigsberg Bridge Problem. The graphical aspect of this theory has given rise to a variety of applications, such as frameworks for decision-making, the visualization of object relationships, and a flexible method for adjusting and changing current systems. In chemical sciences [1,2], data science [3], and architecture [4], GT has diverse applications. Furthermore, Jachymski [5] developed several FP results by applying the graph structure in FPT. Shukla et al. [6] extended a number of FP discoveries in GMSs and applied the graph structure to MSs. Chen et al. [7] introduced the idea of a graphical convex MS and produced FP results for set-valued G-contraction mappings and related applications.

By introducing fuzzy set theory (FST), Zadeh [8] developed a framework for handling the imprecision and uncertainty that are frequently encountered in day-to-day living. Building on this, FMS was introduced by Kramosil and Michalek [9] using MSs and fuzzy sets. In order to improve the FMS framework, George and Veeramani [10,11] added a Hausdorff structure for these spaces. The concept of graphical fuzzy metric spaces (GFMSs) was first proposed by Saleem et al. [12] and used in the fractional differential equation analysis. This idea was then expanded and refined by Shukla et al. [13] through their investigation of fixed point theory (FPT) in GFMSs.

In their work, Huang and Zhang [14] developed the concept of cone metric spaces (CMSs) by substituting the set of real numbers with an ordered Banach space, and they established various FP results for contractive mappings within this setting. Tarkan Oner et al. [15] introduced the concept of FCMSs, which generalizes CMSs, and established some FP results. Satish Shukla et al. [16] introduced the concept of GCMSs over Banach algebras and established several FP results for specific types of contractive mappings defined on these spaces.

In this study, we introduce the concept of graphical fuzzy cone metric spaces (GFCMSs) and investigate their topological properties in depth. Furthermore, we establish new FP theorems within the framework of complete GFCMSs. The integration of fuzzy, cone, and graph structures into a unified framework is driven by the need to handle uncertainty, partial ordering, and relational dependencies simultaneously in metric-type spaces. Fuzzy metrics account for the vagueness and imprecision inherent in many real-world situations, while cone metrics introduce a vector-valued structure that allows for more refined comparisons, especially in ordered Banach spaces. Incorporating a graph structure enables modeling of asymmetric relationships and directional constraints among elements, which are common in applications such as network theory, optimization, and decision processes. By combining these three components, graphical fuzzy cone metric spaces provide a more flexible and robust setting for analyzing convergence, continuity, and fixed point behavior in complex systems that cannot be effectively studied under classical or single-component metric frameworks.

2. Preliminaries

Definition 1. 

Let $\mathcal{E}$ be a real Banach algebra, meaning that $\mathcal{E}$ is a real Banach space equipped with a multiplication operation that meets the following requirements (see [17]): ∀$\zeta ,\eta ,\gamma \in \mathcal{E}$, $a\in \mathbb{R}$,

1. 

$\zeta \left(\eta \gamma \right)=\left(\zeta \eta \right)\gamma$;

2. 

$\zeta (\eta +\gamma )=\zeta \eta +\zeta \gamma$ and $(\zeta +\eta )\gamma =\zeta \gamma +\zeta \eta$;

3. 

$a\left(\zeta \eta \right)=\left(a\zeta \right)\eta =\zeta \left(a\eta \right)$;

4. 

$\left|\right|\zeta \eta \left|\right|\le \left|\right|\zeta \left|\right|\left|\eta \right||$.

In this paper, we work under the assumption that $\mathcal{E}$ is a Banach algebra possessing a unit element; that is, there exists an identity element e in $\mathcal{E}$ satisfying $e\zeta =\zeta e=\zeta$ for every $\zeta \in \mathcal{E}$. An element $\zeta \in \mathcal{E}$ is called invertible if there exists $\eta \in \mathcal{E}$ s.t. $\zeta \eta =\eta \zeta =e$. The inverse of an element $\zeta \in \mathcal{E}$ is represented by ${\zeta }^{-1}$. The quantity $\rho \left(\zeta \right)$ denotes the spectral radius of the element $\zeta$ in $\mathcal{E}$ and

$$\rho \left(\zeta \right)=\underset{n\to \infty }{lim}{\left|\left|{\zeta }^n\right|\right|}^{{\displaystyle \frac{1}{n}}}=in{f}_{n\ge 1}{\left|\left|{\zeta }^n\right|\right|}^{{\displaystyle \frac{1}{n}}}.$$

Definition 2

(Liu and Xu [18]). Let $\mathfrak{E}$ be a subset of $\mathcal{E}$. The set $\mathfrak{E}$ is defined as a cone provided it satisfies the conditions below:

1. 

$\mathfrak{E}$ is non-empty, closed, and distinct from the singleton set $\left\{\theta \right\}$;

2. 

For any non-negative real numbers $a,b\in \mathbb{R}$ and any elements $\zeta ,\eta \in \mathfrak{E}$, the linear combination $a\zeta +b\eta$ belongs to $\mathfrak{E}$;

3. 

If $\zeta \in \mathfrak{E}$ and simultaneously $-\zeta \in \mathfrak{E}$, then it must follow that $\zeta =\theta$.

A cone $\mathfrak{E}$ is said to be solid if its interior is nonempty, i.e., $\mathrm{int}\left(\mathfrak{E}\right)\ne \varnothing$. We consistently assume that the cone in question is solid. In a Banach algebra $\mathcal{E}$, each cone defines a partial order ⪯ on $\mathcal{E}$ s.t. for all $\zeta ,\eta \in \mathcal{E}$, the relation $\zeta ⪯\eta$ holds precisely when $\eta -\zeta$ lies in $\mathfrak{E}$. Also, we write $\zeta \ll \eta$ if and only if $\zeta -\eta \in$ int$\left(\mathfrak{E}\right)$ for all $\zeta ,\eta \in \mathcal{E}$.

Remark 1

(Jungck et al. [19]). Let $\mathfrak{E}$ be a cone of $\mathcal{E}$, and $\zeta ,\eta ,\gamma \in \mathfrak{E}$.

1. 

If $\zeta ⪯\eta$ and $\eta \ll \gamma$, then $\zeta \ll \gamma$.

2. 

If $\zeta \ll \eta$ and $\eta \ll \gamma$, then $\zeta \ll \gamma$.

3. 

If $\theta ⪯u\ll \gamma$ for every $\gamma \in int\left(\mathfrak{E}\right)$, then $u=\theta$.

Remark 2. 

For any $r_1>r_2$, ∃$r_3\in (0,1)$ s.t. $r_1\ast r_3\ge r_2$, and for any $r_4\in (0,1)$, we can find $r_5\in (0,1)$ satisfying $r_5\ast r_5\ge r_4$.

Definition 3

(Dordević et al. [20]). A sequence ${\zeta }_n$ within the cone $\mathfrak{E}$ is called a c-sequence if, for every $c\in \mathcal{E}$ with $\theta \ll c$, ∃$n_0\in \mathbb{N}$ s.t. ${\zeta }_n\ll c$∀$n>n_0$.

Definition 4

([15]). A 3-tuple $(\mathsf{\Omega },\mathcal{O},\ast )$ is defined as a fuzzy cone metric space (FCMS) if the following hold: $\mathfrak{E}$ is a cone within the space $\mathcal{E}$, Ω is a set chosen arbitrarily, ∗ represents a continuous t-norm, and $\mathcal{O}$ is a fuzzy set on the product space ${\mathsf{\Omega }}^2\times \mathit{int}\left(\mathfrak{E}\right)$ that satisfies specific conditions.

• For all $\zeta ,\eta ,\gamma \in \mathsf{\Omega }$ and $t,s\in int\left(\mathfrak{E}\right)$ (that is $t\gg \theta ,s\gg \theta$)

1. 

$\mathcal{O}(\zeta ,\eta ,t)>0$,

2. 

$\mathcal{O}(\zeta ,\eta ,t)=1\iff \zeta =\eta$,

3. 

$\mathcal{O}(\zeta ,\eta ,t)=\mathcal{O}(\eta ,\zeta ,t)$,

4. 

$\mathcal{O}(\zeta ,\eta ,t)\ast \mathcal{O}(\eta ,\zeta ,s)⪯\mathcal{O}(\eta ,\gamma ,t+s)$,

5. 

$\mathcal{O}(\zeta ,\eta ,·):int\left(\mathfrak{E}\right)\to [0,1]$ is continuous.

We modify certain concepts related to graphs based on the work of Jachymski [5] and Shukla et al. [6].

For a non-empty set $\mathsf{\Omega }$, ∆ represents the diagonal of $\mathsf{\Omega }\times \mathsf{\Omega }$, and $▵=\left\{\right(\zeta ,\zeta ):\zeta \in \mathsf{\Omega }\}.$ A directed graph is denoted by $\mathfrak{G}$ if its collection of vertices is $\mathfrak{V}\left(\mathfrak{G}\right)=\mathsf{\Omega }$ and its set of edges is $\mathfrak{Z}\left(\mathfrak{G}\right)$, which includes no parallel edges and $▵\subseteq \mathfrak{Z}\left(\mathfrak{G}\right)$. In this context, we say that $\mathsf{\Omega }$ is equipped with the graph $\mathfrak{G}$. The symmetric graph, denoted by $\tilde{\mathfrak{G}}$, is defined as $\tilde{\mathfrak{G}}=\mathfrak{Z}\left(\mathfrak{G}\right)\cup \mathfrak{Z}\left({\mathfrak{G}}^{-1}\right)$, where ${\mathfrak{G}}^{-1}$ is characterized by $V\left({\mathfrak{G}}^{-1}\right)=\mathsf{\Omega }$ and $\mathfrak{Z}\left({\mathfrak{G}}^{-1}\right)=(\zeta ,\eta ):(\eta ,\zeta )\in \mathfrak{Z}\left(\mathfrak{G}\right)$.

Let $\zeta ,\eta \in \mathfrak{V}\left(\mathfrak{G}\right)$. A sequence of vertices ${\left\{{\zeta }_i\right\}}_{i=0}^n$, taken from $\mathfrak{V}\left(\mathfrak{G}\right)$, is said to be a path of length $n+1$ from $\zeta$ to $\eta$ if it satisfies ${\zeta }_0=\zeta$, ${\zeta }_n=\eta$, and for every index $i=0,1,\dots ,n$, the pair $({\zeta }_i,{\zeta }_{i+1})$ belongs to $\mathfrak{Z}\left(\mathfrak{G}\right)$. The vertices $\zeta$ and $\eta$ are said to be connected if a path of any length connects $\zeta$ to $\eta$. The graph $\mathfrak{G}$ is considered connected if, for any two vertices in $\mathfrak{G}$, there is a path that links them.

We define ${\left[\zeta \right]}_{\mathfrak{G}}^l=\{\eta \in \mathsf{\Omega }:\mathrm{we}\mathrm{can}\mathrm{find}\mathrm{a}\mathrm{directed}\mathrm{path}\mathrm{from}\zeta \mathrm{to}\eta \mathrm{of}\mathrm{length}l\}$ for $l\in \mathbb{N}$. Additionally, we introduce a relation P on $\mathsf{\Omega }$ such that ${\left(\zeta P\eta \right)}_{\mathfrak{G}}$ holds if and only if $\zeta$ and $\eta$ are connected by a directed path in $\mathfrak{G}$. We denote $\gamma \in {\left(\zeta P\eta \right)}_{\mathfrak{G}}$ if $\gamma$ lies along a directed path from $\zeta$ to $\eta$ in $\mathfrak{G}$. A sequence ${\zeta }_n$ in $\mathsf{\Omega }$ is said to be $\mathfrak{G}$-termwise connected if, for every $n\in \mathbb{N}$, the relation ${\left({\zeta }_{n}P{\zeta }_{n+1}\right)}_{\mathfrak{G}}$ holds.

Definition 5

([16]). Let Ω be a non-empty set equipped with the graph $\mathfrak{G}$, and let $\mathcal{E}$ be a Banach algebra. Assume that a mapping $d_{\mathfrak{G}}:\mathsf{\Omega }\times \mathsf{\Omega }\to \mathcal{E}$ satisfies the following conditions:

1. 

$d_{\mathfrak{G}}(\zeta ,\eta )⪰\theta$∀$\zeta ,\eta \in \mathsf{\Omega }$;

2. 

$d_{\mathfrak{G}}(\zeta ,\eta )=\theta \iff \zeta =\eta$;

3. 

$d_{\mathfrak{G}}(\zeta ,\eta )=d_{\mathfrak{G}}(\eta ,\zeta )$∀$\zeta ,\eta \in \mathsf{\Omega }$;

4. 

${\left(\zeta P\eta \right)}_{\mathfrak{G}}$, $\gamma \in {\left(\zeta P\eta \right)}_{\mathfrak{G}}$ implies $d_{\mathfrak{G}}(\zeta ,\eta )⪯d_{\mathfrak{G}}(\zeta ,\gamma )+d_{\mathfrak{G}}(\gamma ,\eta )$∀$\zeta ,\eta ,\gamma \in \mathsf{\Omega }$.

In this case, the mapping $d_{\mathfrak{G}}$ is referred to as a graphical cone metric on Ω, and the pair $(\mathsf{\Omega },d_{\mathfrak{G}})$ is called a GCMS over the Banach algebra $\mathcal{E}$.

Next, we define the concept of graphical fuzzy cone metric spaces (GFCMSs).

3. Graphical Fuzzy Cone Metric Spaces

Definition 6. 

Let Ω be a nonempty set equipped with the graph $\mathfrak{G}$, and let $\mathcal{E}$ be a Banach algebra, ∗ be a continuous t-norm, $\mathfrak{E}$ be a cone in $\mathcal{E}$, and ${\mathcal{M}}_{\mathfrak{G}}$ be a fuzzy set on $\mathsf{\Omega }\times \mathsf{\Omega }\times int\left(\mathfrak{E}\right)$. The function ${\mathcal{M}}_{\mathfrak{G}}$ is referred to as a graphical fuzzy cone metric provided that the following conditions are satisfied.

1. 

${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)>0$;

2. 

${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=1\iff \zeta =\eta$;

3. 

${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)={\mathcal{M}}_{\mathfrak{G}}(\eta ,\zeta ,t)$;

4. 

${\left(\zeta P\eta \right)}_{\mathfrak{G}}$, $\gamma \in {\left(\zeta P\eta \right)}_{\mathfrak{G}}$ implies ${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)\ast {\mathcal{M}}_{\mathfrak{G}}(\eta ,\gamma ,s)⪯{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\gamma ,t+s)$;

5. 

${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,·):int\left(\mathfrak{E}\right)\to [0,1]$ is continuous,

for all $\zeta ,\eta \in \mathsf{\Omega }$ and $t,s\gg \theta$. Then, $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ is known as a GFCMS.

If we take $\mathsf{\Omega }=\mathbb{R}$, $\mathfrak{E}=[0,\infty )$ and $\zeta \ast \eta =\zeta \eta$, then every GFMS becomes a GFCMSs.

Example 1. 

Consider $\mathcal{E}={\mathbb{R}}^2$, where the norm is Euclidean and multiplication is defined component-wise. Define $\mathfrak{E}=\left\{\right(\zeta ,\eta )\in \mathcal{E}:\zeta ,\eta \ge 0\},$ then $\mathfrak{E}$ is a solid cone in $\mathcal{E}$. Let $\mathsf{\Omega }=[0,1]$ and set $\mathfrak{G}$ to be $\mathfrak{V}\left(\mathfrak{G}\right)=\mathsf{\Omega }$ and $\mathfrak{Z}\left(\mathfrak{G}\right)=▵\cup \left\{\right(\zeta ,\eta )\in \mathsf{\Omega }\times \mathsf{\Omega }:0<\eta \le \zeta \}$. Define a function ${\mathcal{M}}_{\mathfrak{G}}:\mathsf{\Omega }\times \mathsf{\Omega }\times int\left(\mathfrak{E}\right)\to [0,1]$ by

$${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=\left\{\begin{array}{cc}1\hfill & \mathit{if}\zeta =\eta ;\hfill \\ min\{\zeta ,\eta \}\hfill & \mathit{if}\zeta \ne \eta \mathit{and}\zeta ,\eta \in \mathsf{\Omega }\left|\right\{0\};\hfill \\ max\{\zeta ,\eta \},\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Then, $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ is a GFCMS over Banach algebra $\mathcal{E}$.

Example 2. 

Consider $\mathcal{E}={\mathbb{R}}^2$, where the norm is Euclidean and multiplication is defined component-wise. Define $\mathfrak{E}=\left\{\right(\zeta ,\eta )\in \mathcal{E}:\zeta ,\eta \ge 0\},$ then $\mathfrak{E}$ is a solid cone in $\mathcal{E}$. Let $\mathsf{\Omega }=[0,1]$ and set $\mathfrak{G}$ to be $\mathfrak{V}\left(\mathfrak{G}\right)=\mathsf{\Omega }$ and $\mathfrak{Z}\left(\mathfrak{G}\right)=▵\cup \left\{\right(\zeta ,\eta )\in \mathsf{\Omega }\times \mathsf{\Omega }:0<\eta \le \zeta \}$ at time t. Let ∗ be a continuous t-norm defined by $\zeta \ast \eta =\zeta ·\eta$. We define a function ${\mathcal{M}}_{\mathfrak{G}}:\mathsf{\Omega }\times \mathsf{\Omega }\times int\left(\mathfrak{E}\right)\to [0,1]$ as follows:

$${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=\left\{\begin{array}{cc}1,\hfill & \mathit{if}\zeta =\eta ,\hfill \\ e^{-\zeta \eta },\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Afterward, we demonstrate that $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ forms a GFCMS over a Banach algebra. The properties 1, 2, and 3 are obvious. For 4, suppose $\zeta ,\eta ,\gamma \in \mathsf{\Omega }$ and $\gamma \in {\left(\zeta P\eta \right)}_{\mathfrak{G}}$, i.e., $0\le \zeta \le \gamma \le \eta$. Then, we must have $\left(\zeta \gamma \right)\ge \left(\zeta \eta \right)\ast \left(\eta \gamma \right)$. This shows that ${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\gamma ,t+s)⪰{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)\ast {\mathcal{M}}_{\mathfrak{G}}(\eta ,\gamma ,s)$. On the other hand, $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ is not a FCMS, as ${\mathcal{M}}_{\mathfrak{G}}(0.5,0.8,t+s){\mathcal{M}}_{\mathfrak{G}}(0.5,0,t)\ast {\mathcal{M}}_{\mathfrak{G}}(0,0.8,s)$.

GFCMS differs from GFMS by allowing for cone-valued time parameters ordered via a cone in a Banach algebra, introducing a partial order into the triangle inequality and enabling comparisons within a richer, vector-valued fuzzy framework.

Definition 7. 

Consider $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ as a GFCMS. Let $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ be a function, and let ${\mathfrak{G}}^{\prime }$ represent a subgraph of $\mathfrak{G}$ with the property that $\mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$ contains Δ. In this setting, the mapping $\mathcal{F}$ is referred to as a $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-graphical fuzzy cone contraction, provided the following conditions are satisfied:

(GFCC1) 

$(\zeta ,\eta )\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$ implies $(\mathcal{F}\zeta ,\mathcal{F}\eta )\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$, i.e., $\mathcal{F}$ is edge-preserving in ${\mathfrak{G}}^{\prime };$

(GFCC2) 

for some constant κ with $0<\kappa <1$ s.t.

$${\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\mathcal{F}\zeta ,\mathcal{F}\eta ,t)}}-1\le \kappa \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)}}-1\right)$$

∀$\zeta ,\eta \in \mathsf{\Omega }$ and $t\gg \theta$ with $(\zeta ,\eta )\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$.

Example 3. 

Let $\mathsf{\Omega }=[0,1]$, and let $\mathcal{E}={\mathbb{R}}^2$ be equipped with the cone

$$\mathfrak{E}=\{(\zeta ,\eta )\in {\mathbb{R}}^2:\zeta \ge 0,\eta \ge 0\},$$

which is a solid, normal cone in the Banach algebra ${\mathbb{R}}^2$ under coordinate-wise operations. We define the continuous t-norm ∗ by $\zeta \ast \eta =\zeta ·\eta$.

We define a graph $\mathfrak{G}$ on Ω such that

$$\mathfrak{Z}\left(\mathfrak{G}\right)=▵\cup \left\{\right(\zeta ,\eta )\in \mathsf{\Omega }\times \mathsf{\Omega }:\zeta \le \eta \}.$$

Let ${\mathfrak{G}}^{\prime }$ be the subgraph of $\mathfrak{G}$ defined as follows:

$$\mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)=\{(\zeta ,\eta )\in \mathsf{\Omega }\times \mathsf{\Omega }:\zeta \le \eta \}.$$

We define the function ${\mathcal{M}}_{\mathfrak{G}}:\mathsf{\Omega }\times \mathsf{\Omega }\times \mathit{int}\left(\mathfrak{E}\right)\to [0,1]$ as follows:

$${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=\left\{\begin{array}{cc}1,\hfill & \mathit{if}\zeta =\eta ,\hfill \\ e^{-|\zeta -\eta |},\hfill & \mathit{if}(\zeta ,\eta )\in \mathfrak{Z}\left(\mathfrak{G}\right),\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Now, we define the mapping $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ as follows:

$$\mathcal{F}\left(\zeta \right)={\displaystyle \frac{\zeta }{2}},\mathit{for}\mathit{all}\zeta \in \mathsf{\Omega }.$$

We now verify that $\mathcal{F}$ satisfies both conditions of Definition 7:

(GFCC1) 

Let $(\zeta ,\eta )\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$, i.e., $\zeta \le \eta$. Then,

$$\mathcal{F}\left(\zeta \right)={\displaystyle \frac{\zeta }{2}}\le {\displaystyle \frac{\eta }{2}}=\mathcal{F}\left(\eta \right),$$

so $(\mathcal{F}\left(\zeta \right),\mathcal{F}\left(\eta \right))\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$. Hence, $\mathcal{F}$ is edge-preserving in ${\mathfrak{G}}^{\prime }$.

(GFCC2) 

Let $(\zeta ,\eta )\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$, i.e., $\zeta \le \eta$. Then,

$${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=e^{-|\zeta -\eta |},{\mathcal{M}}_{\mathfrak{G}}(\mathcal{F}\zeta ,\mathcal{F}\eta ,t)=e^{-|\zeta /2-\eta /2|}=e^{-{\displaystyle \frac{1}{2}}|\zeta -\eta |}.$$

Now, we compute

$${\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\mathcal{F}\zeta ,\mathcal{F}\eta ,t)}}-1=e^{{\displaystyle \frac{1}{2}}|\zeta -\eta |}-1,$$

and

$${\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)}}-1=e^{|\zeta -\eta |}-1.$$

Since for all $\zeta >0$, the inequality

$$e^{\zeta /2}-1<\kappa (e^{\zeta }-1)$$

holds for some $\kappa \in (0,1)$. It follows that

$${\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\mathcal{F}\zeta ,\mathcal{F}\eta ,t)}}-1\le \kappa \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)}}-1\right).$$

Hence, $\mathcal{F}$ satisfies (GFCC2).

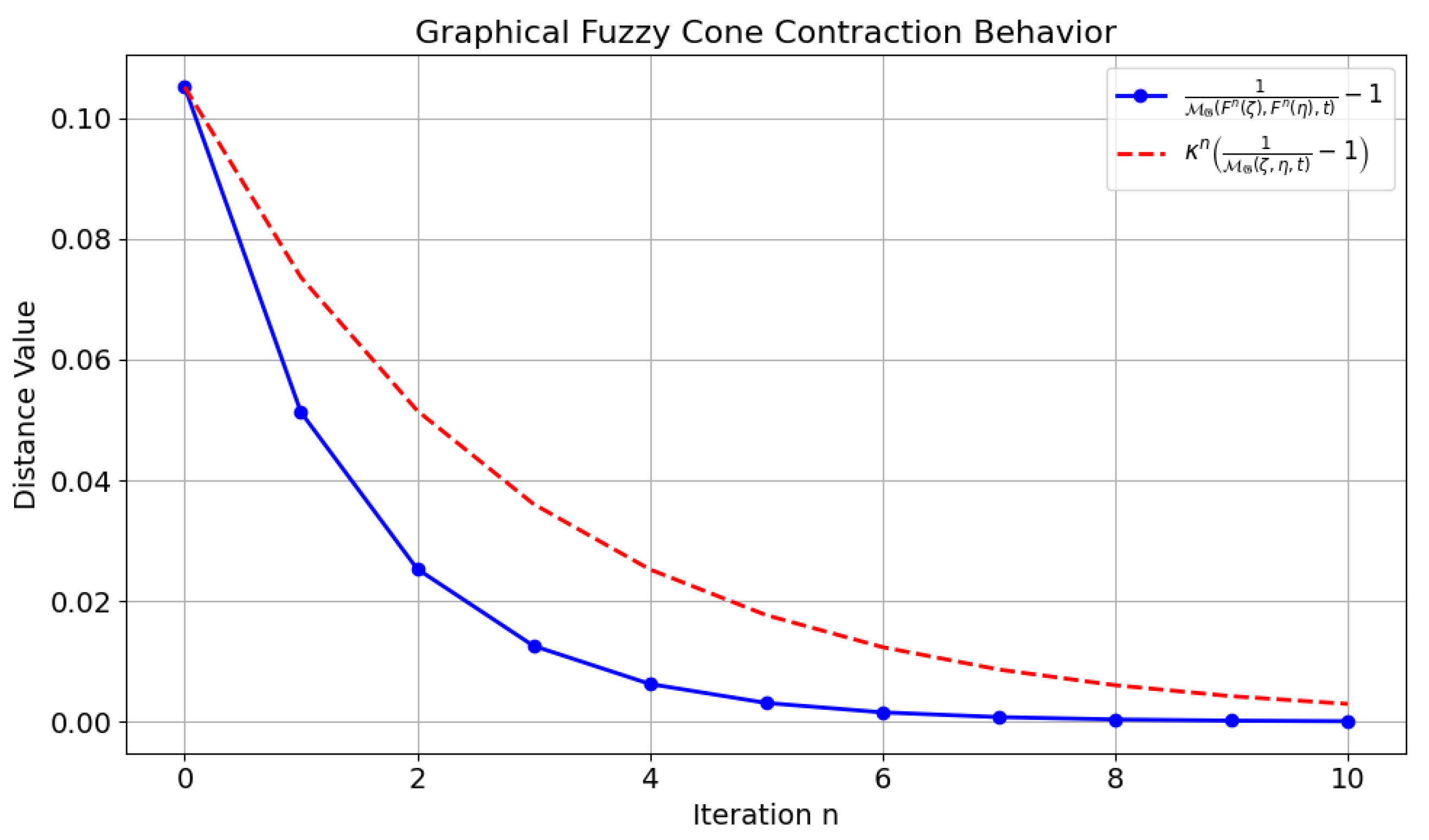
Thus, $\mathcal{F}\left(\zeta \right)=\zeta /2$ is a $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-graphical fuzzy cone contraction.

The contraction behavior of the mapping $\mathcal{F}\left(\zeta \right)={\displaystyle \frac{1}{2}}\zeta$ as a graphical fuzzy cone contraction in GFCMS is depicted in Figure 1.

Definition 8. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS. Given $t\gg \theta$, the open ball $B_{\mathfrak{G}}(\zeta ,r,t)$ centered at ζ with radius $r\in (0,1)$ is described as

$$B_{\mathfrak{G}}(\zeta ,r,t)=\{\eta \in \mathsf{\Omega };\left(\zeta P\eta \right)\mathit{and}{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)>1-r\}.$$

Theorem 1. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS. We define

$$\tau =\{\mathfrak{U}\subseteq \mathsf{\Omega }:\forall \zeta \in \mathfrak{U}\exists r\in (0,1)\mathrm{s}.\mathrm{t}.{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,r)\subseteq \mathfrak{U}\}.$$

Then, τ defines a topology on Ω.

Proof. 

It is clear that $\mathsf{\Omega },\varnothing \in \tau$; hence, $\tau \ne \varnothing$. Suppose ${\mathfrak{U}}_1,{\mathfrak{U}}_2\in \tau$. Let $\zeta \in {\mathfrak{U}}_1\cap {\mathfrak{U}}_2$. Then, there exist $r_1,r_2\in (0,1)$ such that $B_{\mathfrak{G}}(\zeta ,r_1,t)\subseteq {\mathfrak{U}}_1$ and $B_{\mathfrak{G}}(\zeta ,r_2,t)\subseteq {\mathfrak{U}}_2$. Since $r_1,r_2\in (0,1)$, ∃$r\in (0,1)$ s.t. $r\ll r_1$ and $r\ll r_2$ and so $B_{\mathfrak{G}}(\zeta ,r,t)\subseteq B_{\mathfrak{G}}(\zeta ,r_1,t)\cap B_{\mathfrak{G}}(\zeta ,r_2,t)\subseteq {\mathfrak{U}}_1\cap {\mathfrak{U}}_2$. Hence, ${\mathfrak{U}}_1\cap {\mathfrak{U}}_2\in \tau$. In the same way, it can be demonstrated that the union of any family of sets from $\tau$ also belongs to $\tau$. □

Theorem 2. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS. Then, $(\mathsf{\Omega },\tau )$ is a Hausdorff.

Proof. 

Let $\zeta ,\eta \in \mathsf{\Omega }$ such that $\zeta \ne \eta$. Based on the definition of a fuzzy metric, we have $1>{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)>0$, and let us denote ${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)$ by r. According to Remark 2, for every $r_0$ satisfying $1>r_0>r_1$, there exists a value $r_1\in (0,1)$ such that $r_1\ast r_1>r_0$.

Now, consider the sets $B_{\mathfrak{G}}(\zeta ,1-r_1,{\displaystyle \frac{t}{2}})$ and $B_{\mathfrak{G}}(\eta ,1-r_1,{\displaystyle \frac{t}{2}})$. We have to see

$$B_{\mathfrak{G}}(\zeta ,1-r_1,{\displaystyle \frac{t}{2}})\cap B_{\mathfrak{G}}(\eta ,1-r_1,{\displaystyle \frac{t}{2}})=\varnothing$$

Suppose that $B_{\mathfrak{G}}(\zeta ,1-r_1,{\displaystyle \frac{t}{2}})\cap B_{\mathfrak{G}}(\eta ,1-r_1,{\displaystyle \frac{t}{2}})\ne \varnothing$. Then, there exists $\gamma \in B_{\mathfrak{G}}(\zeta ,1-r_1,{\displaystyle \frac{t}{2}})\cap B_{\mathfrak{G}}(\eta ,1-r_1,{\displaystyle \frac{t}{2}})$. Therefore, ${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\gamma ,{\displaystyle \frac{t}{2}})>1-(1-r_1)=r_1$ and ${\mathcal{M}}_{\mathfrak{G}}(\eta ,\gamma ,{\displaystyle \frac{t}{2}})>1-(1-r_1)=r_1.$ Thus, $r={\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)⪰{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\gamma ,{\displaystyle \frac{t}{2}})\ast {\mathcal{M}}_{\mathfrak{G}}(\eta ,\gamma ,{\displaystyle \frac{t}{2}})$. Then, $r>r_1\ast r_1$, so $r>r_0>r.$ This is a contradiction. Hence, $B_{\mathfrak{G}}(\zeta ,1-r_1,{\displaystyle \frac{t}{2}})\cap B_{\mathfrak{G}}(\eta ,1-r_1,{\displaystyle \frac{t}{2}})=\varnothing$. □

Definition 9. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS. Then, the graphical fuzzy cone distance between $\zeta \in \mathsf{\Omega }$ and a set $\mathfrak{K}\subset \mathsf{\Omega }$ is defined by

$${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\mathfrak{K},t)=\underset{{\zeta }_1\in \mathfrak{K}}{sup}\{{\mathcal{M}}_{\mathfrak{G}}(\zeta ,{\zeta }_1,t):\left(\zeta P{\zeta }_1\right)\}$$

, and the distance between $\mathfrak{A},\mathfrak{K}\subset \mathsf{\Omega }$ is defined by

$${\mathcal{M}}_{\mathfrak{G}}(\mathfrak{A},\mathfrak{K},t)=\underset{{\zeta }_1\in \mathfrak{A}}{inf}\left\{{\mathcal{M}}_{\mathfrak{G}}({\zeta }_1,\mathfrak{K},t)\right\}.$$

We shall use $\mathfrak{S}$ to represent the family of all nonempty compact subsets of $\mathsf{\Omega }$.

Example 4. 

Let $\mathsf{\Omega }=[0,1]$, $\mathcal{E}={\mathbb{R}}^2$, and let $\mathfrak{E}=\{(\zeta ,\eta )\in {\mathbb{R}}^2:\zeta ,\eta \ge 0\}$ be a solid cone in the Banach algebra ${\mathbb{R}}^2$ (with component-wise operations). Let ∗ be the product t-norm: $\zeta \ast \eta =\zeta \times \eta$.

We define the graph $\mathfrak{G}$ on Ω such that: $\mathfrak{Z}\left(\mathfrak{G}\right)=▵\cup \left\{\right(\zeta ,\eta )\in \mathsf{\Omega }\times \mathsf{\Omega }:\zeta \le \eta \}$.

We define the graphical fuzzy cone metric ${\mathcal{M}}_{\mathfrak{G}}:\mathsf{\Omega }\times \mathsf{\Omega }\times \mathit{int}\left(\mathfrak{E}\right)\to [0,1]$ as follows:

$${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=\left\{\begin{array}{cc}1,\hfill & \mathit{if}\zeta =\eta ,\hfill \\ e^{-|\zeta -\eta |},\hfill & \mathit{if}(\zeta ,\eta )\in \mathfrak{Z}\left(\mathfrak{G}\right),\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Now, take $\zeta =0.2$, $\mathfrak{K}=\{0.5,0.6,0.8\}$. Since $\left(\zeta P{\zeta }_1\right)$ means $0.2\le {\zeta }_1$ (based on the graph structure), we compute the following: ${\mathcal{M}}_{\mathfrak{G}}(0.2,\mathfrak{K},t)={sup}_{{\zeta }_1\in \mathfrak{K},0.2\le {\zeta }_1}{\mathcal{M}}_{\mathfrak{G}}(0.2,{\zeta }_1,t)=sup\{e^{-0.3},e^{-0.4},e^{-0.6}\}=e^{-0.3}$.

Now, let $\mathfrak{A}=\{0.1,0.2\}$. Then, ${\mathcal{M}}_{\mathfrak{G}}(\mathfrak{A},\mathfrak{K},t)={inf}_{{\zeta }_1\in \mathfrak{A}}{\mathcal{M}}_{\mathfrak{G}}({\zeta }_1,\mathfrak{K},t)$.

We already have ${\mathcal{M}}_{\mathfrak{G}}(0.2,\mathfrak{K},t)=e^{-0.3},{\mathcal{M}}_{\mathfrak{G}}(0.1,\mathfrak{K},t)=sup\{e^{-0.4},e^{-0.5},e^{-0.7}\}=e^{-0.4},$

so ${\mathcal{M}}_{\mathfrak{G}}(\mathfrak{A},\mathfrak{K},t)=inf\{e^{-0.3},e^{-0.4}\}=e^{-0.4}$.

Definition 10. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS, then the graphical fuzzy cone Hausdorff distance between two elements $\mathfrak{A}$ and $\mathfrak{K}$ of $\mathfrak{S}$ is as follows:

$${\mathfrak{H}}_{\mathfrak{G}}(\mathfrak{A},\mathfrak{K},t)=min\{{\mathcal{M}}_{\mathfrak{G}}(\mathfrak{A},\mathfrak{K},t),{\mathcal{M}}_{\mathfrak{G}}(\mathfrak{K},\mathfrak{A},t)\}.$$

Thus, $\mathfrak{S}$, equipped with the graphical fuzzy cone Hausdorff distance, forms a GFCMS. This space will be referred to as the graphical fuzzy cone Hausdorff metric space (GFCHMS) and will be denoted by $(\mathfrak{S},{\mathfrak{H}}_{\mathfrak{G}},\ast )$. It should be noted that the graphical fuzzy cone Hausdorff metric space is complete, provided that the GFCMS $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ is complete.

Lemma 1. 

Let $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ be a $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-graphical fuzzy cone contraction (GFCC) on a GFCMS $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$. Then, $\mathcal{F}:\mathfrak{S}\to \mathfrak{S}$ defined by

$$\mathcal{F}\left(\mathfrak{K}\right)=\left\{\mathcal{F}\right(\zeta ):\zeta \in \mathfrak{K}\}\forall \mathfrak{K}\in \mathfrak{S}$$

is a $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-GFCC on $(\mathfrak{S},{\mathfrak{H}}_{\mathfrak{G}},\ast )$.

Proof. 

Suppose $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ is a $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-GFCC on a GFCMS $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$. Then, $\mathcal{F}$ is edge-preserving in ${\mathfrak{G}}^{\prime }$, and there exist $0<\kappa <1$ s.t.

$${\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\mathcal{F}\zeta ,\mathcal{F}\eta ,t)}}-1\le \kappa \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)}}-1\right)$$

∀$\zeta ,\eta \in \mathsf{\Omega }$ and $t\gg \theta$ with $(\zeta ,\eta )\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$. Since $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ is a $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-graphical fuzzy cone contraction on a GFCMS $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$, $\mathcal{F}$ maps $\mathfrak{S}$ into itself. We will demonstrate that $\mathcal{F}:\mathfrak{S}\to \mathfrak{S}$ is a $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-graphical fuzzy cone contraction on $(\mathfrak{S},{\mathfrak{H}}_{\mathfrak{G}},\ast )$. Clearly, $\mathcal{F}:\mathfrak{S}\to \mathfrak{S}$ is edge-preserving in ${\mathfrak{G}}^{\prime }$. For any $\mathfrak{A},\mathfrak{K}\in \mathfrak{S}$ and $t\gg \theta$, let us have the following:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{{\mathfrak{H}}_{\mathfrak{G}}(\mathcal{F}\mathfrak{A},\mathcal{F}\mathfrak{K},t)}}-1={\displaystyle \frac{1}{min\{{\mathcal{M}}_{\mathfrak{G}}(\mathcal{F}\mathfrak{A},\mathcal{F}\mathfrak{K},t),{\mathcal{M}}_{\mathfrak{G}}(\mathcal{F}\mathfrak{K},\mathcal{F}\mathfrak{A},t)\}}}-1\end{array}$$

(1)

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\mathcal{F}\mathfrak{A},\mathcal{F}\mathfrak{K},t)}}-1& ={\displaystyle \frac{1}{min\{max\{{\mathcal{M}}_{\mathfrak{G}}(\mathcal{F}\zeta ,\mathcal{F}\eta ,t):\eta \in \mathfrak{K}\}:\zeta \in \mathfrak{A}\}}}-1\hfill \\ & \le \kappa \left({\displaystyle \frac{1}{min\{max\{{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t):\eta \in \mathfrak{K}\}:\zeta \in \mathfrak{A}\}}}-1\right)\hfill \\ & =\kappa \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\mathfrak{A},\mathfrak{K},t)}}-1\right)\hfill \end{array}$$

Similarly,

$${\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\mathcal{F}\mathfrak{K},\mathcal{F}\mathfrak{A},t)}}-1\le \kappa \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\mathfrak{K},\mathfrak{A},t)}}-1\right)$$

Equation (1) implies that

$${\displaystyle \frac{1}{{\mathfrak{H}}_{\mathfrak{G}}(\mathcal{F}\mathfrak{A},\mathcal{F}\mathfrak{K},t)}}-1\le \kappa \left({\displaystyle \frac{1}{{\mathfrak{H}}_{\mathfrak{G}}(\mathfrak{A},\mathfrak{K},t)}}-1\right)$$

Thus, $\mathcal{F}:\mathfrak{S}\to \mathfrak{S}$ is a $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-graphical fuzzy cone contraction on $(\mathfrak{S},{\mathfrak{H}}_{\mathfrak{G}},\ast )$. □

Definition 11. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS. A sequence $\left({\zeta }_n\right)$ in Ω is said to converge to $\zeta \in \mathsf{\Omega }$ with respect to ${\mathcal{M}}_{\mathfrak{G}}$ if, for every $t\gg \theta$ and each $r\in (0,1)$, ∃$n_0\in \mathbb{N}$ s.t. ${\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,\zeta ,t)>1-r$ holds ∀$n\ge n_0$; that is, ${lim}_{n\to \infty }{\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,\zeta ,t)=1$ for every $t\gg \theta$. A sequence $\left({\zeta }_n\right)$ in Ω is termed a Cauchy sequence if, for every $t\gg \theta$ and each $r\in (0,1)$, ∃$n_0\in \mathbb{N}$ s.t. ${\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,{\zeta }_m,t)>1-r$∀ indices $n,m\ge n_0$.

Example 5. 

Let $\mathsf{\Omega }=[0,1]$, $\mathcal{E}={\mathbb{R}}^2$ and define the solid cone $\mathfrak{E}=\{(a,b)\in {\mathbb{R}}^2:a\ge 0,b\ge 0\}$ in ${\mathbb{R}}^2$. Define the graph $\mathfrak{G}$ on Ω as follows:

$$(\zeta ,\eta )\in \mathfrak{Z}\left(\mathfrak{G}\right)\iff \zeta \le \eta .$$

Define the graphical fuzzy cone metric ${\mathcal{M}}_{\mathfrak{G}}:\mathsf{\Omega }\times \mathsf{\Omega }\times \mathit{int}\left(\mathfrak{E}\right)\to [0,1]$ as follows:

$${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=\left\{\begin{array}{cc}1,\hfill & \mathit{if}\zeta =\eta ,\hfill \\ e^{-|\zeta -\eta |},\hfill & \mathit{if}\zeta \le \eta ,\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Now, define the sequence ${\zeta }_n=1-{\displaystyle \frac{1}{n}}$ for $n\in \mathbb{N}$. Clearly, ${\zeta }_n\in \mathsf{\Omega }$ and ${\zeta }_n\to 1$ as $n\to \infty$.

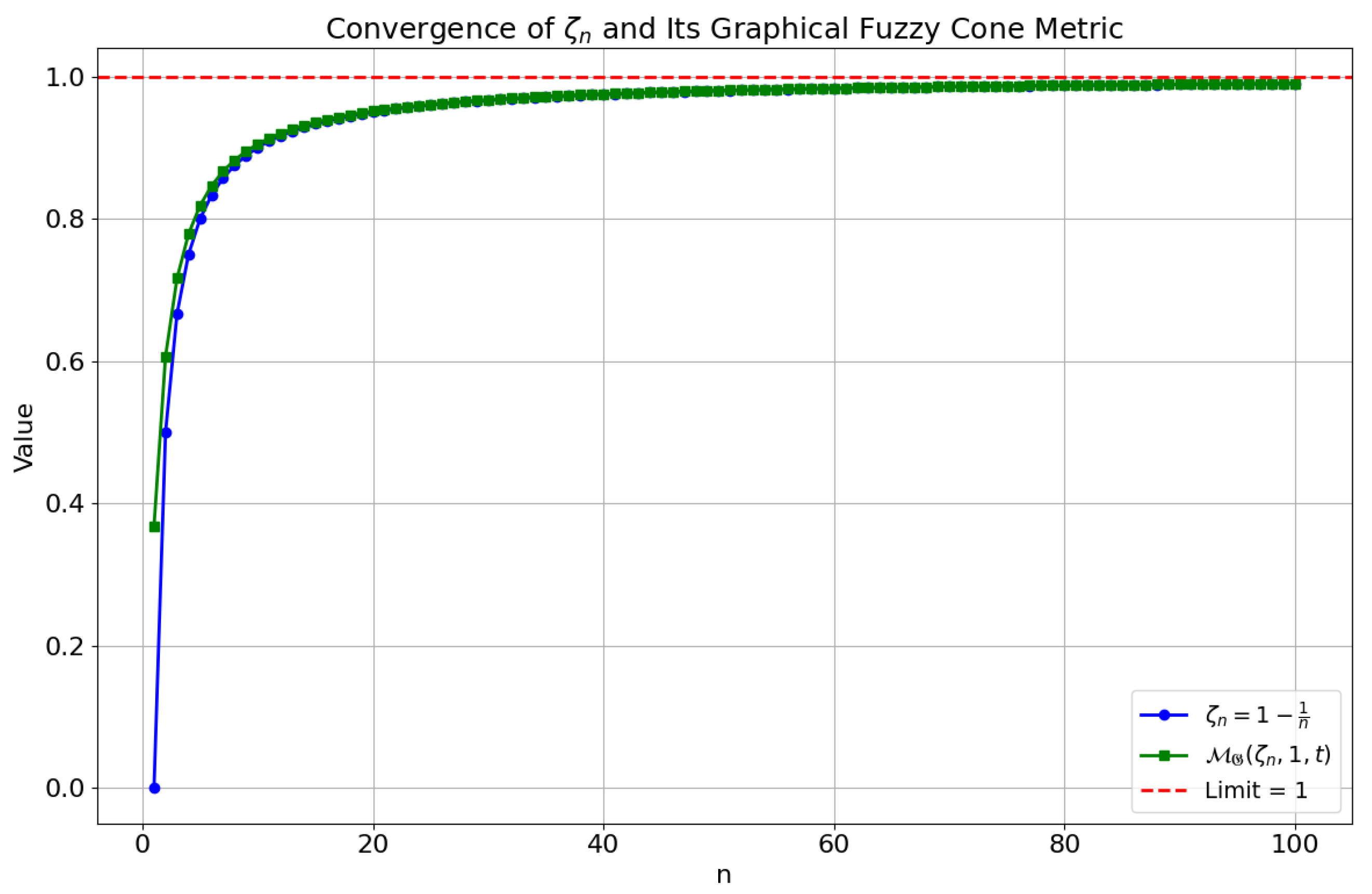
To check convergence, let $t\gg \theta$ and fix $r\in (0,1)$. Choose $n_0\in \mathbb{N}$ such that for all $n\ge n_0$:

$$|{\zeta }_n-1|={\displaystyle \frac{1}{n}}<-ln(1-r).$$

Then, for $n\ge n_0$, we have the following:

$${\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,1,t)=e^{-|{\zeta }_n-1|}>1-r.$$

Thus, ${\zeta }_n\to 1$ in the GFCMS.

To show that $\left({\zeta }_n\right)$ is Cauchy, fix $r\in (0,1)$ and choose $n_0$ such that for all $n,m\ge n_0$,

$$|{\zeta }_n-{\zeta }_m|<-ln(1-r).$$

Since ${\zeta }_n\le {\zeta }_m$ or ${\zeta }_m\le {\zeta }_n$ (as both approach 1 from below), the ordered pair lies in $\mathfrak{Z}\left(\mathfrak{G}\right)$, so:

$${\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,{\zeta }_m,t)=e^{-|{\zeta }_n-{\zeta }_m|}>1-r.$$

Hence, $\left({\zeta }_n\right)$ is a Cauchy sequence in the GFCMS.

The convergence of the sequence ${\zeta }_n=1-{\displaystyle \frac{1}{n}}$ to 1 in the GFCMS is illustrated through the graphical fuzzy cone metric ${\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,1,t)$ in Figure 2.

Definition 12. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS. A space $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ is considered complete if all Cauchy sequences in Ω converge to an element within Ω. Let ${\mathcal{H}}^{\prime }$ be a subgraph with $\mathfrak{V}\left({\mathcal{H}}^{\prime }\right)=\mathsf{\Omega }$. We describe $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ as ${\mathcal{H}}^{\prime }$-complete whenever every ${\mathcal{H}}^{\prime }$-termwise connected Cauchy sequence in Ω tends to a point in Ω.

Definition 13. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS and let ${\mathfrak{G}}^{\prime }$ be a subgraph of $\mathfrak{G}$ such that $\mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)\supseteq ▵$. A sequence $\left\{{\zeta }_n\right\}$ in $\mathsf{\Omega }$ is said to be $\mathfrak{Z}\left({\mathcal{G}}_I^{\prime }\right)$-convergent to $\zeta \in \mathsf{\Omega }$ if, for every $r\in (0,1)$ and $t\gg \theta$, there exists $n_0\in \mathbb{N}$ such that $({\zeta }_n,\zeta )\in \mathfrak{Z}\left({\mathcal{G}}_I^{\prime }\right)$ and ${\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,\zeta ,t)>1-r$ for all $n\ge n_0$. Moreover, if $({\zeta }_n,\zeta )\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)\cap \mathfrak{Z}\left({\mathfrak{G}}^{\prime -1}\right)$ for all $n\ge n_0$, then the sequence is said to be $\mathfrak{Z}\left({\mathcal{G}}_S^{\prime }\right)$-convergent to $\zeta$.

It is straightforward to verify that sequences that are $\mathfrak{Z}\left({\mathcal{G}}_S^{\prime }\right)$-convergent are also $\mathfrak{Z}\left({\mathcal{G}}_I^{\prime }\right)$-convergent; however, the converse is not generally true. Next, we proceed to explore the notion of Cauchy sequences within GFCMSs. In the framework of FMSs, the ideas of Cauchy sequences and completeness have been introduced in two distinct approaches: one following Grabiec (refer to [21]) and the other based on the work of George and Veeramani (refer to [10]). In a similar fashion, we present two categories of Cauchy sequences along with their corresponding forms of completeness.

Clearly, the condition of ${\mathcal{H}}^{\prime }$-completeness is less restrictive compared to the overall completeness of a GFCMS.

In the following section, we present several FP theorems for self-maps on a GFCMS under specific assumptions.

Definition 14. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS and $\left\{{\zeta }_n\right\}$ be a sequence in $\mathsf{\Omega }$. The sequence $\left\{{\zeta }_n\right\}$ is referred to as a Cauchy sequence in $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ if, for every $t\gg \theta$, it satisfies either of the following equivalent conditions:

1. 

For any natural number p, the limit ${lim}_{n\to \infty }{\mathcal{M}}_{\mathfrak{G}}({\zeta }_{n+p},{\zeta }_n,t)$ equals 1 (i.e., $\mathfrak{G}$-Cauchy).

2. 

The limit ${lim}_{n,m\to \infty }{\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,{\zeta }_m,t)=1$ (i.e., $\mathcal{M}$-Cauchy).

Definition 15. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS and $\left\{{\zeta }_n\right\}$ be a sequence in Ω. The sequence ${\zeta }_n$ is described as graphical fuzzy cone contractive. Assuming the existence of a constant $\kappa \in (0,1)$ s.t.

$${\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\zeta }_{n+1},{\zeta }_{n+2},t)}}-1\le \kappa \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,{\zeta }_{n+1},t)}}-1\right)$$

∀$t\gg \theta$, $n\in \mathbb{N}$.

Example 6. 

Let $\mathsf{\Omega }=[0,1]$, $\mathcal{E}={\mathbb{R}}^2$, and define the solid cone $\mathfrak{E}=\{(a,b)\in {\mathbb{R}}^2:a\ge 0,b\ge 0\}$ in the Banach algebra ${\mathbb{R}}^2$. Let the graph $\mathfrak{G}$ on Ω be defined as follows:

$$(\zeta ,\eta )\in \mathfrak{Z}\left(\mathfrak{G}\right)\iff \zeta \le \eta .$$

We define the fuzzy cone metric ${\mathcal{M}}_{\mathfrak{G}}:\mathsf{\Omega }\times \mathsf{\Omega }\times \mathit{int}\left(\mathfrak{E}\right)\to [0,1]$ by

$${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=\left\{\begin{array}{cc}1,\hfill & \mathit{if}\zeta =\eta ,\hfill \\ e^{-|\zeta -\eta |},\hfill & \mathit{if}\zeta \le \eta ,\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Now, we define the sequence ${\zeta }_n=1-{\displaystyle \frac{1}{2^n}}$ for $n\in \mathbb{N}$. Then,

$${\zeta }_1={\displaystyle \frac{1}{2}},{\zeta }_2={\displaystyle \frac{3}{4}},{\zeta }_3={\displaystyle \frac{7}{8}},{\zeta }_4={\displaystyle \frac{15}{16}},\mathit{etc}.$$

Let us compute the quantities:

$${\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,{\zeta }_{n+1},t)}}-1={\displaystyle \frac{1}{e^{-|{\zeta }_n-{\zeta }_{n+1}|}}}-1=e^{|{\zeta }_n-{\zeta }_{n+1}|}-1.$$

We have:

$$|{\zeta }_n-{\zeta }_{n+1}|=\left(1-{\displaystyle \frac{1}{2^n}}\right)-\left(1-{\displaystyle \frac{1}{2^{n+1}}}\right)={\displaystyle \frac{1}{2^{n+1}}}.$$

Therefore:

$$e^{|{\zeta }_n-{\zeta }_{n+1}|}-1=e^{{\displaystyle \frac{1}{2^{n+1}}}}-1.$$

Similarly:

$$|{\zeta }_{n+1}-{\zeta }_{n+2}|={\displaystyle \frac{1}{2^{n+2}}},e^{{\displaystyle \frac{1}{2^{n+2}}}}-1=\mathit{next}\mathit{term}.$$

Thus:

$${\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\zeta }_{n+1},{\zeta }_{n+2},t)}}-1=e^{{\displaystyle \frac{1}{2^{n+2}}}}-1\le \kappa \left(e^{{\displaystyle \frac{1}{2^{n+1}}}}-1\right),$$

which holds for some $\kappa \in (0,1)$ and all n because the exponential function is increasing and ${\displaystyle \frac{1}{2^{n+2}}}<{\displaystyle \frac{1}{2^{n+1}}}$.

Hence, the sequence $\left\{{\zeta }_n\right\}$ satisfies the graphical fuzzy cone contractive condition.

Definition 16. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS, and let ${\mathfrak{G}}^{\prime }$ be a subgraph of $\mathfrak{G}$ s.t. $\mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)\supseteq ▵$. The space $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ is referred to as ${\mathfrak{G}}^{\prime }$-$\mathfrak{G}$-complete, $\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$-$\mathfrak{G}$-complete, or $\mathfrak{Z}\left({\mathfrak{G}}_S^{\prime }\right)$-$\mathfrak{G}$-complete (alternatively, ${\mathfrak{G}}^{\prime }$-$\mathcal{M}$-complete, $\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$-$\mathcal{M}$-complete, or $\mathfrak{Z}\left({\mathfrak{G}}^{\prime }S\right)$-$\mathcal{M}$-complete) if every ${\mathfrak{G}}^{\prime }$-termwise connected $\mathfrak{G}$-Cauchy sequence (or $\mathcal{M}$-Cauchy sequence) within Ω converges in the sense of ${\mathcal{M}}_{\mathfrak{G}}$ or is $\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$-convergent or $\mathfrak{Z}\left({\mathfrak{G}}_S^{\prime }\right)$-convergent, respectively.

Theorem 3. 

Consider $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ as a ${\mathfrak{G}}^{\prime }$-$\mathfrak{G}$-complete GFCMS, where every graphical fuzzy cone contractive sequence is also a $\mathfrak{G}$-Cauchy sequence. Let $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ be an $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-GFCC. Consider that the conditions listed below are fulfilled:

1. 

∃${\zeta }_0\in \mathsf{\Omega }$ s.t. $\mathcal{F}{\zeta }_0\in {\left[{\zeta }_0\right]}_{{\mathfrak{G}}^{\prime }}^q$ for some $q\in \mathbb{N}$;

2. 

${\lim }_{t\to \infty }{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=1$∀$\zeta ,\eta \in \mathsf{\Omega }$ s.t. $(\zeta ,\eta )\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$;

3. 

if a $\mathcal{F}$-Picard sequence $\left\{{\zeta }_n\right\}$, which is ${\mathfrak{G}}^{\prime }$-termwise connected, converges to some $\zeta \in \mathsf{\Omega }$ with respect to ${\mathcal{M}}_{\mathfrak{G}}$, then it also converges to ζ in the sense of $\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$.

As a result, one can find an element ${\zeta }^{*}\in \mathsf{\Omega }$ such that the Picard sequence $\left\{{\zeta }_n\right\}$ generated by $\mathcal{F}$, starting from an initial point ${\zeta }_0\in \mathsf{\Omega }$, is ${\mathfrak{G}}^{\prime }$-termwise connected and converges in the sense of $\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$ to both ${\zeta }^{*}$ and $\mathcal{F}{\zeta }^{*}$.

To prove the existence of a fixed point, we construct a Picard sequence starting from a point ${\zeta }_0\in \mathsf{\Omega }$ and show that it is ${\mathfrak{G}}^{\prime }$-termwise connected, graphical fuzzy cone contractive, and converges to a common point ${\zeta }^{*}$ and $\mathcal{F}{\zeta }^{*}$ under $\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$-convergence.

Proof. 

Consider a point ${\zeta }_0\in \mathsf{\Omega }$ for which $\mathcal{F}{\zeta }_0$ belongs to the q-step neighborhood ${\left[{\zeta }_0\right]}_{{\mathfrak{G}}^{\prime }}^q$, where q is a positive integer. Assume that $\left\{{\zeta }_n\right\}$ represents the Picard sequence generated by $\mathcal{F}$, starting from the initial point ${\zeta }_0$. According to the definition, there exists a sequence ${\left\{{\eta }_i\right\}}_{i=0}^q$ satisfying ${\eta }_0={\zeta }_0$, ${\eta }_q=\mathcal{F}{\zeta }_0$, and $({\eta }_{i-1},{\eta }_i)\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$ for each $i=1,2,\dots ,q$. As $\mathcal{F}$ is an $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-GFCC, based on $\left(GFCC1\right)$, we have $(\mathcal{F}{\eta }_{i-1},\mathcal{F}{\eta }_i)\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$ for $i=1,2,\dots ,q$. Therefore, ${\left\{\mathcal{F}{\eta }_i\right\}}_{i=0}^q$ is a path from $\mathcal{F}{\eta }_0=\mathcal{F}{\zeta }_0={\zeta }_1$ to $\mathcal{F}{\eta }_q={\mathcal{F}}^2{\zeta }_0={\zeta }_2$ of length q, and so ${\zeta }_2\in {\left[{\zeta }_1\right]}_{{\mathfrak{G}}^{\prime }}^q$. Thus, for every $n\in \mathbb{N}$, we can build a sequence ${\left\{{\mathcal{F}}^n{\eta }_i\right\}}_{i=0}^q$ connecting ${\mathcal{F}}^n{\eta }_0={\mathcal{F}}^n{\zeta }_0={\zeta }_n$ to ${\mathcal{F}}^n{\eta }_q={\mathcal{F}}^n\mathcal{F}{\zeta }_0={\zeta }_{n+1}$, having length q. This demonstrates that ${\zeta }_{n+1}\in {\left\{{\zeta }_n\right\}}_{{\mathfrak{G}}^{\prime }}^q$ for all $n\in \mathbb{N}$. Thus, $\left\{{\zeta }_n\right\}$ is an ${\mathfrak{G}}^{\prime }$-termwise connected sequence. Since $({\mathcal{F}}^n{\eta }_{i-1},{\mathcal{F}}^n{\eta }_i)\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$ for $i=1,2,3,\dots ,q$ and $n\in \mathbb{N}$ based on $\left(GFCC2\right)$, we have the following:

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^n{\eta }_{i-1},{\mathcal{F}}^n{\eta }_i,t)}}-1& \le \kappa \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^{n-1}{\eta }_{i-1},{\mathcal{F}}^{n-1}{\eta }_i,t)}}-1\right)\hfill \\ \hfill & \le {\kappa }^2\left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^{n-2}{\eta }_{i-1},{\mathcal{F}}^{n-2}{\eta }_i,t)}}-1\right)\hfill \\ & ⋮\hfill \\ \hfill & \le {\kappa }^n\left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\eta }_{i-1},{\eta }_i,t)}}-1\right)\hfill \end{array}$$

(2)

∀$t\gg \theta$. As the sequence $\left\{{\zeta }_n\right\}$ is ${\mathfrak{G}}^{\prime }$-termwise connected, it follows that for each $n\in \mathbb{N}$, we have the following:

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,{\zeta }_{n+1},t)}}-1& ={\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^n{\eta }_0,{\mathcal{F}}^n{\eta }_q,t)}}-1\hfill \\ & \le \kappa \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^{n-1}{\eta }_0,{\mathcal{F}}^{n-1}{\eta }_q,t)}}-1\right)\hfill \\ & =\kappa \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\zeta }_{n-1},{\zeta }_n,t)}}-1\right),\hfill \end{array}$$

$n\in \mathbb{N}$. It follows that $\left\{{\zeta }_n\right\}$ is a graphical fuzzy cone contractive sequence and, by assumption, is $\mathfrak{G}$-Cauchy in $\mathsf{\Omega }$. Consequently, $\left\{{\zeta }_n\right\}$ is a ${\mathfrak{G}}^{\prime }$-termwise connected sequence that is also $\mathfrak{G}$-Cauchy in $\mathsf{\Omega }$. Based on the ${\mathfrak{G}}^{\prime }$-$\mathfrak{G}$-completeness of $\mathsf{\Omega }$, the sequence $\left\{{\zeta }_n\right\}$${\mathcal{M}}_{\mathfrak{G}}$-converges to some ${\zeta }^{*}\in \mathsf{\Omega }$. Additionally, from Condition (3), it follows that $\left\{{\zeta }_n\right\}$ converges to ${\zeta }^{*}$ under $\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$-convergence. Then, ∃$n_0\in \mathbb{N}$ s.t. $({\zeta }^{*},{\zeta }_n)\in \mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$∀$n\ge n_0$ and

$$\underset{n\to \infty }{lim}{\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,{\zeta }^{*},t)=1\forall t\gg \theta .$$

Thus, based on $\left(GFCC1\right)$, we obtain $(\mathcal{F}{\zeta }^{*},{\zeta }_{n+1})=(\mathcal{F}{\zeta }^{*},\mathcal{F}{\zeta }_n)\in E\left({\mathfrak{G}}_I^{\prime }\right)$ for each $n\ge n_0$, and using $\left(GFCC2\right)$, we get

$$\left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\zeta }_{n+1},\mathcal{F}{\zeta }^{\ast },t)}}-1\right)=\left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\mathcal{F}{\zeta }_n,\mathcal{F}{\zeta }^{\ast },t)}}-1\right)\le \kappa \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,{\zeta }^{\ast },t)}}-1\right),$$

∀$n\ge n_0$. Since ${lim}_{n\to \infty }{\mathcal{M}}_{\mathfrak{G}}({\zeta }_n,{\zeta }^{*},t)=1\forall t\gg \theta ,$ we get

$$\underset{n\to \infty }{lim}{\mathcal{M}}_{\mathfrak{G}}({\zeta }_{n+1},\mathcal{F}{\zeta }^{*},t)=1$$

Therefore, the sequence $\left\{{\zeta }_n\right\}$ also $\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$-converges to $\mathcal{F}{\zeta }^{*}\in \mathsf{\Omega }$. Consequently, the sequence $\left\{{\zeta }_n\right\}$$\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$-converges to both ${\zeta }^{*}$ and $\mathcal{F}{\zeta }^{*}$. □

Corollary 1. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a $\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$-$\mathfrak{G}$-complete GFCMS and $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ be a GFCC. Consider that the conditions listed below are fulfilled:

1. 

∃${\zeta }_0\in \mathsf{\Omega }$ s.t. $\mathcal{F}{\zeta }_0\in {\left[{\zeta }_0\right]}_{{\mathfrak{G}}^{\prime }}^q$, for some $q\in \mathbb{N}$;

2. 

${\lim }_{t\to \infty }{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=1$∀$\zeta ,\eta \in \mathsf{\Omega }$ s.t. $(\zeta ,\eta )\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$.

There exists an element ${\zeta }^{*}\in \mathsf{\Omega }$ s.t. the $\mathcal{F}$-Picard sequence $\left\{{\zeta }_n\right\}$, initiated at ${\zeta }_0\in \mathsf{\Omega }$, is ${\mathfrak{G}}^{\prime }$-termwise connected and converges to both ${\zeta }^{*}$ and $\mathcal{F}{\zeta }^{*}$ with respect to the $\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$-convergence.

It is important to note that the previous results guarantee the convergence of a $\mathcal{F}$-Picard sequence, but they do not guarantee the existence of a FP for $\mathcal{F}$, as demonstrated in the following example.

Example 7. 

Consider $\mathcal{E}={\mathbb{R}}^2$ endowed with the Euclidean norm and the operation of coordinate-wise multiplication. Define $\mathfrak{E}=\left\{\right(\zeta ,\eta )\in \mathcal{E}:\zeta ,\eta \ge 0\},$ then $\mathfrak{E}$ is a solid cone in $\mathcal{E}$. Let $\mathsf{\Omega }=[0,1]$ and $\mathfrak{G}$ be defined by $\mathfrak{V}\left(\mathfrak{G}\right)=\mathsf{\Omega }$ and $\mathfrak{Z}\left(\mathfrak{G}\right)=▵\cup \left\{\right(\zeta ,\eta )\in \mathsf{\Omega }\times \mathsf{\Omega }:0<\eta \le \zeta \}$ at a time t. Let ∗ be a continuous t-norm defined by $\zeta \ast \eta =\zeta ·\eta$. Define a function ${\mathcal{M}}_{\mathfrak{G}}:\mathsf{\Omega }\times \mathsf{\Omega }\times int\left(\mathfrak{E}\right)\to [0,1]$ by

$${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=\left\{\begin{array}{cc}1,\hfill & \mathit{if}\zeta =\eta ,\hfill \\ e^{-\zeta \eta },\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Then, $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ is a GFCMS over Banach algebra. Suppose a self-map $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ is given:

$$\mathcal{F}\zeta =\left\{\begin{array}{cc}{\displaystyle \frac{\zeta }{2}},\hfill & \mathit{if}\zeta \ne 0,\hfill \\ 1,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

It is straightforward to observe that $\mathcal{F}$ is an $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-graphical fuzzy cone contraction with a constant κ s.t. ${\displaystyle \frac{1}{4}}\le \kappa <1$. For any initial point ${\zeta }_0\in [0,1]$, we have $({\zeta }_0,\mathcal{F}{\zeta }_0)\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$, meaning that $\mathcal{F}{\zeta }_0\in {\left[{\zeta }_0\right]}_{{\mathfrak{G}}^{\prime }}^q$, where $q=1$. Furthermore, it can be verified that all the hypotheses of Theorem 3 are fulfilled but $\mathcal{F}$ does not have a FP in Ω.

The previous example demonstrates that even when all the hypotheses of a fixed point theorem are satisfied, a fixed point may still fail to exist if the limit of the Picard sequence is not unique. In particular, the sequence may converge to two different points—one in $\mathsf{\Omega }$ and another in the image of $\mathsf{\Omega }$ under $\mathcal{F}$. To eliminate such pathological cases and guarantee the existence of fixed points, we now introduce an additional condition known as Property $\left(S\right)$.

Definition 17. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS, ${\mathfrak{G}}^{\prime }$ be a subgraph of $\mathfrak{G}$, and $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ be a mapping. The five-tuple $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast ,{\mathfrak{G}}^{\prime },\mathcal{F})$ is said to possess property $\left(S\right)$ if a ${\mathfrak{G}}^{\prime }$-termwise connected $\mathcal{F}$-Picard sequence $\left\{{\zeta }_n\right\}$ happens to converge to two different points,

$${\zeta }^{*}\mathit{and}{\eta }^{*},\mathit{where}{\zeta }^{*}\in \mathsf{\Omega },{\eta }^{*}\in \mathcal{F}\left(\mathsf{\Omega }\right),\mathit{then}{\zeta }^{*}={\eta }^{*}.$$

We represent by $Fix\left(\mathcal{F}\right)$ the collection of all FPs of the mapping $\mathcal{F}$. In addition, let us define ${\mathsf{\Omega }}_{\mathcal{F}}=\{\zeta \in \mathsf{\Omega }:(\zeta ,\mathcal{F}\zeta )\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)\}.$

Theorem 4. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a ${\mathfrak{G}}^{\prime }$-$\mathfrak{G}$-complete GFCMS in which graphical fuzzy cone contractive sequences are $\mathfrak{G}$-Cauchy. $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ be an $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-GFCC. Consider that the conditions listed below are fulfilled:

1. 

∃${\zeta }_0\in \mathsf{\Omega }$ s.t. $\mathcal{F}{\zeta }_0\in {\left[{\zeta }_0\right]}_{{\mathfrak{G}}^{\prime }}^q$ for some $q\in \mathbb{N}$;

2. 

${\lim }_{t\to \infty }{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=1$∀$\zeta ,\eta \in \mathsf{\Omega }$ s.t. $(\zeta ,\eta )\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$;

3. 

if a ${\mathfrak{G}}^{\prime }$-termwise connected $\mathcal{F}$-Picard sequence $\left\{{\zeta }_n\right\}$${\mathcal{M}}_{\mathfrak{G}}$-converges to some $\zeta \in \mathsf{\Omega }$, then $\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$-converges to ζ.

We can identify a point ${\zeta }^{*}\in \mathsf{\Omega }$ s.t. the $\mathcal{F}$-Picard sequence $\left\{{\zeta }_n\right\}$, starting with the initial value ${\zeta }_0\in \mathsf{\Omega }$, is ${\mathfrak{G}}^{\prime }$-termwise connected and converges to both ${\zeta }^{*}$ and $\mathcal{F}{\zeta }^{*}$ with respect to $\mathfrak{Z}\left({\mathfrak{G}}_I^{\prime }\right)$. Furthermore, if the five-tuple $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast ,{\mathfrak{G}}^{\prime },\mathcal{F})$ satisfies property $\left(S\right)$, then $\mathcal{F}$ has a FP in Ω.

Proof. 

The proof of this theorem follows directly from the argument presented in Theorem 3 and is therefore omitted.□

The following example illustrates that Theorem 3 provides a sufficient condition for the existence of a FP, but it does not ensure the uniqueness of the FP.

Example 8. 

Let $\mathsf{\Omega }=[0,\infty )$, and let $\mathfrak{G}$ be the graph with vertex set $\mathfrak{V}\left(\mathfrak{G}\right)=\mathsf{\Omega }$ and

$$\mathfrak{Z}\left(\mathfrak{G}\right)=▵\left\{\right(\zeta ,\eta )\in \mathsf{\Omega }\times \mathsf{\Omega },:\eta \le \zeta \}$$

and ${\mathfrak{G}}^{\prime }=\mathfrak{G}$. Then, $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ is a GFCMS, where ${\mathcal{M}}_{\mathfrak{G}}$ is defined as follows:

$${\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=\left\{\begin{array}{cc}1,\hfill & \mathit{if}\zeta =\eta ;\hfill \\ {exp}^{{\displaystyle \frac{-{(\zeta +\eta )}^2}{t}}}\hfill & \mathit{if}\zeta \ne \eta .\hfill \end{array}\right.$$

Then, $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ is a ${\mathfrak{G}}^{\prime }$-complete GFCMS. Suppose a self-map $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ is given:

$$\mathcal{F}\left(\zeta \right)=\left\{\begin{array}{cc}{\displaystyle \frac{\zeta }{2}}\hfill & \mathit{if}\zeta \in [0,1);\hfill \\ {\zeta }^2\hfill & \mathit{if}\zeta \in [1,\infty ).\hfill \end{array}\right.$$

It is straightforward to observe that $\mathcal{F}$ is a GFCC with a constant κ s.t. ${\displaystyle \frac{1}{4}}\le \kappa <1$. For each ${\zeta }_0\in [0,1)$, we have $({\zeta }_0,\mathcal{F}{\zeta }_0)\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$ and $\mathcal{F}{\zeta }_0\in {\left[{\zeta }_0\right]}_{{\mathfrak{G}}^{\prime }}^1$. Additionally, it is clear that ${lim}_{t\to \infty }{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=1$ for all $\zeta ,\eta \in \mathsf{\Omega }$. It is important to note that property $\left(S\right)$ is also fulfilled. Therefore, all the conditions of Theorem 3 are met, and the mapping $\mathcal{F}$ has two FPs in Ω, specifically, Fix$\left(\mathcal{F}\right)=\{0,1\}$.

Theorem 5. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a ${\mathfrak{G}}^{\prime }$-$\mathfrak{G}$-complete GFCMS in which graphical fuzzy cone contractive sequences are $\mathfrak{G}$-Cauchy. Let $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ be an $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-GFCC. Provided that the assumptions of Theorem 4 are fulfilled and ${\mathsf{\Omega }}_{\mathcal{F}}=\{\zeta \in \mathsf{\Omega }:(\zeta ,\mathcal{F}\zeta )\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)\}$ is connected, $\mathcal{F}$ has a unique FP.

Proof. 

The existence of a FP of $\mathcal{F}$ can be derived from Theorem 4. Assume that ${\mathsf{\Omega }}_{\mathcal{F}}$ is connected, and let ${\zeta }^{*}$ and ${\eta }^{*}$ be two distinct FPs of $\mathcal{F}$. Since $\mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)\supseteq ▵$, $Fix\left(\mathcal{F}\right)\subseteq {\mathsf{\Omega }}_{\mathcal{F}}$, and so ${\zeta }^{*},{\eta }^{*}\in {\mathsf{\Omega }}_{\mathcal{F}}$. Again, ${\mathsf{\Omega }}_{\mathcal{F}}$ is connected, and we have ${\left({\zeta }^{*}P{\eta }^{*}\right)}_{\mathfrak{G}}^{\prime }$; that is, we can identify a sequence ${\left\{{\zeta }_i\right\}}_{i=0}^q$, ${\zeta }_0={\zeta }^{*},{\zeta }_q={\eta }^{*}$ and $({\zeta }_{i-1},{\zeta }_i)\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$ for $i=1,2,3\dots ,q.$ Since $\mathcal{F}$ is an $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-GFCC, through successive use of $\left(GFCC1\right)$, we have $({\mathcal{F}}^n{\zeta }_{i-1},{\mathcal{F}}^n{\zeta }_i)\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$ for $i=1,2,3\dots ,q$∀$n\in \mathbb{N}$. Therefore, based on $\left(GFCC2\right)$, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^n{\eta }_{i-1},{\mathcal{F}}^n{\eta }_i,t)}}-1& \le \kappa \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^{n-1}{\eta }_{i-1},{\mathcal{F}}^{n-1}{\eta }_i,t)}}-1\right)\hfill \\ \hfill & \le {\kappa }^2\left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^{n-2}{\eta }_{i-1},{\mathcal{F}}^{n-2}{\eta }_i,t)}}-1\right)\hfill \\ & ⋮\hfill \\ \hfill & \le {\kappa }^n\left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\eta }_{i-1},{\eta }_i,t)}}-1\right),\hfill \end{array}$$

(3)

for $i=1,2,3,\dots ,q$ and for all $n\in \mathbb{N}$. Therefore, based on Condition (4) of GFCMS, we obtain the following:

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^n{\zeta }^{\ast },{\mathcal{F}}^n{\eta }^{\ast },t)}}-1& \le \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^n{\zeta }_0,{\mathcal{F}}^n{\zeta }_1,t)\ast {\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^n{\zeta }_1,{\mathcal{F}}^n{\zeta }_2,t)\ast \dots \ast {\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^n{\zeta }_{q-1},{\mathcal{F}}^n{\zeta }_q,t)}}-1\right)\hfill \\ & =\left({\displaystyle \frac{1}{{\prod }_{i=1}^q{\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}^n{\zeta }_{i-1},{\mathcal{F}}^n{\zeta }_i,t)}}-1\right)\hfill \\ & \le {\kappa }^n\left({\displaystyle \frac{1}{{\prod }_{i=1}^q{\mathcal{M}}_{\mathfrak{G}}({\zeta }_{i-1},{\zeta }_i,t)}}-1\right)\hfill \end{array}$$

Since ${\zeta }^{*},{\eta }^{*}\in Fix\left(\mathcal{F}\right)$, we have ${\mathcal{F}}^n{\zeta }^{*}={\zeta }^{*},{\mathcal{F}}^n{\eta }^{*}={\eta }^{*}$; by taking the limit as $n\to \infty$, the above inequality implies that ${\mathcal{M}}_{\mathfrak{G}}({\zeta }^{*},{\eta }^{*},t)=1$∀$t\gg \theta$. This leads to the conclusion that ${\zeta }^{*}={\eta }^{*}$. This contradiction establishes the uniqueness of the FP of $\mathcal{F}$. □

Corollary 2. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a $\mathfrak{G}$-complete GFCMS s.t. ${lim}_{t\to \infty }{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)=1$∀$\zeta ,\eta \in \mathsf{\Omega }$. Suppose a self-map $\mathcal{F}:\mathsf{\Omega }\to \mathsf{\Omega }$ is given:

$${\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\mathcal{F}\zeta ,\mathcal{F}\eta ,t)}}-1\le \kappa \left({\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(\zeta ,\eta ,t)}}-1\right)$$

∀$\zeta ,\eta \in \mathsf{\Omega }$ and $0<\kappa <1$. Then, $\mathcal{F}$ has a unique FP.

Proof. 

Let the graphs $\mathfrak{G}$ and ${\mathfrak{G}}^{\prime }$ be defined s.t. $\mathfrak{V}\left(\mathfrak{G}\right)=V\left({\mathfrak{G}}^{\prime }\right)=\mathsf{\Omega }$ and $\mathfrak{Z}\left(\mathfrak{G}\right)=\mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)=\mathsf{\Omega }\times \mathsf{\Omega }$. It is then straightforward to verify that all the conditions of Theorem 5 are met, and consequently, the conclusion holds. □

Although fixed point theorems are well-studied, the present work offers a new and meaningful generalization within the framework of graphical fuzzy cone metric spaces (GFCMS). In particular, Theorem 5 establishes a unique fixed point result for $(\mathfrak{G},{\mathfrak{G}}^{\prime })$-graphical fuzzy cone contractions by employing both fuzzy metric structures and graph-based connectivity. The incorporation of graph completeness, fuzzy cone metrics, and generalized convergence through Property (S) and $\mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$-connectivity significantly extends existing results. This allows us to derive fixed point theorems in settings where classical or even fuzzy contractions may fail, thereby highlighting the novelty and broader applicability of our results.

4. Application to Fractals

In this section, we will generate fractals in graphical fuzzy cone metric space using a graphical fuzzy cone iterated function system. This is entirely novel work, as no one has yet generated fractals in a graphical structure. While the process of generating fractals resembles classical iterated function systems, the advancement here lies in extending the framework to fuzzy cone metric spaces equipped with a graph structure. By introducing the concept of a Graphical Fuzzy Cone Iterated Function System (GFCIFS), we move beyond traditional metric-based models and capture a broader class of fractal behaviors. The use of fuzzy cone metrics allows us to incorporate uncertainty and partial ordering, while the graph component models directional relationships and local connectivity among elements. This setting enables the construction of fractals in environments that are not necessarily metrically uniform or linearly connected, thereby offering a more flexible and realistic approach to modeling self-similar structures in abstract spaces.

Definition 18. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS and $\{{\mathcal{F}}_u:\mathsf{\Omega }\to \mathsf{\Omega }:u=1,2,3,\dots ,t\}$ is a finite collection of graphical fuzzy cone contractions (GFCCs). The operator $\Theta :\mathfrak{S}\to \mathfrak{S}$ defined by

$$\Theta \left(\mathfrak{w}\right)={\mathcal{F}}_1\left(\mathfrak{w}\right)\cup {\mathcal{F}}_2\left(\mathfrak{w}\right)\cup \dots \cup {\mathcal{F}}_t\left(\mathfrak{w}\right),$$

for all $\mathfrak{w}\in \mathfrak{S}$ is a graphical fuzzy cone Hutchinson Barnsley operator (GFCHBO).

Definition 19. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a complete GFCMS. If $\{{\mathcal{F}}_u:\mathsf{\Omega }\to \mathsf{\Omega }:u=1,2,3,\dots ,t\}$ is a finite collection of GFCCs, then $(\mathsf{\Omega }:{\mathcal{F}}_1,{\mathcal{F}}_2,{\mathcal{F}}_3,\dots ,{\mathcal{F}}_t)$ is called a graphical fuzzy cone iterated function system (GFCIFS).

Theorem 6. 

Let $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ be a GFCMS and $(\mathsf{\Omega }:{\mathcal{F}}_1,{\mathcal{F}}_2,{\mathcal{F}}_3,\dots ,{\mathcal{F}}_t)$ be a GFCIFS. If $\Theta :\mathfrak{S}\to \mathfrak{S}$ is GFCHBO, then Θ is GFCC on $\mathfrak{S}$.

Proof. 

We will show that $\Theta$ is GFCC on $\mathfrak{S}$ for $u=2$. Let ${\mathcal{F}}_1,{\mathcal{F}}_2:\mathsf{\Omega }\to \mathsf{\Omega }$ be two GFCCs. Therefore, ${\mathcal{F}}_1$ and ${\mathcal{F}}_2$ will map $\mathfrak{S}$ into itself. Take $\mathfrak{w},\mathfrak{K}\in \mathfrak{S}$ such that ${\mathfrak{H}}_{\mathfrak{G}}(\mathfrak{w},\mathfrak{K},t)$ is not equal to zero. Consider the following:

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\mathfrak{H}}_{\mathfrak{G}}(\Theta \left(\mathfrak{w}\right),\Theta \left(\mathfrak{K}\right),t)}}-1& ={\displaystyle \frac{1}{{\mathfrak{H}}_{\mathfrak{G}}({\mathcal{F}}_1\mathfrak{w}\cup {\mathcal{F}}_2\mathfrak{w},{\mathcal{F}}_1\mathfrak{K}\cup {\mathcal{F}}_2\mathfrak{K},t)}}-1\hfill \\ & \le {\displaystyle \frac{1}{min\{{\mathfrak{H}}_{\mathfrak{G}}({\mathcal{F}}_1\mathfrak{w},{\mathcal{F}}_1\mathfrak{K},t),{\mathfrak{H}}_{\mathfrak{G}}({\mathcal{F}}_2\mathfrak{w},{\mathcal{F}}_2\mathfrak{K},t)\}}}-1\hfill \\ & \le \kappa \left({\displaystyle \frac{1}{{\mathfrak{H}}_{\mathfrak{G}}(\mathfrak{w},\mathfrak{K},t)}}-1\right)\hfill \end{array}$$

Similarly, this can be proven for any natural number t. Hence, $\Theta$ is a GFCC on $\mathfrak{S}$. □

Theorem 7. 

Suppose that $(\mathfrak{S},{\mathfrak{H}}_{\mathfrak{G}},\ast )$ is a ${\mathfrak{G}}^{\prime }$-$\mathfrak{G}$-complete graphical fuzzy cone Hausdorff metric space in which graphical fuzzy cone contractive sequences are $\mathfrak{G}$-Cauchy with the property $\left(S\right)$, and $(\mathsf{\Omega }:{\mathcal{F}}_1,{\mathcal{F}}_2,{\mathcal{F}}_3,\dots ,{\mathcal{F}}_t)$ is a GFCIFS. Let $\Theta :\mathfrak{S}\to \mathfrak{S}$ be GFCHBO. Assume that the following conditions hold:

(i) 

$\Theta {\mathfrak{w}}_0\in {\left[{\mathfrak{w}}_0\right]}_{\mathfrak{G}}^p$, provided there exists ${\mathfrak{w}}_0\in \mathfrak{S}$ for some $q\in \mathbb{N}$;

(ii) 

${lim}_{t\to \infty }{\mathfrak{H}}_{\mathfrak{G}}({\mathfrak{w}}_1,{\mathfrak{w}}_2,t)=1$ for all ${\mathfrak{w}}_1,{\mathfrak{w}}_2\in \mathfrak{S}$;

(iii) 

If a sequence $\left\{{\mathfrak{w}}_n\right\}$, which is ${\mathfrak{G}}^{\prime }$-termwise connected, is Picard convergent in $\mathfrak{S}$, then ∃ a limit $\mathfrak{w}\in \mathfrak{S}$ and $n_0\in \mathbb{N}$ s.t. $(\mathfrak{w},{\mathfrak{w}}_n)\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$ or $({\mathfrak{w}}_n,\mathfrak{w})\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)$ at time t ∀ $n\ge n_0$;

(iv) 

${\mathfrak{S}}_{\Theta }=\{\mathfrak{w}\in \mathfrak{S}:(\mathfrak{w},\Theta \mathfrak{w})\in \mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)\}$ is connected.

Then, $\Theta$ has a unique FP.

Proof. 

Since $\Theta$ is GFCHBO, it follows from Theorem 6 that $\Theta$ is a graphical fuzzy cone contraction on $\mathfrak{S}$. Now, if we take $\mathsf{\Omega }=\mathfrak{S}$, ${\mathcal{M}}_{\mathfrak{G}}={\mathfrak{H}}_{\mathfrak{G}}$ and $\mathcal{F}=\Theta$ in Theorem 5, then the proof is similar. □

Example 9. 

Let $\mathsf{\Omega }={\mathbb{R}}^2$ and $\mathfrak{G}$ be a graph defined by $\mathfrak{V}\left(\mathfrak{G}\right)=\mathsf{\Omega }\times \mathsf{\Omega }$ and $\mathfrak{Z}\left(\mathfrak{G}\right)=▵\cup \{(({\zeta }_1,{\zeta }_2),({\zeta }_3,{\zeta }_4))\in \mathsf{\Omega }\times \mathsf{\Omega }:{\zeta }_3\le {\zeta }_1\mathit{and}{\zeta }_4\le {\zeta }_2\}$. Let ${\mathfrak{G}}^{\prime }$ be a subgraph of a graph $\mathfrak{G}$ s.t. $\mathfrak{V}\left(\mathfrak{G}\right)=\mathsf{\Omega }\times \mathsf{\Omega }$ and $\mathfrak{Z}\left({\mathfrak{G}}^{\prime }\right)=▵\cup \{(({\zeta }_1,{\zeta }_2),({\zeta }_3,{\zeta }_4))\in \mathsf{\Omega }\times \mathsf{\Omega }:{\zeta }_3\le {\zeta }_1\mathit{and}{\zeta }_4\le {\zeta }_2\}.$ Define $\mathfrak{E}=\left\{\right(\zeta ,\eta )\in \mathsf{\Omega }:\zeta ,\eta \ge 0\},$ then $\mathfrak{E}$ is a solid cone in Ω. Then, $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ is a GFCMS, where ${\mathcal{M}}_{\mathfrak{G}}$ is defined as follows:

$${\mathcal{M}}_{\mathfrak{G}}(({\zeta }_1,{\zeta }_2),({\zeta }_3,{\zeta }_4),t)=\left\{\begin{array}{cc}1,\hfill & \mathit{if}({\zeta }_1,{\zeta }_2)=({\zeta }_3,{\zeta }_4)\hfill \\ {exp}^{{\displaystyle \frac{-\sqrt{{({\zeta }_3-{\zeta }_1)}^2+{({\zeta }_4-{\zeta }_2)}^2}}{t}}},\hfill & \mathit{if},({\zeta }_1,{\zeta }_2)\ne ({\zeta }_3,{\zeta }_4).\hfill \end{array}\right.$$

Then, $(\mathsf{\Omega },{\mathcal{M}}_{\mathfrak{G}},\ast )$ is ${\mathfrak{G}}^{\prime }$-complete GFCMS. Let ${\mathcal{F}}_1({\zeta }_1,{\zeta }_2)=({\displaystyle \frac{{\zeta }_1}{2}},{\displaystyle \frac{{\zeta }_2}{2}}),{\mathcal{F}}_2({\zeta }_1,{\zeta }_2)=({\displaystyle \frac{{\zeta }_1}{2}}+{\displaystyle \frac{1}{2}},{\displaystyle \frac{{\zeta }_2}{2}})$ and ${\mathcal{F}}_3({\zeta }_1,{\zeta }_2)=({\displaystyle \frac{{\zeta }_1}{2}}+{\displaystyle \frac{1}{4}},{\displaystyle \frac{{\zeta }_2}{2}}+{\displaystyle \frac{\sqrt{3}}{4}}).$

We aim to demonstrate that the mappings ${\mathcal{F}}_1,{\mathcal{F}}_2$ and ${\mathcal{F}}_3$ are edge-preserving. Let $({\zeta }_1,{\zeta }_2)$ and $({\zeta }_3,{\zeta }_4)$ be elements of Ω, and assume there exists a path between these two points. This implies the ordering relationships:

$${\zeta }_3\le {\zeta }_1\mathit{and}{\zeta }_4\le {\zeta }_2.$$

Therefore,

$${\displaystyle \frac{{\zeta }_3}{2}}\le {\displaystyle \frac{{\zeta }_1}{2}},\mathit{and}{\displaystyle \frac{{\zeta }_4}{2}}\le {\displaystyle \frac{{\zeta }_2}{2}}.$$

Since these inequalities hold, the transformation ${\mathcal{F}}_1$ preserves the adjacency and connectivity of the edges.

By applying the same reasoning, we can similarly conclude that ${\mathcal{F}}_2$ and ${\mathcal{F}}_3$ also preserve edge relations. Thus, all three mappings are edge-preserving mappings.

Let $\kappa ={\displaystyle \frac{1}{8}}$, then

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}({\mathcal{F}}_1({\zeta }_1,{\zeta }_2),{\mathcal{F}}_1({\zeta }_3,{\zeta }_4),t)}}-1& ={\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}((\frac{{\zeta }_1}{2},\frac{{\zeta }_2}{2}),(\frac{{\zeta }_3}{2},\frac{{\zeta }_4}{2}),t)}}-1\hfill \\ & ={\displaystyle \frac{1}{{exp}^{\frac{-\sqrt{{({\zeta }_3-{\zeta }_1)}^2+{({\zeta }_4-{\zeta }_2)}^2}}{2t}}}}-1\hfill \\ & <{\displaystyle \frac{1}{{exp}^{\frac{-\sqrt{{({\zeta }_3-{\zeta }_1)}^2+{({\zeta }_4-{\zeta }_2)}^2}}{t}}}}-1\hfill \\ & ={\displaystyle \frac{1}{{\mathcal{M}}_{\mathfrak{G}}(({\zeta }_1,{\zeta }_2),({\zeta }_3,{\zeta }_4),t)}}-1\hfill \end{array}$$

Similarly, we can conclude that ${\mathcal{F}}_2,{\mathcal{F}}_3$ also satisfy the second condition of Definition 7. Hence, ${\mathcal{F}}_1,{\mathcal{F}}_2$, and ${\mathcal{F}}_3$ are GFCCs. Consider the GFCIFS $\{\mathsf{\Omega };{\mathcal{F}}_1,{\mathcal{F}}_2,{\mathcal{F}}_3\}$ with the mapping $\Theta :\mathfrak{S}\to \mathfrak{S}$ given as

$$\Theta \left(\mathfrak{w}\right)={\mathcal{F}}_1\left(\mathfrak{w}\right)\cup {\mathcal{F}}_2\left(\mathfrak{w}\right)\cup {\mathcal{F}}_3\left(\mathfrak{w}\right)$$

for all $\mathfrak{w}\in \mathfrak{S}$. Based on Theorem 7, we have the following:

$${\displaystyle \frac{1}{{\mathfrak{H}}_{\mathfrak{G}}(\Theta \left(\mathfrak{w}\right),\Theta \left(\mathfrak{K}\right),t)}}-1\le \kappa \left({\displaystyle \frac{1}{{\mathfrak{H}}_{\mathfrak{G}}(\mathfrak{w},\mathfrak{K},t)}}-1\right)$$

As a result, all conditions outlined in Theorem 5 are satisfied. Additionally, the sequence of compact sets $\{{\mathfrak{w}}_0,\Theta {\mathfrak{w}}_0,{\Theta }^2{\mathfrak{w}}_0,\dots \}$ converges, and its limit represents the attractor of Θ for any initial set ${\mathfrak{w}}_0\in \mathfrak{S}$.

The step-by-step construction of the fractal set under the iteration of $\Theta$ is illustrated in Figure 3.

We provided a detailed example to demonstrate the process of constructing fractals within a graphical fuzzy cone metric framework. In this example, we used three specific mappings on the space ${\mathbb{R}}^2$, each of which preserved the structure of a graph that captures partial ordering in both coordinates. The fuzzy cone metric ${\mathcal{M}}_{\mathfrak{G}}$ was defined through an exponential function involving the Euclidean distance, allowing us to incorporate uncertainty in a natural way. It was shown that the mappings ${\mathcal{F}}_1$, ${\mathcal{F}}_2$, and ${\mathcal{F}}_3$ preserve the edges of the graph, meaning that they are consistent with the directional relationships of the structure. Additionally, these mappings satisfy a contractive condition specific to the graphical fuzzy cone setting, which means that the system $\{\mathsf{\Omega };{\mathcal{F}}_1,{\mathcal{F}}_2,{\mathcal{F}}_3\}$ forms a well-defined Graphical Fuzzy Cone Iterated Function System (GFCIFS). The associated operator $\Theta$, defined by the union of these mappings, was shown to meet a contractive requirement with respect to the graphical fuzzy Hausdorff metric ${\mathfrak{H}}_{\mathfrak{G}}$, which ensures the existence of a unique fixed set, called an attractor. This attractor arises as the limit of an iterative sequence starting from any initial compact set. Unlike classical fractals, this attractor incorporates the influence of both fuzzy behavior and graph-based structure, providing a more general setting for modeling self-similar patterns. This example confirms that our approach can be used to construct and analyze fractals in spaces where uncertainty and directional relationships play a key role.

5. Conclusions

In this study, we introduced the Graphical Fuzzy Cone Metric Space (GFCMS) and thoroughly explored its core properties by investigating its topological characteristics and defining the Hausdorff distance. We discussed fixed-point theorems within GFCMS, supported by illustrative examples. In addition, an application to generate fractals in GFCMS is presented. This work not only expands the current knowledge in graph theory, fuzzy metric spaces, and topology but also paves the way for future research in fractal geometry and its potential applications in various scientific and computational fields.