On Complex Dimensions and Heat Content of Self-Similar Fractals
Abstract
1. Introduction
1.1. Background
1.2. Main Results
1.3. Organization of the Work
2. Preliminaries
2.1. The Heat Equation on Bounded Open Sets
2.1.1. An Overview of Perron–Wiener–Brelot Solutions
2.1.2. Heat Content and Its Properties
2.2. Geometry of Self-Similar Fractals
2.2.1. Self-Similar Iterated Function Systems
2.2.2. Lattice/Nonlattice Dichotomy
2.2.3. Relative Fractal Drums
- 1.
- ;
- 2.
- For each with , .
- 1.
- Φ satisfies the open set condition (Definition 2) with respect to Ω;
- 2.
- For each , if , then .
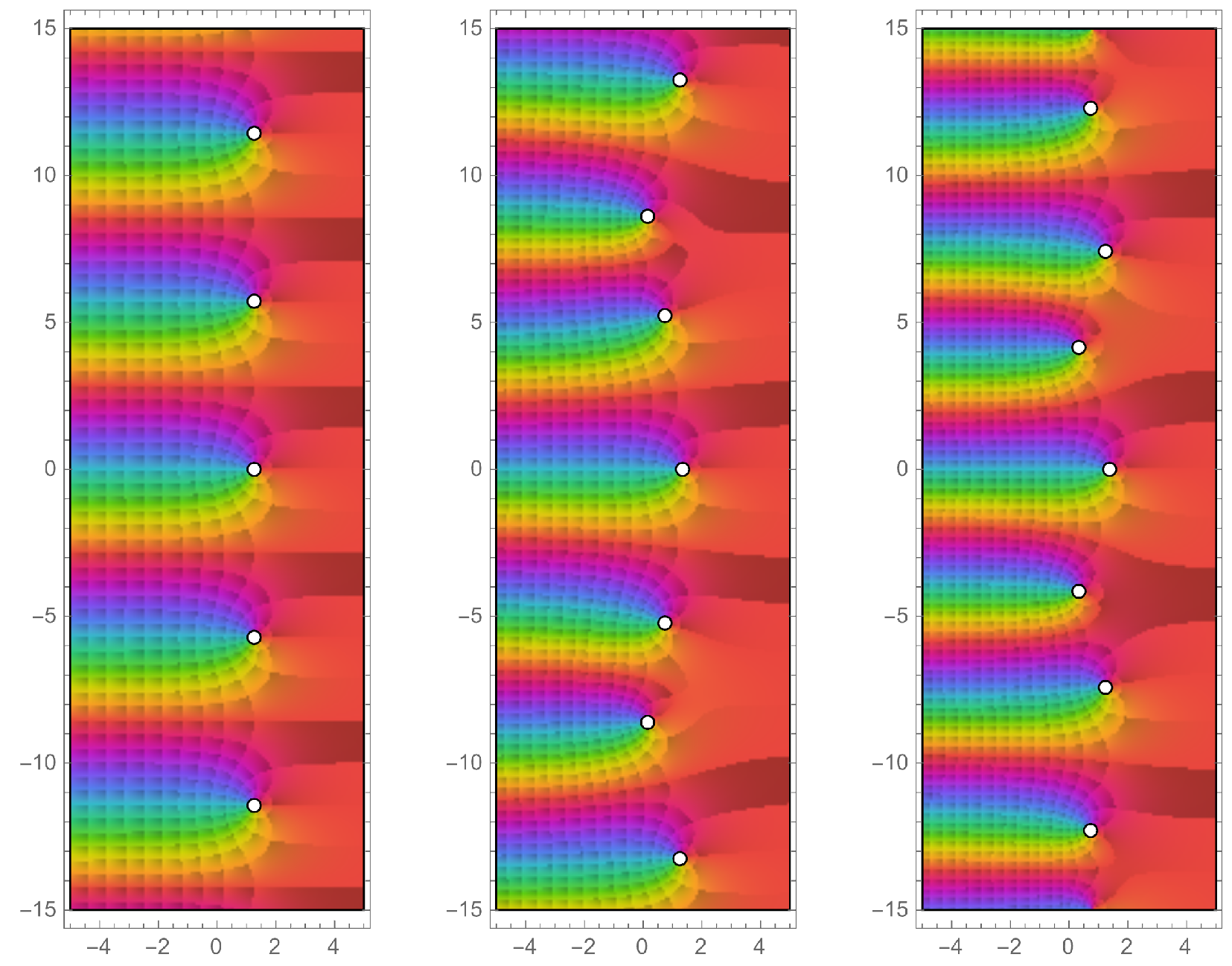
2.2.4. Tube Zeta Functions and Complex Dimensions
3. Analysis of Scaling Functional Equations
3.1. Scaling Functional Equations
3.1.1. Scaling Zeta Functions and Similarity Dimensions
3.1.2. Establishing Scaling Functional Equations
3.1.3. Scaling Functional Equations for Heat Content
3.2. Admissible Remainders
3.2.1. Admissibility and Joint Languidity
- There is a sequence of admissible heights (i.e., a doubly infinite sequence which satisfies (A12) in Appendix C) for which and both satisfy languidity hypothesis L1 with exponent κ and with respect to S using this sequence.
- Both and satisfy languidity hypothesis L2 with exponent κ and with respect to S.
3.2.2. Lower Dimension Criterion
3.2.3. Lattice Criterion
3.3. Explicit Formulae from Scaling Functional Equations
3.3.1. Pointwise Explicit Formulae
3.3.2. Distributional Explicit Formulae
3.3.3. Formulae for the Zeta Functions
3.3.4. Languidity from Scaling Functional Equations
3.3.5. Proof of the Explicit Formulae
4. Heat Content Explicit Formulae
4.1. Heat Zeta Functions
4.2. General Heat Content Results for Self-Similar Sets
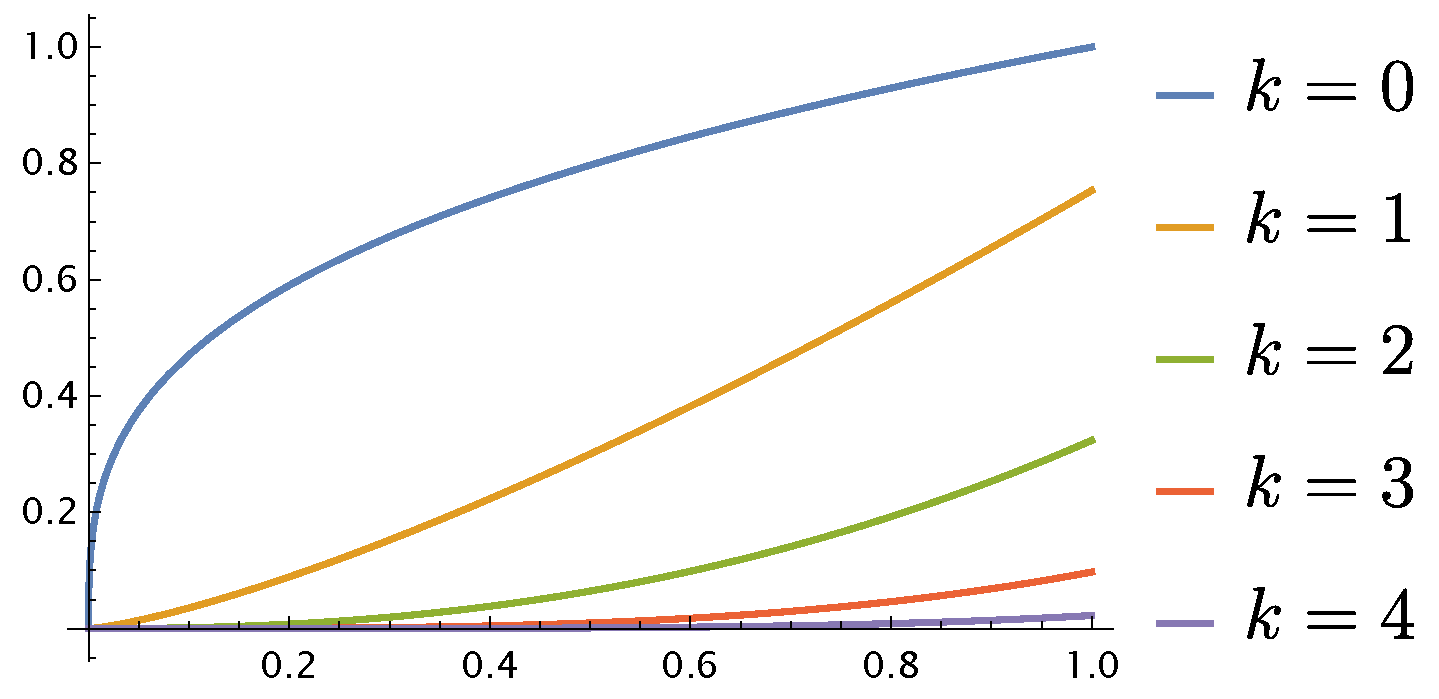
4.3. Heat Content Results for Generalized von Koch Snowflakes
4.3.1. Generalized von Koch Fractals
4.3.2. Heat Content Explicit Formulae for Generalized von Koch Fractals
4.4. Connection to Complex Dimensions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Perron–Wiener–Brelot Solutions to the Heat Equation
Appendix A.1. Classes of Temperature Functions
Appendix A.2. Classification of Boundary Points
- If , we have that for any sequence with , .
- If , we have that for any sequence with and , .
Appendix A.3. Perron–Wiener–Brelot Solutions and Resolutive Functions
Appendix B. Mellin Transforms
Appendix B.1. Truncated Mellin Transforms
Appendix B.2. Convergence of Mellin Transforms
- Let . Suppose that f is bounded away from 0 (i.e., on any interval of the form , where ) and that as , for some . Then, is absolutely convergent and holomorphic in the open right half-plane .
- Let . If f is bounded on , then is entire.
Appendix B.3. Scaling Properties of Mellin Transforms
Appendix C. Languid Growth
Appendix C.1. Languidity Hypotheses
Appendix C.2. Strong Languidity
- L1
- The function satisfies languidity hypothesis L1 with respect to each screen and the (fixed) constant κ. (Equivalently, it satisfies L1 with respect to the formal screen .)
- L2′
- There exist positive constants C and B such that for all and , satisfies
References
- von Koch, H. Sur Une Courbe Continue sans Tangente, Obtenue Par Une Construction Géométrique Élémentaire. Ark. Mat. Astron. Och Fys. 1904, 1, 681–704. [Google Scholar]
- von Koch, H. Une Méthode Géométrique Élémentaire Pour l’Étude de Certaines Questions de La Théorie Des Courbes Planes. Acta Math. 1906, 30, 145–174. [Google Scholar] [CrossRef]
- Fleckinger, J.; Levitin, M.; Vassiliev, D. Heat Content of the Triadic von Koch Snowflake. Inst. Appl. Sci. Comput. 1995, 2, 289–305. [Google Scholar]
- Fleckinger, J.; Levitin, M.; Vassiliev, D. Heat Equation on the Triadic von Koch Snowflake: Asymptotic and Numerical Analysis. Proc. Lond. Math. Soc. 1995, 71, 372–396. [Google Scholar] [CrossRef]
- Levitin, M.; Vassiliev, D. Spectral Asymptotics, Renewal Theorem, and the Berry Conjecture for a Class of Fractals. Proc. Lond. Math. Soc. 1996, 3, 188–214. [Google Scholar] [CrossRef]
- van den Berg, M. Renewal Equation for the Heat Equation of an Arithmetic von Koch Snowflake. In Infinite Dimensional Stochastic Analysis (Amsterdam, 1999); Royal Netherlands Academy of Arts and Sciences (KNAW): Amsterdam, The Netherlands, 2000; Volume 52, pp. 25–37. [Google Scholar]
- van den Berg, M. Heat Equation on the Arithmetic von Koch Snowflake. Probab. Theory Relat. Fields 2000, 118, 17–36. [Google Scholar] [CrossRef]
- van den Berg, M.; den Hollander, F. Asymptotics for the Heat Content of a Planar Region with a Fractal Polygonal Boundary. Proc. Lond. Math. Soc. 1999, 78, 627–661. [Google Scholar] [CrossRef]
- van den Berg, M.; Gilkey, P.B. A Comparison Estimate for the Heat Equation with an Application to the Heat Content of the S-Adic von Koch Snowflake. Bull. Lond. Math. Soc. 1998, 30, 404–412. [Google Scholar] [CrossRef]
- Keleti, T.; Paquette, E. The Trouble with von Koch Curves Built from N-Gons. Amer. Math. Mon. 2010, 117, 124–137. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications. Vol. I; John Wiley & Sons, Inc.: New York, NY, USA, 1950. [Google Scholar]
- Strichartz, R.S. Self-Similar Measures and Their Fourier Transforms I. Indiana Univ. Math. J. 1990, 39, 797–817. [Google Scholar] [CrossRef]
- Strichartz, R.S. Self-Similar Measures and Their Fourier Transforms. II. Trans. Amer. Math. Soc. 1993, 336, 335–361. [Google Scholar] [CrossRef]
- Strichartz, R.S. Self-Similar Measures and Their Fourier Transforms. III. Indiana Univ. Math. J. 1993, 42, 367–411. [Google Scholar] [CrossRef]
- Kigami, J.; Lapidus, M.L. Weyl’s Problem for the Spectral Distribution of Laplacians on p.c.f. Self-Similar Fractals. Comm. Math. Phys. 1993, 158, 93–125. [Google Scholar] [CrossRef]
- Park, H.; Xiao, Y. Spectral Heat Content on a Class of Fractal Sets for Subordinate Killed Brownian Motions. Math. Nachrichten 2023, 296, 4192–4205. [Google Scholar] [CrossRef]
- Rozanova-Pierrat, A.; Teplyaev, A.; Winter, S.; Zähle, M. Fractal Curvatures and Short-Time Asymptotics of Heat Content. arXiv 2025, arXiv:2502.02989. [Google Scholar] [CrossRef]
- Lapidus, M.L.; van Frankenhuijsen, M. Fractal Geometry, Complex Dimensions and Zeta Functions: Geometry and Spectra of Fractal Strings, 2nd ed.; Springer Monographs in Mathematics; Springer: New York, NY, USA, 2013; 1st ed. 2006. [Google Scholar] [CrossRef]
- Lapidus, M.L.; Radunović, G.; Žubrinić, D. Fractal Zeta Functions and Fractal Drums: Higher Dimensional Theory of Complex Dimensions; Springer Monographs in Mathematics; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Lapidus, M.L.; Pearse, E.P.J. A Tube Formula for the Koch Snowflake Curve, with Applications to Complex Dimensions. J. Lond. Math. Soc. 2006, 74, 397–414. [Google Scholar] [CrossRef]
- Hoffer, W.E. Tube Formulae for Generalized von Koch Fractals through Scaling Functional Equations. J. Fractal Geom. 2025, 12, 135–174. [Google Scholar] [CrossRef]
- Lapidus, M.L.; Pearse, E.P.J. Tube Formulas and Complex Dimensions of Self-Similar Tilings. Acta Appl. Math. 2010, 112, 91–136. [Google Scholar] [CrossRef]
- Lapidus, M.L.; Pearse, E.P.J.; Winter, S. Pointwise Tube Formulas for Fractal Sprays and Self-Similar Tilings with Arbitrary Generators. Adv. Math. 2011, 227, 1349–1398. [Google Scholar] [CrossRef]
- Hambly, B.M.; Lapidus, M.L. Random Fractal Strings: Their Zeta Functions, Complex Dimensions and Spectral Asymptotics. Trans. Amer. Math. Soc. 2006, 358, 285–314. [Google Scholar] [CrossRef]
- Deniz, A.; Koçak, Ş.; Özdemir, Y.; Üreyen, A.E. Tube Volumes via Functional Equations. J. Geom. 2015, 106, 153–162. [Google Scholar] [CrossRef]
- Perron, O. Eine neue Behandlung der ersten Randwertaufgabe für Δu=0. Math Z 1923, 18, 42–54. [Google Scholar] [CrossRef]
- Wiener, N. Certain Notions in Potential Theory. J. Math. Phys. 1924, 3, 24–51. [Google Scholar] [CrossRef]
- Wiener, N. The Average Value of a Functional. Proc. Lond. Math. Soc. 1924, 22, 454–467. [Google Scholar] [CrossRef]
- Brelot, M. A New Proof of the Fundamental Theorem of Kellogg–Evans on the Set of Irregular Points in the Dirichlet Problem. Rend. Circ. Mat. Palermo 1955, 4, 112–122. [Google Scholar] [CrossRef]
- Brelot, M. Lectures on Potential Theory, 2nd ed.; Vol. No. 19, Tata Institute of Fundamental Research Lectures on Mathematics; Tata Institute of Fundamental Research: Bombay, India, 1967. [Google Scholar]
- Widder, D.V. Positive Temperatures on an Infinite Rod. Trans. Amer. Math. Soc. 1944, 55, 85–95. [Google Scholar] [CrossRef]
- Watson, N.A. Introduction to Heat Potential Theory. In Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2012; Volume 182. [Google Scholar] [CrossRef]
- Hutchinson, J.E. Fractals and Self-Similarity. Indiana Univ. Math. J. 1981, 30, 713–747. [Google Scholar] [CrossRef]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley & Sons, Ltd.: Chichester, UK, 1990. [Google Scholar]
- Barnsley, M. Fractals Everywhere; Academic Press, Inc.: Boston, MA, USA, 1988. [Google Scholar]
- Lapidus, M.L.; Radunović, G. An Invitation to Fractal Geometry: Fractal Dimensions, Self-Similarity, and Fractal Curves. In Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2024; Volume 247. [Google Scholar]
- Lalley, S.P. The Packing and Covering Functions of Some Self-Similar Fractals. Indiana Univ. Math. J. 1988, 37, 699–710. [Google Scholar] [CrossRef]
- Lalley, S.P. Renewal Theorems in Symbolic Dynamics, with Applications to Geodesic Flows, Non-Euclidean Tessellations and Their Fractal Limits. Acta Math. 1989, 163, 1–55. [Google Scholar] [CrossRef]
- Lalley, S.P. Probabilistic Methods in Certain Counting Problems of Ergodic Theory. In Ergodic Theory, Symbolic Dynamics, and Hyperbolic Spaces (Trieste, 1989); Oxford Science Publications, Oxford University Press: New York, NY, USA, 1991; pp. 223–258. [Google Scholar]
- Dettmers, K.; Giza, R.; Morales, R.; Rock, J.A.; Knox, C. A Survey of Complex Dimensions, Measurability, and the Lattice/Nonlattice Dichotomy. Discret. Contin. Dyn. Syst. Ser. S 2017, 10, 213–240. [Google Scholar] [CrossRef][Green Version]
- Lapidus, M.L.; van Frankenhuysen, M. Fractal Geometry and Number Theory: Complex Dimensions of Fractal Strings and Zeros of Zeta Functions; Birkhäuser Boston, Inc.: Boston, MA, USA, 2000. [Google Scholar] [CrossRef]
- Moran, P.A.P. Additive Functions of Intervals and Hausdorff Measure. Math. Proc. Camb. Philos. Soc. 1946, 42, 15–23. [Google Scholar] [CrossRef]
- Graf, U. Introduction to Hyperfunctions and Their Integral Transforms: An Applied and Computational Approach; Birkhäuser Basel: Basel, Switzerland, 2010. [Google Scholar] [CrossRef]
- Wiener, N. The Dirichlet Problem. J. Math. Phys. 1924, 3, 127–146. [Google Scholar] [CrossRef]
- Kellogg, O.D. Unicité des Fonctions Harmoniques. C. R. Acad. Sci. Paris 1928, 187, 526–527. [Google Scholar]
- Evans, G.C. Application of Poincaré’s Sweeping-out Process. Proc. Natl. Acad. Sci. USA 1933, 19, 457–461. [Google Scholar] [CrossRef] [PubMed]
- Doob, J.L. Applications to Analysis of a Topological Definition of Smallness of a Set. Bull. Amer. Math. Soc. 1966, 72, 579–600. [Google Scholar] [CrossRef]
- Bauer, H. Harmonische Räume Und Ihre Potentialtheorie; Lecture Notes in Mathematics; Springer: Berlin, Germany; New York, NY, USA, 1966; Volume 22. [Google Scholar]
- Constantinescu, C.; Cornea, A. Potential Theory on Harmonic Spaces; Die Grundlehren Der Mathematischen Wissenschaften; Springer: New York, NY, USA; Heidelberg, Germany, 1972; Volume 158. [Google Scholar]
- Doob, J.L. A Probability Approach to the Heat Equation. Trans. Amer. Math. Soc. 1955, 80, 216–280. [Google Scholar] [CrossRef]
- Evans, L.C.; Gariepy, R.F. Wiener’s Criterion for the Heat Equation. Arch. Ration. Mech. Anal. 1982, 78, 293–314. [Google Scholar] [CrossRef]
- Watson, N.A. The Two Versions of the Dirichlet Problem for the Heat Equation. N. Z. J. Math. 2015, 45, 89–110. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoffer, W.E.; Lapidus, M.L. On Complex Dimensions and Heat Content of Self-Similar Fractals. Fractal Fract. 2025, 9, 649. https://doi.org/10.3390/fractalfract9100649
Hoffer WE, Lapidus ML. On Complex Dimensions and Heat Content of Self-Similar Fractals. Fractal and Fractional. 2025; 9(10):649. https://doi.org/10.3390/fractalfract9100649
Chicago/Turabian StyleHoffer, William E., and Michel L. Lapidus. 2025. "On Complex Dimensions and Heat Content of Self-Similar Fractals" Fractal and Fractional 9, no. 10: 649. https://doi.org/10.3390/fractalfract9100649
APA StyleHoffer, W. E., & Lapidus, M. L. (2025). On Complex Dimensions and Heat Content of Self-Similar Fractals. Fractal and Fractional, 9(10), 649. https://doi.org/10.3390/fractalfract9100649







