Granular Fuzzy Fractional Continuous-Time Linear Systems: Roesser and Fornasini–Marchesini Models
Abstract
1. Introduction
Motivation and Contribution
- 1.
- Two classes of FFTDCT linear systems are introduced and investigated to address uncertainty and fuzziness in system parameters.
- 2.
- The fuzzy solution of FFTDCT linear systems based on the Roesser model and the second FM model is obtained under one-dimensional 2D partial fractional granular Caputo derivatives.
- 3.
- The potential solution of the proposed model is determined using the 2D granular Laplace transform.
- 4.
- Real-world applications, including signal processing systems and wireless sensor network data fusion, are solved using the proposed technique.
2. Fuzzy Preliminaries
- (i).
- .
- (ii).
- .
- (iii).
- .
2.1. Fuzzy Fractional Calculus
2.2. Granular 2D Laplace Transform for FVF
3. Granular FFTDCT Linear Systems in the Roesser Framework
4. Granular Fuzzy Fractional 2D Continuous Linear Systems: A Fornasini–Marchesini Second Model Approach
5. Applications of FFTDCT Linear System
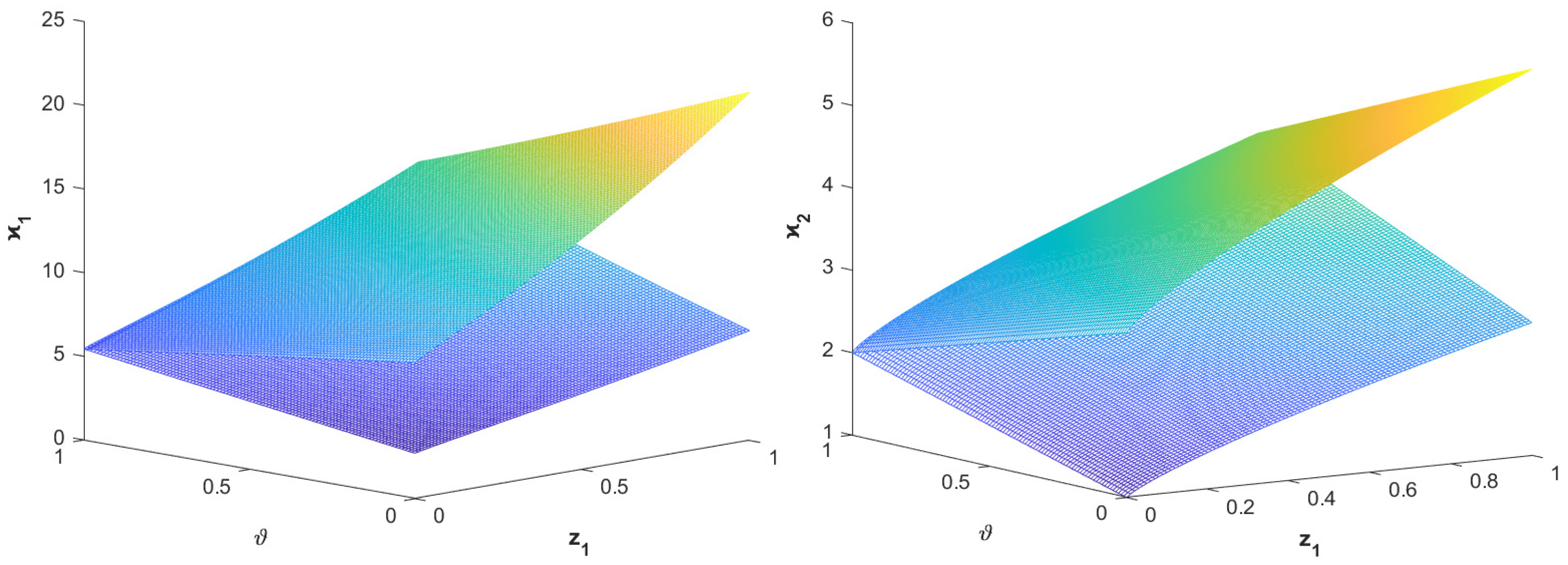
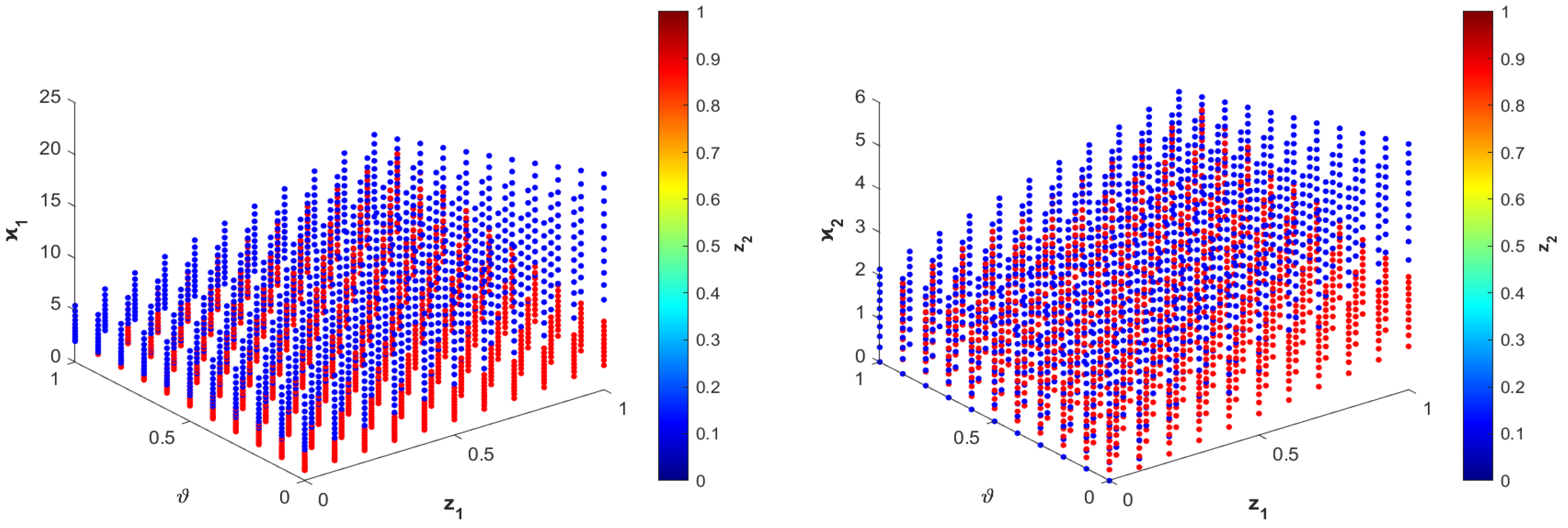
5.1. Application of FFTDCT Linear System Described by the Roesser Model in Signal Processing System
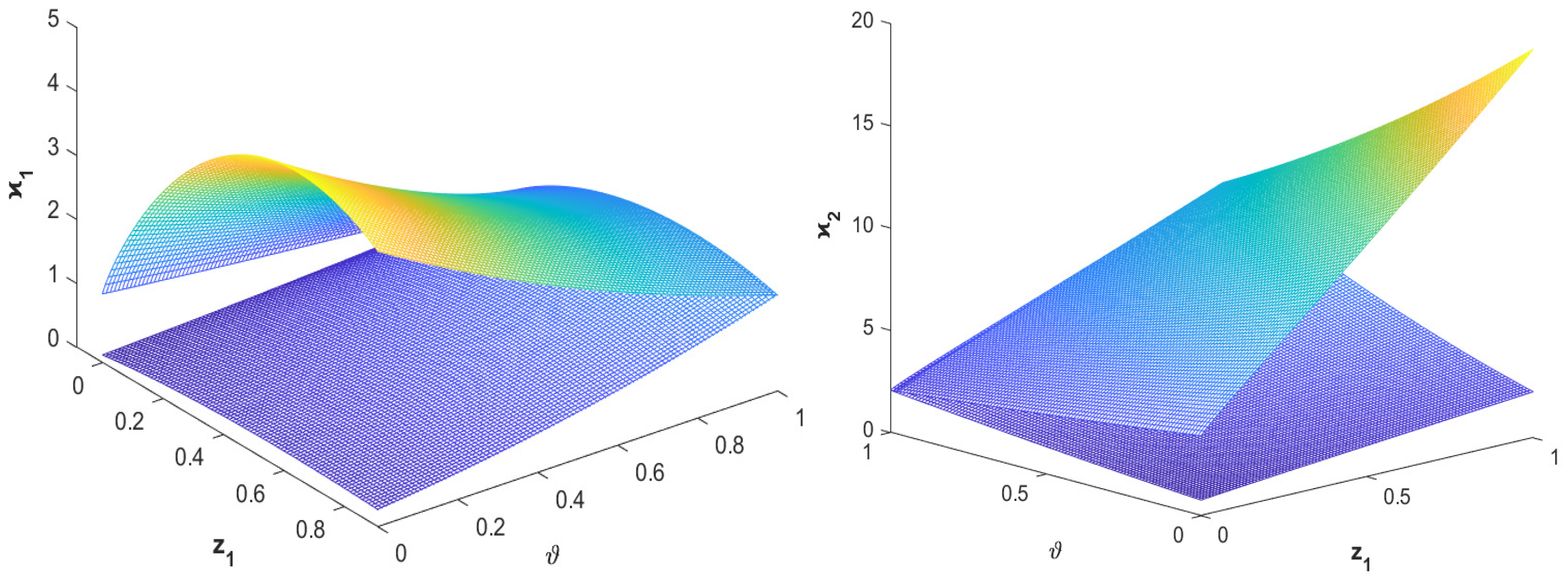
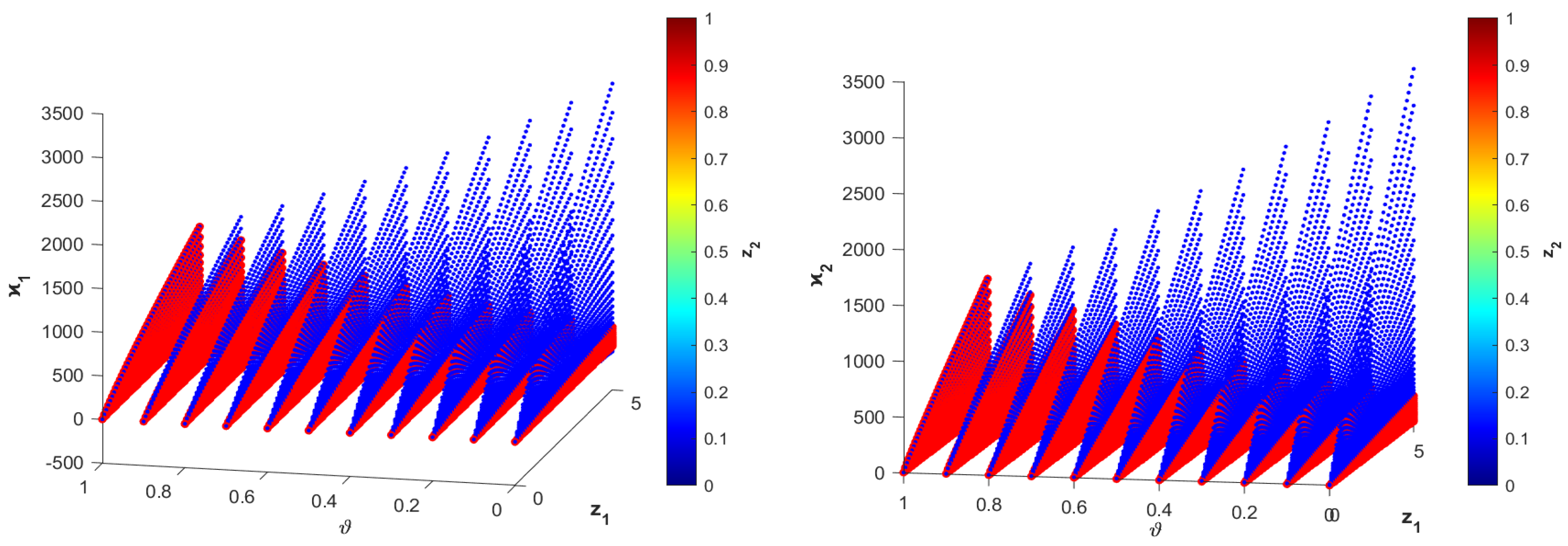
5.2. Application of FFTDCT Linear System in Wireless Sensor Network Data Fusion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeng, G.; Chen, S.; Wu, H.; Yang, M. Continuous-discrete extended Kalman filtering based on the neural ordinary differential equations method. Eng. Appl. Artif. Intell. 2024, 133, 108611. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Towards fuzzy differential calculus part 3: Differentiation. Fuzzy Sets Syst. 1982, 8, 225–233. [Google Scholar] [CrossRef]
- Akram, M.; Muhammad, G.; Allahviranloo, T.; Pedrycz, W. Solution of initial-value problem for linear third-order fuzzy differential equations. Comput. Appl. Math. 2022, 41, 398. [Google Scholar] [CrossRef]
- Muhammad, G.; Akram, M. Fuzzy fractional epidemiological model for Middle East respiratory syndrome coronavirus on complex heterogeneous network using Caputo derivative. Inf. Sci. 2024, 659, 120046. [Google Scholar] [CrossRef]
- Muhammad, G.; Akram, M. Fuzzy fractional generalized Bagley-Torvik equation with fuzzy Caputo gH-differentiability. Eng. Appl. Artif. Intell. 2024, 133, 108265. [Google Scholar] [CrossRef]
- Akram, M.; Muhammad, G.; Allahviranloo, T. Explicit analytical solutions of an incommensurate system of fractional differential equations in a fuzzy environment. Inf. Sci. 2023, 645, 119372. [Google Scholar] [CrossRef]
- Akram, M.; Muhammad, G.; Allahviranloo, T.; Pedrycz, W. Incommensurate non-homogeneous system of fuzzy linear fractional differential equations using the fuzzy bunch of real functions. Fuzzy Sets Syst. 2023, 473, 108725. [Google Scholar] [CrossRef]
- Mazandarani, M.; Pan, J. The challenges of modeling using fuzzy standard interval arithmetic: A case study in electrical engineering. Inf. Sci. 2024, 653, 119774. [Google Scholar] [CrossRef]
- Mazarani, M.; Pariz, N.; Kamyad, A.V. Granular differentiability of fuzzy-number-valued functions. IEEE Trans. Fuzzy Syst. 2017, 26, 310–323. [Google Scholar] [CrossRef]
- Cano, Y.C.; Flores, H.R. On new solutions of fuzzy differential equations. Chaos Solitons Fractals 2008, 38, 112–119. [Google Scholar] [CrossRef]
- Roesser, R. A discrete state-space model for linear image processing. IEEE Trans. Autom. Control 1975, 20, 1–10. [Google Scholar] [CrossRef]
- Fornasini, E.; Marchesini, G. State-space realization theory of two-dimensional filters. IEEE Trans. Autom. Control 1976, 21, 484–491. [Google Scholar] [CrossRef]
- Kurek, J. The general state-space model for two-dimensional linear digital systems. IEEE Trans. Autom. Control 1985, 30, 600–602. [Google Scholar] [CrossRef]
- Bose, N.K. Applied Multidimensional Systems Theory; Van Nostrand Reinhold Co.: New York, NY, USA, 1982. [Google Scholar]
- Kaczorek, T. Two-Dimensional Linear Systems; Springer: London, UK, 1985. [Google Scholar]
- Galkowski, K. State-Space Realizations of Linear 2-D Systems with Extensions to the General nD (n > 2) Case; Springer: London, UK, 2001. [Google Scholar]
- Farina, L.; Rinaldi, S. Positive Linear Systems: Theory and Applications; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: London, UK, 1999. [Google Scholar]
- Kaczorek, T. Fractional 2D linear systems. J. Autom. Mob. Robot. Intell. Syst. 2008, 2, 5–9. [Google Scholar]
- Rogowski, K. General response formula for fractional 2D continuous-time linear systems described by the Roesser model. Acta Mech. Autom. 2011, 5, 112–116. [Google Scholar]
- Kaczorek, T.; Rogowski, K. Fractional Linear Systems and Electrical Circuits; Springer International Publishing: Cham, Switzerland, 2015; pp. 49–80. [Google Scholar]
- Rogowski, K. Selected Problems of Theory of 2D Non-Integer Order Systems Described by the Roesser Model. Ph.D. Thesis, Bialystok University of Technology, Bialystok, Poland, 2011. (In Polish). [Google Scholar]
- Idczak, M.; Kamocki, T.; Majewski, M. On a fractional continuous counterpart of Fornasini-Marchesini model. In Proceedings of the International Conference on Multidimensional Systems, Erlangen, Germany, 9–11 September 2013; pp. 1–5. [Google Scholar]
- Rogowski, K. Positivity analysis of continuous Fornasini-Marchesini fractional model. In Proceedings of the 5th International Symposium on Positive Systems, Rome, Italy, 14–16 September 2016. [Google Scholar]
- Hu, H.; Meng, Y.; Huang, S. Dynamic event-triggered control of 2-D continuous systems in Roesser model. Asian J. Control 2025, 27, 646–660. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, B.; Wang, Y.E.; Liu, L. Practical exponential stability of switched generalized homogeneous positive nonlinear systems with bounded disturbances. Circuits Syst. Signal Process. 2025, 44, 3793–3809. [Google Scholar] [CrossRef]
- Ma, H.; Tian, D.; Li, M.; Zhang, C. Reachable set estimation for 2-D switched nonlinear positive systems with impulsive effects and bounded disturbances described by the Roesser model. Math. Model. Control 2024, 4, 152–162. [Google Scholar] [CrossRef]
- Dami, L.; Benzaouia, A. Stabilization of switched two dimensional fractional order positive systems modeled by the Roesser model. J. Control Autom. Electr. Syst. 2023, 34, 1136–1144. [Google Scholar] [CrossRef]
- Huang, S.; Yan, Z.; Zhang, Z.; Zeng, G. Finite-time boundedness of two-dimensional positive continuous-discrete systems in Roesser model. Trans. Inst. Meas. Control 2021, 43, 1452–1463. [Google Scholar] [CrossRef]
- Gao, J.; Wang, W.; Zhang, G. Finite-time stability and control of 2D continuous–discrete systems in Roesser model. Circuits Syst. Signal Process. 2018, 37, 4789–4809. [Google Scholar] [CrossRef]
- Ahn, C.K.; Shi, P.; Wu, L. l∞-gain performance analysis for two-dimensional Roesser systems with persistent bounded disturbance and saturation nonlinearity. Inf. Sci. 2016, 333, 126–139. [Google Scholar] [CrossRef]
- Nemati, A.; Mamehrashi, K. The use of the Ritz method and Laplace transform for solving 2D fractional-order optimal control problems described by the Roesser model. Asian J. Control 2019, 21, 1189–1201. [Google Scholar] [CrossRef]
- Zhang, J.R.; Lu, J.G.; Zhu, Z. Stability analysis and stabilisation of continuous-discrete fractional-order 2D Fornasini-Marchesini first model. Int. J. Syst. Sci. 2023, 54, 333–344. [Google Scholar] [CrossRef]
- Zhu, Z.; Lu, J.G. Robust stability and stabilization of continuous-discrete fractional-order 2D Fornasini-Marchesini second model with interval uncertainties. Asian J. Control 2024, 26, 3054–3066. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, W. Finite-region stability and boundedness for discrete 2D Fornasini-Marchesini second models. Int. J. Syst. Sci. 2017, 48, 778–787. [Google Scholar] [CrossRef]
- Benyettou, K.; Bouagada, D.; Ghezzar, M.A. Solution of 2D state space continuous-time conformable fractional linear system using Laplace and Sumudu transform. Comput. Math. Model. 2021, 32, 94–109. [Google Scholar] [CrossRef]
- Benyettou, K.; Bouagada, D.; Benamar, M.N. Controllability and minimum energy control problem of two-dimensional continuous-time fractional linear systems. Int. J. Syst. Sci. 2024, 56, 966–981. [Google Scholar] [CrossRef]
- Yan, S.; Sun, L.; Xu, L.; Cai, Y.; Zhao, Q. State-space formulation of 2-D frequency transformation in Fornasini-Marchesini second model. Multidimens. Syst. Signal Process. 2018, 29, 361–383. [Google Scholar] [CrossRef]
- Li, X.; Hou, X. Design of parametric controller for two-dimensional polynomial systems described by the Fornasini-Marchesini second model. IEEE Access 2019, 7, 44070–44079. [Google Scholar] [CrossRef]
- Bede, B.; Stefanini, L. Generalized differentiability of fuzzy-valued functions. Fuzzy Sets Syst. 2013, 230, 119–141. [Google Scholar] [CrossRef]
- Son, N.T.K.; Long, H.V.; Dong, N.P. Fuzzy delay differential equations under granular differentiability with applications. Comput. Appl. Math. 2019, 38, 107. [Google Scholar] [CrossRef]
- Kaczorek, T. Selected Problems in Fractional Systems Theory; Springer: London, UK, 2011. [Google Scholar]
- Rogowski, K. Solution to the fractional-order 2D continuous systems described by the second Fornasini-Marchesini model. IFAC-PapersOnLine 2017, 50, 9748–9752. [Google Scholar] [CrossRef]
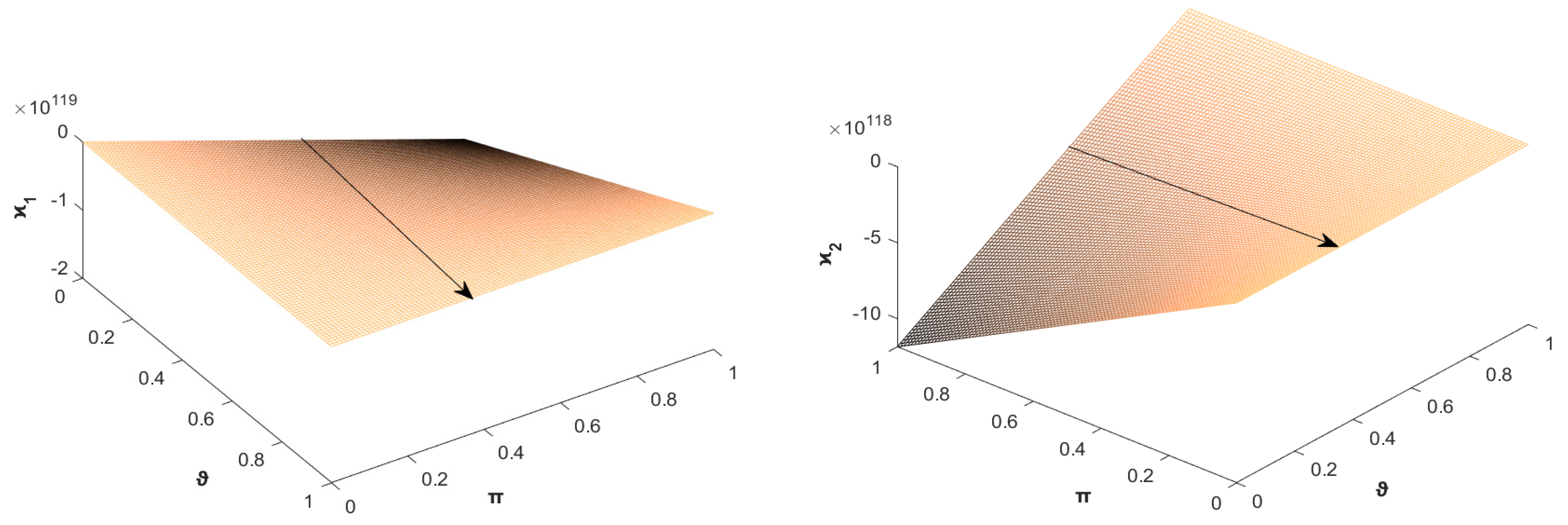
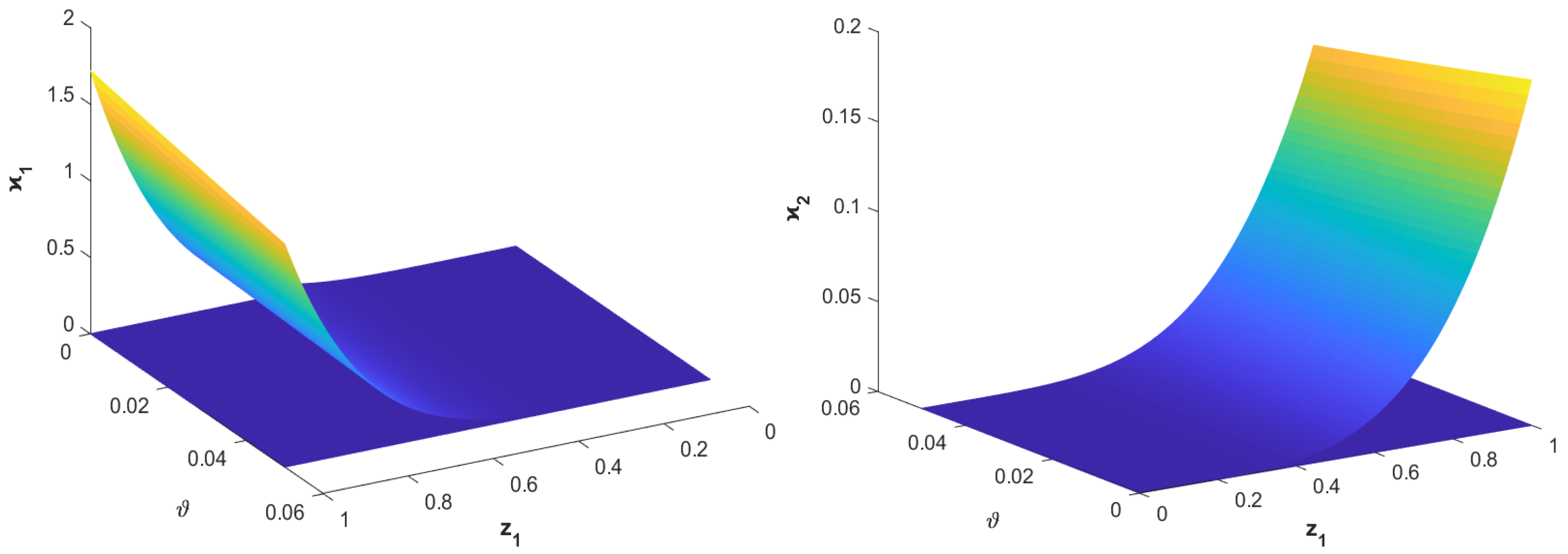
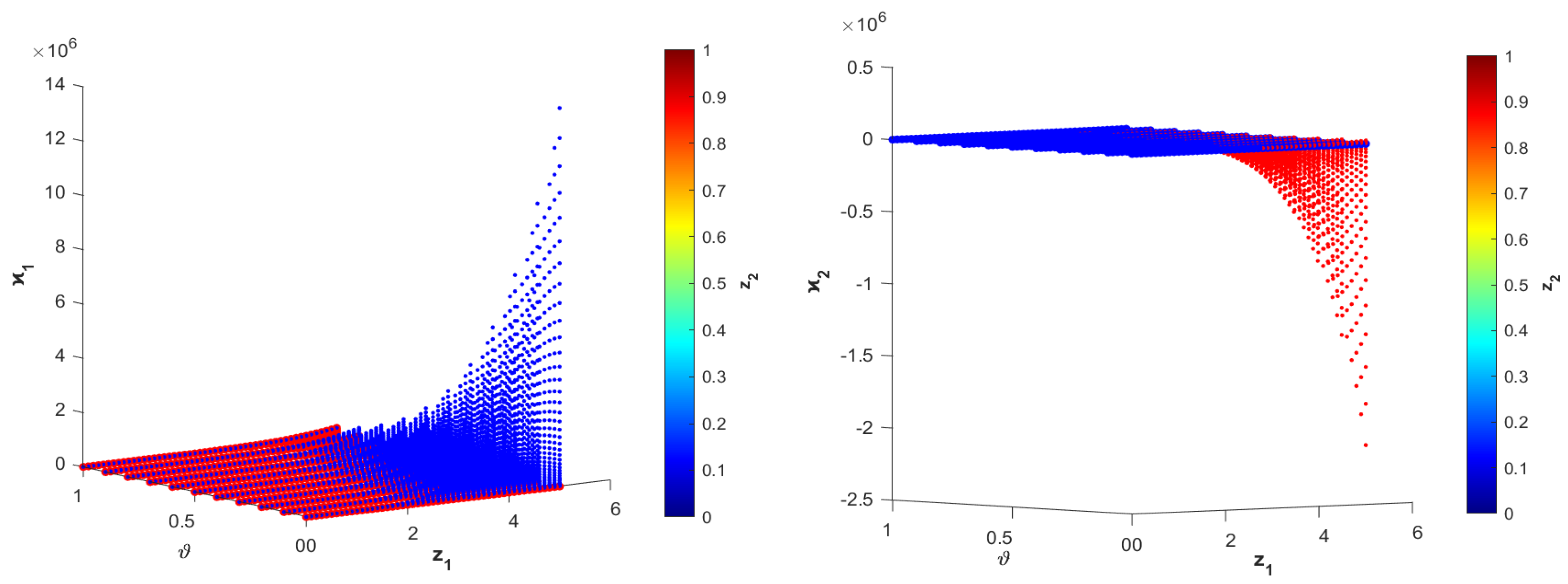
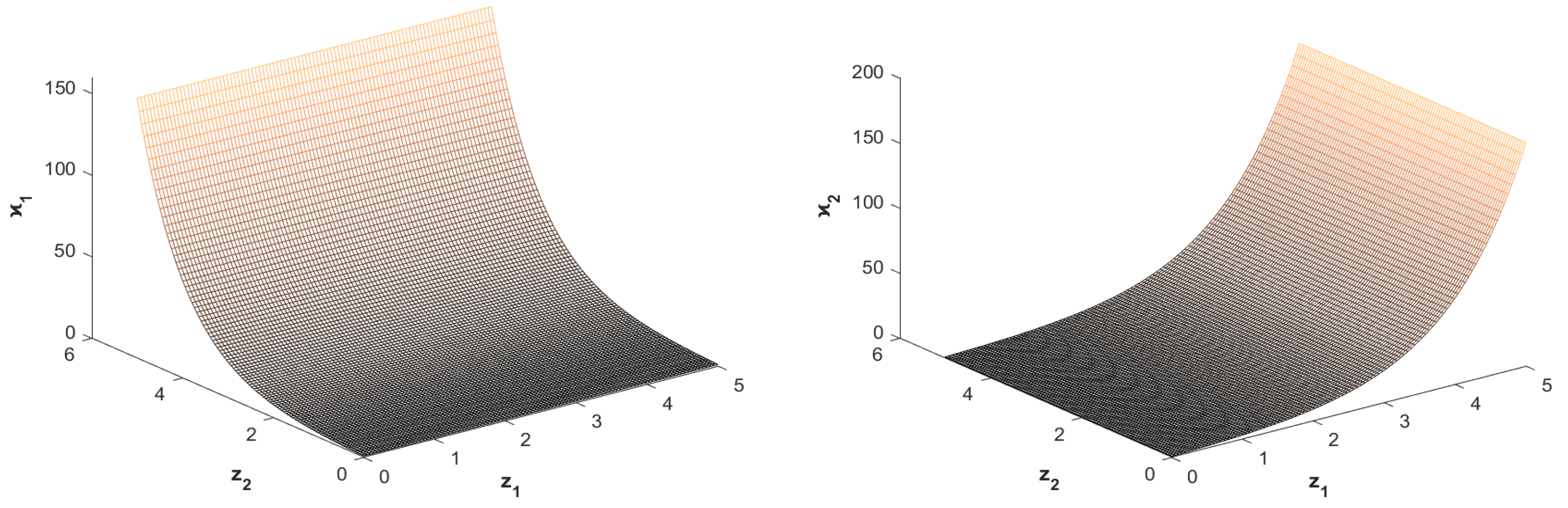

| Notation | Description | Location |
|---|---|---|
| The collection of all FNs on | Section 2 | |
| The HMF of the FN | Section 2 | |
| The 2DRL fractional integral of order regarding the variable (i = 1, 2) | Definition 9 | |
| The 2D Caputo fractional derivative (CFD) of order regarding variable | Definition 12 | |
| The 2D Laplace transform regarding and | Definition 16 | |
| The 2D granular Laplace transform regarding and | Definition 18 | |
| The GFI of order regarding (i = 1, 2) | Definition 13 | |
| The two-dimensional GCFD of order regarding (i = 1, 2) | Definition 14 | |
| FI of order of regarding the variable | Definition 8 |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.5123 | 0.5101 | 0.5112 | 0.5100 |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.2439 | 0.3501 | 0.2422 | 0.3452 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.7201 | 0.8112 | 0.7199 | 0.8108 |
| 0.3 | 0.3 | 0.3 | 0.3 | 1.5607 | 1.4140 | 1.5602 | 1.4112 |
| 0.4 | 0.4 | 0.4 | 0.4 | 2.8969 | 2.1715 | 2.8950 | 2.1612 |
| 0.5 | 0.5 | 0.5 | 0.5 | 4.8501 | 3.1839 | 4.8499 | 3.1822 |
| 0.6 | 0.6 | 0.6 | 0.6 | 7.5899 | 4.1930 | 7.5812 | 4.1901 |
| 0.7 | 0.7 | 0.7 | 0.7 | 11.1483 | 5.3929 | 11.1460 | 5.3924 |
| 0.8 | 0.8 | 0.8 | 0.8 | 15.5037 | 6.6530 | 15.5001 | 6.6501 |
| 0.9 | 0.9 | 0.9 | 0.9 | 20.9987 | 7.8535 | 20.9940 | 7.8427 |
| 1.0 | 1.0 | 1.0 | 1.0 | 24.9339 | 8.8185 | 24.8312 | 8.8130 |
| AE | RE | AE | RE | ||||
|---|---|---|---|---|---|---|---|
| 0.5123 | 0.5112 | 0.0011 | 0.002147 | 0.5101 | 0.5100 | 0.0001 | 0.000196 |
| 0.2439 | 0.2422 | 0.0017 | 0.006970 | 0.3501 | 0.3452 | 0.0049 | 0.014000 |
| 0.7201 | 0.7199 | 0.0002 | 0.000278 | 0.8112 | 0.8108 | 0.0004 | 0.000493 |
| 1.5607 | 1.5602 | 0.0005 | 0.000320 | 1.4140 | 1.4112 | 0.0028 | 0.001982 |
| 2.8969 | 2.8950 | 0.0019 | 0.000656 | 2.1715 | 2.1612 | 0.0103 | 0.004740 |
| 4.8501 | 4.8499 | 0.0002 | 0.000041 | 3.1839 | 3.1822 | 0.0017 | 0.000533 |
| 7.5899 | 7.5812 | 0.0087 | 0.001146 | 4.1930 | 4.1901 | 0.0029 | 0.000693 |
| 11.1483 | 11.1460 | 0.0023 | 0.000206 | 5.3929 | 5.3924 | 0.0005 | 0.000093 |
| 15.5037 | 15.5001 | 0.0036 | 0.000232 | 6.6530 | 6.6501 | 0.0029 | 0.000437 |
| 20.9987 | 20.9940 | 0.0047 | 0.000224 | 7.8535 | 7.8427 | 0.0108 | 0.001375 |
| 24.9339 | 24.8312 | 0.1027 | 0.004119 | 8.8185 | 8.8130 | 0.0055 | 0.000623 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhammad, G.; Akram, M.; Alsulami, H.; Hussain, N. Granular Fuzzy Fractional Continuous-Time Linear Systems: Roesser and Fornasini–Marchesini Models. Fractal Fract. 2025, 9, 398. https://doi.org/10.3390/fractalfract9070398
Muhammad G, Akram M, Alsulami H, Hussain N. Granular Fuzzy Fractional Continuous-Time Linear Systems: Roesser and Fornasini–Marchesini Models. Fractal and Fractional. 2025; 9(7):398. https://doi.org/10.3390/fractalfract9070398
Chicago/Turabian StyleMuhammad, Ghulam, Muhammad Akram, Hamed Alsulami, and Nawab Hussain. 2025. "Granular Fuzzy Fractional Continuous-Time Linear Systems: Roesser and Fornasini–Marchesini Models" Fractal and Fractional 9, no. 7: 398. https://doi.org/10.3390/fractalfract9070398
APA StyleMuhammad, G., Akram, M., Alsulami, H., & Hussain, N. (2025). Granular Fuzzy Fractional Continuous-Time Linear Systems: Roesser and Fornasini–Marchesini Models. Fractal and Fractional, 9(7), 398. https://doi.org/10.3390/fractalfract9070398








