Adaptive Fractional Order Control for Bispectral Index Regulation During Anaesthesia
Abstract
1. Introduction
1.1. Medical Basis
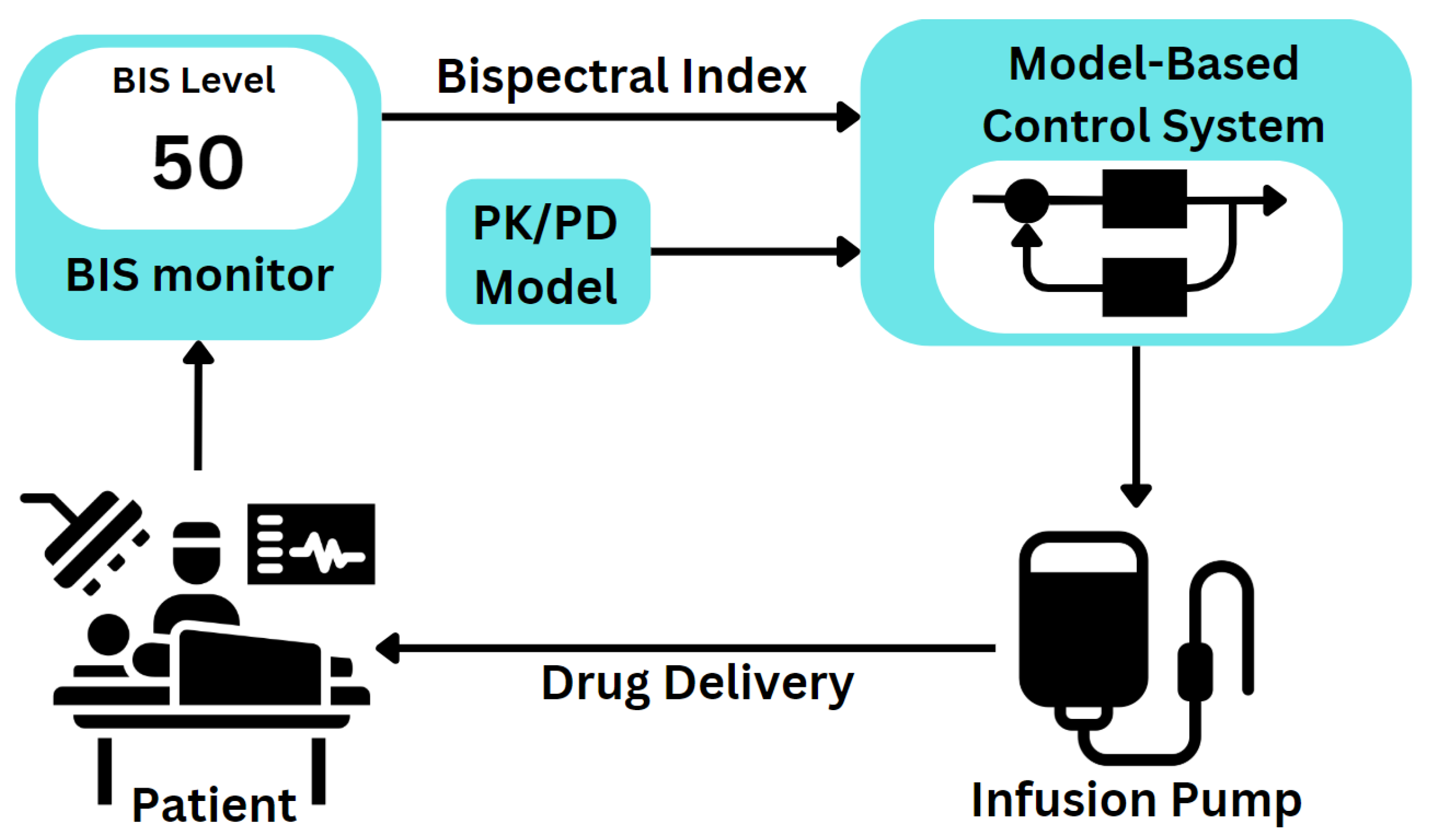
1.2. Automation in Anaesthesia
- The merging fractional order controllers and adaptive schemes for BIS regulation.
- The design, testing and validation of a novel adaptive fractional order PI controller.
- Stability and robustness analyses of the novel controller.
2. Materials and Methods
2.1. Process Model
2.2. Fractional Order Controller
- Proportional term (P): generates an output directly proportional to the current error, providing immediate correction through the P controller.
- Integral term (I): accumulates past errors over time to address persistent biases and achieve the setpoint.
- Derivative term (D): responds to the change rate of the error, anticipating future deviations to minimise overshoot and oscillations.
- An imposed gain crossover frequency .
- A phase margin .
- A condition for robustness against gain variations.
- High-frequency noise rejection.
- A measure for good output disturbance rejection.
2.3. Model Reference Adaptive Control
- Uncertain plant: adaptive control addresses uncertainty in both linear and nonlinear plants, which can manifest as either structured uncertainty (parametric uncertainty) or unstructured uncertainty (where neither parameters nor functional characteristics are known). In this paper’s case, the plant process is the depth of anaesthesia induced through anaesthetic drugs and measured through the BIS signal. Patient variability and unexpected behaviour generate the uncertain aspects of the process, which the MRAC system must compensate for.
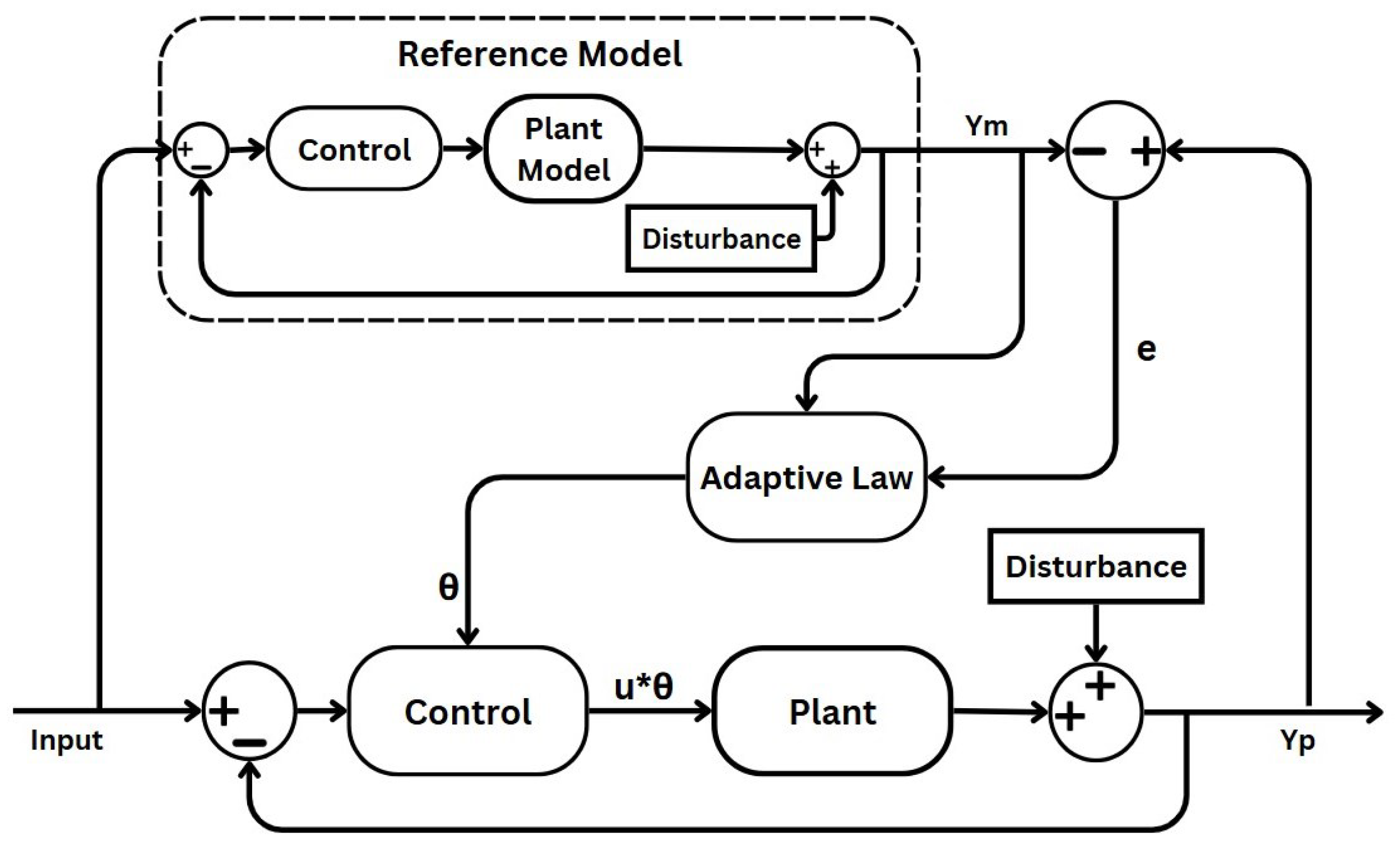
- Reference model: defines the desired response of the MRAC system to a command input, serving as a command shaping filter to achieve the precise command-following behaviour [39,40]. In adaptive control, whether formulated for command following or tracking, the adaptation process relies on minimising the tracking error between the system output and the designated reference model. Designing the reference model thoughtfully is crucial for ensuring accurate tracking. While traditionally structured as a linear time-invariant (LTI) model, nonlinear variants can also be utilised, albeit with added complexity. In this specific case, the reference model reflects the ideal BIS response specific to a given surgical context.
- Controller: ensures stable system performance under nominal conditions, serving as a baseline controller. As shown in Figure 2, the controller in the primary loop generates a control signal by comparing the output of the uncertain plant with that of the reference model. This signal is further influenced by the adaptive law component, mediated through the intermediary output . In the MRAC system, adjustments in propofol infusion rate are made to minimise the discrepancy between the BIS and the desired reference model output. This component will be implemented using the designed FO-PI controller.
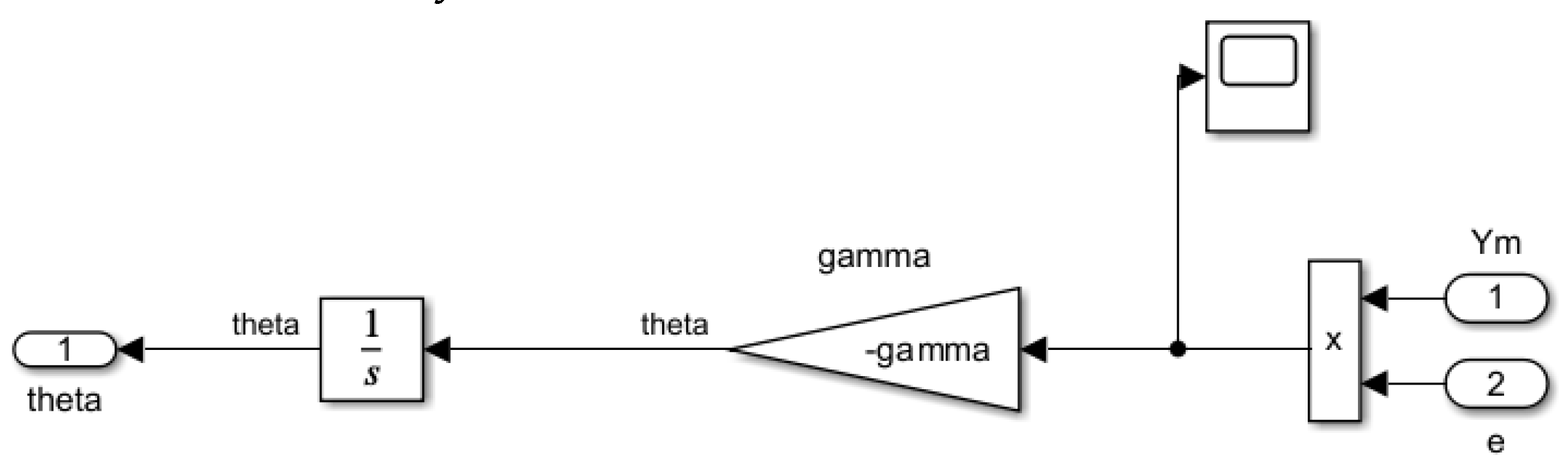
- Adaptation mechanism: dictates in all adaptive schemes how adaptive parameters adjust to minimise tracking errors. In certain schemes, this aspect is crucially influencing stability via Lyapunov stability theory. Adaptive laws vary in complexity and robustness, requiring careful parameter tuning to balance performance and stability in adaptive control systems.
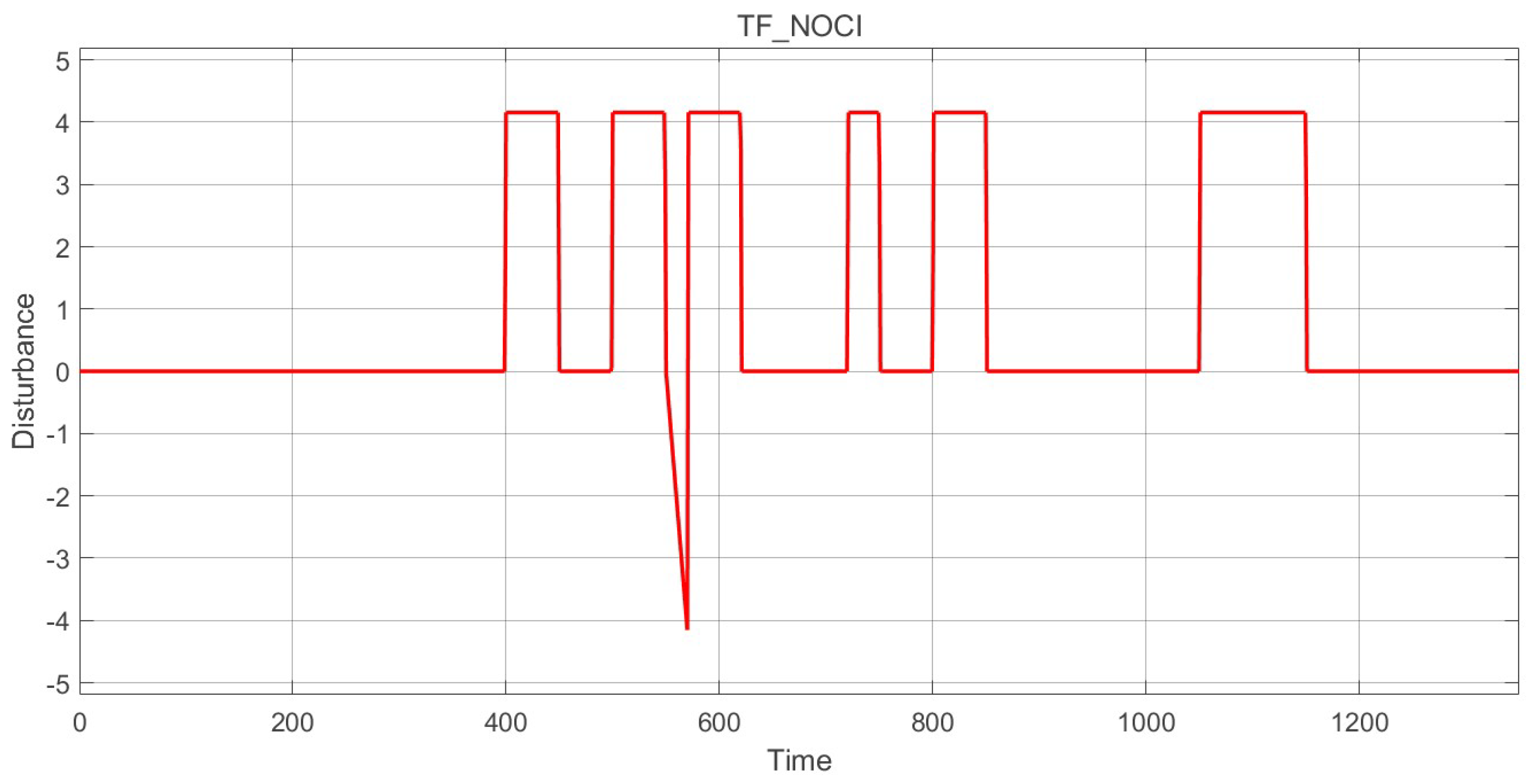
2.4. Disturbance Signal
3. Results
3.1. FO-PI Controller
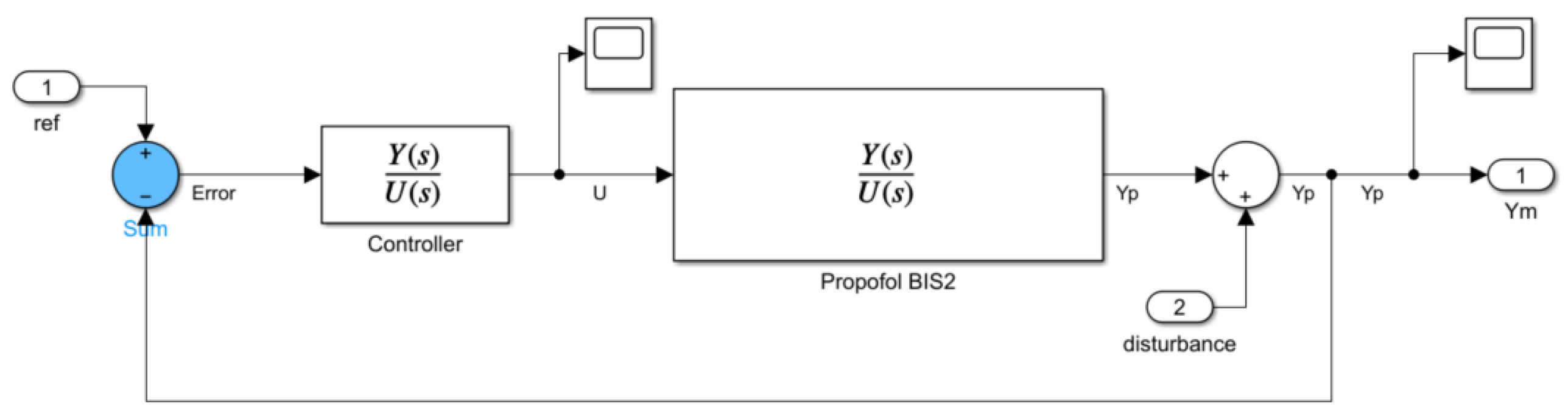
3.2. System Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PK | Pharmacokinetics |
| PD | Pharmacodynamics |
| TCI | Target-Controlled Infusion |
| PID | Proportional–Integral–Derivative |
| MPC | Model Predictive Control |
| MRAC | Model Reference Adaptive Control |
| SISO | Single-Input–Single-Output |
| MIMO | Multiple-Input–Multiple-Output |
| FO | Fractional Order |
| ORA | Oustaloup Recursive Approximation |
| EMG | Electromyogram |
| RASS | Ramsay Agitation Score |
| BIS | Bispectral Index |
| EEG | Electroencephalogram |
| MAP | Mean Arterial Pressure |
| CO | Cardiac Output |
| DSP | Digital Signal Processing |
| MIT | Massachusetts Institute of Technology |
| IIC | Initial Integral Condition |
| ISE | Integral Squared Error |
| MSE | Mean-Squared Error |
References
- Mistri, I.; Badge, A.; Shahu, S. Enhancing Patient Safety Culture in Hospitals. Cureus 2023, 15, e51159. [Google Scholar] [CrossRef] [PubMed]
- Sameera, V.; Bindra, A.; Rath, G.P. Human Errors and Their Prevention in Healthcare. J. Anaesthesiol. Clin. Pharmacol. 2021, 37, 328–335. [Google Scholar] [CrossRef] [PubMed]
- Labuschagne, M.; Robbetze, W.; Rozmiarek, J.; Strydom, M.; Wentzel, M.; Diedericks, J.; Joubert, G. Errors in Drug Administration by Anaesthetists in Public Hospitals in the Free State. S. Afr. Med. J. 2011, 101, 324–327. [Google Scholar] [CrossRef]
- Zaouter, C.; Joosten, A.; Rinehart, J.; Struys, M.M.R.F.; Hemmerling, T.M. Autonomous Systems in Anesthesia: Where Do We Stand in 2020? A Narrative Review. Anesth. Analg. 2020, 130, 1120–1132. [Google Scholar] [CrossRef]
- Dinia, L.; Mangini, F.; Frezza, F. Can the Perception of Risk Be Decreased among Caregivers during Anesthesia Delivery? In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Jones, C.P.L.; Fawker-Corbett, J.; Groom, P.; Morton, B.; Lister, C.; Mercer, S.J. Human factors in preventing complications in anaesthesia: A systematic review. Anaesthesia 2018, 73, 12–24. [Google Scholar] [CrossRef]
- Gautam, B.; Shrestha, B.R. Critical Incidents during Anesthesia and Early Post-Anesthetic Period: A Descriptive Cross-sectional Study. JNMA J. Nepal Med. Assoc. 2020, 58, 240–247. [Google Scholar] [CrossRef]
- Steadman, J.; Catalani, B.; Sharp, C.; Cooper, L. Life-Threatening Perioperative Anesthetic Complications: Major Issues Surrounding Perioperative Morbidity and Mortality. Trauma Surg. Acute Care Open 2017, 2, e000113. [Google Scholar] [CrossRef]
- Dalley, P.; Robinson, B.; Weller, J.; Caldwell, C. The Use of High-Fidelity Human Patient Simulation and the Introduction of New Anesthesia Delivery Systems. Anesth. Analg. 2004, 99, 1737–1741. [Google Scholar] [CrossRef]
- Dinia, L.; Mangini, F.; Mileti, I.; Palermo, E.; Frezza, F. Adverse Patient Events in Anesthesia Delivery – Review and Analysis of Potentially Avoidable Events. In Proceedings of the 2020 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Bari, Italy, 1 June–1 July 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Dinia, L.; Mangini, F.; Marella, M.A.; Frezza, F. Parallelism Between Risk and Perception of Risk Among Caregivers During Anesthesia Delivery. Eur. Rev. Med. Pharmacol. Sci. 2019, 23, 3129–3141. [Google Scholar] [CrossRef]
- Keyser, R.D.; Copot, D.; Ionescu, C. Estimation of Patient Sensitivity to Drug Effect During Propofol Hypnosis. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; pp. 2487–2491. [Google Scholar] [CrossRef]
- Dobson, G.; Chow, L.; Filteau, L.; Hurdle, H.; McIntyre, I.; Milne, A.; Milkovich, R.; Perrault, M.A.; Sparrow, K.; Swart, P.A.; et al. Guidelines to the Practice of Anesthesia—Revised Edition 2021. Can. J. Anesth. 2021, 68, 92–129. [Google Scholar] [CrossRef]
- Bibian, S.; Ries, C.R.; Huzmezan, M.; Dumont, G. Introduction to automated drug delivery in clinical anesthesia. Eur. J. Control 2015, 11, 535–557. [Google Scholar] [CrossRef]
- Cehajic-Kapetanovic, J.; Xue, K.; Edwards, T.L.; Meenink, T.C.; Beelen, M.J.; Naus, G.J.; de Smet, M.D.; MacLaren, R.E. First-in-Human Robot-Assisted Subretinal Drug Delivery Under Local Anesthesia. Am. J. Ophthalmol. 2022, 237, 104–113. [Google Scholar] [CrossRef]
- Hemmerling, T.M.; Charabati, S.; Zaouter, C.; Minardi, C.; Mathieu, P.A. A Randomized Controlled Trial Demonstrates That a Novel Closed-loop Propofol System Performs Better Hypnosis Control Than Manual Administration. Can. J. Anesth. 2010, 57, 725–735. [Google Scholar] [CrossRef]
- Haddad, W.M.; Bailey, J.M. Closed-loop control for intensive care unit sedation. Best Pract. Res. Clin. Anaesthesiol. 2009, 23, 95–114. [Google Scholar] [CrossRef]
- Ahtiainen, H.K.; Kallio, M.M.; Airaksinen, M.; Holmström, A.R. Safety, Time and Cost Evaluation of Automated and Semi-Automated Drug Distribution Systems in Hospitals: A Systematic Review. Eur. J. Hosp. Pharm. 2020, 27, 253–262. [Google Scholar] [CrossRef]
- Fang, M.; Tao, Y.; Wang, Y. An Enriched Simulation Environment for Evaluation of Closed-loop Anesthesia. J. Clin. Monit. Comput. 2014, 28, 13–26. [Google Scholar] [CrossRef]
- Padula, F.; Ionescu, C.; Latronico, N.; Paltenghi, M.; Visioli, A.; Vivacqua, G. Optimized PID Control of Depth of Hypnosis in Anesthesia. Comput. Methods Programs Biomed. 2017, 144, 21–35. [Google Scholar] [CrossRef]
- Paolino, N.; Schiavo, M.; Latronico, N.; Paltenghi, M.; Visioli, A. PK/PD Model-Based Design of PID Control for Closed-Loop Anesthesia. IFAC J. Syst. Control 2024, 27, 100247. [Google Scholar] [CrossRef]
- Patel, B.; Patel, H.G. Intravenous Anesthesia Automation with Internal and Instrumental Delay. In Proceedings of the 2017 IEEE International Conference on Industrial and Information Systems (ICIIS), Peradeniya, Sri Lanka, 15–16 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Navarro-Guerrero, G.; Tang, Y. Adaptive Control for Anesthesia Based on a Simple Fractional-Order Model. In Proceedings of the 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 5623–5628. [Google Scholar] [CrossRef]
- Wei, Z.X.; Doctor, F.; Liu, Y.X.; Fan, S.Z.; Shieh, J.S. An Optimized Type-2 Self-Organizing Fuzzy Logic Controller Applied in Anesthesia for Propofol Dosing to Regulate BIS. IEEE Trans. Fuzzy Syst. 2020, 28, 1062–1072. [Google Scholar] [CrossRef]
- Hegedus, E.T.; Birs, I.R.; Ghita, M.; Muresan, C.I. Fractional-Order Control Strategy for Anesthesia–Hemodynamic Stabilization in Patients Undergoing Surgical Procedures. Fractal Fract. 2022, 6, 614. [Google Scholar] [CrossRef]
- Chen, J.; Ren, W.; Liu, J.; Fu, Z.; Yao, Y.; Chen, X.; Teng, L. Feasibility of Intelligent Drug Control in the Maintenance Phase of General Anesthesia Based on Convolutional Neural Network. Heliyon 2023, 9, e12481. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Peng, S.; Chen, M.; Yang, Z.; Chen, Y. A Transformer-Based Prediction Method for Depth of Anesthesia During Target-Controlled Infusion of Propofol and Remifentanil. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 3363–3374. [Google Scholar] [CrossRef] [PubMed]
- Ghita, M.; Neckebroek, M.; Muresan, C.; Copot, D. Closed-Loop Control of Anesthesia: Survey on Actual Trends, Challenges and Perspectives. IEEE Access 2020, 8, 206264–206279. [Google Scholar] [CrossRef]
- Ionescu, C.M.; Neckebroek, M.; Ghita, M.; Copot, D. An Open Source Patient Simulator for Design and Evaluation of Computer-Based Multiple Drug Dosing Control for Anesthetic and Hemodynamic Variables. IEEE Access 2021, 9, 8680–8694. [Google Scholar] [CrossRef]
- Hegedus, E.; Ghita, M.; Birs, I.R.; Copot, D.; Muresan, C.I. Robustness Analysis of a Fractional Order Control System for the Hemodynamic Variables in Anesthetized Patients. In Proceedings of the 2023 European Control Conference (ECC), Bucharest, Romania, 13–16 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Eleveld, D.J.; Colin, P.; Absalom, A.R.; Struys, M.M.R.F. Pharmacokinetic-Pharmacodynamic Model for Propofol for Broad Application in Anaesthesia and Sedation. Br. J. Anaesth. 2018, 120, 942–959, Erratum in Br. J. Anaesth. 2018, 121, 519. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Van Heusden, K.; Dumont, G.A.; Garone, E. An Explicit Reference Governor Scheme for Closed-Loop Anesthesia. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 1294–1299. [Google Scholar] [CrossRef]
- Vajta, M. Some Remarks on Padé-Approximations. In Proceedings of the 3rd TEMPUS-INTCOM Symposium, Veszprém, Hungary, 9–14 September 2000; p. 1. [Google Scholar]
- Neckebroek, M.M.; Smet, T.D. Automated drug delivery in anesthesia. J. Anesth. 2013, 3, 18–26. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 5th ed.; Pearson: Hoboken, NJ, USA, 2010. [Google Scholar]
- Vilanova, R.; Visioli, A. (Eds.) PID Control in the Third Millennium; Advances in Industrial Control; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Azar, A.; Radwan, A.; Vaidyanathan, S. Fractional Order Systems: Optimization, Control, Circuit Realizations and Applications; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Nguyen, N. Model Reference Adaptive Control—A Primer; Advanced Textbooks in Control and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Mallick, S.; Mondal, U. Design of Lyapunov Based Model Reference Adaptive Controller for First Order Plus Delay Time Liquid Level System. In Proceedings of the 2019 International Conference on Intelligent Computing and Remote Sensing (ICICRS), Bhubaneswar, India, 19–20 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Tao, G. Multivariable adaptive control: A survey. Automatica 2014, 50, 2737–2764. [Google Scholar] [CrossRef]
- Swathi, M.; Ramesh, P. Modeling and Analysis of Model Reference Adaptive Control by Using MIT and Modified MIT Rule for Speed Control of DC Motor. In Proceedings of the 2017 IEEE 7th International Advance Computing Conference (IACC), Hyderabad, India, 5–7 January 2017; pp. 482–486. [Google Scholar] [CrossRef]
- Jain, P.; Nigam, M.J. Real Time Control of Ball and Beam System with Model Reference Adaptive Control Strategy Using MIT Rule. In Proceedings of the 2013 IEEE International Conference on Computational Intelligence and Computing Research, Enathi, India, 26–28 December 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Jenkins, B.M.; Annaswamy, A.M.; Lavretsky, E.; Gibson, T.E. Convergence Properties of Adaptive Systems and the Definition of Exponential Stability. SIAM J. Control Optim. 2018, 56, 2463–2484. [Google Scholar] [CrossRef]
- Ooba, S.; Ueki, R.; Kariya, N.; Tatara, T.; Hirose, M. Mathematical Evaluation of Responses to Surgical Stimuli Under General Anesthesia. Sci. Rep. 2020, 10, 15300. [Google Scholar] [CrossRef]
- Röpcke, H.; Rehberg, B.; Koenen-Bergmann, M.; Bouillon, T.; Bruhn, J.; Hoeft, A. Surgical Stimulation Shifts EEG Concentration–Response Relationship of Desflurane. Anesthesiology 2001, 94, 390–399. [Google Scholar] [CrossRef] [PubMed]
- Schiavo, M.; Padula, F.; Latronico, N.; Paltenghi, M.; Visioli, A. Individualized PID tuning for maintenance of general anesthesia with propofol. IFAC-PapersOnLine 2021, 54, 679–684. [Google Scholar] [CrossRef]
- Bachmann, F.; Koch, G.; Pfister, M.; Szinnai, G.; Schropp, J. OptiDose: Computing the Individualized Optimal Drug Dosing Regimen Using Optimal Control. J. Optim. Theory Appl. 2021, 189, 46–65. [Google Scholar] [CrossRef]
- Khan, A.; Swamy, M.S. Modified MRAC based on Lyapunov theory for improved controller efficiency. In Proceedings of the 2016 International Conference on Automatic Control and Dynamic Optimization Techniques (ICACDOT), Pune, India, 9–10 September 2016; pp. 989–995. [Google Scholar] [CrossRef]
- Pawłowski, A.; Schiavo, M.; Latronico, N.; Paltenghi, M.; Visioli, A. Model predictive control using MISO approach for drug co-administration in anesthesia. J. Process Control 2022, 117, 98–111. [Google Scholar] [CrossRef]
- Maxim, A.; Copot, D. Closed-loop control of anesthesia and hemodynamic system: A Model Predictive Control approach. IFAC-PapersOnLine 2021, 54, 37–42. [Google Scholar] [CrossRef]







| Control Strategy | Benefits | Limitations | Application Domains |
|---|---|---|---|
| PID control | Simple to implement, widely used, real-time response | Poor performance in nonlinear or time-varying systems, limited adaptability | BIS level tracking in stable cases |
| Model predictive control (MPC) | Handles fluctuating time delays and constraints well, anticipatory control | Computationally intensive | Complex surgical scenarios, personalised dosing |
| Adaptive control | Adjusts to patient variability in real-time | Stability can be harder to guarantee, design complexity | Dynamic BIS control for variable PK/PD patient models but no disturbance |
| Fuzzy logic control | Robust to uncertainties, mimics expert knowledge | Computationally expensive, rule design is heuristic | Systems with vague/noisy data, paediatric or elderly patients |
| Fractional order control | Adequate induction phase performance | Parameter working range constraints and high sensitivity | Control of combined anaesthesia–haemodynamic systems |
| Intelligent control | Learns from data, superior prediction during sudden BIS changes | Requires large training datasets, prediction issues during the induction period due to time lag | Real-time closed-loop BIS control in advanced systems |
| Phase Margin | Parameters | ||||
|---|---|---|---|---|---|
| Nr Crt | (°) | ||||
| 1 | 65 | 0.0185 | 0.016 | 1.204 | 0.003 |
| 2 | 80 | 0.0265 | 0.0033 | 1.0765 | 0.0035 |
| 3 | 90 | 0.0297 | 0.0057 | 1 | 0.004 |
| Variables | Error Values | ||||
|---|---|---|---|---|---|
| Nr Crt | IIC | (°) | ISE () | MSE () | |
| 1 | 0 | 65 | 0.000005 | 4.142 | 10.107 |
| 2 | 0 | 80 | 0.000005 | 4.034 | 9.579 |
| 3 | 0 | 90 | 0.000005 | 4.002 | 9.284 |
| 4 | 0.5 | 65 | 0.000005 | 2.625 | 1.717 |
| 5 | 0.5 | 80 | 0.000005 | 2.540 | 1.601 |
| 6 | 0.5 | 90 | 0.000005 | 2.512 | 1.547 |
| 7 | 0.5 | 65 | 0.00001 | 2.494 | 1.205 |
| 8 | 0.5 | 80 | 0.00001 | 2.394 | 1.130 |
| 9 | 0.5 | 90 | 0.00001 | 2.354 | 1.095 |
| 10 | 0.5 | 65 | 0.000015 | 2.447 | 0.979 |
| 11 | 0.5 | 80 | 0.000015 | 2.345 | 0.923 |
| 12 | 0.5 | 90 | 0.000015 | 2.299 | 0.896 |
| 13 | 1 | 65 | 0.00001 | 1.809 | |
| 14 | 1 | 80 | 0.00001 | 1.737 | |
| 15 | 1 | 90 | 0.00001 | 1.712 | |
| 16 | 1 | 65 | 0.000015 | 1.798 | |
| 17 | 1 | 80 | 0.000015 | 1.727 | |
| 18 | 1 | 90 | 0.000015 | 1.702 | |
| Nr Crt | IIC | (°) | Overshoot (%) | Settling Time (s) | () | |
|---|---|---|---|---|---|---|
| 1 | 0 | 65 | 0.000005 | 4.9 | 335 | 6.22 |
| 2 | 0 | 80 | 0.000005 | 0 | 220 | 5.816 |
| 3 | 0 | 90 | 0.000005 | 0 | 320 | 5.476 |
| 4 | 0.5 | 65 | 0.000015 | 4 | 315 | 5.871 |
| 5 | 0.5 | 80 | 0.000015 | 0 | 250 | 2.191 |
| 6 | 0.5 | 90 | 0.000015 | 0 | 320 | 5.334 |
| 7 | 1 | 65 | 0.000015 | 3 | 330 | 5.78 |
| 8 | 1 | 80 | 0.000015 | 0 | 240 | 5.536 |
| 9 | 1 | 90 | 0.000015 | 0 | 315 | 5.288 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malița, A.-C.; Muresan, C.I.; Duarte-Mermoud, M.A.; Ceballos Benavides, G. Adaptive Fractional Order Control for Bispectral Index Regulation During Anaesthesia. Fractal Fract. 2025, 9, 330. https://doi.org/10.3390/fractalfract9060330
Malița A-C, Muresan CI, Duarte-Mermoud MA, Ceballos Benavides G. Adaptive Fractional Order Control for Bispectral Index Regulation During Anaesthesia. Fractal and Fractional. 2025; 9(6):330. https://doi.org/10.3390/fractalfract9060330
Chicago/Turabian StyleMalița, Alin-Ciprian, Cristina Ioana Muresan, Manuel A. Duarte-Mermoud, and Gustavo Ceballos Benavides. 2025. "Adaptive Fractional Order Control for Bispectral Index Regulation During Anaesthesia" Fractal and Fractional 9, no. 6: 330. https://doi.org/10.3390/fractalfract9060330
APA StyleMalița, A.-C., Muresan, C. I., Duarte-Mermoud, M. A., & Ceballos Benavides, G. (2025). Adaptive Fractional Order Control for Bispectral Index Regulation During Anaesthesia. Fractal and Fractional, 9(6), 330. https://doi.org/10.3390/fractalfract9060330







