An Efficient Structure-Preserving Scheme for the Fractional Damped Nonlinear Schrödinger System
Abstract
1. Introduction
- An exponential variable is introduced to derive an equivalent formulation of the DFNLS equation, accompanied by a rigorous proof of the conservation of two quantities in this form.
- A semi-discrete scheme utilizing the Fourier spectral method in space is proposed, demonstrating its conservation properties and spectral accuracy convergence.
- A fully-discrete scheme is developed by integrating the Fourier spectral method in space with the Crank–Nicolson method in time, establishing its conservation and convergence properties.
- The theoretical findings are validated through numerical experiments, which also confirm the method’s effectiveness in addressing fractional high-dimensional problems.
2. Reformulated System
3. Construction of Semi-Discrete Fourier Spectral Scheme and Theoretical Analysis
3.1. Some Useful Lemmas
3.2. Semi-Discrete Fourier Spectral Scheme
4. Construction of Full-Discrete Fourier Spectral Scheme and Theoretical Analysis
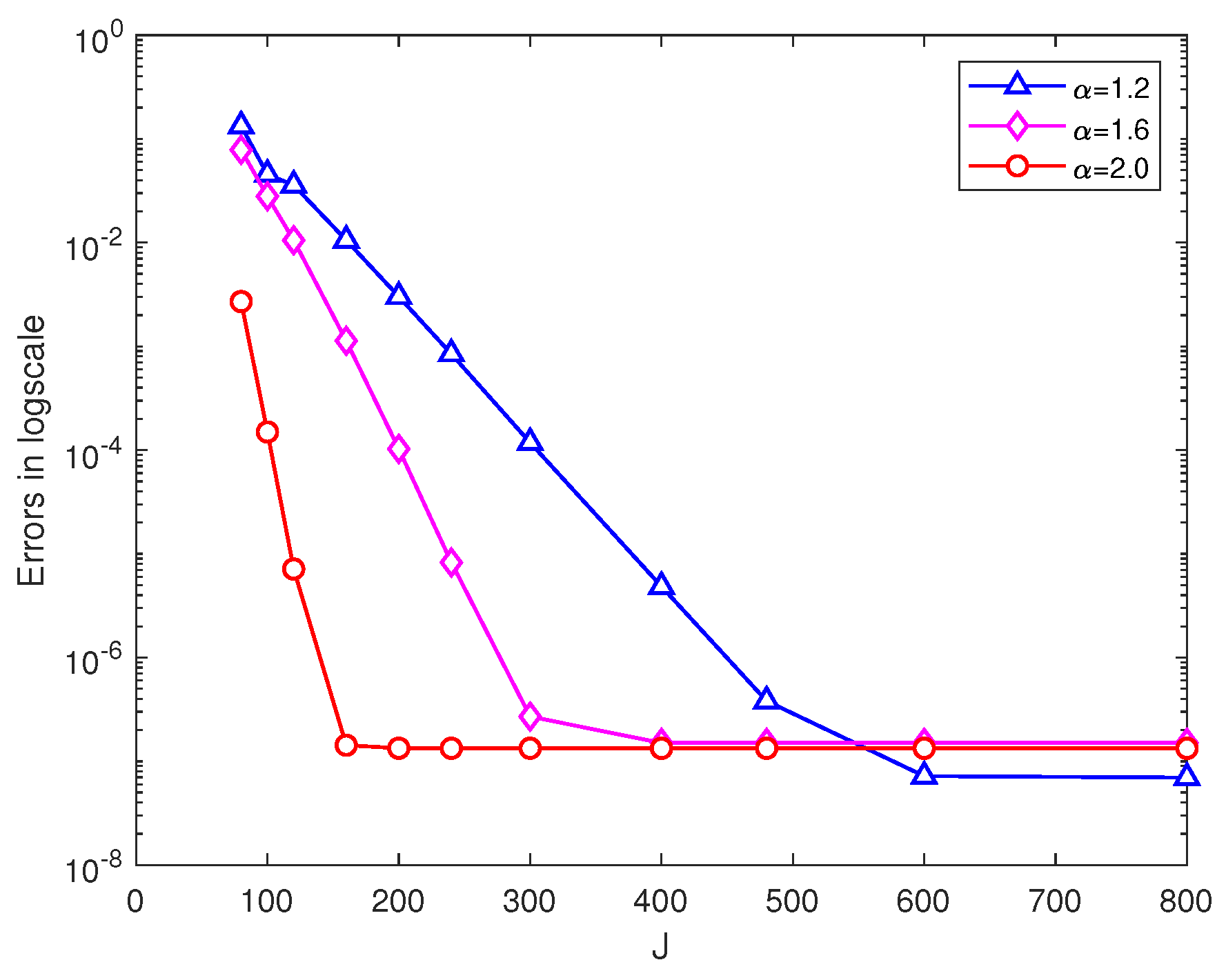
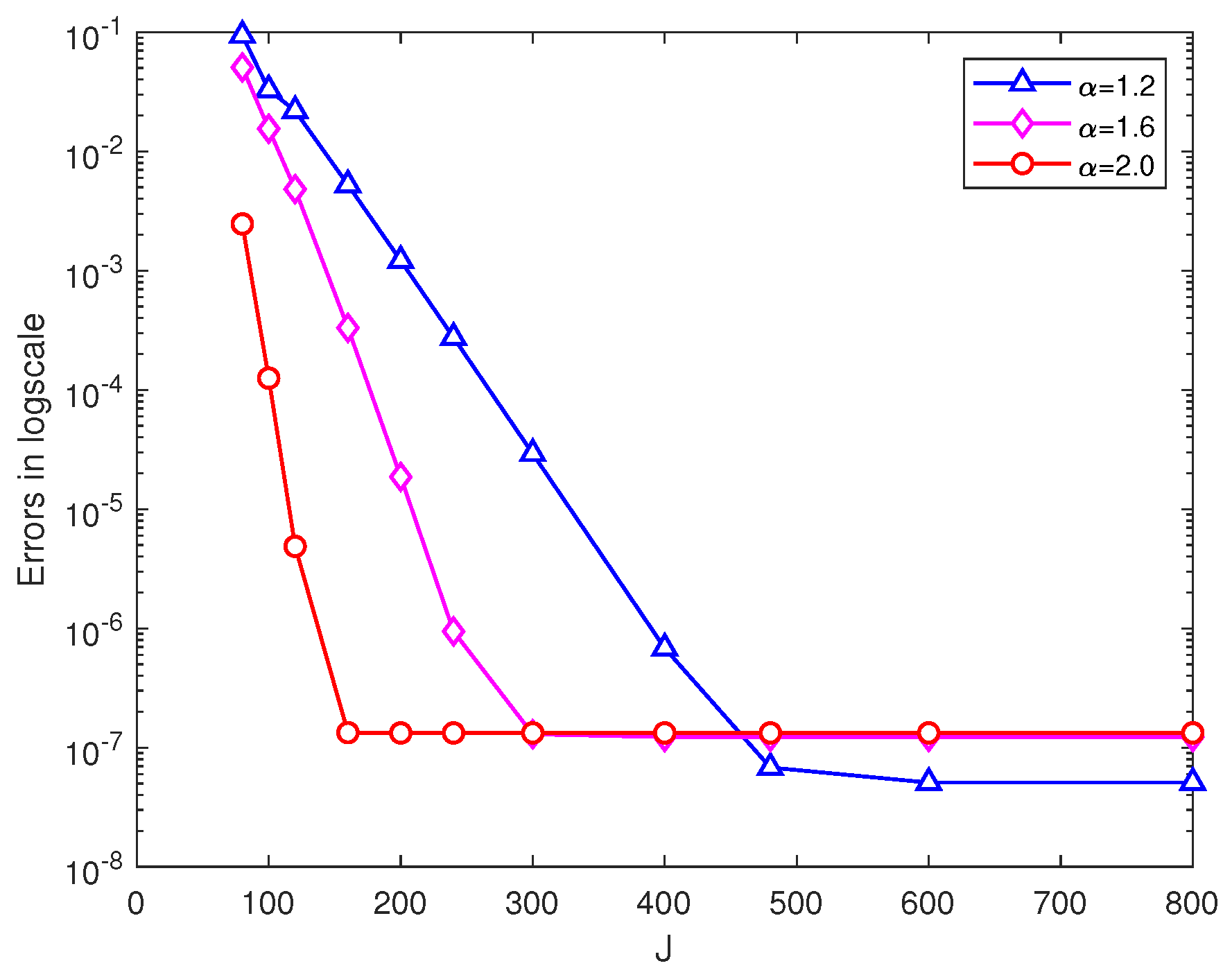
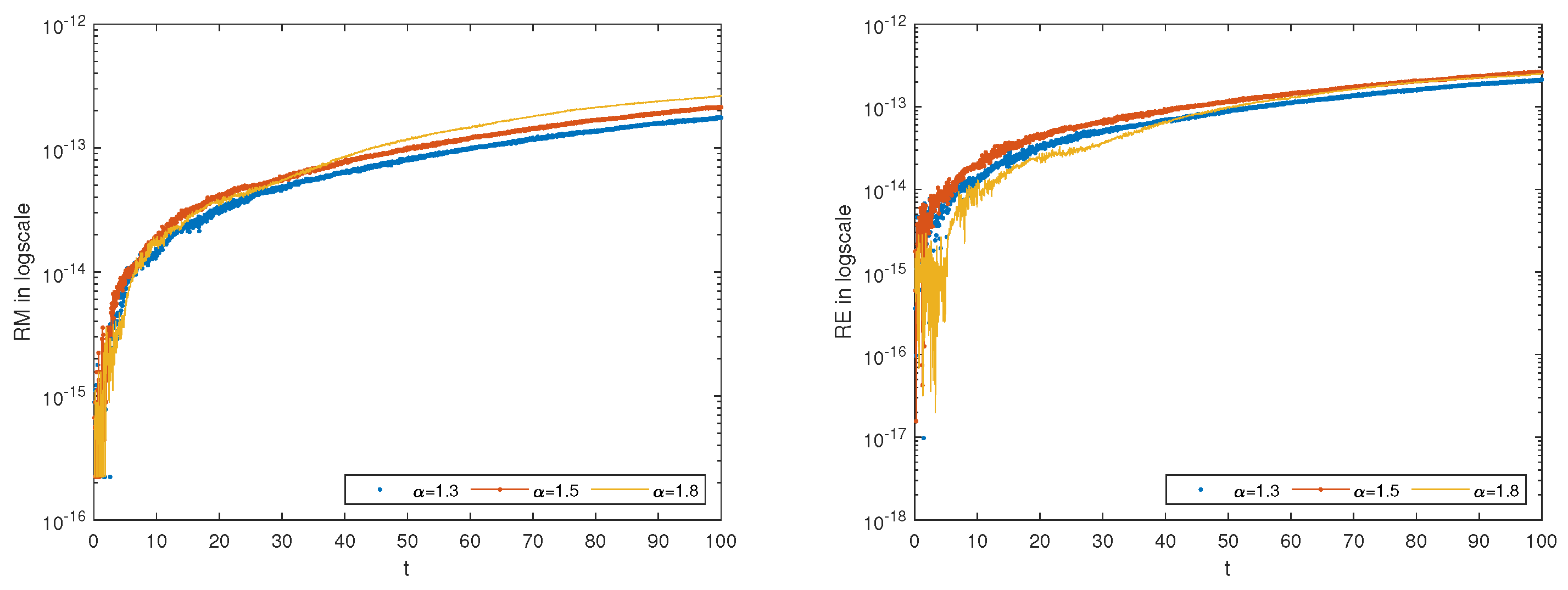
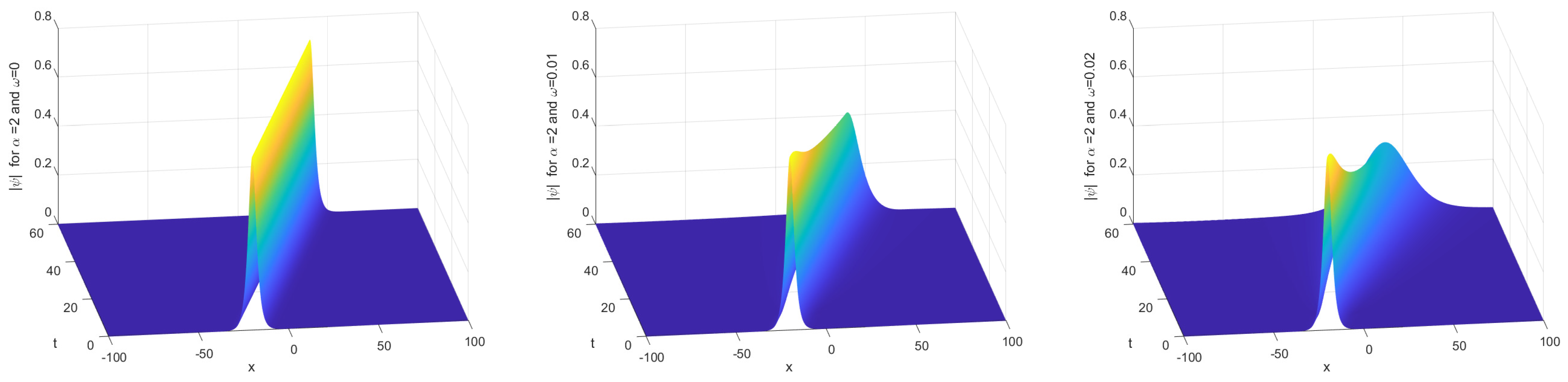
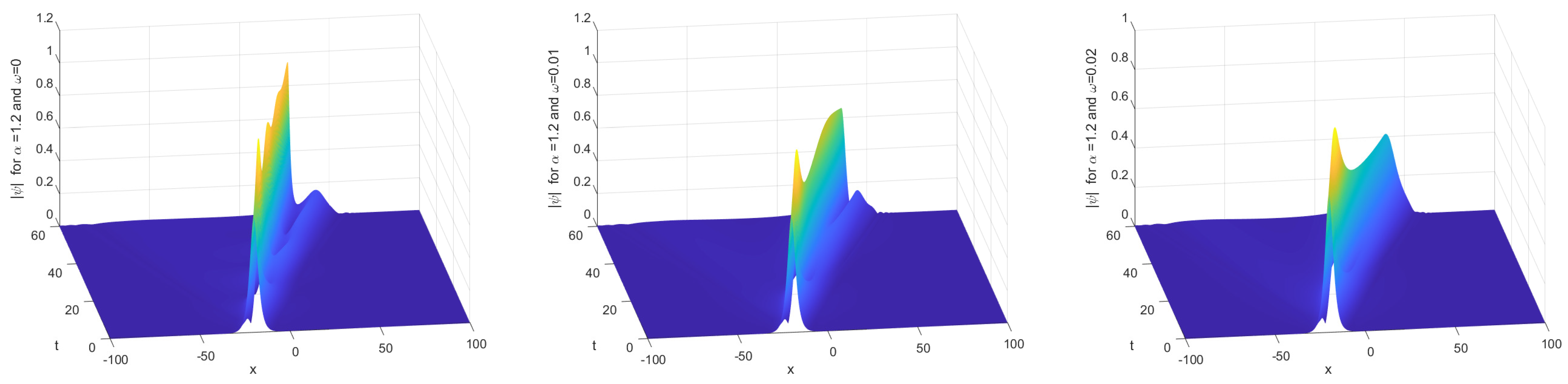
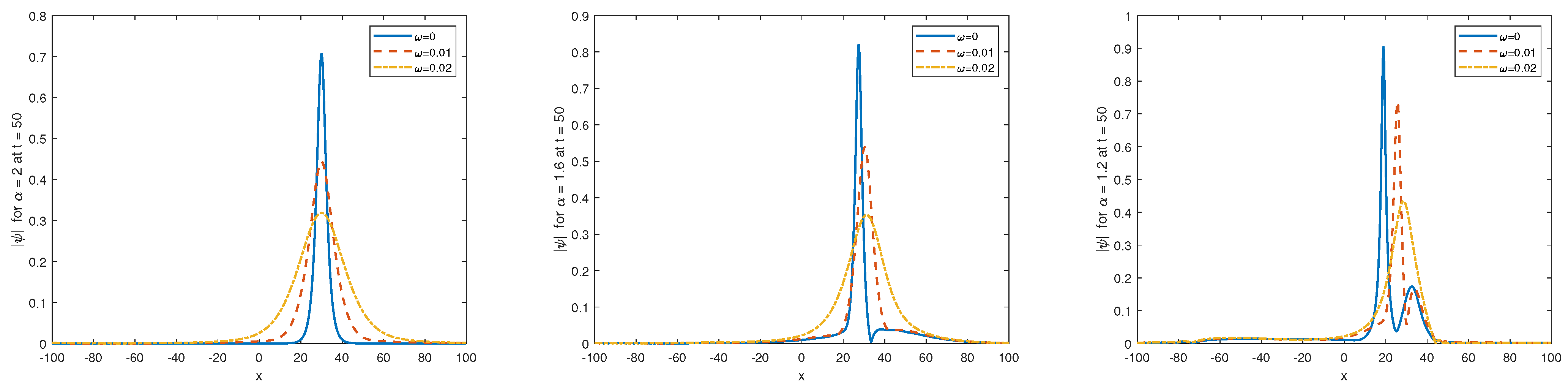
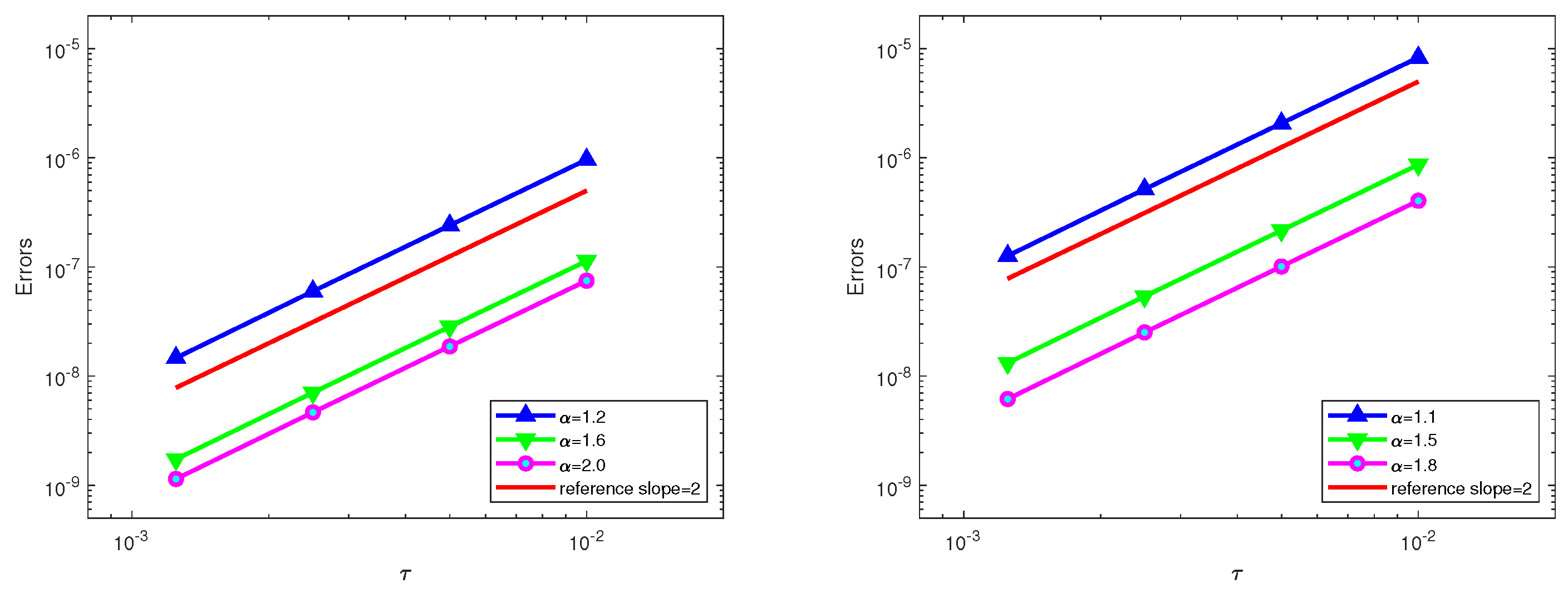
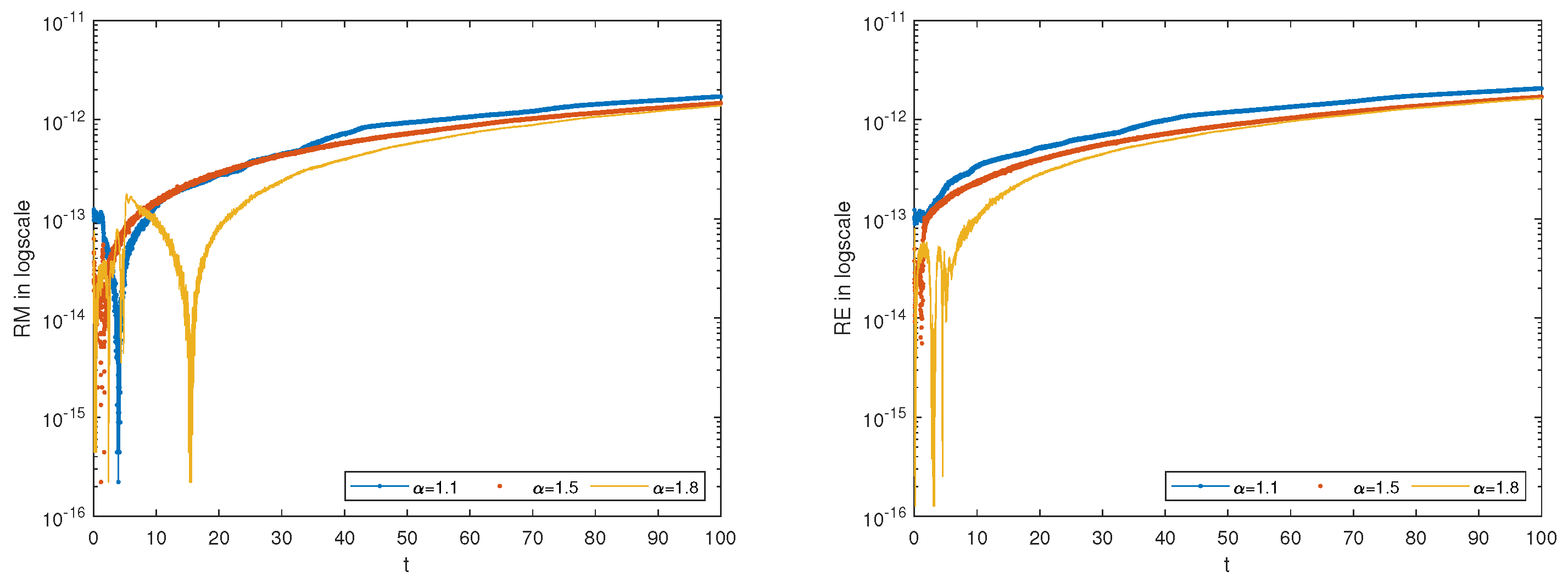
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Laskin, N. Fractional Schrödinger equation. Phys. Rev. E 2002, 66, 056108. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Xu, M. Some physical applications of fractional Schrödinger equation. J. Math. Phys. 2006, 47, 082104. [Google Scholar] [CrossRef]
- Longhi, S. Fractional Schrödinger equation in optics. Opt. Lett. 2015, 40, 1117–1120. [Google Scholar] [CrossRef]
- Zhang, L.; Li, C.; Zhong, H.; Xu, C.; Lei, D.; Li, Y.; Fan, D. Propagation dynamics of super-Gaussian beams in fractional Schrödinger equation: From linear to nonlinear regimes. Opt. Express. 2016, 24, 14406–14418. [Google Scholar] [CrossRef]
- Ionescu, A.D.; Pusateri, F. Nonlinear fractional Schrödinger equations in one dimension. J. Funct. Anal. 2014, 266, 139–176. [Google Scholar] [CrossRef]
- Pozrikidis, C. The Fractional Laplacian; Chapman and Hall/CRC: New York, NY, USA, 2016. [Google Scholar]
- Tsutsumi, M. Nonexistence of global solutions to the Cauchy problem for the damped nonlinear Schrödinger equations. SIAM J. Math. Anal. 1984, 15, 357–366. [Google Scholar] [CrossRef]
- Fu, H.; Zhou, W.; Qian, X.; Song, S.H.; Zhang, L.Y. Conformal structure-preserving method for damped nonlinear Schrödinger equation. Chin. Phys. B 2016, 25, 110201. [Google Scholar] [CrossRef]
- Fu, H.; Zhou, W.; Qian, X.; Song, S. Novel conformal structure-preserving algorithms for coupled damped nonlinear Schrödinger system. Adv. Appl. Math. Mech. 2017, 9, 1383–1403. [Google Scholar] [CrossRef]
- Jiang, C.; Cai, W.; Wang, Y. Optimal error estimate of a conformal Fourier pseduo-spectral method for the damped nonlinear Schrödinger equation. Numer. Methods Partial. Differ. Equ. 2018, 34, 1422–1454. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J.; Guo, B. Two completely explicit and unconditionally convergent Fourier pseudo-spectral methods for solving the nonlinear Schrödinger equation. J. Comput. Phys. 2020, 404, 109116. [Google Scholar] [CrossRef]
- Tarek, S. Remarks on damped fractional Schrödinger equation with pure power nonlinearitys. J. Math. Phys. 2015, 56, 061502. [Google Scholar]
- Liang, J.; Song, S.; Zhou, W.; Fu, H. Analysis of the damped nonlinear space-fractional schrödinger equation. Appl. Math. Comput. 2018, 320, 495–511. [Google Scholar] [CrossRef]
- Fu, Y.; Song, Y.; Wang, Y. Maximum-norm error analysis of a conservative scheme for the damped nonlinear fractional Schrödinger equation. Math. Comput. Simul. 2019, 166, 206–223. [Google Scholar] [CrossRef]
- Wu, L.; Ma, Q.; Ding, X. Conformal structure-preserving method for two-dimensional damped nonlinear fractional Schrödinger equation. Numer. Methods Partial Differ. Equ. 2023, 39, 3195–3221. [Google Scholar] [CrossRef]
- Ding, H.; Qu, H.; Yi, Q. Construction and analysis of structure-preserving numerical algorithm for two-dimensional damped nonlinear space fractional Schrödinger equation. J. Sci. Comput. 2024, 99, 60. [Google Scholar] [CrossRef]
- Fei, M.; Huang, C.; Wang, P. Error estimates of structure-preserving Fourier pseudospectral methods for the fractional Schrödinger equation. Numer. Methods Partial Differ. Equ. 2019, 36, 369–393. [Google Scholar] [CrossRef]
- Wang, Y.; Mei, L.; Bu, L. Split-step spectral Galerkin method for the two-dimensional nonlinear space-fractional Schrödinger equation. Appl. Numer. Math. 2019, 136, 257–278. [Google Scholar] [CrossRef]
- Zou, G.; Wang, B.; Sheu, T. On a conservative Fourier spectral Galerkin method for cubic nonlinear Schrödinger equation with fractional Laplacian. Math. Comput. Simul. 2020, 168, 122–134. [Google Scholar] [CrossRef]
- Abdolabadi, F.; Zakeri, A.; Amiraslani, A. A split-step Fourier pseudo-spectral method for solving the space fractional coupled nonlinear Schrödinger equations. Commun. Nonlinear Sci. Numer. Simul. 2023, 120, 107150. [Google Scholar] [CrossRef]
- Lawson, J. Generalized Runge-Kutta processes for stable systems with large Lipschitz constants. SIAM J. Numer. Anal. 2006, 4, 372–380. [Google Scholar] [CrossRef]
- Wang, P.; Huang, C. Structure-preserving numerical methods for the fractional Schrödinger equation. Appl. Numer. Math. 2018, 129, 137–158. [Google Scholar] [CrossRef]
- Li, C. Numerical Analysis for Some Fractional Anomalous Diffusion Equations. Ph.D. Thesis, Lanzhou University, Lanzhou, China, 2009. [Google Scholar]
- Wang, J.; Xiao, A. Conservative Fourier spectral method and numerical investigation of space fractional Klein-Gordon-Schrödinger equations. Appl. Math. Comput. 2019, 350, 348–365. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T.; Wang, L. Spectral Methods: Algorithms, Analysis and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Noorizadegan, A.; Chen, C.; Young, D.; Chen, C. Effective condition number for the selection of the RBF shape parameter with the fictitious point method. Appl. Numer. Math. 2022, 178, 280–295. [Google Scholar] [CrossRef]
- Tian, J.; Ding, H. Improved high-order difference scheme for the conservation of mass and energy in the two-dimensional spatial fractional Schrödinger equation. Fractal Fract. 2025, 9, 280. [Google Scholar] [CrossRef]





| 4.3356 | – | 9.5038 | – | 8.4776 | – | |
| 1.0957 | 1.9843 | 2.3742 | 2.0011 | 2.1081 | 2.0077 | |
| 2.7467 | 1.9962 | 5.9340 | 2.0003 | 5.2631 | 2.0019 | |
| 6.8712 | 1.9990 | 1.4834 | 2.0001 | 1.3153 | 2.0005 | |
| 3.1939 | – | 7.7686 | – | 8.4607 | – | |
| 8.0681 | 1.9850 | 1.9399 | 2.0017 | 2.1034 | 2.0080 | |
| 2.0222 | 1.9963 | 4.8479 | 2.0005 | 5.2514 | 2.0020 | |
| 5.0587 | 1.9991 | 1.2119 | 2.0001 | 1.3124 | 2.0005 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Liu, X.; Wang, Z. An Efficient Structure-Preserving Scheme for the Fractional Damped Nonlinear Schrödinger System. Fractal Fract. 2025, 9, 328. https://doi.org/10.3390/fractalfract9050328
Shi Y, Liu X, Wang Z. An Efficient Structure-Preserving Scheme for the Fractional Damped Nonlinear Schrödinger System. Fractal and Fractional. 2025; 9(5):328. https://doi.org/10.3390/fractalfract9050328
Chicago/Turabian StyleShi, Yao, Xiaozhen Liu, and Zhenyu Wang. 2025. "An Efficient Structure-Preserving Scheme for the Fractional Damped Nonlinear Schrödinger System" Fractal and Fractional 9, no. 5: 328. https://doi.org/10.3390/fractalfract9050328
APA StyleShi, Y., Liu, X., & Wang, Z. (2025). An Efficient Structure-Preserving Scheme for the Fractional Damped Nonlinear Schrödinger System. Fractal and Fractional, 9(5), 328. https://doi.org/10.3390/fractalfract9050328






