Abstract
Human error remains a significant concern in the medical field, particularly in anaesthesia, where even minor miscalculations can jeopardise patient safety. To address these challenges, the integration of automated control systems has emerged as a viable solution. Most existing control algorithms are tuned using a nominal patient model and inter-patient variability is tackled by incorporating robustness in the controller design. A personalised approach is, however, desirable. In this paper, a hybrid control framework that combines fractional-order control with a model-reference adaptive control (MRAC) approach is proposed as a solution for personalised control of the bispectral index (BIS). The system is designed to meet stringent performance requirements while ensuring stability and robustness. Comparative result with a non-adaptive fractional order controller are presented to demonstrate the efficiency of the proposed adaptive strategy. Simulation results demonstrate promising outcomes, both with respect to the selected criteria and in alignment with the anticipated future developments.
1. Introduction
The modern healthcare sector faces challenging demands to reduce medical errors, optimise resource use, ensure quality of care, and improve workflow efficiency. As one of the guiding principles of medical practice, the concern for patient safety underscores the importance of adapting to technological advances and evolving regulatory standards [1].
1.1. Medical Basis
Medical errors are generally categorised into system errors, equipment errors, and human errors. Among these, human errors involve unintentional deviations from established safety practices, whether through actions, decisions, or omissions, that can lead to adverse outcomes or compromise patient safety [2]. Akin to other fields but more pronounced in medicine, human errors are often influenced by factors such as knowledge, experience, haste, fatigue, stress, or illness, making them a critical concern in healthcare [3]. High workloads and time constraints in healthcare can hinder the adherence to patient safety protocols. The drive for efficiency often clashes with the need for thorough attention to detail, increasing the risk of errors or oversights. Moreover, the pressure to meet deadlines fosters a high-stress work environment, which may impact the well-being and decision-making abilities of healthcare professionals [1,4]. Human factors are estimated to contribute to approximately 87% of patient safety incidents in monitored medical settings [5,6].
The observed trend of patient safety concerns extends to the branch of anaesthesia, especially general anaesthesia, which is more predisposed to side effects and risks. While advancements in monitoring and protocols have significantly improved safety, anaesthesia still necessitates thorough risk assessment and management. Compared to many other medical specialities, anaesthesia involves a unique set of challenges, including the potential for adverse events related to drug administration and physiological responses. Safe practice requires a deep understanding of medical diagnosis, pharmacology, anatomy, and physiology, combined with exceptional technical skills to effectively administer anaesthetic agents and respond to complications in real time [5,7,8]. Patient safety in anaesthesia relies on the intricate interaction between a skilled practitioner and the equipment used. Equipment-related issues account for approximately 14–30% of intraoperative complications, with anaesthetic delivery systems being the most frequent source of problems. While pure equipment failure is less common, the improper use of equipment is a significant contributor. Human error is linked to about 90% of equipment-related failures, while equipment malfunctions constitute roughly 15% of preventable incidents, and 82% of all anaesthesia procedure incidents involve human error [8]. Targeted case studies focusing on narrower scopes also indicate considerable figures, as human factors are responsible for nearly 42% of reported errors [3,7]. Although safety measures have improved, critical incidents and adverse events persist, still posing a substantial risk to patient well-being [9]. Controllability (the perception of being in control) and miscommunication among operating room staff affect the reporting of issues, indicating a risk of under-reporting. Human error is linked to about 90% of equipment-related failures, while equipment malfunctions constitute roughly 15% of preventable incidents, and 82% of all anaesthesia procedure incidents involve human error [9]. The majority of incidents involving high-end medical machines are attributed to mishandling and misinterpretation by medical personnel rather than to flaws in the machines’ design or functionality [10,11].
Before exploring the utility of automated systems in addressing these challenges, it is important to first review the key elements of anaesthesia. The concept of anaesthesia entails the use of specific drugs during surgical procedures. The anaesthesia paradigm includes hypnosis, neuromuscular blockade, and analgesia to induce unconsciousness, impede movement, and reduce pain perception during surgical procedures, respectively, [12]. Three phases make up the anaesthetic procedure: the pre-anaesthetic, anaesthetic, and post-anaesthetic phases. The pre-anaesthetic phase is devoted to gathering important patient information, like the patient’s surgical and medical history. The type of surgery and pre-existing medical conditions (comorbidities) are also factors in need of consideration. However, laboratory testing is usually not part of the routine for asymptomatic patients with low-risk surgeries, and in these common scenarios, complacency can take root. Overdosing can have long-term negative effects and lengthen recovery, whereas underdosing can leave a patient traumatised and paralysed, causing anxiety [13]. The essential study of patients’ unique responses to anaesthetic drugs can be conducted through the concepts of pharmacokinetics (PK) and pharmacodynamics (PD). Pharmacokinetics focuses on the body’s absorption, distribution, metabolism, and excretion of a drug, while pharmacodynamics examines how the drug interacts with the body, including its biochemical and physiological effects at the site of action. Together, PK and PD inform the appropriate use of medications, guiding infusion pumps to administer drugs effectively and safely for patients [14].
1.2. Automation in Anaesthesia
Practical robots in anaesthesia can be categorised into three types: pharmacological robots (closed-loop systems for individualised anaesthetic drug titration), mechanical robots (automate tasks requiring high manual dexterity), and cognitive robots (decision support systems identifying critical clinical situations needing human intervention). Pharmacological robots precisely titrate anaesthetic drugs and control relevant biological parameters, ensuring optimal homeostasis during general anaesthesia and, recently, even local anaesthesia cases (which entail numbing an area of a body while keeping the patient conscious) [15]. Current studies suggest that autonomous systems are more effective in regulating haemodynamic parameters in operating rooms compared to their traditional counterparts [4,16]. By dynamically adjusting drug dosages in real-time, their goal is to attain and sustain desired clinical outcomes.
One primary objective of integrating pharmacological robots in clinical settings is to reduce complications and mortality rates associated with anaesthesia procedures [17]. These robots alleviate the workload of clinicians by reducing the mental strain required for constant monitoring of vital signs and titration values, as well as the repetitive task of adjusting drug dosages. As a result, clinicians can dedicate their attention to more complex tasks that necessitate human expertise, including pivotal decision making and interpersonal interactions. This underscores the potential of robotics to enhance patient safety and the effectiveness of medical procedures, as well as circumvent human bias and errors [17]. Automation in the dispensing process primarily reduces errors related to the dispensing and storage of medications, yet it does not address other types of errors, such as prescribing errors, which occur prior to the dispensing phase. Additional automated solutions, such as computerised patient records, electronic prescriptions, computerised physician order entry (CPOE), and barcode (BC) verification are needed to guarantee the security of the entire medication-use process [18].
Automating anaesthesia delivery through PD monitoring enhances medical oversight by continuously measuring physiological variables. This approach enables safer and more consistent control over the patient’s anaesthetic state throughout surgical procedures. Figure 1 displays an example of how a closed-loop system for automated drug delivery would be structured.
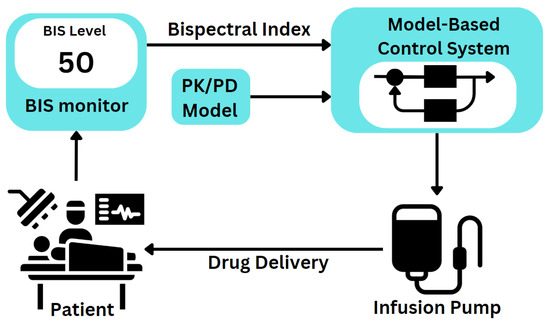
Figure 1.
Automated closed-loop system for anaesthesia management in clinical practice.
Designing closed-loop anaesthesia systems necessitates personalised PK-PD models. Propofol is a commonly chosen sedative drug paired with target-controlled infusion (TCI) systems due to its well-established models for achieving hypnosis. However, remifentanil, isoflurane, and atracurium models are also viable options in specific contexts, contributing to the reliability of these systems [19].
Numerous control strategies for closed-loop anaesthesia have been developed and evaluated; the following examples serve as representative approaches alongside their reported performance characteristics. Traditional proportional–integral–derivative (PID) controllers such as [20,21] are documented to ensure rapid induction, minimal overshoot, and effective disturbance rejection during the maintenance phase. Model predictive control (MPC) enables rapid BIS response with minimal oscillations across diverse patient profiles. The Smith predictor with an enhanced filter for nonlinear hypnosis control further reduces the total propofol required to sustain adequate anaesthesia depth [22]. Adaptive control (through online estimation and update of parameters integrated in models or control laws, or gain scheduling techniques) proves robust to interpatient variations and anaesthesia time delays [23]. However, the implemented method exhibits slow convergence due to the trade-off between tracking error speed and transient performance [23]. Fuzzy-logic control and merged schemes may effectively enhance the robustness and handling of inter-patient variability but can be time-consuming when more parameters are included due to single-input, single-output regression nature [24]. Fractional order control (FO) specifically tuned for induction-phase and maintenance-phase specifications has also demonstrated satisfactory outcomes [25]. Intelligent control methods utilising diverse neural network architectures have been developed and evaluated for their reliability and feasibility, albeit with anticipated limitations [26,27]. These approaches have been validated both in simulations and clinical studies. Table 1 displays a comparative overview of the discussed control strategies, highlighting their respective benefits, limitations, and potential application domains.

Table 1.
Comparative summary of control strategies for BIS regulation in anaesthesia.
The significance of stability control in anaesthesia delivery cannot be overstated, considering its vital role in ensuring patient safety and successful surgical results. Any proposed control strategy must adhere to stability requirements. For the purpose of testing additional control algorithms, extensive collections of virtual subject models and control algorithms have been developed, establishing a simulation platform that replicates real-world anaesthesia scenarios [19,28].
Among the approaches discussed, this paper proposes a potential model-based adaptive control (MRAC) strategy in combination with a fractional-order (FO) controller, with the goal of ascertaining their viability in the context of anaesthesia regulation. This selection is supported by the limited availability of research addressing this specific control structure in anaesthesia applications. The novelty of the current research consists of the following:
- The merging fractional order controllers and adaptive schemes for BIS regulation.
- The design, testing and validation of a novel adaptive fractional order PI controller.
- Stability and robustness analyses of the novel controller.
2. Materials and Methods
2.1. Process Model
Understanding the complexities of anaesthesia requires careful consideration of the physiological responses and pharmacological interactions involved in achieving optimal patient outcomes. Before any control strategy is considered, the relevant models must be identified based on the behaviour of the target system. Multiple clinical variables are involved in measuring the depth of anaesthesia, but for the purposes of this paper, the focus will remain on only the BIS signal as a hypnosis indicator. Several factors contribute to mismatches between the required and delivered amounts of anaesthesia, including the intensity of surgical stimuli, the haemodynamic effects of medications, equipment failures, and dosing errors.
In the open source patient simulation provided by [29], propofol, remifentanil, and atracurium are employed to manage hypnosis, analgesia, and neuromuscular blockade, respectively. Thanks to their quick onset and recovery times, these medications are appropriate for computerised closed-loop control systems. Bispectral index (BIS), Ramsay agitation score (RAAS), and electromyogram (EMG) are used to track their effects. This simulator serves as the basis of the modelling. The 2021 study [29] acknowledges collaborative efforts with Ghent University Hospital (Belgium) and University Medical Centre Groningen (The Netherlands) in developing a comprehensive database of patient profiles aimed at closely reflecting real-world scenarios. This database encompasses 24 patients with a variety of characteristics, integrating PK models correlating propofol to BIS, biometric data models, and PD model sensitivity values. These elements collectively improve the accuracy and realism of anaesthesia modelling.
Among the parameters that can be controlled and monitored in the context of anaesthesia, this paper aims to employ the BIS signal as the main biological indicator of the awareness level of patients. Control of consciousness holds significant importance in the comfort, safety, and recovery of patients under anaesthesia, underscoring the significance of research [14]. While research extends from single-input–single-output (SISO) to multiple-input–multiple-output (MIMO) closed-loop systems [4], the current manuscript centres on the particular scenario of a single closed-loop control system for BIS regulation. This choice is made deliberately in order to create an isolated case, examining the specific performance and characteristics.
Propofol’s pharmacokinetics are represented by a three-compartment model, characterised by a nonlinear sigmoidal response to dose. Factors such as age, sex, height, weight, body mass index (BMI), lean body mass (LBM) and other variables influence these models. In pharmacology, the Hill function is frequently employed to describe the dose–response relationship, including the effect of propofol on parameters such as depth of anaesthesia [29]. This function provides a robust framework for modelling how drug concentration correlates with pharmacodynamic effects. Similarly, the pharmacokinetics of remifentanil are modelled with parameters influenced by LBM and age. These models incorporate different compartment volumes and clearance rates, each defined by specific equations tailored to the characteristics of each drug [29]. By integrating these detailed pharmacokinetic models, researchers can simulate and predict how propofol and remifentanil will behave in diverse patient populations, enhancing the accuracy of anaesthesia management strategies in clinical practice.
By employing the previously outlined simulator, a recent study [30] was able to determine decoupled patient models for four target biological indicators: BIS, RASS, mean arterial pressure (MAP), and cardiac output (CO), respectively. The transfer function in (1) identifies the relationship between administered propofol (in correlation to remifentanil and dopamine) and the output signal BIS for the case of a nominal patient, which is descriptive for the whole sample of patients.
BIS-controlled systems estimate electroencephalogram (EEG) states using epoch-based moving windows, resulting in a usual time signal processing delay between 10 and 30 s in the BIS signal [29,31]. In the model, this aspect is represented by the time delay = 20 [s], (1).
In control theory, time delays represent the lag between the input signal and the system’s output. They can significantly affect system stability and performance, especially in closed-loop systems where delays can lead to oscillations or instability. A number of methods, including the Padè approximation (used by [32]), lead compensation, Smith predictor (also used in [22,25]), and digital signal processing (DSP) methods, can be used to address time delays in transfer functions. Each approach has its advantages and is chosen based on the specific attributes of the system and the target performance criteria. To address the time delay in the chosen process model, this paper uses the Padè approximation. Padè approximation in particular represents the time delay as a rational function, which is a method to approximate the delay with a series of terms [33].
The second-order Padè approximation of the process transfer function, using the pade() function provided by MATLAB®, is presented in (2):
(REVISIT) This is the Padè approximation order that is utilised for the majority of the design phase and for the reference model inside the MRAC scheme.
To simulate performance according to practical cases, the system must demonstrate the ability to reject input disturbances (introduced after the settling of the signal at the 400 s mark) and return to the target value within the testing period of 1350 s. The closed-loop system should attain either full or partial asymptotic stability or ultimate boundedness despite system uncertainty, disturbances, and nonlinearity [17]. The output signal should present no stationary error and should hold the set point with no oscillations [34]. The anaesthetic should gradually and smoothly reduce the BIS level from 100 (the percentage value representing an awake state for the patient) to the target reference of 50 (indicating that adequate general anaesthesia prevents awareness under the hypnotic effect) to ensure patient safety [10]. Consequently, the control behaviour should not be overly aggressive to avoid rapid adjustments, and the settling time for the closed-loop output should be approximately 5–6 min (300–360 s). During the maintenance phase, it is crucial to keep the BIS signal within the range of 40–60% (maximal values for undershoot and overshoot) by promptly addressing any disruptions in output, such as surgical stimuli and anaesthesiologist-delivered boluses [22]. These compose the base specifications to ensure that the anaesthetic control system maintains a stable and safe level of anaesthesia throughout the surgical procedure, minimising the risk of awareness of the patient during surgery and optimising patient outcomes. Implementing these strategies effectively has the potential to contribute to advancing the precision and reliability of anaesthesia control systems in clinical practice.
2.2. Fractional Order Controller
For over 70 years, proportional–integral–derivative (PID) controllers have been integral components of control systems. PID controllers are widely valued for their straightforwardness and efficacy in diverse applications [35]. These controllers continually compute an error by comparing a desired setpoint with the measured process variable, utilising proportional, integral, and derivative terms to modify their output. These three distinct components modulate the controller’s response to ensure the process variable achieves and maintains the setpoint with minimal oscillation and steady-state error. The functions of the PID components are as follows:
- Proportional term (P): generates an output directly proportional to the current error, providing immediate correction through the P controller.
- Integral term (I): accumulates past errors over time to address persistent biases and achieve the setpoint.
- Derivative term (D): responds to the change rate of the error, anticipating future deviations to minimise overshoot and oscillations.
These elements work together to create a flexible and effective control strategy that can keep the system operating and stable even in the face of disturbances and shifting circumstances. The ideal PID controller can be formulated in the time domain as in Equation (3), where is the control output, acts as the proportional gain, as the integral gain, is the derivative gain, and ultimately is the time-varying error.
Once converted into the Laplace domain, the PID controller can be represented as shown in Equation (4), with s as the complex frequency variable in the Laplace transform.
From the previous form, the proportional gain constant () is still present. Stronger responses to errors may result from higher values of (), which also carries the risk of causing instability [36].
These parameters are crucial as they directly influence the controller’s performance, affecting how quickly and accurately the system responds to changes and disturbances. The choice and tuning of these parameters depend on the specific application and the desired balance between responsiveness and stability [36].
Traditional control systems typically restrict the orders of differentiation and integration to integer values. However, fractional order (FO) control extends classical integer-order control to include fractional values, offering greater flexibility and enhanced performance in certain applications. FO-PID control methods have gained popularity in the biomedical field, though further research is needed to combine FO methodology with other control structures [22].
In order to create controllers with non-integer order dynamics, fractional order control makes use of the principles of fractional calculus. Unlike traditional integer-order controllers, such as PID controllers, fractional-order controllers provide additional flexibility in managing complex dynamics and enhancing system performance. They can offer superior transient response, robustness to parameter variations, and improved tracking accuracy. Systems that display non-ideal behaviours, such as delay, nonlinearity, or memory effects, benefit greatly from fractional order control [37].
A challenge in implementing FO controllers lies in the infinite temporal scope, which implies a need for unlimited memory. Within a suitable frequency range, approximating fractional order systems with finite integer order transfer functions can solve this issue. The regular expression of a FO-PID controller follows the formula:
In the classical PID form, the and factors would be both equal to 1; however, the FO-PID imposes real values for the two factors. It must be noted that the parameters for the controller, , , , and can each be calculated according to specified performance criteria. In order to cover for the five unknown parameters of the FO-PID controller, the potential choices for the performance criteria are given as follows:
- An imposed gain crossover frequency .
- A phase margin .
- A condition for robustness against gain variations.
- High-frequency noise rejection.
- A measure for good output disturbance rejection.
Between the unknown parameters and the performance criteria, independent equations can be determined. Optimisation algorithms or graphical methods may be used to solve these equations. After arriving at the values of the control parameters through experimentation, the controller is finally computed and then added in the closed loop accordingly.
In addition, for practical reasons, the Oustaloup recursive approximation (ORA) can be employed as a continuous time approximation. ORA can facilitate turning the fractional order element into an approximated higher-order rational system. This approach has the benefit of enhancing the design of controllers with non-integer order dynamics by providing greater flexibility, stability, adaptability, and particularly robustness [38]. The standard formula for ORA (6) presents its key parameters: the gain factor K, the order of approximation N, the range of frequency of interest defined between the lower bound and higher bound , and the fractional order to be approximated [38]. The optimal values for these parameters are determined through trial and error.
Given that achieving an exceptionally small settling time is not a primary requirement, the derivative (D) component can be omitted. For this specific application, a proportional–integral (PI) controller is deemed sufficient to effectively meet the performance criteria. Tuning fractional order controllers for SISO plants involves finding the three values required for the FO-PI controller. The FO-PI controller takes the form (7).
Its key parameters, , and , can be calculated once specific performance requirements are set. Since there are three unknown parameters, it suffices to set three performance requirements: an imposed gain crossover frequency , an imposed phase margin, , and a condition for robustness against gain variations.
The frequency response of the patient, as described in (1), can be rewritten as (8), highlighting the real K and imaginary L components of the system’s frequency domain response.
To meet the FO-PI controller’s performance requirements, three conditions are defined. The robustness condition (10) ensures that the phase derivative of the open-loop system is zero. This allows the determination of . The phase margin condition (9) imposes that the open-loop phase equals , which is used to calculate the integral gain . Finally, the gain frequency condition (11) requires the modulus of the open-loop system to be unity at frequency , enabling the calculation of the proportional gain [37].
The solution to (10) for the parameter requires the consideration of a graphical technique. The mentioned performance criteria are set the same. Based on (10), is computed as a function of . A graphical representation method is applied using the result , the intersection of the plots ultimately leads to the solution for the systems of Equations (9)–(11). The last parameter can be computed according to (12).
The fractional order integrator is split into an integer order component and a fractional order component in order to prevent a sluggish response. To implement the FO-PI controller in (7), the following estimation is used:
The term has been computed using the ORA method as indicated in (6). In this case, the ORA is applied with the parameters chosen as , , , , and .
2.3. Model Reference Adaptive Control
Adaptive control, predominantly used in nonlinear systems applications, addresses the challenge of managing systems with inherent uncertainties, such as internal changes or external disturbances. Adaptive controllers extend linear feedback integrators by generating output through integrating nonlinear functions of tracking errors within the system. To handle systems with uncertainties brought on by internal changes or external disturbances, adaptive control uses nonlinear techniques. To manage uncertainty, these systems dynamically modify control parameters, such as control gains, in response to plant input. The adjustment mechanism, which is usually nonlinear and complex to design and analyse, is referred to as the adaptive law. These adjustable parameters are known as adaptive parameters. Traditional linear control design (for example, techniques such as Bode plot analysis, phase and gain margins, eigenvalue analysis, etc.) cannot be applied to these nonlinear systems [39].
Initially developed for high-performance aircraft with sophisticated autopilots, adaptive control dates back to the 1950s. Due to the complexities of nonlinearity in adaptive control, gain-scheduling control, which uses classical techniques to schedule control gains based on operating conditions, became more popular [39,40]. In the 1960s, modern control theory and Lyapunov stability theory propelled adaptive control forward, followed by the 1970s, which saw the establishment of Lyapunov stability theory as a foundation for MRAC, leading to more effective schemes. By the 1980s, however, it was evident that small disturbances or unmodelled dynamics could cause adaptive control to become unstable, despite utilising the Lyapunov stability criterion. This demonstrated how the accuracy of system modelling affects model-reference adaptive control and how the real system and its model are not the same [39,40].
Innovative algorithms such as the (sigma) modification and the e modification have been developed to enhance robustness. These led to the emergence of a new category of adaptive control systems known as "robust adaptive control [39].
Adaptive control can be labelled as either direct or indirect adaptive control, yet there is also a growing trend towards hybrid adaptive control architectures that integrate both approaches, often termed as hybrid, combined, or composite direct–indirect adaptive control. Other classifications encompass state feedback (for state tracking) or output feedback (for output tracking), suitable for various system types, including linear or nonlinear, continuous or discrete-time, time-invariant or time-varying, deterministic or stochastic, with some exceptions noted [41].
As a specific approach to adaptive control theory, MRAC employs a reference model that defines the ideal behaviour of the controlled process, aligning with application specifications. The adaptive scheme consists of two sections: the simple negative feedback loop of the nominal controller and the real plant and the adaptive section, depending on the reference model (its own isolated control loop) as part of the adjustment mechanism. This loop structure enables MRAC to continually refine its control parameters based on real-time feedback, ensuring robust performance in dynamic environments [42].
A standard block diagram of a MRAC system is illustrated in Figure 2, showcasing its basic components. The signal is the output of the reference model, while represents the output of the plant.
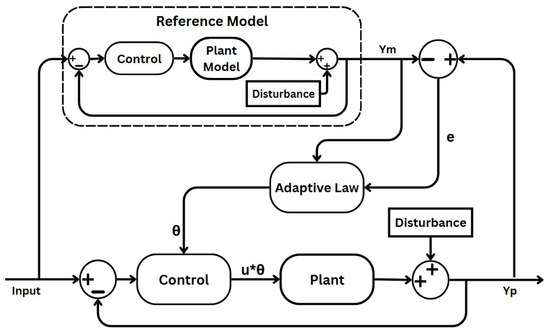
Figure 2.
Block diagram of an MRAC scheme.
The central concept of MRAC strategies is to guarantee that the system’s behaviour aligns with a predefined model, regardless of uncertainties and changes in system dynamics. The key parts of a MRAC scheme are given as follows [39,40]:
- Uncertain plant: adaptive control addresses uncertainty in both linear and nonlinear plants, which can manifest as either structured uncertainty (parametric uncertainty) or unstructured uncertainty (where neither parameters nor functional characteristics are known). In this paper’s case, the plant process is the depth of anaesthesia induced through anaesthetic drugs and measured through the BIS signal. Patient variability and unexpected behaviour generate the uncertain aspects of the process, which the MRAC system must compensate for.
- Reference model: defines the desired response of the MRAC system to a command input, serving as a command shaping filter to achieve the precise command-following behaviour [39,40]. In adaptive control, whether formulated for command following or tracking, the adaptation process relies on minimising the tracking error between the system output and the designated reference model. Designing the reference model thoughtfully is crucial for ensuring accurate tracking. While traditionally structured as a linear time-invariant (LTI) model, nonlinear variants can also be utilised, albeit with added complexity. In this specific case, the reference model reflects the ideal BIS response specific to a given surgical context.
- Controller: ensures stable system performance under nominal conditions, serving as a baseline controller. As shown in Figure 2, the controller in the primary loop generates a control signal by comparing the output of the uncertain plant with that of the reference model. This signal is further influenced by the adaptive law component, mediated through the intermediary output . In the MRAC system, adjustments in propofol infusion rate are made to minimise the discrepancy between the BIS and the desired reference model output. This component will be implemented using the designed FO-PI controller.
- Adaptation mechanism: dictates in all adaptive schemes how adaptive parameters adjust to minimise tracking errors. In certain schemes, this aspect is crucially influencing stability via Lyapunov stability theory. Adaptive laws vary in complexity and robustness, requiring careful parameter tuning to balance performance and stability in adaptive control systems.
One fundamental approach for the adjustment mechanism in MRAC theory is the MIT rule, named after the Massachusetts Institute of Technology, where it was developed. The MIT rule facilitates this by defining an adaptation mechanism that modifies the controller parameters based on the error signal. By applying MRAC with the MIT rule, the system can dynamically adapt to the patient’s response to anaesthesia, accounting for individual variations and maintaining optimal anaesthesia levels throughout the procedure [43]. The adjustment law is derived to minimise a cost function J, typically the squared error between the plant output and the reference model output . This formulation enables the controller to iteratively reduce deviation from the desired behaviour. The error and the cost function are presented in (14) and (15), respectively.
The adjustable parameter in the adaptive law is updated according to the negative gradient of a performance index J, often representing the squared discrepancy between the plant output and the reference model output. Additionally, the adaptation gain influences the rate at which is adjusted. The error e and the model reference signal both play critical roles in this adjustment mechanism [39,42]. The term , called sensitivity derivative, represents the error changing in sync with the change in the parameter, adding a layer of feedback to guide the adaptation more precisely.
The MIT rule for updating can be represented as:
The above equation indicates that the rate of change of the parameter is proportional to the product of the error signal and the reference model output , scaled by the adaptation gain . Convergence in adaptive systems refers to the system’s ability to minimise the tracking error to zero, ensuring that the plant output follows the reference model despite uncertainties. The adaptation gain influences the convergence rate. Higher values speed up adaptation but may cause instability, while lower values improve stability at the cost of a slower response. Effective convergence balances speed, accuracy, and robustness, which is critical in dynamic settings like anaesthesia [44].
In the frequency domain, the relationship (16) can be rewritten as (17). In this formula, represents the Laplace transform of the parameter , allowing for frequency-domain analysis and control design.
The reference model functions on an unaltered control signal, uninfluenced by the adaptive mechanism. The primary control signal u is designed in accordance with the reference model. The actual control signal is then obtained by multiplying this control signal u with the adaptive parameter [39,43]:
The output of the MRAC closed-loop is given by (19):
In the given setup, represents the plant/process transfer function. The equation demonstrates how the control signal , influenced by the adaptive parameter , interacts with the plant’s transfer function to achieve the desired model reference behaviour.
2.4. Disturbance Signal
Before surgical procedures, anaesthesiologists adjust anaesthetic doses to meet specific goals, like inducing amnesia, unconsciousness, and immobility, anticipating increased requirements due to surgical stimuli. A surgical stimulus refers to a specific type of sensory input intentionally applied during surgical procedures. EEG monitoring is used to gauge how anaesthetics indirectly impact brain function. During surgery, tissue invasion triggers nociception, which anaesthesia suppresses. General anaesthesia involves a dynamic interplay between the nociceptive response and its inhibition, which can activate the autonomic nervous system [45,46].
The desired MRAC scheme must maintain stability through disturbance rejection (surgical stimulation) and other interventions. The suggested control structure must be tested by modelling and introducing a surgical stimulus disturbance, as EEG-based indices (such as BIS) are insufficient for indicating the degree of analgesia without a continuous nociception stimulus. Thus, it is important to employ an accurate simulated model of the surgical stimulus [28]. For this purpose, the simulator created by [29] is chosen. The simulator operates using disturbance models specifically initialised for surgical procedures. The disturbance signal, tailored for surgical actions, serves as the stimulus that passes through the nociceptor pathway. The disturbance simulation attempts to capture the steps of the surgical protocol: intubation, surgical incision followed by a pause for awaiting pathology results, a sudden stimulus after a low-stimulation period, continuous surgical activity, brief intense stimulation during surgery, and finally, the tapering of stimulation during closure [29]. Such events increase the BIS due to pain from interventions which trigger nociceptor responses. Additionally, the disturbance profile includes a bolus of propofol administered by the anaesthesiologist in anticipation of a surgical cut, thus pre-emptively decreasing the BIS level [29]. The final isolated disturbance signal is presented in Figure 3, with amplitude values in the range of [−4.15, 4.15].
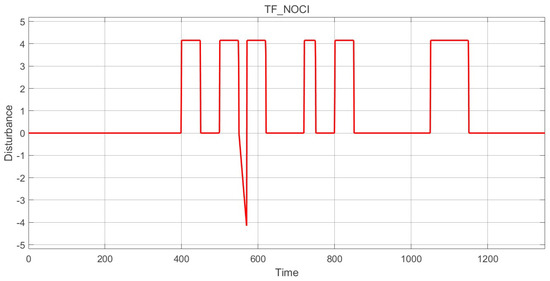
Figure 3.
Surgical stimuli: disturbance signal.
3. Results
3.1. FO-PI Controller
The implementation medium for this paper’s application was MATLAB®, version R2023b, for designing the required controllers, and Simulink® for the simulation of the resulting MRAC schemes.
During the fractional order (FO) control design method, the second-order Padè approximation is selected for the process model. The algorithm’s implementation for designing the controller begins with calculating the process transfer function’s phase and magnitude. The value of cutting frequency = 0.013 [25] is considered, and three values for the phase margin are compared to determine the best set of conditions for the FO-PI controller.
With the controller parameters computed using the formulas presented in Section 2.2, the FO-PI controller and subsequently the closed loop are ascertained. Three phase margins (, or ) are proposed, and after following the design steps detailed previously, each results in their respective control transfer function. The parameters of these controllers are recorded in Table 2.

Table 2.
FO control parameters.
Figure 4 captures the normalised closed-loop response of the system under the effect of the FO-PI controller with a phase margin .
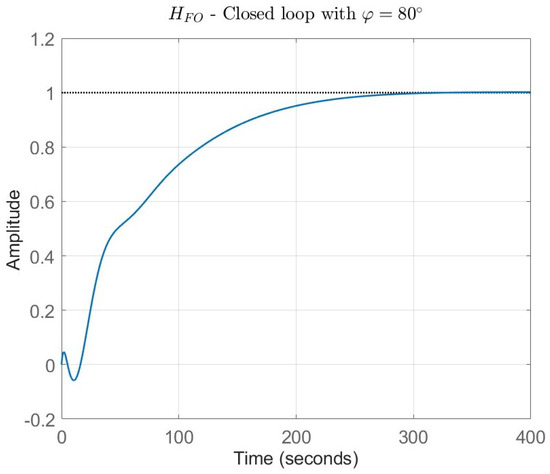
Figure 4.
FO closed loop results with = 80°.
3.2. System Simulation
Within the framework of MRAC, real-time adjustments ensure that the system remains stable and performs optimally despite variations in system dynamics and external disturbances. The overall closed-loop scheme of MRAC is depicted in Simulink® in Figure 5. The MRAC structure includes four elements of note: the reference model, the adaptive mechanism, the nominal controller, and the process model. With regard to the disturbance, the surgical stimuli simulator described in Section 2.4 is used.
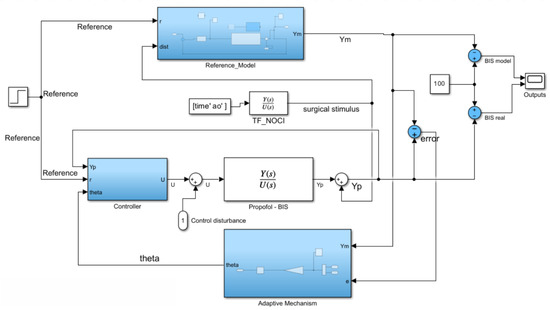
Figure 5.
Simulink® block diagram of MRAC.
The reference input signal is a simple step reference of amplitude 50, equal to the desired stationary value for the BIS signal. This reference is fed to both the nominal controller and to the reference model. Inside the reference model block, depicted in Figure 6, a regular closed-loop negative feedback control scheme is implemented. In this model, the controller receives the expected error, computed as the difference between output and reference. The control command becomes the input of the model plant, for which we use the second-order Padè approximation of the process, previously presented in (2). The process plant (outside the reference model) is put as a Padè approximation of order 10, a form of much higher complexity than the reference plant. This decision was made with the understanding that the process model would inevitably be a simplification of the actual real-time system, thereby reducing computational complexity for the model. The 10th-order Padè approximation acting as the unknown process plant is considerably more accurate and complex, with higher polynomials, being closer to a real-time example. However, the value of the reference plant lies in generality, not utmost precision, as no perfect model can assess the diverse array of dynamics found in patients; therefore, the MRAC system must avoid overfitting to the nominal patient case. This can only be achieved using the lower-order Padè approximation for the reference plant while employing the more complex transfer function (10th-order Padè approximation) for the process plant.
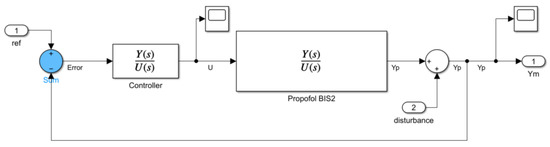
Figure 6.
Simulink® block diagram of reference model.
The MRAC system depends on the tracking of the model’s behaviour. As such, the real output of the MRAC system and the output of the reference model are subtracted from the value of 100 to simulate the decrease in the BIS signal (and consciousness), while the anaesthetic agent is taking effect. The surgical stimuli signal is applied to the output, challenging the disturbance rejection capability and the stability of the adaptive controller. The adjusted step response of each adaptive controller configuration is compared to the respective model’s response as a way to gauge the model-tracking performance. The simulation covers a time period of 1350 s within which the MRAC system must reach the stationary point and maintain it after the introduction of complex disturbances. Overshoot (or undershoot) should be kept to a minimum in order to avoid any risks of overdosing (or underdosing) the patient; thus, this aspect must be accounted for in the tuning process [47].
For tuning the adaptive mechanism, both the gain and the initial integral condition (IIC) can be gradually adjusted. The IIC represents the initial condition of the integration block within the adaptive mechanism. Setting the integrator with an initial condition of 0.5 for the adaptive parameter implies that will start at a value of 0.5 when the simulation begins, i.e., . This initial value can influence the initial behaviour of the control system and affect the convergence rate of the adaptive algorithm. Inputting higher values for IIC results in faster convergence for this specific system towards the model/desired output. On the other hand, a high IIC value may interfere with the system’s ability to adapt to new processes that differ too much from the reference plant, impeding the goal of the adaptive structure.
The control law block, depicted in Figure 7, showcases the application of the adaptive law onto the controller output signal. The parameter is multiplied with the controller’s output, obtaining a final command signal, akin to (18). Applying a saturation block for the command signal is optional, as the signal amplitude remains within reasonable, achievable values for practical application .
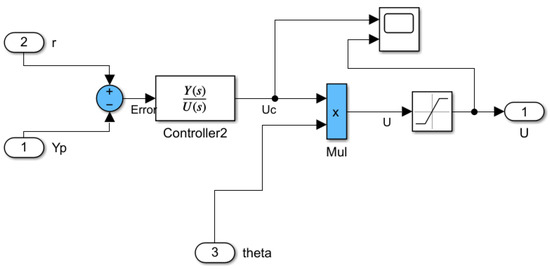
Figure 7.
Simulink® block diagram of control law.
The adaptive law refers to the adaptive gain resulting from the application of the gradient rules according to the MIT rule (16). The adaptive mechanism of the MRAC structure requires knowledge of the error of the system (the difference between the reference model output , and the overall MRAC system output ) in Figure 8. The dynamic adjustment capability of the system is vital for achieving consistent and reliable performance in the drug titration process. Tuning the feedback loop parameters and the adaptive gain facilitates quick yet stable responses from the system, preventing oscillations or overshooting in anaesthetic delivery.
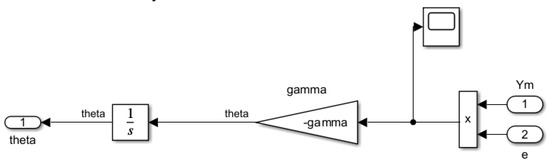
Figure 8.
Simulink® block diagram of adaptive law.
Three configurations of the FO-PI controllers within the MRAC framework are tested and compared by adjusting the imposed phase margin. The result of the presented design, with the setting of adaptive parameters as and , is shown across Figure 9, Figure 10 and Figure 11. The first figure captures the first implementation of the FO-MRAC, considering the phase margin = 65°, in which a slight overshoot = 1.9 (3.8%) can be observed. In contrast, the other cases show no overshoot, smoothly reaching the steady-state of 50. The FO-MRAC structure with = 80° is depicted in Figure 10, while the last proposed FO-MRAC with = 90° is depicted in Figure 11.
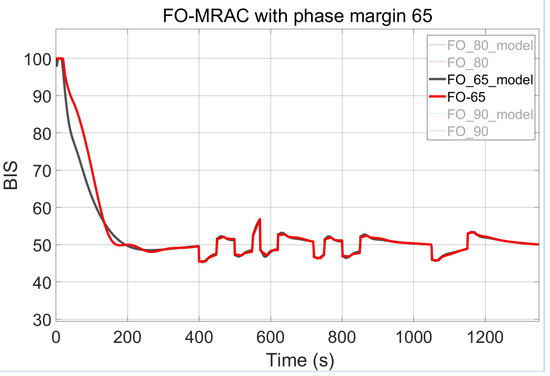
Figure 9.
FO-MRAC results with = 65°.
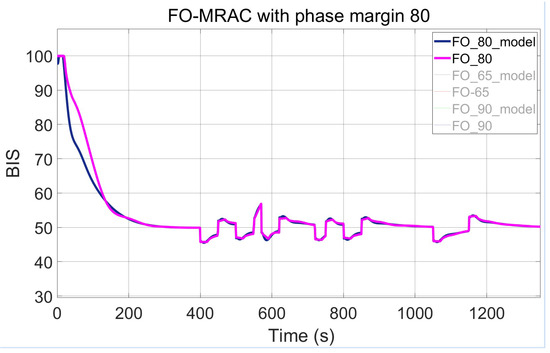
Figure 10.
FO-MRAC results with = 80°.
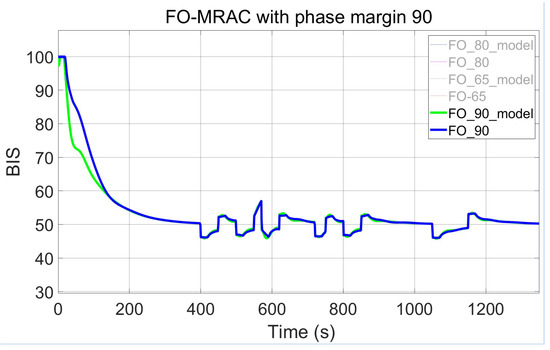
Figure 11.
FO-MRAC results with = 90°.
The significance of the phase margin variable on the design of MRAC-FO-PI controllers is emphasised by presenting the responses from the previous figures in a combined display in Figure 12.
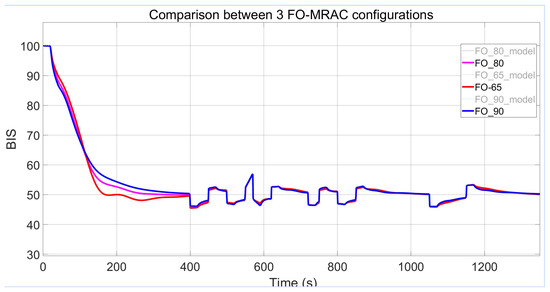
Figure 12.
Output comparison between all FO-MRAC configurations.
For a final step value of 50 and an IIC of zero, the system remains stable for values of , although saturated oscillations may appear at steady state. Instability is observed for 0.00002 in all three discussed cases. A higher results in larger adjustments made to the command signal in each iteration, and facilitates a lower settling time. A lower limit for the gain is reached when the system becomes far too slow, with response times outside the acceptable range and significant overshoot. This behaviour is recorded in cases of gain values for most of the tested controllers. Therefore, it is recommended to maintain the adaptive gain in the range of .
The quality of the performance of the closed-loop systems is measured analytically through two types of errors. The simulation period encompasses the entire duration of 1350 s. The integral squared errors (ISE) evaluates the system’s capability to follow and maintain the reference over time, providing a cumulative measure of the squared deviations from the desired trajectory. The summation runs from to its final time step , as described by (21). The ISE metric is particularly useful for assessing long-term performance and stability, as it penalises larger errors more severely, thereby encouraging a control strategy that minimises significant deviations from the target BIS level. Conversely, the mean squared error (MSE) offers a snapshot of the average discrepancy between the true output and the reference model at each point in time. By averaging the squared differences, as shown in (22), the MSE provides insight into the overall accuracy and precision of the control system in real-time operation. Together, these metrics offer a comprehensive view of the control system’s performance, although the magnitudes of these errors are affected by measuring during the entire simulation period.
A range of variable configurations across three phase margin alternatives is evaluated to explore their influence on system performance and stability, with the most notable results recorded in Table 3. The aforementioned table for the designed controllers is split into the variables defining the control and adaptive law and the corresponding error values whose meaning has been described above. The adaptive law is modified through the handling of the variables for the gain adaptation , and through the IIC inside the adaptive block. The error values ISE and MSE are displayed as the last two columns.

Table 3.
Performance measures for the FO-MRAC strategy.
Additional performance metrics are included in the analysis. Firstly, a secondary error measure, referred to as , is calculated using Equation (21), with the evaluation constrained to the interval between 400 and 1350 s, in order to specifically assess the system’s effectiveness in suppressing the disturbance effect. In parallel, overshoot and settling time values for nine selected FO-MRAC configurations are reported in Table 4.

Table 4.
Additional metrics for indicative FO-MRAC tuning configurations.
To establish a quantitative comparison, a conventional FO-PID controller is designed and implemented within a closed-loop system that incorporates the same patient and disturbance models used in the testing and validation of the FO-MRAC strategy. The considered parameters for the FO-PID controller are the following: proportional gain , integral gain , derivative gain , integral order , and derivative order .
The FO-PID controller exhibits an overshoot of approximately 12%, with a settling time of approximately 250 s. The performance metrics include an ISE = and an = . Although the overall ISE value of the FO-PID controller is significantly lower—less than half—compared to the best-performing FO-MRAC configurations, its performance in disturbance rejection, as indicated by the metric, is inferior. More importantly, the presence of significant overshoot and prolonged settling time, combined with a more aggressive control strategy, characterised by rapid transient response, suggests a higher likelihood of compromising patient comfort and safety when compared to the more balanced performance of the MRAC structure.
4. Discussion
In accordance with the objectives underlined in Section 2.1, it is vital to address the stability, disturbance rejection capabilities, and response times of the designed system to ensure patient safety and effective anaesthesia management.
The objective is to guarantee that the system can perform reliably under various conditions while maintaining the stability of the signal and meeting the established benchmarks for clinical use.
The system should be robust to changes in the process and to the great variance between patients, such as comorbidities, individual variability in pharmacokinetics, and physical characteristics [14].
Just as the MRAC structure relies on real-time adjustments based on system errors to maintain stability, anaesthesiologists dynamically modify anaesthetic levels in response to physiological signals. This parallel highlights the importance of feedback and adaptation in maintaining desired outcomes, whether in engineering systems or patient care [48]. MRAC systems excel in managing a broad spectrum of uncertainties and variations in system parameters, providing robust performance across different conditions. This adaptability ensures that the system can maintain its desired performance even as the environment changes. The continuous adjustment of controller parameters allows MRAC systems to dynamically respond to new challenges, enhancing overall system efficiency and effectiveness.
However, the design of MRAC systems involves considerable complexity, particularly in formulating the adaptation law and ensuring system stability. This complexity requires a deep understanding of both control theory and the process to create an effective MRAC system. Additionally, MRAC systems can be sensitive to unmodelled dynamics and disturbances. This sensitivity means that, if certain dynamics are not accounted for in the model, the system can become unstable, posing significant challenges in practical implementation.
It is imperative that the reference plant model and the practical plant model (the plant transfer function found in the main MRAC loop, titled “Propofol-BIS” in Figure 5) are not the same, as to guarantee the validity of the testing results and the simulation of the real variability in the patient model. The unpredictable behaviour of the anaesthesia process is owed to the wide range of physical and PK-PD characteristics in different patients. Therefore, the control structure should adapt to each new plant process provided without having to make considerable modifications to the reference model. The reference model serves as an ideal case for guiding the control structure to adjust the output towards the desired performance.
Another drawback of the implemented adaptive scheme is its sensitivity to the adaptive gain . The tolerance for is relatively linked to the IIC within the adaptive mechanism. When the initial condition is increased from 0 to 0.5 or more, the system can tolerate a larger range of gain values without becoming unstable. This adjustment allows for a broader operational interval for the gain, which can enhance the flexibility and robustness of the control system. However, this also implies that the careful tuning of both the adaptive gain and the IIC is necessary to achieve optimal performance. The need for meticulous tuning can complicate the implementation process in clinical settings, where variations in patient responses and conditions are commonplace. This weakness in the control schemes suggests practical implications and potential hazards which must be explored.
As can be interpreted from Table 3, the performance for the controllers improves with the application of higher gain and IIC values. One case that stands out as a promising middle ground is the controller with = 80°, which shows no overshoot in Figure 12, unlike the case with = 65°, and settles faster than the FO-PI structure with = 90°.
During testing, the FO-MRAC strategy registers preferable output error values for the smallest imposed phase margin ( = 65°). While its ISE values are not the lowest among all strategies, the MSE is notably low without a high overfitting risk.
An alternative approach for presenting the errors would have been separating the output values between the sections before and after the introduction of disturbance, in other words, after the point of 400 s. This method could highlight both transient and steady-state behaviour separately, but there are benefits to viewing the full picture as well. Analysing the entire simulation period allows for a holistic assessment of the control system’s performance, capturing the interactions between the transient and steady-state phases. This comprehensive view is crucial for understanding the overall effectiveness and robustness of the control strategy in real-world scenarios, where disturbances and dynamic changes occur continuously. It provides a complete picture of how the system responds to initial changes, adapts over time, and maintains stability and performance in the presence of ongoing variations. An optimal control system aims to minimise both ISE and MSE, thereby ensuring both accuracy in tracking the reference model and robustness in maintaining that performance under varying conditions and disturbances.
Applying more advanced adaptive control theories, such as Lyapunov stability analysis or other sophisticated methodologies, offers an opportunity for further progress [49]. Additionally, comprehensive performance comparisons should be conducted with other advanced control structures, such as predictive control, Lyapunov-based adaptive designs, or MISO [50], and MIMO strategies [28,51].
Translating the presented approach into clinical practice may encounter the same real-world implementation barriers that affect other documented closed-loop control structures. Regulatory certification for such medical systems is rigorous, requiring thorough validation and risk assessment. The computational demands of fractional-order modelling and real-time adaptation may require specialised hardware or optimisation for integration with current anaesthesia systems. Successful clinical deployment would also depend on adequate staff training to ensure proper understanding and safe use. Healthcare professionals remain the centre of health decisions for patients [28].
5. Conclusions
As outlined in the introduction of this paper, the study aims to advance an adaptive technique capable of estimating a simplified patient model during the induction phase, utilising the drug infusion rate and the corresponding BIS measurements. This model estimation is then used to adapt the controller parameters in real-time, enabling personalised control. Future work will involve evaluating the approach on a broader patient dataset, incorporating bench-testing scenarios to simulate real-world conditions. Particular attention will be given to clinical variability and the robustness of the control strategy.
Configurations and parameters for adaptive systems governing propofol-to-BIS process approximations have been meticulously tailored to meet rigorous operational criteria and uphold safety standards in anaesthesia management. The evaluated adaptive control schemes demonstrate potential in managing surgical stimuli during the maintenance phase, albeit with a slower rise time compared to the ideal model reference. Nevertheless, the system effectively maintains the BIS signal within safety parameters and displays smooth operation, indicating a less aggressive control approach. The FO-MRAC method demonstrates notable reference model tracking and ensures smooth, stable performance, especially with a phase margin of .
The proposed control system proved its potential as a drug delivery control strategy, but not without disadvantages. As the graphical representation of the outputs revealed, overshoots are not fully nullified by all applied controllers. Furthermore, the true output of the MRAC system is only theoretically within the approved margins for an appropriate settling time, and physical implementations may be met with unexpected dips in performance. These practical challenges are exacerbated by unexpected variation in patient physiology. However, the robustness against the introduced surgical stimuli is evident, partially validating the underlying premise of the paper.
The foundation established by this paper has potential use in future studies for creating more complex adaptive control systems. As mentioned in Section 4, while initial results are promising, further validation and comparative analysis against existing methodologies are essential to fully establish the effectiveness of the proposed approach. It is hoped that, when balanced against other strategies, the adaptive control strategies offer desirable attributes that further research may uncover. Even if the outcome is contrary to expectations, the research remains valuable as it provides critical insights into the limitations of adaptive control systems.
Further investigation is needed to evaluate the integrated application of various types of robots in maintaining the homeostasis of biological variables, emphasising their combined effectiveness and safety in clinical settings. Naturally, the human element of medical procedures cannot be ignored or fully replaced. Pharmacological robots should be regarded as powerful tools, not substitutes, working harmoniously with healthcare professionals [14,28].
Author Contributions
Conceptualisation, A.-C.M. and C.I.M.; methodology, A.-C.M.; software, A.-C.M.; validation, A.-C.M.; formal analysis, A.-C.M.; investigation, A.-C.M.; resources, C.I.M.; data curation, C.I.M.; writing—original draft preparation, A.-C.M.; writing—review and editing, C.I.M., M.A.D.-M. and G.C.B.; visualisation, A.-C.M.; supervision, C.I.M., M.A.D.-M. and G.C.B.; project administration, C.I.M.; funding acquisition, C.I.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant of the Romanian Ministry of Research, Innovation and Digitization, PNRR-III-C9-2022-I8, grant number 760068/23 May 2023.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in the study are openly available in reference [29].
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PK | Pharmacokinetics |
| PD | Pharmacodynamics |
| TCI | Target-Controlled Infusion |
| PID | Proportional–Integral–Derivative |
| MPC | Model Predictive Control |
| MRAC | Model Reference Adaptive Control |
| SISO | Single-Input–Single-Output |
| MIMO | Multiple-Input–Multiple-Output |
| FO | Fractional Order |
| ORA | Oustaloup Recursive Approximation |
| EMG | Electromyogram |
| RASS | Ramsay Agitation Score |
| BIS | Bispectral Index |
| EEG | Electroencephalogram |
| MAP | Mean Arterial Pressure |
| CO | Cardiac Output |
| DSP | Digital Signal Processing |
| MIT | Massachusetts Institute of Technology |
| IIC | Initial Integral Condition |
| ISE | Integral Squared Error |
| MSE | Mean-Squared Error |
References
- Mistri, I.; Badge, A.; Shahu, S. Enhancing Patient Safety Culture in Hospitals. Cureus 2023, 15, e51159. [Google Scholar] [CrossRef] [PubMed]
- Sameera, V.; Bindra, A.; Rath, G.P. Human Errors and Their Prevention in Healthcare. J. Anaesthesiol. Clin. Pharmacol. 2021, 37, 328–335. [Google Scholar] [CrossRef] [PubMed]
- Labuschagne, M.; Robbetze, W.; Rozmiarek, J.; Strydom, M.; Wentzel, M.; Diedericks, J.; Joubert, G. Errors in Drug Administration by Anaesthetists in Public Hospitals in the Free State. S. Afr. Med. J. 2011, 101, 324–327. [Google Scholar] [CrossRef]
- Zaouter, C.; Joosten, A.; Rinehart, J.; Struys, M.M.R.F.; Hemmerling, T.M. Autonomous Systems in Anesthesia: Where Do We Stand in 2020? A Narrative Review. Anesth. Analg. 2020, 130, 1120–1132. [Google Scholar] [CrossRef]
- Dinia, L.; Mangini, F.; Frezza, F. Can the Perception of Risk Be Decreased among Caregivers during Anesthesia Delivery? In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Jones, C.P.L.; Fawker-Corbett, J.; Groom, P.; Morton, B.; Lister, C.; Mercer, S.J. Human factors in preventing complications in anaesthesia: A systematic review. Anaesthesia 2018, 73, 12–24. [Google Scholar] [CrossRef]
- Gautam, B.; Shrestha, B.R. Critical Incidents during Anesthesia and Early Post-Anesthetic Period: A Descriptive Cross-sectional Study. JNMA J. Nepal Med. Assoc. 2020, 58, 240–247. [Google Scholar] [CrossRef]
- Steadman, J.; Catalani, B.; Sharp, C.; Cooper, L. Life-Threatening Perioperative Anesthetic Complications: Major Issues Surrounding Perioperative Morbidity and Mortality. Trauma Surg. Acute Care Open 2017, 2, e000113. [Google Scholar] [CrossRef]
- Dalley, P.; Robinson, B.; Weller, J.; Caldwell, C. The Use of High-Fidelity Human Patient Simulation and the Introduction of New Anesthesia Delivery Systems. Anesth. Analg. 2004, 99, 1737–1741. [Google Scholar] [CrossRef]
- Dinia, L.; Mangini, F.; Mileti, I.; Palermo, E.; Frezza, F. Adverse Patient Events in Anesthesia Delivery – Review and Analysis of Potentially Avoidable Events. In Proceedings of the 2020 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Bari, Italy, 1 June–1 July 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Dinia, L.; Mangini, F.; Marella, M.A.; Frezza, F. Parallelism Between Risk and Perception of Risk Among Caregivers During Anesthesia Delivery. Eur. Rev. Med. Pharmacol. Sci. 2019, 23, 3129–3141. [Google Scholar] [CrossRef]
- Keyser, R.D.; Copot, D.; Ionescu, C. Estimation of Patient Sensitivity to Drug Effect During Propofol Hypnosis. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; pp. 2487–2491. [Google Scholar] [CrossRef]
- Dobson, G.; Chow, L.; Filteau, L.; Hurdle, H.; McIntyre, I.; Milne, A.; Milkovich, R.; Perrault, M.A.; Sparrow, K.; Swart, P.A.; et al. Guidelines to the Practice of Anesthesia—Revised Edition 2021. Can. J. Anesth. 2021, 68, 92–129. [Google Scholar] [CrossRef]
- Bibian, S.; Ries, C.R.; Huzmezan, M.; Dumont, G. Introduction to automated drug delivery in clinical anesthesia. Eur. J. Control 2015, 11, 535–557. [Google Scholar] [CrossRef]
- Cehajic-Kapetanovic, J.; Xue, K.; Edwards, T.L.; Meenink, T.C.; Beelen, M.J.; Naus, G.J.; de Smet, M.D.; MacLaren, R.E. First-in-Human Robot-Assisted Subretinal Drug Delivery Under Local Anesthesia. Am. J. Ophthalmol. 2022, 237, 104–113. [Google Scholar] [CrossRef]
- Hemmerling, T.M.; Charabati, S.; Zaouter, C.; Minardi, C.; Mathieu, P.A. A Randomized Controlled Trial Demonstrates That a Novel Closed-loop Propofol System Performs Better Hypnosis Control Than Manual Administration. Can. J. Anesth. 2010, 57, 725–735. [Google Scholar] [CrossRef]
- Haddad, W.M.; Bailey, J.M. Closed-loop control for intensive care unit sedation. Best Pract. Res. Clin. Anaesthesiol. 2009, 23, 95–114. [Google Scholar] [CrossRef]
- Ahtiainen, H.K.; Kallio, M.M.; Airaksinen, M.; Holmström, A.R. Safety, Time and Cost Evaluation of Automated and Semi-Automated Drug Distribution Systems in Hospitals: A Systematic Review. Eur. J. Hosp. Pharm. 2020, 27, 253–262. [Google Scholar] [CrossRef]
- Fang, M.; Tao, Y.; Wang, Y. An Enriched Simulation Environment for Evaluation of Closed-loop Anesthesia. J. Clin. Monit. Comput. 2014, 28, 13–26. [Google Scholar] [CrossRef]
- Padula, F.; Ionescu, C.; Latronico, N.; Paltenghi, M.; Visioli, A.; Vivacqua, G. Optimized PID Control of Depth of Hypnosis in Anesthesia. Comput. Methods Programs Biomed. 2017, 144, 21–35. [Google Scholar] [CrossRef]
- Paolino, N.; Schiavo, M.; Latronico, N.; Paltenghi, M.; Visioli, A. PK/PD Model-Based Design of PID Control for Closed-Loop Anesthesia. IFAC J. Syst. Control 2024, 27, 100247. [Google Scholar] [CrossRef]
- Patel, B.; Patel, H.G. Intravenous Anesthesia Automation with Internal and Instrumental Delay. In Proceedings of the 2017 IEEE International Conference on Industrial and Information Systems (ICIIS), Peradeniya, Sri Lanka, 15–16 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Navarro-Guerrero, G.; Tang, Y. Adaptive Control for Anesthesia Based on a Simple Fractional-Order Model. In Proceedings of the 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 5623–5628. [Google Scholar] [CrossRef]
- Wei, Z.X.; Doctor, F.; Liu, Y.X.; Fan, S.Z.; Shieh, J.S. An Optimized Type-2 Self-Organizing Fuzzy Logic Controller Applied in Anesthesia for Propofol Dosing to Regulate BIS. IEEE Trans. Fuzzy Syst. 2020, 28, 1062–1072. [Google Scholar] [CrossRef]
- Hegedus, E.T.; Birs, I.R.; Ghita, M.; Muresan, C.I. Fractional-Order Control Strategy for Anesthesia–Hemodynamic Stabilization in Patients Undergoing Surgical Procedures. Fractal Fract. 2022, 6, 614. [Google Scholar] [CrossRef]
- Chen, J.; Ren, W.; Liu, J.; Fu, Z.; Yao, Y.; Chen, X.; Teng, L. Feasibility of Intelligent Drug Control in the Maintenance Phase of General Anesthesia Based on Convolutional Neural Network. Heliyon 2023, 9, e12481. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Peng, S.; Chen, M.; Yang, Z.; Chen, Y. A Transformer-Based Prediction Method for Depth of Anesthesia During Target-Controlled Infusion of Propofol and Remifentanil. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 3363–3374. [Google Scholar] [CrossRef] [PubMed]
- Ghita, M.; Neckebroek, M.; Muresan, C.; Copot, D. Closed-Loop Control of Anesthesia: Survey on Actual Trends, Challenges and Perspectives. IEEE Access 2020, 8, 206264–206279. [Google Scholar] [CrossRef]
- Ionescu, C.M.; Neckebroek, M.; Ghita, M.; Copot, D. An Open Source Patient Simulator for Design and Evaluation of Computer-Based Multiple Drug Dosing Control for Anesthetic and Hemodynamic Variables. IEEE Access 2021, 9, 8680–8694. [Google Scholar] [CrossRef]
- Hegedus, E.; Ghita, M.; Birs, I.R.; Copot, D.; Muresan, C.I. Robustness Analysis of a Fractional Order Control System for the Hemodynamic Variables in Anesthetized Patients. In Proceedings of the 2023 European Control Conference (ECC), Bucharest, Romania, 13–16 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Eleveld, D.J.; Colin, P.; Absalom, A.R.; Struys, M.M.R.F. Pharmacokinetic-Pharmacodynamic Model for Propofol for Broad Application in Anaesthesia and Sedation. Br. J. Anaesth. 2018, 120, 942–959, Erratum in Br. J. Anaesth. 2018, 121, 519. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Van Heusden, K.; Dumont, G.A.; Garone, E. An Explicit Reference Governor Scheme for Closed-Loop Anesthesia. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 1294–1299. [Google Scholar] [CrossRef]
- Vajta, M. Some Remarks on Padé-Approximations. In Proceedings of the 3rd TEMPUS-INTCOM Symposium, Veszprém, Hungary, 9–14 September 2000; p. 1. [Google Scholar]
- Neckebroek, M.M.; Smet, T.D. Automated drug delivery in anesthesia. J. Anesth. 2013, 3, 18–26. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 5th ed.; Pearson: Hoboken, NJ, USA, 2010. [Google Scholar]
- Vilanova, R.; Visioli, A. (Eds.) PID Control in the Third Millennium; Advances in Industrial Control; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Azar, A.; Radwan, A.; Vaidyanathan, S. Fractional Order Systems: Optimization, Control, Circuit Realizations and Applications; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Nguyen, N. Model Reference Adaptive Control—A Primer; Advanced Textbooks in Control and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Mallick, S.; Mondal, U. Design of Lyapunov Based Model Reference Adaptive Controller for First Order Plus Delay Time Liquid Level System. In Proceedings of the 2019 International Conference on Intelligent Computing and Remote Sensing (ICICRS), Bhubaneswar, India, 19–20 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Tao, G. Multivariable adaptive control: A survey. Automatica 2014, 50, 2737–2764. [Google Scholar] [CrossRef]
- Swathi, M.; Ramesh, P. Modeling and Analysis of Model Reference Adaptive Control by Using MIT and Modified MIT Rule for Speed Control of DC Motor. In Proceedings of the 2017 IEEE 7th International Advance Computing Conference (IACC), Hyderabad, India, 5–7 January 2017; pp. 482–486. [Google Scholar] [CrossRef]
- Jain, P.; Nigam, M.J. Real Time Control of Ball and Beam System with Model Reference Adaptive Control Strategy Using MIT Rule. In Proceedings of the 2013 IEEE International Conference on Computational Intelligence and Computing Research, Enathi, India, 26–28 December 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Jenkins, B.M.; Annaswamy, A.M.; Lavretsky, E.; Gibson, T.E. Convergence Properties of Adaptive Systems and the Definition of Exponential Stability. SIAM J. Control Optim. 2018, 56, 2463–2484. [Google Scholar] [CrossRef]
- Ooba, S.; Ueki, R.; Kariya, N.; Tatara, T.; Hirose, M. Mathematical Evaluation of Responses to Surgical Stimuli Under General Anesthesia. Sci. Rep. 2020, 10, 15300. [Google Scholar] [CrossRef]
- Röpcke, H.; Rehberg, B.; Koenen-Bergmann, M.; Bouillon, T.; Bruhn, J.; Hoeft, A. Surgical Stimulation Shifts EEG Concentration–Response Relationship of Desflurane. Anesthesiology 2001, 94, 390–399. [Google Scholar] [CrossRef] [PubMed]
- Schiavo, M.; Padula, F.; Latronico, N.; Paltenghi, M.; Visioli, A. Individualized PID tuning for maintenance of general anesthesia with propofol. IFAC-PapersOnLine 2021, 54, 679–684. [Google Scholar] [CrossRef]
- Bachmann, F.; Koch, G.; Pfister, M.; Szinnai, G.; Schropp, J. OptiDose: Computing the Individualized Optimal Drug Dosing Regimen Using Optimal Control. J. Optim. Theory Appl. 2021, 189, 46–65. [Google Scholar] [CrossRef]
- Khan, A.; Swamy, M.S. Modified MRAC based on Lyapunov theory for improved controller efficiency. In Proceedings of the 2016 International Conference on Automatic Control and Dynamic Optimization Techniques (ICACDOT), Pune, India, 9–10 September 2016; pp. 989–995. [Google Scholar] [CrossRef]
- Pawłowski, A.; Schiavo, M.; Latronico, N.; Paltenghi, M.; Visioli, A. Model predictive control using MISO approach for drug co-administration in anesthesia. J. Process Control 2022, 117, 98–111. [Google Scholar] [CrossRef]
- Maxim, A.; Copot, D. Closed-loop control of anesthesia and hemodynamic system: A Model Predictive Control approach. IFAC-PapersOnLine 2021, 54, 37–42. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).