Abstract
This work examines the fractional Sawada–Kotera and Korteweg–de Vries (KdV)–Burgers equations, which are essential models of nonlinear wave phenomena in many scientific domains. The homotopy perturbation transform method (HPTM) and the Yang transform decomposition method (YTDM) are two sophisticated techniques employed to derive analytical solutions. The proposed methods are novel and remarkable hybrid integral transform schemes that effectively incorporate the Adomian decomposition method, homotopy perturbation method, and Yang transform method. They efficiently yield rapidly convergent series-type solutions through an iterative process that requires fewer computations. The Caputo operator, used to express the fractional derivatives in the equations, provides a robust framework for analyzing the behavior of non-integer-order systems. To validate the accuracy and reliability of the obtained solutions, numerical simulations and graphical representations are presented. Furthermore, the results are compared with exact solutions using various tables and graphs, illustrating the effectiveness and ease of implementation of the proposed approaches for various fractional partial differential equations. The influence of the non-integer parameter on the solutions behavior is specifically examined, highlighting its function in regulating wave propagation and diffusion. In addition, a comparison with the natural transform iterative method and optimal auxiliary function method demonstrates that the proposed methods are more accurate than these alternative approaches. The results highlight the potential of YTDM and HPTM as reliable tools for solving nonlinear fractional differential equations and affirm their relevance in wave mechanics, fluid dynamics, and other fields where fractional-order models are applied.
1. Introduction
In a letter dating back to 1695, mathematicians Leibniz and L’Hospital discussed the concept of fractional calculus (FC), which extends classical calculus from integer-order to arbitrary-order derivatives. In recent years, FC has attracted growing interest among researchers due to its ability to model a wide range of nonlinear phenomena. FC has become a foundational platform for major advances in science and engineering, owing to its valuable properties such as analyticity, heredity, non-locality, and memory effect. These features have made it one of the most effective tools for analyzing and characterizing complex nonlinear behaviors. The complexity of systems with heterogeneities led to the development of the concept of derivatives of arbitrary order. Differential operators of non-integer order can effectively capture the fundamental behavior of complex media with diffusion mechanisms. The rapid progress in mathematical techniques, computational methods, and software has further enabled researchers to explore both the foundations and diverse applications of fractional-order calculus [,,,,,]. Various innovative definitions of FC have been introduced, laying a solid theoretical foundation for its application in nanotechnology [], optics [], human diseases [], chaos theory [], and other areas [,,,,].
Fractional differential equations (FDEs) are an extension of standard differential equations that exhibit both non-local and genetic effects on material properties. Several renowned researchers have investigated and discussed the concept of FC, proposing novel definitions that serve as the foundation of the field [,,]. By taking into consideration their complex characteristics, such as memory and non-locality, nonlinear FDEs provide a more realistic depiction of biological and physical systems []. FDEs are becoming increasingly important for both constructing nonlinear models and for examining dynamical systems. The concept of FC has been used to analyze and evaluate a wide range of phenomena. Real-world applications of the FC theory include financial models [], noisy environments [], optics [], and others [,]. Numerous solutions to FDEs illustrate the features of nonlinear problems that occur in nature. Researchers have examined general classes of FDEs, such as mixed, sequential, and hybrid, that remain largely unexplored in this area. In the domain of nonlinear analysis, experiential methods are crucial for understanding the dynamics of systems governed by various schemes. Due to the challenges of solving FDEs describing nonlinear systems with accuracy, several analytical and numerical techniques have been employed. Computational methods that yield analytical solutions offer certain advantages over traditional numerical approaches. The lack of discretization eliminates rounding errors and reduces memory and processing requirements. The Adomian decomposition method (ADM) has recently proven effective in solving fractional ordinary differential equations []. A general set of FDEs containing a Caputo fractional derivative with a linear functional argument was solved using the spectral Tau approach []. The Caputo-Fabrizio and the Atangana-Baleanu derivatives, two distinct forms of non-integer derivatives, were applied using the natural decomposition approach in [] to address the time-fractional nonlinear Korteweg–de Vries (KdV)-Burgers equation. In addition, ref. [] proposed a hybrid technique for solving fractional local Poisson equations.
This paper focuses on the fractional Sawada–Kotera and KdV–Burgers equations. The KdV–Burgers model has attracted considerable attention in recent decades. It is used in several real-world scenarios, including wave propagation through an elastic pipe filled with a viscous liquid [], the transport of liquids carrying gas bubbles [], weakly nonlinear plasma waves with specific dissipative properties [], and the turbulence of undular bores in shallow water []. In addition, it serves as a nonlinear model in circuit theory, turbulence, ferroelectricity theory, and other domains [,]. Assume the fractional KdV-Burgers equation as follows
where indicates the non-integer derivative, taken in the Caputo sense. Here, is a function of and , where denotes the spatial variable and the time variable. The classical Sawada–Kotera equation is another important model that describes the dynamics of long waves in shallow water under gravity, as well as in a one-dimensional nonlinear lattice. It also has numerous applications in nonlinear optics and quantum physics. The use of kink-shaped tanh solutions or bell-shaped sech solutions to represent wave phenomena and fluid dynamics in plasma media is well known. This equation is also used to simulate waves propagating in opposite directions. Assume the fractional Sawada–Kotera equation as follows []:
This is the fifth-order variation of the Sawada–Kotera equation [,,]. The condition indicates the non-integer derivative. The fractional derivative is considered in the Caputo sense and is denoted by , indicates the ordinary integer-order derivative of , and signifies time.
The ADM was proposed by Grorge Adomian in 1980 [] and has since attracted significant attention in applied mathematics. Cherruault [] conducted an important investigation into the convergence of the method. ADM enables the efficient and accurate solution of a wide class of linear and nonlinear partial and ordinary differential equations (PDEs and ODEs). Notably, it can be applied to most physical models of PDEs without relying on linearization or other restrictive assumptions that might distort the actual physical behavior of the systems under study [,]. In parallel, Ji-Huan He introduced the homotopy perturbation method (HPM) [,,], which combines the homotopy method with traditional perturbation techniques []. The primary advantage of the HPM lies in its simplicity of handling nonlinear terms. Burgers-type equations [,,,] were among the linear or nonlinear ODEs and PDEs successfully investigated using this method. The HPM and its convergence have been examined and refined by numerous researchers. In this study, the Yang transform decomposition method (YTDM) and homotopy perturbation transform method (HPTM) are employed to obtain analytical and approximate solutions for the nonlinear fractional Sawada–Kotera and KdV–Burgers equations. Interestingly, YTDM combines Hes polynomials, the Yang transformation, and the homotopy perturbation method, whereas HPTM combines the Yang transformation, the ADM, and Adomian polynomials. The primary aim of this paper is to address certain limitations by proposing a novel modification of the ADM and HPM. These requirements are met through the application of new techniques that merge the Yang transform with ADM and HPM. The main advantages of these approaches are their ease of use and low computational effort. Moreover, the analytical solutions derived using these methods show complete agreement with those found in existing literature. These techniques offer more accurate and exact numerical results compared to alternative methods. The numerical results are contrasted with those obtained through other approaches to assess both methods’ accuracy. The findings demonstrate that the outcomes of the proposed techniques are largely consistent, confirming their efficacy and reliability. The novel methods also outperform existing approaches, making them more valuable and effective. In addition, just one or two iteration steps yield highly accurate results over a broad range. In the numerical scenarios considered, our methods produced infinite series solutions. Once expressed in closed form, these series yield accurate solutions to the corresponding equations. The remainder of this paper is structured as follows. In Section 2, we outline several key concepts and notations related to FC and the Yang transform used in the current context. Section 3 presents the Laplace–Yang duality property. Section 4 and Section 5 provide a concise overview of the general principles underlying the proposed methods. In Section 6, we present the main results of the recommended strategies. Section 7 introduces the proposed techniques along with the validity of the error-bound theorem. Section 8 includes the implementation of the proposed techniques on the fractional Sawada–Kotera and KdV–Burgers equations, supported by numerical results and observations. Finally, the conclusion is presented in Section 9.
2. Preliminaries
Some well-known definitions from FC, which are related to our analysis, are presented in this section.
Definition 1.
The Riemann–Liouville’s (RL) non-integer derivative is defined as [,]
with , and
Definition 2.
The Caputo non-integer derivative is defined as [,]
with
Definition 3.
The Laplace transform (LT) of function for is defined as []
Definition 4.
The Yang transform (YT) of the is defined as []:
with u indicating the transform variable.
Few properties of YT are defined as
and the inverse is given by
Definition 5.
The YT of Caputo derivative is defined as []
3. Laplace-Yang Duality
Lemma 1.
Suppose the LT of is , then .
4. Methodology of HPTM
Consider the FDE of the form:
with
Here, represents the Caputo operator, is linear, and is the nonlinear operator.
After some simplification,
Apply inverse YT to Equation (20)
By implementing the homotopy perturbation method [], we obtain
having parameter .
Assume a series solution of the form:
with
He’s polynomials are defined as []:
where
By applying the recursive relationship:
The final solution can be written as
5. Methodology of YTDM
Take into account the FDE of the form:
with
Here, denotes the Caputo operator, is a linear operator, and is a nonlinear operator.
Taking the YT of Equation (29), we obtain
After some simplification, we obtain
Apply the inverse YT to Equation (31):
Assume a series solution of the form:
The nonlinear term is calculated as []
with
By applying the recursive relationship:
The final solution can be written as
6. Convergence Analysis
The existence results of the proposed techniques are discussed in this section.
Theorem 1.
Assume the exact result of (17) is and suppose , and , where H indicates the Hilbert space. The attained outcome converges to if , i.e., for all , with
Proof.
Assume
We must ascertain that forms a Cauchy sequence to achieve the preferred outcome. Let
For , then:
Since and are bounded, it follows that: , and we obtain
Hence, forms a Cauchy sequence in H. Thus, it is a convergent sequence with , for . □
Theorem 2.
Assume that is finite and is the corresponding series solution. Considering and , the maximum absolute error is given by:
Proof.
Let be finite, then .
Assume
which completes the proof. □
Theorem 3.
Suppose is Banach space and is a self-map of H. Then, the iteration procedure of YTDM is defined by:
is P-stable if.
- for some
- for some
Proof.
For proof, see []. □
Theorem 4.
Suppose is Banach space and is a mapping associated with the YTDM, defined by (38). Then, P has a unique fixed point, and the sequence converges to that fixed point in H, starting from an initial value , if such that .
Proof.
For proof, see []. □
7. Error Estimation
To evaluate the performance and accuracy of the proposed approaches, we present the error functions in this portion. Assuming that is the accurate solution and is the -order approximation of generated via the suggested methods, the absolute error in the -order approximation is as follows:
Then, maximum absolute error is given by:
The authors of [,,] discussed error bounds for their numerical approaches based on well-known lemmas and theorems. In our work, we provide an upper bound on the absolute error for the proposed methods using the following theorem.
Theorem 5
Proof.
Suppose is a continuous function on . Then, the upper bound of is defined as
By applying the norm property, we obtain
Since , we apply the Taylor expansion to obtain
with
From (50), we have
Now, we calculate the value of .
Let with so
8. Application
8.1. Case I
Examine the fractional KdV–Burgers equation:
with
Application of HPTM
Taking the YT of Equation (54), we obtain
After some simplification, we obtain
Apply the inverse YT to Equation (57):
By implementing the homotopy perturbation method, we obtain
Using the recursive relationship:
The final solution can be written as
Application of YTDM
Taking the YT of Equation (54), we obtain
After some simplification, we obtain
Apply the inverse YT to Equation (63):
Assume a series solution of the form:
The nonlinear term is calculated as Thus,
Using the recursive relationship:
On
On
The final solution can be written as
Hence, we obtain the exact solution for as shown below:
8.2. Case II
Examine the fractional Sawada–Kotera equation.
with
Application of HPTM
Taking the YT of Equation (69), we obtain
After some simplification, we obtain
Apply the inverse YT to Equation (72):
By implementing the homotopy perturbation method, we obtain
Using the recursive relationship
The final solution can be written as
Application of YTDM
Taking the YT of Equation (69), we obtain
After some simplification, we obtain
Apply the inverse YT to Equation (78):
Assume a series solution of the form:
The nonlinear term is calculated as Thus,
Using the recursive relationship:
On
On
The final solution can be expressed as
Hence, we obtain the exact solution for as follows
- Results and Discussion
The first numerical solutions to the Caputo fractional problems using the newly proposed techniques, HPTM and YTDM, are presented in this article. The inclusion of the Caputo fractional operator in the models is crucial for capturing anomalous diffusion and memory effects. MATHEMATICA 13.3 software was used to generate 2D and 3D graphs to visualize the numerical results. These graphical representations illustrate that the surface structures vary significantly with different values of . The solution for different fractional orders is graphically compared in Figure 1, which is divided into four sections. The 3D surface of the suggested methods solution at is shown in Figure 1a. The behavior at is depicted in Figure 1b, and the solution at is shown in Figure 1c. A 2D comparison of the solution at is shown in Figure 1d, highlighting the similarity of the proposed approaches. The exact and approximate solutions for of Equation (54) are shown in both 3D and 2D in Figure 2. Similarly, Figure 3 shows the error comparison between the exact and approximate solutions for Case (I). The obtained approximations are shown in Figure 1, Figure 2 and Figure 3 for a range of values, with and temporal variable . Table 1 displays both the exact solution and the approximate solutions derived using the proposed methods. Table 2 compares the absolute error of the proposed techniques with the natural transform iterative method (NTIM) and optimal auxiliary function method (OAFM). The comparison of the exact and analytical results reveals a high level of agreement. Accordingly, the proposed methods offer reliable and innovative approaches that require less computational time and are more straightforward and flexible than NTIM and OAFM. Figure 4 illustrates the solution for different fractional orders . The result at is shown in Figure 4a, while Figure 4b examines the behavior at , demonstrating improved wave characteristics compared to lower orders. Figure 4c corresponds to , representing the classical integer-order scenario with different waveforms. A 2D comparison of the solution at is shown in Figure 4d, emphasizing the similarity of the various approaches. Both 3D and 2D visualizations of the exact and estimated solutions for of Equation (69) are shown in Figure 5. Similarly, Figure 6 shows the error comparison of the exact and approximate results of Case (II). Figure 4, Figure 5 and Figure 6 cover a range of values with and temporal variable . The exact solution and the approximate solutions generated via the suggested methods are displayed in Table 3. In addition, the comparison of the proposed techniques with NTIM and OAFM in terms of absolute error is shown in Table 4. The graphical and tabular representations confirm that HPTM and YTDM are not only simple to implement but also capable of producing solutions that are highly accurate and closely aligned with the exact solution.
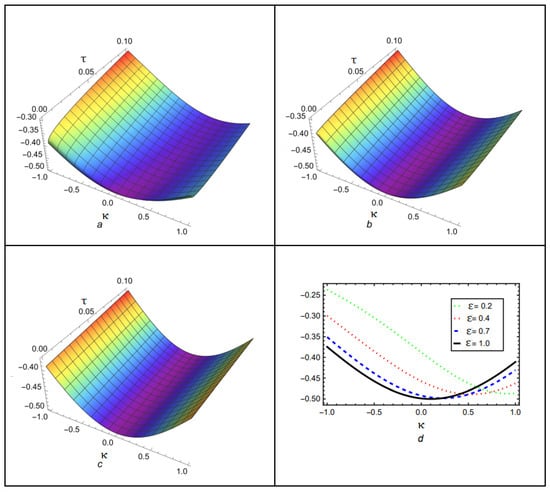
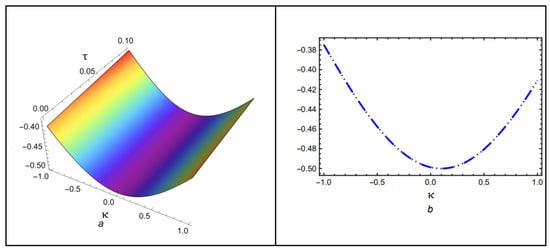
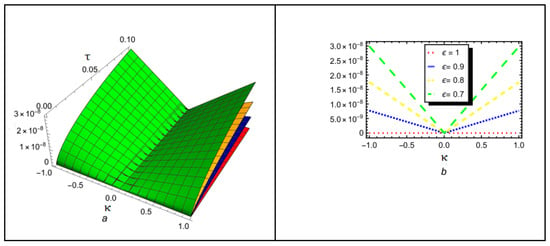

Table 1.
Comparison between the exact and HPTM/YTDM solutions for .

Table 2.
Comparison among HPTM/YTDM, NITM, and OFAM solutions for .
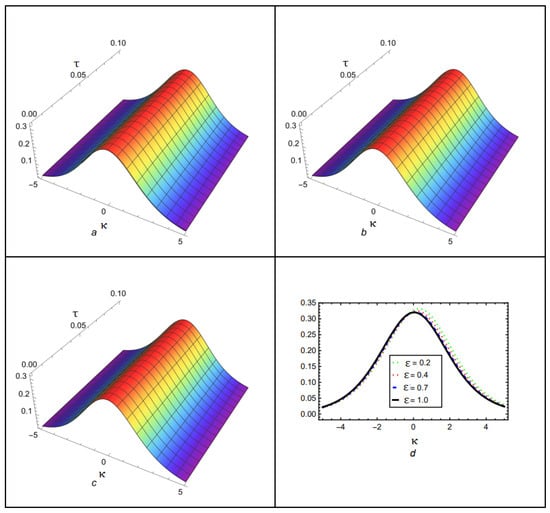
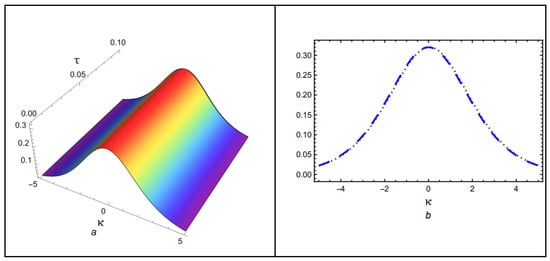
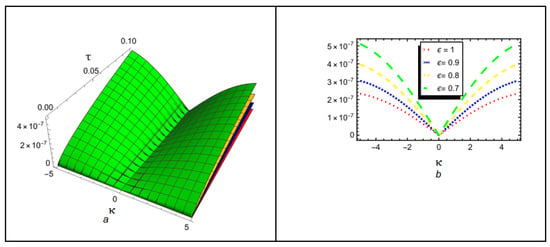

Table 3.
Comparison between the exact and HPTM/YTDM solutions for .

Table 4.
Comparative analysis of HPTM/YTDM with NITM and OFAM for .
9. Conclusions
Finding exact solutions to fractional partial differential equations (FPDEs), especially when applied to complex models such as the Sawada–Kotera equation and the KdV–Burgers equations, is often a challenging task. The YTDM and HPTM approaches offer innovative techniques for solving FPDEs with high accuracy and efficacy. These approaches offer a robust framework for addressing complex nonlinear FDEs, particularly when applied with the Caputo fractional operator. The findings enhance our understanding of diffusion and wave dynamics in non-integer systems by demonstrating the significant impact of the fractional parameter on solution behavior. The characteristics of the resulting series solutions were illustrated using 2D and 3D graphs for various fractional orders. The proposed solutions, as confirmed by the presented tables and figures, are highly accurate. To support the theoretical results, graphical illustrations were used to confirm the practical relevance of the solutions in modeling physical phenomena. This study demonstrates the efficiency and reliability of YTDM and HPTM as powerful tools for analyzing fractional-order equations. These methods not only simplify the solution process but also offer new perspectives into the dynamics of fractional systems. They hold significant potential for applications in diverse fields, such as nonlinear dynamics, fluid mechanics, and wave propagation. Future studies could explore the application of these methodologies in interdisciplinary contexts and extend them to even more complex fractional models.
Funding
This project was funded by KAU Endowment (WAQF) at King Abdulaziz University, Jeddah, Saudi Arabia. The authors, therefore, acknowledge with thanks WAQF and the Deanship of Scientific Research (DSR) for technical and financial support.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liouville, J. Mémoire sur quelques questions de géométrie et de mécanique, et sur un nouveau genre de calcul pour résoudre ces questions. J. L’École Polytech. 1832, 13, 1–69. [Google Scholar]
- Riemann, G.F.B. Versuch einer allgemeinen Auffassung der Integration und Differentiation. In Gesammelte Mathematische Werke; Weber, H., Dedekind, R., Eds.; Teubner: Leipzig, Germany, 1896; pp. 331–344. [Google Scholar]
- Caputo, M. Elasticitá e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley-Interscience: New York, NY, USA, 1993; pp. 1–366. [Google Scholar]
- Podlubny, I. Fractional differential equations: An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. In Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1998; pp. 1–366. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. (Eds.) Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; pp. 1–523. [Google Scholar]
- Baleanu, D.; Güvenç, Z.B.; Tenreiro Machado, J.A. (Eds.) New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Dordrecht, The Netherlands; Heidelberg, Germany; London, UK; New York, NY, USA, 2010; pp. 1–546. [Google Scholar]
- Bulut, H.; Sulaiman, T.A.; Baskonus, H.M.; Rezazadeh, H.; Eslami, M.; Mirzazadeh, M. Optical solitons and other solutions to the conformable space–time fractional Fokas–Lenells equation. Optik 2018, 172, 20–27. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Solving smoking epidemic model of fractional order using a modified homotopy analysis transform method. Math. Sci. 2019, 13, 115–128. [Google Scholar] [CrossRef]
- Baleanu, D.; Wu, G.-C.; Zeng, S.-D. Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos Solitons Fractals 2017, 102, 99–105. [Google Scholar] [CrossRef]
- Alshammari, N.A.; Alharthi, N.S.; Saeed, A.M.; Khan, A.; Ganie, A.H. Numerical solutions of a fractional order SEIR epidemic model of measles under Caputo fractional derivative. PLoS ONE 2025, 20, e0321089. [Google Scholar] [CrossRef]
- AlBaidani, M.M. Analytical Insight into Some Fractional Nonlinear Dynamical Systems Involving the Caputo Fractional Derivative Operator. Fractal Fract. 2025, 9, 320. [Google Scholar] [CrossRef]
- Ganie, A.H.; Khan, A.; Alharthi, N.S.; Tolasa, F.T.; Jeelani, M.B. Comparative Analysis of Time-Fractional Coupled System of Shallow-Water Equations Including Caputos Fractional Derivative. J. Math. 2024, 2024, 2440359. [Google Scholar] [CrossRef]
- Fadhal, E.; Ganie, A.H.; Alharthi, N.S.; Khan, A.; Fathima, D.; Elamin, A.E.A. On the analysis and deeper properties of the fractional complex physical models pertaining to nonsingular kernels. Sci. Rep. 2024, 14, 22182. [Google Scholar] [CrossRef]
- Povstenko, Y. Linear Fractional Diffusion—Wave Equation for Scientists and Engineers; Birkhäuser: Cham, Switzerland, 2015; pp. 1–453. [Google Scholar]
- Mohammed, P.O.; Machado, J.A.T.; Guirao, J.L.G.; Agarwal, R.P. Adomian decomposition and fractional power series solution of a class of nonlinear fractional differential equations. Mathematics 2021, 9, 1070. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Abou Hasan, M.M.; Baleanu, D. New studies for general fractional financial models of awareness and trial advertising decisions. Chaos Solitons Fractals 2017, 104, 772–784. [Google Scholar] [CrossRef]
- Liu, D.Y.; Gibaru, O.; Perruquetti, W.; Laleg-Kirati, T.M. Fractional order differentiation by integration and error analysis in noisy environment. IEEE Trans. Autom. Control 2015, 60, 2945–2960. [Google Scholar] [CrossRef]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons to the space-time fractional (1+1)-dimensional coupled nonlinear Schrödinger equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Gallo, A. New results on the synthesis of FO-PID controllers. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 997–1007. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Novel simulations to the time-fractional Fishers equation. Math. Sci. 2019, 13, 33–42. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Analytical solution of a time-fractional Navier–Stokes equation by Adomian decomposition method. Appl. Math. Comput. 2006, 177, 488–494. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Gusu, D.M.; Mohammed, P.O.; Wedajo, G.; Nonlaopon, K.; Hamed, Y.S. Solutions of general fractional-order differential equations by using the spectral Tau method. Fractal Fract. 2021, 6, 7. [Google Scholar] [CrossRef]
- Ganie, A.H.; Mofarreh, F.; Khan, A. On new computations of the time-fractional nonlinear KdV–Burgers equation with exponential memory. Phys. Scr. 2024, 99, 045217. [Google Scholar] [CrossRef]
- Arshad, M.; Khan, S.; Sohail, M.; Khan, H.; Tchier, F.; Haidary, M.K.; Nadeem, M. The solution comparison of fractional heat transfer and porous media equations using analytical techniques. Comput. Math. Math. Phys. 2024, 64, 1614–1630. [Google Scholar] [CrossRef]
- Johnson, R.S. A non-linear equation incorporating damping and dispersion. J. Fluid Mech. 1970, 42, 49–60. [Google Scholar] [CrossRef]
- Van Wijngaarden, L. On the motion of gas bubbles in a perfect fluid. Annu. Rev. Fluid Mech. 1972, 4, 369–373. [Google Scholar]
- Hu, P.N. Collisional theory of shock and nonlinear waves in a plasma. Phys. Fluids 1972, 15, 854–864. [Google Scholar] [CrossRef]
- Johnson, R.S. Shallow water waves on a viscous fluid—The undular bore. Phys. Fluids 1972, 15, 1693–1699. [Google Scholar] [CrossRef]
- Gao, G. A theory of interaction between dissipation and dispersion of turbulence. Sci. Sin. Ser. Math. Phys. Tech. Sci. 1985, 28, 616–627. [Google Scholar]
- Liu, S.; Liu, S. KdV–Burgers equation modelling of turbulence. Sci. China Ser. A Math. 1992, 5, 576–586. [Google Scholar]
- Zheng, B.; Wen, C. Exact solutions for fractional partial differential equations by a new fractional sub-equation method. Adv. Differ. Equ. 2013, 2013, 199. [Google Scholar] [CrossRef]
- Naher, H.; Abdullah, F.A.; Mohyud-Din, S.T. Extended generalized Riccati equation mapping method for the fifth-order Sawada–Kotera equation. AIP Adv. 2013, 3, 052104. [Google Scholar] [CrossRef]
- Dinarvand, S.; Khosravi, S.; Doosthoseini, A.; Rashidi, M.M. The homotopy analysis method for solving the Sawada–Kotera and Laxs fifth-order KdV equations. Adv. Theor. Appl. Mech. 2008, 1, 327–335. [Google Scholar]
- Wazwaz, A.-M. Partial Differential Equations and Solitary Waves Theory; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Adomian, G. Nonlinear Stochastic Operator Equations; Academic Press: San Diego, CA, USA, 2014. [Google Scholar]
- Cherruault, Y. Convergence of Adomian’s method. Kybernetes 1989, 18, 31–38. [Google Scholar] [CrossRef]
- Adomian, G. Solution of coupled nonlinear partial differential equations by decomposition. Comput. Math. Appl. 1996, 31, 117–120. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- Desai, K.R. Solution of Burger’s equation and coupled Burger’s equations by Homotopy perturbation method. Int. J. Eng. Res. Appl. 2012, 2, 2033–2040. [Google Scholar]
- Elzaki, T.M. The new integral transform Elzaki transform. Glob. J. Pure Appl. Math. 2011, 7, 57–64. [Google Scholar]
- Alshikh, A.A.; Mahgob, M.M.A. A comparative study between Laplace transform and two new integrals “Elzaki” transform and “Aboodh” transform. Pure Appl. Math. J. 2016, 5, 145–150. [Google Scholar] [CrossRef]
- Schiff, J.L. The Laplace Transform: Theory and Applications; Springer Science & Business Media: New York, NY, USA, 1999. [Google Scholar]
- Ganie, A.H. An efficient analytical approaches to investigate nonlinear two-dimensional time-fractional Rosenau–Hyman equations within the Yang transform. AIP Adv. 2024, 14, 095220. [Google Scholar] [CrossRef]
- Ghorbani, A. Beyond Adomian polynomials: He polynomials. Chaos Solitons Fractals 2009, 39, 1486–1492. [Google Scholar] [CrossRef]
- Adomian, G. A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 1988, 135, 501–544. [Google Scholar] [CrossRef]
- Bekela, A.S.; Deresse, A.T. A hybrid Yang transform Adomian decomposition method for solving time-fractional nonlinear partial differential equation. BMC Res. Notes 2024, 17, 226. [Google Scholar] [CrossRef]
- Cooper, G.J. Error bounds for numerical solutions of ordinary differential equations. Numer. Math. 1971, 18, 162–170. [Google Scholar] [CrossRef]
- Warne, P.G.; Warne, D.A.P.; Sochacki, J.S.; Parker, G.E.; Carothers, D.C. Explicit a-priori error bounds and adaptive error control for approximation of nonlinear initial value differential systems. Comput. Math. Appl. 2006, 52, 1695–1710. [Google Scholar] [CrossRef]
- Yüzbaşı, Ş. A numerical approach for solving a class of the nonlinear Lane–Emden type equations arising in astrophysics. Math. Methods Appl. Sci. 2011, 34, 2218–2230. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).