Abstract
Fractal dimension has proven to be a valuable tool in the analysis of geological data. For instance, it can be used for assessing the distribution and connectivity of fractures in rocks, which is important for evaluating hydrocarbon storage potential. However, while calculating a single fractal dimension for an entire geological profile provides a general overview, it can obscure local variations. These localized fluctuations, if analyzed, can offer a more detailed and nuanced understanding of the profile’s characteristics. Hence, this study proposes a fractal characterization procedure using a new strategy based on moving windows applied to the analysis domain, enabling the evaluation of data multifractality through the Dynamical Approach Method. Validations for the proposed methodology were performed using controlled artificial data generated from Weierstrass–Mandelbrot functions. Then, the methodology was applied to real geological profile data measuring permeability and porosity in oil wells, revealing the fractal dimensions of these data along the depth of each analyzed case. The results demonstrate that the proposed methodology effectively captures a wide range of fractal dimensions, from high to low, in artificially generated data. Moreover, when applied to geological datasets, it successfully identifies regions exhibiting distinct fractal characteristics, which may contribute to a deeper understanding of reservoir properties and fluid flow dynamics.
1. Introduction
The complex nature of well logs [1], often characterized by irregular patterns and non-linear relationships, poses significant challenges for traditional geometric modeling. For example, Euclidean classic geometry [2], limited to integer dimensions, struggles to adequately represent complex data [3] such as intricate geological structures and uneven distribution of resources found in oil wells. Fractal geometry, on the other hand, offers a more suitable framework for modeling these complex systems [4]. By capturing the self-similar and scale-invariant characteristics of petroleum data, fractal geometry can enhance predictive models and improve our understanding of reservoir dynamics [5].
Dimri [6] provided an analysis of fractal applications in earth sciences, focusing on geological fault assessment, geophysical well log interpretation, and seismic signal analysis. Wu etal. [7] further employed fractal dimensions to characterize pore structures in tight oil and gas reservoirs, revealing a correlation between fractal dimensions and pore structure parameters. They demonstrated that the fractal dimension of nuclear magnetic resonance (NMR)-echoed data are particularly effective for evaluating pore structure in tight sandstone formations, providing insights crucial for reservoir quality assessment.
Due to the varied applications of fractal dimension analysis in the oil extraction process, fractal analysis has established itself as a powerful tool for reservoir characterization [8] in recent decades. A significant portion of this research concentrates on multifractal analysis [9,10,11,12,13].
The analysis of petrophysical parameters using multifractal techniques can provide valuable insights into lithological transitions [14], pore structure identification [15], fluid properties [16], hydrocarbon-bearing zones [17], and reservoir quality [18]. These methods allow for a more comprehensive and accurate characterization of well data, leading to improved decision-making in oil and gas exploration and production. Consequently, it is evident that identifying fractal dimensions and multifractality of geophysical data from oil wells plays an important role. Such knowledge can facilitate the development of models that correlate properties like porosity and permeability with the likelihood of discovering oil and gas.
In that way, detecting changes in fractal dimension during oil well exploration is important for understanding reservoir characteristics and improving extraction methods. Variations in fractal dimension can reveal changes in rock porosity, permeability, and fracture distribution [19], which affect how fluids move through the reservoir. By analyzing these changes, geologists can identify the best drilling locations, evaluate the stability of the reservoir, and predict its behavior more accurately. This helps optimize oil production while reducing risks and operational costs.
Recent advancements in multifractal analysis have significantly enhanced the interpretation of geological data by enabling more precise characterization of spatial heterogeneity and complexity across scales. Key developments include the integration of multifractal features with machine learning algorithms for improved prediction and classification [20,21], the use of adaptive and localized methods to detect subtle geological anomalies [22,23], and the application of robust techniques like multifractal-detrended fluctuation analysis and wavelet-based analysis to handle noisy or non-stationary signals such as seismic data [24,25]. Additionally, the rise of 3D multifractal modeling, supported by increased computational capabilities, has enabled more realistic simulations of subsurface structures, benefiting tasks such as mineral prospectivity mapping, reservoir characterization, and geohazard detection [26,27]. These innovations position multifractal analysis, such as the one proposed in this paper, as a powerful and evolving tool in data-driven geoscience.
A variety of methods have been proposed in the literature to calculate fractal and multifractal properties. Prominent techniques include Box Counting [28], Compass [29], Detrended Fluctuation Analysis (DFA) [30], Mass and Modified Mass [31], Hurst and Persistences [32], and the Dynamical Fractal Approach (DFA) [33]. While all these methods are capable of identifying fractal features, their performance can vary significantly based on data type, noise levels, and computational demands [34]. Silva et al. [34] have demonstrated that among all the aforementioned methods, the Dynamical Fractal Approach [33] exhibits the best performance for the majority of tested situations in extracting fractal dimensions, both for synthetic data and geophysical science applications.
All of the previous methods can be applied to data segments to identify changes in fractal behavior. However, the selection of signal segments can introduce inaccuracies in the evaluations. Larger segments generally yield more accurate fractal dimension calculations, attributing an average monofractal behavior to the analyzed window. Conversely, smaller segments are better at detecting fluctuations in fractality across the domain, but they are also more susceptible to inaccuracies caused by noise and the inherent challenges of calculating fractal dimensions with limited data points.
To mitigate the issues arising from the choice of data segment size used to identify multifractality, this paper presents an efficient methodology based on the use of multiple moving windows coupled with the Dynamical Fractal Approach Method [33,35]. Instead of dividing the signal into segments, a set of overlapping moving windows across relatively high peaks in the ranges the domain is used, reducing the influence of noise and enabling a more accurate calculation of the variation in fractality using the Dynamical Approach. To validate the proposed methodology, controlled artificial data are generated using Weierstrass–Mandelbrot functions [36], which are known for their fractal characteristics. The Weierstrass–Mandelbrot function is often used to generate artificial data for verification due to its inherent fractal nature, simulating real-world complexity. Its non-differentiability and self-similarity at all scales create realistic, though controlled, datasets. This allows researchers to test algorithms’ and methods’ robustness against complex, fractal-like patterns, serving as a reliable benchmark for evaluating how well methods handle fractal characteristics. In the work by Silva et al. [34], these functions were used as benchmarks to assess different fractal methods. Then, the methodology is applied to real-world geological profile data collected from oil wells, specifically focusing on permeability and porosity measurements. By analyzing these data along the depth of each well, the fractal dimensions are determined, providing valuable insights about the complex geological structures and their potential impact on oil and gas reserves.
In fact, all methods used for multifractal analysis can benefit from the approach proposed in this paper. The idea is based on the segmentation of the analysis domain using different segment sizes. Hence, aiming to increase the reliability of the results, the averages of the fractal dimensions obtained for each segment are applied. The proposed segmentation strategy enables localized application of fractal analysis methods, producing more robust and reliable results, thereby enhancing the quality of input parameters for machine learning models.
By computing multifractal parameters within a sliding window, this approach enables the identification of spatial variations in scaling behavior, allowing for a more localized assessment of heterogeneity. This is particularly relevant in subsurface formations, where geological properties often change abruptly over short distances. Unlike conventional multifractal models that provide a single set of descriptors for an entire dataset, the moving window approach captures the dynamic evolution of multifractal features, offering greater sensitivity to subtle changes in the data. In practical terms, this facilitates the determination of reservoir boundaries, the detection of stratigraphy discontinuities, and the assessment of flow unit connectivity with improved spatial resolution. Furthermore, the moving window framework can be integrated with other geophysical or petrophysical indicators, making it a flexible tool in multidisciplinary workflows aimed at reducing uncertainty in exploration and development decisions.
It is important to highlight that the primary focus of this paper is not to compare different fractal dimension estimation methods (which was the focus of the work of Silva et al. [34]). Instead, the proposed methodology is designed to be flexible and generalizable, as it can be applied in conjunction with any fractal analysis technique. Therefore, rather than evaluating the relative performance of different methods, this paper aims to demonstrate how the use of multiple windows enhances the consistency and quality of results within the chosen analytical framework.
2. Methodology
2.1. Dynamical Approach Method
The Dynamical Fractal Approach suggests that by constructing mechanical systems based on the data points of a time series, the ratios of the natural frequencies of these systems will correspond to the fractal dimension of the original data. In other words, it establishes a relationship between the vibrational properties of a constructed mechanical system and the complexity of the underlying data. In this mechanical analogy, the constructed system is a sequence of connected bars, with one end clumped, where each of the system’s nodes is a point in the time series. This method was proposed by Bevilacqua et al. [33,35] and is briefly described below.
The dynamic direct problem for fractal structures involves iteratively segmenting the geometry of a given self-similar data point, where points are selected along the domain, separated by fixed-size steps. These steps determine the resolution of the fractal representation: smaller step sizes lead to a structure that is closer to the original data, while larger steps simplify the mechanical analogy, approximating it to a single bar connecting the first and last points of the data.
At each iteration, the domain is partitioned using a uniform step size , where represents the distance between consecutive points in the domain. As decreases, more points are included, refining the geometric structure to better represent the full dataset. Conversely, larger step sizes reduce the number of points, simplifying the representation. Bevilacqua et al. [33,35] prove that the relationship between the first oscillation period () and the segment length () provides the fractal properties of the data. This relationship takes the form of a power law:
where is the single bar connecting the first and last points of the data and its first vibration period; a is the slope of the log-log plot graphic; and b is the linear coefficient. The dynamic fractal dimension D for rotational movements can then be derived from this slope as
2.2. Moving Windows-Based Strategy
Consider a dataset , where i ranges from 1 to the total number of data points . Here, represents the inputs of the problem’s domain and their respective images. The proposed methodology involves a series of steps associated with segments of the dataset bounded by moving windows (for and ) concentric at , where W and S are the number of windows and steps, respectively, as presented in Figure 1. For simplicity, Figure 1 only shows the case where , i.e., three windows.
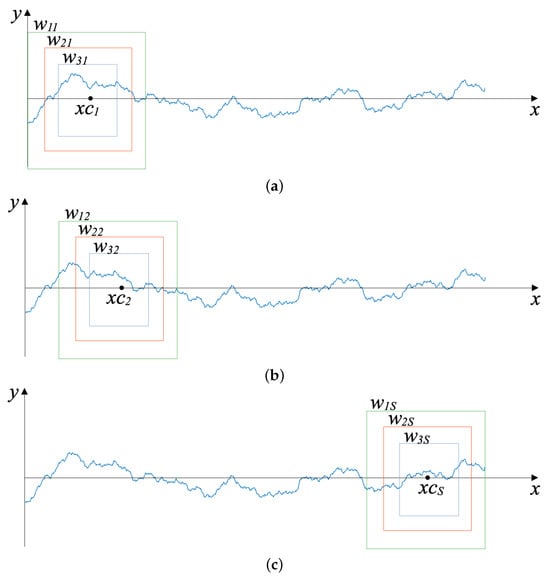
Figure 1.
Moving widows scheme for multifractality evaluation: (a) first step, (b) second step, (c) step.
All calculations of the fractal dimensions in this work are made by applying the rotational dynamic approach, briefly described in the previous section [35]. However, other methods could be used to determine the fractal dimension without compromising the proposed methodology of moving windows, such as the Hurst Method [37], the Detrended Fluctuation Analysis [38], the Persistences Method [32], Box Counting [39], or the Compass Method [40]. The choice to use the Dynamical Approach Method was based on the results of Silva et al. [34], which demonstrated the superiority of this method when compared to the others analyzed. In that paper, the authors conducted a comprehensive comparative analysis of eight fractal analysis methods, including Box Counting, Compass, Detrended Fluctuation Analysis, Dynamical Fractal Approach, Hurst, Mass, Modified Mass, and Persistence. These methods were applied to artificially generated fractal data, such as Weierstrass–Mandelbrot functions, as well as natural datasets related to environmental and geophysical domains. They indicated that the Dynamical Fractal Approach consistently demonstrated the highest accuracy across different datasets.
Figure 2 provides a visual representation of the results (fractal dimensions) yielded by the proposed methodology for a hypothetical signal.
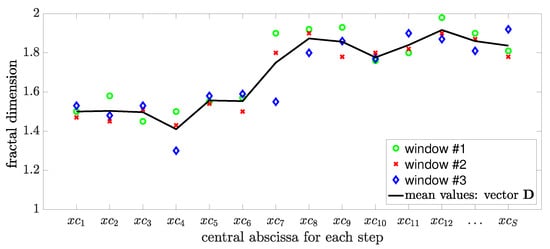
Figure 2.
Visual representation of the proposed methodology.
The methodology comprises four phases:
- First phase: Evaluate , which is the average fractal dimension associated with the data within the window , centered at . Thus, is related to (see Figure 1).
- Second phase: Define a new set of windows , centered at . This new set of windows is obtained by shifting all windows from the previous set by positions.
- Third phase: Evaluate , which is the average fractal dimension associated with the data within the window , centered at . Thus, is related to .
- Fourth phase: Repeat the second and third phases for subsequent steps, until the step is reached. Hence, a vector with fractal dimensions , respectively, associated with the vector is obtained.
The vector represents the multifractal dimension estimates along the domain x.
The vector has components varying within the range [, ], where and ; is the number of points in the largest window; and and denote the ceiling and floor functions, respectively. As a result, no fractal dimension is calculated for and using the proposed methodology.
Some parameters are critical for the functioning of the proposed methodology and must be adjusted for each particular case, according to the focus of the analysis. They are as follows:
- •
- The number of windows W. There must be a balance between computational efficiency and the accuracy of the vector . A larger W will comprise more data points, potentially improving the reliability of the fractal dimension estimates for . However, it will also increase the computational load. Thus, selecting W involves a trade-off: minimizing computational costs without compromising the accuracy of the estimates for .
- •
- The window size. The window size should be selected based on the desired resolution and the intrinsic characteristics of the data. Larger windows capture broader trends in fractal dimensions but may smooth out local details. Smaller windows are more sensitive to local variations but may be more susceptible to noise and imprecision inherent in the calculation of fractal dimension with few data points.
- •
- The step size . This parameter dictates the amount by which the windows are shifted along the dataset at each step. Typically, is less than or equal to the length of the smallest window to ensure overlapping, which provides smoother transitions between segments. The choice of is a trade-off between available computational resources and the desired resolution for locating points that indicate a change in the fractal behavior of the signal.
3. Validation
The validation of the proposed methodology is performed by using artificial data for which the fractal dimensions are known. Data with multifractal characteristics are generated using the Weierstrass–Mandelbrot function [36,41], shown in Equation (3) [42]:
where D is the fractal dimension, b is a frequency parameter with a value larger than 1, and is a real number indicating a phase shift for the harmonic term n between A and B values.
The closer the value of D is to 1, the smoother is; on the contrary, the closer to 2 the function is, the more irregular is. Figure 3 shows two distinct scenarios according to the fractal dimension. The first image is a Weierstrass function with dimension 1.3, whose behavior is smoother, while the second image has a dimension value equal to 1.7 with opposite behavior near irregular characteristics.
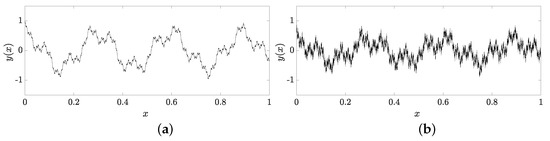
Figure 3.
Typical Weierstrass–Mandelbrot functions (a) D = 1.3, (b) D = 1.7.
Four signals with 16,384 data points () each were used to validate the proposed methodology. Also, the following parameters were defined:
- •
- Number of windows. After several preliminary numerical tests, it was verified that six windows provided a good precision for the evaluation of fractal dimensions without significantly increasing the computational costs.
- •
- Window size. Two analyses were conducted to evaluate the methodology using windows with smaller lengths and larger lengths. For smaller windows, six windows were used with lengths of 401, 501, 601, 701, 801, and 901 data points. For larger windows, sizes of 1001, 1101, 1201, 1301, 1401, and 1501 data points were adopted.
- •
- The step size. To ensure a robust description of the multifractality, the number of steps was adjusted according to the domain size. By using , it resulted in 155 components for smaller windows and 149 for larger ones, providing sufficient detail for the vector .
3.1. Case 1
The first validation case involves a monofractal signal with , as depicted in Figure 4. The goals of this initial analysis are to assess the accuracy and variability of fractal dimension estimation along the signal using both small and large window sizes, to compare this with using individual windows separately, to estimate theoretical limitations of the presented methodology, and to evaluate the influence of noise on the identification of fractal dimension.
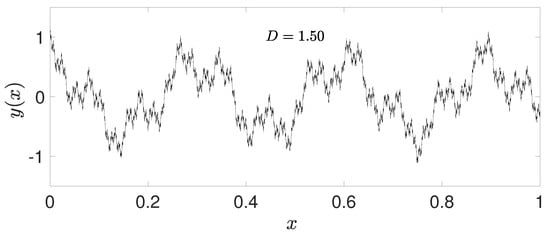
Figure 4.
Case 1—artificial monofractal signal with .
Figure 5 shows that for both groups of windows, the fractal dimension is correctly identified. As expected, a higher fluctuation of results around 1.50 is observed for smaller windows are they are more sensitive to local variations.
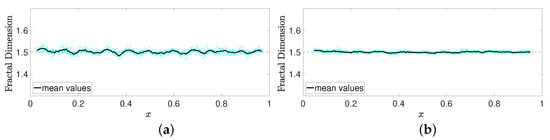
Figure 5.
Identified fractal dimensions for Case 1 with different set of window sizes. (a) Small windows. (b) Larger windows.
Figure 6 details three outcomes for the fractal dimension of Case 1, obtained by analyzing the smallest (401 points), intermediate (901 points), and largest (1501 points) windows separately. While all three tend towards the mean value of 1.50, the dispersion of results varies significantly. Notably, the dispersion decreases as the window size grows.

Figure 6.
Identified fractal dimensions for Case 1 with different window sizes. (a) Smallest window (401 points). (b) Medium window (901 points). (c) Largest window (1501 points).
Table 1 and Table 2 present a summary of the average fractal dimensions for individual windows and the window sets proposed in this study. The mean values in both tables converge accurately to the dimension of 1.50, with no significant differences. As expected, larger windows exhibit lower dispersion, as indicated by the standard deviations. More importantly, the proposed methodology utilizing multiple windows substantially reduces the standard deviations, enhancing the reliability of our findings.

Table 1.
Fractal dimensions identified for Case 1 using small windows.

Table 2.
Fractal dimensions identified for Case 1 using larger windows.
Clearly, for simple monofractal cases like Case 1, employing larger windows generally yields better results as more data points are included in the analysis. Despite that, using multiple windows still enhances result quality by filtering out random fluctuations, as shown in Table 1 and Table 2. However, when dealing with multifractal scenarios, large windows can obscure the underlying complexity, providing only average fractal dimensions.
The theoretical limit of the presented methodology is closely linked to the number and size of the adopted windows. For Case 1, Table 1 and Table 2 show that the average fractal dimension has a percentage error of 0.15% when small windows are used and 0.03% for large windows, which can be considered good performance in identifying the average fractal dimension. However, it is necessary to observe the confidence interval of the results across the domain. In the case of small windows, the standard deviation obtained was 0.0063, resulting in an approximate 95% confidence interval between 1.5148 and 1.4896 (mean ± two standard deviations), giving a variation range of 0.0252. For large windows, the 95% confidence interval has upper and lower limits of 1.5061 and 1.4949, respectively, resulting in a smaller variation range of 0.0112. Thus, based on the evaluated results of Case 1, it can be stated that the presented methodology has good sensitivity to detect changes in the fractal dimension greater than 0.0252 when using small windows and 0.0112 for large windows.
The analysis of the influence of noise on the identification of the fractal dimension is performed using the signal presented in Figure 4 with added random noise defined by Equation (4):
where is the noisy signal; p is a value between 0 and 2%; a is the root mean square of ; and U is random uniform distribution over the interval .
Figure 7a,b show the variation of the identified fractal dimension for the signal as a function of the noise percentage p. In each graph, three series are displayed: the identified average values (in blue) and the upper and lower limits of an approximate 95% confidence interval (mean ± 2 times the standard deviations) in green and magenta, respectively.
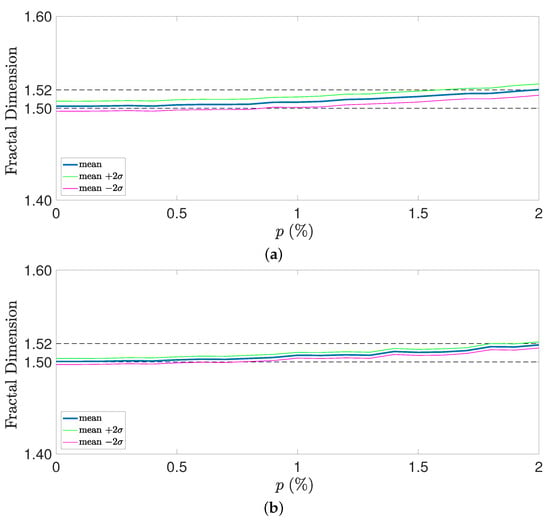
Figure 7.
Influence of noise in fractal dimension identified using the proposed approach. (a) For small windows. (b) For large windows.
As expected, increasing the magnitude of noise leads to a rise in the identified fractal dimension in both analyzed cases. This occurs because the introduction of noise amplifies the oscillatory behavior of the resulting signal, thereby increasing its fractal dimension. As a result, values reach approximately 1.52 with 2% noise for both smaller and larger window sizes. However, it is observed that larger windows exhibit a more gradual increase in the fractal dimension, along with a smaller standard deviation, thereby enhancing the reliability of the results.
The subsequent case study examines the performance of our proposed method in a bifractal context.
3.2. Case 2
The primary objective of the second analysis is to assess the methodology’s ability to accurately identify the exact point within the domain where a change in the fractal dimension occurs. To this end, a signal was generated with two distinct fractal dimensions: 1.80 for and 1.20 for , as depicted in Figure 8. The abscissa represents the point at which the fractal dimension changes. Using smaller windows, a more precise identification of the fractal dimension transition point was observed, and with these windows, the transition from a dimension of 1.80 to 1.20 occurred between abscissas 0.500 and 0.528. For larger windows, the transition was detected with a small delay, between abscissas 0.516 and 0.546. As previously noted, while both window groups accurately captured the overall fractal dimensions, smaller windows exhibited greater variability in the results (see Figure 9).
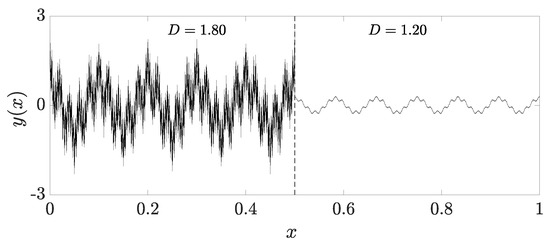
Figure 8.
Case 2—artificial multifractal signal (fractal dimensions 1.8 and 1.2).
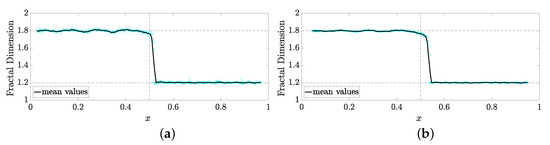
Figure 9.
Identified fractal dimensions for Case 2 with different window sizes. (a) Small windows. (b) Larger windows.
The variation ranges of the fractal dimensions obtained for small windows and large windows, excluding the transition region, were 0.0233 and 0.0115, respectively. These values are consistent with the theoretical limits evaluated within a 95% confidence interval in the previous case (0.0252 when using small windows and 0.0112 for large windows).
The identification of fractal dimension variations across the domain using the proposed methodology exhibits similarities to Short-Time Fourier Transform (STFT) techniques employed for frequency determination. The calculation of the variation of can be considered a form of “instantaneous fractal dimension”, analogous to the calculation of instantaneous frequencies [43] using STFT. In both methodologies, larger windows lead to more accurate estimations of or but reduce spatial resolution. Conversely, smaller windows provide better spatial localization but at the expense of accuracy in estimating or .
3.3. Case 3
The third validation case aims to assess the methodology’s ability to detect subtle variations in the fractal dimension across the domain. To this end, a multifractal signal was generated (Figure 10) with two segments having a fractal dimension of 1.30 and two others with a dimension of 1.33. The results show that both window groups accurately captured the fractal dimensions in their respective sections (see Figure 11). However, a higher fluctuation was observed compared to the previous cases for both window groups. This may be due to the proximity of the dimensions 1.30 and 1.33, making it more challenging for the dynamical approach method to accurately distinguish them. Nevertheless, especially for larger windows, the results obtained both in terms of the location of fractal transitions and the magnitudes of the calculated dimensions can be consider satisfactory.
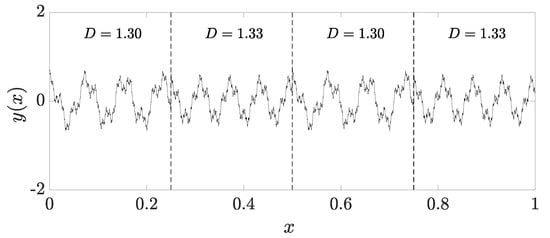
Figure 10.
Case 3—artificial multifractal signal (fractal dimensions 1.30 and 1.33).
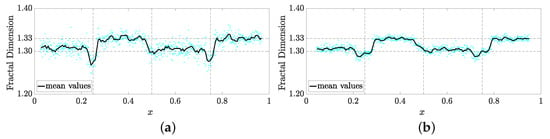
Figure 11.
Identified fractal dimensions for Case 3 with different window sizes. (a) Small windows. (b) Larger windows.
The results for Case 3 once again confirm the analysis regarding the theoretical limitations discussed in Case 1. Greater fluctuation in results is observed for small windows around the exact fractal dimension values compared to those obtained with large windows. Furthermore, the range of variation for these fluctuations, excluding transition regions, is consistent with what was detected in the analysis of Case 1, specifically: 0.0244 when using small windows and 0.0148 for large windows.
3.4. Case 4
The final validation case seeks to evaluate the methodology’s capacity to distinguish fractality in signals with multiple levels of fractal dimension. To this end, the signal in Figure 12 was generated with eight distinct fractal dimensions ranging from 1.20 to 1.90. In this example, both window groups correctly identified each of the eight fractal dimension levels, as shown in Figure 13. However, smaller windows exhibited superior performance in identifying transition zones, while larger windows displayed lower result fluctuations.
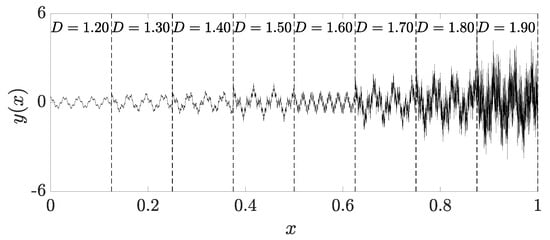
Figure 12.
Case 4—artificial multifractal signal with several fractal dimensions.
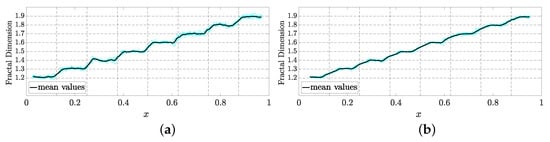
Figure 13.
Identified fractal dimensions for Case 4 with different window sizes. (a) Small windows. (b) Larger windows.
All calculations were implemented and performed using MATLAB software (version 2022a). The Weierstrass–Mandelbrot functions were generated using the MATLAB algorithm provided by Monge-Álvarez, J. (2024) [42]. No preprocessing technique was used prior to the application of the proposed methodology.
4. Multifractality of Geological Data
As already mentioned, detecting subtle changes in fractal dimension is important in geology for analyzing rock structures and resource exploration. These variations reveal shifts in porosity, permeability, and fractures, aiding in reservoir assessment, hazard prediction, and risk management. Hence, the proposed methodology was applied to geological data on permeability and porosity from three oil wells operated by Petrobras S/A, and the geological data correspond to depths ranging approximately from 5000 m to 6000 m.
The three wells were chosen because they exhibit qualitative differences in the fractal dimension as well as in the petrophysical properties. The wells are from a Brazilian Pre-salt carbonate reservoir. This reservoir was subject to tectonics which resulted in faults and fractures. These structures served as conduits to diagenetic corrosive fluids that formed vuggy fractures, caves, and karstic structures. In this kind of reservoir, the porosity ranges from a matrix thin-section scale, passing to the cave and fracture meter scale, and increasing up to the seismic fault scale. The dissolution processes create after-deposition porosities, which increases the porosity heterogeneity.
In this study, we analyzed the petrophysical logging measurements of Nuclear Magnetic Resonance (NMR) T2 distribution [44], Ultrasonic Borehole Image (UBI) [45], and caliper in the same depth where fractal dimensions were analyzed to verify if there is correlation between the measurements. In the present petrophysical measurement scale, it is possible to classify the porosity in matrix-dominated and vuggy/fracture-dominated porosity [46]. The matrix scale considered is in the order of centimeters, and the cave/fracture scale considered is in the order of meters.
Porosity for each well was obtained through nuclear magnetic resonance (NMR) log measurements and presented as a percentage between 0 and 100. Permeability was obtained using the SDR model on NMR data, with units in milliDarcy (mD), presented in log scale.
The following parameters were used to identify fractal dimensions using the proposed approach. The definition of these parameters was made based on the good results achieved with validation data.
- Number of windows. This number was kept at 6 (six).
- Window size. Smaller windows were used (401, 501, 601, 701, 801, and 901 data points) to focus on local variations in fractal behavior.
- The step size. A step size of was used to provide sufficient detail for the fractal dimension vector .
4.1. Evaluation of Well #1
Figure 14 presents the petrophysical measurements and the interpreted dominant porosity types for Well #1. Figure 14a shows the T2 distribution, which exhibits relatively high peaks in the range of 3–100 ms between 5650 and 5760 m. A possible explanation for these high peaks is that the NMR tool loses contact with the reservoir wall, for instance, in front of caves and wide-open fractures, and then it registers the relaxation decay time of hydrogen within the drilling fluid, which has a very short T2 [47]. This T2 distribution is very similar to the one shown in Figure 1 of the reference [47]. In contrast, the T2 distributions in the other depth ranges display a pattern consistent with a regular pore-scale matrix distribution [44]. In Figure 14b, the Ultrasonic Borehole Image (a full azimuth acoustic image of the borehole wall), reveals several darker vertical lines. The wider lines, indicated by blue arrows, are on the order of meters and correlate with the high peaks in the T2 distribution as well as the caliper peaks in Figure 14c. Based on the above analysis, we interpret a depth range characterized by cave/fracture-dominated porosity and another depth range characterized by matrix-dominated porosity, as indicated in the figure.
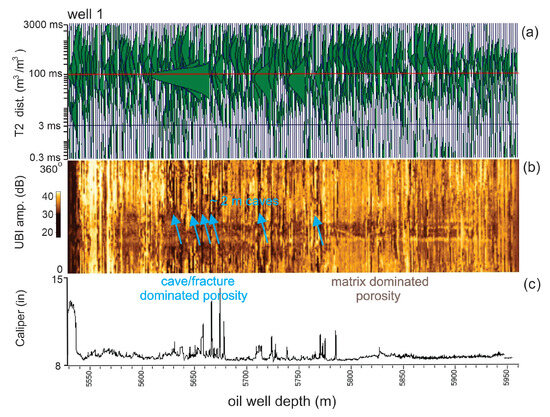
Figure 14.
Petrophysical log measurements from Well #1: (a) the Nuclear Magnetic Resonance T2 distribution, (b) the full azimuth Ultrasonic Borehole Image amplitude, and (c) the caliper. The interpreted cave/fracture- and matrix-dominated porosity intervals are indicated.
Figure 15 presents the geological profiles of porosity and the corresponding fractal dimension as a function of well depth. This figure indicates low variations in fractal dimension, ranging approximately from 1.32 to 1.47, which characterizes an almost monofractal behavior of the data, with an average value of 1.40. In the context of oil wells, the distinction between monofractal and multifractal porosity behavior lies in the complexity and variability of pore distribution across different scales (from pore scale to reservoir scale). Monofractal porosity implies a consistent fractal dimension, indicating a uniform level of heterogeneity throughout the reservoir. This simplifies modeling, as the pore structure’s complexity remains relatively constant. Conversely, multifractal porosity would reflect a more complex and scale-dependent heterogeneity. This would mean that the pore distribution’s complexity changes with the scale of observation, making reservoir modeling more challenging but potentially more accurate in capturing the complex flow dynamics of hydrocarbons.
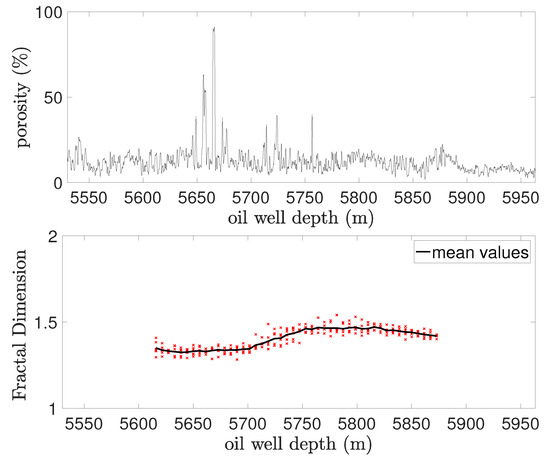
Figure 15.
Variation of porosity and fractal dimension with depth for Well #1.
Figure 16 presents the geological profiles of permeability and the respective fractal dimension as a function of the depth of the well. The results for fractal dimensions indicate multifractal behavior for permeability. A clear step indicating an abrupt change in fractality was detected between 5700 m and 5750 m of depth. These steps are known as the Devil’s Staircase and can indicate the presence of fractures, which play a critical role in hydrocarbon flow. Fractal dimensions for permeability in Well #1 varied between 1.18 and 1.63, averaging 1.41.
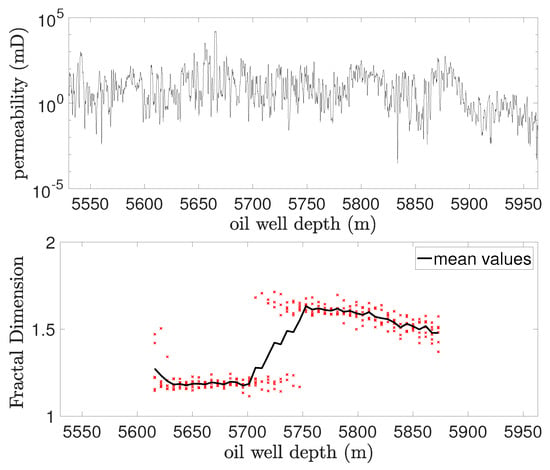
Figure 16.
Variation of permeability and fractal dimension with depth for Well #1.
4.2. Evaluation of Well #2
Figure 17 presents the petrophysical measurements and the dominated porosity interpretation of Well #2. In Figure 17a, the T2 distribution presents relatively high peaks in the range of 3–100 ms between 5160 and 5340 m. This is consistent with the presence of caves and fractures, as discussed in Figure 14. In Figure 17b, the Ultrasonic Borehole Image shows a concentration of wide darker vertical lines between 5160 and 5340 m and less concentration between 5550 and 5630 m. Even concentration appears around 5450 m and 5700 m. Taking into account the caliper of Figure 17c, we interpret two depth ranges of cave/fracture-dominated porosity as well as two depth ranges of matrix-dominated porosity, as indicated in this figure.
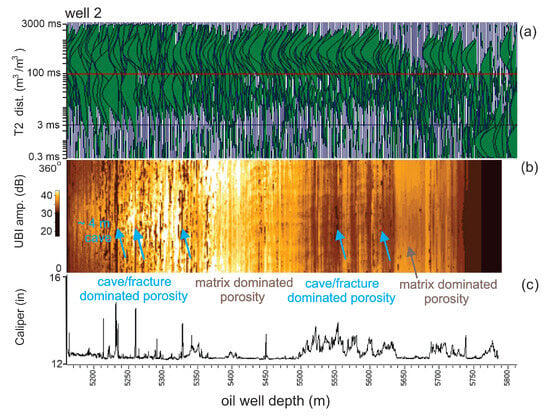
Figure 17.
Petrophysical log measurements from Well #2: (a) the Nuclear Magnetic Resonance T2 distribution, (b) the full azimuth Ultrasonic Borehole Image amplitude, and (c) the caliper. The interpreted cave/fracture- and matrix-dominated porosity intervals are indicated.
The fractal analysis of the porosity profile shown in Figure 18 exhibits a behavior similar to that of Well #1, with small variations in the fractal dimension (maximum: 1.54; minimum: 1.36; average: 1.44), also indicating a tendency towards monofractal behavior.
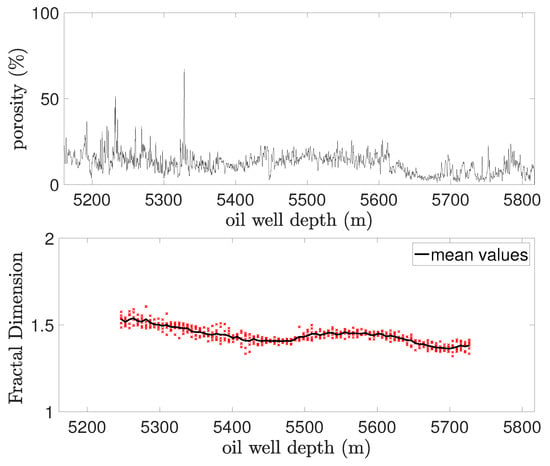
Figure 18.
Variation of porosity and fractal dimension with depth for Well #2.
Conversely, the permeability behavior for Well #2, presented in Figure 19, revealed two abrupt reductions in fractality, one at a depth between 5380 m and 5400 m and another between 5640 m and 5680 m, confirming the multifractal nature of permeability. This could be associated with changes in the fracture density within the rocks at these depths.
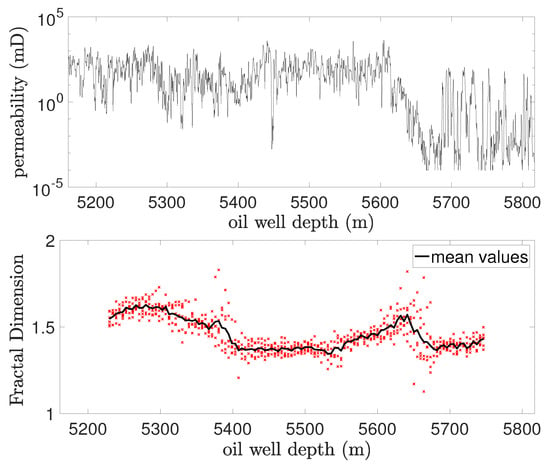
Figure 19.
Variation of permeability and fractal dimension with depth for Well #2.
4.3. Evaluation of Well #3
Figure 20 presents the petrophysical measurements and the dominated porosity interpretation of Well #3. In Figure 20a, the T2 distribution presents relatively high peaks in the range of 3–100 ms around 5570 and around 5700 m. This is consistent with the presence of caves and fractures, as discussed in the other wells. In Figure 20b, the Ultrasonic Borehole Image shows a concentration of wide darker vertical lines at depths that include 5500 m; 5560 m; and 5650–5700 m. However there are tool artifacts that hinder the interpretation. Taking into account the caliper of Figure 20c, we interpret two depth ranges of cave/fracture-dominated porosity as well as two depth ranges of matrix-dominated porosity, as indicated in Figure 20. However, due to the artifacts and the lower contrast in properties, we are less confident in the classification of the dominated porosity.
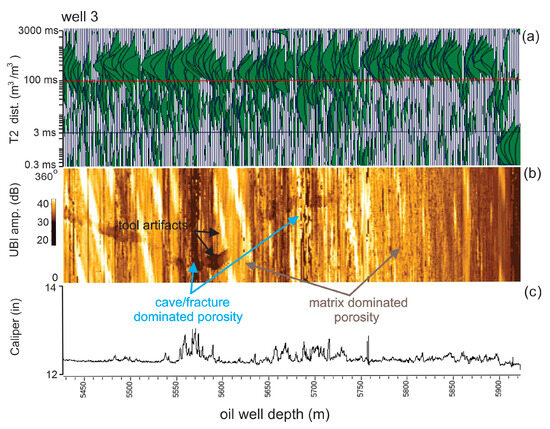
Figure 20.
Petrophysical log measurements from Well #3: (a) the Nuclear Magnetic Resonance T2 distribution, (b) the full azimuth Ultrasonic Borehole Image amplitude, and (c) the caliper. This well presents artifacts in the UBI that hinder interpretation. The interpreted cave/fracture- and matrix-dominated porosity intervals are indicated.
The porosity profile in Figure 21 exhibits a relatively narrow range of fractal dimensions (1.40–1.48, average 1.44), suggesting a predominantly monofractal character, akin to Wells #1 and #2.
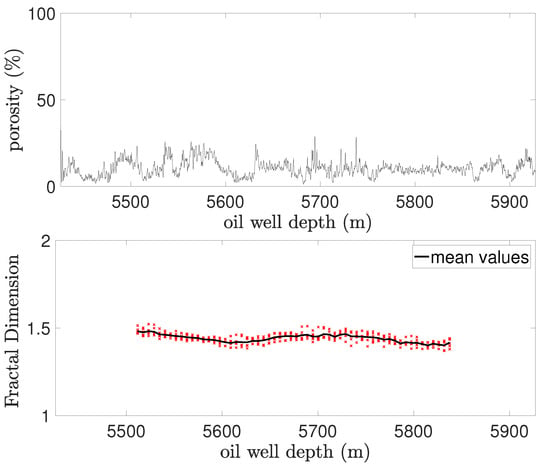
Figure 21.
Variation of porosity and fractal dimension with depth for Well #3.
Conversely, the permeability analysis revealed a decrease in fractality between 5600 m and 5700 m depth, followed by an increase between 5700 m and 5800 m, as shown in Figure 22. This indicates two distinct fractal regimes: one below 5600 m and above 5800 m, with an average fractal dimension of approximately 1.27; and another regime centered around 5700 m, with a fractal dimension of about 1.06. These findings suggest that the degree of fracturing in the rocks varied with depth, decreasing near 5700 m before returning to a level similar to the upper and lower regimes below 5800 m depth.
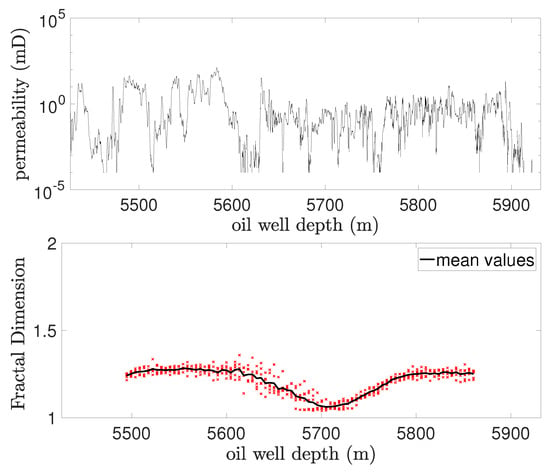
Figure 22.
Variation of permeability and fractal dimension with depth for Well #3.
In this case, by comparing the petrophysical results shown in Figure 20 and the fractal dimensions presented in Figure 21 and Figure 22, we did not detect a clear correspondence between the fractal dimension and the dominated porosity. This suggests that while fractal dimension can be indicative, it should not be considered as a decisive parameter in the evaluation of a petrophysical profile.
5. Conclusions
This study introduced a novel methodology for multifractal analysis based on a moving window strategy combined with the Dynamical Approach Method. Validation with artificial datasets confirmed its high accuracy in detecting local variations in fractal dimensions and its robustness against noise. In addition, the method proved effective in identifying subtle changes and transition zones in monofractal and multifractal artificial signals, offering a reliable framework for fractal characterization.
When applied to real geological data from oil wells, the methodology enabled the identification of zones with varying fractal characteristics in porosity and permeability profiles. For Wells #1 and #2, the estimates of the fractal dimension showed a strong correlation with petrophysical indicators such as the NMR distributions and the caliper logs, reflecting the changes between the matrix and the porosity dominated by fracture/cave. For Well #3, this correlation was less clear, highlighting both the potential and limitations of fractal dimension as a standalone diagnostic tool.
The main contribution of this work lies in enhancing the spatial resolution of multifractal analyses without compromising robustness, which has significant implications for geological modeling, reservoir assessment, and fluid flow predictions. The moving window framework is adaptable and can be integrated with other analytical methods or machine learning models, thereby offering a versatile tool for multidisciplinary geoscientific workflows.
Author Contributions
Conceptualization, A.C. and F.B.; methodology, A.C. and F.B.; validation, J.P., J.F. and L.M.; formal analysis, A.C., F.B., A.O. and F.V.; investigation, A.C., F.B., A.O., F.V., G.S., F.P.d.M. and M.M.; resources, G.S., F.P.d.M. and M.M.; data curation, J.P., J.F., L.M., G.S., F.P.d.M. and M.M.; writing—original draft preparation, J.P., J.F. and L.M.; writing—review and editing, A.C. and F.B.; supervision, A.C. and F.B.; project administration, F.B. and G.S.; funding acquisition, G.S., F.P.d.M. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by PETROBRAS S.A. grant number 0050.0119736.21.9, and the APC was also funded by PETROBRAS S.A. The authors would like to thank Conselho Nacional de Desenvolvimento Científico e Tecnológico—CNPq (Brazil)—407256/2022-9, 402533/2023-2, 303982/2022-5, and 308008/2021-9 and Fundação de Amparo à Pesquisa do Estado de Minas Gerais—FAPEMIG—APQ-00032-24.
Data Availability Statement
Data can be provided upon request.
Conflicts of Interest
Authors Gil Silva, Fernando Pellon de Miranda and Mateus Michelon were employed by PETROBRAS—Petróleo Brasileiro S/A. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Ji, X.; Wang, H.; Ge, Y.; Liang, J.; Xu, X. Empirical mode decomposition-refined composite multiscale dispersion entropy analysis and its application to geophysical well log data. J. Pet. Sci. Eng. 2022, 208, 109495. [Google Scholar] [CrossRef]
- Dai, W.; Shen, Y.; Win, M. A Computational Geometry Framework for Efficient Network Localization. IEEE Trans. Inf. Theory 2018, 64, 1317–1339. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, X.; Gong, M. Two-phase clustering algorithm with density exploring distance measure. CAAI Trans. Intell. Technol. 2018, 3, 59–64. [Google Scholar] [CrossRef]
- Subhakar, D.; Chandrasekhar, E. Reservoir characterization using multifractal detrended fluctuation analysis of geophysical well-log data. Phys. A Stat. Mech. Its Appl. 2016, 445, 57–65. [Google Scholar] [CrossRef]
- Habib, M.; Guangqing, Y.; Xie, C.; Charles, S.; Jakada, H.; Danlami, M.; Ahmed, H.; Omeiza, I. Optimizing oil and gas field management through a fractal reservoir study model. J. Pet. Explor. Prod. Technol. 2016, 7, 43–53. [Google Scholar] [CrossRef]
- Dimri, V. Fractal Solutions for Understanding Complex Systems in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Wu, B.; Xie, R.; Wang, X.; Wang, T.; Yue, W. Characterization of pore structure of tight sandstone reservoirs based on fractal analysis of NMR echo data. J. Nat. Gas Sci. Eng. 2020, 81, 103483. [Google Scholar] [CrossRef]
- Boulassel, A.; Zaourar, N.; Gaci, S.; Boudella, A. A new multifractal analysis-based for identifying the reservoir fluid nature. J. Appl. Geophys. 2021, 185, 104185. [Google Scholar] [CrossRef]
- Marsan, D.; Bean, C. Multiscaling nature of sonic velocities and lithology in the upper crystalline crust: Evidence from the KTB main borehole. Geophys. Res. Lett. 1999, 26, 275–278. [Google Scholar] [CrossRef]
- Guadagnini, A.; Neuman, S.; Riva, M. Numerical investigation of apparent multifractality of samples from processes subordinated to truncated fBm. Hydrol. Processes 2011, 26, 2894–2908. [Google Scholar] [CrossRef]
- Elyas, H.; Hossein, H.; Yousef, S.; Seyed, J. Self-similar segmentation and multifractality of post-stack seismic data. Pet. Explor. Dev. 2020, 47, 781–790. [Google Scholar] [CrossRef]
- Boufadel, M.; Lu, S.; Molz, F.; Lavallee, D. Multifractal scaling of the intrinsic permeability. Water Resour. Res. 2000, 36, 3211–3222. [Google Scholar] [CrossRef]
- Dashtian, H.; Jafari, G.; Sahimi, M.; Masihi, M. Scaling, multifractality, and long-range correlations in well log data of large-scale porous media. Phys. A Stat. Mech. Its Appl. 2011, 390, 2096–2111. [Google Scholar] [CrossRef]
- Zaourar, N.; Hamoudi, M.; Briqueu, L. Détection des transitions lithologiques par l’analyse de la composante fractale des diagraphies par transformée continue en ondelettes. Comptes Rendus Géosci. 2006, 338, 514–520. [Google Scholar] [CrossRef]
- Sha, F.; Xiao, L.; Mao, Z.; Jia, C. Petrophysical Characterization and Fractal Analysis of Carbonate Reservoirs of the Eastern Margin of the Pre-Caspian Basin. Energies 2018, 12, 78. [Google Scholar] [CrossRef]
- Mahsal Khan, M.; Fadzil, A.; Hani, M.; Firdaus, M.; Halim, M. Using Singularity Spectrum Attributes for Analyzing Homogeneity/Heterogeneity of Reservoir. ASEG Ext. Abstr. 2007, 2007, 1–4. [Google Scholar] [CrossRef]
- Ojha, S.; Misra, S.; Tinni, A.; Sondergeld, C.; Rai, C. Pore connectivity and pore size distribution estimates for Wolfcamp and Eagle Ford shale samples from oil, gas and condensate windows using adsorption-desorption measurements. J. Pet. Sci. Eng. 2017, 158, 454–468. [Google Scholar] [CrossRef]
- Golsanami, N.; Fernando, S.; Jayasuriya, M.; Yan, W.; Dong, H.; Cui, L.; Dong, X.; Barzgar, E. Fractal Properties of Various Clay Minerals Obtained from SEM Images. Geofluids 2021, 2021, 5516444. [Google Scholar] [CrossRef]
- Xie, W.; Yin, Q.; Zeng, J.; Yang, F.; Zhang, P.; Yan, B. An Improved Rock Resistivity Model Based on Multi-Fractal Characterization Method for Sandstone Micro-Pore Structure Using Capillary Pressure. Fractal Fract. 2024, 8, 118. [Google Scholar] [CrossRef]
- Sun, T.; Feng, M.; Pu, W.; Liu, Y.; Chen, F.; Zhang, H.; Huang, J.; Mao, L.; Wang, Z. Fractal-Based Multi-Criteria Feature Selection to Enhance Predictive Capability of AI-Driven Mineral Prospectivity Mapping. Fractal Fract. 2024, 8, 224. [Google Scholar] [CrossRef]
- Lal, U.; Chikkankod, A.; Longo, L. Fractal dimensions and machine learning for detection of Parkinson?s disease in resting-state electroencephalography. Neural Comput. Appl. 2024, 36, 8257–8280. [Google Scholar] [CrossRef]
- Zuo, R.; Wang, J. Fractal/multifractal modeling of geochemical data: A review. J. Geochem. Explor. 2016, 164, 33–41. [Google Scholar] [CrossRef]
- Wang, J.; Zuo, R.; Liu, Q. Mapping geochemical anomalies by accounting for the uncertainty of mineralization-related elemental associations. Solid Earth 2024, 15, 731–746. [Google Scholar] [CrossRef]
- Morales Martínez, J.; Segovia-Domínguez, I.; Rodríguez, I.; Horta-Rangel, F.; Sosa-Gómez, G. A modified Multifractal Detrended Fluctuation Analysis (MFDFA) approach for multifractal analysis of precipitation. Phys. A Stat. Mech. Its Appl. 2021, 565, 125611. [Google Scholar] [CrossRef]
- Nicolis, O.; Gonzalez, C. Wavelet-based fractal and multifractal analysis for detecting mineral deposits using multispectral images taken by drones. In Methods and Applications in Petroleum and Mineral Exploration and Engineering Geology; Elsevier: Amsterdam, The Netherlands, 2021; pp. 295–307. [Google Scholar] [CrossRef]
- Sadeghi, B. Simulated-multifractal models: A futuristic review of multifractal modeling in geochemical anomaly classification. Ore Geol. Rev. 2021, 139, 104511. [Google Scholar] [CrossRef]
- Karimpouli, S.; Tahmasebi, P. 3D multi?fractal analysis of porous media using 3D digital images: Considerations for heterogeneity evaluation. Geophys. Prospect. 2018, 67, 1082–1093. [Google Scholar] [CrossRef]
- Zhang, G.; Guo, J.; Xu, B.; Xu, L.; Dai, Z.; Yin, S.; Soltanian, M. Quantitative Analysis and Evaluation of Coal Mine Geological Structures Based on Fractal Theory. Energies 2021, 14, 1925. [Google Scholar] [CrossRef]
- Hotar, V. Application of Fractal Dimension in Industry Practice. In Fractal Analysis—Applications in Physics, Engineering and Technology; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef]
- Raubitzek, S.; Corpaci, L.; Hofer, R.; Mallinger, K. Scaling Exponents of Time Series Data: A Machine Learning Approach. Entropy 2023, 25, 1671. [Google Scholar] [CrossRef]
- Barros, M. The Fractal Dimension of Physical Phenomena in Fractal Geometric Systems. Master’s Thesis, Laboratório Nacional de Computação Científica, Petrópolis, Brazil, 2011. [Google Scholar]
- Barros, M.; Venturelli, F.; Bevilacqua, L. Characterization of complex data functions through local persistence of increments. Commun. Nonlinear Sci. Numer. Simul. 2021, 94, 105590. [Google Scholar] [CrossRef]
- Bevilacqua, L.; Barros, M. The inverse problem for fractal curves solved with the dynamical approach method. Chaos Solitons Fractals 2023, 168, 113113. [Google Scholar] [CrossRef]
- Silva, G.; Miranda, F.; Michelon, M.; Ovídio, A.; Venturelli, F.; Parêdes, J.; Ferreira, J.; Moraes, L.; Barbosa, F.; Cury, A. A Comparative Study of Fractal Models Applied to Artificial and Natural Data. Fractal Fract. 2025, 9, 87. [Google Scholar] [CrossRef]
- Bevilacqua, L.; Barros, M. Dynamical characterization of mixed fractal structures. J. Mech. Mater. Struct. 2011, 6, 51–69. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, C.; Sun, J. Generalized Weierstrass-Mandelbrot Function Model For Actual Stocks Markets Indexes With Nonlinear Characteristics. Fractals 2015, 23, 1550006. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Peng, C.; Buldyrev, S.; Havlin, S.; Simons, M.; Stanley, H.; Goldberger, A. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [PubMed]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications. Biometrics 1990, 46, 886. [Google Scholar] [CrossRef]
- Mandelbrot, B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
- Maragos, P.; Sun, F. Measuring the Fractal Dimension of Signals: Morphological Covers and Iterative Optimization. IEEE Trans. Signal Process. 1993, 41, 108. [Google Scholar] [CrossRef]
- Monge-Álvarez, J.; Weierstrass Cosine Function (WCF). MATLAB Central File Exchange. 2024. Available online: https://www.mathworks.com/matlabcentral/fileexchange/50292-weierstrass-cosine-function-wcf (accessed on 30 October 2024).
- Nogueira, F.; Barbosa, F. Novel approach for precise identification of vibration frequencies and damping ratios from free vibration decay time histories data of nonlinear single degree of freedom models. Int. J.-Non-Linear Mech. 2024, 167, 104867. [Google Scholar] [CrossRef]
- George, R.C.; Xiao, L.; Prammer, M. NMR Logging Principles and Applications; Elsevier Science: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Winkler, K.; D’Angelo, R. Ultrasonic borehole velocity imaging. Geophysics 2006, 71, F25–F30. [Google Scholar] [CrossRef]
- Warren, J.; Root, P. The Behavior of Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Menezes de Jesus, C.; Compan, A.L.M.; Surmas, R. Permeability Estimation Using Ultrasonic Borehole Image Logs in Dual-Porosity Carbonate Reservoirs. Petrophysics 2016, 57, 620–637. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).