Dynamical Behavior Analysis of Generalized Chen–Lee–Liu Equation via the Riemann–Hilbert Approach
Abstract
1. Introduction
2. The Riemann–Hilbert Problem
2.1. The Lax Pair of gCLL Equation
2.2. Spectral Analysis
3. Inverse Scattering Transform
4. Soliton Solutions
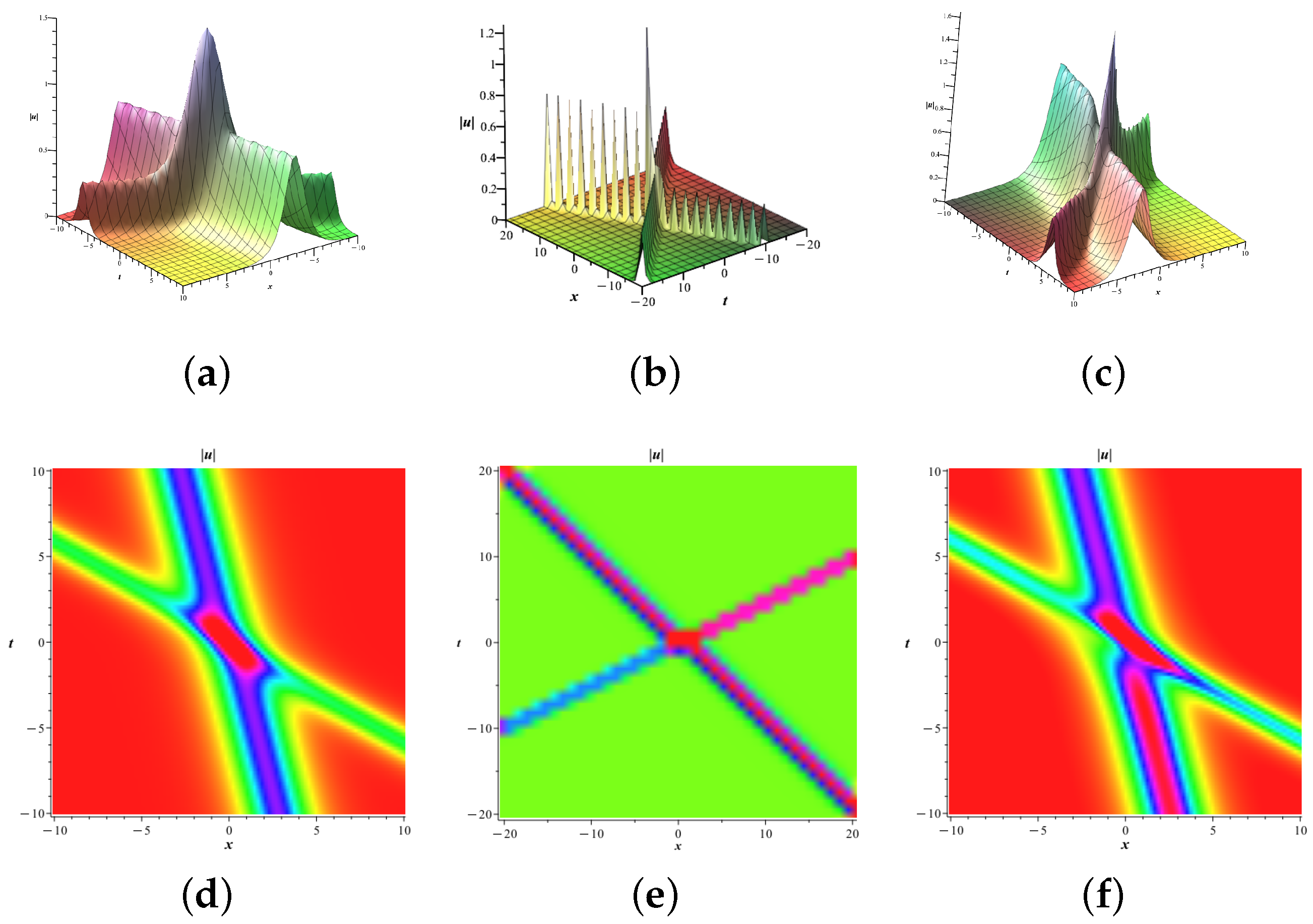
4.1. N-Soliton Solutions
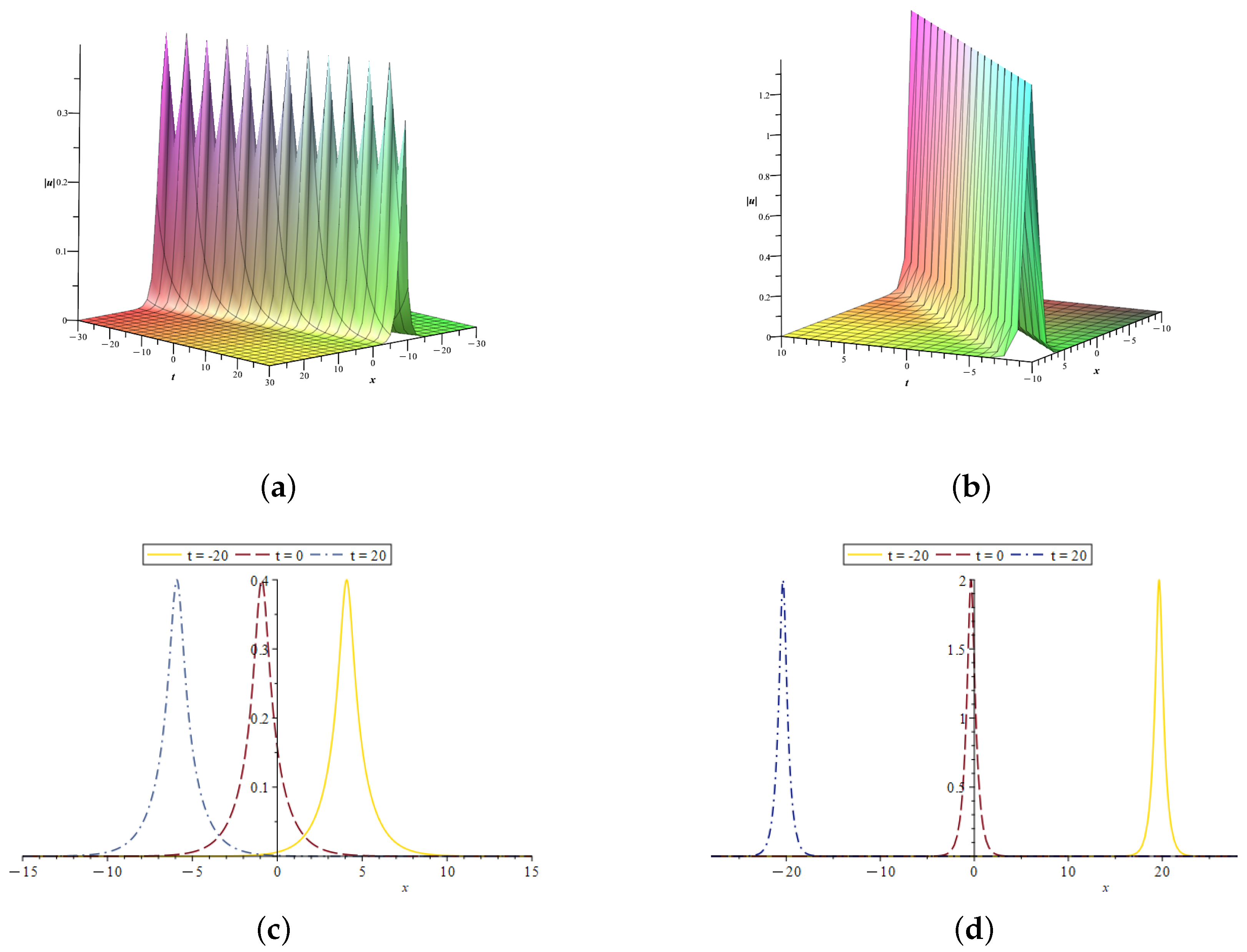
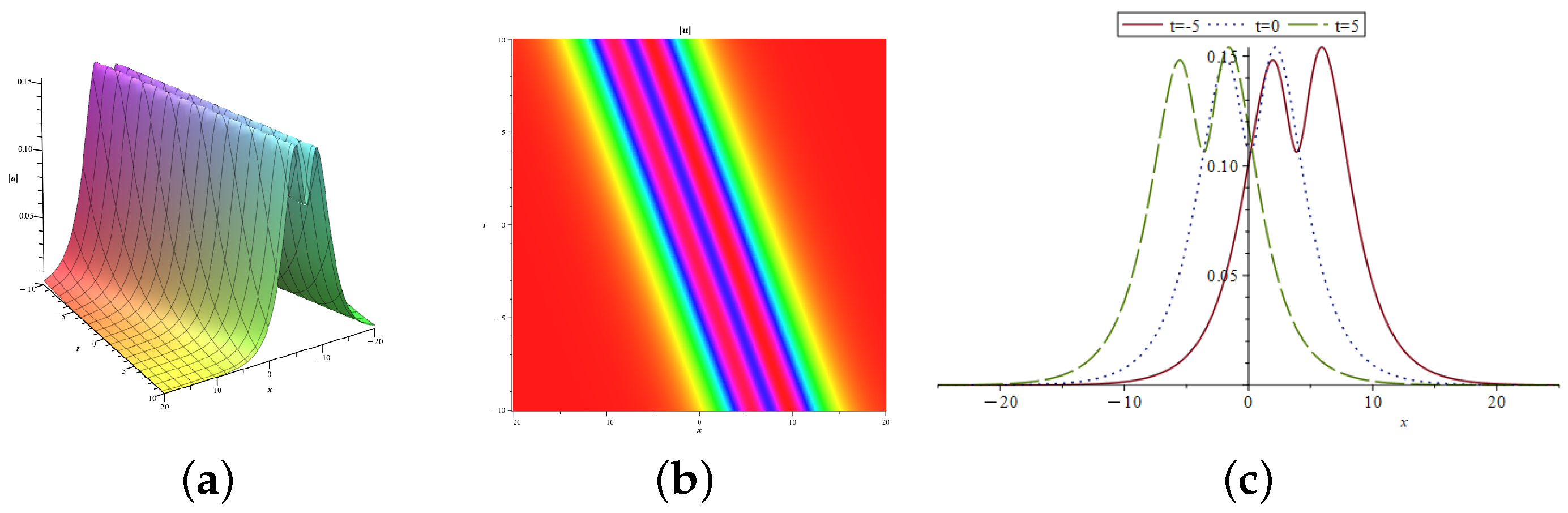
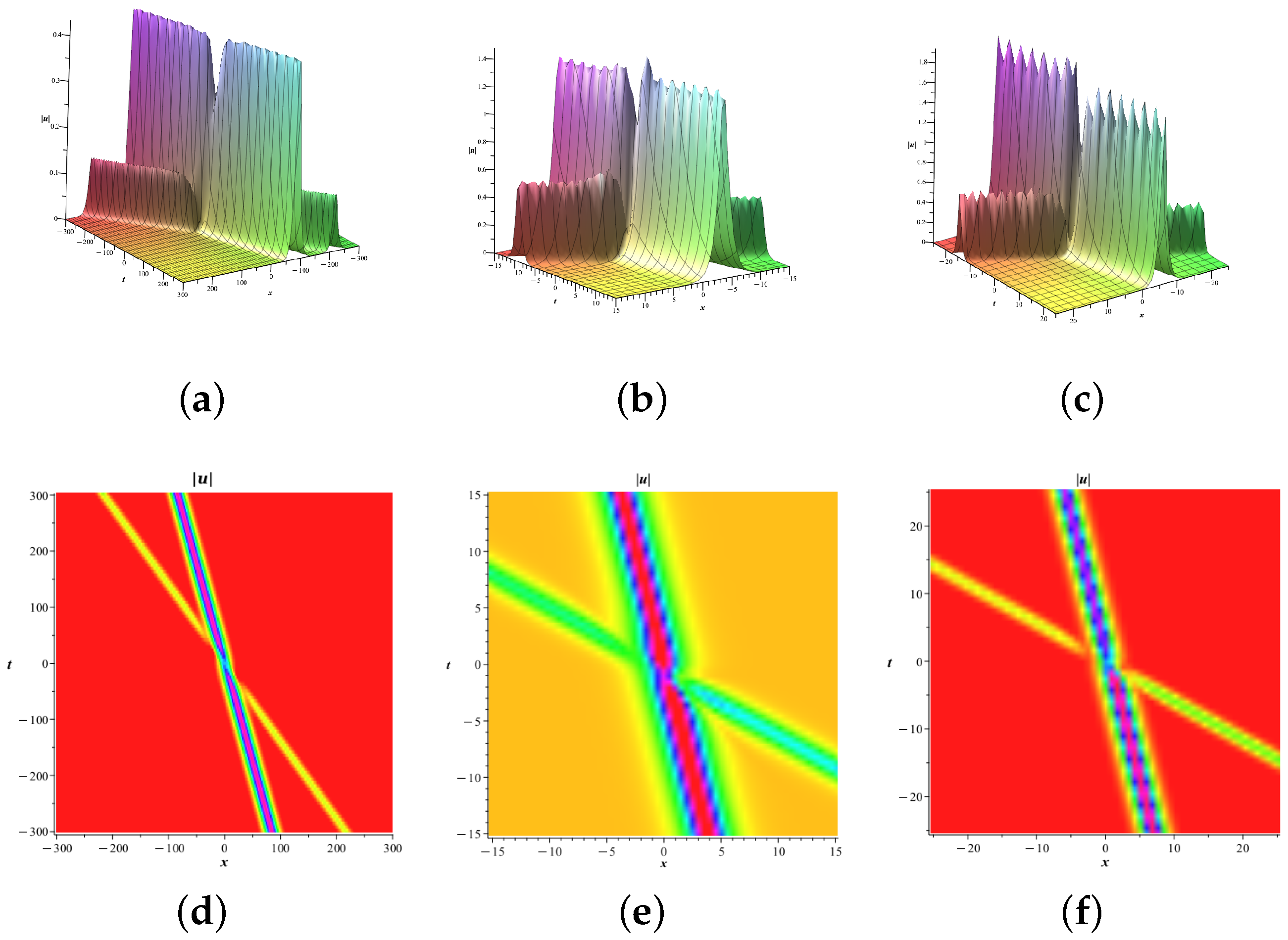
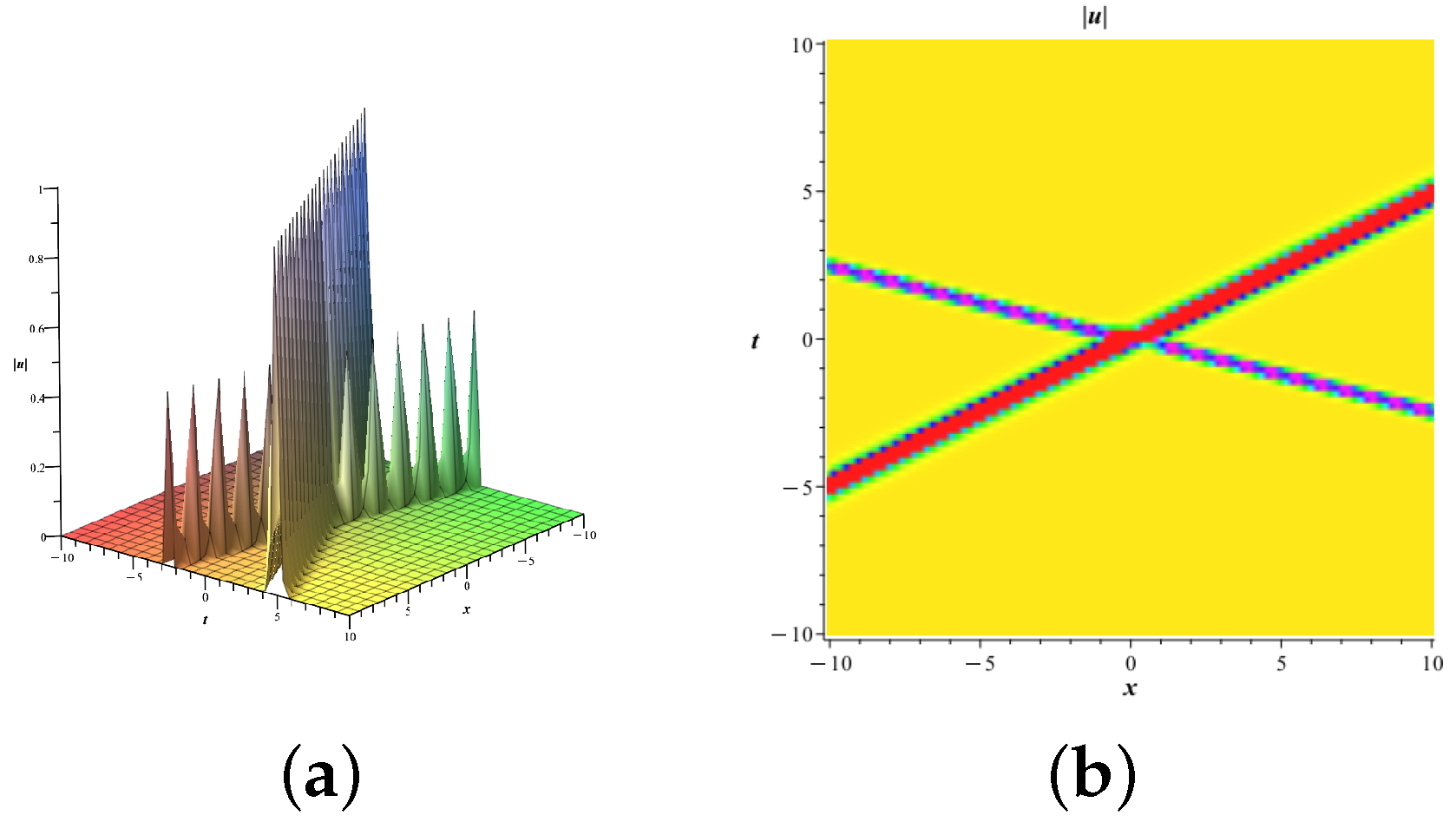
4.2. Single-Soliton Solutions
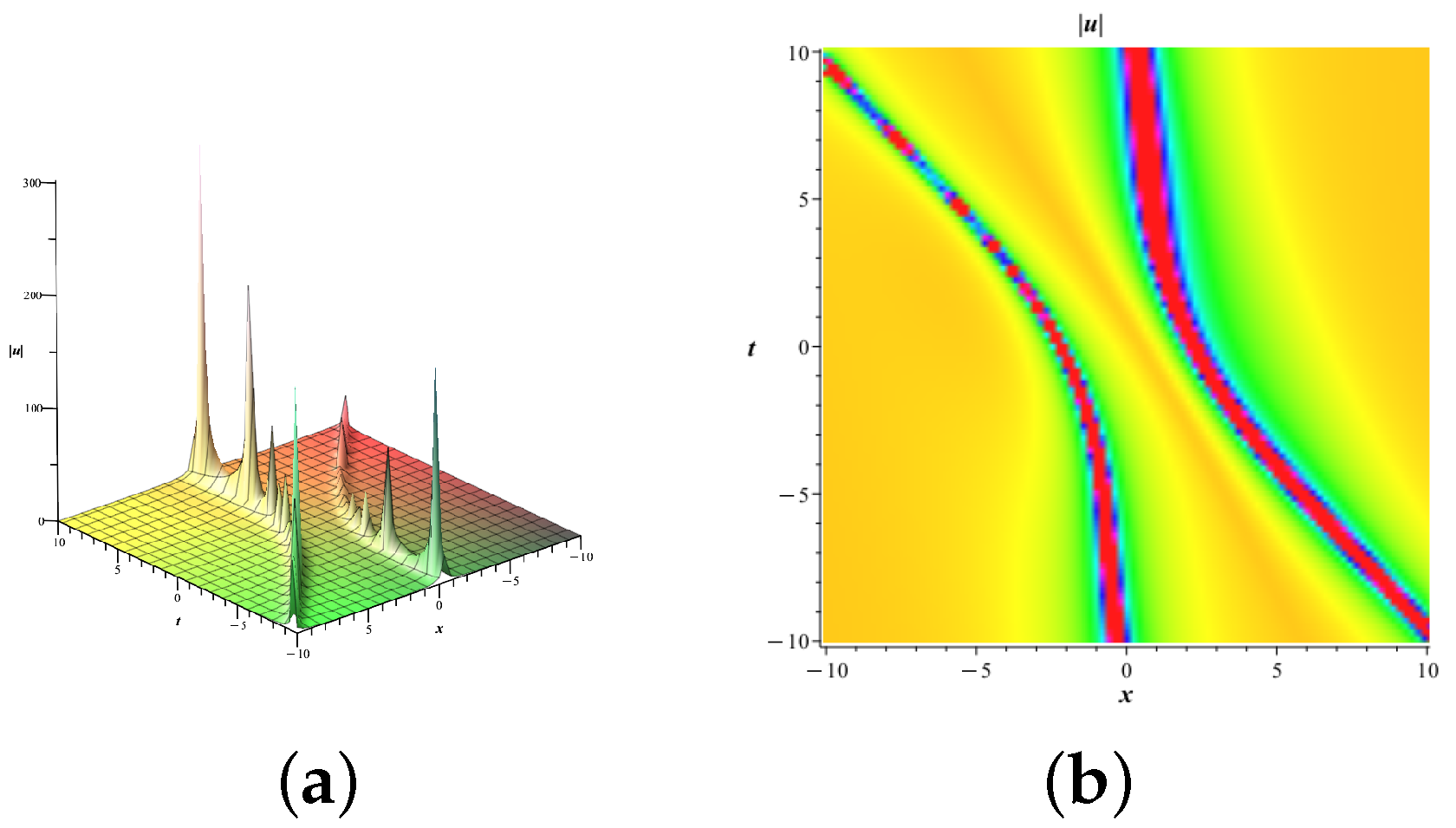
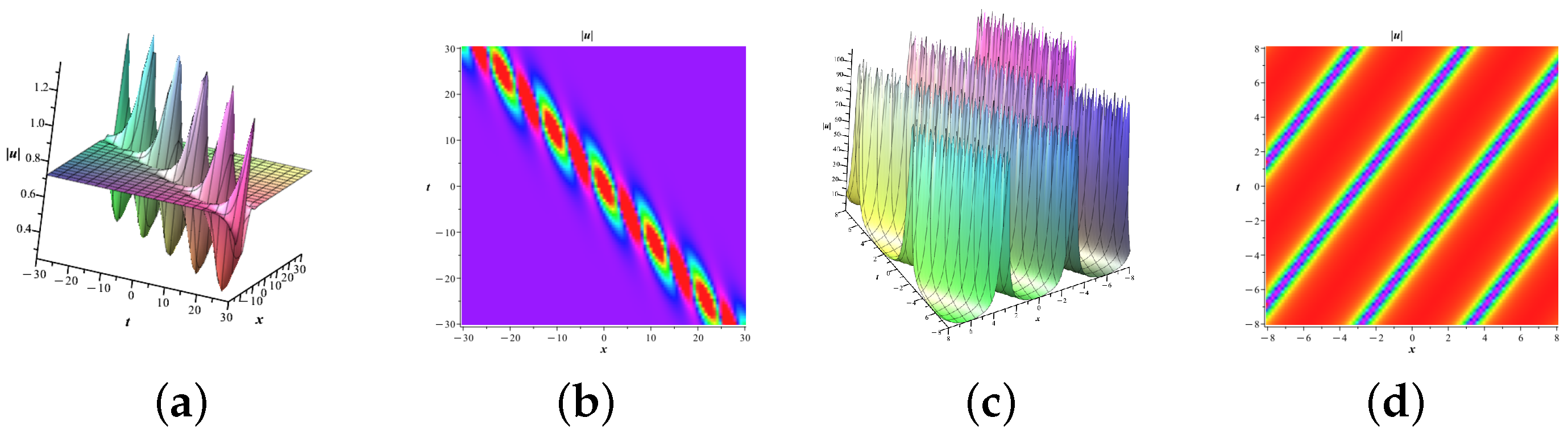
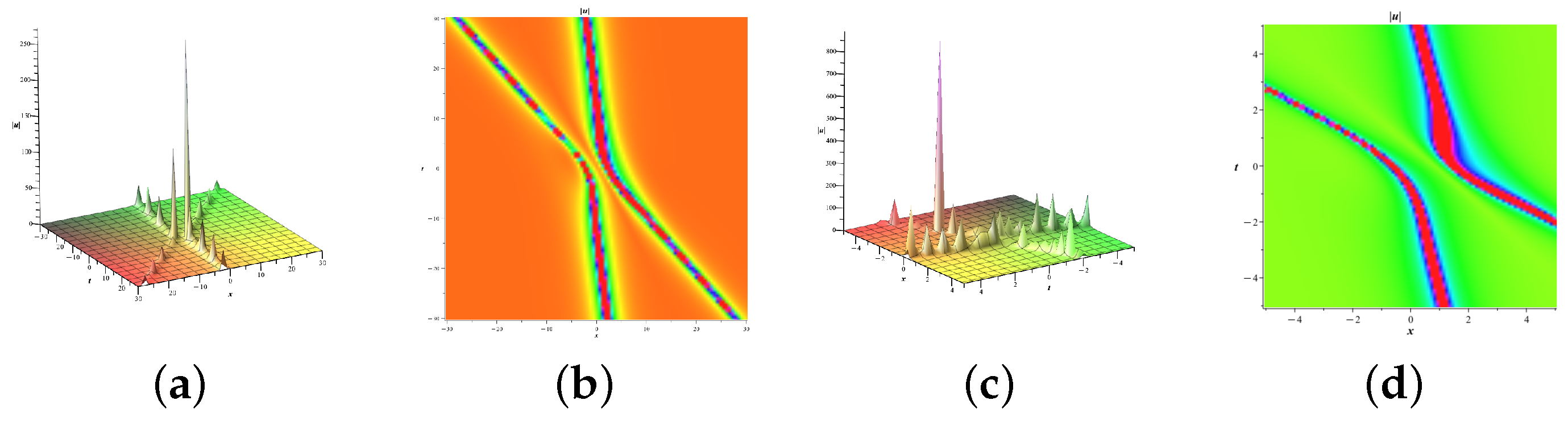
4.3. Double-Soliton Solutions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Lee, Y.; Liu, C. Integrability of nonlinear Hamiltonian systems by inverse scattering method. Phys. Scr. 1979, 20, 490. [Google Scholar] [CrossRef]
- Fan, E. Integrable systems of derivative nonlinear Schrödinger type and their multi-Hamiltonian structure. J. Phys. A Math. Gen. 2001, 34, 513. [Google Scholar] [CrossRef]
- Triki, H.; Babatin, M.; Biswas, A. Chirped bright solitons for Chen–Lee–Liu equation in optical fibers and PCF. Optik 2017, 149, 300–303. [Google Scholar] [CrossRef]
- Newell, A.C. The general structure of integrable evolution equations. Proc. R. Soc. Lond. A Math. Phys. Sci. 1979, 365, 283–311. [Google Scholar]
- Kawata, T.; Kobayashi, N.; Inoue, H. Soliton solutions of the derivative nonlinear Schrödinger equation. J. Phys. Soc. Jpn. 1979, 46, 1008–1015. [Google Scholar] [CrossRef]
- Fan, E. Darboux transformation and soliton-like solutions for the Gerdjikov-Ivanov equation. J. Phys. A Math. Gen. 2000, 33, 6925. [Google Scholar] [CrossRef]
- Xu, M.J.; Xia, T.C.; Hu, B.B. Riemann–Hilbert approach and N-soliton solutions for the Chen–Lee–Liu equation. Mod. Phys. Lett. B 2019, 33, 1950002. [Google Scholar] [CrossRef]
- Han, S.H.; Park, Q.H. Effect of self-steepening on optical solitons in a continuous wave background. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2011, 83, 066601. [Google Scholar] [CrossRef]
- Paliathanasis, A. Periodic solutions from Lie symmetries for the generalized Chen–Lee–Liu equation. Eur. Phys. J. Plus 2021, 136, 934. [Google Scholar] [CrossRef]
- Rogers, C.; Chow, K. Localized pulses for the quintic derivative nonlinear Schrödinger equation on a continuous-wave background. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2012, 86, 037601. [Google Scholar] [CrossRef]
- Ivanov, S.K. Riemann problem for the light pulses in optical fibers for the generalized Chen-Lee-Liu equation. Phys. Rev. A 2020, 101, 053827. [Google Scholar] [CrossRef]
- Forest, M.; Rosenberg, C.J.; Wright, O. On the exact solution for smooth pulses of the defocusing nonlinear Schrödinger modulation equations prior to breaking. Nonlinearity 2009, 22, 2287. [Google Scholar] [CrossRef]
- González-Gaxiola, O.; Biswas, A. W-shaped optical solitons of Chen–Lee–Liu equation by Laplace–Adomian decomposition method. Opt. Quantum Electron. 2018, 50, 314. [Google Scholar] [CrossRef]
- Liu, N.; Sun, J.; Yu, J.D. Inverse scattering and soliton dynamics for the mixed Chen–Lee–Liu derivative nonlinear Schrödinger equation. Appl. Math. Lett. 2024, 152, 109029. [Google Scholar] [CrossRef]
- Zhang, N.; Xia, T.c.; Fan, E.g. A Riemann-Hilbert approach to the Chen-Lee-Liu equation on the half line. Acta Math. Appl. Sin. Engl. Ser. 2018, 34, 493–515. [Google Scholar] [CrossRef]
- Ozdemir, N.; Esen, H.; Secer, A.; Bayram, M.; Yusuf, A.; Sulaiman, T.A. Optical soliton solutions to Chen Lee Liu model by the modified extended tanh expansion scheme. Optik 2021, 245, 167643. [Google Scholar] [CrossRef]
- Yıldırım, Y. Optical solitons to Chen–Lee–Liu model in birefringent fibers with trial equation approach. Optik 2019, 183, 881–886. [Google Scholar] [CrossRef]
- Bansal, A.; Biswas, A.; Zhou, Q.; Arshed, S.; Alzahrani, A.K.; Belic, M.R. Optical solitons with Chen–Lee–Liu equation by Lie symmetry. Phys. Lett. A 2020, 384, 126202. [Google Scholar] [CrossRef]
- Gomez, C.A.; Rezazadeh, H.; Inc, M.; Akinyemi, L.; Nazari, F. The generalized Chen-Lee-Liu model with higher order nonlinearity: Optical solitons. Opt. Quantum Electron. 2022, 54, 492. [Google Scholar] [CrossRef]
- Scott, A.C.; Chu, F.Y.; McLaughlin, D.W. The soliton: A new concept in applied science. Proc. IEEE 1973, 61, 1443–1483. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004; p. 155. [Google Scholar]
- Gu, C. Soliton Theory and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM: Bangkok, Thailand, 1981. [Google Scholar]
- Wazwaz, A.M. Multiple-soliton solutions for the KP equation by Hirota’s bilinear method and by the tanh–coth method. Appl. Math. Comput. 2007, 190, 633–640. [Google Scholar] [CrossRef]
- Gu, C.; Hu, H.; Zhou, Z. Darboux Transformations in Integrable Systems: Theory and Their Applications to Geometry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Rogers, C.; Schief, W.K. Bäcklund and Darboux Transformations: Geometry and Modern Applications in Soliton Theory; Cambridge University Press: Cambridge, UK, 2002; Volume 30. [Google Scholar]
- Aygar, Y.; Bairamov, E. Jost solution and the spectral properties of the matrix-valued difference operators. Appl. Math. Comput. 2012, 218, 9676–9681. [Google Scholar] [CrossRef]
- Miller, R.K. Volterra integral equations in a Banach space. Funkcial. Ekvac 1975, 18, 163–193. [Google Scholar]
- Zhang, Y.; Cheng, Y.; He, J. Riemann—Hilbert method and N—soliton for two—component Gerdjikov-Ivanov equation. J. Nonlinear Math. Phys. 2017, 24, 210–223. [Google Scholar] [CrossRef]
- Lenells, J.; Fokas, A. An integrable generalization of the nonlinear Schrödinger equation on the half-line and solitons. Inverse Probl. 2009, 25, 115006. [Google Scholar] [CrossRef]
- Guo, B.; Ling, L. Riemann-Hilbert approach and N-soliton formula for coupled derivative Schrödinger equation. J. Math. Phys. 2012, 53, 073506. [Google Scholar] [CrossRef]
- Fokas, A.S. Two–dimensional linear partial differential equations in a convex polygon. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2001, 457, 371–393. [Google Scholar] [CrossRef]
- Shchesnovich, V.S.; Yang, J. General soliton matrices in the Riemann–Hilbert problem for integrable nonlinear equations. J. Math. Phys. 2003, 44, 4604–4639. [Google Scholar] [CrossRef]
- Faddeev, L.D.; Takhtajan, L.A. Hamiltonian Methods in the Theory of Solitons; Springer: Berlin/Heidelberg, Germany, 1987; Volume 23. [Google Scholar]
- Wang, D.S.; Ma, Y.Q.; Li, X.G. Prolongation structures and matter-wave solitons in F = 1 spinor Bose–Einstein condensate with time-dependent atomic scattering lengths in an expulsive harmonic potential. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 3556–3569. [Google Scholar] [CrossRef]
- Geng, X.; Wu, J. Riemann–Hilbert approach and N-soliton solutions for a generalized Sasa–Satsuma equation. Wave Motion 2016, 60, 62–72. [Google Scholar] [CrossRef]
- Boutet de Monvel, A.; Shepelsky, D.; Zielinski, L. The short pulse equation by a Riemann–Hilbert approach. Lett. Math. Phys. 2017, 107, 1345–1373. [Google Scholar] [CrossRef]
- Kang, Z.Z.; Xia, T.C.; Ma, X. Multi-soliton solutions for the coupled modified nonlinear Schrödinger equations via Riemann–Hilbert approach. Chin. Phys. B 2018, 27, 070201. [Google Scholar] [CrossRef]
- Ma, W.X. Riemann–Hilbert problems and N-soliton solutions for a coupled mKdV system. J. Geom. Phys. 2018, 132, 45–54. [Google Scholar] [CrossRef]
- Zhuang, Y.; Zhang, Y.; Zhang, H.; Xia, P. Multi-soliton solutions for the three types of nonlocal Hirota equations via Riemann–Hilbert approach. Commun. Theor. Phys. 2022, 74, 115004. [Google Scholar] [CrossRef]
- Lin, Y.; Dong, H.; Fang, Y. N-Soliton Solutions for the NLS-Like Equation and Perturbation Theory Based on the Riemann–Hilbert Problem. Symmetry 2019, 11, 826. [Google Scholar] [CrossRef]
- Qiu, D. Riemann-Hilbert approach and N-soliton solution for the Chen-Lee-Liu equation. Eur. Phys. J. Plus 2021, 136, 825. [Google Scholar] [CrossRef]
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons; Springer Series in Nonlinear Dynamics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Lenells, J. Dressing for a novel integrable generalization of the nonlinear Schrödinger equation. J. Nonlinear Sci. 2010, 20, 709–722. [Google Scholar] [CrossRef]
- Liu, W.J.; Tian, B.; Zhang, H.Q.; Li, L.L.; Xue, Y.S. Soliton interaction in the higher-order nonlinear Schrödinger equation investigated with Hirota’s bilinear method. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2008, 77, 066605. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Zhang, C.; Tian, L. Dynamical Behavior Analysis of Generalized Chen–Lee–Liu Equation via the Riemann–Hilbert Approach. Fractal Fract. 2025, 9, 282. https://doi.org/10.3390/fractalfract9050282
Chen W, Zhang C, Tian L. Dynamical Behavior Analysis of Generalized Chen–Lee–Liu Equation via the Riemann–Hilbert Approach. Fractal and Fractional. 2025; 9(5):282. https://doi.org/10.3390/fractalfract9050282
Chicago/Turabian StyleChen, Wenxia, Chaosheng Zhang, and Lixin Tian. 2025. "Dynamical Behavior Analysis of Generalized Chen–Lee–Liu Equation via the Riemann–Hilbert Approach" Fractal and Fractional 9, no. 5: 282. https://doi.org/10.3390/fractalfract9050282
APA StyleChen, W., Zhang, C., & Tian, L. (2025). Dynamical Behavior Analysis of Generalized Chen–Lee–Liu Equation via the Riemann–Hilbert Approach. Fractal and Fractional, 9(5), 282. https://doi.org/10.3390/fractalfract9050282






