Computational Study of Time-Fractional Kawahara and Modified Kawahara Equations with Caputo Derivatives Using Natural Homotopy Transform Method

Abstract

This article presents a computational analysis of approximate solutions for the time-fractional nonlinear Kawahara problem (KP) and the modified Kawahara problem (modified KP). This study utilizes the natural homotopy transform scheme (NHTS), which integrates the natural transform (NT) with the homotopy perturbation scheme (HPS). We derive the algebraic expression of nonlinear terms through the implementation of HPS. The fractional derivatives are considered in the Caputo form. Numerical results and visualizations present the practical interest and effectiveness of the fractional derivatives. The accuracy of the approximate results, coupled with their precise outcomes, emphasizes the reliability of the method. These findings demonstrate that NHTS is a robust and effective approach for solving time-fractional problems through series expansions.

1. Introduction

Fractional calculus has grown into a strong mathematical resource with applications in almost every field of science and technology. Unlike classical calculus, which focuses on integer-order derivatives and integrals, fractional calculus extends these operators to non-integer orders. This extension makes it possible to model systems with memory and hereditary characteristics. Such a capability is especially useful for representing phenomena that involve anomalous diffusion, viscoelastic behavior, and long-range dependencies—features that traditional models often fail to capture. Fractional differential equations (FDEs) have been employed in various fields, including computational biological disciplines, nuclear research, and astrophysical science, as well as in the study of solid-state fluid dynamics, plasma physics, and optical beams [1,2,3,4,5]. The use of fractional calculus has become significantly more critical in the field of applied science and, therefore, FDEs are particularly attractive for modeling multiple natural phenomena. Khatun and Akbar [6] proposed an expansion strategy for the solution of the beta time-fractional simplified modified Camassa–Holm problem. Momani and Al-Khaled [7] adopted the Adomian decomposition method for the numerical solutions of fractional differential equations. Pant et al. [8] combined Laplace transform with a residual power series scheme to obtain the numerical results for two-dimensional differential problems of time-fractional order. Nadeem and Iambor [9] derived traveling wave solutions for the Boussinesq model through the application of an effective analytical technique. Lin and Xu [10] proposed a finite difference strategy and Legendre spectral approach to derive the approximation of the fractional diffusion problem. Pandir and Ekin [11] explored new solitary wave solutions of the Korteweg–de-Vries problem using an updated version of the trial equation technique. Liu and Feng [12] introduced the concept of a modified generalized Kudryashov scheme to solve the nonlinear time-fractional Schrö dinger-type problems. Tian and Liu [13] proposed the exponential rational function method to derive the series solutions for the time-fractional Cahn–Allen and time-fractional Phi-4 problems.

The dispersive wave problems are vital to applications in mathematical and physical science. The Kawahara equation is particularly intriguing due to its reduced dispersion and significant nonlinearity, which are essential in characterizing the development of nonlinear wave propagation within the long-spectrum domain. Many researchers have focused on studying the Kawahara and modified Kawahara problems for a long time [14,15]. In 1972, Kawahara [16] initially presented the Kawahara problems to explore solitary waves in various phenomena in physical science. This concept is present in the modeling of shallow-water waves influenced by surface tension, and it is utilized in the study of plasma magneto-acoustic waves. Furthermore, the modified Kawahara equation demonstrates extensive applicability in the study of capillary–gravity wave propagation [17,18]. In this paper, we consider the nonlinear Kawahara problem and the modified Kawahara problem with a Caputo fractional derivative as follows:

$$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^{\alpha }\vartheta }{\partial {\tau }^{\alpha }}}+\vartheta {\displaystyle \frac{\partial \vartheta }{\partial \varsigma }}+{\displaystyle \frac{{\partial }^3\vartheta }{\partial {\varsigma }^3}}-{\displaystyle \frac{{\partial }^5\vartheta }{\partial {\varsigma }^5}}=0,0<\alpha \le 1,\end{array}$$

(1)

with

$$\begin{array}{c}\hfill \vartheta (\varsigma ,0)=f\left(\varsigma \right),\end{array}$$

(2)

and

$$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^{\alpha }\vartheta }{\partial {\tau }^{\alpha }}}+{\vartheta }^2{\displaystyle \frac{\partial \vartheta }{\partial \varsigma }}+a{\displaystyle \frac{{\partial }^3\vartheta }{\partial {\varsigma }^3}}+b{\displaystyle \frac{{\partial }^5\vartheta }{\partial {\varsigma }^5}}=0,0<\alpha \le 1,\end{array}$$

(3)

with

$$\begin{array}{c}\hfill \vartheta (\varsigma ,0)=g\left(\varsigma \right),\end{array}$$

(4)

in which a and b are positive parameters. The function $\vartheta (\varsigma ,\tau )$ defines the variables $\varsigma$ as a space and $\tau$ as a time. The functions $f\left(\varsigma \right)$ and $g\left(\varsigma \right)$ are typically expressed as hyperbolic functions specified over the period $-\infty <\varsigma <\infty$. The fractional derivatives are analyzed in the context of Caputo’s definition. For $\alpha =1$, Equations (1) and (3) convert to integer-order problems. Varol [19] obtained various solitary wave results for the extended Kawahara problem of time-fractional order. Zafar et al. [20] used the homotopy analysis method to solve two versions of time-fractional Kawahara and modified Kawahara. Karunakar and Chakraverty [21] used the homotopy perturbation transform approach for the solution of interval-modified Kawahara differential problems. The authors in [22] proposed the idea of Quintic B-spline and Galerkin’s method for the series solution of nonlinear Kawahara equations with time-fractional order. Aljahdaly and Alweldi [23] introduced a modification of Laplace transform with a perturbation scheme to address the damped modified Kawahara problem and presented applications in fluid dynamics. Wang [24] solved Kawahara and modified Kawahara problems with dual-power law nonlinearities using the sine–cosine method and finite difference schemes. Kumar and Gupta [25] used the Haar scale wavelet scheme for the numerical investigation of the time-fractional KP.

This research aims to provide a computational analysis and evaluate the efficacy of the natural homotopy transform scheme (NHTS) for the nonlinear KP and the modified KP of time-fractional order. Our proposed strategy is widely favored and straightforward to implement, as it simplifies the management of the convergence domain for the sequence of analytical solutions in any given problem. This approach effectively addresses both linear and nonlinear problems without any restrictions or assumptions. A key distinguishing feature of this method is its ability to provide a series solution for both small and large physical variables. This paper is organized as follows: Section 2 provides the basic definitions of fractional calculus and natural transform. We formulate the idea of the natural homotopy transform scheme (NHTS) step by step in Section 3. We provide the existence and uniqueness theorem in Section 4. We consider a nonlinear application of KP and modified KP with Caputo fractional derivative to show the accuracy of our proposed scheme in Section 5. The research findings and remarks are offered in Section 6. We present the concluding remarks in the last section, Section 7.

2. Basic Definitions of Fractional Calculus and Natural Transform

In this section, we present several definitions and principles of fractional calculus and natural transform that are fundamental for the design of this structure.

Definition 1.

The Reimann–Liouville fractional differential operator of order $\alpha$ is defined as [26,27]

$$\begin{array}{c}\hfill D^{\alpha }\vartheta \left(\tau \right)={\displaystyle \frac{1}{\mathsf{\Gamma }(\phi -\alpha )}}{\displaystyle \frac{d}{d{\tau }^{\phi }}}{\int }_m^n\vartheta \left(\varphi \right){(\tau -\varphi )}^{\phi -\alpha -1}d\varphi ,\end{array}$$

where $\alpha$ shows the Caputo fractional derivative and $\tau \in [m,n]$.

Definition 2.

The Caputo fractional differential operator of order $\alpha$ is defined as follows [27]:

$$\begin{array}{c}\hfill D^{\alpha }\vartheta \left(\tau \right)={\displaystyle \frac{1}{\mathsf{\Gamma }(\phi -\alpha )}}{\int }_m^n{\displaystyle \frac{d}{d{\tau }^{\phi }}}\vartheta \left(\varphi \right){(\tau -\varphi )}^{\phi -\alpha -1}d\varphi ,\end{array}$$

where $\alpha$ denotes the order of derivative and $\tau \in [m,n]$.

Definition 3.

Consider the set A consisting of functions such as those defined in [28]:

$$\begin{array}{c}\hfill A=\vartheta \left(\tau \right):\exists M,h_1,h_2>0,\mid \vartheta \left(\tau \right)\mid <M{e}^{{\displaystyle \frac{\mid \tau \mid }{h_j}}},\mathrm{if}\tau \in {(-1)}^j\times [0,\infty ),\end{array}$$

where M is a constant and must have a specific value, while the constants $h_1$ and $h_2$ can be finite or infinite. Moreover, the natural transform is described as an integral formula such as

$$\begin{array}{c}\hfill N^{+}\left[\vartheta \left(\tau \right)\right]=R(s,v)={\displaystyle \frac{1}{v}}{\int }_0^{\infty }\vartheta \left(\tau \right)e^{-{\displaystyle \frac{s\tau }{v}}}d\tau ,s,\tau >0,\end{array}$$

in which s and v are the transformation parameters.

Definition 4.

The inverse formula of natural transform $R(s,v)$ is expressed as follows [28]:

$$\begin{array}{c}\hfill N^{-1}\left[R(s,v)\right]=\vartheta \left(\tau \right)={\displaystyle \frac{1}{2\pi i}}{\int }_{c-i\infty }^{c+i\infty }R(s,v)e^{{\displaystyle \frac{s\tau }{v}}}ds,\end{array}$$

where N⁻¹ gives the inverse natural transform and $s=a+bi$ represents the complex plan for operating the integral over $s=c$, in which $c\in R$.

Definition 5.

Let ${\vartheta }^n\left(\tau \right)$ shows the n-th derivative of $\vartheta \left(\tau \right)$, so the natural transformation in its nth form is expressed as follows [29]:

$$\begin{array}{cc}\hfill & N^{+}\left({\vartheta }^n\left(\tau \right)\right)=R_n(s,v)={\displaystyle \frac{s^n}{v^n}}R(s,v)-\sum _{k=0}^{n-1}{\displaystyle \frac{s^{n-(k+1)}}{v^{n-k}}}\left({\vartheta }^n\left(0\right)\right),n\ge 1.\hfill \end{array}$$

Corollary 1.

Suppose that $k_1\left(\tau \right)$ and $k_2\left(\tau \right)$ are specified on set A and contain the corresponding transformations $K_1(s,v)$ and $K_2(s,v)$; accordingly, ultimately,

$$\begin{array}{c}\hfill N^{+}\left[k^{*}h\right]=v{K}_1(s,v)K_2(s,v),\end{array}$$

with $\left[k_1^{*}{k}_2\right]$ as the convolution of $k_1$ and $k_2$.

3. Formulation of Natural Homotopy Transform Scheme

The current section investigates the formulation of NHTS for the computational analysis of the time-fractional KP and modified KP. The present scheme is remarkable and it is straightforward to compute the solution in the form of a series for the fractional-order derivatives. The development of NHTS requires minimal theory, predictions, and constraints on parameters. We initiate the procedure of the present approach by analyzing a nonlinear differential equation of fractional order:

$$\begin{array}{c}\hfill D_{\tau }^{\alpha }\vartheta (\varsigma ,\tau )=R_1\vartheta (\varsigma ,\tau )+R_2\vartheta (\varsigma ,\tau )+g(\varsigma ,\tau ),\end{array}$$

(5)

with the following constraints:

$$\begin{array}{c}\hfill \vartheta (\varsigma ,0)=f\left(\varsigma \right).\end{array}$$

(6)

In this context, $R_1$ and $R_2$ represent linear and nonlinear operators, respectively; however $g(\varsigma ,\tau )$ indicates a source parameter.

• Step 1. By applying the N⁺T to Equation (5), we obtain

  $$\begin{array}{c}\hfill N^{+}\left[D_{\tau }^{\alpha }\vartheta (\varsigma ,\tau )\right]=N^{+}[R_1\vartheta (\varsigma ,\tau )+R_2\vartheta (\varsigma ,\tau )+g(\varsigma ,\tau )].\end{array}$$

  Now, utilizing the property of N⁺T, we derive

  $$\begin{array}{c}\hfill {\displaystyle \frac{s^{\alpha }}{v^{\alpha }}}{N}^{+}\left[\vartheta (\varsigma ,\tau )\right]-{\displaystyle \frac{s^{\alpha -1}}{v^{\alpha }}}\vartheta (\varsigma ,0)=N^{+}[R_1\vartheta (\varsigma ,\tau )+R_2\vartheta (\varsigma ,\tau )+g(\varsigma ,\tau )].\end{array}$$

  Upon handling this calculation and applying Condition (6), we have

  $$\begin{array}{c}\hfill N^{+}\left[\vartheta (\varsigma ,\tau )\right]={\displaystyle \frac{f\left(\varsigma \right)}{s}}+{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left[g(\varsigma ,\tau )\right]+{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}[R_1\vartheta (\varsigma ,\tau )+R_2\vartheta (\varsigma ,\tau )].\end{array}$$
• Step 2. By employing the N⁻¹T, we generate

  $$\begin{array}{cc}\hfill \vartheta (\varsigma ,\tau )& =G(\varsigma ,\tau )+N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left[R_1\vartheta (\varsigma ,\tau )+R_2\vartheta (\varsigma ,\tau )\right]\right].\hfill \end{array}$$

  (7)

  Equation (7) shows the recurring correlation of NHTS for Equation (5), wherein

  $$\begin{array}{c}\hfill G(\varsigma ,\tau )=N^{-1}\left[{\displaystyle \frac{f\left(\varsigma \right)}{s}}+{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left[g(\varsigma ,\tau )\right]\right].\end{array}$$
• Step 3. The exact solution of Equation (5) is specified as

  $$\begin{array}{c}\hfill \vartheta (\varsigma ,\tau )=\sum _{n=0}^{\infty }{p}^n{\vartheta }_n(\varsigma ,\tau ).\end{array}$$

  (8)

  In this context, $p\in [0,1]$ denotes a homotopy variable; however, ${\vartheta }_0(\varsigma ,\tau )$ serves as its first value. On the other side, the nonlinear factor associated with the homotopy parameter is defined as

  $$\begin{array}{c}\hfill R_2\vartheta (\varsigma ,\tau )=\sum _{n=0}^{\infty }{p}^n{H}_n\vartheta (\varsigma ,\tau ).\end{array}$$

  (9)

  The following formula can be employed to compute He’s parameters:

  $$\begin{array}{c}\hfill H_n(\varsigma ,\tau )={\displaystyle \frac{1}{n!}}{\displaystyle \frac{{\partial }^n}{\partial p^n}}{\left(R_2\left(\sum _{n=0}^{\infty }{p}^n{\vartheta }_n\right)\right)}_{p=0},n=0,1,2,\cdots .\end{array}$$

  Through connecting Equations (8) and (9), we derive Equation (7) as follows:

  $$\begin{array}{c}\hfill \sum _{n=0}^{\infty }{p}^n{\vartheta }_n(\varsigma ,\tau )=G(\varsigma ,\tau )+p{N}^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left\{R_1\left(\sum _{n=0}^{\infty }{p}^n{\vartheta }_n(\varsigma ,\tau )\right)+\sum _{n=0}^{\infty }{p}^n{H}_n{\vartheta }_n(\varsigma ,\tau )\right\}\right].\end{array}$$
• Step 4. Upon conducting an analysis of p on the two sides, the resulting outcome is presented as

  $$\begin{array}{cc}\hfill p^0& :{\vartheta }_0(\varsigma ,\tau )=G(\varsigma ,\tau ),\hfill \\ \hfill p^1& :{\vartheta }_1(\varsigma ,\tau )=N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left\{R_1{\vartheta }_0(\varsigma ,\tau )+H_0\left(\vartheta \right)\right\}\right],\hfill \\ \hfill p^2& :{\vartheta }_2(\varsigma ,\tau )=N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left\{R_1{\vartheta }_1(\varsigma ,\tau )+H_1\left(\vartheta \right)\right\}\right],\hfill \\ \hfill p^3& :{\vartheta }_3(\varsigma ,\tau )=N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left\{R_1{\vartheta }_2(\varsigma ,\tau )+H_2\left(\vartheta \right)\right\}\right],\hfill \\ \hfill & ⋮\hfill \\ \hfill p^n& :{\vartheta }_n(\varsigma ,\tau )=N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left\{R_1{\vartheta }_{n-1}(\varsigma ,\tau )+H_{n-1}\left(\vartheta \right)\right\}\right].\hfill \end{array}$$
• Step 5. As a result, we are able to summarize the findings of this iterative series as follows:

  $$\begin{array}{c}\hfill \vartheta (\varsigma ,\tau )={\vartheta }_0+{\vartheta }_1+{\vartheta }_2+\cdots =\underset{p\to 1}{\lim }\sum _{i=1}^{\infty }{\vartheta }_i(\varsigma ,\tau ).\end{array}$$

  (10)

4. Natural Transformation over Existence and Convergence Analysis

This section investigates the natural transformation under existence conditions and the uniqueness theorem, utilizing convergence examination to demonstrate the accuracy of our suggested scheme. The derived findings demonstrate that NHTS is a successful and significant approach to handling nonlinear problems of fractional order.

4.1. Existence of NT with Sufficient Condition

Theorem 1.

Let $\vartheta \left(\tau \right)$ be a continuous function specified across the interval $0\le \tau \le \beta$ that grows geometrically as $\tau >\beta$. As a result, we report that NT holds for $\vartheta \left(\tau \right)$.

Proof. 

Let $\beta$ be a positive integer with the subsequent algebraic expression

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{v}}{\int }_0^{\infty }\exp \left(-{\displaystyle \frac{s\tau }{v}}\right)\vartheta \left(\tau \right)d\tau ={\displaystyle \frac{1}{v}}{\int }_0^{\beta }\exp \left(-{\displaystyle \frac{s\tau }{v}}\right)\vartheta \left(\tau \right)d\tau +{\displaystyle \frac{1}{v}}{\int }_{\beta }^{\infty }\exp \left(-{\displaystyle \frac{s\tau }{v}}\right)\vartheta \left(\tau \right)d\tau .\end{array}$$

Since $\vartheta \left(\tau \right)$ is a piecewise continuous function that holds true for the bounded values of $0\le \tau \le \beta$, we can locate an element of the main integral to the proper edge. Furthermore, the parameter $\alpha$ of $\vartheta \left(\tau \right)$ for $\tau >\beta$ indicates the presence of the second integral component of the opposite edge. We evaluate this argument by exploring the following case:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left|{\displaystyle \frac{1}{v}}{\int }_{\beta }^{\infty }\exp \left(-{\displaystyle \frac{s\tau }{v}}\right)\vartheta \left(\tau \right)d\tau \right|,& \le {\int }_{\beta }^{\infty }\left|{\displaystyle \frac{1}{v}}\exp \left(-{\displaystyle \frac{s\tau }{v}}\right)\vartheta \left(\tau \right)\right|d\tau ,\hfill \\ \hfill & \le {\int }_0^{\infty }{\displaystyle \frac{1}{v}}\exp \left(-{\displaystyle \frac{s\tau }{v}}\right)\left|\vartheta \left(\tau \right)\right|d\tau ,\hfill \\ \hfill & \le {\int }_{\beta }^{\infty }{\displaystyle \frac{1}{v}}\exp \left(-{\displaystyle \frac{s\tau }{v}}\right)\exp \left(\alpha \tau \right)d\tau ,\hfill \\ \hfill & ={\int }_{\beta }^{\infty }{\displaystyle \frac{1}{v}}\exp \left(-{\displaystyle \frac{(s-\alpha v)\tau }{v}}\right)d\tau ,\hfill \\ \hfill & =-{\displaystyle \frac{v}{(s-\alpha v)}}\underset{\gamma \to \infty }{\lim }{\left[{\displaystyle \frac{1}{v}}\exp \left(-{\displaystyle \frac{(s-\alpha v)\tau }{v}}\right)\right]}_0^{\gamma },\hfill \\ \hfill & ={\displaystyle \frac{1}{s-\alpha v}}.\hfill \end{array}\end{array}$$

So, the theorem is true. □

4.2. Uniqueness Theorem for NHTS

Theorem 2.

Equation (10) yields a unique result, such as $0<\left({\delta }_1+{\delta }_2\right){\displaystyle \frac{{\tau }^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}<1$.

Proof. 

Let $Y=\left(\mathcal{C}\right[I],\parallel .\parallel )$ denote a structure that involves mappings with a continuous norm $\parallel .\parallel$ defined on the interval $I=[0,\nsim ]$, which is recognized as a Banach space. We define a mapping $Q:Y\to Y$ in the following manner:

$$\begin{array}{c}\hfill {\vartheta }_{k+1}^C(\varsigma ,\tau )={\vartheta }_0^C+N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[L_1\left({\vartheta }_k(\varsigma ,\tau )\right)\right]\right]+N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[L_2\left({\vartheta }_k(\varsigma ,\tau )\right)\right]\right],k\ge 0.\end{array}$$

Let us consider the conditions where the absolute difference between $L\left(\vartheta \right)$ and $L\left({\vartheta }^{*}\right)$ is less than ${\delta }_1$ multiplied by the absolute difference between $\vartheta$ and ${\vartheta }^{*}$. Similarly, the absolute difference between $N\left(\vartheta \right)$ and $N\left({\vartheta }^{*}\right)$ is constrained by ${\delta }_2$ times the absolute difference between $\vartheta$ and ${\vartheta }^{*}$. Here, ${\delta }_1$ and ${\delta }_2$ represent Lipschitz parameters, while $\vartheta$ and ${\vartheta }^{*}$ denote the unknown elements of the mapping.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill ∥Q\left(\vartheta \right)-Q\left({\vartheta }^{*}\right)∥& =\underset{\tau \in I}{\max }\left|N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}[L_1\left(\vartheta \right)+L_2\left(\vartheta \right)]\right]-N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[L_1\left({\vartheta }^{*}\right)+L_2\left({\vartheta }^{*}\right)\right]\right]\right|,\hfill \\ \hfill & \le \underset{\tau \in I}{\max }\left|N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[L_1\left(\vartheta \right)-L_1\left({\vartheta }^{*}\right)\right]+{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[L_2\left(\vartheta \right)-L_2\left({\vartheta }^{*}\right)\right]\right]\right|,\hfill \\ \hfill & \le \underset{\tau \in I}{\max }\left[{\delta }_1{N}^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left|\vartheta -{\vartheta }^{*}\right|\right]+{\delta }_2{N}^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left|\vartheta -{\vartheta }^{*}\right|\right]\right],\hfill \\ \hfill & \le \underset{\tau \in I}{\max }\left({\delta }_1+{\delta }_2\right)\left[N^{-1}\left\{{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }\left[N^{+}\left|\vartheta -{\vartheta }^{*}\right|\right]\right\}\right],\hfill \\ \hfill & \le \left({\delta }_1+{\delta }_2\right)\left[N^{-1}\left\{{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}∥\vartheta -{\vartheta }^{*}∥\right\}\right],\hfill \\ \hfill & =\left({\delta }_1+{\delta }_2\right){\displaystyle \frac{{\tau }^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}∥\vartheta -{\vartheta }^{*}∥,\hfill \end{array}\end{array}$$

which shows that this mapping is in reduction form within the framework of $0<\left({\delta }_1+{\delta }_2\right){\displaystyle \frac{{\tau }^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}}<1$. So, we can conclude that Equation (10) is considered a particular solution of Equation (5). Therefore, the statement has been completed. □

4.3. Convergence Study of NHTS

Theorem 3.

In this subsection, we demonstrate that the solution to Equation (5) is convergent.

Proof. 

The n-th sum of partials is represented by ${\vartheta }_n$, where ${\vartheta }_n={\sum }_{m=0}^n{\vartheta }_m(\varsigma ,\tau )$. At this stage, we indicate the sequence $\left\{{\vartheta }_n\right\}$ as a Cauchy series within the context of a Banach space M. By employing the uniqueness theorem to derive HPS outcomes through He’s factors, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \overline{R}\left({\vartheta }_n\right)={\check{H}}_n+\sum _{p=0}^{n-1}{\breve{H}}_p,\hfill \\ \hfill & \overline{N}\left({\vartheta }_n\right)={\breve{H}}_n+\sum _{c=0}^{n-1}{\breve{H}}_c.\hfill \end{array}\end{array}$$

Thus,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill ∥{\vartheta }_n-{\vartheta }_q∥=\underset{\widehat{f}\in I}{\max }\left|{\vartheta }_n-{\vartheta }_q\right|& =\underset{\overline{f}\in I}{\max }\left|\sum _{m=q+1}^n{\vartheta }_m\right|,m=1,2,3,\dots \hfill \\ \hfill & \le \underset{\overline{f}\in I}{\max }\left|\begin{array}{c}{N}^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[\sum _{m=q+1}^n{L}_1\left[{\vartheta }_{n-1}(\varsigma ,\tau )\right]\right]\right]\\ +N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[\sum _{m=q+1}^n{L}_2\left[{\vartheta }_{n-1}(\varsigma ,\tau )\right]\right]\right]\\ +N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[\sum _{m=q+1}^n{\check{H}}_{n-1}(\varsigma ,\tau )\right]\right]\end{array}\right|,\hfill \\ \hfill & =\underset{\tau \in I}{\max }\left|\begin{array}{c}{N}^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[\sum _{m=q}^{n-1}{L}_1\left[{\vartheta }_n(\varsigma ,\tau )\right]\right]\right]\\ +N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[\sum _{m=q}^{n-1}{L}_2\left[{\vartheta }_n(\varsigma ,\tau )\right]\right]\right]\\ +N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[\sum _{m=q}^{n-1}{\breve{H}}_n(\varsigma ,\tau )\right]\right]\end{array}\right|,\hfill \\ \hfill \\ \hfill & \le \underset{\overline{\tau }\in I}{\max }\left|\begin{array}{c}{N}^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[\sum _{m=q}^{n-1}{L}_1\left({\vartheta }_{n-1}\right)-L_1\left({\vartheta }_{q-1}\right)\right]\right]\hfill \\ +N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[\sum _{m=q}^{n-1}{L}_2\left({\vartheta }_{n-1}\right)-L_2\left({\vartheta }_{q-1}\right)\right]\right]\hfill \\ +N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[\sum _{m=q}^{n-1}{L}_3\left({\vartheta }_{n-1}\right)-L_3\left({\vartheta }_{q-1}\right)\right]\right]\hfill \end{array}\right|,\hfill \\ \hfill \\ \hfill & \le \underset{\overline{f}\in I}{\max }\left|\begin{array}{c}{N}^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[L_1\left({\vartheta }_{n-1}\right)-L_1\left({\vartheta }_{q-1}\right)\right]\right]\\ +N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[L_2\left({\vartheta }_{n-1}\right)-L_2\left({\vartheta }_{q-1}\right)\right]\right]\\ +N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[L_3\left({\vartheta }_{n-1}\right)-L_3\left({\vartheta }_{q-1}\right)\right]\right]\end{array}\right|,\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \le {\delta }_1\underset{\overline{f}\in I}{\max }{N}^{-1}\left|\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[\left({\vartheta }_{n-1}\right)-\left({\vartheta }_{q-1}\right)\right]\right]\right|\hfill \\ \hfill & +{\delta }_2\underset{\tau \in I}{\max }\left|N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[\left({\vartheta }_{n-1}\right)-\left({\vartheta }_{q-1}\right)\right]\right]\right|\hfill \\ \hfill & +{\delta }_3\underset{\tau \in I}{\max }\left|N^{-1}\left[{\left({\displaystyle \frac{v}{s}}\right)}^{\alpha }{N}^{+}\left[\left({\vartheta }_{n-1}\right)-\left({\vartheta }_{q-1}\right)\right]\right]\right|,\hfill \\ \hfill & ={\displaystyle \frac{\left({\delta }_1+{\delta }_2+{\delta }_3\right){\tau }^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}∥{\vartheta }_{n-1}-{\vartheta }_{q-1}∥.\hfill \end{array}\end{array}$$

Let $n=q+1$; then,

$$\begin{array}{c}\hfill ∥{\vartheta }_{q+1}-{\vartheta }_q∥\le ϵ∥{\vartheta }_q-{\vartheta }_{q-1}∥\le {ϵ}^2∥{\vartheta }_{q-1}-{\vartheta }_{q-2}∥\le \dots \le {ϵ}^q∥{\vartheta }_1-{\vartheta }_0∥,\end{array}$$

in which $ϵ={\displaystyle \frac{\left({\delta }_1+{\delta }_2+{\delta }_3\right){\tau }^{(\alpha -1)}}{\alpha !}}$.

By applying the triangle inequality, we arrive at the following result:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill ∥{\vartheta }_n-{\vartheta }_q∥& \le ∥{\vartheta }_{q+1}-{\vartheta }_q∥+∥{\vartheta }_{q+2}-{\vartheta }_{q+1}∥+\dots +∥{\vartheta }_n-{\vartheta }_{n-1}∥,\hfill \\ \hfill & \le \left[{ϵ}^q+{ϵ}^{q+1}+\dots +{ϵ}^{n-1}\right]∥{\vartheta }_1-{\vartheta }_0∥,\hfill \\ \hfill & \le {ϵ}^q\left({\displaystyle \frac{1-{ϵ}^{n-q}}{1-ϵ}}\right)∥{\vartheta }_1∥.\hfill \end{array}\end{array}$$

Since we have $\left(1-{ϵ}^{n-q}\right)<1$ with $0<ϵ<1$, we obtain

$$\begin{array}{c}\hfill ∥{\vartheta }_n-{\vartheta }_q∥\le {\displaystyle \frac{{ϵ}^q}{1-ϵ}}\underset{\overline{f}\in I}{\max }∥{\vartheta }_1∥.\end{array}$$

From the fact that $\left|{\vartheta }_1\right|<\infty$, as $q\to \infty$, it follows that $∥{\vartheta }_n-{\vartheta }_q∥\to 0$. Considering that $\left\{{\vartheta }_1\right\}$ is a Cauchy series over $\mathbb{Z}$, it implies that ${\sum }_{n=0}^{\infty }{\vartheta }_n$ represents a sequence of convergence. Therefore, the statements regarding convergence are proven. □

5. Numerical Problems

The present section provides a fractional analysis of the time-fractional KP and modified KP to compute the series results in convergence form. The computed results demonstrate the significance, ability, and credibility of NHTS. We present visual representations of the illustrated problems with varying fractional parameters. The software Mathematica 11 wasutilized for intricate mathematical computations and concepts.

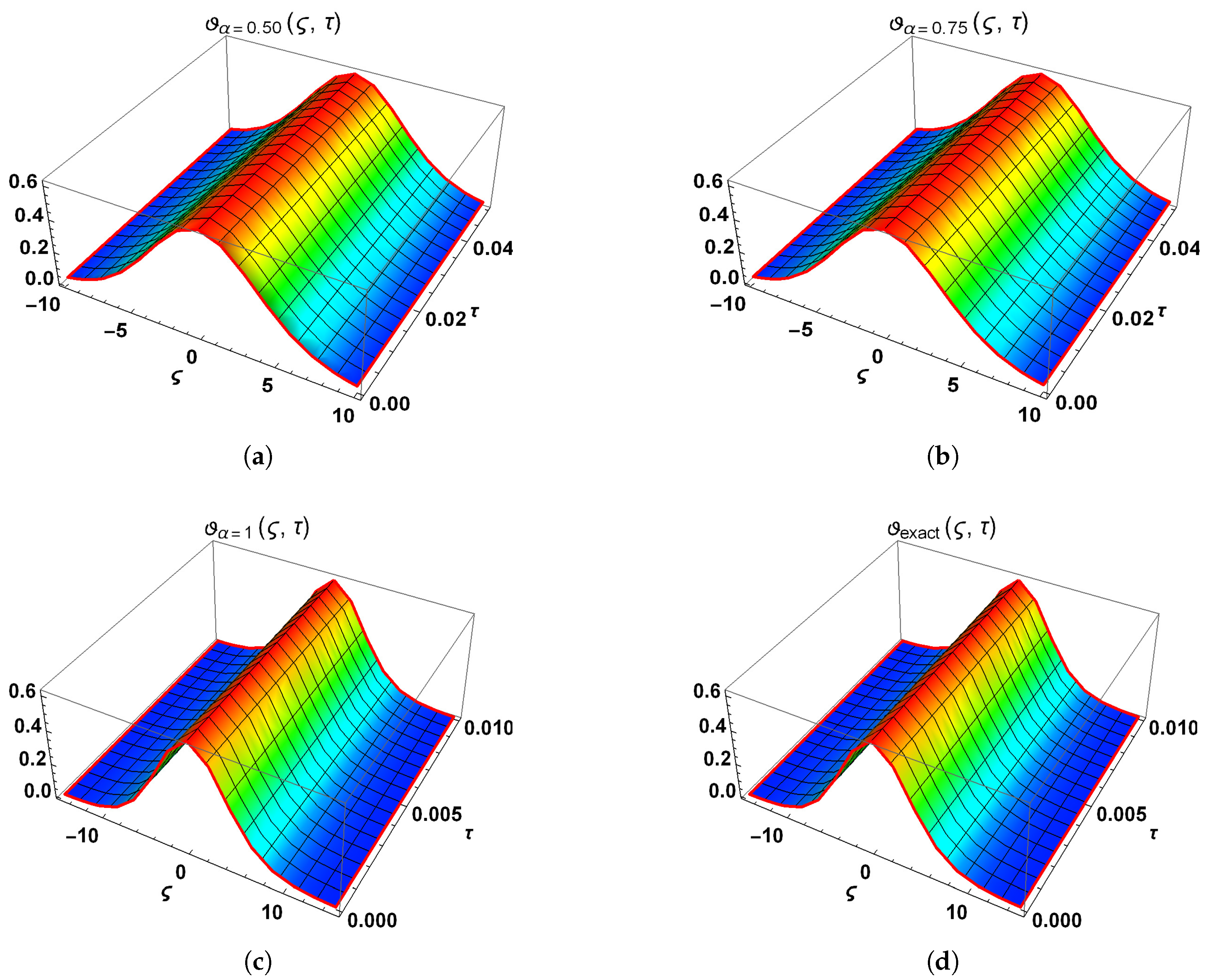
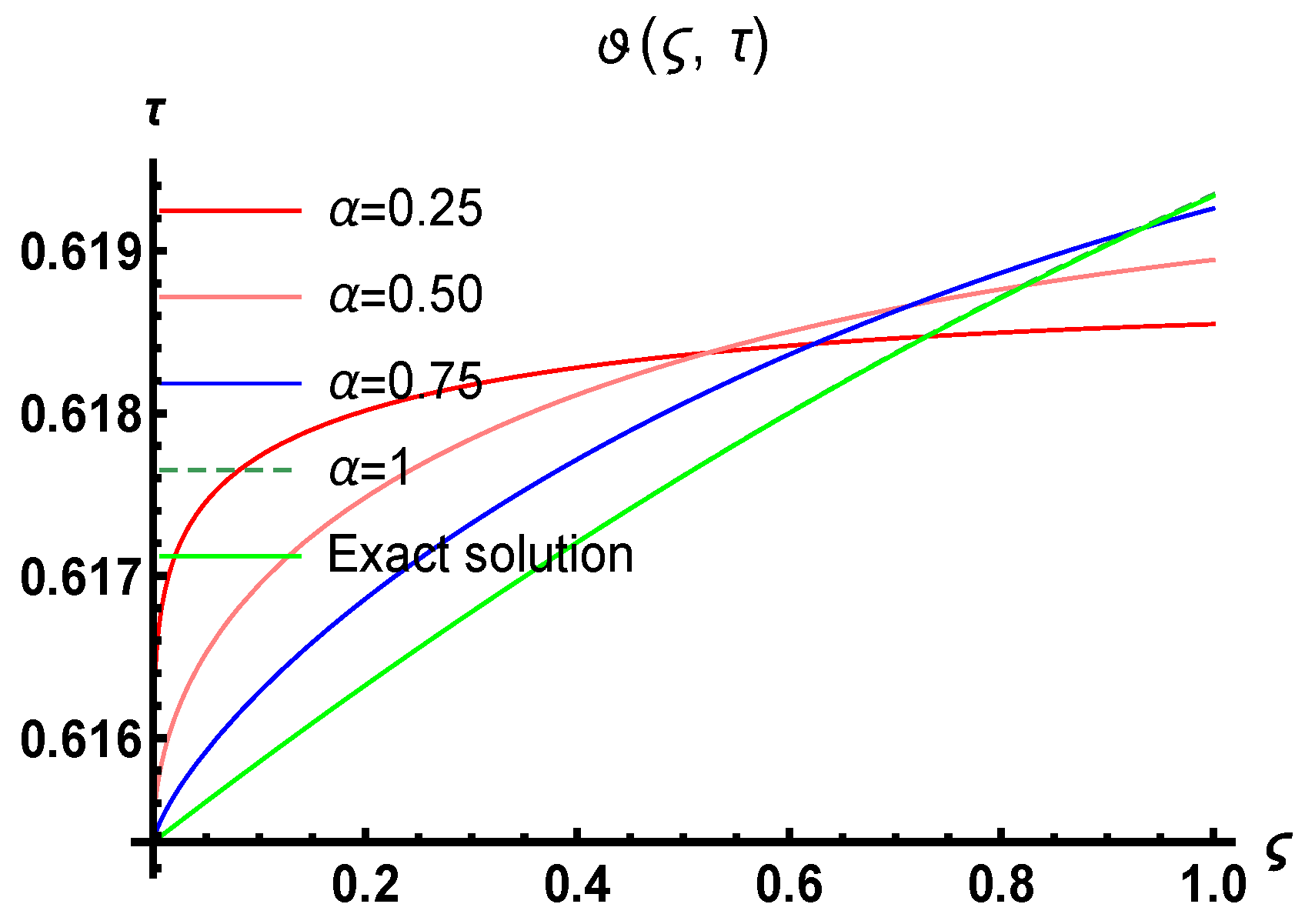
5.1. Problem 1

Consider the following time-fractional KP [30]:

$$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^{\alpha }\vartheta }{\partial {\tau }^{\alpha }}}+\vartheta {\displaystyle \frac{\partial \vartheta }{\partial \varsigma }}+{\displaystyle \frac{{\partial }^3\vartheta }{\partial {\varsigma }^3}}-{\displaystyle \frac{{\partial }^5\vartheta }{\partial {\varsigma }^5}}=0,\end{array}$$

(11)

where the initial conditions are

$$\begin{array}{c}\hfill \vartheta (\varsigma ,0)={\displaystyle \frac{105}{169}}{\mathrm{sech}}^4\left({\displaystyle \frac{\varsigma }{2\sqrt{13}}}\right).\end{array}$$

(12)

Using the natural transform, we obtain

$$\begin{array}{c}\hfill N^{+}\left[{\displaystyle \frac{{\partial }^{\alpha }\vartheta }{\partial {\tau }^{\alpha }}}\right]=-N^{+}\left[\vartheta {\displaystyle \frac{\partial \vartheta }{\partial \varsigma }}+{\displaystyle \frac{{\partial }^3\vartheta }{\partial {\varsigma }^3}}-{\displaystyle \frac{{\partial }^5\vartheta }{\partial {\varsigma }^5}}\right].\end{array}$$

The operator $N^{+}$ may be employed as

$$\begin{array}{c}\hfill {\displaystyle \frac{s^{\alpha }}{v^{\alpha }}}{N}^{+}\left[\vartheta (\varsigma ,\tau )\right]-{\displaystyle \frac{s^{\alpha -1}}{v^{\alpha }}}\vartheta (\varsigma ,0)=-N^{+}\left[\vartheta {\displaystyle \frac{\partial \vartheta }{\partial \varsigma }}+{\displaystyle \frac{{\partial }^3\vartheta }{\partial {\varsigma }^3}}-{\displaystyle \frac{{\partial }^5\vartheta }{\partial {\varsigma }^5}}\right].\end{array}$$

Employing the inverse natural transform, we obtain

$$\begin{array}{c}\hfill \vartheta (\varsigma ,\tau )={\displaystyle \frac{\frac{105}{169}{\mathrm{sech}}^4\left(\frac{\varsigma }{2\sqrt{13}}\right)}{s}}-N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left(\vartheta {\displaystyle \frac{\partial \vartheta }{\partial \varsigma }}+{\displaystyle \frac{{\partial }^3\vartheta }{\partial {\varsigma }^3}}-{\displaystyle \frac{{\partial }^5\vartheta }{\partial {\varsigma }^5}}\right)\right].\end{array}$$

(13)

Utilizing the concept of HPS on Equation (13), we have

$$\begin{array}{c}\hfill \sum _{i=0}^{\infty }{p}^i\vartheta (\varsigma ,\tau )={\displaystyle \frac{105}{169}}{\mathrm{sech}}^4\left({\displaystyle \frac{\varsigma }{2\sqrt{13}}}\right)-N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left(\sum _{i=0}^{\infty }{p}^i{\vartheta }_i\sum _{i=0}^{\infty }{p}^i{\displaystyle \frac{\partial {\vartheta }_i}{\partial \varsigma }}+\sum _{i=0}^{\infty }{p}^i{\displaystyle \frac{{\partial }^3{\vartheta }_i}{\partial {\varsigma }^3}}-\sum _{i=0}^{\infty }{p}^i{\displaystyle \frac{{\partial }^5{\vartheta }_i}{\partial {\varsigma }^5}}\right)\right].\end{array}$$

By analyzing the relevant parameters of p, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill p^0={\vartheta }_0(\varsigma ,\tau )& =\vartheta (\varsigma ,0),\hfill \\ \hfill p^1={\vartheta }_1(\varsigma ,\tau )& =-N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left({\vartheta }_0{\displaystyle \frac{\partial {\vartheta }_0}{\partial \varsigma }}+{\displaystyle \frac{{\partial }^3{\vartheta }_0}{\partial {\varsigma }^3}}-{\displaystyle \frac{{\partial }^5{\vartheta }_0}{\partial {\varsigma }^5}}\right)\right],\hfill \\ \hfill p^2={\vartheta }_2(\varsigma ,\tau )& =-N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left({\vartheta }_0{\displaystyle \frac{\partial {\vartheta }_1}{\partial \varsigma }}+{\vartheta }_1{\displaystyle \frac{\partial {\vartheta }_0}{\partial \varsigma }}+{\displaystyle \frac{{\partial }^3{\vartheta }_1}{\partial {\varsigma }^3}}-{\displaystyle \frac{{\partial }^5{\vartheta }_1}{\partial {\varsigma }^5}}\right)\right],\hfill \\ & ⋮\hfill \end{array}\end{array}$$

Therefore, one can obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill p^0={\vartheta }_0(\varsigma ,\tau )& ={\displaystyle \frac{105}{169}}{\mathrm{sech}}^4\left({\displaystyle \frac{\varsigma }{2\sqrt{13}}}\right),\hfill \\ \hfill p^1={\vartheta }_1(\varsigma ,\tau )& ={\displaystyle \frac{7560}{\sqrt{13}\mathrm{28,561}}}{\mathrm{sech}}^4\left({\displaystyle \frac{\varsigma }{2\sqrt{13}}}\right)\tanh \left({\displaystyle \frac{\varsigma }{2\sqrt{13}}}\right){\displaystyle \frac{{\tau }^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}},\hfill \\ \hfill p^2={\vartheta }_2(\varsigma ,\tau )& ={\displaystyle \frac{\mathrm{136,080}}{\mathrm{62,758,517}}}\left(-3+2\cosh \left({\displaystyle \frac{\varsigma }{\sqrt{13}}}\right)\right){\mathrm{sech}}^6\left({\displaystyle \frac{\varsigma }{2\sqrt{13}}}\right){\displaystyle \frac{{\tau }^{2\alpha }}{\mathsf{\Gamma }(1+2\alpha )}},\hfill \\ & ⋮·\hfill \end{array}\end{array}$$

Thus, the approximate series solution is given as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \vartheta (\varsigma ,\tau )& ={\vartheta }_0(\varsigma ,\tau )+{\vartheta }_1(\varsigma ,\tau )+{\vartheta }_2(\varsigma ,\tau )+{\vartheta }_3(\varsigma ,\tau )+\cdots \hfill \\ \hfill & ={\displaystyle \frac{105}{169}}{\mathrm{sech}}^4\left({\displaystyle \frac{\varsigma }{2\sqrt{13}}}\right)+{\displaystyle \frac{7560}{\sqrt{13}\mathrm{28,561}}}{\mathrm{sech}}^4\left({\displaystyle \frac{\varsigma }{2\sqrt{13}}}\right)\tanh \left({\displaystyle \frac{\varsigma }{2\sqrt{13}}}\right){\displaystyle \frac{{\tau }^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}}\hfill \\ & +{\displaystyle \frac{\mathrm{136,080}}{\mathrm{62,758,517}}}\left(-3+2\cosh \left({\displaystyle \frac{\varsigma }{\sqrt{13}}}\right)\right){\mathrm{sech}}^6\left({\displaystyle \frac{\varsigma }{2\sqrt{13}}}\right){\displaystyle \frac{{\tau }^{2\alpha }}{\mathsf{\Gamma }(1+2\alpha )}}+\cdots ·\hfill \end{array}\end{array}$$

(14)

This derived series yields the following result if $\alpha =1$:

$$\begin{array}{c}\hfill \vartheta (\varsigma ,\tau )={\displaystyle \frac{105}{169}}{\mathrm{sech}}^4\left({\displaystyle \frac{1}{2\sqrt{13}}}\left(\varsigma -{\displaystyle \frac{36\tau }{169}}\right)\right).\end{array}$$

(15)

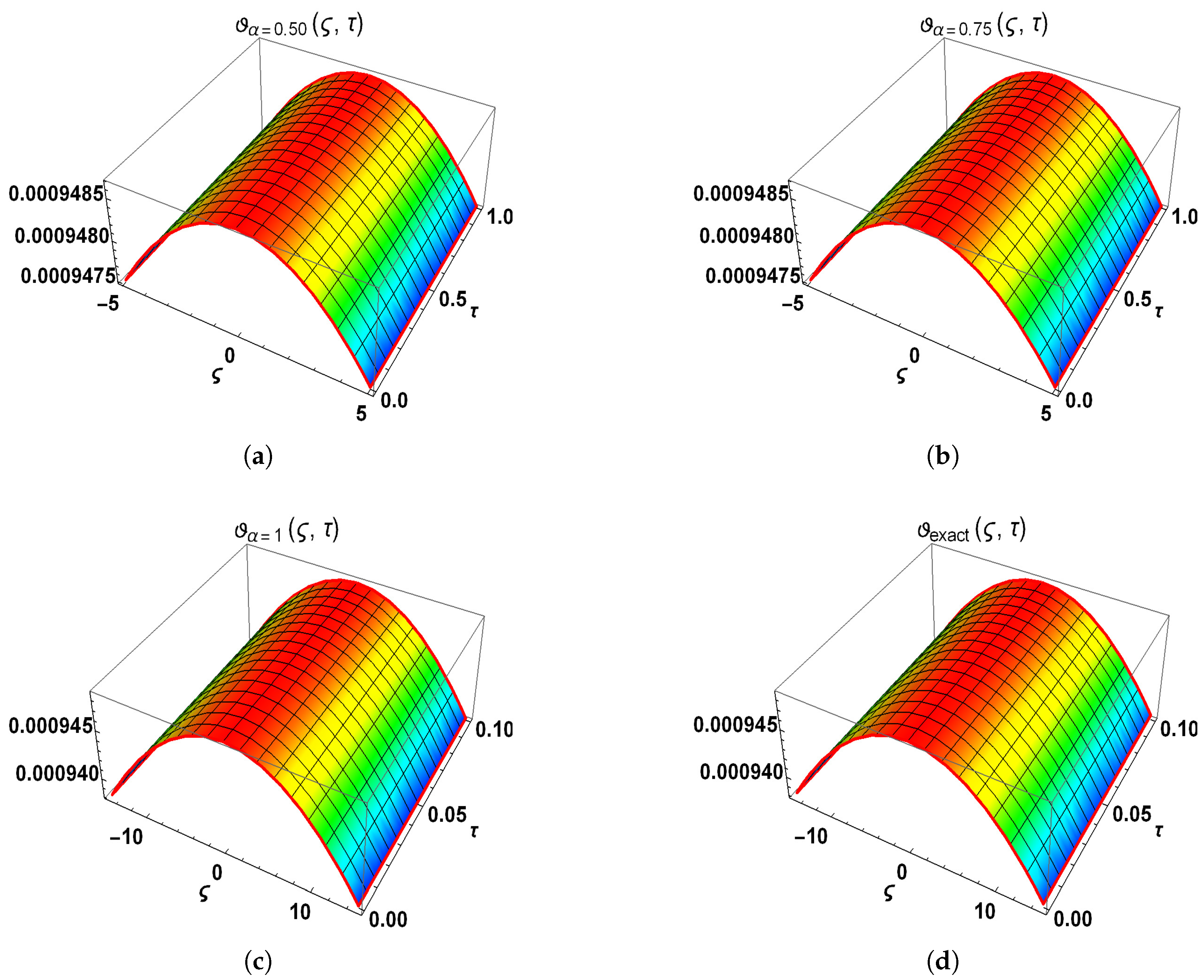
5.2. Problem 2

Consider the following time-fractional modified KP [30]:

$$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^{\alpha }\vartheta }{\partial {\tau }^{\alpha }}}+{\vartheta }^2{\displaystyle \frac{\partial \vartheta }{\partial \varsigma }}+a{\displaystyle \frac{{\partial }^3\vartheta }{\partial {\varsigma }^3}}+b{\displaystyle \frac{{\partial }^5\vartheta }{\partial {\varsigma }^5}}=0,\end{array}$$

(16)

where the initial conditions are

$$\begin{array}{c}\hfill \vartheta (\varsigma ,0)={\displaystyle \frac{3a}{\sqrt{-10b}}}{\mathrm{sech}}^2\left({\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{-a}{5b}}}\varsigma \right).\end{array}$$

(17)

Using the natural transform, we obtain

$$\begin{array}{c}\hfill N^{+}\left[{\displaystyle \frac{{\partial }^{\alpha }\vartheta }{\partial {\tau }^{\alpha }}}\right]=-N^{+}\left[{\vartheta }^2{\displaystyle \frac{\partial \vartheta }{\partial \varsigma }}+a{\displaystyle \frac{{\partial }^3\vartheta }{\partial {\varsigma }^3}}+b{\displaystyle \frac{{\partial }^5\vartheta }{\partial {\varsigma }^5}}\right].\end{array}$$

The operator $N^{+}$ may be employed as

$$\begin{array}{c}\hfill {\displaystyle \frac{s^{\alpha }}{v^{\alpha }}}{N}^{+}\left[\vartheta (\varsigma ,\tau )\right]-{\displaystyle \frac{s^{\alpha -1}}{v^{\alpha }}}\vartheta (\varsigma ,0)=-N^{+}\left[{\vartheta }^2{\displaystyle \frac{\partial \vartheta }{\partial \varsigma }}+a{\displaystyle \frac{{\partial }^3\vartheta }{\partial {\varsigma }^3}}+b{\displaystyle \frac{{\partial }^5\vartheta }{\partial {\varsigma }^5}}\right].\end{array}$$

Employing the inverse natural transform, we obtain

$$\begin{array}{c}\hfill \vartheta (\varsigma ,\tau )={\displaystyle \frac{\frac{3a}{\sqrt{-10b}}{\mathrm{sech}}^2\left(\frac{1}{2}\sqrt{\frac{-a}{5b}}\varsigma \right)}{s}}-N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}S\left({\vartheta }^2{\displaystyle \frac{\partial \vartheta }{\partial \varsigma }}+a{\displaystyle \frac{{\partial }^3\vartheta }{\partial {\varsigma }^3}}+b{\displaystyle \frac{{\partial }^5\vartheta }{\partial {\varsigma }^5}}\right)\right].\end{array}$$

(18)

Utilizing the concept of HPS in Equation (18), we have

$$\begin{array}{c}\hfill \sum _{i=0}^{\infty }{p}^i\vartheta (\varsigma ,\tau )={\displaystyle \frac{3a}{\sqrt{-10b}}}{\mathrm{sech}}^2\left({\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{-a}{5b}}}\varsigma \right)-N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left(\sum _{i=0}^{\infty }{p}^i{\vartheta }_i^2\sum _{i=0}^{\infty }{p}^i{\displaystyle \frac{\partial {\vartheta }_i}{\partial \varsigma }}+a\sum _{i=0}^{\infty }{p}^i{\displaystyle \frac{{\partial }^3{\vartheta }_i}{\partial {\varsigma }^3}}+b\sum _{i=0}^{\infty }{p}^i{\displaystyle \frac{{\partial }^5{\vartheta }_i}{\partial {\varsigma }^5}}\right)\right].\end{array}$$

By analyzing the relevant parameters of p, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill p^0={\vartheta }_0(\varsigma ,\tau )& =\vartheta (\varsigma ,0),\hfill \\ \hfill p^1={\vartheta }_1(\varsigma ,\tau )& =-N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left({\vartheta }_0^2{\displaystyle \frac{\partial {\vartheta }_0}{\partial \varsigma }}+a{\displaystyle \frac{{\partial }^3{\vartheta }_0}{\partial {\varsigma }^3}}+b{\displaystyle \frac{{\partial }^5{\vartheta }_0}{\partial {\varsigma }^5}}\right)\right],\hfill \\ \hfill p^2={\vartheta }_2(\varsigma ,\tau )& =-N^{-1}\left[{\displaystyle \frac{v^{\alpha }}{s^{\alpha }}}{N}^{+}\left({\vartheta }_0^2{\displaystyle \frac{\partial {\vartheta }_1}{\partial \varsigma }}+2{\vartheta }_0{\vartheta }_1{\displaystyle \frac{\partial {\vartheta }_0}{\partial \varsigma }}+a{\displaystyle \frac{{\partial }^3{\vartheta }_1}{\partial {\varsigma }^3}}+b{\displaystyle \frac{{\partial }^5{\vartheta }_1}{\partial {\varsigma }^5}}\right)\right],\hfill \\ & ⋮\hfill \end{array}\end{array}$$

Therefore, one can obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill p^0={\vartheta }_0(\varsigma ,\tau )& ={\displaystyle \frac{3a}{\sqrt{-10b}}}{\mathrm{sech}}^2\left({\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{-a}{5b}}}\varsigma \right),\hfill \\ \hfill p^1={\vartheta }_1(\varsigma ,\tau )& ={\displaystyle \frac{6\sqrt{2}{a}^3\sqrt{-\frac{a}{b}}}{125{(-b)}^{\frac{3}{2}}}}{\mathrm{sech}}^2\left({\displaystyle \frac{\sqrt{-\frac{a}{b}}\varsigma }{\sqrt[2]{5}}}\right)\tanh \left({\displaystyle \frac{\sqrt{-\frac{a}{b}}\varsigma }{\sqrt[2]{5}}}\right){\displaystyle \frac{{\tau }^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}},\hfill \\ \hfill p^2={\vartheta }_2(\varsigma ,\tau )& ={\displaystyle \frac{12\sqrt{\frac{2}{5}}{a}^6}{3125{(-b)}^{\frac{7}{2}}}}\left(-2+\cosh \left({\displaystyle \frac{\sqrt{-\frac{a}{b}}\varsigma }{\sqrt{5}}}\right)\right){\mathrm{sech}}^4\left({\displaystyle \frac{\sqrt{-\frac{a}{b}}\varsigma }{\sqrt[2]{5}}}\right){\displaystyle \frac{{\tau }^{2\alpha }}{\mathsf{\Gamma }(1+2\alpha )}},\hfill \\ & ⋮\hfill \end{array}\end{array}$$

Thus, the approximate series solution yields

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \vartheta (\varsigma ,\tau )& ={\vartheta }_0+{\vartheta }_1+{\vartheta }_2+{\vartheta }_3+\cdots \hfill \\ \hfill & ={\displaystyle \frac{3a}{\sqrt{-10b}}}{\mathrm{sech}}^2\left({\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{-a}{5b}}}\varsigma \right)+{\displaystyle \frac{6\sqrt{2}{a}^3\sqrt{-\frac{a}{b}}}{125{(-b)}^{\frac{3}{2}}}}{\mathrm{sech}}^2\left({\displaystyle \frac{\sqrt{-\frac{a}{b}}\varsigma }{\sqrt[2]{5}}}\right)\tanh \left({\displaystyle \frac{\sqrt{-\frac{a}{b}}\varsigma }{\sqrt[2]{5}}}\right){\displaystyle \frac{{\tau }^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}}\hfill \\ & +{\displaystyle \frac{12\sqrt{\frac{2}{5}}{a}^6}{3125{(-b)}^{\frac{7}{2}}}}\left(-2+\cosh \left({\displaystyle \frac{\sqrt{-\frac{a}{b}}\varsigma }{\sqrt{5}}}\right)\right){\mathrm{sech}}^4\left({\displaystyle \frac{\sqrt{-\frac{a}{b}}\varsigma }{\sqrt[2]{5}}}\right){\displaystyle \frac{{\tau }^{2\alpha }}{\mathsf{\Gamma }(1+2\alpha )}}+\cdots \hfill \end{array}\end{array}$$

(19)

This derived series yields the following results if $\alpha =1$:

$$\begin{array}{c}\hfill \vartheta (\varsigma ,\tau )={\displaystyle \frac{3a}{\sqrt{-10b}}}{\mathrm{sech}}^2\left({\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{-a}{5b}}}\left(\varsigma -{\displaystyle \frac{25b-4a^2}{25b}}\tau \right)\right).\end{array}$$

(20)

6. Results and Discussion

The present section offers an in-depth analysis of the graphical representations of the findings derived using NHTS. Our proposed approach effectively manages the time-fractional KP and modified KP equations, delivering a rapid sequence of results that converge to an accurate solution. We illustrate the surface plots of $\vartheta (\varsigma ,\tau )$ for varying fractional time orders in a Brownian framework.

Figure 1a,b present a visual representation when $\alpha =0.50$ and $\alpha =0.75$ within the range of $-10\le \varsigma \le 10$ and $0\le \tau \le 0.05$. Similarly, Figure 1c,d showcase the visualization when $\alpha =1$ and when the precise outcomes are within the range of $-15\le \varsigma \le 15$ and $0\le \tau \le 0.01$. We can observe that the function $\vartheta (\varsigma ,\tau )$ decreased when the values of the defined spatial domain $\varsigma$ with interval $\tau$ decreased in the example given in Section 5.1. We display the graphical distribution of $\vartheta (\varsigma ,\tau )$ over the range $0\le \varsigma \le 0.5$ and $0\le \tau \le 1$ for different parameters of $\alpha$ in Figure 2.

Figure 3a,b present the visual representation when $\alpha =0.50$ and $\alpha =0.75$ within the range of $-5\le \varsigma \le 5$ and $0\le \tau \le 1$. Similarly, Figure 1c,d display the results when $\alpha =1$ and the exact results fall within the range of $-15\le \varsigma \le 15$ and $0\le \tau \le 0.1$. We note that the function $\vartheta (\varsigma ,\tau )$ increased when the values of the defined spatial domain $\varsigma$ with interval $\tau$ increased in the example featured in Section 5.2. Furthermore, we provide the graphical distribution of $\vartheta (\varsigma ,\tau )$ over the range of $0\le \varsigma \le 0.1$ and $0\le \tau \le 0.01$ for different parameters of $\alpha$ in Figure 4.

Our analysis demonstrates that only a minimal number of iterations are required to obtain an approximate solution for the fractional problem. The proposed method effectively achieves remarkable alignment with the exact results in just two iterations. In addition, incorporating additional parameters significantly improves accuracy, leading to an error reduction approaching zero. As the value of $\alpha$ increases, non-linear effects become more pronounced, despite a decrease in wave amplitude. The consistency between the 2D and 3D graphical representations confirms that our proposed approach successfully handles both the KP and modified KP equations.

7. Conclusions

In this study, we investigated the series solution for the time-fractional Kawahara (KP) and modified KP problems using a semi-analytical approach within the Caputo framework. We compared the results using 2D and 3D graphical representations at different fractional orders to verify the effectiveness of our method. In particular, our method does not impose assumptions or restrictions on variables during its formulation. The graphical solutions reveal the inherent symmetric structure of these problems, a critical characteristic of the time-fractional KP and modified KP. This advancement paves the way for future research, particularly in areas such as positivity preservation, fractal theory, and singular solutions, with broad applications in various scientific and engineering domains.