Optical Solutions of the Nonlinear Kodama Equation with the M-Truncated Derivative via the Extended (G^′/G)-Expansion Method

Abstract

The main purpose of this article is to study the optical solutions of the nonlinear Kodama equation with the M-truncated derivative by using the extended $(G^{\prime }/G)$-expansion method. Firstly, the nonlinear Kodama equation with the M-truncated derivative is transformed into a nonlinear ordinary differential equation based on the principle of homogeneous equilibrium and the traveling wave transformation. Secondly, the optical solutions of the nonlinear Kodama equation with the M-truncated derivative are constructed by using the extended $(G^{\prime }/G)$-expansion method. Finally, three-dimensional, two-dimensional, and contour maps of partial solutions are obtained by using Matlab R2023b mathematical software.

1. Introduction

Complex fractional partial differential equations (CFPDEs) [1,2] are widely used in fields such as physics, chemistry, biology, geophysics, communication, and engineering. For example, in physics, CFPDEs are used to describe various physical phenomena with memory and diffusion processes. In the field of communications [3], CFPDEs can effectively reduce and enhance signals. In finance [4], CFPDEs are used to establish financial market models incorporating memory and volatility. In addition to the aforementioned fields, CFPDEs have broad application prospects in multiple areas. The most typical CFPDE is the well-known fractional-order Schrödinger equation [5,6]. In recent years, many fractional-order derivatives [7,8,9,10] have been proposed and combined with nonlinear partial differential equations to form fractional order partial differential equations. There are many types of fractional derivatives, such as the conformable fractional derivative [11], the Riemann–Liouville fractional derivative [12], and the M-truncated derivative [13,14]. The nonlinear Kodama equation with the M-truncated derivative (NLKE-MTD) is a very important class of CFPDE, which is usually described as follows [15]:

$$i{T}_{k,t}^{\alpha ,\beta }u+u_{xx}+i{u}_{xxx}+{\epsilon }_1{\left|u\right|}^{2}u+i{\epsilon }_2{\left|u\right|}^2{u}_x+i{\epsilon }_3{u}^2{u}_x=0,$$

(1)

where $u=u(x,t)$ stands for the complex function. $T_{k,t}^{\alpha ,\beta }(·)$ represents the M-truncated derivative, its definition and properties will be provided in Section 2. Parameters ${\epsilon }_1$, ${\epsilon }_2$, and ${\epsilon }_3$ are arbitrary constants. i represents the imaginary unit satisfying $i^2=-1$. In [15], Mohammed and his collaborators obtained soliton solutions of Equation (1) by using the generalized Riccati equation method and the Jacobi elliptic function method, respectively. In [16], Algolam et al. obtained the soliton solutions of the stochastic version of the nonlinear Kodama equation (NLKE) by using the $(G^{\prime }/G)$-expansion method and the mapping method, respectively.

The subsequent sections are arranged as follows: In Section 2, NLKE-MTD is transformed into a nonlinear ordinary differential equation. In Section 3, the optical solutions of NLKE-MTD are constructed by using the extended $(G^{\prime }/G)$-expansion method. In Section 4, three-dimensional, two-dimensional, and contour maps of two sets of solutions are obtained by using Matlab mathematical software. In Section 5, a brief conclusion is given.

2. Preliminary

2.1. The M-Truncated Fractional-Derivative and Its Properties

Definition 1

([17]). Let $f:[0,+\infty )\to (-\infty ,+\infty )$. For $0<\alpha \le 1$, the truncated M-fractional derivative is denoted as

$$T_{k,t}^{\alpha ,\beta }f(t)=\underset{h\to 0}{lim}{\displaystyle \frac{f(t{E}_{k,\beta }(h{t}^{1-\alpha }))-f(t)}{h}},\beta \in (0,+\infty ),$$

(2)

where the constant α stands for a fractional-order derivative. $E_{k,\beta }(t)$ is a truncated Mittag–Leffler function defined as follows [18]:

$$E_{k,\beta }(t)=\sum _{k=0}^j{\displaystyle \frac{t^k}{\mathrm{\Gamma }(\gamma k+1)}},t\in \mathbb{C},$$

(3)

where $\mathbb{C}$ represents the complex number.

Remark 1.

MTD has the following properties [19]:

1. 

$T_{k,t}^{\alpha ,\beta }(af+bg)=a{T}_{k,t}^{\alpha ,\beta }f+b{T}_{k,t}^{\alpha ,\beta }g$;

2. 

$T_{k,t}^{\alpha ,\beta }(f)(t)={\displaystyle \frac{t^{1-\beta }}{\mathrm{\Gamma }(\beta +1)}}{\displaystyle \frac{df}{dt}}$;

3. 

$T_{k,t}^{\alpha ,\beta }(fg)=f{T}_{k,t}^{\alpha ,\beta }g+g{T}_{k,t}^{\alpha ,\beta }f$;

4. 

$T_{k,t}^{\alpha ,\beta }(f\circ g)(t)=f^{\prime }(g(t))T_{k,t}^{\alpha ,\beta }g(t)$;

5. 

$T_{k,t}^{\alpha ,\beta }{t}^{\gamma }={\displaystyle \frac{\gamma }{\mathrm{\Gamma }(\beta +1)}}{t}^{\gamma -\alpha }$.

2.2. The Extended $(G^{\prime }/G)$-Expansion Method [20]

We assume that there is a complex partial differential equation with M-truncated fractional-derivatives

$$\mathbf{P}(t,x,T_{k,t}^{\alpha ,\beta }u,u_x,u_{xx},\cdots )=0,$$

(4)

where $u=u(x,t)$ is the unknown function. We then introduce the fractional-order traveling wave transformation

$$u(x,t)=\mathcal{U}(\xi )e^{i\eta },\xi ={\zeta }_{1}x+{\displaystyle \frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }}{t}^{\alpha },\eta ={\mu }_{1}x+{\displaystyle \frac{\mathrm{\Gamma }(\beta +1){\mu }_2}{\alpha }}{t}^{\alpha },$$

(5)

${\zeta }_1$, ${\zeta }_2$, ${\mu }_1$, and ${\mu }_2$ are nonzero constants.

Plugging Equation (5) into Equation (4), we can obtain the following nonlinear ordinary differential equation:

$$\mathbf{Q}(\mathcal{U}(\xi ),{\displaystyle \frac{d\mathcal{U}(\xi )}{d\xi }},{\displaystyle \frac{d^2\mathcal{U}(\xi )}{d{\xi }^2}},{\displaystyle \frac{d^3\mathcal{U}(\xi )}{d{\xi }^3}},\cdots )=0.$$

(6)

Next, we assume that the approximate solution of Equation (6) is

$$\mathcal{U}(\xi )=\sum _{i=0}^N{a}_i{({\displaystyle \frac{G^{\prime }}{G}})}^i+\sum _{i=1}^N{b}_i{({\displaystyle \frac{G^{\prime }}{G}})}^{-i},$$

(7)

and $G=G(\xi )$ satisfies

$$G{G}^{″}={\chi }_{1}G{G}^{\prime }+{\chi }_2{(G^{\prime })}^2+{\chi }_3{G}^2,$$

(8)

where ${\chi }_1$, ${\chi }_2$, and ${\chi }_3$ are real numbers.

The N in Equation (7) can be balanced by the highest order derivative term and the highest order nonlinear term in Equation (6). By substituting Equations (7) and (8) into Equation (6), a polynomial about ${(G^{\prime }/G)}^i$($i=0,1,2,\cdots ,N$) and ${(G^{\prime }/G)}^{-i}$($i=1,2,\cdots ,N$) can be obtained. Let all coefficients of the polynomial be zero. By solving this system of equations, we can obtain the coefficients of Equation (6). The above are the main steps of the extended ($G^{\prime }/G$)-expansion method. The detailed steps can refer to the literature [20].

2.3. Traveling Wave Transformation

Firstly, a very important fractional order traveling wave transformation is presented:

$$\begin{array}{c}\hfill u(x,t)=\mathcal{U}(\xi )e^{i\eta },\xi ={\zeta }_{1}x+{\displaystyle \frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }}{t}^{\alpha },\eta ={\mu }_{1}x++{\displaystyle \frac{\mathrm{\Gamma }(\beta +1){\mu }_2}{\alpha }}{t}^{\alpha }\end{array}$$

(9)

where $U(\xi )$ represents the unknown function. ${\zeta }_1$, ${\zeta }_2$, ${\mu }_1$, and ${\mu }_2$ are nonzero constants.

Plugging Equation (9) into Equation (1) and separating the real and imaginary parts, we can obtain

$$\begin{array}{cc}\hfill & \mathrm{Imaginary}\mathrm{part}:{\epsilon }_1{\zeta }_1^3{\mathcal{U}}^{\prime \prime \prime }+({\zeta }_2+2{\mu }_1{\zeta }_1-3{\epsilon }_1{\mu }_1^2{\zeta }_1){\mathcal{U}}^{\prime }+{\zeta }_1({\epsilon }_2+{\epsilon }_3){\mathcal{U}}^2{\mathcal{U}}^{\prime }=0,\hfill \\ \hfill & \mathrm{Real}\mathrm{part}:({\zeta }_1^2-3{\epsilon }_1{\mu }_1{\zeta }_1^2){\mathcal{U}}^{″}+({\epsilon }_1{\mu }_1^3-{\mu }_2-{\mu }_1^2)\mathcal{U}+({\epsilon }_1-{\epsilon }_2{\mu }_1+{\epsilon }_3{\mu }_1){\mathcal{U}}^3=0,\hfill \end{array}$$

(10)

where $\mathcal{U}=\mathcal{U}(\xi )$.

Integrating Equation (10) with respect to $\xi$ simultaneously once and assuming the integral constant is zero, the following can be obtained:

$${\epsilon }_1{\zeta }_1^3{\mathcal{U}}^{″}+({\zeta }_2+2{\mu }_1{\zeta }_1-3{\epsilon }_1{\mu }_1^2{\zeta }_1)\mathcal{U}+{\displaystyle \frac{{\zeta }_1({\epsilon }_2+{\epsilon }_3)}{3}}{\mathcal{U}}^3=0.$$

(11)

Then, Equation (11) is equivalent to the second equation of Equation (9) and must satisfy the following conditions:

$${\displaystyle \frac{{\zeta }_1^2-3{\epsilon }_1{\mu }_1{\zeta }_1^2}{{\epsilon }_1{\zeta }_1^3}}={\displaystyle \frac{{\epsilon }_1{\mu }_1^3-{\mu }_2-{\mu }_1^2}{{\zeta }_2+2{\mu }_1{\zeta }_1-3{\epsilon }_1{\mu }_1^2{\zeta }_1}}={\displaystyle \frac{3({\epsilon }_1-{\epsilon }_2{\mu }_1+{\epsilon }_3{\mu }_1)}{{\zeta }_1({\epsilon }_2+{\epsilon }_3)}}.$$

(12)

If the conditions of Equation (12) are satisfied, then Equation (11) can be rewritten as

$${\mathcal{U}}^{″}+{\aleph }_2{\mathcal{U}}^3+{\aleph }_1\mathcal{U}=0,$$

(13)

where ${\aleph }_2={\displaystyle \frac{{\epsilon }_2+{\epsilon }_3}{3{\epsilon }_1{\zeta }_1^2}}$ and ${\aleph }_1={\displaystyle \frac{{\zeta }_2+2{\mu }_1{\zeta }_1-3{\epsilon }_1{\mu }_1^2{\zeta }_1}{{\epsilon }_1{\zeta }_1^3}}$.

3. Optical Solutions of NLKE-MTD

Using the principle of homogeneous equilibrium, we can obtain $N=1$ by balancing the highest order derivative term ${\mathcal{U}}^{″}$ and the highest order nonlinear term ${\mathcal{U}}^3$. Then, Equation (7) can be expressed as

$$\mathcal{U}(\xi )=a_1({\displaystyle \frac{G^{\prime }}{G}})+a_0+b_1{({\displaystyle \frac{G^{\prime }}{G}})}^{-1}.$$

(14)

By using Equations (8) and (14), we can obtain

$$\begin{array}{cc}\hfill & {\mathcal{U}}^{″}(\xi )=2a_1({\chi }_2-1){({\displaystyle \frac{G^{\prime }}{G}})}^3+[2a_1{\chi }_1({\chi }_2-1)+a_1{\chi }_1({\chi }_2-1)]{({\displaystyle \frac{G^{\prime }}{G}})}^2\hfill \\ \hfill & +[a_1{\chi }_1^2+2a_1{\chi }_3({\chi }_2-1)]({\displaystyle \frac{G^{\prime }}{G}})+[a_1{\chi }_1{\chi }_3+b_1{\chi }_1({\chi }_2-1)]\hfill \\ \hfill & +[b_1{\chi }_1^2+2b_1{\chi }_3({\chi }_2-1)]{({\displaystyle \frac{G^{\prime }}{G}})}^{-1}+(b_1{\chi }_1^2+2b_1{\chi }_1{\chi }_3){({\displaystyle \frac{G^{\prime }}{G}})}^{-2}\hfill \\ \hfill & +2b_1{\chi }_3^2{({\displaystyle \frac{G^{\prime }}{G}})}^{-3}.\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\mathcal{U}}^3(\xi )& =a_1^3{({\displaystyle \frac{G^{\prime }}{G}})}^3+3a_0{a}_1^2{({\displaystyle \frac{G^{\prime }}{G}})}^2+(3a_0^2{a}_1+3a_1^2{b}_1)({\displaystyle \frac{G^{\prime }}{G}})+(a_0^3+6a_0{a}_1{b}_1)\hfill \\ \hfill & +(3a_0^2{b}_1+3a_1{b}_1^2){({\displaystyle \frac{G^{\prime }}{G}})}^{-1}+3a_0{b}_1^2{({\displaystyle \frac{G^{\prime }}{G}})}^{-2}+b_1^3{({\displaystyle \frac{G^{\prime }}{G}})}^{-3}.\hfill \end{array}$$

(16)

According to the extended ($G^{\prime }/G$)-expansion method in Section 2, we obtain

$$a_1=\pm \sqrt{{\displaystyle \frac{2(1-{\chi }_2)}{{\aleph }_2}}},a_0=\pm {\displaystyle \frac{\sqrt{2}{\chi }_1}{2}}\sqrt{{\displaystyle \frac{1-{\chi }_2}{{\aleph }_2}}},{\aleph }_1={\displaystyle \frac{{\chi }_1^2({\chi }_2-3)}{2}},b_1=0.$$

$$a_1=0,a_0=\pm {\displaystyle \frac{{\chi }_1^2+2{\chi }_1{\chi }_3}{6{\chi }_3^2}}\sqrt{{\displaystyle \frac{2{\chi }_3^2}{{\aleph }_2}}},{\aleph }_1=2{\chi }_3(1-{\chi }_2)-{\chi }_1^2-{\displaystyle \frac{{\chi }_1^2{({\chi }_1+2{\chi }_2)}^2}{6{\chi }_3^2}},b_1=\pm \sqrt{{\displaystyle \frac{2{\chi }_3^2}{{\aleph }_2}}}.$$

Case 1. When $\Delta ={\chi }_2^2-4({\chi }_1-1){\chi }_3>0$ and ${\chi }_1\ne 1$, we can obtain the solution of Equation (1):

$$\begin{array}{cc}\hfill u_1(x,t)& =[\pm {\displaystyle \frac{\sqrt{2}{\chi }_1}{2}}\sqrt{{\displaystyle \frac{1-{\chi }_2}{{\aleph }_2}}}\pm \sqrt{{\displaystyle \frac{2(1-{\chi }_2)}{{\aleph }_2}}}({\displaystyle \frac{{\chi }_2}{2(1-{\chi }_1)}}+{\displaystyle \frac{\sqrt{\Delta }}{2(1-{\chi }_1)}}\hfill \\ \hfill & {\displaystyle \frac{C_{1}sinh(\frac{\sqrt{\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))+C_{2}cosh(\frac{\sqrt{\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))}{C_{1}cosh(\frac{\sqrt{\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))+C_{2}sinh(\frac{\sqrt{\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))}})]\hfill \\ \hfill & e^{i({\mu }_{1}x++{\displaystyle \frac{\mathrm{\Gamma }(\beta +1){\mu }_2}{\alpha }}{t}^{\alpha })}.\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill u_2(x,t)& =[\pm {\displaystyle \frac{{\chi }_1^2+2{\chi }_1{\chi }_3}{6{\chi }_3^2}}\sqrt{{\displaystyle \frac{2{\chi }_3^2}{{\aleph }_2}}}\pm \sqrt{{\displaystyle \frac{2{\chi }_3^2}{{\aleph }_2}}}({\displaystyle \frac{{\chi }_2}{2(1-{\chi }_1)}}+{\displaystyle \frac{\sqrt{\Delta }}{2(1-{\chi }_1)}}\hfill \\ \hfill & {\displaystyle \frac{C_{1}sinh(\frac{\sqrt{\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))+C_{2}cosh(\frac{\sqrt{\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))}{C_{1}cosh(\frac{\sqrt{\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))+C_{2}sinh(\frac{\sqrt{\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))}}{)}^{-1}]\hfill \\ \hfill & e^{i({\mu }_{1}x++{\displaystyle \frac{\mathrm{\Gamma }(\beta +1){\mu }_2}{\alpha }}{t}^{\alpha })}.\hfill \end{array}$$

(18)

Case 2. When $\Delta ={\chi }_2^2-4({\chi }_1-1){\chi }_3<0$ and ${\chi }_1\ne 1$, we can obtain the solution of Equation (1):

$$\begin{array}{cc}\hfill u_3(x,t)& =[\pm {\displaystyle \frac{\sqrt{2}{\chi }_1}{2}}\sqrt{{\displaystyle \frac{1-{\chi }_2}{{\aleph }_2}}}\pm \sqrt{{\displaystyle \frac{2(1-{\chi }_2)}{{\aleph }_2}}}({\displaystyle \frac{{\chi }_2}{2(1-{\chi }_1)}}+{\displaystyle \frac{\sqrt{-\Delta }}{2(1-{\chi }_1)}}\hfill \\ \hfill & {\displaystyle \frac{-C_{1}sin(\frac{\sqrt{-\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))+C_{2}cos(\frac{\sqrt{-\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))}{C_{1}cos(\frac{\sqrt{-\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))+C_{2}sin(\frac{\sqrt{-\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha })))}}]\hfill \\ \hfill & e^{i({\mu }_{1}x++{\displaystyle \frac{\mathrm{\Gamma }(\beta +1){\mu }_2}{\alpha }}{t}^{\alpha })}.\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill u_4(x,t)& =[\pm {\displaystyle \frac{{\chi }_1^2+2{\chi }_1{\chi }_3}{6{\chi }_3^2}}\sqrt{{\displaystyle \frac{2{\chi }_3^2}{{\aleph }_2}}}\pm \sqrt{{\displaystyle \frac{2{\chi }_3^2}{{\aleph }_2}}}({\displaystyle \frac{{\chi }_2}{2(1-{\chi }_1)}}+{\displaystyle \frac{\sqrt{-\Delta }}{2(1-{\chi }_1)}}\hfill \\ \hfill & {\displaystyle \frac{-C_{1}sin(\frac{\sqrt{-\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))+C_{2}cos(\frac{\sqrt{-\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))}{C_{1}cos(\frac{\sqrt{-\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))+C_{2}sin(\frac{\sqrt{-\Delta }}{2}({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha }))}}{)}^{-1}]\hfill \\ \hfill & e^{i({\mu }_{1}x++{\displaystyle \frac{\mathrm{\Gamma }(\beta +1){\mu }_2}{\alpha }}{t}^{\alpha })}.\hfill \end{array}$$

(20)

Case 3. When $\Delta ={\chi }_2^2-4({\chi }_1-1){\chi }_3=0$ and ${\chi }_1\ne 1$, we can obtain the solution of Equation (1):

$$\begin{array}{cc}\hfill u_5(x,t)& =[\pm {\displaystyle \frac{\sqrt{2}{\chi }_1}{2}}\sqrt{{\displaystyle \frac{1-{\chi }_2}{{\aleph }_2}}}\pm \sqrt{{\displaystyle \frac{2(1-{\chi }_2)}{{\aleph }_2}}}{\displaystyle \frac{1}{1-{\chi }_1}}({\displaystyle \frac{{\chi }_2}{2}}+{\displaystyle \frac{C_1}{C_1({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha })+C_2}})]\hfill \\ \hfill & e^{i({\mu }_{1}x++{\displaystyle \frac{\mathrm{\Gamma }(\beta +1){\mu }_2}{\alpha }}{t}^{\alpha })}.\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill u_6(x,t)& =[\pm {\displaystyle \frac{{\chi }_1^2+2{\chi }_1{\chi }_3}{6{\chi }_3^2}}\sqrt{{\displaystyle \frac{2{\chi }_3^2}{{\aleph }_2}}}\pm \sqrt{{\displaystyle \frac{2{\chi }_3^2}{{\aleph }_2}}}(1-{\chi }_1){({\displaystyle \frac{{\chi }_2}{2}}+{\displaystyle \frac{C_1}{C_1({\zeta }_{1}x+\frac{\mathrm{\Gamma }(\beta +1){\zeta }_2}{\alpha }{t}^{\alpha })+C_2}})}^{-1}]\hfill \\ \hfill & e^{i({\mu }_{1}x++{\displaystyle \frac{\mathrm{\Gamma }(\beta +1){\mu }_2}{\alpha }}{t}^{\alpha })}.\hfill \end{array}$$

(22)

4. Numerical Simulation

In this section, we illustrate three-dimensional, two-dimensional, and contour maps of the modulus length as well as the real and imaginary parts of $u_1(x,t)$ when ${\zeta }_1=-1,{\zeta }_2=1,{\epsilon }_1=-1,$${\epsilon }_2=3,{\epsilon }_3=0,{\mu }_1=1,{\mu }_2=-4,{\chi }_1=2,{\chi }_2=2,{\chi }_3={\displaystyle \frac{1}{2}},C_1\ne 0,\alpha =\beta ={\displaystyle \frac{1}{2}}$, and $C_2=0$, as shown in Figure 1, Figure 2 and Figure 3. Moreover, we plot three-dimensional, two-dimensional, and contour maps of the modulus length as well as the real and imaginary parts of $u_5(x,t)$ when ${\zeta }_1=-1,$${\zeta }_2=1,{\epsilon }_1=-1,{\epsilon }_2=3,{\epsilon }_3=0,{\mu }_1=1,{\mu }_2=-4,{\chi }_1=2,{\chi }_2=1,{\chi }_3={\displaystyle \frac{1}{2}},C_1\ne 0,$$\alpha =\beta ={\displaystyle \frac{1}{2}}$, and $C_2=0$, as shown in Figure 4, Figure 5 and Figure 6.

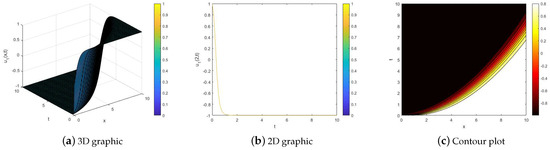
Figure 1. The modulus of the solution $u_1(x,t)$ of Equation (1) for ${\zeta }_1=-1,{\zeta }_2=1,{\epsilon }_1=-1,$${\epsilon }_2=3,{\epsilon }_3=0,{\mu }_1=1,{\mu }_2=-4,{\chi }_1=2,{\chi }_2=2,{\chi }_3={\displaystyle \frac{1}{2}},C_1\ne 0,C_2=0,\alpha =\beta ={\displaystyle \frac{1}{2}}$.

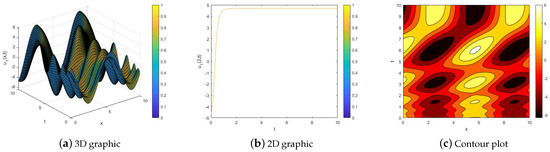
Figure 2. The real part of the solution $u_1(x,t)$ of Equation (1) for ${\zeta }_1=-1,{\zeta }_2=1,{\epsilon }_1=-1,$${\epsilon }_2=3,{\epsilon }_3=0,{\mu }_1=1,{\mu }_2=-4,{\chi }_1=2,{\chi }_2=2,{\chi }_3={\displaystyle \frac{1}{2}},C_1\ne 0,C_2=0,\alpha =\beta ={\displaystyle \frac{1}{2}}$.

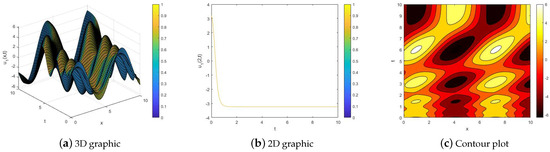
Figure 3. The imaginary part of the solution $u_1(x,t)$ of Equation (1) for ${\zeta }_1=-1,{\zeta }_2=1,{\epsilon }_1=-1,$${\epsilon }_2=3,{\epsilon }_3=0,{\mu }_1=1,{\mu }_2=-4,{\chi }_1=2,{\chi }_2=2,{\chi }_3={\displaystyle \frac{1}{2}},C_1\ne 0,C_2=0,\alpha =\beta ={\displaystyle \frac{1}{2}}$.

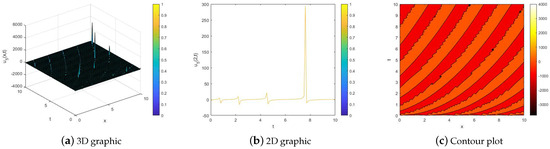
Figure 4. The modulus of the solution $u_5(x,t)$ of Equation (1) for ${\zeta }_1=-1,{\zeta }_2=1,{\epsilon }_1=-1,$${\epsilon }_2=3,{\epsilon }_3=0,{\mu }_1=1,{\mu }_2=-4,{\chi }_1=2,{\chi }_2=1,{\chi }_3={\displaystyle \frac{1}{2}},C_1\ne 0,C_2=0,\alpha =\beta ={\displaystyle \frac{1}{2}}$.

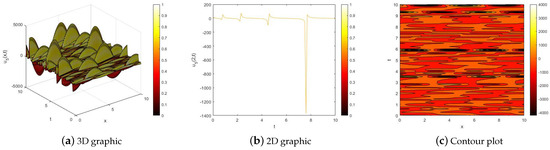
Figure 5. The real part of the solution $u_5(x,t)$ of Equation (1) for ${\zeta }_1=-1,{\zeta }_2=1,{\epsilon }_1=-1,$${\epsilon }_2=3,{\epsilon }_3=0,{\mu }_1=1,{\mu }_2=-4,{\chi }_1=2,{\chi }_2=1,{\chi }_3={\displaystyle \frac{1}{2}},C_1\ne 0,C_2=0,\alpha =\beta ={\displaystyle \frac{1}{2}}$.

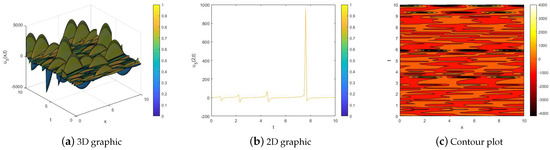
Figure 6. The imaginary part of the solution $u_5(x,t)$ of Equation (1) for ${\zeta }_1=-1,{\zeta }_2=1,{\epsilon }_1=-1,$${\epsilon }_2=3,{\epsilon }_3=0,{\mu }_1=1,{\mu }_2=-4,{\chi }_1=2,{\chi }_2=1,{\chi }_3={\displaystyle \frac{1}{2}},C_1\ne 0,C_2=0,\alpha =\beta ={\displaystyle \frac{1}{2}}$.

5. Conclusions

In the article, we used the extended $(G^{\prime }/G)$-expansion method to study the optical solutions of NLKE-MTD. These solutions mainly include hyperbolic function solutions, rational function solutions, trigonometric function solutions, and negative power solutions. Moreover, we illustrated three-dimensional, two-dimensional, and contour maps of the modulus length as well as the real and imaginary parts of $u_1(x,t)$ and $u_5(x,t)$, respectively. Compared with [16], this paper considers the traveling wave solution of the fractional-order version of NLKE, and the $(G^{\prime }/G)$-expansion method used in this paper is an extended form method. In addition, this paper also provides solutions with negative power forms. These graphs clarify the propagation of waves in the solution of NLKE-MTD.