Mechanical Response and Damage Characteristics of Frozen–Thawed Sandstone Across Various Temperature Ranges Under Impact Loads

Abstract

Freeze–thaw action is a key factor in the deterioration of the dynamic mechanical behavior of rocks in cold regions. This study used yellow sandstone, which is prevalent in the seasonally cold region of Xinjiang, China. The yellow sandstone samples were subjected to various temperatures and a range of freeze–thaw cycles. Impact mechanical tests were performed using a Split Hopkinson Pressure Bar (SHPB) system on the treated samples. The effects of freezing temperature and changes in impact load on the mechanical properties of frozen–thawed sandstone were examined. Additionally, the damage fractal characteristics of the sandstone were analyzed using fractal theory. The results indicate that as the freezing temperature decreases, the stress–strain curves of frozen–thawed specimens exhibit a clear initial compaction stage. The dynamic strength of the specimens decreases with lower freezing temperatures and shows a logarithmic relationship with the loading strain rate; however, the dynamic deformation modulus exhibits no significant correlation with the strain rate. The fractal dimension is positively correlated with the strain rate, indicating that lower freezing temperatures correspond to a higher rate of increase in the fractal dimension. These findings offer valuable insights into the damage deterioration characteristics of frozen–thawed rocks under varying temperature conditions.

1. Introduction

Freeze–thaw cycles are one of the most potent forms of physical weathering [1]. This process can alter the mechanical properties of rocks and impact their durability [2]. At lower temperatures, the transformation of water into ice within the pore spaces leads to changes in the internal pore structure of the rock [3,4]. The increase in volume as the water turns to ice causes internal damage to the rock, such as the development of pores and cracks, which ultimately reduces the rock’s mechanical properties [5]. During construction, rocks weathered by freeze–thaw cycles are more susceptible to damage from stress waves [6,7].

Scholars have researched the effect of freeze–thaw cycles on rocks’ static mechanical properties. These studies primarily consider factors such as rock type, pore characteristics, saturation, internal damage, temperature change rate, number of cycles, duration of freeze–thaw cycles, and the surrounding hydrochemical environment. Ghobadi [8] and Wang et al. [9,10] conducted freeze–thaw cycles and mechanical tests on various types of rocks, including sandstone, granite, and marble. The results showed that sedimentary rocks are more sensitive to freeze–thaw weathering than magmatic and metamorphic rocks. A gradual decrease in properties such as uniaxial compressive strength, tensile strength, and longitudinal wave velocity with increased cycles indicates this sensitivity. The main reasons for this phenomenon are the differences in lithology, critical minerals, microstructural surfaces, and bonding types. Al-Omari et al. [11] conducted freeze–thaw tests on porous limestone with varying porosities and saturations, finding that rock damage was evident in the early stages of freeze–thaw cycles when saturation exceeded 80%. An 80% to 85% saturation level represents the critical water content for freeze–thaw damage. This critical water content is independent of the number of cycles and porosity, representing an intrinsic property of the rock. Liu [12], T. Yamabe [13], Chen [14], etc., also considered that saturation is the critical factor in freeze–thaw action determining the degree of freeze–thaw damage. Freeze–thaw action has little effect below the critical saturation or on dry rocks [15]. Temperature is the key factor affecting the volume fraction of ice crystals in the rock pores, which determines the effect of freeze–thaw conditions on the mechanical properties of the rock [16,17]. Weng et al. [18] and Çelik et al. [19] carried out freeze–thaw cycling tests on materials such as rocks at different lower temperature limits and found that the lower the temperature limit, the greater the loss of mass and water absorption of the specimen and the more significant the reduction in strength and modulus of elasticity. M. Akin et al. [20] considered rock damage under freeze–thaw cycle conditions as fatigue damage, which is positively correlated with the number of cycles and manifests as a gradual decrease in strength and modulus. Static mechanical tests are typically used to study the mechanical properties of rocks under the freeze–thaw effect. However, rock engineering is susceptible to dynamic loading perturbations, which represent a significant difference from static mechanical behavior. The deformation and damage behaviors are more complex, especially under variable-temperature freeze–thaw conditions. Therefore, it is essential to conduct dynamic mechanical tests to fully understand the influence of variable-temperature freeze–thaw conditions on the mechanical properties of rock.

Rocks in mining operations are subjected to various loads, of which impact loads are significant [21]. The Split Hopkinson Pressure (Tension) Bar experimental system (SHPB) is one of the leading facilities for studying the mechanical properties of rock under impact loading conditions [18]. Ma et al. [22] conducted SHPB impact tests on different rocks after freeze–thawing. They found that with the increase in freeze–thaw damage, the dynamic strength of different rocks showed an exponential decrease pattern, which is consistent with the results of Wang [9], Xu [23], etc. Li et al. [24] combined NMR and SHPB impact tests and found that the distribution characteristics of the pore structure are affected by freeze–thaw action, which in turn affects the dynamic mechanical properties. Liu [25] and Zhang [26], etc., also conducted static and impact tests on post-freeze–thaw rocks and pointed out that the sensitivity of dynamic mechanical properties of rocks to freeze–thaw damage is greater than that of static mechanics of stones. Zhao et al. [27] conducted low-temperature impact tests on sandstones with prefabricated fissures and noted that the presence of fissure ice significantly affected the dynamic mechanical properties of the rocks. Like static loading, the dynamic mechanical properties of the rock are almost unaffected by freeze–thaw action when the saturation is below a critical value. In addition, Zhou et al. [28] conducted SHPB tests at different loading strain rates to analyze the effect of changes in the microstructure of rock specimens under freeze–thaw conditions on the energy dissipation during the impact process. The research on the dynamic mechanics of rocks affected by freeze–thaw conditions is mainly focused on the impact test of saturated rocks under single-temperature freeze–thaw conditions. It is evident that the majority of current studies focus on freeze–thaw cycles within a particular temperature range, such as −20 °C to 0 °C. The effects of freeze–thaw cycles at varying temperatures have not been thoroughly investigated. Therefore, in this paper, the impact of varying freezing temperatures (−0~20 °C, −3~20 °C, −5~20 °C, and −20~20 °C) on sandstone is systematically examined.

Freeze–thaw cycles and shock perturbations in cold regions do not necessarily occur simultaneously [29,30]. This phenomenon exhibits a superimposition effect on the time scale, indicating that it is independent rather than a coupling relationship, which allows for separate analysis. In this study, we conducted impact mechanical tests on yellow sandstone specimens at varying strain rates while undergoing freeze–thaw cycles at different temperatures. Additionally, we employed scanning electron microscopy to examine how variations in freezing temperature affect the dynamic mechanical response of yellow sandstone.

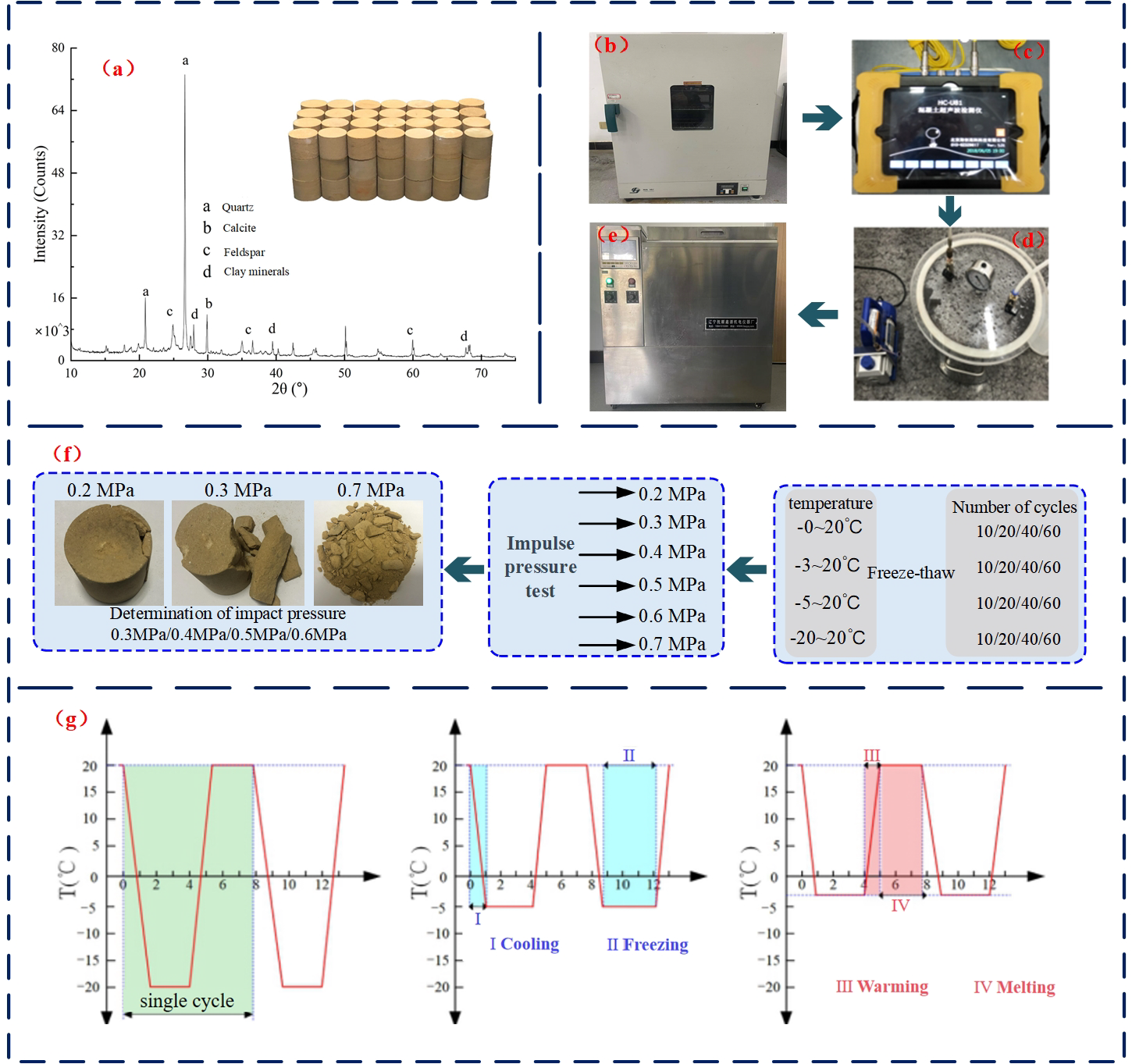
2. Material Preparation and Experimental Scheme

2.1. Material Preparation

Careful material preparation is key to successful testing [31,32]. The yellow sandstone for the work was sampled from the slope of an open pit mine in Urumqi, China. The selected yellow sandstone is a common sedimentary rock in the Xinjiang region of China. At the same time, the Xinjiang region is situated in seasonally cold areas, and the rock structures are susceptible to freeze–thaw weathering. X-ray diffraction studies show the main mineral composition of the yellow sandstone as shown in Figure 1a. The main components include quartz, sodium feldspar, plagioclase, calcite, and clay minerals.

(1) According to the standards of the International Society of Rock Mechanics, homogeneous sandstone blocks were selected, drilled in the direction of the laminations, and machined into cylinders of 50 mm diameter × 50 mm height, with a surface error of 0.3 mm or less and good surface integrity.

(2) The sieved samples were tested for dry mass and volume. The samples were dried in a drying oven at 105 °C for 48 h.

(3) Sandstone longitudinal wave velocities were determined by ultrasonic velocimetry. Samples within 10% of the average wave velocity were selected.

(4) The specimen was saturated using a vacuum saturator. It was placed in pure water for 24 h, and its saturated mass was measured.

(5) The prepared specimens were divided into different groups. Freeze–thaw cycle tests were performed at different freezing temperatures.

The numbers of cycles were 0, 10, 20, 40, and 60 times. The different temperatures were −0~20 °C, −3~20 °C, −5~20 °C, and −20~20 °C. The duration of freezing during the test was set to 4 h, the duration of thawing was set to 4 h, the rate of temperature change was set to 0.5 °C/min, and each freeze–thaw cycle was set to 8 h. The temperature change rate was set to 0.5 °C/min. This study used a fast freeze–thaw test chamber as shown in Figure 1e. The chamber was operated over a temperature range of −30 to 80 °C and controlled to an accuracy of ±0.5 °C. After completing the specified number of cycles, the impact test was performed. It is important to note that the impact is a transient impact. Following the impact, scanning electron microscopy from Vega Compact in the Czech Republic was utilized to perform SEM observation of the damaged section of each group of specimens.

To determine a suitable range for test air pressure, unfrozen and thawed rock samples were exposed to varying pressure impacts. The air pressure interval was set to 0.1 MPa, and the crushing outcomes are depicted in the figure. Figure 1f shows that at 0.2 MPa, the specimen exhibited only minor spalling at the edges. At 0.3 MPa, the rock specimen started to fracture, with the degree of fragmentation being minimal. At 0.7 MPa, the rock specimen was completely crushed, lacking any significant structure. Considering the effects of freezing and thawing, air pressures of 0.3 MPa, 0.4 MPa, 0.5 MPa, and 0.6 MPa were chosen to investigate the impact of dynamic loading on the mechanical response of sandstone subjected to variable-temperature freezing and thawing conditions.

Equation (1) was used to calculate the basic physical properties of the yellow sandstone samples. The results are shown in

Table 1. Physical properties of yellow sandstone.

Parameter	Longitudinal Wave Speed (km/s)	Dry Mass (g/cm3)	Porosity (%)	Saturated Density (g/cm3)	Natural Moisture Content (%)	Saturated Water Content (%)
Value	2.61	2.15	17.84	2.33	4.28	8.67

.

$$\left\{\begin{array}{l}\omega ={\displaystyle \frac{m-m_{\mathrm{d}0}}{m_{\mathrm{d}0}}};{\omega }_{\mathrm{d}}={\displaystyle \frac{m_{\mathrm{s}0}-m_{\mathrm{d}0}}{m_{\mathrm{s}0}}}\hfill \\ n_{\mathrm{w}}={\displaystyle \frac{4\times (m_{\mathrm{s}0}-m_{\mathrm{d}0})}{\pi d^2{\rho }_{\mathrm{w}}}}\times 100\%\hfill \\ v_{\mathrm{p}}={\displaystyle \frac{l}{t_{\mathrm{p}}}}\hfill \end{array}\right.$$

(1)

where ω and m are the natural water content (%) and mass (g) of the yellow sandstone; m_s0 and m_d0 are the saturated mass and dry mass (g) of the yellow sandstone; ρ_w is the density of pure water, g/cm³; d and l are the diameter and length of the rock sample (mm), respectively; and t_p is the propagation time of the longitudinal wave in the rock sample (s).

2.2. SHPB System and Test Scheme

The SHPB system primarily conducts impact tests, as illustrated in Figure 2. When high-pressure gas activates the striking head to strike the incident rod, an elastic compression wave is generated. A portion of the compression wave travels through the sample to the transmission rod. Based on the principle of one-dimensional stress wave propagation, the dynamic loads (P₁ and P₂), strain rate, and strain at both ends of the specimen (as demonstrated in Equation (2) were calculated using the three-wave analysis method [33].

$$\left\{\begin{array}{l}{P}_1=A_{\mathrm{r}}{E}_0\left[{\epsilon }_{\mathrm{i}}(t)+{\epsilon }_{\mathrm{r}}(t)\right],P_2(t)=A_{\mathrm{r}}{E}_0{\epsilon }_{\mathrm{t}}(t)\\ \dot{\epsilon }(t)={\displaystyle \frac{C_0}{L}}\left[{\epsilon }_{\mathrm{i}}(t)-{\epsilon }_{\mathrm{r}}(t)-{\epsilon }_{\mathrm{t}}(t)\right]\\ \epsilon (t)={\displaystyle {\int }_0^t\dot{\epsilon }(t)dt=-2\frac{C_0}{L}{\displaystyle {\int }_0^t{\epsilon }_r(t)dt}}\end{array}\right.$$

(2)

where the incident wave is ε_i(t); the reflected wave is ε_r(t), and the transmitted wave is ε_t(t); the cross-sectional area and the modulus of elasticity of the SHPB rod are denoted as A₀ and E₀, respectively; the velocity of propagation of the elastic wave in the rod is C₀; the average strain in the rock sample is ε(t); and the average strain rate in the rock sample is $\dot{\epsilon }(t)$. The length of the rock sample is denoted as L.

Furthermore, the measurement accuracy of the dynamic strain gauge of the SHPB system used in this test is 0.001%, and the accuracy of the pneumatic control system is 0.005 MPa. Validation of the SHPB test results is mandatory [34]. The stress uniformity verification was carried out on the basis of several repetitive tests before the start of the test, as shown in Figure 2c. Considering the effects of F-T cycles, various loading air pressures (0.3 MPa, 0.4 MPa, 0.5 MPa, and 0.6 MPa) were utilized to examine the impact of dynamic loading on the mechanical response of frozen–thawed sandstone across a range of temperatures (−0~20 °C, −3~20 °C, −5~20 °C, −20~20 °C).

3. Impact Mechanical Responses of Frozen–Thawed Sandstone

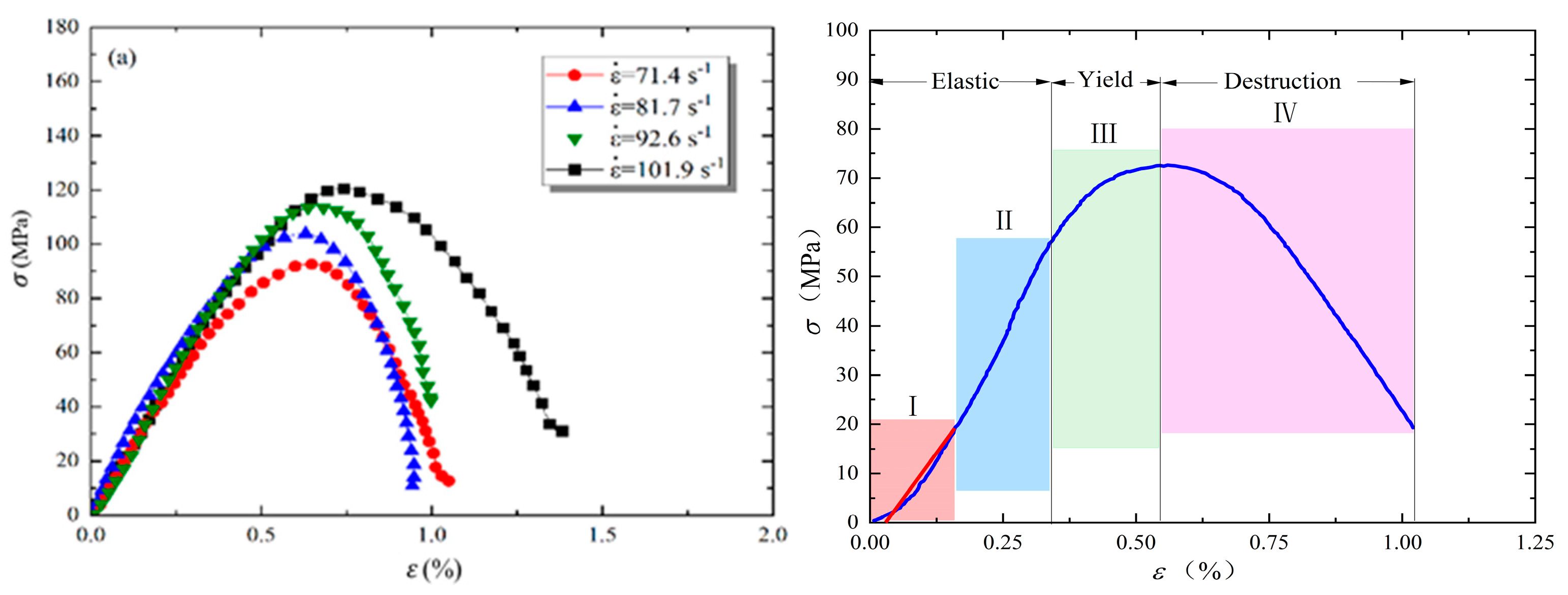
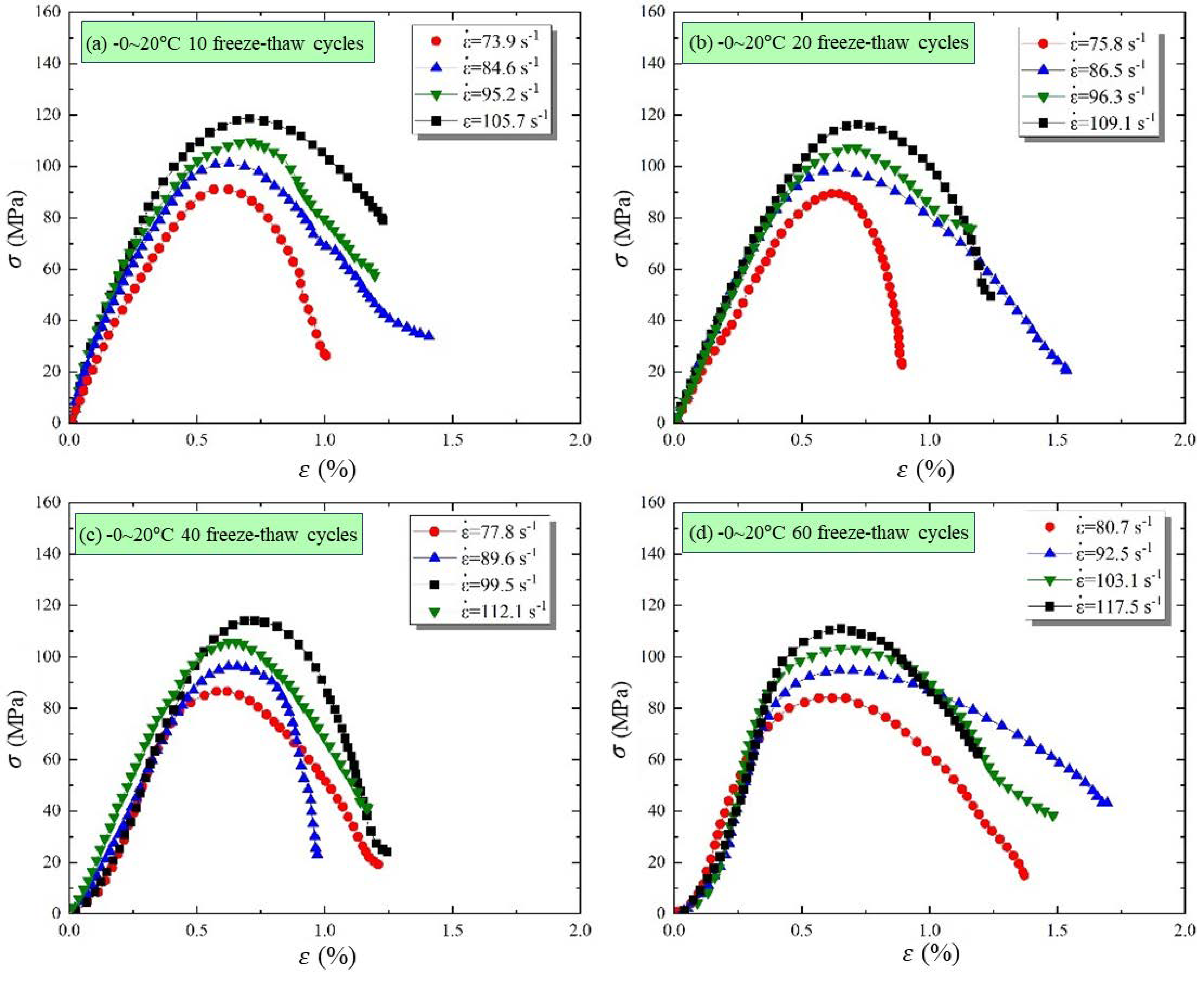
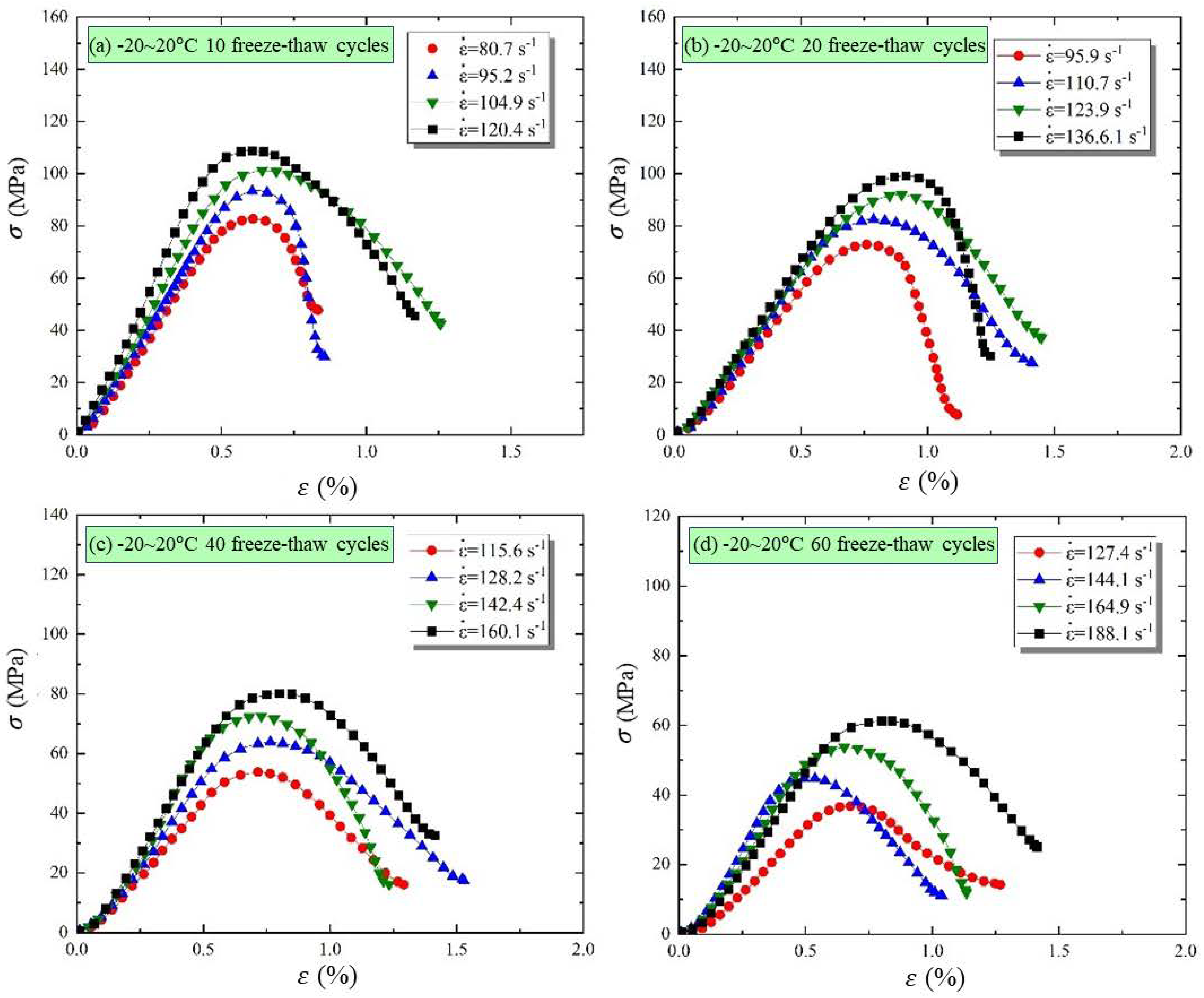
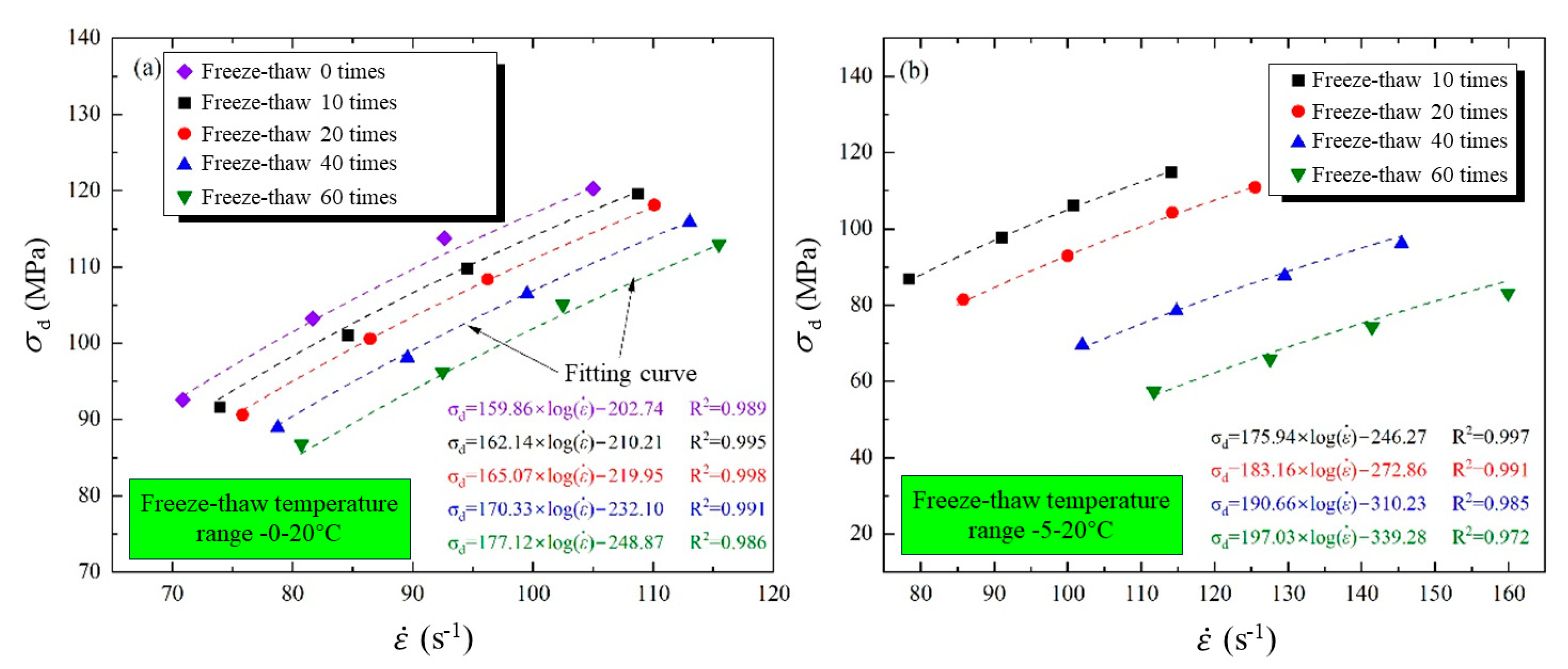
3.1. Characteristics of Dynamic Compressive Stress–Strain Curves

We obtained the dynamic stress–strain curves of the rock samples using the three-wave method (Equation (2)). As shown in Figure 3, the stress–strain curves of unfrozen–thawed samples under impact loading conditions can be divided into three stages: the elastic stage, the yielding stage, and the destruction stage. As shown in Figure 3a, it can be found that the dynamic compressive strength of the samples increases with the growth in the strain rate, presenting an obvious strain rate enhancement effect. To further analyze the effect of freeze–thaw cycles on dynamic stress–strain behavior, Figure 3b compares the typical difference between the before and after freeze–thaw cycles. Notably, the initial elastic deformation section of the sample becomes steeper after the freeze–thaw test, and initial redundant strain is observed, which can be viewed as indicative of crack compaction and pore closure. As for the yield deformation section, the strain rate has more impact on the stress–strain curve, and the stress value under unit strain conditions significantly increases with the strain rate, while the maximum strain value of the yield segment decreases obviously. In the destruction deformation section, the sample at a high strain rate shows prominent deformation capacity, and its strain variation is significantly higher than that at a low strain rate.

Figure 4, Figure 5, Figure 6 and Figure 7 show that the change in freezing temperature significantly affects the stress–strain relationship of rock samples under impact loading conditions. In comparison to the static test, the dynamic curve of the unfrozen and thawed sandstone directly entered the approximate elastic deformation stage, skipping the initial compaction stage. This phenomenon occurs because the initial microcracks in the specimens are relatively few and do not intersect, resulting in initial defects that cannot close promptly at high strain rates. At this juncture, the overall structure of the sandstone specimen remains the primary factor influencing its load-bearing capacity, leading the rock sample to proceed directly to stage II. In other words, the rate of matrix deformation in sandstone specimens is lower than the propagation rate of stress waves, resulting in deformation hysteresis [35,36,37]. This phenomenon has been previously observed and demonstrated in earlier studies [38]. However, under the influence of freeze–thaw cycles, the dynamic stress–strain curve of the rock samples evolved from three stages to four. An obvious compaction stage (stage I) was observed; the lower the freezing temperature, the more pronounced this compaction stage became. For example, under freeze–thaw conditions ranging from −0 to 20 °C, the rock samples did not exhibit a distinct compaction stage I after 60 cycles. This can be attributed to the minimal development of internal pores and the negligible generation of new pores at this temperature. Consequently, the stress–strain relationship was comparable to that of unfrozen rock samples under impact loading conditions. When the freezing temperature decreased to −20 °C, the rock samples displayed a distinct compaction stage I after 60 cycles, exhibiting characteristics similar to those observed in static compression tests. This implies that the internal pores and microfractures began to develop and merge following freeze–thaw cycles, gradually becoming critical factors in determining the load-bearing capacity [39,40,41]. Variations in freezing temperature induce permanent damage to the sandstone, thereby impacting its mechanical response to dynamic loading. As the impact load increases, the rock samples progressively transition into either the elastic or yielding phase [42,43].

The elastic stage II corresponds to a linear increase in stress with strain, where the elastic strain energy stored within the rock sample gradually accumulates. As illustrated in Figure 4, Figure 5, Figure 6 and Figure 7, under the same freeze–thaw cycle conditions, the slope of stage II significantly decreases with lower freezing temperatures, implying a reduction in the rate of elastic strain energy storage, which reflects the weakening of the rock samples’ deformation resistance. This occurs because a lower freezing temperature intensifies the effects of the freeze–thaw process on the rock’s structure, leading to an increase in the volume of internal defects and a reduction in the strength of the collodion and mineral grains. This weakening of the energy storage function results in an earlier transition to yielding stage III. Upon entering yielding stage III, the elastic strain energy starts to be released. At this point, defects within the rock sample, such as microfractures and pores, enter a state of instability while new fractures form, causing its slope to gradually decrease to zero, reaching the peak point. Stage III demonstrates a significant strain softening phenomenon, related to freeze–thaw action and strain rate, reflecting a comprehensive interplay among strain rate strength, strain rate hardening, and thermal softening [44,45,46]. After reaching the peak point, the rock sample transitions to destruction stage IV, where cracks gradually propagate and develop into macroscopic fractures, ultimately leading to sample failure and a loss of bearing capacity.

Freeze–thaw conditions have a serious effect on the mechanical properties of yellow sandstone. In contrast, red sandstone and shale show similar trends but with different degrees of sensitivity to freeze–thaw conditions. Red sandstone is more severely damaged by freeze–thaw cycles than shale. Both rocks show similar trends in compressive and tensile properties, but red sandstone is more sensitive to freeze–thaw cycles [47,48]. This study takes yellow sandstone as the research object, and the experimental conclusions obtained have certain commonalities under the same experimental conditions, which can provide an important reference basis for engineering construction in cold regions.

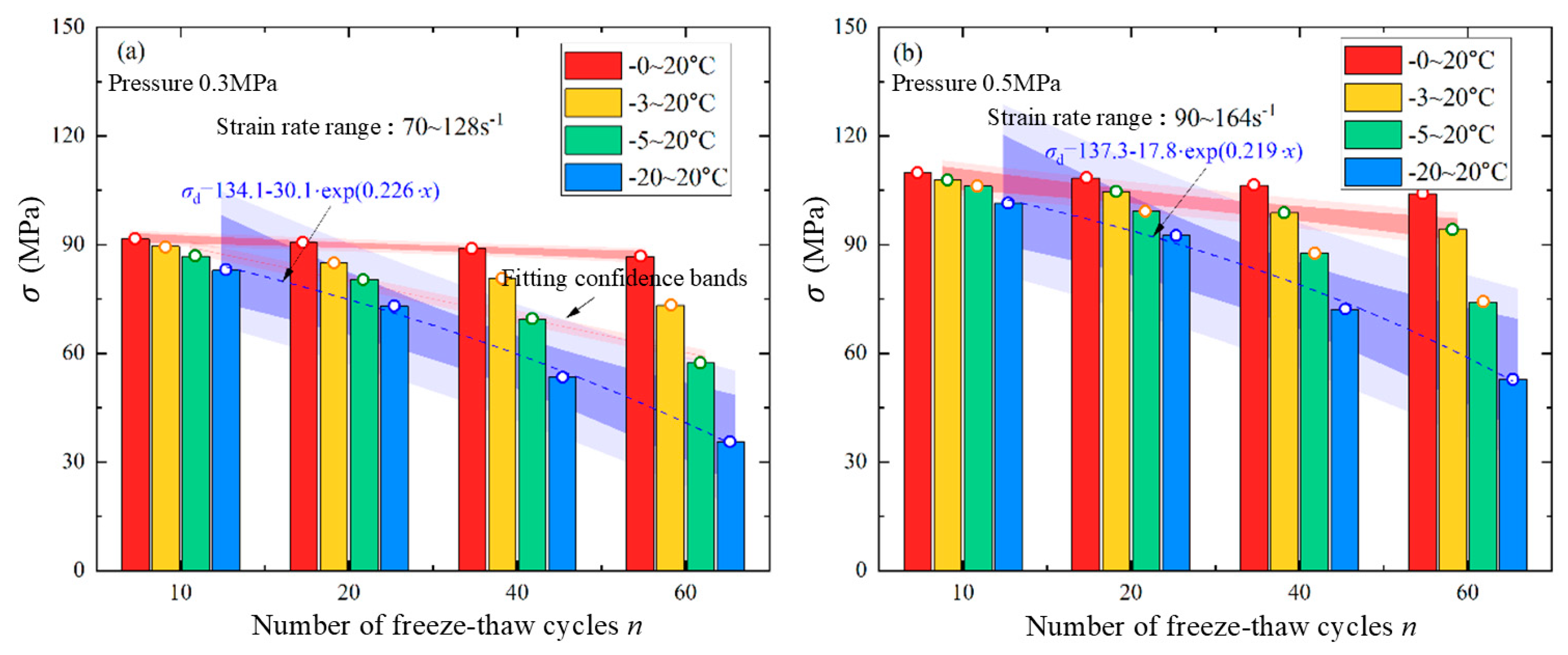
3.2. Evolution Characteristics of Dynamic Peak Strength

To more effectively illustrate the impact of freezing temperature on the dynamic deformation resistance and bearing capacity of frozen–thawed rocks, this paper fits the dynamic strength results of frozen–thawed rock samples at different freezing temperatures using Equation (3)

$${\sigma }_{\mathrm{d}}=h\times \log \dot{\epsilon }+f$$

(3)

where h and f are the fitting parameters in units of MPa·s and MPa, respectively. The parameter h specifies the rate of increase in dynamic strength, whereas f defines the magnitude of dynamic strength. Analysis of the fitted function in Figure 8 indicates that freeze–thaw cycling enhances the growth rate of dynamic strength in rock samples, while concurrently reducing their dynamic peak strength.

Given the similarity in the rules governing changes in dynamic strength and strain rate, only two freeze–thaw temperature intervals were selected to illustrate the effect of freezing temperature on the dynamic loading of frozen–thawed rock samples. Figure 8a illustrates that the strain rate of rock samples subjected to the same air pressure increases with the number of freeze–thaw cycles. For instance, as the number of freeze–thaw cycles increased from 0 to 60, the strain rate of rock samples subjected to 0.3 MPa impact air pressure increased from 71.4 s⁻¹ to 80.7 s⁻¹, representing a 13.0% increase; moreover, the increase was more pronounced at higher air pressures. This finding aligns with the observation that larger impact loads result in faster deformation rates of rocks in practical engineering applications. Furthermore, as the freezing temperature decreased, the strain rate of rock samples under impact loading conditions increased from 47.1 s⁻¹ (−0 to 20 °C) to 80.8 s⁻¹ (−5 to 20 °C), indicating that the dynamic deformation rate of rock samples is more sensitive to changes in freezing temperature. This increase in strain rate may be attributed to the freeze–thaw action that softens rocks in cold regions.

Figure 9 illustrates the changes in the dynamic strength of rock samples under two types of impact loads, considering freeze–thaw temperature and the number of cycles. The dynamic strength exhibits a decreasing trend as the number of freeze–thaw cycles increases. This decreasing trend shifts from a linear function to an exponential function as the freezing temperatures decrease from 0 °C to −20 °C. This indicates that lower freezing temperatures accelerate the deterioration of the dynamic mechanical properties of the rock samples. Simultaneously, as the impact load increases, the decreasing trend in the dynamic strength of the rock samples becomes more pronounced. The exponent of the fitted function falls from 0.226 to 0.219. For instance, the dynamic strength of the rock samples subjected to freeze–thaw cycles from −3 °C to 20 °C in Figure 9a decreases from 89.6 MPa to 73.2 MPa. However, in Figure 9b, it decreases from 107.9 MPa to 93.5 MPa. This phenomenon occurs because the reduction in freezing temperature enhances the freezing and expansion forces within the pores. When freezing progresses from the outside inward, an “ice barrier” forms on the outer surface, which elevates internal ice pressure and contributes to the phenomenon of “hydraulic fracturing” [49,50]. Furthermore, the cyclic nature of freezing and thawing exacerbates these effects, as repeated cycles of expansion and contraction can result in cumulative damage [29,30].

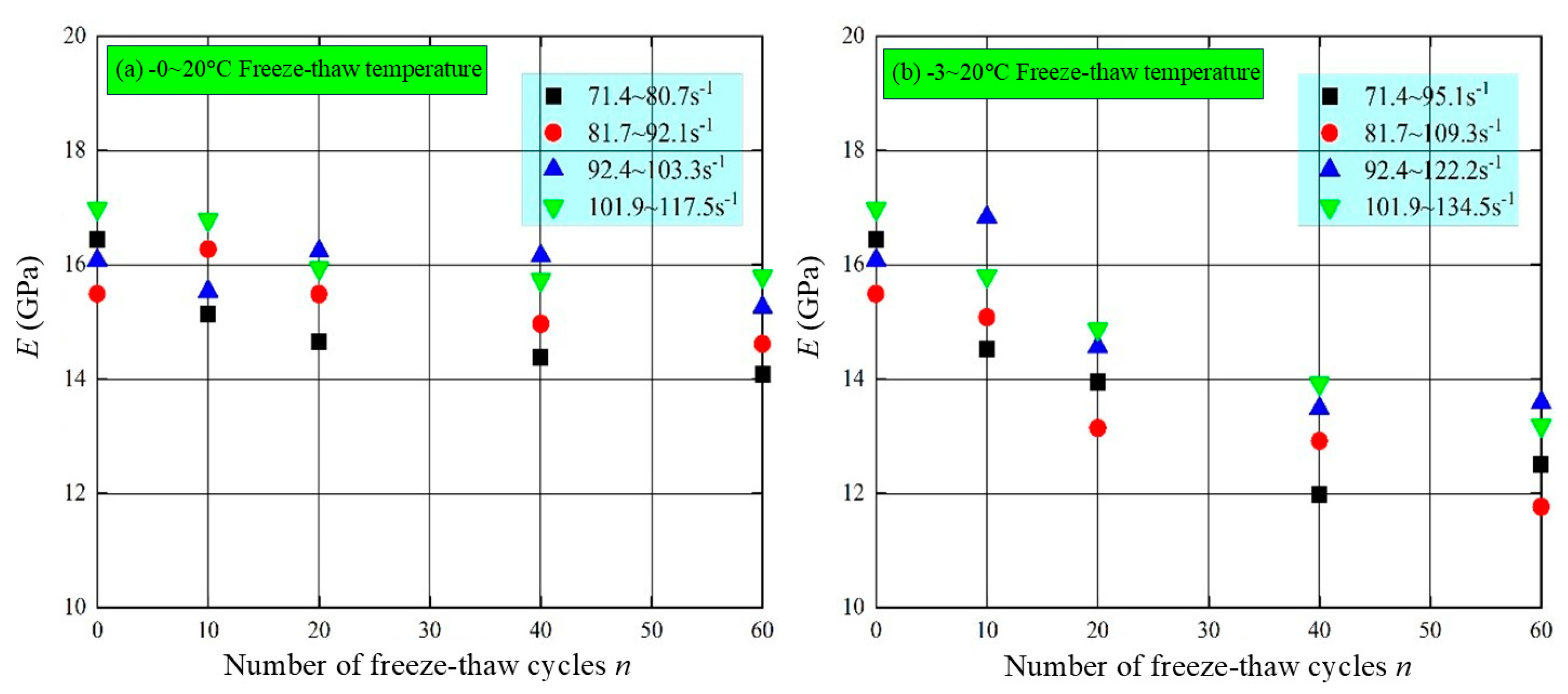
3.3. Evolution Characteristics of Dynamic Deformation Modulus

The deformation modulus can more accurately characterize the dynamic deformation resistance of rocks [20,51]. Thus, we selected the dynamic deformation modulus to characterize how changes in freezing temperature affect the deformation characteristics of yellow sandstone during the freeze–thaw process. This study defines the deformation modulus as the ratio of peak strength to the corresponding peak strain in the stress–strain curve.

Figure 10 illustrates the changes in the dynamic deformation modulus with the number of cycles at varying freezing temperatures. With a fixed number of cycles, a lower freezing temperature during freeze–thaw cycles results in a more significant decrease in the dynamic deformation modulus of rock samples. This indicates that lower freezing temperatures reduce the effective bearing area within the rock and weaken the strength of key structural components, such as mineral particles and cement. Therefore, deformation resistance declines as freezing temperatures decrease. In Figure 10a,c, when the freezing temperature decreased from −0 °C to −5 °C, the dynamic deformation modulus decreased by 3.38 GPa, 3.43 GPa, 2.84 GPa, and 3.92 GPa after 60 cycles. These values represent 2.12, 1.21, 1.67, and 1.58 times the changes in deformation modulus observed when the temperature was lowered to −3 °C under the same conditions. Integrating previous research with the findings of this experiment, we can demonstrate that variations in ambient temperature have a significant impact on the attenuation of rock deformation resistance; as the temperature decreases, the attenuation phenomenon becomes more pronounced [52,53].

The deformation modulus of rock samples shows an increasing trend with the rise in strain rates; however, this trend is not pronounced. As shown in Figure 10c,d, when the strain rate is low, the change in the deformation modulus is minimal. These results are consistent with the findings of Xing et al. [54]. To capture the general trend and to mitigate the effects of irregularities observed at specific strain rates, it is convenient to study the evolution of the deformation modulus as a function of the number of freeze–thaw and temperature intervals. The average deformation modulus under five freeze–thaw cycle conditions was calculated, and the results are presented in

Table 2. Dynamic deformation modulus at different freezing temperatures.

Freeze–Thaw Temperature	Mean Value of Dynamic Deformation Modulus of Samples (GPa)
	71.4~127.4 s−1	81.7~144.1 s−1	92.4~164.9 s−1	101.9~188.1 s−1
−0~20 °C	14.64	15.58	15.27	16.25
−3~20 °C	13.87	13.68	14.91	14.87
−5~20 °C	13.09	12.96	13.83	14.19
−20~20 °C	10.73	11.15	11.86	12.09

.

When the strain rate was varied from 71.4~127.4 s⁻¹ to 92.4~164.9 s⁻¹, the mean Young’s modulus at different freezing temperatures changed from 14.64 GPa, 13.87 GPa, 13.09 GPa, 10.73 GPa, to 15.27 GPa, 14.91 GPa, 13.83 GPa, and 11.86 GPa. The relative percentage changes were 21.1%, 22.6%, 25.8%, and 25.1%, respectively. This suggests that examining the relationship between the deformation modulus and a specific strain rate may be meaningless. Additionally, the table demonstrates how the deformation modulus of rock samples changes with the freezing temperature; the maximum decrease of 28.4% occurred at a freezing temperature of −20 °C, indicating that variations in freezing and thawing temperatures significantly deteriorate the dynamic deformation modulus of yellow sandstone. The loading strain rate has little effect on the specimen’s dynamic elastic modulus. The conclusion is consistent with the experimental results in the literature [42,55]. Therefore, to more clearly explore the trend of how temperature change affects the dynamic Young’s modulus, the mean values of the dynamic deformation modulus and the number of freeze–thaw cycles at four types of freezing temperatures are presented in Figure 11.

Figure 11 shows that the average deformation modulus under four types of impact loads gradually declines as the number of freeze–thaw cycles increases, and the rate of decline is positively correlated with the freezing temperature. When the freezing temperature is between −0 and 20 °C, the deformation modulus of the rock sample decreases from 16.25 GPa to 14.93 GPa after 60 freeze–thaw cycles, representing a drop of 8.1%. Under freeze–thaw conditions of −5 to 20 °C, the deformation modulus of the rock sample experiences a decline of 31.8%. Furthermore, as the number of freeze–thaw cycles increases, the rate of decline in the deformation modulus begins to decelerate, indicating that the deterioration of the rock sample due to freeze–thaw effects has its limits [41,56]. During the freeze–thaw process, numerous new defects develop within the rock sample, which can partially release a portion of the frost heave stress and help mitigate the effects of freeze–thaw damage [57].

4. Dynamic Damage Features of Frozen–Thawed Sandstone

Rock samples were collected and sieved after being subjected to impact crushing. Based on these samples, an evolution equation describing the fractal characteristics of rock sample crushing was established.

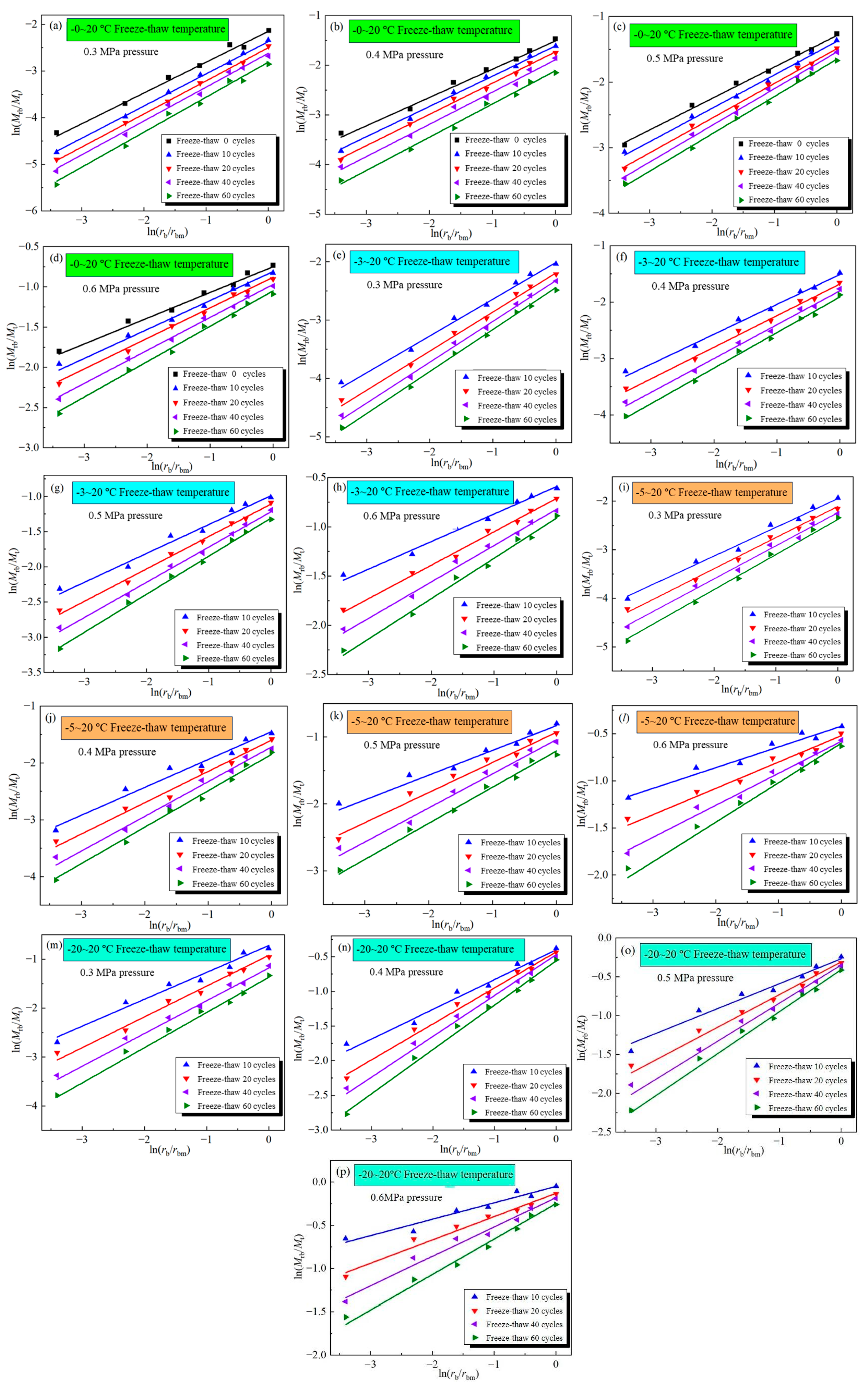
4.1. Dynamic Crushing Characteristics of Frozen–Thawed Sandstone

Due to the similarity in test conditions, only a selection of broken rock samples is presented in

Table 3. Distribution of failure patterns of samples at different freezing temperatures.

Freeze–Thaw Temperature	77.8~115.6 s−1	89.6~128.2 s−1	99.5~142.4 s−1	112.1~160.1 s−1
non-frozen–thawed
−0~20 °C 40 cycles
−3~20 °C 40 cycles
−5~20 °C 40 cycles
−20~20 °C 40 cycles

. Without exposure to freeze–thawing, the broken rock samples are significantly larger and predominantly exhibit columnar shapes along the axial direction. This indicates that the most significant damage cracks develop along the axial direction; thus, the damage mode of the rock samples is tensile. As the loading strain rate increases, the size of the broken blocks gradually decreases, resulting in the formation of a granular broken body. When the freeze–thaw temperature ranges from −0 to 20 °C, the formation of wedge-shaped broken blocks is due to the propagation and deviation of tensile cracks, which contribute to the macro-damage of rock samples [57,58]. As the freezing temperature continues to decrease, more granular fragments and the increased destruction of rock samples occur due to enhanced crack propagation and mechanical weakening [59].

The damage pattern of yellow sandstone under dynamic loading conditions is primarily influenced by the impact load and the inherent properties of the rock itself [60]. As the freezing temperature decreases, the degree of fragmentation increases. The damage mode transitions from compound damage (tensile or shear) to comminution damage. This transition is largely attributed to the increased internal defects and reduced strength of both particles and cement [61,62].

Additionally, the crushed rock samples were graded and screened using multi-stage screens with sizes of 0–0.5 mm, 0.5–1.5 mm, 1.5–3.0 mm, 3.0–5.0 mm, 5.0–8.0 mm, 8.0–10.0 mm, 10.0–15.0 mm, and 15.0–50 mm. The mass of crushed blocks in each range was weighed. The distribution of the sieved particle sizes is shown in Figure 12.

Fractals are geometric shapes that exhibit self-similarity, meaning that their structure is made up of parts that resemble the whole at different scales [63]. Research indicates that dynamic loading, such as blasting, induces a high number of microcracks in rocks. These microcracks form rapidly and do not coalesce into larger cracks due to the swift loading process [64]. The inability of microcracks to coalesce results in a fractal distribution of fragment sizes. The complexity and irregularity of fractal objects are quantified by the fractal dimension (D_f). D_f is often measured by examining the relationship between an intrinsic value (e.g., mass or area) and a characteristic value (e.g., length or size) [65] and can reflect the damage characteristics of rocks to some extent [66]. To determine the fractal dimension of fragments, researchers often use the mass-equivalent dimension parameter, which adheres to specific relationships as shown in Equation (4) [67].

$${\displaystyle \frac{M_{rb}}{M_{\mathrm{t}}}}=1-\exp {(-{\displaystyle \frac{r_{\mathrm{b}}}{r_{\mathrm{bm}}}})}^{\alpha }$$

(4)

where r_b is the particle size of crushed particles, rbm is the maximum crushed block size, D_f is the crushing fractal dimension, M_rb is the cumulative mass of the crushed blocks with a particle size smaller than rb, and M_t is the total mass of the crushed blocks.

At a small r_b/r_bm, this can be approximated as

$${\displaystyle \frac{M_{rb}}{M_{\mathrm{t}}}}={({\displaystyle \frac{r_{\mathrm{b}}}{r_{\mathrm{bm}}}})}^{\alpha }$$

(5)

The left and right sides of Equation (5) are logarithmized and deformed to

$$\ln {\displaystyle \frac{M_{\mathrm{rb}}}{M_{\mathrm{t}}}}=\alpha \ln ({\displaystyle \frac{r_{\mathrm{b}}}{r_{\mathrm{bm}}}})$$

(6)

Meanwhile, after deriving Equation (5), the equation is obtained as

$$d{M}_{\mathrm{rb}}\propto {r_b}^{\alpha -1}d{r}_b$$

(7)

Concerning the definition of a fractal, there are the following relations:

$$N\propto {r_b}^{-D_f}\to dN\propto {r_b}^{-D_f-1}d{r}_b$$

(8)

Considering that the increase in block size is closely related to the rise in mass, the following relationship exists:

$$dN\propto {r_b}^{-3}d{M}_{rb}$$

(9)

The slope α of the fitted line for the coordinate system from Equation (6) is obtained as follows:

$$D_f=3-\alpha$$

(10)

The ln-ln plots and corresponding fitted curves for the crushed particle size and mass of rock samples at different freezing temperatures and impact loads are shown in Figure 13. From Equation (6), the slope of the straight line allows for the calculation of the fractal dimension of the crushed particle size. The high correlation coefficient of the linear fit in the graph indicates that the crushed particle size exhibits good self-similarity. The figure reveals that a decrease in freezing temperature and an increase in loading air pressure during the freeze–thaw process significantly alter the slope of the curve, which gradually declines. Simultaneously, the intercept decreases slowly, indicating that the crushed material mainly consists of relatively smaller particles. Figure 14 presents a count of the slopes from the fitted straight lines.

As shown in Figure 14, the fractal dimension of the crushed grain size in the rock samples at different freezing temperatures increased with the number of freeze–thaw cycles. For example, when the loading strain rate increased from 79.8 s⁻¹ to 116.2 s⁻¹ during 20 freeze–thaw cycles at temperatures ranging from −3 to 20 °C, the fractal dimension rose from 2.27 to 2.56. Similarly, the fractal dimension increased from 2.34 to 2.67 at a freezing temperature of −20 °C under the same conditions. The increase in the fractal dimension indicates a greater proportion of smaller particle sizes, suggesting more significant damage. This also indicates that lowering the freezing temperature exacerbates freeze–thaw damage in rock samples. When the impact load remains constant, all curves exhibit an upward trend with the increase in freeze–thaw cycles. This suggests that more freeze–thaw cycles lead to greater fragmentation of rock samples after impact. These findings align with the distribution of rock sample fragmentation shown in Table 3.

4.2. Microstructure Failure Characteristics

The variation in the fractal dimension of sandstone crushing reflects the influence of freeze–thaw action on the macroscopic damage characteristics of sandstone. The macroscopic damage pattern of a material represents a superposition of its fine-scale defects under loading conditions. Consequently, crushed rock samples subjected to different test conditions were analyzed using the SEM method. The effects of freezing temperature, the number of cycles, and impact loading on the fine-scale structural features of the samples were examined to elucidate the evolution of the macroscopic damage pattern from a fine-scale perspective. Figure 15 illustrates the SEM images of rock samples conducted under various test conditions. Figure 15a demonstrates the influence of freezing temperature on the structural surface of the rock samples, while Figure 15b exhibits the fine-grained morphology of the crushed rock mass under the corresponding impact load. All SEM images are presented at the same magnification.

As shown in Figure 15a, the rock sample surfaces gradually evolves from a relatively dense state to a looser state as the freezing temperature decreases while maintaining the same number of freeze–thaw cycles. The relatively isolated pore structures in their initial state develop into a connected network of cleavages. The number of pores and cracks increases significantly. For instance, the width of the surface cracks at −20 °C approaches 8 μm, indicating a relatively large value. In addition, the surface defects shift from the initial damage along the collodion to damage affecting mineral particles. The subject impacted by the reduction in freeze–thaw temperature shifts from pore cracks to collodion and ultimately to mineral grains, further elucidating the shift in micromechanical behavior. When subjected to impact loading, two primary types of morphology are observed in the damaged surfaces of the rock samples: smooth through-grain damage surfaces and rough collodion damage surfaces. As the freezing temperature continues to drop, the micro-morphology of the rock samples changes; the density of micro-cracks increases, with crack sizes exceeding 4 μm and maximum sizes reaching up to 13 μm. At the same time, the surface of the sandstone exhibits large-scale holes.

The SEM results indicate that as the freezing temperature decreases, the freeze–thaw effect progressively influences the material, starting from the pores and cracks and ultimately leading to a deterioration in the strength of mineral particles. This results in the loosening of the surface structure and the formation of a network of pores and fissures. This deterioration effect is exacerbated under impact loading conditions, particularly through the evolution of the fracture network, which results in increased dynamic fragmentation and various forms of damage [57,68,69].

5. Conclusions

Engineering rock bodies in cold regions are subjected to dynamic loads such as blasting, mechanical construction, and earthquakes. This study performed impact tests on sandstone under variable-temperature freezing and thawing conditions using the SHPB system. Studies of freeze–thaw cycles in sandstones provide comprehensive insights into the microstructural, mechanical, and environmental factors that influence rock degradation. These contributions are essential for predicting geohazards, designing durable infrastructure, and understanding the long-term evolution of rock formations in cold climates. The primary conclusions are as follows:

(1)

As the freezing temperature decreases, the stress–strain curve transitions from three stages to four, characterized by the emergence of an initial compaction stage, a reduction in peak stress, and an increase in the yield stage. The dynamic strength of freeze–thaw sandstone shows a logarithmic relationship with strain rate across different impact gas pressures.

(2)

The dynamic deformation modulus of frozen–thawed sandstone exhibits a decreasing trend as the freezing temperature decreases. Additionally, there is no significant relationship between the loading strain rate and the dynamic deformation modulus. The average dynamic deformation modulus across the four air pressures decreases with an increase in freeze–thaw cycles and shifts from a linear decrease to an exponential decrease as the freezing temperature declines.

(3)

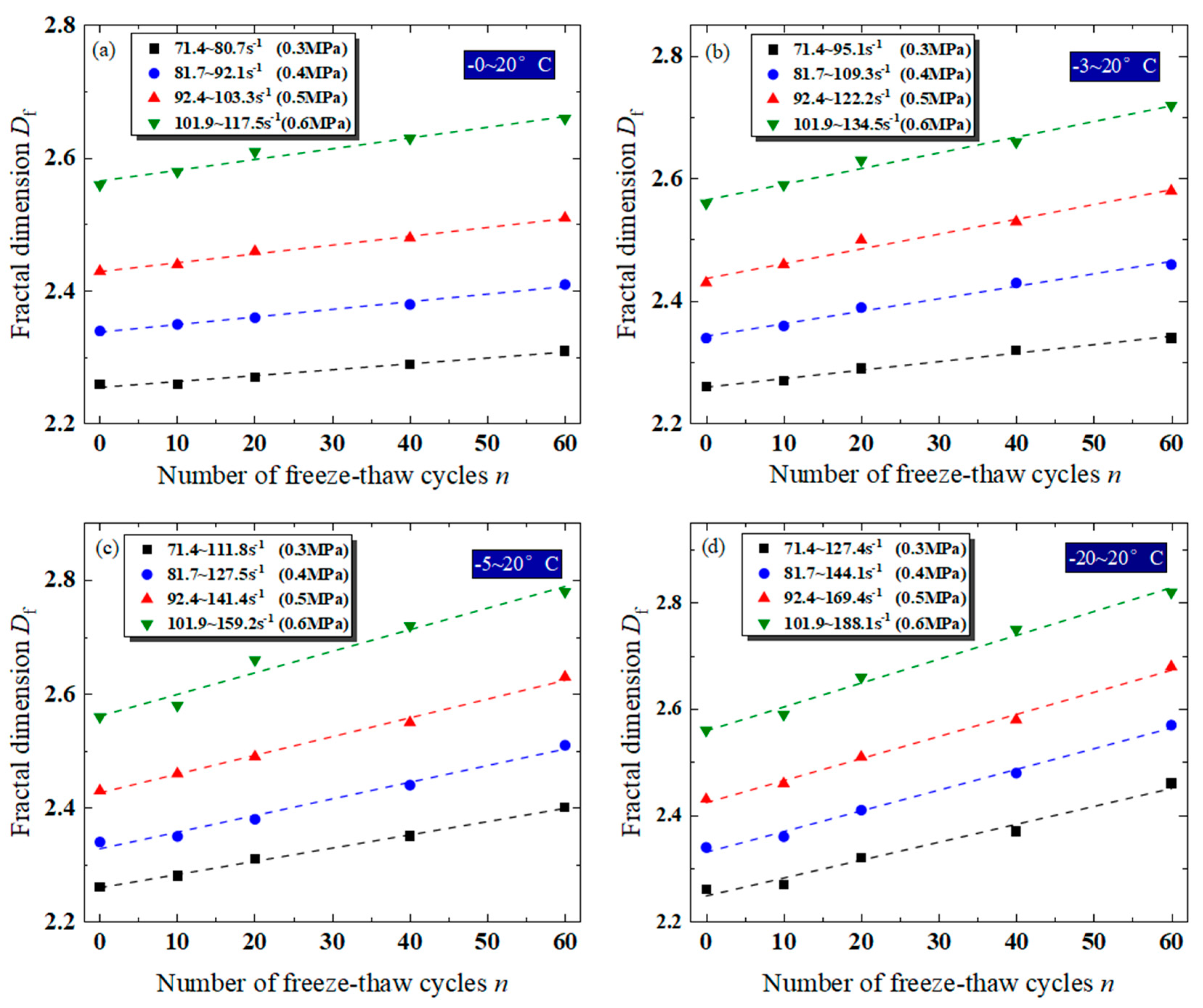
Macroscopically, the fractal dimension of sandstone fragmentation increases with higher loading strain rates and a greater number of freeze–thaw cycles; the rate of increase in the fractal dimension is faster at lower freezing temperatures.

(4)

Microscopically, as the freezing temperature decreases, the influence of freeze–thaw action transitions from pore cracks to cementitious materials, ultimately degrading the strength of mineral particles. This degradation, in turn, affects the macroscopic dynamic failure characteristics.