On a Certain Class of GA-Convex Functions and Their Milne-Type Hadamard Fractional-Integral Inequalities
Abstract
1. Introduction
2. Preliminaries
3. Main Results
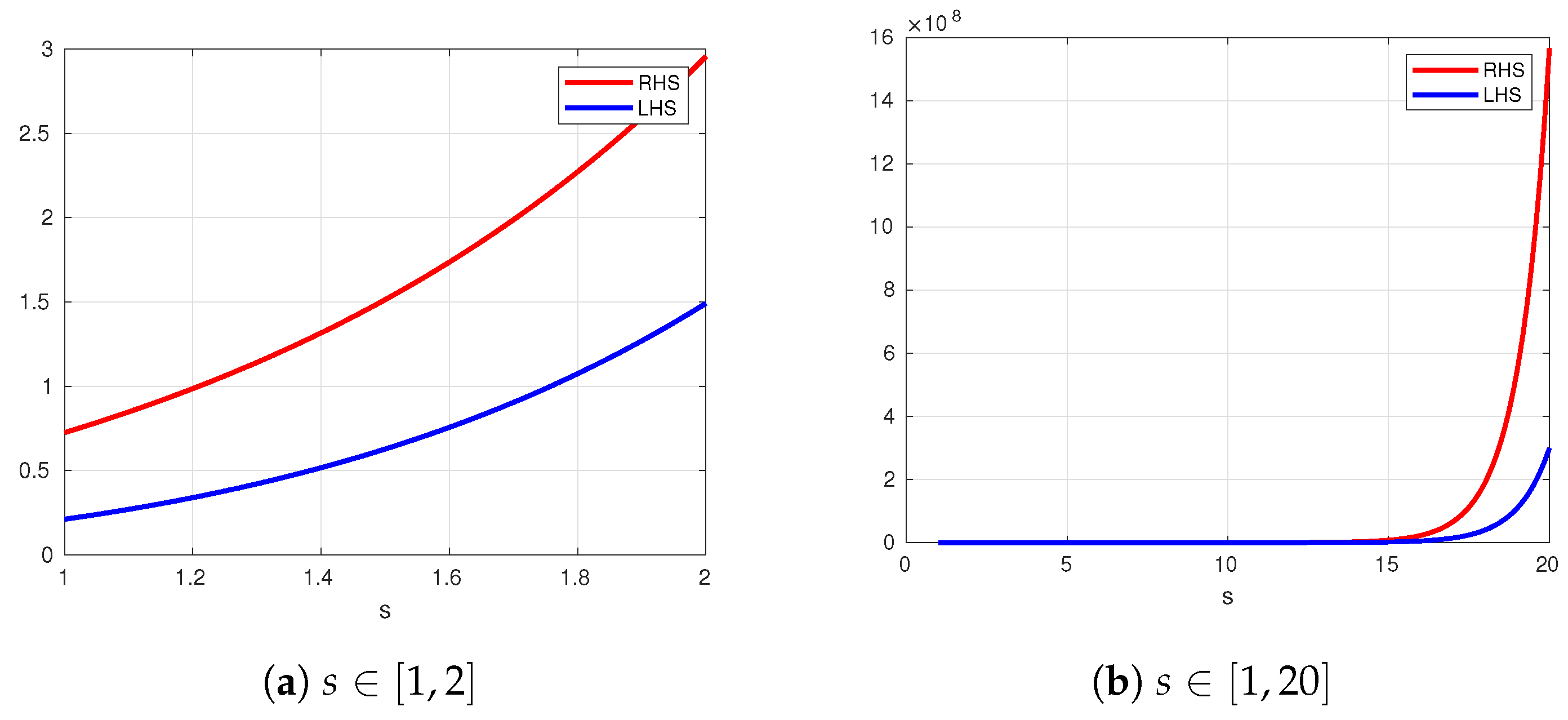
4. Graphical Illustration Example
5. Application
- The arithmetic mean
- The geometric mean , where
- The harmonic mean
- The logarithmic mean , where with
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sadek, L.; Baleanu, D.; Abdo, M.S.; Shatanawi, W. Introducing novel θ-fractional operators: Advances in fractional calculus. J. King Saud-Univ.-Sci. 2024, 36, 103352. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies, 204; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives. Theory and Applications; Edited and with a Foreword by S. M. Nikol’skiĭ. Translated from the 1987 Russian Original. Revised by the Authors; Gordon and Breach Science Publishers: Yverdon, Switzerland, 1993. [Google Scholar]
- Sadek, L.; Algefary, A. Extended Hermite–Hadamard inequalities. AIMS Math. 2024, 9, 36031–36046. [Google Scholar] [CrossRef]
- Katugampola, U.N. New approach to a generalized fractional integral. Appl. Math. Comput. 2011, 218, 860–865. [Google Scholar] [CrossRef]
- Alraqad, T.; Almalahi, M.A.; Mohammed, N.; Alahmade, A.; Aldwoah, K.A.; Saber, H. Modeling Ebola Dynamics with a Φ-Piecewise Hybrid Fractional Derivative Approach. Fractal Fract. 2024, 8, 596. [Google Scholar] [CrossRef]
- Hamza, A.; Osman, O.; Ali, A.; Alsulami, A.; Aldwoah, K.; Mustafa, A.; Saber, H. Fractal-Fractional-Order Modeling of Liver Fibrosis Disease and Its Mathematical Results with Subinterval Transitions. Fractal Fract. 2024, 8, 638. [Google Scholar] [CrossRef]
- Saber, H.; Imsatfia, M.; Boulares, H.; Moumen, A.; Alraqad, T. On the Existence and Ulam Stability of BVP within Kernel Fractional Time. Fractal Fract. 2023, 7, 852. [Google Scholar] [CrossRef]
- Nassima, N.; Meftah, B.; Moumen, A.; Saber, H. Fractional 3/8-Simpson type inequalities for differentiable convex functions. AIMS Math. 2024, 9, 5349–5375. [Google Scholar]
- Saber, H.; Almalahi, M.A.; Albala, H.; Aldwoah, K.; Alsulami, A.; Shah, K.; Moumen, A. Investigating a Nonlinear Fractional Evolution Control Model Using W-Piecewise Hybrid Derivatives: An Application of a Breast Cancer Model. Fractal Fract. 2024, 8, 735. [Google Scholar] [CrossRef]
- Sadek, L. A cotangent fractional derivative with the application. Fractal Fract. 2023, 7, 444. [Google Scholar] [CrossRef]
- Fallahgoul, H.A.; Focardi, S.M.; Fabozzi, F.J. Fractional Calculus and Fractional Processes with Applications to Financial Economics; Theory and Application; Elsevier/Academic Press: London, UK, 2017. [Google Scholar]
- Ruszczyński, A.; Shapiro, A. Optimization of convex risk functions. Math. Oper. Res. 2006, 31, 433–452. [Google Scholar] [CrossRef]
- Pham, H. Continuous-Time Stochastic Control and Optimization with Financial Applications; Stochastic Modelling and Applied Probability, 61; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Carr, P.; Zhu, Q.J. Convex Duality and Financial Mathematics; SpringerBriefs in Mathematics; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Bertsekas, D.P. Convex Optimization Theory; Athena Scientific: Nashua, NH, USA, 2009. [Google Scholar]
- Cambini, A.; Martein, L. Generalized Convexity and Optimization; Theory and Applications; With a Foreword by Siegfried Schaible; Lecture Notes in Economics and Mathematical Systems, 616; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Owen, G. Game Theory, 4th ed.; Emerald Group Publishing Limited: Bingley, UK, 2013. [Google Scholar]
- Alomari, M.W.; Dragomir, S.S. Various error estimations for several Newton-Cotes quadrature formulae in terms of at most first derivative and applications in numerical integration. Jordan J. Math. Stat. 2014, 7, 89–108. [Google Scholar]
- Deng, J.; Wang, J. Fractional Hermite-Hadamard inequalities for (α,m)-logarithmically convex functions. J. Inequal. Appl. 2013, 364, 11. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Agarwal, R.P.; Cerone, P. On Simpson’s inequality and applications. J. Inequal. Appl. 2000, 5, 533–579. [Google Scholar] [CrossRef]
- Meftah, B.; Benssaad, M.; Kaidouchi, W.; Ghomrani, S. Conformable fractional Hermite-Hadamard type inequalities for product of two harmonic s-convex functions. Proc. Amer. Math. Soc. 2021, 149, 1495–1506. [Google Scholar] [CrossRef]
- Booth, A.D. Numerical Methods, 3rd ed.; Butterworths: La Canada Flintrige, CA, USA, 1966. [Google Scholar]
- Alomari, M.; Liu, Z. New error estimations for the Milne’s quadrature formula in terms of at most first derivatives. Konuralp J. Math. 2013, 1, 17–23. [Google Scholar]
- Djenaoui, M.; Meftah, B. Milne-type inequalities for differentiable s-convex functions. Honam Math. J. 2022, 44, 325–338. [Google Scholar]
- Özarslan, M.A.; Ustaoğlu, C. Some incomplete hypergeometric functions and incomplete Riemann-πLiouville fractional integral operators. Mathematics 2019, 7, 483. [Google Scholar] [CrossRef]
- Budak, H.; Kösem, P.; Kara, H. On new Milne-type inequalities for fractional integrals. J. Inequal. Appl. 2023, 10, 15. [Google Scholar] [CrossRef]
- Meftah, B.; Lakhdari, A.; Saleh, W.; Kiliçman, A. Some new fractal Milne-type integral inequalities via generalized convexity with applications. Fractal Fract. 2023, 7, 166. [Google Scholar] [CrossRef]
- Al-Sa’di, S.; Bibi, M.; Seol, Y.; Muddassar, M. Milne-type fractal integral inequalities for generalized m-convex mapping. Fractals 2023, 31, 2350081. [Google Scholar] [CrossRef]
- Sial, I.B.; Budak, H.; Ali, M.A. Some Milne’s rule type inequalities in quantum calculus. Filomat 2023, 37, 9119–9134. [Google Scholar] [CrossRef]
- Lakhdari, A.; Budak, H.; Mlaiki, N.; Meftah, B.; Abdeljawad, T. New insights on fractal–fractional integral inequalities: Hermite–Hadamard and Milne estimates. Chaos Solitons Fractals 2025, 193, 116087. [Google Scholar] [CrossRef]
- Bin-Mohsin, B.; Javed, M.Z.; Awan, M.U.; Khan, A.G.; Noor, C.C.M.A. Exploration of Quantum Milne–Mercer-Type Inequalities with Applications. Symmetry 2023, 15, 1096. [Google Scholar] [CrossRef]
- Bosch, P.; Rodríguez, J.M.; Sigarreta, J.M. On new Milne-type inequalities and applications. J. Inequal. Appl. 2023, 3, 18. [Google Scholar] [CrossRef]
- Budak, H.; Hyder, A.A. Enhanced bounds for Riemann-Liouville fractional integrals: Novel variations of Milne inequalities. AIMS Math. 2023, 8, 30760–30776. [Google Scholar] [CrossRef]
- Budak, H.; Karagözoğlu, P. Fractional Milne-type inequalities. Acta Math. Univ. Comen. 2024, 93, 1–15. [Google Scholar]
- Demir, I. A new approach of Milne-type inequalities based on proportional Caputo-Hybrid operator: A new approach for Milne-type inequalities. J. Adv. App. Comput. 2023, 10, 102–119. [Google Scholar] [CrossRef]
- Desta, H.D.; Budak, H.; Kara, H. New perspectives on fractional Milne-type inequalities: Insights from twice-differentiable functions. Univers. J. Math. Appl. 2024, 7, 30–37. [Google Scholar] [CrossRef]
- Shehzadi, A.; Budak, H.; Haider, W.; Chen, H. Milne-type inequalities for co-ordinated convex functions. Filomat 2024, 38, 8295–8303. [Google Scholar]
- Munir, A.; Qayyum, A.; Rathour, L.; Atta, G.; Supadi, S.S.; Ali, U. A study on Milne-type inequalities for a specific fractional integral operator with applications. Korean J. Math. 2024, 32, 297–314. [Google Scholar]
- Hezenci, F.; Budak, H.; Kara, H.; Baş, U. Novel results of Milne-type inequalities involving tempered fractional integrals. Bound. Value Probl. 2024, 12, 15. [Google Scholar] [CrossRef]
- Niculescu, C.P. Convexity according to the geometric mean. Math. Inequal. Appl. 2000, 3, 155–167. [Google Scholar] [CrossRef]
- İşcan, İ. New general integral inequalities for quasi-geometrically convex functions via fractional integrals. J. Inequal. Appl. 2013, 491, 15. [Google Scholar] [CrossRef]
- Chiheb, T.; Meftah, B.; Moumen, A.; Bouye, M. Maclaurin type integral inequalities for GA-convex functions involving confluent hypergeometric function via Hadamard fractional integrals. Fractal Fract. 2023, 7, 860. [Google Scholar] [CrossRef]
- İşcan, İ. Hermite-Hadamard and Simpson type inequalities for differentiable P-GA-functions. Int. J. Anal. 2014, 2014, 125439. [Google Scholar] [CrossRef]
- İşcan, İ.; Aydin, M. Some new generalized integral inequalities for GA-s-convex functions via Hadamard fractional integrals. Chin. J. Math. 2016, 2016, 4361806. [Google Scholar] [CrossRef]
- Kalsoom, H.; Latif, M.A. Some weighted Hadamard and Ostrowski-type fractional inequalities for quasi-geometrically convex functions. Filomat 2023, 37, 5921–5942. [Google Scholar] [CrossRef]
- Latif, M.A. Some Companions of Fejér Type Inequalities Using GA-Convex Functions. Mathematics 2023, 11, 392. [Google Scholar] [CrossRef]
- Latif, M.A. Extensions of Fejér type inequalities for GA-convex functions and related results. Filomat 2023, 37, 8041–8055. [Google Scholar] [CrossRef]
- Latif, M.A. Properties of GA-h-Convex Functions in Connection to the Hermite–Hadamard–Fejér-Type Inequalities. Mathematics 2023, 11, 3172. [Google Scholar] [CrossRef]
- Jameson, G.J.O. The incomplete gamma functions. Math. Gaz. 2016, 100, 298–306. [Google Scholar] [CrossRef]
- Park, J. Some Hermite-Hadamard-like type inequalities for logarithmically convex functions. Int. J. Math. Anal. 2013, 7, 2217–2233. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moumen, A.; Debbar, R.; Meftah, B.; Zennir, K.; Saber, H.; Alraqad, T.; Alshawarbeh, E. On a Certain Class of GA-Convex Functions and Their Milne-Type Hadamard Fractional-Integral Inequalities. Fractal Fract. 2025, 9, 129. https://doi.org/10.3390/fractalfract9020129
Moumen A, Debbar R, Meftah B, Zennir K, Saber H, Alraqad T, Alshawarbeh E. On a Certain Class of GA-Convex Functions and Their Milne-Type Hadamard Fractional-Integral Inequalities. Fractal and Fractional. 2025; 9(2):129. https://doi.org/10.3390/fractalfract9020129
Chicago/Turabian StyleMoumen, Abdelkader, Rabah Debbar, Badreddine Meftah, Khaled Zennir, Hicham Saber, Tariq Alraqad, and Etaf Alshawarbeh. 2025. "On a Certain Class of GA-Convex Functions and Their Milne-Type Hadamard Fractional-Integral Inequalities" Fractal and Fractional 9, no. 2: 129. https://doi.org/10.3390/fractalfract9020129
APA StyleMoumen, A., Debbar, R., Meftah, B., Zennir, K., Saber, H., Alraqad, T., & Alshawarbeh, E. (2025). On a Certain Class of GA-Convex Functions and Their Milne-Type Hadamard Fractional-Integral Inequalities. Fractal and Fractional, 9(2), 129. https://doi.org/10.3390/fractalfract9020129






