Permeability Prediction Model of Fractal Rough Fractures Under Coupled Shear and Normal Stress
Abstract
1. Introduction
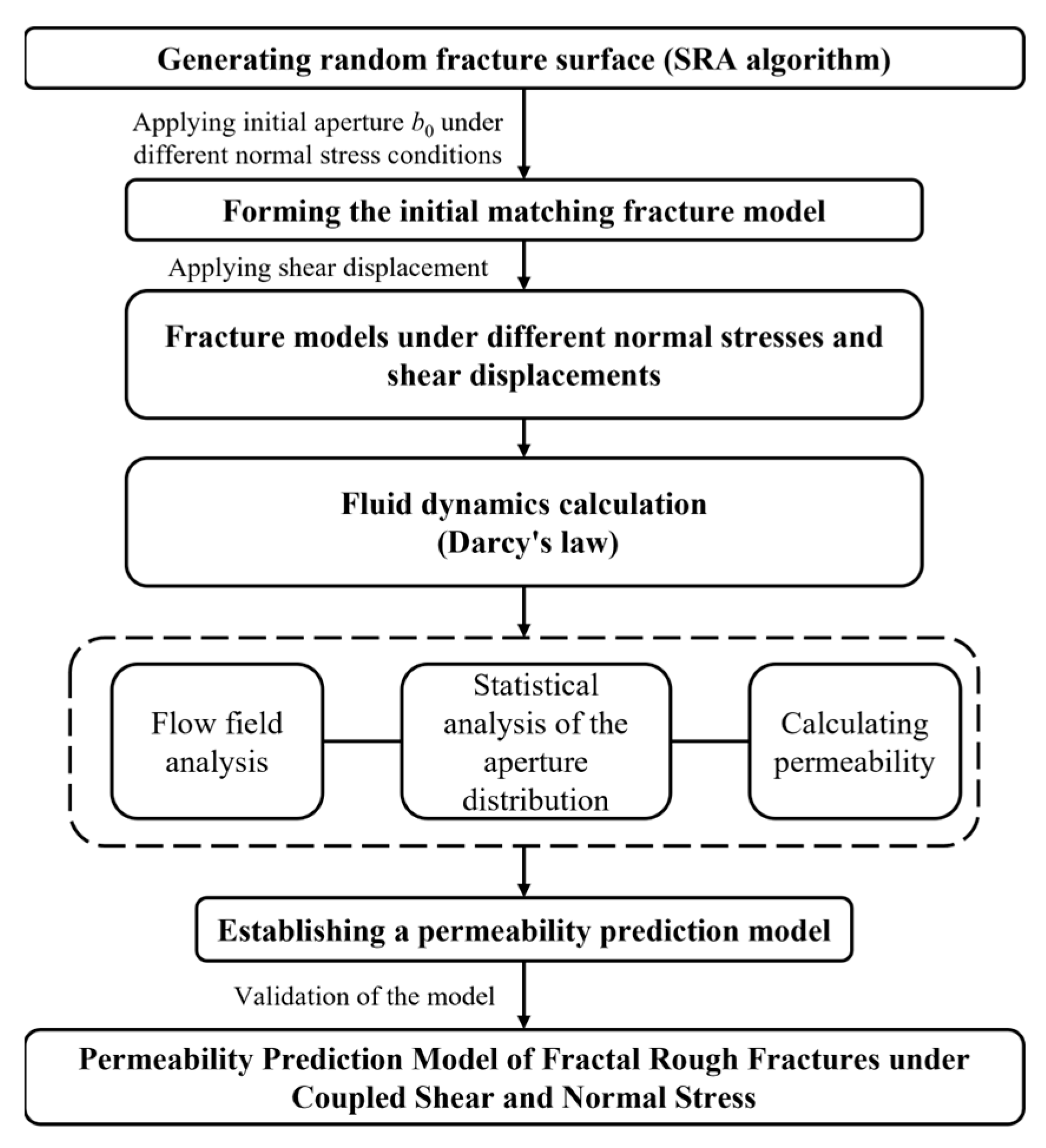
2. Rough Fracture Numerical Model Generation
2.1. Rock Fracture Model Construction
2.2. Fluid Dynamics Computation
3. Stress-Induced Mechanical Behavior and Fracture Aperture Evolution
3.1. Normal Stress-Induced Fracture Closure Model
- denotes the height of a local maximum on the composite topography;
- represents the number density of local maxima per unit area;
- is the average tangential stress correction factor;
- denotes the effective elastic modulus (or the mean value of the elastic constants);
- refers to the average curvature of the contact points;
- is the normal closure (i.e., the reduction in fracture aperture under compression);
- indicates the initial separation between the reference planes (undeformed fracture surfaces);
- denotes the applied normal stress;
- is the probability density function describing the statistical distribution of local maxima heights in the composite surface profile.
3.2. Shear-Induced Fracture Dilation Model
4. Hydraulic Behavior of Rock Fracture
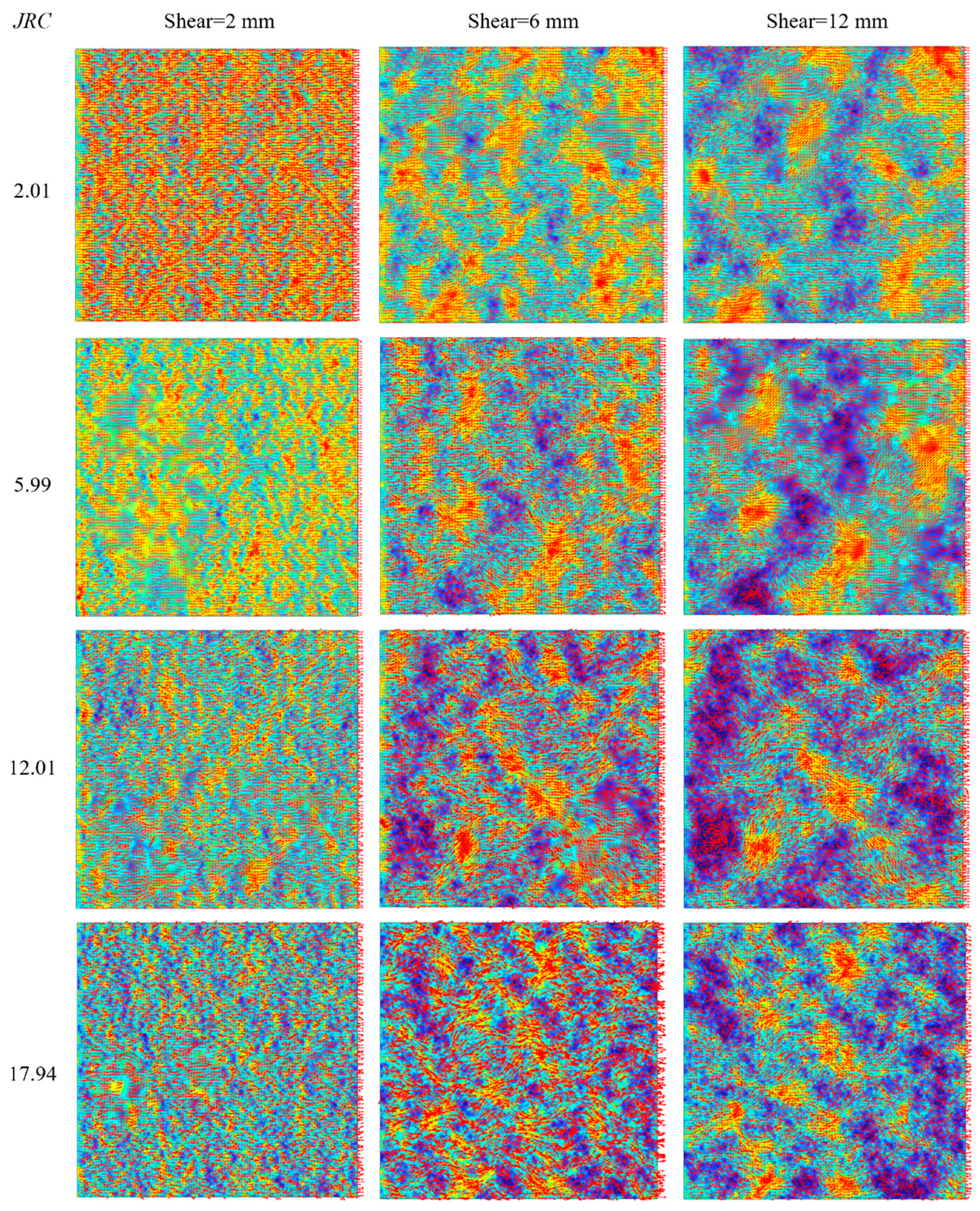
4.1. Flow Flied Distribution
4.2. Evolution of Fracture Aperture Distribution
4.3. Evolution of Mechanical Aperture
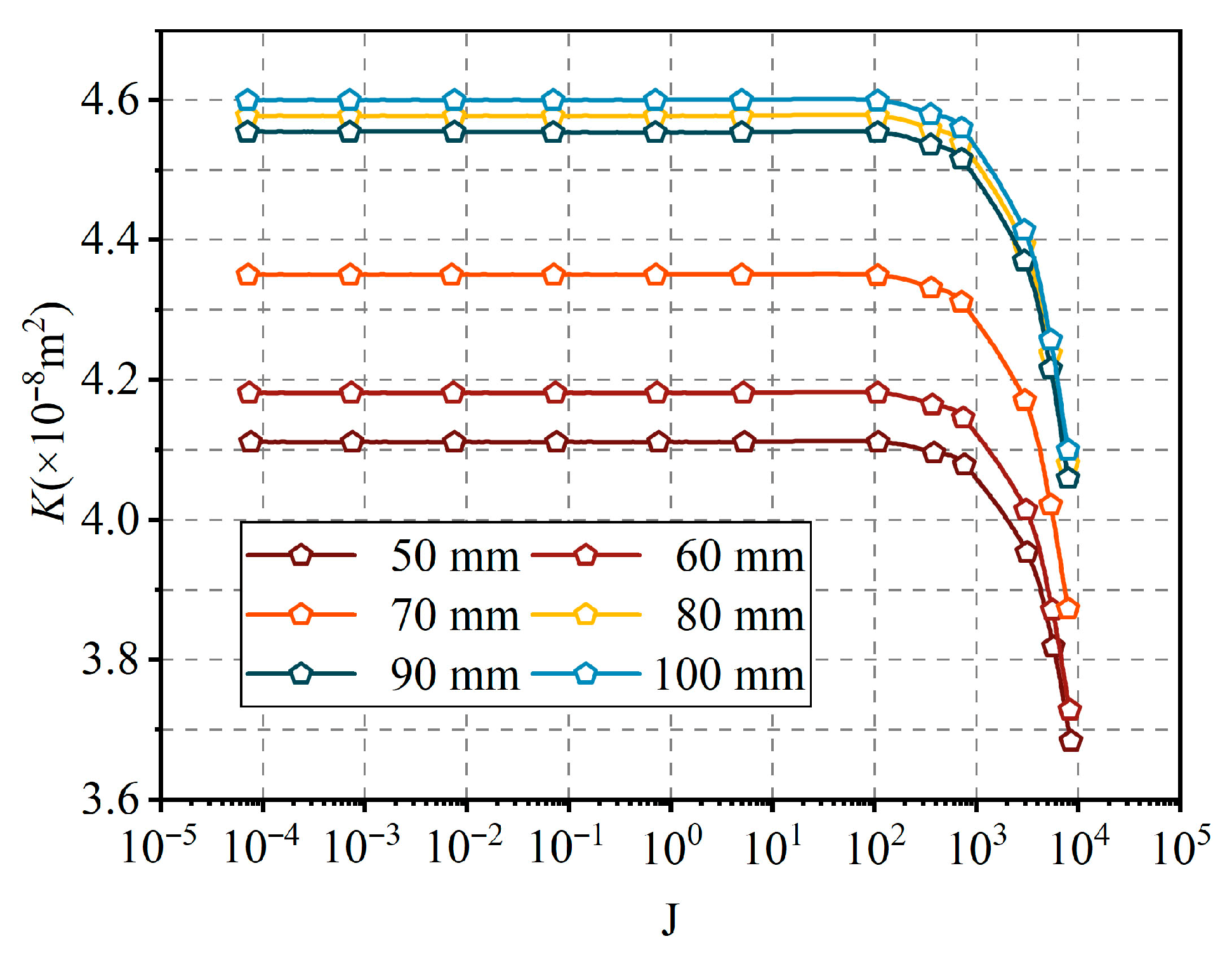
5. Predict Model for Fracture Permeability Estimate
5.1. Predict Model Construction
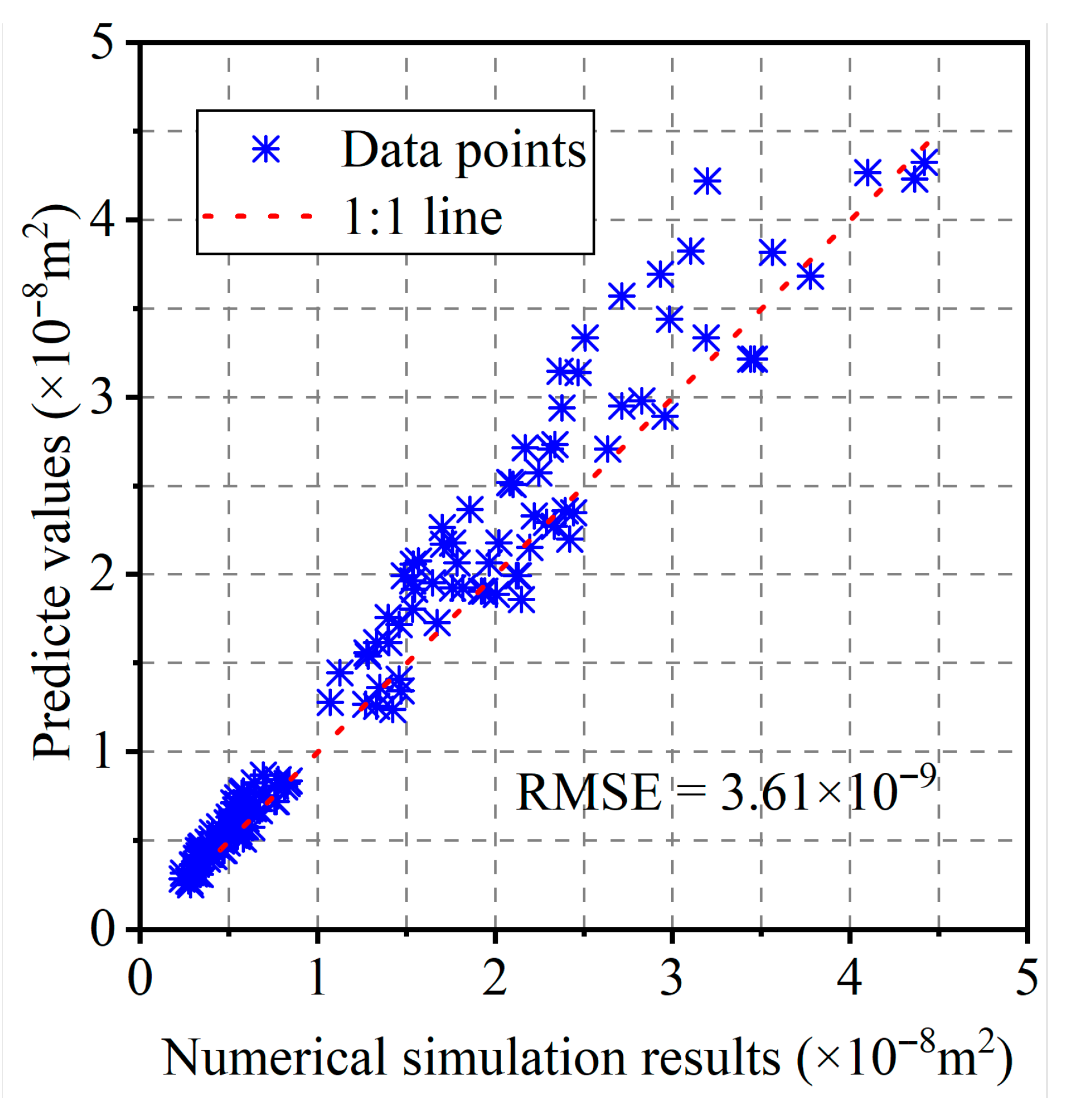
5.2. Predict Model Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, Y.; Zhang, Z.; Zhang, L.; Xue, K.; Long, K. Influence of fracture roughness and void space morphology on nonlinear fluid flow through rock fractures. Eur. Phys. J. Plus 2022, 137, 1288. [Google Scholar] [CrossRef]
- Pu, H.; Xue, K.; Wu, Y.; Zhang, S.; Liu, D.; Xu, J. Estimating the permeability of fractal rough rock fractures with variable apertures under normal and shear stresses. Phys. Fluids 2025, 37, 036635. [Google Scholar] [CrossRef]
- Xue, K.; Pu, H.; Li, M.; Luo, P.; Liu, D.; Yi, Q. Fractal-based analysis of stress-induced dynamic evolution in geometry and permeability of porous media. Phys. Fluids 2025, 37, 036630. [Google Scholar] [CrossRef]
- Tóth, E.; Hrabovszki, E.; Schubert, F.; Tóth, T.M. Discrete fracture network (DFN) modelling of a high-level radioactive waste repository host rock and the effects on its hydrogeological behaviour. J. Struct. Geol. 2022, 156, 104556. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, F.; Yin, S.; Wallace, C.D.; Soltanian, M.R.; Dai, Z.; Ritzi, R.W.; Ma, Z.; Zhan, C.; Lü, X. Application of upscaling methods for fluid flow and mass transport in multi-scale heterogeneous media: A critical review. Appl. Energy 2021, 303, 117603. [Google Scholar] [CrossRef]
- Cardona, A.; Finkbeiner, T.; Santamarina, J.C. Natural Rock Fractures: From Aperture to Fluid Flow. Rock Mech. Rock Eng. 2021, 54, 5827–5844. [Google Scholar] [CrossRef]
- Liu, E. Effects of fracture aperture and roughness on hydraulic and mechanical properties of rocks: Implication of seismic characterization of fractured reservoirs. J. Geophys. Eng. 2005, 2, 38–47. [Google Scholar] [CrossRef]
- He, X.; Zhang, Z.; Wang, Y.; Liu, X.; Hao, S. Modeling the relative permeability of gas and water flow in rock fractures with surface morphology parameters. Phys. Fluids 2024, 36, 123305. [Google Scholar] [CrossRef]
- Ghorbani, Y.; Nwaila, G.T.; Zhang, S.E.; Bourdeau, J.E.; Cánovas, M.; Arzua, J.; Nikadat, N. Moving towards deep underground mineral resources: Drivers, challenges and potential solutions. Resour. Policy 2023, 80, 103222. [Google Scholar] [CrossRef]
- Peng, F.-L.; Dong, Y.-H.; Wang, W.-X.; Ma, C.-X. The next frontier: Data-driven urban underground space planning orienting multiple development concepts. Smart Constr. Sustain. Cities 2023, 1, 3. [Google Scholar] [CrossRef]
- Zhang, W.; Gu, X.; Tang, L.; Yin, Y.; Liu, D.; Zhang, Y. Application of machine learning, deep learning and optimization algorithms in geoengineering and geoscience: Comprehensive review and future challenge. Gondwana Res. 2022, 109, 1–17. [Google Scholar] [CrossRef]
- Wang, J.; Leung, C. Progress in feature research topics in deep underground. Deep. Undergr. Sci. Eng. 2025, 4, 339–340. [Google Scholar] [CrossRef]
- Feng, X.-T.; Yang, C.-X.; Kong, R.; Zhao, J.; Zhou, Y.; Yao, Z.; Hu, L. Excavation-induced deep hard rock fracturing: Methodology and applications. J. Rock Mech. Geotech. Eng. 2022, 14, 1–34. [Google Scholar] [CrossRef]
- Li, P.; Xu, Q.; Fang, Q. Deep Rock Mass Engineering: Excavation, Monitoring, and Control. Appl. Sci. 2022, 12, 11721. [Google Scholar] [CrossRef]
- Gui, Y.; Yin, Z.; Du, K. Editorial: Deep rock mass engineering: Excavation, monitoring, and control. Front. Earth Sci. 2022, 10, 1047612. [Google Scholar] [CrossRef]
- Viswanathan, H.S.; Ajo-Franklin, J.; Birkholzer, J.T.; Carey, J.W.; Guglielmi, Y.; Hyman, J.D.; Karra, S.; Pyrak-Nolte, L.J.; Rajaram, H.; Srinivasan, G.; et al. From Fluid Flow to Coupled Processes in Fractured Rock: Recent Advances and New Frontiers. Rev. Geophys. 2022, 60, e2021RG000744. [Google Scholar] [CrossRef]
- Zhou, C.-B.; Chen, Y.-F.; Hu, R.; Yang, Z. Groundwater flow through fractured rocks and seepage control in geotechnical engineering: Theories and practices. J. Rock Mech. Geotech. Eng. 2023, 15, 1–36. [Google Scholar] [CrossRef]
- Yu, L.; Liu, R.; Jiang, Y. A Review of Critical Conditions for the Onset of Nonlinear Fluid Flow in Rock Fractures. Geofluids 2017, 2017, 2176932. [Google Scholar] [CrossRef]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Liu, J.; Xie, H.; Li, C.; Hu, J.; Luo, Y.; Liu, B.; Wang, Z. Effect of complex void structures on flow channeling and heterogeneous heat transfer in fractured rocks. J. Hydrol. 2024, 639, 131654. [Google Scholar] [CrossRef]
- Xue, K.; Zhang, Z.; Zhong, C.; Jiang, Y.; Geng, X. A fast numerical method and optimization of 3D discrete fracture network considering fracture aperture heterogeneity. Adv. Water Resour. 2022, 162, 104164. [Google Scholar] [CrossRef]
- Develi, K.; Babadagli, T. Experimental and visual analysis of single-phase flow through rough fracture replicas. Int. J. Rock Mech. Min. Sci. 2015, 73, 139–155. [Google Scholar] [CrossRef]
- Gudala, M.; Govindarajan, S.K. Numerical modelling of coupled single-phase fluid flow and geomechanics in a fractured porous media. J. Pet. Sci. Eng. 2020, 191, 107215. [Google Scholar] [CrossRef]
- Al-Yaari, A.; Ching, D.L.C.; Sakidin, H.; Muthuvalu, M.S.; Zafar, M.; Haruna, A.; Merican, Z.M.A.; Yunus, R.B.; Al-dhawi, B.N.S.; Jagaba, A.H. The effects of nanofluid thermophysical properties on enhanced oil recovery in a heterogenous porous media. Case Stud. Chem. Environ. Eng. 2024, 9, 100556. [Google Scholar] [CrossRef]
- Xu, C.; Dong, S.; Wang, H.; Wang, Z.; Xiong, F.; Jiang, Q.; Zeng, L.; Faulkner, L.; Tian, Z.F.; Dowd, P. Modelling of Coupled Hydro-Thermo-Chemical Fluid Flow through Rock Fracture Networks and Its Applications. Geosciences 2021, 11, 153. [Google Scholar] [CrossRef]
- Liu, X.; Chen, D.; Li, M.; Li, Y.; Yang, X. Characteristics of Fluid Flow and Solute Transport in Multicrossed Rough Rock Fractures Based on Three-Dimensional Simulation. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 072095. [Google Scholar] [CrossRef]
- Huang, N.; Wang, X.; Jiang, Y.; Zhang, Y.; Zhuang, Y. Experimental and numerical studies on fluid flow through fractured rock masses based on an enhanced three-dimensional discrete fracture network model. J. Contam. Hydrol. 2025, 273, 104582. [Google Scholar] [CrossRef]
- Gao, M.; Zhang, C.; Oh, J. Assessments of the effects of various fracture surface morphology on single fracture flow: A review. Int. J. Min. Sci. Technol. 2023, 33, 1–29. [Google Scholar] [CrossRef]
- Zou, Q.; Luo, G. Geometric Modeling for Microstructure Design and Manufacturing: A Review of Representations and Modeling Algorithms. Comput.-Aided Des. 2025, 180, 103834. [Google Scholar] [CrossRef]
- He, X.; Sinan, M.; Kwak, H.; Hoteit, H. A corrected cubic law for single-phase laminar flow through rough-walled fractures. Adv. Water Resour. 2021, 154, 103984. [Google Scholar] [CrossRef]
- Trinchero, P.; Zou, L.; de La Iglesia, M.; Iraola, A.; Bruines, P.; Deissmann, G. Experimental and numerical analysis of flow through a natural rough fracture subject to normal loading. Sci. Rep. 2024, 14, 5587. [Google Scholar] [CrossRef]
- Landry, C.J.; Prodanović, M.; Karpyn, Z.; Eichhubl, P. Estimation of Fracture Permeability from Aperture Distributions for Rough and Partially Cemented Fractures. Transp. Porous Med. 2024, 151, 689–717. [Google Scholar] [CrossRef]
- Magsipoc, E.; Zhao, Q.; Grasselli, G. 2D and 3D Roughness Characterization. Rock Mech. Rock Eng. 2020, 53, 1495–1519. [Google Scholar] [CrossRef]
- Kangsheng, X.; Zhenyu, Z.; Xuefeng, H.; Wenfeng, G. A fractal model for estimating the permeability of tortuous fracture networks with correlated fracture length and aperture. Phys. Fluids 2023, 35, 043615. [Google Scholar] [CrossRef]
- Yan, Y.; Ma, L.; Qian, J.; Zhao, G.; Fang, Y.; Ma, H.; Wang, J. Estimating permeability of rock fracture based on geometrical aperture using geoelectrical monitoring. J. Hydrol. 2024, 644, 132067. [Google Scholar] [CrossRef]
- Huo, J.; Meguid, M.A. Systematic investigation of stress-induced fracture closure and permeability evolution in Lac du Bonnet granite. Int. J. Rock Mech. Min. Sci. 2025, 191, 106113. [Google Scholar] [CrossRef]
- Chen, L.; He, A.; Zhao, J.; Kang, Q.; Li, Z.-Y.; Carmeliet, J.; Shikazono, N.; Tao, W.-Q. Pore-scale modeling of complex transport phenomena in porous media. Prog. Energy Combust. Sci. 2022, 88, 100968. [Google Scholar] [CrossRef]
- Makki, S.; Yehya, A.; Maalouf, E. Complex Fracture Networks Prohibit Safe Fracturing Fluid Recovery. Eng. Rep. 2025, 7, e70036. [Google Scholar] [CrossRef]
- Gowrisankar, A.; Banerjee, S. Frontiers of fractals for complex systems: Recent advances and future challenges. Eur. Phys. J. Spec. Top. 2021, 230, 3743–3745. [Google Scholar] [CrossRef]
- Liu, R.; He, M.; Huang, N.; Jiang, Y.; Yu, L. Three-dimensional double-rough-walled modeling of fluid flow through self-affine shear fractures. J. Rock Mech. Geotech. Eng. 2020, 12, 41–49. [Google Scholar] [CrossRef]
- Han, X.; Xue, K.; Zhang, S. The behavior of fluid flow and solute transport in 3D crossed rock fractures. Processes 2024, 13, 67. [Google Scholar] [CrossRef]
- Liu, H.-H.; Bodvarsson, G.S.; Lu, S.; Molz, F.J. A Corrected and Generalized Successive Random Additions Algorithm for Simulating Fractional Levy Motions. Math. Geol. 2004, 36, 361–378. [Google Scholar] [CrossRef]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. Rock Eng. 1977, 92, 54. [Google Scholar] [CrossRef]
- Tse, R.; Cruden, D.M. Estimating joint roughness coefficients. Int. J. Rock Mech. Min. Sci. 1979, 16, 5. [Google Scholar] [CrossRef]
- Luo, P.; Zhang, Z.; Geng, X.; Xue, K.; Guang, W. Evaluation of ScCO2-water performance on bituminous coal: Insights from experiments and 3D CT image reconstruction. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 118. [Google Scholar] [CrossRef]
- Xue, K.; Liu, X.; Yan, X.; Chi, X.; Teng, B. The Effect of Fracture Surface Roughness and Mechanical Aperture on the Onset of Nonlinear Flow Behaviors in 3D Self-Affine Rough Fractures. Geofluids 2022, 2022, 4837207. [Google Scholar] [CrossRef]
- Brown, S.R.; Scholz, C.H. Closure of random elastic surfaces in contact. J. Geophys. Res. Solid Earth 1985, 90, 5531–5545. [Google Scholar] [CrossRef]
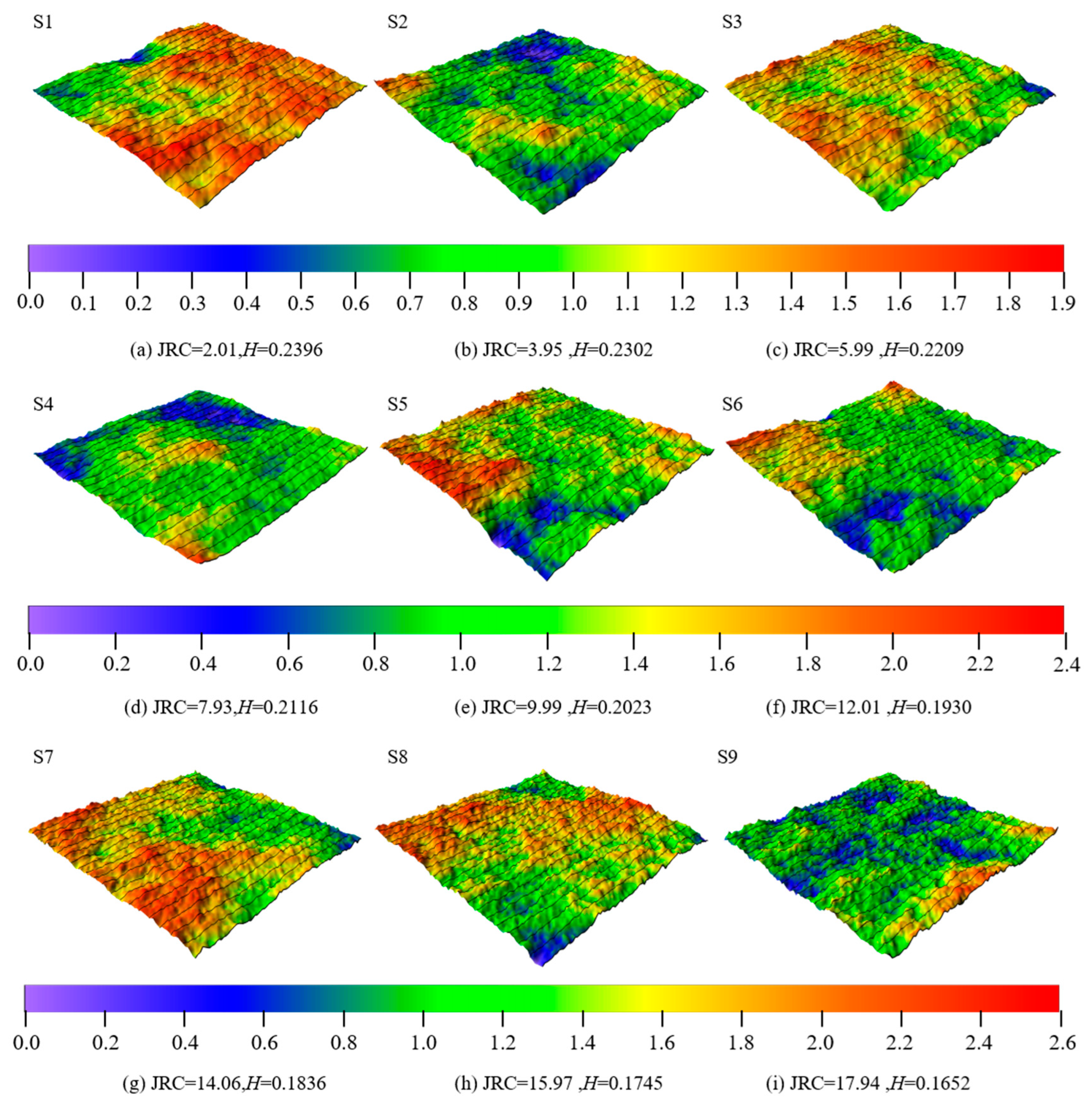
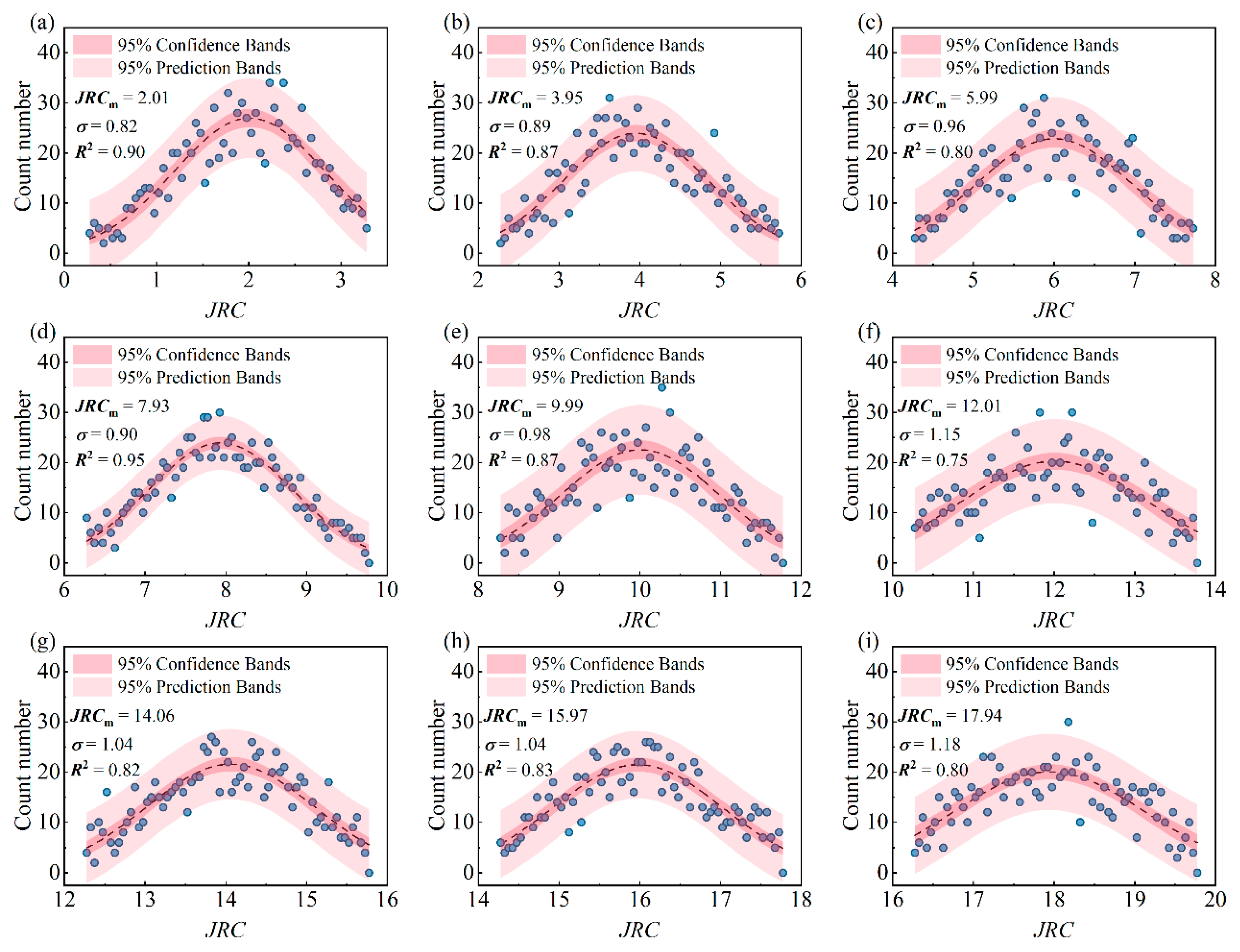
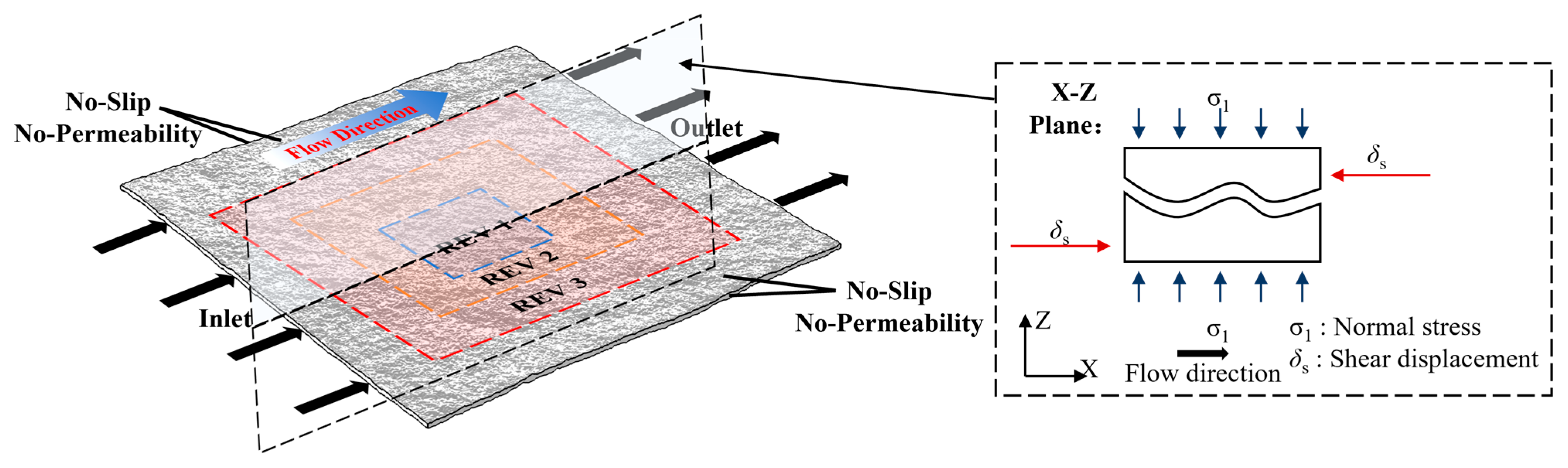


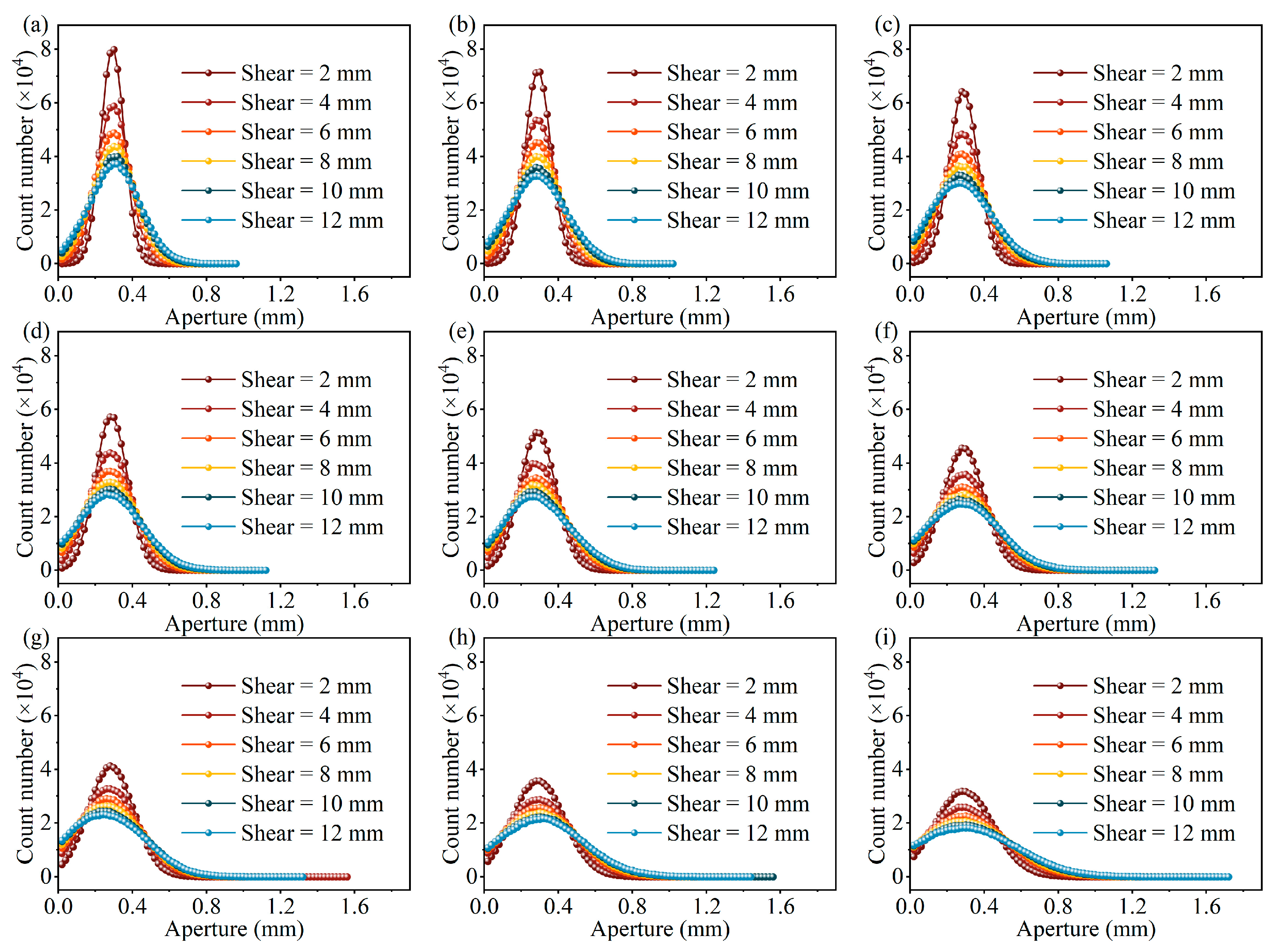
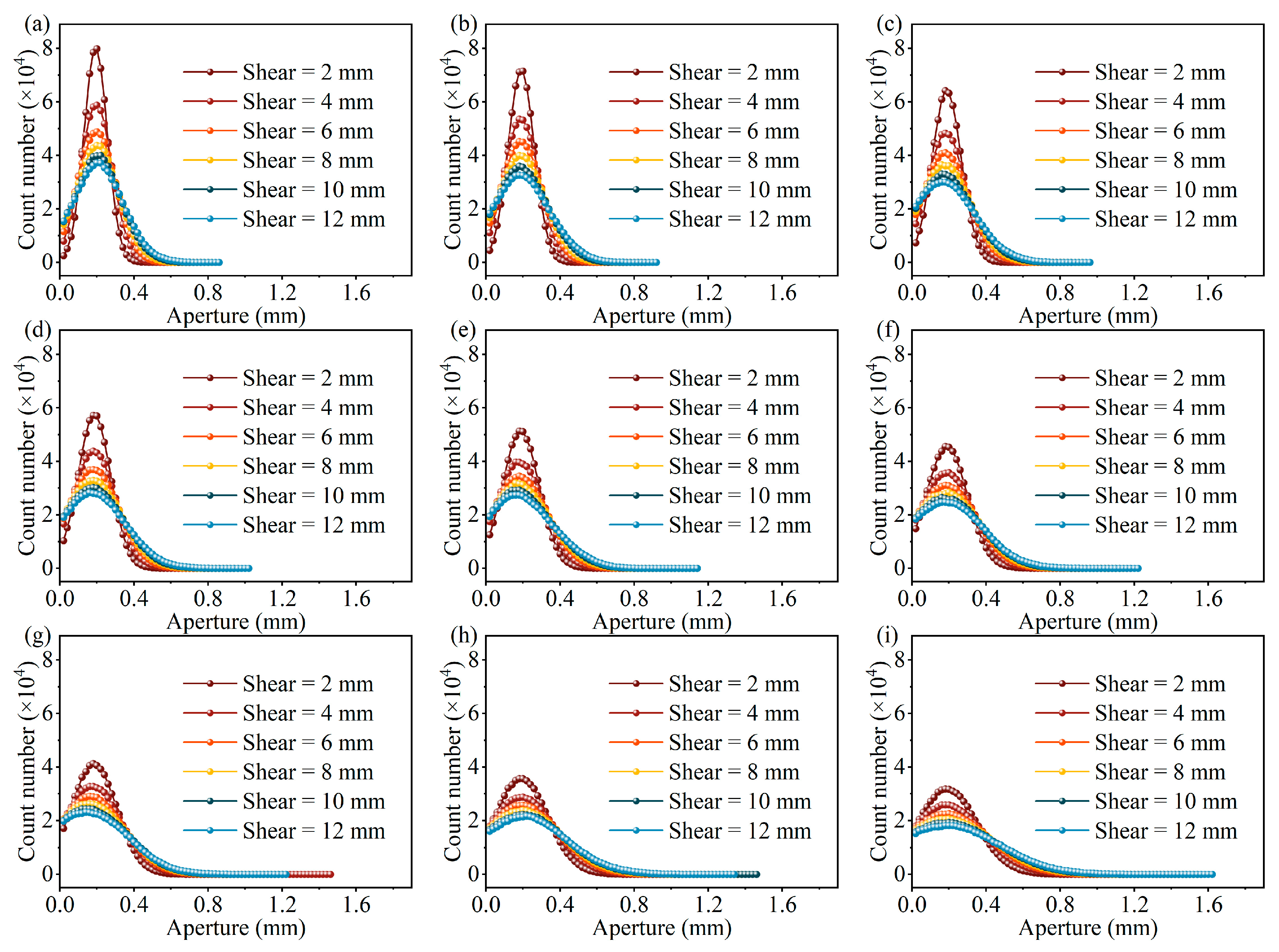
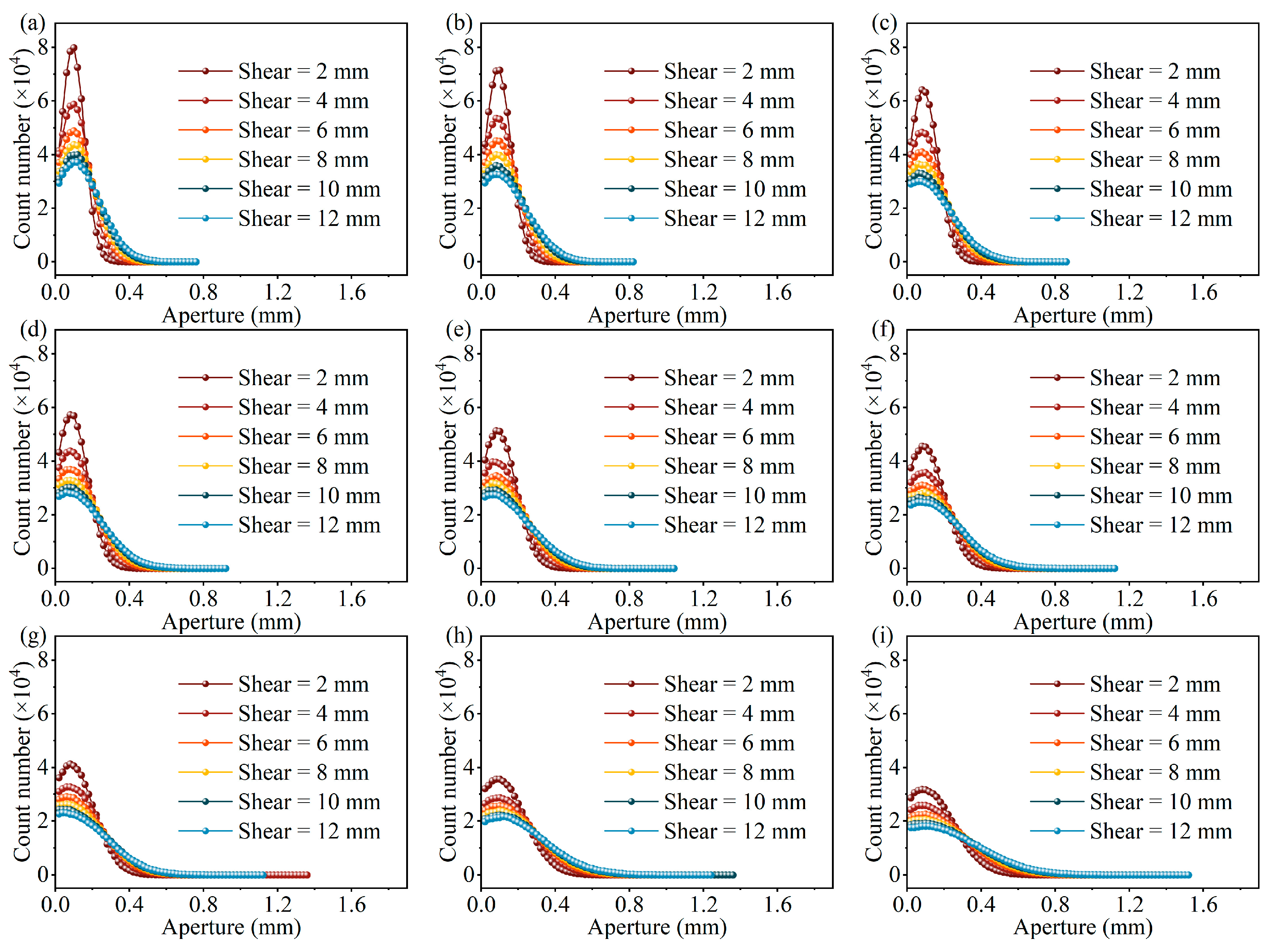
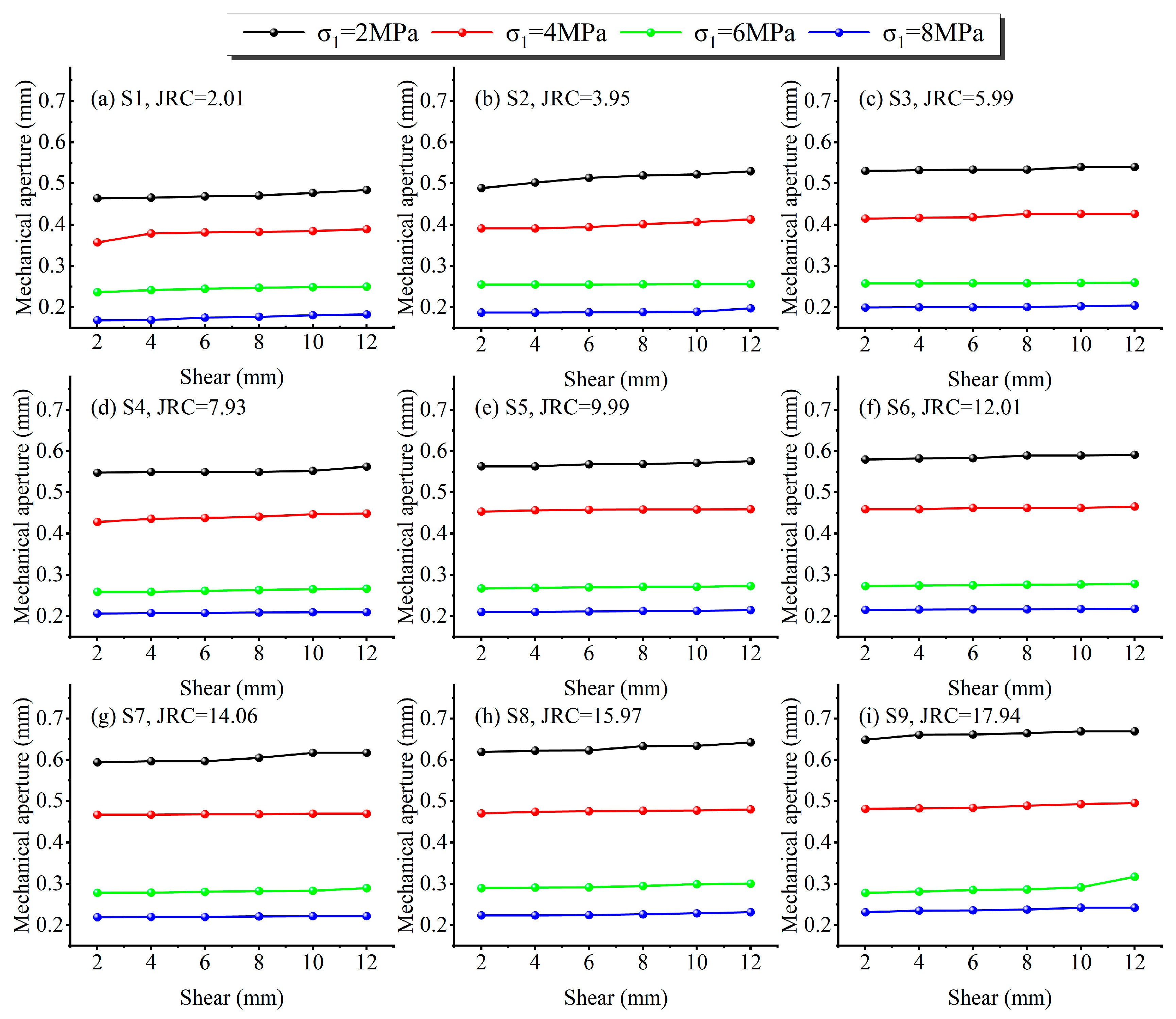

| Parameters | Value |
|---|---|
| Normal stress | σ1 = 2 MPa, σ1 = 4 MPa, σ1 = 6 MPa, σ1 = 8 MPa |
| Shear displacement | 2 mm, 4 mm, 6 mm, 8 mm, 10 mm, 12 mm |
| Hurst exponent | 0.2396, 0.2302, 0.2209, 0.2116, 0.2023, 0.1930, 0.1836, 0.1745, 0.1652 |
| JRC of fracture | 2.01, 3.95, 5.99, 7.93, 9.99, 12.01, 14.06, 15.97, 17.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, X.; Wu, L.; Yang, J.; He, X. Permeability Prediction Model of Fractal Rough Fractures Under Coupled Shear and Normal Stress. Fractal Fract. 2025, 9, 739. https://doi.org/10.3390/fractalfract9110739
Hao X, Wu L, Yang J, He X. Permeability Prediction Model of Fractal Rough Fractures Under Coupled Shear and Normal Stress. Fractal and Fractional. 2025; 9(11):739. https://doi.org/10.3390/fractalfract9110739
Chicago/Turabian StyleHao, Xiaotian, Lizhou Wu, Juan Yang, and Xingji He. 2025. "Permeability Prediction Model of Fractal Rough Fractures Under Coupled Shear and Normal Stress" Fractal and Fractional 9, no. 11: 739. https://doi.org/10.3390/fractalfract9110739
APA StyleHao, X., Wu, L., Yang, J., & He, X. (2025). Permeability Prediction Model of Fractal Rough Fractures Under Coupled Shear and Normal Stress. Fractal and Fractional, 9(11), 739. https://doi.org/10.3390/fractalfract9110739






