Analysis of Finite Integrals with Incomplete Aleph Functions, Mittag-Leffler Generalizations, and the Error Function

Abstract

In this paper, we evaluate a general class of finite integrals involving the error function, generalized Mittag-Leffler functions, and incomplete Aleph functions. The main result provides a unified framework that extends several known formulas related to the incomplete Gamma, I-, and H-functions. Under suitable conditions, these results reduce to many classical special cases. We discuss convergence conditions that justify the validity of the obtained formulas and include explicit corollaries that highlight connections with earlier results in the literature. To illustrate applicability, we present numerical examples and graphs, demonstrating the behavior of the error function integral and Mittag-Leffler functions for specific parameter values. These integrals arise naturally in fractional calculus, probability theory, viscoelasticity, and anomalous diffusion, underscoring the importance of the present work in both mathematical analysis and applications.

1. Introduction and Preliminaries

Special functions such as the Gamma, Mittag-Leffler, error, and Aleph functions play a central role in mathematics, physics, and engineering. They appear in the study of differential and integral equations, probability distributions, statistical mechanics, viscoelasticity, and fractional diffusion processes. For example, the error function is fundamental in probability theory as the distribution function of the normal law, while Mittag-Leffler functions occur as solutions of fractional differential equations modeling anomalous diffusion and relaxation phenomena. Similarly, the Aleph function and its incomplete forms provide a unifying framework that generalizes many other classes of special functions, including Saxena’s I-function and Fox’s H-function.

Srivastava et al. [1] explored the incomplete Gamma function and incomplete hypergeometric function. In more recent work, Kumar et al. [2] investigated improper integrals associated with the incomplete Aleph functions; Kumar et al. [3] investigated the Boros integral involving a class of polynomials and incomplete ℵ-functions; Kumar et al. [4] investigated the Boros integral involving the generalized multi-index Mittag-Leffler function and incomplete I-functions. Srivastava et al. [5] introduced and investigated the incomplete H-function and incomplete $\overline{H}$-function. Several other researchers, including Bansal et al. [6], Bansal and Kumar [7], and Bansal et al. [8], have contributed to the study of the incomplete ℵ-function, the incomplete I-function, and the evaluation of integrals involving the incomplete H-function.

The purpose of this paper is twofold. First, we extend classical finite integrals involving the error function to the broader setting of generalized Mittag-Leffler and incomplete Aleph functions. Second, we unify several related results scattered in the literature by deriving them as corollaries of a single general theorem. The importance of such integrals lies in their potential applications: they arise in the evaluation of solutions of fractional partial differential equations, in diffusion problems, and in applied probability models.

The paper is organized as follows: Section 1 introduces the necessary definitions and preliminaries, with a discussion of convergence and validity conditions. In Section 2, we present the main integral theorem, while Section 3 lists corollaries obtained as special cases, connecting to incomplete I- and H-functions and various Mittag-Leffler generalizations. Section 4 provides applications and numerical illustrations, including explicit examples and graphs that verify the derived formulas. Finally, Section 5 summarizes the contributions of this work and indicates directions for future research.

The Gamma function was introduced by Leonhard Euler in 1729 as an extension of the factorial function [9]. Euler’s integral representation of the Gamma function,

$$\mathrm{\Gamma }\left(\alpha \right)={\int }_0^{\infty }{t}^{\alpha -1}{e}^{-t}\mathrm{d}t\left(\mathrm{\Re }\left(\alpha \right)>0\right),$$

(1)

was later generalized to the incomplete Gamma function, which is defined as

$$\gamma \left(\alpha ,x\right)={\int }_0^x{t}^{\alpha -1}{e}^{-t}\mathrm{d}t\left(\mathrm{\Re }\left(\alpha \right)>0;x⩾0\right),$$

(2)

and

$$\mathrm{\Gamma }\left(\alpha ,x\right)={\int }_x^{\infty }{t}^{\alpha -1}{e}^{-t}\mathrm{d}t\left(x⩾0;\mathrm{\Re }\left(\alpha \right)>0\mathrm{when}x=0\right).$$

(3)

We have the following relation:

$$\gamma \left(\alpha ,x\right)+\mathrm{\Gamma }\left(\alpha ,x\right)=\mathrm{\Gamma }\left(\alpha \right)\left(Re\left(\alpha \right)>0\right).$$

(4)

Now, we give the expression of the incomplete Aleph functions ${}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}(z,x)$ and ${}^{\left(\gamma \right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}(z,x)$ given by Bansal et al. [6] (see also [3]), as follows:

$$\begin{array}{cc}\hfill & {}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z,x\right)={}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z\left|\begin{array}{c}\left(a_1,A_1,x\right),{\left(a_j,A_j\right)}_{2,n},{\left[{\tau }_i\left(a_{ji},A_{ji}\right)\right]}_{n+1,p_i;r}\\ \\ {\left(g_j,G_j\right)}_{1,m},{\left[{\tau }_i\left(g_{ji},G_{ji}\right)\right]}_{m+1,q_i;r}\end{array}\right.\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2\pi \omega }}{\int }_L{\displaystyle \frac{\mathrm{\Gamma }\left(1-a_1-A_{1}s,x\right){\prod }_{j=2}^n\mathrm{\Gamma }\left(1-a_j-A_{j}s\right){\prod }_{j=1}^m\mathrm{\Gamma }\left(g_j+G_{j}s\right)}{{\sum }_{i=1}^r{\tau }_i\left[{\prod }_{j=m+1}^{q_i}\mathrm{\Gamma }\left(1-g_{ji}-G_{ji}s\right){\prod }_{j=n+1}^{p_i}\mathrm{\Gamma }\left(a_{ji}+A_{ji}s\right)\right]}}{z}^{-s}\mathrm{d}s,\hfill \end{array}$$

(5)

and

$$\begin{array}{cc}\hfill & {}^{\left(\gamma \right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z,x\right){=}^{\left(\gamma \right)}{\mathrm{\aleph }}_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z\left|\begin{array}{c}\left(a_1,A_1,x\right),{\left(a_j,A_j\right)}_{2,n},{\left[{\tau }_i\left(a_{ji},A_{ji}\right)\right]}_{n+1,p_i;r}\\ \\ {\left(g_j,G_j\right)}_{1,m},{\left[{\tau }_i\left(g_{ji},G_{ji}\right)\right]}_{m+1,q_i;r}\end{array}\right.\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2\pi \omega }}{\int }_L{\displaystyle \frac{\gamma \left(1-a_1-A_{1}s,x\right){\prod }_{j=2}^n\mathrm{\Gamma }\left(1-a_j-A_{j}s\right){\prod }_{j=1}^m\mathrm{\Gamma }\left(g_j+G_{j}s\right)}{{\sum }_{i=1}^r{\tau }_i\left[{\prod }_{j=m+1}^{q_i}\mathrm{\Gamma }\left(1-g_{ji}-G_{ji}s\right){\prod }_{j=n+1}^{p_i}\mathrm{\Gamma }\left(a_{ji}+A_{ji}s\right)\right]}}{z}^{-s}\mathrm{d}s.\hfill \end{array}$$

(6)

The incomplete ℵ-functions ${}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}(z,x)$ and ${}^{\left(\gamma \right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}(z,x)$, as defined above, exist for $x\ge 0$ under the following validity conditions.

The contour L lies in the s-plane and extends from $\sigma -i\infty$ to $\sigma +i\infty$, where $\sigma$ is a real number. A loop may be introduced, if necessary, to ensure that the poles of $\mathrm{\Gamma }(1-a_j-A_{j}s)$ for $j=2,\dots ,n$ lie to the right of the contour L and the poles of $\mathrm{\Gamma }(g_j+G_{j}s),j=1,\dots ,m$ lie to the left of it. The parameters ${\tau }_i,m,n,p_i$, and $q_i$ are positive numbers that satisfy the conditions $0\le n\le p_i$ and $0\le m\le q_i$. The values of $a_j,g_j$ and $a_{ji},g_{ji}$ are complex numbers. It is assumed that the poles of the integrand are simple. The following conditions apply:

$${\mathrm{\Omega }}_i>0,\left|arg\left(z\right)\right|<{\displaystyle \frac{\pi }{2}}{\mathrm{\Omega }}_i\left(i=1,\dots ,r\right),$$

(7)

$${\mathrm{\Omega }}_j\ge 0,\left|arg\left(z\right)\right|<{\displaystyle \frac{\pi }{2}}{\mathrm{\Omega }}_i\mathrm{and}\mathrm{\Re }\left({\zeta }_i\right)+1<0,$$

(8)

where

$${\mathrm{\Omega }}_i=\sum _{j=1}^n{A}_j+\sum _{j=1}^m{G}_j-{\tau }_i\underset{1\le i\le r}{max}\left(\sum _{j=n+1}^{p_i}{A}_{ji}+\sum _{j=m+1}^{q_i}{G}_{ji}\right)$$

(9)

and

$${\zeta }_i=\sum _{j=1}^m{b}_j-\sum _{j=1}^n{a}_j+{\tau }_i\left(\sum _{j=m+1}^{q_i}{b}_{ji}-\sum _{j=n+1}^{p_i}{a}_{ji}\right)+{\displaystyle \frac{p_i-q_i}{2}}\left(i=1,\dots ,r\right).$$

(10)

We can easily derive the following relation:

$${}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}(z,x)+{}^{\left(\gamma \right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}(z,x)={\mathrm{\aleph }}_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z\right),$$

(11)

where ${\mathrm{\aleph }}_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z\right)$ is the Aleph function [10]. Also, if we set $x=0$, then (5) reduces to the ℵ-function.

Taking ${\tau }_i\to 1$, then the incomplete Aleph functions ${}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}(z,x)$ and ${}^{\left(\gamma \right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}(z,x)$ reduce to the incomplete I-functions ${}^{\left(\mathrm{\Gamma }\right)}I_{p_i,q_i;r}^{m,n}(z,x)$ and ${}^{\left(\gamma \right)}I_{p_i,q_i;r}^{m,n}(z,x)$, respectively, defined as

$$\begin{array}{cc}\hfill & {}^{\left(\mathrm{\Gamma }\right)}I_{p_i,q_i;r}^{m,n}(z,x){=}^{\left(\mathrm{\Gamma }\right)}{I}_{p_i,q_i;r}^{m,n}\left(z\left|\begin{array}{c}\left(a_1,A_1,x\right),{\left(a_j,A_j\right)}_{2,n},{\left(a_{ji},A_{ji}\right)}_{n+1,p_i;r}\\ \\ {\left(g_j,G_j\right)}_{1,m},{\left(g_{ji},G_{ji}\right)}_{m+1,q_i;r}\end{array}\right.\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2\pi \omega }}{\int }_L{\displaystyle \frac{\mathrm{\Gamma }\left(1-a_1-A_{1}s,x\right){\prod }_{j=2}^n\mathrm{\Gamma }\left(1-a_j-A_{j}s\right){\prod }_{j=1}^m\mathrm{\Gamma }\left(g_j+G_{j}s\right)}{{\sum }_{i=1}^r\left[{\prod }_{j=m+1}^{q_i}\mathrm{\Gamma }\left(1-g_{ji}-G_{ji}s\right){\prod }_{j=n+1}^{p_i}\mathrm{\Gamma }\left(a_{ji}+A_{ji}s\right)\right]}}{z}^{-s}\mathrm{d}s,\hfill \end{array}$$

(12)

and

$$\begin{array}{cc}\hfill & {}^{\left(\gamma \right)}I_{p_i,q_i;r}^{m,n}(z,x)={}^{\left(\gamma \right)}I_{p_i,q_i;r}^{m,n}\left(z\left|\begin{array}{c}\left(a_1,A_1,x\right),{\left(a_j,A_j\right)}_{2,n},{\left(a_{ji},A_{ji}\right)}_{n+1,p_i;r}\\ \\ {\left(g_j,G_j\right)}_{1,m},{\left(g_{ji},G_{ji}\right)}_{m+1,q_i;r}\end{array}\right.\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2\pi \omega }}{\int }_L{\displaystyle \frac{\gamma \left(1-a_1-A_{1}s,x\right){\prod }_{j=2}^n\mathrm{\Gamma }\left(1-a_j-A_{j}s\right){\prod }_{j=1}^m\mathrm{\Gamma }\left(g_j+G_{j}s\right)}{{\sum }_{i=1}^r\left[{\prod }_{j=m+1}^{q_i}\mathrm{\Gamma }\left(1-g_{ji}-G_{ji}s\right){\prod }_{j=n+1}^{p_i}\mathrm{\Gamma }\left(a_{ji}+A_{ji}s\right)\right]}}{z}^{-s}\mathrm{d}s.\hfill \end{array}$$

(13)

Under the same conditions as stated earlier, with ${\tau }_i\to 1$, we now consider $r=1$. In this case, the incomplete I-functions ${}^{\left(\mathrm{\Gamma }\right)}I_{p_i,q_i;r}^{m,n}(z,x)$ and ${}^{\left(\gamma \right)}I_{p_i,q_i;r}^{m,n}(z,x)$ simplify to incomplete H-functions, namely, ${}^{\left(\mathrm{\Gamma }\right)}H_{p,q}^{m,n}(z,x)$ and ${}^{\left(\gamma \right)}H_{p,q}^{m,n}(z,x)$, respectively. Such functions are given as

$$\begin{array}{cc}\hfill & {}^{\left(\mathrm{\Gamma }\right)}H_{p,q}^{m,n}(z,x)={}^{\left(\mathrm{\Gamma }\right)}H_{p,q}^{m,n}\left(z\left|\begin{array}{c}\left(a_1,A_1,x\right),{\left(a_j,A_j\right)}_{2,p}\\ \\ {\left(g_j,G_j\right)}_{1,q}\end{array}\right.\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2\pi \omega }}{\int }_L{\displaystyle \frac{\mathrm{\Gamma }\left(1-a_1-A_{1}s,x\right){\prod }_{j=2}^n\mathrm{\Gamma }\left(1-a_j-A_{j}s\right){\prod }_{j=1}^m\mathrm{\Gamma }\left(g_j+G_{j}s\right)}{{\prod }_{j=m+1}^q\mathrm{\Gamma }\left(1-g_j-G_{j}s\right){\prod }_{j=n+1}^p\mathrm{\Gamma }\left(a_j+A_{j}s\right)}}{z}^{-s}\mathrm{d}s\hfill \end{array}$$

(14)

and

$$\begin{array}{cc}\hfill & {}^{\left(\gamma \right)}H_{p,q}^{m,n}(z,x)={}^{\left(\gamma \right)}H_{p,q}^{m,n}\left(z\left|\begin{array}{c}\left(a_1,A_1,x\right),{\left(a_j,A_j\right)}_{2,p}\\ \\ {\left(g_j,G_j\right)}_{1,q}\end{array}\right.\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2\pi \omega }}{\int }_L{\displaystyle \frac{\gamma \left(1-a_1-A_{1}s,x\right){\prod }_{j=2}^n\mathrm{\Gamma }\left(1-a_j-A_{j}s\right){\prod }_{j=1}^m\mathrm{\Gamma }\left(g_j+G_{j}s\right)}{{\prod }_{j=m+1}^q\mathrm{\Gamma }\left(1-g_j-G_{j}s\right){\prod }_{j=n+1}^p\mathrm{\Gamma }\left(a_j+A_{j}s\right)}}{z}^{-s}\mathrm{d}s,\hfill \end{array}$$

(15)

under the same conditions confirmed by the incomplete I-functions when $r=1$.

By using Formula (11), we have the following relations:

$${}^{\left(\mathrm{\Gamma }\right)}I_{p_i,q_i;r}^{m,n}(z,x)+{}^{\left(\gamma \right)}I_{p_i,q_i;r}^{m,n}(z,x)=I_{p_i,q_i;r}^{m,n}\left(z\right),$$

(16)

with the function $I_{p_i,q_i,r}^{m,n}\left(z\right)$ being the function defined by Saxena [11] and

$${}^{\left(\mathrm{\Gamma }\right)}H_{p,q}^{m,n}(z,x)+{}^{\left(\gamma \right)}H_{p,q}^{m,n}(z,x)=H_{p,q}^{m,n}\left(z\right).$$

(17)

Gujar et al. [12] proposed a multivariate generalization of the Mittag-Leffler function, defined as follows:

$$E_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(z_1,\dots ,z_t\right)=\sum _{p_1,\dots ,p_t=0}^{\infty }{\displaystyle \frac{{\left({\delta }_1\right)}_{{\rho }_1{p}_1}\dots {\left({\delta }_t\right)}_{{\rho }_t{p}_t}{z}_1^{p_1}\dots z_t^{p_t}}{\mathrm{\Gamma }\left({\sum }_{k=1}^t{\xi }_k{p}_k+\upsilon \right){\left(K_1\right)}_{{ϵ}_1{p}_1}\dots ,{\left(K_t\right)}_{{ϵ}_t{p}_t}}},$$

(18)

where ${\delta }_k,{\xi }_k,\upsilon ,K_k,z_k\in \mathbb{C}$,

$$\underset{1⩽k⩽t}{min}\left\{\mathrm{\Re }\left({\delta }_k\right),\mathrm{\Re }\left(\upsilon \right),\mathrm{\Re }\left(K_k\right),\mathrm{\Re }\left({\xi }_k\right)\right\}>0,{\rho }_k,{ϵ}_k>0,{\rho }_k<\mathrm{\Re }\left({\xi }_k\right)+{ϵ}_k\mathrm{with}k=1,\dots ,t.$$

We note that

$$A_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(p_1,\dots ,p_t\right)={\displaystyle \frac{{\left({\delta }_1\right)}_{{\rho }_1{p}_1}\dots {\left({\delta }_t\right)}_{{\rho }_t{p}_t}}{\mathrm{\Gamma }\left({\sum }_{k=1}^t{\xi }_k{p}_k+\upsilon \right){\left(K_1\right)}_{{ϵ}_1{p}_1}\dots ,{\left(K_t\right)}_{{ϵ}_t{p}_t}}}.$$

(19)

When $k=1$, we obtain a generalization of the Mittag-Leffler function as defined by Salim and Faraj [13] (see also [14]), which yields

$$E_{\xi ,\upsilon ,ϵ}^{\delta ,K,\rho }\left(z\right)=\sum _{k^{\prime }=0}^{\infty }{\displaystyle \frac{{\left(\delta \right)}_{\rho k^{\prime }}{z}^{k^{\prime }}}{\mathrm{\Gamma }\left(\xi k^{\prime }+\upsilon \right){\left(K\right)}_{ϵk^{\prime }}}},$$

(20)

where $\delta ,\xi ,\upsilon ,K,z\in \mathbb{C}$, $min\left\{\mathrm{\Re }\left(\delta \right),\mathrm{\Re }\left(\upsilon \right),\mathrm{\Re }\left(K\right),Re\left(\xi \right)\right\}>0,\rho ,ϵ,\rho <\mathrm{\Re }\left(\xi \right)+ϵ$.

Also

$$A_{\xi ,\upsilon ,ϵ}^{\delta ,K,\rho }\left(k^{\prime }\right)={\displaystyle \frac{{\left(\delta \right)}_{\rho k^{\prime }}}{\mathrm{\Gamma }\left(\xi k^{\prime }+\upsilon \right){\left(K\right)}_{ϵk^{\prime }}}}.$$

(21)

Salim [15] studied a unification of the Mittag-Leffler function, defined as follows (see also [16]):

$$E_{\xi ,\beta }^{\gamma ,\delta }\left(z\right)=\sum _{k^{\prime }=0}^{\infty }{\displaystyle \frac{{\left(\gamma \right)}_{k^{\prime }}{z}^{k^{\prime }}}{\mathrm{\Gamma }\left(\xi k^{\prime }+\beta \right){\left(\delta \right)}_{k^{\prime }}}},$$

(22)

where $\xi ,\beta ,\gamma ,\delta ,z\in \mathbb{C},\mathrm{\Re }(\xi ,\beta ,\gamma ,\delta )>0$.

We have

$$A_{\xi ,\beta }^{\gamma ,\delta }\left(k^{\prime }\right)={\displaystyle \frac{{\left(\gamma \right)}_{k^{\prime }}}{\mathrm{\Gamma }\left(\xi k^{\prime }+\beta \right){\left(\delta \right)}_{k^{\prime }}}}.$$

(23)

We present the generalization of the Mittag-Leffler function as defined by Srivastava and Tomovski [17] (see also [18]), expressed as follows:

$$E_{\xi ,\upsilon }^{\delta ,K}\left(z\right)=\sum _{k^{\prime }=0}^{\infty }{\displaystyle \frac{{\left(\delta \right)}_{K{k}^{\prime }}{z}^{k^{\prime }}}{\mathrm{\Gamma }\left(\xi k^{\prime }+\upsilon \right)k^{\prime }!}},$$

(24)

where $\delta ,\xi ,\upsilon ,z\in \mathbb{C}$, $\mathrm{\Re }\left(\xi \right)>max\left\{0,\mathrm{\Re }\left(K\right)-1\right\}$, $\mathrm{\Re }\left(K\right)>0$.

We note that

$$A_{\xi ,\upsilon }^{\delta ,K}\left(k^{\prime }\right)={\displaystyle \frac{{\left(\delta \right)}_{K{k}^{\prime }}}{\mathrm{\Gamma }\left(\xi k^{\prime }+\upsilon \right)k^{\prime }!}},$$

(25)

and if we set $K=1$ in (24) and (25), we obtain the Mittag-Leffler function (see Prabhakar [19]), as follows:

$$E_{\xi ,\upsilon }^{\delta ,}\left(z\right)=\sum _{k^{\prime }=1}^{\infty }{\displaystyle \frac{{\left(\delta \right)}_{k^{\prime }}{z}^{k^{\prime }}}{\mathrm{\Gamma }\left(\xi k^{\prime }+\upsilon \right)k^{\prime }!}},$$

(26)

where $z,\upsilon ,\delta ,\xi \in \mathbb{C}$ and $min\left\{\mathrm{\Re }\left(\xi \right),\mathrm{\Re }\left(\upsilon \right)\right\}>0$.

Also,

$$A_{\xi ,\upsilon }^{\delta ,}\left(k^{\prime }\right)={\displaystyle \frac{{\left(\delta \right)}_{k^{\prime }}}{\mathrm{\Gamma }\left(\xi k^{\prime }+\upsilon \right)k^{\prime }!}}.$$

(27)

By setting $\delta =1$ in (26) and (27), we retrieve the Mittag-Leffler function defined by Wiman [20], given as

$$E_{\xi ,\upsilon }\left(z\right)=\sum _{k^{\prime }=1}^{\infty }{\displaystyle \frac{z^{k^{\prime }}}{\mathrm{\Gamma }\left(\xi k^{\prime }+\upsilon \right)}},$$

(28)

where $z,\xi ,\upsilon \in \mathbb{C},min\left\{\mathrm{\Re }\left(\xi \right),\mathrm{\Re }\left(\upsilon \right)\right\}>0$.

Let

$$A_{\xi ,\upsilon }\left(k^{\prime }\right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\xi k^{\prime }+\upsilon \right)}},$$

(29)

and by setting $\upsilon =1$ in (29), we obtain the Mittag-Leffler function [21], defined as

$$E_{\xi }\left(z\right)=\sum _{k^{\prime }=1}^{\infty }{\displaystyle \frac{z^{k^{\prime }}}{\mathrm{\Gamma }\left(\xi k^{\prime }+1\right)}},$$

(30)

where $z,\xi ,\in \mathbb{C}$.

We also have

$$A_{\xi }\left(k^{\prime }\right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\xi k^{\prime }+1\right)}}.$$

(31)

The error function, denoted by $\mathrm{erf}\left(z\right)$, is defined both by an integral and a series, as detailed in Abramowitz and Stegun ([22], p. 86), given as

$$\mathrm{erf}\left(z\right)={\displaystyle \frac{2}{\sqrt{\pi }}}{\int }_0^z{e}^{-t^2}\mathrm{d}t={\displaystyle \frac{2}{\sqrt{\pi }}}\sum _{k=0}^{\infty }{\displaystyle \frac{{(-)}^k{z}^{2k+1}}{k!(2k+1)}}.$$

(32)

Required Integral

We present a general finite integral, as outlined in Brychkov ([23], sec. 4.4.1, eqn. 2, page 184).

Lemma 1.

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x(a-x)}\right)\mathrm{d}x\hfill \\ \hfill & =2^{-2s-{\displaystyle \frac{1}{2}}}{a}^{2s+2}b{\displaystyle \frac{\mathrm{\Gamma }\left(2s+\frac{5}{2}\right)}{\mathrm{\Gamma }\left(2s+3\right)}}{}_2{F}_2\left(\left.\begin{array}{c}{\displaystyle \frac{1}{2}},2s+{\displaystyle \frac{5}{2}}\\ \\ {\displaystyle \frac{3}{2}},2s+3\end{array}\right|-{\displaystyle \frac{a{b}^2}{2}}\right)\hfill \end{array}$$

(33)

where $\mathrm{\Re }\left(s\right)>-{\displaystyle \frac{5}{4}},a>0$.

2. Main Integral

In this section, we establish a general finite integral involving the error function, Mittag-Leffler functions, and the incomplete Aleph function. The following theorems serve as the main results of this work.

Theorem  1.

Let $a>0$ and $\mathrm{\Re }\left(s\right)>-1/2$, and assume that the parameters satisfy the convergence conditions stated in Section 1. Then the following finite integral holds:

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{(a-x)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)E_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(z_1{x}^{B_1}{\left(a-x\right)}^{B_1},\dots ,z_t{x}^{B_t}{\left(a-x\right)}^{B_t}\right)\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z{x}^A{(a-x)}^A,x^{\prime }\right)\mathrm{d}x=2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{n^{\prime },p_1,\dots ,p_t=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}\hfill \\ \hfill & \times A_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(p_1,\dots ,p_t\right)\prod _{i=1}^t{z}_i^{p_i}{2}^{-2{\sum }_{i=1}^t{B}_i{p}_i}{a}^{2{\sum }_{i=1}^t{B}_i{p}_i}\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i+1,q_i+1,{\tau }_i;r}^{m,n+1}\left(z{\left({\displaystyle \frac{a}{2}}\right)}^{2A}\left|\begin{array}{c}\left(a_1,A_1,x^{\prime }\right),\left(-{\displaystyle \frac{3}{2}}-2s-2\sum _{i=1}^t{B}_i{p}_i-n^{\prime };2A\right),\\ \\ {\left(g_j,G_j\right)}_{1,m},{\left[{\tau }_i\left(g_{ji},G_{ji}\right)\right]}_{m+1,q_i;r},\end{array}\right.\right.\hfill \\ \hfill & \left.\begin{array}{c}{\left(a_j,A_j\right)}_{2,n},{\left[{\tau }_i\left(a_{ji},A_{ji}\right)\right]}_{n+1,p_i;r}\\ \\ \left(-2-2s-2\sum _{i=1}^t{B}_i{p}_i-n^{\prime };2A\right)\end{array}\right),\hfill \end{array}$$

(34)

provided that $x^{\prime }⩾0,\mathrm{\Re }\left(s\right)>-{\displaystyle \frac{5}{4}},\left|arg\left(2+a{b}^2\right)\right|<\pi ,a>0$,

$$\mathrm{\Re }\left(s+\sum _{i=1}^t{B}_i{p}_i\right)+2A\underset{1⩽j⩽m}{min}\mathrm{\Re }\left({\displaystyle \frac{g_j}{G_j}}\right)>-{\displaystyle \frac{5}{4}},A>0,{\mathrm{\Omega }}_i>0,\left|arg\left(z\right)\right|<{\displaystyle \frac{\pi }{2}}{\mathrm{\Omega }}_i,i=1,\dots ,r,$$

or ${\mathrm{\Omega }}_i\ge 0,\left|arg\left(z\right)\right|<{\displaystyle \frac{\pi }{2}}{\mathrm{\Omega }}_i$ and $\mathrm{\Re }\left({\zeta }_i\right)+1<0;{\mathrm{\Omega }}_i$ and ${\zeta }_i$ are defined by (9) and (10), respectively; $B_i>0,i=1,\dots ,t$. ${\delta }_k,{\xi }_k,\upsilon ,K_k,z_k\in \mathbb{C},$

$$\underset{1⩽k⩽t}{min}\left\{\mathrm{\Re }\left({\delta }_k\right),\mathrm{\Re }\left(\upsilon \right),\mathrm{\Re }\left(K_k\right),\mathrm{\Re }\left({\xi }_k\right)\right\}>0,{\rho }_k,{ϵ}_k>0,{\rho }_k<\mathrm{\Re }\left({\xi }_k\right)+{ϵ}_k,k=1,\dots ,t,A>0.$$

Notation reminder. Here ${(a_j,A_j)}_{2,n}$ denotes the sequence $(a_2,A_2),(a_3,A_3),\dots ,(a_n,A_n)$, while ${(g_{ji},G_{ji})}_{m+1,qi;r}$ represents the corresponding sequence of coefficients defined in Section 1.

Proof. 

To prove the theorem, we express the extension of the Mittag-Leffler function of t variables defined Gujar et al. [12] in series with the help of (18) and the modified incomplete Gamma Aleph-function in the Mellin–Barnes contour integral with the help of (5), and we interchange the order of integrations and series, which is justifiable due to the absolute convergence of the integral involved in the process. Now by collecting the power of x, we obtain $\mathcal{I}$:

$$\begin{array}{cc}\hfill & \mathcal{I}={\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)E_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(z_1{x}^{B_1}{\left(a-x\right)}^{B_1},\dots ,z_t{x}^{B_t}{\left(a-x\right)}^{B_t}\right)\hfill \\ \hfill & {}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z{x}^A{(a-x)}^A,x^{\prime }\right)\mathrm{d}x=\sum _{p_1,\dots ,p_t=0}^{\infty }{A}_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(p_1,\dots ,p_t\right)\hfill \\ \hfill & \times {\displaystyle \frac{1}{2\pi \omega }}{\int }_L{\displaystyle \frac{\mathrm{\Gamma }\left(1-a_1-A_{1}t,x^{\prime }\right){\prod }_{j=2}^n\mathrm{\Gamma }\left(1-a_j-A_{j}t\right){\prod }_{j=1}^m\mathrm{\Gamma }\left(g_j+G_{j}t\right)}{{\sum }_{i=1}^r{\tau }_i\left[{\prod }_{j=m+1}^{q_i}\mathrm{\Gamma }\left(1-g_{ji}-G_{ji}t\right){\prod }_{j=n+1}^{p_i}\mathrm{\Gamma }\left(a_{ji}+A_{ji}t\right)\right]}}{z}^{-t}\hfill \\ \hfill & \times {\int }_0^a{x}^{s+{\sum }_{i=1}^t{B}_i{p}_i-At+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^{s+{\sum }_{i=1}^t{B}_i{p}_i-At}\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)\mathrm{d}x\mathrm{d}t.\hfill \end{array}$$

(35)

We apply Lemma 1, which results in

$$\begin{array}{cc}\hfill & \mathcal{I}={\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)\hfill \\ \hfill & \times E_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(z_1{x}^{B_1}{\left(a-x\right)}^{B_1},\dots ,z_t{x}^{B_t}{\left(a-x\right)}^{B_t}\right){}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z{x}^A{\left(a-x\right)}^A,x^{\prime }\right)\mathrm{d}x\hfill \\ \hfill & =2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{p_1,\dots ,p_t=0}^{\infty }{A}_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(p_1,\dots ,p_t\right)\prod _{i=1}^t{z}_i^{p_i}{2}^{-2{\sum }_{i=1}^t{B}_i{p}_i}{a}^{2{\sum }_{i=1}^t{B}_i{p}_i}\hfill \\ \hfill & \times {\displaystyle \frac{1}{2\pi \omega }}{\int }_L{\displaystyle \frac{\mathrm{\Gamma }\left(1-a_1-A_{1}t,x^{\prime }\right){\prod }_{j=2}^n\mathrm{\Gamma }\left(1-a_j-A_{j}t\right){\prod }_{j=1}^m\mathrm{\Gamma }\left(g_j+G_{j}t\right)}{{\sum }_{i=1}^r{\tau }_i\left[{\prod }_{j=m+1}^{q_i}\mathrm{\Gamma }\left(1-g_{ji}-G_{ji}t\right){\prod }_{j=n+1}^{p_i}\mathrm{\Gamma }\left(a_{ji}+A_{ji}t\right)\right]}}{z}^{-t}{2}^{2At}{a}^{-2At}\hfill \\ \hfill & \times {\displaystyle \frac{\mathrm{\Gamma }\left(2s+2{\sum }_{i=1}^t{B}_i{p}_i-2At+\frac{5}{2}\right)}{\mathrm{\Gamma }\left(2s+2{\sum }_{i=1}^t{B}_i{p}_i-2At+3\right)}}{}_4{F}_3\left(-{\displaystyle \frac{a{b}^2}{2}}\left|\begin{array}{c}{\displaystyle \frac{1}{2}},1,2s+2\sum _{i=1}^t{B}_i{p}_i-2At+{\displaystyle \frac{5}{2}}\\ \\ {\displaystyle \frac{3}{2}},2s+2\sum _{i=1}^t{B}_i{p}_i-2At+3\end{array}\right.\right)\mathrm{d}t.\hfill \end{array}$$

(36)

We substitute the Gauss hypergeometric function with the series ${\sum }_{n=0}^{\infty }$ (see Slater [24]). Under the given hypothesis, we are able to interchange the series and the t integrals, which leads to the following equation:

$$\begin{array}{cc}\hfill & \mathcal{I}={\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)\hfill \\ \hfill & \times E_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(z_1{x}^{B_1}{\left(a-x\right)}^{B_1},\dots ,z_t{x}^{B_t}{\left(a-x\right)}^{B_t}\right){}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z{x}^A{\left(a-x\right)}^A,x^{\prime }\right)\mathrm{d}x\hfill \\ \hfill & =2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{n^{\prime },p_1,\dots ,p_t=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}{A}_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(p_1,\dots ,p_t\right)\hfill \\ \hfill & \times \prod _{i=1}^t{z}_i^{p_i}{2}^{-2{\sum }_{i=1}^t{B}_i{p}_i}{a}^{2{\sum }_{i=1}^t{B}_i{p}_i}\hfill \\ \hfill & \times {\displaystyle \frac{1}{2\pi \omega }}{\int }_L{\displaystyle \frac{\mathrm{\Gamma }\left(1-a_1-A_{1}t,x^{\prime }\right){\prod }_{j=2}^n\mathrm{\Gamma }\left(1-a_j-A_{j}t\right){\prod }_{j=1}^m\mathrm{\Gamma }\left(g_j+G_{j}t\right)}{{\sum }_{i=1}^r{\tau }_i\left[{\prod }_{j=m+1}^{q_i}\mathrm{\Gamma }\left(1-g_{ji}-G_{ji}t\right){\prod }_{j=n+1}^{p_i}\mathrm{\Gamma }\left(a_{ji}+A_{ji}t\right)\right]}}{z}^{-t}{2}^{2At}{a}^{-2At}\hfill \\ \hfill & \times {\displaystyle \frac{\mathrm{\Gamma }\left(2s+2{\sum }_{i=1}^t{B}_i{p}_i-2At+\frac{5}{2}\right)}{\mathrm{\Gamma }\left(2s+2{\sum }_{i=1}^t{B}_i{p}_i-2At+3\right)}}{\displaystyle \frac{{\left(2s+2{\sum }_{i=1}^t{B}_i{p}_i-2At+\frac{5}{2}\right)}_{n^{\prime }}}{{\left(2s+2{\sum }_{i=1}^t{B}_i{p}_i-2At+3\right)}_{n^{\prime }}}}\mathrm{d}t.\hfill \end{array}$$

(37)

Next, we utilize the relation $\mathrm{\Gamma }\left(a\right){\left(a\right)}_n=\mathrm{\Gamma }(a+n)$, which leads to the following result:

$$\begin{array}{cc}\hfill & \mathcal{I}={\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)\hfill \\ \hfill & \times E_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}{\left(z_1{x}^{B_1}{\left(a-x\right)}^{B_1},\dots ,z_t{x}^{B_t}{\left(a-x\right)}^{B_t}\right)}^{\left(\mathrm{\Gamma }\right)}{\mathrm{\aleph }}_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z{x}^A{\left(a-x\right)}^A,x^{\prime }\right)\mathrm{d}x\hfill \\ \hfill & =2^{-2s-{\displaystyle \frac{3}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{n^{\prime },p_1,\dots ,p_t=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}{2}^{-2{\sum }_{i=1}^t{B}_i{p}_i}{a}^{2{\sum }_{i=1}^t{B}_i{p}_i}\hfill \\ \hfill & \times A_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(p_1,\dots ,p_t\right)\prod _{i=1}^t{z}_i^{p_i}\hfill \\ \hfill & \times {\displaystyle \frac{1}{2\pi \omega }}{\int }_L{\displaystyle \frac{\mathrm{\Gamma }\left(1-a_1-A_{1}t,x^{\prime }\right){\prod }_{j=2}^n\mathrm{\Gamma }\left(1-a_j-A_{j}t\right){\prod }_{j=1}^m\mathrm{\Gamma }\left(g_j+G_{j}t\right)}{{\sum }_{i=1}^r{\tau }_i\left[{\prod }_{j=m+1}^{q_i}\mathrm{\Gamma }\left(1-g_{ji}-G_{ji}t\right){\prod }_{j=n+1}^{p_i}\mathrm{\Gamma }\left(a_{ji}+A_{ji}t\right)\right]}}{z}^{-t}{2}^{2At}{a}^{-2At}\hfill \\ \hfill & \times {\displaystyle \frac{\mathrm{\Gamma }\left(2s-2At+2{\sum }_{i=1}^t{B}_i{p}_i+\frac{5}{2}+n^{\prime }\right)}{\mathrm{\Gamma }\left(2s-2At+2{\sum }_{i=1}^t{B}_i{p}_i+3+n^{\prime }\right)}}\mathrm{d}t.\hfill \end{array}$$

(38)

Upon evaluating the contour integral of the incomplete Gamma Aleph function, the desired result is obtained. □

Theorem  2.

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)E_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(z_1{x}^{B_1}{\left(a-x\right)}^{B_1},\dots ,z_t{x}^{B_t}{\left(a-x\right)}^{B_t}\right)\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z{x}^A{\left(a-x\right)}^A,x^{\prime }\right)\mathrm{d}x=2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{n^{\prime },p_1,\dots ,p_t=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}\hfill \\ \hfill & \times A_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(p_1,\dots ,p_t\right)\prod _{i=1}^t{z}_i^{p_i}{2}^{-2{\sum }_{i=1}^t{B}_i{p}_i}{a}^{2{\sum }_{i=1}^t{B}_i{p}_i}\hfill \\ \hfill & \times {}^{\left(\gamma \right)}\mathrm{\aleph }_{p_i+1,q_i+1,{\tau }_i;r}^{m,n+1}\left(z{\left({\displaystyle \frac{a}{2}}\right)}^{2A}\left|\begin{array}{c}\left(a_1,A_1,x^{\prime }\right),\left(-{\displaystyle \frac{3}{2}}-2s-2\sum _{i=1}^t{B}_i{p}_i-n^{\prime };2A\right),\\ \\ {\left(g_j,G_j\right)}_{1,m},{\left[{\tau }_i\left(g_{ji},G_{ji}\right)\right]}_{m+1,q_i;r},\end{array}\right.\right.\hfill \\ \hfill & \left.\begin{array}{c}{\left(a_j,A_j\right)}_{2,n},{\left[{\tau }_i\left(a_{ji},A_{ji}\right)\right]}_{n+1,p_i;r}\\ \\ \left(-2-2s-2\sum _{i=1}^t{B}_i{p}_i-n^{\prime };2A\right)\end{array}\right).\hfill \end{array}$$

(39)

Proof. 

The result can be obtained in a similar manner to that derived from Theorem 1, using the incomplete gamma Aleph function as defined in (6). □

3. Special Cases

In the subsequent section, we discuss several particular cases. Theorems 1 and 2 admit a number of important reductions. Instead of presenting them as separate theorems, we state them as corollaries to highlight their dependence on the general result.

First, we analyze the incomplete and complete functions, followed by a discussion of several special cases of the generalized Mittag-Leffler function presented in Section 1. By setting ${\tau }_i\to 1$ in (34), the incomplete Aleph functions ${}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}(z,x)$ and ${}^{\left(\gamma \right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}(z,x)$ reduce to the incomplete I-functions ${}^{\left(\mathrm{\Gamma }\right)}I_{p_i,q_i;r}^{m,n}(z,x)$ and ${}^{\left(\gamma \right)}I_{p_i,q_i;r}^{m,n}(z,x)$, respectively. The following results are then obtained for the incomplete I-functions, which are defined as follows.

Corollary 1.

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)E_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(z_1{x}^{B_1}{\left(a-x\right)}^{B_1},\dots ,z_t{x}^{B_t}{\left(a-x\right)}^{B_t}\right)\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}I_{p_i,q_i;r}^{m,n}\left(z{x}^A{\left(a-x\right)}^A,x^{\prime }\right)\mathrm{d}x=2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{n^{\prime },p_1,\dots ,p_t=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}\hfill \\ \hfill & A_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(p_1,\dots ,p_t\right)\prod _{i=1}^t{z}_i^{p_i}{2}^{-2{\sum }_{i=1}^t{B}_i{p}_i}{a}^{2{\sum }_{i=1}^t{B}_i{p}_i}\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}I_{p_i+1,q_i+1;r}^{m,n+1}\left(z{\left({\displaystyle \frac{a}{2}}\right)}^{2A}\left|\begin{array}{c}\left(a_1,A_1,x^{\prime }\right),\left(-{\displaystyle \frac{3}{2}}-2s-2\sum _{i=1}^t{B}_i{p}_i-n^{\prime };2A\right),\\ \\ {\left(g_j,G_j\right)}_{1,m},{\left[\left(g_{ji},G_{ji}\right)\right]}_{m+1,q_i;r},\end{array}\right.\right.\hfill \\ \hfill & \left.\begin{array}{c}{\left(a_j,A_j\right)}_{2,n},{\left[\left(a_{ji},A_{ji}\right)\right]}_{n+1,p_i;r}\\ \\ \left(-2-2s-2\sum _{i=1}^t{B}_i{p}_i-n^{\prime };2A\right)\end{array}\right),\hfill \end{array}$$

(40)

provided that $\mathrm{\Re }\left(s\right)>-1,\left|arg(2+a{b}^2)\right|<\pi$, $a>0$,

$$\mathrm{\Re }\left(s+\sum _{i=1}^t{B}_i{p}_i\right)-A\underset{1⩽j⩽m}{min}\mathrm{\Re }\left({\displaystyle \frac{g_j}{G_j}}\right)>-{\displaystyle \frac{5}{4}},$$

$A>0$, ${\mathrm{\Omega }}_i>0,\left|arg\left(z\right)\right|<{\displaystyle \frac{\pi }{2}}{\mathrm{\Omega }}_i$, $i=1,\dots ,r$ or ${\mathrm{\Omega }}_i\ge 0,\left|arg\left(z\right)\right|<{\displaystyle \frac{\pi }{2}}{\mathrm{\Omega }}_i$ and $\mathrm{\Re }\left({\zeta }_i\right)+1<0$, and $B_i>0$ for $i=1,\dots ,t,{\delta }_k,{\xi }_k,\upsilon ,K_k,z_k\in \mathbb{C}$,

$$\underset{1⩽k⩽t}{min}\left\{\mathrm{\Re }\left({\delta }_k\right),\mathrm{\Re }\left(\upsilon \right),\mathrm{\Re }\left(K_k\right),\mathrm{\Re }\left({\xi }_k\right)\right\}>0,$$

${\rho }_k,{ϵ}_k>0,{\rho }_k<\mathrm{\Re }\left({\xi }_k\right)+{ϵ}_k$, where $k=1,\dots ,t$. Also we have

$${\mathrm{\Omega }}_i=\sum _{j=1}^n{A}_j+\sum _{j=1}^m{G}_j-\underset{1\le i\le r}{max}\left(\sum _{j=n+1}^{p_i}{A}_{ji}+\sum _{j=m+1}^{q_i}{G}_{ji}\right),$$

(41)

$${\zeta }_i=\sum _{j=1}^m{b}_j-\sum _{j=1}^n{a}_j+\left(\sum _{j=m+1}^{q_i}{b}_{ji}-\sum _{j=n+1}^{p_i}{a}_{ji}\right)+{\displaystyle \frac{p_i-q_i}{2}}\left(i=1,\dots ,r\right).$$

(42)

Corollary 2.

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x(a-x)}\right)E_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(z_1{x}^{B_1}{\left(a-x\right)}^{B_1},\dots ,z_t{x}^{B_t}{\left(a-x\right)}^{B_t}\right)\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}I_{p_i,q_i;r}^{m,n}\left(z{x}^A{\left(a-x\right)}^A,x^{\prime }\right)\mathrm{d}x=2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{n^{\prime },p_1,\dots ,p_t=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}\hfill \\ \hfill & \times A_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(p_1,\dots ,p_t\right)\prod _{i=1}^t{z}_i^{p_i}{2}^{-2{\sum }_{i=1}^t{B}_i{p}_i}{a}^{2{\sum }_{i=1}^t{B}_i{p}_i}\hfill \\ \hfill & \times {}^{\left(\gamma \right)}I_{p_i+1,q_i+1;r}^{m,n+1}\left(z{\left({\displaystyle \frac{a}{2}}\right)}^{2A}\left|\begin{array}{c}\left(a_1,A_1,x^{\prime }\right),\left(-{\displaystyle \frac{3}{2}}-2s-2\sum _{i=1}^t{B}_i{p}_i-n^{\prime };2A\right),\\ \\ {\left(g_j,G_j\right)}_{1,m},{\left[\left(g_{ji},G_{ji}\right)\right]}_{m+1,q_i;r},\end{array}\right.\right.\hfill \\ \hfill & \left.\begin{array}{c}{\left(a_j,A_j\right)}_{2,n},{\left[\left(a_{ji},A_{ji}\right)\right]}_{n+1,p_i;r}\\ \\ \left(-2-2s-2\sum _{i=1}^t{B}_i{p}_i-n^{\prime };2A\right),\end{array}\right)\hfill \end{array}$$

(43)

under the conditions cited in Corollary 1.

If we take $r=1$, the incomplete I-functions ${}^{\left(\mathrm{\Gamma }\right)}I_{p_i,q_i;r}^{m,n}(z,x)$ and ${}^{\left(\gamma \right)}I_{p_i,q_i;r}^{m,n}(z,x)$ reduce to incomplete H-functions, namely, ${}^{\left(\mathrm{\Gamma }\right)}H_{p,q}^{m,n}(z,x)$ and ${}^{\left(\gamma \right)}H_{p,q}^{m,n}(z,x)$, respectively. The subsequent results are, therefore, obtained for the incomplete H-functions, which are expressed as follows.

Corollary 3.

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{(a-x)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)E_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(z_1{x}^{B_1}{(a-x)}^{B_1},\dots ,z_t{x}^{B_t}{\left(a-x\right)}^{B_t}\right)\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}H_{p,q}^{m,n}\left(z{x}^A{(a-x)}^A,x^{\prime }\right)\mathrm{d}x=2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{n^{\prime },p_1,\dots ,p_t=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}\hfill \\ \hfill & \times A_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(p_1,\dots ,p_t\right)\prod _{i=1}^t{z}_i^{p_i}{2}^{-2{\sum }_{i=1}^t{B}_i{p}_i}{a}^{2{\sum }_{i=1}^t{B}_i{p}_i}\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}H_{p+1,q+1}^{m,n+1}\left(z{\left({\displaystyle \frac{a}{2}}\right)}^{2A}\left|\begin{array}{c}\left(a_1,A_1,x^{\prime }\right),\left(-{\displaystyle \frac{3}{2}}-2s-2\sum _{i=1}^t{B}_i{p}_i-n^{\prime };2A\right),{\left(a_j,A_j\right)}_{2,p}\\ \\ {\left(g_j,G_j\right)}_{1,q},\left(-2-2s-2\sum _{i=1}^t{B}_i{p}_i-n^{\prime };2A\right)\end{array}\right.\right),\hfill \end{array}$$

(44)

provided that $\mathrm{\Re }\left(s\right)>-1$, $\left|arg(2+a{b}^2)\right|<\pi$, $a>0$,

$$\mathrm{\Re }\left(s+\sum _{i=1}^t{B}_i{p}_i\right)-A\underset{1⩽j⩽m}{min}\mathrm{\Re }\left({\displaystyle \frac{g_j}{G_j}}\right)>-{\displaystyle \frac{5}{4}},A>0,$$

$\mathrm{\Omega }>0,\left|arg\left(z\right)\right|<{\displaystyle \frac{\pi }{2}}\mathrm{\Omega }$, or $\mathrm{\Omega }\ge 0,\left|arg\left(z\right)\right|<{\displaystyle \frac{\pi }{2}}\mathrm{\Omega }$ and $\mathrm{\Re }\left(\zeta \right)+1<0$, and $A,B_i>0\left(i=1,\dots ,t\right)$. ${\delta }_k,{\xi }_k,\upsilon ,K_k,z_k\in \mathbb{C}$,

$$\underset{1⩽k⩽t}{min}\left\{\mathrm{\Re }\left({\delta }_k\right),\mathrm{\Re }\left(\upsilon \right),\mathrm{\Re }\left(K_k\right),\mathrm{\Re }\left({\xi }_k\right)\right\}>0,{\rho }_k,{ϵ}_k>0,{\rho }_k<\mathrm{\Re }\left({\xi }_k\right)+{ϵ}_k\mathrm{where}k=1,\dots ,t.$$

Also

$$\mathrm{\Omega }=\sum _{j=1}^n{A}_j+\sum _{j=1}^m{G}_j-\left(\sum _{j=n+1}^p{A}_j+\sum _{j=m+1}^q{G}_j\right),$$

(45)

and

$$\zeta =\sum _{j=1}^m{g}_j-\sum _{j=1}^n{a}_j+\left(\sum _{j=m+1}^q{g}_j-\sum _{j=n+1}^p{a}_j\right)+{\displaystyle \frac{p-q}{2}}.$$

(46)

Corollary 4.

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)E_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(z_1{x}^{B_1}{\left(a-x\right)}^{B_1},\dots ,z_t{x}^{B_t}{\left(a-x\right)}^{B_t}\right)\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}H_{p,q}^{m,n}\left(z{x}^A{(a-x)}^A,x^{\prime }\right)\mathrm{d}x=2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{n^{\prime },p_1,\dots ,p_t=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}\hfill \\ \hfill & \times A_{{\xi }_k,\upsilon ,{ϵ}_k}^{{\delta }_k,K_k,{\rho }_k}\left(p_1,\dots ,p_t\right)\prod _{i=1}^t{z}_i^{p_i}{2}^{-2{\sum }_{i=1}^t{B}_i{p}_i}{a}^{2{\sum }_{i=1}^t{B}_i{p}_i}\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}H_{p+1,q+1}^{m,n+1}\left(z{\left({\displaystyle \frac{a}{2}}\right)}^{2A}\left|\begin{array}{c}\left(a_1,A_1,x^{\prime }\right),\left(-{\displaystyle \frac{3}{2}}-2s-2\sum _{i=1}^t{B}_i{p}_i-n^{\prime };2A\right),{\left(a_j,A_j\right)}_{2,p}\\ \\ {\left(g_j,G_j\right)}_{1,q},\left(-2-2s-2\sum _{i=1}^t{B}_i{p}_i-n^{\prime };2A\right)\end{array}\right.\right),\hfill \end{array}$$

(47)

under the conditions cited in Corollary 3.

By setting $k=1$, the multivariate generalized Mittag-Leffler function simplifies to the generalized Mittag-Leffler function as defined by Salim and Faraj [13], leading to the following result.

Corollary 5.

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)E_{\xi ,\upsilon ,ϵ}^{\delta ,K,\rho }\left(Z{x}^B{(a-x)}^B\right)\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z{x}^A{\left(a-x\right)}^A,x^{\prime }\right)\mathrm{d}x=2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{k^{\prime },n^{\prime }=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}{Z}^{k^{\prime }}\hfill \\ \hfill & \times A_{\xi ,\upsilon ,ϵ}^{\delta ,K,\rho }\left(k^{\prime }\right)2^{-2B{k}^{\prime }}{a}^{2B{k}^{\prime }}{}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i+1,q_i+1,{\tau }_i;r}^{m,n+1}\left(z{\left({\displaystyle \frac{a}{2}}\right)}^{2A}\left|\begin{array}{c}\left(a_1,A_1,x^{\prime }\right),\\ \\ {\left(g_j,G_j\right)}_{1,m},\end{array}\right.\right.\hfill \\ \hfill & \left.\begin{array}{c}\left(-{\displaystyle \frac{3}{2}}-2s-2B{k}^{\prime }-n^{\prime };2A\right),{\left(a_j,A_j\right)}_{2,n},{\left[{\tau }_i\left(a_{ji},A_{ji}\right)\right]}_{n+1,p_i;r}\\ \\ {\left[{\tau }_i\left(g_{ji},G_{ji}\right)\right]}_{m+1,q_i;r},\left(-2-2s-2B{k}^{\prime }-n^{\prime };2A\right)\end{array}\right),\hfill \end{array}$$

(48)

under the conditions $\mathrm{\Re }\left(s\right)>-{\displaystyle \frac{5}{4}},\left|arg\left(2+a{b}^2\right)\right|<\pi$, $\mathrm{\Re }\left(s\right)>-1,\left|arg\left(2+a{b}^2\right)\right|<\pi ,a>0$, $A,B>0$.

$$\mathrm{\Re }\left(s+B{k}^{\prime }\right)-A\underset{1⩽j⩽m}{min}\mathrm{\Re }\left({\displaystyle \frac{g_j}{G_j}}\right)>-{\displaystyle \frac{5}{4}},{\mathrm{\Omega }}_i>0,\left|arg\left(z\right)\right|<{\displaystyle \frac{\pi }{2}}{\mathrm{\Omega }}_i\left(i=1,\dots ,r\right)$$

or ${\mathrm{\Omega }}_i\ge 0,\left|arg\left(z\right)\right|<{\displaystyle \frac{\pi }{2}}{\mathrm{\Omega }}_i$. $\mathrm{\Re }\left({\zeta }_i\right)+1<0;{\mathrm{\Omega }}_i$ and ${\zeta }_i$ are defined by (9) and (10), respectively; and $\delta ,\xi ,\upsilon ,K,z\in \mathbb{C}$, $A,B>0$ and $min\left\{\mathrm{\Re }\left(\delta \right),\mathrm{\Re }\left(\upsilon \right),\mathrm{\Re }\left(K\right),\mathrm{\Re }\left(\xi \right)\right\}>0$, $\rho ,ϵ,\rho <\mathrm{\Re }\left(\xi \right)+ϵ$.

Next, we explore a generalized version of the Mittag-Leffler function as defined by Salim [15], and we have the following.

Corollary 6.

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)E_{\xi ,\beta }^{\gamma ,\delta }\left(Z{x}^B{\left(a-x\right)}^B\right)\hfill \\ \hfill & {}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z{x}^A{\left(a-x\right)}^A,x^{\prime }\right)\mathrm{d}x=2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\hfill \\ \hfill & \times \sum _{k^{\prime },n^{\prime }=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}{Z}^k{A}_{\xi ,\beta }^{\gamma ,\delta }\left(k^{\prime }\right)2^{-2B{k}^{\prime }}{a}^{2B{k}^{\prime }}\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i+1,q_i+1,{\tau }_i;r}^{m,n+1}\left(z{\left({\displaystyle \frac{a}{2}}\right)}^{2A}\left|\begin{array}{c}\left(a_1,A_1,x^{\prime }\right),\left(-{\displaystyle \frac{3}{2}}-2s-2B{k}^{\prime }-n^{\prime };2A\right),\\ \\ {\left(g_j,G_j\right)}_{1,m},{\left[{\tau }_i\left(g_{ji},G_{ji}\right)\right]}_{m+1,q_i;r},\end{array}\right.\right.\hfill \\ \hfill & \left.\begin{array}{c}{\left(a_j,A_j\right)}_{2,n},{\left[{\tau }_i\left(a_{ji},A_{ji}\right)\right]}_{n+1,p_i;r}\\ \\ \left(-2-2s-2B{k}^{\prime }-n^{\prime };2A\right)\end{array}\right),\hfill \end{array}$$

(49)

under the conditions $\mathrm{\Re }\left(s\right)>-{\displaystyle \frac{5}{4}},\left|arg\left(2+a{b}^2\right)\right|<\pi ,\mathrm{\Re }\left(s\right)>-1,\left|arg\left(2+a{b}^2\right)\right|<\pi$, $a>0,A,B>0$. Also,

$$\mathrm{\Re }\left(s+B{k}^{\prime }\right)-A\underset{1⩽j⩽m}{min}\mathrm{\Re }\left({\displaystyle \frac{g_j}{G_j}}\right)>-{\displaystyle \frac{5}{4}},{\mathrm{\Omega }}_i>0,\left|arg\left(z\right)\right|<{\displaystyle \frac{\pi }{2}}{\mathrm{\Omega }}_i\left(i=1,\dots ,r\right).$$

or ${\mathrm{\Omega }}_i\ge 0,\left|arg\left(z\right)\right|<{\displaystyle \frac{\pi }{2}}{\mathrm{\Omega }}_i,\mathrm{\Re }\left({\zeta }_i\right)+1<0$. ${\mathrm{\Omega }}_i$ and ${\zeta }_i$ are defined by (9) and (10), respectively, and $\xi ,\beta ,\gamma ,\delta ,z\in \mathbb{C},\mathrm{\Re }\left(\xi ,\beta ,\gamma ,\delta \right)>0$.

Consider the formulation of the generalized Mittag-Leffler function provided by Srivastava and Tomovski [17], which gives the following.

Corollary 7.

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)E_{\xi ,\upsilon }^{\delta ,K}\left(Z{x}^B{\left(a-x\right)}^B\right)\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z{x}^A{\left(a-x\right)}^A,x^{\prime }\right)\mathrm{d}x=2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{k^{\prime },n^{\prime }=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}{Z}^k\hfill \\ \hfill & \times A_{\xi ,\upsilon }^{\delta ,K}\left(k^{\prime }\right)2^{-2B{k}^{\prime }}{a}^{2B{k}^{\prime }}{}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i+1,q_i+1,{\tau }_i;r}^{m,n+1}\left(z{\left({\displaystyle \frac{a}{2}}\right)}^{2A}\left|\begin{array}{c}\left(a_1,A_1,x^{\prime }\right),\\ \\ {\left(g_j,G_j\right)}_{1,m},\end{array}\right.\right.\hfill \\ \hfill & \left.\begin{array}{c}\left(-{\displaystyle \frac{3}{2}}-2s-2B{k}^{\prime }-n^{\prime };2A\right),{\left(a_j,A_j\right)}_{2,n},{\left[{\tau }_i\left(a_{ji},A_{ji}\right)\right]}_{n+1,p_i;r}\\ \\ {\left[{\tau }_i\left(g_{ji},G_{ji}\right)\right]}_{m+1,q_i;r},\left(-2-2s-2B{k}^{\prime }-n^{\prime };2A\right)\end{array}\right),\hfill \end{array}$$

(50)

under the conditions verified by Theorem 1 and where $\delta ,\xi ,\upsilon ,K,z\in \mathbb{C}$, $A,B>0$,$min\left\{\mathrm{\Re }\left(\delta \right),\mathrm{\Re }\left(K\right),\mathrm{\Re }\left(\xi \right)\right\}>0$ and $\mathrm{\Re }\left(\delta \right)>max\left\{0,\mathrm{\Re }\left(K\right)-1\right\}$.

Furthermore, by setting $K=1$ in the result given in equation (50), the generalized Mittag-Leffler function [17] simplifies to the Mittag-Leffler function defined by Prabhakar [19], yielding the following.

Corollary 8.

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)E_{\xi ,\upsilon }^{\delta ,}\left(Z{x}^B{(a-x)}^B\right)\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z{x}^A{\left(a-x\right)}^A,x^{\prime }\right)\mathrm{d}x=2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{k^{\prime },n^{\prime }=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}{Z}^k\hfill \\ \hfill & \times A_{\xi ,\upsilon }^{\delta }\left(k^{\prime }\right)2^{-2B{k}^{\prime }}{a}^{2B{k}^{\prime }}{}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i+1,q_i+1,{\tau }_i;r}^{m,n+1}\left(z{\left({\displaystyle \frac{a}{2}}\right)}^{2A}\left|\begin{array}{c}\left(a_1,A_1,x^{\prime }\right),\\ \\ {\left(g_j,G_j\right)}_{1,m},{\left[{\tau }_i\left(g_{ji},G_{ji}\right)\right]}_{m+1,q_i;r},\end{array}\right.\right.\hfill \\ \hfill & \left.\begin{array}{c}\left(-{\displaystyle \frac{3}{2}}-2s-2B{k}^{\prime }-n^{\prime };2A\right),{\left(a_j,A_j\right)}_{2,n},{\left[{\tau }_i\left(a_{ji},A_{ji}\right)\right]}_{n+1,p_i;r}\\ \\ \left(-2-2s-2B{k}^{\prime }-n^{\prime };2A\right)\end{array}\right),\hfill \end{array}$$

(51)

under the conditions verified by Theorem 1, $z,\upsilon ,\delta ,\xi \in \mathbb{C},min\left\{\mathrm{\Re }\left(\xi \right),\mathrm{\Re }\left(\upsilon \right)\right\}>0$, and $A,B>0$.

Next, by choosing $\delta =1$ in the expression from equation (51), the Mittag-Leffler function [19] reduces to the form defined by Wiman [20], and we obtain the following.

Corollary 9.

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x(a-x)}\right)E_{\xi ,\upsilon }\left(Z{x}^B{\left(a-x\right)}^B\right)\hfill \\ \hfill & \times {}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z{x}^A{\left(a-x\right)}^A,x^{\prime }\right)\mathrm{d}x=2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{k^{\prime },n^{\prime }=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}{Z}^k\hfill \\ \hfill & \times A_{\xi }\left(k^{\prime }\right)2^{-2B{k}^{\prime }}{a}^{2B{k}^{\prime }}{}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i+1,q_i+1,{\tau }_i;r}^{m,n+1}\left(z{\left({\displaystyle \frac{a}{2}}\right)}^{2A}\left|\begin{array}{c}\left(a_1,A_1,x^{\prime }\right),\\ \\ {\left(g_j,G_j\right)}_{1,m},\end{array}\right.\right.\hfill \\ \hfill & \left.\begin{array}{c}\left(-{\displaystyle \frac{3}{2}}-2s-2B{k}^{\prime }-n^{\prime };2A\right),{\left(a_j,A_j\right)}_{2,n},{\left[{\tau }_i\left(a_{ji},A_{ji}\right)\right]}_{n+1,p_i;r}\\ \\ {\left[{\tau }_i\left(g_{ji},G_{ji}\right)\right]}_{m+1,q_i;r},\left(-2-2s-2B{k}^{\prime }-n^{\prime };2A\right)\end{array}\right),\hfill \end{array}$$

(52)

under the assumptions verified in Theorem 1, where $z,\xi ,\upsilon \in \mathbb{C}$, and $min\left\{\mathrm{\Re }\left(\xi \right),\mathrm{\Re }\left(\upsilon \right)\right\}>0$, and $A,B>0$.

If we choose $\upsilon =1$ in the result from Equation (52), the Mittag-Leffler function [20] becomes the Mittag-Leffler function defined by Mittag-Leffler [21], and we get the following.

Corollary 10.

$$\begin{array}{cc}\hfill & {\int }_0^a{x}^{s+{\displaystyle \frac{1}{2}}}{\left(a-x\right)}^s\mathrm{erf}\left(b\sqrt[4]{x\left(a-x\right)}\right)E_{\xi }\left(Z{x}^B{\left(a-x\right)}^B\right)\hfill \\ & \times {}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}\left(z{x}^A{\left(a-x\right)}^A,x^{\prime }\right)\mathrm{d}x=2^{-2s-{\displaystyle \frac{1}{2}}}\sqrt{\pi }{a}^{2s+2}b\sum _{k^{\prime },n^{\prime }=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}\right)}_{n^{\prime }}}{{\left(\frac{3}{2}\right)}_{n^{\prime }}}}{\left({\displaystyle \frac{-a^{2}b}{2}}\right)}^{n^{\prime }}{Z}^k\hfill \\ \hfill & \times A_{\xi ,\upsilon }\left(k^{\prime }\right)2^{-2B{k}^{\prime }}{a}^{2B{k}^{\prime }}{}^{\left(\mathrm{\Gamma }\right)}\mathrm{\aleph }_{p_i+1,q_i+1,{\tau }_i;r}^{m,n+1}\left(z{\left({\displaystyle \frac{a}{2}}\right)}^{2A}\left|\begin{array}{c}\left(a_1,A_1,x^{\prime }\right),\\ \\ {\left(g_j,G_j\right)}_{1,m},\end{array}\right.\right.\hfill \\ \hfill & \left.\begin{array}{c}\left(-{\displaystyle \frac{3}{2}}-2s-2B{k}^{\prime }-n^{\prime };2A\right),{\left(a_j,A_j\right)}_{2,n},{\left[{\tau }_i\left(a_{ji},A_{ji}\right)\right]}_{n+1,p_i;r}\\ \\ {\left[{\tau }_i\left(g_{ji},G_{ji}\right)\right]}_{m+1,q_i;r},\left(-2-2s-2B{k}^{\prime }-n^{\prime };2A\right)\end{array}\right),\hfill \end{array}$$

(53)

in accordance with the conditions validated by Theorem 1, and $z,\xi ,\in \mathbb{C}$.

Remark 1.

We observe that the six corollaries yield comparable formulas involving the incomplete gamma Aleph function ${}^{\left(\gamma \right)}\mathrm{\aleph }_{p_i,q_i,{\tau }_i;r}^{m,n}(z,x^{\prime })$, the incomplete Gamma I-function ${}^{\left(\mathrm{\Gamma }\right)}I_{p_i,q_i;r}^{m,n}(.)$, the incomplete Gamma I-function, ${}^{\left(\gamma \right)}I_{p_i,q_i;r}^{m,n}(.)$, and the incomplete H-functions ${}^{\left(\mathrm{\Gamma }\right)}H_{p,q}^{m,n}(.)$ and ${}^{\left(\gamma \right)}H_{p,q}^{m,n}(.)$.

Also, we can obtain similar generalized finite integrals that include the extension of the Mittag-Leffler function, the Aleph function introduced by Südland [25], Saxena’s I-function [11], and Fox’s H-function.

4. Applications and Numerical Illustrations

To complement the theoretical results, we now present numerical examples and graphical illustrations for selected parameter values. These computations demonstrate the practical behavior of the studied integrals and functions and confirm that the formulas derived in Theorems 1 and 2 are verifiable.

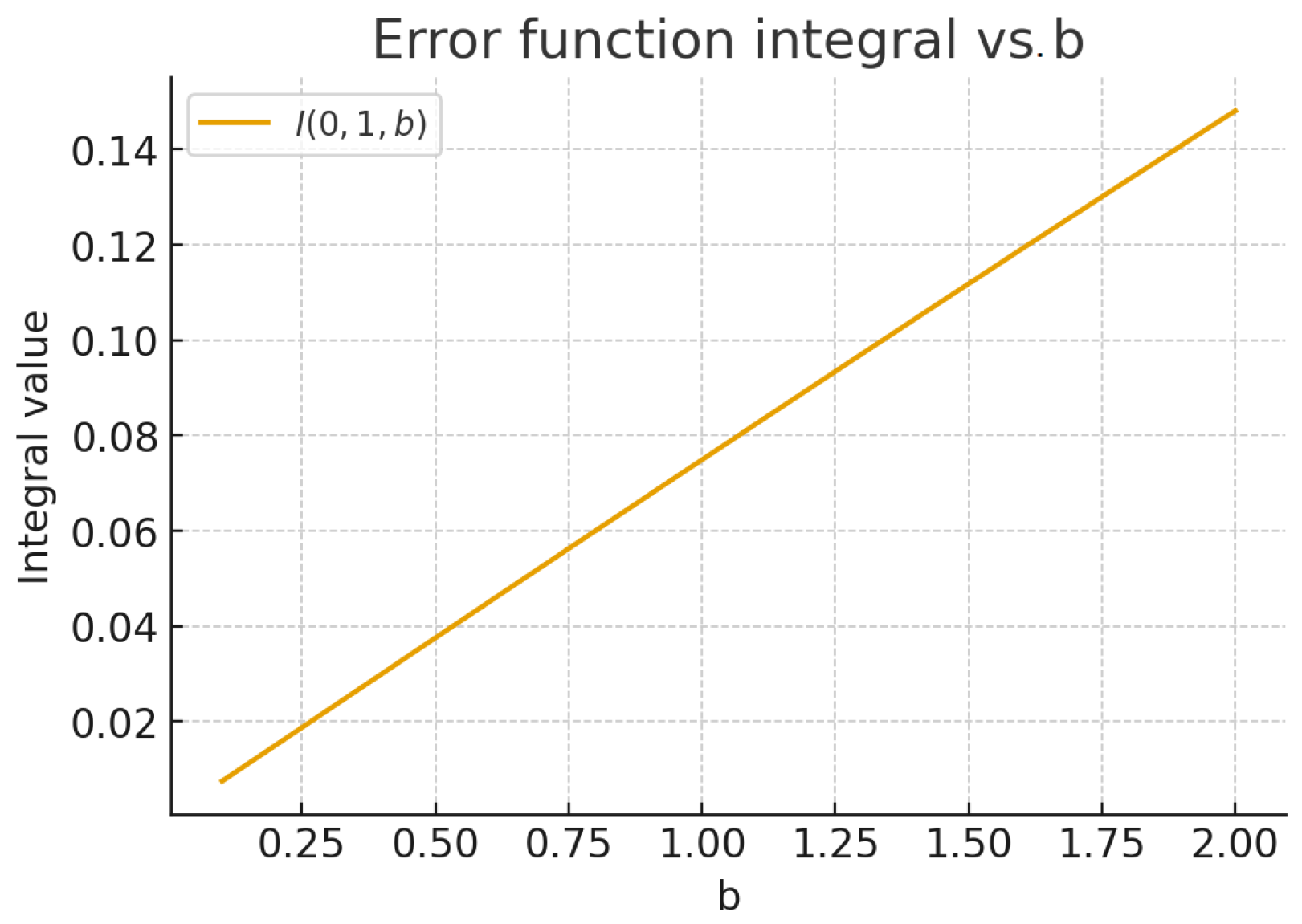
4.1. Error Function Integral

Consider the special case of Lemma 1 (Equation (33)) with parameters $s=0$, $a=1$, and varying b. The integral reduces to

$$I(0,1,b)={\int }_0^1\sqrt{x}\mathrm{erf}\left({\displaystyle \frac{b}{4}}\sqrt{x(1-x)}\right)dx.$$

For $b=1$, numerical evaluation gives

$$I(0,1,1)\approx 0.0749.$$

As shown in Figure 1, the integral increases monotonically with b. This demonstrates how the error function modifies the value of the integral depending on the parameter b. Such integrals appear in probability theory, especially in problems related to the normal distribution and cumulative probabilities.

4.2. Mittag-Leffler Function

The Mittag-Leffler function $E_{\alpha ,\beta }\left(z\right)$ arises naturally in fractional differential equations and is defined by the series

$$E_{\alpha ,\beta }\left(z\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{z^k}{\mathrm{\Gamma }(\alpha k+\beta )}},\alpha ,\beta >0.$$

For $\alpha =0.8$ and $\beta =1$, we plot $E_{0.8,1}\left(z\right)$ for $z\in [0,5]$.

Figure 2 shows the rapid growth of the Mittag-Leffler function, consistent with its role as a generalization of the exponential function. This example highlights the importance of Mittag-Leffler functions in fractional differential equations, where they frequently appear as fundamental solutions to anomalous diffusion and relaxation models.

4.3. Discussion

These examples illustrate the following points:

• The formulas derived in Theorems 1 and 2 can be verified numerically and yield meaningful values for specific parameters.
• The error function integral connects directly to probability theory and diffusion processes.
• The Mittag-Leffler function illustrates the role of fractional calculus in modeling anomalous diffusion and relaxation phenomena.

Thus, the theoretical results obtained in this work are not merely formal but are supported by explicit computations, enhancing their applicability in both pure and applied mathematics.

5. Concluding Remarks

In this paper, we have evaluated a general finite integral involving the error function, generalized Mittag-Leffler functions, and incomplete Aleph functions. The main contribution lies in the unifying theorem presented in Section 2, from which a wide range of special cases are obtained as corollaries. These include reductions to the incomplete Gamma function, I-function, and H-function, thereby demonstrating that our results extend and generalize several known formulas in the literature.

The novelty of our contribution lies in the following:

• Extending classical integrals with the error function to settings involving incomplete Aleph and Mittag-Leffler functions of several variables.
• Demonstrating that numerous known results from the literature (Srivastava–Tomovski, Saxena’s I-function, Fox’s H-function, and others) appear as corollaries of our general theorem.
• Providing explicit examples, numerical illustrations, and graphs to show the verifiability and usefulness of the results beyond formal theory.

The applications of these integrals are broad: they arise in fractional differential equations, anomalous diffusion models, viscoelasticity, and probability theory. Our results, therefore, provide a valuable tool both for pure mathematicians and for applied scientists working with fractional models.

Future research may include

• Numerical methods for evaluating the incomplete Aleph function and its special cases.
• Applications to specific physical models (heat conduction, viscoelastic materials, stochastic processes, etc.).
• Further generalizations to q-analogs and multidimensional integrals.

By combining theoretical rigor with illustrative examples, this work bridges abstract analysis with applications, making the study of incomplete Aleph and Mittag-Leffler functions more accessible and impactful.