A Physics-Informed Neural Network Based on the Separation of Variables for Solving the Distributed-Order Time-Fractional Advection–Diffusion Equation

Abstract

In this work, we propose a new physics-informed neural network framework based on the method of separation of variables (SVPINN) to solve the distributed-order time-fractional advection–diffusion equation. We develop a new method for calculating the distributed-order derivative, which enables the fractional integral to be modeled by a network and directly solved by combining automatic differentiation technology. In this way, the approximation of the distributed-order derivative is integrated into the parameter training system of the network, and the data-driven adaptive learning mechanism is used to replace the numerical discretization scheme. In the SVPINN framework, we decompose the kernel function of the Caputo integral into three independent functions using the method of separation of variables, and apply a neural network as a surrogate model for the modified integral and the function related to the time variable. The new physical constraint generated by the modified integral serves as an extra supervised learning task for the network. We systematically evaluated the feasibility of the SVPINN on several numerical experiments and demonstrated its performance.

1. Introduction

In the fields of science and engineering, efficient modeling and solving of complex physical systems have always been a core challenge. Traditional numerical methods, such as the finite element method and the finite difference method, face bottlenecks such as high computational costs and weak model generalization ability when dealing with high-dimensional problems and complex boundary conditions. In recent years, with the rapid development of machine learning, especially the breakthroughs in function approximation and data-driven modeling in deep learning, physics-informed neural network (PINN) [1] that combines physical prior knowledge with a neural network has emerged, providing a new paradigm for solving the above problems.

Since the PINN framework was proposed, it has made breakthrough progress in fields such as fluid mechanics [2,3,4,5], solid mechanics [6,7,8], heat conduction [9,10], and materials science [11]. To enhance the performance of the PINN, researchers have proposed a series of advanced optimization methods based on the model and problem characteristics. From the perspective of the PINN model, the main ways to improve the generalization ability and training efficiency of the model are through adjusting the network structure [12,13,14,15,16], introducing attention mechanism [17] or adaptive idea [18], optimizing the construction of loss functions [19,20,21,22], and making improvements to training strategies [23,24,25]. Starting from the perspective of problem characteristics, domain decomposition techniques are adopted to refine the problem-solving space [26,27], and additional constraint conditions are introduced to further optimize the model [28,29,30], thereby achieving a comprehensive improvement in overall performance.

However, despite the enormous potential demonstrated by the PINN, it fails to directly solve fractional partial differential equations (FPDEs) due to the inability of the automatic differentiation technique to calculate integrals. Pang et al. [31] proposed using the finite difference method, the Grünwald–Letnikov scheme, to approximate fractional derivatives and developed fractional PINNs (fPINNs). Ma et al. [32] used the L1 formula and the L2$-1_{\sigma }$ formula to approximate Caputo derivatives. Sivalingam et al. [33] applied the theory of functional connection to solve Caputo-type problems. Guo et al. [34] used a Monte Carlo strategy to approximate fractional derivatives. Subsequent studies continue to use different numerical schemes to solve FPDEs [35,36,37].

The advection–diffusion equation can effectively characterize transport processes in both engineering and natural phenomena. However, the description of transport processes in various physical or biological systems often exhibits anomalous diffusion behavior. For instance, particle propagation speed deviates from Fick’s law, and the growth rate of mean square displacement shows a nonlinear relationship with time. These phenomena also occur in other transportation scenarios, such as pollutant migration, groundwater flow, and turbulent transport. The fractional advection–diffusion equation can more accurately describe these complex dynamic processes. The fractional derivative utilizes a memory kernel in the form of a power function to weight the entire historical process, which gives the model a memory effect and significantly improves its ability to model and predict transport behavior in complex systems, attracting widespread attention.

As a significant extension of fractional derivatives, distributed-order derivatives break through the limitation of fixed-order derivatives and expand the derivative order from a single numerical value to a continuous interval description based on distributed functions. Although this feature enhances the ability of equations to describe complex physical processes, it also increases the difficulty of solving them. To address this challenge, some scholars have drawn on the discretization idea of fractional derivatives in fPINN. In the recently proposed PINN-based framework, Ramezani et al. [38] used composite midpoint and L1 formulae to approximate the distributed-order derivative, while Momeni et al. [39] combined the Legendre–Gauss quadrature rule and operational matrices to discretize the distributed-order derivative. Other scholars also use numerical schemes to convert the distributed-order derivatives into a processable form, and then embed them into a neural network [40,41,42,43].

However, there are two issues with this approach: (1) PINN-based frameworks rely on numerical schemes such as finite difference to discretize the distributed-order derivative; (2) the approximation of the distributed-order derivative cannot be achieved by optimizing the parameters of the network. Therefore, the accuracy of the solution is limited by the precision of the numerical discretization method, rather than the approximation ability of the network. These issues drive the primary objective of this work.

In this paper, we present a new framework based on the PINN, called SVPINN, to solve the distributed-order time-fractional advection–diffusion equation. The proposed method changes the integral form by separating variables, which allows the neural network to directly approximate the distributed-order derivative. The main contributions of this paper are as follows: (1) We propose a variable separation-based PINN framework suitable for the distributed-order derivative. Unlike the classical separation of variables method that seeks analytical solutions, a neural network is utilized to approximate the variable-based basis functions to achieve the variable separation process, as the kernel function in the Caputo derivative is not strictly separable. (2) The proposed SVPINN decomposes the kernel function in the Caputo derivative into the product form of basis functions consisting of time variable, integral variable, and order. This avoids using a numerical discretization scheme to approximate the distributed-order derivative, thereby eliminating integral discretization. (3) In the SVPINN framework, the approximation of the distributed-order derivative is gradually completed by training the parameters of the network during the training process, which is different from the PINN-based frameworks proposed in [40,41,42,43] that directly complete the approximation of the distributed-order derivative using a numerical scheme before the training process. (4) Compared with the PINN that simulates the fractional derivative using numerical discretization scheme, the SVPINN significantly improves prediction accuracy and convergence speed in irregular domains and high-dimensional problems.

The structure of this paper is as follows: In Section 2, the detailed framework of the SVPINN is presented. In Section 3, several numerical examples are used to test the performance of our proposed method. In Section 4, we summarize several concluding remarks.

2. Method

In this section, we first clarify the distributed-order advection–diffusion equation and the definition of the distributed-order derivative. Then we present a detailed introduction to the structure of our proposed method. Finally, we analyze the stability of the proposed SVPINN.

2.1. Problem Setup

In this study, we focus on the following distributed-order time-fractional advection–diffusion equation

$$D_t^{\omega \left(\alpha \right)}u-\Delta u+R·\nabla u=h(\mathit{x},t),(\mathit{x},t)\in \mathrm{\Omega }\times \tau ,$$

(1)

with the boundary condition

$$u(\mathit{x},t)=\mathcal{B}(x,t),(\mathit{x},t)\in \partial \overline{\mathrm{\Omega }}\times \overline{\tau },$$

(2)

and the initial condition

$$u(\mathit{x},0)=\mathcal{I}\left(\mathit{x}\right),\mathit{x}\in \overline{\mathrm{\Omega }},$$

(3)

where $R=(1,1,\cdots ,1)\in {\mathbb{R}}^d$ denotes a constant advection velocity. Also $D_t^{\omega \left(\alpha \right)}$ represents the distributed-order derivative, having

$$D_t^{\omega \left(\alpha \right)}u(\mathit{x},t)={\int }_0^1\omega {\left(\alpha \right)}_0^C{D}_t^{\alpha }u(\mathit{x},t)d\alpha ,$$

(4)

with the Caputo fractional derivative [40,41,42,43]

$${}_a{}^{C}D_t^{\alpha }u(\mathit{x},t)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\int }_a^t{(t-\eta )}^{-\alpha }{u}_{\eta }(\mathit{x},\eta )d\eta ,\hfill & 0\le \alpha <1,\hfill \\ {\displaystyle \frac{{\partial }^{\alpha }u(\mathit{x},t)}{\partial t^{\alpha }}},\hfill & \alpha =1,\hfill \end{array}\right.$$

(5)

where ${(t-\eta )}^{-\alpha }$ represents the kernel function, $\omega \left(\alpha \right)>0$, and $0<{\int }_0^1\omega \left(\alpha \right)d\alpha <\infty$. In the framework of the distributed-order derivative, the order $\alpha$ varies as an integral variable, rather than remaining fixed. The influence of any individual order $\alpha$ is determined by the weight function $\omega \left(\alpha \right)$.

2.2. The SVPINN Framework

Based on the integral (4), without considering other variables such as the space variable $\mathit{x}$ and the time variable t, we can simply regard the integral as

$${\int }_0^1\omega \left(\alpha \right){}_0{}^{C}D_t^{\alpha }u(\mathit{x},t)d\alpha ={\int }_0^1\omega \left(\alpha \right)\mathcal{A}\left(\alpha \right)d\alpha ,$$

(6)

where the function $\mathcal{A}\left(\alpha \right)$ is only related to the integral variable $\alpha$. Similarly, for the integral in (5), if we can separate t and $\eta$ in the kernel function ${(t-\eta )}^{-\alpha }$, then we have

$${\int }_a^t{(t-\eta )}^{-\alpha }{u}_{\eta }(\mathit{x},\eta )d\eta =\mathcal{T}\left(t\right){\int }_a^t\mathcal{N}\left(\eta \right)u_{\eta }(\mathit{x},\eta )d\eta ,$$

(7)

where $\mathcal{T}\left(t\right)$ and $\mathcal{N}\left(\eta \right)$ are only related to variables t and n, respectively. On the basis of the above conjecture, we plan to construct a new integral form of the distributed-order derivative by separating variables.

For the kernel function ${(t-\eta )}^{-\alpha }$, we apply the method of separation of variables to decompose it into the following form

$${(t-\eta )}^{-\alpha }\approx \mathcal{T}\left(t\right)\mathcal{N}\left(\eta \right)\mathcal{A}\left(\alpha \right).$$

(8)

Then, the Caputo fractional derivative can be rewritten as

$${}_a{}^{C}D_t^{\alpha }u(\mathit{x},t)\approx {\displaystyle \frac{1}{\Gamma (1-\alpha )}}\mathcal{A}\left(\alpha \right)\mathcal{T}\left(t\right){\int }_a^t\mathcal{N}\left(\eta \right)u_{\eta }(\mathit{x},\eta )d\eta .$$

(9)

For the distributed-order derivative $D_t^{\omega \left(\alpha \right)}u(\mathit{x},t)$, we have

$${\int }_0^1\omega \left(\alpha \right){}_0{}^{C}D_t^{\alpha }u(\mathit{x},t)d\alpha \approx \mathfrak{D}(\mathit{x},t,u){\int }_0^1{\displaystyle \frac{\omega \left(\alpha \right)}{\Gamma (1-\alpha )}}\mathcal{A}\left(\alpha \right)d\alpha ,$$

(10)

where

$$\mathfrak{D}(\mathit{x},t,u)=\mathcal{T}\left(t\right){\int }_a^t\mathcal{N}\left(\eta \right)u_{\eta }(\mathit{x},\eta )d\eta .$$

(11)

Given that $\psi (\mathit{x},t)={\int }_a^t\mathcal{N}\left(\eta \right)u_{\eta }(\mathit{x},\eta )d\eta$, we can obtain the following condition [44]

$${\psi }_t(\mathit{x},t)=\mathcal{N}\left(t\right)u_t(\mathit{x},t).$$

(12)

Finally, the distributed-order derivative $D_t^{\omega \left(\alpha \right)}u(\mathit{x},t)$ is rewritten as

$$D_t^{\omega \left(\alpha \right)}u(\mathit{x},t)\approx \mathcal{T}\left(t\right)\psi (\mathit{x},t){\int }_0^1{\displaystyle \frac{\omega \left(\alpha \right)}{\Gamma (1-\alpha )}}\mathcal{A}\left(\alpha \right)d\alpha .$$

(13)

To achieve the separation process of (8), we use a network to approximate $\mathcal{T}\left(t\right)$ and set $\mathcal{N}\left(\eta \right)=\eta$ and $\mathcal{A}\left(\alpha \right)=\alpha$. The reason for this definition are as follows:

• The variables $\eta$ and $\alpha$ are both integral variables. If $\mathcal{N}\left(\eta \right)$ and $\mathcal{A}\left(\alpha \right)$ are approximated by a network, the integral operation needs to be performed on the network. However, the existing technology limits the integral calculation of the network.
• Based on the approximation capability of neural network and the properties of distributed-order derivative, we set $\mathcal{N}\left(\eta \right)$ and $\mathcal{A}\left(\alpha \right)$ as an identity mapping form, i.e., $\mathcal{N}\left(\eta \right)=\eta$ and $\mathcal{A}\left(\alpha \right)=\alpha$. This approach aims to simplify the calculation of the integrals ${\int }_a^t\mathcal{N}\left(\eta \right)u_{\eta }(\mathit{x},\eta )d\eta$ and ${\int }_0^1{\displaystyle \frac{\omega \left(\alpha \right)}{\Gamma (1-\alpha )}}\mathcal{A}\left(\alpha \right)d\alpha$, and avoid the increase in computational complexity when using the separated variable method to process the kernel function. And using the network to approximate $\mathcal{T}\left(t\right)$ can satisfy the variable separation process of the kernel function (8).

In the SVPINN framework, we construct a neural network with multi-output terms $\left[u\right(\mathit{x},t;\vartheta ),\psi (\mathit{x},t;\vartheta ),\mathcal{T}(\mathit{x},t;\vartheta \left)\right]$ to approximate the analytical solution $u(\mathit{x},t)$, $\psi (\mathit{x},t)$ and $\mathcal{T}\left(t\right)$. The parameter $\vartheta$ represents the trainable parameters of the network. Considering the physical information (12) as a new constraint condition, then we define

$$\left\{\begin{array}{c}f(\mathit{x},t)=\mathcal{T}\left(t\right)\psi (\mathit{x},t){\int }_0^1{\displaystyle \frac{\omega \left(\alpha \right)}{\Gamma (1-\alpha )}}\mathcal{A}\left(\alpha \right)d\alpha -\Delta u+R·\nabla u-h(\mathit{x},t),\hfill \\ g(\mathit{x},t)={\psi }_t(\mathit{x},t)-\mathcal{N}\left(t\right)u_t(\mathit{x},t).\hfill \end{array}\right.$$

(14)

Remark 1.

It is worth noting that in the proposed framework, no additional constraints are imposed on the function $\mathcal{T}\left(t\right)$. The governing Equation (1) can provide a good constraint effect on $\mathcal{T}(\mathit{x},t;\vartheta )$, and the network that approximates $u(\mathit{x},t)$ is the same as the network that approximates $\mathcal{T}\left(t\right)$. This makes it equivalent to treating the initial and boundary conditions as an implicit constraint condition for $\mathcal{T}(\mathit{x},t;\vartheta )$ during the overall training process. Moreover, in the input layer of the approximator $\mathcal{T}(\mathit{x},t;\vartheta )$, we still add the variable $\mathit{x}$, with the aim of making $\mathcal{T}(\mathit{x},t;\vartheta )$ closer to the physical laws described by (1)–(3).

The total loss function of the SVPINN method can be formulated as

$$\begin{array}{c}\mathcal{L}\left(\vartheta \right)={\mathcal{L}}_f\left(\vartheta \right)+{\mathcal{L}}_e\left(\vartheta \right)+{\mathcal{L}}_u\left(\vartheta \right),\hfill \\ {\mathcal{L}}_f\left(\vartheta \right)={\displaystyle \frac{1}{N_f}}{\displaystyle \sum _{i=1}^{N_f}}{\left|f({\mathit{x}}_f^i,t_f^i;\vartheta )\right|}^{ 2},\hfill \\ {\mathcal{L}}_e\left(\vartheta \right)={\displaystyle \frac{1}{N_f}}{\displaystyle \sum _{i=1}^{N_f}}{\left|g({\mathit{x}}_f^i,t_f^i;\vartheta )\right|}^{ 2},\hfill \\ {\mathcal{L}}_u\left(\vartheta \right)={\displaystyle \frac{1}{N_u}}{\displaystyle \sum _{i=1}^{N_u}}{|u({\mathit{x}}_u^i,t_u^i;\vartheta )-u({\mathit{x}}_u^i,t_u^i)|}^{ 2},\hfill \end{array}$$

(15)

where ${\mathcal{L}}_f\left(\vartheta \right)$ is a loss term based on the residual equation f, which is used to ensure that the neural network $u(\mathit{x},t;\vartheta )$ satisfies the physical laws described by the governing equation in the spatio-temporal domain. The characteristic equation loss ${\mathcal{L}}_e\left(\vartheta \right)$ is physical information introduced to implement the separation of variables, providing a regularized constraint for approximating the distributed-order derivative to accelerate convergence efficiency. The loss ${\mathcal{L}}_u\left(\vartheta \right)$ is a constraint on the data related to the initial and boundary conditions for the network, providing an initial direction for training and ensuring consistency between the predicted results and the problem. The data set ${\left\{({\mathit{x}}_f^i,t_f^i)\right\}}_{i=1}^{N_f}$ denotes the collocation points randomly sampled from the domain $\mathrm{\Omega }\times \tau$, and ${\{({\mathit{x}}_u^i,t_u^i),u({\mathit{x}}_u^i,t_u^i)\}}_{i=1}^{N_u}$ represent the boundary and initial data. In Algorithm 1, the SVPINN framework for solving the distributed-order time-fractional advection–diffusion equation is described in detail.

Remark 2.

We use an equal weight approach in the loss function to ensure that ${\mathcal{L}}_f$, ${\mathcal{L}}_e$, and ${\mathcal{L}}_u$ maintain the same proportion during the training process, while also avoiding the model overfitting to a specific constraint. In addition, we mainly focus on verifying the effectiveness and feasibility of the proposed framework, therefore using an equal weight approach as a benchmark.

Algorithm 1 The SVPINN framework

Input: Time variable t and spatial variable x. Output: The prediction $u(\mathit{x},t;\vartheta )$.  1: Construct a neural network with multiple outputs $\left[u\right(\mathit{x},t;\vartheta ),\psi (\mathit{x},t;\vartheta ),\mathcal{T}(\mathit{x},t;\vartheta \left)\right]$.  2: Divide the kernel function into the product form of basis functions and network: $${(t-\eta )}^{-\alpha }\approx \mathcal{T}(\mathit{x},t;\vartheta )\mathcal{N}\left(\eta \right)\mathcal{A}\left(\alpha \right).$$  3: Calculate the Caputo fractional derivative: $${}_a{}^{C}D_t^{\alpha }u(\mathit{x},t;\vartheta )={\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\int }_a^t\mathcal{T}(\mathit{x},t;\vartheta )\mathcal{N}\left(\eta \right)\mathcal{A}\left(\alpha \right)u_{\eta }(\mathit{x},\eta ;\vartheta )d\eta .$$  4: Define $\psi (\mathit{x},t;\vartheta )={\int }_a^t\mathcal{N}\left(\eta \right)u_{\eta }(\mathit{x},\eta ;\vartheta )d\eta$.  5: Obtain the distributed-order derivative $D_t^{\omega \left(\alpha \right)}u(\mathit{x},t;\vartheta )$: $$\begin{array}{cc}{D}_t^{\omega \left(\alpha \right)}u(\mathit{x},t;\vartheta )& ={\int }_0^1\omega \left(\alpha \right){}_0{}^{C}D_t^{\alpha }u(\mathit{x},t;\vartheta )d\alpha \hfill \\ & \hfill =\mathcal{T}(\mathit{x},t;\vartheta )\psi (\mathit{x},t;\vartheta ){\int }_0^1{\displaystyle \frac{\omega \left(\alpha \right)}{\Gamma (1-\alpha )}}\mathcal{A}\left(\alpha \right)d\alpha .\end{array}$$  6: Construct the loss function $\mathcal{L}\left(\vartheta \right)$ by combing (1)–(3) and (12).  7: Apply the L-BFGS method to optimize the network parameters $\vartheta$.

2.3. Analysis of Stability

In this section, we aim to analyze the stability of the proposed SVPINN method. We first introduce the following lemmas:

Lemma 1.

For the constant $C_{\mathcal{B}}>0$, the boundary error caused by the approximation of the network satisfies

$$\left|{\int }_{\partial \mathrm{\Omega }}\tilde{u}{\displaystyle \frac{\partial \tilde{u}}{\partial \mathbf{n}}}ds\right|+\left|{\int }_{\partial \mathrm{\Omega }}{\tilde{u}}^{2}R·\mathbf{n}ds\right|\le C_{\mathcal{B}}{\mathcal{E}}_{\mathcal{B}},$$

(16)

where ${\mathcal{E}}_{\mathcal{B}}$ denotes the upper bound of the error corresponding to the boundary condition.

Lemma 2.

There exists a constant $C_{sv}$ such that

$$|{\epsilon }_{sv}{|=|(t-\eta )}^{-\alpha }-\mathcal{T}\left(t\right)\mathcal{N}\left(\eta \right)\mathcal{A}\left(\alpha \right)|\le C_{sv}.$$

(17)

Theorem 1.

Let $(u_1,{\psi }_1)$ and $(u_2,{\psi }_2)$ be the predictions given by the SVPINN for the problem (1) corresponding to the source terms $h_1$ and $h_2$, respectively. Then for a constant C > 0, we have the following stability holds:

$$\parallel (u_1-u_2)(·,t){\parallel }_{L^2\left(\mathrm{\Omega }\right)}+\parallel ({\psi }_1-{\psi }_2)(·,t){\parallel }_{L^2\left(\mathrm{\Omega }\right)}\le C(\parallel h_1-h2{\parallel }_{L^2(\mathrm{\Omega }\times [0,t])}+{\mathcal{E}}_{\mathcal{B}}+{\mathcal{E}}_{\mathcal{I}}+C_{sv}),$$

(18)

where ${\mathcal{E}}_{\mathcal{I}}$ represents the upper bound of the error corresponding to the initial condition.

Proof.

Defining $\tilde{u}=u_1-u_2$, $\tilde{\psi }={\psi }_1-{\psi }_2$, and $\tilde{h}=h_1-h_2$, we have

$$\left\{\begin{array}{c}\mathcal{T}\left(t\right)\tilde{\psi }(\mathit{x},t){\int }_0^1{\displaystyle \frac{\omega \left(\alpha \right)}{\Gamma (1-\alpha )}}\mathcal{A}\left(\alpha \right)d\alpha -\Delta \tilde{u}+R·\nabla \tilde{u}=\tilde{h}(\mathit{x},t)+{\mathcal{E}}_{sv},\hfill \\ {\tilde{\psi }}_t(\mathit{x},t)=\mathcal{N}\left(t\right){\tilde{u}}_t(\mathit{x},t),\hfill \end{array}\right.$$

(19)

where ${\mathcal{E}}_{sv}$ denotes the disturbance term caused by the error ${\epsilon }_{sv}$. By multiplying the first equation in (19) by $\tilde{u}$ and integrating it over $\mathrm{\Omega }$, we obtain

$${\int }_{\mathrm{\Omega }}\left[\mathcal{T}\left(t\right)\tilde{\psi }\tilde{u}{C}_A-\tilde{u}\Delta \tilde{u}+\tilde{u}R·\nabla \tilde{u}\right]d\mathit{x}={\int }_{\mathrm{\Omega }}\tilde{h}\tilde{u}d\mathit{x}+{\int }_{\mathrm{\Omega }}{\mathcal{E}}_{sv}\tilde{u}d\mathit{x},$$

(20)

where $C_A={\int }_0^1{\displaystyle \frac{\omega \left(\alpha \right)}{\Gamma (1-\alpha )}}\mathcal{A}\left(\alpha \right)d\alpha$. Noting that

$$-{\int }_{\mathrm{\Omega }}\tilde{u}\Delta \tilde{u}d\mathit{x}={\int }_{\mathrm{\Omega }}{|\nabla \tilde{u}|}^{2}d\mathit{x}-{\int }_{\partial \mathrm{\Omega }}\tilde{u}{\displaystyle \frac{\partial \tilde{u}}{\partial \mathbf{n}}}ds,$$

(21)

and

$${\int }_{\mathrm{\Omega }}\tilde{u}R·\nabla \tilde{u}d\mathit{x}={\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}R·\nabla \left({\tilde{u}}^2\right)d\mathit{x}={\displaystyle \frac{1}{2}}{\int }_{\partial \mathrm{\Omega }}{\tilde{u}}^{2}R·\mathbf{n}ds-{\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}(\nabla ·R){\tilde{u}}^{2}d\mathit{x},$$

(22)

we have

$$\mathcal{T}\left(t\right)C_A{\int }_{\mathrm{\Omega }}\tilde{\psi }\tilde{u}d\mathit{x}+{\int }_{\mathrm{\Omega }}{|\nabla \tilde{u}|}^{2}d\mathit{x}={\int }_{\mathrm{\Omega }}\tilde{h}\tilde{u}d\mathit{x}+{\int }_{\mathrm{\Omega }}{\mathcal{E}}_{sv}\tilde{u}d\mathit{x}.$$

(23)

There exists constants ${\delta }_1>0$ and ${\delta }_2>0$ such that

$$\begin{array}{c}\hfill \left|{\int }_{\mathrm{\Omega }}\tilde{h}\tilde{u}d\mathit{x}\right|\le {\displaystyle \frac{1}{2{\delta }_1}}\parallel \tilde{h}{\parallel }_{L^2\left(\mathrm{\Omega }\right)}^2+{\displaystyle \frac{{\delta }_1}{2}}{\parallel \tilde{u}\parallel }_{L^2\left(\mathrm{\Omega }\right)}^2,\\ \hfill \left|{\int }_{\mathrm{\Omega }}{\mathcal{E}}_{sv}\tilde{u}d\mathit{x}\right|\le {\displaystyle \frac{1}{2{\delta }_2}}{C}_{sv}^2+{\displaystyle \frac{{\delta }_2}{2}}{\parallel \tilde{u}\parallel }_{L^2\left(\mathrm{\Omega }\right)}^2.\end{array}$$

(24)

Then we can obtain

$$\mathcal{T}\left(t\right)C_A{\int }_{\mathrm{\Omega }}\tilde{\psi }\tilde{u}d\mathit{x}+{\int }_{\mathrm{\Omega }}|\nabla \tilde{u}{|}^{2}d\mathit{x}\le {\displaystyle \frac{1}{2{\delta }_1}}\parallel \tilde{h}{\parallel }_{L^2\left(\mathrm{\Omega }\right)}^2+{\displaystyle \frac{1}{2{\delta }_2}}{C}_{sv}^2+\left({\displaystyle \frac{{\delta }_1+{\delta }_2}{2}}\right){\parallel \tilde{u}\parallel }_{L^2\left(\mathrm{\Omega }\right)}^2+C_1{\mathcal{E}}_{\mathcal{B}}.$$

(25)

For the two terms on the left side of the Formula (25), we have

$$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}{|\nabla \tilde{u}|}^{2}d\mathit{x}& \ge {\displaystyle \frac{1}{C_P^2}}{\parallel \tilde{u}\parallel }_{L^2\left(\mathrm{\Omega }\right)}^2-C_b{\mathcal{E}}_{\mathcal{B}}^2,\hfill \\ \hfill \left|\mathcal{T}\left(t\right)C_A{\int }_{\mathrm{\Omega }}\tilde{\psi }\tilde{u}d\mathit{x}\right|& \le {\displaystyle \frac{|\mathcal{T}\left(t\right)C_A|}{2\gamma }}\parallel \tilde{\psi }{\parallel }_{L^2\left(\mathrm{\Omega }\right)}^2+{\displaystyle \frac{|\mathcal{T}\left(t\right)C_A|\gamma }{2}}{\parallel \tilde{u}\parallel }_{L^2\left(\mathrm{\Omega }\right)}^2.\hfill \end{array}$$

(26)

We define the energy functional as follows

$$E\left(t\right)={\displaystyle \frac{1}{2}}\left(\parallel \tilde{u}{\parallel }_{L^2\left(\mathrm{\Omega }\right)}^2+\lambda {\parallel \tilde{\psi }\parallel }_{L^2\left(\mathrm{\Omega }\right)}^2\right),$$

(27)

where λ is an undetermined constant. Combining the Formulae (25) and (26), we can arrive at

$$E\left(t\right)\le {\displaystyle \frac{1}{4\alpha {\delta }_1}}{\parallel \tilde{h}\parallel }_{L^2\left(\mathrm{\Omega }\right)}^2+{\displaystyle \frac{1}{4\alpha {\delta }_2}}{C}_{sv}^2+{\displaystyle \frac{C_B}{2\alpha }}{\mathcal{E}}_{\mathcal{B}},$$

(28)

where $\alpha ={\displaystyle \frac{1}{C_P^2}}-{\displaystyle \frac{{\delta }_1+{\delta }_2}{2}}-{\displaystyle \frac{|\mathcal{T}\left(t\right)C_A|\gamma }{2}}>0$. According to the definition of the energy functional, it can be inferred that

$$\parallel \tilde{u}{\parallel }_{L^2\left(\mathrm{\Omega }\right)}\le \sqrt{2E\left(t\right)},{\parallel \tilde{\psi }\parallel }_{L^2\left(\mathrm{\Omega }\right)}\le \sqrt{{\displaystyle \frac{2E\left(t\right)}{\lambda }}}.$$

(29)

Then we have

$$\parallel \tilde{u}{\parallel }_{L^2\left(\mathrm{\Omega }\right)}+{\parallel \tilde{\psi }\parallel }_{L^2\left(\mathrm{\Omega }\right)}\le \left(1+{\displaystyle \frac{1}{\sqrt{\lambda }}}\right)\sqrt{2E\left(t\right)}.$$

(30)

Based on the error caused by the initial conditions, we complete the proof. □

3. Results

In this section, several numerical experiments are studied to illustrate the performance of the proposed method. To assess the capability of the SVPINN method, the relative $L^2$ error is formulated as

$$\parallel u_p{-u\parallel }_{L^2}=\frac{\sqrt{{\displaystyle \sum _{i=1}^N}{|u_p^i-u^i|}^2}}{\sqrt{{\displaystyle \sum _{i=1}^N}{\left|u^i\right|}^2}},$$

(31)

where $u_p$ denotes the predicted solution. For convenience, we define

$$\parallel D_t^{\omega \left(\alpha \right)}\parallel =\parallel \mathcal{T}(\mathit{x},t;\vartheta )\psi (\mathit{x},t;\vartheta ){\int }_0^1{\displaystyle \frac{\omega \left(\alpha \right)}{\Gamma (1-\alpha )}}\mathcal{A}\left(\alpha \right)d\alpha -D_t^{\omega \left(\alpha \right)}{u(\mathit{x},t)\parallel }_{L^2},$$

(32)

and $\parallel u\parallel ={\parallel u(\mathit{x},t;\vartheta )-u(\mathit{x},t)\parallel }_{L^2}$.

In the absence of a specific statement, the network consists of 4 hidden layers and 10 neurons on each hidden layer, the activation function is the tanh function, and the parameters $N_u$ and $N_f$ are set to 1000 and 2000, respectively. The test data are 10,000 points randomly selected from the solution domain using the Latin Hypercube Sampling strategy. We choose the L-BFGS optimizer to update the trainable parameter $\vartheta$.

Remark 3.

The L-BFGS automatically determines the optimal step size for each iteration during the training process, so there is no need to set a learning rate. And its convergence criterion is that the gradient norm of the iteration point or the change in adjacent objective function values is less than the preset threshold.

The analytical solution for the problem (1)–(3) is as follows

$$u(\mathit{x},t)=t^2+sin({\displaystyle \frac{1}{d}}\sum _{i=1}^d{x}_i).$$

(33)

Given $\omega \left(\alpha \right)=\Gamma (3-\alpha )$, the boundary condition $\mathcal{B}(\mathit{x},t)$, initial condition $\mathcal{I}(\mathit{x},t)$, and source term $h(\mathit{x},t)$ are given by the exact solution. We compare the SVPINN with the PINN based on the FBN-$\theta$ scheme [43,45,46,47] (PINN-FBN) and the PINN based on the WSGD operator [48,49] (PINN-WSGD). Both methods approximate the distributed-order derivative by discrete schemes and then use the PINN to solve the problem (1)–(3). The structure of the two discrete schemes and parameter settings are presented in Appendix A.

3.1. Feasibility Analysis

In this example, we aim to adopt a function approximation case to validate the feasibility of the proposed variable separation method for the kernel function. Consider the following function:

$$U(x,y,z)={(x-y)}^z,x\in (0,1),0\le y\le x,z\in (0,1).$$

(34)

For this function, we decompose it as follows

$${(x-y)}^z=\mathcal{T}\left(x\right)\mathcal{N}\left(y\right)\mathcal{A}\left(z\right).$$

(35)

where $\mathcal{N}\left(y\right)=y$ and $\mathcal{A}\left(z\right)=z$. We construct a network $\mathcal{T}(x;\vartheta )$ to predict the basis function $\mathcal{T}\left(x\right)$. Then the loss function is formulated as

$$\begin{array}{c}\hfill \mathcal{L}\left(\vartheta \right)={\displaystyle \frac{1}{N_f}}\sum _{i=1}^{N_f}|U(x_f^i,y_f^i,z_f^i)-\mathcal{T}{((x_f^i;\vartheta )\mathcal{N}\left(y_f^i\right)\mathcal{A}\left(z_f^i\right)|}^{ 2}.\end{array}$$

(36)

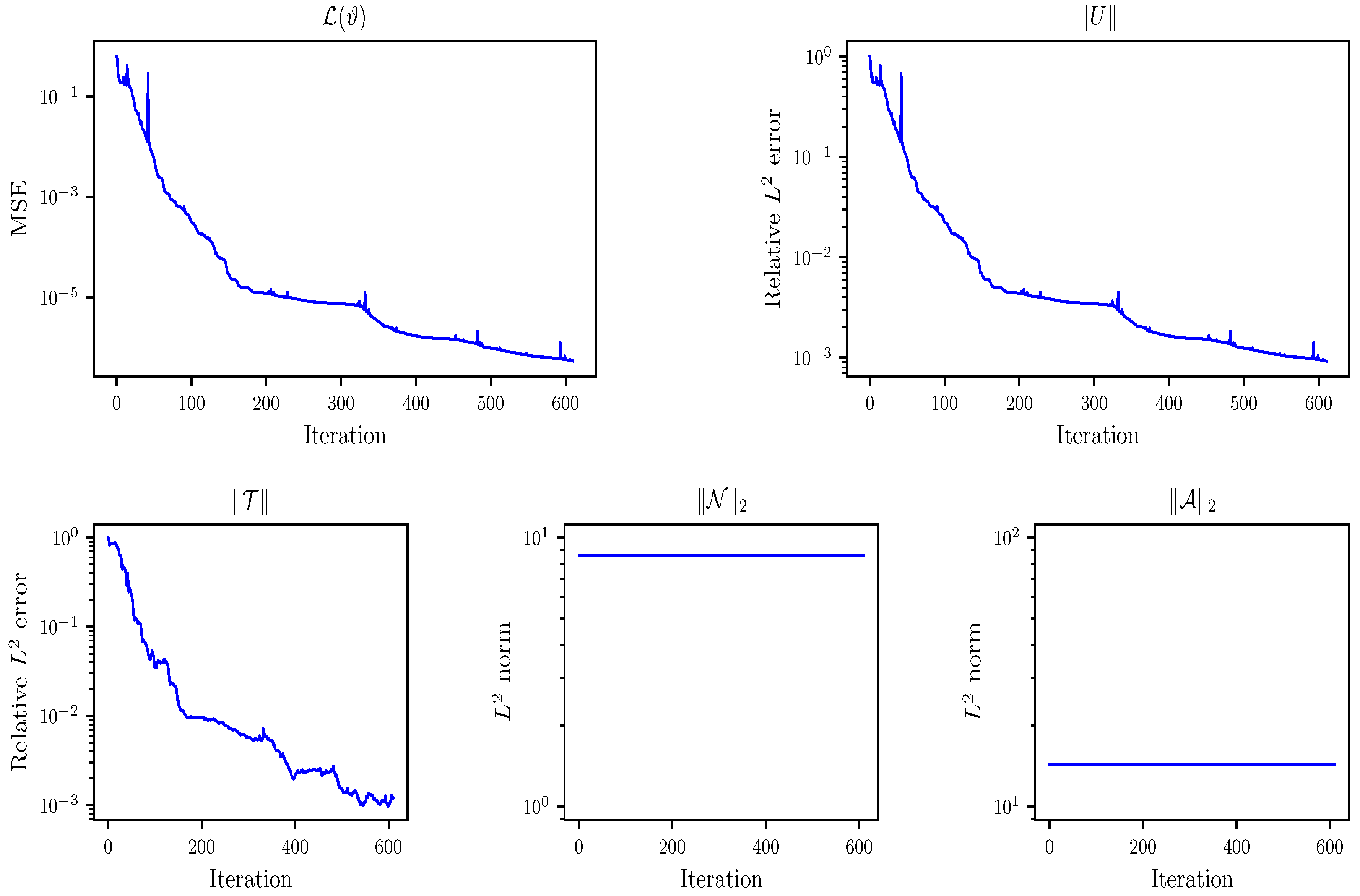
The history of the loss function $\mathcal{L}\left(\vartheta \right)$ and the relative $L^2$ error $\parallel U\parallel$ during the training process is presented in Figure 1. From the decreasing trend of the loss function and the error, the proposed method of decomposing the kernel function into three basis functions is validated as feasible. It also illustrates the stability of the method during the training process. Moreover, we also display the dynamic change in the relative error of the basis function $\mathcal{T}\left(x\right)$ and the $L^2$ norm of the basis functions $\mathcal{N}\left(y\right)$ and $\mathcal{A}\left(z\right)$ during the training process in Figure 1. It can be observed from the figure that the network $\mathcal{T}(x;\vartheta )$ provides an ideal level of prediction accuracy. Since the basis functions $\mathcal{N}\left(y\right)$ and $\mathcal{A}\left(z\right)$ are only related to y and z, respectively, their norms remain fixed during the training process. Based on the above analysis, it can be demonstrated that our proposed neural network-based variable separation method for the kernel function is reasonable.

3.2. 2D Problem

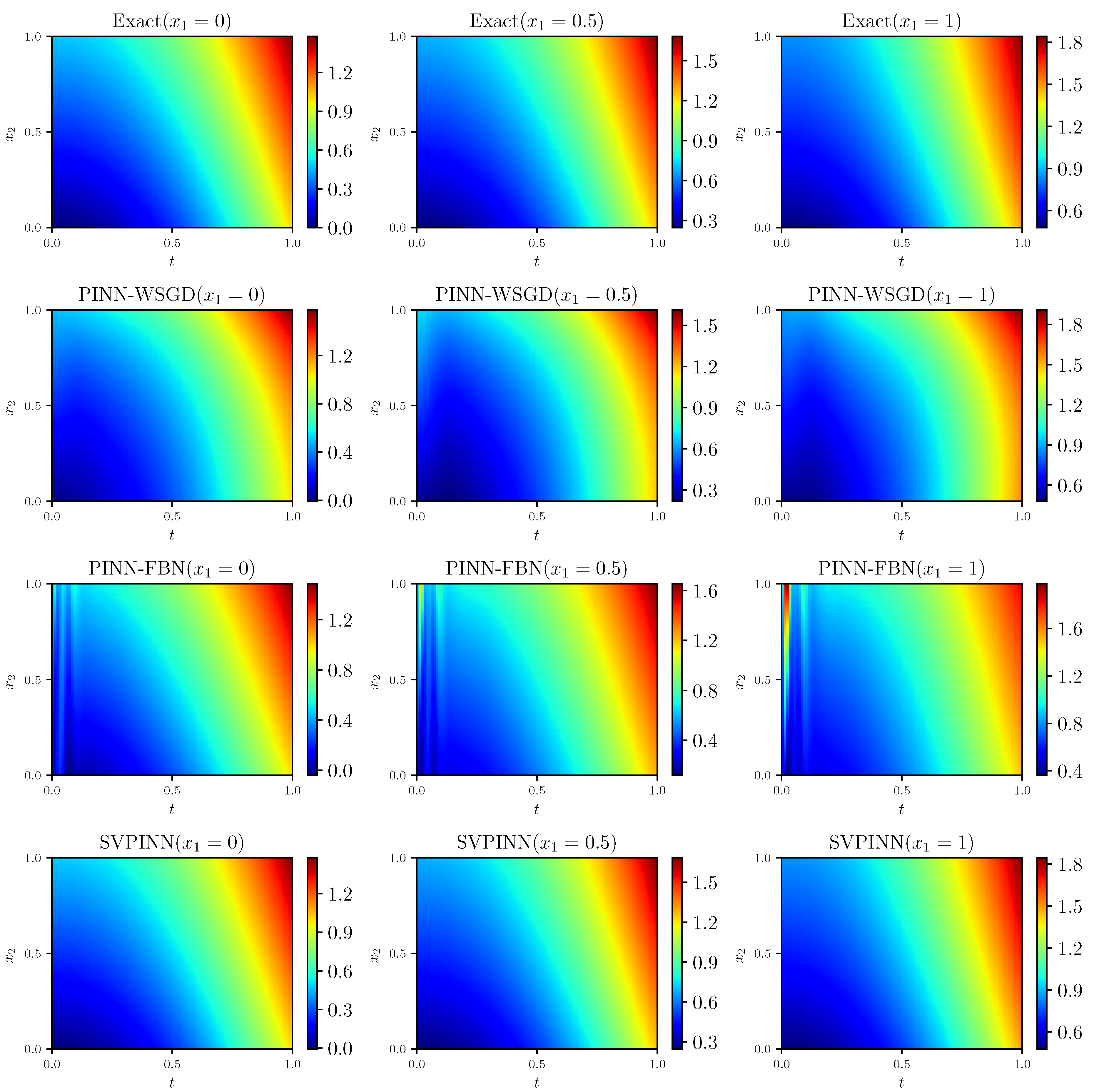
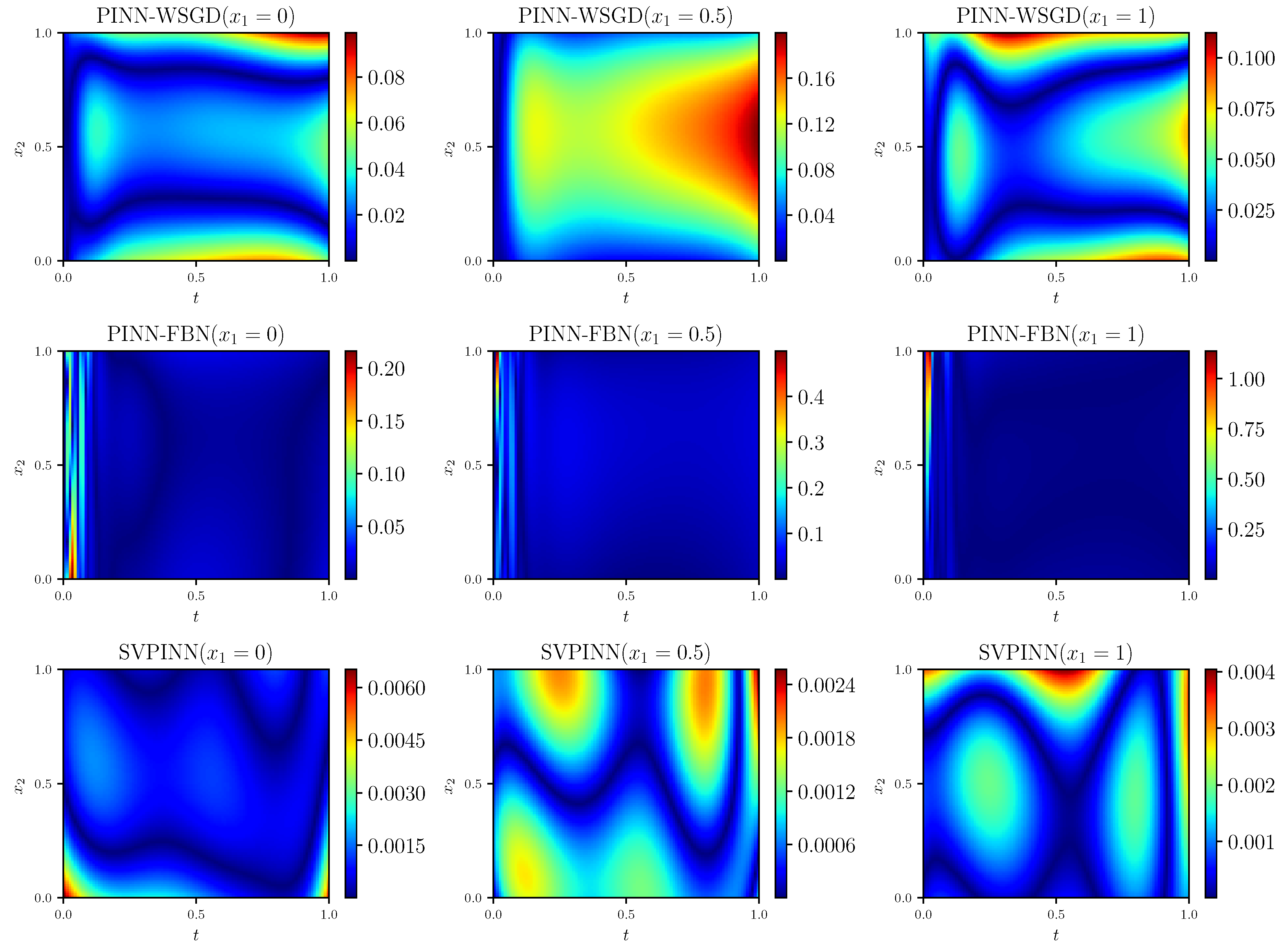
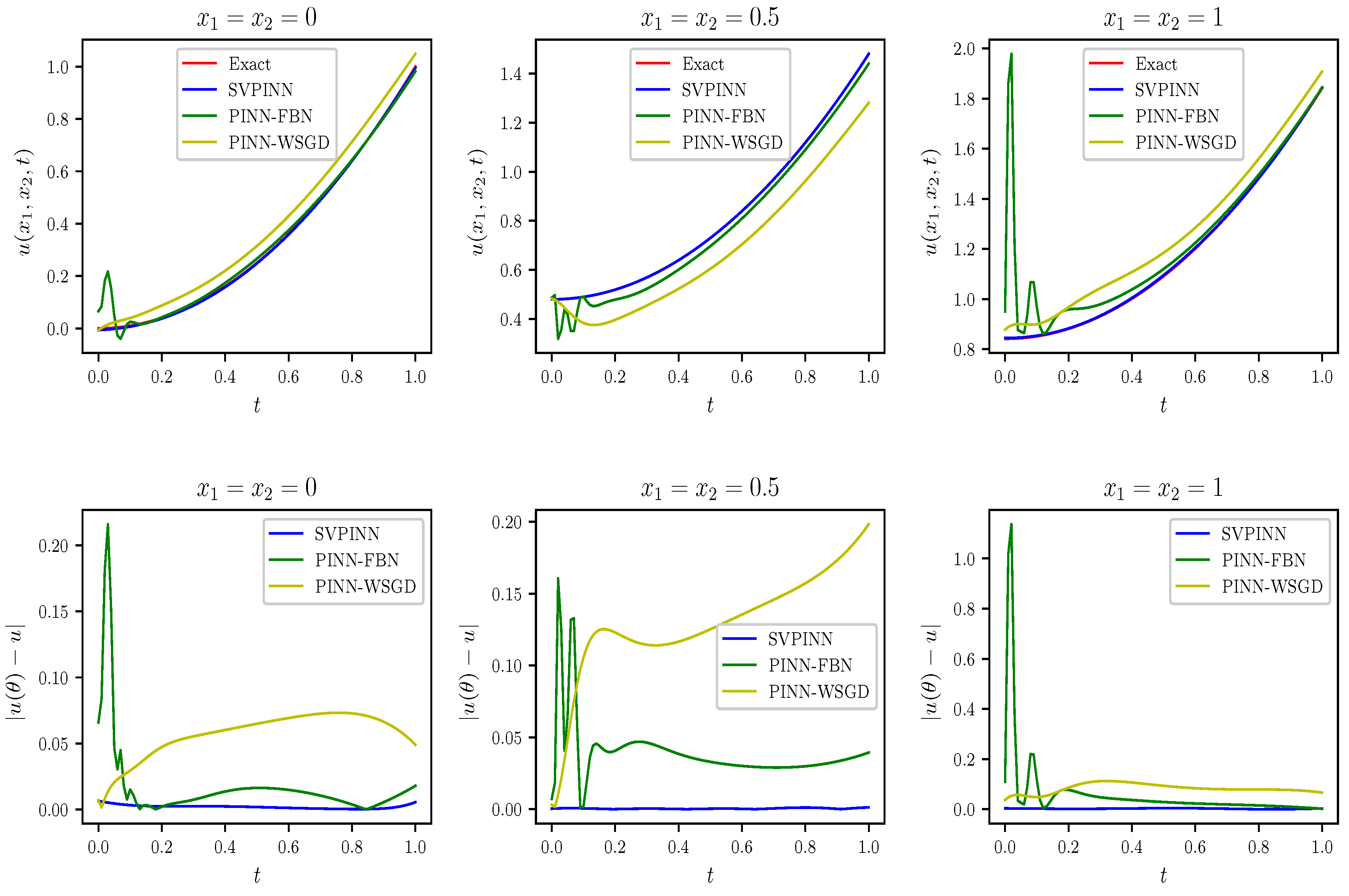
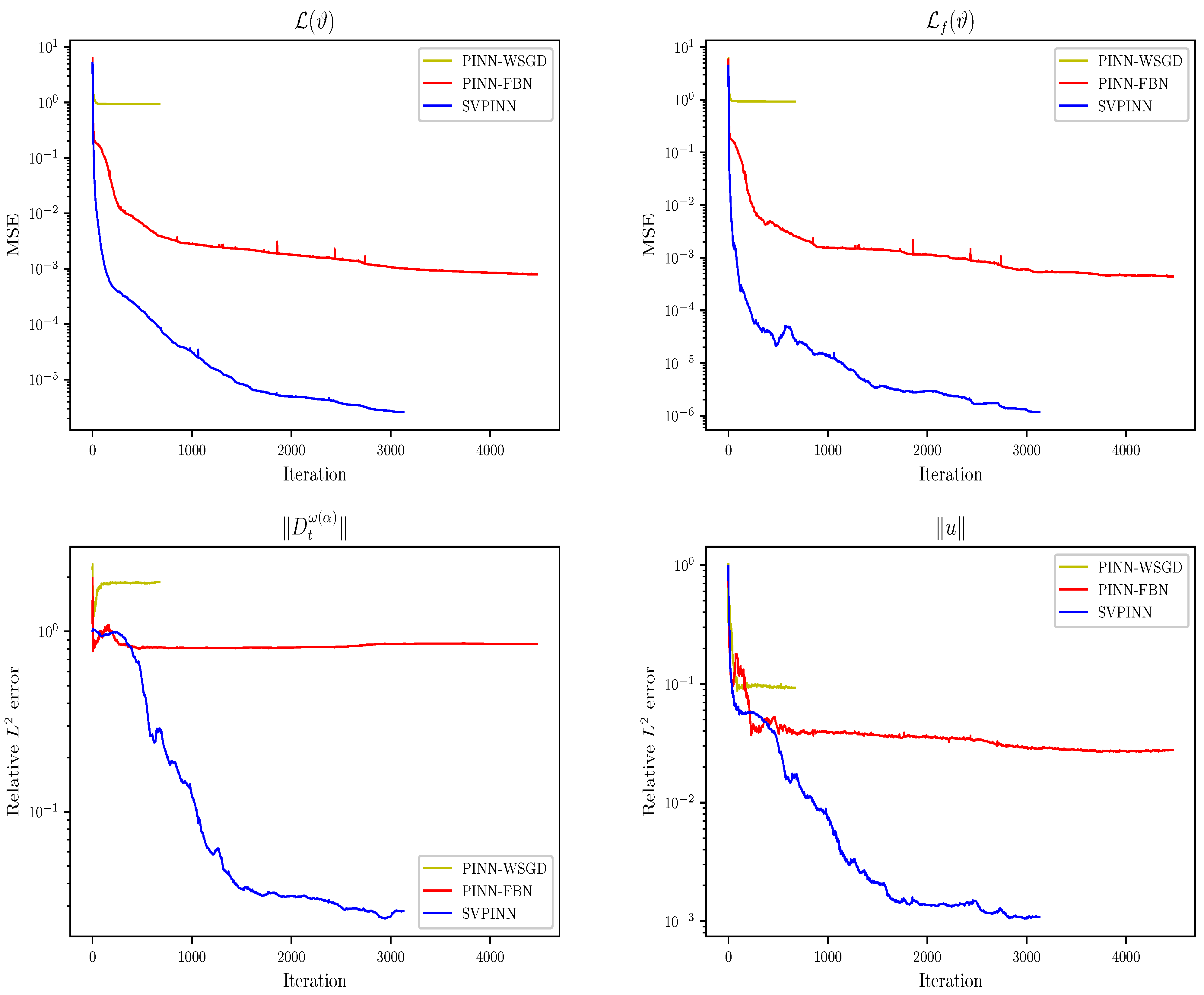
For this example, we set $\mathrm{\Omega }={(0,1)}^2$ and $\tau =(0,1]$. Figure 2 displays the solutions predicted by the SVPINN, PINN-FBN, and PINN-WSGD methods. Moreover, the corresponding absolute error between the predicted and exact solutions is depicted in Figure 3. It reveals that the proposed method can obtain better prediction accuracy. Figure 4 provides a more explicit comparison between the SVPINN, PINN-FBN, and PINN-WSGD, illustrating that the proposed SVPINN is closer to the exact solution. 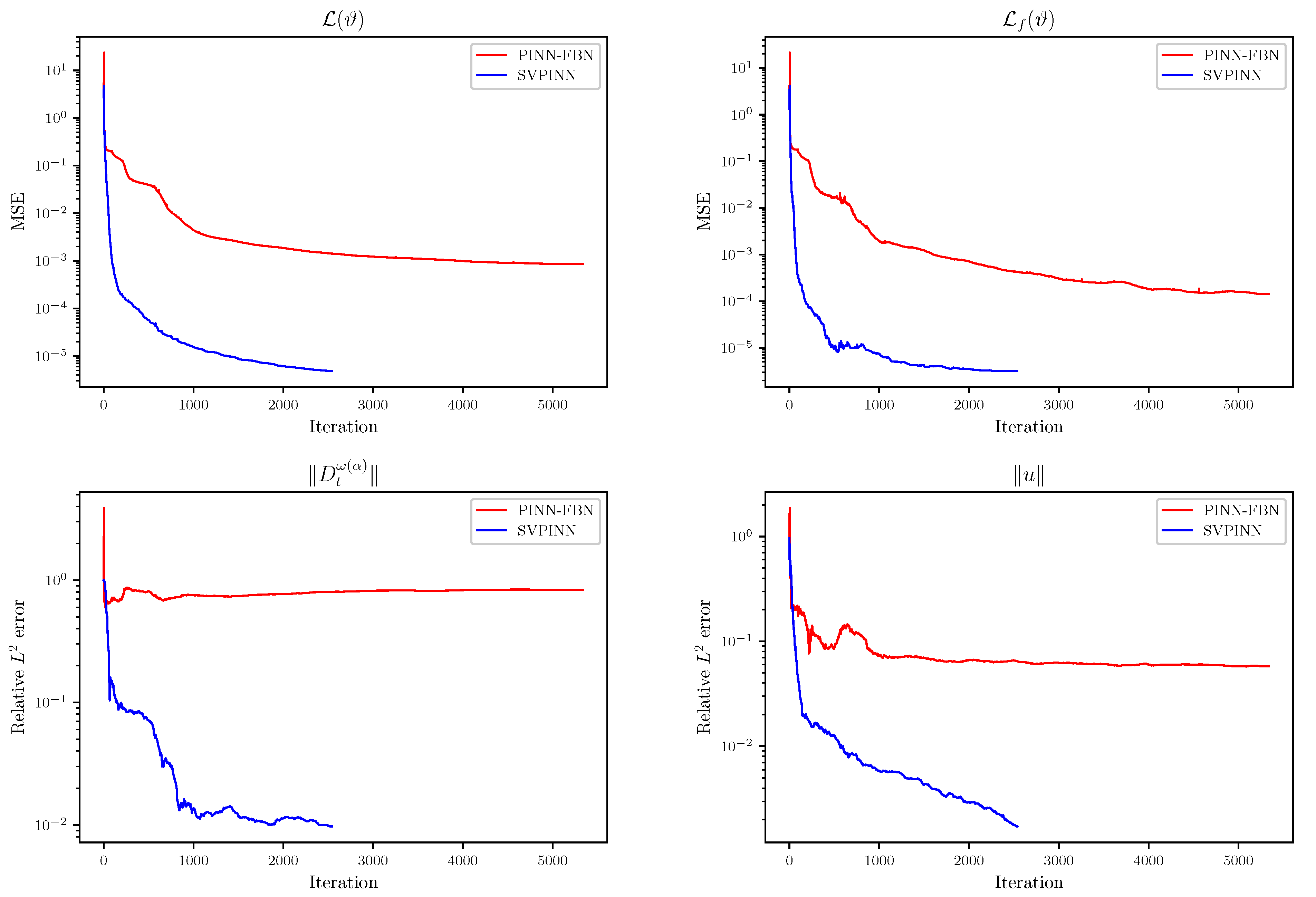Figure 5 presents a comparative analysis of the SVPINN, PINN-WSGD, and PINN-FBN methods, which depicts the dynamic changes in the total function $\mathcal{L}\left(\vartheta \right)$, loss term ${\mathcal{L}}_f\left(\vartheta \right)$, and relative errors. This figure demonstrates that the PINN-WSGD has poor convergence performance in solving FPDE (1), making it difficult to effectively reduce errors and achieve efficient and accurate prediction. Although the PINN-FBN can solve the problem (1), its convergence speed is relatively slow during the training process, and more iterations are required to reach the same level of accuracy. Compared to the PINN-FBN, the SVPINN exhibits better performance and faster convergence speed. It can achieve a lower mean square error with fewer iterations and achieve a more ideal prediction result.

In

Table 1. The relative $L^2$ errors and computational cost of the PINN-WSGD, the PINN-FBN, and the SVPINN with different network structures for Section 3.2.

Layer	Method		Neuron
			10	20	40	60	80
2	SVPINN	Relative $L^2$ error	$1.183$ × ${10}^{-2}$	$8.324$ × ${10}^{-4}$	$6.019$ × ${10}^{-4}$	$1.589$ × ${10}^{-2}$	$1.081$ × ${10}^{-3}$
		Time (s)	9	7	10	58	15
		Memory (MB)	215	223	225	227	223
	PINN-WSGD	Relative $L^2$ error	$1.012$ × ${10}^{-1}$	$9.289$ × ${10}^{-2}$	$9.460$ × ${10}^{-2}$	$9.152$ × ${10}^{-2}$	$9.227$ × ${10}^{-2}$
		Time (s)	5	7	10	17	13
		Memory (MB)	236	243	241	244	244
	PINN-FBN	Relative $L^2$ error	$5.037$ × ${10}^{-2}$	$4.229$ × ${10}^{-2}$	$4.556$ × ${10}^{-2}$	$3.852$ × ${10}^{-2}$	$3.613$ × ${10}^{-2}$
		Time (s)	27	84	77	127	120
		Memory (MB)	238	245	251	242	267
4	SVPINN	Relative $L^2$ error	$1.066$ × ${10}^{-3}$	$6.724$ × ${10}^{-4}$	$1.614$ × ${10}^{-3}$	$1.661$ × ${10}^{-3}$	$1.680$ × ${10}^{-3}$
		Time (s)	13	12	9	18	20
		Memory (MB)	228	240	249	267	239
	PINN-WSGD	Relative $L^2$ error	$9.416$ × ${10}^{-2}$	$9.333$ × ${10}^{-2}$	$9.239$ × ${10}^{-2}$	$9.405$ × ${10}^{-2}$	$9.377$ × ${10}^{-2}$
		Time (s)	8	10	17	16	21
		Memory (MB)	247	255	267	281	301
	PINN-FBN	Relative $L^2$ error	$4.943$ × ${10}^{-2}$	$4.802$ × ${10}^{-2}$	$3.614$ × ${10}^{-2}$	$3.715$ × ${10}^{-2}$	$3.616$ × ${10}^{-2}$
		Time (s)	42	68	172	211	193
		Memory (MB)	251	260	273	263	302
6	SVPINN	Relative $L^2$ error	$1.567$ × ${10}^{-3}$	$1.171$ × ${10}^{-3}$	$9.085$ × ${10}^{-4}$	$1.549$ × ${10}^{-3}$	$9.524$ × ${10}^{-4}$
		Time (s)	19	23	37	33	59
		Memory (MB)	252	245	276	295	329
	PINN-WSGD	Relative $L^2$ error	$9.548$ × ${10}^{-2}$	$9.744$ × ${10}^{-2}$	$9.354$ × ${10}^{-2}$	$9.307$ × ${10}^{-2}$	$9.279$ × ${10}^{-2}$
		Time (s)	14	10	23	18	50
		Memory (MB)	260	271	289	270	331
	PINN-FBN	Relative $L^2$ error	$4.383$ × ${10}^{-2}$	$3.999$ × ${10}^{-2}$	$4.213$ × ${10}^{-2}$	$3.790$ × ${10}^{-2}$	$3.750$ × ${10}^{-2}$
		Time (s)	75	99	160	185	476
		Memory (MB)	264	274	265	313	275
8	SVPINN	Relative $L^2$ error	$8.506$ × ${10}^{-3}$	$1.223$ × ${10}^{-3}$	$1.133$ × ${10}^{-3}$	$1.490$ × ${10}^{-3}$	$1.190$ × ${10}^{-3}$
		Time (s)	28	21	21	41	50
		Memory (MB)	267	274	306	327	357
	PINN-WSGD	Relative $L^2$ error	$9.927$ × ${10}^{-2}$	$9.321$ × ${10}^{-2}$	$9.478$ × ${10}^{-2}$	$9.429$ × ${10}^{-2}$	$9.420$ × ${10}^{-2}$
		Time (s)	14	19	27	40	81
		Memory (MB)	273	275	310	287	367
	PINN-FBN	Relative $L^2$ error	$4.370$ × ${10}^{-2}$	$6.401$ × ${10}^{-2}$	$4.186$ × ${10}^{-2}$	$4.540$ × ${10}^{-2}$	$5.264$ × ${10}^{-2}$
		Time (s)	91	52	89	246	267
		Memory (MB)	283	289	315	351	371

and

Table 2. The relative $L^2$ errors and computational cost of the PINN-WSGD, the PINN-FBN, and the SVPINN with different numbers of training points for Section 3.2.

${\mathit{N}}_{\mathit{f}}$	Method		${\mathit{N}}_{\mathit{u}}$
			200	400	600	800	1000
2000	SVPINN	Relative $L^2$ error	$7.109$ × ${10}^{-4}$	$1.151$ × ${10}^{-3}$	$8.220$ × ${10}^{-4}$	$8.676$ × ${10}^{-4}$	$1.066$ × ${10}^{-3}$
		Time (s)	16	12	9	14	13
		Memory (MB)	233	227	235	235	228
	PINN-WSGD	Relative $L^2$ error	$9.219$ × ${10}^{-2}$	$9.164$ × ${10}^{-2}$	$9.402$ × ${10}^{-2}$	$9.456$ × ${10}^{-2}$	$9.416$ × ${10}^{-2}$
		Time (s)	9	11	10	7	8
		Memory (MB)	250	248	254	252	247
	PINN-FBN	Relative $L^2$ error	$5.580$ × ${10}^{-2}$	$5.348$ × ${10}^{-2}$	$3.912$ × ${10}^{-2}$	$5.917$ × ${10}^{-2}$	$4.943$ × ${10}^{-2}$
		Time (s)	80	16	94	43	42
		Memory (MB)	255	255	257	256	251
3000	SVPINN	Relative $L^2$ error	$9.348$ × ${10}^{-4}$	$7.352$ × ${10}^{-4}$	$1.278$ × ${10}^{-3}$	$6.464$ × ${10}^{-4}$	$9.381$ × ${10}^{-4}$
		Time (s)	22	21	18	20	20
		Memory (MB)	232	232	236	237	238
	PINN-WSGD	Relative $L^2$ error	$9.073$ × ${10}^{-2}$	$9.350$ × ${10}^{-2}$	$9.299$ × ${10}^{-2}$	$9.508$ × ${10}^{-2}$	$9.408$ × ${10}^{-2}$
		Time (s)	16	20	20	18	14
		Memory (MB)	295	293	294	287	294
	PINN-FBN	Relative $L^2$ error	$4.496$ × ${10}^{-2}$	$5.193$ × ${10}^{-2}$	$3.893$ × ${10}^{-2}$	$7.293$ × ${10}^{-2}$	$5.390$ × ${10}^{-2}$
		Time (s)	37	36	108	40	48
		Memory (MB)	289	297	296	295	295
4000	SVPINN	Relative $L^2$ error	$1.223$ × ${10}^{-3}$	$1.170$ × ${10}^{-3}$	$1.574$ × ${10}^{-3}$	$9.621$ × ${10}^{-4}$	$1.347$ × ${10}^{-3}$
		Time (s)	17	17	19	24	15
		Memory (MB)	239	238	239	239	240
	PINN-WSGD	Relative $L^2$ error	$9.375$ × ${10}^{-2}$	$9.644$ × ${10}^{-2}$	$1.000$ × ${10}^{-1}$	$1.039$ × ${10}^{-1}$	$9.601$ × ${10}^{-2}$
		Time (s)	32	31	32	18	28
		Memory (MB)	348	348	349	350	351
	PINN-FBN	Relative $L^2$ error	$5.817$ × ${10}^{-2}$	$4.344$ × ${10}^{-2}$	$5.467$ × ${10}^{-2}$	$4.126$ × ${10}^{-2}$	$4.888$ × ${10}^{-2}$
		Time (s)	130	158	58	292	147
		Memory (MB)	351	351	351	353	352
5000	SVPINN	Relative $L^2$ error	$1.615$ × ${10}^{-3}$	$9.707$ × ${10}^{-4}$	$1.423$ × ${10}^{-3}$	$1.093$ × ${10}^{-3}$	$6.616$ × ${10}^{-4}$
		Time (s)	25	22	18	23	29
		Memory (MB)	238	240	236	229	238
	PINN-WSGD	Relative $L^2$ error	$9.063$ × ${10}^{-2}$	$9.507$ × ${10}^{-2}$	$9.357$ × ${10}^{-2}$	$9.429$ × ${10}^{-2}$	$9.482$ × ${10}^{-2}$
		Time (s)	36	42	40	58	51
		Memory (MB)	417	418	418	417	415
	PINN-FBN	Relative $L^2$ error	$6.481$ × ${10}^{-2}$	$4.208$ × ${10}^{-2}$	$5.259$ × ${10}^{-2}$	$4.856$ × ${10}^{-2}$	$4.721$ × ${10}^{-2}$
		Time (s)	281	207	132	129	148
		Memory (MB)	421	422	416	421	421

, we present our ablation study on the key components of the three PINN methods, such as the network structure and number of training points, and quantitatively analyze their impact on the accuracy, convergence speed, and generalization ability of the model by adjusting parameters. The training time represents the CPU time. From Table 1, it can be found that our proposed method significantly outperforms the PINN-FBN and PINN-WSGD methods in prediction accuracy, while maintaining comparable memory usage. In terms of convergence speed, the SVPINN has the potential to accelerate convergence under appropriate network structures. The PINN-WSGD has a short computation time but fails to achieve effective convergence, while the PINN-FBN generally takes a long time to converge.

3.3. Irregular Domain

To systematically evaluate the adaptability and solving capability of the SVPINN in complex geometric scenes

$$\mathrm{\Omega }=\{(x,y)\in {\mathbb{R}}^d:x=rcos\left(\theta \right),y=rsin\left(\theta \right),\theta \in [0,2\pi ],x^2+y^2\le r^2\},$$

(37)

we select five irregular domains as the research object. The parametric equations of these domains are as follows

$$\begin{array}{cc}\hfill & r_1=0.6-0.2cos\left(7\theta \right),\hfill \\ \hfill & r_2=1+tanh(cos\left(2.5\theta \right))sin\left(5.5\theta \right),\hfill \\ \hfill & r_3=0.5\sqrt{sin\left(5\theta \right)+\sqrt{1.1-{sin}^3\left(5\theta \right)}},\hfill \\ \hfill & r_4=1.5\sqrt{sin\left(6\theta \right)+\sqrt{1.1-{sin}^3\left(6\theta \right)}},\hfill \\ \hfill & r_5=2\sqrt{sin\left(8\theta \right)+\sqrt{1.1-{sin}^3\left(8\theta \right)}}.\hfill \end{array}$$

(38)

The time interval is the same as that in Section 3.2.

Table 3. The relative $L^2$ errors and computational cost of the MoPINN, the PINN-FBN, and the SVPINN with different solution domains for Section 3.3.

Method		${\mathit{r}}_1$	${\mathit{r}}_2$	${\mathit{r}}_3$	${\mathit{r}}_4$	${\mathit{r}}_5$
SVPINN	Relative $L^2$ error	$1.834$ × ${10}^{-3}$	$1.673$ × ${10}^{-3}$	$1.700$ × ${10}^{-3}$	$6.722$ × ${10}^{-4}$	$2.256$ × ${10}^{-3}$
	Time (s)	9	10	10	21	22
	Memory (MB)	229	230	237	231	236
PINN-FBN	Relative $L^2$ error	$1.978$ × ${10}^{-2}$	$8.121$ × ${10}^{-2}$	$1.145$ × ${10}^{-2}$	$1.381$ × ${10}^{-1}$	$3.235$ × ${10}^{-1}$
	Time (s)	69	54	42	45	77
	Memory (MB)	258	251	256	256	250
MoPINN	Relative $L^2$ error	$1.140$ × ${10}^{-1}$	$1.527$ × ${10}^{-1}$	$5.161$ × ${10}^{-2}$	$3.650$ × ${10}^{-1}$	$4.154$ × ${10}^{-1}$
	Time (s)	10	22	25	20	39
	Memory (MB)	263	262	263	270	256

reports the relative $L^2$ error and calculation cost provided by the SVPINN, the MoPINN [43], and the PINN-FBN. From the table, it can be seen that the relative error of our proposed method always remains between the levels of ${10}^{-4}$ and ${10}^{-3}$, which are one and two orders of magnitude higher than the prediction accuracy of the other two methods. The results demonstrate that our proposed method can better predict the exact solution. 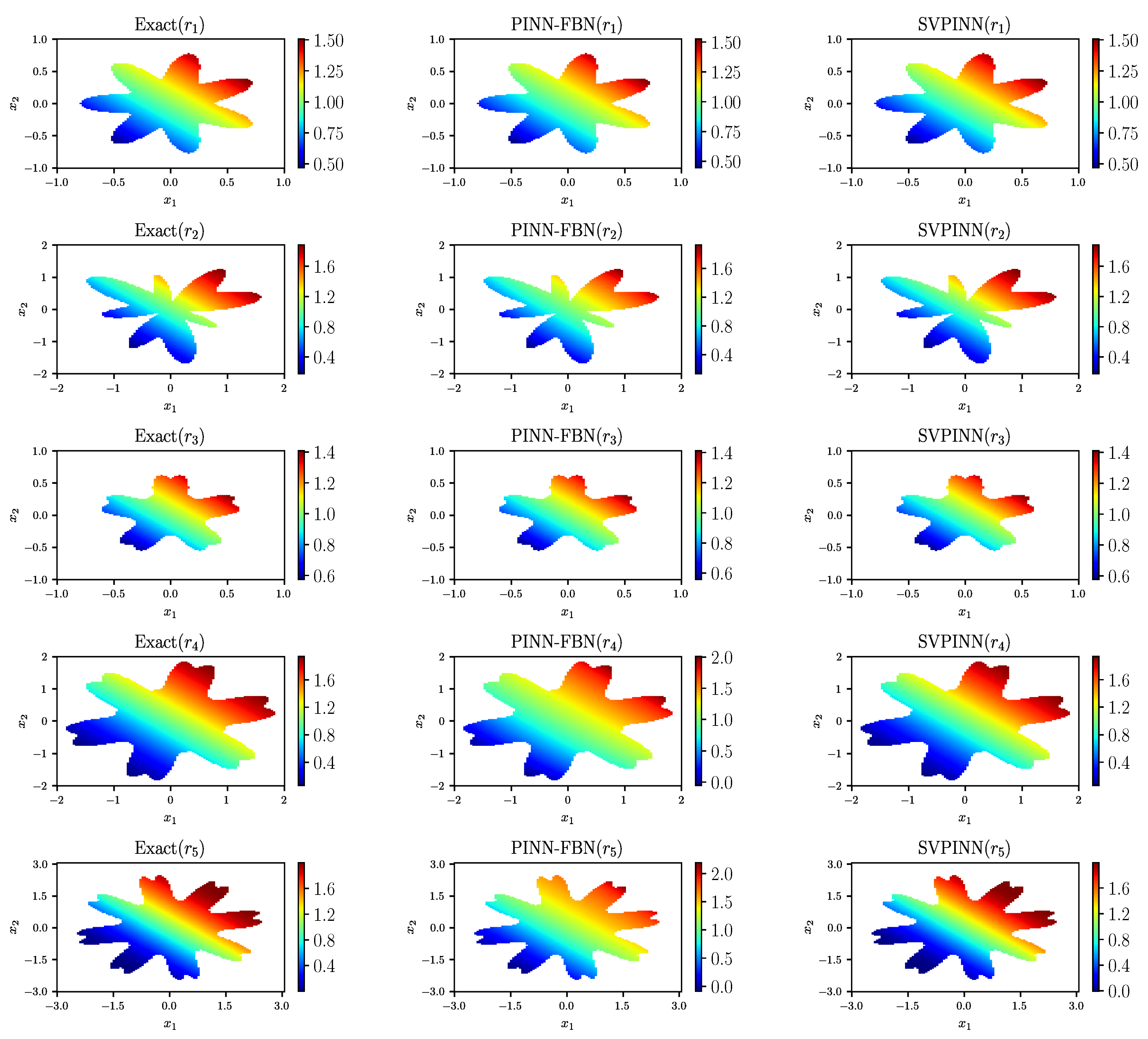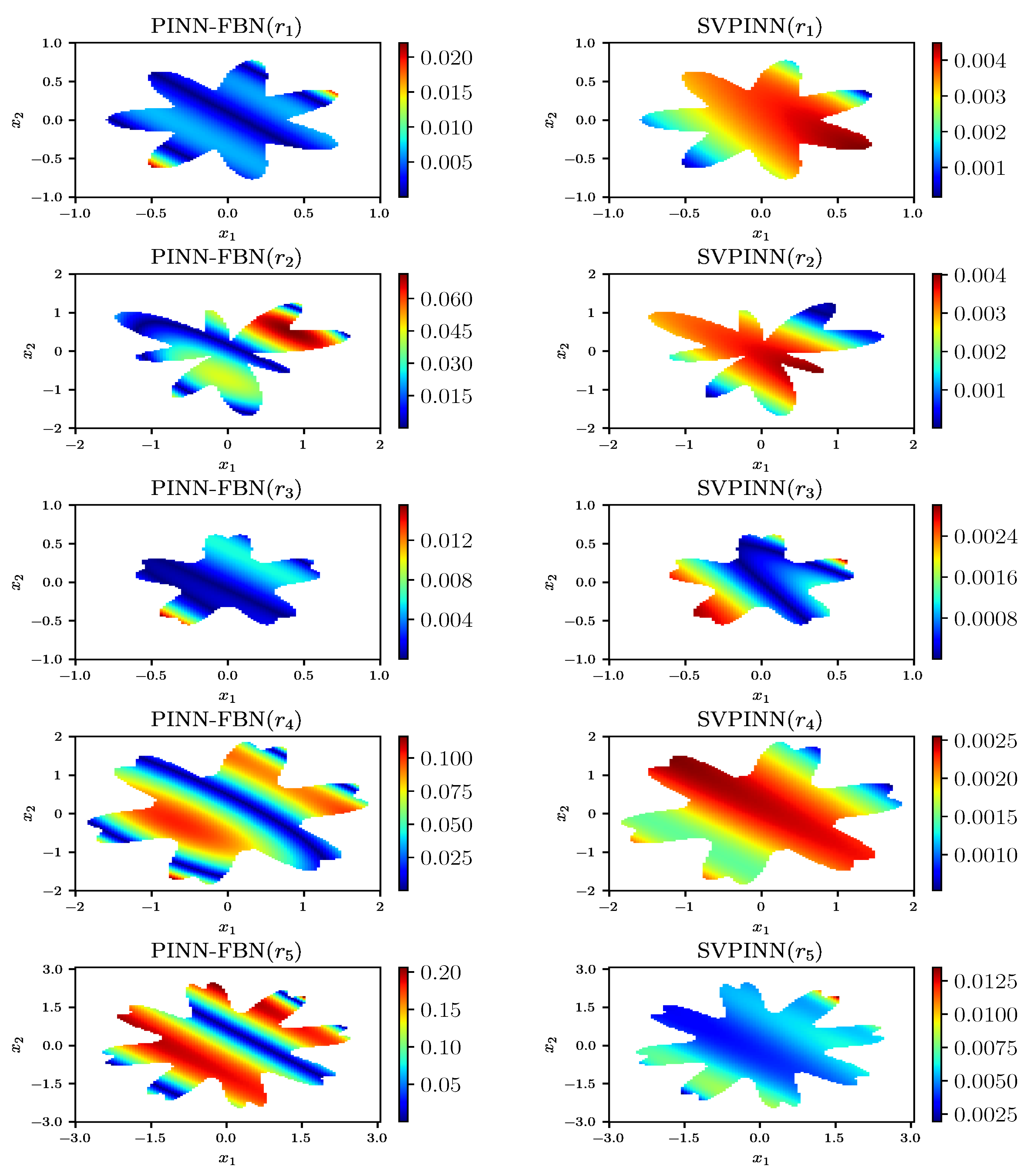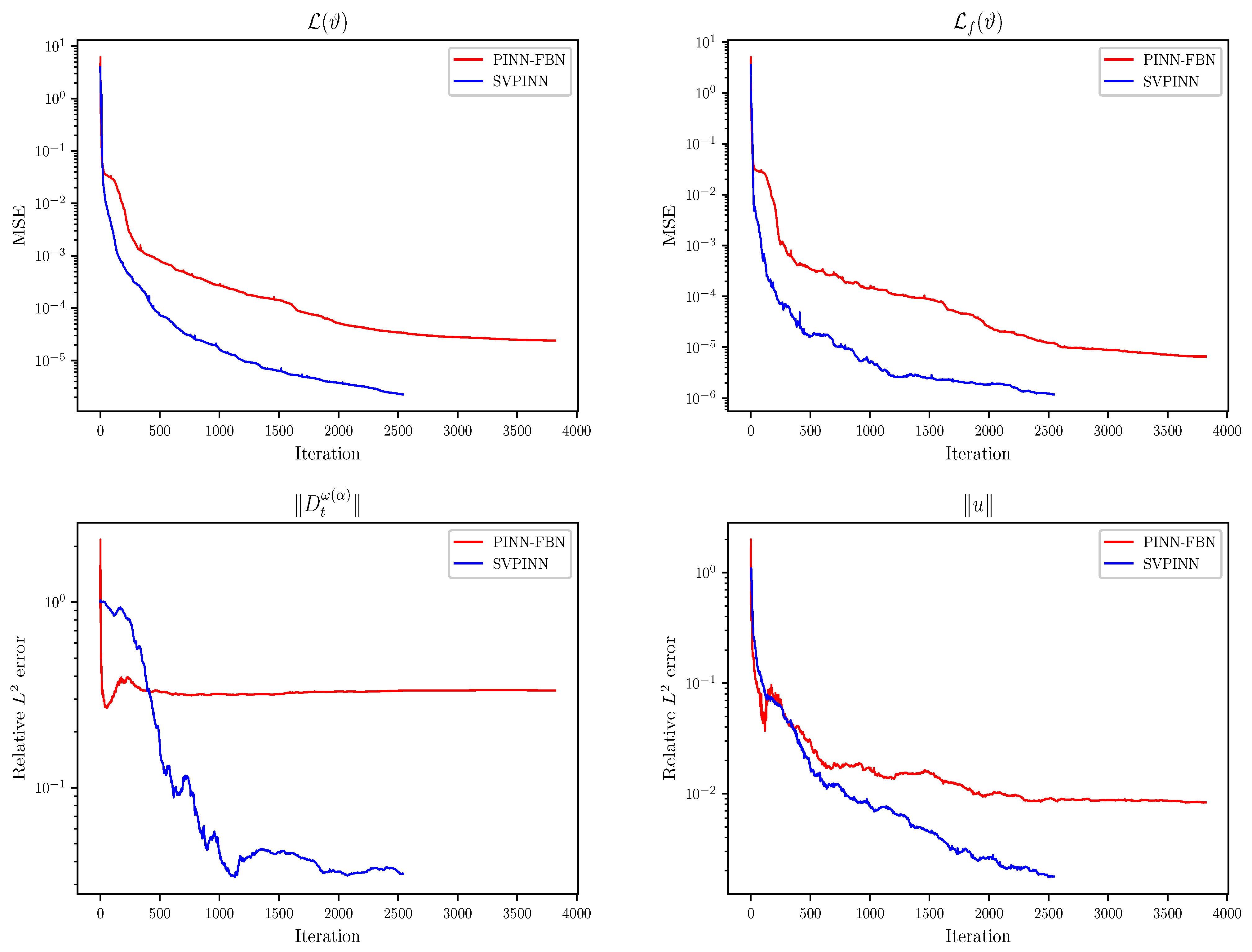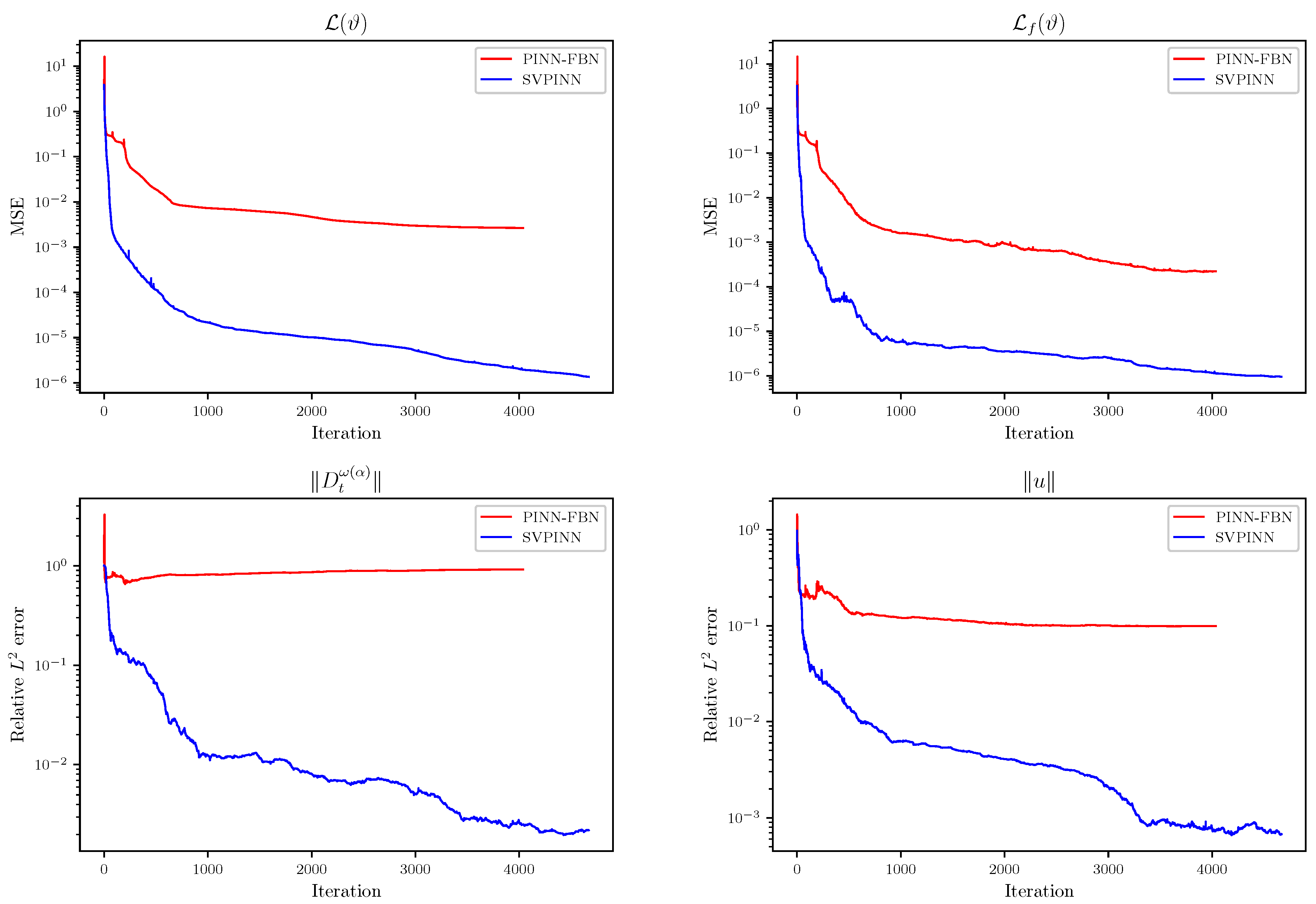Figure 6 presents the predictions given by the proposed SVPINN and the PINN-FBN, and Figure 7 displays the distribution of the absolute error between the exact solution and the prediction. From the figure, it can be observed that the prediction results of our proposed method have higher consistency with the exact solution, which intuitively verifies the effectiveness of the proposed SVPINN in solving the distributed-order advection–diffusion equation with irregular domains. To evaluate the feasibility of the SVPINN by monitoring the changes in the loss function during the training process and demonstrate physical consistency via a quantitative analysis of the residual equation and the errors, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 display the decreasing trend of the loss function $\mathcal{L}\left(\vartheta \right)$, the loss term ${\mathcal{L}}_f\left(\vartheta \right)$, and the relative errors of the distributed-order derivative $D_t^{\omega \left(\alpha \right)}$ and the exact solution $u(\mathit{x},t)$ in the process of optimizing the network. In general, the SVPINN has more advantages in the optimization effect. It not only performs better than the PINN-FBN in reducing the loss, but also converges faster and can reach a lower error level. Moreover, we also test the impact of network parameters, the number of collocation points, and the number of the initial and boundary points on the performance of the SVPINN in

Table 4. The relative $L^2$ errors and computational cost of the PINN-FBN and the SVPINN with different numbers of neurons and different irregular domains for Section 3.3.

Neuron	Method		${\mathit{r}}_1$	${\mathit{r}}_2$	${\mathit{r}}_3$	${\mathit{r}}_4$	${\mathit{r}}_5$
20	SVPINN	Relative $L^2$ error	$1.438$ × ${10}^{-3}$	$1.451$ × ${10}^{-3}$	$1.437$ × ${10}^{-3}$	$1.669$ × ${10}^{-3}$	$1.221$ × ${10}^{-3}$
		Time (s)	7	12	7	16	16
		Memory (MB)	238	240	238	241	232
	PINN-FBN	Relative $L^2$ error	$1.917$ × ${10}^{-2}$	$8.980$ × ${10}^{-2}$	$9.846$ × ${10}^{-3}$	$1.661$ × ${10}^{-1}$	$3.033$ × ${10}^{-1}$
		Time (s)	83	77	92	127	168
		Memory (MB)	261	253	262	262	262
40	SVPINN	Relative $L^2$ error	$3.117$ × ${10}^{-3}$	$1.306$ × ${10}^{-3}$	$2.871$ × ${10}^{-3}$	$1.379$ × ${10}^{-3}$	$1.062$ × ${10}^{-3}$
		Time (s)	7	13	7	13	21
		Memory (MB)	239	249	238	252	251
	PINN-FBN	Relative $L^2$ error	$1.730$ × ${10}^{-2}$	$7.690$ × ${10}^{-2}$	$1.084$ × ${10}^{-2}$	$1.702$ × ${10}^{-1}$	$2.689$ × ${10}^{-1}$
		Time (s)	129	144	82	212	155
		Memory (MB)	260	274	273	275	260
60	SVPINN	Relative $L^2$ error	$1.785$ × ${10}^{-3}$	$1.047$ × ${10}^{-3}$	$1.525$ × ${10}^{-3}$	$1.025$ × ${10}^{-3}$	$1.399$ × ${10}^{-3}$
		Time (s)	19	21	26	24	25
		Memory (MB)	233	269	268	241	240
	PINN-FBN	Relative $L^2$ error	$1.587$ × ${10}^{-2}$	$7.668$ × ${10}^{-2}$	$1.078$ × ${10}^{-2}$	$1.469$ × ${10}^{-1}$	$4.818$ × ${10}^{-1}$
		Time (s)	219	194	99	224	764
		Memory (MB)	289	265	286	288	268
80	SVPINN	Relative $L^2$ error	$3.603$ × ${10}^{-3}$	$1.414$ × ${10}^{-3}$	$2.113$ × ${10}^{-3}$	$1.626$ × ${10}^{-3}$	$1.304$ × ${10}^{-3}$
		Time (s)	15	31	16	24	43
		Memory (MB)	280	239	281	281	239
	PINN-FBN	Relative $L^2$ error	$1.910$ × ${10}^{-2}$	$8.377$ × ${10}^{-2}$	$1.073$ × ${10}^{-2}$	$1.650$ × ${10}^{-1}$	$4.314$ × ${10}^{-1}$
		Time (s)	201	346	192	469	644
		Memory (MB)	303	301	259	303	306

,

Table 5. The relative $L^2$ errors and computational cost of the PINN-FBN and the SVPINN with different numbers of hidden layers and different irregular domains for Section 3.3.

Layer	Method		${\mathit{r}}_1$	${\mathit{r}}_2$	${\mathit{r}}_3$	${\mathit{r}}_4$	${\mathit{r}}_5$
2	SVPINN	Relative $L^2$ error	$2.830$ × ${10}^{-3}$	$3.326$ × ${10}^{-3}$	$2.382$ × ${10}^{-3}$	$1.145$ × ${10}^{-3}$	$1.491$ × ${10}^{-3}$
		Time (s)	4	3	4	7	5
		Memory (MB)	216	215	216	215	215
	PINN-FBN	Relative $L^2$ error	$2.595$ × ${10}^{-2}$	$9.296$ × ${10}^{-2}$	$1.813$ × ${10}^{-2}$	$1.478$ × ${10}^{-1}$	$2.943$ × ${10}^{-1}$
		Time (s)	27	40	31	31	24
		Memory (MB)	242	238	238	242	238
5	SVPINN	Relative $L^2$ error	$1.966$ × ${10}^{-2}$	$1.729$ × ${10}^{-3}$	$1.426$ × ${10}^{-2}$	$1.448$ × ${10}^{-2}$	$3.950$ × ${10}^{-3}$
		Time (s)	46	21	41	44	21
		Memory (MB)	245	236	239	245	245
	PINN-FBN	Relative $L^2$ error	$3.161$ × ${10}^{-2}$	$9.558$ × ${10}^{-2}$	$1.404$ × ${10}^{-2}$	$1.791$ × ${10}^{-1}$	$2.345$ × ${10}^{-1}$
		Time (s)	38	117	52	81	131
		Memory (MB)	264	264	264	264	257
6	SVPINN	Relative $L^2$ error	$2.172$ × ${10}^{-3}$	$5.210$ × ${10}^{-3}$	$1.606$ × ${10}^{-3}$	$1.253$ × ${10}^{-3}$	$7.215$ × ${10}^{-3}$
		Time (s)	14	23	13	34	15
		Memory (MB)	252	253	251	244	252
	PINN-FBN	Relative $L^2$ error	$4.472$ × ${10}^{-2}$	$1.028$ × ${10}^{-1}$	$1.974$ × ${10}^{-2}$	$1.646$ × ${10}^{-1}$	$2.977$ × ${10}^{-1}$
		Time (s)	40	99	47	99	125
		Memory (MB)	263	270	270	263	270
8	SVPINN	Relative $L^2$ error	$2.270$ × ${10}^{-3}$	$2.641$ × ${10}^{-3}$	$1.303$ × ${10}^{-2}$	$5.875$ × ${10}^{-3}$	$2.936$ × ${10}^{-3}$
		Time (s)	57	21	29	17	22
		Memory (MB)	269	269	270	268	269
	PINN-FBN	Relative $L^2$ error	$3.575$ × ${10}^{-2}$	$1.384$ × ${10}^{-1}$	$2.476$ × ${10}^{-2}$	$1.233$ × ${10}^{-1}$	$2.960$ × ${10}^{-1}$
		Time (s)	26	41	62	102	67
		Memory (MB)	276	276	284	277	276

,

Table 6. The relative $L^2$ errors and computational cost of the PINN-FBN and the SVPINN with different numbers of boundary and initial data and different irregular domains for Section 3.3.

${\mathit{N}}_{\mathit{u}}$	Method		${\mathit{r}}_1$	${\mathit{r}}_2$	${\mathit{r}}_3$	${\mathit{r}}_4$	${\mathit{r}}_5$
200	SVPINN	Relative $L^2$ error	$1.704$ × ${10}^{-3}$	$1.266$ × ${10}^{-3}$	$1.749$ × ${10}^{-3}$	$1.451$ × ${10}^{-3}$	$2.086$ × ${10}^{-3}$
		Time (s)	13	14	11	20	14
		Memory (MB)	235	233	233	234	227
	PINN-FBN	Relative $L^2$ error	$4.951$ × ${10}^{-2}$	$1.721$ × ${10}^{-1}$	$2.906$ × ${10}^{-2}$	$3.017$ × ${10}^{-1}$	$7.235$ × ${10}^{-1}$
		Time (s)	68	63	48	60	75
		Memory (MB)	255	255	257	255	256
400	SVPINN	Relative $L^2$ error	$2.267$ × ${10}^{-3}$	$1.770$ × ${10}^{-3}$	$1.657$ × ${10}^{-3}$	$1.605$ × ${10}^{-3}$	$3.668$ × ${10}^{-3}$
		Time (s)	15	15	14	23	25
		Memory (MB)	229	229	227	230	229
	PINN-FBN	Relative $L^2$ error	$2.242$ × ${10}^{-2}$	$1.099$ × ${10}^{-1}$	$1.170$ × ${10}^{-2}$	$2.695$ × ${10}^{-1}$	$3.624$ × ${10}^{-1}$
		Time (s)	47	40	71	115	28
		Memory (MB)	255	255	257	258	255
600	SVPINN	Relative $L^2$ error	$1.810$ × ${10}^{-3}$	$1.894$ × ${10}^{-3}$	$2.092$ × ${10}^{-3}$	$3.230$ × ${10}^{-3}$	$9.176$ × ${10}^{-4}$
		Time (s)	11	13	7	15	38
		Memory (MB)	235	233	227	235	230
	PINN-FBN	Relative $L^2$ error	$2.590$ × ${10}^{-2}$	$1.090$ × ${10}^{-1}$	$1.210$ × ${10}^{-2}$	$1.225$ × ${10}^{-1}$	$2.370$ × ${10}^{-1}$
		Time (s)	63	59	61	77	57
		Memory (MB)	257	250	257	256	257
800	SVPINN	Relative $L^2$ error	$1.421$ × ${10}^{-3}$	$1.859$ × ${10}^{-3}$	$1.933$ × ${10}^{-3}$	$2.612$ × ${10}^{-3}$	$1.393$ × ${10}^{-3}$
		Time (s)	9	27	16	23	34
		Memory (MB)	229	237	229	231	236
	PINN-FBN	Relative $L^2$ error	$2.196$ × ${10}^{-2}$	$9.512$ × ${10}^{-2}$	$1.099$ × ${10}^{-2}$	$1.777$ × ${10}^{-1}$	$2.657$ × ${10}^{-1}$
		Time (s)	54	102	82	129	79
		Memory (MB)	251	250	257	259	256

and

Table 7. The relative $L^2$ errors and computational cost of the PINN-FBN and the SVPINN with different numbers of collocation points and different irregular domains for Section 3.3.

${\mathit{N}}_{\mathit{f}}$	Method		${\mathit{r}}_1$	${\mathit{r}}_2$	${\mathit{r}}_3$	${\mathit{r}}_4$	${\mathit{r}}_5$
3000	SVPINN	Relative $L^2$ error	$3.087$ × ${10}^{-3}$	$1.571$ × ${10}^{-3}$	$1.502$ × ${10}^{-3}$	$2.474$ × ${10}^{-3}$	$2.019$ × ${10}^{-3}$
		Time (s)	6	23	10	22	27
		Memory (MB)	237	238	230	239	239
	PINN-FBN	Relative $L^2$ error	$2.324$ × ${10}^{-2}$	$8.725$ × ${10}^{-2}$	$1.180$ × ${10}^{-2}$	$1.189$ × ${10}^{-1}$	$3.131$ × ${10}^{-1}$
		Time (s)	90	139	105	118	190
		Memory (MB)	297	298	296	297	298
4000	SVPINN	Relative $L^2$ error	$3.313$ × ${10}^{-3}$	$1.897$ × ${10}^{-3}$	$1.333$ × ${10}^{-3}$	$1.321$ × ${10}^{-3}$	$1.642$ × ${10}^{-3}$
		Time (s)	8	18	13	37	34
		Memory (MB)	238	238	240	231	235
	PINN-FBN	Relative $L^2$ error	$2.339$ × ${10}^{-2}$	$1.023$ × ${10}^{-1}$	$1.160$ × ${10}^{-2}$	$1.587$ × ${10}^{-1}$	$3.765$ × ${10}^{-1}$
		Time (s)	182	151	141	337	239
		Memory (MB)	352	344	351	355	353
5000	SVPINN	Relative $L^2$ error	$2.526$ × ${10}^{-3}$	$9.265$ × ${10}^{-4}$	$1.172$ × ${10}^{-3}$	$7.407$ × ${10}^{-4}$	$8.975$ × ${10}^{-4}$
		Time (s)	9	31	18	49	39
		Memory (MB)	235	238	236	238	237
	PINN-FBN	Relative $L^2$ error	$2.273$ × ${10}^{-2}$	$9.765$ × ${10}^{-2}$	$1.184$ × ${10}^{-2}$	$1.499$ × ${10}^{-1}$	$2.559$ × ${10}^{-1}$
		Time (s)	237	320	383	299	398
		Memory (MB)	425	423	418	423	423

. From the table, it can be seen that the relative error of the SVPINN is generally maintained at the level of ${10}^{-3}$ to ${10}^{-4}$, which are one and two orders of magnitude lower than the other two methods. The SVPINN has excellent advantages in computational efficiency. The data in the table clearly indicates that the training time required by the SVPINN is significantly shorter than that of the PINN-FBN, often as little as $10\%$ or even less. Furthermore, the SVPINN achieves higher accuracy without incurring additional memory consumption, maintaining essentially the same memory usage as the PINN-FBN. When the hyperparameters change, the error of the SVPINN consistently stays at the order of ${10}^{-3}$, indicating its strong stability.

3.4. High-Dimensional Problems

In this example, we investigate the effectiveness of the SVPINN for high-dimensional distributed-order advection–diffusion equation. The spatial domain and time interval are set to $\mathrm{\Omega }={(-1,1)}^d$ and $\tau =(0,1]$, respectively.

In

Table 8. The relative $L^2$ errors and computational cost of the PINN-FBN and the SVPINN with different dimensions for Section 3.4.

Method		$\mathit{d}=3$	$\mathit{d}=5$	$\mathit{d}=10$
SVPINN	Relative $L^2$ error	$1.865$ × ${10}^{-3}$	$8.815$ × ${10}^{-4}$	$1.351$ × ${10}^{-3}$
	Time (s)	35	20	27
	Memory (MB)	258	296	394
PINN-FBN	Relative $L^2$ error	$8.332$ × ${10}^{-2}$	$4.641$ × ${10}^{-2}$	$6.704$ × ${10}^{-2}$
	Time (s)	47	121	223
	Memory (MB)	275	317	415

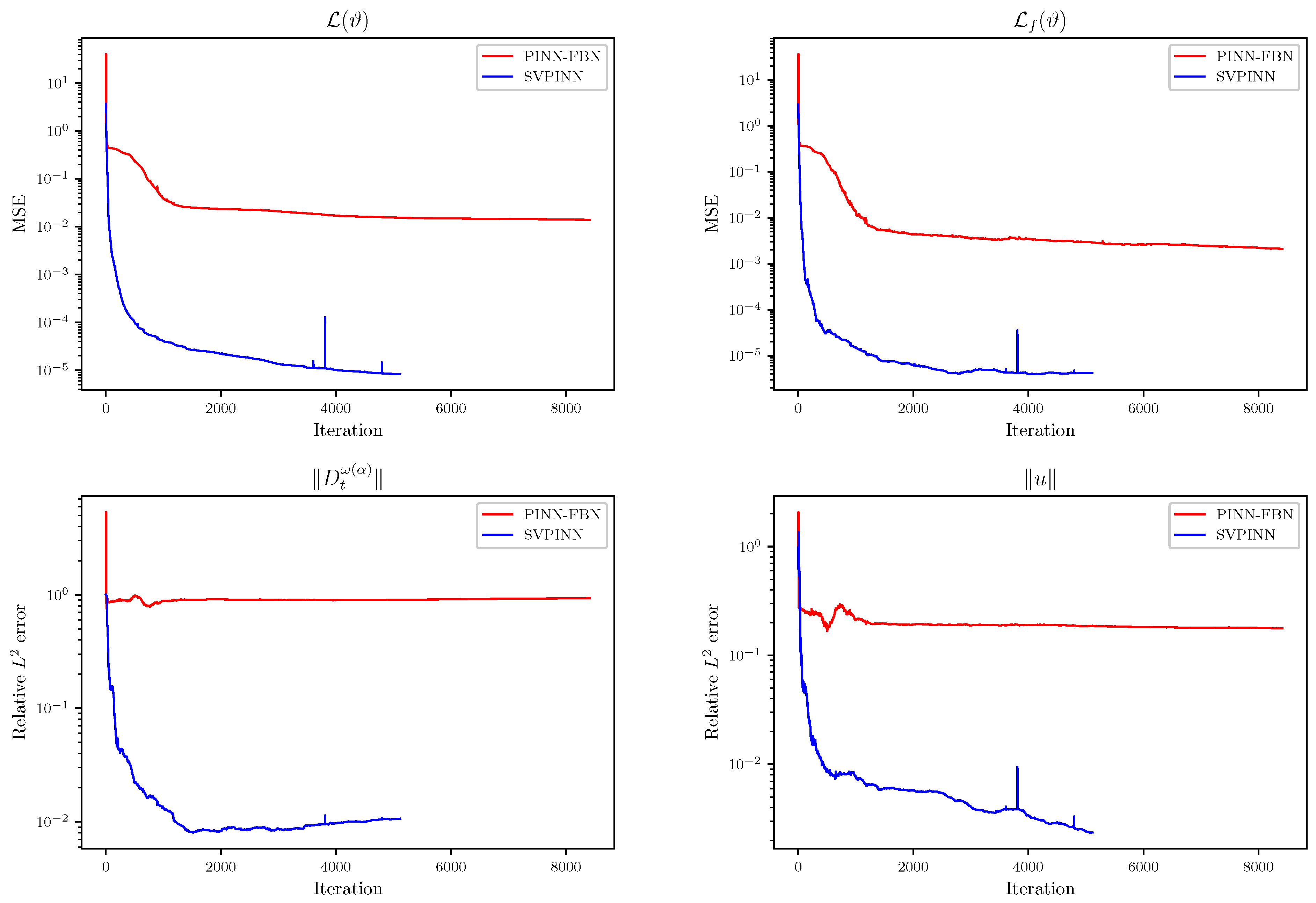
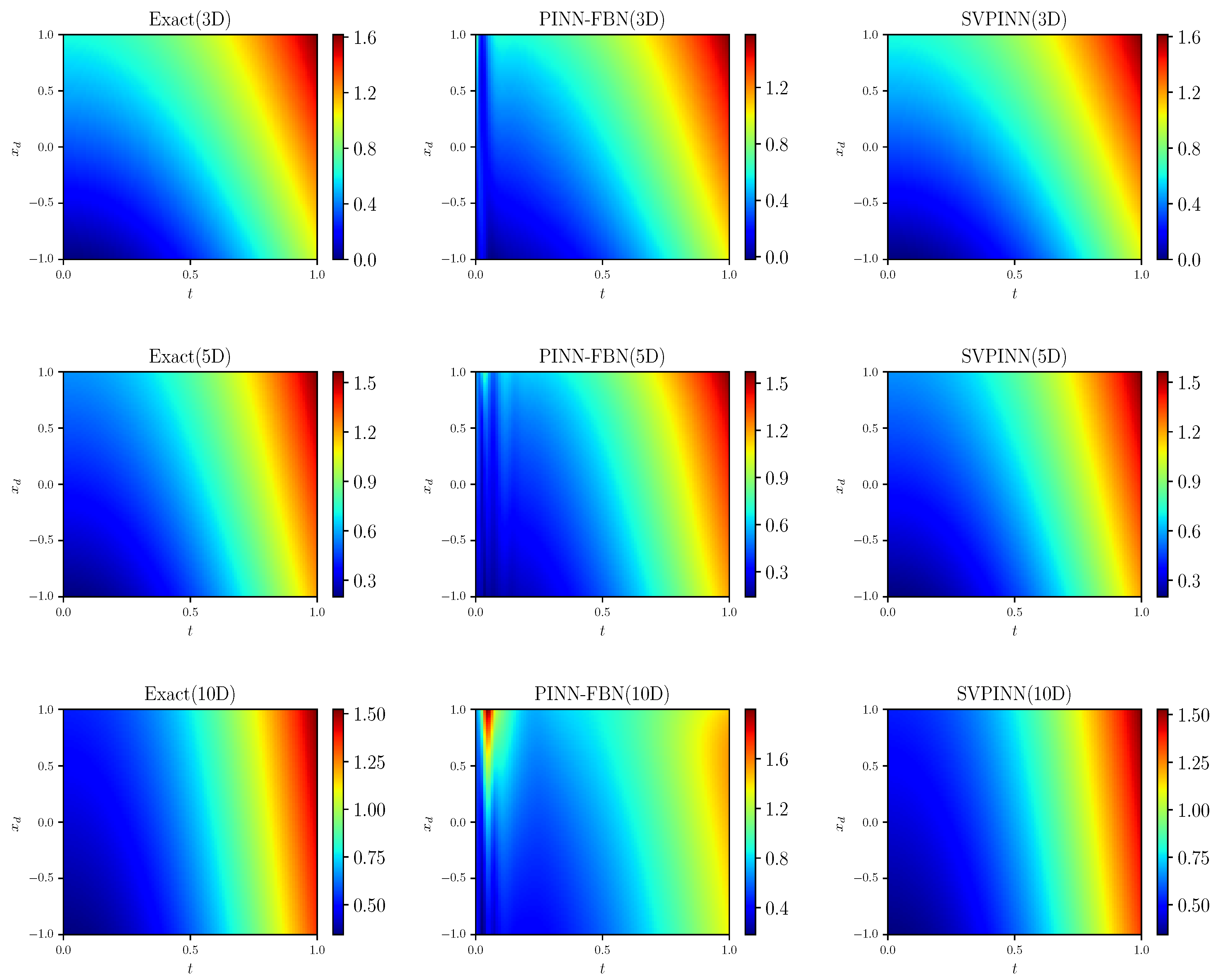
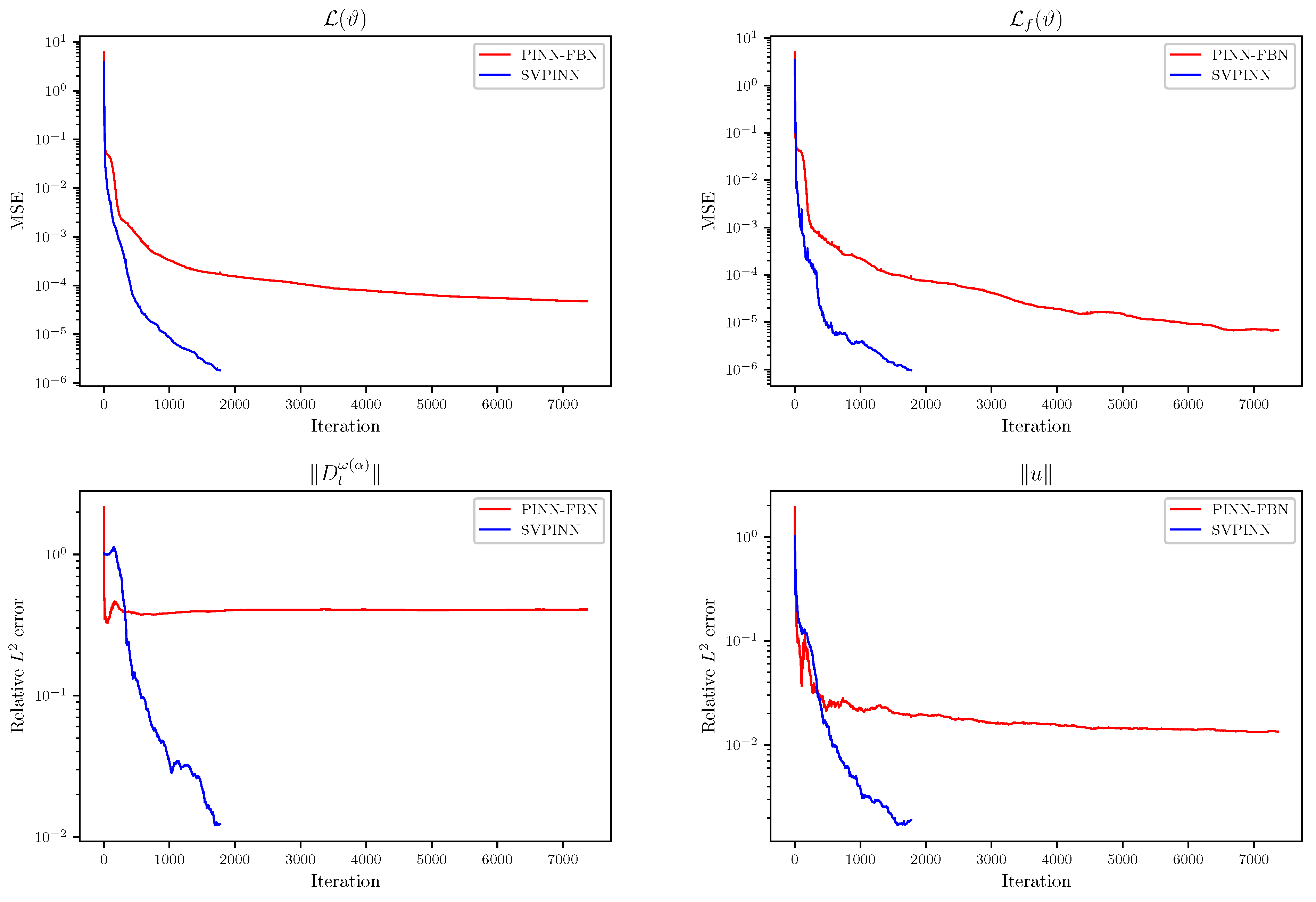
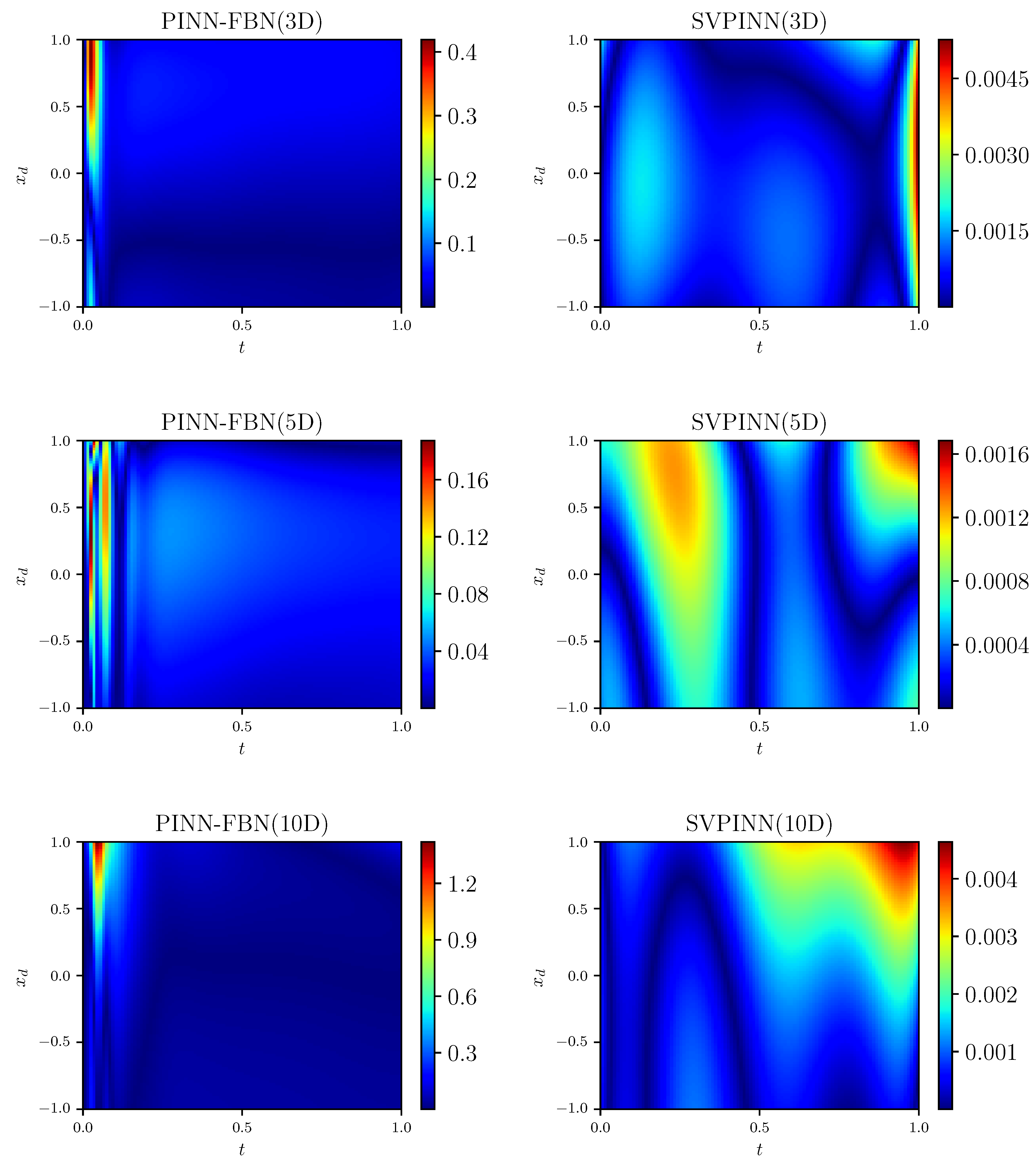
, we present the relative $L^2$ error, training time, and memory usage obtained by the SVPINN and PINN-FBN methods at $d=3,5,10$. The error between the exact solution and the prediction given by the SVPINN is $1.351\times {10}^{-3}$, when $d=10$. The results demonstrate that for high-dimensional cases, our proposed method also has good prediction accuracy. In Figure 13 and Figure 14, we plot the distributions of the analytical solution, the prediction, and the absolute error. 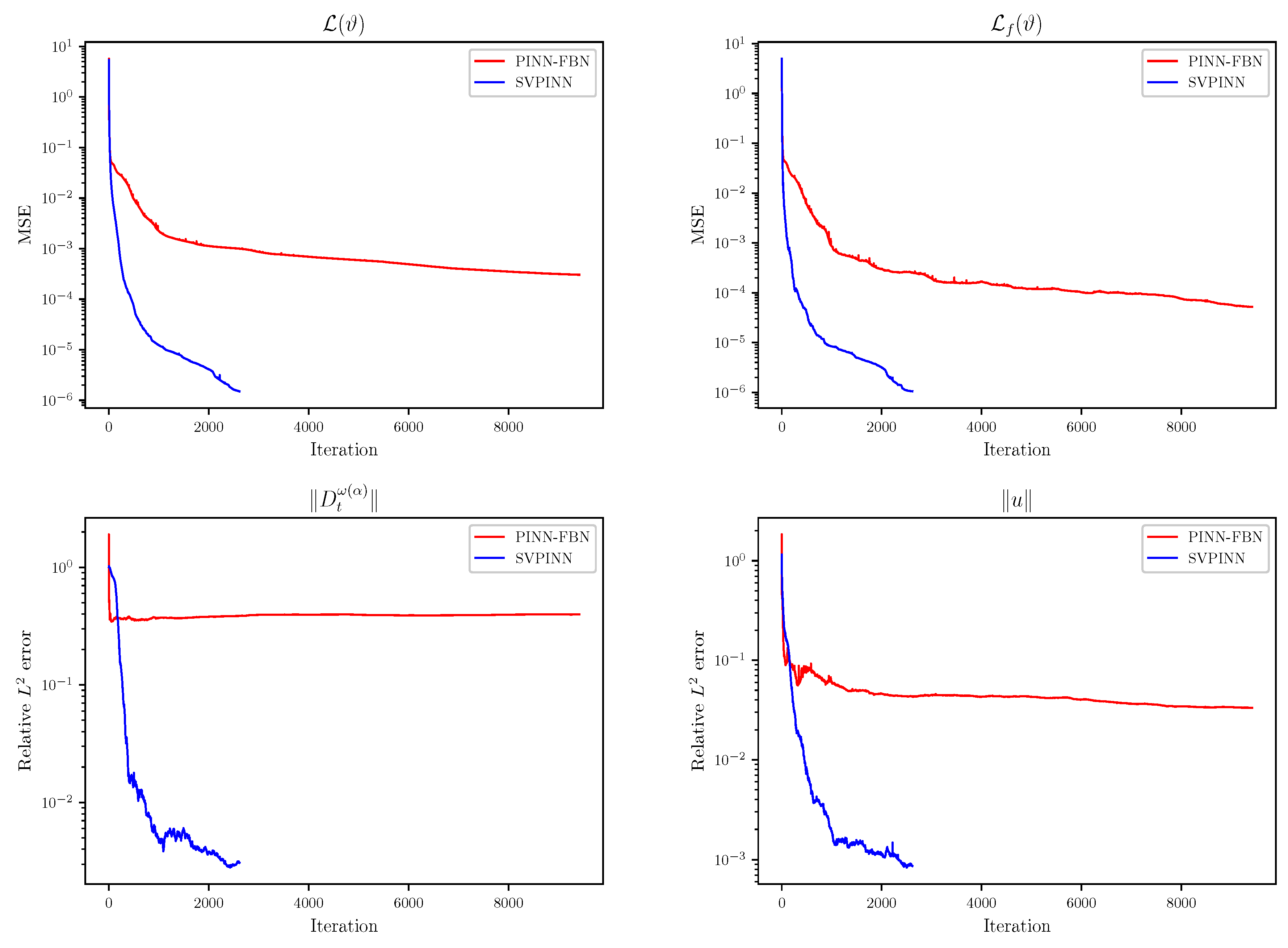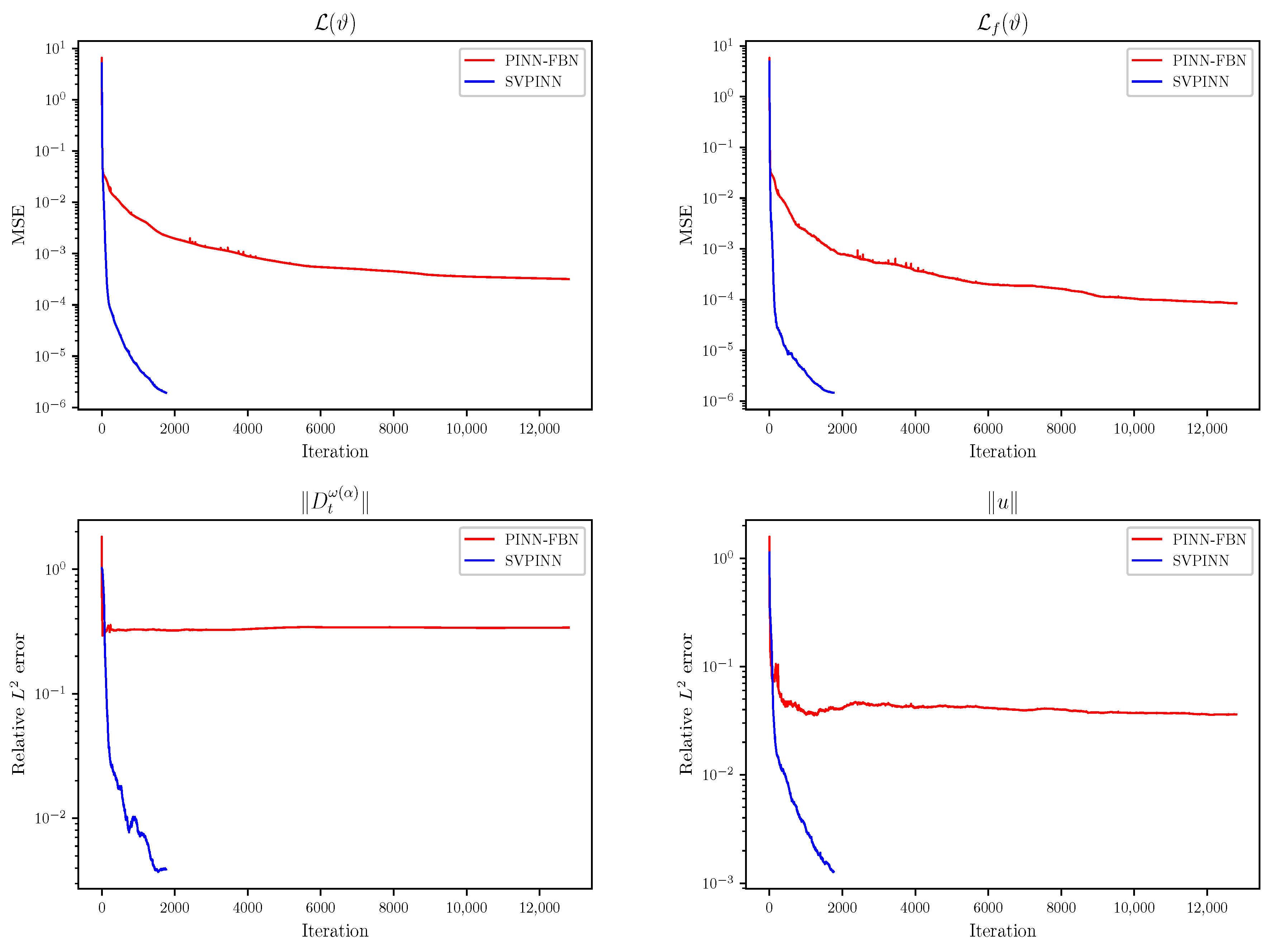In addition, we provide a comparison of the loss and relative error between the SVPINN and PINN-FBN methods in Figure 15, Figure 16 and Figure 17, which shows that the SVPINN has higher accuracy in approximating the distributed-order derivative and can better optimize the network parameters. During the training process, we can observe a stable decrease and rapid convergence of the total loss function, demonstrating the feasibility of the proposed SVPINN. Quantitative analysis of the loss of the residual equation and the relative error, as shown in the figures, verifies that the neural network adheres to the physical laws described by the governing equation during the training process.

Table 9. The relative $L^2$ errors and computational cost of the PINN-FBN and the SVPINN with different numbers of neurons and different dimensions for Section 3.4.

d	Method		Neuron
			20	40	60	80
3	SVPINN	Relative $L^2$ error	$7.190$ × ${10}^{-4}$	$1.276$ × ${10}^{-3}$	$1.291$ × ${10}^{-3}$	$1.138$ × ${10}^{-3}$
		Time (s)	15	13	23	37
		Memory (MB)	250	280	262	320
	PINN-FBN	Relative $L^2$ error	$4.320$ × ${10}^{-2}$	$3.621$ × ${10}^{-2}$	$4.119$ × ${10}^{-2}$	$4.092$ × ${10}^{-2}$
		Time (s)	161	346	427	403
		Memory (MB)	280	301	319	337
5	SVPINN	Relative $L^2$ error	$1.831$ × ${10}^{-3}$	$1.557$ × ${10}^{-3}$	$1.351$ × ${10}^{-3}$	$1.585$ × ${10}^{-3}$
		Time (s)	19	25	40	70
		Memory (MB)	299	300	301	398
	PINN-FBN	Relative $L^2$ error	$3.298$ × ${10}^{-2}$	$3.877$ × ${10}^{-2}$	$3.566$ × ${10}^{-2}$	$3.486$ × ${10}^{-2}$
		Time (s)	160	212	546	809
		Memory (MB)	320	352	384	418
10	SVPINN	Relative $L^2$ error	$1.494$ × ${10}^{-3}$	$1.643$ × ${10}^{-3}$	$2.266$ × ${10}^{-3}$	$2.237$ × ${10}^{-3}$
		Time (s)	33	40	73	76
		Memory (MB)	407	460	514	568
	PINN-FBN	Relative $L^2$ error	$4.890$ × ${10}^{-2}$	$3.656$ × ${10}^{-2}$	$4.934$ × ${10}^{-2}$	$7.027$ × ${10}^{-2}$
		Time (s)	258	590	910	1194
		Memory (MB)	428	478	533	581

,

Table 10. The relative $L^2$ errors and computational cost of the PINN-FBN and the SVPINN with different numbers of hidden layers and different dimensions for Section 3.4.

d	Method		Layer
			2	5	6	8
3	SVPINN	Relative $L^2$ error	$1.323$ × ${10}^{-3}$	$3.505$ × ${10}^{-2}$	$7.507$ × ${10}^{-4}$	$2.331$ × ${10}^{-3}$
		Time (s)	6	51	27	42
		Memory (MB)	229	269	278	302
	PINN-FBN	Relative $L^2$ error	$7.306$ × ${10}^{-2}$	$7.357$ × ${10}^{-2}$	$7.214$ × ${10}^{-2}$	$5.623$ × ${10}^{-2}$
		Time (s)	39	65	95	98
		Memory (MB)	252	286	292	317
5	SVPINN	Relative $L^2$ error	$9.644$ × ${10}^{-4}$	$1.225$ × ${10}^{-3}$	$1.232$ × ${10}^{-3}$	$1.567$ × ${10}^{-3}$
		Time (s)	11	51	39	68
		Memory (MB)	256	313	330	362
	PINN-FBN	Relative $L^2$ error	$7.421$ × ${10}^{-2}$	$4.427$ × ${10}^{-2}$	$5.459$ × ${10}^{-2}$	$5.232$ × ${10}^{-2}$
		Time (s)	77	129	162	113
		Memory (MB)	285	332	348	379
10	SVPINN	Relative $L^2$ error	$1.969$ × ${10}^{-3}$	$1.710$ × ${10}^{-3}$	$1.140$ × ${10}^{-3}$	$1.378$ × ${10}^{-3}$
		Time (s)	30	41	99	133
		Memory (MB)	334	423	451	513
	PINN-FBN	Relative $L^2$ error	$6.858$ × ${10}^{-2}$	$4.588$ × ${10}^{-2}$	$5.602$ × ${10}^{-2}$	$6.979$ × ${10}^{-2}$
		Time (s)	144	289	226	250
		Memory (MB)	353	443	469	525

,

Table 11. The relative $L^2$ errors and computational cost of the PINN-FBN and the SVPINN with different numbers of boundary and initial data and different dimensions for Section 3.4.

d	Method		${\mathit{N}}_{\mathit{u}}$
			200	400	600	800
3	SVPINN	Relative $L^2$ error	$5.126$ × ${10}^{-3}$	$1.644$ × ${10}^{-3}$	$5.286$ × ${10}^{-3}$	$1.634$ × ${10}^{-3}$
		Time (s)	28	41	18	28
		Memory (MB)	256	257	258	256
	PINN-FBN	Relative $L^2$ error	$7.024$ × ${10}^{-2}$	$7.856$ × ${10}^{-2}$	$7.056$ × ${10}^{-2}$	$7.062$ × ${10}^{-2}$
		Time (s)	75	73	114	81
		Memory (MB)	275	276	276	275
5	SVPINN	Relative $L^2$ error	$2.717$ × ${10}^{-3}$	$1.005$ × ${10}^{-3}$	$1.291$ × ${10}^{-3}$	$7.463$ × ${10}^{-4}$
		Time (s)	21	25	39	42
		Memory (MB)	285	297	299	301
	PINN-FBN	Relative $L^2$ error	$1.129$ × ${10}^{-1}$	$5.254$ × ${10}^{-2}$	$5.179$ × ${10}^{-2}$	$4.449$ × ${10}^{-2}$
		Time (s)	137	128	88	110
		Memory (MB)	318	319	318	317
10	SVPINN	Relative $L^2$ error	$2.055$ × ${10}^{-3}$	$1.506$ × ${10}^{-3}$	$1.350$ × ${10}^{-3}$	$1.537$ × ${10}^{-3}$
		Time (s)	32	34	32	26
		Memory (MB)	393	394	395	393
	PINN-FBN	Relative $L^2$ error	$1.605$ × ${10}^{-1}$	$6.963$ × ${10}^{-2}$	$8.097$ × ${10}^{-2}$	$5.270$ × ${10}^{-2}$
		Time (s)	154	241	197	260
		Memory (MB)	415	417	413	415

and

Table 12. The relative $L^2$ errors and computational cost of the PINN-FBN and the SVPINN with different numbers of collocation points and different dimensions for Section 3.4.

d	Method		${\mathit{N}}_{\mathit{f}}$
			3000	4000	5000
3	SVPINN	Relative $L^2$ error	$4.057$ × ${10}^{-3}$	$1.249$ × ${10}^{-3}$	$1.750$ × ${10}^{-3}$
		Time (s)	50	36	64
		Memory (MB)	262	260	263
	PINN-FBN	Relative $L^2$ error	$5.442$ × ${10}^{-2}$	$4.749$ × ${10}^{-2}$	$8.404$ × ${10}^{-2}$
		Time (s)	185	270	305
		Memory (MB)	316	359	442
5	SVPINN	Relative $L^2$ error	$8.344$ × ${10}^{-4}$	$1.334$ × ${10}^{-3}$	$1.080$ × ${10}^{-3}$
		Time (s)	44	32	50
		Memory (MB)	298	297	310
	PINN-FBN	Relative $L^2$ error	$8.972$ × ${10}^{-2}$	$5.283$ × ${10}^{-2}$	$4.481$ × ${10}^{-2}$
		Time (s)	185	265	442
		Memory (MB)	355	410	495
10	SVPINN	Relative $L^2$ error	$1.217$ × ${10}^{-3}$	$1.448$ × ${10}^{-3}$	$1.203$ × ${10}^{-3}$
		Time (s)	35	37	50
		Memory (MB)	397	409	422
	PINN-FBN	Relative $L^2$ error	$7.417$ × ${10}^{-2}$	$8.836$ × ${10}^{-2}$	$5.790$ × ${10}^{-2}$
		Time (s)	206	594	400
		Memory (MB)	454	523	597

report the performance of the SVPINN and PINN-FBN methods with respect to the network structure, the number of collocation points, and the number of initial and boundary data. From the table, it can be seen that the prediction accuracy of the PINN-FBN is maintained at the level of ${10}^{-2}$, while that of the SVPINN is maintained at the level of ${10}^{-3}$. The training time for the SVPINN is generally maintained between 20 s and 100 s, while the PINN-FBN requires approximately 60 s to 800 s, which is 3 to 8 times longer than the SVPINN. When the network structure and the number of training points change, the prediction accuracy of the SVPINN remains almost stable at the level of ${10}^{-3}$, demonstrating strong robustness.

3.5. Comprehensive Analysis

In this section, to further comprehensively evaluate the performance and the computational complexity of the proposed method, we summarized, in

Table 13. Comparison of representative numerical results of the PINN-WSGD, the PINN-FBN, the MoPINN, and the SVPINN for Section 3.2, Section 3.3 and Section 3.4.

Example	Method	Relative ${\mathit{L}}^2$ Error	Time (s)	Memory (MB)
Section 3.2	SVPINN	$1.066$ × ${10}^{-3}$	13	228
	PINN-WSGD	$9.416$ × ${10}^{-2}$	8	247
	PINN-FBN	$4.943$ × ${10}^{-2}$	42	251
Section 3.3	SVPINN	$6.722$ × ${10}^{-4}$	21	231
	PINN-FBN	$1.381$ × ${10}^{-1}$	45	256
	MoPINN	$3.650$ × ${10}^{-1}$	20	270
Section 3.4	SVPINN	$8.815$ × ${10}^{-4}$	20	296
	PINN-FBN	$4.641$ × ${10}^{-2}$	121	317

, the key indicators such as prediction accuracy, computation time, and memory, which reflect the overall performance of SVPINN in Section 3.2, Section 3.3 and Section 3.4. As shown in the table, in Section 3.2, Section 3.3 and Section 3.4, our proposed method not only achieves better prediction accuracy, but also has lower memory consumption than the PINN-FBN. Moreover, the SVPINN significantly improves computational efficiency with similar computational costs, reducing training time to $16\%$ to $50\%$ of that required by the PINN-FBN. Although the PINN-WSGD has less training time than the SVPINN, it fails to accurately predict the exact solution. Overall, our proposed method shows better performance in both prediction accuracy and computational cost, while also exhibiting lower computational complexity and excellent scalability.

4. Conclusions

In this work, we proposed a novel PINN framework and applied it to solve the distributed-order advection–diffusion equation. In the SVPINN framework, we separate the time variable and the other two integration variables in the kernel function of the Caputo integral into three independent functions, transforming the kernel function into the product of these functions. Further, we change the integral form by defining two functions determined by the integral variables $\alpha$ and $\eta$ and use the network to approximate the function related only to the time variable. In the proposed PINN method, the solution process of the distributed-order derivative is embedded into the network training framework, and an adaptive learning mode based on neural network parameter training is adopted to approximate the distributed-order derivative term. Several numerical experiments are carried out to verify the effectiveness of the SVPINN method. The results demonstrate that the integral scheme we constructed can effectively approximate the distributed-order derivative, and it makes the proposed SVPINN model achieve higher accuracy than the PINN models that use the numerical schemes, such as the FBN-$\theta$ scheme or the WSGD scheme, to discretize the fractional derivative. The focus of future research is to enhance the ability of the SVPINN model to deal with more complex physical systems, such as fractional underground seepage problems with complex mixed boundary conditions.