A Distributed-Order Fractional Hyperchaotic Detuned Laser Model: Dynamics, Multistability, and Dual Combination Synchronization
Abstract
1. Introduction
2. Application of the Caputo Fractional Derivative to the Model (3)
2.1. Numerical Solutions of the Fractional-Order Detuned Laser Model (3)
2.1.1. Solutions That Approach Fixed Points
2.1.2. Solutions That Approach a Chaotic Attractor
2.1.3. The Difference Between Caputo and DO Dynamics
3. Preliminaries
- 1.
- 2.
4. Analysis of the DOHD Laser Model (4)
4.1. Invariance and Dissipation
4.2. Fixed Points and Their Stability
4.3. Numerical Solutions of the DOHD Laser Model (4)
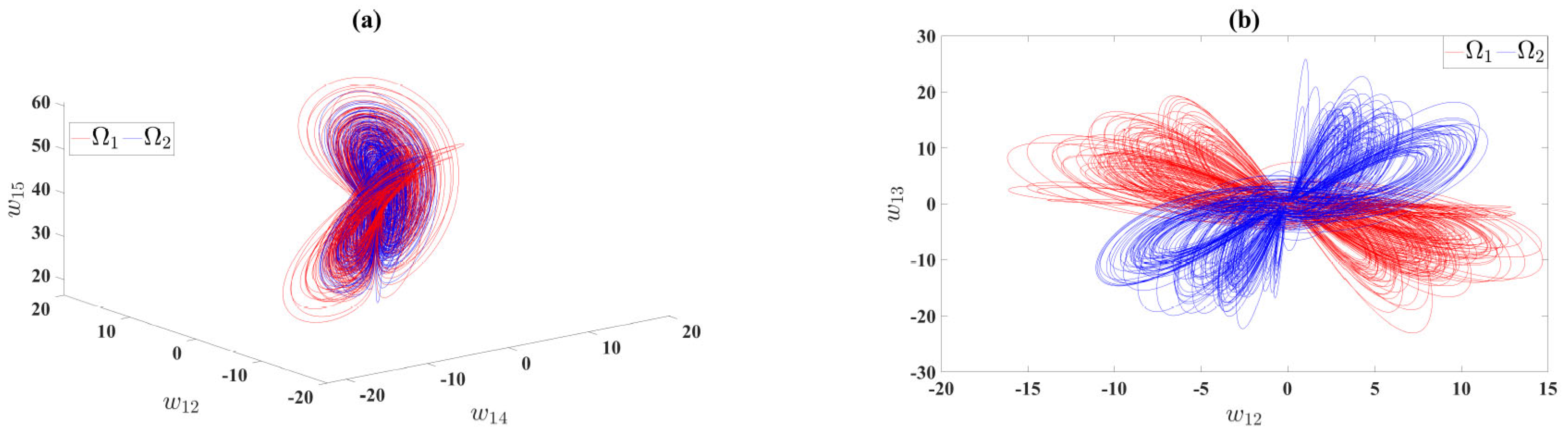
5. Coexisting Attractors of the DOHD Laser Model (4)
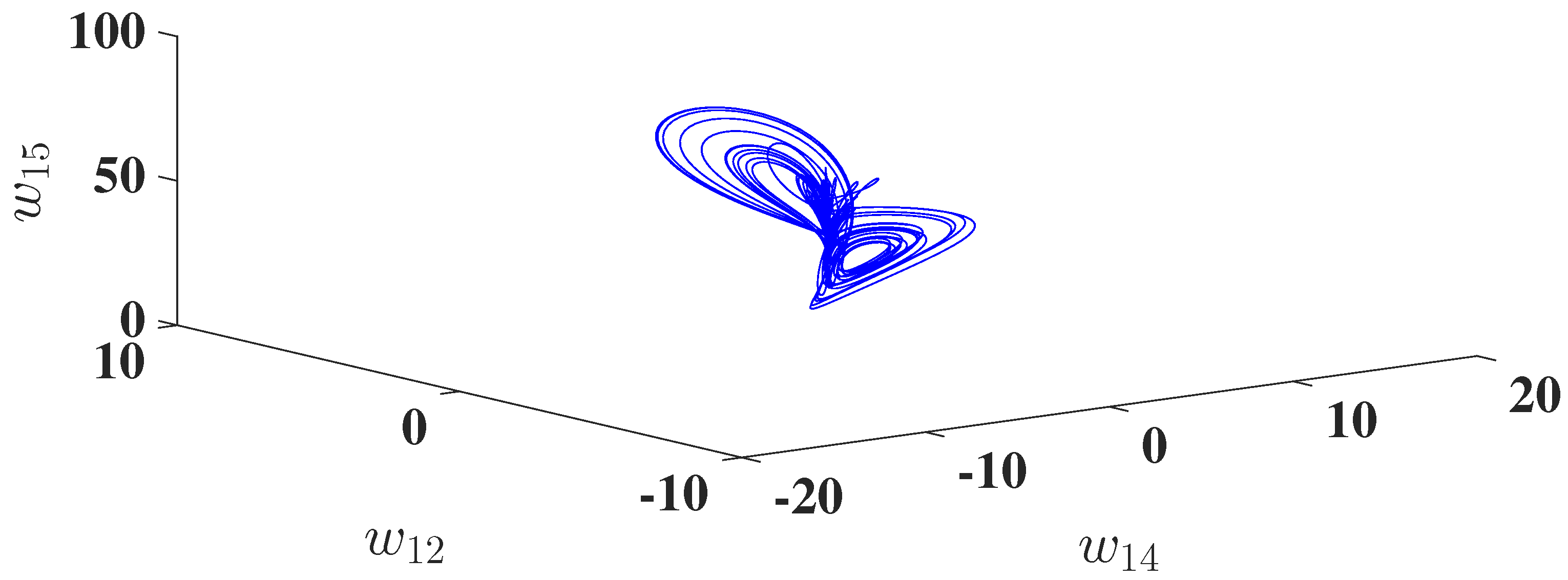
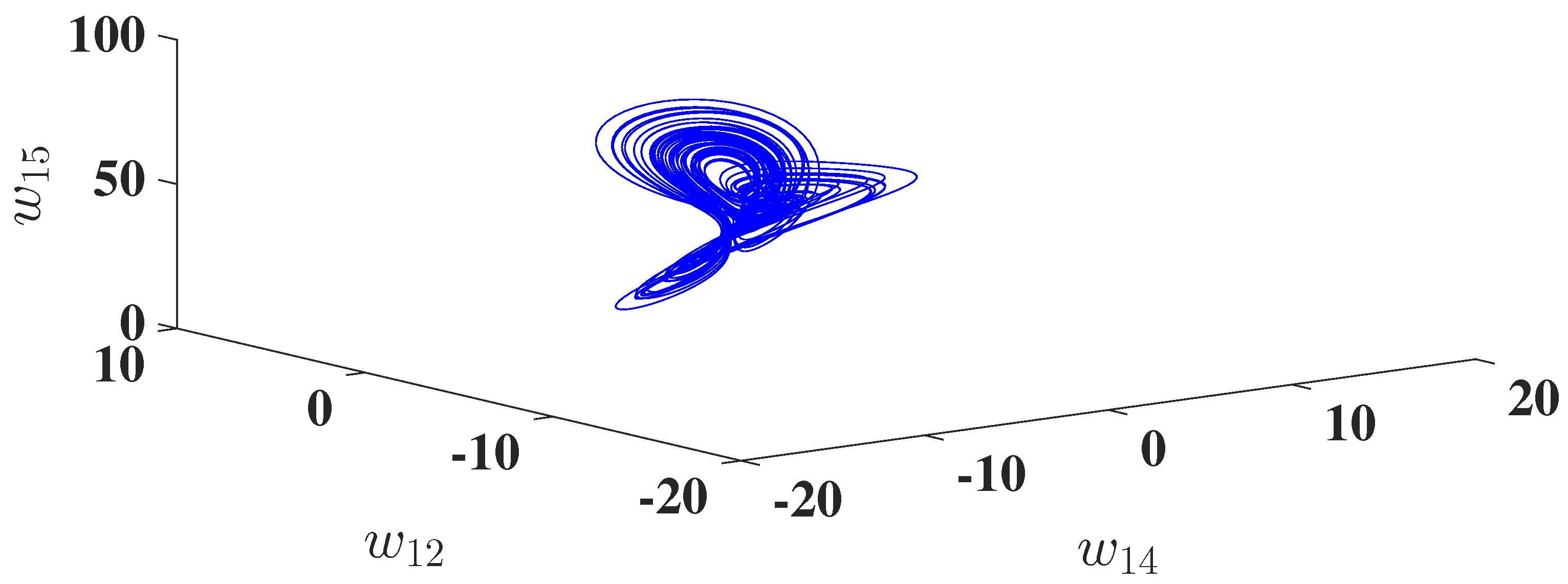
5.1. Chaotic and Hyperchaotic Attractors
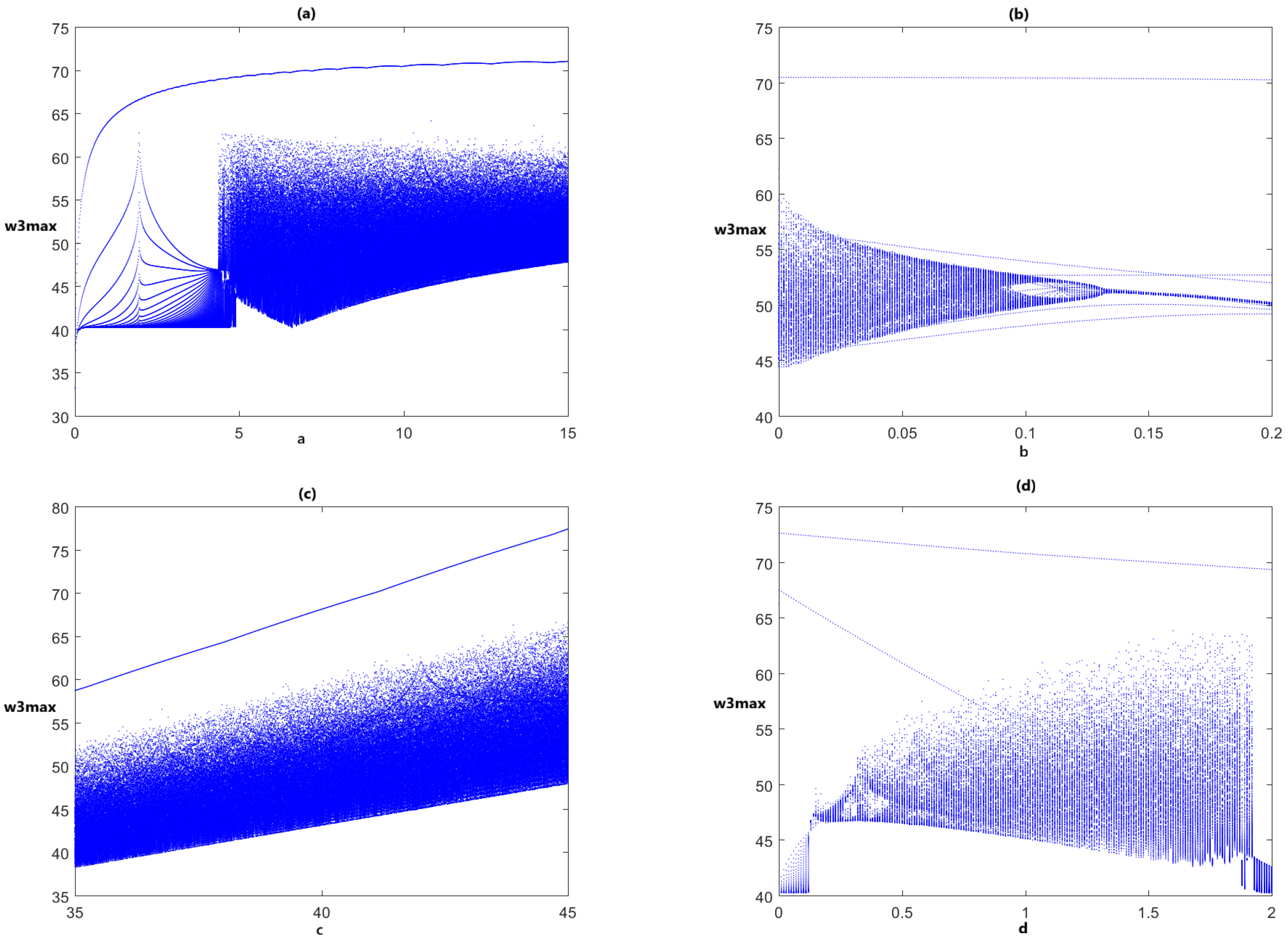
5.1.1. Fix , , , , and Vary
5.1.2. Fix , , , , and Vary
5.1.3. Fix , , , , and Vary
5.1.4. Fix , , , , and Vary
5.1.5. Fix , , , , and Vary
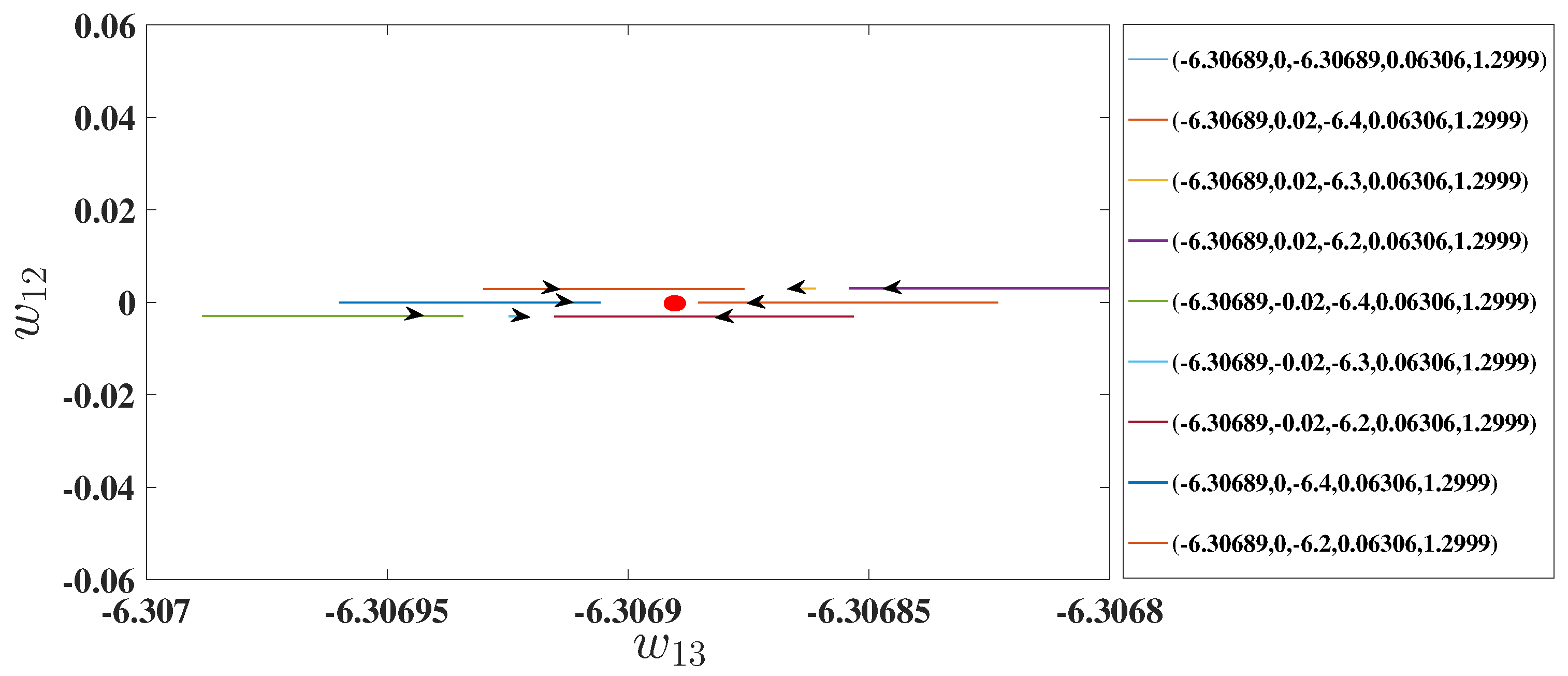
5.2. Solution That Approaches Fixed Points
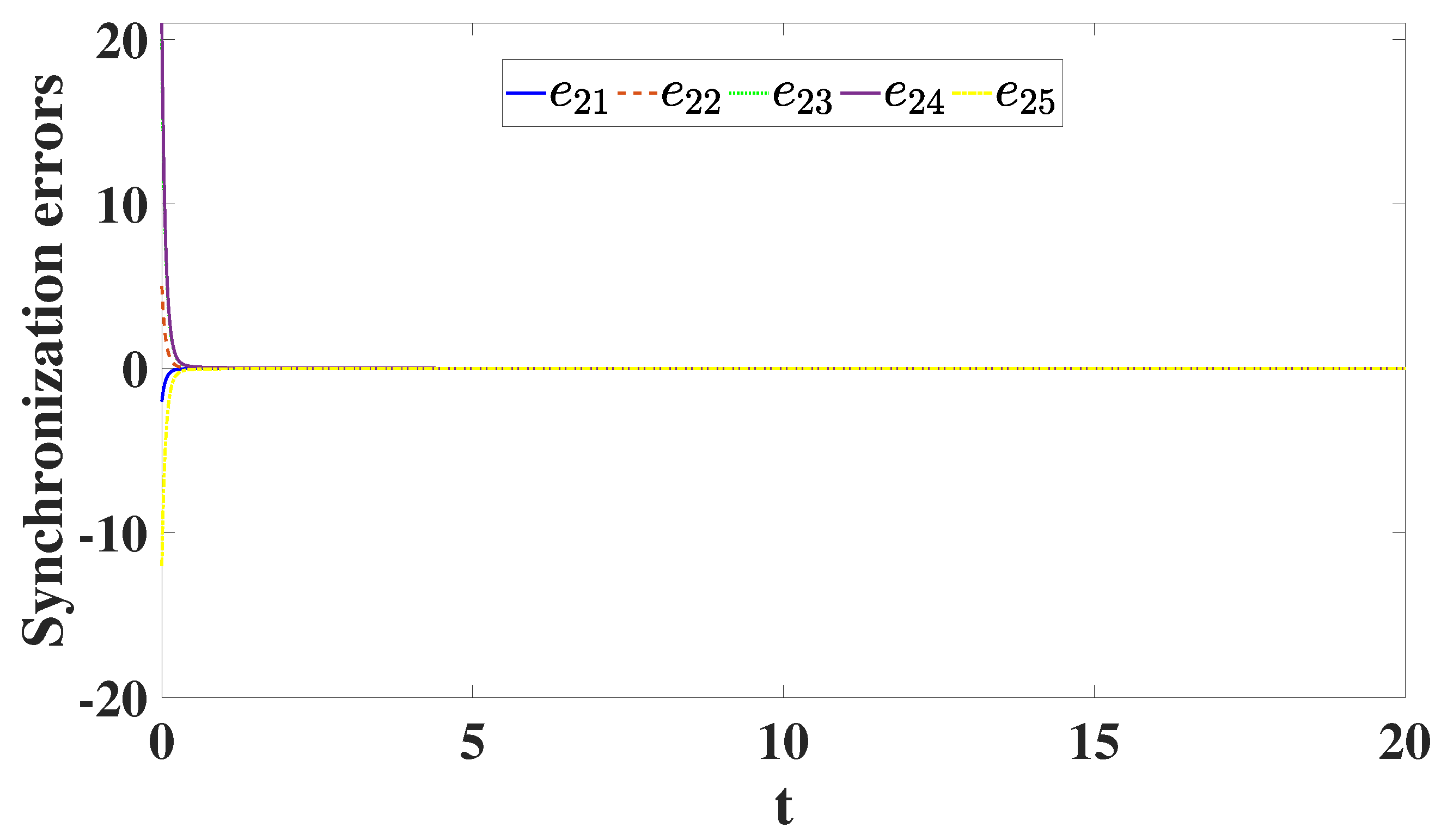
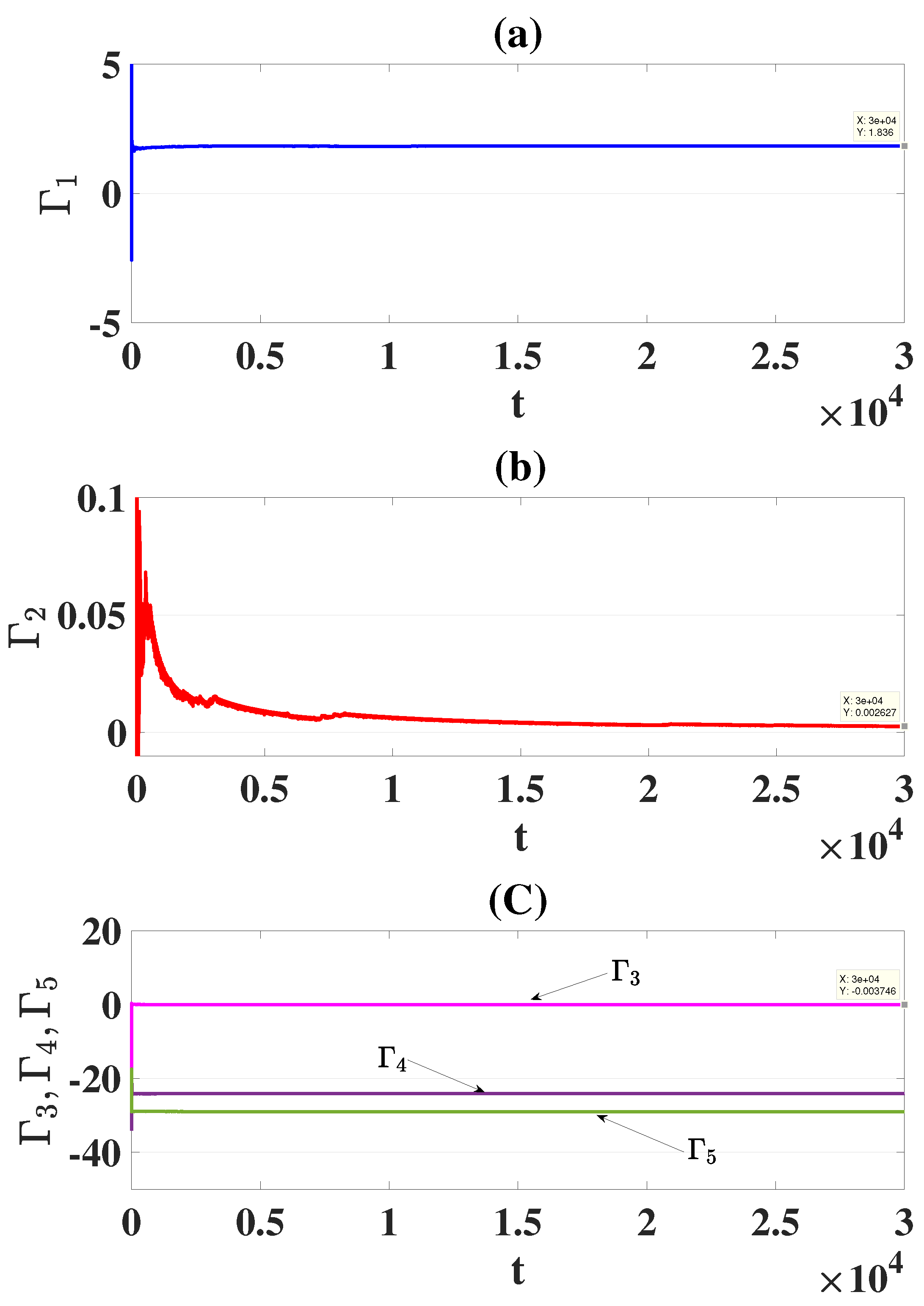
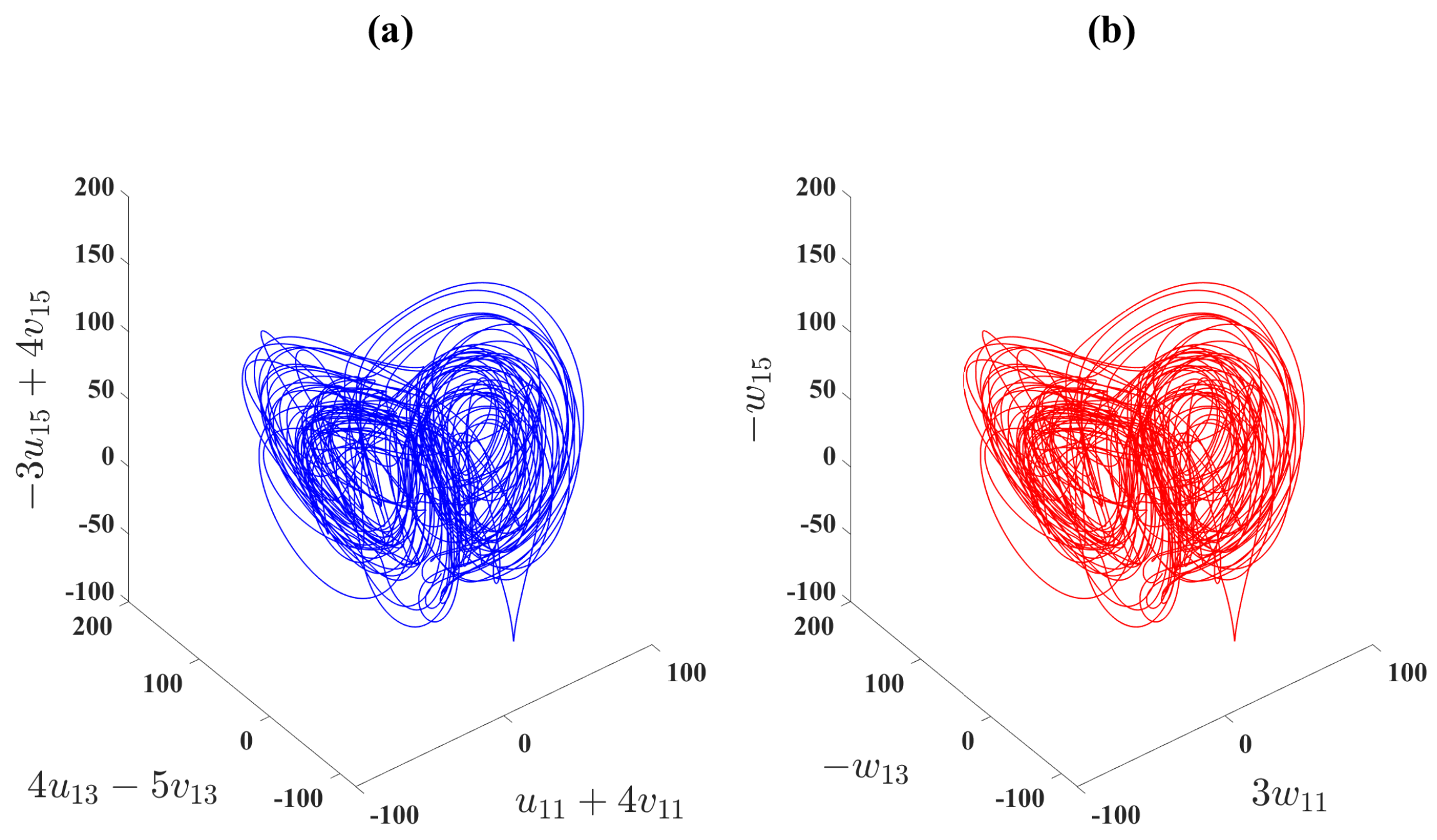
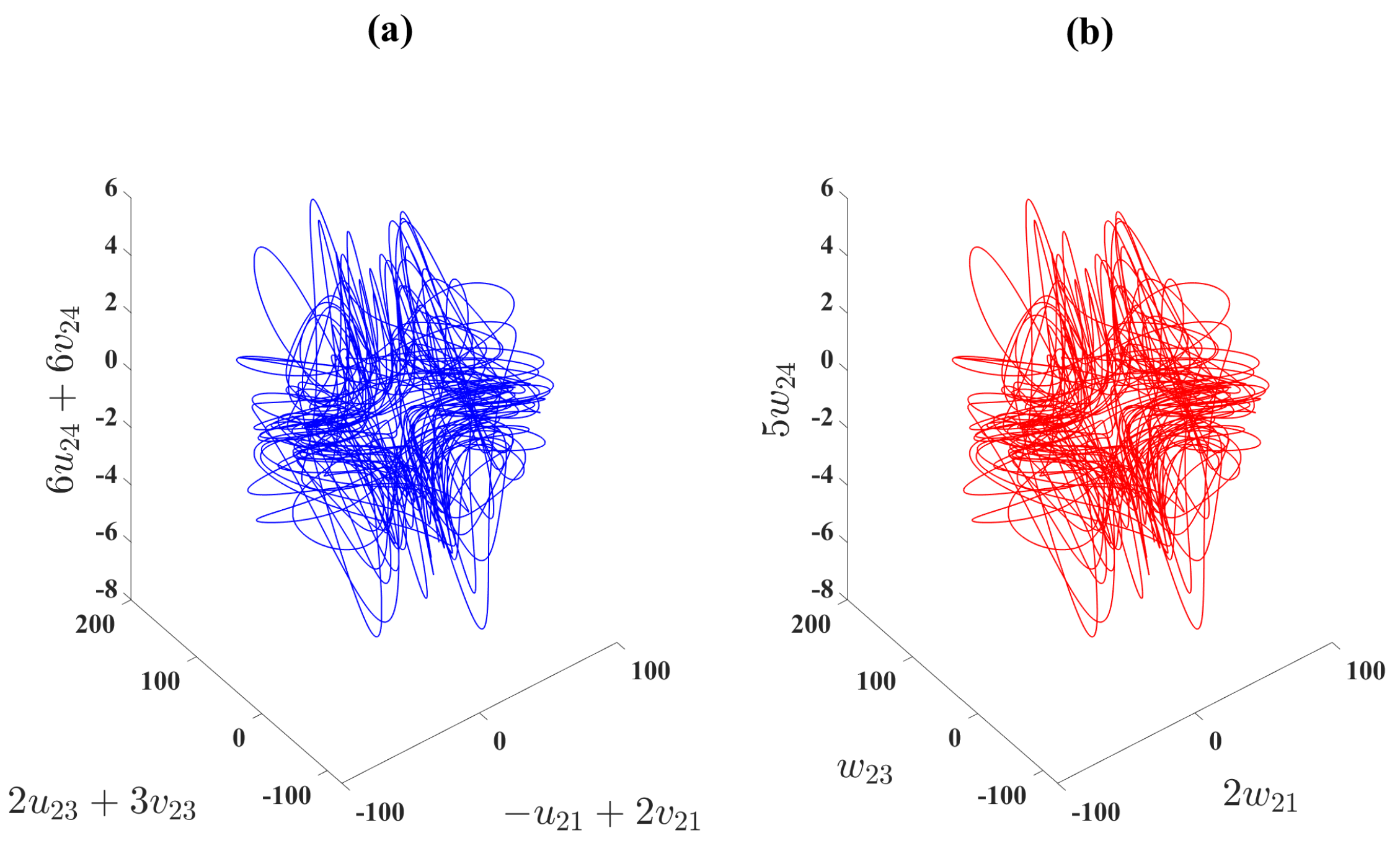
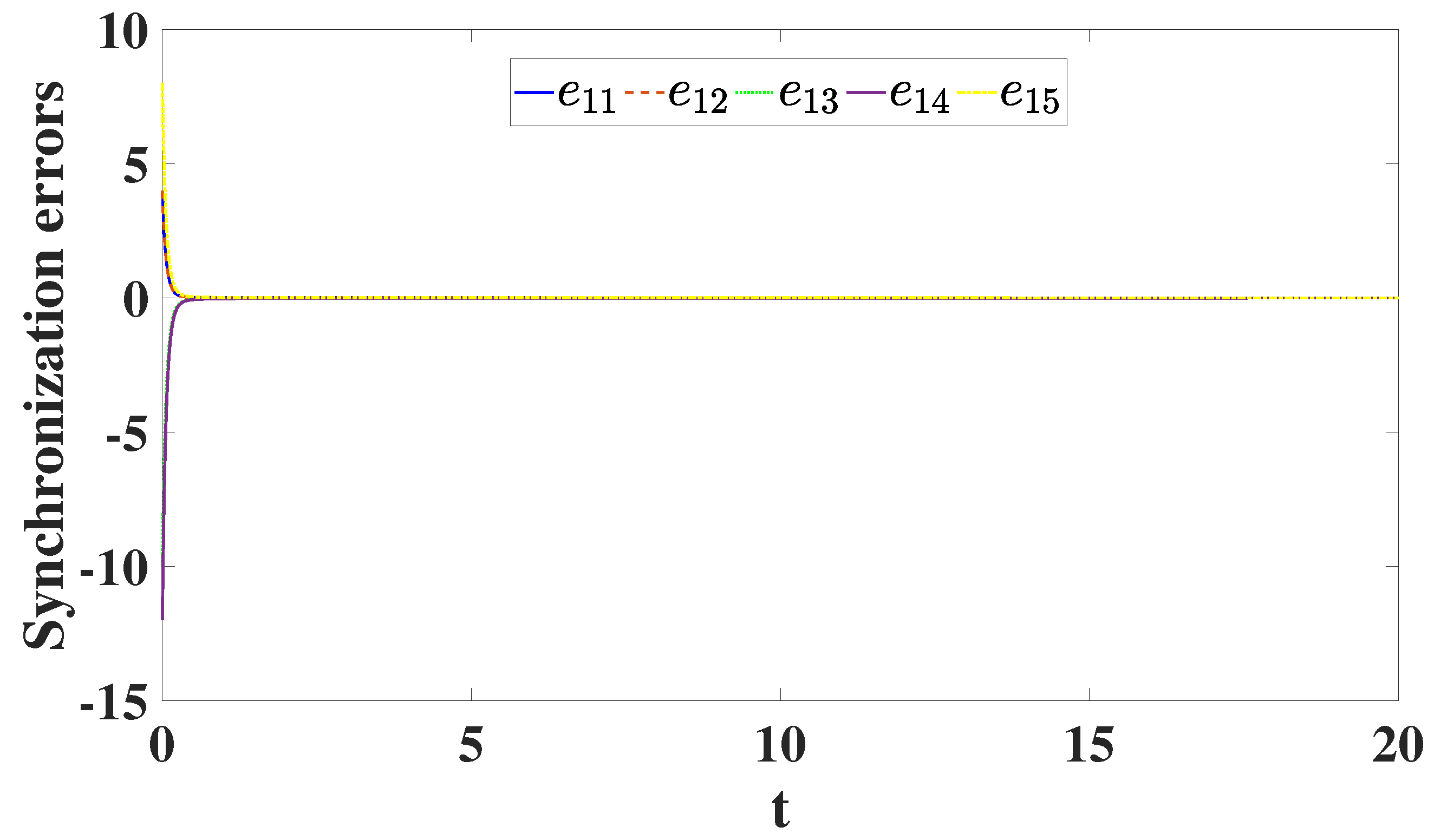
6. A Scheme for DCS Between Integer and Distributed-Order Hyperchaotic Models
A Special Case
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Caputo, M. Elasticita e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Caputo, M. Distributed order differential equations modelling dielectric induction and diffusion. Fract. Calc. Appl. Anal. 2001, 4, 421–442. [Google Scholar]
- Mahmoud, G.M.; Aboelenen, T.; Abed-Elhameed, T.M.; Farghaly, A.A. Generalized Wright stability for distributed fractional-order nonlinear dynamical systems and their synchronization. Nonlinear Dyn. 2019, 97, 413–429. [Google Scholar] [CrossRef]
- Ding, W.; Patnaik, S.; Sidhardh, S.; Semperlotti, F. Applications of distributed-order fractional operators: A review. Entropy 2021, 23, 110. [Google Scholar] [CrossRef] [PubMed]
- Qiao, Y.; Wang, X.; Xu, H.; Qi, H. Numerical analysis for viscoelastic fluid flow with distributed/variable order time fractional Maxwell constitutive models. Appl. Math. Mech. 2021, 42, 1771–1786. [Google Scholar] [CrossRef]
- Li, M.; Pu, H.; Cao, L.; Sha, Z.; Yu, H.; Zhang, J.; Zhang, L. Damage creep model of viscoelastic rock based on the distributed order calculus. Appl. Sci. 2023, 13, 4404. [Google Scholar] [CrossRef]
- Jiang, J. The distributed order models to characterize the flow and heat transfer of viscoelastic fluid between coaxial cylinders. Phys. Scr. 2023, 99, 015233. [Google Scholar] [CrossRef]
- Duan, J.-S.; Hu, D.-C. Vibration systems with fractional-order and distributed-order derivatives characterizing viscoinertia. Fractal Fract. 2021, 5, 67. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Farghaly, A.A.; Abed-Elhameed, T.M.; Aly, S.A.; Arafa, A.A. Dynamics of distributed-order hyperchaotic complex van der Pol oscillators and their synchronization and control. Eur. Phys. J. Plus 2020, 135, 32. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Khalaf, H.; Darwish, M.M.; Abed-Elhameed, T.M. Synchronization and desynchronization of chaotic models with integer, fractional and distributed-orders and a color image encryption application. Phys. Scr. 2023, 98, 095211. [Google Scholar] [CrossRef]
- Tomovski, Ž.; Sandev, T. Distributed-order wave equations with composite time fractional derivative. Int. J. Comput. Math. 2018, 95, 1100–1113. [Google Scholar] [CrossRef]
- Abed-Elhameed, T.M.; Mahmoud, G.M.; Elbadry, M.M.; Ahmed, M.E. Nonlinear distributed-order models: Adaptive synchronization, image encryption and circuit implementation. Chaos Solitons Fractals 2023, 175, 114039. [Google Scholar] [CrossRef]
- Aboelenen, T. Local discontinuous Galerkin method for distributed-order time and space-fractional convection–diffusion and Schrödinger-type equations. Nonlinear Dyn. 2018, 92, 395–413. [Google Scholar] [CrossRef]
- Zeghlache, H.; Mandel, P. Influence of detuning on the properties of laser equations. J. Opt. Soc. Am. B 1985, 2, 18–22. [Google Scholar] [CrossRef]
- Ning, C.-Z.; Haken, H. Detuned lasers and the complex Lorenz equations: Subcritical and supercritical Hopf bifurcations. Phys. Rev. A 1990, 41, 3826. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Bountis, T.; Al-Kashif, M.; Aly, S.A. Dynamical properties and synchronization of complex non-linear equations for detuned lasers. Dyn. Syst. 2009, 24, 63–79. [Google Scholar] [CrossRef]
- Li, X.; Mou, J.; Banerjee, S.; Wang, Z.; Cao, Y. Design and DSP implementation of a fractional-order detuned laser hyperchaotic circuit with applications in image encryption. Chaos Solitons Fractals 2022, 159, 112133. [Google Scholar] [CrossRef]
- Feudel, U. Complex dynamics in multistable systems. Int. J. Bifurc. Chaos 2008, 18, 1607–1626. [Google Scholar] [CrossRef]
- Ngonghala, C.N.; Feudel, U.; Showalter, K. Extreme multistability in a chemical model system. Phys. Rev. E 2011, 83, 056206. [Google Scholar] [CrossRef]
- Bao, B.; Li, Q.; Wang, N.; Xu, Q. Multistability in Chua’s circuit with two stable node-foci. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 043111. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, S. Coexisting attractors generated from a new 4D smooth chaotic system. Int. J. Control Autom. Syst. 2016, 14, 1124–1131. [Google Scholar] [CrossRef]
- Chen, Y.-M. Dynamics of a Lorenz-type multistable hyperchaotic system. Math. Methods Appl. Sci. 2018, 41, 6480–6491. [Google Scholar] [CrossRef]
- Bao, B.; Bao, H.; Wang, N.; Chen, M.; Xu, Q. Hidden extreme multistability in memristive hyperchaotic system. Chaos Solitons Fractals 2017, 94, 102–111. [Google Scholar] [CrossRef]
- Jin, M.; Sun, K.; Wang, H. Dynamics and synchronization of the complex simplified Lorenz system. Nonlinear Dyn. 2021, 106, 2667–2677. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, G.; Iu, H.; Shen, Y.; Liang, Y. Complex dynamics of a non-volatile memcapacitor-aided hyperchaotic oscillator. Nonlinear Dyn. 2020, 100, 3937–3957. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Aboelenen, T.; Abed-Elhameed, T.M.; Farghaly, A.A. On boundedness and projective synchronization of distributed order neural networks. Appl. Math. Comput. 2021, 404, 126198. [Google Scholar] [CrossRef]
- Yang, L.-X.; He, W.-S.; Liu, X.-J. Synchronization between a fractional-order system and an integer order system. Comput. Math. Appl. 2011, 62, 4708–4716. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Jiao, Z.; Chen, Y.; Podlubny, I. Distributed Order Dynamic Systems, Modeling, Analysis and Simulation; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Fernández-Anaya, G.; Nava-Antonio, G.; Jamous-Galante, J.; Muñoz-Vega, R.; Hernández-Martínez, E.G. Asymptotic stability of distributed order nonlinear dynamical systems. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 541–549. [Google Scholar] [CrossRef]
- Yu, J.; Hu, C.; Jiang, H.; Fan, X. Projective synchronization for fractional neural networks. Neural Netw. 2014, 49, 87–95. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Ma, C. Modified projective synchronization of fractional-order chaotic systems via active sliding mode control. Nonlinear Dyn. 2012, 69, 511–517. [Google Scholar] [CrossRef]
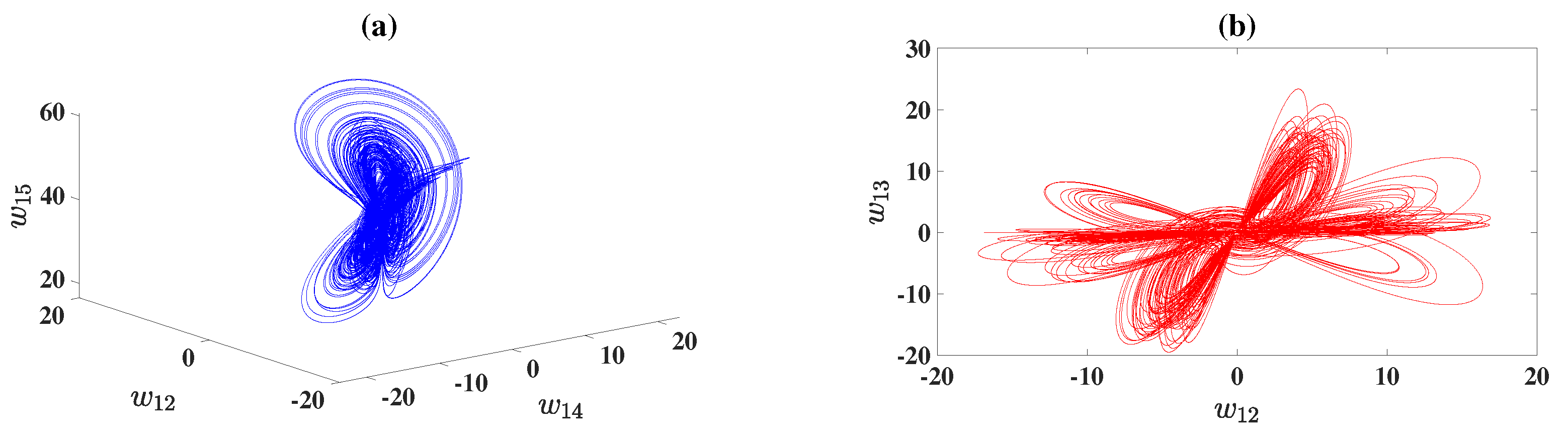

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalaf, H.; Mahmoud, G.M.; Bountis, T.; AboElkher, A.M. A Distributed-Order Fractional Hyperchaotic Detuned Laser Model: Dynamics, Multistability, and Dual Combination Synchronization. Fractal Fract. 2025, 9, 668. https://doi.org/10.3390/fractalfract9100668
Khalaf H, Mahmoud GM, Bountis T, AboElkher AM. A Distributed-Order Fractional Hyperchaotic Detuned Laser Model: Dynamics, Multistability, and Dual Combination Synchronization. Fractal and Fractional. 2025; 9(10):668. https://doi.org/10.3390/fractalfract9100668
Chicago/Turabian StyleKhalaf, Hesham, Gamal M. Mahmoud, Tassos Bountis, and Atef M. AboElkher. 2025. "A Distributed-Order Fractional Hyperchaotic Detuned Laser Model: Dynamics, Multistability, and Dual Combination Synchronization" Fractal and Fractional 9, no. 10: 668. https://doi.org/10.3390/fractalfract9100668
APA StyleKhalaf, H., Mahmoud, G. M., Bountis, T., & AboElkher, A. M. (2025). A Distributed-Order Fractional Hyperchaotic Detuned Laser Model: Dynamics, Multistability, and Dual Combination Synchronization. Fractal and Fractional, 9(10), 668. https://doi.org/10.3390/fractalfract9100668