1. Introduction
Over the past decades, collaborative dynamics within multi-agent systems (MASs) have garnered extensive research interest, fueled by their pervasive real-world applications like unmanned vehicles, sensor networks, and flocking/swarming behaviors [
1,
2,
3,
4,
5]. It is widely acknowledged that consensus serves as the foundational cornerstone of coordination in this field. A significant extension of consensus, containment control, involves scenarios with multiple leaders and followers. The objective here is to engineer control strategies ensuring all followers asymptotically enter the convex hull spanned by the leaders. The inclusion of multiple leaders allows for a richer convex hull representation, enabling more flexible containment regions in practical applications such as multi-target surveillance or cooperative transport. Owing to its practical utility in areas such as robotic movement and unmanned aerial vehicles (UAVs), containment control has emerged as an increasingly prominent research field [
6,
7,
8].
A considerable body of work now exists addressing containment control [
9,
10,
11,
12,
13]. Nevertheless, prevailing research continues to concentrate predominantly on integer-order multi-agent systems (IOMASs). In-depth studies of many phenomena reveal inaccuracies when describing these complex problems using integer-order calculus. Examples span diverse areas, including biological behaviors such as food searching and flocking movement, as well as engineering challenges such as UAV operations in complex environments and the dynamics of vehicles incorporating viscoelastic materials. With the advancement of research, fractional-order systems, which have emerged in this context, can address these issues because of their excellent memory and hereditary properties [
14,
15,
16,
17]. Therefore, fractional calculus can be effectively applied to capture the behavior of complex multi-agent systems, particularly in cases involving organisms at microscopic scales, substances with high viscoelasticity, or movement across challenging substrates such as sand, mud, and vegetated ground. While containment control strategies have proven effective in IOMASs, their extension to fractional-order frameworks remains largely unexplored, necessitating the current investigation.
Recent studies reflect increasing focus on containment control within fractional-order multi-agent systems (FOMASs), with foundational contributions emerging in this domain [
18,
19,
20,
21]. In [
18,
19], Liu et al. established necessary and sufficient conditions for achieving containment in FOMASs with time-varying delays. In [
20], Pang et al. developed both nondelayed and delayed communication protocols for nonlinear FOMASs by leveraging fractional-order Razumikhin methods. A common feature of these approaches is their exclusive reliance on continuous state feedback. Practical implementation challenges arise, however, from the persistent requirement for agents to acquire neighbors’ state data via communication networks. This process not only strains communication bandwidth but also imposes considerable computational loads on onboard sensors and processing units. To address these operational constraints, this study proposes novel practical and resource-efficient control strategies for FOMASs that explicitly overcome the limitations of continuous communication and computational burden.
To deal with the above difficulties, an event-triggered mechanism (ETM) has been presented [
22,
23,
24,
25]. Bipartite containment control is examined in [
22] using an ETM. For nonlinear multi-agent systems featuring input-bounded leaders and time-varying delays, containment control is tackled in [
23] through a dynamic ETM. An ETM framework is utilized in [
24] to investigate containment control of general linear multi-agent systems. Within the domain of FOMASs, ETMs have further facilitated command-filtered adaptive containment control solutions. By design, ETMs restrict controller actuation to event-driven instants determined by local errors, thereby yielding substantial reductions in communication overhead and computational load. This paper introduces a novel event-triggered control framework to overcome the limitations of existing ETMs in fractional-order systems. By incorporating optimized trigger conditions, the proposed design not only guarantees control precision but also improves efficiency in both communication and computational resource utilization.
Although ETMs reduce communication burden, low-frequency triggering mechanisms must be devised to efficiently achieve control objectives. The pull-based event-triggered mechanism (PETM) has recently gained prominence as an effective strategy for minimizing controller update frequency and energy consumption [
26,
27,
28,
29]. In [
26], consensus problems are primarily examined using pull-based event-triggered feedback control, with results further extended to scenarios involving discontinuous communication. Containment control for IOMASs under active leaders is addressed in [
27] via PETM combined with aperiodic sampled-data transmission. In [
28], Jiang et al. tackle the bipartite fixed-time output control problem for heterogeneous systems with an active leader, employing a fully distributed PETM. In [
29], the fully distributed consensus control problem for linear multi-agent systems is investigated using a dynamic double-event-triggered mechanism. Crucially, PETM operates differently from conventional ETMs: follower controllers update solely at their own next triggering instant, independent of neighbors’ events. Despite these valuable contributions, research targeting FOMASs remains notably absent, thus motivating the central focus of the current study.
Given the inherent constraints of limited onboard storage and computational resources in individual agents, researchers have proposed the dynamic event-triggered mechanism (DETM) [
23,
29,
30,
31]. This approach enhances standard event-triggering by incorporating auxiliary dynamic variables into the triggering conditions. The primary benefit is significantly extended inter-event intervals. Particularly beneficial for large-scale networks, this reduction in triggering frequency translates directly to substantial energy savings. However, a practical challenge arises: the computationally intensive eigenvalue calculations required can become prohibitive, hindering real-world deployment. To the best of our knowledge, the design of fully distributed pull-based dynamic event-triggered control protocols for FOMASs remains an open issue and awaits a breakthrough; this forms one key motivation for the present work.
Within real-world multi-agent deployments, communication-induced time delays prove unavoidable [
6,
32]. Such latency not only compromises system efficacy but may also induce instability, necessitating serious attention in design considerations. Despite these critical implications, current containment control research exhibits a notable gap: scant investigation exists into FOMASs subject to time delays. This research void underscores the pressing need for more effective methodologies to address FOMAS containment control under delay constraints. In response, we develop a novel control framework for FOMASs that explicitly incorporates communication delay considerations.
Despite the aforementioned advancements, a significant gap remains in the literature concerning the integration of fractional-order dynamics, communication delays, and a fully distributed pull-based dynamic event-triggered mechanism (PETM) for containment control. Existing works on FOMAS containment control, such as [
18,
19,
20,
21], primarily rely on continuous communication or conventional ETMs, which do not fully address the challenges of limited bandwidth and energy consumption in large-scale networks. While PETM has been successfully applied to integer-order systems [
26,
27,
28,
29] to reduce update frequency, its extension to fractional-order systems with time delays is notably absent. Furthermore, most existing event-triggered containment control strategies for FOMAS either overlook communication delays or require global network information for controller design, limiting their practical applicability in scenarios with limited onboard resources and variable communication latency. Therefore, the development of a fully distributed, delay-tolerant, and resource-efficient containment control protocol for FOMASs represents an open and compelling research problem.
Building upon the preceding analysis, this work explores fully distributed containment control for FOMASs utilizing a novel pull-based dynamic event-triggered strategy. Distinct from existing approaches, our primary contributions encompass the following: (1) Novel Integration of PETM and DETM in FOMASs: This is the first work, to the best of our knowledge, to synergistically combine the advantages of the pull-based mechanism (PETM) and the dynamic event-triggered mechanism (DETM) specifically for fractional-order multi-agent systems. This integration significantly reduces controller updates and communication burden without compromising control performance. (2) Fully Distributed and Delay-Tolerant Design: The proposed protocol is fully distributed, meaning each follower agent relies solely on local information and interactions with its neighbors. It does not require global knowledge of the network topology (e.g., Laplacian eigenvalues) or system parameters. Explicitly incorporating time delays into the control law enhances its robustness and practical relevance. (3) Rigorous Theoretical Guarantees: We provide a rigorous stability analysis using a Lyapunov approach to ensure asymptotic convergence of followers into the leaders’ convex hull. Furthermore, we rigorously prove the exclusion of Zeno behavior, ensuring the practical implementability of the proposed scheme.
The remainder of this paper is organized as follows:
Section 2 provides essential background information, covering graph theory fundamentals and fractional calculus concepts. Moving to the core contribution,
Section 3 details the main findings, specifically outlining the developed control protocols and conducting stability analysis. To validate the theoretical results,
Section 4 offers a simulation case study. Finally,
Section 5 summarizes the key conclusions drawn from this research.
3. Fully Distributed Event-Triggered Containment Control for Time-Delayed FOMASs via a Pull-Based Communication Mechanism
3.1. Problem Statement
Consider a FOMAS comprising
N followers (
) and
M leaders (
), forming a total of
agents. Each agent
exhibits dynamics governed by
where
denotes the fractional order,
the state vector, and
the control input, with
A and
B being constant matrices of compatible dimensions. Leaders are autonomous agents with
, while followers employ the proposed control protocol in Equation (
12) to achieve containment.
Remark 1. Extensive research on fractional calculus establishes that systems of arbitrary order can be reduced to the case through order transformation techniques. Consequently, this work focuses exclusively on the order range. Our objective is to devise distributed control protocols that guarantee containment control for Equation (8). Assumption 1. The subgraph induced by the N followers exhibits connectivity. Furthermore, every follower in the full graph G maintains a directed path to at least one leader.
Assumption 2. (A, B) is stabilizable.
According to Assumption 2, there exists a positive definite solution
P to Equation (
14), which is used to construct the feedback gain
.
Lemma 1 ([
34]).
Under Assumption 1, the follower interconnection matrix is positive definite and invertible, with eigenvalues () exhibiting strictly positive real parts (). Consequently, the product contains exclusively nonnegative entries while maintaining row sums identically equal to unity. Proof Sketch. The positive definiteness of follows from the connectivity of the follower subgraph (Assumption 1) and the fact that is a principal submatrix of the Laplacian L in (2). The row sum property derives from the structure of L: since , we have , thus . Nonnegativity follows from the M-matrix properties of under connected graphs. □
Lemma 2 ([
29]).
For any connected undirected graph G, the Laplacian matrix L possesses a simple eigenvalue , with its smallest nonzero eigenvalue given by the Rayleigh quotient minimization Proof (Proof Sketch). This is a standard result in spectral graph theory. The zero eigenvalue corresponds to the uniform vector due to the row-sum property of L. The constraint ensures that x is orthogonal to the kernel of L, which is spanned by the all-one vector. The positivity of follows from graph connectivity: disconnected graphs would have multiple zero eigenvalues. The Rayleigh quotient formulation emerges from the variational characterization of eigenvalues for symmetric matrices. □
Lemma 3 ([
35]).
If is a continuous function for all , and if , where , and p and M are positive constants, then . To achieve energy-efficient containment control in the FOMAS (Equation (
8)), our controller design employs an event-triggered framework. This approach incorporates a dynamic triggering parameter within the event function, significantly reducing inter-agent communication requirements. We initiate the formulation by defining the aggregated measurement error for each follower agent [
36].
Using the Kronecker product of matrices, Equation (
9) can be written in the following compact form
where
,
,
, and ⊗ denotes the Kronecker product.
Define
as the convex hull (Definition A3) spanned by the leaders’ states. The containment error is then given by
. This work aims to develop a control protocol ensuring asymptotic convergence:
. Through Equation (
10) and the error definition, we derive the fundamental relationship
Thus, the problem of proving reduces to proving .
To realize containment control in the FOMASs (
8), we develop the following fully distributed control strategy
where
,
is time delay,
is the feedback gain matrix,
is the
kth triggered instant of agent
i.
are the adaptive gains of controller with
and they update with the following law:
where
are positive constants.
The adaptive gains represent local control intensities that self-adjust based on containment errors . Each increases with error magnitude, amplifying control effort when needed, and stabilizes as errors diminish. This monotonic non-decreasing behavior ensures sustained control authority while enabling fully distributed implementation without global network knowledge. The fully distributed nature ensures the per-agent computational burden remains constant regardless of network size, providing excellent theoretical scalability.
Leveraging the stabilizability of the matrix pair
, we obtain a positive definite solution
to the algebraic Riccati equation:
where
Q is positive definite [
29]. This solution directly determines the feedback gain matrix
for the control protocol in Equation (
12). The algebraic Riccati Equation (
14) inherently possesses a computational complexity of
, where
n denotes the state dimension.
Remark 2. Generally, control protocol feedback gains require explicit knowledge of Laplacian matrix eigenvalues. However, the proposed adaptive gains enable autonomous self-adjustment, eliminating dependence on global topological information.
The state measurement error for each agent is defined as
The next triggering time
for the
ith agent is determined by
where the triggering condition is defined by
where
,
,
is the arbitrary positive real number,
is the dynamic variable.
Remark 3. Unlike existing approaches [23,24], our pull-based DETM uniquely ensures each follower’s controller updates only at its self-generated triggering instants, irrespective of neighboring agents’ events. This architecture fundamentally reduces controller update frequency and energy consumption while achieving full distribution through adaptive parameters, eliminating dependence on global network characteristics such as Laplacian eigenvalues or agent population size. Employing the Kronecker product, Equation (
9) admits the compact matrix representation:
Thus, the
-order derivative of
satisfies
where
is the diagonal matrix of adaptive gains.
Theorem 1. Subject to the fulfillment of Assumptions 1 and 2, the FOMAS ((Equation8)) attains asymptotic containment control when governed by the PETM ((Equation 12)). This convergence property holds for any bounded delay τ, where the control gain is structured as with P being the solution to the algebraic Riccati Equation (14) for a prescribed positive definite matrix . The sequence of triggering instants is generated through Equations (16)–(18). Proof. Consider the following time-dependent Lyapunov candidate function
where
c and
denote positive constants to be determined.
Under Assumption 1, the follower interconnection matrix
is positive definite. Since
P is the solution to Equation (
14) and is positive definite, the Kronecker product
is also positive definite. Therefore, the first term
is nonnegative and equals zero only when
. The second term
is a sum of squares and is always nonnegative.
From the dynamic triggering condition in Equation (
18), since
,
,
, and
is positive semidefinite, the right-hand side of Equation (
18) is bounded above by
. Using the comparison lemma [
20], it can be shown that if
, then
for all
. Thus, the third term
is nonnegative. Since all three terms are nonnegative and the first term is positive definite in
,
is positive definite for all
.
For the convenience of analysis, denote
,
,
, According to the dynamic triggering conditions in Equations (
16)–(
18), one has
.
Applying the comparison lemma [
20], we obtain
, which implies the positive definiteness of
V.
The time derivative of
admits the following representation:
Recognizing the relationship
, we derive the subsequent expansion
In light of Young’s inequality, it follows that
where
is a positive constant.
Invoking Equation (
13), the fractional derivative of
takes the form
Applying Young’s inequality to the second summation yields
where
.
The derivative of
can be shown as
Integrating the results from Equations (
22) and (
28), we derive the composite fractional derivative bound
where
.
By choosing
with
, we ensure
, which eliminates the third term on the right-hand side of Equation (
29). Thus, we have
Now, recall that
from Equation (
10). Therefore, the second term can be rewritten as
Given the positive definiteness of
, there exists an orthogonal matrix
U such that
, where
for all
i. Let
. Then, the first term becomes
Using the algebraic Riccati Equation (
14),
, we have
Select
, where
is the minimum eigenvalue of
. Then
Through eigenvalue analysis, we can show that the matrix in the bracket is negative definite, and there exists a positive constant
such that
Specifically, by choosing
, we obtain
Equation (
30) indicates that the fractional derivative of
is non-positive for all
. To apply Lemma 3, we integrate both sides of Equation (
30) from
to
t using the fractional integral operator
Since
for all
, we have
Taking the limit as
Now, applying Lemma 3 with
,
, and
, we conclude that
which implies
since
is bounded. This completes the proof that containment control for FOMAS in Equation (
8) is achieved. □
Remark 4. Unlike the consensus methods in [37,38] that necessitate global eigenvalue information of the asymmetric Laplacian matrix, the adaptive strategy in Equation (12) operates solely based on individual agent dynamics and local neighbor interactions. This design enables fully decentralized computation and execution by every agent. Event-triggered control in FOMAS may induce Zeno behavior—an impractical phenomenon in real-world applications. Consequently, establishing exclusion conditions for such behavior becomes essential. Motivated by this objective, we develop the subsequent theorem.
Theorem 2. The fully distributed pull-based event-triggered control strategy in Equation (12) effectively eliminates Zeno phenomena. Proof. According to Lemma 2, agent states
remain bounded, implying boundedness of their fractional derivatives
. Consequently, we can select a positive constant
W satisfying
,
where
. For any interval
, combining the error definition
with norm contraction properties yields
With the help of the definition of fractional order calculus, Equation (
32) can be further expressed as
Since
for all
i and
t, we have
We compute each integral separately, and substitute these results into Equation (
34)
Using the property that for
and
, we have
, we can further simplify
Therefore, the upper bound becomes
Recalling that
, we finally obtain
Since the trigger condition , i.e., , and , we have and the inequality , so . Clearly, for all , holds, i.e., Zeno behavior is excluded. □
3.2. Guidance on Parameter Tuning
The practical implementation and performance of the proposed control protocol hinge on the appropriate selection of parameters , , , and .
The parameter , originating from Young’s inequality, modulates the trade-off between control effort and triggering frequency. Larger values of (e.g., between 1 and 3) relax the triggering condition, reducing controller updates but potentially slowing convergence. The parameter , introduced in the error bound estimation, influences the weighting between current and delayed state errors. Increasing (typically between 1.5 and 3) enhances tolerance to measurement errors, further reducing communication at the cost of transient performance.
The scaling factor directly affects the sensitivity of the triggering condition. Larger values lead to more frequent updates and higher precision, suitable for critical agents, while smaller values conserve energy. A uniform initial choice of is often effective. The decay rate governs the dynamics of the auxiliary variable . A larger (e.g., 0.5 to 1) accelerates the decay of , tightening the triggering condition and increasing updates, whereas smaller values (e.g., 0.1 to 0.3) promote longer inter-event intervals.
A recommended tuning procedure begins with conservative values: , , , and for all i. Convergence speed can be improved by slightly decreasing or , while communication overhead can be reduced by increasing them. If oscillations occur, increasing or enhances stability. Since these parameters are fully distributed and independent of global network information, they can be adjusted online or via simulation-based sensitivity analysis, ensuring the protocol remains practical and adaptable to various network conditions.
4. Simulation Examples
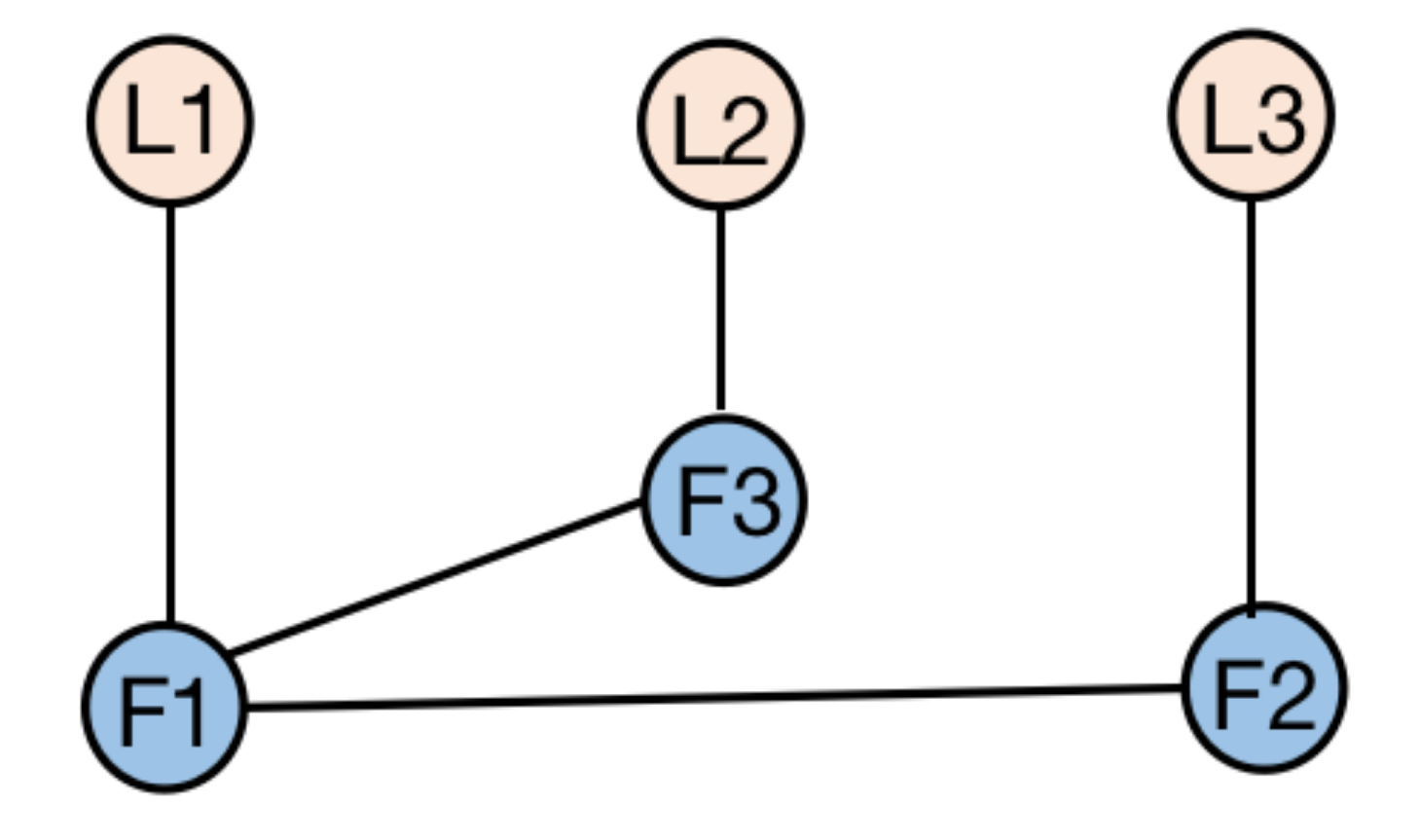
This section presents a numerical validation case study to verify the feasibility and effectiveness of the theoretical framework. The associated communication topology, comprising three leaders (
) and three followers (
), is depicted in
Figure 1.
Taking the system matrices
A and
B in the FOMAS dynamics Equation (
8), respectively, as
The control gains were configured as follows: the Riccati equation solution
feedback gain matrix
, and adaptive gain parameters
,
,
. The event-triggering threshold was set to
for all followers.
With
, the parameters are set to
,
,
,
. Other algorithm parameters were selected to ensure stability while maintaining reasonable triggering frequency, with their evolution governed by the adaptive laws in Equations (
13) and (
18). The initial values of each agent state are
,
,
,
,
,
, and denote by
the
jth state component of the
ith agent.
Implementing the distributed control protocol from
Section 3.1 yields the simulation outcomes shown in
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6 and
Figure 7. These results confirm that follower states successfully converge to the leaders’ convex hull, validating the containment control strategy’s performance.
This simulation employs
and
.
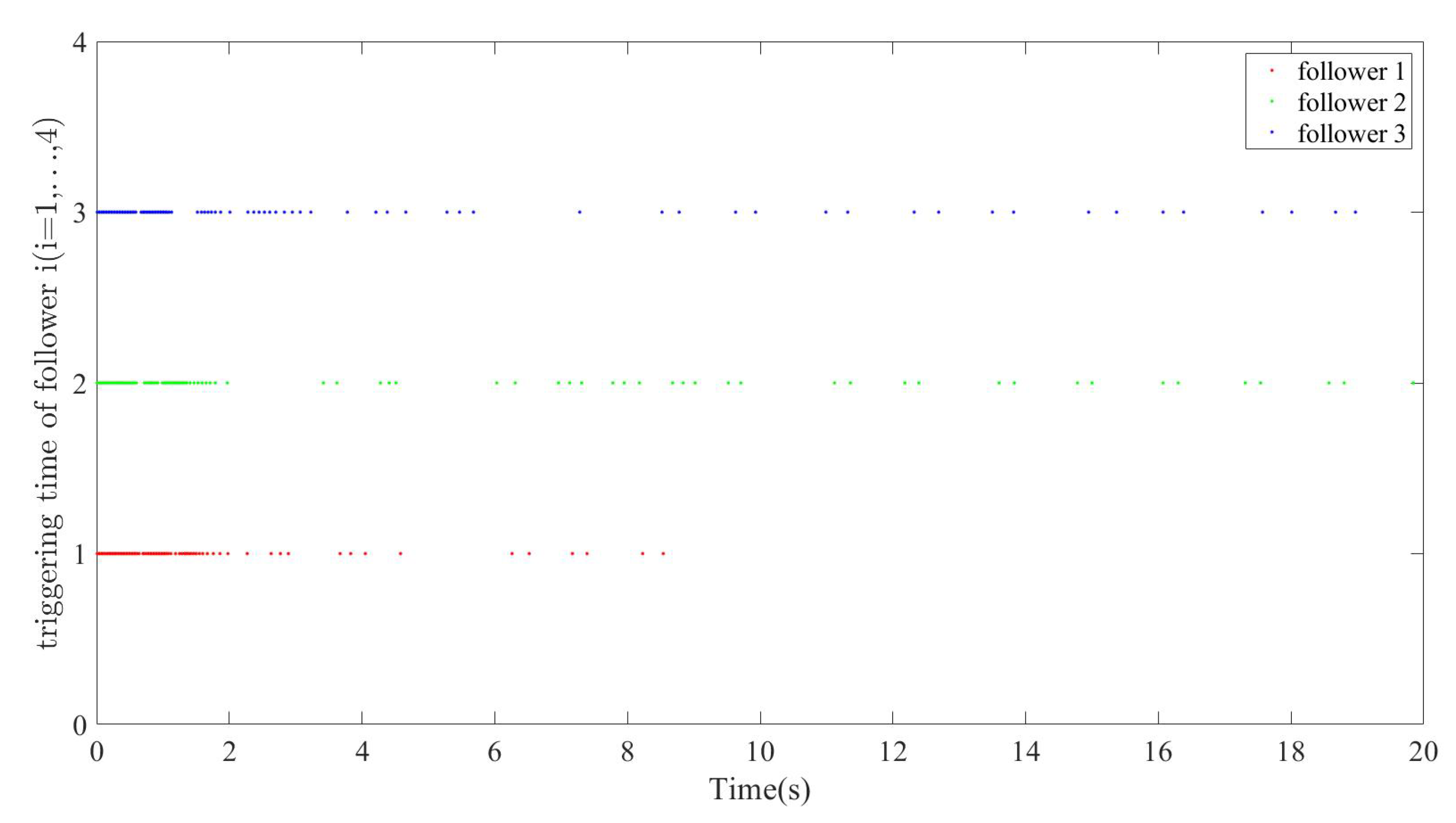
Table 1 documents all controller triggering instants for followers during this finite horizon, alongside the update count without triggering. The substantial computational reduction afforded by the ETM is evident from comparative analysis. The recorded minimum inter-event times are 0.010 s for Follower 1, 0.010 s for Follower 2, and 0.010 s for Follower 3. These strictly positive values provide numerical evidence that the proposed event-triggered mechanism successfully avoids Zeno behavior in practice, confirming the theoretical guarantees.
Figure 4 visually documents the triggering chronology for each follower agent.
Through
Figure 4, not only can we visualize the reduction in the number of triggers, but we can also conclude that the FOMAS avoids the Zeno behavior very well under the effect of control protocol (
12).
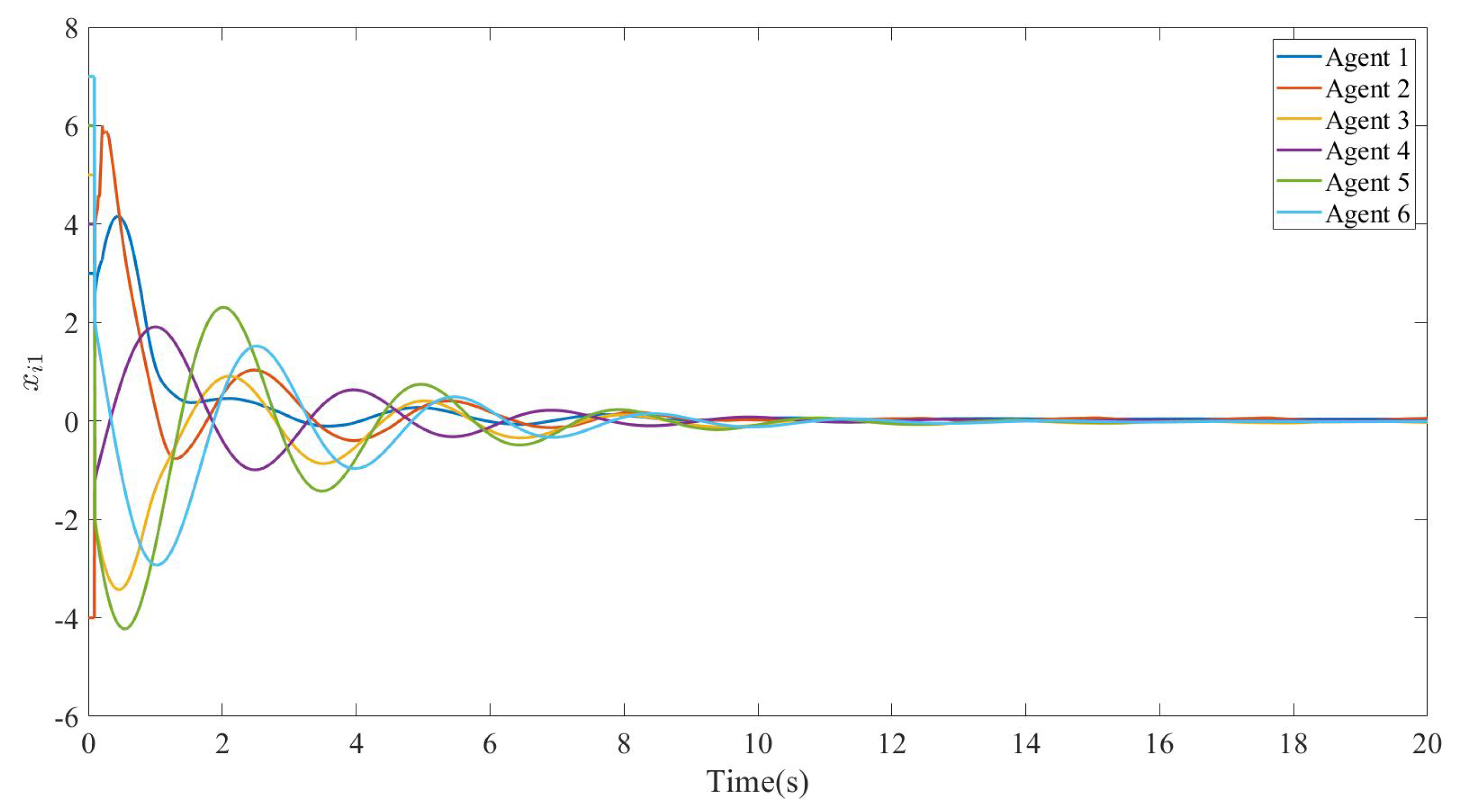
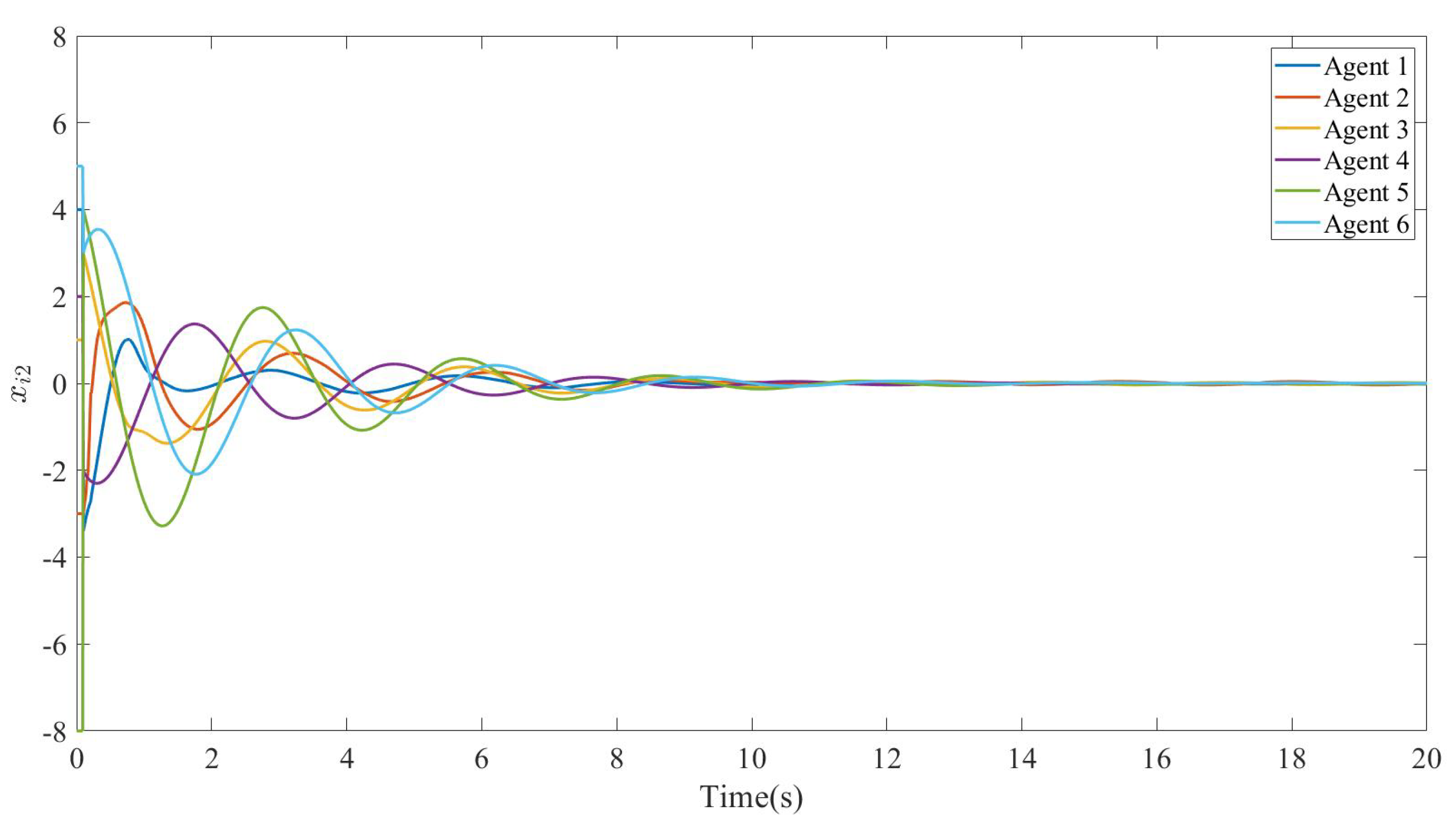
Since the states of the numerically simulated agents in this algorithm are two-dimensional,
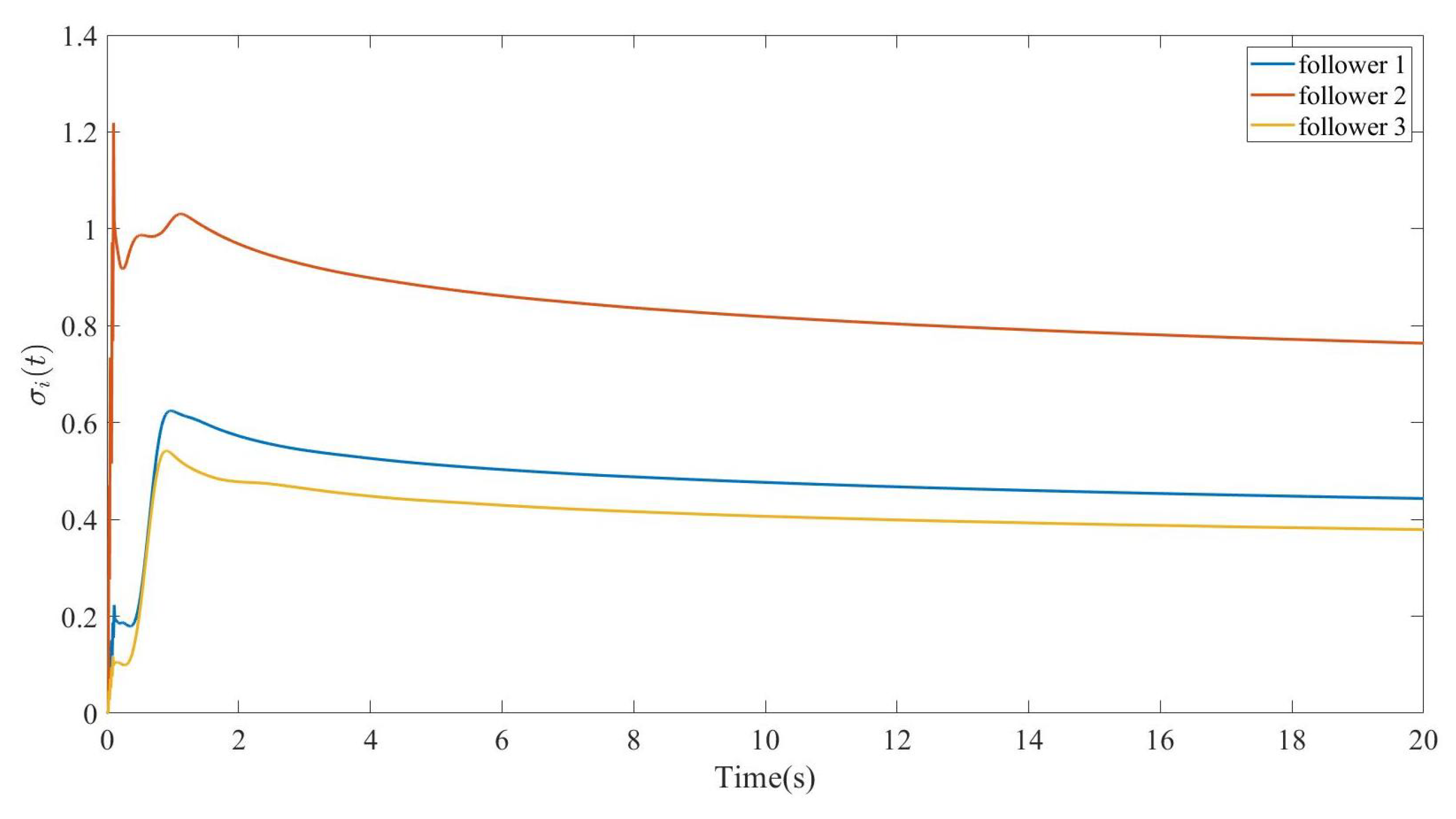
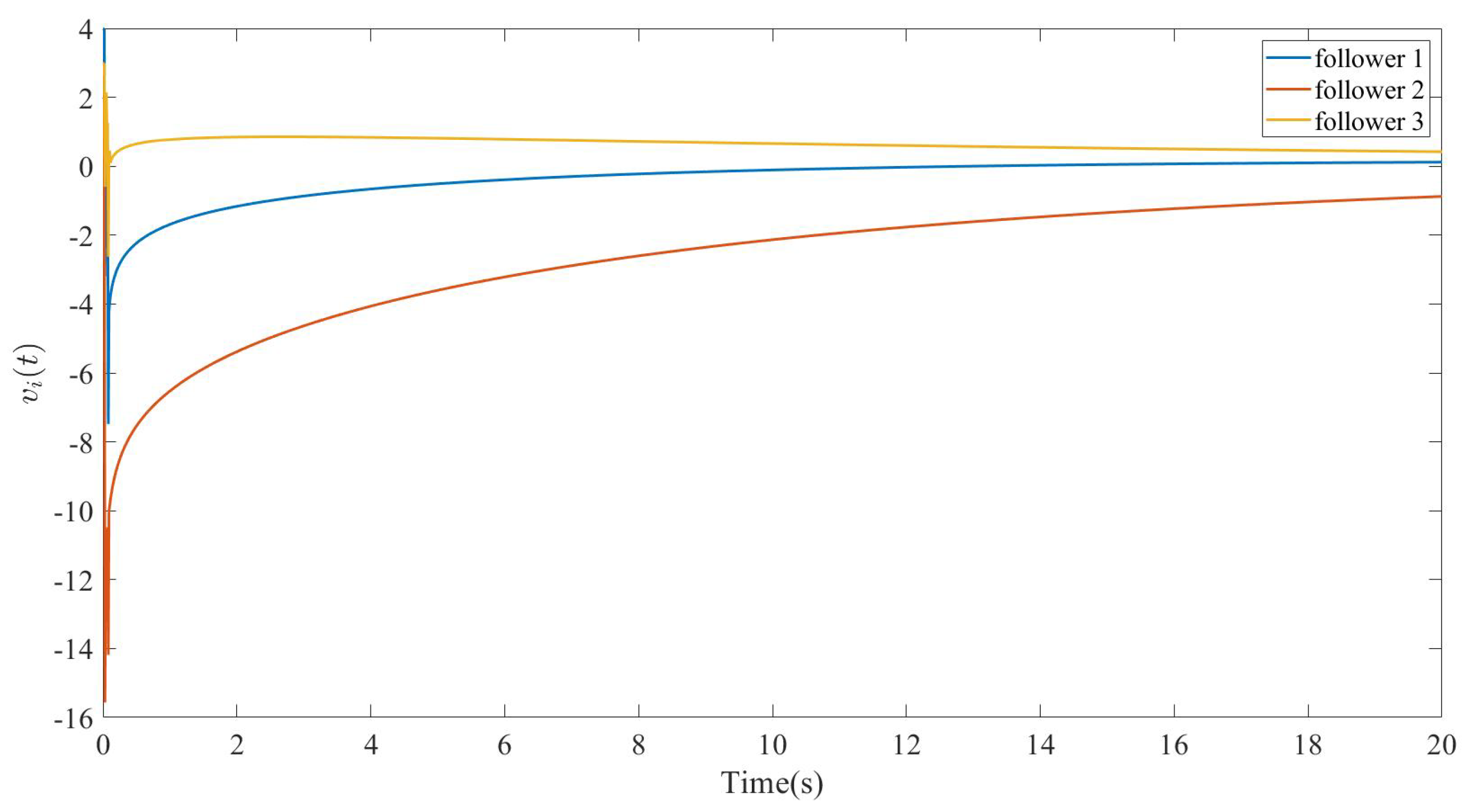
Figure 5 and
Figure 6 depict the information of the first and second components of the states of each agent, respectively. The figures show all follower state components converging to the convex hull spanned by the leaders’ states, confirming successful containment control in FOMASs.
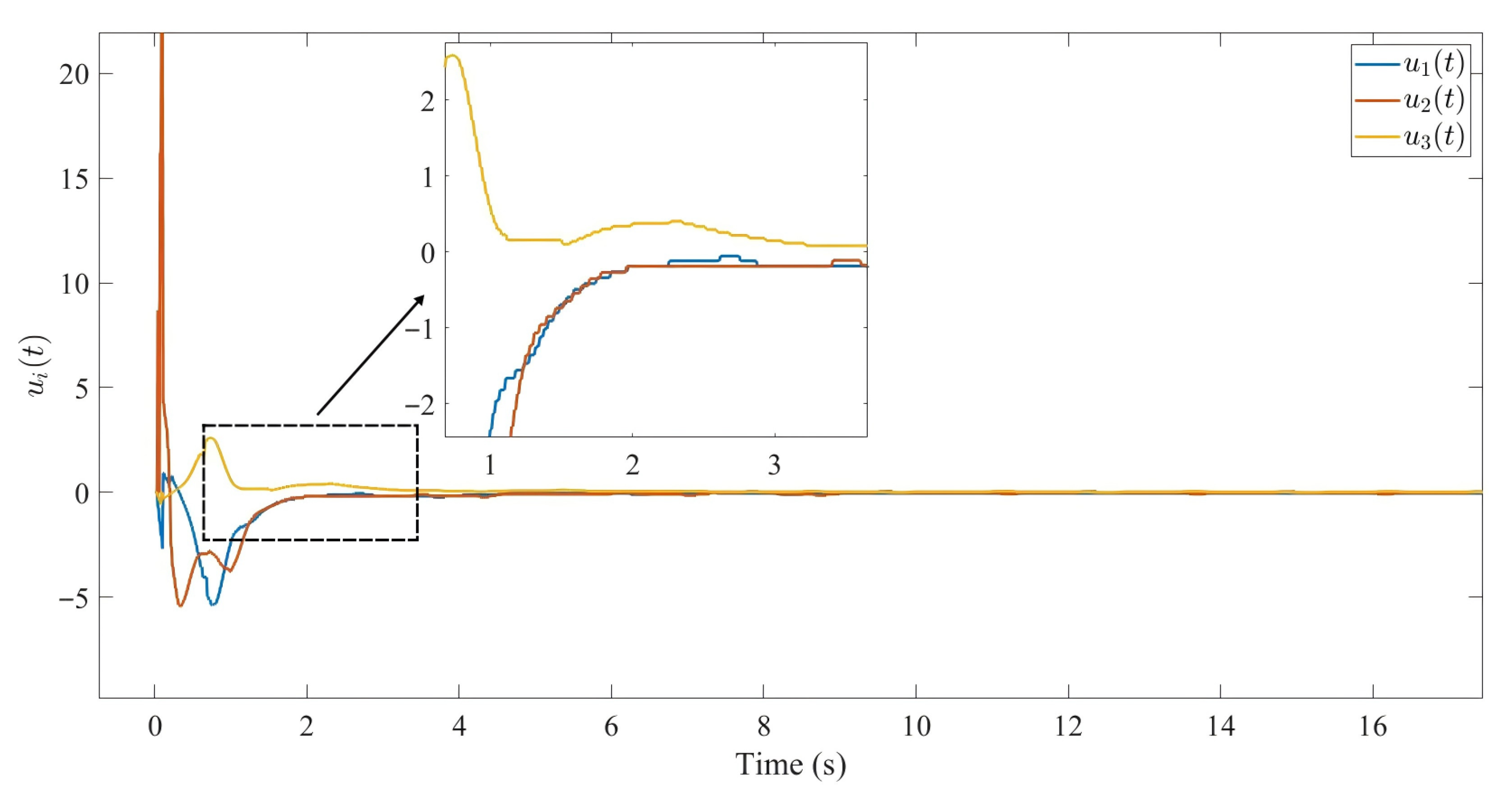
Figure 7 illustrates the bounded containment errors fluctuating near zero. The evolution of control inputs
is shown in
Figure 8, further validating the effectiveness of the event-triggered mechanism in reducing control updates. The ensemble of results conclusively establishes asymptotic containment control realization in FOMAS (
8) for any bounded input delay.
In summary, it can be seen that under the fully distributed pull-based dynamic event-triggered control protocol (
12), the containment control of FOMASs (
8) can be realized, and the computational cost and communication consumption can be greatly reduced.