Finite-Time Modified Function Projective Synchronization Between Different Fractional-Order Chaotic Systems Based on RBF Neural Network and Its Application to Image Encryption
Abstract
1. Introduction
2. Some Preliminaries
2.1. Fractional Calculus
2.2. Modified Function Projective Synchronization (MFPS)
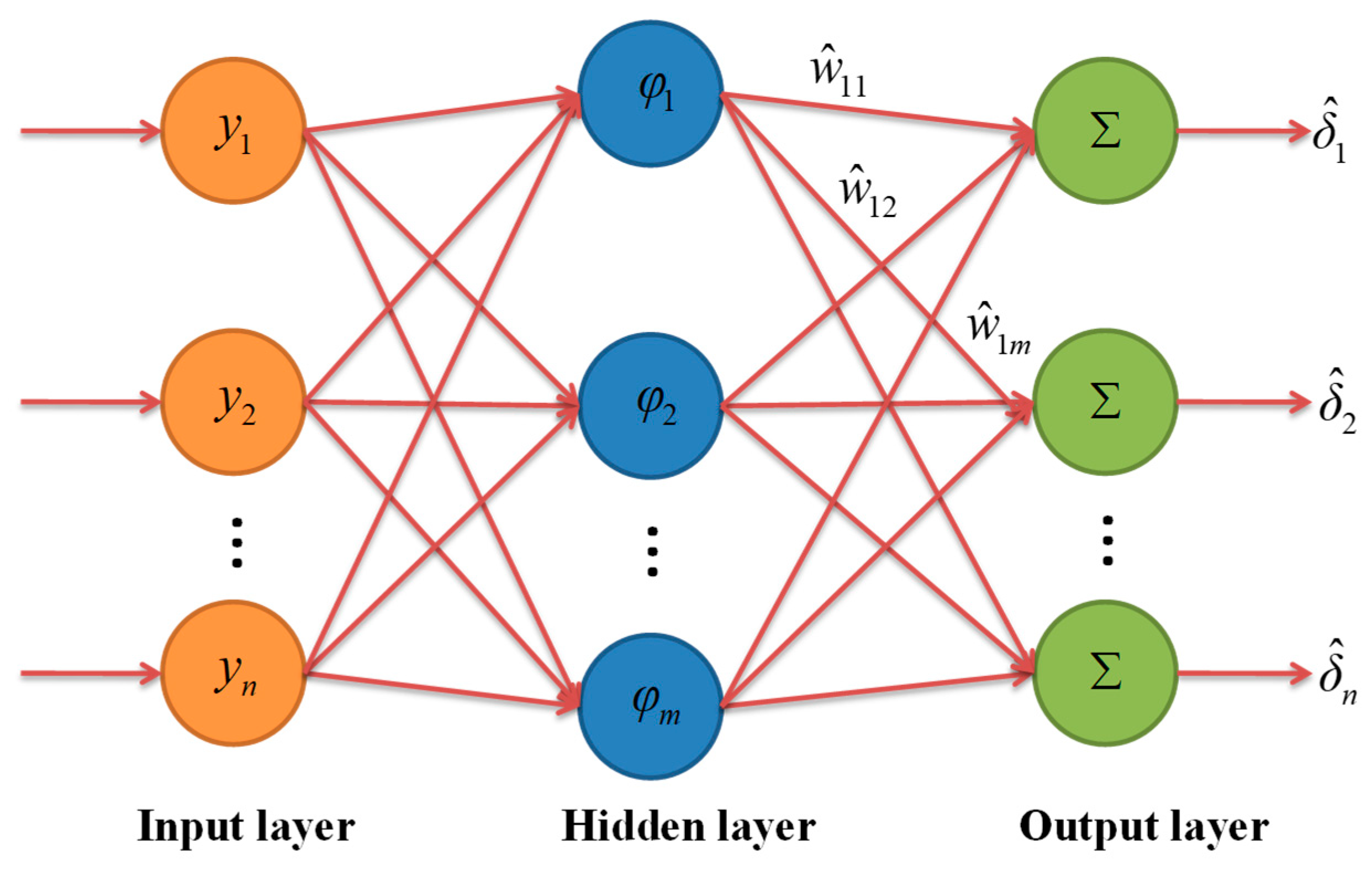
2.3. RBF Neural Networks Estimator
3. Finite-Time MFPS Controller Design
3.1. Problem Description
3.2. Fractional Terminal Sliding Surface
3.3. Terminal Sliding Mode Control with RBF Neural Network
4. Simulation Results
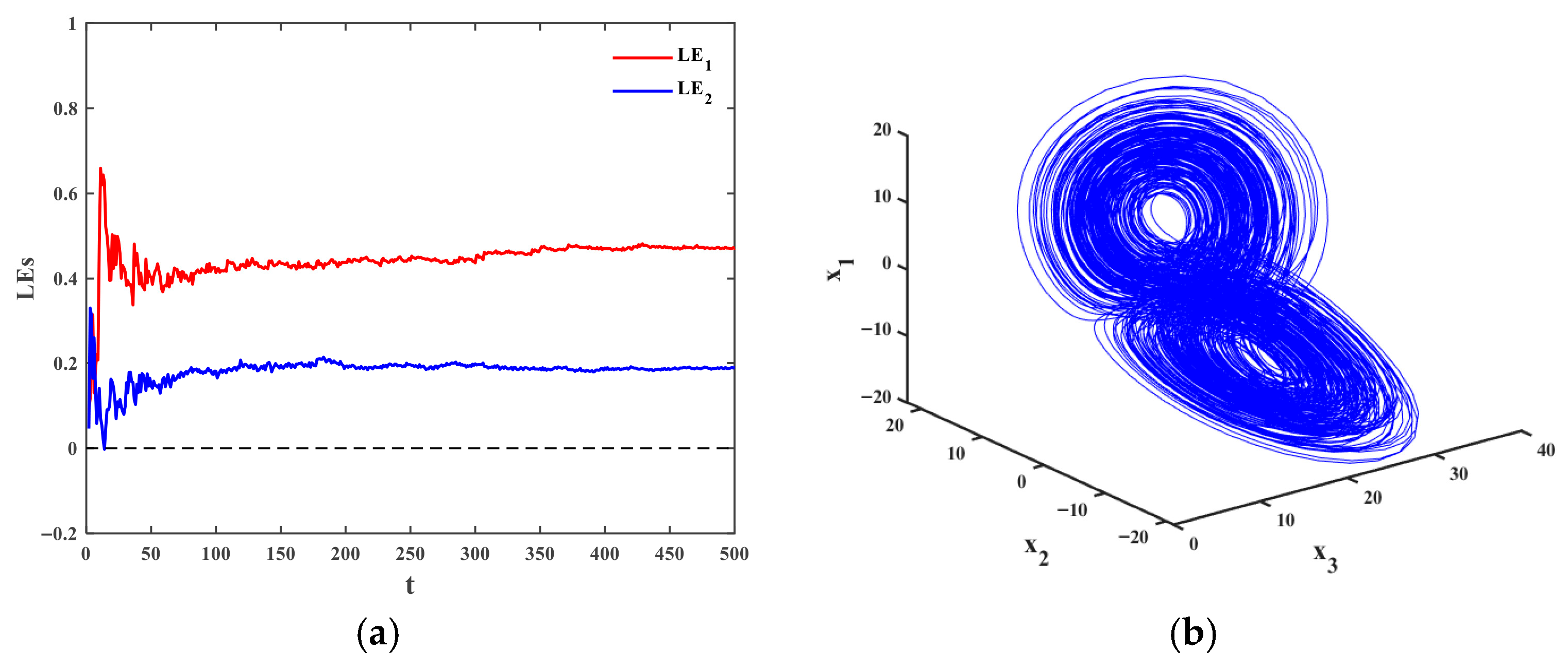
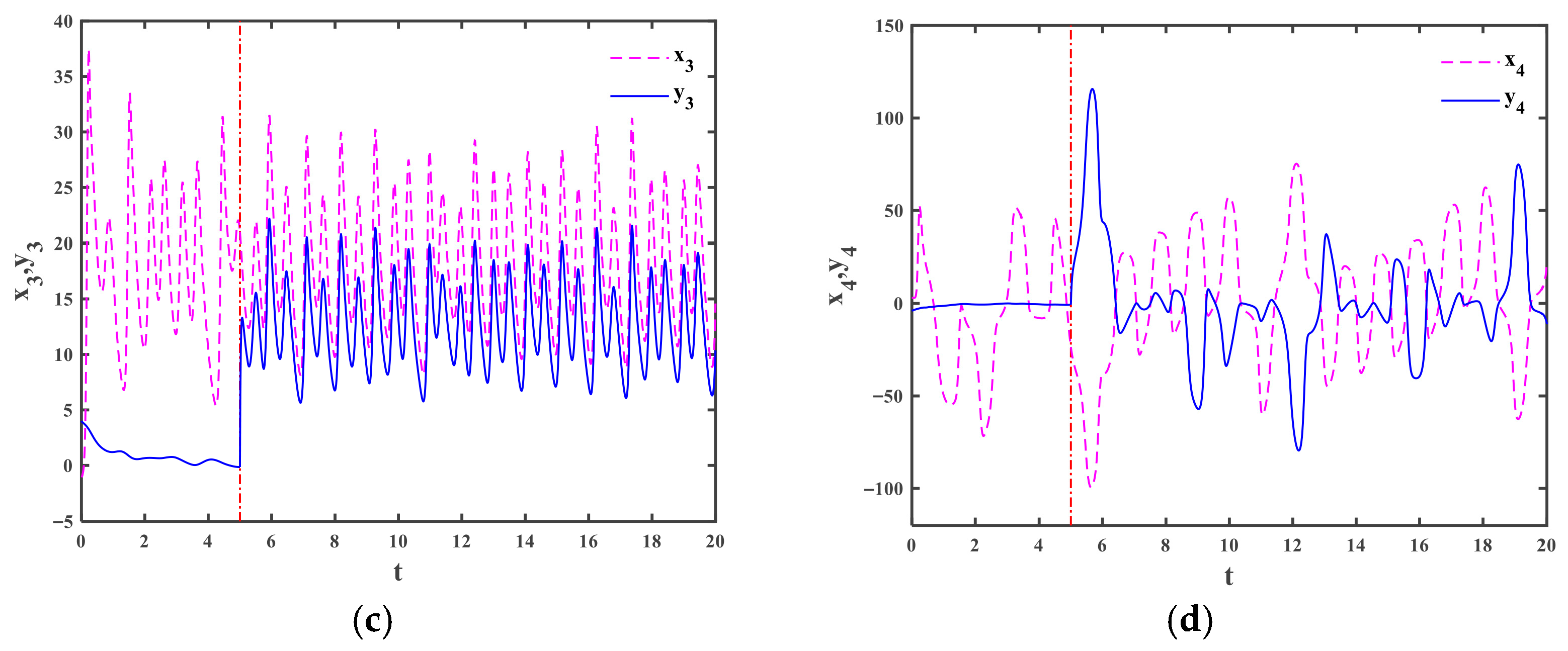
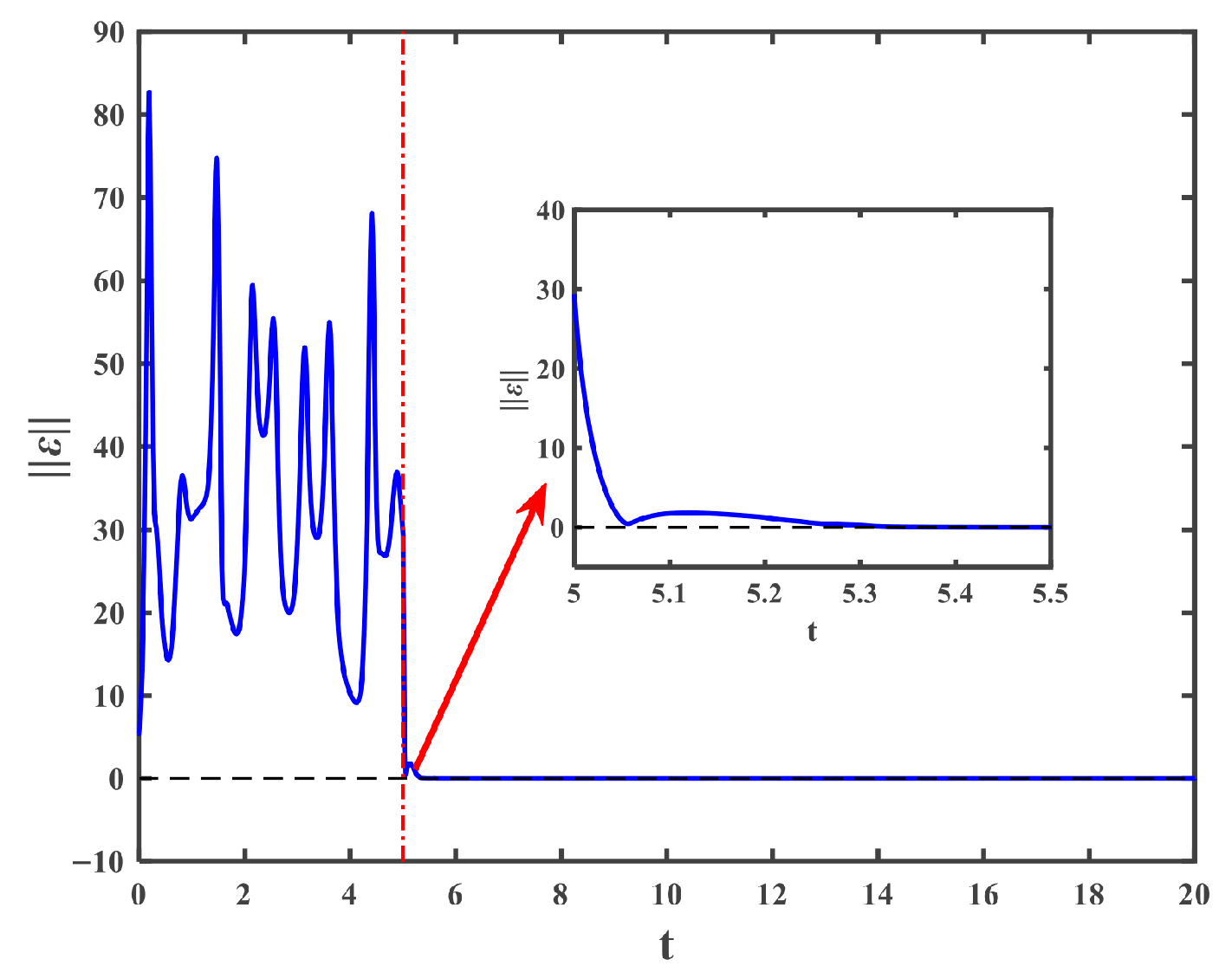
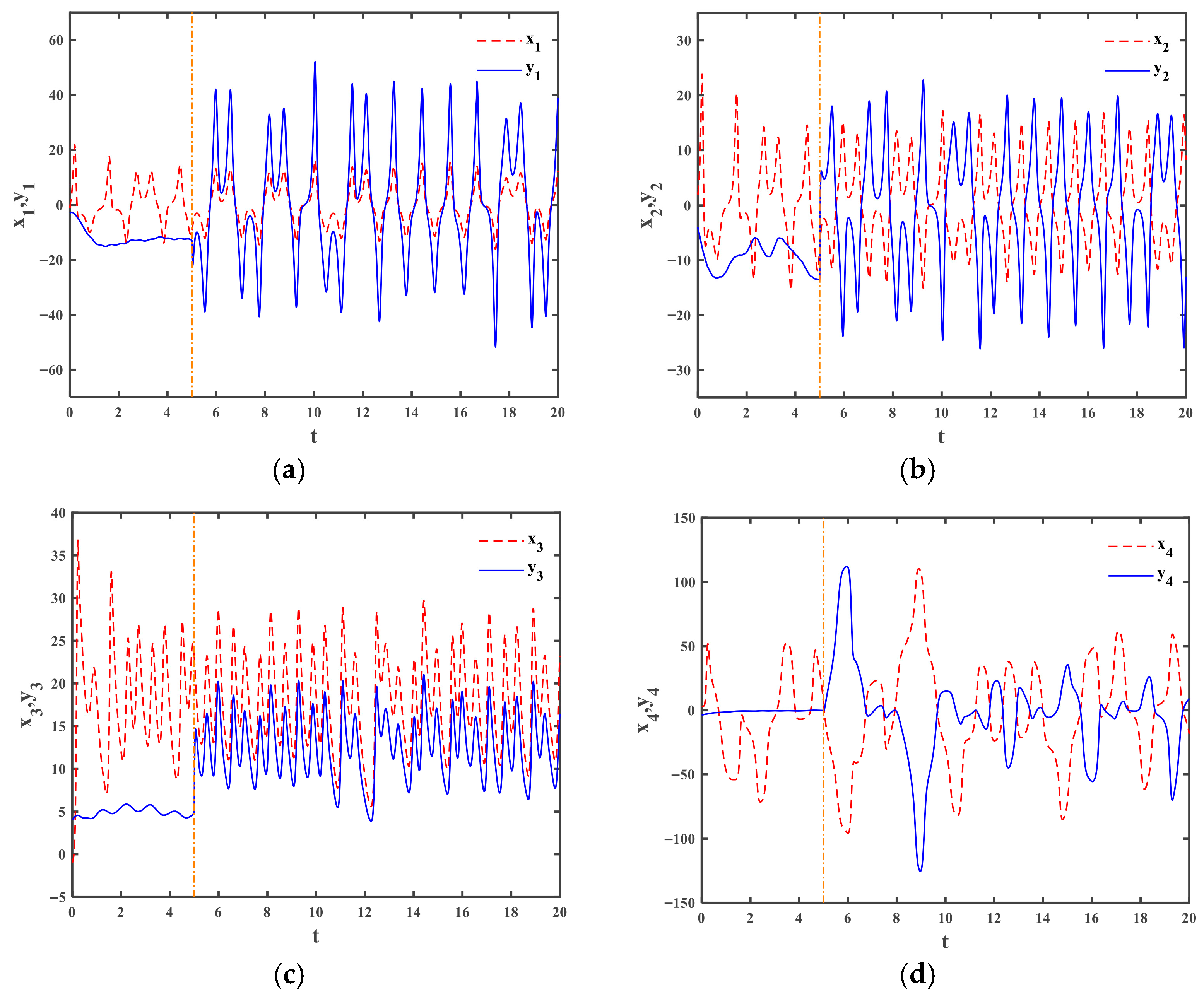
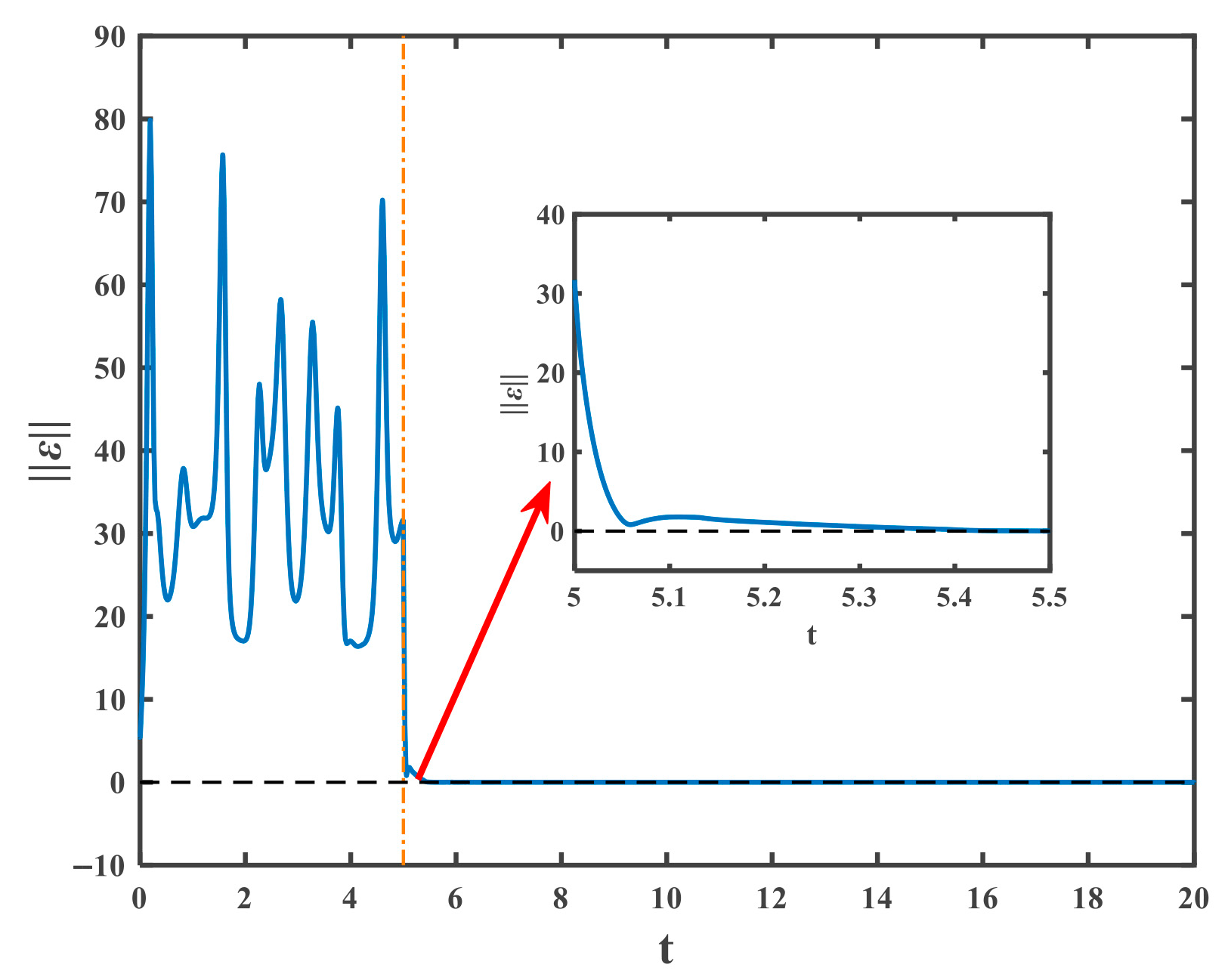
4.1. The Drive and the Response Systems with Periodic Disturbances
4.2. The Drive and Response Systems with Noise Disturbance
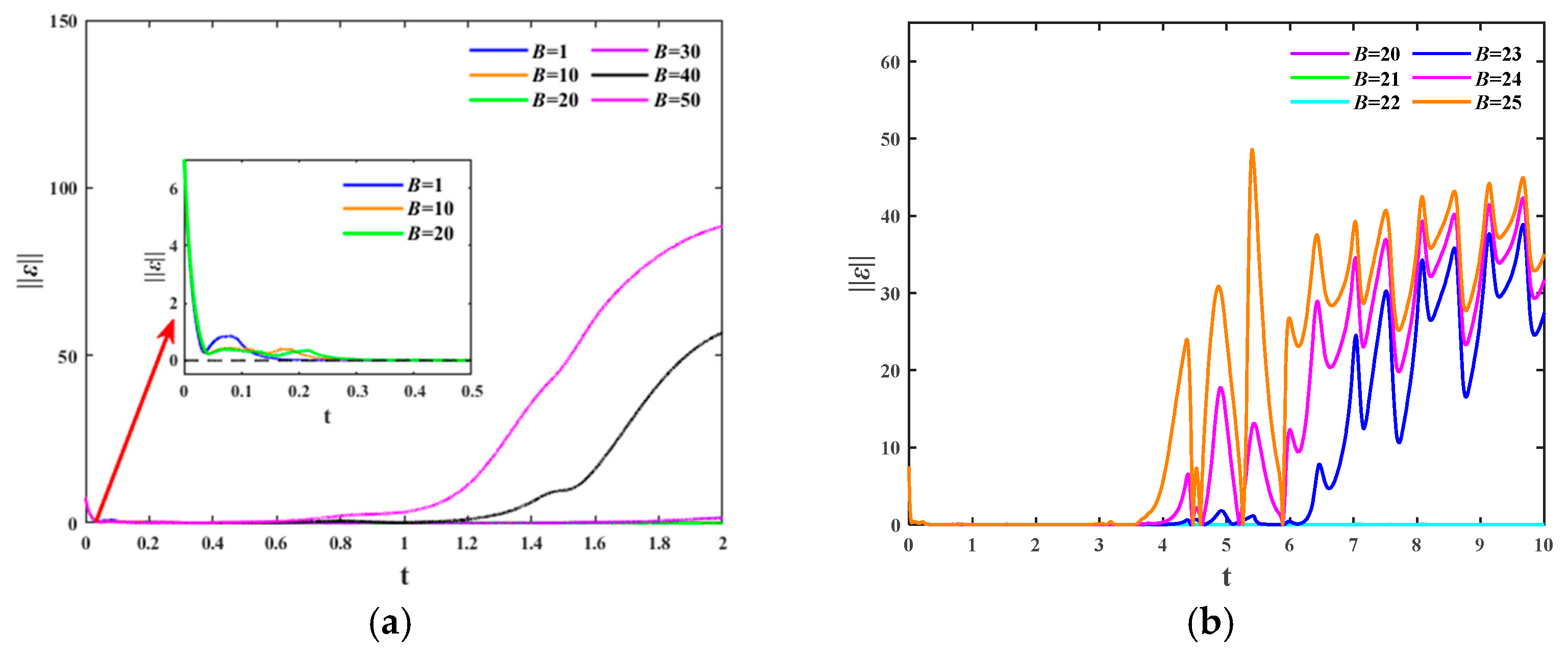
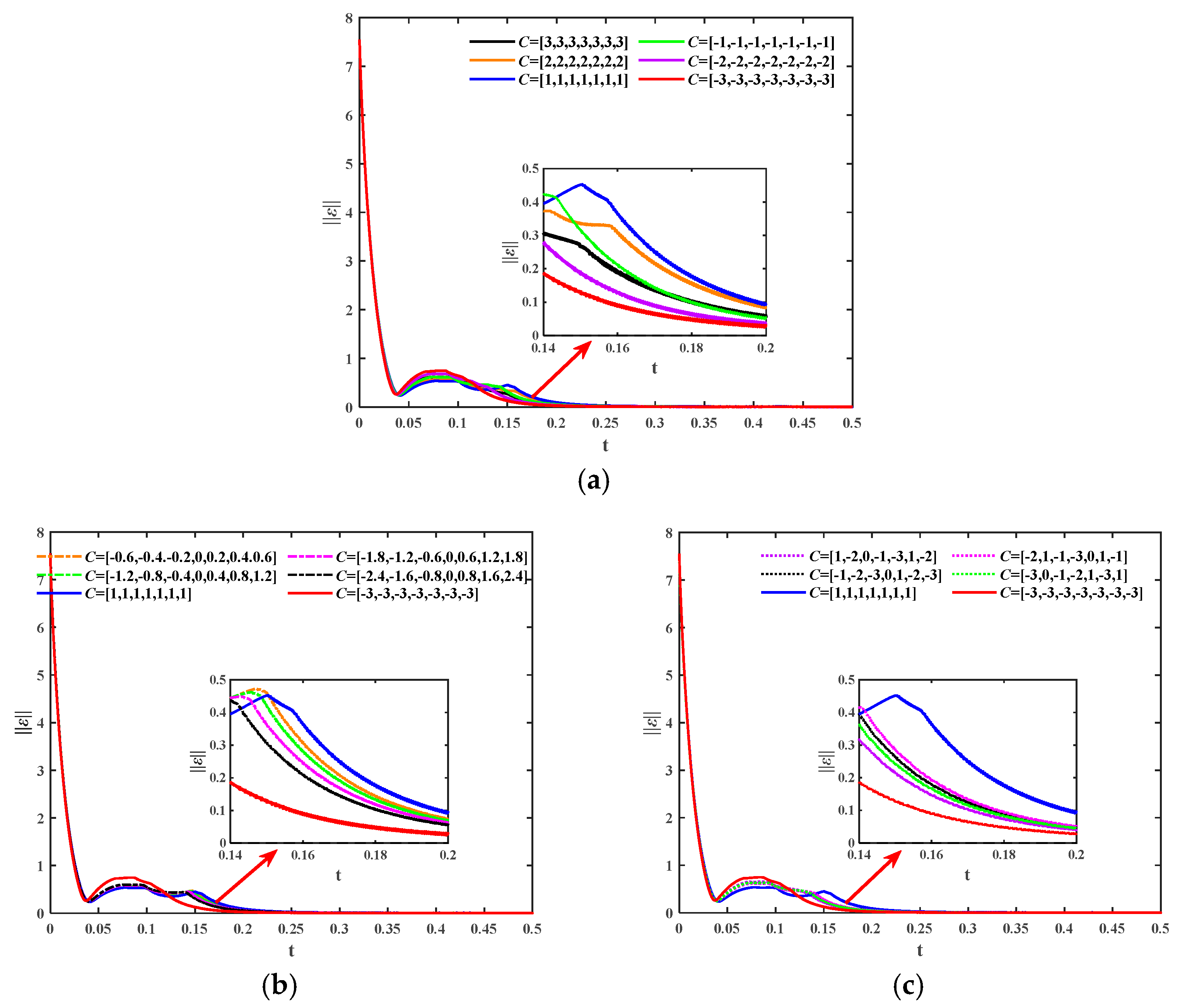
4.3. The Effect of RBF Neural Network Parameters
5. Image Cryptography Based on the Finite-Time MFPS
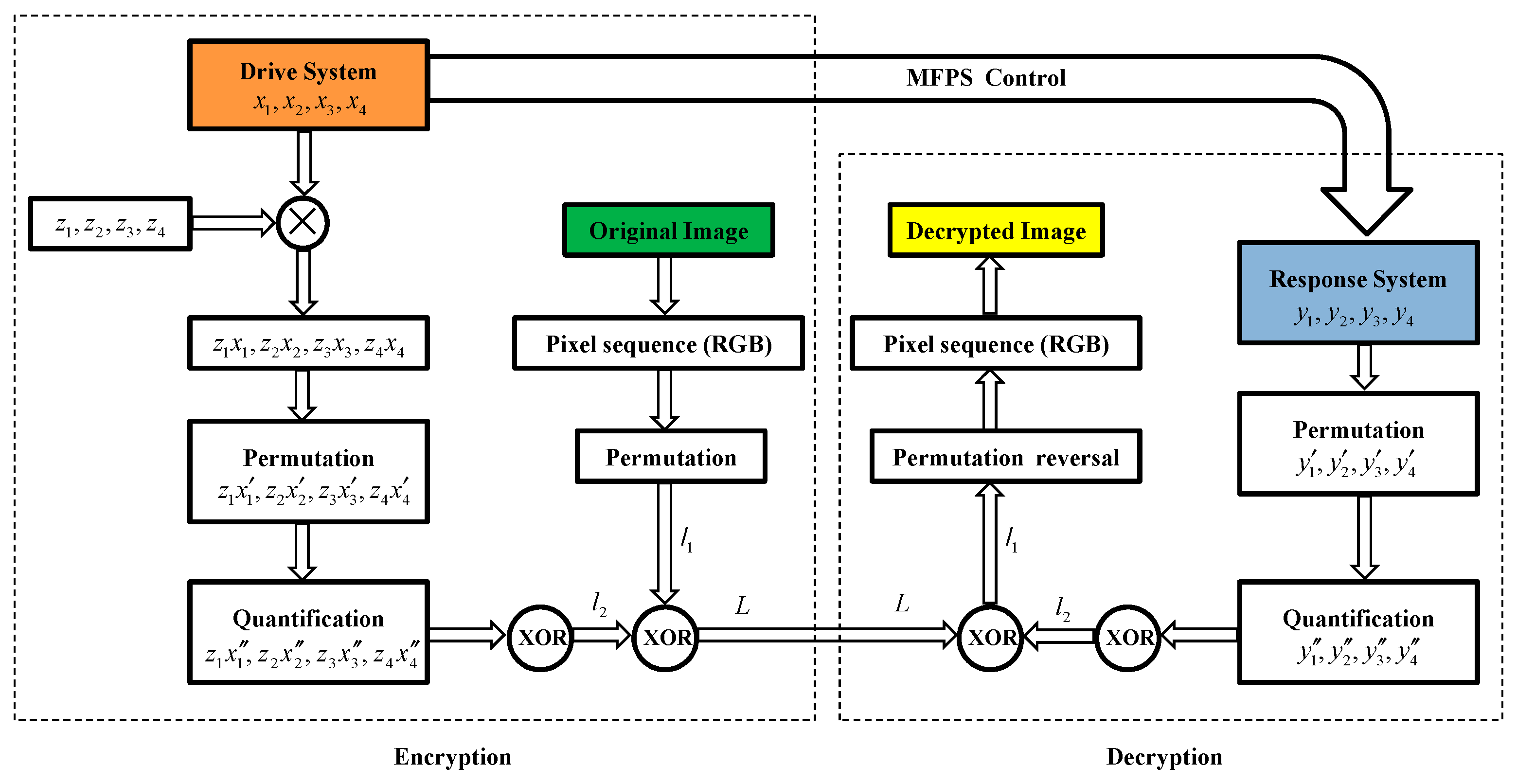
5.1. Proposed Encryption and Decryption Scheme
5.2. Simulated Experiments
5.3. Statistics and Security Analysis
5.3.1. Key Space Analysis
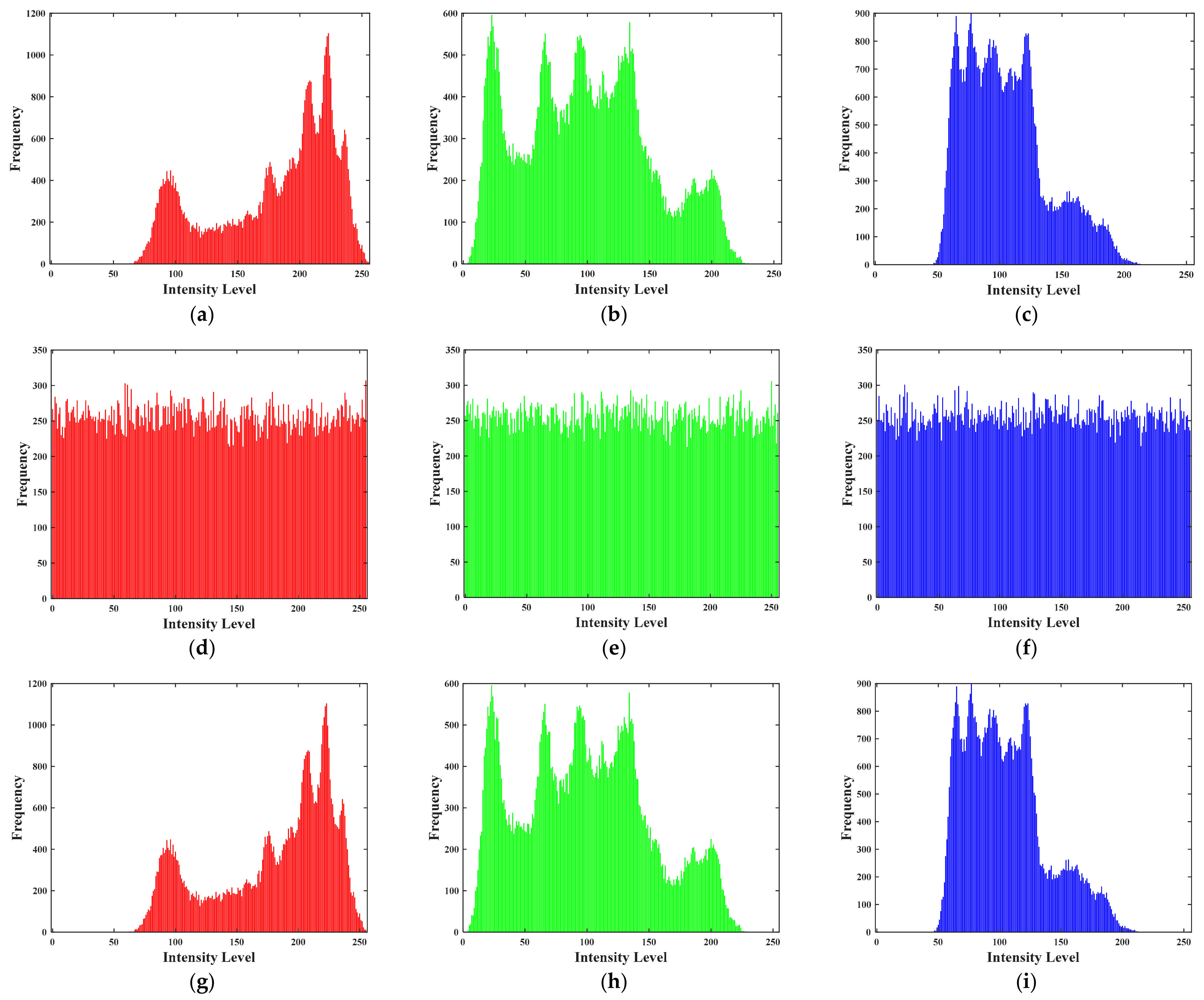
5.3.2. Histogram Analysis
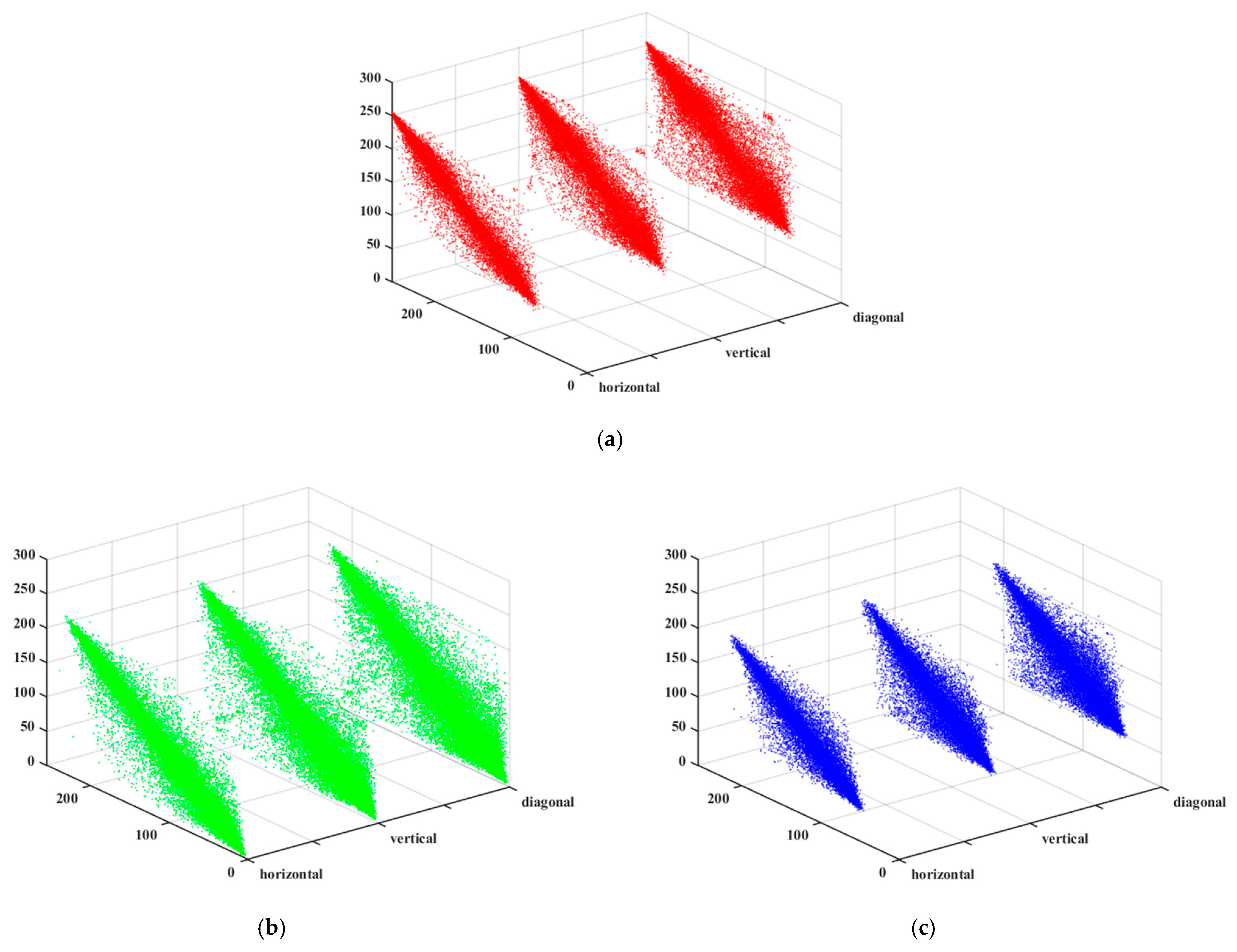
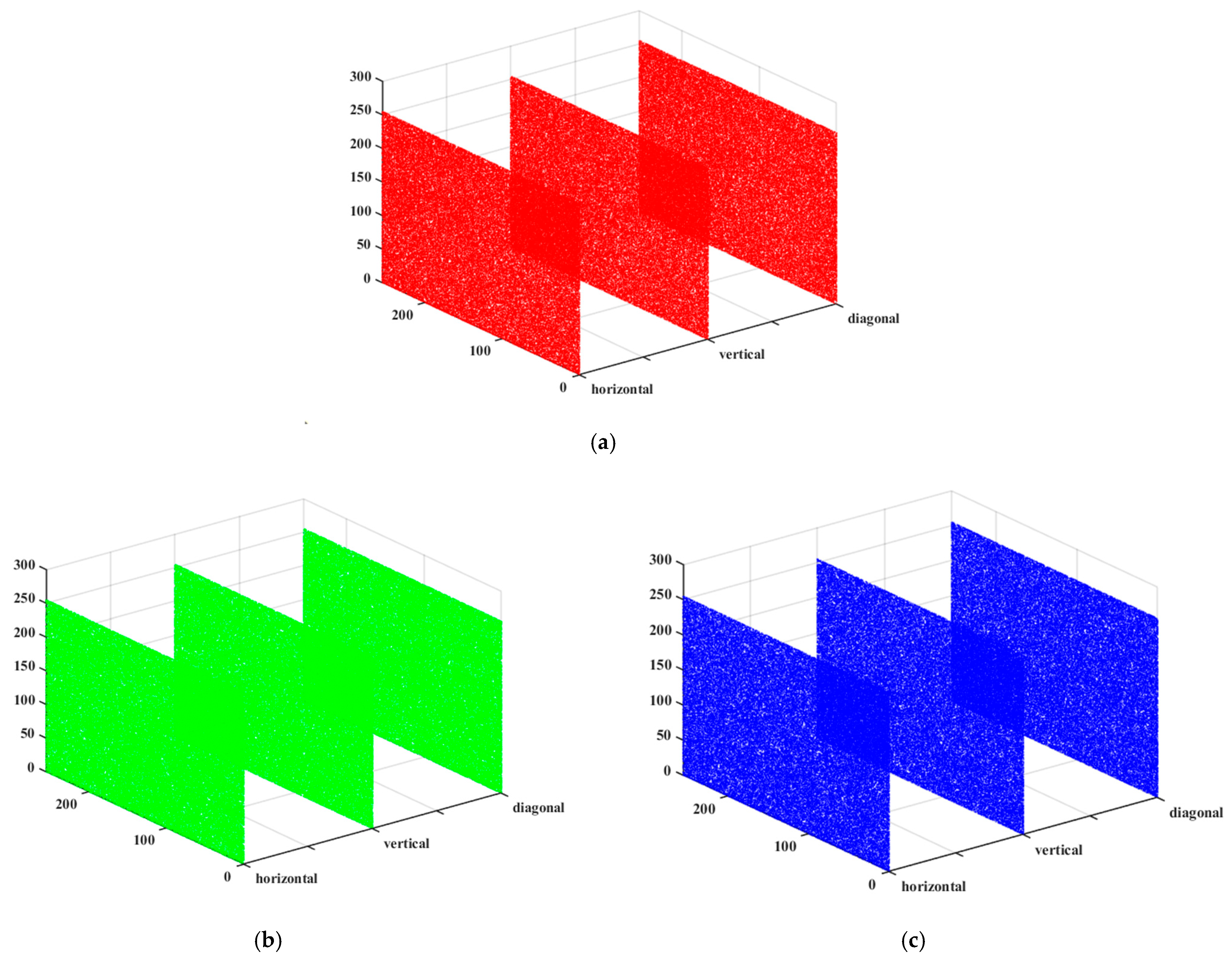
5.3.3. Adjacent Pixel Correlation Analysis
5.3.4. Information Entropy Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FPS | function projection synchronization |
| MFPS | modified function projection synchronization |
| RBF | radial basis function |
| IE | Information Entropy |
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Diethelm, K.; Kiryakova, V.; Luchko, Y.; Machado, J.A.T.; Tarasov, V.E. Trends, directions for further research, and some open problems of fractional calculus. Nonlinear Dyn. 2022, 107, 3245–3270. [Google Scholar] [CrossRef]
- Sun, H.G.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y.Q. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Wang, H. Research on application of fractional calculus in signal real-time analysis and processing in stock financial market. Chaos Soliton Fract. 2019, 128, 92–97. [Google Scholar]
- Sakariya, H.; Prasad, R.S.; Kumar, S. A study on brain tumor dynamics in two-dimensional irregular domain with variable-order time-fractional derivative. Comput. Meth. Prog. Bio. 2005, 264, 108700. [Google Scholar]
- Fu, L.X.; Zhu, W.T.; Yu, B.; Zhang, Y.Y.; Sosa, P.A.V.; Li, C.B.; Ricci, L.; Frasca, M.; Minati, L. Modeling and experimental circuit implementation of fractional single-transistor chaotic oscillators. Appl. Math. Comput. 2025, 500, 129438. [Google Scholar] [CrossRef]
- Lenka, B.K.; Upadhyay, R.K. Hidden memory chaotic attractors in simple nonequilibrium fractional order systems. Commun. Nonlinear Sci. Numer. Simulat. 2025, 150, 108970. [Google Scholar]
- Tavazoei, M.S. Fractional order chaotic systems: History, achievements, applications, and future challenges. Eur. Phys. J.-Spec. Top. 2020, 229, 887–904. [Google Scholar]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, G.M.; Mahmoud, E.E. Complete synchronization of chaotic complex nonlinear systems with uncertain parameters. Nonlinear Dyn. 2010, 62, 875–882. [Google Scholar] [CrossRef]
- Chishti, S.; Ramaswamy, R. Design strategies for generalized synchronization. Phys. Rev. E 2018, 98, 032217. [Google Scholar] [CrossRef]
- Wei, X.F.; Zhang, Z.Y.; Lin, C.; Chen, J. Synchronization and anti-synchronization for complex-valued inertial neural networks with time-varying delays. Appl. Math. Comput. 2021, 403, 126194. [Google Scholar]
- Luan, H.Y.; Ouyang, Y.H.; Zhao, Z.W.; Mao, W.Z.; Ma, R.M. Reconfigurable moiré nanolaser arrays with phase synchronization. Nature 2023, 624, 282–288. [Google Scholar] [CrossRef] [PubMed]
- Mainieri, R.; Rehacek, J. Projective synchronization in three-dimensional chaotic systems. Phys. Rev. Lett. 1999, 82, 3042–3045. [Google Scholar] [CrossRef]
- Si, G.Q.; Sun, Z.Y.; Zhang, Y.B.; Chen, W.Q. Projective synchronization of different fractional-order chaotic systems with non-identical orders. Nonlinear Anal. Real World Appl. 2012, 13, 1761–1771. [Google Scholar]
- Du, H.Y.; Zeng, Q.S.; Wang, C.H. Function projective synchronization of different chaotic systems with uncertain parameters. Phys. Lett. A 2008, 372, 5402–5410. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.L.; Fan, W.H.; Ma, P. Finite-time function projective synchronization control method for chaotic wind power systems. Chaos Soliton Fract. 2020, 135, 109756. [Google Scholar] [CrossRef]
- Du, H.Y.; Zeng, Q.S.; Wang, C.H. Modified function projective synchronization of chaotic system. Chaos Soliton Fract. 2009, 42, 2399–2404. [Google Scholar]
- Tran, X.T.; Kang, H.J. A novel observer-based finite-time control method for modified function projective synchronization of uncertain chaotic (hyperchaotic) systems. Nonlinear Dyn. 2015, 80, 905–916. [Google Scholar] [CrossRef]
- Dessoky, M.M.E.; Almohammadi, N.; Alzahrani, E. Control and adaptive modified function projective synchronization of different hyperchaotic dynamical systems. AIMS Math. 2023, 8, 23621–23634. [Google Scholar] [CrossRef]
- Liu, S.T.; Zhang, F.F. Complex function projective synchronization of complex chaotic system and its applications in secure communication. Nonlinear Dyn. 2014, 76, 1087–1097. [Google Scholar]
- Tirandaz, H.; Mollaee, A.K. Modified function projective feedback control for time-delay chaotic Liu system synchronization and its application to secure image transmission. Optik 2017, 147, 187–196. [Google Scholar] [CrossRef]
- Sudheer, K.S.; Sabir, M. Modified function projective synchronization of hyperchaotic systems through Open-Plus-Closed-Loop coupling. Phys. Lett. A 2010, 374, 2017–2023. [Google Scholar] [CrossRef]
- He, J.M.; Wu, Y.P.; Yang, C.S. Function matrix projective synchronization for disturbed fractional laser chaotic systems and image encryption. Chin. J. Phys. 2025, 95, 1078–1095. [Google Scholar] [CrossRef]
- Zhou, P.; Ding, R. Adaptive function projective synchronization between different fractional-order chaotic systems. Indian J. Phys. 2012, 86, 497–501. [Google Scholar] [CrossRef]
- Geng, L.L.; Yu, Y.G.; Zhang, S. Function projective synchronization between integer-order and stochastic fractional-order nonlinear systems. ISA Trans. 2016, 64, 34–46. [Google Scholar] [CrossRef]
- Ouannas, A.; Grassi, G.; Ziar, T.; Odibat, Z. On a function projective synchronization scheme for non-identical fractional-order chaotic (hyperchaotic) systems with different dimensions and orders. Optik 2017, 136, 513–523. [Google Scholar] [CrossRef]
- Du, H.Y. Modified function projective synchronization between two fractional-order complex dynamical networks with unknown parameters and unknown bounded external disturbances. Phys. A 2019, 526, 120997. [Google Scholar] [CrossRef]
- Dessoky, M.M.E.; Khan, M.A. Application of fractional calculus to combined modified function projective synchronization of different systems. Chaos 2019, 29, 013107. [Google Scholar] [CrossRef] [PubMed]
- He, J.M.; Pei, L.J. Function matrix projection synchronization for the multi-time delayed fractional order memristor-based neural networks with parameter uncertainty. Appl. Math. Comput. 2023, 454, 128110. [Google Scholar] [CrossRef]
- Amato, F.; Ariola, M. Finite-time control of discrete-time linear systems. IEEE Trans. Autom. Control 2005, 50, 724–729. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Ai, C.Y.; He, S.; Wang, W.Q.; Fan, X.C. Finite time adaptive synchronous control for fractional-order chaotic power systems. IET Gener. Transm. Dis. 2023, 17, 3626–3637. [Google Scholar] [CrossRef]
- Lin, F.N.; Xue, G.M.; Qin, B.; Li, S.G.; Liu, H. Event-triggered finite-time fuzzy control approach for fractional-order nonlinear chaotic systems with input delay. Chaos Soliton Fract. 2023, 175, 114036. [Google Scholar] [CrossRef]
- Aghababa, M.P. Finite-time chaos control and synchronization of fractional-order nonautonomous chaotic (hyperchaotic) systems using fractional nonsingular terminal sliding mode technique. Nonlinear Dyn. 2012, 69, 247–261. [Google Scholar] [CrossRef]
- Delavari, H.; Mohadeszadeh, M. Robust finite-time synchronization of non-identical fractional-order hyperchaotic systems and its application in secure communication. IEEE/CAA J. Autom. Sinica 2019, 6, 228–235. [Google Scholar] [CrossRef]
- Taheri, M.; Chen, Y.C.; Zhang, C.Q.; Berardehi, Z.R.; Roohi, M.; Khooban, M.H. A finite-time sliding mode control technique for synchronization chaotic fractional-order laser systems with application on encryption of color images. Optik 2023, 285, 170948. [Google Scholar] [CrossRef]
- Huang, L.L.; Li, W.Y.; Xiang, J.H.; Zhu, G.L. Adaptive finite-time synchronization of fractional-order memristor chaotic system based on sliding-mode control. Eur. Phys. J.-Spec. Top. 2022, 231, 3109–3118. [Google Scholar] [CrossRef]
- Wu, X.F.; Bao, H.B.; Cao, J.D. Finite-time inter-layer projective synchronization of Caputo fractional-order two-layer networks by sliding mode control. J. Frankl. Inst. 2021, 358, 1002–1020. [Google Scholar] [CrossRef]
- Liu, N.X.; Fei, J.T. Adaptive fractional sliding mode control of active power filter based on dual RBF neural networks. IEEE Access 2017, 5, 27590–27598. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Pacheco, J.M.M.; Bekiros, S.; Wei, Z.C. A fractional-order hyper-chaotic economic system with transient chaos. Chaos Soliton Fract. 2020, 130, 109400. [Google Scholar] [CrossRef]
- Nian, F.Z.; Liu, X.M.; Zhang, Y.Q.; Yu, X.L. Module-phase synchronization of fractional-order complex chaotic systems based on RBF neural network and sliding mode control. Int. J. Mod. Phys. B 2020, 34, 2050050. [Google Scholar] [CrossRef]
- Yang, S.S.; Li, N. Chaotic behavior of a new fractional-order financial system and its predefined-time sliding mode control based on the RBF neural network. Electron. Res. Arch. 2025, 33, 2762–2799. [Google Scholar] [CrossRef]
- Camacho, N.A.; Mermoud, M.A.D.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simulat. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Wu, H.Q.; Wang, L.F.; Niu, P.F.; Wang, Y. Global projective synchronization in finite time of nonidentical fractional-order neural networks based on sliding mode control strategy. Neurocomputing 2017, 235, 264–273. [Google Scholar] [CrossRef]
- Wu, X.J.; Lu, Y. Generalized projective synchronization of the fractional-order Chen hyperchaotic system. Nonlinear Dyn. 2009, 57, 25–35. [Google Scholar] [CrossRef]
- Tang, X.Y.; Li, R.H.; Huang, D.M. A novel entanglement functions-based 4D fractional-order chaotic system and its bifurcation analysis. Phys. Scripta 2024, 99, 055251. [Google Scholar]
- Deng, W.H. Short memory principle and a predictor-corrector approach for fractional differential equations. J. Comput. Appl. Math. 2007, 206, 174–188. [Google Scholar] [CrossRef]
- Wei, F.; Chen, G.C.; Zeng, Z.G.; Gunasekaran, N. Finite/fixed-time synchronization of inertial memristive neural networks by interval matrix method for secure communication. Neural Netw. 2023, 167, 168–182. [Google Scholar] [CrossRef]



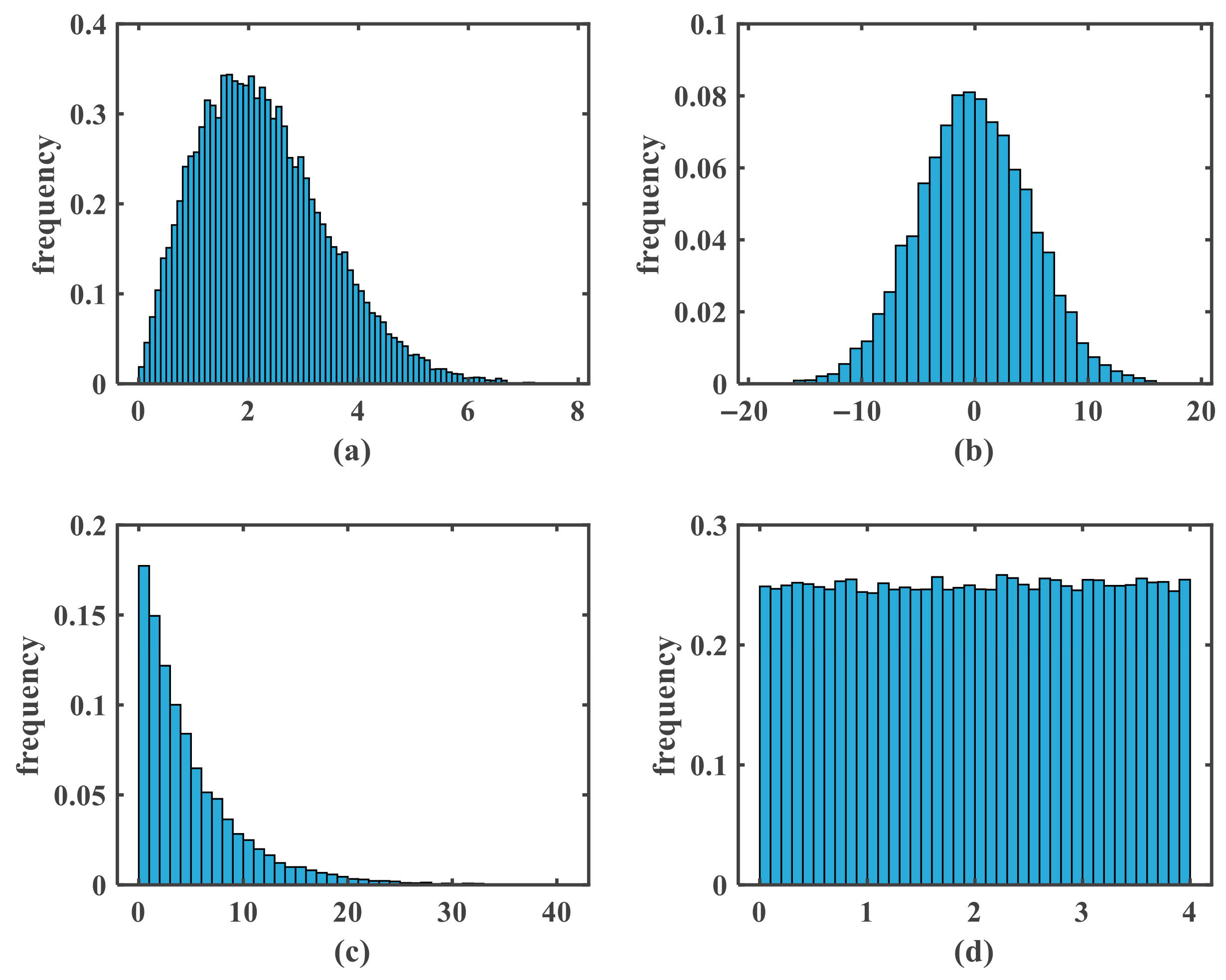
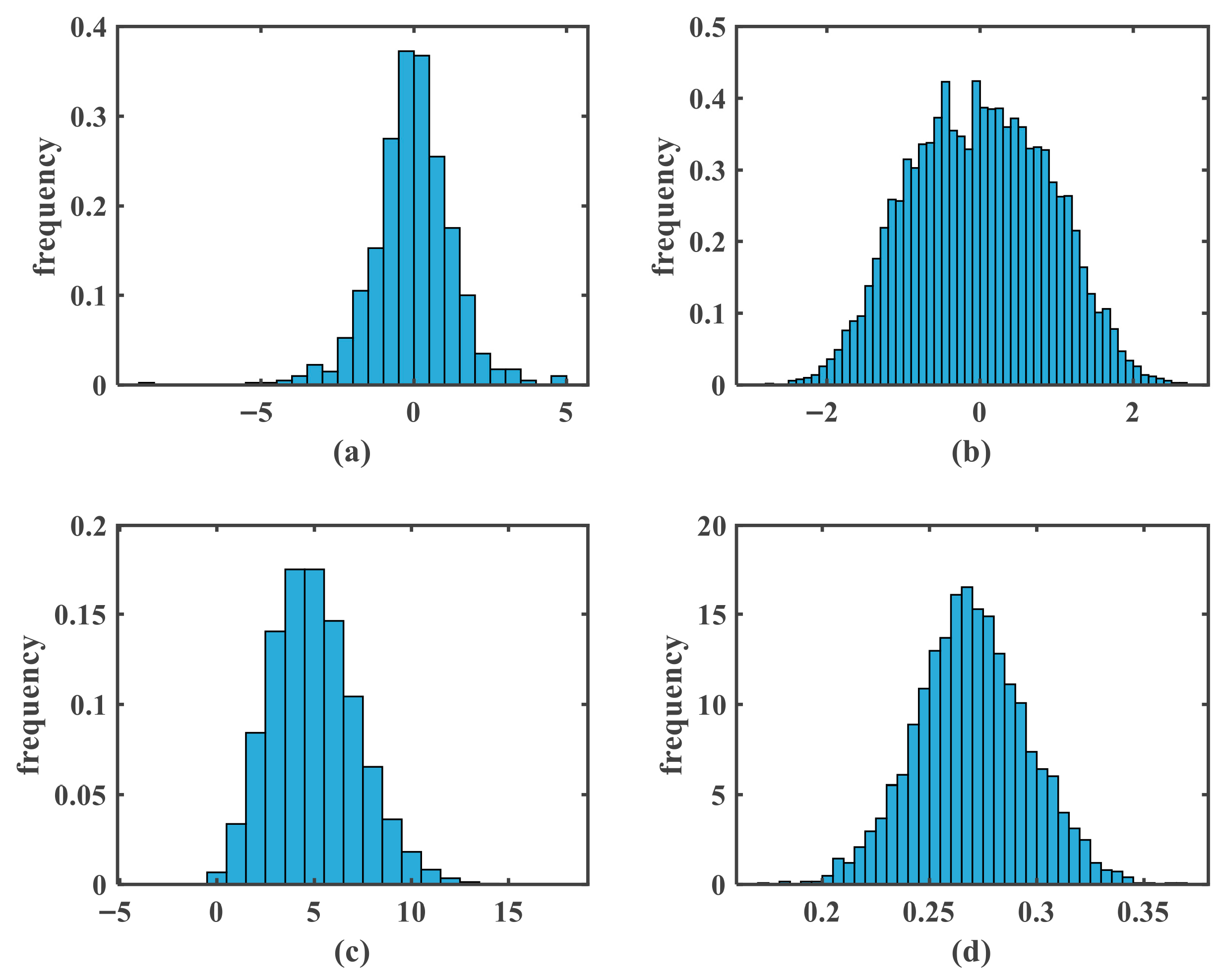

| Noise | Mean | Variance |
|---|---|---|
| Rayleigh noise | 2.26 | 1.39 |
| Gaussian noise | 0.00 | 25.00 |
| Gamma noise | 5.06 | 25.90 |
| Uniform noise | 2.00 | 1.33 |
| Cauchy noise | 0.05 | 1.68 |
| Gaussian white noise | 0.00 | 0.81 |
| Poisson noise | 5.00 | 4.99 |
| Beta noise | 0.26 | 0.0007 |
| Image | Channel | Horizontal | Vertical | Diagonal |
|---|---|---|---|---|
| Original image | R | 0.9740 | 0.9510 | 0.9262 |
| G | 0.9680 | 0.9406 | 0.9072 | |
| B | 0.9527 | 0.9166 | 0.8868 | |
| Encrypted image | R | −0.0012 | −0.0019 | 0.0041 |
| G | 0.0067 | −0.0062 | 0.0063 | |
| B | 0.0020 | 0.0025 | 0.0009 | |
| Encrypted image [51] | R | −0.0033 | 0.0119 | −0.0148 |
| G | −0.0029 | 0.0113 | −0.0213 | |
| B | −0.0040 | 0.0016 | 0.01628 |
| Image | R | G | B |
|---|---|---|---|
| Original image | 7.2349 | 7.5683 | 6.9176 |
| Encrypted image | 7.9993 | 7.9991 | 7.9993 |
| Encrypted image [51] | 7.9993 | 7.9992 | 7.9994 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Wang, H.; Huang, D. Finite-Time Modified Function Projective Synchronization Between Different Fractional-Order Chaotic Systems Based on RBF Neural Network and Its Application to Image Encryption. Fractal Fract. 2025, 9, 659. https://doi.org/10.3390/fractalfract9100659
Li R, Wang H, Huang D. Finite-Time Modified Function Projective Synchronization Between Different Fractional-Order Chaotic Systems Based on RBF Neural Network and Its Application to Image Encryption. Fractal and Fractional. 2025; 9(10):659. https://doi.org/10.3390/fractalfract9100659
Chicago/Turabian StyleLi, Ruihong, Huan Wang, and Dongmei Huang. 2025. "Finite-Time Modified Function Projective Synchronization Between Different Fractional-Order Chaotic Systems Based on RBF Neural Network and Its Application to Image Encryption" Fractal and Fractional 9, no. 10: 659. https://doi.org/10.3390/fractalfract9100659
APA StyleLi, R., Wang, H., & Huang, D. (2025). Finite-Time Modified Function Projective Synchronization Between Different Fractional-Order Chaotic Systems Based on RBF Neural Network and Its Application to Image Encryption. Fractal and Fractional, 9(10), 659. https://doi.org/10.3390/fractalfract9100659







