1. Introduction
Ultrasound imaging is a vital, non-invasive tool used in medical diagnostics for its real-time imaging and detailed information on tissue structures and blood flow. The process involves emitting high-frequency sound waves that reflect off tissues and are converted into visual images. Dehazing and denoising are essential in this workflow to enhance image clarity and preserve structural details, which improves diagnostic accuracy. Numerous techniques have been developed to tackle noise in coherent imaging, addressing the challenges posed by speckle noise and other artifacts [
1] as shown in
Figure 1. These techniques can be categorized into traditional methods and modern deep learning approaches.
Traditional methods for image denoising, which include spatial domain filters, diffusion filters, non-local means (NLM) filters, transform domain techniques, and hybrid filter approaches, have made significant strides in enhancing image quality [
2]. Spatial domain filter methods such as those of Loupas et al. [
3] and Zhu et al. [
4] operate directly on pixel values, using a moving window to adjust each pixel based on local statistics. They are effective for noise reduction through local pixel adjustments but may blur global image structures due to their reliance on local information. Additionally, these spatial domain filter methods can be computationally intensive and may not be well suited for real-time applications. Diffusion filter techniques, such as the speckle-reducing anisotropic diffusion filter (SRAD) [
5], effectively reduce noise while preserving edges, but they can introduce stair-step artifacts and result in information loss during the diffusion process. Stevens et al. [
6] present a diffusion model-based method for dehazing ultrasound images, improving clarity and diagnostic utility, especially for challenging cases like obesity, where conventional methods fall short. These diffusion filter methods also struggle with real-time processing due to their computational complexity. Non-local means filters use similarity between image patches to reduce noise. The non-local means (NLM) filter [
7] excels at preserving fine details by averaging similar patches across the image. However, its high computational complexity and potential to produce blurry results if patches are not sufficiently similar can limit its practicality. The Optimal Bayesian NLM (OBNLM) [
8] builds upon NLM by incorporating Bayesian optimization to improve denoising performance, yet it still suffers from significant computational demands. The Non-Local Low-Rank Framework (NLLRF) [
4] extends NLM by leveraging low-rank matrix properties to enhance noise reduction, but it may lead to excessive smoothing if the low-rank assumption does not hold, affecting the preservation of image details.
Low-rank-based techniques effectively denoise images by exploiting the assumption that natural images have an underlying low-rank structure [
9], which can be approximated from noisy data. However, their performance is highly dependent on the low-rank characteristic of the image, and these methods will fail if the image does not adhere to this property. Transform domain techniques denoise images by leveraging the properties of transformed domain representations, such as wavelet thresholds, to effectively reduce noise while preserving significant features [
10,
11]. Zhou et al. [
12] propose a degradation model based on the non-linear transformation to adjust the intensity of SAR image pixel values. Bi et al. [
13] introduce a mixed-order denoising algorithm that incorporates both fractional-order and higher-order regularization terms. This approach significantly mitigates the staircase artifacts commonly associated with the TV model and its variations, while enhancing edge and detail preservation. However, these methods often introduce artifacts and may degrade image quality due to the challenges of balancing noise reduction with artifact suppression.
Hybrid filter approaches combine multiple denoising techniques to leverage their complementary strengths, often resulting in improved performance over individual methods [
1]. For example, Wang et al. introduce a multi-scale hybrid method (MHM) designed to effectively reduce speckle noise in medical ultrasound images while preserving important structural details [
14]. However, these hybrid filter approaches tend to be complex and computationally intensive, which can limit their practical applicability and efficiency. All these algorithms have their own limitations and are not specifically designed for ultrasound images, making them less effective for denoising speckle noise in ultrasound images.
Deep learning has made significant advancements in the field of image denoising. Techniques such as image-adapted denoising CNNs [
15], channel and space attention neural networks [
16], and multi-scale networks [
17] have emerged as powerful tools for tackling the challenges of ultrasound image denoising. These methods leverage the capacity of deep networks to learn complex noise patterns and image structures from data, leading to significant improvements in denoising performance. Liang et al. [
18] are pioneers in applying deep learning networks to image denoising, followed by Zhang et al. [
19] with their feed-forward Denoising Convolutional Neural Networks (DnCNNs). This DnCNN excels at removing various types of noise by learning complex noise patterns from training data. Its strengths include effective noise reduction and adaptability to different noise conditions, but it faces limitations such as high computational demands, dependence on training data quality, and the potential introduction of artifacts. To overcome the limitations of DnCNN, Anwar et al. [
20] introduced a blind real image denoising network (RIDNet), a one-stage network designed specifically for blind real image denoising. RIDNet demonstrates effective performance in natural image denoising by leveraging its architecture. Additionally, the integration of attention mechanisms into deep learning-based denoising approaches has further enhanced results, showing considerable promise in improving image quality.
Subsequently, the incorporation of attention mechanisms into deep learning denoising techniques has shown great potential. For example, Sharif et al. [
21] introduce the Deep Residual Attention Network (DRAN), which enhances denoising in multidisciplinary medical images by integrating attention mechanisms with spatially refined residual features. Similarly, Lan et al. [
22] propose the Mixed-Attention Mechanism-based Residual UNet (MARU), effectively denoising ultrasound images through a mixed-attention approach. Furthermore, the Multi-Scale Attention-Guided Neural Network (MSANN) [
23] leverages a multi-scale attention module to capture and address the spatial distribution of speckle noise, proving effective in managing complex noise patterns. Yuting et al. [
24] propose a dual-branch architecture for joint image dehazing and denoising, using a dark channel prior and unsupervised networks for dehazing, and a mean/extreme sampler with a self-supervised network for denoising. While these methods have demonstrated effectiveness with synthetic data, their performance on real ultrasound images remains uncertain. The denoised images produced by these deep learning techniques often exhibit excessive smoothness, which can undermine their practical utility. In contrast to traditional approaches that frequently lead to oversmoothing, our proposed method aims to achieve a balanced approach, effectively reducing speckle noise while minimizing the risk of excessive smoothing.
In summary, existing filters struggle to effectively detect and preserve edges while simultaneously reducing speckle noise. To address these challenges, we propose an efficient multi-scale wavelet approach for dehazing and denoising ultrasound images using fractional-order filtering. Our approach utilizes multi-scale wavelet decomposition to detect edges and ascertain their orientation at various levels of the image analysis, enabling effective differentiation between edge and noise. We use the structure tensor, which ranges from 0 (no significant edge) to 1 (highly significant edge), to enhance edge detection and evaluate edge importance.
The main contributions of this work are summarized in the following:
Multi-Scale Wavelet Approach: We introduce a multi-scale wavelet approach that enhances edge detection and the separation of objects from noise at different physical scales.
Integrated Filtering Techniques: Our method integrates guided filtering, directional filtering, fractional-order filtering, and haze removal, which collectively improve the quality of denoised images.
Extensive Evaluation: We emphasize that our approach has been rigorously evaluated on both synthetic and real images, demonstrating superior performance in quantitative metrics and visual quality.
The structure of this paper is as follows:
Section 2 provides background information.
Section 3 details our proposed method.
Section 4 presents the experimental results on synthetic and real images. The conclusion is given in
Section 5.
3. Proposed Method
The proposed method utilizes a multi-scale pyramid framework to address image processing tasks through a hierarchical decomposition of images, ranging from coarse to fine resolutions. This method integrates anisotropic diffusion for edge detection, directional filtering for edge enhancement, guided filtering for image denoising, fractional filtering for texture preservation, dehazing for image clarity, and contrast enhancement to improve overall image quality, all applied at each level of the pyramid. The method consists of two key phases: pyramid analysis and pyramid synthesis. In the pyramid analysis phase, the algorithm focuses on edge detection, noise identification, and edge orientation assessment at each resolution scale. The wavelet domain is utilized to effectively separate edges from noise by leveraging structure tensors. This allows for the precise localization of edges while distinguishing them from noise artifacts. The pyramid synthesis phase aims to achieve two main objectives: reducing speckle noise and enhancing edges across different scales. By processing each layer independently, the algorithm can apply tailored smoothing and contrast adjustments that correspond to the specific features present at that scale. This multi-scale method ensures that prominent boundaries, usually larger than speckle noise, are treated separately from smaller features. The smoothing process is uniform but non-linear, specifically designed to reduce speckle noise while preserving critical details.
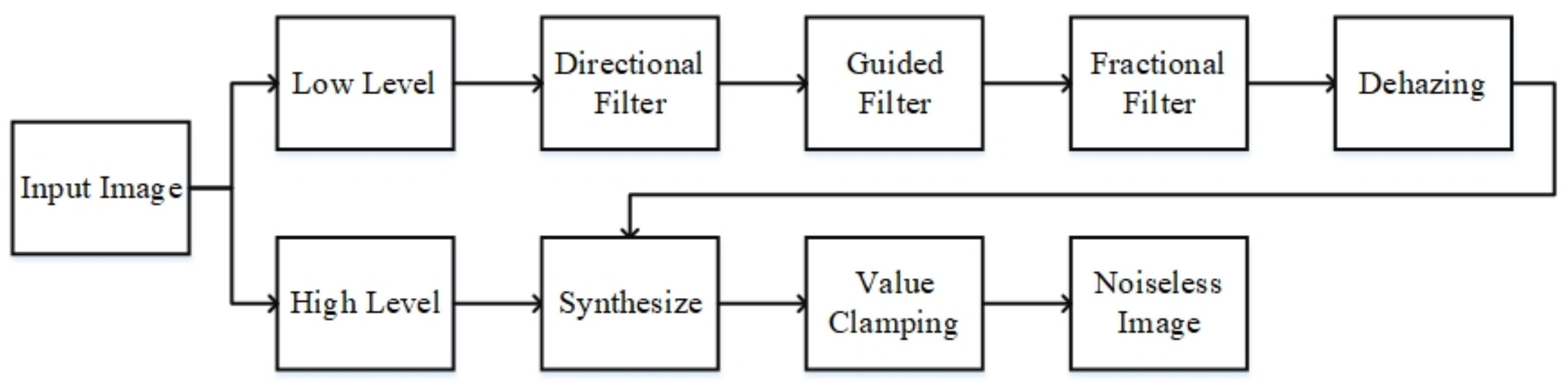
Figure 2 illustrates the flowchart detailing the procedure employed in this study for dehazing and denoising. The methodology can be summarized as follows:
Obtain the Ultrasound Image: Begin by acquiring the ultrasound image to be processed.
Construct the Wavelet Pyramid: Develop a wavelet pyramid for the image from Step 1. This constitutes the analysis phase of the pyramid process. For detailed algorithmic specifics, refer to
Section 3.1.
Process Each Pyramid Level: For each level of the pyramid, apply the following methods to the approximation layer:
Diffusion Tensor: Utilized for edge detection.
Directional Filter: Enhances edge sharpness.
Guided Filter: Performs image denoising.
Fractional Filter: Preserves texture details.
Image Dehazing: Removes haze effects.
Synthesize the Pyramid Levels: During the synthesis phase of each pyramid level, combine the results from Step 3 with the associated detail layers.
Value Clamping: Constrain the pixel values to the range of 0 to 255 following the processing of each pyramid level.
Iterate Through Pyramid Levels: Move to the next finer pyramid level and perform Steps 3 through 5 until processing is finished at the most detailed stage.
A notable advantage of this method is its flexibility, derived from the use of a non-dyadic decomposition. This allows for adaptation to varying physical dimensions across different imaging probes and modalities, such as linear, convex, and phased arrays. The method employs anisotropic, directional filtering for edge enhancement, adapting processing to the direction of boundaries, while maintaining spatial and temporal consistency to prevent artifacts and ensure uniform image quality.
Overall, the multi-scale pyramid approach enhances image clarity by effectively balancing speckle reduction and edge preservation. The tailored processing at each scale, combined with the ability to adapt to different imaging conditions, highlights the method’s robustness and effectiveness in improving image quality.
3.1. Image Pyramid
The image pyramid framework is a comprehensive approach that encompasses both the analysis and synthesis stages. In the analysis stage, the image is decomposed into multiple levels through successive downsampling, each representing a different scale. Mathematically, if
denotes the original image, the image pyramid decomposition can be expressed as
where
is the downsampling operator at level
k, and
represents the image at the
k-th scale. This multi-scale decomposition is essential for achieving several key objectives: enhancing structural features at coarser scales, improving edge details at intermediate scales, and refining fine edge structures at the finest scale. Such a hierarchical representation enables both “local” contrast and edge contrast enhancement effectively.
In our proposed method, the image pyramid is designed to ensure perfect reconstruction, allowing for accurate image reconstruction from its multi-scale components. The pyramid is built using downsampling factors that can be either one or two for height and width dimensions. The choice of a downsampling factor of one is particularly useful when the original image dimensions are highly imbalanced between height and width. The downsampling operation
can be expressed as
where
k is the factor of the pyramid. Additionally, applying a downsampling factor of zero allows for iterative filtering processes at the same scale, which effectively repeats the filtering operation and enhances the processing of the image.
To generate the multi-scaled images, we employ the guided filter, which produces two sub-bands—LL (low level) and HL (high level)—via wavelet decomposition. This method leverages the wavelet transform to separate image components at different scales. The wavelet decomposition can be mathematically represented as
where
W denotes the wavelet transform, and
and
are the low-level and high-level sub-bands. This separation facilitates targeted processing at each level of the pyramid. By adapting to varying scales, our image pyramid framework enhances both global structures and localized details, leading to improved overall image quality.
3.2. Edge Detection
Anisotropic diffusion is widely recognized for its effectiveness in edge detection tasks [
29]. This technique distinguishes itself by avoiding histogram-based methods and relying instead on low-pass filtering combined with additional calculations. It is particularly adept at identifying edges with low contrast, as it operates independently of pixel intensity levels.
The diffusion tensor, incorporated into the coherence-enhancing diffusion (CED) framework, enables precise directionally adaptive smoothing by capturing and quantifying the directional properties of diffusion processes. This approach is essential in medical imaging for analyzing brain structure and connectivity. For each pixel, the diffusion tensor is given by
where
represents the image gradient, with
and
denoting gradients in the x and y directions, respectively.
refers to the Gaussian convolution kernel, and ‘*’ signifies convolution.
Eigenvalue decomposition of the tensor produces eigenvalues and along with corresponding eigenvectors and . The eigenvector is oriented along the normal direction, whereas aligns with the tangent direction.
The edge detection proceeds as follows:
Evaluate the pairwise multiplication of gradient components for each pixel.
Apply a 2D Gaussian filter to smooth each of the four resulting matrices.
Derive the eigenvalues and corresponding eigenvectors from the smoothed matrices.
Designate the eigenvectors as and and the eigenvalues as and .
To evaluate if a pixel corresponds to an edge, we compute the normalized coherence factor given by
The values of fall between zero and one, with values near one indicating a sharp edge, while zero corresponds to a non-edge region. A high occurs when one eigenvalue substantially exceeds the other, suggesting that gradients are strongly oriented in one direction. When exceeds a predefined threshold, the pixel is categorized as an edge.
3.3. Edge Enhancement
In the previous section, we categorized regions into edge and non-edge areas. For enhancing edge regions, we applied a directional filtering technique. This approach is tailored to sharpen edges according to their specific orientation while concurrently smoothing the adjacent areas to diminish noise [
30]. The filter is consistently applied across different scales, including the LL band, which is less affected by noise.
For a pixel denoted as , where the normalized coherence factor surpasses a threshold (which varies with the scale level), the edge enhancement process proceeds as follows:
Identify the positions , , , and , where is calculated as , as , and similarly for and .
Apply linear interpolation to determine the values , , , and at the corresponding positions , , , and .
The resultant value at pixel after applying the directional filter is given by
where
x represents the original intensity at
, and
denotes the enhanced value. The weights
and
are used to balance the contribution from the edge and non-edge directions, respectively.
3.4. Image Denoising
In non-edge regions, smoothing methods such as the guided filter [
31] are particularly effective at maintaining edge details, improving image structure, and reducing unwanted noise. This filter leverages a guidance image, which can either be the input image itself or a separate reference, to produce the final output. The mathematical formulation of the guided filter is as follows:
In Equation (
18), the filter kernel
depends on the guidance image
G and is independent of the input image
p. The indices
i and
j correspond to pixel locations. This filter ensures that edges in the output image
q are preserved if they exist in the guidance image
G. The kernel weights
are computed using Equation (
19), where
and
represent the mean and variance of the guidance image
G within a local window
,
indicates the number of pixels in this region, and
is a regularization term.
3.5. Texture Preservation
Fractional calculus has attracted considerable interest in signal and image processing because of its features, including weak singularity, extended memory, and non-local behavior [
25]. So, fractional derivatives can effectively emphasize details and edge information in images by adjusting the order of differentiation. Unlike traditional integer-order derivatives, fractional derivatives offer more flexible tuning capabilities, making them advantageous for capturing subtle variations and complex structures in images. For example, lower-order fractional derivatives can smooth the image, while higher-order fractional derivatives can enhance edges and textures. Therefore, applying fractional derivatives to ultrasound image denoising can provide an efficient and precise solution, helping to improve the quality and reliability of medical imaging.
From Ref. [
26], Pu introduces the use of a differential mask for both image denoising and texture enhancement. This approach has proven to be highly effective. The fractional differential mask leverages fractional calculus to enhance texture details at multiple scales while simultaneously reducing noise. By applying this method, the paper demonstrates substantial improvements in preserving texture features and achieving cleaner images, showcasing its effectiveness in enhancing image quality through advanced mathematical techniques. The fractional differential mask can be represented as
where
is a differentiable-integrable function [
32],
denotes the domain of
, and
v is any real number (including fractional) representing the order of differentiation. The gamma function is denoted by
. This equation is employed in our fractional filtering method to preserve texture in ultrasound images. The filter attenuates low-frequency signals (
) while amplifying high-frequency components (
), with the amplification increasing as
v rises. Thus, fractional differentiation enhances texture preservation during denoising by boosting high-frequency details. Experimental results show that the optimal value of
provides the best texture retention.
3.6. Image Dehazing
In ultrasound imaging, haze can obscure important details and reduce image clarity. To address this, we employ a single-channel dehazing approach based on atmospheric scattering principles, specifically targeting the low-frequency haze typical in ultrasound images. The dehazing process involves the following steps:
1. Calculate the Dark Channel: For a single color channel
of the ultrasound image, we first compute the dark channel
as follows:
where
denotes a local patch centered at pixel
x.
He et al. [
28] establish that for haze-free images, the dark channel value
of the image
S is typically very low, approaching zero:
2. Estimate the Transmission: Assuming the global noise level
A is known, we modify the single-channel model of the ultrasound image
as follows:
To estimate the transmission
, we assume it is constant within a local window, denoted as
. Applying the minimum operator to both sides of Equation (
23), we obtain
Since
approaches zero, this simplifies to
Thus, the transmission
is given by
3. Introduce Correction Parameter and Recover Image: To improve visual realism by accounting for depth of field effects, we introduce a correction parameter
:
where
is set to 0.95. The global noise level
A is estimated using the brightest 0.1% of pixels in the dark channel, selecting the pixels with the highest intensity in
I.
Using the estimated transmission and the global noise level A, the ideal noiseless envelope is recovered.
4. Experiments
In this section, we assess the performance of our proposed method in comparison to existing baselines on both synthetic and real-world speckle noise reduction tasks. We benchmark our method against several well-known despeckling techniques, including OBNLM [
8], SRAD [
5], NLLRF [
4], the prominent deep learning-based natural image denoising method DnCNN [
19], and the latest ultrasound image denoising technique MHM [
14]. To evaluate the image quality, we utilize two commonly used metrics: peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) [
33]. Additionally, we provide ablation studies to examine the contribution of different components with our method.
4.1. Dataset and Experimental Configuration
In this study, we perform experiments on two types of datasets. The first type includes synthetic noise images, created using the multiplicative speckle noise model outlined in [
5]. This involves simulating noisy images by convolving a 2D point spread function with ground truth images using a radio-frequency (RF) image. For validation, we use five widely recognized datasets. The McMaster dataset [
34] includes 25 grayscale images, each with a size of 256 × 256 pixels in TIFF format. The Kodak24 dataset [
35] comprises 24 color images, each 512 × 768 pixels, in JPEG format. The BSD68 dataset [
36] contains 68 color images, sized 481 × 321 pixels, available in PNG format. The Set12 dataset [
19] features 12 grayscale images, each with dimensions of 256 × 256 pixels in PNG format. Finally, the Urban100 dataset [
37] includes 100 color images, each 1024 × 1024 pixels in size, provided in JPEG format. This diverse selection of datasets ensures a thorough evaluation across different image types and formats.
The second type of dataset consists of real ultrasound speckle noise images, captured using the Saset INSIGHT 37C system (Saset Healthcare Inc., Chengdu, China). During data collection, all optimization functions of the machine were turned off to capture raw ultrasound images with significant speckle noise. Over 3000 noisy liver images were collected. These noisy images were then processed using the noise reduction function of the INSIGHT 37C to generate images approximating noise-free ultrasound images, which were considered the ground truth. Experienced doctors were invited to select the most representative pairs of noisy and ground truth images for inclusion in the final ultrasound image dataset.
In this study, we utilized the following hardware for our experiments. The CPU used was an Intel Core i7-4770, which is based on the fourth-generation Haswell architecture. It features 4 physical cores and 8 threads, with a base clock speed of 3.4 GHz and a maximum turbo boost frequency of up to 3.9 GHz. It also has 8 MB of L3 cache. The GPU employed was an NVIDIA GeForce RTX 2070, which uses the Turing architecture. For each dataset, we conducted a single experimental test. The quantitative results, including average SNR and SSIM, were reported for these tests.
4.2. Experimental Results on Synthetic Noisy Images
We generated synthetic noisy images by introducing speckle noise with the following parameters: MHz, = 0.1 μs, and ms.
(I) Quantitative Analysis: Table 1 presents the PSNR and SSIM values for each method across these datasets. We highlight that our method consistently achieves the highest values in these metrics compared to other approaches. Specifically, in the McMaster, Kodak24, BSD68, Set12, and Urban100 datasets, our method demonstrates superior performance in both PSNR and SSIM, indicating its effectiveness in producing high-quality despeckled images with better preservation of structural details and reduction in noise.
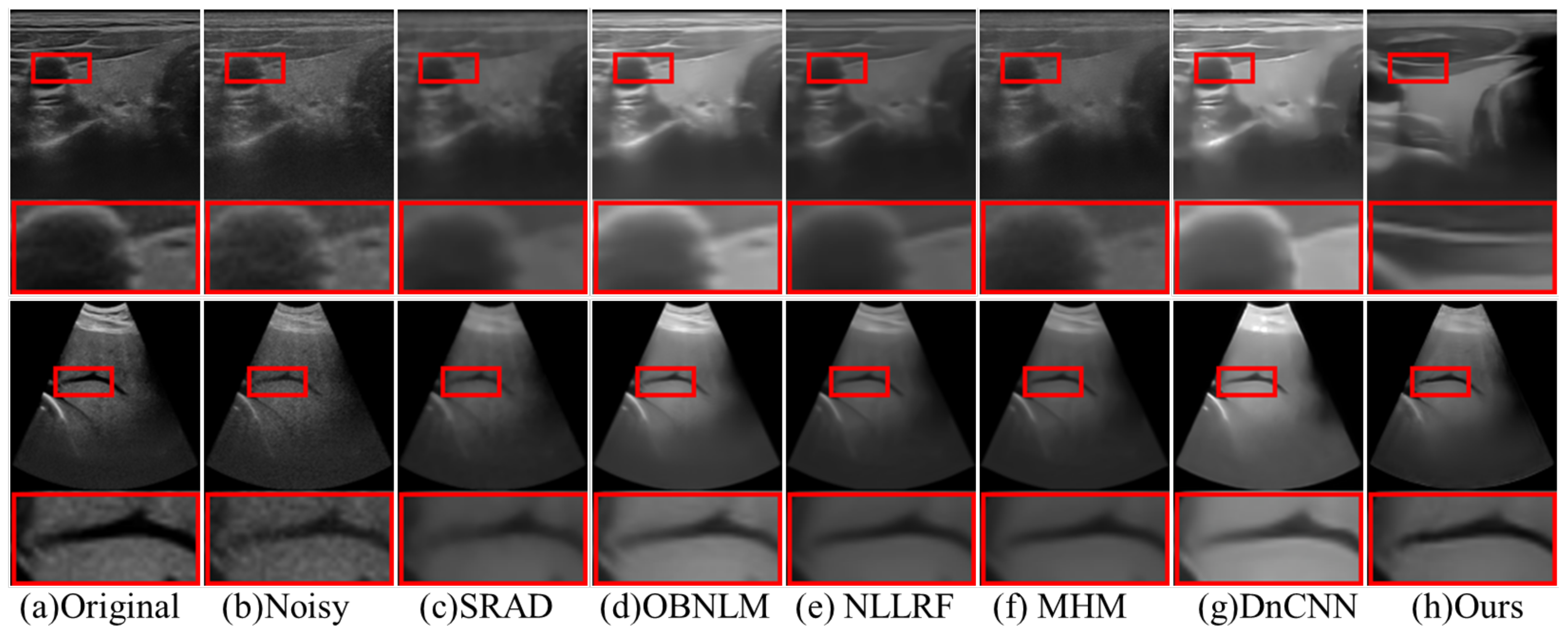
(II) Visual Analysis: This section presents a visual comparison of the denoised results achieved using our proposed method versus several competing techniques, evaluated on a challenging ultrasound image from our dataset.
Figure 3 illustrates the performance of different despeckling methods on synthetic noise images. The SRAD [
8] and OBNLM [
5] methods are observed to excessively smooth edges and textures, which results in a noticeable loss of fine details. The NLLR method [
4], while attempting to reduce noise, fails to sufficiently mitigate it, leaving the image with noticeable speckle artifacts and overall lower quality. DnCNN [
19] excels at noise reduction but tends to over-smooth the images, particularly in regions with fine textures or detailed features, leading to a reduction in image clarity. Similarly, MHM [
14] demonstrates improvements in denoising but suffers from inconsistencies, with some areas of the image being under-smoothed while others are over-smoothed. In contrast, our proposed method effectively reduces noise while preserving the integrity of edges, textures, and fine details. This visual comparison highlights the ability of our method to achieve a balance between noise reduction and detail preservation, outperforming existing techniques in maintaining the structural fidelity of ultrasound images.
4.3. Realistic Experiments on Various Types of Images
(I) Quantitative Analysis: To quantitatively evaluate the performance of our proposed method on a real ultrasound dataset, we conducted experiments using the established ultrasound speckle noise dataset. The quantitative results, including PSNR and SSIM, are presented in
Table 2. Our method achieved the highest values for both PSNR and SSIM compared to other state-of-the-art approaches. The results in
Table 2 clearly demonstrate the robustness and effectiveness of our approach in the challenging task of ultrasound image denoising. By taking into account the characteristics of speckles and using wavelet decomposition, using diffusion tensor to identify edges, and then applying different filtering methods to various regions, we achieved the best results.
(II) Visual Analysis: Figure 4 shows the experimental comparison results on our ultrasound speckle noise dataset. Our method demonstrates superior performance in restoring ultrasound images with enhanced structural preservation. In contrast, SRAD, OBNLM, and NLLRF show over-smoothing effects that diminish fine details and textures. SRAD and OBNLM excessively smooth the images, while NLLRF, DnCNN, and MHM struggle with maintaining image structure, resulting in blurriness and less-defined features. Our approach effectively reduces speckle noise while preserving fine details and textures, avoiding excessive smoothing artifacts. This visual evidence highlights the effectiveness of our method in balancing noise reduction and structural integrity, outperforming existing techniques in detail preservation and noise suppression.
Figure 5 illustrates the effectiveness of our proposed method in reducing speckle noise across various imaging systems, including radar, medical ultrasound, and underwater sonar. The performance of our approach in realistic imaging scenarios is also demonstrated in this figure. It highlights that our method preserves more image details and features compared to traditional techniques, which often struggle with adaptability to speckle noise. Methods such as OBNLM [
5], NLLR [
4], and SRAD [
8] fail to sufficiently remove noise, leading to lower-quality images. While DnCNN [
19] and MHM [
14] exhibit strong learning capabilities and generate visually enhanced images, they still face challenges related to over-smoothing and incomplete noise reduction.
Clinical evaluations were conducted with four radiologists to assess the effectiveness of our approach in processing liver and carotid artery images. The evaluation criteria included image clarity, detail preservation, and contrast enhancement. The radiologists consistently identified superior texture preservation and enhanced feature delineation in the images processed using our method. Overall, our approach demonstrates improved performance over existing speckle reduction and structural preservation techniques, indicating its strong suitability for clinical ultrasound imaging applications.
4.4. Ablation Study
To evaluate the efficacy of our proposed module, we perform a series of ablation experiments on the suggested method. Our multi-scale wavelet approach includes four distinct filter components: directional filter, guided filter, fractional filter, and dehazing. The ablation results are detailed in
Table 3. A checkmark indicates that the module is selected, while a cross indicates that the module is not selected. The proposed method achieves optimal performance when all filter blocks are included, while the removal of any block results in degraded performance. Omitting any of these components leads to a noticeable decline in performance, underscoring the importance of each filter in achieving effective denoising.
5. Conclusions
This paper introduces an advanced multi-scale wavelet approach for dehazing and denoising ultrasound images, utilizing fractional-order filtering to enhance image quality. The proposed method begins by constructing a wavelet pyramid to facilitate multi-resolution analysis, allowing for detailed examination from coarse to fine scales. Key features are accentuated through a directional filter applied to edges detected by a structure tensor, while areas lacking distinct edges are processed with a guided filter to reduce speckles. Using a fractional filter further aids in preserving texture, and a final dehazing step eliminates residual haze.
Our ablation study confirms the effectiveness of each filtering component, with the proposed method demonstrating superior performance across all evaluated metrics. The experimental results validate that our approach significantly reduces speckle noise while maintaining the structural integrity of medical ultrasound images. Compared to existing advanced denoising techniques, our method stands out for its enhanced performance in preserving image details and reducing noise.
This approach improves the clarity and diagnostic utility of ultrasound images and has significant implications for the advancement of medical imaging. By minimizing diagnostic errors and providing informed consent stance to clinicians, our method contributes to more accurate and reliable patient evaluations.
We have addressed the computational challenges associated with the wavelet pyramid technique by implementing the algorithm within the CUDA parallel computing framework. This adaptation enables the real-time processing of ultrasound data at 40 frames per second, making the method practical for clinical applications. Despite the inherent computational complexity, our parallelized optimization ensures that the approach is feasible for real-time use, enhancing its applicability in dynamic medical imaging scenarios.