Abstract
In this study, a model-free
-sliding mode control (
-SMC) methodology is proposed to synchronize a specific class of chaotic fractional-order memristive neural network systems (FOMNNSs) with delays and input saturation. The fractional-order Lyapunov stability theory is used to design a two-level
-SMC which can effectively manage the inherent chaotic behavior of delayed FOMNNSs and achieve finite-time synchronization. At the outset, an initial sliding surface is introduced. Subsequently, a robust
-sliding surface is designed as a second sliding surface, based on proportional–integral (PI) rules. The finite-time asymptotic stability of both surfaces is demonstrated. The final step involves the design of a dynamic-free control law that is robust against system uncertainties, input saturations, and delays. The independence of control rules from the functions of the system is accomplished through the application of the norm-boundedness property inherent in chaotic system states. The soft actor-critic (SAC) algorithm based deep Q-Learning is utilized to optimally adjust the coefficients embedded in the two-level
-SMC controller’s structure. By maximizing a reward signal, the optimal policy is found by the deep neural network of the SAC agent. This approach ensures that the sliding motion meets the reachability condition within a finite time. The validity of the proposed protocol is subsequently demonstrated through extensive simulation results and two numerical examples.
1. Introduction
Delayed neural networks (DNNs) represent an approach to designing networks specifically tailored for tasks where the order and timing of information play a crucial role. Unlike networks that process data in a linear fashion, DNNs incorporate deliberate delays in their connections. This feature enables the network to consider occurrences over timeframes, enhancing its ability to detect evolving patterns. For instance, when forecasting the word in a sentence or predicting stock values, DNNs shine by leveraging and recalling the timing of inputs. This capacity to analyze and understand sequences positions DNNs as tools in areas such as speech recognition, financial prediction, and any field where grasping the sequence of events is vital. By capturing the subtleties of dynamics, DNNs provide an advanced method for modeling and forecasting time-related phenomena [1,2,3].
Delayed fractional-order memristive neural network systems (FOMNNSs) are advanced neural networks that integrate fractional calculus, memristive components, and time delays to enhance their processing capabilities [4]. The fractional-order aspect allows these networks to model more complex dynamics with memory effects, while the memristive elements, which remember past voltages, provide non-volatile storage and adaptive learning capabilities [5]. This combination makes these systems highly suitable for applications requiring sophisticated temporal pattern recognition and adaptive learning, such as advanced signal processing, adaptive control, and complex system modeling [6,7,8,9].
Time delays are introduced to manage and utilize temporal dependencies in the data [10,11]. In delayed FOMNNSs, control and synchronization are imperative for ensuring stability, accuracy, and operational efficiency. The integration of complex dynamics, memory effects, and time delays necessitates precise control mechanisms to prevent erratic behavior and ensure reliable performance. Synchronization enhances the coordination of interconnected subsystems, thereby facilitating accurate information processing, which is critical for real-time applications. Furthermore, effective control and synchronization optimize resource utilization, enhance robustness to environmental changes, and support coherent adaptive learning [3]. These contributions collectively ensure that the network remains reliable and effective in handling complex, dynamic tasks. Applications benefiting from these controlled and synchronized systems include advanced signal processing, adaptive control systems, and real-time data analysis, where precise timing and coordination are crucial for optimal performance [12,13,14].
Various control techniques have been devised to mitigate undesirable behaviors in FO nonlinear systems. These methods include the fuzzy technique [15,16], Proportional–Integral–Derivative technique [17], adaptive technique [18], backstepping technique [19], sliding mode technique [20], optimal technique [21], and so on. Sliding mode control (SMC) has become popular among these techniques because of its precision, simplicity of execution, robustness against uncertainties, and adaptability. The PID control with SMC, known as PID-SMC, offers significant benefits including high precision, robust performance under system uncertainties, and ease of implementation [22]. It enhances stability and provides a fast response to dynamic changes, while mitigating the chattering issue often associated with traditional SMC. This combined approach results in improved control accuracy, adaptability, and overall performance, making it a versatile solution for managing complex systems effectively. For instance, in [1], a sliding mode control method is investigated for uncertain delayed fractional-order reaction–diffusion memristor neural networks. Unlike most existing literature, this study constructs a linear sliding mode switching function and designs the corresponding control law. In [23], the asymptotic stability of fractional-order (FO) systems with uncertainty and time-varying delay is studied using sliding mode control (SMC). An integral type fractional-order sliding mode surface (FOSMS) is designed, and the stability condition is established using inequality techniques. Ref. [24] explores fixed-time synchronization in delayed FO complex-valued neural networks. It proposes a sliding mode surface, based on sliding mode control and Lyapunov stability.
In [25], the research focuses on the finite-time synchronization of uncertain delayed FOMNNs, which exhibit leak, and an adaptive-SMC method is proposed to approximate the upper bounds of uncertainties. Ref. [26], investigates synchronizing FO chaotic systems with input delay. To optimize communication resources and achieve synchronization, an adaptive neural network backstepping sliding mode controller is proposed using an event-triggered scheme without Zeno behavior. In [27], fixed-time stabilization of fuzzy neural networks with distributed delay is achieved using an adaptive sliding mode controller. A new fixed-time stability theorem provides the settling time, and an integral sliding mode surface is designed. In [28], a FO hyperbolic neuro-fuzzy backstepping sliding mode controller is designed for chaotic systems with time-varying delays and uncertainties. The controller uses adaptive rules for estimating system dynamics and updating uncertainty bounds, and employs hyperbolic tangential FO sliding surfaces to minimize tracking errors. The authors of [29] have studied the consensus problem for FO multi-agent systems with input delay and nonlinear dynamics. A dynamic event-triggered SMC scheme without Zeno behavior reduces communication usage. In [30], fixed- and preassigned-time synchronization of stochastic FOMNNs with uncertain parameters and mixed delays is addressed using SMC. A sliding surface and adaptive laws are constructed for fixed-time stability, and a preassigned-time SMC is proposed for fast synchronization. In [31], generalized projective synchronization of Caputo FOMNNs with multiple delays is studied, and a new function-matrix-projection-based SMC method is introduced. Also, a mixed controller, combining open-loop feedback and robust control, is introduced to derive the scheme using state and sampling information.
However, the cited research works exhibit one or more of the following limitations:
- ○
- Existing research often relies heavily on either linear or nonlinear components in the suggestion of control techniques, limiting the comprehensiveness of the approaches.
- ○
- In many instances, the utilization of SMC methods is accompanied by chattering phenomena that are not acceptable.
- ○
- Most of these works simplify system definitions by neglecting uncertainties, external distributions, and input saturations, which are essential aspects of real-world systems.
- ○
- Almost all these methods have selected the control parameters by classic error trials for simulation.
Recently, reinforcement learning (RL) was developed for the optimization problem of various engineering problems [32,33]. Q-learning is one of the most prevalent off-policy algorithms which can solve RL problems in a tabular manner. In Q-learning, agent actions and system states are stored in a Q-table and then the best action is selected among the possible actions. However, Q-learning fails to handle high-dimensional problems with a large number of states. To address this issue, deep neural nets (DNNs) were incorporated into RL algorithms as approximators, which is called a deep Q-network (DQN). In this regard, the Deep Deterministic Policy Gradient (DDPG) was introduced which can handle the system with continuous action space. The problem of overestimation was the main reason for the emergence of twin delayed DDPG, called TD3 [34]. However, both the DDPG and TD3 have high sensitivity to their hyper-parameters which limits their application. More recently, the soft actor-critic (SAC) was introduced which exploits a stochastic policy and maximum entropy RL. As a result, a superior level of exploration and convergence can be obtained by SAC than previous RL algorithms [35,36].
To address these issues, we propose a novel finite-time two-level SMC technique. This method aims to develop a chattering-free
-SMC technique that is dynamic and robust against unpredictability, external disturbances, and input saturations. Beginning at the first step, sliding surface will be introduced. Then, based on the PI rules, a robust
-sliding surface will be designed as the second sliding surface. The finite-time asymptotic stability of both surfaces will be proven. Also, the final step in this part is designing a dynamic-free control law, which is robust against system uncertainties, input saturations, and system delay.
Furthermore, to optimize parameters for SMC, the Q-learning (QL) algorithm is integrated with the SMC strategy. This eliminates constraints on the initial conditions of the control input, ensuring that the sliding motion meets the reachability condition within a finite time.
The main contributions and innovations of this research are as follows:
- •
- Development of a Novel Control Methodology: The study proposes a model-free -SMC methodology, specifically designed for synchronizing chaotic with delays and input saturation.
- •
- Two-Level Sliding Surface Design: The methodology introduces a two-level control approach. The initial sliding surface addresses chaotic system dynamics, while the second -sliding surface, based on proportional-integral (PI) rules, enhances system stability and robustness.
- •
- Finite-Time Synchronization: The proposed control method guarantees finite-time synchronization of delayed FOMNNSs, overcoming the challenge of delays, input saturations, and system uncertainties that previous approaches have struggled to handle effectively.
- •
- System Independence: The control laws are designed to be independent of the specific functions governing the system’s behavior. This is achieved through the norm-boundedness property of chaotic system states, making the methodology more adaptable to a wide range of chaotic systems.
- •
- Optimization via Soft Actor-Critic (SAC) Algorithm: The study utilizes SAC algorithm-based deep Q-learning to optimally adjust the controller parameters. This approach improves the adaptability and performance of the controller by maximizing a reward signal through the deep neural network of the SAC agent.
- •
- Extensive Validation: The effectiveness of the proposed control strategy is demonstrated through comprehensive simulation results and two numerical examples, confirming its applicability in practical engineering scenarios.
- •
- Practical Relevance: The proposed method’s robustness in handling chaotic dynamics, delays, and input saturation shows significant potential for real-world engineering applications, particularly in areas requiring advanced control of complex systems.
The rest of the study is organized as follows: Section 2 provides the necessary concepts about FO initials, stability theorems, and presents the problem statement and system description. Section 3 introduces a novel model-free P-SMC technique designed to synchronize of different delayed FOMNNSs, in three steps. Section 4 details the deep SAC method employed in this study and elucidates the process for determining the optimal parameters. Section 5 includes numerical simulations and illustrates the analytical results through two case studies involving the synchronization of unknown delayed FOMNNSs. Section 6 concludes the paper with a discussion of the findings and draws final conclusions based on the results.
2. Preliminary Concepts and Description of the Problem
This section is divided into two subsections. Initially, fundamental definitions and principles concerning FO calculus and stability are outlined. Following that, the problem statement regarding synchronization is introduced.
2.1. Preliminaries
Definition 1
([37]). Suppose
is a continuous function in real space
. The Rieman–Liouville non-integer-order integral of
for a fractional constant
is defined as
where
represents the starting time, and
is the Gamma function.
Definition 2
([37,38]). Suppose
is a continuous function in real space
. The Caputo-defined fractional-order derivative of
for a non-integer number
is given by
in which
and
represents the Caputo derivative operator throughout the rest of this study.
Property 1
([39]). If
and
is a real number, then
.
Property 2
([39]). Consider
and
, then
Lemma 1
([40]). Assuming
consider the fractional-order system
which satisfies the Lipschitz condition and has an equilibrium point at
. Under these conditions, let us examine the existence of a Lyapunov function
that adheres to the following criteria:
Here,
,
and
represent positive constants. If these conditions are met, the equilibrium point of the fractional-order system
will demonstrate (asymptotic) stability as per the Mittag–Leffler specifications.
2.2. Description of the Problem
For
, let us examine the subsequent group of delayed FOMNNSs.
where
denotes the number of neural network units, and
represents the state of the i-th neuron within the delayed FOMNNSs.
and
denote the activation functions of the j-th neuron, while
and
signify the elements of connection weight matrices corresponding to the j-th neuron’s influence on the i-th neuron.
denotes an unspecified parameter indicating the rate at which the i-th neuron restores its prospective to the resting state upon disconnection from the network.
represents the i-th element of external distributions, and τ signifies the transmission delay.
To tackle the challenge of synchronization/stabilization in delayed FOMNNSs, we designate system (8) as the drive system. Subsequently, the ensuing system serves as the response system.
In this context,
denotes the i-th state of neurons within the delayed FOMNNSs, while
and
represent the activation functions of the j-th neuron. The parameters
and
correspond to the components of connection weight matrices, where
is analogous to
in Equation (8). Additionally,
denotes the i-th component of external distributions, and τ represents the transmission delay.
Furthermore,
signifies the control input, and
represents the input-saturation function, defined as
where
In (11),
and
represent the upper and lower bounds, respectively, of the input saturation process in Equation (10). The parameter
denotes the slope saturation.
By specifying the error function, we obtain the following:
Hence, for
, the dynamics to synchronize the error parameters can be derived by
The overarching aim is to design a sliding mode control mechanism that is both pertinent and operational, ensuring that, for
, the following convergence holds in the limit as time approaches infinity:
If Equation (15) can be derived, it will pave the way for the comprehensive resolution and implementation of error suppression between the drive system (8) and the response system (9).
Assumption 1.
The error states’ trajectories in chaotic systems are often constrained within certain regions of phase space [41,42], owing to the irregular attractors produced by chaotic behavior. As a result, there are positive constants
and
that fulfill the conditions outlined in the subsequent relations.
and
Moreover, it is anticipated that the uncertainty terms
and
will be bounded. Consequently, there exists a positive constant
such that
As a result of (16), (17), and (18),
where
is a positive constant for
Assumption 2.
Ensuring the boundedness property of the control method is among the most crucial prerequisites for the relevance of a control law. Therefore, it is desirable that
remains bounded. Consequently, one has
Remark 1.
The input saturation function
was introduced into the control input to address the practical constraints associated with real-world systems where the control signals are limited by the physical capabilities of actuators. By incorporating this function, the control strategy effectively models and manages these input constraints, ensuring that the control signals remain within allowable bounds and do not exceed the system’s limits. This approach helps prevent issues such as actuator overload and maintains system stability and performance under realistic operating conditions. It ensures that the proposed control methodology remains feasible and effective even in the presence of input saturation, which is crucial for practical applications where input constraints are an inherent aspect of system design.
3. Finite Time -SMC Technique Design
This section will first outline the design of a robust sliding surface, and then introduce the
sliding surface. Moreover, a finite time control scheme will be presented to synchronize FOMNNSs (8) and (9). Also, the related theorems and proofs are provided.
Hence, for
, the hypothesized equation for the sliding surface in the field-oriented control system is proposed as follows:
in which
is a positive constant.
During the occurrence of sliding motion, it is widely acknowledged that the condition
is met; thus, employing Property 1,
Theorem 1.
The dynamic equation governing sliding (Equation (24)) will exhibit stability, and the states of the fractional-order error neural network (Equation (14)) will asymptotically converge to the origin within finite time.
Proof of Theorem 1.
By taking into account the Lyapunov structure
and applying an integer derivative to Equation (25), and utilizing Equation (3) in Property 2, one obtains the following:
Substituting
from Equation (24) into Equation (26), we have
Hence, according to Equation (29), the inequality
holds true, ensuring
. Consequently, the stability criteria outlined in Lemma 1 are satisfied, leading to the attainment of asymptotic stability for the sliding surface dynamics (Equation (24)).
Now, in accordance with Equations (26) and (29),
Integrating both sides of Equation (31) yields
Since
one obtains
Hence, the states of
converge to zero within a finite time
, thus completing the proof. □
Remark 2.
Equation (26) is valid for
Also, it holds true specifically when
, as the right-hand side simplifies to the first derivative
. However, for
1, whether fractional or integer, the equation does not generally hold. This is because
involves a fractional derivative and applying
results in a fractional integral of order
, which does not simplify back to the first derivative [39]. Thus, the equation does not accurately represent
for
.
Now, let us introduce the second proportional–integral (PI) sliding surface. The PI sliding surface offers several advantages in control systems. By integrating both proportional and integral control actions, the PI sliding surface enhances system robustness by mitigating steady-state errors and improving tracking performance. It reduces overshooting, ensures steady-state accuracy, and simplifies controller tuning compared to more complex strategies. The continuous integration of error signals over time leads to smoother responses and improved transient behavior. Additionally, its versatility allows for application across a wide range of control problems, making it a practical choice for diverse industrial applications.
Here’s the second sliding surface, implemented as a PI equation:
in which
and
are PI parameters and
is a real number.
As it mentioned before, in the event of sliding motion, it is widely recognized that the condition
is satisfied, thereby leveraging Property 1:
Theorem 2.
The dynamic equation governing sliding (Equation (39)) is expected to demonstrate stability, with the states of the PI sliding dynamics (Equation (36)) asymptotically converging to the origin within finite time.
Proof of Theorem 2.
Examine the following Lyapunov framework:
Now, through the application of an integer derivative to Equation (40) and attention to Equation (3) in Property 2, one obtains
Substituting
from Equation (39) into Equation (41) yields the following:
Hence, based on Equation (44), the inequality
always holds true, and
. Consequently, the stability criteria outlined in Lemma 1 are met, resulting in the attainment of asymptotic stability for dynamic Equation (39) and the PI sliding dynamics (Equation (36)).
Now, for
, based on Equations (40) and (44),
Integrating both sides of Equation (31) yields
Since
one obtains
Thus, the convergence of
states to zero within a finite time
concludes the proof. □
Remark 3.
In this study, the sliding surfaces for the
-SMC method are carefully designed to achieve robust synchronization of chaotic FOMNNSs. The design process involves the following key elements:
- Initial Sliding Surface:
- •
- State Trajectories: The initial sliding surface is introduced to guide the state trajectories of the chaotic system towards a more controlled behavior. This surface is a function of the system’s state variables and is typically designed to simplify the system’s dynamics, making it easier to manage the chaotic behavior.
- •
- Robustness: Although the initial sliding surface provides some level of control, it primarily serves as the foundation for more robust control mechanisms. It reduces the complexity of the system’s chaotic dynamics, but further refinement is needed to handle uncertainties and external disturbances effectively.
- -Sliding Surface:
- •
- Proportional-Integral (PI) Rules: The -sliding surface is designed using PI rules, which combine proportional and integral actions to improve control performance. The addition of the fractional-order element (denoted by φ) allows the surface to better manage the memory and hereditary effects inherent in fractional-order systems, resulting in more precise control over the state trajectories.
- •
- Robustness Against Uncertainties: This surface is designed to be robust against system uncertainties, input saturations, and delays. By incorporating both PI control and fractional-order dynamics, the -sliding surface ensures that the system can reach and maintain desired states even in the presence of significant disturbances and nonlinearities.
- Lyapunov Stability:
- •
- Finite-Time Asymptotic Stability: The stability of both the initial and -sliding surfaces is analyzed using the fractional-order Lyapunov stability theory. This theory helps demonstrate that the system’s state trajectories will converge to the sliding surfaces within a finite time and remain there, ensuring that the chaotic behavior is effectively controlled and synchronization is achieved.
- •
- Lyapunov Function: A Lyapunov function is typically constructed to prove that the sliding surfaces are stable. The function is chosen such that it decreases over time, guaranteeing that the system’s state will move towards the sliding surface and stay there, leading to finite-time synchronization of the delayed FOMNNS.
Remark 4.
The decision to design two sliding surfaces—a primary sliding surface and a
sliding surface—was made to enhance both the robustness and precision of the control system for FOMNNSs with delays and input saturation. The primary sliding surface ensures initial stabilization by guiding the chaotic system’s trajectory towards a stable region, while the
sliding surface introduces proportional–integral control to refine the system’s response, compensating for steady-state errors and further improving robustness against uncertainties. This two-level structure also better handles input saturation and accelerates convergence to finite-time synchronization, offering significant advantages over a single sliding surface, which may struggle with control precision and only achieve asymptotic synchronization. This dual-layer approach thus optimizes both stability and performance, making it more suitable for complex system dynamics.
Now, for
a novel and dynamic-free control method will be introduced in the following theorem, formulated as:
The structure of the suggested controller applied to the FOMNNs is depicted in Figure 1.
Figure 1.
Closed-loop schematic of the suggested dynamic-free control for FOMNNs.
Theorem 3.
Consider the fractional-order error mechanism (Equation (14)). Utilizing the subsequent control approach (Equation (52)), the trajectories of the error FOMNNs (Equation (14)) will achieve asymptotic stability within a finite duration.
Proof of Theorem 3.
Examine the following Lyapunov framework:
By applying a first order derivative to Equation (53), and utilizing Equation (3) in Property 2, one obtains:
By inserting
from Equation (38) into Equation (54), we obtain
Now, by inserting
from Equation (23) into Equation (55), we obtain
Here, by substituting
from Equation (14) into Equation (56), and according to Equations (19) and (20), one has
By substituting
from Equation (52), one obtains the following:
Hence, based on Equation (61), the inequality
always holds true, and
. Consequently, the stability criteria outlined in Lemma 1 are met, resulting in the attainment of asymptotic stability for error FOMNNs (14).
Now, for
, based on the Equations (53) and (61)
Integrating both sides of Equation (64) yields
Dou to the fact that
one obtains
Thus, the convergence of
states to zero within a finite time
concludes the proof. □
4. Design of Finite Time -SMC Based on Deep SAC Learning
4.1. Principle Concepts of MDP and RL Algorithm
In many problems, all states of the system are not observable by the agent which are necessary to describe by Markov decision process (MDP) learning. By utilizing the MDP, the dynamics of any practical system can be captured in a straightforward manner where the agent policy is obtained according to the inherent characteristics of the system. According to the definition of the MDP, the next observation of a system only depends on the current observation [43]. Typically, the MDP is elaborated by a five-tuple
with the following expressions:
- •
- is the set of system observations (states).
- •
- is the set of actions.
- •
- is the transition function, where this function indicates the probability of mapping from current observation to next step observation under action .
- •
- is a reward signal which is emitted from the environment after applying the action .
- •
- A history stores all the transitions of actions and observations.
At each step, a signal is produced by the RL agent under current state
to obtain a reward signal
from the environment (system). To select the appropriate action, the policy
is defined which represents the behavior of the RL agent.
In RL problems, the agent aims to maximize the sum of discounted returns, given as
To complete the RL task, the state-value function
and action-value function
are defined according to Equation (70) and Equation (71), respectively.
4.2. Soft Actor-Critic Strategy
The soft actor-critic is one of the RL algorithms which can solve high-dimensional problems using the training capability of deep neural nets (DNNs). In the SCA, the concept of entropy regularization is utilized where the policy of this algorithm is characterized by preserving a balance between expected reward signals and entropy. This policy mechanism prevents premature convergence while improving the exploration capability. The SAC algorithm training is realized using entropy and reward terms [43,44].
where
is the hyper-parameter to adjust the entropy. The SAC algorithm is constructed from three DNNs including Q-net, V net, and Policy net. Also, an experience buffer is utilized to store all historical transitions during the training process.
The training Q-net parameterized by
is conduced by minimizing a soft Bellman equation, given as follows:
where
where
is the gradient of V net parameterized by
.
The value function V is defined using the following expression:
where
denotes the distribution of experience buffer.
The policy net parameterized by
is trained by
Moreover, two additional nets including target Q-net and target policy net are adopted in the SAC algorithm which are updated by the soft updates of main nets.
4.3. Design of -Sliding Model Control Based on SAC
The parameters of SMC play a critical role in the overall performance of the system. Thus, tunable coefficients embedded in the control law of SMC are adjusted by the soft actor-critic learning. The actor net generates regulatory signals to adaptively update the parameters of the control’s law to improve system performance. In this application, the terms of
,
,
,
,
,
} are selected as the tunable parameters of the controller which will be automatically adjusted by the deep SAC. The overall schematic of suggested
-SMC designed by soft actor-critic is depicted in Figure 2.
Figure 2.
Architecture of
-SMC controller for regulation of FC system using SAC algorithm.
By training the ability of the DNNs, the actor and critic nets are trained to maximize the reward function. The reward function is defined as follows:
The deep neural nets (Q-net, V net, Policy net and their target nets) are made from two hidden layers (HLs) with 200 and 300 neurons. The rectified linear units (ReLU) are adopted as the activation function of the DNNs. The weights of three DNNs are trained by ADAM optimizer. The hyper-parameters of the deep SAC are listed in Table 1.

Table 1.
Hyper-parameters of SAC learning.
Remark 5.
The SAC algorithm was chosen to optimize the parameters of the
-SMC controller due to its unique advantages in handling complex and high-dimensional control problems. SAC combines the benefits of both value-based and policy-based reinforcement learning approaches, which makes it particularly effective for optimizing control parameters in dynamic systems with challenging conditions.
Unique Advantages of SAC Compared to Other Optimization Algorithms:
- Sample Efficiency: SAC is known for its sample efficiency, meaning it requires fewer interactions with the environment to learn effective policies. This is crucial for optimizing control parameters in systems where obtaining data can be costly or time-consuming.
- Stability and Robustness: SAC utilizes off-policy learning and stable target networks, which contribute to its robustness and stability during training. This is particularly advantageous for managing the inherent uncertainties and chaotic behavior of FOMNNSs, ensuring reliable parameter optimization.
- Continuous Action Space: SAC is well suited for continuous action spaces, making it an ideal choice for optimizing control parameters in scenarios where control inputs are continuous rather than discrete. This aligns well with the needs of fine-tuning the PI^φ-SMC controller.
- Entropy Regularization: SAC incorporates entropy regularization to encourage exploration and prevent premature convergence to suboptimal solutions. This feature helps in finding more robust and optimal control policies by balancing exploration and exploitation.
- High Dimensionality Handling: SAC effectively manages high-dimensional state and action spaces, which is beneficial for complex systems like FOMNNSs where the control problem may involve numerous parameters and intricate dynamics.
Overall, SAC’s combination of sample efficiency, stability, suitability for continuous action spaces, and robust exploration makes it a superior choice for optimizing the
—SMC controller compared to other optimization algorithms such as genetic algorithms or particle swarm optimization, which may not handle the high-dimensional and continuous nature of the control problem as effectively.
5. Numerical Simulations
Here, two different numerical situations involving delayed FOMNNs are examined to demonstrate how the multi-level SMC method can be effectively applied. The numerical simulations utilized the algorithm described in [45,46], with a time-step of h = 0.01 implemented in MATLAB R2023bsoftware.
5.1. Scenario 1: In the Case of 2D Complex Delayed FOMNNSs
In this exemplar, we contemplate the illustration of two-dimensional unknown delayed FOMNNSs. Based on the delayed FOMNN (8), the following delayed FOMNN is regarded as the driving system:
where,
,
,
,
, and
. Also,
, and
, and
.
and the response system is as follows:
where,
, and
. Also,
, and
and
.
The control technique parameters in Equation (52) are established as
The parameters of the control methodology (52) are set as
and
. Furthermore, the parameters of the SS (21) are selected by
,
. Moreover, the nonlinear input
is introduced as
Figure 3 and Figure 4 illustrate the synchronization and controlled error of the states of FO drive-response in delayed FOMNNSs (78) and (80). It is clear that the chaotic attractors of the complex FO error mechanisms quickly converged to stability points. Additionally, Figure 4 presents the time-history of the
-SMC method (52) used to synchronize the delayed FOMNNSs. The control input (52) is seen to reach equilibrium without any signs of the chattering phenomenon. This demonstrates the
-SMC method can effectively synchronize the two-dimensional delayed FOMNNSs (78) and (80). Moreover, as depicted in Figure 5, when the signals of the control laws approach the saturation boundaries, they are suppressed by the saturation condition, leading to leaping phenomena. Thus, jumping and switching states can be easily applied, especially when relays and specified saturation conditions are employed.
Figure 3.
The time-history of the synchronized delayed FOMNNSs (78) and (80).
Figure 4.
The time-history of the errors between the delayed FOMNNSs (78) and (80).
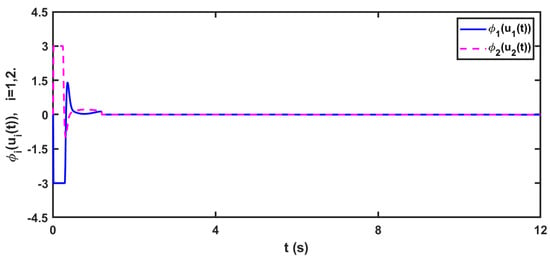
Figure 5.
The time-response of the control signals (52) applied for synchronization of the delayed FOMNNSs (78) and (80).
Figure 6 shows the time-response of the SS (21) for both function and surface plots. Clearly, each component of the SS (21) converges to zero, and there are no signs of the chattering phenomenon in the SS (21).
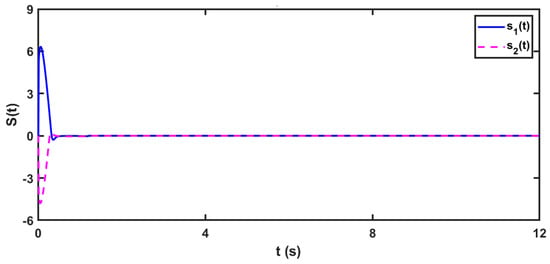
Figure 6.
The time-evolution of the SS (21) applied for synchronization of the delayed FOMNNSs (78) and (80).
5.2. Scenario 2: In the Case of 3D Unknown Delayed FOMNNSs
Here, we examine the representation of two-dimensional unfamiliar delayed FOMNNSs. Using the delayed FOMNN (8) as a reference point, the subsequent delayed FOMNN is considered the leading system.
where,
,
,
,
, and
. Furthermore,
,
, and
and
.
And for the response system,
where,
, and
. Also,
, and
,
and
.
And, for
, the structure of the input controller is
Also,
, and
show the starting values.
The parameters of the control signal (52) were selected as
and
and
. Plus, the parameters of the SS (21) were
,
and
.
Figure 7 and Figure 8 depict the synchronization and controlled error of the states of FO drive-response in three-dimensional delayed FOMNNSs (83) and (85). The chaotic attractors of the chaotic FO error system are quickly stabilized. Additionally, Figure 8 presents the time-history of the
-SMC method controller (52) used for synchronizing the delayed FOMNNSs (83) and (85). The control input (52) achieves equilibrium without exhibiting any signs of the chattering phenomena, demonstrating the effectiveness of the
-SMC method in synchronizing the three-dimensional delayed FOMNNSs (83) and (85). Moreover, as shown in Figure 9, when the control law signals approach the saturation limits, they are controlled by the saturation protocol, leading to leaping happening. Therefore, jumping and switching states can be easily operated, particularly when using transmits and specified saturation criteria.
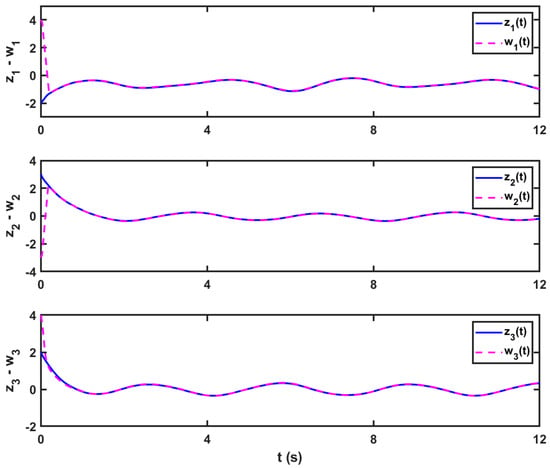
Figure 7.
The time-history of the synchronized delayed FOMNNSs (83) and (85).
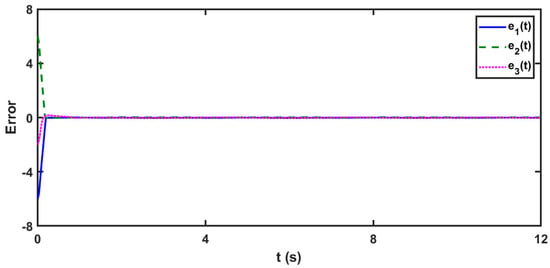
Figure 8.
The time-evolution of the errors between the delayed FOMNNSs (83) and (85).
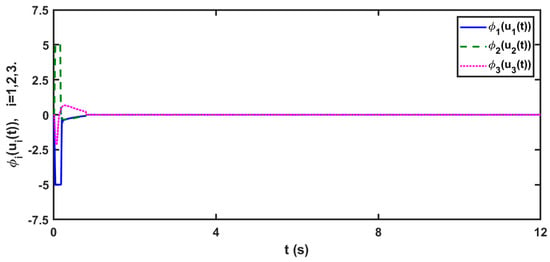
Figure 9.
The time-response of the control signals (52) for the synchronization of delayed FOMNNSs (83) and (85).
Figure 10 illustrates the time-response of the sliding surface (21) used for synchronizing the delayed FOMNNSs (83) and (85). Clearly, each parameter of the sliding surface (21) converges to zero, and there are no indications of the chattering phenomenon. The sliding surfaces surface (21) converges to zero, and there are no indications of the chattering phenomenon on the sliding surfaces.
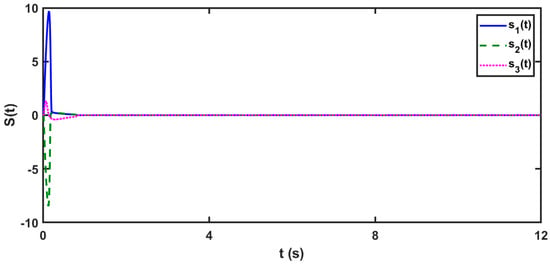
Figure 10.
The time evolution of the SS (21) for synchronization of the delayed FOMNNSs (83) and (85).
6. Discussion and Conclusions
This study presents a model-free
-SMC methodology for achieving synchronization in chaotic delayed FOMNNSs with input saturation. The approach leverages fractional-order Lyapunov stability theory to develop a two-tiered
-SMC framework, effectively addressing the inherent chaotic behavior of delayed FOMNNSs and ensuring finite-time synchronization. The methodology began with the introduction of a primary sliding surface. This was followed by the design of a robust
sliding surface, grounded in proportional-integral (PI) rules, and the demonstration of finite-time asymptotic stability for both sliding surfaces. Subsequently, a dynamic-free control law was formulated, which is robust against system uncertainties, input saturations, and delays. This approach decouples the control signals from both nonlinear and linear components of the system, taking advantage of the norm-boundedness of chaotic states. To further enhance the performance of the
-SMC, the deep SAC learning is integrated with the control strategy, effectively removing constraints on the initial conditions of the control input and ensuring that the sliding motion adheres to the reachability condition within finite time. The proposed methodology’s validity is confirmed through comprehensive simulation results and two numerical examples, demonstrating its robustness and effectiveness in practical scenario.
For future work, we plan to extend the
-SMC methodology to other complex systems, including higher-dimensional and nonlinear systems. Future research will also focus on integrating adaptive control techniques to handle time-varying uncertainties and input saturations, and on conducting experimental validations to bridge theoretical results with practical applications. Additionally, we will explore methods to reduce computational complexity for real-time implementation and consider incorporating machine learning for system identification and adaptive control. Finally, we will perform a sensitivity analysis to better understand the robustness of our approach under varying conditions. Additionally, we plan to design and conduct experiments to calibrate the model parameters using real-world data. This can be realized through collecting data from physical systems similar to those modeled in our study and applying advanced parameter estimation techniques to fine-tune the control law coefficients.
Author Contributions
Conceptualization, M.R., A.R.H. and A.B.-O.; Methodology, M.R. and A.B.-O.; Software, M.R. and S.M.; Validation, A.R.H.; Formal analysis, M.R., S.M. and A.B.-O.; Investigation, A.B.-O.; Resources, A.B.-O.; Writing—original draft, M.R. and S.M.; Writing—review & editing, A.R.H. and A.B.-O.; Supervision, A.B.-O.; Project administration, A.B.-O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cao, Y.; Kao, Y.; Wang, Z.; Yang, X.; Park, J.H.; Xie, W. Sliding mode control for uncertain fractional-order reaction–diffusion memristor neural networks with time delays. Neural Netw. 2024, 178, 106402. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Liu, S.; Wu, X.; Sun, J.; Qiao, W. Synchronization of Fractional Delayed Memristive Neural Networks with Jump Mismatches via Event-Based Hybrid Impulsive Controller. Fractal Fract. 2024, 8, 297. [Google Scholar] [CrossRef]
- Roohi, M.; Zhang, C.; Taheri, M.; Basse-O’Connor, A. Synchronization of Fractional-Order Delayed Neural Networks Using Dynamic-Free Adaptive Sliding Mode Control. Fractal Fract. 2023, 7, 682. [Google Scholar] [CrossRef]
- He, Y.; Zhang, W.; Zhang, H.; Cao, J.; Alsaadi, F.E. Finite-time projective synchronization of fractional-order delayed quaternion-valued fuzzy memristive neural networks. Nonlinear Anal. Model. Control. 2024, 29, 401–425. [Google Scholar] [CrossRef]
- Chen, L.; Gong, M.; Zhao, Y.; Liu, X. Finite-Time Synchronization for Stochastic Fractional-Order Memristive BAM Neural Networks with Multiple Delays. Fractal Fract. 2023, 7, 678. [Google Scholar] [CrossRef]
- Liu, X.; He, H.; Cao, J. Event-Triggered Bipartite Synchronization of Delayed Inertial Memristive Neural Networks With Unknown Disturbances. IEEE Trans. Control. Netw. Syst. 2023, 1–12. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; De Jesus, A.M.P.; Fazeres-Ferradosa, T.; Zhu, S.-P. A novel hybrid adaptive Kriging and water cycle algorithm for reliability-based design and optimization strategy: Application in offshore wind turbine monopile. Comput. Methods Appl. Mech. Eng. 2023, 412, 116083. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Y.; Frangopol, D.M. An error-based stopping criterion for spherical decomposition-based adaptive Kriging model and rare event estimation. Reliab. Eng. Syst. Saf. 2024, 241, 109610. [Google Scholar] [CrossRef]
- Jia, D.-W.; Wu, Z.-Y. An improved adaptive Kriging model for importance sampling reliability and reliability global sensitivity analysis. Struct. Saf. 2024, 107, 102427. [Google Scholar] [CrossRef]
- Alikhanov, A.A.; Asl, M.S.; Huang, C.; Khibiev, A. A second-order difference scheme for the nonlinear time-fractional diffusion-wave equation with generalized memory kernel in the presence of time delay. J. Comput. Appl. Math. 2024, 438, 115515. [Google Scholar] [CrossRef]
- Alikhanov, A.A.; Asl, M.S.; Huang, C. Stability analysis of a second-order difference scheme for the time-fractional mixed sub-diffusion and diffusion-wave equation. Fract. Calc. Appl. Anal. 2024, 27, 102–123. [Google Scholar] [CrossRef]
- Narayanan, G.; Ali, M.S.; Karthikeyan, R.; Rajchakit, G.; Sanober, S.; Kumar, P. Adaptive Strategies and its Application in the Mittag-Leffler Synchronization of Delayed Fractional-Order Complex-Valued Reaction-Diffusion Neural Networks. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 1–14. [Google Scholar] [CrossRef]
- Birs, I.; Muresan, C.; Nascu, I.; Ionescu, C. A Survey of Recent Advances in Fractional Order Control for Time Delay Systems. IEEE Access 2019, 7, 30951–30965. [Google Scholar] [CrossRef]
- Rasooli Berardehi, Z.; Zhang, C.; Taheri, M.; Roohi, M.; Khooban, M.H. Implementation of TS fuzzy approach for the synchronization and stabilization of non-integer-order complex systems with input saturation at a guaranteed cost. Trans. Inst. Meas. Control. 2023, 45, 2536–2553. [Google Scholar] [CrossRef]
- Xie, S.; Sun, H.; Xie, Y.; Chen, X. Tuning of fuzzy controller with arbitrary triangular input fuzzy sets based on proximal policy optimization for time-delays system. J. Process Control. 2023, 129, 103059. [Google Scholar] [CrossRef]
- Roohi, M.; Mirzajani, S.; Haghighi, A.R.; Basse-O’Connor, A. Robust stabilization of fractional-order hybrid optical system using a single-input TS-fuzzy sliding mode control strategy with input nonlinearities. AIMS Math. 2024, 9, 25879–25907. [Google Scholar] [CrossRef]
- Makhbouche, A.; Boudjehem, B.; Birs, I.; Muresan, C.I. Fractional-Order PID Controller Based on Immune Feedback Mechanism for Time-Delay Systems. Fractal Fract. 2023, 7, 53. [Google Scholar] [CrossRef]
- Liu, S.; Wang, H.; Li, T. Adaptive composite dynamic surface neural control for nonlinear fractional-order systems subject to delayed input. ISA Trans. 2023, 134, 122–133. [Google Scholar] [CrossRef]
- Dong, H.Q.; Gam, N.T.; Cuong, H.M.; Tuan, L.A. Fractional-order fast terminal back-stepping sliding mode control of autonomous robotic excavators. J. Frankl. Inst. 2024, 361, 106686. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, H.; Sun, J.; Wang, Y. Sliding Mode Control Based on Reinforcement Learning for T-S Fuzzy Fractional-Order Multiagent System With Time-Varying Delays. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 1–12. [Google Scholar] [CrossRef]
- Johnson, M.; Mohan Raja, M.; Vijayakumar, V.; Shukla, A.; Nisar, K.S.; Jahanshahi, H. Optimal control results for impulsive fractional delay integrodifferential equations of order 1 < r < 2 via sectorial operator. Nonlinear Anal. Model. Control. 2023, 28, 468–490. [Google Scholar] [CrossRef]
- Roohi, M.; Mirzajani, S.; Basse-O’Connor, A. A No-Chatter Single-Input Finite-Time PID Sliding Mode Control Technique for Stabilization of a Class of 4D Chaotic Fractional-Order Laser Systems. Mathematics 2023, 11, 4463. [Google Scholar] [CrossRef]
- Ren, Z.; Tong, D.; Chen, Q.; Zhou, W. Sliding Mode Control for Uncertain Fractional-Order Systems with Time-Varying Delays. Circuits Syst. Signal Process. 2024, 43, 3979–3995. [Google Scholar] [CrossRef]
- Cheng, Y.; Hu, T.; Xu, W.; Zhang, X.; Zhong, S. Fixed-time synchronization of fractional-order complex-valued neural networks with time-varying delay via sliding mode control. Neurocomputing 2022, 505, 339–352. [Google Scholar] [CrossRef]
- Jia, T.; Chen, X.; He, L.; Zhao, F.; Qiu, J. Finite-Time Synchronization of Uncertain Fractional-Order Delayed Memristive Neural Networks via Adaptive Sliding Mode Control and Its Application. Fractal Fract. 2022, 6, 502. [Google Scholar] [CrossRef]
- Chen, T.; Yang, H.; Yuan, J. Event-Triggered Adaptive Neural Network Backstepping Sliding Mode Control for Fractional Order Chaotic Systems Synchronization With Input Delay. IEEE Access 2021, 9, 100868–100881. [Google Scholar] [CrossRef]
- Ren, F.; Wang, X.; Zeng, Z. Improved Fixed-Time Stabilization of Fuzzy Neural Networks With Distributed Delay via Adaptive Sliding Mode Control. IEEE Trans. Fuzzy Syst. 2023, 31, 2029–2043. [Google Scholar] [CrossRef]
- Dalir, M.; Bigdeli, N. An Adaptive neuro-fuzzy backstepping sliding mode controller for finite time stabilization of fractional-order uncertain chaotic systems with time-varying delays. Int. J. Mach. Learn. Cybern. 2021, 12, 1949–1971. [Google Scholar] [CrossRef]
- Chen, T.; Yuan, J.; Yang, H. Event-triggered adaptive neural network backstepping sliding mode control of fractional-order multi-agent systems with input delay. J. Vib. Control. 2021, 28, 23–24. [Google Scholar] [CrossRef]
- Gao, J.; Chen, X.; Qiu, J.; Wang, C.; Jia, T. Adaptive Sliding Mode Fixed-/Preassigned-Time Synchronization of Stochastic Memristive Neural Networks with Mixed-Delays. Neural Process. Lett. 2024, 56, 205. [Google Scholar] [CrossRef]
- Fan, H.; Rao, Y.; Shi, K.; Wen, H. Time-Varying Function Matrix Projection Synchronization of Caputo Fractional-Order Uncertain Memristive Neural Networks with Multiple Delays via Mixed Open Loop Feedback Control and Impulsive Control. Fractal Fract. 2024, 8, 301. [Google Scholar] [CrossRef]
- Wen, G.; Chen, C.P.; Li, W.N. Simplified optimized control using reinforcement learning algorithm for a class of stochastic nonlinear systems. Inf. Sci. 2020, 517, 230–243. [Google Scholar] [CrossRef]
- Bian, T.; Jiang, Z.-P. Reinforcement learning and adaptive optimal control for continuous-time nonlinear systems: A value iteration approach. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 2781–2790. [Google Scholar] [CrossRef]
- Yuan, X.; Wang, Y.; Zhang, R.; Gao, Q.; Zhou, Z.; Zhou, R.; Yin, F. Reinforcement learning control of hydraulic servo system based on TD3 algorithm. Machines 2022, 10, 1244. [Google Scholar] [CrossRef]
- Chen, S.; Qiu, X.; Tan, X.; Fang, Z.; Jin, Y. A model-based hybrid soft actor-critic deep reinforcement learning algorithm for optimal ventilator settings. Inf. Sci. 2022, 611, 47–64. [Google Scholar] [CrossRef]
- Ren, Y.; Duan, J.; Li, S.E.; Guan, Y.; Sun, Q. Improving generalization of reinforcement learning with minimax distributional soft actor-critic. 2020 IEEE 23rd Int. Conf. Intell. Transp. Syst. 2020, 1–6. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier Science: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Asl, M.S.; Javidi, M. Numerical evaluation of order six for fractional differential equations: Stability and convergency. Bull. Belg. Math. Soc. -Simon Stevin 2019, 26, 203–221. [Google Scholar] [CrossRef]
- Li, C.; Deng, W. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Curran, P.F.; Chua, L.O. Absolute Stability Theory and the Synchronization Problem. Int. J. Bifurc. Chaos 1997, 7, 1375–1382. [Google Scholar] [CrossRef]
- Roohi, M.; Aghababa, M.P.; Haghighi, A.R.J.C. Switching adaptive controllers to control fractional—order complex systems with unknown structure and input nonlinearities. Complexity 2015, 21, 211–223. [Google Scholar] [CrossRef]
- Haklidir, M.; Temeltaş, H. Guided soft actor critic: A guided deep reinforcement learning approach for partially observable Markov decision processes. IEEE Access 2021, 9, 159672–159683. [Google Scholar] [CrossRef]
- Tang, H.; Wang, A.; Xue, F.; Yang, J.; Cao, Y. A novel hierarchical soft actor-critic algorithm for multi-logistics robots task allocation. Ieee Access 2021, 9, 42568–42582. [Google Scholar] [CrossRef]
- Alikhanov, A.A.; Asl, M.S.; Huang, C.; Apekov, A.M. Temporal second-order difference schemes for the nonlinear time-fractional mixed sub-diffusion and diffusion-wave equation with delay. Phys. D Nonlinear Phenom. 2024, 464, 134194. [Google Scholar] [CrossRef]
- Asl, M.S.; Javidi, M.; Ahmad, B. New predictor-corrector approach for nonlinear fractional differential equations: Error analysis and stability. J. Appl. Anal. Comput. 2019, 9, 1527–1557. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).