Abstract
This paper presents an application of a fractional-order system on modeling an industrial process system with large inertia and time delay. The traditional integer-order model of the process system is extended to a fractional-order one in this work. To identify the parameters of the proposed fractional-order model, an output-error identification algorithm is presented. Based on the experimental step response data of the selective catalytic reduction (SCR) denitrification process in a power plant, this proposed fractional-order model shows a better fitting result compared with the typical integer-order models. An integer-order proportional–integral (PI) controller is designed for the process plant using a simple scheme according to the identified fractional-order and integer-order models, respectively. Validation tests are performed based on the obtained fractional-order and integer-order models, demonstrating the advantages of the proposed fractional-order model with the corresponding system identification approach for industrial processes with large inertia and time delay.
1. Introduction
Fractional-order modeling has gained significant attention in recent years due to its ability to capture complex dynamics more accurately compared to its traditional integer-order counterparts [1]. Zheng et al. [2] proposed a fractional-order modeling approach for a permanent magnet synchronous motor (PMSM) speed servo system combining electromagnetic part modeling and mechanical part modeling; system identification, closed-loop control simulation, and experiments were conducted, showing the advantage of the proposed fractional-order model. Gan et al. [3] also presented a fractional-order electromagnetic modeling method for a PMSM speed servo system but from the perspective of voltage source inverter nonlinearity, and they proposed an improved inverter nonlinearity model and compensation method. Shi et al. [4] derived a fractional-order Euler–Lagrange equation and applied the proposed equation to describe the dynamics of a multiple-backbone continuum robot; the simulation illustrated that the fractional-order Lagrange dynamic model of the continuum robot had higher modeling accuracy. Sierociuk et al. [5] explored heat conduction under different initial and boundary conditions by analogizing it to electrical conduction, using an RC network as an electro-analog model of the diffusion process model of heat dissipation processes; in addition, a fractional-order model of the diffusion process and its modeling via a lumped RC network was used. A matrix method for solving fractional-order diffusion equations was introduced, and comparisons were made among analytical solutions, numerical solutions, and experimental measurements, demonstrating the effectiveness of the numerical approach. Wang et al. [6] established a fractional-order model of lithium-ion batteries based on a modified Randles model using the form of an equivalent circuit model. The parameters of the fractional-order model were identified based on time-domain test data by using a hybrid multiswarm particle swarm optimization algorithm. A comparison with the commonly used first-order RC equivalent circuit model demonstrates the superiority of the fractional-order model. Zeng et al. [7] established a high-precision fractional-order hysteresis-equivalent circuit model (FH-ECM) based on the second-order RC equivalent circuit model and Grunwald–Letnikov (G-L) definition, considering the open-circuit voltage hysteresis effect; identification was conducted using a particle swarm algorithm optimized by a genetic algorithm (GA-PSO), and the feasibility of the model and algorithm was verified under complex working conditions. Gude et al. [8] introduced a novel method for identifying dynamic systems aimed at deriving reduced-fractional-order models and applied them to processes exhibiting an S-shaped step response. The proposed method demonstrated its efficacy and simplicity through several illustrative examples. Haider et al. [9] proposed a novel method based on a hybrid of Bernoulli polynomials and block pulse functions (HBPBPFs) to identify fractional-order systems with time delays, and the approach was applied to a numerical and a real example of an industrial air heating process. Shalaby et al. [10] proposed a fractional-order model of an inverted pendulum system (IPS), extending the traditional integer-order IPS model to the fractional-order one. The parameters of the proposed fractional-order model were identified using the sine cosine algorithm (SCA), and comparison results showed superior fitting performance compared to the integer-order model. Controllers were designed using the same design approach for the identified fractional-order model, integer-order model, and theoretical nonlinear model (TNM), demonstrating the advantages of the proposed fractional-order modeling approach in control system design.
In the field of process control, considering the knowledge reserve of on-site operators, equipment computing power, and industrial control requirements for safety and stability, a low-order model such as a first-order plus time delay (FOPTD) model is normally used for identification and controller design [11]. However, due to the complex mechanisms, varying conditions, and multisource disturbances typically present in industrial processes, it is a struggle for lower-order models to accurately fit the responses of real systems. On the other hand, employing higher-order models increases the difficulty of controller design. From the above discussion, there is a significant advantage of fractional-order modeling in process control: a fractional-order model with much fewer parameters can achieve satisfactory fitting of system dynamics with significantly decreasing model complexity compared with a high-order model with many more parameters [8]. The selective catalytic reduction (SCR) denitrification process is a typical plant with complex dynamic characteristics, which has a strong need for modeling accuracy and control performance improvements. SCR technology has emerged as a cornerstone in the mitigation of nitrogen oxide () emissions from industrial sources, crucial for environmental sustainability and regulatory compliance. Studying the modeling and control of the SCR denitrification process holds significant engineering importance. Pan et al. [12] proposed a simplified dynamical transfer function model of SCR denitrification reaction system adopting mechanism modeling. Li et al. [13] utilized historical data from the distributed control system (DCS) database of a 350 MW coal-fired power plant. The proposed method selects sufficiently excited data from the original historical operation data based on the condition number of the Fisher information matrix, and the asymptotic method is applied to identify the high-order auto-regressive with extra inputs (ARX) model of the SCR denitrification process. Wang et al. [14] proposed an identification method for the SCR flue gas denitration system of a 600 MW power plant under closed-loop operation conditions, based on a new fading memory recursive least squares (FMRLS) algorithm using the squared error loss function (SELF). The results demonstrate that this method offers advantages including a small deviation range, fast convergence speed, and high accuracy. Kang et al. [15] proposed a method that combines dynamic joint mutual information and Bi-LSTM, where the dynamic joint mutual information theory is used to estimate the reactor dynamic characteristics and system delay. Through the analysis of the formation mechanism of NOx and the reaction mechanism of the SCR reactor, Xie et al. [16] proposed a sequence-to-sequence dynamic prediction model, which can fit multivariable coupling, nonlinear, and large delay systems. An et al. [17] proposed a method based on hybrid data-driven approaches and model ensemble to dynamically estimate
concentrations at the outlet of SCR systems. The approach includes outlier detection, time delay estimation, phase space reconstruction, and feature selection. Through model ensemble strategies integrating genetic algorithm-optimized neural networks, support vector machines, and gradient boosting models, a model accurately predicts
emissions from SCR systems. Validation results demonstrate excellent dynamic tracking performance and prediction consistency in practical industrial applications.
Based on the above discussion, this paper explores an application of fractional-order systems in modeling the SCR denitrification process in a power plant which can be characterized by large inertia and time delays. It extends the traditional FOPTD model of such processes to a fractional-order model. To identify the parameters of the proposed model, an output-error identification algorithm is introduced. Using experimental step response data from the SCR denitrification process, the fractional-order model demonstrates superior fitting results compared to the integer-order model. An integer-order proportional–integral (PI) controller is designed for the process plant based on both the identified fractional-order model and the integer-order model. Validation tests confirm the advantages of the fractional-order model and the corresponding system identification approach for this industrial process.
The main contributions of this paper are summarized as follows:
- (1)
- A fractional-order plus time delay modeling with a parameter identification approach for experimental step response data from an industrial power plant SCR denitrification process is proposed;
- (2)
- Closed-loop control illustration using the PI controllers designed for the traditional integer-order models and the fractional-order one is conducted to show the advantages of the proposed fractional-order model with the corresponding system identification approach.
The rest of this paper is organized as follows: the main chemical reaction equation and dynamic mechanism model of the SCR denitrification process are discussed in Section 2; the fundamentals of fractional calculus, an integer-order approximation approach of fractional-order operators, and a time-domain identification method of fractional-order model are presented in Section 3; and parameter identification and control simulation based on experimental data of an SCR denitrification process in a power plant are conducted in Section 4. The conclusion is provided in the last section.
2. SCR Denitrification Process
The denitrification process of coal-fired units exhibits complex characteristics with large inertia and time delay, posing practical challenges in modeling and control. This section introduces the structure of the SCR denitrification system and its dynamic reaction mechanism.
2.1. Reaction Process of SCR Denitrification System
The schematic diagram of the SCR denitrification system for coal-fired units is shown in Figure 1 [18]. Flue gas generated by boiler combustion and ammonia gas diluted with air are introduced into the SCR reactor vessel simultaneously, and harmless nitrogen gas and water are produced, thereby strictly controlling the concentration of
in the outlet flue gas. The main chemical reactions in this process are as follows [18]:
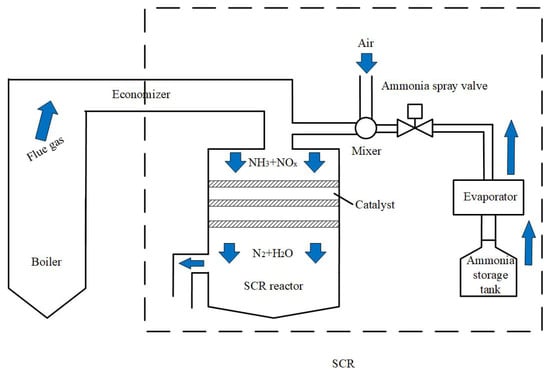
Figure 1.
Schematic diagram of the selective catalytic reduction (SCR) denitrification system.
In the practical denitrification process, approximately 95% of the
introduced into the reactor is
; thus, the primary chemical reactions that occur are the first two reactions mentioned above.
The basic control diagram of the SCR denitrification process is shown in Figure 2. Adjusting the opening of the ammonia injection valve to control the amount of ammonia injected ensures sufficient reaction of
in the flue gas. In the above-mentioned process, excessive ammonia injection leads to high outlet ammonia concentration, while insufficient injection results in
concentration exceeding the standard [19].
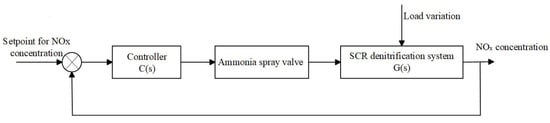
Figure 2.
Basic control diagram of the SCR denitrification process.
2.2. Dynamic Mechanism of the SCR Denitrification Reaction
Investigating the reaction mechanism of the SCR denitrification process enhances comprehension of the intricate dynamic characteristics inherent to this process. Yao et al. [20] proposed a set of nonlinear differential equations to describe the dynamics of the SCR denitrification reaction:
where
and
are the concentrations of
and
in the SCR process;
and
are the inlet concentration of
and
;
is the coverage fraction of
on the catalyst surface; F and V are the flue gas flow and the volume of the reactor, respectively;
characterizes the adsorption capacity of the catalyst for
in the reactor;
,
,
, and
are the rates of oxidation, reduction, adsorption, and desorption, which can be calculated by
where
,
,
, and
refer to oxidation rate coefficient, denitrification rate coefficient, adsorption rate coefficient, and desorption rate coefficient;
,
,
, and
stand for the activation energies in the corresponding reaction; and R and T refer to the universal gas constant and temperature, respectively. The units of the quantities are provided in Appendix B.
The adsorption and desorption of ammonia are intermediate processes in the entire denitrification reaction; hence, the coverage fraction of
() is regarded as an intermediate state variable in the dynamic model of the denitrification reaction. To simplify the model complexity, the concentration of the material inside the reactor is assumed to be equal to the outlet concentration. The inlet
molar concentration () and inlet
molar concentration () are the inputs to the mechanism model, while the outlet
molar concentration () and outlet
molar concentration () are the outputs of the mechanism model.
,
,
,
,
,
,
,
, and
remain constant during the reaction and can be obtained through identification. However, the concentration and flue gas flow fields within the reactor are nonuniform, and the flue gas temperature can only be measured at the reactor inlet, while the temperature inside the reactor is unmeasurable. Additionally, the aforementioned dynamics do not account for side reactions involving ammonia and other substances such as sulfur compounds in the flue gas, leading to poor generalization of the nonlinear model and difficulty in meeting control requirements. Consequently, black-box modeling methods are widely used in the denitrification process [13,14,18]. In practical applications, since the inlet
concentration is relatively constant, the ammonia injection amount is often used as the input and the outlet
concentration as the output for modeling.
3. Fractional Order Modeling and Identification
First, the fundamental concept of fractional calculus is introduced in this section, and then an implementation approximation method is presented, which approximates the fractional-order operators in the frequency domain. Furthermore, the approximation method of a fractional-order transfer function and time-domain identification method based on the fractional-order model are presented in the last two subsections.
3.1. Fundamental Concept of Fractional Calculus
The continuous fractional order integral–differential operator is defined as follows:
where
and t are the time limits of the integration and
is the fractional order, and
is the real part of
.
The Caputo definition of a fractional derivative is
where n is an integer, satisfying
, and
is the Gamma function with the definition
The Laplace transform of the above-mentioned derivative is
where
.
3.2. Approximation of Fractional-Order Operator and System
The fractional-order system is infinite-dimensional, so approximation within a certain range is required in numerical simulation to approximate the behavior of a fractional-order system.
In this subsection, the fractional-order operator under discussion is
, where
, and the fractional-order operator outside this range can be approximated by cascading with an integer-order operator [1].
Theoretically, the slope of the Bode magnitude characteristics of
is 20
dB/dec, while the slope of the asymptotic Bode plot for an integer-order transfer function is always a multiple of 20 dB/dec. Hence, it is not possible to achieve a completely consistent approximation of a fractional-order operator using an integer-order transfer function.
An Oustaloup filter [21] is a commonly used integer-order approximation method that approximates the Bode magnitude characteristics of fractional-order operators within a specific frequency range, using a set of integer-order poles and zeros to generate asymptotic Bode plots as shown in Figure 3 [22]. The slanted line in Figure 3 represents the ideal magnitude-frequency characteristic curve of the fractional-order operator, while the polyline is the approximation of the ideal magnitude-frequency curve within the specified frequency range.
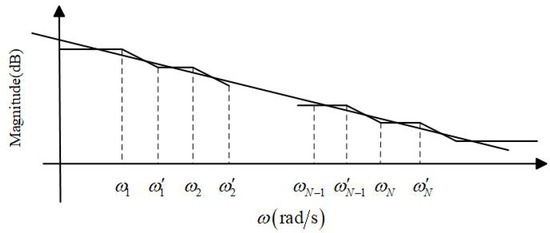
Figure 3.
Illustration of the Bode plot of the Oustaloup filter.
The standard form of the Oustaloup filter is given as follows:
where
,
, and
refer to the gain, zeros, and poles of the filter, respectively; N is the order of the filter.
Giving the frequency range
and the order N, the parameters of the Oustaloup filter can be calculated by
Fractional-order transfer functions can be used to describe the dynamics of the system. By replacing the fractional-order operator with the Oustaloup filter in a fractional-order transfer function, an integer-order approximation of the fractional-order model can be realized.
The frequency range affects the filter’s ability to process signal frequencies, while the order determines the approximation capability and impacts model accuracy. When designing the Oustaloup filter, the rough estimation of the cutoff frequency of the plant is chosen as the midpoint of the frequency range for the filter. Since a larger frequency range and a higher order do not significantly increase the computation time of the filter parameters [22], a frequency range with the size of at least six decades and an order of 15 or higher are chosen to ensure that the output of the model closely approximates the actual plant.
3.3. Identification of the Fractional-Order Model with Time Delay
The proposed fractional-order plus time delay model to be identified is described as follows:
where
is extended from a positive integer to any positive rational number; the FOPTD model is a specific instance of the above-mentioned model with
.
Known from the previous section, model (10) can be approximated by the following integer-order transfer function using an Oustaloup filter:
where
is the model parameter vector to be identified, while the frequency range
and the order N of the Oustaloup filter should be determined before the optimization procedure begins and stay consistent during the optimization process.
The classic graphical method is employed to obtain the initial model parameter vector
and determine the frequency range and the order of the Oustaloup filter. The estimation of the cutoff frequency of the plant is denoted as
, the frequency range of the filter is determined as
, and the order is chosen to be 15.
The MATLAB function
is used to calculate the model (11) output
based on the input signal
and the model parameter vector
, where k represents the individual sample time point. The objective function of this optimization procedure is the root mean square error (RMSE) between the model output
and experimental output
, i.e.,
where n is the number of sample points.
The MATLAB function
for finding the minimum value of an unconstrained multivariable function is applied in this work. Optimization is performed using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) [23,24,25,26] quasi-Newton method within this function. The gradient of the objective function
and an approximation of the inverse of the Hessian matrix H are used in the iteration.
The gradient is calculated using the forward finite difference method:
where h is the step size, with a recommended value of
[27], and
is the relative floating-point precision in MATLAB; m is the dimension of
, and
is an m-dimensional unit vector with the l-th element equal to 1,
.
Before the iteration starts, the gradient at the initial point is calculated. If
, where
denotes the infinity norm of a vector and
is the tolerance value, then the identification program terminates, and
is returned as the optimal value
; otherwise, the matrix H is initialized to
, where
is the m-dimensional identity matrix. The iterative process is described as follows:
- Line search: search along the given direction, determine the optimal step size, and update the solution.
- (a)
- Search direction : quasi-Newton direction is determined as follows:where , J is the maximum number of iterations (400 in this paper).
- (b)
- Step size : the Wolfe conditions are used to determine the search step size to ensure effective descent and improve convergence speed. The Wolfe conditions are defined as follows:where . ensures a significant descent in the objective function at the step size, while ensures that the gradient of the objective function changes sufficiently at the new point. In this paper, and . In each iteration, the initial step size is set to 1. If the current step size does not satisfy the Wolfe conditions, the step size is updated according to the following formula until the Wolfe conditions are met:
- (c)
- Update solution : according to the search direction and step size, the solution is updated as follows:
- Update the approximation of the inverse of the Hessian matrix: the BFGS method uses information from the previous iteration and related increments to update the approximation of the inverse of the Hessian matrix:where and .
- Termination: In each iteration, early termination is determined by checking if the gradient, solution increment, and objective function increment fall below predefined tolerance:where .
Algorithm 1 presents the pseudo-code for the identification procedure.
| Algorithm 1 The pseudo-code of the identification procedure. |
|
4. Fractional-Order Model Identification of the SCR Denitrification Process
In industrial processes, the FOPTD model’s simplicity facilitates proper controller design. However, the SCR denitrification system’s large inertia and delay characteristics lead to poor fitting when using FOPTD modeling, while the higher-order modeling method increases the complexity of controller design. Fractional-order modeling shows the advantages of both better fitting and easier controller design compared with traditional integer-order modeling.
4.1. Experimental Setup
In this paper, the research focuses on the SCR denitrification system employed in a 660 MW generator unit at the Honghaiwan Power Plant, Southern China Grid. Emerson’s OVATION1.9 distributed control system (DCS) collects historical operation data, which provides advanced monitoring, control, and data analysis capabilities. It supports real-time data acquisition and optimization control strategies to enhance industrial process efficiency, safety, and reliability. The OVATION system is characterized by openness and scalability, seamlessly integrating with other equipment and systems to meet the demands of the complex industrial environment. The historical operational data used for identification are steady-state step open-loop test data conducted at 400 MW and 580 MW loads, with a sampling period of 3 s. Maintaining a steady-state condition of total airflow and coal quantity during data acquisition is essential to ensure the stable operation of the SCR denitrification process. Figure 4 shows the experimental conditions under 400 MW and 580 MW. The experimental data are extracted from the point that the input signal starts to change. The input and output signals should undergo incremental preprocessing before parameter identification.
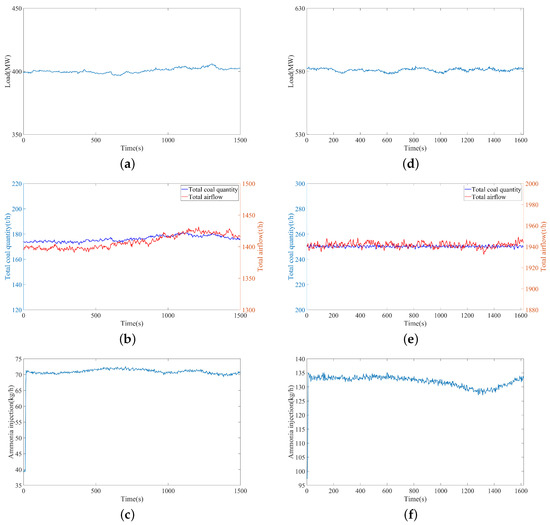
Figure 4.
Experimental conditions under 400 MW and 580 MW. (a) 400 MW load curve. (b) Total airflow and coal quantity curves under 400 MW. (c) Input volume curve under 400 MW. (d) 580 MW load curve. (e) Total airflow and coal quantity curves under 580 MW. (f) Input volume curve under 580 MW.
4.2. System Identification
To confirm the effectiveness of the proposed fractional-order model, this subsection provides comparisons of the identification results between the proposed fractional-order model with the traditional FOPTD model and other integer-order models presented in [13,14].
Ref. [13] proposed an ARX model with parameters to be identified, which is
where
is a unit delay, k represents the time series, and d is the number of samples for the time delay.
and
stand for the input and output signals, respectively.
and
, where
to
,
to
, and d are the parameters to be determined. The sampling period of the ARX model in our paper is 3 s as well.
Ref. [14] proposed a second-order transfer function model, which is
where
,
, A, and B are the parameters to be identified.
Figure 5 shows the identification results of the fractional-order model, the FOPTD model, and the two models mentioned above, respectively. Table 1 and Table 2 present the identified models and the RMSE of each model, showing the advantage of the fractional-order model in better fitting.

Figure 5.
Comparison curves between model outputs and actual data under 400 MW and 580 MW. (a) 400 MW output curves. (b) 580 MW output curves.

Table 1.
Identification result of dynamic characteristics of SCR denitrification system under 400 MW.

Table 2.
Identification result of dynamic characteristics of SCR denitrification system under 580 MW.
The order of the fractional derivative has a significant impact on the solutions of fractional differential equations. Ref. [28] discusses the impact of the value of fractional order on the characteristics and dynamics of soliton solutions in the fractional nonlinear Schrödinger equation (fNLSE). Ref. [29] studies the boundary value problem for a fractional oscillator with random order and provides the random behavior of the solution to the fractional differential equation under different random processes for varying orders. Ref. [30] investigates an efficient iterative method for solving nonlinear fractional optimal control problems affected by external persistent disturbances and provides numerical simulation results for different fractional orders. The results indicate that the proposed method performs well for problems where the order is close to 1.
In this paper, to investigate the fitting performance of the fractional-order model under different given orders, model identification is performed for the experimental data based on each specified order.
Figure 6 shows the outputs of the fractional-order model for different given orders, while Table 3 and Table 4 present the RMSE between the model output and the experimental data. The results indicate that as the given order approaches the previously identified order, the RMSE between the identified model output and the experimental data correspondingly decreases.
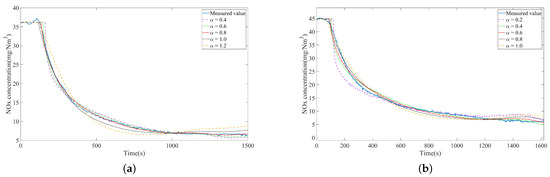
Figure 6.
Fitting performance of the fractional-order model output under different given orders. (a) 400 MW load. (b) 580 MW load.

Table 3.
RMSE between the fractional-order model output with given orders and the experimental data under 400 MW.

Table 4.
RMSE between the fractional-order model output with given orders and the experimental data under 580 MW.
4.3. Model Verification Based on Closed-Loop Control Step Response
To demonstrate the advantages of fractional-order modeling, this paper utilizes the MATLAB function
to fit a high-order model as a surrogate model for the actual plant. The MATLAB functions used in this paper can be found in Appendix A. The RMSE of the high-order model are 0.2306 mg/Nm3 and 0.3914 mg/Nm3 under 400 MW and 580 MW, respectively. Two groups of PI controllers are designed using the same scheme according to the identified fractional-order model and the other three models and applied to the high-order models. The fractional-order model is chosen to demonstrate the controller’s design strategy. The transfer functions of the high-order models are as follows:
and
where
and
are the transfer functions of the high-order models under 400 MW and 580 MW, respectively.
The transfer function of the PI controller is
where
and
are the proportional and integral gains, respectively.
The PI controller is designed with two frequency specifications: gain crossover frequency
and phase margin
, which satisfy
The gain and phase of the PI controller and the identified fractional-order model are
Based on the gain–frequency and phase–frequency relationships of the PI controller and the fractional-order model given in (27)–(30), considering the gain and phase conditions in (25) and (26) at the gain crossover frequency, the algebraic equations for the PI controller parameters are derived as follows:
Solving the algebraic Equations (31) and (32), the PI controller parameters that ensure the control system meets the frequency domain specifications are obtained:
and the symbol of
should ensure that the closed-loop system is a negative feedback system, which means
should have the same sign as K.
,
,
, and
are the transfer functions of the PI controller designed for the fractional-order model, FOPTD model, ARX model, and second-order model, respectively.
- For 400 MW, = 0.004 rad/s, and = :The open-loop Bode plots of the control system under 400 MW load with identified models are shown in Figure 7a.
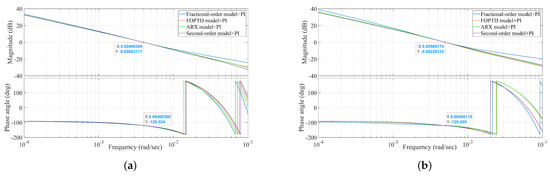 Figure 7. The open-loop plots of each control system under 400 MW and 580 MW. (a) 400 MW. (b) 580 MW.Applying the designed PI controllers for the high-order system, a comparison between the identified model output and the high-order model output of each control system is shown in Figure 8. The RMSE between the identified model outputs and the high-order model output are shown in Table 5.
Figure 7. The open-loop plots of each control system under 400 MW and 580 MW. (a) 400 MW. (b) 580 MW.Applying the designed PI controllers for the high-order system, a comparison between the identified model output and the high-order model output of each control system is shown in Figure 8. The RMSE between the identified model outputs and the high-order model output are shown in Table 5.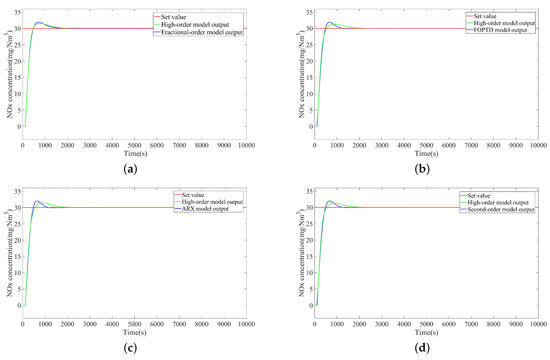 Figure 8. Step tracking responses under 400 MW. (a) Fractional-order model output and high-order model output. (b) FOPTD model output and high-order model output. (c) ARX model output and high-order model output. (d) Second-order model output and high-order model output.
Figure 8. Step tracking responses under 400 MW. (a) Fractional-order model output and high-order model output. (b) FOPTD model output and high-order model output. (c) ARX model output and high-order model output. (d) Second-order model output and high-order model output. Table 5. RMSE (mg/Nm3) between identified model output and high-order model output of each system.
Table 5. RMSE (mg/Nm3) between identified model output and high-order model output of each system. - For 580 MW, = 0.005 rad/s, and = :The open-loop Bode plots of the control system under 580 MW load with identified models are shown in Figure 7b.Applying the designed PI controllers for the high-order system, a comparison between the identified model output and the high-order model output of each control system is shown in Figure 9. The RMSE between the identified model outputs and the high-order model output are shown in Table 5.
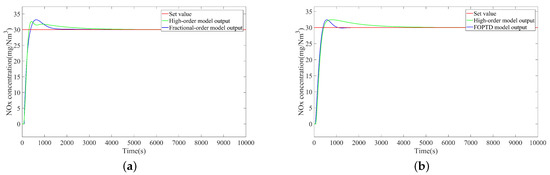
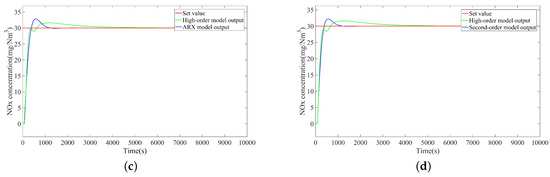 Figure 9. Step tracking responses under 580 MW. (a) Fractional-order model output and high-order model output. (b) FOPTD model output and high-order model output. (c) ARX model output and high-order model output. (d) Second-order model output and high-order model output.
Figure 9. Step tracking responses under 580 MW. (a) Fractional-order model output and high-order model output. (b) FOPTD model output and high-order model output. (c) ARX model output and high-order model output. (d) Second-order model output and high-order model output.
5. Conclusions
To simultaneously achieve better fitting effects and facilitate controller design, this paper proposes a fractional-order system with a time-domain identification method for process control systems. The method extends the traditional integer-order first-order plus time delay model to the fractional-order one, improving the modeling accuracy while keeping the simple form. The proposed method is applied to the SCR denitrification process in a power plant and achieves a more accurate modeling effect over the traditional integer order method. Based on the identified integer-order and fractional-order models, controllers are designed using the same strategy and criteria, applied to control a high-order model that accurately characterizes system dynamics from the real experimental data. Closed-loop control results indicate that the response of the fractional order model-based controller is much closer to that of the high-order model compared with the integer-order model-based controller.
Future work will focus on the design of control strategies to mitigate the impact of large inertia and time delay. It is also necessary to consider identifying the system under more different loads and operating conditions and adjust control strategies based on identification results to improve control performance and reduce
emissions.
Author Contributions
Conceptualization, Y.L.; Writing—original draft, X.L.; Writing—review & editing, W.A., Y.L. and X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China grant number 62173151.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
This appendix provides a brief introduction to the MATLAB functions used in the paper.
is used to find the minimum value of an unconstrained multivariable function;
calculates the simulated time response of a dynamic system to arbitrary inputs;
estimates the transfer function model by input and output data. Basic syntax and description of the parameters of each function are presented in Table A1.

Table A1.
Introduction to the MATLAB functions used in this paper.
Table A1.
Introduction to the MATLAB functions used in this paper.
| Name | Basic Syntax | Parameter Descriptions |
|---|---|---|
| x = fminunc(fun,x0) | x: Solution fun: Objective function x0: Initial solution | |
| y = lsim(sys,u,t) | y: Simulated response data sys: Dynamic system u: Input signal t: Time samples | |
| sys = tfest(tt,np,nz,iodelay) | sys: Identified transfer function tt: Timetable-based estimation data np: Number of poles nz: Number of zeros iodelay: Transport delay |
Appendix B
This appendix provides the units for the quantities related to Section 2.2 and Table A2.

Table A2.
Units of quantities in the dynamic equations for the denitrification reaction.
Table A2.
Units of quantities in the dynamic equations for the denitrification reaction.
| Quantity | Unit |
|---|---|
| F | m3/s |
| V | m3 |
| R | J/(mol · K) |
| T | K |
| mol/m3 | |
| mol/m3 | |
| mol/m3 | |
| mol/m3 | |
| dimensionless | |
| mol/m3 | |
| m3/(mol · s) | |
| m3/(mol · s) | |
| m3/(mol · s) | |
| m3/(mol · s) | |
| J/mol | |
| J/mol | |
| J/mol | |
| J/mol |
References
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Zheng, W.; Luo, Y.; Chen, Y.; Pi, Y. Fractional-order modeling of permanent magnet synchronous motor speed servo system. J. Vib. Control 2016, 22, 2255–2280. [Google Scholar] [CrossRef]
- Gan, H.; Cao, Z.; Chen, P.; Luo, Y.; Luo, X. Fractional-order electromagnetic modeling and identification for PMSM servo system. ISA Trans. 2024, 147, 527–539. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Liu, Y.; Chen, P.; Luo, Y.; Chen, Y. Fractional-Order Dynamics Modeling for Continuum Robots. In Proceedings of the 2023 International Conference on Fractional Differentiation and Its Applications (ICFDA), Ajman, United Arab Emirates, 14–16 March 2023; pp. 1–5. [Google Scholar]
- Sierociuk, D.; Skovranek, T.; Macias, M.; Podlubny, I.; Petras, I.; Dzielinski, A.; Ziubinski, P. Diffusion process modeling by using fractional-order models. Appl. Math. Comput. 2015, 257, 2–11. [Google Scholar] [CrossRef]
- Wang, B.; Li, S.E.; Peng, H.; Liu, Z. Fractional-order modeling and parameter identification for lithium-ion batteries. J. Power Sources 2015, 293, 151–161. [Google Scholar] [CrossRef]
- Zeng, J.; Wang, S.; Cao, W.; Zhang, M.; Fernandez, C.; Guerrero, J.M. Improved fractional-order hysteresis-equivalent circuit modeling for the online adaptive high-precision state of charge prediction of urban-electric-bus lithium-ion batteries. Int. J. Circuit Theory Appl. 2024, 52, 420–438. [Google Scholar] [CrossRef]
- Gude, J.J.; Bringas, P.G.; Herrera, M.; Rincón, L.; Di Teodoro, A.; Camacho, O. Fractional-order model identification based on the process reaction curve: A unified framework for chemical processes. Results Eng. 2024, 21, 101757. [Google Scholar] [CrossRef]
- Haider, M.; Abid, M.; Khan, A.Q.; Mustafa, G. Identification of Fractional-Order Systems with Time Delays Using the Method of Hybrid of Bernoulli Polynomials and Block Pulse Functions. Available online: https://ssrn.com/abstract=4416424 (accessed on 3 September 2024).
- Shalaby, R.; El-Hossainy, M.; Abo-Zalam, B. Fractional order modeling and control for under-actuated inverted pendulum. Commun. Nonlinear Sci. Numer. Simul. 2019, 74, 97–121. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. Am. Soc. Mech. Eng. 1942, 64, 759–765. [Google Scholar] [CrossRef]
- Pan, Y.; Yan, F.; Yang, J.; Zeng, X.; Li, X.; Qi, X. Mechanism Modeling of SCR Flue Gas Denitration Reaction System. In Proceedings of the International Conference on Frontier Computing, Seoul, Republic of Korea, 13–17 July 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 828–838. [Google Scholar]
- Li, J.; Shi, R.; Xu, C.; Wang, S. Process identification of the SCR system of coal-fired power plant for de-NOx based on historical operation data. Environ. Technol. 2019, 40, 3287–3296. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, J.; Zhu, X.; Jiao, Y. Model identification of SCR denitration system for 600 MW thermal power unit. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 1721–1726. [Google Scholar]
- Kang, J.; Niu, Y.; Hu, B.; Li, H.; Zhou, Z. Dynamic modeling of SCR denitration systems in coal-fired power plants based on a bi-directional long short-term memory method. Process. Saf. Environ. Prot. 2021, 148, 867–878. [Google Scholar] [CrossRef]
- Xie, P.; Gao, M.; Zhang, H.; Niu, Y.; Wang, X. Dynamic modeling for NOx emission sequence prediction of SCR system outlet based on sequence to sequence long short-term memory network. Energy 2020, 190, 116482. [Google Scholar] [CrossRef]
- An, B.; Tang, M.; Qiu, J.; Li, Z.; Wang, W.; Zhang, Y.; Yan, Y. Dynamic NO x Prediction Model for SCR Denitrification Outlet of Coal-Fired Power Plants Based on Hybrid Data-Driven and Model Ensemble. Ind. Eng. Chem. Res. 2023, 62, 14286–14299. [Google Scholar] [CrossRef]
- Wu, Z.; Sui, S.; Li, S.; Li, B.; Liu, Y.; Yang, L.; Li, D.; Chen, Y. Modified Active Disturbance Rejection Control Design Based on Gain Scheduling for Selective Catalytic Reduction Denitrification Processes. IEEE Trans. Ind. Electron. 2024, 1–11. [Google Scholar] [CrossRef]
- Tang, M.; An, B.; Yan, Y.; Zhang, Y.; Wang, W. Predictive control of SCR denitrification system in thermal power plants based on GA-BP and PSO. Can. J. Chem. Eng. 2023, 101, 5818–5831. [Google Scholar] [CrossRef]
- Yao, C.; Long, D.; Lv, Y.; Liu, J. Study on mechanism modelling and control of SCR denitrification system in thermal power plant. J. Eng. Therm. Energy Power 2018, 33, 78–84. [Google Scholar]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Xue, D. Fractional Calculus and Fractional-Order Control; Science Press: Beijing, China, 2018. [Google Scholar]
- Broyden, C.G. The convergence of a class of double-rank minimization algorithms 1. general considerations. IMA J. Appl. Math. 1970, 6, 76–90. [Google Scholar] [CrossRef]
- Fletcher, R. A new approach to variable metric algorithms. Comput. J. 1970, 13, 317–322. [Google Scholar] [CrossRef]
- Goldfarb, D. A Family of Variable-Metric Methods Derived by Variational Means. Math. Comput. 1970, 24, 23–26. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of quasi-Newton methods for function minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]
- Conn, A.R.; Gould, N.I.; Toint, P.L. Trust Region Methods; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Bayındır, C.; Farazande, S.; Altintas, A.A.; Ozaydin, F. Petviashvili method for the fractional Schrödinger equation. Fractal Fract. 2022, 7, 9. [Google Scholar] [CrossRef]
- Lopez-Cresencio, O.U.; Ariza-Hernandez, F.J.; Sanchez-Ortiz, J.; Arciga-Alejandre, M.P. A boundary value problem for a random-order fractional differential equation. Results Appl. Math. 2022, 16, 100328. [Google Scholar] [CrossRef]
- Jajarmi, A.; Hajipour, M.; Mohammadzadeh, E.; Baleanu, D. A new approach for the nonlinear fractional optimal control problems with external persistent disturbances. J. Frankl. Inst. 2018, 355, 3938–3967. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).