Abstract
Due to system complexity, research on fuzzy fractional-order, singular perturbation, multi-agent systems (FOSPMASs) remains limited in control theory. This article focuses on the leader-following consensus of fuzzy FOSPMASs with orders in the range of . By employing the T-S fuzzy modeling approach, a fuzzy FOSPMAS is constructed. In order to achieve the consensus of a FOSPMAS with multiple time-scale characteristics, a fuzzy observer-based controller is designed, and the error system corresponding to each agent is derived. Through a series of equivalent transformations, the error system is decomposed into fuzzy singular fractional-order systems (SFOSs). The consensus conditions of the fuzzy FOSPMASs are obtained based on linear matrix inequalities (LMIs) without an equality constraint. The theorems provide a way to tackle the uncertainty and nonlinearity in FOSPMASs with orders in the range of . Finally, the effectiveness of the theorems is verified through an RLC circuit model and a numerical example.
1. Introduction
In recent decades, the control of multi-agent systems (MASs) has become a leading research subject, stemming from the superior efficiency of multiple agents collaborating to execute tasks compared to an individual agent [1]. The applications of MASs are significant, spanning various domains, including service robotics [2,3], hazardous environment detection [4], and unmanned aerial vehicle formation flying [5]. Consensus control of MASs is a fundamental and core issue based on tracking control [6,7]. A significant amount of research has emerged on the consensus of MASs [8,9,10,11,12]. Ren [8] constructed MASs with second-order integrator dynamics by analyzing the swarming model and designed a consensus protocol. Tian and Liu [9] obtained two decentralized consensus conditions of MASs with diverse input and communication delays. Wen et al. [10] introduced an innovative protocol designed by using synchronous intermittent local feedback for second-order consensus of MASs. Zhang et al. [11] proposed event-trigger output feedback control approaches, enabling all connected communication graphs to reach a consensus. Tan et al. [12] derived the consensus criteria for cyber-physical systems under sampled data control, employing a suitable Lyapunov function. The above studies predominantly concentrate on achieving consensus of MASs with integer order, which encounters challenges in describing actual systems in nature and industry.
Fractional-order systems (FOSs) are capable of more accurately modeling and computing genetic and memory effects in various complex processes than integer-order systems [13]. Singular fractional-order systems (SFOSs), also called descriptor systems, have a broader range of applications. In physics, SFOSs are employed to accurately simulate a range of complex physical phenomena, including anomalous diffusion [14] and wave propagation [15]. In engineering, SFOSs are used to enhance the efficiency and accuracy of both signal processing and image recognition [16]. In addition, the consensus of fractional-order MASs (FOMASs) has attracted widespread interest [17,18,19,20,21,22]. Su and Ye proposed a control strategy with input delays to achieve the consensus of general linear and nonlinear FOMASs under event-triggered conditions in [17,18], respectively. Yang et al. [19] considered the consensus of nonlinear distributed and input-delayed FOMASs and further explored the performance of FOMASs in terms of leader-following and leaderless global consensus in [20]. Hu et al. [21] developed an adaptive controller that employs an event-triggered scheme without Zeno behavior, aiming to realize the consensus of FOMASs. Bahrampour et al. [22] proposed new Lyapunov-based LMI conditions to determine the state feedback controller gains on the distributed consensus control of heterogeneous FOMASs with interval uncertainties. However, many practical MASs exhibit multiple time-scale characteristics that refer to the coupled coexistence of fast dynamics and slow dynamics. The design of controllers for these systems frequently encounters difficulties due to the presence of high dimensionality and pathological values [23,24].
Singular perturbation systems (SPSs) have multiple time scales and inherently pathological dynamical properties [25,26,27]. SPSs with a certain parasitic parameter () are modeled to describe real systems. In power system modeling, is used to represent transient phenomena in machine reactors or voltage regulators [28]. In industrial control systems, it signifies small time constants between control and response [29]. Numerous scholars have intensively studied SPSs [30,31,32,33,34,35]. On one hand, two commonly employed strategies for solving control problems of SPSs are the quasi-steady-state method [30] and the block diagonalization method [31], which decompose the system into slow and fast subsystems. But these methods rely on the assumption that the fast subsystem matrix is non-singular, and they are not applicable to non-standard SPSs that cannot be easily decomposed. On the other hand, Yang et al. [32], Gao et al. [33], and Liu et al. [34] proposed the integral sliding mode control method for full-order SPSs with mismatched disturbances, uncertainty, and nonlinear input, respectively. Their methods are based on a full-order model, which eliminates the need to decompose the system. Furthermore, techniques such as the use of Lyapunov functions and LMIs are also applied to system analysis. Fridman [35] derived the LMI criteria for the stability of SPSs for delays proportional to and delays independent of . Additionally, for singular perturbation MASs (SPMASs), both Ben Rejeb et al. [36] and Tognetti et al. [37] designed decentralized controllers, enabling systems to synchronize and ensuring global performance. Xu et al. [38] presented a sliding-mode controller with memory output for to address the consensus of SPMASs in finite time. Zhang et al. [39] achieved global Mittag–Leffler consensus tracking for fractional SPMASs modeled by a discontinuous function with a non-decreasing property. However, in practical applications, the exact value of the parameter is often difficult to obtain directly. By analyzing the background information of specific problems in depth, the reasonable change range of can be effectively estimated. Given in a known interval, the design of controllers to achieve the consensus of nonlinear FOSPMASs remains an open problem in the field of control theory.
T-S fuzzy models possess the ability to approximate nonlinear dynamics; therefore, the well-established control methods for linear systems can be extended to the analysis and design of nonlinear systems. Wang et al. [40] proposed a parallel distributed compensation (PDC) method based on a T-S fuzzy model for the stability of nonlinear systems, where the fuzzy controller adopts the same fuzzy set as the fuzzy system. Using the PDC method, Wang et al. [41] further analyzed the effectiveness of using a T-S fuzzy model to approximate nonlinear functions. Numerous scholars have undertaken extensive research endeavors focusing on T-S fuzzy SPSs [42,43,44,45]. Yang and Zhang [42] proposed a design method for a state feedback controller depending on for T-S fuzzy SPSs. Chen et al. [43] focused on nonlinear SPSs and presented two novel methods to design a static output feedback () controller based on LMIs. Visavakitcharoen et al. [44] designed an event-triggered controller based on integral feedback for nonlinear SPSs with a fuzzy model. Zhang and Han [45] proposed two diverse feedback controllers aiming to obtain the stabilization criteria of fuzzy FOSPSs with . Nevertheless, research on the consensus control of fuzzy FOSPMASs is still relatively limited.
Inspired by previous discussions, this paper focuses on filling this research gap. The following is an overview of the main contributions of this research:
- 1
- To provide a more accurate portrayal of complex systems in practice, a T-S fuzzy FOSPMAS with is formulated to reduce the difficulty of directly studying nonlinear systems. Compared to integer-order systems, the constructed model exhibits enhanced accuracy and complexity. A fuzzy FOSPS with error as a variable is derived by designing a fuzzy observer-based controller.
- 2
- The fuzzy FOSPS is analyzed by transforming it into a fuzzy SFOS using the system augmentation method. In comparison to the existing methods [46], the proposed approach not only relaxes the assumption that the fast subsystem matrix must be non-singular but also avoids the ill-conditioned issue arising from the parameter.
- 3
- The consensus conditions for fuzzy FOSPMASs with and are formulated in this study for any , where and are the lower and upper boundaries, respectively. The results are presented based on LMIs without equality constraints, reducing solution difficulties. It is demonstrated through an RLC circuit model that the proposed methods are effective in practice.
The remaining parts are structured in the following manner. Section 2 provides foundational definitions in graph theory and correlative lemmas. The establishment of the system model and the primary findings on the consensus of FOSPMASs are detailed in Section 3. Section 4 presents two practical examples. Lastly, Section 5 summarizes the study.
2. Preliminaries
2.1. Notations
and signify that the matrix X is positive definite and positive semi-definite, respectively. stands for the transpose of the matrix (X), and . spec is the spectrum of . The ∗ symbol represents the symmetric element of a matrix. ⊗ denotes the Kronecker product. For , , and denotes . represents a diagonal matrix. stands for the rounding of up to the nearest integer.
2.2. Graph Theory
Consider the case of an MAS comprising a single leader and N followers. The information exchanged between N agents is presented as an undirected graph (). The Laplace matrix of the graph () is defined as , where and is the element of weighted adjacency matrix of graph . means that follower i communicates with follower j; otherwise, . When is undirected, is symmetric. Similarly, represents the communication between the leader and follower i, and means follower i receives information from the leader; otherwise, .
2.3. Preliminary Lemmas
Consider a continuous linear SFOS with described by
where are the system matrices and . represents the state. denotes the Caputo fractional-order derivative, which is defined as
where is the Euler Gamma function and (1) is represented by the triple .
When , system (1) is simplified to a normal FOS as follows:
Lemma 1
([47]). System (2) is stable iff
Lemma 2
([48]). is asymptotically stable at the equilibrium points if all the eigenvalues (, ) of the Jacobian matrix () satisfy
where .
Lemma 3
([49]). Choose two non-singular matrices (U and V) such that
then, system (1) is regular, impulse-free and stable, and defined as admissible iff is non-singular and
Lemma 4
Lemma 5
Remark 1.
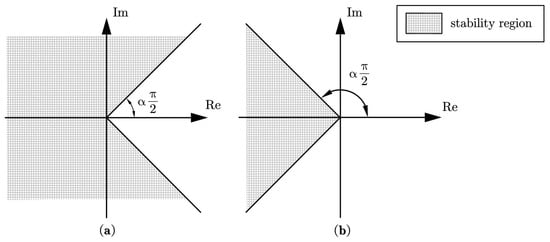
According to Lemma 1, Figure 1 shows the stability region of system (2) with a fractional order of or . Lemmas 4 and 5 are regarded as the natural extension of Lyapunov stability from normal integer-order systems to SFOSs [49,50].

Figure 1.
Stability region of system (2): (a) ; (b) .
Lemma 6
([51]). Given a symmetric constant matrix (Z) and constant matrices (), the inequality
holds for all F satisfying iff there exist some such that
3. Main Results
3.1. System Model Description
Consider an MAS consisting of a leader and N followers, with the dynamic of each agent modeled by a T-S fuzzy FOSPS. This nonlinear system is described by the fuzzy rules as follows:
Rule k: If is and ⋯ and is ,
Then, the dynamic description of each agent is written as
where
, , and represent the state, control input and output of follower i, respectively; and represent the state and output of the leader, respectively; and system matrices , , and are constant. Additionally, represents the fuzzy sets of the premise variables , where and . Here, r represents the number of rules.
According to the procedures of defuzzification, the global model of T-S fuzzy FOSPMASs (4) and (5) is derived as follows:
where is the weighting function and is the membership function, satisfying , , , and .
Utilizing the complete state information for controller design is often challenging, owing to economic constraints and measurement limitations. To address this issue and design a consensus protocol for fuzzy FOSPMASs (6) and (7), a fuzzy observer is formulated as follows:
where signifies the estimated state of follower i and represents the error between the actual output () and the weighted sum of estimated outputs. Furthermore, denotes the gain matrix.
To achieve the consensus of (6) and (7), the following distributed control protocol based on (8) is designed:
Let , where
3.2. Equivalent Transformations
In this section, equivalence conditions of the consensus of fuzzy FOSPMASs are derived by addressing the stability problem of system (14).
Based on graph theory, it is known that matrix M is positive definite. Therefore, an orthogonal matrix (V) exists such that , and all eigenvalues () of the matrix (M) possess positive real parts, where .
Let , where and According to the properties of the Kronecker product, system (14) is transformed into the following form:
where
Proof.
According to Lemma 1, system (15) is stable iff
According to Definition 1 and Lemma 7, in order to achieve the consensus of fuzzy FOSPMASs (6) and (7), it is necessary for systems (16) and (17) to both be stable. Therefore, in order to derive the stability conditions of (16) and (17), the following equivalent transformation is presented.
Matrix is decomposed into
where the scalar is , , and .
Let and . Then, (16) is derived as
where , , , , and .
Similarly, and . Then, (17) is reformulated as
where , , and .
3.3. Consensus Conditions of T-S Fuzzy FOSPMASs
In this section, the LMI criteria for the consensus of fuzzy FOSPMASs (6) and (7) are proposed by studying the admissibility of systems (18) and (19).
Assumption 1.
and are in the range of , and ρ is a sufficiently small scalar.
Theorem 1.
Given , the consensus of fuzzy FOSPMASs (6) and (7) with and any is achieved via protocol (9) if there exist matrices (, , , and ) and positive scalars ( and ) such that
where
The gain matrices are derived as
Proof.
Then, (18) is reformulated with as
Based on Assumption 1, the Jacobian matrix of system (28) is seen as a constant (). Based on Lemma 2, system (28) is admissible at the equilibrium points if
By pre- and post-multiplying (30) by , it is transformed as follows:
According to the Schur complement, (31) is equivalent to
Considering in (32) and Lemma 6 yields
Substituting into (33) yields the following expression:
According to Lemma 4, (29) is guaranteed, and system (28) with is admissible according to (22) and (34).
Similarly, substituting into system (19) yields
By pre- and post-multiplying (36) by , it is transformed as
In the same way, (37) is equivalent to
Lemma 6 and yield
Substituting into (39) yields
Remark 2.
The conditions in Theorem 1 involve LMIs with equality constraints, rendering them fragile and potentially prone to computational difficulty. Consequently, the subsequent theorem presents strict LMI conditions to address these issues and enhance computational accuracy.
Theorem 2.
Given , the consensus of fuzzy FOSPMASs (6) and (7) with and any is achieved via protocol (9) if there exist matrices (, , , , , and ) and positive scalars ( and ) such that
where
are arbitrary matrices with full column ranks satisfying . The gain matrices are derived as
Proof.
Theorem 3.
Given , the consensus of fuzzy FOSPMASs (6) and (7) with and any is achieved via protocol (9) if there exist matrices (, , and ) and positive scalars ( and ) such that
where
The the gain matrices are chosen as
Proof.
The proof parallels that of Theorem 1 based on Lemma 5, which is omitted here for brevity. □
Theorem 4.
Given , the consensus of fuzzy FOSPMASs (6) and (7) with and any is achieved via protocol (9) if there exist matrices (, , , , , , , and ), and positive scalars ( and ) such that
where
and satisfy the conditions in Theorem 2. The gain matrices are chosen as
Proof.
Remark 3.

Table 1 shows that this paper focuses on FOSPMASs with or , which are more complex and have a wider range of order . Some early literature, including [30,36], decomposed SPSs into fast subsystems and slow subsystems. However, this approach needs to assume that the fast subsystem matrix is non-singular, which is not applicable to non-standard SPSs. In contrast, the method proposed in this paper is based on a full-order model, which overcomes the limitation of decomposition and avoids the above assumption.

Table 1.
Comparison of existing methods.
4. Numerical Examples
This section presents two demonstrative instances that highlight the effectiveness of the control protocol in achieving the consensus of fuzzy FOSPMASs with an orders of in and .
Example 1.
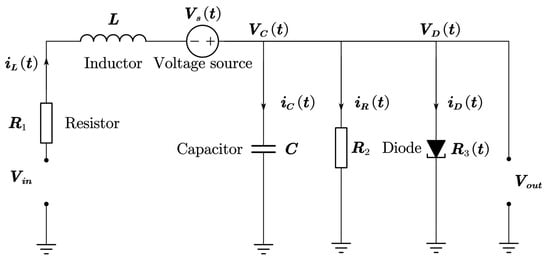
The capacitor and inductor have fractional characteristics in the circuit; the inductance value is very small and prone to pathological problems. The volt-ampere characteristic of the diode is nonlinear. This nonlinear circuit model is taken as a node of an MAS. With parasitic parameters and fractional-order characteristics, the MAS is very complex, and the consensus problem is difficult to solve. Thus, by approximating the volt-ampere characteristic as a quadratic function and constructing a T-S fuzzy model, Theorem 4 is used to achieve the consensus of the nonlinear FOSPMASs.
Consider a T-S fuzzy FOSPMAS composed of one leader and four followers; the behavior of each agent is described by the fractional-order RLC circuit model as shown in Figure 2.

Figure 2.
RLC circuit with a diode.
The capacitor and inductor have fractional characteristics with an order of α. L represents a very small parasitic inductance. , and denote the resistances of the corresponding resistors. is a diode, and its characteristic function is approximated as . It is known that the relationships between voltages are and . The dynamic of each agent is subsequently described as follows:
The parameters are chosen as , , , , and . It is assumed that belongs to . Subsequently, the fuzzy rules are set as follows:
Rule 1: If the value of is approximately 0, then
Rule 2: If the value of is approximately , then
where
The fuzzy weighting function is selected as , . The matrix (M) is expressed as follows:
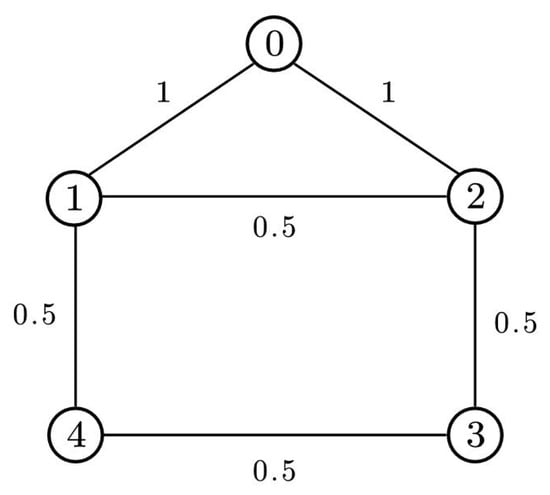
Based on the modeling and analysis of the power system, the connection relationships and interactions of the system are abstracted into a undirected topology graph, as depicted in Figure 3.

Figure 3.
Weighted undirected graph.
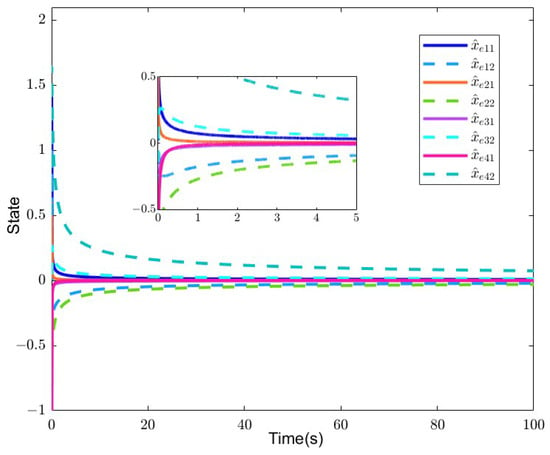
Let . The tracking errors and estimation errors are depicted in Figure 4 and Figure 5, respectively. A consensus error of zero means that each follower converges toward the leader, which demonstrates that the system achieves consensus by using the observer-based protocol (9), indicating the practical applicability and efficacy of the proposed method with . Model simulation is shown in the Appendix A.

Figure 4.
State errors between leader and followers in Example 1.

Figure 5.
Estimation errors of followers in Example 1.
Example 2.
Considering T-S fuzzy FOSPMASs (6) and (7) within the topology presented in Figure 3, the fuzzy rules of the system are established in the following manner:
Rule 1: If is , then
Rule 2: If is , then
The remaining parameters are proposed as follows:
Assuming that state belongs to , the fuzzy weighting function is selected as , .
Considering and , the feasible solutions are presented based on LMIs (41) and (44) in Theorem 2 as follows:
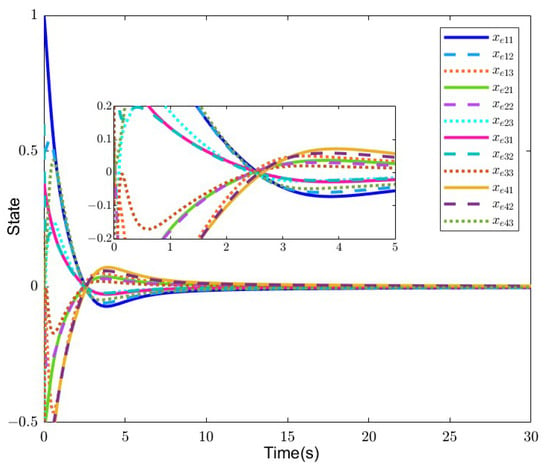
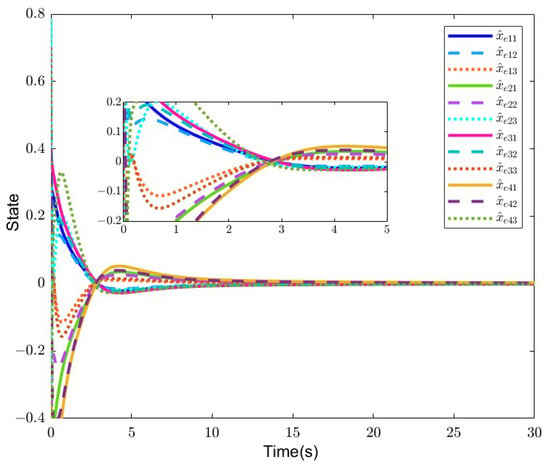
Figure 6 and Figure 7 present the simulation results of the error system (14) with . As depicted in Figure 6, the state of follower agents exhibits a successful tracking of the state of the leader agent, indicating that the consensus issue of fuzzy FOSPMASs (6) and (7) with is solved by the criteria in Theorem 2.

Figure 6.
State errors between leader and followers in Example 2.

Figure 7.
Estimation errors of followers in Example 2.
5. Conclusions
In this paper, a T-S fuzzy FOSPMAS with is modeled and studied to more accurately describe actual complex systems. The consensus problem of T-S fuzzy FOSPMASs is transformed into admissibility assessment of fuzzy SFOSs (18) and (19). In contrast to the methodologies in proposed in previous literature, the proposed method not only overcomes the pathological problem arising from multiple time scales but is also applicable to both standard and non-standard SPMASs. Theorems 1 and 3 provide sufficient conditions for achieving consensus with and . Furthermore, strict LMI criteria are proposed in Theorems 2 and 4, which are solved easily with the LMI toolbox. In practical applications, the proposed method can be used to simulate the dynamic behavior of helicopter swarms in complex flight environments. There are still some difficulties in dealing with the consensus problem of fuzzy FOSPMASs with input saturation and actuator faults. In the future, the fault-tolerant control and fault detection problem of fuzzy FOSPMASs will be studied.
Author Contributions
Conceptualization, methodology, and validation, X.W. and X.Z.; writing—original draft preparation, X.W.; writing—review and editing, X.W. and X.Z.; visualization, X.W. and S.-H.Y.; supervision, W.P. and D.B.; project administration, X.Z.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 62103093, the National Key Research and Development Program of China under Grant 2022YFB3305905, the Fundamental Research Funds for the Central Universities under Grant N2224005-3, and the National Key Research and Development Program Topic under Grant 2020YFB1710003.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
The simulation of the fuzzy FOSPMAS model is depicted in Figure A1. This simulation model essentially encompasses fuzzy logic controllers, m functions, fractional-order operators, and integer-order integrators, the latter two of which are combined into fractional-order integrators with initial values. Notably, due to constraints in space, only a part of the simulation model pertaining to fuzzy FOSPMASs is shown. In practical cases, the precise number of state variables and fuzzy rules and the corresponding system description are tailored to suit actual scenarios or application requirements.
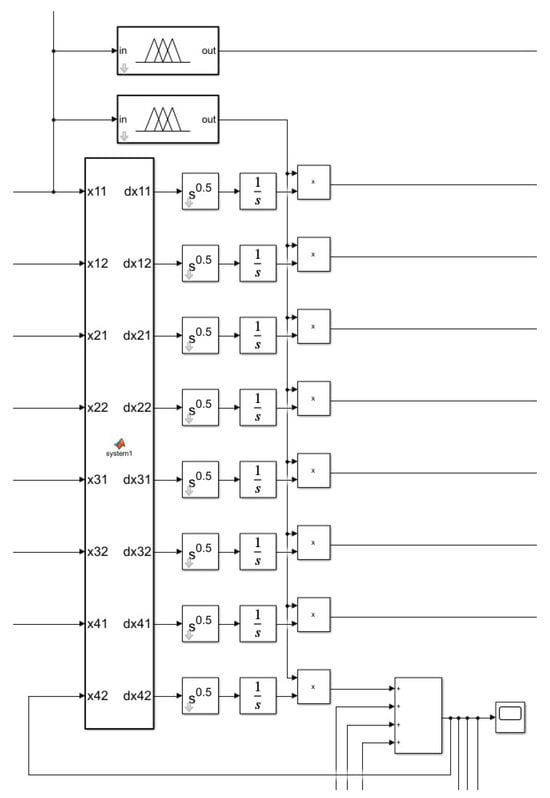
Figure A1.
Fuzzy FOSPMAS model simulation.
References
- Santos, G.; Pinto, T.; Praça, I.; Vale, Z. MASCEM: Optimizing the performance of a multi-agent system. Energy 2016, 111, 513–524. [Google Scholar] [CrossRef]
- Jiménez, A.C.; García-Díaz, V.; Bolaños, S. A decentralized framework for multi-agent robotic systems. Sensors 2018, 18, 417. [Google Scholar] [CrossRef] [PubMed]
- Iñigo-Blasco, P.; Diaz-del-Rio, F.; Romero-Ternero, M.C.; Cagigas-Muñiz, D.; Vicente-Diaz, S. Robotics software frameworks for multi-agent robotic systems development. Robot. Auton. Syst. 2012, 60, 803–821. [Google Scholar] [CrossRef]
- Florez-Lozano, J.; Caraffini, F.; Parra, C.; Gongora, M. Cooperative and distributed decision-making in a multi-agent perception system for improvised land mines detection. Inf. Fusion 2020, 64, 32–49. [Google Scholar] [CrossRef]
- Yan, Z.W.; Han, L.; Li, X.D.; Dong, X.W.; Li, Q.D.; Ren, Z. Event-triggered formation control for time-delayed discrete-time multi-agent system applied to multi-UAV formation flying. J. Frankl. Inst. 2023, 360, 3677–3699. [Google Scholar] [CrossRef]
- Zhang, J.X.; Xu, K.D.; Wang, Q.G. Prescribed Performance Tracking Control of Time-Delay Nonlinear Systems with Output Constraints. IEEE/CAA J. Autom. Sin. 2024, 11, 1557–1565. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Low-Complexity Tracking Control of Strict-Feedback Systems with Unknown Control Directions. IEEE Trans. Autom. Control. 2019, 64, 5175–5182. [Google Scholar] [CrossRef]
- Ren, W. On Consensus Algorithms for Double-Integrator Dynamics. IEEE Trans. Autom. Control. 2008, 53, 1503–1509. [Google Scholar] [CrossRef]
- Tian, Y.P.; Liu, C.L. Consensus of Multi-Agent Systems with Diverse Input and Communication Delays. IEEE Trans. Autom. Control. 2008, 53, 2122–2128. [Google Scholar] [CrossRef]
- Wen, G.H.; Duan, Z.S.; Yu, W.W.; Chen, G.R. Consensus in multi-agent systems with communication constraints. Int. J. Robust Nonlinear Control. 2012, 22, 170–182. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, G.; Yan, H.C.; Chen, Q.J. Observer-Based Output Feedback Event-Triggered Control for Consensus of Multi-Agent Systems. IEEE Trans. Ind. Electron. 2014, 61, 4885–4894. [Google Scholar] [CrossRef]
- Tan, M.C.; Song, Z.Q.; Zhang, X.M. Robust leader-following consensus of cyber–physical systems with cyber attack via sampled-data control. ISA Trans. 2021, 109, 61–71. [Google Scholar] [CrossRef] [PubMed]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Aslefallah, M.; Abbasbandy, S.; Shivanian, E. Numerical solution of a modified anomalous diffusion equation with nonlinear source term through meshless singular boundary method. Eng. Anal. Bound. Elem. 2019, 107, 198–207. [Google Scholar] [CrossRef]
- Lu, J.F.; Hanyga, A. Numerical modelling method for wave propagation in a linear viscoelastic medium with singular memory. Geophys. J. Int. 2004, 159, 688–702. [Google Scholar] [CrossRef]
- Liu, J.; Chen, S.; Tan, X. Fractional order singular value decomposition representation for face recognition. Pattern Recognit. 2008, 41, 378–395. [Google Scholar] [CrossRef]
- Ye, Y.Y.; Su, H.S. Leader-following consensus of general linear fractional-order multiagent systems with input delay via event-triggered control. Int. J. Robust Nonlinear Control. 2018, 28, 5717–5729. [Google Scholar] [CrossRef]
- Ye, Y.Y.; Su, H.S. Leader-following consensus of nonlinear fractional-order multi-agent systems over directed networks. Nonlinear Dyn. 2019, 96, 1391–1403. [Google Scholar] [CrossRef]
- Yang, R.; Liu, S.; Tan, Y.Y.; Zhang, Y.J.; Jiang, W. Consensus analysis of fractional-order nonlinear multi-agent systems with distributed and input delays. Neurocomputing 2019, 329, 46–52. [Google Scholar] [CrossRef]
- Yang, R.; Liu, S.; Li, X.Y.; Zhao, X.W.; Pan, G. Consensus of fractional-order delayed multi-agent systems in Riemann–Liouville sense. Neurocomputing 2020, 396, 123–129. [Google Scholar] [CrossRef]
- Hu, T.T.; He, Z.; Zhang, X.J.; Zhong, S.M. Leader-following consensus of fractional-order multi-agent systems based on event-triggered control. Nonlinear Dyn. 2020, 99, 2219–2232. [Google Scholar] [CrossRef]
- Bahrampour, E.; Asemani, M.H.; Dehghani, M.; Tavazoei, M. Consensus control of incommensurate fractional-order multi-agent systems: An LMI approach. J. Frankl. Inst. 2023, 360, 4031–4055. [Google Scholar] [CrossRef]
- Fridman, E. Robust sampled-data H∞ control of linear singularly perturbed systems. IEEE Trans. Autom. Control. 2006, 51, 470–475. [Google Scholar] [CrossRef]
- Yang, C.Y.; Zhang, L.L.; Sun, J. Anti-windup controller design for singularly perturbed systems subject to actuator saturation. IET Control. Theory Appl. 2016, 10, 469–476. [Google Scholar] [CrossRef]
- Saksena, V.R.; O’reilly, J.; Kokotovic, P.V. Singular perturbations and time-scale methods in control theory: Survey 1976–1983. Automatica 1984, 20, 273–293. [Google Scholar] [CrossRef]
- Naidu, D. Singular perturbations and time scales in control theory and applications: An overview. Dyn. Contin. Discret. Impuls. Syst. Ser. B 2002, 9, 233–278. [Google Scholar]
- Wang, Y.Y.; Shi, P.; Yan, H.C. Reliable control of fuzzy singularly perturbed systems and its application to electronic circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 3519–3528. [Google Scholar] [CrossRef]
- Munje, R.; Patre, B.; Tiwari, A.; Munje, R.; Patre, B.; Tiwari, A. State feedback control using linear quadratic regulator. In Investigation of Spatial Control Strategies with Application to Advanced Heavy Water Reactor; Springer: Singapore, 2018; pp. 61–77. [Google Scholar]
- Xia, G.Q.; Zhang, Y.; Zhang, W.; Chen, X.M.; Yang, H.Y. Multi-time-scale 3-D coordinated formation control for multi-underactuated AUV with uncertainties: Design and stability analysis using singular perturbation methods. Ocean. Eng. 2021, 230, 109053. [Google Scholar] [CrossRef]
- Nagarale, R.M.; Patre, B.M. Composite fuzzy sliding mode control of nonlinear singularly perturbed systems. ISA Trans. 2014, 53, 679–689. [Google Scholar] [CrossRef] [PubMed]
- Litkouhi, B.; Khalil, H. Multirate and composite control of two-time-scale discrete-time systems. IEEE Trans. Autom. Control. 1985, 30, 645–651. [Google Scholar] [CrossRef]
- Yang, C.Y.; Che, Z.Y.; Shen, L.P. Integral sliding mode control for singularly perturbed systems with matched disturbances. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 2452–2456. [Google Scholar] [CrossRef]
- Gao, Y.B.; Sun, B.H.; Lu, G.P. Passivity-Based Integral Sliding-Mode Control of Uncertain Singularly Perturbed Systems. IEEE Trans. Circuits Syst. II Express Briefs 2011, 58, 386–390. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.Y.; Wang, Z.M. H∞ observer-based sliding mode control for singularly perturbed systems with input nonlinearity. Nonlinear Dyn. 2016, 85, 573–582. [Google Scholar] [CrossRef]
- Fridman, E. Effects of small delays on stability of singularly perturbed systems. Automatica 2002, 38, 897–902. [Google Scholar] [CrossRef]
- Ben Rejeb, J.; Morărescu, I.-C.; Daafouz, J. Control design with guaranteed cost for synchronization in networks of linear singularly perturbed systems. Automatica 2018, 91, 89–97. [Google Scholar] [CrossRef]
- Tognetti, E.S.; Calliero, T.R.; Morărescu, I.-C.; Daafouz, J. Synchronization via output feedback for multi-agent singularly perturbed systems with guaranteed cost. Automatica 2021, 128, 109549. [Google Scholar] [CrossRef]
- Xu, J.; Niu, Y.G.; Zou, Y.Y. Finite-time consensus for singularity-perturbed multiagent system via memory output sliding-mode control. IEEE Trans. Cybern. 2021, 52, 8692–8702. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wu, H.Q.; Cao, J.D. Global Mittag-Leffler consensus for fractional singularly perturbed multi-agent systems with discontinuous inherent dynamics via event-triggered control strategy. J. Frankl. Inst. 2021, 358, 2086–2114. [Google Scholar] [CrossRef]
- Wang, H.; Tanaka, K.; Griffin, M. Parallel distributed compensation of nonlinear systems by Takagi-Sugeno fuzzy model. In Proceedings of the 1995 IEEE International Conference on Fuzzy Systems, Yokohama, Japan, 20–24 March 1995; Volume 2, pp. 531–538. [Google Scholar] [CrossRef]
- Wang, H.; Li, J.; Niemann, D.; Tanaka, K. T-S fuzzy model with linear rule consequence and PDC controller: A universal framework for nonlinear control systems. In Proceedings of the Ninth IEEE International Conference on Fuzzy Systems, FUZZ-IEEE 2000 (Cat. No.00CH37063), San Antonio, TX, USA, 7–10 May 2000; Volume 2, pp. 549–554. [Google Scholar] [CrossRef]
- Yang, C.Y.; Zhang, Q.L. Multiobjective Control for T–S Fuzzy Singularly Perturbed Systems. IEEE Trans. Fuzzy Syst. 2009, 17, 104–115. [Google Scholar] [CrossRef]
- Chen, J.X.; Sun, Y.G.; Min, H.B.; Sun, F.C.; Zhang, Y.G. New results on static output feedback H∞ control for fuzzy singularly perturbed systems: A linear matrix inequality approach. Int. J. Robust Nonlinear Control. 2013, 23, 681–694. [Google Scholar] [CrossRef]
- Visavakitcharoen, A.; Assawinchaichote, W.; Shi, Y.; Angeli, C. Event-triggered fuzzy integral control for a class of nonlinear singularly perturbed systems. ISA Trans. 2023, 139, 71–85. [Google Scholar] [CrossRef]
- Zhang, X.F.; Han, Z.R. Output feedback control of fractional order Takagi–Sugeno fuzzy singularly perturbed systems. J. Vib. Control. 2022, 28, 3162–3172. [Google Scholar] [CrossRef]
- Koskie, S.; Coumarbatch, C.; Gajic, Z. Exact slow-fast decomposition of the singularly perturbed matrix differential Riccati equation. Appl. Math. Comput. 2010, 216, 1401–1411. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Proceedings of the Computational Engineering in Systems Applications, Lille, France, 9–12 July 1996; Volume 2, pp. 963–968. [Google Scholar]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Zhang, X.F.; Chen, Y.Q. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0 < α < 1 case. ISA Trans. 2018, 82, 42–50. [Google Scholar] [PubMed]
- Marir, S.; Chadli, M.; Bouagada, D. New admissibility conditions for singular linear continuous-time fractional-order systems. J. Frankl. Inst. 2017, 354, 752–766. [Google Scholar] [CrossRef]
- Lee, H.J.; Park, J.B.; Chen, G.R. Robust fuzzy control of nonlinear systems with parametric uncertainties. IEEE Trans. Fuzzy Syst. 2001, 9, 369–379. [Google Scholar]
- Wang, Y.; Zhang, J.X.; Zhang, X. Fuzzy control of singular fractional order multi-agent systems with actuator saturation. Inf. Sci. 2024, 665, 120397. [Google Scholar] [CrossRef]
- Fan, X.; Wang, Z. A Fuzzy Lyapunov Function Method to Stability Analysis of Fractional-Order T–S Fuzzy Systems. IEEE Trans. Fuzzy Syst. 2022, 30, 2769–2776. [Google Scholar] [CrossRef]
- Zhu, L.J.; Lu, J.G.; Zhu, Z. Robust stability and stabilization of uncertain fractional-order singularly perturbed systems. Comput. Appl. Math. 2024, 43, 58. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).