Synchronization Control of Complex Spatio-Temporal Networks Based on Fractional-Order Hyperbolic PDEs with Delayed Coupling and Space-Varying Coefficients

Abstract

This paper studies synchronization behaviors of two sorts of non-linear fractional-order complex spatio-temporal networks modeled by hyperbolic space-varying PDEs (FCSNHSPDEs), respectively, with time-invariant delays and time-varying delays, including one delayed coupling. One distributed controller with space-varying control gains is firstly designed. For time-invariant delayed cases, sufficient conditions for synchronization of FCSNHSPDEs are presented via LMIs, which have no relation to time delays. For time-varying delayed cases, synchronization conditions of FCSNHSPDEs are presented via spatial algebraic LMIs (SALMIs), which are related to time delay varying speeds. Finally, two examples show the validity of the control approaches.

1. Introduction

There exists an array of important complex networks in real life, such as power networks [1], people group networks [2], influential spreader networks [3], transportation networks [4], and logistics networks [5]. Complex networks are an effective and significant instrument for perceiving the interconnections of elements. In view to their powerful function, complex networks have been applied to many fields, including virus spread [6], brain science [7], image processing [8], water quality assessment [9], network attack [10], feature extraction [11], and multi-agent systems [12,13,14,15].

As is well-known, synchronization is one of the most important dynamics behaviors [16,17,18]. Most of the literature has held the idea that the dynamics of nodes depends only on time. Actually, the dynamics of most processes depend not only on time but also on space [19,20,21,22,23], such as in the cases of flexible manipulators [24], flexible spacecraft [25], and reaction-diffusion systems [26]. Therefore, it is meaningful to study partial differential equation (PDE)-based complex spatio-temporal networks(CSNs), considering both time and space [27,28,29]. Kocarev et al. proposed synchronization methods of spatio-temporal chaos [30]. Xia and Scardovi studied synchronization analysis of linear CSNs [31]. Demetriou investigated control methods for synchronization of CSNs [32]. Kabalan et al. proposed synchronization of CSNs with in-domain coupling by boundary control [33]. Zheng et al. gave an control approach for synchronization of fractional-order CSNs with time delays [34]. Hu et al. proposed an adaptive approach for synchronization of intermittent CSNs using piecewise auxiliary functions [35]. Yang et al. proposed two boundary coupling ways of stochastic CSNs [36]. Yang et al. proposed exponential synchronization of fractional-order CSNs with hybrid delay-dependent impulses [37].

Most of the above references were modeled by parabolic PDEs, whereas few works studied the synchronization of CSNs based on hyperbolic space-varying PDEs (CSNHSPDEs). Li et al. studied synchronization of second-order CSNHSPDEs [38] and first-order CSNHSPDEs [39] by using boundary control. Lu proposed boundary control for local exact synchronization of quasi-linear CSNHSPDEs [40]. Ma and Yang studied synchronization control of CSNHSPDEs, respectively considering a single weight and multiple weights [41]. As a whole, these works studied synchronization of space-varying CSNHSPDEs, which fractional-order models have not considered.

Fractional-order systems are commonly found in a wide range of fields such as physics, electronics, biology, and engineering [42,43]. Yan et al. proposed boundary control of fractional-order parabolic multi-agent systems [44] as well as studying observer-based control [45]. Zhao et al. proposed an event-triggered boundary controller of fractional-order parabolic multi-agent systems [46]. Finite-time boundary control was studied for hyperbolic multi-agent systems [47]. However, the research of fractional-order CSNs based on hyperbolic space-varying PDEs (FCSNHSPDEs) with time-delayed couplings is significant and it remains challenging, not being solved yet.

The objective of this paper is to investigate a distributed controller for synchronization of a kind of FCSNHSPDEs with time-varying parameters and time delays. Firstly, a class of FCSNHSPDE models with time-invariant delays is given, and a distributed controller is studied to drive the following node to reach synchronization with the isolated node. Sufficient conditions are obtained for synchronization of FCSNHSPDEs in terms of spatial algebraic LMIs (SALMIs). A class of FCSNHSPDE models with time-varying delays is given. The same distributed controller is employed, and sufficient conditions are respectively obtained for synchronization of FCSNHSPDEs with time-varying delays. The key contributions of this paper are listed as:

(1)

Non-linear fractional-order complex spatio-temporal networks are modeled by hyperbolic space-varying PDEs in this paper, and have potential applications for flexible manipulators, flexible strings, flexible articulated wings, and flexible appendages.

(2)

One distributed controller with space-varying control gains is designed in this paper. It allows different nodes to own different gains.

(3)

Synchronization conditions of FCSNHSPDEs are presented by spatial algebraic LMIs, which contain space-varying coefficients. By using spatial algebraic LMIs, time-invariant delays and multiple time-varying delays within FCSNHSPDEs have been addressed, respectively.

2. Problem Formulation

This paper firstly studies one fractional-order CSTN based on hyperbolic space-varying PDEs (FCSNHSPDEs) with time-invariant delays, and the i-th node has the behavior as

$$\left\{\begin{array}{l}{}_{t_0}{}^{c}D_t^{\alpha }{z}_i(\omega ,t)=\mathsf{\Theta }\left(\omega \right){\displaystyle \frac{\partial z_i(\omega ,t)}{\partial \omega }}+A\left(\omega \right)z_i(\omega ,t)+A_d\left(\omega \right)z_i(\omega ,t-{\tau }_1)+B\left(\omega \right)f\left(z_i(\omega ,t)\right)\hfill \\ +B_d\left(\omega \right)f\left(z_i(\omega ,t-{\tau }_2)\right)+c_1{\displaystyle \sum _{j=1}^N}{g}_{ij}\left(\omega \right)\mathsf{\Gamma }\left(\omega \right)z_j(\omega ,t)\hfill \\ +c_2{\displaystyle \sum _{j=1}^N}{g}_{ij}\left(\omega \right)\mathsf{\Gamma }\left(\omega \right)z_j(\omega ,t-{\tau }_3)+u_i(\omega ,t),\hfill \\ z_i(L,t)=0,\hfill \\ z_i(\omega ,t)=z_i^0(\omega ,t),(\omega ,t)\in [0,L]\times [-\tau ,0],\hfill \end{array}\right.$$

(1)

where $(\omega ,t)\in [0,L]\times [0,\infty )$ are space and time, respectively. $z_i(\omega ,t)$, $u_i(\omega ,t)\in {\mathbb{R}}^n$. $\mathsf{\Theta }\left(\omega \right)>0,A\left(\omega \right),A_d\left(\omega \right),B\left(\omega \right),$ and $\mathsf{\Gamma }\left(\omega \right)\in {\mathbb{R}}^{n\times n}$. $f(·)$ is a non-linear function, $0<L$ and $0<\alpha <1$ are real scalars, time delays $0⩽{\tau }_1,{\tau }_2,{\tau }_3⩽\tau$, and constants $c_1>0$ and $c_2>0$ are the coupling strengths. $G\left(\omega \right)={\left(g_{ij}\left(\omega \right)\right)}_{N\times N}$ is such that $g_{ii}\left(\omega \right)=-{\displaystyle \sum _{j=1,j\ne i}^N}{g}_{ij}\left(\omega \right)$.

The isolated node, $s(\omega ,t)\in {\mathbb{R}}^n$, is assumed to be

$$\left\{\begin{array}{c}{}_{t_0}{}^{c}D_t^{\alpha }s(\omega ,t)=\mathsf{\Theta }\left(\omega \right){\displaystyle \frac{\partial s(\omega ,t)}{\partial \omega }}+A\left(\omega \right)s(\omega ,t)+A_d\left(\omega \right)s(\omega ,t-{\tau }_1)+B\left(\omega \right)f\left(s(\omega ,t)\right)\hfill \\ +B_d\left(\omega \right)f\left(s(\omega ,t-{\tau }_2)\right),\hfill \\ s(L,t)=0,\hfill \\ s(\omega ,t)=s^0(\omega ,t),(\omega ,t)\in [0,L]\times [-\tau ,0].\hfill \end{array}\right.$$

(2)

This study aims to explore a distributed controller driving FCSNHSPDE (1) synchronization to the isolated node (2) as

$$u_i(\omega ,t)=d_i\left(\omega \right)(s(\omega ,t)-z_i(\omega ,t)),$$

(3)

in which $d_i\left(\omega \right)$ are space-varying control gains.

Definition 1.

FCSNHSPDE (1) reaches synchronization if

$$\underset{t\to \infty }{lim}\left|\right|z_i(\omega ,t)-s(\omega ,t)\left|\right|=0,i\in \{1,2,\cdots ,N\}.$$

(4)

Definition 2

([48]). For $\alpha \in (0,1)$, the Caputo partial derivative is defined as follows:

$$\begin{array}{cc}\hfill & {}_{t_0}{}^{c}D_t^{\alpha }p(\omega ,t)={\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}{\int }_{t_0}^t{\displaystyle \frac{\partial p(\omega ,\tau )}{\partial \tau }}{\displaystyle \frac{1}{{(t-\tau )}^{\alpha }}}d\tau ,\hfill \end{array}$$

(5)

where $p(x,t)$: $\mathbb{R}\times [t_0,\infty )$ is a differentiable function with regard to t.

Assumption 1.

For any ${\omega }_1,{\omega }_2\in \mathbb{R}$, there exists $0<\mathcal{X}\in \mathbb{R}$ satisfying

$$\begin{array}{c}\hfill |f\left({\omega }_1\right)-f\left({\omega }_2\right)|\le \mathcal{X}|{\omega }_1-{\omega }_2|.\end{array}$$

(6)

Lemma 1

([49]). For $\alpha \in (0,1)$, $z(\omega ,t):{\mathbb{R}}^m\times {\mathbb{R}}_{+}\to {\mathbb{R}}^n$ is differentiable, then the following inequation holds:

$$\begin{array}{c}\hfill {}_{t_0}{}^{c}D_t^{\alpha }\left(z^T(\omega ,t)z(\omega ,t)\right)\le 2z^T{(\omega ,t)}_{t_0}^c{D}_t^{\alpha }z(\omega ,t).\end{array}$$

(7)

3. Synchronization of FCSNHSPDEs with Time-Invariant Delays

Let $e_i(\omega ,t)\stackrel{\Delta }{=}{z}_i(\omega ,t)-s(\omega ,t)$. The behavior of $e_i$ is obtained as

$$\left\{\begin{array}{c}{}_{t_0}{}^{c}D_t^{\alpha }{e}_i(\omega ,t)=(I_N\otimes \mathsf{\Theta }\left(\omega \right)){\displaystyle \frac{\partial e(\omega ,t)}{\partial \omega }}+(I_N\otimes A\left(\omega \right))e(\omega ,t)+(I_N\otimes A_d\left(\omega \right))e(\omega ,t-{\tau }_1)\hfill \\ +(I_N\otimes B\left(\omega \right))F\left(e(\omega ,t)\right)+(I_N\otimes B_d\left(\omega \right))F\left(e(\omega ,t-{\tau }_2)\right)\hfill \\ +c_1(G_1\left(\omega \right)\otimes {\mathsf{\Gamma }}_1\left(\omega \right))e(\omega ,t)+c_2(G_2\left(\omega \right)\otimes {\mathsf{\Gamma }}_2\left(\omega \right))e(\omega ,t-{\tau }_3)+u(\omega ,t),\hfill \\ e(L,t)=0,\hfill \\ e(\omega ,t)=e^0(\omega ,t),(\omega ,t)\in [0,L]\times [-\tau ,0],\hfill \end{array}\right.$$

(8)

where $e_i^0\left(\omega \right)\stackrel{\Delta }{=}{z}_i^0\left(\omega \right)-s^0\left(\omega \right)$, $u\stackrel{\Delta }{=}{[u_1^T,u_2^T,\cdots ,u_N^T]}^T$, $e\stackrel{\Delta }{=}{[e_1^T,e_2^T,\cdots ,e_N^T]}^T$, $F\left(e_i\right)\stackrel{\Delta }{=}f\left(z_i(\omega ,t)\right)-f\left(s(\omega ,t)\right)$, and $F\left(e\right)\stackrel{\Delta }{=}{[F^T\left(e_1\right),F^T\left(e_2\right),\cdots ,F^T\left(e_N\right)]}^T$.

Theorem 1.

Under Assumption 1, FCSNHSPDE (1) achieves synchronization via the controller (2), if there exist $d_i\left(\omega \right)>0$ such that the following SALMI holds:

$$\begin{array}{ccc}\hfill \mathsf{\Psi }\left(\omega \right)& \triangleq & \left[\begin{array}{ccc}{\mathsf{\Psi }}_{11}\left(\omega \right)& A_d\left(\omega \right)& 0.5c_2{G}_2\left(\omega \right)\otimes {\mathsf{\Gamma }}_2\left(\omega \right)\\ \ast & -I& 0\\ \ast & \ast & -I\end{array}\right]<0,\hfill \end{array}$$

(9)

where

$$\begin{array}{c}{\mathsf{\Psi }}_{11}\left(\omega \right)\triangleq 0.5[I_N\otimes A\left(\omega \right)+c_1{G}_1\left(\omega \right)\otimes {\mathsf{\Gamma }}_1\left(\omega \right)-D\left(\omega \right)\otimes I_n+\ast ]\hfill \\ +0.5{\chi }^2{I}_N\otimes (B\left(\omega \right)B^T\left(\omega \right)+B_d\left(\omega \right)B_d^T\left(\omega \right))+3.5I_{Nn},\hfill \\ D\left(\omega \right)\stackrel{\Delta }{=}diag\{d_1\left(\omega \right),d_2\left(\omega \right),\cdots ,d_N\left(\omega \right)\}.\hfill \end{array}$$

Proof. 

Let the Lyapunov functional candidate be

$$\begin{array}{cc}\hfill V_1\left(t\right)=& {}_{t_0}{}^{c}D_t^{\alpha }{V}_a\left(t\right)+V_b\left(t\right),\hfill \\ \hfill V_a\left(t\right)=& 0.5{\int }_0^L{e}^T(\omega ,t)e(\omega ,t)d\omega ,\hfill \\ \hfill V_b\left(t\right)=& {\int }_0^L{\int }_{t-{\tau }_1}^t{e}^T(\omega ,\rho )e(\omega ,\rho )d\rho d\omega \hfill \\ \hfill & +{\int }_0^L{\int }_{t-{\tau }_2}^t{e}^T(\omega ,\rho )e(\omega ,\rho )d\rho d\omega \hfill \\ \hfill & +{\int }_0^L{\int }_{t-{\tau }_3}^t{e}^T(\omega ,\rho )e(\omega ,\rho )d\rho d\omega .\hfill \end{array}$$

(10)

By using Lemma 1, one has

$$\begin{array}{cc}\hfill {\dot{V}}_1\left(t\right)⩽& {\int }_0^L{e}^T(\omega ,t){}_{t_0}{}^{c}D_t^{\alpha }e(\omega ,t)d\omega +3{\int }_0^L{e}^T(\omega ,t)e(\omega ,t)d\omega \hfill \\ \hfill & -{\int }_0^L{e}^T(\omega ,t-{\tau }_1)e(\omega ,t-{\tau }_1)d\omega -{\int }_0^L{e}^T(\omega ,t-{\tau }_2)e(\omega ,t-{\tau }_2)d\omega \hfill \\ \hfill & -{\int }_0^L{e}^T(\omega ,t-{\tau }_3)e(\omega ,t-{\tau }_3)d\omega \hfill \\ \hfill =& {\int }_0^L{e}^T(\omega ,t){\displaystyle \frac{\partial e(\omega ,t)}{\partial \omega }}d\omega \hfill \\ \hfill & +{\int }_0^L{e}^T(\omega ,t)(I_N\otimes A\left(\omega \right)+c_1{G}_1\left(\omega \right)\otimes {\mathsf{\Gamma }}_1\left(\omega \right))e(\omega ,t)d\omega \hfill \\ \hfill & +{\int }_0^L{e}^T(\omega ,t)(I_N\otimes A_d\left(\omega \right))e(\omega ,t-{\tau }_1)d\omega \hfill \\ \hfill & +{\int }_0^L{e}^T(\omega ,t)(c_2{G}_2\left(\omega \right)\otimes {\mathsf{\Gamma }}_2\left(\omega \right))e(\omega ,t-{\tau }_3)d\omega +{\int }_0^L{e}^T(\omega ,t)B\left(\omega \right)F\left(e(\omega ,t)\right)d\omega \hfill \\ \hfill & +{\int }_0^L{e}^T(\omega ,t)B_d\left(\omega \right)F\left(e(\omega ,t-{\tau }_2)\right)d\omega -{\int }_0^L{e}^T(\omega ,t)(D\left(\omega \right)\otimes I_n)e(\omega ,t)d\omega \hfill \\ \hfill & +3{\int }_0^L{e}^T(\omega ,t)e(\omega ,t)d\omega -{\int }_0^L{e}^T(\omega ,t-{\tau }_1)e(\omega ,t-{\tau }_1)d\omega \hfill \\ \hfill & -{\int }_0^L{e}^T(\omega ,t-{\tau }_2)e(\omega ,t-{\tau }_2)d\omega -{\int }_0^L{e}^T(\omega ,t-{\tau }_3)e(\omega ,t-{\tau }_3)d\omega .\hfill \end{array}$$

(11)

Using integration by parts,

$$\begin{array}{cc}\hfill & {\int }_0^L{e}^T(\omega ,t)\mathsf{\Theta }\left(\omega \right){\displaystyle \frac{\partial e(\omega ,t)}{\partial \omega }}d\omega \hfill \\ \hfill =& e^T{(\omega ,t)\mathsf{\Theta }\left(\omega \right)e(\omega ,t)|}_{\omega =0}^{\omega =L}\hfill \\ \hfill & -{\int }_0^L{\displaystyle \frac{\partial e^T(\omega ,t)}{\partial \omega }}\mathsf{\Theta }\left(\omega \right)e(\omega ,t)\hfill \\ \hfill =& -e^T(0,t)\mathsf{\Theta }\left(\omega \right)e(0,t)\hfill \\ \hfill & -{\int }_0^L{e}^T(\omega ,t)\mathsf{\Theta }\left(\omega \right){\displaystyle \frac{\partial e(\omega ,t)}{\partial \omega }}d\omega \hfill \\ \hfill \le & -{\int }_0^L{e}^T(\omega ,t)\mathsf{\Theta }\left(\omega \right){\displaystyle \frac{\partial e(\omega ,t)}{\partial \omega }}d\omega ,\hfill \end{array}$$

(12)

which implies

$${\int }_0^L{e}^T(\omega ,t)\mathsf{\Theta }\left(\omega \right){\displaystyle \frac{\partial e(\omega ,t)}{\partial \omega }}d\omega \le 0.$$

(13)

By applying the triangle inequality, under Assumption 1, one has

$$\begin{array}{cc}\hfill & {\int }_0^L{e}^T(\omega ,t)B\left(\omega \right)F\left(e(\omega ,t)\right)d\omega +{\int }_0^L{e}^T(\omega ,t)B_d\left(\omega \right)F\left(e(\omega ,t-{\tau }_2)\right)d\omega \hfill \\ \hfill \le & 0.5{\chi }^2{\int }_0^L{e}^T(\omega ,t)(B\left(\omega \right)B^T\left(\omega \right)+B_d\left(\omega \right)B_d^T\left(\omega \right))e(\omega ,t)d\omega \hfill \\ & +0.5{\chi }^{-2}{\int }_0^L(F^T(\omega ,t)F(\omega ,t)+F^T(\omega ,t-{\tau }_2)F(\omega ,t-{\tau }_2))d\omega \hfill \\ \hfill =& {\int }_0^L{e}^T(\omega ,t)(0.5{\chi }^2{I}_N\otimes (B\left(\omega \right)B^T\left(\omega \right)+B_d\left(\omega \right)B_d^T\left(\omega \right))+0.5I_{Nn})e(\omega ,t)d\omega \hfill \\ & +0.5{\int }_0^L{e}^T(\omega ,t-{\tau }_2)e(\omega ,t-{\tau }_2)d\omega .\hfill \end{array}$$

(14)

Substitution of (12)–(14) into (11) yields,

$$\begin{array}{c}\hfill {\dot{V}}_1\left(t\right)⩽{\int }_0^L{\overline{e}}^T(\omega ,t)\mathsf{\Psi }\overline{e}(\omega ,t)d\omega -0.5{\int }_0^L{e}^T(\omega ,t-{\tau }_2)e(\omega ,t-{\tau }_2)d\omega ,\end{array}$$

(15)

where $\widehat{e}(\omega ,t)\triangleq {[e^T(\omega ,t),e^T(\omega ,t-{\tau }_1),e^T(\omega ,t-{\tau }_3)]}^T$. Substituting (9) to (15), one has $\dot{V}\left(t\right)⩽-{\lambda }_{min}(-\mathsf{\Psi })\left|\right|\widehat{e}(·,t)\left|\right|⩽-{\lambda }_{min}(-\mathsf{\Psi })\left|\right|e(·,t)\left|\right|<0$, for all non-zero $e(\omega ,t)$, implying synchronization of FCSNHSPDE (1). □

4. Synchronization of FCSNHSPDEs with Time-Varying Delays

This section studies time-varying delayed FCSNHSPDEs, such as

$$\left\{\begin{array}{c}{}_{t_0}{}^{c}D_t^{\alpha }{z}_i(\omega ,t)=\mathsf{\Theta }\left(\omega \right){\displaystyle \frac{\partial z_i(\omega ,t)}{\partial \omega }}+A\left(\omega \right)z_i(\omega ,t)+A_d\left(\omega \right)z_i(\omega ,t-{\tau }_1\left(t\right))+B\left(\omega \right)f\left(z_i(\omega ,t)\right)\hfill \\ +B_d\left(\omega \right)f\left(z_i(\omega ,t-{\tau }_2\left(t\right))\right)+c_1{\displaystyle \sum _{j=1}^N}{g}_{ij}\left(\omega \right)\mathsf{\Gamma }\left(\omega \right)z_j(\omega ,t)\hfill \\ +c_2{\displaystyle \sum _{j=1}^N}{g}_{ij}\left(\omega \right)\mathsf{\Gamma }\left(\omega \right)z_j(\omega ,t-{\tau }_3\left(t\right))+u_i(\omega ,t),\hfill \\ z_i(L,t)=0,\hfill \\ z_i(\omega ,t)=z_i^0(\omega ,t),(\omega ,t)\in [0,L]\times [-\tau ,0],\hfill \end{array}\right.$$

(16)

where $0⩽{\tau }_1\left(t\right)⩽\tau$, $0⩽{\tau }_2\left(t\right)⩽\tau$, $0⩽{\tau }_1\left(t\right)⩽\tau$, $0⩽{\dot{\tau }}_3\left(t\right)⩽{\mu }_1$, $0⩽{\dot{\tau }}_2\left(t\right)⩽{\mu }_2$, and $0⩽{\dot{\tau }}_3\left(t\right)⩽{\mu }_3$.

The isolated node is assumed to be

$$\left\{\begin{array}{c}{}_{t_0}{}^{c}D_t^{\alpha }s(\omega ,t)=\mathsf{\Theta }\left(\omega \right){\displaystyle \frac{\partial s(\omega ,t)}{\partial \omega }}+A\left(\omega \right)s(\omega ,t)+A_d\left(\omega \right)s(\omega ,t-{\tau }_1\left(t\right))+B\left(\omega \right)f\left(s(\omega ,t)\right)\hfill \\ +B_d\left(\omega \right)f\left(s(\omega ,t-{\tau }_2\left(t\right))\right),\hfill \\ s(L,t)=0,\hfill \\ s(\omega ,t)=s^0(\omega ,t),(\omega ,t)\in [0,L]\times [-\tau ,0].\hfill \end{array}\right.$$

(17)

The error system between FCSNHSPDE (16) and (17) with time-varying delays can be obtained as

$$\left\{\begin{array}{c}{}_{t_0}{}^{c}D_t^{\alpha }e(\omega ,t)=(I_N\otimes \mathsf{\Theta }\left(\omega \right)){\displaystyle \frac{\partial e(\omega ,t)}{\partial \omega }}+(I_N\otimes A\left(\omega \right))e(\omega ,t)+(I_N\otimes A_d\left(\omega \right))e(\omega ,t-{\tau }_1\left(t\right))\hfill \\ +(I_N\otimes B\left(\omega \right))F\left(e(\omega ,t)\right)+(I_N\otimes B_d\left(\omega \right))F\left(e(\omega ,t-{\tau }_2\left(t\right))\right)\hfill \\ +c_1(G_1\left(\omega \right)\otimes {\mathsf{\Gamma }}_1\left(\omega \right))e(\omega ,t)+c_2(G_2\left(\omega \right)\otimes {\mathsf{\Gamma }}_2\left(\omega \right))e(\omega ,t-{\tau }_3\left(t\right))+u(\omega ,t),\hfill \\ e(L,t)=0,\hfill \\ e(\omega ,t)=e^0(\omega ,t),(\omega ,t)\in [0,L]\times [-\tau ,0].\hfill \end{array}\right.$$

(18)

Theorem 2.

Under Assumption 1, the FCSNHSPDE (17) achieves synchronization with the isolated node (18) via the controller (2), if there exist $d_i\left(\omega \right)>0$ such that the following SALMI holds:

$$\begin{array}{ccc}\hfill \mathrm{\Xi }& \triangleq & \left[\begin{array}{ccc}{\mathrm{\Xi }}_{11}& A_d\left(\omega \right)& 0.5c_2{G}_2\left(\omega \right)\otimes {\mathsf{\Gamma }}_2\left(\omega \right)\\ \ast & -I& 0\\ \ast & \ast & -I\end{array}\right]<0,\hfill \end{array}$$

(19)

where $D\left(\omega \right)$ is defined in (9) and

$$\begin{array}{cc}\hfill {\mathrm{\Xi }}_{11}\triangleq & 0.5[I_N\otimes A\left(\omega \right)+c_1{G}_1\left(\omega \right)\otimes {\mathsf{\Gamma }}_1\left(\omega \right)-D\left(\omega \right)\otimes I_n+\ast ]\hfill \\ & +0.5{\chi }^2{I}_N\otimes (B\left(\omega \right)B^T\left(\omega \right)+B_d\left(\omega \right)B_d^T\left(\omega \right))+3.5I_{Nn}.\hfill \end{array}$$

Proof. 

Let the Lyapunov functional candidate be

$$\begin{array}{cc}\hfill V_2\left(t\right)=& {}_{t_0}{}^{c}D_t^{\alpha }{V}_a\left(t\right)+V_c\left(t\right),\hfill \\ \hfill V_a\left(t\right)=& 0.5{\int }_0^L{e}^T(\omega ,t)e(\omega ,t)d\omega ,\hfill \\ \hfill V_c\left(t\right)=& {\int }_0^L{\int }_{t-{\tau }_1\left(t\right)}^t{e}^T(\omega ,\rho )e(\omega ,\rho )d\rho d\omega \hfill \\ \hfill & +{\int }_0^L{\int }_{t-{\tau }_2\left(t\right)}^t{e}^T(\omega ,\rho )e(\omega ,\rho )d\rho d\omega \hfill \\ \hfill & +{\int }_0^L{\int }_{t-{\tau }_3\left(t\right)}^t{e}^T(\omega ,\rho )e(\omega ,\rho )d\rho d\omega .\hfill \end{array}$$

(20)

By using Lemma 1, one has

$$\begin{array}{cc}\hfill {\dot{V}}_2\left(t\right)\le & {\int }_0^L{e}^T(\omega ,t){}_{t_0}{}^{c}D_t^{\alpha }e(\omega ,t)d\omega +3{\int }_0^L{e}^T(\omega ,t)e(\omega ,t)d\omega \hfill \\ \hfill & -(1-{\dot{\tau }}_1\left(t\right)){\int }_0^L{e}^T(\omega ,t-{\tau }_1\left(t\right))e(\omega ,t-{\tau }_1\left(t\right))d\omega \hfill \\ \hfill & -(1-{\dot{\tau }}_2\left(t\right)){\int }_0^L{e}^T(\omega ,t-{\tau }_2\left(t\right))e(\omega ,t-{\tau }_2\left(t\right))d\omega \hfill \\ \hfill & -(1-{\dot{\tau }}_3\left(t\right)){\int }_0^L{e}^T(\omega ,t-{\tau }_3\left(t\right))e(\omega ,t-{\tau }_3\left(t\right))d\omega \hfill \\ \hfill =& {\int }_0^L{e}^T(\omega ,t){\displaystyle \frac{\partial e(\omega ,t)}{\partial \omega }}d\omega \hfill \\ \hfill & +{\int }_0^L{e}^T(\omega ,t)(I_N\otimes A\left(\omega \right)+c_1{G}_1\left(\omega \right)\otimes {\mathsf{\Gamma }}_1\left(\omega \right))e(\omega ,t)d\omega \hfill \\ \hfill & +{\int }_0^L{e}^T(\omega ,t)(I_N\otimes A_d\left(\omega \right))e(\omega ,t-{\tau }_1\left(t\right))d\omega \hfill \\ \hfill & +{\int }_0^L{e}^T(\omega ,t)(c_2{G}_2\left(\omega \right)\otimes {\mathsf{\Gamma }}_2\left(\omega \right))e(\omega ,t-{\tau }_3\left(t\right))d\omega +{\int }_0^L{e}^T(\omega ,t)B\left(\omega \right)F\left(e(\omega ,t)\right)d\omega \hfill \\ \hfill & +{\int }_0^L{e}^T(\omega ,t)B_d\left(\omega \right)F\left(e(\omega ,t-{\tau }_2\left(t\right))\right)d\omega -{\int }_0^L{e}^T(\omega ,t)(D\left(\omega \right)\otimes I_n)e(\omega ,t)d\omega \hfill \\ \hfill & +3{\int }_0^L{e}^T(\omega ,t)e(\omega ,t)d\omega -(1-{\dot{\tau }}_1\left(t\right)){\int }_0^L{e}^T(\omega ,t-{\tau }_1\left(t\right))e(\omega ,t-{\tau }_1\left(t\right))d\omega \hfill \\ \hfill & -(1-{\dot{\tau }}_2\left(t\right)){\int }_0^L{e}^T(\omega ,t-{\tau }_2\left(t\right))e(\omega ,t-{\tau }_2\left(t\right))d\omega \hfill \\ \hfill & -(1-{\dot{\tau }}_3\left(t\right)){\int }_0^L{e}^T(\omega ,t-{\tau }_3\left(t\right))e(\omega ,t-{\tau }_3\left(t\right))d\omega ,\hfill \end{array}$$

(21)

where $D\left(\omega \right)\stackrel{\Delta }{=}diag\{d_1\left(\omega \right),d_2\left(\omega \right),\cdots ,d_N\left(\omega \right)\}$.

Under Assumption 1,

$$\begin{array}{cc}& {\int }_0^L{e}^T(\omega ,t)B\left(\omega \right)F\left(e(\omega ,t)\right)d\omega +{\int }_0^L{e}^T(\omega ,t)B_d\left(\omega \right)F\left(e(\omega ,t-{\tau }_2\left(t\right))\right)d\omega \hfill \\ \hfill ⩽& 0.5{\chi }^2{(1-{\mu }_2)}^{-1}{\int }_0^L{e}^T(\omega ,t)(B\left(\omega \right)B^T\left(\omega \right)+B_d\left(\omega \right)B_d^T\left(\omega \right))e(\omega ,t)d\omega \hfill \\ & +0.5{\chi }^{-2}(1-{\mu }_2){\int }_0^L(F^T(\omega ,t)F(\omega ,t)+F^T(\omega ,t-{\tau }_2\left(t\right))F(\omega ,t-{\tau }_2\left(t\right)))d\omega \hfill \\ \hfill =& {\int }_0^L{e}^T(\omega ,t)(0.5{\chi }^2{(1-{\mu }_2)}^{-1}{I}_N\otimes (B\left(\omega \right)B^T\left(\omega \right)+B_d\left(\omega \right)B_d^T\left(\omega \right))+0.5I_{Nn})e(\omega ,t)d\omega \hfill \\ & +0.5(1-{\mu }_2){\int }_0^L{e}^T(\omega ,t-{\tau }_2\left(t\right))e(\omega ,t-{\tau }_2\left(t\right))d\omega .\hfill \end{array}$$

(22)

According to the conditions of time-varying delays, one has

$$\begin{array}{cc}\hfill & -(1-{\dot{\tau }}_1\left(t\right)){\int }_0^L{e}^T(\omega ,t-{\tau }_1\left(t\right))e(\omega ,t-{\tau }_1\left(t\right))d\omega \hfill \\ & -(1-{\dot{\tau }}_2\left(t\right)){\int }_0^L{e}^T(\omega ,t-{\tau }_2\left(t\right))e(\omega ,t-{\tau }_2\left(t\right))d\omega \hfill \\ \hfill & -(1-{\dot{\tau }}_3\left(t\right)){\int }_0^L{e}^T(\omega ,t-{\tau }_3\left(t\right))e(\omega ,t-{\tau }_3\left(t\right))d\omega \hfill \\ \hfill ⩽& -(1-{\mu }_1){\int }_0^L{e}^T(\omega ,t-{\tau }_1\left(t\right))e(\omega ,t-{\tau }_1\left(t\right))d\omega \hfill \\ & -(1-{\mu }_2){\int }_0^L{e}^T(\omega ,t-{\tau }_2\left(t\right))e(\omega ,t-{\tau }_2\left(t\right))d\omega \hfill \\ \hfill & -(1-{\mu }_3){\int }_0^L{e}^T(\omega ,t-{\tau }_3\left(t\right))e(\omega ,t-{\tau }_3\left(t\right))d\omega .\hfill \end{array}$$

(23)

Substitution of (22) and (23) into (21) yields,

$$\begin{array}{c}\hfill \dot{V_2}\left(t\right)⩽{\int }_0^L{\tilde{e}}^T(\omega ,t)\mathrm{\Xi }\left(\omega \right)\tilde{e}(\omega ,t)d\omega -0.5(1-{\mu }_2){\int }_0^L{e}^T(\omega ,t-{\tau }_2\left(t\right))e(\omega ,t-{\tau }_2\left(t\right))d\omega ,\end{array}$$

(24)

where $\tilde{e}(\omega ,t)\triangleq {[e^T(\omega ,t),e^T(\omega ,t-{\tau }_1\left(t\right)),e^T(\omega ,t-{\tau }_3\left(t\right))]}^T$.

The rest of the proof is similar to that of Theorem 1, and so it is omitted. □

Remark 1.

There are many important works on synchronization of hyperbolic PDE-based CSTNs [38,39,50]; however, time delays are still not addressed, which has been considered in this paper.

Remark 2.

This paper addresses synchronization of FCSNHSPDEs not only with multiple time-invariant delays but also with multiple time-varying delays, as well as considering delayed coupling.

Remark 3.

PDEs’ space-invariant parameters with based CSTNs have been studied for synchronization or consensus [50,51], while space-varying parameters models have not been considered. As is well-known, space-varying parameter models exist in processing [52,53,54]. This paper deals with space-varying parameter-based models.

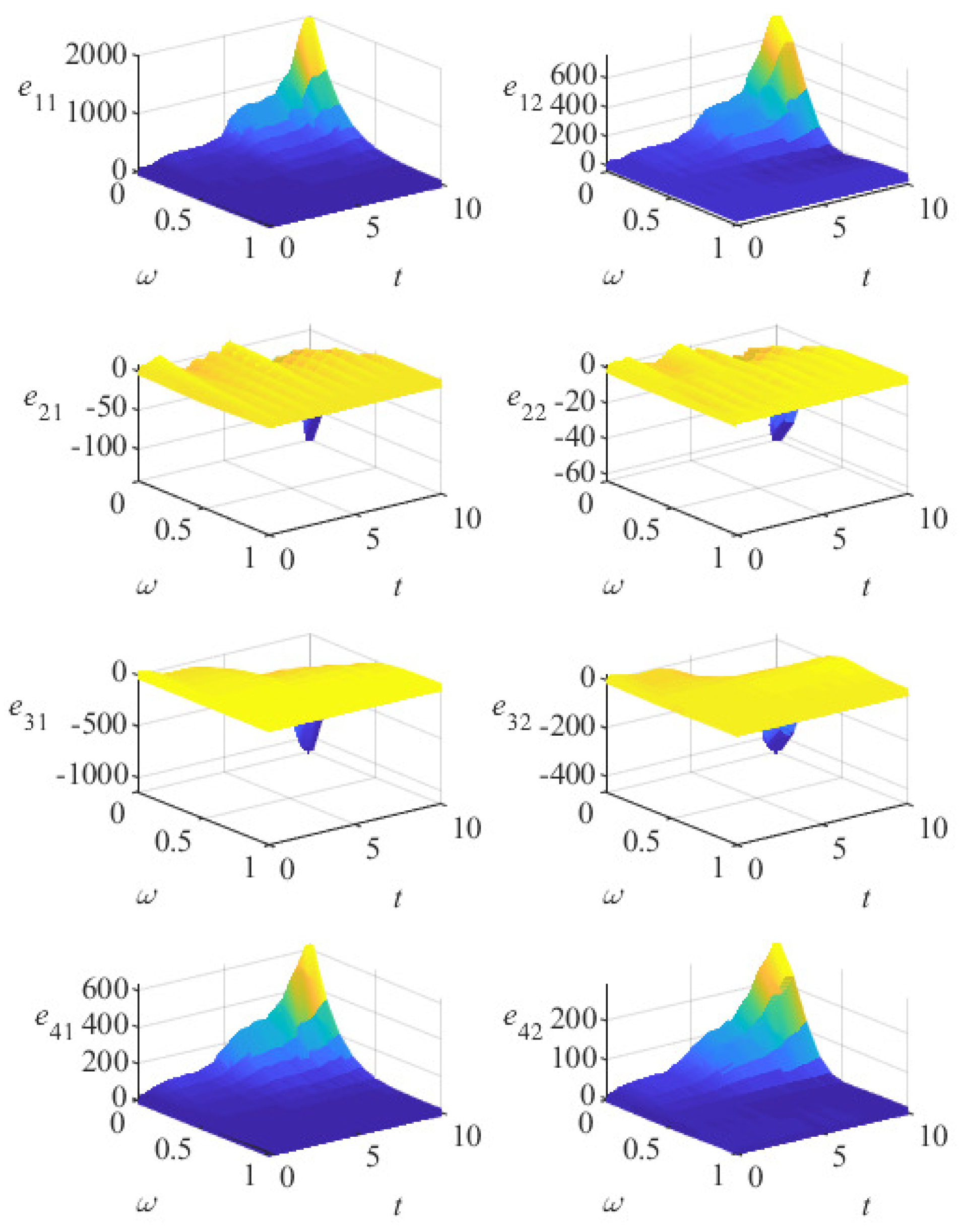
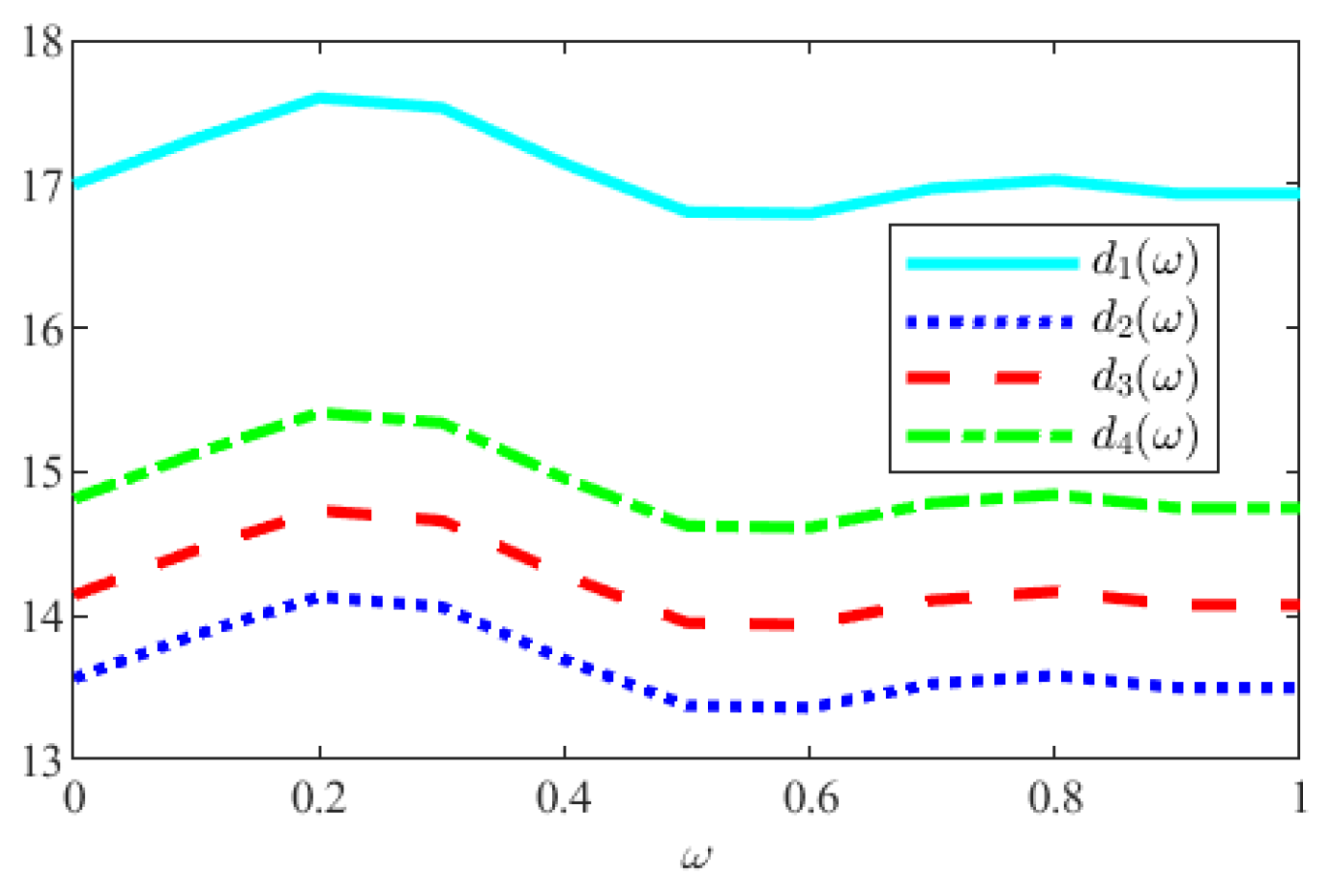
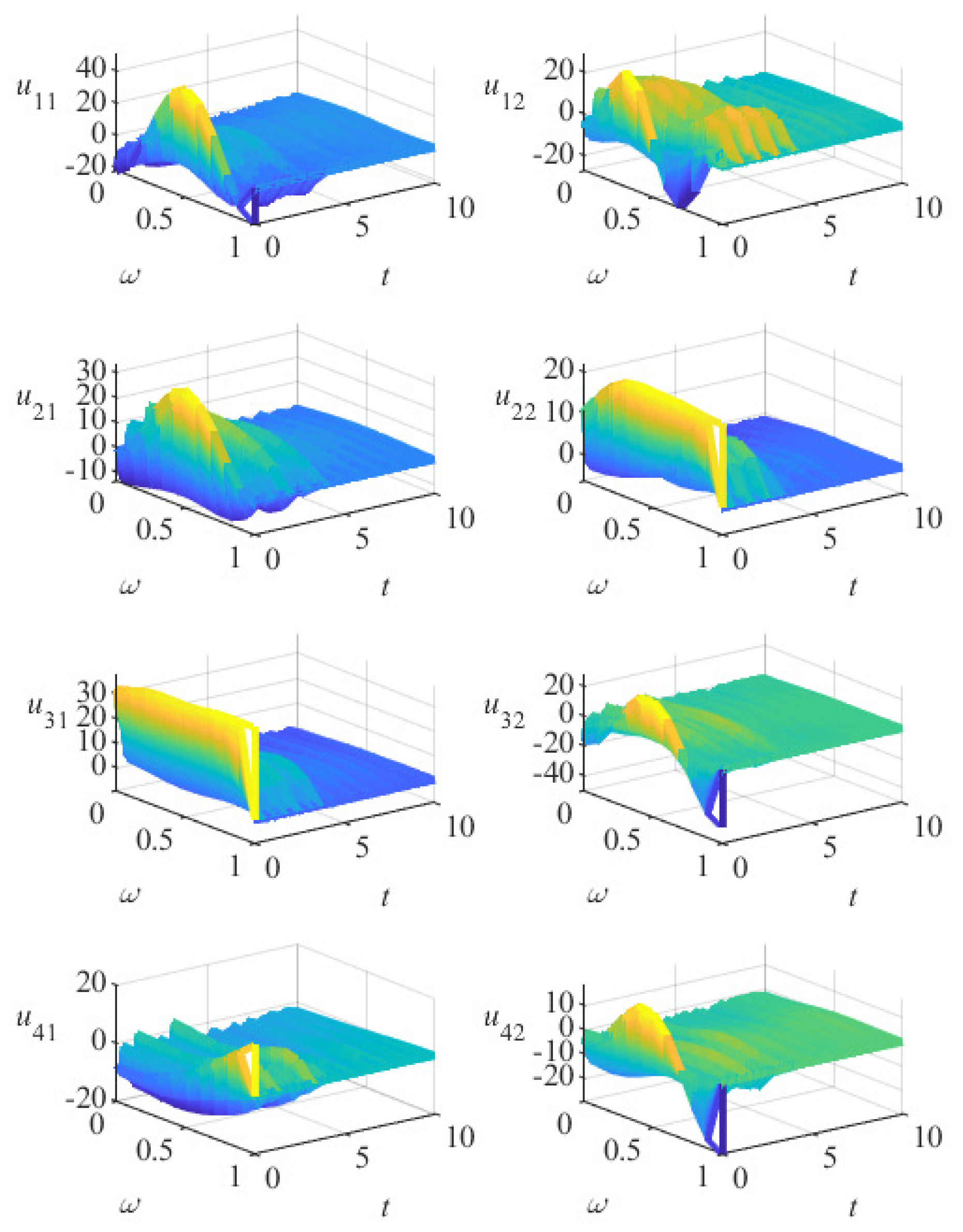
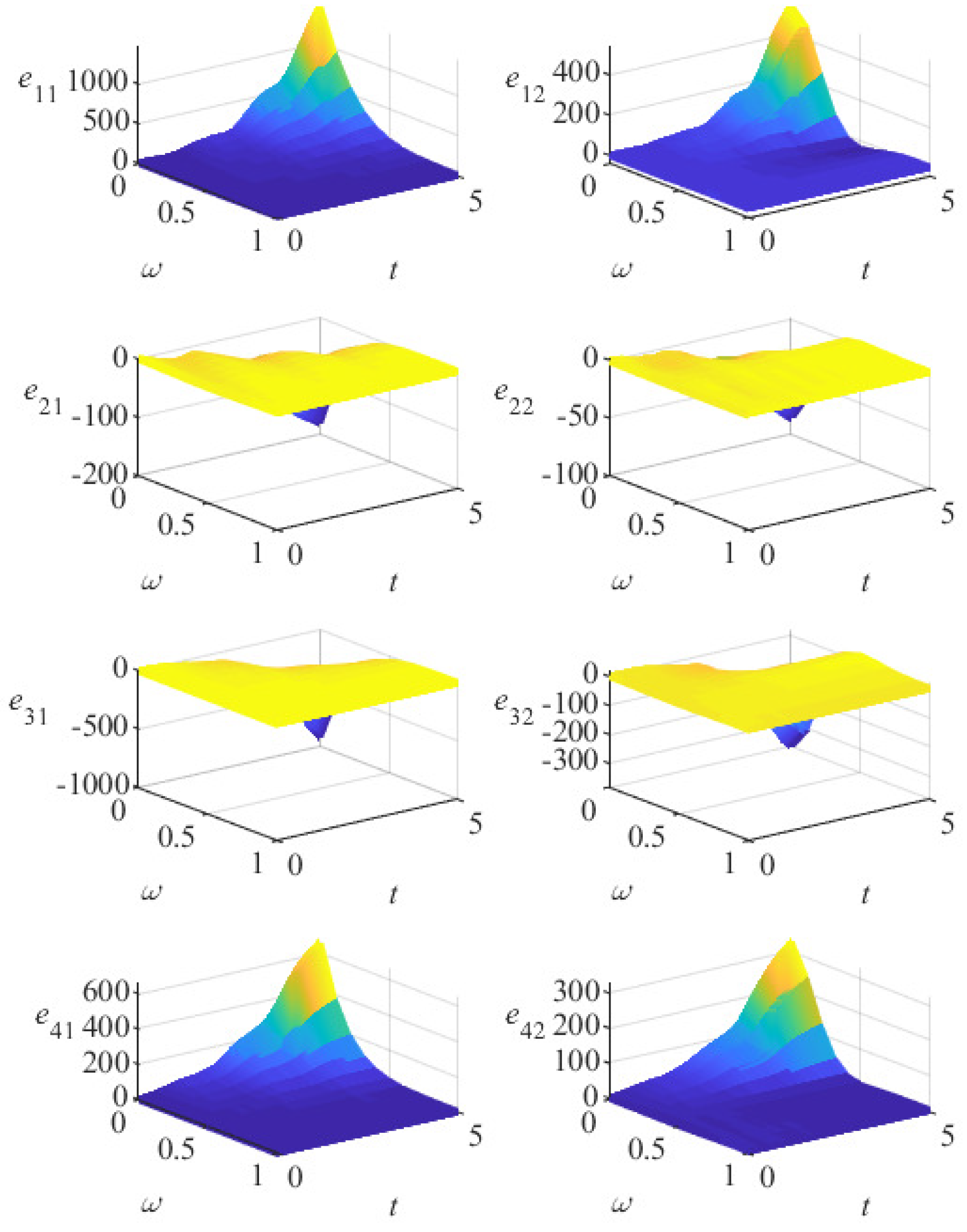
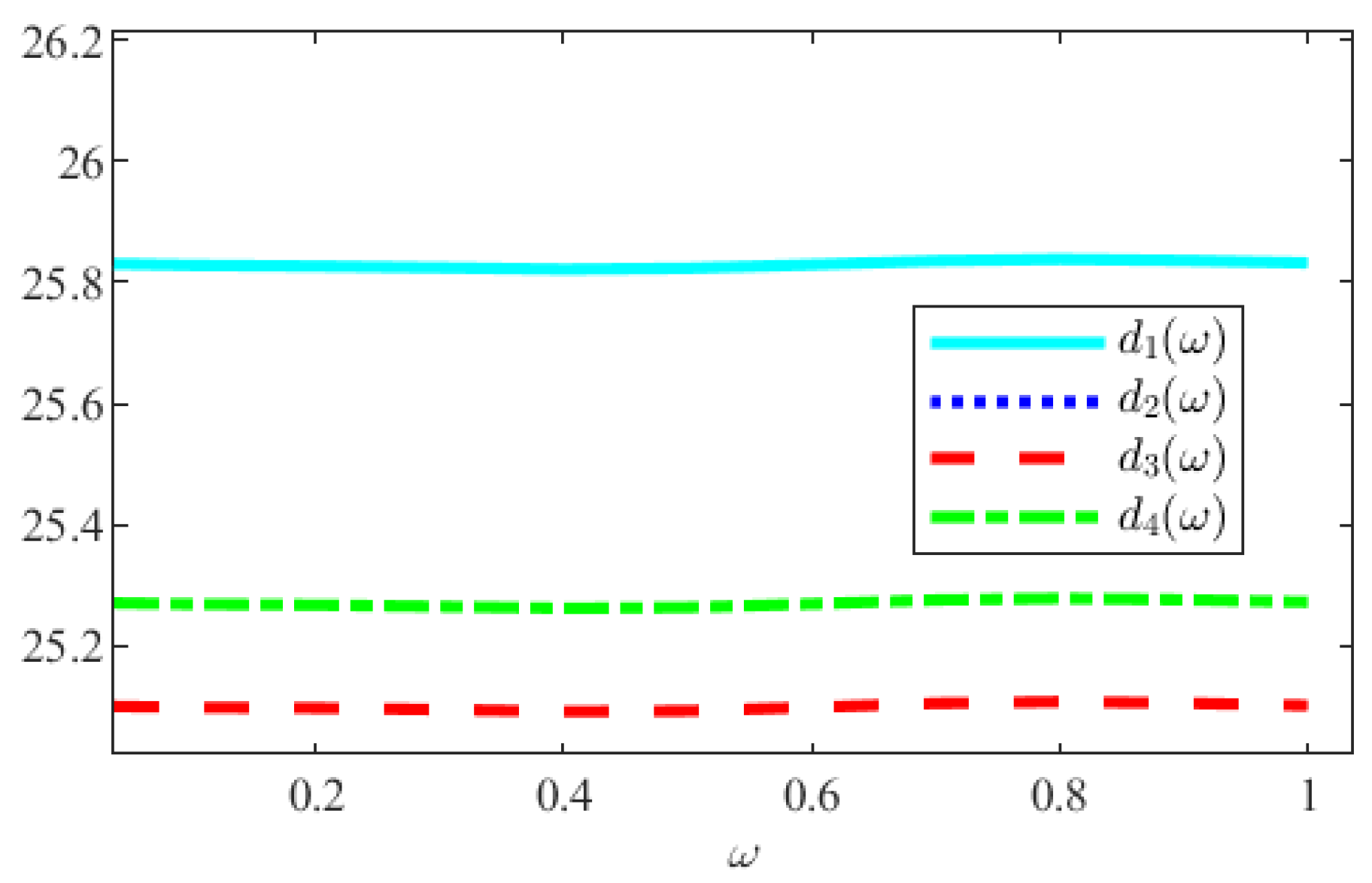
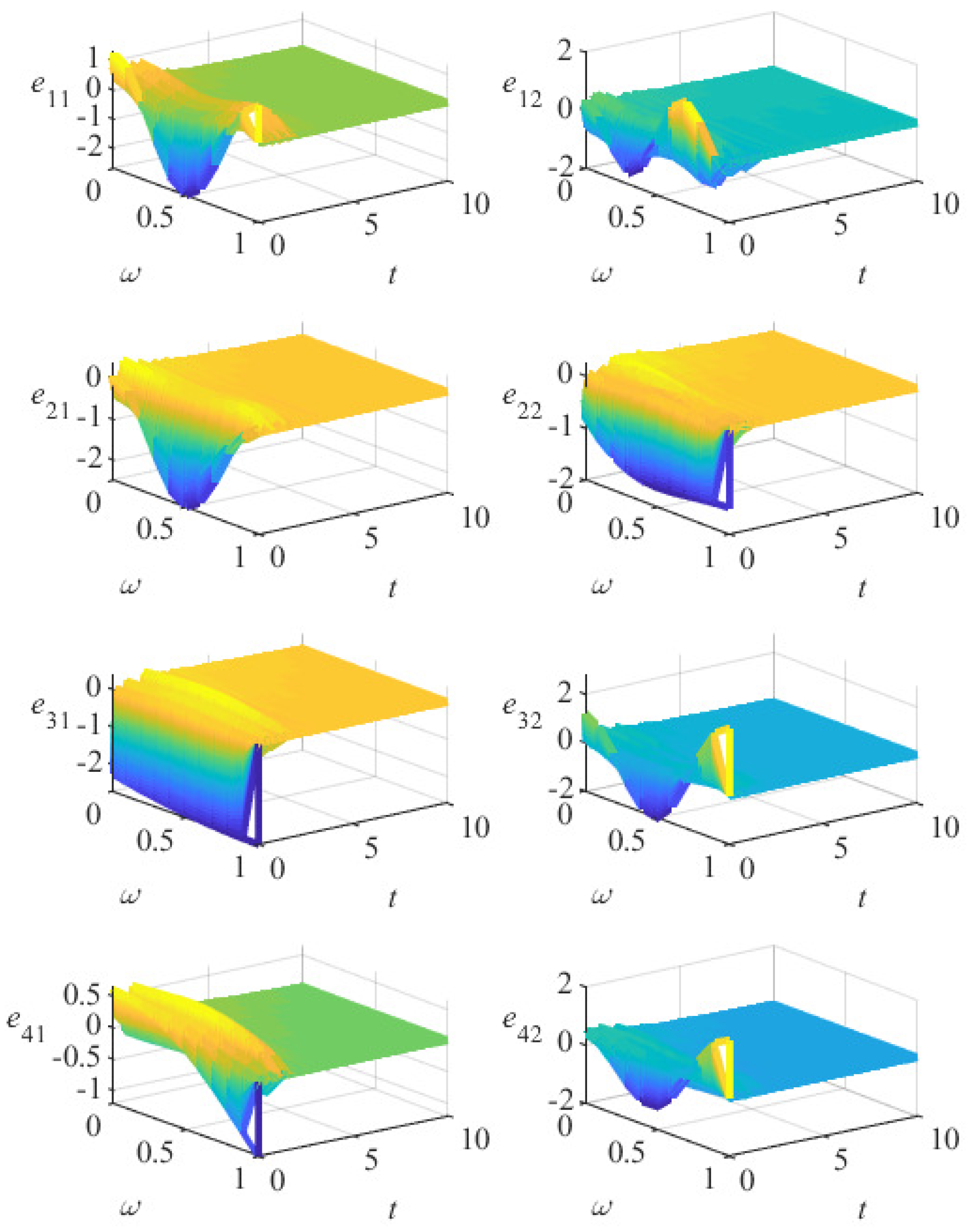
5. Numerical Examples

Example 1.

To demonstrate the effectiveness of Theorem 1, consider FCSNHSPDE (1) with random initial conditions and time-invariant delays as follows

$$\left\{\begin{array}{c}{}_{t_0}{}^{c}D_t^{\alpha }{z}_{i1}(\omega ,t)={\displaystyle \frac{\partial z_{i1}(\omega ,t)}{\partial \omega }}+1.2z_{i}1(\omega ,t)-0.2z_{i2}(\omega ,t)+0.8z_{i1}(\omega ,t-{\tau }_1)\hfill \\ +0.5z_{i2}(\omega ,t-{\tau }_1)+f\left(z_{i1}(\omega ,t)\right)-0.2f\left(z_{i1}(\omega ,t)\right)\hfill \\ +f\left(z_{i1}(\omega ,t-{\tau }_2)\right)-0.2f\left(z_{i2}(\omega ,t-{\tau }_2)\right)+0.2{\displaystyle \sum _{j=1}^N}{g}_{ij}\left(\omega \right)z_{j1}(\omega ,t)\hfill \\ +0.3{\displaystyle \sum _{j=1}^N}{g}_{ij}\left(\omega \right)z_{j1}(\omega ,t-{\tau }_3)+u_{i1}(\omega ,t),\hfill \\ {}_{t_0}{}^{c}D_t^{\alpha }{z}_{i2}(\omega ,t)={\displaystyle \frac{\partial z_{i2}(\omega ,t)}{\partial \omega }}+2.5sin\left(2\pi \omega \right)z_{i}1(\omega ,t)-1.8z_{i2}(\omega ,t)\hfill \\ +cos\left(\pi \omega \right)z_{i1}(\omega ,t-{\tau }_1)+1.6z_{i2}(\omega ,t-{\tau }_1)+0.2sin\left(2\pi \omega \right)f\left(z_{i1}(\omega ,t)\right)\hfill \\ -2.5f\left(z_{i1}(\omega ,t)\right)+0.2sin\left(2\pi \omega \right)f\left(z_{i1}(\omega ,t-{\tau }_2)\right)-2.5f\left(z_{i2}(\omega ,t-{\tau }_2)\right)\hfill \\ +0.2{\displaystyle \sum _{j=1}^N}{g}_{ij}\left(\omega \right)z_{j2}(\omega ,t)+0.3{\displaystyle \sum _{j=1}^N}{g}_{ij}\left(\omega \right)z_{j2}(\omega ,t-{\tau }_3)+u_{i2}(\omega ,t),\hfill \end{array}\right.$$

(25)

where

$$\begin{array}{cc}\hfill & \mathsf{\Theta }\left(\omega \right)=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],A\left(\omega \right)=\left[\begin{array}{cc}1.2& -0.2\\ 2.5sin\left(2\pi \omega \right)& -1.8\end{array}\right],A_d\left(\omega \right)=\left[\begin{array}{cc}0.8& 0.5\\ cos\left(\pi \omega \right)& 1.6\end{array}\right],\hfill \\ \hfill & B\left(\omega \right)=B_d\left(\omega \right)=\left[\begin{array}{cc}1& -0.2\\ 0.2sin\left(2\pi \omega \right)& -2.5\end{array}\right],{\mathsf{\Gamma }}_1\left(\omega \right)={\mathsf{\Gamma }}_2\left(\omega \right)=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],\hfill \\ \hfill & L=1,\alpha =0.95,c_1=0.2,c_2=0.3,t_0=0,{\tau }_1=3,{\tau }_2=2,{\tau }_3=4,f(·)=tanh(·),\hfill \\ \hfill & z_i=\left[\begin{array}{c}{z}_{i1}\\ z_{i2}\end{array}\right],G_1\left(\omega \right)=G_2\left(\omega \right)=\left[\begin{array}{cccc}10& -1& -3& -6\\ -1& 5& -2& -2\\ -2& -3& 6& -1\\ -1& -3& -3& 7\end{array}\right].\hfill \end{array}$$

(26)

This illustrates that FCSNHSPDE (1) cannot achieve synchronization without control in Figure 1. From (26), $\chi =1$ is obtained. By Theorem 1, solve (9) by using Matlab, and the time-varying control gains are obtained as shown in Figure 2, where the parameter feasibility radius = 100 of feasp in the LMI toolkit. Figure 3 shows that FCSNHSPDE (1) reaches synchronization via the proposed controller (3) with the feedback gains shown in Figure 2, and the controller (3) is shown in Figure 4.

Example 2.

To demonstrate the effectiveness of Theorem 2, consider FCSNHSPDE (16) with time-varying delays, and with the same coefficients to those of Example 1, except:

$${\tau }_1\left(t\right)=1.2+0.2sin\left(1.2\pi t\right),{\tau }_2=1.5+0.8sin\left(0.2\pi t\right),{\tau }_3=1.8+sin\left(0.3\pi t\right).$$

(27)

Figure 5 shows that FCSNHSPDE (16) with time-varying delays cannot achieve synchronization without control. From (27), ${\mu }_1=0.24\pi ,{\mu }_2=0.16\pi ,{\mu }_3=0.3\pi$, and $\chi =1$ are obtained. By Theorem 2, solve (20) and the time-varying control gains are obtained as shown in Figure 6, where the parameter feasibility radius=200 of feasp in the LMI toolkit. Figure 7 shows that FCSNHSPDE (16) with time-varying delays achieves synchronization via controller (3) with the control gains, while controller (3) is shown in Figure 8.

6. Conclusions

This study addressed synchronization of two sorts of semi-linear space-varying FCSNHSPDEs, one with time-invariant delays, and the other with time-varying delays. To ensure FCSNHSPDEs achieve synchronization, a space-varying control gains-based control method was proposed. Sufficient conditions for synchronization of FCSNHSPDE with both time-invariant and time-varying delays were derived using SALMIs. The effectiveness of these methods was demonstrated through two examples. The proposed method has a potential application for flexible manipulators, flexible strings, flexible articulated wings, and flexible appendages, which will be considered in the future. The actuator is often prone to faults due to harsh environmental conditions, and so fault-tolerant control of FCSNHSPDEs will be studied in future.