On the Numerical Investigations of a Fractional-Order Mathematical Model for Middle East Respiratory Syndrome Outbreak
Abstract
1. Introduction
2. Preliminaries
3. Model Derivation
3.1. Stability and Equilibrium Points
3.2. Sensitivity Analysis
4. Existence and Uniqueness Analysis
- Similarly, we obtain
4.1. Existence of Solution
- Similarly, we can prove that . Then, the operator maps itself.
- Also, we evolute the following equality:
4.2. Uniqueness of Solution
5. Numerical Algorithms
5.1. Numerical Algorithm of MVM
Stability Analysis of MVM
5.2. Numerical Algorithm of ITM
Stability Analysis of ITM
6. Numerical Results
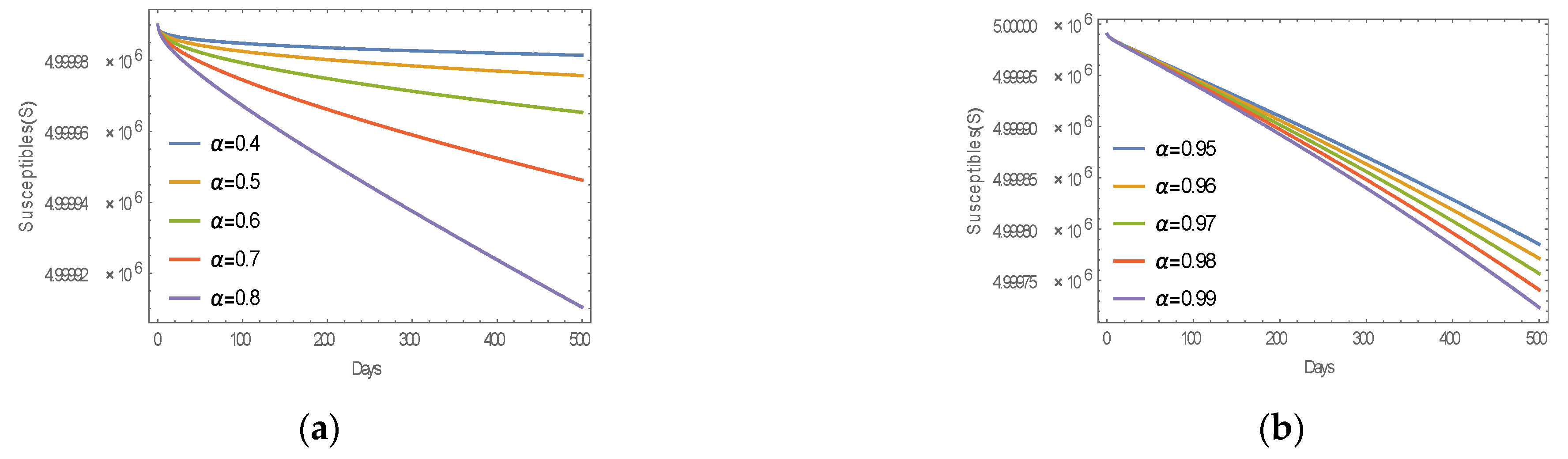
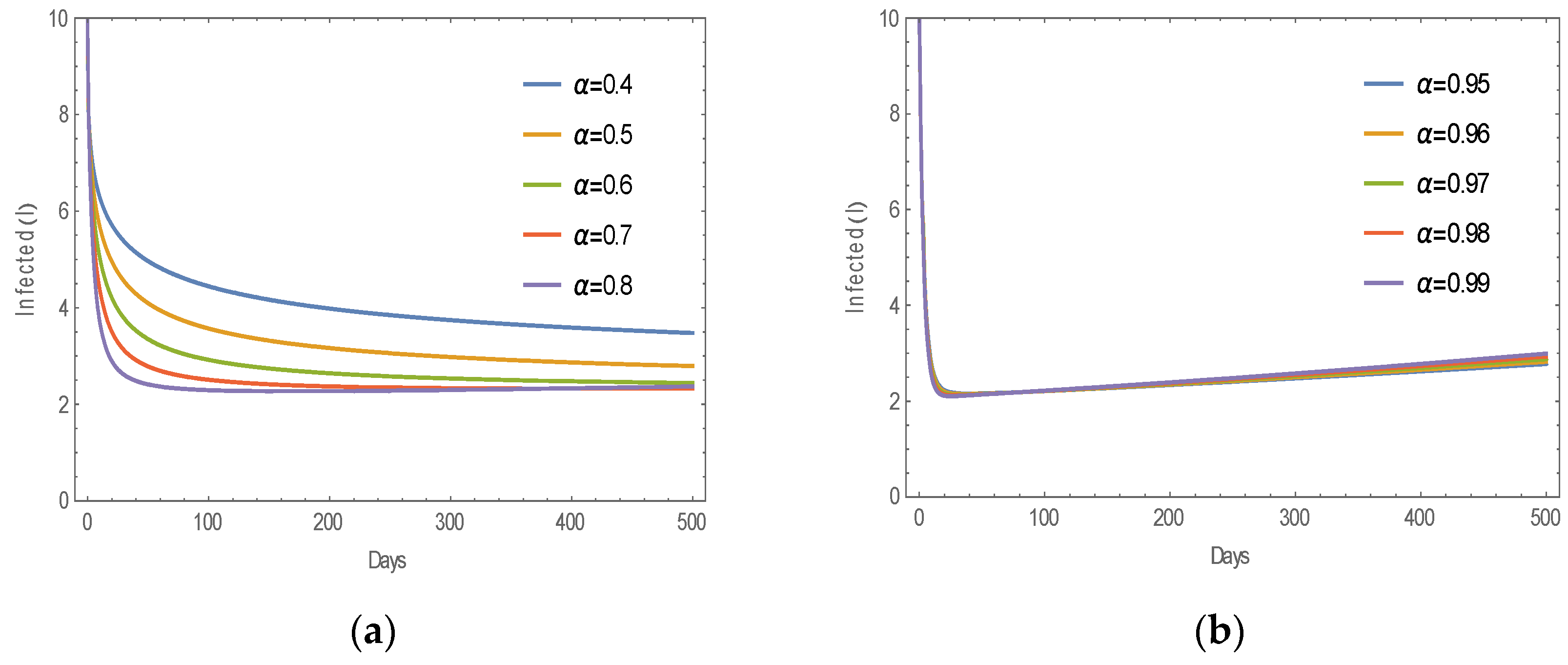
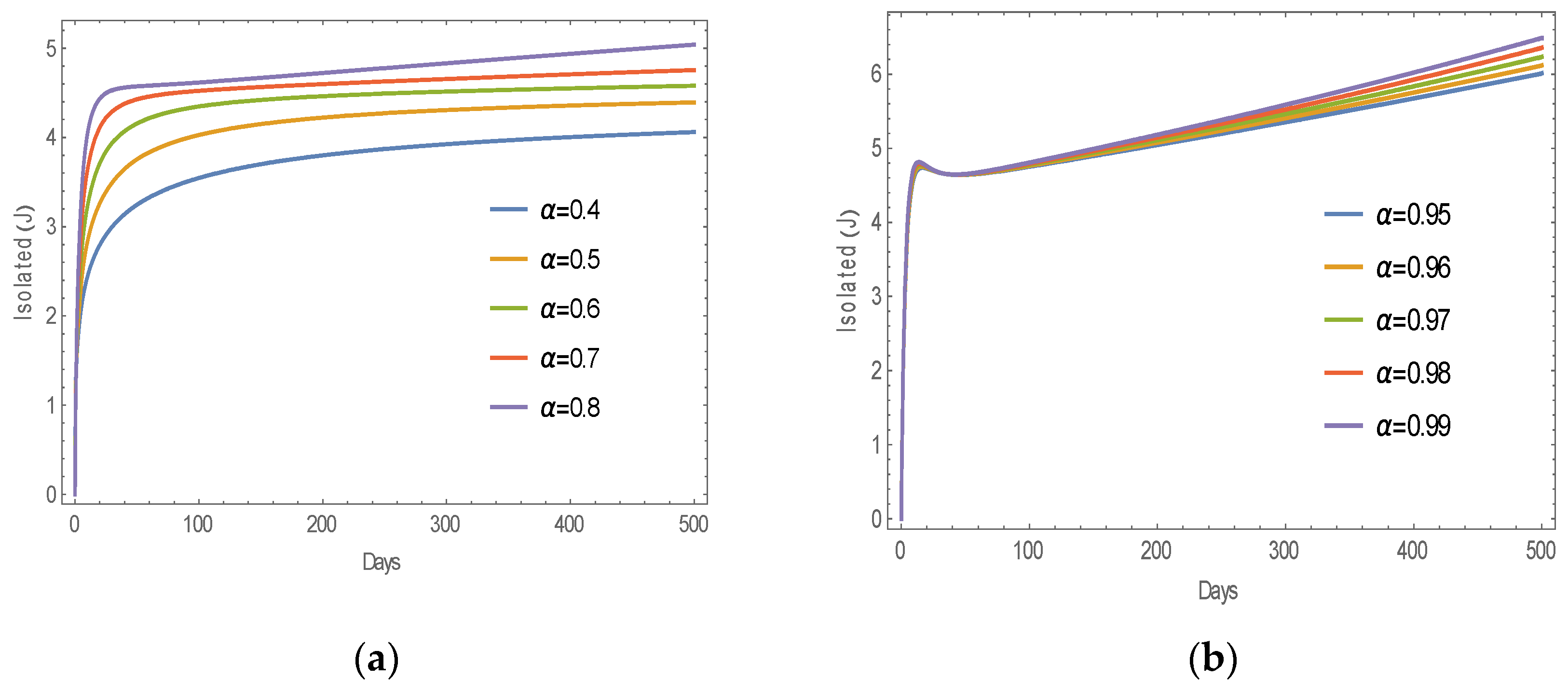
6.1. Numerical Simulation of MERS
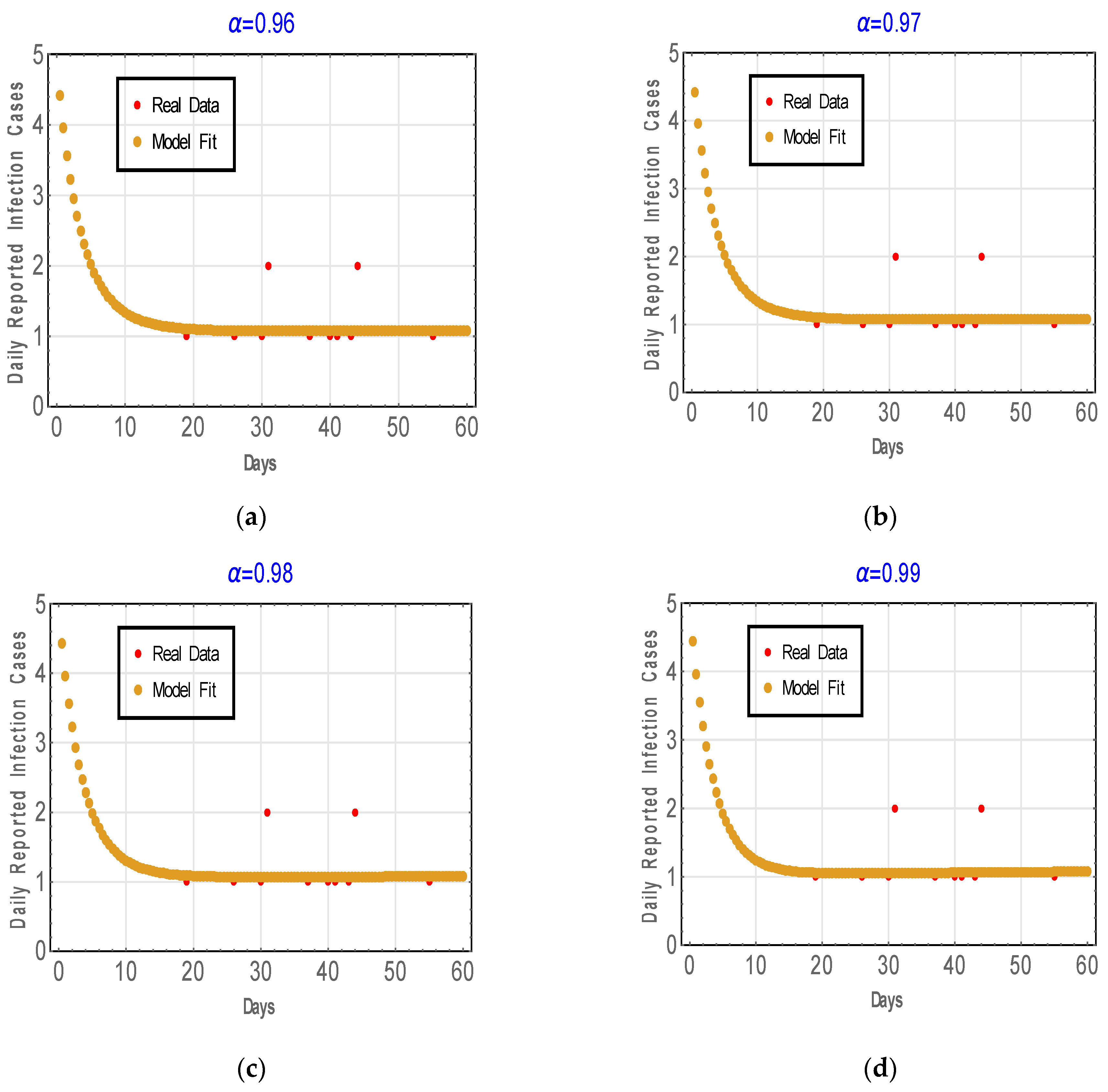
6.2. Fitting Model to Real Data
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- WHO. Available online: https://www.who.int/news-room/fact-sheets/detail/middle-east-respiratory-syndrome-coronavirus-(mers-cov)?gad_source=1&gclid=Cj0KCQjwmMayBhDuARIsAM9HM8c1PPHDJWHIKsKn146_w6EYp7Rnza8cbhHUKd1qO-OcN7KFiOR6Yj8aAkBAEALw_wcB (accessed on 1 August 2024).
- El-Saka HA, A.; Obaya, I.; Lee, S.; Jang, B. Fractional model for Middle East respiratory syndrome coronavirus on a complex heterogeneous network. Sci. Rep. 2022, 12, 24–25. [Google Scholar] [CrossRef] [PubMed]
- Elkholy, A.A.; Grant, R.; Assiri, A.; Elhakim, M.; Malik, M.R.; Van Kerkhove, M.D. MERS-CoV infection among healthcare workers and risk factors for death: Retrospective analysis of all laboratory-confirmed cases reported to WHO from 2012 to 2 June 2018. J. Infect. Public Health 2020, 13, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Al-Asuoad, N.; Rong, L.; Alaswad, S.; Shillor, M. Mathematical model and simulations of MERS outbreak: Predictions and implications for control measures. BIOMATH 2017, 5, 1612141. [Google Scholar] [CrossRef][Green Version]
- Arafa AA, M.; Rida, S.Z.; Khalil, M. Fractional modeling dynamics of HIV and CD4+ T-cells during primary infection. Nonlinear Biomed. Phys. 2012, 6, 1. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Nagy, A.M.; Elfahri, L.E. Fractional-order delayed Salmonella transmission model: A numerical simulation. Progr. Fract. Differ. Appl. 2022, 8, 63–76. [Google Scholar]
- Khalil, M.; Arafa, A.; Sayed, A. On a Fractional Variable-Order Model of MERS-CoV. Prog. Fract. Differ. Appl. 2023, 9, 331–344. [Google Scholar]
- Chechkin, A.V.; Gorenflo, R.; Sokolov, I.M. Fractional diffusion in inhomogeneous media. J. Phys. A. Math. Gen. 2005, 38, L679. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Hadhoud, A.R.; Abd Alaal, F.E.; Abdelaziz, A.A.; Radwan, T. A Cubic Spline Collocation Method to Solve a Nonlinear Space-Fractional Fisher’s Equation and Its Stability Examination. Fractal Fract. 2022, 6, 470. [Google Scholar] [CrossRef]
- Hadhoud, A.R.; Abd Alaal, F.E.; Abdelaziz, A.A. On the numerical investigations of the time-fractional modified Burgers’ equation with conformable derivative, and its stability analysis. J. Math. Comput. Sci. 2021, 12, 36. [Google Scholar]
- Azhar, E.I.; Hui, D.S.C.; Memish, Z.A.; Drosten, C.; Zumla, A. The middle east respiratory syndrome (MERS). Infect. Dis. Clin. 2019, 33, 891–905. [Google Scholar] [CrossRef]
- Chowell, G.; Abdirizak, F.; Lee, S.; Lee, J.; Jung, E.; Nishiura, H.; Viboud, C. Transmission characteristics of MERS and SARS in the healthcare setting: A comparative study. BMC Med. 2015, 13, 210. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. WHO MERS Global Summary and Assessment of Risk; World Health Organization: Geneva, Switzerland, 2019.
- Tahir, M.; Shah SI, A.; Zaman, G.; Khan, T. Stability behaviour of mathematical model MERS corona virus spread in population. Filomat 2019, 33, 3947–3960. [Google Scholar] [CrossRef]
- Tahir, M.; Ali Shah, S.I.; Zaman, G.; Khan, T. A dynamic compartmental mathematical model describing the transmissibility of MERS-CoV virus in public. Punjab Univ. J. Math. 2020, 51, 51–71. [Google Scholar]
- Liang, K. Mathematical model of infection kinetics and its analysis for COVID-19, SARS and MERS. Infect. Genet. Evol. 2020, 82, 104306. [Google Scholar] [CrossRef] [PubMed]
- DarAssi, M.H.; Shatnawi, T.A.M.; Safi, M.A. Mathematical analysis of a MERS-Cov coronavirus model. Demonstr. Math. 2022, 55, 265–276. [Google Scholar] [CrossRef]
- Dighe, A.; Jombart, T.; Van Kerkhove, M.; Ferguson, N. A mathematical model of the transmission of middle East respiratory syndrome coronavirus in dromedary camels (Camelus dromedarius). Int. J. Infect. Dis. 2019, 79, 1. [Google Scholar] [CrossRef]
- Chang, H.J. Estimation of basic reproduction number of the Middle East respiratory syndrome coronavirus (MERS-CoV) during the outbreak in South Korea, 2015. Biomed. Eng. Online 2017, 16, 79. [Google Scholar] [CrossRef]
- Mackay, I.M.; Arden, K.E. MERS coronavirus: Diagnostics, epidemiology and transmission. Virol. J. 2015, 12, 222. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach: London, UK, 1993. [Google Scholar]
- Diethelm, K.; Ford, N.J. The Analysis of Fractional Differential Equations; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2010; Volume 2004. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. The finite difference methods for fractional ordinary differential equations. Numer. Funct. Anal. Optim. 2013, 34, 149–179. [Google Scholar] [CrossRef]
- Gumel, A.B.; Ruan, S.; Day, T.; Watmough, J.; Brauer, F.; Driessche, P.v.D.; Gabrielson, D.; Bowman, C.; Alexander, M.E.; Ardal, S.; et al. Modelling strategies for controlling SARS outbreaks. Proc. R. Soc. B Biol. Sci. 2004, 271, 2223–2232. [Google Scholar] [CrossRef]
- Agarwal, P.; Ramadan, M.A.; Rageh, A.A.M.; Hadhoud, A.R. A fractional-order mathematical model for analyzing the pandemic trend of COVID-19. Math. Methods Appl. Sci. 2022, 45, 4625–4642. [Google Scholar] [CrossRef] [PubMed]
- Rezapour, S.; Mohammadi, H. A study on the AH1N1/09 influenza transmission model with the fractional Caputo–Fabrizio derivative. Adv. Differ. Equ. 2020, 2020, 488. [Google Scholar] [CrossRef]
- Tuan, N.H.; Mohammadi, H.; Rezapour, S. A mathematical model for COVID-19 transmission by using the Caputo fractional derivative. Chaos Solitons Fractals 2020, 140, 110107. [Google Scholar] [CrossRef] [PubMed]
- Burden, R.L.; Faires, J.D. Numerical Analysis, 8th ed.; Thomson Brooks/Cole: Belmont, CA, USA, 2005. [Google Scholar]
- Hadhoud, A.R.; Alaal, F.E.A.; Abdelaziz, A.A.; Radwan, T. Numerical treatment of the generalized time—Fractional Huxley—Burgers’ equation and its stability examination. Demonstr. Math. 2021, 54, 436–451. [Google Scholar] [CrossRef]
- Hadhoud, A.R.; Gaafar, F.M.; Alaal, F.E.A.; Abdelaziz, A.A.; Boulaaras, S.; Radwan, T. A Robust Collocation Method for Time Fractional PDEs Based on Mean Value Theorem and Cubic B-Splines. Partial Differ. Equ. Appl. Math. 2024, in press. [Google Scholar] [CrossRef]
- MacroTrends. Available online: https://www.macrotrends.net/globalmetrics/cities/22432/riyadh/population#google_vignette (accessed on 1 August 2024).
- Van Kerkhove, M.D.; Alaswad, S.; Assiri, A.; Perera, R.A.; Peiris, M.; El Bushra, H.E.; BinSaeed, A.A. Transmissibility of MERS-CoV infection in closed setting, Riyadh, Saudi Arabia, 2015. Emerg. Infect. Dis. 2019, 25, 1802–1809. [Google Scholar] [CrossRef]



| Parameter | Parameter Value | Unit | Source |
|---|---|---|---|
| 1/day | Nofe et al. [4] | ||
| 1/day | Estimated | ||
| 1/day | Nofe et al. [4] | ||
| 1/day | Nofe et al. [4] | ||
| 1/day | Nofe et al. [4] | ||
| 1/day | Nofe et al. [4] | ||
| 1/day | Nofe et al. [4] | ||
| - | Nofe et al. [4] | ||
| - | Nofe et al. [4] | ||
| 1/day | Nofe et al. [4] | ||
| individual/day | Nofe et al. [4] |
| MVM | ITM | MVM | ITM | MVM | ITM | |
|---|---|---|---|---|---|---|
| MVM | ITM | MVM | ITM | MVM | ITM | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | |
| MVM | ITM | MVM | ITM | MVM | ITM | |
|---|---|---|---|---|---|---|
| 10 | 10 | 10 | 10 | 10 | 10 | |
| MVM | ITM | MVM | ITM | MVM | ITM | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | |
| MVM | ITM | MVM | ITM | MVM | ITM | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | |
| Day | Reported MERS Cases |
|---|---|
| 19 September 2015 | |
| 26 September 2015 | |
| 30 September 2015 | |
| 1 October 2015 | |
| 7 October 2015 | |
| 10 October 2015 | |
| 11 October 2015 | |
| 13 October 2015 | |
| 14 October 2015 | |
| 22 October 2015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd Alaal, F.E.; Hadhoud, A.R.; Abdelaziz, A.A.; Radwan, T. On the Numerical Investigations of a Fractional-Order Mathematical Model for Middle East Respiratory Syndrome Outbreak. Fractal Fract. 2024, 8, 521. https://doi.org/10.3390/fractalfract8090521
Abd Alaal FE, Hadhoud AR, Abdelaziz AA, Radwan T. On the Numerical Investigations of a Fractional-Order Mathematical Model for Middle East Respiratory Syndrome Outbreak. Fractal and Fractional. 2024; 8(9):521. https://doi.org/10.3390/fractalfract8090521
Chicago/Turabian StyleAbd Alaal, Faisal E., Adel R. Hadhoud, Ayman A. Abdelaziz, and Taha Radwan. 2024. "On the Numerical Investigations of a Fractional-Order Mathematical Model for Middle East Respiratory Syndrome Outbreak" Fractal and Fractional 8, no. 9: 521. https://doi.org/10.3390/fractalfract8090521
APA StyleAbd Alaal, F. E., Hadhoud, A. R., Abdelaziz, A. A., & Radwan, T. (2024). On the Numerical Investigations of a Fractional-Order Mathematical Model for Middle East Respiratory Syndrome Outbreak. Fractal and Fractional, 8(9), 521. https://doi.org/10.3390/fractalfract8090521







