Inverse Scattering Integrability and Fractional Soliton Solutions of a Variable-Coefficient Fractional-Order KdV-Type Equation
Abstract
1. Introduction
2. The vcfKdV-Type Equation and Anomalous Dispersion Relation
3. IST for the vcfKdV-Type Equation
3.1. The Direct Scattering Problem
3.2. Time Dependences of the Scattering Data
3.3. Reconstruction of Potential
4. Explicit Form of the vcfKdV-Type Equation
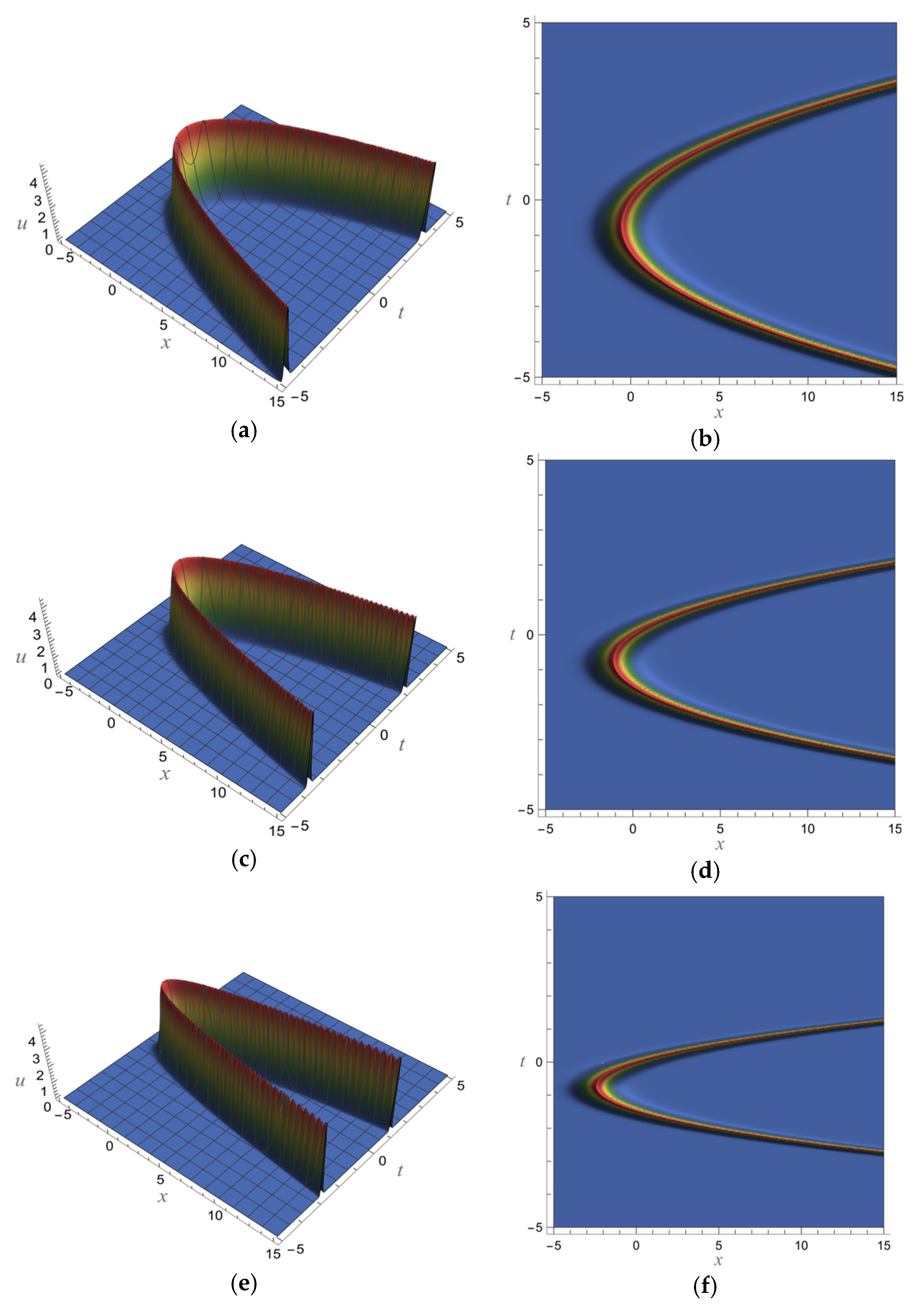
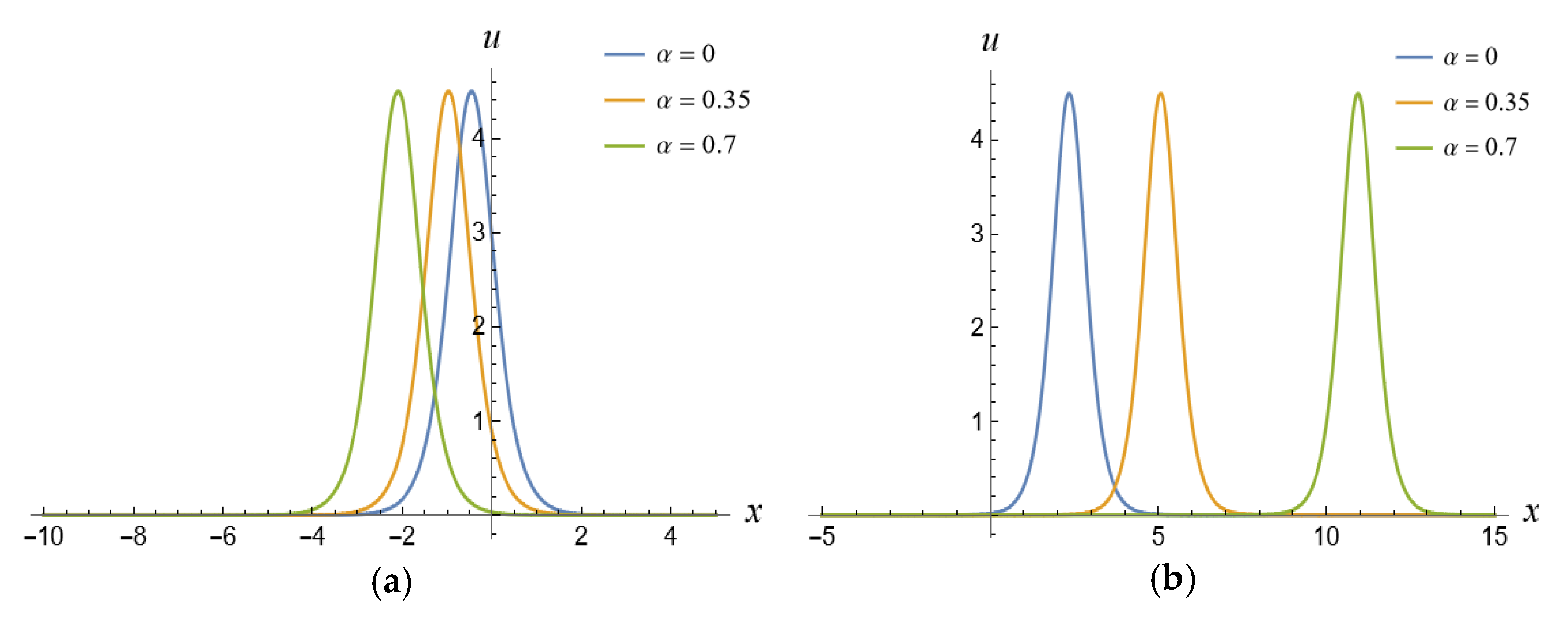
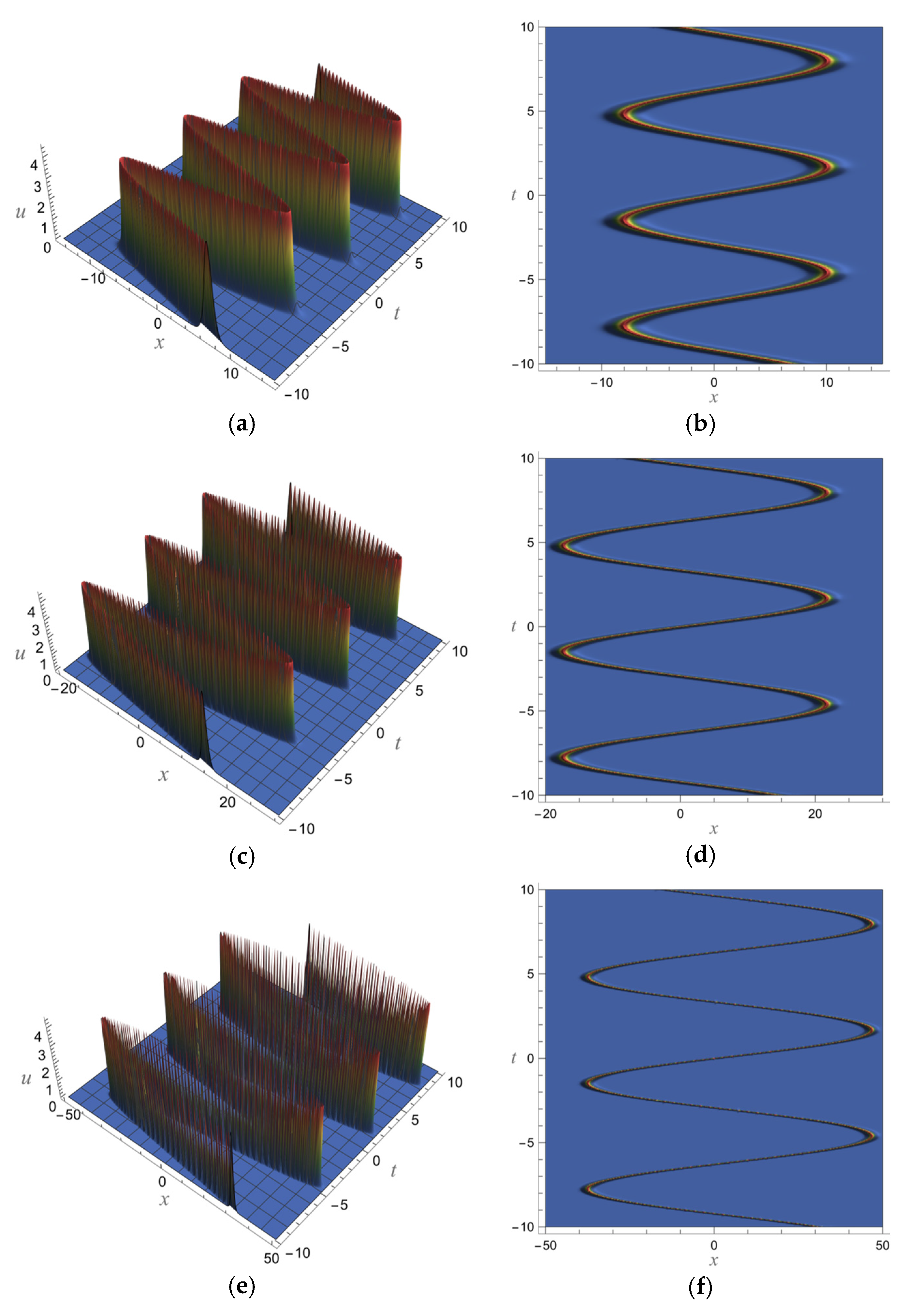
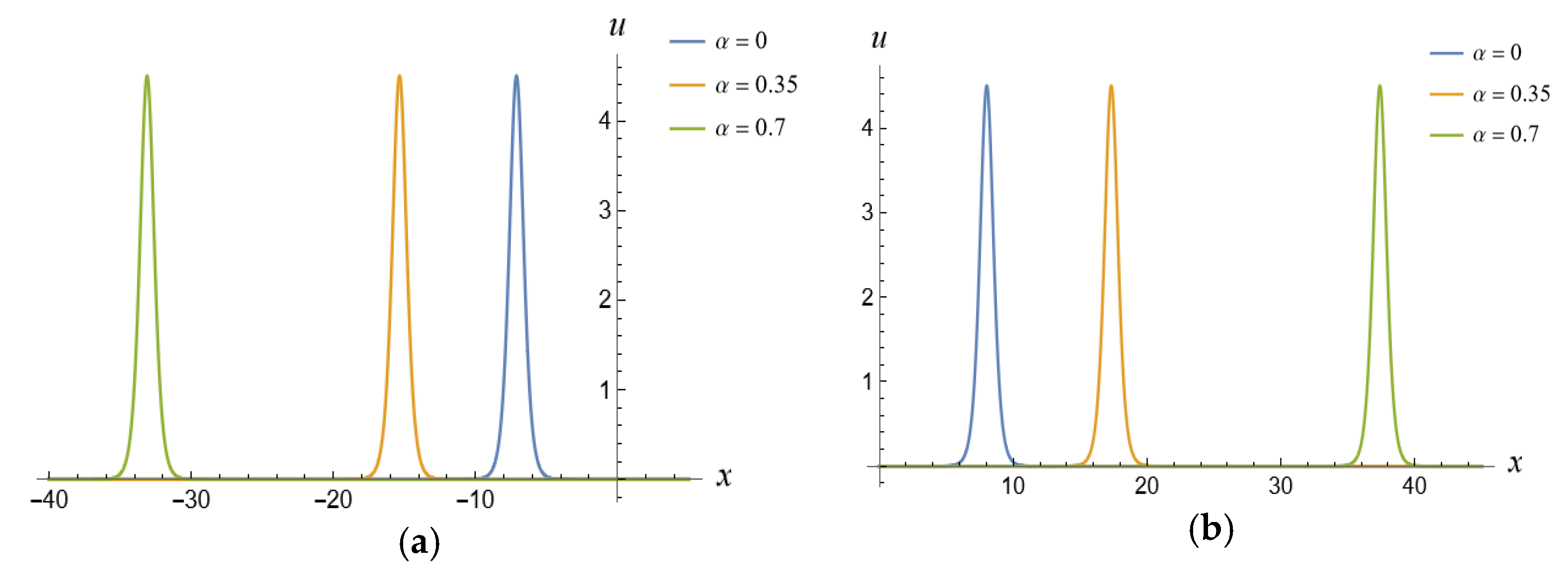
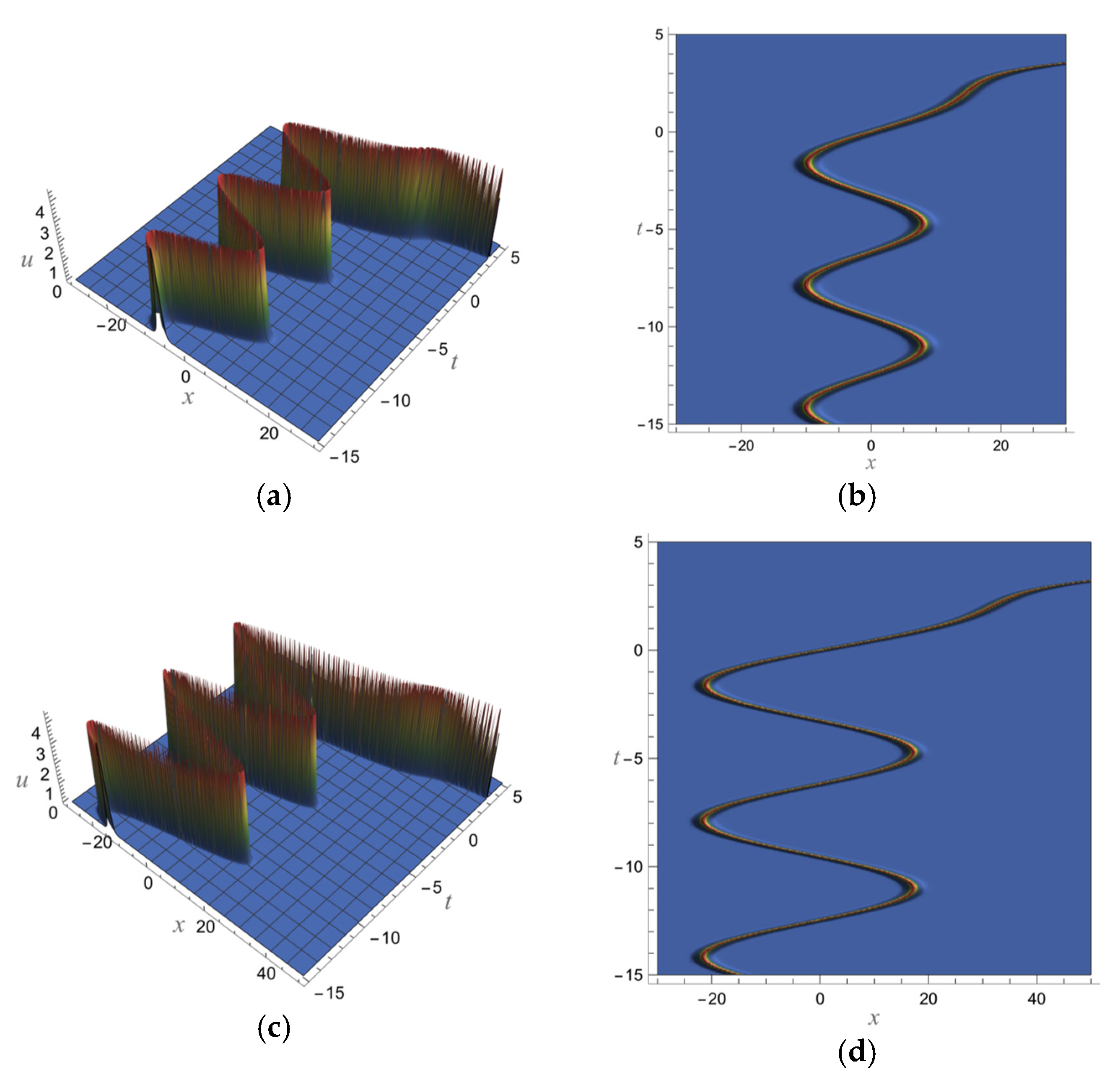
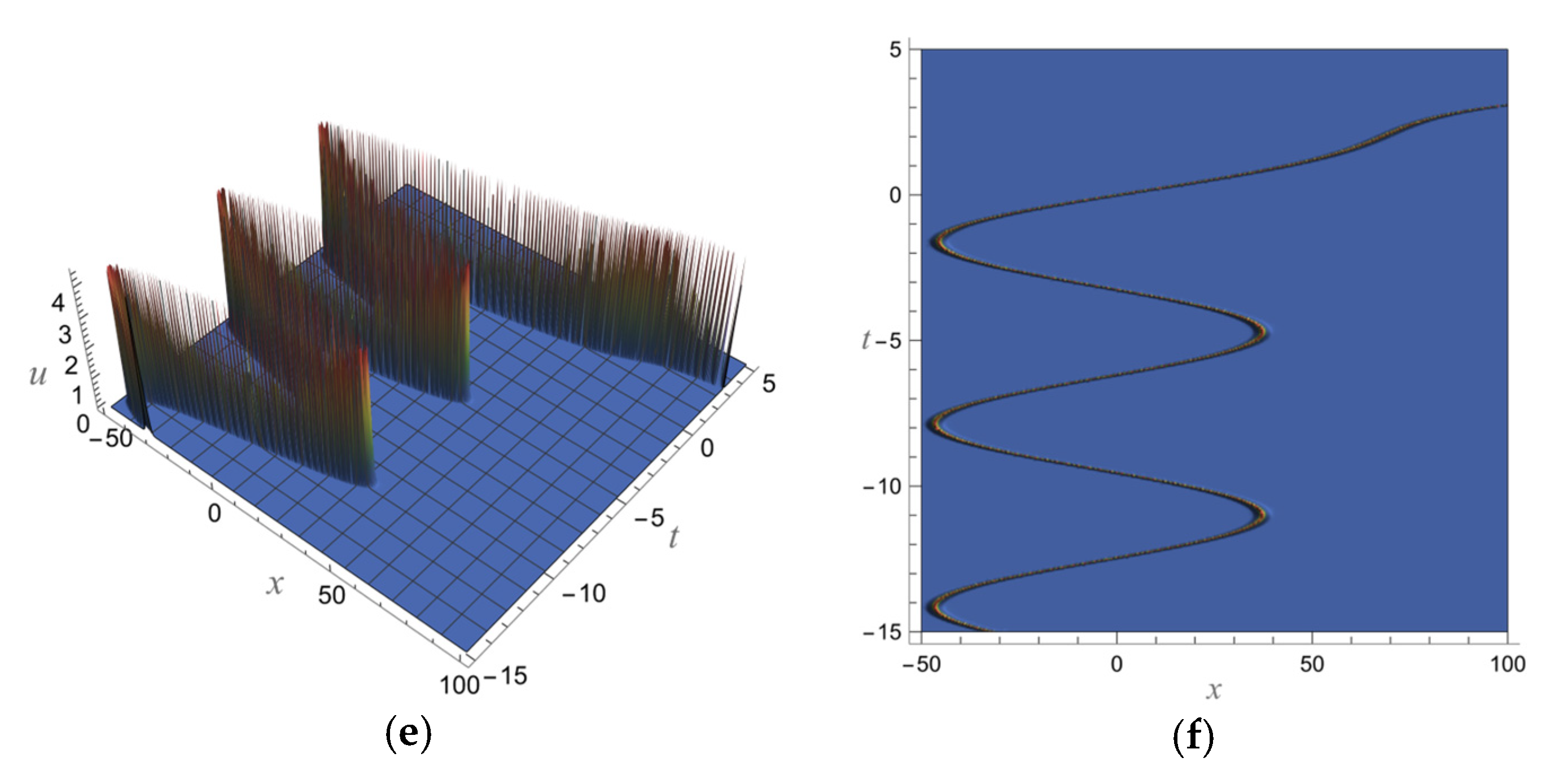
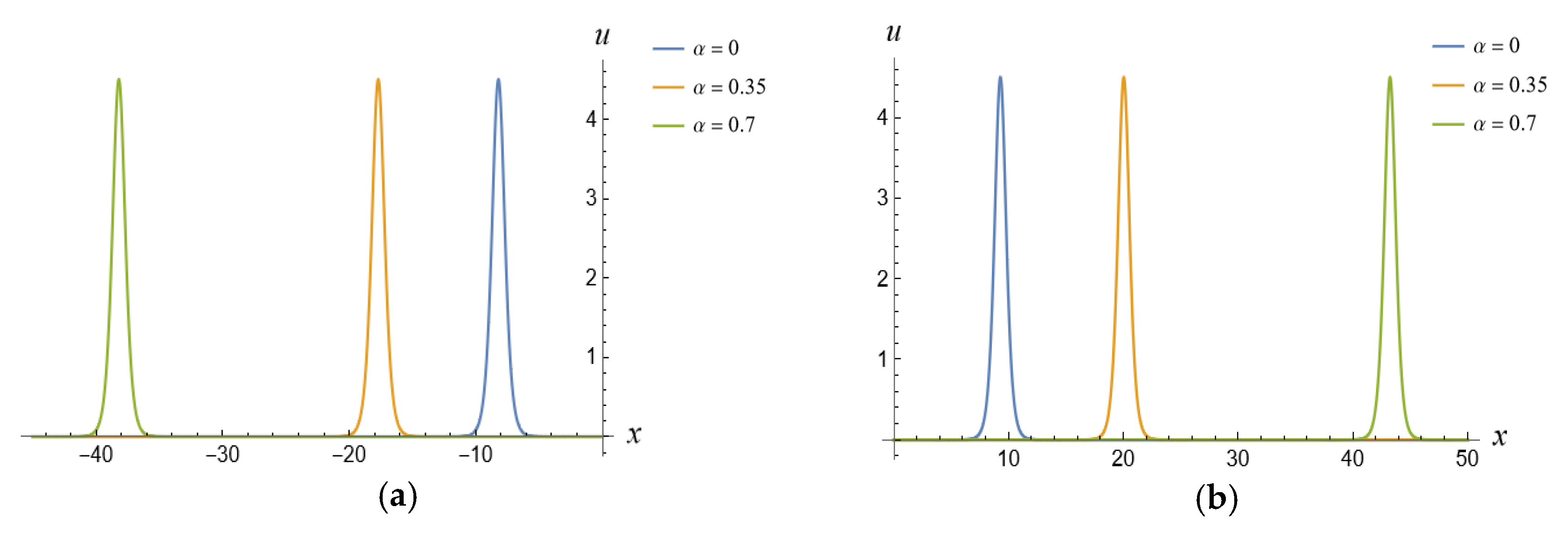
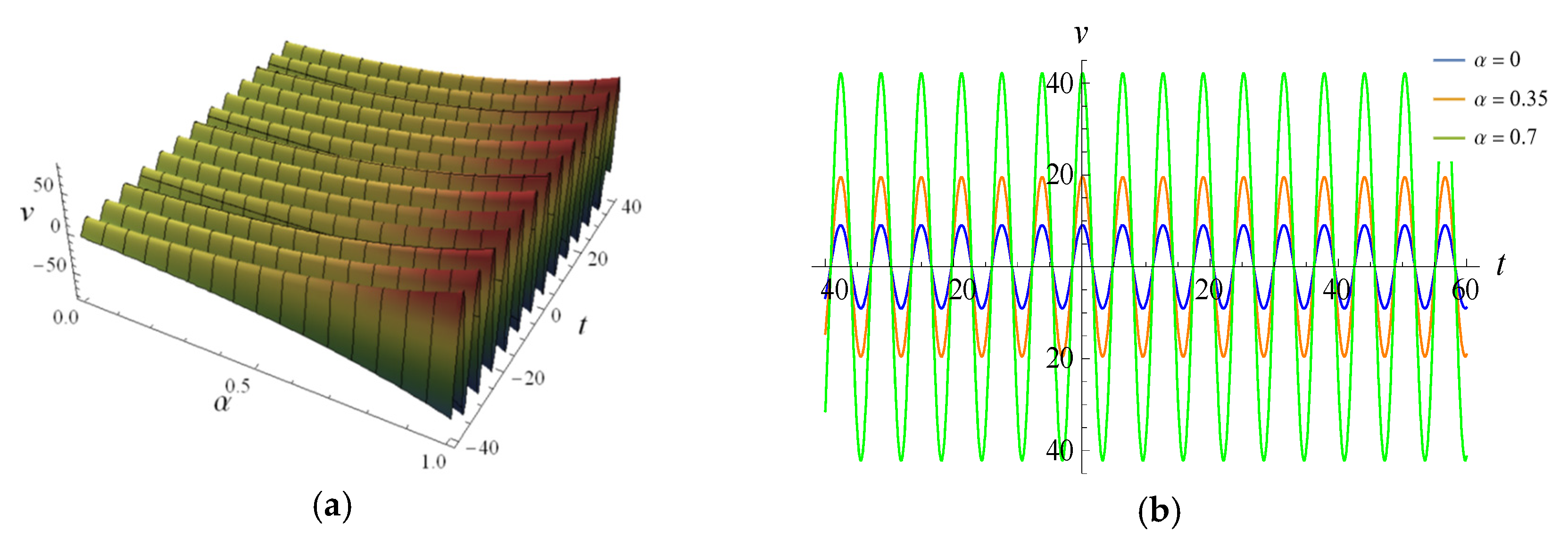
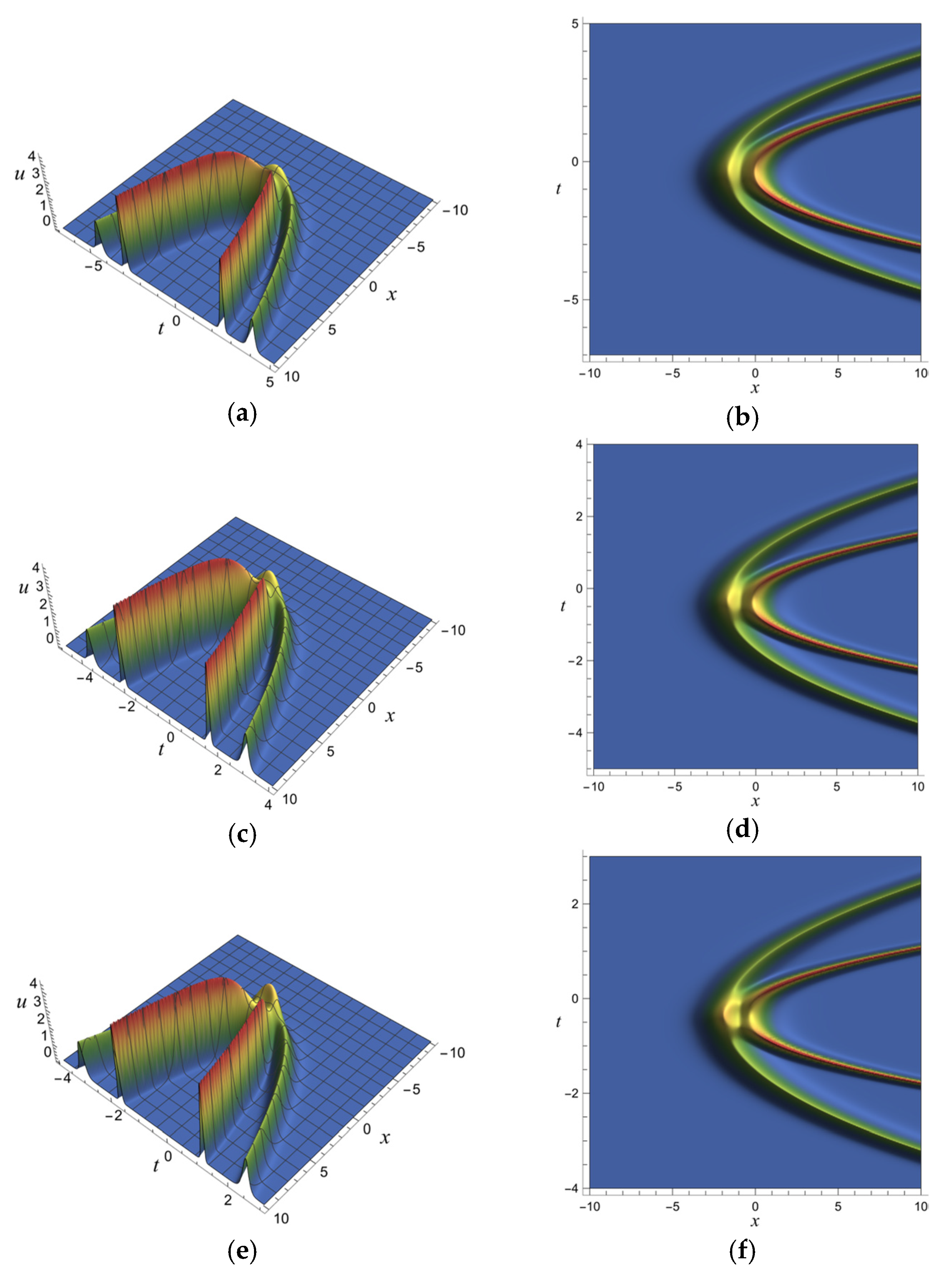
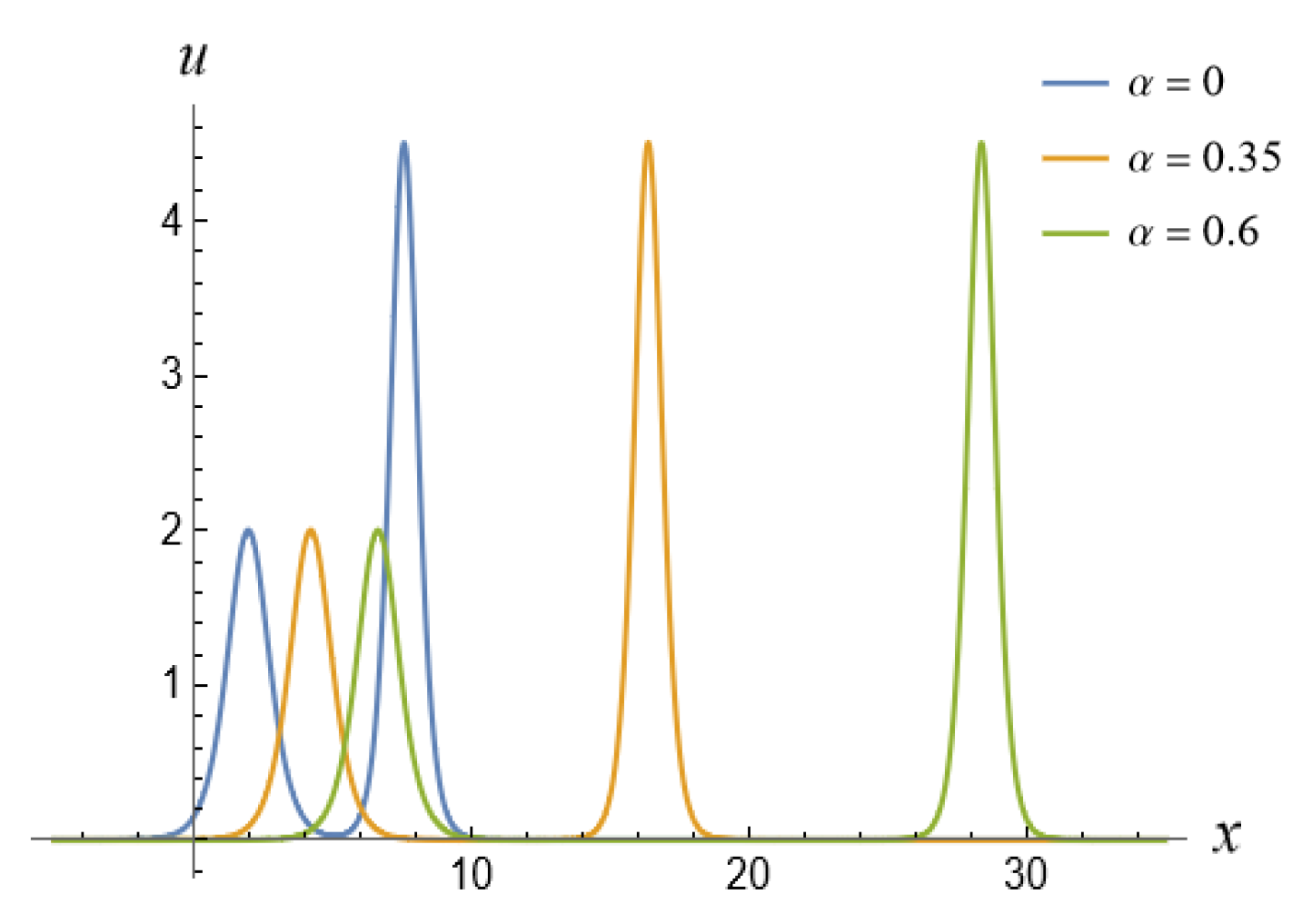
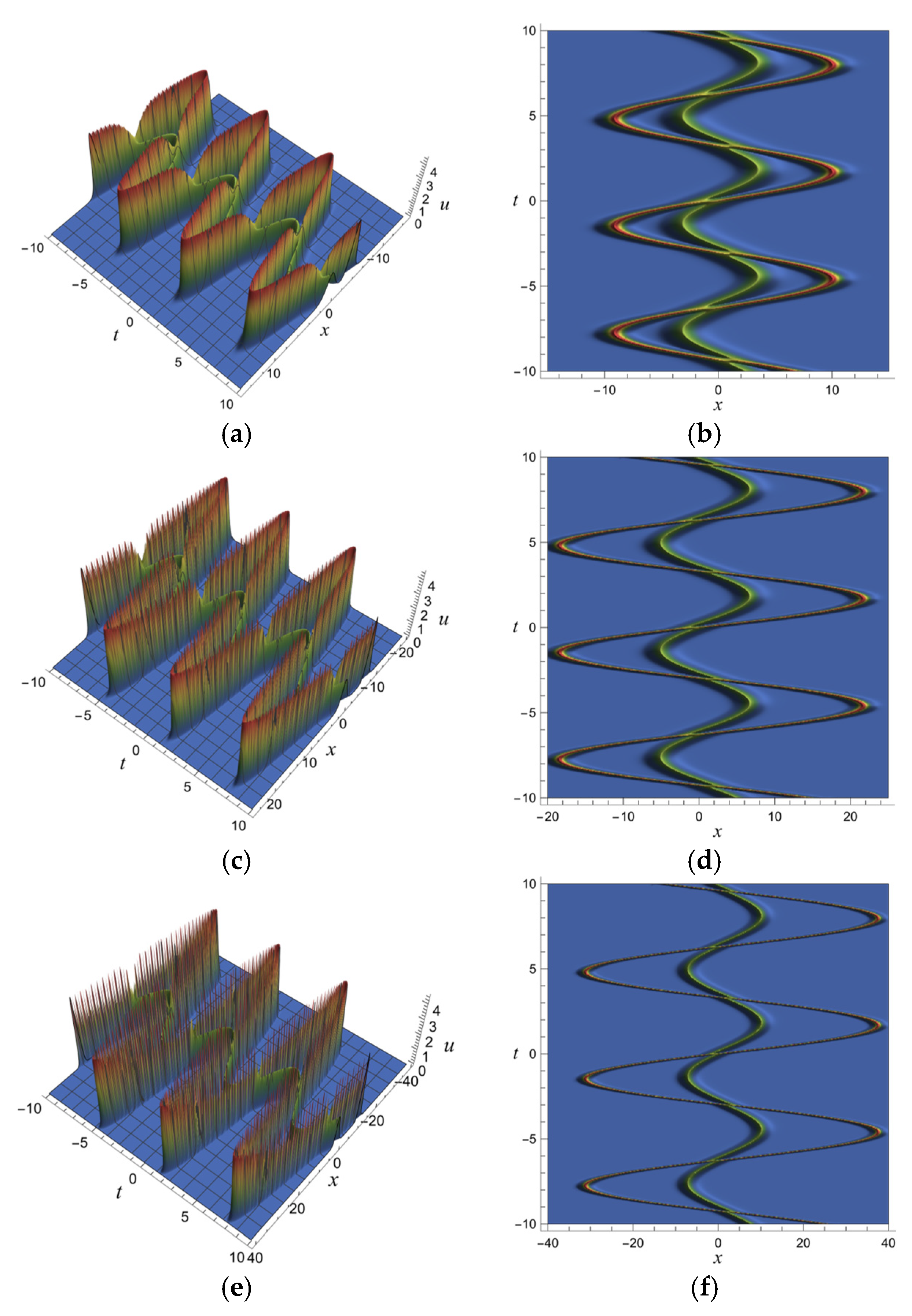
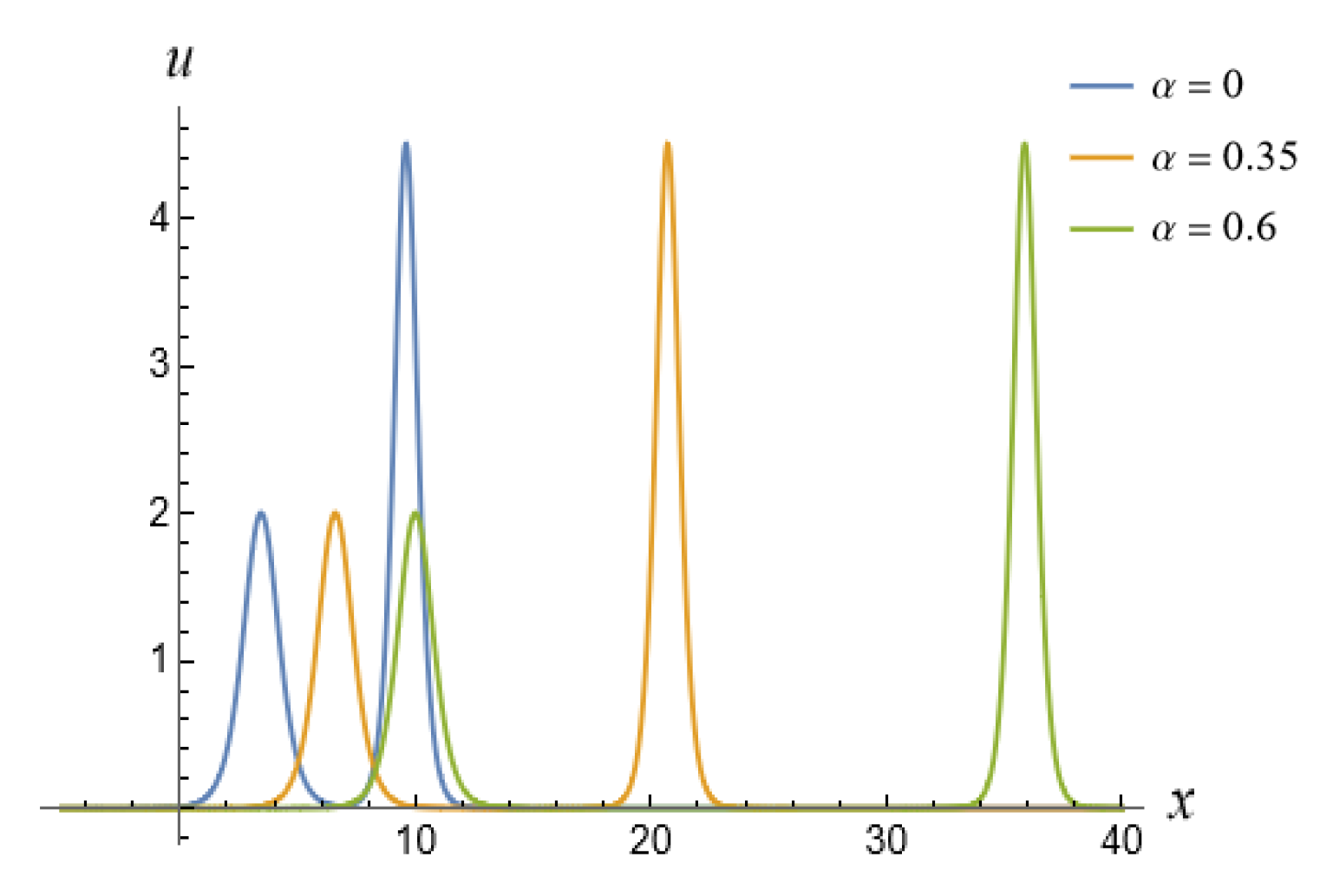
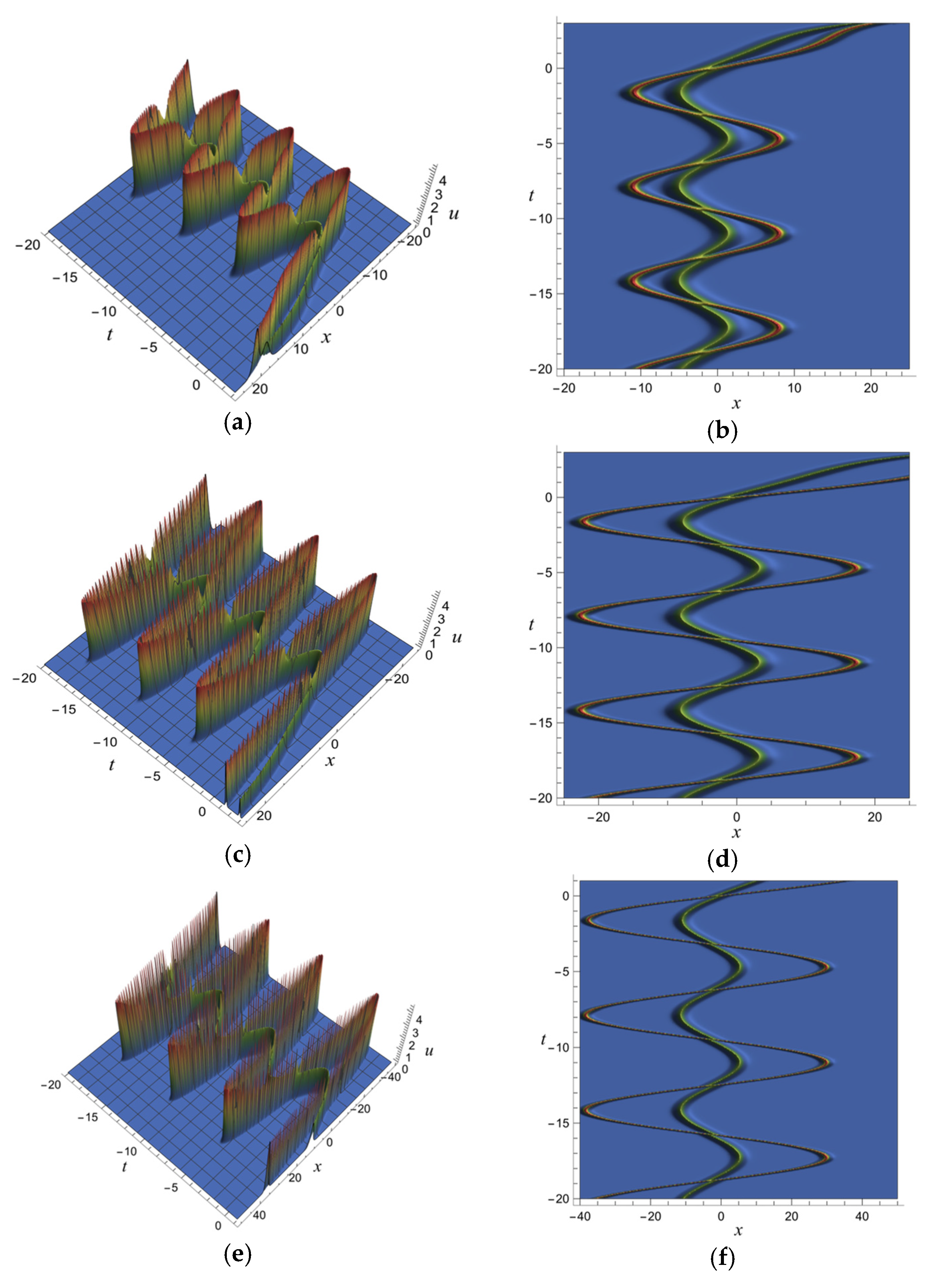
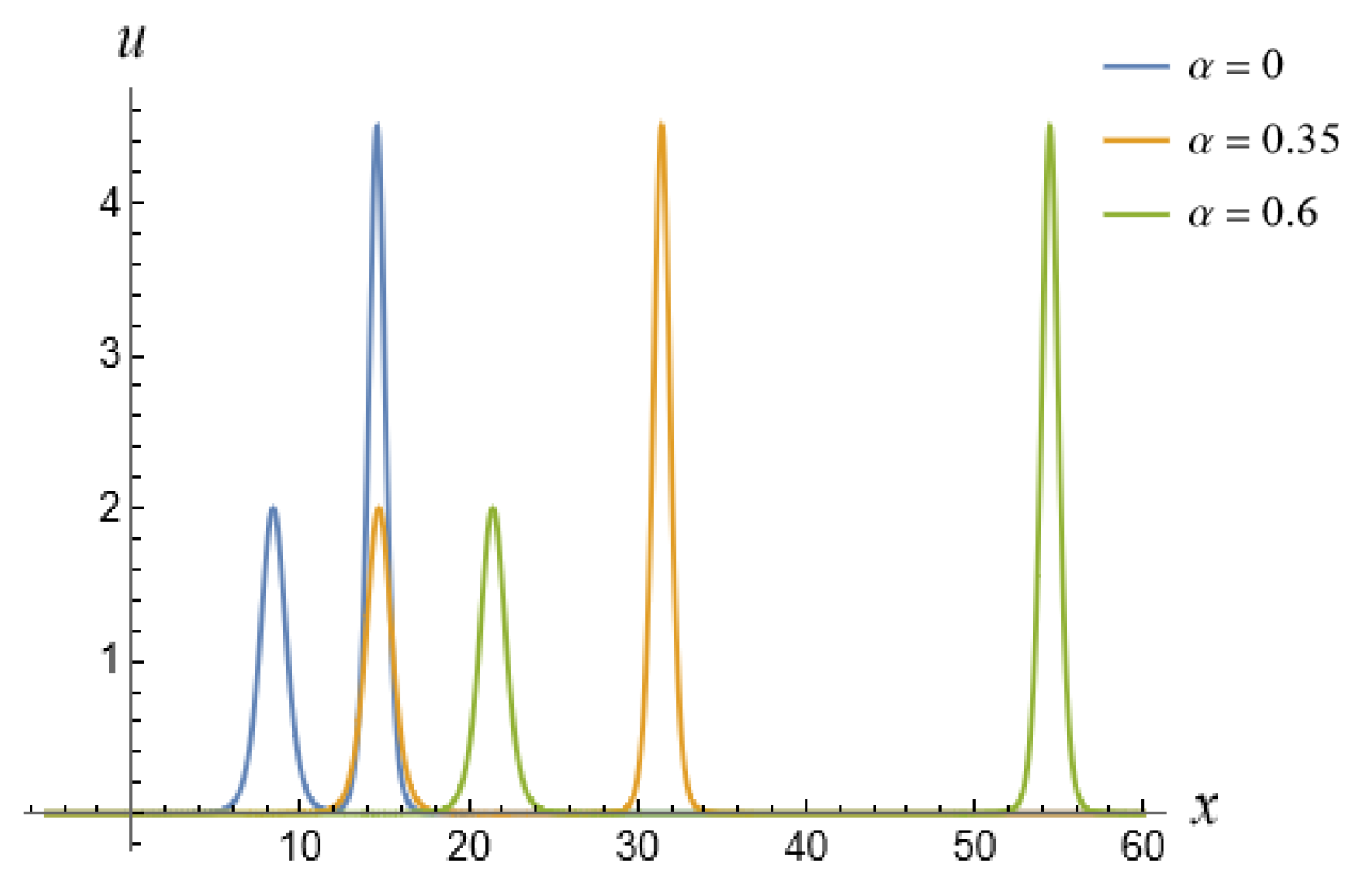
5. Fractional Soliton Solutions of the vcfKdV-Type Equation
5.1. One-Soliton Solution of the vcfKdV-Type Equation
5.2. Two-Soliton Solutions of the vcfKdV-Type Equation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteweg–deVries equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. The inverse scattering transform––Fourier analysis for nonlinear problems. Stud. Appl. Math. 1974, 53, 249–315. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: New York, NY, USA, 1991; pp. 24–346. [Google Scholar]
- Hirota, R. Exact envelope-soliton solutions of a nonlinear wave equation. J. Math. Phys. 1973, 14, 805–809. [Google Scholar] [CrossRef]
- Matveev, V.B.; Salle, M.A. Darboux Transformation and Soliton; Springer: Berlin/Heidelberg, Germany, 1991; pp. 7–106. [Google Scholar]
- Wadati, M. The modified Korteweg–de Vries equation. J. Phys. Soc. Jpn. 1973, 34, 1289–1296. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Shabat, A.B. Exact theory of two-dimensional self-focusing and onedimensional self-modulation of waves in nonlinear media. J. Exp. Theor. Phys. 1972, 34, 62–69. [Google Scholar]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. Method for solving the sine-Gordon equation. Phys. Rev. Lett. 1973, 30, 1262–1264. [Google Scholar] [CrossRef]
- Flaschka, H. On the Toda lattice. II. Inverse-scattering solution. Prog. Theor. Phys. 1974, 51, 703–716. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Ablowitz, M.J. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons; Cambridge University Press: New York, NY, USA, 2011; pp. 261–312. [Google Scholar]
- Bronski, J.C.; Carr, L.D.; Deconinck, B.; Kutz, J.N. Bose-Einstein condensates in standing waves: The cubic nonlinear Schrödinger equation with a periodic potential. Phys. Rev. Lett. 2001, 86, 1402–1405. [Google Scholar] [CrossRef]
- Boardman, A.; Wang, Q.; Nikitov, S.; Shen, J.S.; Chen, W.; Mills, D.; Bao, J. Nonlinear magnetostatic surface waves in ferromagnetic films. IEEE Trans. Magn. 1994, 30, 14–22. [Google Scholar] [CrossRef]
- Shlesinger, M.F.; West, B.J.; Klafter, J. L’evy dynamics of enhanced diffusion: Application to turbulence. Phys. Rev. Lett. 1987, 58, 1100–1103. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- West, B.J.; Grigolini, P.; Metzler, R.; Nonnenmacher, T.F. Fractional diffusion and L’evy stable processes. Phys. Rev. E 1997, 55, 99–106. [Google Scholar] [CrossRef]
- Wang, W.; Cherstvy, A.G.; Chechkin, A.V.; Thapa, S.; Seno, F.; Liu, X.; Metzler, R. Fractional Brownian motion with random diffusivity: Emerging residual nonergodicity below the correlation time. J. Phys. A Math. Theor. 2020, 53, 474001. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Been, J.B.; Carr, L.D. Fractional integrable nonlinear soliton equations. Phys. Rev. Lett. 2022, 128, 184101. [Google Scholar] [CrossRef]
- Ablowitz, M.; Been, J.; Carr, L. Integrable fractional modified Korteweg–de Vries, sine-Gordon, and sinh-Gordon equations. J. Phys. A Math. Theor. 2022, 55, 384010. [Google Scholar] [CrossRef]
- Riesz, M. L’intégrale de Riemann–Liouville et le probléme de Cauchy. Acta Math. 1949, 81, 1–222. [Google Scholar] [CrossRef]
- Cai, M.; Li, C.P. On Riesz derivative. Fract. Calc. Appl. Anal. 2019, 22, 287–301. [Google Scholar] [CrossRef]
- Weng, W.F.; Zhang, M.H.; Zhang, G.Q.; Yan, Z.Y. Dynamics of fractional N-soliton solutions with anomalous dispersions of integrable fractional higher-order nonlinear Schrödinger equations. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 123110. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.H.; Weng, W.F.; Yan, Z.Y. Interactions of fractional N-solitons with anomalous dispersions for the integrable combined fractional higher-order mKdV hierarchy. Phys. D 2023, 444, 133614. [Google Scholar] [CrossRef]
- Mou, D.S.; Dai, C.Q.; Wang, Y.Y. Integrable fractional n-component coupled nonlinear Schrödinger model and fractional n-soliton dynamics. Chaos Solitons Fractals 2023, 171, 113451. [Google Scholar] [CrossRef]
- An, L.; Ling, L.M.; Zhang, X.E. Nondegenerate solitons in the integrable fractional coupled Hirota equation. Phys. Lett. A 2023, 460, 128629. [Google Scholar] [CrossRef]
- Chen, D.Y. Introduction of Soliton; Science Press: Beijing, China, 2006. [Google Scholar]
- Meerschaert, M.M.; Sikorskii, A. Stochastic Models for Fractional Calculus; Walter de Gruyter GmbH & Co. KG: Berlin/Boston, Germany, 2011. [Google Scholar]
- De Pablo, A.; Quirós, F.; Rodríguez, A.; Vázquez, J.L. A fractional porous medium equation. Adv. Math. 2011, 226, 1378–1409. [Google Scholar] [CrossRef]
- Constantin, P.; Wu, J.H. Behavior of solutions of 2D quasigeostrophic equations. SIAM J. Math. Anal. 1999, 30, 937–948. [Google Scholar] [CrossRef]
- Holm, S. Waves with Power-Law Attenuation; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Pozrikidis, C. The Fractional Laplacian; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Bucur, C.; Valdinoci, E. Nonlocal Diffusion and Applications; Springer Nature: Cham, Switzerland, 2016. [Google Scholar]
- Carrillo, J.A.; Manresa, M.D.P.; Figalli, A.; Mingione, G.; Vázquez, J.L. Nonlocal and Nonlinear Diffusions and Interactions: New Methods and Directions; Springer Nature: Cham, Switzerland, 2017. [Google Scholar]
- Zhang, S.; Gao, X.D. Exact N-soliton solutions and dynamics of a new AKNS equation with time-dependent coefficients. Nonlinear Dyn. 2016, 83, 1043–1052. [Google Scholar] [CrossRef]
- Zhu, J.M.; Zheng, C.L.; Ma, Z.Y. A general mapping approach and new travelling wave solutions to the general variable coefficient KdV equation. Chin. Phys. 2004, 13, 2008–2012. [Google Scholar]
- Li, Y.S. Solitons and Integrable Systems; Shanghai Science and Technology Education Press: Shanghai, China, 1999. [Google Scholar]
- Sachs, R.L. Completeness of derivatives of squared Schrödinger eigenfunctions and explicit solutions of the linearized KdV equation. SIAM J. Math. Anal. 1983, 14, 674–683. [Google Scholar] [CrossRef]





| Time | ||
|---|---|---|
| 1 | 7.25164 × 10–4 | 1.45336 × 10–2 |
| 2 | 1.14268 × 10–3 | 2.29014 × 10–2 |
| 3 | 1.5602 × 10–3 | 3.12692 × 10–2 |
| 4 | 1.97772 × 10–3 | 3.69371 × 10–2 |
| 5 | 2.39254 × 10–3 | 4.80049 × 10–2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Li, H.; Xu, B. Inverse Scattering Integrability and Fractional Soliton Solutions of a Variable-Coefficient Fractional-Order KdV-Type Equation. Fractal Fract. 2024, 8, 520. https://doi.org/10.3390/fractalfract8090520
Zhang S, Li H, Xu B. Inverse Scattering Integrability and Fractional Soliton Solutions of a Variable-Coefficient Fractional-Order KdV-Type Equation. Fractal and Fractional. 2024; 8(9):520. https://doi.org/10.3390/fractalfract8090520
Chicago/Turabian StyleZhang, Sheng, Hongwei Li, and Bo Xu. 2024. "Inverse Scattering Integrability and Fractional Soliton Solutions of a Variable-Coefficient Fractional-Order KdV-Type Equation" Fractal and Fractional 8, no. 9: 520. https://doi.org/10.3390/fractalfract8090520
APA StyleZhang, S., Li, H., & Xu, B. (2024). Inverse Scattering Integrability and Fractional Soliton Solutions of a Variable-Coefficient Fractional-Order KdV-Type Equation. Fractal and Fractional, 8(9), 520. https://doi.org/10.3390/fractalfract8090520







