Abstract
We extend two KdVSKR models to fractional KdVSKR models with the Caputo derivative. The KdVSKR equation in (2+1)-dimension, which is a recent extension of the KdVSKR equation in (1+1)-dimension, can model the soliton resonances in shallow water. Applying the Hirota bilinear method, finite symmetry group method, and consistent Riccati expansion method, many new interaction solutions have been derived. Soliton and elliptical function interplaying solution for the fractional KdVSKR model in (1+1)-dimension has been derived for the first time. For the fractional KdVSKR model in (2+1)-dimension, two-wave interaction solutions and three-wave interaction solutions, including dark-soliton-sine interaction solution, bright-soliton-elliptic interaction solution, and lump-hyperbolic-sine interaction solution, have been derived. The effect of the order on the dynamical behaviors of the solutions has been illustrated by figures. The three-wave interaction solution has not been studied in the current references. The novelty of this paper is that the finite symmetry group method is adopted to construct interaction solutions of fractional nonlinear systems. This research idea can be applied to other fractional differential equations.
1. Introduction
In recent decades, fractional nonlinear systems have developed into effective mathematical tools to describe real-world problems with the rapid development of fractional calculus. Fractional differential equations (FDEs) have been widely used in many fields, such as economics and finance [1,2], epidemiology of disasters [3,4], physics [5,6,7,8], engineering [9], and so on. To better model practical problems, different fractional derivatives have been defined and applied, such as Riemann-Liouville [10,11], Caputo [12], modified Riemann-Liouville [13], Atangana-Baleanu derivative [14], and so on [15]. For further information on the fractional derivatives, readers can refer to [10,11,12].
Since FDEs play an important role in expressing practical problems mathematically, the extraction of exact solutions for these FDEs is imperative. Exact solutions of the governing FDEs can be used to verify the accuracy of the numerical solution [16]. In addition, exact solutions are significant for a more profound understanding of many physical phenomena. For example, the coactions of water waves observed in shallow water are often described by interaction solutions of different functions [17,18]. In recent decades, many effective algorithms, such as the Lie symmetry method [5,19,20,21,22,23], fractional auxiliary equation method [24,25,26], -expansion method [27], exp-function method [28], the modified extended direct algebraic method [29], the trial equation method [30], and many more [31,32], have been presented to extract analytical solutions of FDEs. Among those, the fractional complex transform is often used to change FDEs into integer order systems [6]. Therefore, methods which are used to solve PDEs, such as the Bernoulli sub-equation function method [33], Hirota bilinear method (HBM) [34], finite symmetry group method (FSGM) [35], Exp (−ϕ(η)) expansion method [36], consistent Riccati expansion method (CREM) [37,38], and so on, can be applied to solve FDEs.
The HBM was first proposed by Hirota in 1971 [34]. For almost all nonlinear PDEs, the HBM is very effective in exploring explicit soliton excitation solutions, including lump, breather, and soliton molecules. These solutions are very beneficial in explaining physical problems better. Several fractional partial differential equations (PDEs) have been exactly solved by combining the fractional complex transform and the HBM [39,40,41,42]. The finite symmetry group method (FSGM) was proposed by Lou in 2005, which is a direct method used to find finite symmetry groups of PDEs [35]. By the FSGM, we can obtain the relationship between the known solutions and new solutions. Recently, the CREM has been proposed to find soliton or soliton–elliptical interaction solutions [37,38]. The CREM has been applied to many PDEs, for example, the KdV equation, SK equation, KP equation, and so on [37,38]. To our knowledge, the FSGM and CREM have not been applied to derive interaction solutions for FDEs. The new contribution of this paper is that we will use the FSGM and CREM to extract new interaction solutions for FDEs.
The research objects are the (1+1)-dimensional fractional Korteweg-de Vries-Sawada-Kotera-Ramani (FKdVSKR) equation
and the (2+1)-dimensional FKdVSKR equation
where is the Caputo time-fractional derivative [12], , is a constant, and and are both constants. As for the fractional derivatives of time, the value of at some time is dependent upon the value of at all the times preceding that time, so the time-fractional derivative is easier to express the memory and inheritance effect. Equations (1) and (2) are shallow water wave models and have critical applications in describing the interactions of water waves. For example, y-shaped waves have been observed recently in the Qiantang River in China, which are interaction waves of two large tides. In the field of mathematical physics, y-shaped waves correspond to y-type solutions, which are resonances of solitons and include fission solutions and fusion solutions.
FKdVSKR Equations (1) and (2) include a lot of KdV-type equations as their particular cases. When (1) becomes the KdV model
When (1) becomes the well-known Sawada–Kotera (SK) equation
When (1) is the (1+1)-dimensional KdVSKR equation [43,44,45,46,47,48,49]
which is also named the KdV-SK equation [46] or extended KdV equation [48,49].
Soliton molecules and an asymmetric soliton for (3) are obtained in [43] using the condition of velocity resonance. Finite symmetry groups of (3) are also obtained [43]. Lie symmetry, optimal system, symmetry reductions, power series solutions, and the N-soliton solution of (3) are derived in [44]. Quasi-periodic solutions of (3) are studied in [45] by a new method. A Kaup-Kupershmidt soliton wave solution has been obtained in [46]. The authors in [46] regard (3) as the higher-order KdV equation, or the KdV-SK equation. Soliton-cnoidal solutions of (3) have been obtained by the CREM [47]. For the variable-coefficient KdVSKR equation, rational function solutions, and multi-wave solutions have been derived by a generalized unified method [48]. We should point out that all the above work is on (3), and it is the first time that FKdVSKR equation (1) has been researched.
When (2) becomes the integrable Sawada–Kotera (SK) equation [50]
When (2) becomes the (2+1)-dimensional KdVSKR equation
which has been proposed recently; by generalizing (3) to direction, this may model the resonances of solitons in shallow water [51]. In Refs. [51,52,53,54,55], the authors study soliton excitations or interaction solutions of (4) based on the HBM. The long wave limit method has been adopted to obtain interaction solutions between the lump and solitons of (4) [51]. The velocity resonance mechanism is employed to find localized excitation solutions of (4) [52]. In [53], the fission solutions and fusion solutions of (4) are studied. The dynamic behaviors of two different molecules are also illustrated. In Ref. [54], a new condition has been presented to show the interactions between a lump soliton and other excitations. Several interaction solutions between lump and other functions have been obtained by choosing appropriate functions in the bilinear form [55]. In Ref. [56], Painlevé analysis, Lie point symmetry and symmetry reductions for (4) have been studied. As far as we know, no more studies have been carried out on (4). Therefore, CREM and FSGM have not been applied to the KdVSKR equation in (2+1)-dimension.
The following is the framework of this paper. We construct novel explicit solutions of (1) by the fractional complex transform and the known solutions in Section 2. In Section 3, we construct novel analytical solutions of (2) using the CREM and fractional complex transform. In Section 4, explicit solutions of (2) will be found by the fractional complex transform and FSGM. We will generate new solutions from the known ones. New interaction solutions will be derived. Section 5 is arranged to discuss the results and methods used in this paper. Some conclusions and future work of the paper are explained in the last section.
2. Exact Solutions of (1)
According to the fractional complex transform, we set
Substituting (5) into (1), we have the following KdVSKR equation in (1+1)-dimension [43,44,45,46,47,48,49,55]
In fact, (6) and (3) are exactly the same if we ignore the difference between and . Works on (6) have been analyzed in the Introduction. Because of simplicity and directness, the HBM is used frequently to seek significative solutions of a given PDE. A critical step in applying the HBM is converting a PDE to its bilinear form by the following transformation.
(6) can be converted into its bilinear form
where is the bilinear operator concerning and is the bilinear operator concerning
2.1. Soliton Solutions
KdVSKR Equation (6) has an N-order soliton solution as follows:
where and are arbitrary constants , is the sum of every possible pair under the restriction is a sum of total pairs of
2.1.1. One-Soliton Solution
When (6) has a single-soliton solution
and the fractional one-soliton solution for the FKdVSKR model (1) is
Graphs (a), (b), and (c) in Figure 1 illustrate the dynamical behaviors of (8) with different when taking Graph (d) in Figure 1 shows the relative locations for a different fractional order parameter at The effect of on the dynamical behaviors of (8) can be observed. The larger is , the more backward the soliton is; the smaller is , the more forward the solution is. Interestingly, the fractional soliton solution for the KMM system is just the opposite [17]. For the KMM system, the location of the soliton is more backward when the fractional order becomes smaller.
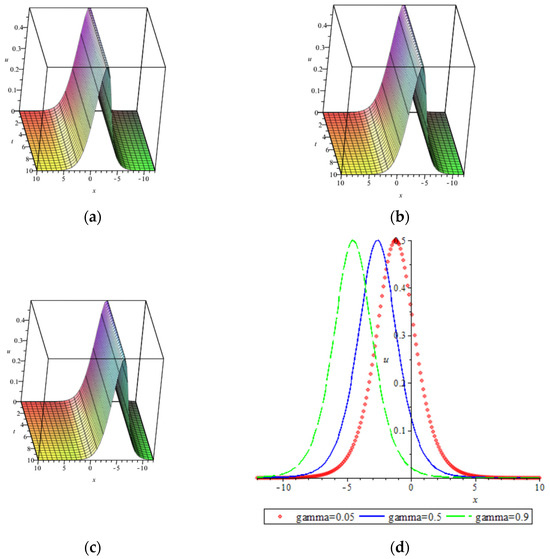
Figure 1.
One-soliton solution (10) with different (a) One-soliton with (b) One-soliton with (c) One-soliton with (d) One-soliton with different .
2.1.2. Two-Soliton Solution
When the fractional two-soliton solution for FKdVSKR Equation (1) is
where , and are determined by (7).
When taking diagrams of the two-soliton solution can be plotted as follows.
Figure 2 illustrates the two-soliton solution with As we can see from Figure 3, changes in the locations of the two-soliton are the same as the one-soliton. The location of the two-soliton is more forward when becomes smaller.
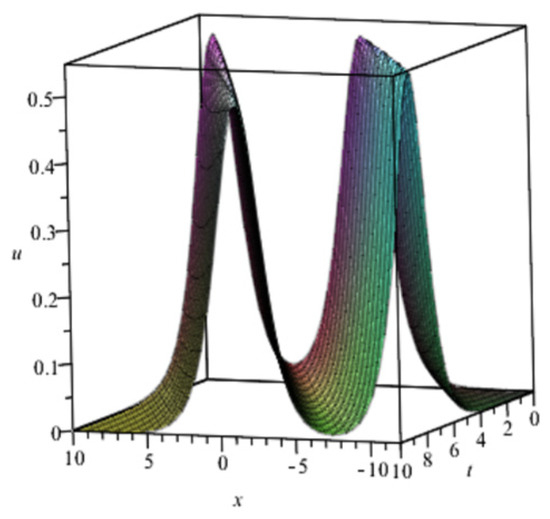
Figure 2.
Two-soliton with .
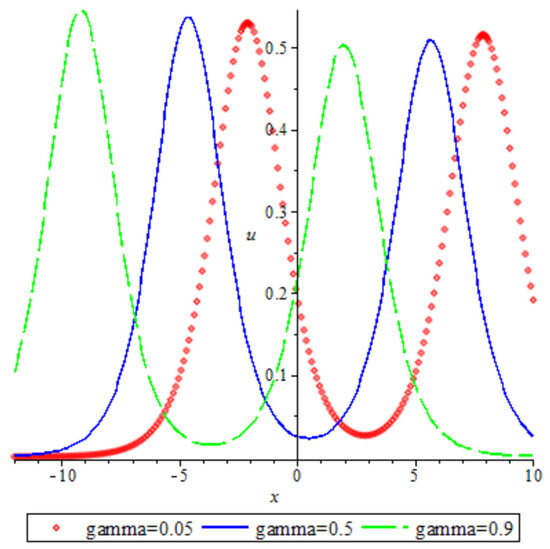
Figure 3.
Two-soliton .
2.1.3. Three-Soliton Solution
When
where , , and are determined by (7); the fractional three-soliton solution for FKdVSKR Equation (1) can be derived by (7) and (5). When taking and diagrams of the above three-soliton solution can be obtained as follows. Figure 4 illustrates the three-soliton solution with As we can see from Figure 5, the changing tendency of the locations of the three-soliton is the same as the one-soliton and two-soliton. The location of the three -soliton is more forward when becomes smaller. However, in the neighborhood of the trend of this change is not obvious.
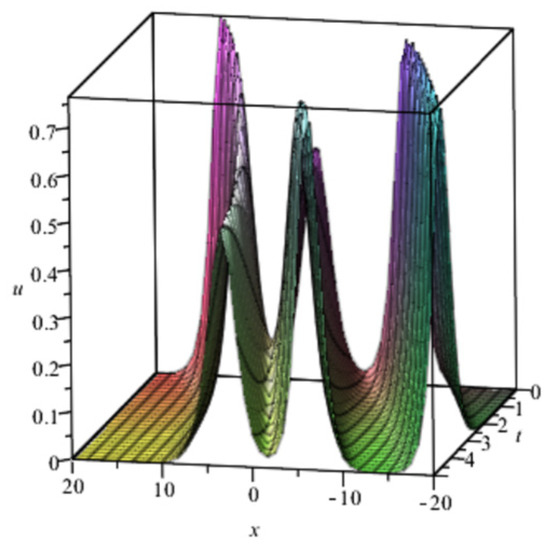
Figure 4.
Three-soliton with .

Figure 5.
Three-soliton .
2.1.4. Generalized Kaup-Kupershmidt Solitary Waves
Based on [46], (6) has a generalized Kaup-Kupershmidt (GKK) solitary wave as follows:
where is a constant. Through (5), one can obtain a GKK solitary wave solution for (1).
We should remark that it is different from the one-soliton solution (8).
2.2. Interaction Solution between Soliton and Elliptical Solution
The CREM is an effective and straightforward way to find interaction solutions between soliton and elliptic waves [37,38]. In [48], a soliton-cnoidal wave solution for (6) has been found by the CREM.
Taking advantage of the known solution in [48], an interaction solution between soliton and Jacobi elliptic function for (1) is
with
and and denote the modulus of the Jacobi elliptic function, where and are constants.
2.3. Lump–Periodic Interaction Solution
In the expression of the N-soliton solution (7), if we set
where , and are constants, we can obtain a lump-periodic interaction solution for KdVSKR Equation (6). Employing (5), a lump-periodic interaction solution of (1) is as follows.
When , the solution (11) becomes a solution for KdVSKR Equation (6), and it is precisely the same as that in [55].
3. New Solutions of (2) by the CREM
According to the fractional complex transform, we set
Substituting (12) into (2), we obtain the KdVSKR equation in (2+1)-dimension:
In fact, (13) and (4) are exactly the same if we ignore the difference between and Removing the integral operation, we can transform (13) into the following KdVSKR system:
If solutions of (14) can be obtained, solutions of (13) will be derived in the meantime. In the following, we first give an explanation of the CREM and then derive solutions of (14) by the CREM.
3.1. Explanation of the CREM
The CREM is proposed to derive exact solutions by applying the known solutions of the Riccati equation [37,38]. Consider a nonlinear PDE system as follows:
Suppose that the solutions of (15) have the following form:
where , and are undetermined functions concerning , and The positive integers and are determined by balancing the highest-order derivative term with the highest-order nonlinear term in (15). is a solution of the Riccati equation
with and being constants. Exact solutions of (17) have been reported in many references, such as [57].
Substituting (16) with (17) into (15), we can obtain a system of PDEs composed of the coefficients of different If and can be determined by and its derivatives, then solutions of (15) can be obtained by choosing the suitable forms of For more examples of the CREM, readers can refer to [37].
3.2. Exact Solutions by the CREM
By balancing the highest nonlinearity and dispersive term, we suppose that solutions of (14) are as follows:
where , and are functions of , and and is a solution of (17).
Taking (18) with (17) into (14) and vanishing the coefficients of different powers of yields
and the function W is a solution of the following three equations
where
To sum up, the (2+1)-dimensional KdVSKR system (14) can be solved by the CREM, and the following nonauto Backlund transform theorem has been proven.
Theorem 1.
If is a solution of (17) and is a solution of (19), then
are solutions of the (2+1)-dimensional KdVSKR system (14).
Taking and applying Theorem 1, two solutions of (13) can be obtained. The first one is a dark soliton solution:
and another is a singular soliton solution:
where , and are constants.
Employing (12), fractional dark soliton and singular soliton solutions for (2) can be obtained, and they are as follows:
4. Interaction Solutions of (2) by the FSGM
The finite symmetry group method (FSGM) is an effective way to obtain new exact solutions from the known solutions. In addition, the generator of the Lie group can also be obtained from the finite symmetry group.
4.1. Finite Symmetry Group of (14)
According to the FSGM, we suppose that the finite symmetry group of (14) has the following form:
where and are functions to be determined. and are supposed to satisfy the same (2+1)-dimensional PDEs as and with the transformation
That is to say, and are solutions of the following nonlinear system:
Substituting (22) into (14), ruling out and via (24), and collecting the other coefficients of and their derivatives, we have a set of overdetermined PDEs. From them, we have
where , and are arbitrary functions of So we obtain the finite symmetry group for (14).
Theorem 2.
If and are solutions of the (2+1)-dimensional KdVSKR system (14), then so are and expressed by (22) with (25).
To see the relation between the classical Lie group and the finite symmetry group, we set
where is an infinitesimal parameter; , and are arbitrary functions of Then (22) can be written as
then
and
so the Lie symmetry generators of (14) are as follows:
they are exactly the same as the results in [56], which have been obtained by the standard Lie group method.
Remark 1.
In [43], the finite symmetry group of (6) has been derived, but there are no arbitrary functions. The case in the (2+1)-dimensional KdVSKR system (14) is quite different, since the finite symmetry group of (14) has three arbitrary functions. The arbitrary functions in the finite symmetry group are very useful in extracting new types of interaction solutions.
4.2. Dark–Soliton–Sine Interaction Solution for (2)
Applying Theorem 2 and the given solution (20), we can obtain new solutions for (13). Taking a new solution for (13) is
Substituting into (26), an interaction solution between dark soliton and the trigonometric sine periodic function of (2) is obtained. To illustrate the effect of on the dynamical behaviors of the new interaction solution, graphs with different fractional order parameters have been plotted. When taking graphs in 3D are given in Figure 6.
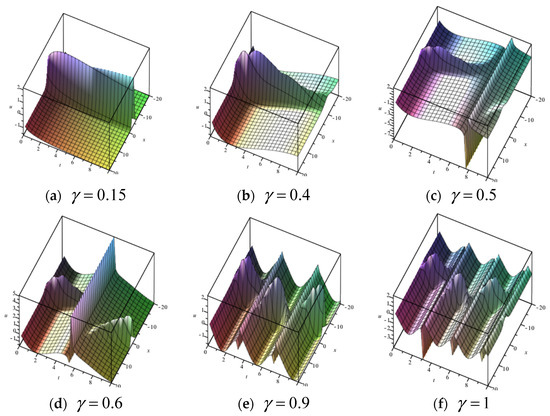
Figure 6.
Three-dimensional graphs of solution (26) with different fractional order .
From graphs (a)–(f) in Figure 6, we find an interesting fact. When the fractional order the soliton dominates the solution. When the periodicity of the solution begins to emerge. When the periodicity of the solution becomes strong when the fractional order parameter grows large. This conclusion can also be proven by Figure 7, which is at , with the same parameters as in Figure 6.
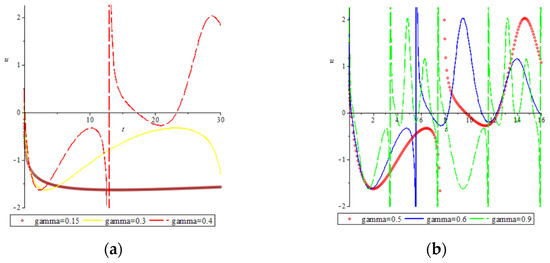
Figure 7.
Influence of fractional order on solution’s dynamical behaviors. (a) Small influence of periodicity. (b) Strong influence of periodicity.
4.3. Bright–Soliton–Elliptical Interaction Solution for (2)
From [52], we know that (2+1)-dimensional KdVSKR Equation (13) has a bright soliton solution
where and are constants.
Taking (27) into Theorem 2, we can obtain new solutions for (13). For example, taking a new two-wave interaction solution for (13) is
where are short for the Jacobi elliptic function and , respectively, and is the modulus of the Jacobi elliptic function.
Substituting into (28), a new interplaying solution between bright soliton and elliptic periodic function for (2) is obtained. To illustrate the influence of fractional order parameter on the dynamical behaviors of the new interaction solution, graphs with different fractional order parameters have been plotted. When taking graphs in 3D are given in Figure 8.
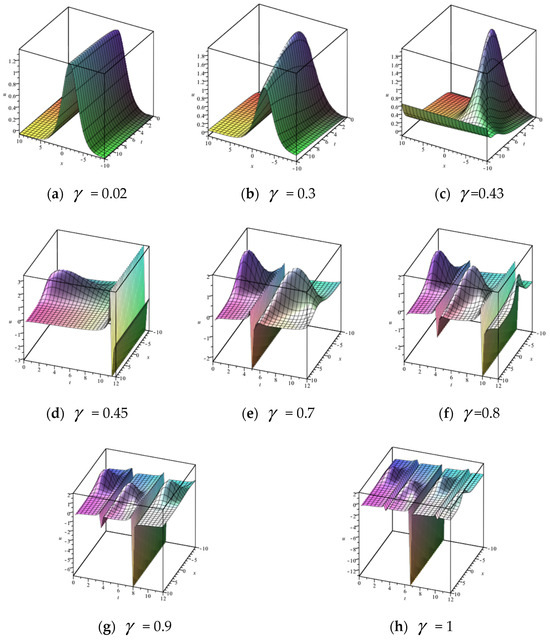
Figure 8.
Three-dimensional graphs of solution (28) with different fractional order .
From graphs (a)–(h) in Figure 8, the effect of on the dynamical behaviors of the solutions can be observed. When the fractional order it is the shape of the soliton, and we cannot see the influence of the elliptic function. When the fractional orders are and , the shape of the soliton has changed. When the periodicity of the solution begins to emerge. When the periodicity of the solution becomes stronger when the fractional order parameter grows larger. This conclusion can also be proven by Figure 9. It is plotted at , and other parameters are the same in Figure 8.
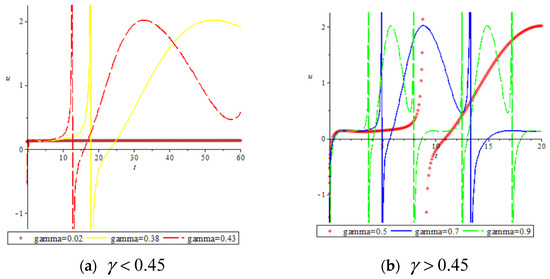
Figure 9.
Influence of fractional order on solution’s dynamical behaviors.
5. Results and Discussion
From Section 2 to Section 4, analytical solutions of the two FKdVSKR equations have been derived. The CREM and FSGM are used to study exact solutions of KdVSKR Equations (6) and (14). For (6), the authors in [48] show that the equation can be solved by the CREM, and a soliton-cnoidal interaction solution has been derived. From the known solution, we obtain a fractional soliton and elliptic function interaction solution (10) for FKdVSKR Equation (1). It is a fractional soliton lying on a fractional elliptical periodic wave. It is the first time that we have obtained a fractional soliton-cnoidal interaction solution for a fractional differential system. The FSGM has been applied to (6) in [43], and there are not any arbitrary functions in the expression of the finite symmetry group, so we cannot obtain new solutions from the FSGM. Fortunately, the finite symmetry group of (14) has three arbitrary functions, so we can obtain a lot of new solutions, making use of the known solutions of (13) and Theorem 2.
From [55], we know that (13) has a lump–hyperbolic solution
with
where and are constants.
Substituting into (29), alump–hyperbolic interaction solution for (2+1)-dimensional FKdVSKR Equation (2) is obtained. When taking graphs are as follows.
From graphs (a)–(c) in Figure 10, we find that the influence of on the dynamical behaviors of the solution is not obvious.
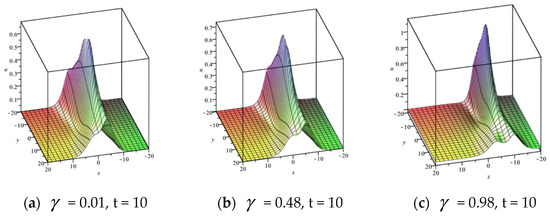
Figure 10.
Lump-hyperbolic solution with different fractional order .
Applying Theorem 2 and the above solution (29), we can obtain new solutions for (2). Taking a three-wave interaction solution for (13) is as follows:
with
Substituting into (30), a lump-hyperbolic-sine interplaying solution for (2) can be obtained. When taking graphs are as follows.
From graphs (a)–(i) in Figure 11, the effect of on the dynamical behaviors of the new interaction solution can be observed. We find that as the fractional order increases, the shape of the solution changes regularly. From to , it goes from periodic solution to soliton solution gradually. From to , the soliton becomes a periodic solution gradually. From to , the wave spans from disappearing to emerging.
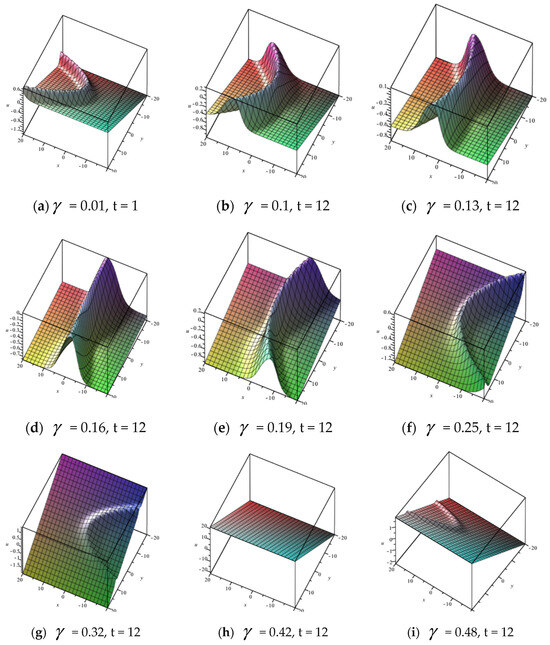
Figure 11.
Lump-hyperbolic-periodic solution with different fractional order .
Comparing the graphs in Figure 10 with those in Figure 11, we find that the dynamical behaviors of the lump-hyperbolic interaction solution are very different to that of the lump-hyperbolic-sine interaction solution. With the change in fractional order , the three-wave interaction solution changes regularly, while the two-wave interaction solution changes a little.
Remark 2.
The new interaction solutions (26), (28) and (30) of (13) cannot be obtained by other methods, such as the sub-equation method
-expansion method, Lie symmetry method, the exp-function method, and the Bernoulli sub-equation function method. We should point out that making use of Theorem 2, lots of new solutions with unexpected dynamic behavior and properties have been obtained. It is necessary to study these further.
6. Conclusions
Recently, a new (2+1)-dimensional PDE has been proposed, which is called the KdVSKR equation and can model the soliton resonances in shallow water. The available results show that this equation possesses rich local excitation patterns. Since fractional KdVSKR equations have not been studied so far, we perform in-depth studies on their exact solutions by means of the HBM, CREM, and FSGM. For the (1+1)-dimensional FKdVSKR equation, the effect of fractional order on the dynamical behaviors of fractional one-soliton, fractional two-soliton, and fractional three-soliton has been illustrated by graphs. We find that one-soliton, two-soliton, and three-soliton have the same variation tendency: the location of the fractional soliton is more backward when the fractional order becomes larger. In addition, we also obtain fractional lump–periodic and fractional soliton–cnoidal interaction wave solutions. To the best of our knowledge, soliton–cnoidal interaction wave solutions of fractional PDEs have not been reported previously.
For the (2+1)-dimensional KdVSKR equation, its finite symmetry group is derived. From the finite symmetry group, Lie point symmetry has been obtained and is exactly the same as the results in [56]. Using Theorem 2, a lot of novel solutions have been derived for (2+1)-dimensional KdVSKR Equation (13), and these solutions are all different from those in [51,52,53,54,55,56]. Making use of the fractional complex transform (12), new types of interaction solutions for (2) have been extracted. The solutions include dark soliton with trigonometric sine function interaction solution (26), bright soliton with elliptic function interaction solution (28), and lump-hyperbolic-sine three-wave interaction solution (29) under the condition . The impact of fractional order on the dynamical behaviors of these solutions has been illustrated by plenty of graphs. As far as we know, the lump-hyperbolic-sine three-wave interaction solution has not been seen in the published references.
The innovation of this study is that we have found two new ways to obtain interaction solutions of fractional nonlinear systems. The FSGM and CREM can both be used to obtain new interaction solutions for FDEs. This is the first time that the FSGM and CREM have been applied to extract interaction solutions for FDEs. We will study the fractional higher-order beam equation by applying the research idea of this paper in the future.
Author Contributions
Writing–original draft preparation, L.Z.; formal analysis, Z.Z. and B.S.; investigation, G.W.; writing—review and editing, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 12105073), Natural Science Foundation of Hebei Province of China (No. A2023207002), ‘333 Talent Project’ of Hebei Province (No. C20221021), Key Program of Hebei University of Economics and Business (No. 2023ZD10), Hebei Social Science Fund Program (No. HB20TJ002), Science Research Project of the Hebei Education Department (No. BJS2024068), and Natural Science Foundation of Shandong Province of China (No. ZR2022MA081).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Acknowledgments
The authors are in debt to the helpful discussions with X.P. Xin. The authors are very grateful to the referees and to the editors for their useful comments and suggestions towards the improvement of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| KdV | Korteweg-de Vries |
| KdVSKR | Korteweg-de Vries Sawada-Kotera-Ramani |
| FKdVSKR | fractional Korteweg-de Vries Sawada-Kotera-Ramani |
| SK | Sawada-Kotera |
| KP | Kadomtsev-Petviashvili |
| FDEs | fractional differential equations |
| PDEs | partial differential equations |
| ODEs | ordinary differential equations |
| HBM | Hirota bilinear method |
| FSGM | finite symmetry group method |
| CREM | consistent Riccati expansion method |
| GKK | generalized Kaup–Kupershmidt |
References
- Ma, P.C.; Taghipour, M.; Cattani, C. Option pricing in the illiquid markets under the mixed fractional Brownian motion model. Chaos Solitons Fractals 2024, 182, 114806. [Google Scholar] [CrossRef]
- Chen, Q.L.; Dipesh; Kumar, P.; Baskonus, H.M. Modeling and analysis of demand-supply dynamics with a collectability factor using delay differential equations in economic growth via the Caputo operator. AIMS Math. 2024, 9, 7471–7491. [Google Scholar] [CrossRef]
- Kavya, K.N.; Veeresha, P.; Baskonus, H.M.; Alsulami, M. Mathematical modeling to investigate the influence of vaccination and booster doses on the spread of Omicron. Commun. Nonlinear Sci. Numer. Simul. 2024, 130, 107755. [Google Scholar] [CrossRef]
- Cattani, C.; Baskonus, H.M.; Ciancio, A. Introduction to the special issue on recent developments on computational biology-i. CMES Comput. Model. Eng. Sci. 2024, 139, 2261–2264. [Google Scholar] [CrossRef]
- Wang, G.W.; Liu, X.Q.; Zhang, Y.Y. Lie symmetry analysis to the time fractional generalized fifth-order KdV equation. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2321–2326. [Google Scholar] [CrossRef]
- Li, Z.B.; He, J.H. Fractional complex transform for fractional differential equations. Math. Comput. Appl. 2016, 15, 970–973. [Google Scholar] [CrossRef]
- Saad, K.M.; Baleanu, D.; Atangana, A. New fractional derivatives applied to the Korteweg-deVries and Korteweg-de Vries-Burger’s equations. Comp. Appl. Math. 2018, 37, 5203–5216. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.T.; Baleanu, D.; Cattani, C. A new method for exact solutions of variant types of time-fractional Korteweg-de Vries equations in shallow water waves. Chaos. Interdiscip. J. Nonlinear Sci. 2016, 26, 084312. [Google Scholar] [CrossRef] [PubMed]
- He, J.H. The simpler, the better: Analytical methods for nonlinear oscillators and fractional oscillators. J. Low Freq. Noise Vib. Act. 2019, 38, 1252–1260. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: New York, NY, USA, 1993. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Jumarie, G. Modified Riemann-Liouville derivative and fractional Taylor series of non differentiable functions further results. Comput. Math. Appl. 2006, 51, 1367–1376. [Google Scholar] [CrossRef]
- Baleanu, D.; Atangana, A. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar]
- Yang, X.J.; Aty, M.A.; Cattani, C. New general fractional-order derivative with rabotnov fractional-exponential kernel applied to model the anomalous heat transfer. Therm. Sci. 2019, 23, 1677–1681. [Google Scholar] [CrossRef]
- Gou, C.H.; Cai, R.X.; Zhang, N. Explicit analytical solutions of transport equations considering non-Fourier and non-Fick effects in porous media. Prog. Nat. Sci. 2005, 15, 545–549. [Google Scholar]
- Zhang, L.H.; Shen, B.; Jiao, H.B.; Wang, G.W.; Wang, Z.L. Exact solutions for the KMM system in (2+1)-dimensions and its fractional form with Beta-derivative. Fractal Fract. 2022, 6, 520. [Google Scholar] [CrossRef]
- Zhang, L.H.; Wang, Z.L.; Shen, B. Fractional complex transforms, reduced equations and exact solutions of the fractional Kraenkel-Manna-Merle system. Fractals 2022, 30, 22501791. [Google Scholar] [CrossRef]
- Baleanu, D.; Inc, M.; Yusuf, A.; Aliyu, A.I. Lie symmetry analysis, exact solutions and conservation laws for the time fractional Caudrey-Dodd-Gibbon-Sawada-Kotera equation. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 222–234. [Google Scholar] [CrossRef]
- Liu, J.G.; Yang, X.J.; Geng, L.L.; Fan, Y.R. Group analysis of the time fractional (3+1)-dimensional KdV-type equation. Fractals 2021, 29, 2150169. [Google Scholar] [CrossRef]
- Wang, G.W.; Kara, A.H.; Fakhar, K. Symmetry analysis and conservation laws for the class of time-fractional nonlinear dispersive equation. Nonlinear Dyn. 2015, 82, 281–287. [Google Scholar] [CrossRef]
- Inc, M.; Yusuf, A.; Aliyu, A.I.; Baleanu, D. Time-fractional Cahn-Allen and time-fractional Klein-Gordon equations: Lie symmetry analysis, explicit solutions and convergence analysis. Physica A 2018, 493, 94–106. [Google Scholar] [CrossRef]
- Sahadevan, R.; Bakkyaraj, T. Invariant analysis of time fractional generalized burgers and Korteweg-de vries equations. J. Math. Anal. Appl. 2012, 393, 341–347. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S. Improved fractional sub-equation method for (3+1) -dimensional generalized fractional KdV-Zakharov-Kuznetsov equations. Comput. Math. Appl. 2015, 70, 158–166. [Google Scholar] [CrossRef]
- Murad, M.A.S.; Ismael, H.F.; Hamasalh, F.K.; Shah, N.A.; Eldin, S.M. Optical soliton solutions for time-fractional Ginzburg-Landau equation by a modified sub-equation method. Results Phys. 2023, 53, 106950. [Google Scholar] [CrossRef]
- Zheng, B. G′/G-expansion method for solving fractional partial differential equations in the theory of mathematical physics. Commun. Theor. Phys. 2012, 58, 623–630. [Google Scholar] [CrossRef]
- Zulfiqar, A.; Ahmad, J.; Ul-Hassan, Q.M. Analysis of some new wave solutions of fractional order generalized Pochhammer-Chree equation using exp-function method. Opt. Quant. Electron. 2022, 54, 735. [Google Scholar] [CrossRef]
- Noor, S.; Alyousef, H.A.; Shafee, A.; Shah, R.; El-Tantawy, S.A. A novel analytical technique for analyzing the (3+1)-dimensional fractional Calogero- Bogoyavlenskii-Schiff equation: Investigating solitary/shock waves and many others physical phenomena. Phys. Scr. 2024, 99, 065257. [Google Scholar] [CrossRef]
- Afzal, U.; Raza, N.; Murtaza, I.G. On soliton solutions of time fractional form of Sawada–Kotera equation. Nonlinear Dyn. 2019, 95, 391–405. [Google Scholar] [CrossRef]
- Özkan, A.; Özkan, E.M. A novel study of analytical solutions of some important nonlinear fractional differential equations in fluid dynamics. Mod. Phys. Lett. B 2024, 2450461. [Google Scholar] [CrossRef]
- Rao, A.; Vats, R.K.; Yadav, S. Analytical solution for time-fractional cold plasma equations via novel computational method. Int. J. Appl. Comput. Math. 2024, 10, 2. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Mahmud, A.A.; Muhamad, K.A.; Tanriverdi, T. A study on Caudrey-Dodd-Gibbon-Sawada-Kotera partial diferential equation. Math. Methods Appl. Sci. 2022, 45, 8737–8753. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Lou, S.Y.; Ma, H.C. Non-Lie symmetry groups of (2+1)-dimensional nonlinear systems obtained from a simple direct method. J. Phys. A Math. Gen. 2005, 38, 129–137. [Google Scholar] [CrossRef]
- Din, M.S.T.; Ali, A. Exp(−ϕ(η)) expansion method and shifted Chebyshev Wavelets for generalized Sawada-Kotera of fractional order. Fund. Inform. 2017, 151, 173–190. [Google Scholar]
- Lou, S.Y. Consistent Riccati expansion for integrable systems. Stud. Appl. Math. 2015, 134, 372–402. [Google Scholar] [CrossRef]
- Ren, B.; Lin, J.; Lou, Z.M. Consistent Riccati expansion and rational solutions of the Drinfel’d-Sokolov-Wilson equation. Appl. Math. Lett. 2020, 105, 106326. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.H.; Si, J.; Shi, F.; Wang, G.D. N-Soliton, breather, lump solutions and diverse travelling wave solutions of the fractional (2+1)-dimensional Boussinesq equation. Fractals 2023, 31, 23500238. [Google Scholar]
- Biswas, S.; Ghosh, U.; Raut, S. Construction of fractional Granular model and bright, dark, lump, breather types soliton solutions using Hirota bilinear method. Chaos Solitons Fractals 2023, 172, 13520. [Google Scholar] [CrossRef]
- Younas, U.; Sulaiman, T.A.; Ismael, H.F.; Shah, N.A.; Eldin, S.M. On the lump interaction phenomena to the conformable fractional (2+1)-dimensional KdV equation. Results Phys. 2023, 52, 106863. [Google Scholar] [CrossRef]
- Jaradat, H.M.; Shara, S.A.; Jaradat, M.M.M.; Mustafa, Z.; Alsayyed, O.; Alquran, M.; Abohassan, K.M.; Momani, S. New solitary wave and multiple soliton solutions for the time-space coupled fractional mKdV system with time-dependent coefficients. J. Comput. Theor. Nanosci. 2016, 13, 9082–9089. [Google Scholar]
- Xiong, N.; Yu, Y.X.; Li, B. Soliton molecules and full symmetry groups to the KdV -Sawada-Kotera-Ramani equation. Adv. Math. Phys. 2021, 1, 5534996. [Google Scholar] [CrossRef]
- Ma, P.L.; Tian, S.F.; Zhang, T.T.; Zhang, X.Y. On Lie symmetries, exact solutions and integrability to the KdV -Sawada-Kotera-Ramani equation. Eur. Phys. J. Plus 2016, 131, 98. [Google Scholar] [CrossRef]
- Zhang, L.J.; Chaudry, M.K. Exact solitary wave and quasi-periodic wave solutions of the KdV-Sawada-Kotera-Ramani equation. Adv. Differ. Equ. 2015, 195, 13662. [Google Scholar] [CrossRef][Green Version]
- Burde, G.I. Generalized Kaup-Kupershmidt solitons and other solitary wave solutions of the higher-order KdV equations. J. Phys. A Math. Gen. 2010, 43, 085208. [Google Scholar] [CrossRef]
- Osman, M.S. Analytical study of rational and double-soliton rational solutions governed by the KdV-Sawada-Kotera-Ramani equation with variable coefficients. Nonlinear Dyn. 2017, 89, 2283–2289. [Google Scholar] [CrossRef]
- Cheng, W.G.; Xu, T.Z. Consistent Riccati expansion solvable classification and soliton-cnoidal wave interaction solutions for an extended Korteweg-de Vries equation. Chin. J. Phys. 2018, 56, 2753–2759. [Google Scholar] [CrossRef]
- Wang, H.; Xia, T.C. Bell polynomial approach to an extended Korteweg-de Vries equation. Math. Method Appl. Sci. 2014, 37, 1476–1487. [Google Scholar] [CrossRef]
- Xia, Y.R.; Yao, R.X.; Xin, X.P.; Li, Y. Trajectory equation of a lump before and after collision with other waves for (2+1)-dimensional Sawada-Kotera equation. Appl. Math. Lett. 2023, 135, 108408. [Google Scholar] [CrossRef]
- Zhu, C.; Long, C.X.; Zhou, Y.T.; Wei, P.F.; Ren, B.; Wang, W.L. Dynamics of multi-solitons, multi-lumps and hybrid solutions in (2+1)-dimensional korteweg-de vries-Sawada-Kotera-Ramani equation. Results Phys. 2022, 34, 105248. [Google Scholar] [CrossRef]
- Wei, P.F.; Long, C.X.; Zhu, C.; Zhou, Y.T.; Yu, H.Z.; Ren, B. Soliton molecules, multi-breathers and hybrid solutions in (2+1)-dimensional Korteweg-de Vries-Sawada-Kotera-Ramani equation. Chaos Solitons Fractals 2022, 158, 112062. [Google Scholar] [CrossRef]
- Ma, H.C.; Deng, A.P.; Gao, Y.D. Novel y-type and hybrid solutions for the (2+1) -dimensional Korteweg-de Vries-Sawada-Kotera-Ramani equation. Nonlinear Dyn. 2023, 111, 4645–4656. [Google Scholar] [CrossRef]
- Li, L.X.; Dai, Z.D.; Cheng, B.T.; Li, R.B. Nonlinear superposition between lump soliton and other nonlinear localized waves for the (2+1)-dimensional Korteweg-deVries-Sawada-Kotera-Ramani equation. Results Phys. 2023, 49, 106516. [Google Scholar] [CrossRef]
- Chen, W.X.; Tang, L.P.; Tian, L.X. New interaction solutions of the KdV-Sawada-Kotera-Ramani equation in various dimensions. Phys. Scr. 2023, 98, 055217. [Google Scholar] [CrossRef]
- Ren, B.; Lin, J.; Wang, W.L. Painlevé analysis, infinite dimensional symmetry group and symmetry reductions for the (2+1)-dimensional Korteweg-de Vries-Sawada-Ramani equation. Commun. Theor. Phys. 2023, 75, 085006. [Google Scholar] [CrossRef]
- Chen, H.T.; Zhang, H.Q. New double periodic and multiple soliton solutions of the generalized (2+1)-dimensional Boussinesq equation. Appl. Math. Comput. 2004, 157, 765–769. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).