Abstract
The reservoir quality of tight sandstone is usually affected by pore throat structures, and understanding pore throat structures and their fractal characteristics is crucial for the exploration and development of tight sandstone gas. In this study, fractal dimensions of pore throat structures and the effect of diagenesis on the fractal dimension of tight sandstone sweet spot in Huagang Formation, Jiaxing area, East China Sea Basin were studied by means of thin sections, scanning electron microscopes, X-ray diffraction analysis, scanning electron microscope quantitative mineral evaluation, and high pressure mercury injection experiments. The results show that the total fractal dimension ranges of type I, type II, and type III sweet spots were 2.62–2.87, 2.22–2.56, and 2.71–2.77, respectively. The negative correlation between total fractal dimensions, porosity, and permeability of type I sweet spots was different from those of type II and type III sweet spots. The negative correlation between total fractal dimensions of type II and type III sweet spots and maximum mercury saturation, average pore throat radius, and skewness were significant, whereas the correlation between total fractal dimensions of type I sweet spots, and maximum mercury saturation, average pore throat radius and skewness were not significant. The positive correlation between the total fractal dimensions of type II and type III sweet spots and the relative sorting coefficient, displacement pressure, and efficiency of mercury withdrawal were significant, whereas the correlation between the total fractal dimension of type I sweet spots and relative sorting coefficients, displacement pressures and efficiency of mercury withdrawal were not significant. The effect of diagenesis on fractal dimensions was investigated. Compaction reduced the pore space of tight sandstone and increased fractal dimensions. Quartz cementation and calcite cementation blocked pores and throats, reduced pore space, and increased fractal dimensions. Chlorite coat can inhibit compaction, protect pore throat structures, and maintain fractal dimensions. Most clay minerals filled primary pores and secondary pores and increased fractal dimensions. Dissolution increased the pore space of tight sandstone and decreased the fractal dimensions of the pore throat structures. The pore throat structures of type I sweet spots were mainly composed of macropores, mesopores, transitional pores, and micropores, and the fractal dimension of type I sweet spots was chiefly controlled by chlorite coat formation, dissolution, and a small amount of compaction. This study provides a reference for pore throat structure and fractal dimension analysis of tight sandstone sweet spots.
1. Introduction
Tight sandstone usually experiences strong diagenesis, such as compaction, cementation, and dissolution, which results in small pores and complex pore throat structures at the microscopic level [1]. The characteristics of pore throat structures are crucial for a comprehensive understanding of tight sandstone reservoirs. This is because heterogeneous pore throat structures can affect reservoir quality evaluation and final exploration risk assessment [2,3]. Fractal theory is a useful tool for irregular and self-similar phenomena widely present in the natural and social sciences [4]. The pore throat structure of sandstone is proved to be a statistical fractal in a certain range [4]. Therefore, the fractal dimension is a key parameter and an effective means to describe pore throat complexity and microscopic heterogeneity, and has been applied to pore throat structure evaluation, permeability prediction, and classification and evaluation of tight reservoirs [1,5,6,7].
At present, qualitative and quantitative research on pore throat morphology and size of tight sandstone can be divided into three categories: image observation methods, fluid injection methods, and spectral analysis methods [8,9,10,11]. Image observation methods, such as thin section, scanning electron microscope and energy spectrum analysis, and micro/nano CT, can be used to characterize the geometric characteristics of the pore throat visually [10,12]. Fluid injection methods, including high pressure mercury injection, constant rate mercury injection, gas adsorption/desorption measurement, and nuclear magnetic resonance, can quantitatively characterize pore throat size and distribution characteristics [13,14,15]. Spectral analysis methods chiefly include X-ray small-angle scattering, neutron small-angle scattering, and focused ion beam scanning electron microscopes [11]. However, these analytical methods have their advantages and limitations for measuring pore throat diameters [8,16]. Fractal theory is an effective tool to quantitatively characterize the complexity of pore throat structures in tight sandstone [17,18].
The fractal dimension is an important parameter to characterize the heterogeneity of pore throat structures [19,20]. With the increase in protuberances and concavities, pore surface and structure become more rough and complex [21], and fractal dimensions can quantify the roughness of the material surface. Fractal theory provides an effective bridge between microscopic characteristics and physical properties of tight reservoirs [22]. The fractal dimension of pore throat structures is between 2 and 3, and the increase in fractal dimension indicates a discrete distribution of pore throats and poor connectivity [18]. At present, there is much research on pore throat structures, fractal characteristics, and diagenesis of tight sandstone [16,23,24]. However, there are few studies on the fractal dimension of the pore throat structure of tight sandstone sweet spots and the effect of diagenesis on fractal dimensions.
The fourth (H4) and fifth (H5) members of the Huagang Formation in the Jiaxing area of the East China Sea Basin are tight sandstone reservoirs. The reservoir quality of these tight sandstones is often affected by pore throat structures, and understanding pore throat structure characteristics of sweet spots is crucial for effective development. This work takes the Jiaxing area of the East China Sea Basin as an example to investigate the fractal dimension of the pore throat structure of tight sandstone sweet spots and the effect of diagenesis on fractal dimensions. The structure of this article is as follows. Firstly, reservoir characteristics of tight sandstone were investigated. Secondly, the diagenesis of tight sandstone was analyzed, and the diagenetic evolution sequence was established. Thirdly, pore throat structure characteristics of tight sandstone were investigated. Fourthly, fractal characteristics of tight sandstone sweet spots were elaborated. In addition, a discussion was given, including the relationship between fractal dimensions, reservoir properties, and pore structure parameters, the effect of diagenesis on fractal characteristics, and implications for sweet spot prediction. Finally, the main conclusion was drawn. The main objectives of this work are the following: (1) Outline compaction, clay mineral transformation, quartz cementation, calcite cementation, and dissolution of tight sandstone; (2) Investigate the fractal dimension of pore throat structure of tight sandstone sweet spot, and elaborate the relationship between fractal dimension, reservoir properties, and pore structure parameters; (3) Investigate the effect of diagenesis on fractal dimension. This study provides a reference for pore throat structure and fractal dimension analysis of tight sandstone sweet spots.
2. Materials and Methods
2.1. Geological Setting and Samples
The East China Sea Basin is located in eastern China (Figure 1a) [25]. The Xihu Sag is located in the middle of the Zhedong Depression in the East China Sea Basin (Figure 1a) [26,27]. The length of the Xihu Sag is about 440 km, the width is approximately 70–130 km, and the area is about 59,000 km2. The Xihu Sag is a basin dominated by Cenozoic strata, and its basement is the Proterozoic metamorphic rock series crystalline basement and Jurassic and Cretaceous inland clastic rock and volcanic rock series Mesozoic basement. East of the Xihu Sag is bounded by the Diaoyudao uplift, the west is bounded by the Haijiao uplift and the Yushan low uplift, the south is connected with the Diaobei Sag, and the north is adjacent to the Fujiang Sag (Figure 1b) [28]. The N gas field is located in the Jiaxing area of the central–northern parts of the central uplift belt in the Xihu Sag, East China Sea Basin (Figure 1b). The Huagang Formation in the N gas field is primarily a braided river delta sedimentary system with a large development range and continuous sandstone distribution (Figure 1b). The upper part of the Huagang Formation can be divided into H1–H5 and the lower part of the Huagang Formation can be divided into H6–H12. The thick sandstone deposits in the upper part of the Huagang Formation are primarily subaqueous distributary channels in the braided river delta front part, which are the main natural gas reservoirs. H1–H2 is chiefly composed of thin interbeds of sandstone and mudstone. H3-H5 develops thick positive rhythm superimposed sandstone, with glutenite and gravel-bearing sandstone common at the bottom. The tight sandstone of the H4 and H5 members is the target interval of this study (Figure 1c). The burial depth of the H4 and H5 sandstones ranges from 3800 m to 4150 m, and the formation temperature ranges from 135 °C to 155 °C.
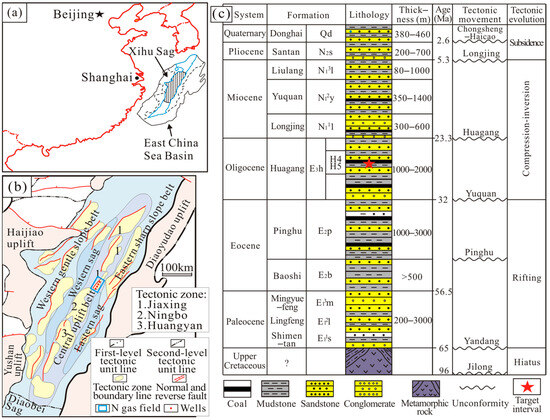
Figure 1.
(a) Location of East China Sea Basin and Xihu Sag. (b) Division of structural units and location of N gas field in Xihu Sag [29]. (c) Comprehensive stratigraphic column of Xihu Sag [30]. The red star indicates the studied target intervals.
More than 500 core samples and 2713 conventional core analysis data were collected from China National Offshore Oil Corporation Shanghai Branch. Sandstone samples were taken from core sections of the H4 and H5 members of four wells in the N gas field in Xihu Sag. The total length of the core section in the target interval of four wells is 129.9 m, including 27.1 m in the N1 well, 48.3 m in the N2 well, 45.5 m in the N3 well, and 9.0 m in the N4 well. These sandstone samples were prepared for 296 thin-section analyses, 158 scanning electron microscopes, 64 X-ray diffraction analyses, 6 scanning electron microscope mineral quantitative evaluations, and 16 high pressure mercury injection measurements.
2.2. Experiment Methods
X-ray diffraction analysis data were used to analyze reservoir characteristics of tight sandstone. Thin sections, scanning electron microscopes, and scanning electron microscope mineral quantitative evaluations were used to investigate the diagenesis and diagenetic minerals of tight sandstone. Then, pore throat structure of tight sandstone was investigated by high pressure mercury injection experiment, and fractal dimension of pore throat structure of tight sandstone sweet spot was investigated by fractal theory.
2.2.1. Thin Section
A total of 296 blue epoxy-infected thin sections were used for petrographic analysis. Thin sections were stained with alizarin red for the determination of carbonate minerals. Petrographic point counting analysis was performed on thin sections of sandstone samples, and mineral composition, authigenic minerals, primary pores, and secondary pores of each thin section were determined. Point counting was performed on a thin section for detrital composition with at least 300 points, which can provide a standard deviation of approximately 5.5% or less [31]. The pore types contained primary intergranular pore, intragranular dissolution pore, intergranular dissolution pore, and moldic pore. The initial porosity evaluation equation proposed by Scherer (1987) was used to calculate the initial porosity (or initial intergranular volume) [32]. The initial porosity of H4 and H5 tight sandstones calculated by this method ranged from 31.8% to 35.5%. The porosity loss caused by compaction in H4 and H5 sandstone was calculated using the Houseknecht (1987) method [33].
2.2.2. Scanning Electron Microscopy
A total of 158 gold-coated core sandstone bulk samples were analyzed for scanning electron microscopes. The core sample treatment process included oil washing, sample selection, piling, drying, dust removal, and gold plating. A scanning electron microscope was used to describe the pore morphology, pore size, and mineral distribution of tight sandstone [29,34]. High-resolution imaging was performed on the Quanta FEG 450 scanning electron microscopy to determine pore throat space, cement morphology, and mineral composition.
2.2.3. X-ray Diffraction Analysis
A total of 64 core samples were selected for whole-rock X-ray diffraction analysis and clay X-ray diffraction analysis. Whole rock (massive) and clay fractions (<2 μm) were analyzed for whole rock mineral content and clay mineral content using X-ray diffractometer Ultima IV.
2.2.4. Scanning Electron Microscopy Mineral Quantitative Evaluation
Based on petrographic analysis, six representative core samples were selected for scanning electron microscope minerals quantitative evaluation (QEMSCAN). The quantification analysis of mineral composition was performed by scanning the surface of the sample with a high-energy electron beam accelerated along the preset grating scanning mode to obtain a color map of the distribution characteristics of mineral assemblage. By combining back-scattered electron (BSE) image grayscale with X-ray intensity, the content of the element can be obtained and converted into mineral phases. By scanning the surface of the sample, almost all parameters related to mineral texture characteristics can be calculated, including mineral grain morphology, mineral distribution characteristics, mineral dissociation degree, element occurrence state, porosity, and matrix density. The quantification analysis results obtained mineralogy images of investigated thin sections.
QEMSCAN analysis was carried out by iRock Technologies company, Beijing city, China, and test instruments were Hitachi FlexSEM1000II desktop electron microscope, Bruker Energy Spectrometer EDSQ80detectors, and AMICS 3.2.0.222 mineral analysis software. The Hitachi FlexSEM1000II desktop electron microscope was operated at an accelerated voltage of 0.1 kV–20 kV, and the highest resolution of the BSE was 5 nm. A resolution of 0.5 μm or 0.83 μm was used for analysis to obtain clear BSE images. Mineral identification was carried out using the Mapping (debris)/Particles (core) of the analytical mineral library (Shale 2021 SY) in the AMICS 3.2.0.222 mineral analysis software. For each region analyzed, the BSE image was converted to a mineral image by merging energy dispersive spectrometer spectra into a single mineral.
2.2.5. High Pressure Mercury Injection Experiment
Based on petrographic analysis, high pressure mercury injection experiment was performed on 16 core samples to obtain pore throat size data. Before conducting high pressure mercury injection experiment, oil and gas should be removed from the sample, and the parameters such as porosity, permeability, and density need to be measured in advance. High pressure mercury injection analysis was conducted at the Exploration and Development Experiment Center of Geological Science Research Institute, Jiangsu Oilfield Branch of China Petroleum and Chemical Corporation. According to the Chinese petroleum industry standard GBT 29171-2012 [35], pore throat size of core samples with a diameter of approximately 2.54 cm and a length of approximately 4.5 cm were tested by using AutoPore IV9520 mercury porosimeter at a temperature of 25 °C and a relative humidity of 35–50%. Mercury was injected to obtain the intrusion curves until the maximum pressure was reached, and then the experiment of decreasing pressure was carried out to obtain the mercury extrusion curves. The maximum intrusion pressure was 116.67 MPa, which corresponded to a pore throat radius of 0.006 μm. During the experiment, the volume accuracy of the entry or exit of mercury was greater than 0.1 μL. The pore distribution characteristics of the cores can be converted from the capillary pressure curve.
The complex pore throat structure is thought to be composed of a series of interconnected irregular pore networks with self-similarity. When non-wetting phase mercury was injected into a porous sample, capillary force prevented mercury from entering the pore throat. Therefore, an injection pressure was required to overcome capillary resistance, and each injection pressure corresponded to a corresponding magnitude of capillary force. Under capillary pressure equilibrium, the injection pressure and injection amount of mercury were recorded, and then the capillary pressure curve characterizing pore throat structures was obtained according to the relationship between injection pressure and mercury saturation. The pore throat radius curve was obtained by the relationship between capillary pressure and pore throat radius (Equation (1)), and the pore structure of tight sandstone was evaluated:
where Pc is capillary pressure, MPa, θ is the wetting angle, °, σ is surface tension, N/m, and r is pore throat radius, μm. In general, θ = 140° and σ = 0.48 N/m.
2.3. Fractal Methodology
The pore throat structure of a sandstone reservoir has self-similarity, which can be described by fractal theory, and the fractal dimension is related to the surface roughness of the reservoir pore throat [36]. In this paper, based on the advantages of high mercury injection pressure and large pore diameter range, a fractal dimension study of obtained experiment data was carried out to quantitatively characterize the heterogeneity of the pore throat structure of the H4 and H5 tight sandstone in the study area.
In high pressure mercury injection experiments, capillary pressure can reflect the difficulty of mercury entering different pore throat radii. According to the principle of fractal geometry, when the pore throat radius property of tight sandstone conforms to the fractal characteristics, the number of pore throats with a radius greater than r is calculated as N. The correlation between N and r can be expressed as Equation (2):
where rmax is the maximum pore throat radius, μm, and F(r) is the distribution density function of the pore throat radius, and a is the proportionality constant. Since the minimum value of pore throat radius, rmin, is much smaller than rmax, Equation (3) can be obtained.
where S is the wetting phase saturation corresponding to capillary pressure Pc, %.
Assuming that θ is not affected by pore throat size, the fractal Equation (4) of pore throat radius distribution can be obtained.
where Pmin is capillary pressure corresponding to rmax, MPa. Take the logarithm of both sides of Equation (4) to obtain Equation (5).
The fractal dimension calculation procedure is as follows. Firstly, according to the experiment data of capillary pressure, the correlation between lg(S) and lg(Pc) can be determined. In the high pressure mercury injection experiment, the wetting phase is air, and the non-wetting phase is mercury, so lg(S) can be expressed as lg(1−SHg), where SHg is mercury saturation. Secondly, the slope of the lg(1−SHg) and lg(Pc) correlation trendline was obtained by linear fitting, which is the Hurst index (H). Finally, the fractal dimension is calculated based on Equation (6).
According to fractal theory, pore throat structure fractals can be divided into total fractals and segmented fractals [37]. The segmented fractal curve of the lg(1−SHg) and lg(Pc) plot curve is not a straight line and has obvious turning points. The curve can be divided into several segments, and the fractal dimension of different sizes of pore throats needs to be calculated. Many classification criteria for pores were proposed [38,39]. In this study, the Xoaoth classification criteria was used to classify pore types, namely micropores (<10 nm), transitional pores (10–100 nm), mesopores (100–1000 nm), and macropores (>1000 nm). These four types of pores had obvious turning points on lg(1−SHg) and lg(Pc) curves, and then fractal dimensions of micropores, transitional pores, mesopores, and macropores were calculated by linear fitting according to above-mentioned fractal dimension calculation procedure.
The weighted average method can consider the fractal dimension and pore space content of different pores, and the total fractal dimension obtained is accurate. Finally, based on the fractal dimension and porosity of macropores, mesopores, transitional pores and micropores, and the total fractal dimension (D) of the entire pore throat can be obtained by using the weighted average method (Equation (7)).
where, D is total fractal dimension, D1 is fractal dimension of the macropore, D2 is fractal dimension of the mesopore, D3 is fractal dimension of the transitional pore, D4 is fractal dimension of the micropore, φ1 is the porosity of the macropore, %, φ2 is the porosity of the mesopore, %, φ3 is the porosity of the transitional pore, %, φ4 is the porosity of the micropore, %.
3. Results
3.1. Reservoir Characteristics
The rocks of the H4 and H5 members are chiefly feldspathic lithic quartzose, with a small amount of feldspathic litharenite and litharenite (Figure 2a). The content of detrital quartz, feldspar, and rock fragments ranges from 53% to 75%, from 8.0% to 20.0%, and from 14.0% to 37.0%, with an average value of 65.04%, 16.29% and 18.68%, respectively (Figure 2b). The types of rock fragments are primarily metamorphic rock (average 8.87%) and volcanic rock (average 7.97%), followed by sedimentary rock (average 2.54%) (Figure 2c). The pore space is mainly composed of primary pores and secondary pores. The content of the argillaceous matrix ranges from 0.0% to 28.0%, with an average value of 5.14%. The cement content ranges from 3.2% to 34.6%, with an average value of 12.58%. The clastic grains were medium or well sorted, and the roundness was subangular and subrounded. The content of clay minerals in the H4 and H5 sandstones ranged from 2.1% to 35.2%, with an average value of 7.45%. Illite is the predominant clay mineral in the tight sandstone, followed by chlorite and illite–smectite mixed layers (Figure 2d). The illite content in the H4 and H5 sandstones varies from 0.231% to 9.37%.
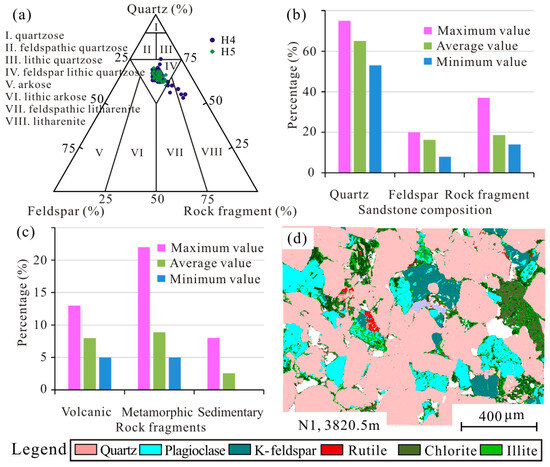
Figure 2.
(a) Ternary plot of rock types in the H4 and H5 members of N gas field in Xihu Sag [40]. (b) Histogram of framework mineral composition. (c) Histogram of rock fragment type. (d) Scanning electron microscope mineral quantitative evaluation data.
3.2. Diagenesis
3.2.1. Compaction
The average burial depth of H4 and H5 in the N gas field is greater than 3780 m. Point-to-line contact, line contact, concave–convex contact, and a small number of point and sutured contacts can be observed under petrographic observation (Figure 3). The clastic grains of the H4 and H5 sandstone experienced mechanical compaction, which is mainly evidenced by the point and line contacts between mineral grains, bending of mica grain, and breakage of quartz and feldspar grains (Figure 3a–d). Evidence of chemical compaction is concave–convex contact and sutured contact between mineral grains (Figure 3e,f).

Figure 3.
Compaction evidence of the H4 and H5 sandstones. (a) Point contact and point-to-line contact. (b) Line contact. (c) Mica bending. (d) Breakage of quartz and feldspar grains. (e) Concave–convex contact. (f) Sutured contact.
According to calculated values, the compaction porosity reduction rate of H4 and H5 sandstone ranges from 27.48% to 96.57% and from 47.93% to 93.27%, respectively, and the average values are 83.93% and 85.12%, respectively.
3.2.2. Quartz Cement
Quartz cement is a common authigenic mineral in H4 and H5 tight sandstones (Figure 4a–d). Quartz cement primarily contains two forms of quartz overgrowth and authigenic quartz crystals (Figure 4a,b). The thickness of quartz overgrowth is primarily distributed between 10 μm and 100 μm (Figure 4a), and the size of authigenic quartz crystals is usually less than 35 μm (Figure 4b). Authigenic quartz crystals are chiefly distributed in the intergranular pores. Two-phase quartz overgrowth can be easily identified by dust line (Figure 4c). The H4 and H5 sandstones developed quartz overgrowth and authigenic quartz crystals (Figure 4a–d).
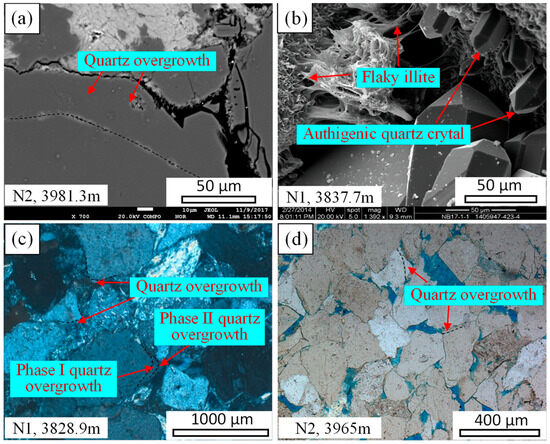
Figure 4.
(a) Quartz overgrowth. (b) Authigenic quartz crystals and flaky illite in intergranular pores. (c) Two-phase quartz overgrowth. (d) Quartz overgrowth.
3.2.3. Illite
Illite is one of the main clay minerals in the H4 and H5 tight sandstones. Detrital illite and authigenic illite can be observed under a scanning electron microscope (Figure 5). Detrital illite is characterized by thick flake, dark color, tight packing, and distinct squeeze features (Figure 5a), whereas authigenic illite is distinctly different. The morphologies of authigenic illite are inner illite coat, honeycomb, flaky, hair-like, filamentous, and pore-bridging (Figure 5b–f). The inner illite coat can be observed on mineral grains (Figure 5b), and the inner illite coat is not common in H4 and H5 tight sandstone. Flaky and honeycomb illites chiefly appear in residue intergranular pores (Figure 5c,d). Filamentous and hair-like illites are widely developed in intergranular dissolution pores and intragranular dissolution pores (Figure 5e,f). Pore-bridging illite is distributed at the narrow pores and throats (Figure 5f). Hair-like and filamentous illites are common at the end of flaky illite on and around the mineral grain. The length of flaky illite is primarily 2–15 μm, and the length of filamentous illite is mainly 5–20 μm.

Figure 5.
Evidence of illite in H4 and H5 tight sandstone of N gas field in Xihu Sag. (a) Detrital illite. (b) Inner illite coat. (c) Flaky illite. (d) Honeycomb illite. (e) Intragranular dissolution pores of plagioclase and filamentous illite. (f) Filamentous illite and pore-bridging illite.
Based on the morphology of illite and the relationship between illite and mineral grains, the illite distribution was analyzed. Inner illite coats are mainly distributed on the grain surface (Figure 6a,b). The inner illite coat is mainly developed in sheet sand sedimentary facies and the upper part of subaqueous distributary channel sedimentary facies. Flaky illite and honeycomb illite mainly appear in residue intergranular pores (Figure 6c). Flaky and honeycomb illites chiefly develop in the upper part of channel bar sedimentary facies, the upper part of subaqueous distributary channel sedimentary facies, and sheet sand sedimentary facies. Filamentous and hair-like illites mainly distribute in intergranular dissolution pores and intragranular dissolution pores, indicating the formation of secondary pores to a certain extent (Figure 6d–f). Filamentous and hair-like illites mainly develop in the middle and upper parts of channel bar sedimentary facies and the middle and upper parts of subaqueous distributary channel sedimentary facies. Illite distribution has a certain influence on reservoir quality. Authigenic illites are associated with the presence of primary pores and secondary pores (Figure 6d–f).
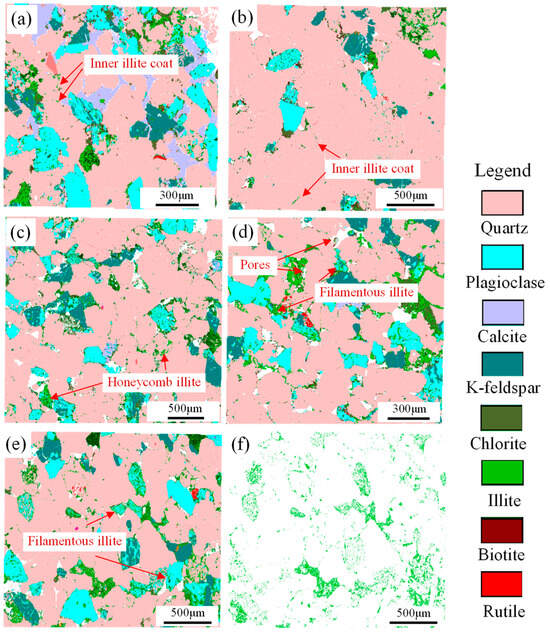
Figure 6.
Mineral quantification evaluation images showing the presence of different illites. (a) Mineral composition and inner illite coat in sheet sand sandstone. (b) Mineral composition and inner illite coat in the upper sandstone of subaqueous distributary channel. (c) Mineral composition, flaky and honeycomb illite in the upper sandstone of subaqueous distributary channel. (d) Mineral composition, primary pores, secondary pores, filamentous, and pore-bridging illite in the channel bar sandstone. (e) Mineral composition, filamentous and pore-bridging illite in the channel bar sandstone. (f) Filamentous and pore-bridging illite in the channel bar sandstone.
3.2.4. Chlorite and Illite–Smectite Mixed Layers
Chlorite is an important clay mineral in the H4 and H5 sandstones. The morphologies of chlorite are primarily detrital grain coat, authigenic grain coat, and pore filling. The size of the detrital chlorite coat is chiefly 1–2 μm, whereas the size of the authigenic chlorite coat is primarily 6–8 μm (Figure 7a,b). It is common that an authigenic chlorite coat grows on a detrital chlorite coat (Figure 7b). Pore-filling chlorite fills the pores and blocks the throats (Figure 7c). The H4 and H5 sandstone primarily develops pore-filling chlorite and minor chlorite coat (Figure 7a–c).

Figure 7.
(a) Authigenic chlorite coat. (b) Detrital chlorite coat and authigenic chlorite coat. (c) Pore-filling chlorite. (d) Illite–smectite mixed layer.
Illite–smectite mixed layer is an intermediate transition mineral in the diagenetic evolution from smectite to illite. The morphology characteristics of the illite–smectite mixed layer are between smectite (honeycomb and mesh) and illite (flaky, filamentous, and hair-like). Illite–smectite mixed layers appear in the form of flaky and honeycomb crystals (Figure 7d), and the size of curled edges ranges from 2 μm to 15 μm. The illite–smectite mixed layer is primarily distributed in the intergranular pores.
3.2.5. Carbonate Cement
Under thin sections, calcite is a red pore-filling poikilitic bulk crystal, and ferrocalcite appears purplish red (Figure 8a). Under cathodoluminescence thin sections, red calcite can be observed surrounded by light to dark purple ferrocalcite (Figure 8b). The development of calcite cement is uneven, showing basal distribution and clustered distribution (Figure 8c,d). The cathodoluminescence of calcite is orange to orange-yellow (Figure 8d). The ferrocalcite cement is primarily developed at the edge of calcite cement or dispersedly distributed in residual primary pores and secondary pores (Figure 8d), and the cathodoluminescence of ferrocalcite is orange-red (Figure 8d).

Figure 8.
(a) Thin section image showing calcite and ferrocalcite cement. (b) Cathodoluminescence thin section image showing calcite and ferrocalcite cement. (c) Cathodoluminescence thin section image showing calcite cement. (d) Cathodoluminescence thin section image showing calcite and ferrocalcite cement. (e) Intragranular dissolution pores of k-feldspar. (f) Intragranular dissolution pores of k-feldspar.
3.2.6. Feldspar Dissolution
Feldspar in the H4 and H5 tight sandstones in Xihu Sag chiefly includes k-feldspar and plagioclase (Figure 8e,f). Partially or completely dissolved plagioclase and k-feldspar are common in the H4 and H5 sandstones, and pore spaces are chiefly intergranular dissolution pores, intragranular dissolution pores, and moldic pores. K-feldspar grains are usually partially dissolved and filled with authigenic illite, usually with intragranular dissolution pores and moldic pores (Figure 8e,f). The dissolution of k-feldspar and potassium-rich rock fragments may produce authigenic illite. Authigenic illite is primarily distributed in the bicrystal structure and cleavage plane of k-feldspar (Figure 8e,f). Under certain circumstances, k-feldspar dissolved to form a network structure (Figure 8f).
3.2.7. Diagenetic Evolution Sequence
Based on thin sections, cathodoluminescence thin sections, scanning electron microscopes, mineral quantification analysis, and previous diagenetic evolution sequences, a diagenetic evolution sequence was established (Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8) [34]. The characteristics observed during early diagenesis chiefly include (1) compaction, (2) formation of chlorite coat and calcite cementation due to connate alkaline pore water, (3) formation of inner illite coat, (4) conversion of smectite to illite, and (5) dissolution of feldspar due to late Oligocene meteoric water leaching, accompanied by the precipitation of kaolinite and quartz cement (Figure 9) (Wang et al., 2021). The middle diagenesis characteristics primarily contain the following: (1) Dissolution of feldspar, rock fragment, and carbonate cement due to organic acid and CO2 acid fluid and precipitation of kaolinite and quartz cement; (2) Continuous compaction; (3) Illitization of k-feldspar; (4) Illitization of k-feldspar and kaolinite; (5) Formation of chlorite, illite, and late ferrocalcite in alkaline diagenetic environment from late Miocene to present day (Figure 9).
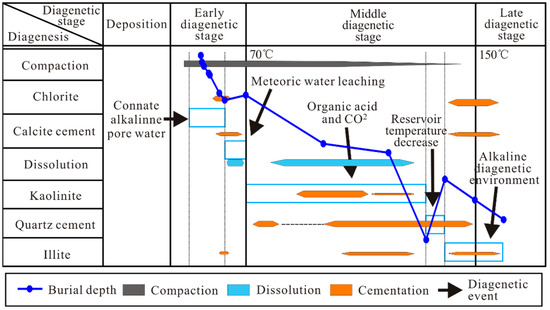
Figure 9.
Diagenetic evolution sequence of the H4 and H5 tight sandstone.
3.3. Pore Throat Structure Characteristics
The pore throat structure and pore size distribution of the sample were obtained by high pressure mercury injection experiment. According to high pressure mercury injection experiment data of 16 representative samples, the displacement pressure and average pore throat radius of the samples are 0.02–2.0 MPa and 0.11–4.7 μm, respectively (Table 1). Maximum mercury saturation, relative sorting coefficient, and skewness of the samples range from 65.6% to 99.5%, from 0.16 to 0.53, and from 0.85 to 2.02, respectively.

Table 1.
Parameters of the high pressure mercury injection experiment.
The pore throat distribution curves of tight sandstone in the study area were obtained by using a high pressure mercury injection curve. It can be seen from the mercury injection curve (Figure 10a) that the trend of the mercury injection curve for most samples is consistent. The front section of the mercury injection curve is relatively gentle, while the back section gradually rises. The pore throat radius was mainly distributed in the range of 0.01–63.0 μm (Figure 10b), and the curve showed a multi-peak distribution. Small pore throats are mainly concentrated in about 0.03 μm, medium pore throats are chiefly concentrated in about 0.8 μm, and large pore throats are mainly concentrated in about 6.5 μm. Although the variation range of pore throats radius is basically similar, the distribution frequency of different pore throats is very different.
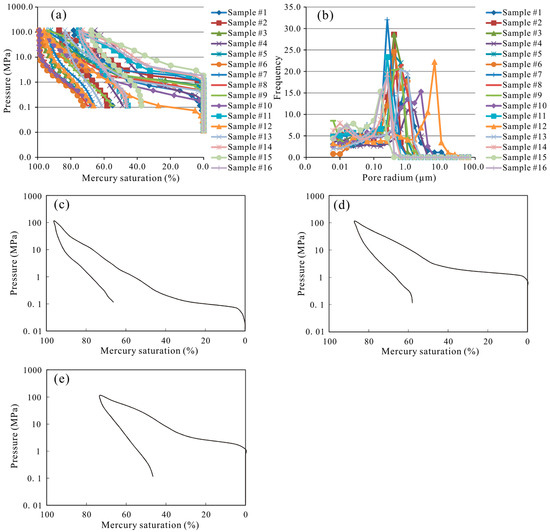
Figure 10.
(a) Typical high pressure mercury injection experiment curves. (b) The characteristics of pore radius of high pressure mercury injection experiment. (c) Capillary pressure curve of mercury intrusion and extrusion of type I sweet spots. (d) Capillary pressure curve of mercury intrusion and extrusion of type II sweet spots. (e) Capillary pressure curve of mercury intrusion and extrusion of type III sweet spots.
Based on reservoir properties, the classification and evaluation criteria for the sweet spot in Huagang Formation were established, namely, type I sweet spots (Φ > 10%, K > 1 mD), type II sweet spots (8% < Φ < 10%, 0.4 mD < K < 1 mD), and type III sweet spots (Φ < 8%, K < 0.4 mD). According to the matching conventional core analysis data and high pressure mercury injection experiment data, the experiment samples were divided into type I, type II, and type III (Figure 10c–e).
3.4. Fractal Characteristics
Figure 11 shows the relationship between lg(1−SHg) and lg(Pc) of typical samples. The average fractal dimensions of macropores, mesopores, transitional pores, and micropores of type I sweet spots are 2.93, 2.72, 2.632, and 2.45, respectively, and the corresponding average porosities are the following: 3.24%, 5.6%, 2.6%, and 0.87% (Figure 11a). The average fractal dimensions of mesopores, transitional pores, and micropores of type II sweet spots are 2.46, 2.46, and 2.05, respectively, and the corresponding average porosities are 6.16%, 2.35%, and 0.85% (Figure 11b). The average fractal dimensions of mesopores, transitional pores, and micropores of type III sweet spots are 2.78, 2.75, and 2.64, respectively, and the corresponding average porosities are 2.98%, 2.77%, and 1.05% (Figure 11c). According to the fractal dimension analysis of the macropores, mesopores, transitional pores, and micropores of the experiment samples, the fractal dimension range of different pore types is between 2 and 3. The fractal dimension of the macropore is large, the fractal dimension of the micropore is small, and the fractal dimension of the mesopore and transitional pore is intermediate (Figure 11d).
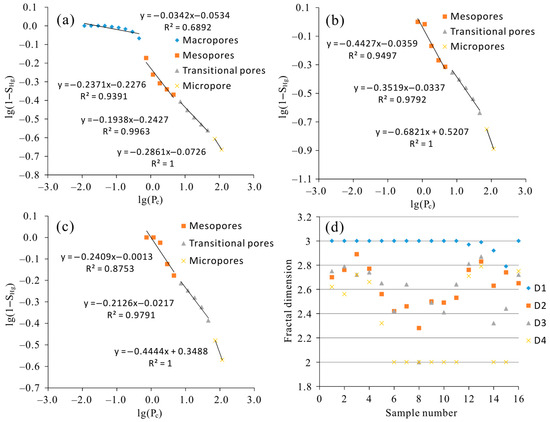
Figure 11.
(a) Fractal dimension curve of type I sweet spots. (b) Fractal dimension curve of type II sweet spots. (c) Fractal dimension curve of type III sweet spots. (d) Fractal dimension distribution of macropore, mesopore, transitional pore, and micropore of the sample in the study area.
The total fractal dimension of the entire pore throat was obtained by the weighted average method. The total fractal dimensions of type I, type II, and type III sweet spots were distributed in the ranges of 2.62–2.87, 2.22–2.56, and 2.71–2.77, respectively (Table 2). The average value of the total fractal dimension of type I sweet spots was 2.726, and the high total fractal dimension was mainly caused by macropores, mesopores, transitional pores, and micropores, especially the contribution of macropores. The average value of the total fractal dimension of the type II sweet spot was 2.43, and the low total fractal dimension was chiefly caused by mesopores, transitional pores, and micropores. The average value of the total fractal dimension of the type III sweet spot was 2.738, and the high total fractal dimension was primarily caused by mesopores, transitional pores, and micropores, especially the contribution of micropores.

Table 2.
Statistical table of fractal dimensions of different pore types of experiment samples in the study area.
4. Discussion
4.1. Relationship between Fractal Dimension, Reservoir Properties and Pore Structure Parameters
4.1.1. Relationship between Fractal Dimension and Reservoir Properties
The relationship between total fractal dimension, porosity, and permeability was investigated. The relationship between total fractal dimension, porosity, and permeability of type I, type II, and type III sweet spots were significantly different. Among them, the negative correlation between total fractal dimension, porosity, and permeability of type I sweet spots was different from that of type II and type III sweet spots (Figure 12a,b). This indicated that pore space types of type I sweet spots were different from those of type II and type III sweet spots. The pore types of type I sweet spots included macropore, mesopore, transitional pore, and micropore, especially the contribution of macropores, whereas type II and type III sweet spots contained mesopores, transitional pores, and micropores. The total fractal dimension of type I sweet spots was large, indicating that the complexity of the macropores had a great influence on porosity and permeability. The total fractal dimension of type II and type III sweet spots had a significant negative correlation with porosity and permeability, and mesopores and transitional pores had a great influence on reservoir properties. The total fractal dimension of type III sweet spots was larger than that of type II sweet spots, indicating that the complexity of micropores had a greater influence on porosity and permeability.
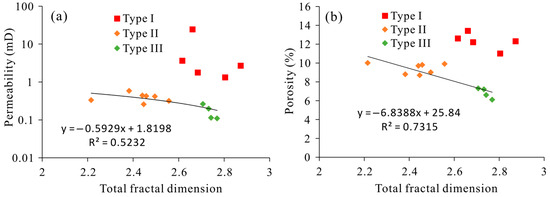
Figure 12.
(a) Relationship between total fractal dimension and porosity. (b) Relationship between total fractal dimension and permeability.
4.1.2. Relationship between Fractal Dimension and Pore Structure Parameters
The relationship between total fractal dimension and pore structure parameters was investigated. Figure 13a shows the negative correlation between the total fractal dimension and maximum mercury saturation. Due to different pore types, the negative correlation between total fractal dimension and maximum mercury saturation of type I sweet spots was different from that of type II and type III sweet spots. The maximum mercury saturation for type I and type II sweet spots was high. This indicated that mesopores and transitional pores had a significant impact on the storage space of type II sweet spots, macropores, mesopores, and transitional pores had a significant impact on the storage space of type I sweet spots, and transitional pores, micropores and mesopores had a significant impact on the storage space of type III sweet spots. Figure 13b shows the negative correlation between the total fractal dimension and the average pore throat radius. The negative correlation between the total fractal dimension and average pore throat radius of type II and type III sweet spots was significant, while there was no significant correlation between the total fractal dimension and average pore throat radius of type I sweet spots. This indicated that the smaller the total fractal dimension of the pore throat structure of type II and III sweet spots, the larger the average pore throat radius. The average pore throat radius of type I sweet spots was large, the average pore throat radius of type III sweet spots was small, and the average pore throat radius of type II sweet spots was between type I and type III sweet spots. The negative correlation between total fractal dimension and skewness of type II and type III sweet spots was significant, whereas there was no correlation between total fractal dimension and skewness of type I sweet spots (Figure 13c). This indicated that the symmetry of micropores, transitional pores, and mesopores distribution had an impact on the fractal characteristics of the pore throat structure of type II and III sweet spots, and the symmetry of macropores distribution had an important impact on the fractal characteristics of the pore throat structure of type I sweet spots.
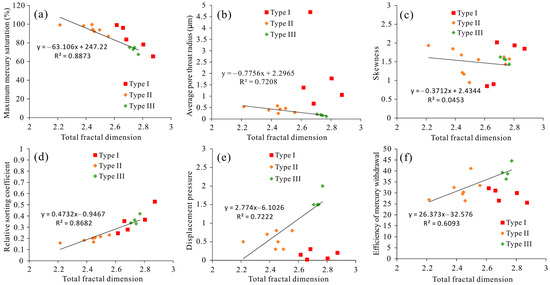
Figure 13.
Relationship between total fractal dimensions and pore structure parameters. (a) Relationship between total fractal dimension and maximum mercury saturation. (b) Relationship between total fractal dimension and average pore throat radius. (c) Relationship between total fractal dimension and skewness. (d) Relationship between total fractal dimension and relative sorting coefficient. (e) Relationship between total fractal dimension and displacement pressure. (f) Relationship between total fractal dimension and efficiency of mercury withdrawal.
The positive correlation between the total fractal dimension of type I, type II, and type III sweet spots and the relative sorting coefficient was significant. The relative sorting coefficient of type II sweet spots was smaller than that of type I and type III sweet spots (Figure 13d). The relative sorting coefficient is a parameter that accurately reflects the uniformity of pore throat distribution. The smaller the relative sorting coefficient, the more uniform the pore throat distribution. This indicated that the pore throat distribution uniformity of type II sweet spots was better than that of type I and III sweet spots. Figure 13e shows the relationship between the total fractal dimension and displacement pressure. The correlation between the total fractal dimension of type I sweet spots and displacement pressure was not significant, whereas the positive correlation between the total fractal dimension of type II and type III sweet spots and displacement pressure was significant. This indicated that the larger the total fractal dimension of type II and type III sweet spots, the larger the displacement pressure. The displacement pressure of the type I sweet spot was small, and the displacement pressure of the type III sweet spot was large. The correlation between the total fractal dimension of type I sweet spots and the efficiency of mercury withdrawal was not significant, whereas the positive correlation between the total fractal dimension of type II and type III sweet spots and the efficiency of mercury withdrawal was significant (Figure 13f). The efficiency of mercury withdrawal of type I sweet spots was similar to that of type II sweet spots. Mercury withdrawal efficiency can reflect the pore throat connectivity of tight sandstone. This indicated that the pore throat connectivity of type II sweet spots was the best, the pore throat connectivity of type III sweet spots was the worst, and the pore throat connectivity of type I sweet spots was similar to that of type II sweet spots.
4.2. Effect of Diagenesis on Fractal Characteristics
The H4 and H5 tight sandstone in Xihu Sag was mainly composed of quartz, feldspar, and rock fragment minerals and experienced various diagenesis during burial. According to thin section and scanning electron microscope observation, pore space and reservoir properties of tight sandstone were affected by compaction, quartz cementation, clay mineral conversion, carbonate cementation, and dissolution (Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8). There is a good relationship between fractal dimension and pore space (porosity and average pore throat radius) and its homogeneity (sorting coefficient). Therefore, the effect of diagenesis on fractal dimension was studied through the effect of different diagenesis on pore space and its homogeneity.
4.2.1. Effect of Compaction on Fractal Characteristics
With the increase in burial depth, the compaction of tight sandstone caused the change of contact type from point contact, point–line contact, line contact to concave–convex contact, or mica bending and grain breakage (Figure 3a–d), which reduced pore space of tight sandstone and increased fractal dimension. The concave–convex contact and sutured contact formed by pressure dissolution increased reservoir heterogeneity and fractal dimension (Figure 3e,f).
4.2.2. Effect of Cementation on Fractal Characteristics
Quartz cement is a major type of cement in the H4 and H5 tight sandstones, including quartz overgrowth and authigenic quartz crystals. Quartz overgrowth and authigenic quartz crystals blocked pores and throats (Figure 4), reduced pore space, and increased fractal dimension.
The effect of clay minerals on pore throat structures was quite complex, and the effect of different types and contents of clay minerals on pore structure was different [41,42,43]. Chlorite coat can inhibit compaction, protect pore throat structures, and maintain fractal dimension (Figure 7a,b). Pore-filling chlorite mainly filled intergranular pores, reduced pore space (Figure 7c,d), and increased reservoir heterogeneity and fractal dimension. Illite and illite–smectite mixed layers were filamentous or flaky and mainly dispersed on the surface of dissolved grains (Figure 5a,b). When the potassium ions produced by complete dissolution of k-feldspar cannot be effectively transported and discharged, the dissolved products of k-feldspar often form illite (Figure 5e). A large number of clay minerals filled primary pores and secondary pores, destroyed sandstone porosity and permeability, and increased the fractal dimension.
Calcite is an important cement in H4 and H5 tight sandstones, including calcite and ferrocalcite (Figure 8a–d). Calcite and ferrocalcite appeared orange to orange-yellow and light to dark purple under a cathodoluminescence thin section (Figure 8b–d). Calcite and ferrocalcite filled residual primary pores and secondary pores, reduced sandstone porosity and permeability, and increased reservoir heterogeneity and fractal dimension.
4.2.3. Effect of Dissolution on Fractal Characteristics
The dissolution of H4 and H5 tight sandstone in Xihu Sag was mainly caused by organic acids and CO2 acidic fluids [34,44,45,46]. The organic acids and CO2 acidic fluids led to the dissolution of feldspar, rock fragments, and carbonate cement to form intergranular dissolution pores and intragranular dissolution pores, increasing the pore space of tight sandstones (Figure 8e,f). Therefore, the dissolution of feldspar and rock fragments improved pore space and reduced the fractal dimension of the pore throat structure (Figure 8e,f).
4.3. Implication for Sweet Spot Prediction
The accuracy of the fractal dimension of tight sandstone sweet spots was analyzed based on analytical test data and fractal dimension calculation procedure. The accuracy analysis of the fractal dimension primarily includes the following three aspects: (1) High pressure mercury injection experiment is to inject non-wetting phase fluid mercury into the pore throat radius distribution of the core sample under a certain pressure. By directly injecting mercury into pore space, three-dimensional pore structure information can be obtained from large core samples, which ensures the accuracy of fractal dimensions of pore throat structures. (2) The fractal dimension calculation procedure considers in detail the turning point determination on lg(1−SHg) and lg(Pc) curves and fractal dimension fitting. The turning points of micropores, transitional pores, mesopores, and macropores can be clearly determined on lg(1−SHg) and lg(Pc) curves. Considering the fractal dimension and pore space content of different pores comprehensively, the weighted average method was used to calculate the total fractal dimension of core samples, which indicates that the reliability of the fractal dimension of pore structure in this study is relatively high. (3) The average value of the total fractal dimension of type I, type II, and type III sweet spots in tight sandstone are 2.726, 2.43, and 2.738. The fractal dimension is an important index to characterize the heterogeneity of microstructure, and the fractal dimension of the pore throat structure is between 2 and 3. This supports the accuracy of the fractal dimensions of pore throat structures in this study.
The clastic components of H4 and H5 tight sandstone in Xihu Sag are mainly composed of quartz, feldspar, rock fragments, and clay minerals. These tight sandstones experienced complex diagenesis, resulting in differences in pore throat structures and fractal dimensions.
The fractal dimension of H4 and H5 tight sandstone sweet spots in Xihu Sag and the effect of diagenesis on the fractal dimension were investigated. Type I sweet spots developed macropores, mesopores, transitional pores, and micropores, with macropores leading to a more complex pore throat structure, with a total fractal dimension range of 2.62–2.87. The average fractal dimensions of macropores, mesopores, transitional pores, and micropores of type I sweet spots are 2.93, 2.72, 2.63, and 2.45, with corresponding average porosity values of 3.24%, 5.6%, 2.6%, and 0.87%, respectively. The fractal dimensions of type I sweet spots were mainly controlled by chlorite coat formation, dissolution, and a small amount of compaction. Type II sweet spots developed mesopores, transitional pores, and micropores, and the total fractal dimension range was 2.22–2.56. The average fractal dimensions of mesopores, transitional pores, and micropores of type II sweet spots are 2.46, 2.46, and 2.05, respectively, with corresponding average porosity values of 6.16%, 2.35%, and 0.85%. The fractal dimension of the type II sweet spot was chiefly controlled by quartz cementation, clay mineral transformation, and a small amount of dissolution. Type III sweet spots developed mesopores, transitional pores, and micropores, and micropores led to a more complex pore throat structure, with total fractal dimensions ranging from 2.71 to 2.77. The average fractal dimensions of mesopores, transitional pores, and micropores of type III sweet spots are 2.78, 2.75, and 2.64, respectively, with corresponding average porosity values of 2.98%, 2.77%, and 1.05%. The fractal dimension of the type III sweet spot was primarily controlled by compaction, calcite cementation, and quartz cementation. This study indicates that the fractal dimension of the pore throat structure of the sweet spot and the effect of diagenesis on the fractal dimension can improve the understanding of the reservoir quality of tight sandstone.
5. Conclusions
In this study, fractal dimensions of pore throat structures and the effect of diagenesis on the fractal dimension of the fourth (H4) and fifth (H5) members tight sandstone sweet spots of the Huagang Formation in the Jiaxing area of Xihu Sag were investigated by integrating thin section, scanning electron microscope, X-ray diffraction data, scanning electron microscope quantitative mineral evaluation, and high pressure mercury injection experiment. Five main conclusions were obtained.
- (1)
- The H4 and H5 tight sandstone is composed of moderately to well sorted, subangular to subrounded feldspathic lithic quartzose. The average values of quartz, feldspar, and rock fragment grains are 65.04%, 16.29%, and 18.68%, respectively. The H4 and H5 sandstone experienced early diagenesis and middle diagenesis. The early diagenesis stage included compaction, chlorite coat formation, calcite cementation, inner illite coat formation, smectite to illite conversion, feldspar dissolution, kaolinite, and quartz cement precipitation. The middle diagenesis stage contained the dissolution of feldspar, rock fragment and carbonate cement, precipitation of kaolinite and quartz cement, illitization of k-feldspar, and formation of illite, chlorite, and ferrocalcite.
- (2)
- The fractal dimension of tight sandstone sweet spots was investigated. The average fractal dimensions of macropores, mesopores, transitional pores, and micropores of type I sweet spots are 2.93, 2.72, 2.632, and 2.45, respectively, and the corresponding average porosities are 3.24%, 5.6%, 2.6%, and 0.87%, respectively. The average fractal dimensions of mesopores, transitional pores, and micropores are 2.46, 2.46, and 2.05, respectively, and the corresponding average porosities are 6.16%, 2.35%, and 0.85%, respectively. The average fractal dimensions of mesopores, transitional pores, and micropores are 2.78, 2.75, and 2.64, respectively, and the corresponding average porosities are 2.98%, 2.77%, and 1.05%, respectively.
- (3)
- The relationship between fractal dimension, reservoir properties, and pore structure parameters was determined. The negative correlation between total fractal dimension, porosity, and permeability of type I sweet spots was different from that of type II and type III sweet spots. The negative correlation between the total fractal dimensions of type II and type III sweet spots and maximum mercury saturation, average pore throat radius, and skewness were significant, whereas the correlation between total fractal dimensions of type I sweet spots and maximum mercury saturation, average pore throat radius and skewness were not significant. The positive correlation between the total fractal dimension of type II and type III sweet spots and the relative sorting coefficient, displacement pressure, and efficiency of mercury withdrawal were significant, whereas the correlation between the total fractal dimension of type I sweet spots and relative sorting coefficient, displacement pressure and efficiency of mercury withdrawal were not significant.
- (4)
- The effect of diagenesis on fractal dimensions was investigated. Compaction reduced pore space of tight sandstone and increased fractal dimension. Quartz cementation and calcite cementation blocked pores and throats, reduced pore space, and increased fractal dimensions. Chlorite coat can inhibit compaction, protect pore throat structures, and maintain fractal dimensions. Most clay minerals filled primary pores and secondary pores, destroyed sandstone porosity and permeability, and increased fractal dimensions. Dissolution increased the pore space of tight sandstone and decreased the fractal dimension of the pore throat structure.
- (5)
- The pore throat structures of type I sweet spots was mainly composed of macropores, mesopores, transitional pores, and micropores, and fractal dimensions of type I sweet spots was chiefly controlled by chlorite coat formation, dissolution, and a small amount of compaction. This study shows that fractal dimensions of pore throat structures of the sweet spots and the effect of diagenesis on fractal dimensions can improve the understanding of the reservoir quality of tight sandstone.
Author Contributions
Conceptualization, W.W., C.L. and X.Z.; methodology, W.W.; software, W.W.; validation, W.W., C.L. and X.Z.; formal analysis, W.W.; investigation, W.W.; resources, W.W., C.L. and X.Z.; data curation, W.W.; writing—original draft preparation, W.W.; writing—review and editing, W.W. and C.L.; visualization, W.W.; supervision, C.L. and X.Z.; project administration, W.W., C.L. and X.Z.; funding acquisition, W.W. and C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the National Natural Science Foundation of China (42202144), Innovative Research Groups of the National Natural Science Foundation of China (U19B2006), and the Natural Science Foundation of Shandong Province (ZR2022QD048).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors gratefully thank the main editors and anonymous reviewers for their valuable comments and suggestions leading to improvement of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kong, X.; Xiao, D.; Jiang, S.; Lu, S.; Sun, B.; Wang, J. Application of the combination of high-pressure mercury injection and nuclear magnetic resonance to the classification and evaluation of tight sandstone reservoirs: A case study of the Linxing Block in the Ordos Basin. Nat. Gas Ind. B 2020, 7, 433–442. [Google Scholar] [CrossRef]
- Li, J.J.; Jiang, H.Q.; Wang, C.; Zhao, Y.Y.; Gao, Y.J.; Pei, Y.L.; Wang, C.C.; Dong, H. Pore-scale investigation of microscopic remaining oil variation characteristics in water-wet sandstone using CT scanning. J. Nat. Gas Sci. Eng. 2017, 48, 36–45. [Google Scholar] [CrossRef]
- Zhao, N.; Wang, L.; Zhang, W.; Peng, Y.; Sima, L. Investigation of pore structure characteristics in marine deep-water high-temperature and high-pressure sandstone: A comprehensive characterization combining various experimental techniques. Geoenergy Sci. Eng. 2023, 222, 211433. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, J.; Lan, Y.; Zi, H.; Cui, Y.; Chen, Q.; You, L.; Fan, X.; Wang, G. New insights into pore fractal dimension from mercury injection capillary pressure in tight sandstone. Geoenergy Sci. Eng. 2023, 228, 212059. [Google Scholar] [CrossRef]
- Ge, X.; Fan, Y.; Deng, S.; Han, Y.; Liu, J. An improvement of the fractal theory and its application in pore structure evaluation and permeability estimation. J. Geophys. Res. Solid Earth 2016, 121, 6333–6345. [Google Scholar] [CrossRef]
- Fan, X.; Wang, G.; Li, Y.; Dai, Q.; Song, L.; Duan, C.; Zhang, C.; Zhang, F. Pore structure evaluation of tight reservoirs in the mixed siliciclasticcarbonate sediments using fractal analysis of NMR experiments and logs. Mar. Pet. Geol. 2019, 109, 484–493. [Google Scholar] [CrossRef]
- Dai, Q.; Wang, G.; Zhao, X.; Han, Z.; Lu, K.; Lai, J.; Wang, S.; Li, D.; Li, Y.; Wu, K. Fractal model for permeability estimation in low-permeable porous media with variable pore sizes and unevenly adsorbed water lay. Mar. Pet. Geol. 2021, 130, 105135. [Google Scholar] [CrossRef]
- Liu, W.; Lu, S.; Wang, M.; Zhang, S.; Liu, Y.; Zhou, N.; Guan, Y.; Wang, H. Overall pore characterization of tight sandstone reservoir space and its significance: A case study of the outer expansion area of Long 26 in Longhupao oilfield, Songliao Basin. J. Northeast Pet. Univ. 2018, 42, 41–51. [Google Scholar]
- Guo, R.; Xie, Q.; Qu, X.; Chu, M.; Li, S.; Ma, D.; Ma, X. Fractal characteristics of pore-throat structure and permeability estimation of tight sandstone reservoirs: A case study of Chang 7 of the Upper Triassic Yanchang Formation in Longdong area, Ordos Basin, China. J. Pet. Sci. Eng. 2019, 184, 106555. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, C.; Ouyang, S.; Luo, B.; Zhao, D.; Sun, W.; Awan, R.S.; Lu, Z.; Li, G.; Zang, Q. Investigation of pore-throat structure and fractal characteristics of tight sandstones using HPMI, CRMI, and NMR methods: A case study of the Lower Shihezi Formation in the Sulige area, Ordos Basin. J. Pet. Sci. Eng. 2022, 210, 110053. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, X. Study on characteristics parameters of coal core structure on fractal theory. J. Henan Univ. Nat. Sci. 2023, 53, 729–737. [Google Scholar]
- Mayo, S.; Josh, M.; Nesterets, Y.; Esteban, L.; Pervukhina, M.; Clennell, M.B.; Maksimenko, A.; Hall, C. Quantitative micro-porosity characterization using synchrotron micro-CT and xenon K-edge subtraction in sandstones, carbonates, shales and coal. Fuel 2015, 154, 167–173. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Freeman, M.; He, L.; Agamalian, M.; Melnichenko, Y.B.; Mastalerz, M.; Bustin, R.M.; Radliński, A.P.; Blach, T.P. Characterization of tight gas reservoir pore structure using USANS/SANS and gas adsorption analysis. Fuel 2012, 95, 371–385. [Google Scholar] [CrossRef]
- Huang, H.; Sun, W.; Ji, W.; Zhang, R.; Du, K.; Zhang, S.; Ren, D.; Wang, Y.; Chen, L.; Zhang, X. Effects of pore-throat structure on gas permeability in the tight sandstone reservoirs of the Upper Triassic Yanchang formation in the Western Ordos Basin, China. J. Pet. Sci. Eng. 2018, 162, 602–616. [Google Scholar] [CrossRef]
- Zhang, F.; Jiang, Z.; Sun, W.; Li, Y.; Zhang, X.; Zhu, L.; Wen, M. A multiscale comprehensive study on pore structure of tight sandstone reservoir realized by nuclear magnetic resonance, high pressure mercury injection and constant-rate mercury injection penetration test. Mar. Pet. Geol. 2019, 109, 208–222. [Google Scholar] [CrossRef]
- Qu, Y.; Sun, W.; Tao, R.; Luo, B.; Chen, L.; Ren, D. Pore–throat structure and fractal characteristics of tight sandstones in Yanchang Formation, Ordos Basin. Mar. Pet. Geol. 2020, 120, 104573. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman & Co. Ltd.: San Francisco, CA, USA, 1983. [Google Scholar]
- Li, P.; Zheng, M.; Bi, H.; Wu, S.; Wang, X. Pore throat structure and fractal characteristics of tight oil sandstone: A case study in the Ordos Basin, China. J. Pet. Sci. Eng. 2017, 149, 665–674. [Google Scholar] [CrossRef]
- Li, K. Analytical derivation of Brooks-Corey type capillary pressure models using fractal geometry and evaluation of rock heterogeneity. J. Pet. Sci. Eng. 2010, 73, 20–26. [Google Scholar] [CrossRef]
- Giri, A.; Tarafdar, S.; Gouze, P.; Dutta, T. Fractal pore structure of sedimentary rocks: Simulation in 2-D using a relaxed bidisperse ballistic deposition model. J. Appl. Geophys. 2012, 87, 40–45. [Google Scholar] [CrossRef]
- Wang, F.; Cheng, Y.; Lu, S.; Jin, K.; Zhao, W. Influence of coalification on the pore characteristics of middle-high rank coal. Energy Fuels 2014, 28, 5729–5736. [Google Scholar] [CrossRef]
- Hu, Q.; Ewing, R.P.; Dultz, S. Low pore connectivity in natural rock. J. Contam. Hydrol. 2012, 133, 76–83. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Huang, Z.; Zhao, L.; Han, W.; Ding, C.; Sun, X.; Yan, R.; Zhang, T.; Yang, X.; Wang, R. Pore structure and multi-fractal analysis of tight sandstone using MIP, NMR and NMRC methods: A case study from the Kuqa depression, China. J. Pet. Sci. Eng. 2019, 178, 544–558. [Google Scholar] [CrossRef]
- Qiao, J.; Zeng, J.; Jiang, S.; Wang, Y. Impacts of sedimentology and diagenesis on pore structure and reservoir quality in tight oil sandstone reservoirs: Implications for macroscopic and microscopic heterogeneities. Mar. Pet. Geol. 2020, 111, 279–300. [Google Scholar] [CrossRef]
- Deng, Y. Analysis on differences of petroleum type and geological conditions between two depression belts in China offshore. Acta Pet. Sin. 2009, 30, 1–8. [Google Scholar] [CrossRef]
- Gao, M.; Lu, Y.; Du, X.; Ma, Y.; Zhang, J.; Deng, K. Multi-factor evaluation for fine grading of tight sandstone reservoirs: A case study from H3 sand group in the upper section of Oligocene Huagang Formation, Xihu Sag, East China Sea Basin. Pet. Geol. Exp. 2021, 43, 1097–1106. [Google Scholar]
- Wang, W.; Lin, C.; Zhang, X.; Dong, C.; Ren, L.; Lin, J. Seismic diagenetic facies prediction of tight sandstone in the offshore sparse well area: An example from the Xihu Depression of the East China Sea Basin. J. Pet. Sci. Eng. 2022, 216, 110825. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, S. Natural gas migration and accumulation patterns in the central-north Xihu Sag, East China Sea Basin. Nat. Gas Geosci. 2021, 32, 1163–1176. [Google Scholar] [CrossRef]
- Zhang, Z.; He, X.; Tang, X.; Zhu, H. Structural trap characteristics and reservoir types in Xihu Sag, East China Sea Basin. Mar. Geol. Front. 2022, 38, 27–35. [Google Scholar] [CrossRef]
- Su, A.; Chen, H.; Chen, X.; He, C.; Liu, H.; Li, Q.; Wang, C. The characterisitcs of low permeability reservoirs, gas origin, generation and charge in the central and western Xihu depression, East China Sea Basin. J. Nat. Gas Sci. Eng. 2018, 53, 94–109. [Google Scholar] [CrossRef]
- Stroker, T.M.; Harris, N.B.; Crawford Elliott, W.; Marion Wampler, J. Diagenesis of a tight gas sand reservoir: Upper Cretaceous Mesaverde Group, Piceance Basin, Colorado. Mar. Pet. Geol. 2013, 40, 48–68. [Google Scholar] [CrossRef]
- Scherer, M. Parameters influencing porosity in sandstones: A model for sandstone porosity prediction. AAPG Bull. 1987, 71, 1508. [Google Scholar] [CrossRef]
- Houseknecht, D.W. Assessing the relative importance of compaction processes and cementation to reduction of porosity in sandstone. AAPG Bull. 1987, 71, 633–642. [Google Scholar] [CrossRef]
- Wang, W.; Lin, C.; Zhang, X.; Dong, C.; Ren, L.; Lin, J. Provenance, clastic composition and their impact on diagenesis: A case study of the Oligocene sandstone in the Xihu sag, East China Sea Basin. Mar. Pet. Geol. 2021, 126, 104890. [Google Scholar] [CrossRef]
- GBT 29171-2012; Rock Capillary Pressure Measurement. Chinese Petroleum Industry Standard: Beijing, China, 2013.
- Liu, S.; Wang, F.; Yu, R.; Gao, J.; Shi, H.; Zhu, Y. Micro pore throat structure and fractal characteristics of tight sandstone reservoir. J. Jilin Univ. Earth Sci. Ed. 2024, 54, 96–107. [Google Scholar]
- Zhu, W.; Zhang, X.; Zhou, D.; Fang, C.; Li, J.; Huang, Z. New cognition on pore structure characteristics of Permian marine shale in the Lower Yangtze Region and its implications for shale gas exploration. Nat. Gas Ind. 2021, 41, 41–55. [Google Scholar] [CrossRef]
- Xoaoth, B. Coal and Gas Outburst; Song, S., Wang, Y., Eds. and Translators; China Industry Press: Beijing, China, 1966. [Google Scholar]
- Loucks, R.G.; Reed, R.M.; Ruppel, S.C.; Hammes, U. Spectrum of pore types and networks in mudrocks and a descriptive classification for matrix-related mudrock pores. AAPG Bull. 2012, 96, 1071–1098. [Google Scholar] [CrossRef]
- Folk, R.L.; Andrews, P.B.; Lewis, D.W. Detrital sedimentary rock classification and nomenclature for use in New Zealand. N. Z. J. Geol. Geophys. 1970, 13, 937–968. [Google Scholar] [CrossRef]
- Spencer, C.W. Review of characteristics of low-permeability gas reservoirs in western United States. AAPG Bull. 1989, 73, 613–629. [Google Scholar] [CrossRef]
- Mahmic, O.; Dypvik, H.; Hammer, E. Diagenetic influence on reservoir quality evolution, examples from Triassic conglomerates/arenites in the Edvard Grieg field, Norwegian North Sea. Mar. Pet. Geol. 2018, 93, 247–271. [Google Scholar] [CrossRef]
- Zhao, D.; Hou, J.; Sarma, H.; Guo, W.; Liu, Y.; Xie, P.; Dou, L.; Chen, R.; Zhang, Z. Pore throat heterogeneity of different lithofacies and diagenetic effects in gravelly braided river deposits: Implications for understanding the formation process of high-quality reservoirs. Geoenergy Sci. Eng. 2023, 221, 111309. [Google Scholar] [CrossRef]
- Wang, W.; Lin, C.; Zhang, X.; Dong, C.; Ren, L.; Lin, J. Effect of burial history on diagenetic and reservoir-forming process of the Oligocene sandstone in Xihu sag, East China Sea Basin. Mar. Pet. Geol. 2019, 112, 104034. [Google Scholar] [CrossRef]
- Wang, W.; Lin, C.; Zhang, X.; Dong, C.; Ren, L.; Lin, J. Discussion of seismic diagenetic facies of deep reservoir in the East China Sea Basin. J. Pet. Sci. Eng. 2022, 208, 109352. [Google Scholar] [CrossRef]
- Wang, W.; Lin, C.; Zhang, X.; Dong, C.; Ren, L.; Lin, J. Diagenesis, diagenetic facies and their relationship with reservoir sweet spot in low-permeability and tight sandstone: Jiaxing area of the Xihu Sag, East China Sea Basin. Minerals 2023, 13, 404. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).