Logging Evaluation of Irreducible Water Saturation: Fractal Theory and Data-Driven Approach—Case Study of Complex Porous Carbonate Reservoirs in Mishrif Formation

Abstract

Evaluating irreducible water saturation is crucial for estimating reservoir capacity and developing effective extraction strategies. Traditional methods for predicting irreducible water saturation are limited by their reliance on specific logging data, which affects accuracy and applicability. This study introduces a predictive method based on fractal theory and deep learning for assessing irreducible water saturation in complex carbonate reservoirs. Utilizing the Mishrif Formation of the Halfaya oilfield as a case study, a new evaluation model was developed using the nuclear magnetic resonance (NMR) fractal permeability model and validated with surface NMR and mercury injection capillary pressure (MICP) data. The relationship between the logarithm mean of the transverse relaxation time (T_2lm) and physical properties was explored through fractal theory and the Thomeer Function. This relationship was integrated with conventional logging curves and an advanced deep learning algorithm to construct a T_2lm prediction model, offering a robust data foundation for irreducible water saturation evaluation. The results show that the new method is applicable to wells with and without specialized NMR logging data. For the Mishrif Formation, the predicted irreducible water saturation achieved a coefficient of determination of 0.943 compared to core results, with a mean absolute error of 2.37% and a mean relative error of 8.46%. Despite introducing additional errors with inverted T_2lm curves, it remains within acceptable limits. Compared to traditional methods, this approach provides enhanced predictive accuracy and broader applicability.

1. Introduction

In petrophysics, the distribution characteristics of immovable fluids are predominantly characterized by the irreducible water saturation parameter, which is defined as the volume of immovable water relative to the total pore volume of the rock [1]. Precisely evaluating irreducible water saturation is a crucial parameter in the exploration and development of oil and gas reservoirs [2,3]. The computation of irreducible water saturation directly influences the calculation of related parameters such as rock wettability, movable water saturation, and relative permeability [4,5]. Furthermore, it plays an essential role in identifying reservoir fluid properties, discerning water-flooded zones, and predicting production capacity [1,6].

Currently, the precise irreducible water saturation of core samples is typically determined through core experiments. The primary methods include the mercury injection capillary pressure (MICP) method [7], the semi-permeable membrane technique [8], nuclear magnetic resonance (NMR) testing [9], and phase infiltration testing. However, these core-based experimental methods do not consider economic and scalability factors. The long time needed and financial costs of these experiments, along with the expensive sampling process, limit the number of core samples [10,11]. Consequently, these methods cannot be directly applied to producing wells without coring data. To obtain continuous vertical irreducible water saturation parameters, the prediction model is typically constructed using high-resolution geophysical logging data in conjunction with core data. For conventional logging data, physical parameters such as porosity and permeability are calculated to construct the irreducible water saturation prediction model [12,13]. However, this method is generally inapplicable to unconventional reservoirs with significant heterogeneity. Therefore, some scholars have constructed irreducible water saturation models for each reservoir type by dividing flow units [14,15]. These flow units are categorized by minimizing physical property differences within the units and maximizing differences between units. The core idea is to mitigate the interference of reservoir pore structure variations on fluid evaluation [16].

Subsequently, some scholars have employed the oil column height method to calculate the irreducible water saturation, also referred to as original water saturation [17]. It is posited that the process of oil and gas continuously overcoming the capillary pressure within the rock and displacing water due to driving forces constitutes the transport of oil and gas. The current state of oil and gas distribution is thus seen as the relative equilibrium between driving forces and capillary pressure [18]. Therefore, an intrinsic connection exists between capillary pressure and the volume of displaced water, which corresponds to oil and gas saturation. For Middle Eastern carbonate rocks characterized by complex pore structures and multi-peak distribution, a relatively mature evaluation process has been established: Initially, the physical model is employed to fit the capillary pressure curve. Subsequently, combined with the saturation height function, a comprehensive quantitative evaluation of the original water saturation of the reservoir is performed based on reservoir classification [19]. However, this method involves a significant workload and low efficiency, requiring high accuracy in permeability calculation and oil–water interface determination. Subsequent studies have demonstrated that NMR data from specialized logging series can effectively evaluate irreducible water saturation [20,21]. The most common method is to differentiate between irreducible and movable fluids by determining the cut-off value of the transverse relaxation time (T_2cutoff), a standard initially recommended by major international oilfield companies [22,23]. Based on extensive experimental samples from the Gulf of Mexico, a fixed value of 92 ms is recommended as the T_2cutoff for carbonate reservoirs. As more experiments are conducted, it has been shown that the fixed value is not applicable to complex reservoirs with significant heterogeneity [24]. For instance, in the pore-type carbonate reservoirs of the Mishrif Formation in the Middle East, which feature a complex pore structure, selecting a single fixed T_2cutoff leads to substantial errors in practical applications. Subsequently, Zhang et al. [25] determined irreducible water saturation by fitting variable T_2cutoff to NMR experimental sample data. However, due to the small number of samples used, the prediction model is difficult to extend to other regions. Wu et al. [26] selected different T_2cutoffs by dividing the reservoirs based on lithological differences. Nonetheless, it is challenging to reflect the complex pore structure of carbonate reservoirs based solely on lithological differences. The complexity of carbonate reservoirs’ pore structures results in varying transverse relaxation time (T₂) spectrum morphologies, making this method poorly applicable in practice.

In the study of heterogeneous carbonate reservoirs, many international scholars have discovered a common phenomenon known as “diffusion coupling” in these reservoirs [27,28]. Consequently, it is challenging to accurately evaluate the irreducible water saturation of the reservoir using the T_2cutoff. Coates [29] analyzed and proposed the spectral coefficient (SBVI) method for addressing this phenomenon, asserting that each term of the relaxation time incorporates the contribution of irreducible water, and introduced an empirical formula specifically applicable to carbonate rocks. Additionally, some scholars utilized NMR data to construct a pseudo-capillary pressure curve, with Zhu et al. [30] specifically constructing such a curve based on NMR logging. The criterion of calculating the cumulative permeability at 99.9% was adopted, resulting in a continuous and accurate evaluation of irreducible water saturation. In addition to NMR logging data, imaging logging data have also been employed to evaluate irreducible water saturation. Li et al. [31] analyzed the porosity characteristics of irreducible fluids using mercury intrusion capillary pressure curves. Based on the capillary pressure approximation theory, the inverse accumulation curve of the porosity spectrum was derived. The physical significance of its “inflection point” was clarified. Subsequently, the irreducible water saturation at each reservoir depth was predicted using Archie’s formula.

Table 1. Evaluation methods for irreducible water saturation.

Method Type	Specific Methods	Advantages	Disadvantages	References
Core experiment	Mercury injection capillary pressure experiment	High accuracy	High costs, poor generalization	[7,8,9]
	Semi-permeable membrane technique
	Nuclear magnetic resonance testing
	Phase infiltration testing
Conventional logging method	Physical property parameter fitting method	Strong generalization, cost-effective	Low precision	[12,13]
	Division of flow unit construction model method	Raises the accuracy, cost-effective	Non-uniform division standards	[14,15]
	Physical model method	Strong anti-interference ability, cost-effective	Low precision, high operation complexity	[18,19]
Special logging method	Nuclear magnetic resonance logging method	Theoretically strong, diversified forms, high recognition	Difficult to promote, high costs, destabilization	[21,22,23,24,25,26,29,30]
	Imaging logging method	Theoretically strong, moderate cost performance	Difficult to promote, poor feasibility	[31]

summarizes the advantages and disadvantages of various methods.

Currently, numerous evaluation methods for irreducible water saturation exist, yet two primary issues persist. The method based on conventional logging data for calculating physical property parameters is relatively popular but suffers from low overall accuracy. Even with the consideration of flow unit division, it is challenging to account for the promotion error of the flow unit and the carry-over error of the calculation. Although artificial intelligence models, such as machine learning [32], are now widely employed in the logging interpretation industry, the limited amount of core data complicates the construction of these models, significantly reducing their reliability. The introduction of a specialized logging series can resolve the accuracy issue, but general applicability remains problematic. Additionally, due to production cost considerations, specialized logging series are rarely collected in production wells. Consequently, evaluation models based on specialized logging data are challenging to apply to oilfield wells. The irreducible water saturation evaluation model is predominantly used in core wells with abundant logging series.

This paper introduces a novel method for evaluating irreducible water saturation to address existing challenges. Initially, an evaluation model for irreducible water saturation is derived from the NMR fractal permeability model, incorporating the logarithm mean of the transverse relaxation time (T_2lm) as a key parameter. Subsequently, the study verifies the numerical relationship between the modal parameter of pore throat diameter and the T_2lm in the Thomeer Function theory, using data from ground NMR and MICP experiments. The fractal theory is then applied to derive calculation formulas for the three key parameters in the Thomeer Function, establishing a numerical relationship between the T_2lm and the Thomeer Function. To operationalize this theory, the paper integrates it with logging data to construct a T_2lm prediction model based on conventional logging curves and advanced deep learning algorithms. This approach results in a versatile method for evaluating irreducible water saturation. In wells lacking specialized logging data, the T_2lm curve can be constructed using conventional curves and the deep learning model for assessing irreducible water saturation. The efficacy of this method was demonstrated in the Mishrif reservoir within the Halfaya oilfield, Middle East, yielding promising outcomes. Overall, this study introduces a novel perspective and methodology for evaluating irreducible water saturation.

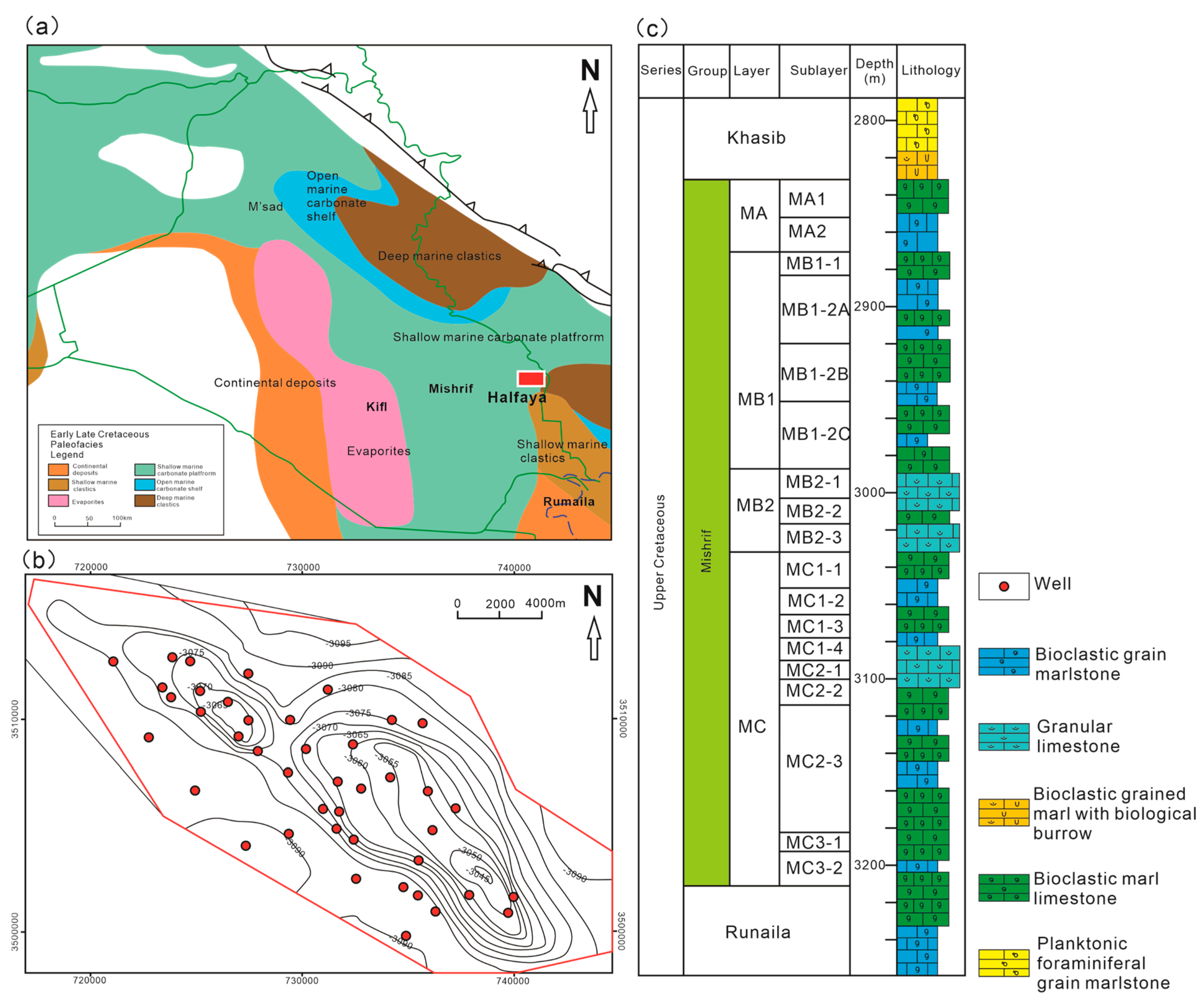
2. Overview of Geological Area

The methods explained in this paper are applied to the Mishrif Formation of the Halfaya oilfield. Regionally, from the Jurassic to Early Cretaceous, the Persian Gulf Basin was generally in a large transgressive cycle [33]. South Iraq was at the west gentle slope of the deepest water area (Figure 1a). Mishrif is a sedimentary cycle deposited in the Cenomanian period of the Early Cretaceous. Some of the wells in the Halfaya oilfield are depicted in Figure 1b. The Mishrif Formation Group can reach a thickness of 400 m [34]. It is overlain by the Khasib Formation and underlain by the Runaila Formation. The Mishrif Formation Group can be subdivided into three major sections: MA, MB, and MC. The MB section can be further divided into MB1 and MB2 (Figure 1c). According to the previous literature, the Mishrif Formation is a porous carbonate reservoir. The primary mineral is calcite, constituting over 90% of the formation. The pore types of the reservoir predominantly consist of connected or disconnected moldic pores, fossil endopores, intergranular pores, intragranular pores, and matrix micropores. However, the influence of sedimentation, diagenesis, and tectonic modification, coupled with the complexity and variety of pore types, results in a complex pore structure, intricate pore-permeability relationships, and strong heterogeneity of the reservoir [35,36,37]. The reservoir exhibits a complicated pore structure, complex pore–permeability relationships, and strong heterogeneity.

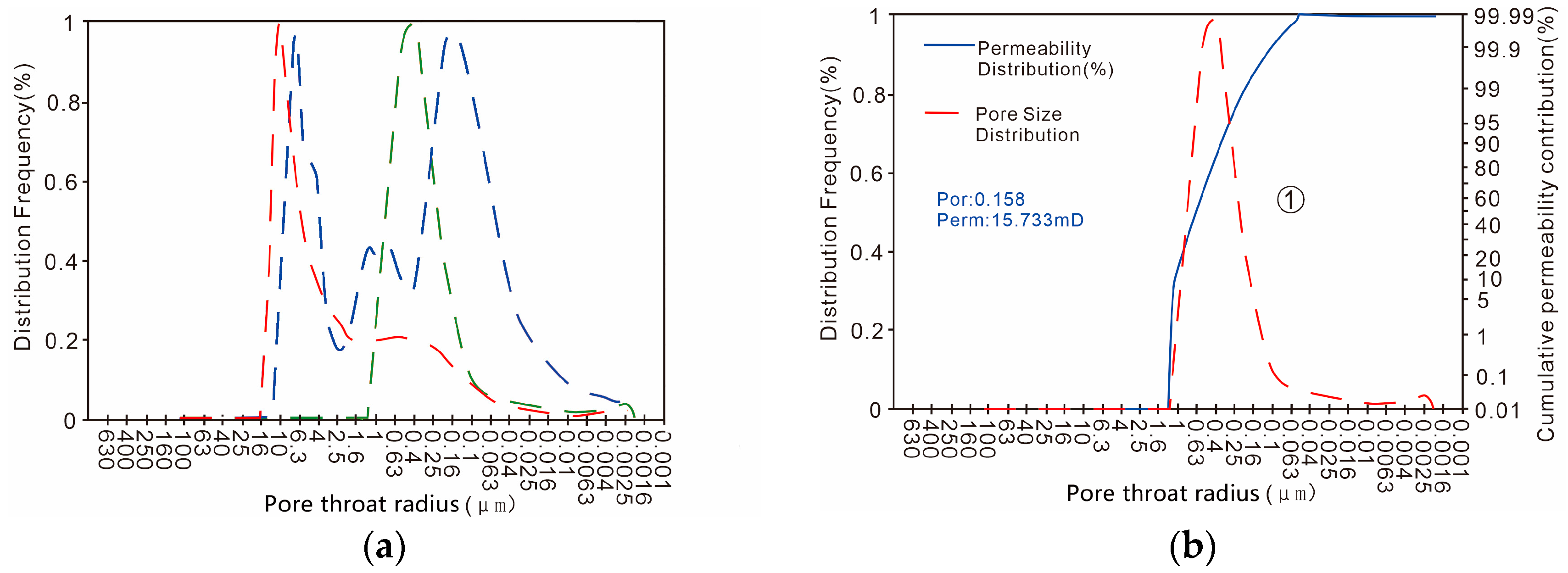
3. Material Source and Experiment

The core samples in this study are sourced from the Mishrif Formation in the Halfaya oilfield, with plunger cores extracted from boreholes (Figure 2a). In Figure 2a, ➀ indicates the core sample, and ➁ indicates the plunger core, which is taken from the MB2_1 reservoir. For the plunger cores, column samples of appropriate size for the instrument are extracted separately to determine the core’s water content and T₂ after centrifugation (Figure 2c). T_2lm and other parameters can also be determined post-centrifugation. The T₂ values after centrifugation (Figure 2c) were used to determine the distribution of T₂ in water-saturated cores, calculate the T_2lm, and establish the irreducible water saturation and corresponding T_2cutoff. Concurrently, the same plunger cores were subjected to MICP experiments using a Micromeritics 9320 mercury compression instrument (Figure 2d). The mercury compression curve of the core sample (Figure 2e) was obtained to calculate the distribution of pore throat radius, irreducible water saturation, and other physical parameters. For the samples and experimental processes shown in Figure 2, a total of 21 co-tested samples were obtained.

4. Methods and Principles

4.1. Derivation and Verification of Irreducible Water Saturation Formula Based on Fractal Nuclear Magnetic Permeability

4.1.1. Derivation of Irreducible Water Saturation Formula

Previous studies have demonstrated that NMR logging data can effectively calculate permeability. The Timur-Coates model [38,39] and the Schlumberger Doll Research (SDR) model [40,41] are the most widely used, corresponding to Equations (1) and (2), as shown in Figure 3A,B.

$$K_c=a_1\times {\phi }^4\times {\left({\displaystyle \frac{FFI}{BVI}}\right)}^2=a_1\times {\phi }^4\times {\left({\displaystyle \frac{1-S_{wirr}}{S_{wirr}}}\right)}^2$$

(1)

$$K_{\mathrm{s}}=a_2\times {\phi }^4\times T_{2lm}^2$$

(2)

In Equations (1) and (2), $\phi$ is the porosity, FFI is the free fluid index, and BVI is the irreducible volume index. Both can be converted to the form of irreducible water saturation (S_wirr, fractional), which can be determined by the T_2cutoff. T_2lm is the logarithmic mean of the transverse relaxation time, and $a_1$ and $a_2$ are the fitting coefficients.

Numerous studies have been conducted to improve the classical equations, primarily updating the coefficient solution for reservoirs with different lithologies or introducing correction coefficients. Wu et al. [42] modified the classical NMR permeability formula using fractal theory. Based on Equations (1) and (2), they introduced fractal dimensions and rewrote the formula as Equations (3) and (4):

$$K_{cD}=a_3\times {\phi }^{(b_1+c_{1}D)}\times {\left({\displaystyle \frac{1-S_{wirr}}{S_{wirr}}}\right)}^{d_1}$$

(3)

$$K_{sD}=a_4\times {\phi }^{(b_2+c_{2}D)}\times T_{2lm}^{d_2}$$

(4)

Unlike the classical formulas, the permeability formulas incorporating fractal theory replace the original constant exponent of porosity with a linear function of the fractal dimension D. The terms a₃, a₄, b₁, b₂, c₁, c₂, d₁, and d₂ are the fitting coefficients.

In this study, Equations (3) and (4) are conjugated to derive an expression for irreducible water saturation, as shown in Equation (5):

$$S_{wirr}={\displaystyle \frac{1}{1+{\left\{\left(\frac{a_4}{a_3}\right)\times {\phi }^{\left[(b_2-b_1)+(c_2-c_1)\times D\right]}\times T_{2lm}^{d_2}\right\}}^{\frac{1}{d_1}}}}={\displaystyle \frac{1}{1+{\left(\frac{a_4}{a_3}\right)}^{\frac{1}{d_1}}\times {\phi }^{\frac{\left[(b_2-b_1)+(c_2-c_1)\times D\right]}{d_1}}\times T_{2lm}^{\frac{d_2}{d_1}}}}$$

(5)

In Equation (5), the constant terms in the formula can be replaced. A*, B*, C*, and D* are constants, $A^{*}={\left({\displaystyle \frac{a_4}{a_3}}\right)}^{{\displaystyle \frac{1}{d_1}}}$, $B^{*}=\left({\displaystyle \frac{b_2-b_1}{d_1}}\right)$, $C^{*}=\left({\displaystyle \frac{c_2-c_1}{d_1}}\right)$, $D^{*}=\left({\displaystyle \frac{d_2}{d_1}}\right)$, whereas D is a variable (fractal dimension). Irreducible water saturation can be expressed as a function of porosity, fractal dimension, and T_2lm (Equation (6)).

$$S_{wirr}={\displaystyle \frac{1}{1+A^{*}\times {\phi }^{B^{*}+C^{*}\times D}\times T_{2lm}^{D^{*}}}}$$

(6)

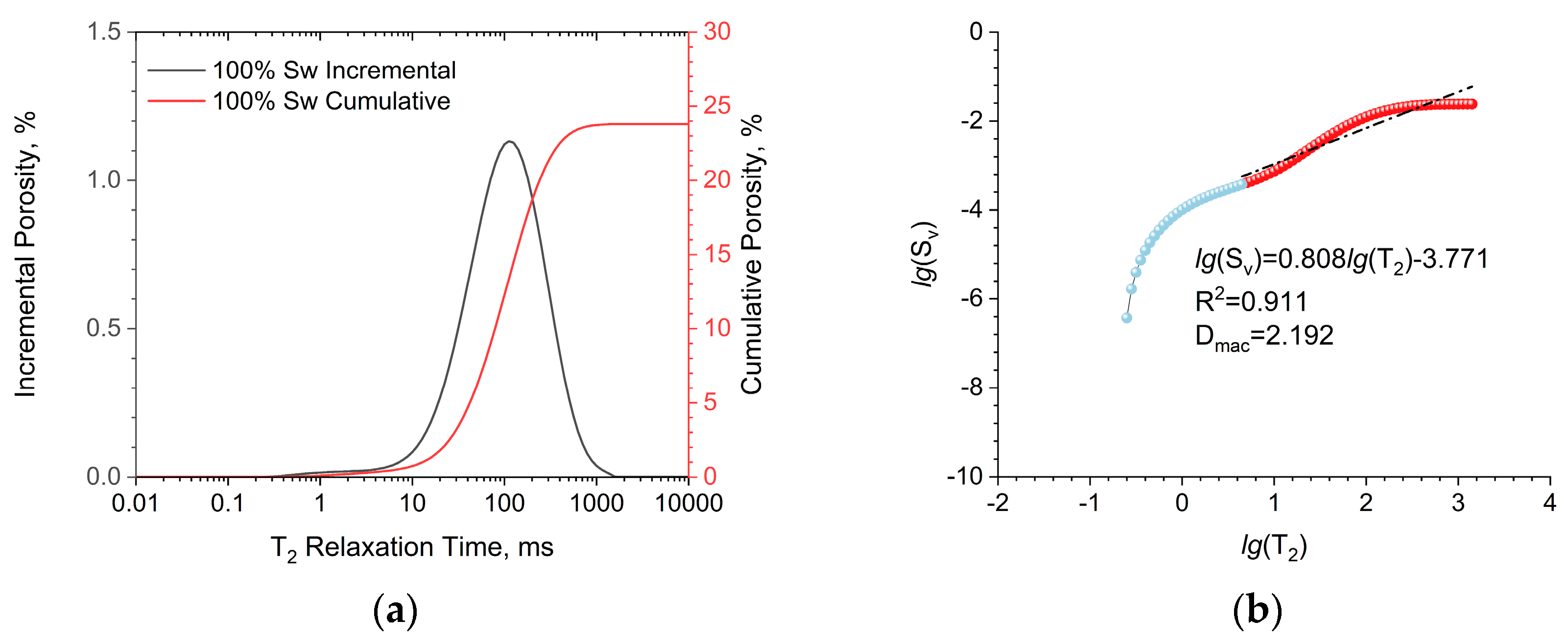
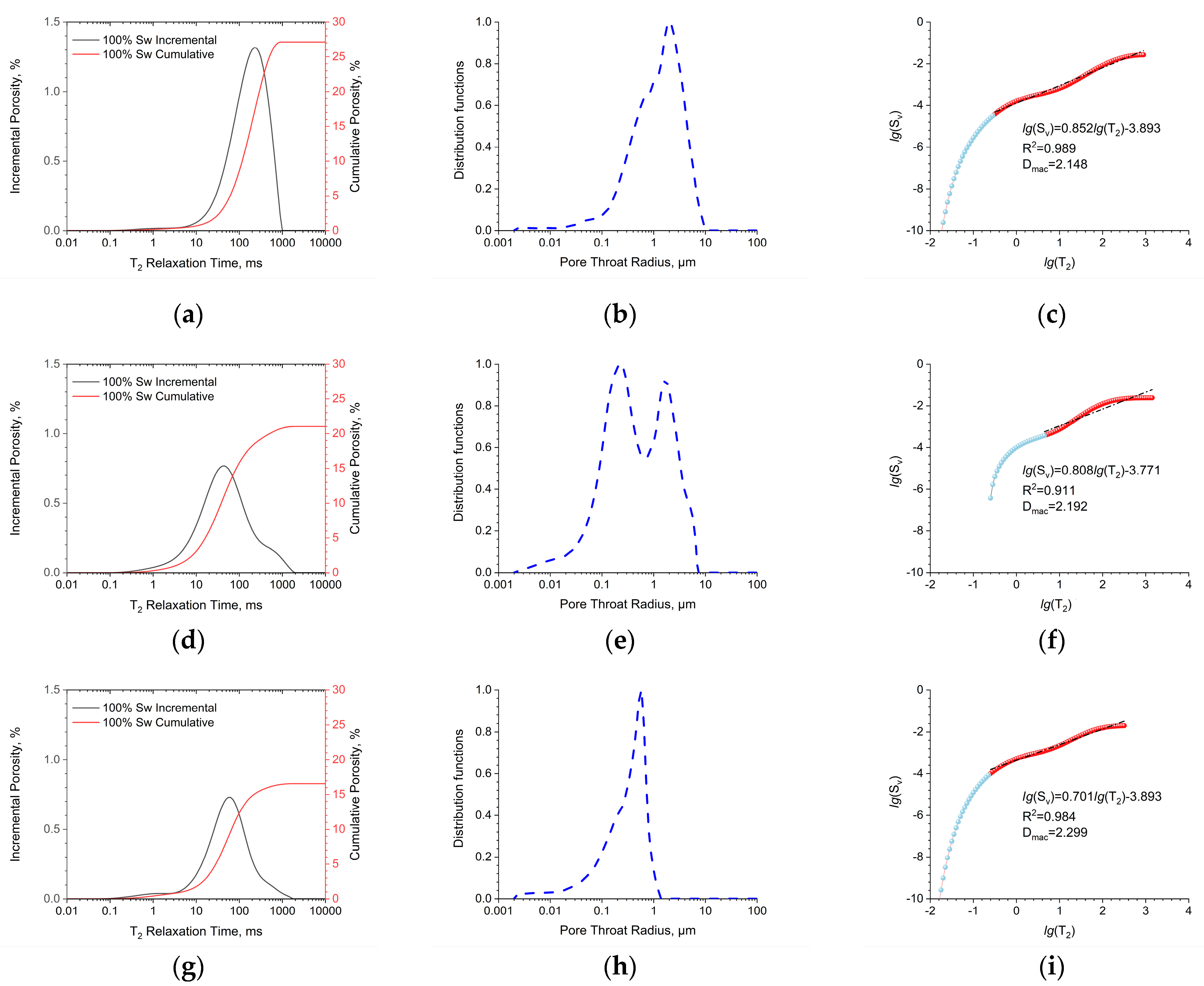
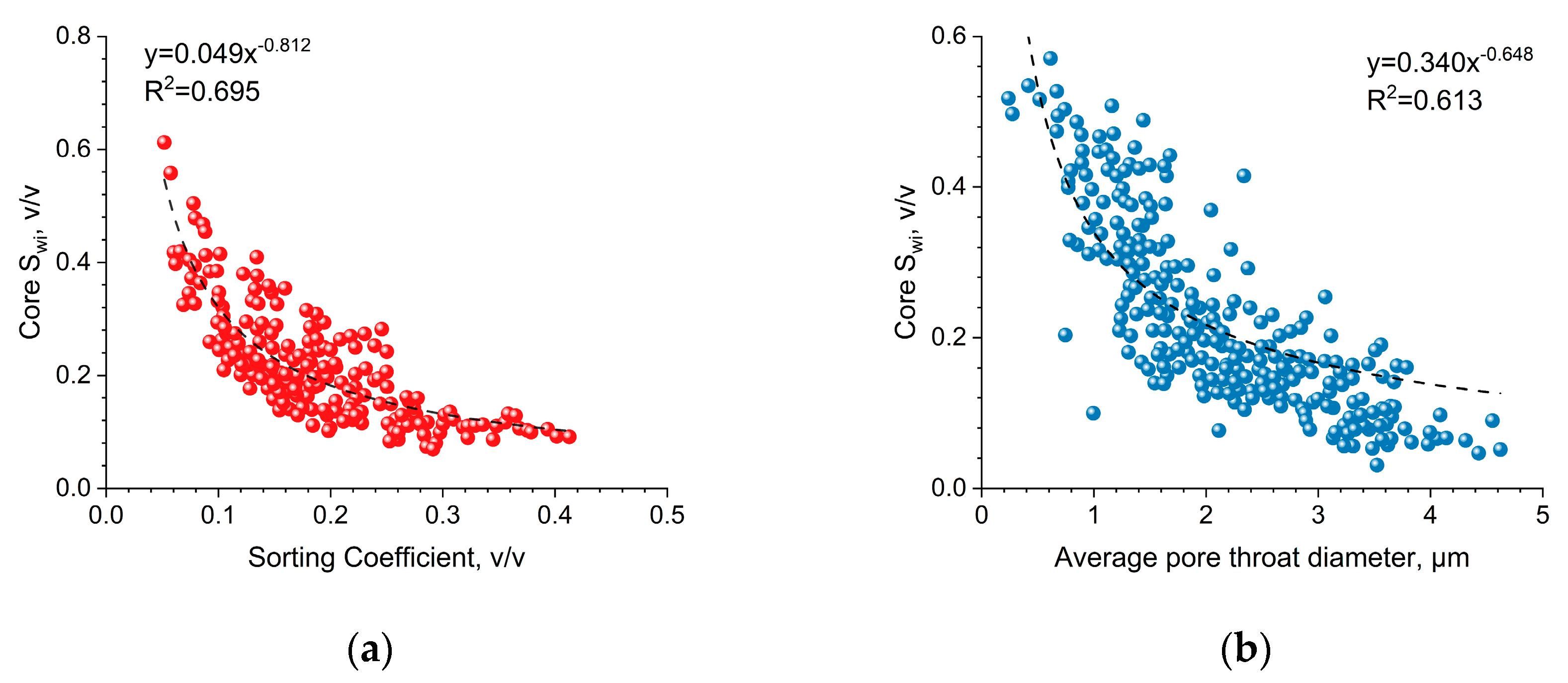
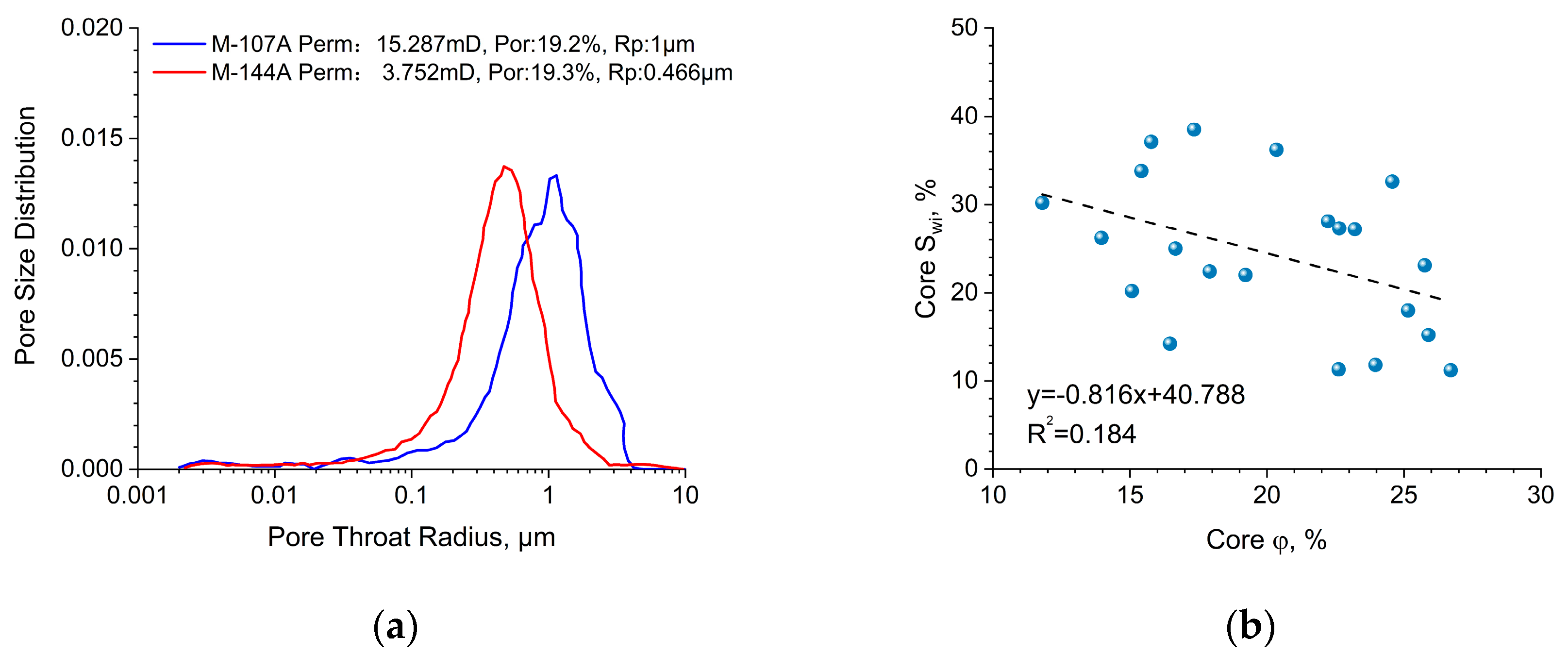
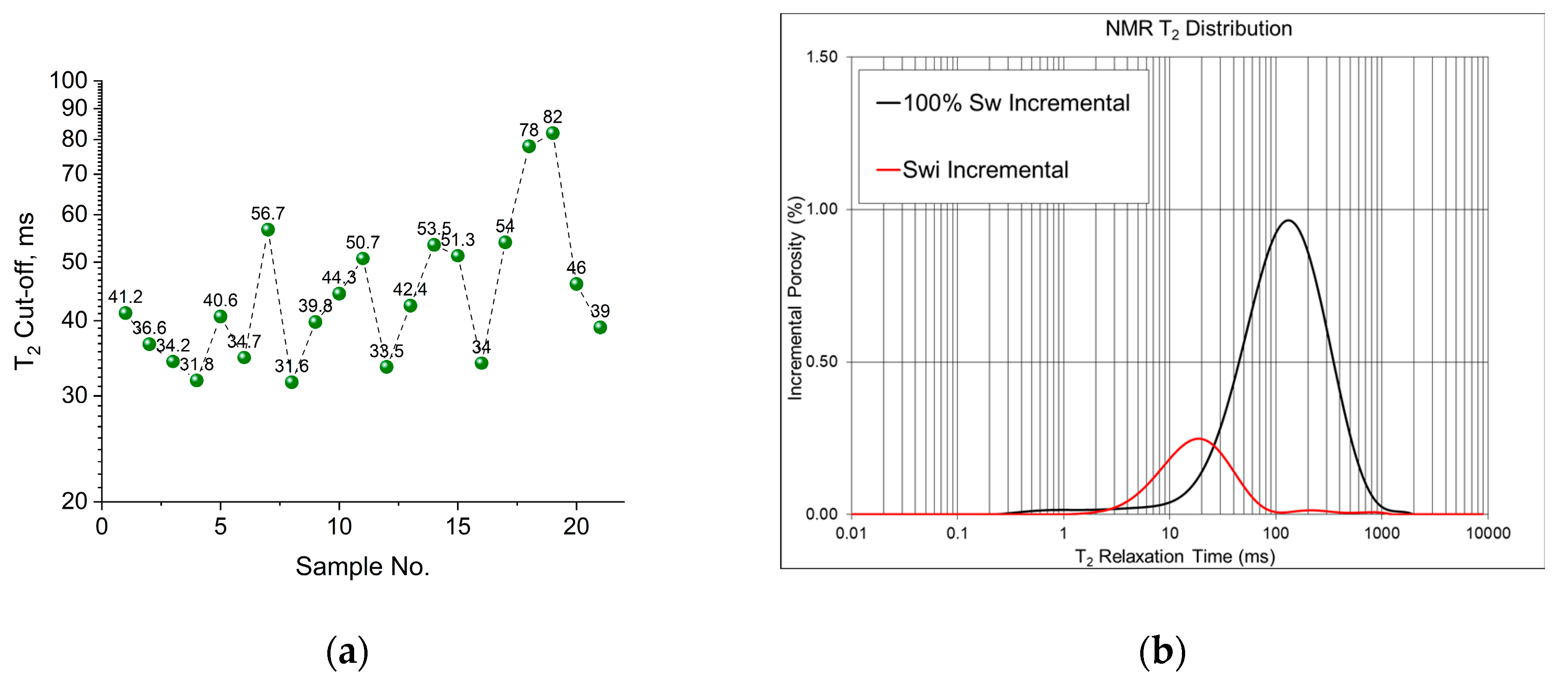
4.1.2. Verification of Irreducible Water Saturation Formula

After deriving the expression for irreducible water saturation, it was validated using data from core ground NMR experiments and MICP experiments. Initially, T₂ spectra obtained from the core NMR experiments were utilized to calculate the fractal dimension. Previous studies have consistently demonstrated that the reservoir’s pore size distribution adheres to a fractal structure [43,44]. Derivations indicate that the density function of pore size distribution in a reservoir with pore sizes larger than $r$ can be expressed as follows:

$$P(r)={\displaystyle \frac{dN}{dr}}=-D\times a\times r^{-D-1}$$

(7)

In Equation (7), $N$ is the number of pores with a diameter greater than $r$; $r$ is a specific pore diameter; $D$ is the pore fractal dimension; $a$ is the proportionality constant; and $P(r)$ is the pore size distribution density function.

The cumulative pore volume fraction $S_v$ for pore diameters less than $r$ is simplified and expressed by Equation (8) [45]:

$$S_v={\displaystyle \frac{r^{3-D}}{r_{\max }^{3-D}}}$$

(8)

In Equation (8), $r$ is the pore diameter, and $S_v$ is the cumulative pore volume fraction for pore diameters less than $r$.

For the T₂ spectrum from NMR experiments, the superposition mechanism and simplification based on the transverse relaxation rate can be considered:

$${\displaystyle \frac{1}{T_2}}=\rho ({\displaystyle \frac{S}{V}})=F_s{\displaystyle \frac{\rho }{r}}$$

(9)

In Equation (9), T₂ is the transverse relaxation time, milliseconds; $\rho$ is the transverse surface relaxation strength of the rock, μm/ms; $S$ is the pore surface area, cm²; $V$ is the pore volume, cm³; and $F_s$ is the geometrical shape factor, typically 2 or 3 depending on the specific model.

For capillary pressure, this can be expressed by Equation (10) [46]:

$$p_c={\displaystyle \frac{2\sigma \cos \theta }{r}}$$

(10)

In Equation (10), $p_c$ is the capillary pressure corresponding to pore diameter $r$; $\sigma$ is the surface tension and contact angle of the liquid; and $\theta$ is the wetting contact angle, °.

According to Equations (9) and (10), the expression between $p_c$ and T₂ can be obtained:

$$p_c=\left|{\displaystyle \frac{2\sigma \cos \theta }{F_s\rho }}\right|\times {\displaystyle \frac{1}{T_2}}$$

(11)

The correlation between the distribution of NMR T₂ spectra and capillary pressure curves obtained from mercury compression experiments reflects their expressions of the rock’s pore structure. Xiao et al. and Zhu et al. [21,30] successfully reconstructed pseudo-capillary curves using these T₂ spectra, as demonstrated in

$$p_{c\min }=\left|{\displaystyle \frac{2\sigma \cos \theta }{F_s\rho }}\right|\times {\displaystyle \frac{1}{T_{2\max }}}$$

(12)

In Equation (12), $p_{c\min }$ is the capillary pressure corresponding to the maximum pore size in the reservoir, i.e., the mercury feed pressure, and $T_{2\max }$ is the maximum transverse relaxation time.

Equations (7), (8), and (10) are conjugated to obtain $S_v$, and then Equations (11) and (12) are substituted:

$$S_{v{T}_2}={({\displaystyle \frac{T_{2\max }}{T_2}})}^{D-3}$$

(13)

At this stage, $S_{v{T}_2}$ represents the cumulative volume of pores with a transverse relaxation time less than T₂, expressed as a percentage of the total pore volume [47]. Applying a logarithm to both sides of Equation (13) results in

$$\lg (S_{v{T}_2})=(3-D)\lg (T_2)+(D-3)\lg T_{2\max }$$

(14)

According to Equation (14), the fractal dimension can then be calculated in conjunction with the T₂ spectrum of the core experiment.

In the past, when calculating the fractal dimension of rock, only the large pore part was usually considered, and few scholars discussed it from the physical properties of the rock itself. In this paper, the relationship between the cumulative permeability contribution and pore system is described by using MICP experimental data of a core. The permeability of reservoir rocks correlates closely with their microscopic pore structure [48,49]. Core MICP experiments provide capillary pressure curves that offer insights into this relationship. The cumulative permeability contribution derived from MICP experimental data reflects the physical properties of the rock [50,51]. It quantifies how specific pore throat intervals within a rock sample contribute to its overall capacity for fluid flow. Thicker pore throats contribute to higher permeability, whereas thinner ones contribute to lower permeability. Equation (15) enables determination of the cumulative permeability contribution across pore throat intervals, ranging from larger to smaller sizes.

$$\Delta K_j={\displaystyle \frac{r_j^2\times Sh{g}_j}{{\displaystyle \sum (r_j^2\times Sh{g}_j)}}}$$

(15)

In Equation (15), $r_j$ denotes the radius of the pore throat corresponding to the $j^{th}$ point, μm; $Sh{g}_j$ denotes the increment of mercury feed corresponding to the $j^{th}$ point, pu; and $\Delta K_j$ denotes the permeability contribution corresponding to the $j^{th}$ point, pu.

Figure 4a shows pore throat frequency distribution curves for three rock samples: single peak (green dashed line), double peak (red dashed line), and triple peak (blue dashed line). Figure 4b–d depict how these distributions relate to cumulative permeability contribution. The blue curve in the double logarithmic scale represents the cumulative permeability contribution, indicating how permeability accumulates from large to small pore throats. The red curve in the semi-logarithmic scale illustrates the pore throat distribution, revealing the pore space structure. Analysis of these curves reveals multiple pore systems in the Mishrif Formation. Single-peak samples (Figure 4b) exhibit a 100% permeability contribution. In double-peak samples (Figure 4c), the first and second pore systems contribute 99.7% and 0.3% to permeability, respectively. Triple-peak samples (Figure 4d) show contributions of 97.6%, 2.2%, and 0.2% from their respective pore systems. This finding aligns with Tang et al.s’ [52] results, suggesting a negligible impact of secondary pore throats on permeability in double-peak samples, focusing instead on the largest pore throat system. This supports Wu et al.’s [42] premise that calculating fractal dimension should primarily consider the macroporous portion.

Among the co-tested core samples, the 151VA sample from well X-95 is used as an example. In Figure 5a, the T₂ spectrum of this sample when saturated with water is shown. The black solid line indicates the pore fraction, while the red solid line represents the cumulative pore volume of the core under saturation. Figure 5b outlines the process for determining the fractal dimension of this core based on the NMR T₂ spectra’s volume percentage. The fractal dimension is derived from the intercept obtained through Equation (13) and its fit.

In previous studies of inhomogeneous carbonate reservoirs, researchers have categorized them into distinct petrophysical types to enhance understanding. In this study, we employed the classical Winland R35 method to classify reservoir types based on the pore throat radius (R35), which corresponds to a 35% cumulative mercury saturation. Martin’s [53] criteria were also used due to the scarcity of samples with R35 values exceeding 10 μm. Specifically, R35 values between 2 μm and 10 μm were classified as first Rock-Type (RT1), those between 0.5 μm and 2 μm as second Rock-Type (RT2), and values below 0.5 μm as third Rock-Type (RT3). The study includes NMR T₂ spectra of three fully saturated core samples, X-1 (RT1), X-9 (RT2), and X-14 (RT3). The porosity and permeability of these samples vary: X-1 (25.9%, 54 mD), X-9 (19.7%, 8.4 mD), and X-14 (15.8%, 0.56 mD). Their corresponding R35 values are 2.4 μm, 0.71 μm, and 0.37 μm, respectively. Figure 6a, 6d, and 6g illustrate the saturated water NMR T₂ spectra of samples X-1, X-9, and X-14, respectively. The NMR spectra of X-1 show a notable shift to longer T₂ compared to X-9 and X-14. Pore throat frequency distributions (Figure 6b,e,h) reveal complex porosity systems in X-9, with indications of dual sets of pores. The peak pore throat sizes decrease gradually from RT1 to RT3. The fractal dimensions calculated for the samples are 2.148 (X-1), 2.256 (X-9), and 2.299 (X-14). This trend aligns with existing research, suggesting higher fractal dimensions correlate with poorer reservoir physical properties. In contrast to dense sandstone reservoirs (typically 2.5–3), the porous carbonate rocks in our study range between 2 and 2.39.

For the co-tested samples, the fractal dimension, T_2lm, and porosity can be determined for each core sample. There are 21 groups of samples in total. In Equation (6), a total of four groups of coefficients are involved; therefore, the number of samples used for determining the coefficients should be no less than four. In this study, 10 groups of samples were randomly selected and combined with the Least-Squares Optimization method to determine the four groups of coefficients in Equation (6). The other 11 groups of samples were used to test the accuracy of the method. The parameter results and the formula’s form are shown in

Table 2. The coefficients in the irreducible water saturation model with the final form of the equation.

Coefficient Value
$A^{*}$	$B^{*}$	$C^{*}$	$D^{*}$
0.034	0.607	−0.256	0.903
$S_{wirr}={\displaystyle \frac{1}{1+0.034\times {\phi }^{(0.607-0.256\times D)}\times T_{2lm}^{0.903}}}$			(16)

. Figure 7 plots the predicted irreducible water saturation results against the core-irreducible water saturation. The blue spheres in Figure 7 represent the ten groups of sample points involved in the model construction, and the red spheres represent the other 11 groups of samples used for validation. The calculated irreducible water saturations are in good agreement with the core samples. The goodness of fit for the two groups of samples is 0.947 and 0.920, with relative errors ranging from 0.01% to 18.17%, and the average relative error is 8.44%. These results indicate that the irreducible water saturation formula derived in this paper is valid.

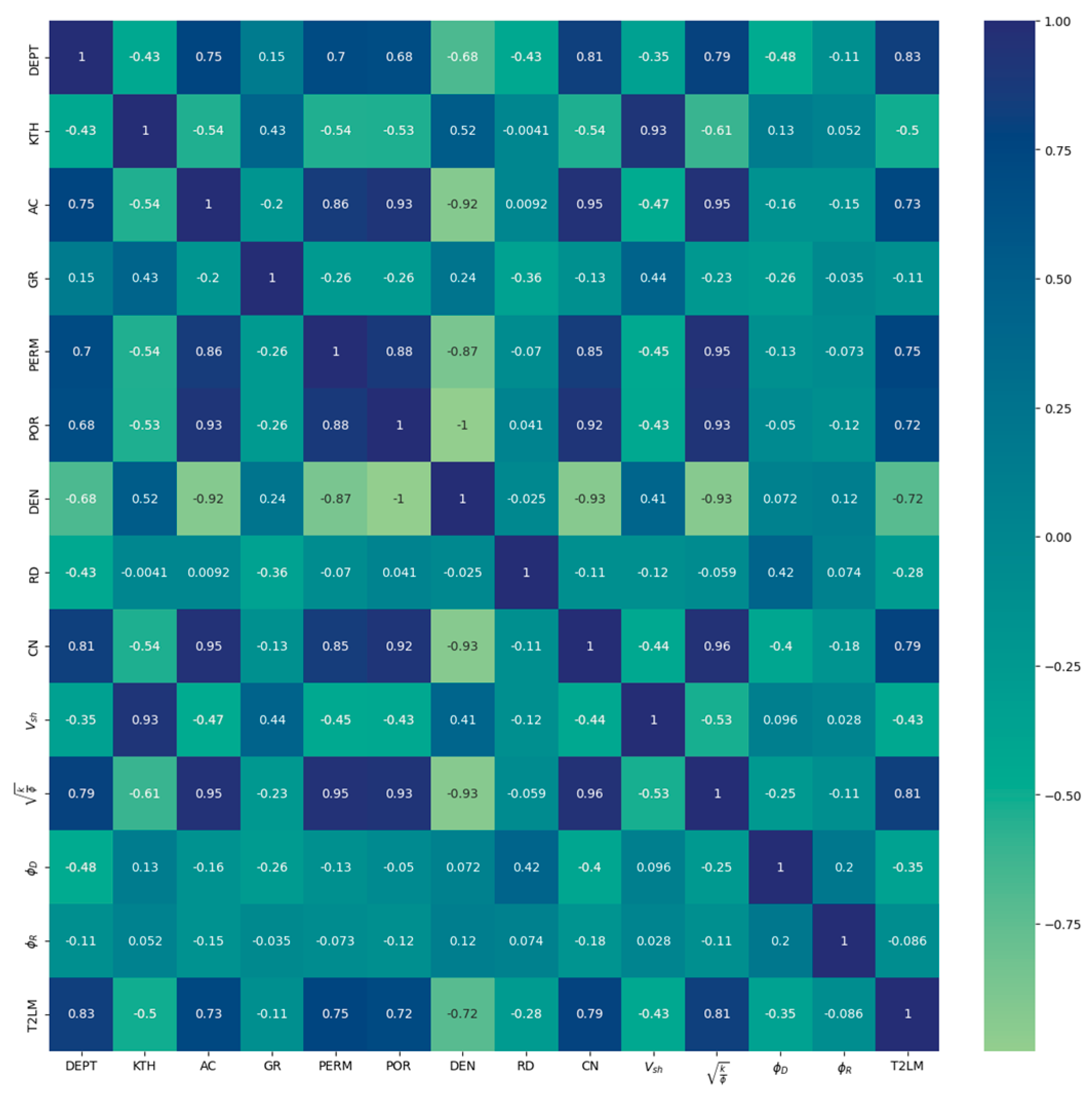
4.2. The Conventional Expression Form of T_2lm and the Promotion of Deep Learning Algorithm

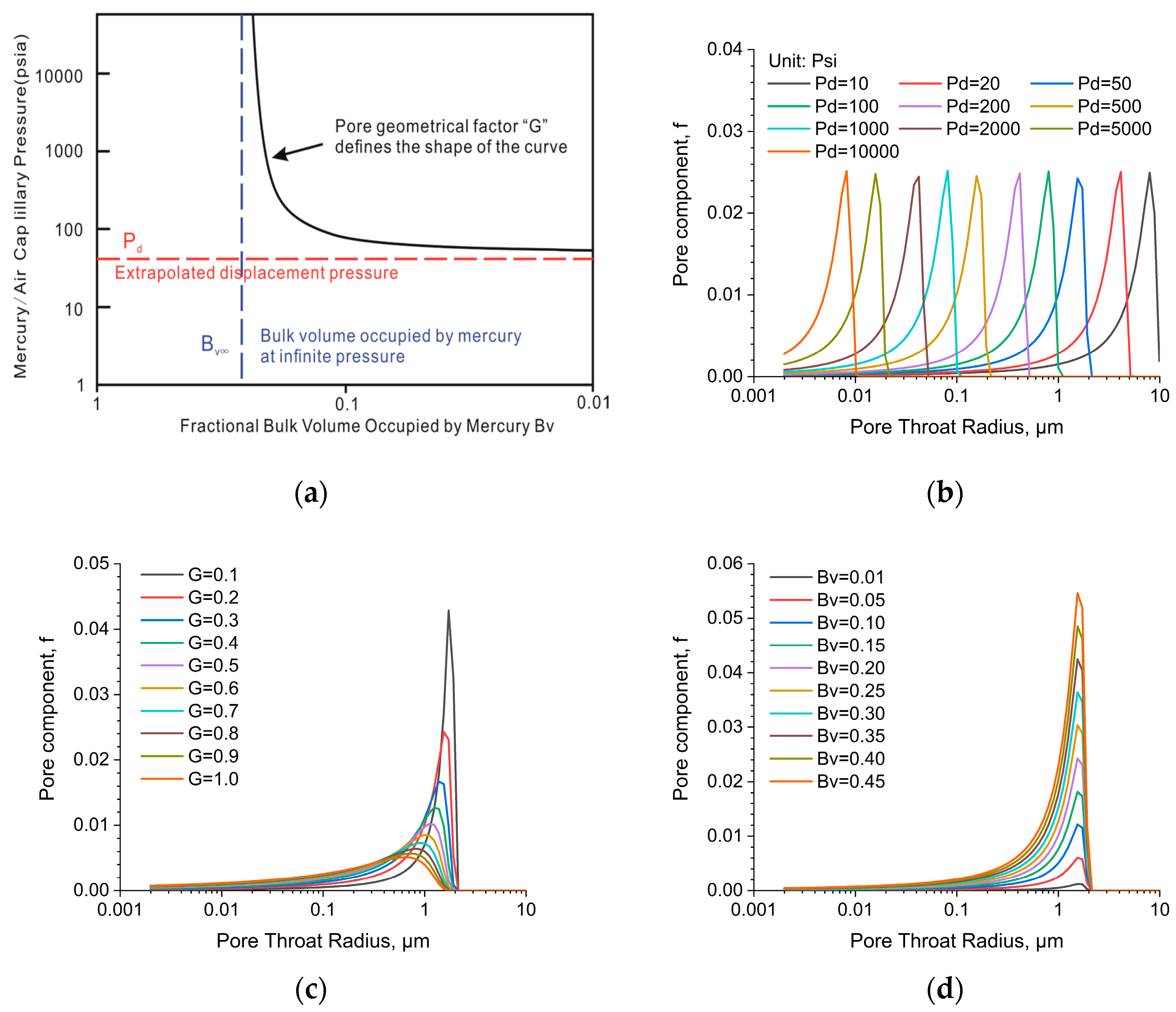
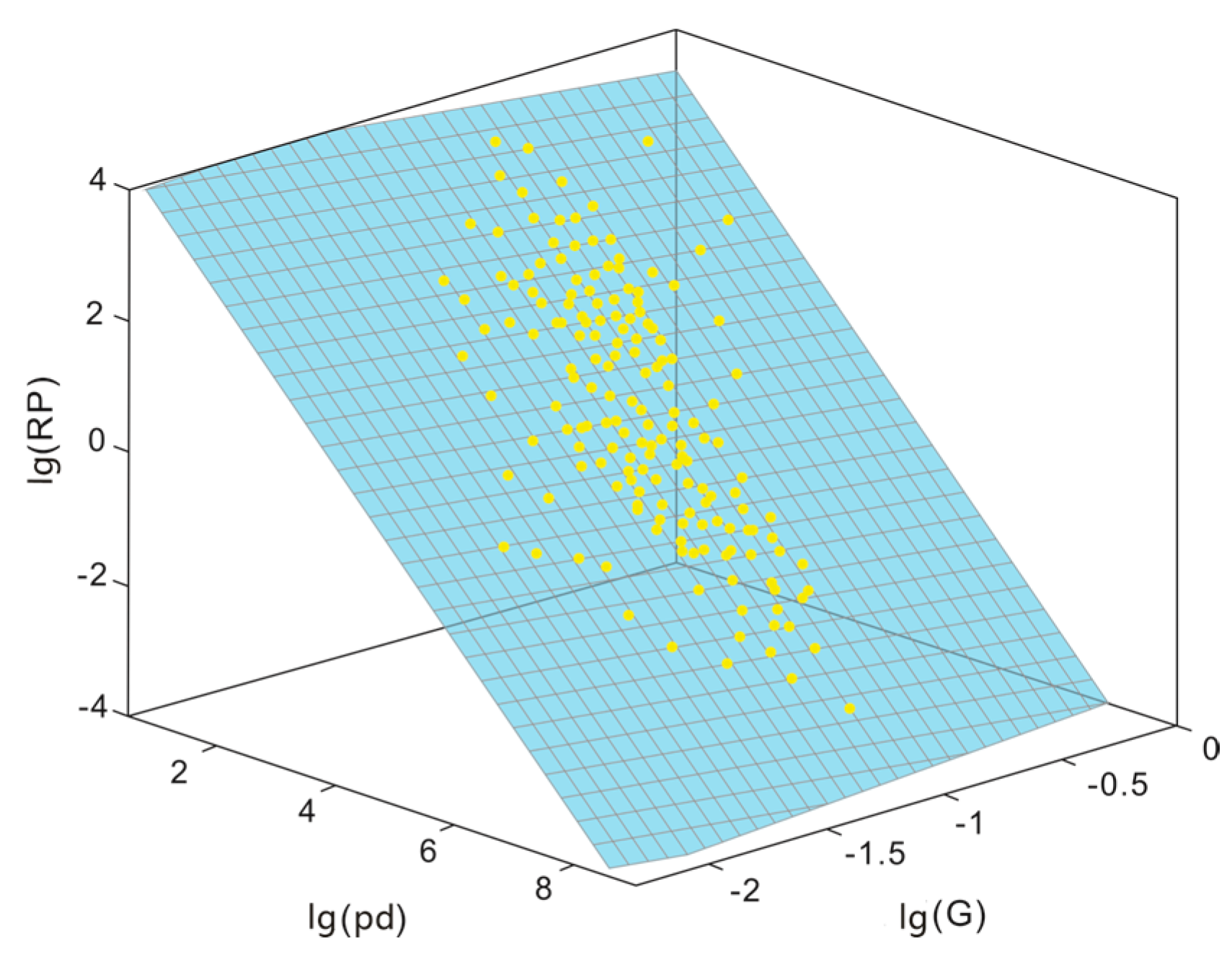
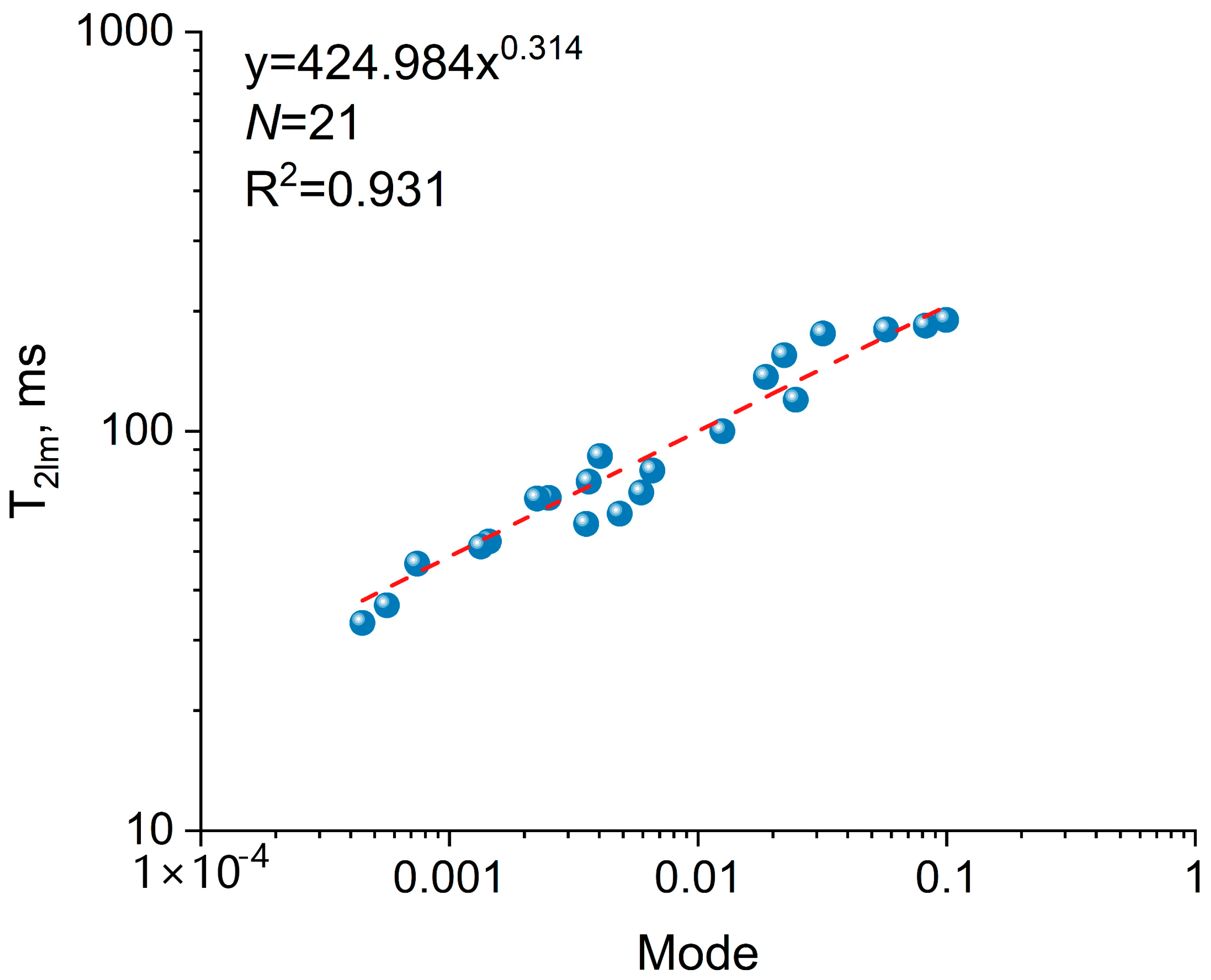
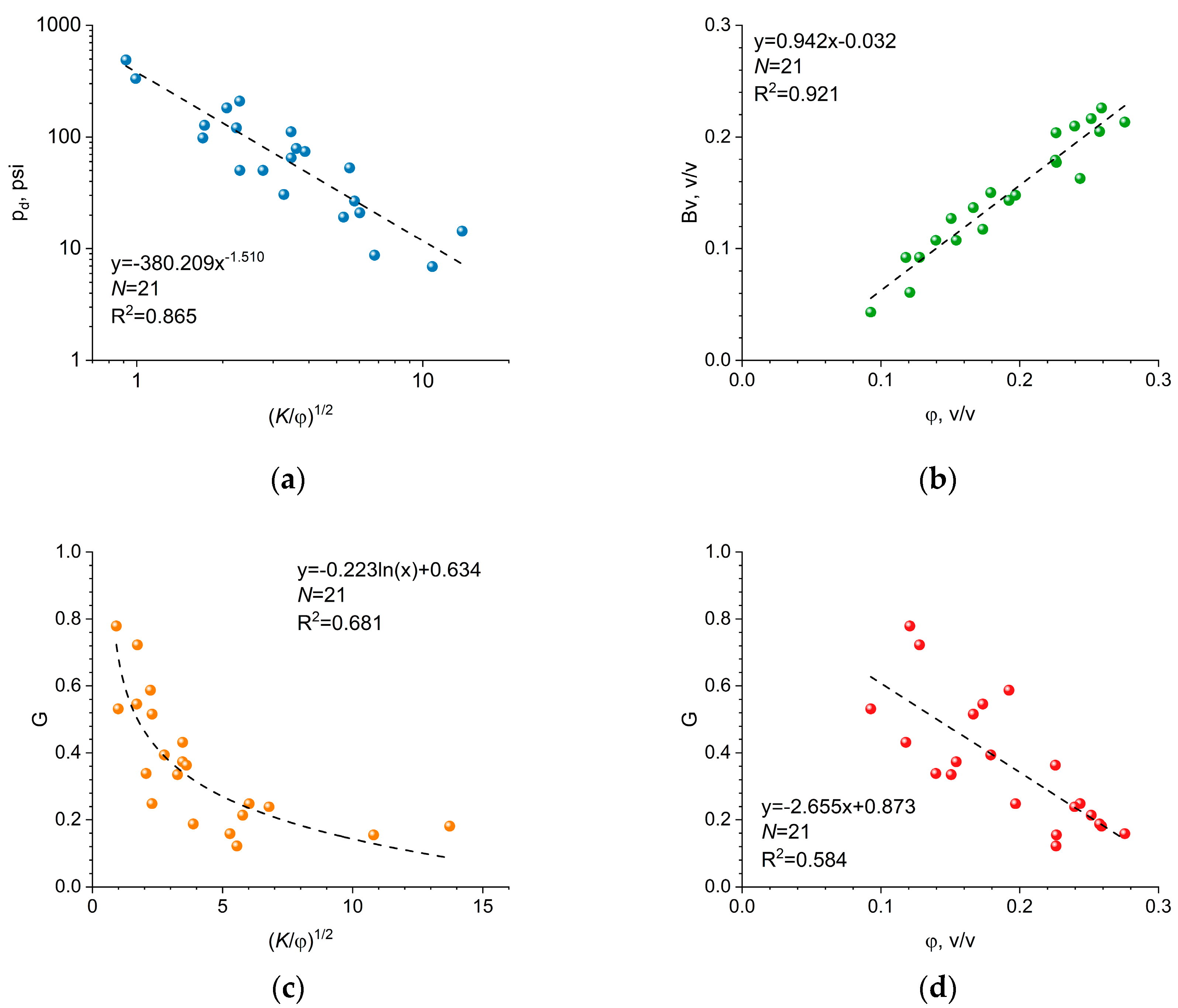
4.2.1. Numerical Expression of T_2lm Based on Thomeer Function and Fractal Theory

The expression for irreducible water saturation was derived and validated in Section 4.1. T_2lm in the equation requires NMR logging data, which are scarce and costly to obtain in practical applications. Thus, promoting Equation (16) presents a technical challenge. In this study, a numerical expression for the T_2lm is derived using Thomeer Function theory combined with fractal theory.

Thomeer [54] observed a capillary pressure curve in double logarithmic coordinates, which can be approximately characterized by a hyperbolic model (Figure 8a). The model is defined as follows:

$${\displaystyle \frac{{(B_v)}_{p_c}}{{(B_v)}_{p{c}_{\infty }}}}=e^{-G/(\lg p_c/p_d)}$$

(17)

In Equation (17), $p_c$ is the mercury–air capillary pressure, psi; $p_d$ is the discharge pressure, i.e., the inlet pressure of mercury, psi; ${(B_v)}_{pc\infty }$ is the volume fraction of injected mercury at infinite pressure, v/v; ${(B_v)}_{Pc}$ is the volume fraction of injected mercury at the $p_c$ pressure, v/v; and $G$ is the dimensionless pore geometry factor.

For the expression form of Equation (16), numerical simulations were carried out with controlled variables, plotting the pore throat radius versus pore fraction under different parameters:

(1)

Changing only the discharge pressure ( $p_d$); the larger the discharge pressure, the smaller the radius of the pore channel, indicating worse physical properties of the sample (Figure 8b).

(2)

Changing only the geometry factor $G$; the smaller G, the narrower the shape of the pore throat distribution curve, indicating that the pore channel is more concentrated and the sorting of rock samples is better (Figure 8c).

(3)

Changing only the maximum mercury feed volume ${(B_v)}_{pc\infty }$; the larger ${(B_v)}_{pc\infty }$, the larger the pore volume, indicating better physical properties of rock samples (Figure 8d).

In the context of the Thomeer Function parameters, the minimum mercury injection pressure corresponds to the maximum pore throat radius, marking the boundary of the larger radius in the pore throat frequency distribution. The parameter $G$ signifies the narrowness of this curve. Typically, these two parameters are combined to pinpoint the peak radius (RP) location within the orifice frequency distribution. A multivariate relationship between RP and $p_d$ relative to $G$ can be established to align with the graphical representation in Figure 9, corresponding to Equation (18):

$$RP={\displaystyle \frac{1.244}{G^{0.211}\times p_d^{1.355}}}$$

(18)

Tang et al. [52] proposed a new parameter, Mode, which is highly correlated with permeability. This was based on Equation (18) using a large amount of core data from the Mishrif Formation in the Middle East, in conjunction with the permeability model form. This parameter is defined as

$$Mode={\displaystyle \frac{1.244\times \left(0.037Bv-0.370G\right)}{G^{0.211}\times p_d^{1.355}}}$$

(19)

This parameter, Mode, can be regarded as a comprehensive characterization of the pore throat size, and the T_2lm has similar physical significance. Chen et al. [55] also showed that this type of element characterizing the pore throat diameter has a significant correlation with the T_2lm. For the 21 groups of samples, the Thomeer Function parameters were extracted based on the MICP experiments. The Mode of the samples was calculated according to Equation (18) and correlated with the T_2lm. Figure 10 shows the results of the correlation analysis between the two parameters. The goodness of fit between the two parameters is 0.931, indicating a significant correlation. This relationship can be characterized by Equation (20), meaning that T_2lm can be characterized using the Mode parameter. Since this parameter consists of the parameters in the Thomeer Function, T_2lm can be written as an expression involving these three parameters.

$$T_{2lm}=424.984\times Mod{e}^{0.314}$$

(20)

Previous calculations of parameters in the Thomeer Function were primarily extracted from core samples and fitted to the response of conventional logging curves, lacking a basis in theoretical derivation [52,56]. This study incorporates fractal theory to propose a new argument. The derivation in Appendix A shows that

$$p_d={\displaystyle \frac{\sigma \cos \theta }{\sqrt{\frac{2K}{f\phi }\frac{5-D}{3-D}}}}$$

(21)

$${(B_v)}_{p_c\infty }=\phi \left\{1-\underset{r\to 0}{\lim }{\left[{\displaystyle \frac{\sqrt{\left(8K/f\phi \right)\left(5-D)/(3-D\right)}}{r}}\right]}^{(D-3)}\right\}$$

(22)

Equation (21) proves that $p_d$ and $\sqrt{{\displaystyle \raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$\phi $}\right.}}$ have a correlation. Especially in the same type of reservoir, when the difference in fractal dimension is not significant, the two are linearly correlated.

In Equation (22), since (D-3) is a negative number, ${(B_v)}_{pc\infty }$ represents a function entirely determined by porosity from a mathematical perspective. Due to the presence of irreducible water, $r$ is not equal to zero, and the porosity $\phi$ remains the parameter with the greatest influence on the calculation results.

The geometric factor $G$, while mathematically simplified, lacks direct physical significance. Numerical simulations indicate that $G$ reflects the concentration of pore throat distribution; a smaller $G$ suggests better sorting. According to Thomeer’s theory, $G$ is influenced by both the $P_d$ and ${(B_v)}_{pc\infty }$ parameters. Given their relationships with $\phi$ and $\sqrt{{\displaystyle \raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$\phi $}\right.}}$, we established a correlation between $G$ and $\phi$, $\sqrt{{\displaystyle \raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$\phi $}\right.}}$ as expressed in Equation (23):

$$G=-1.215\times \phi -0.154\times \lg (\sqrt{{\displaystyle \frac{K}{\phi }}})+0.784$$

(23)

After completing the above theoretical derivation, the demonstration was carried out using the co-tested samples. Figure 11a shows that the $P_d$ has a significant correlation with the $\sqrt{{\displaystyle \raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$\phi $}\right.}}$, which is consistent with the theoretical derivation of Equation (21). Figure 11b shows a strong linear correlation between ${(B_v)}_{pc\infty }$ and $\phi$, with an R² as high as 0.921, which aligns with the theoretical derivation of Equation (22). Figure 11c,d show a correlation between the geometric factor $G$ with the $\sqrt{{\displaystyle \raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$\phi $}\right.}}$ and $\phi$, consistent with the theory mentioned above.

Combining Thomeer Function with fractal theory, the functional relationship between each parameter in the Thomeer Function and the physical property parameters and the fractal dimension is deduced. The combination of Equations (19) and (20) shows that T_2lm can be expressed by $G$, ${(B_v)}_{pc\infty }$, and $p_d$. The combination of Equations (19)–(23) can be written as

$$\begin{array}{l}{T}_{2lm}=28.574\times {(\frac{\phi }{k})}^{1.023}\times {(-\phi -0.062\lg k+0.062\lg \phi +0.645)}^{-0.211}\\ \times {(\phi +0.057\lg k-0.057\lg \phi -0.601)}^{0.314}\end{array}$$

(24)

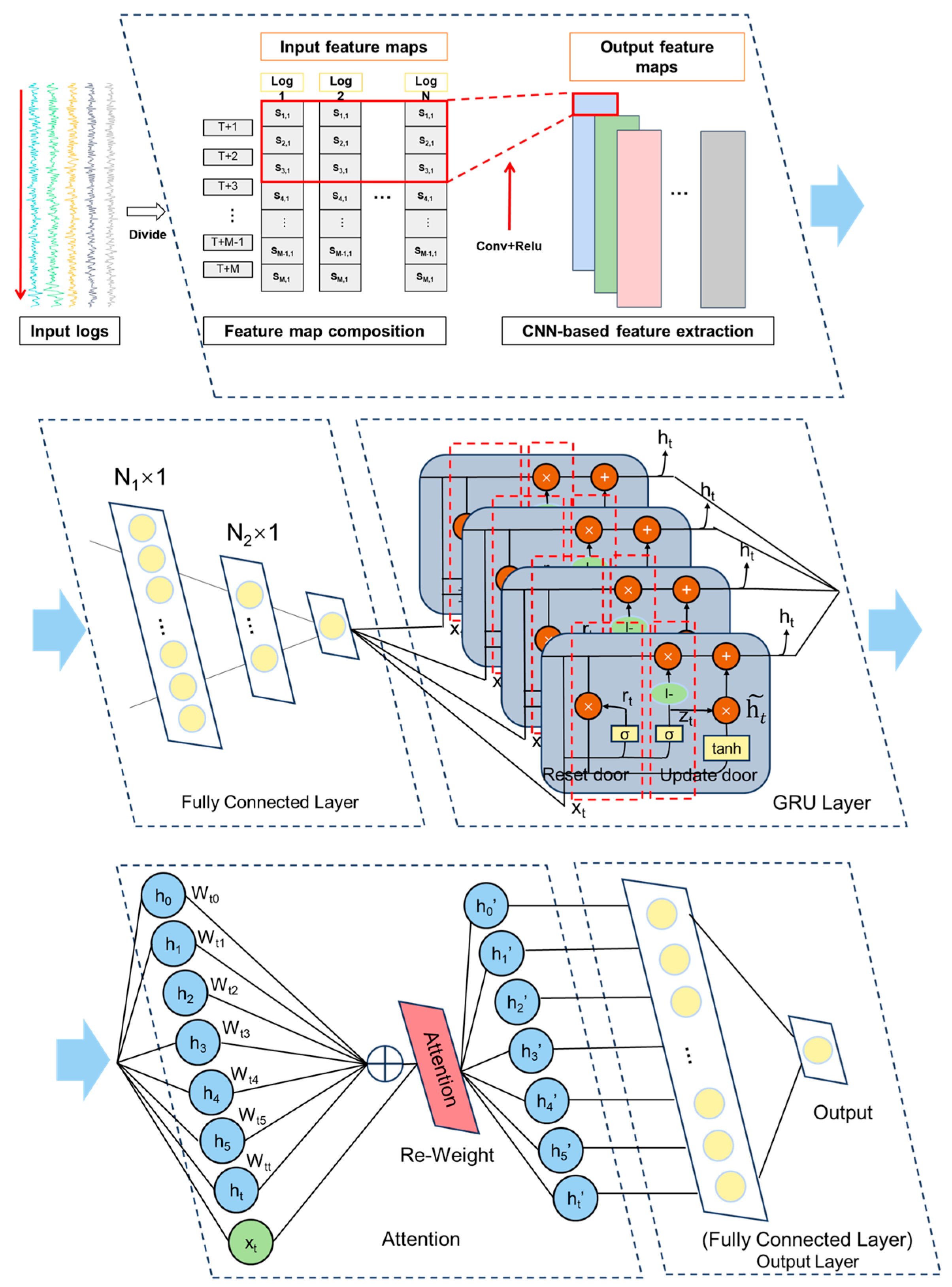
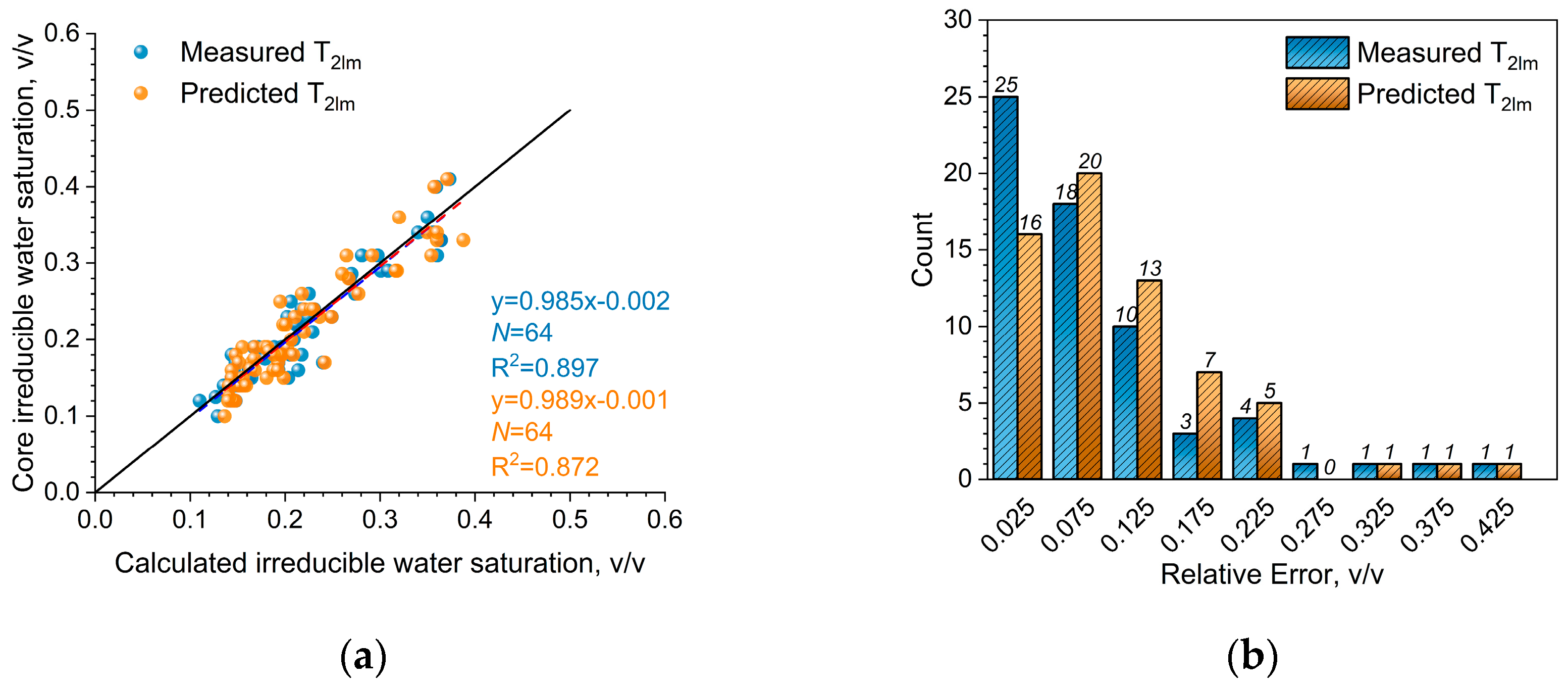
4.2.2. T_2lm Inversion Based on Deep Learning Algorithm

In Section 4.2.1, it was theoretically proven that T_2lm can be calculated from porosity and permeability, and this was verified using experimental data from actual co-tested rock samples. However, in practical applications, there is a significant error in permeability calculation, and the numerical relationship in Equation (24) also has fitting errors. This leads to an increase in the calculation error of the Thomeer Function parameter, an increase in the error in the T_2lm inversion results, and ultimately a decrease in the accuracy of the irreducible water saturation calculation.

Unconventional reservoirs pose challenges in calculating physical property parameters, prompting the use of machine learning or deep learning methods in conjunction with conventional curves to build predictive models. The usefulness of these models has been demonstrated in successful applications. This study focuses on constructing a T_2lm inversion model using deep learning algorithms based on conventional curves. Previously, core data were directly integrated with conventional curves to develop parameter inversion models, requiring substantial core datasets that are costly and time-consuming to obtain, thus limiting their availability. In contrast, inversion curves offer a more abundant source of data samples. The NMR logging instrument’s small sampling interval ensures each set of points collected represents a dataset. Therefore, sufficient samples are available for constructing deep learning models whenever NMR logging data are gathered from boreholes, overcoming the data sample limitations encountered in traditional model construction.

In this study, data extracted from the Mishrif Formation in the study area were analyzed to compute the Pearson correlation coefficient (Equation (25)) across conventional, derived, and T_2lm curves. The conventional curves analyzed include the uranium-free gamma curve (KTH), acoustic time-difference logging curve (AC), natural gamma logging curve (GR), compensated density logging curve (DEN), deep resistivity curve (RD), and compensated neutron logging curve (CN). Derived curves encompass the porosity curve (Por) derived from the regression analysis of the porosity logging series, the permeability curve (K) determined by Winland R35 reservoir classification, the mud content curve (Vsh) calculated from uranium-free gamma curves, $\sqrt{{\displaystyle \raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$\phi $}\right.}}$, the triple porosity difference ${\varphi }_D$, and the triple porosity ratio ${\varphi }_R$.

$$Pearson={\displaystyle \frac{M{\displaystyle \sum _{i=1}^M{x}_i{y}_i-}{\displaystyle \sum _{i=1}^M{x}_i{\displaystyle \sum _{i=1}^M{y}_i}}}{\sqrt{M{\displaystyle \sum _{i=1}^M{x}_i^2-({\displaystyle \sum _{i=1}^M{x}_i^2)}}}\sqrt{M{\displaystyle \sum _{i=1}^M{y}_i^2-({\displaystyle \sum _{i=1}^M{y}_i^2)}}}}}$$

(25)

$x_i$ is for each logging parameter, $y_i$ is T_2lm, i corresponds to the serial number of each sample, and M is the total number of samples for statistics.

A heat map based on the Pearson index was generated (Figure 12), demonstrating significant correlations between the porosity series logging curves, calculated porosity, and T_2lm. Similarly, permeability curves and the $\sqrt{{\displaystyle \raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$\phi $}\right.}}$ also exhibit strong correlations with T_2lm, achieving Pearson indices of 0.81 for both. Furthermore, T_2lm shows a robust correlation with depth. The logging signal and depth form a time series within the logging curve. Consequently, a T_2lm curve inversion model was developed using the CNN-GRU–Attention algorithm [57].

This study introduces an innovative CNN-GRU-ATT model, integrating Convolutional Neural Networks (CNNs), Gated Recurrent Units (GRUs), and Attention mechanisms (Figure 13). The CNN component performs feature extraction through its convolutional layers, utilizes pooling layers to reduce the spatial dimensions of the feature maps, and employs fully connected layers for classification or regression tasks. CNNs are characterized by weight sharing and local receptive fields, which enhance their ability to automatically learn data features, thus improving prediction accuracy [58]. Specifically, input data are represented as N-dimensional vectors, and the CNN processes these through sliding window techniques to generate M×N-dimensional feature maps [59], extracting spatial features as illustrated in the first row of Figure 13.

The GRU, an advanced variant of Recurrent Neural Networks (RNNs), optimizes memory retention and mitigates gradient vanishing issues. It uses reset and update gates to regulate the flow of information, enabling the model to capture long-term dependencies more effectively, which is beneficial for sequence modeling tasks such as language processing and time-series forecasting [60,61], as depicted in the second row of Figure 13.

The Attention mechanism enhances model performance by assigning varying degrees of importance to different parts of the input sequence, improving its ability to focus on critical elements of complex data [62]. This dynamic weighting significantly boosts prediction accuracy and generalization, as shown in the third row of Figure 13.

In the figure, $x_t$ is the input at time $t$; $h_t$ is the hidden layer output at time $t$; $z_t$ is the update gate; $r_t$ is the reset gate; σ is the sigmoid function; and $\tanh$ is the activation function. $h_0$, $h_1$,…, $h_t$ are the hidden layer output vectors of the GRU at each time step, and $W_{t0}$, $W_{t1}$,…, $W_{tt}$ are the corresponding weight coefficients; $h_0^{\prime }$, $h_1^{\prime }$,…, $h_t^{\prime }$ are the weight coefficients of the Soft-max normalized, $\widetilde{h_t}$ are the candidate hidden states, and $x_t$ are the query vectors. By combining CNN’s localized feature extraction capabilities, GRU’s sequence modeling strengths, and the dynamic weighting provided by Attention, the CNN-GRU-ATT model offers a refined and efficient approach for T_2lm prediction. This integrated methodology markedly advances the processing of well log data by effectively capturing both spatial and temporal dynamics. The model architecture consists of an input layer, convolutional layers, max pooling layers, Dropout layers, GRU layers, Attention layers, fully connected layers, and an output layer.

Considering that only a small number of coring boreholes have collected NMR logging data, the T_2lm curve cannot be directly obtained for uncored boreholes. Conventional logging data are usually collected from uncored boreholes. Therefore, for such boreholes, combined with conventional logging curves and calculated parameters as input, the constructed CNN-GRU-ATT network is used to invert the T_2lm curve, and then the inverted T_2lm curve is used to evaluate the irreducible water saturation.

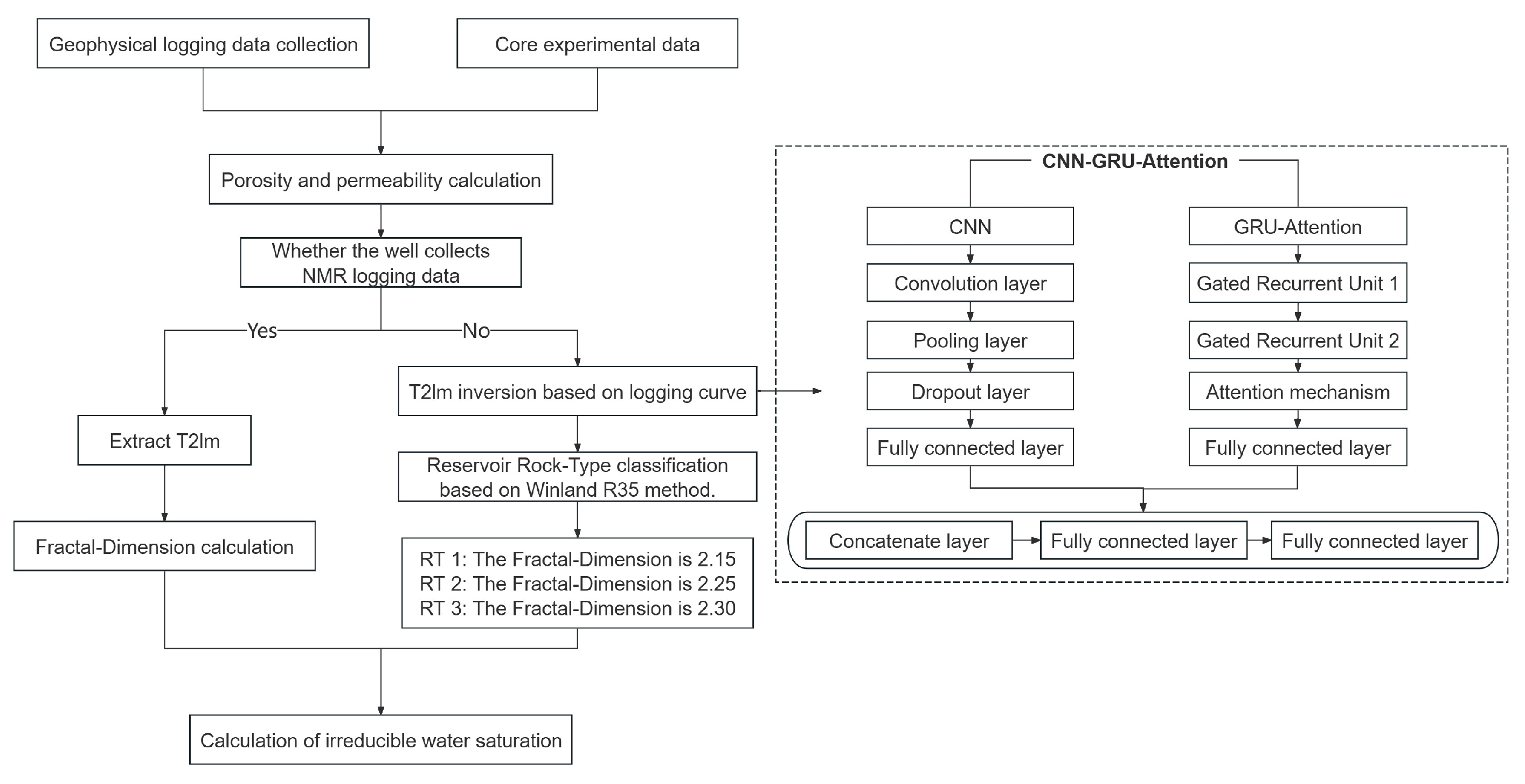
4.3. The Calculation Process of Irreducible Water Saturation

For the evaluation of irreducible water saturation, this paper proposes a new method and process, as shown in Figure 14. The first step is to collect the logging curves and core data of the target reservoir in the study block, calculate and evaluate the porosity curve, and decide the next process based on whether the borehole collects NMR logging data:

• If the borehole collects NMR logging data, extract T_2lm from the T₂ spectrum collected by the NMR logging instrument, calculate the fractal dimensions of each sample point, and ultimately calculate the irreducible water saturation.
• If the borehole did not collect NMR logging data, it is necessary to perform T_2lm inversion based on the logging curve with the deep learning model, determine the fractal dimension for each type of reservoir using the Winland R35 method, and ultimately calculate the irreducible water saturation. This entire process considers both coring and production wells in the study area. Usually, the coring wells have a complete logging series and collect special logging series curves, while the production wells typically contain only conventional curves. The irreducible water evaluation method and process proposed in this paper take full account of this practical situation.

5. Results and Applications

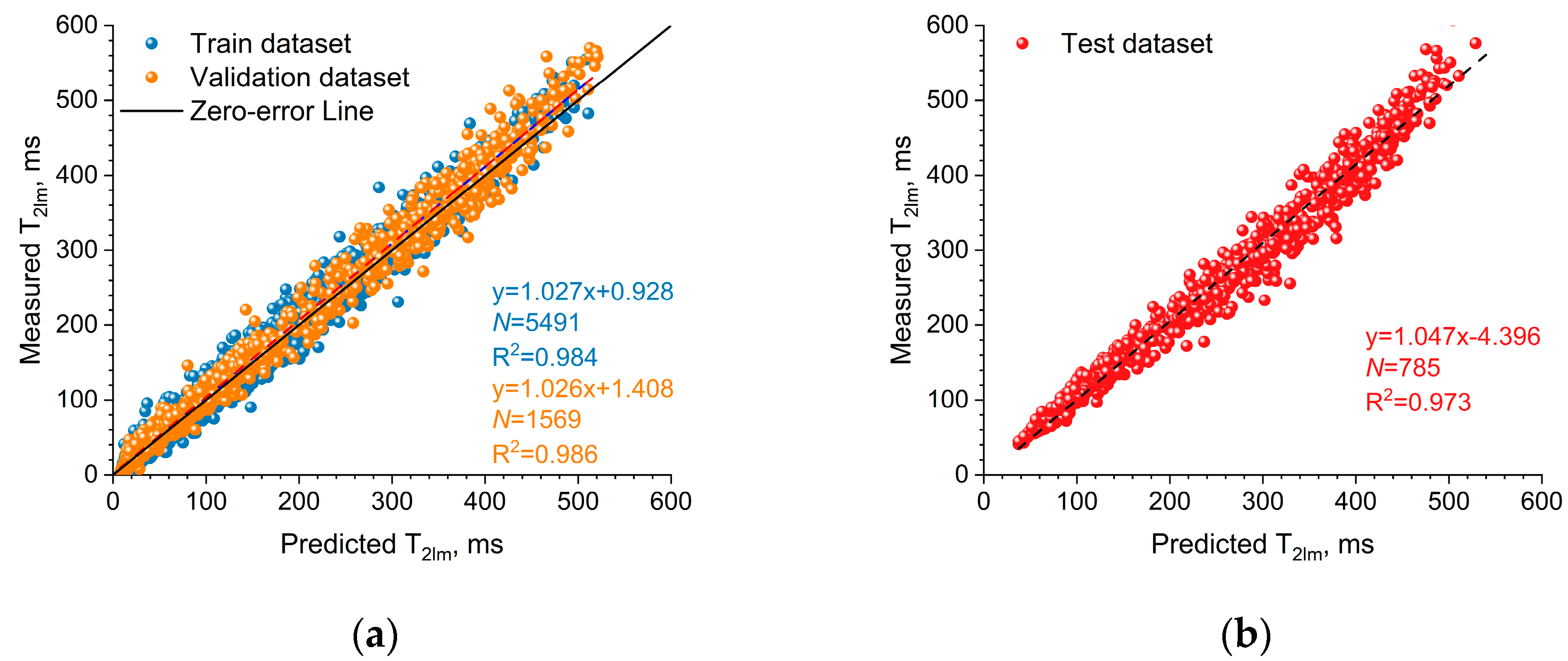
5.1. The Inversion Results of T_2lm Curve

The inversion of T_2lm curves utilized a CNN-GRU–Attention neural network. A dataset comprising 7060 sets of NMR logging sampling points from the Mishrif Formation in the study area was split into training and validation sets at a 4:1 ratio. Hyperparameter tuning for the CNN-GRU–Attention network involved optimizing the width of the convolutional layer’s scanning window, the number and size of CNN kernels, the quantity of GRU neurons, and the batch size, guided by established parameter selection practices. Scanning window widths of 16, 32, 64, and 128, alongside batch sizes of 32, 64, or 128, were evaluated. Training employed the Adam optimizer, with a dynamically adjusted learning rate for enhanced convergence [63]. Hyperparameters were selected through a grid search, prioritizing mean squared error (MSE, Equation (26)) loss to maximize prediction accuracy. The model architecture (see

Table 3. The hyperparameter usage table of CNN-GRU-ATT neural network.

Layer	Parameters	Value
CNN Layer	Number of Convolutional Kernels	32
	Convolutional Kernel Size	3 × 3
	Activation Function of Convolutional Layer	ReLu
	Padding Method of Convolutional Layer	Valid
	Pooling Layer Pooling Window Size	2 × 2
	Pooling Layer Activation Function	ReLu
	Dropout Rate	0.3
GRU Layer	Number of Hidden Neurons	10
	Number of Hidden Neurons	20
Attention	Dimensionality	50
Output Layer	Dense1	10
(Fully Connected Layer)	Dense2	1

) featured 32 CNN kernels with a kernel size of 3 and a regularization rate of 0.3. The GRU layer comprised 10 to 20 hidden neurons, varying as per experimental conditions.

$$MSE={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^N{(y_i-{\widehat{y}}_i)}^2}}{N}}$$

(26)

Based on the parameters in Table 3, the deep learning network inversion T_2lm is constructed, and the results of the training dataset and the verification dataset are displayed. Figure 15a shows the application effect of the training data and the verification data. The blue sphere is the result of the training data. With a total of 5491 sets of samples, the goodness of fit between the predicted results and the measured results reached 0.984, and 1569 sets of samples formed a verification dataset. The goodness of fit between the predicted results and the measured results reached 0.986. The samples of the two types of datasets are evenly distributed on both sides of the zero-error line. To further determine the accuracy and generalization of the T_2lm inversion network, a blind well in the study area was used for validation. This new well was not involved in the training and construction of the model. There were a total of 785 groups of samples in the new well, with the goodness of fit between the predicted and measured results reaching 0.973 (Figure 15b), showing no significant deviation. This demonstrates the generalizability of the T_2lm inversion model.

5.2. Evaluation Results and Application of Irreducible Water Saturation

After validating the general applicability of the T_2lm inversion model, we applied and evaluated the proposed method for assessing irreducible water saturation. Figure 16 illustrates an exemplary application well within the study area. The channels are organized as follows: the first for depth, the second for stratigraphy. The third channel logs lithological data, including the GR, KTH, SP, and CAL curves and the drill bit diameter (BS). The fourth channel records porosity (CN, DEN, DT), while the fifth displays resistivity at maximum depth (RD) and microsphere resistivity (RXO). The sixth channel presents NMR logging data, featuring T₂ spectra and the T_2lm curve. Porosity calculations and core sample porosity are detailed in the seventh channel. The eighth channel includes permeability calculations and core permeability. Channels nine and ten depict irreducible water saturation evaluation: one is based on the T_2lm curve extracted from NMR and porosity data, alongside core measurements; the other uses T_2lm inversion results. The eleventh channel is for explanations and conclusions.

The practical application of the proposed method demonstrates its effectiveness in calculating irreducible water saturation, aligning closely with the core results. Furthermore, to underscore the method’s generalizability, two scenarios are compared: firstly, when borehole NMR data allow direct extraction of T_2lm for saturation evaluation, the average relative error across 64 samples is 9.55%, with a minimum and maximum of 0.10% and 41.06%, respectively. The calculated results exhibit a strong fit with core data (R² = 0.897). Secondly, utilizing a deep learning network for T_2lm curve inversion (yellow samples in Figure 17a,b) results in an average relative error of 10.92%, ranging between 0.49% and 42.19%. Despite a slightly higher error, this method remains within acceptable bounds. Comparatively, direct T_2lm extraction yields higher precision in irreducible water saturation evaluation, with lower relative errors evident in Figure 17b. Importantly, applying the inverted T_2lm curve, despite increased error, remains viable for practical applications in new wells within the study area, affirming the method’s reliability and broad applicability.

6. Discussion

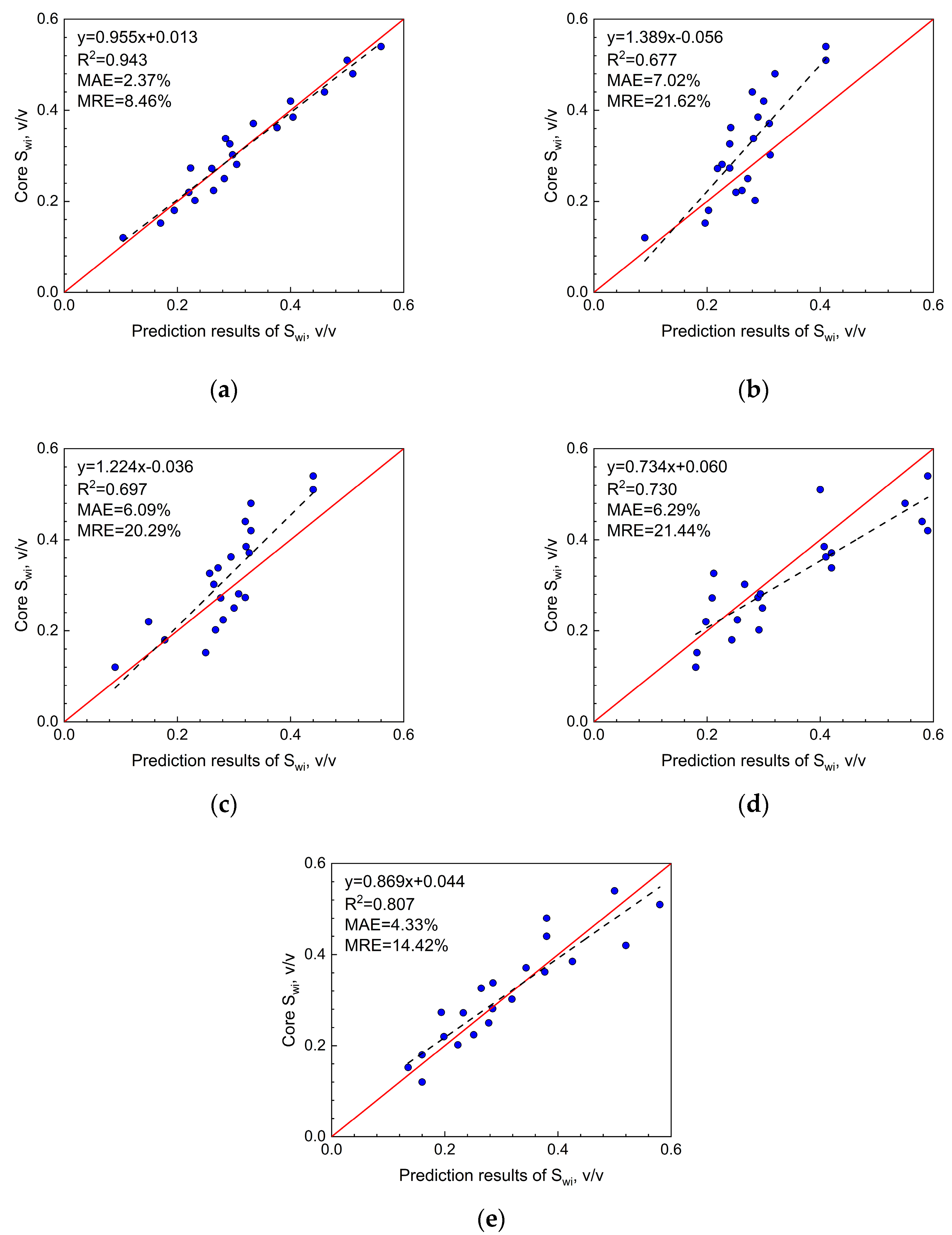
6.1. Methods Comparison

Previous methods for predicting irreducible water saturation primarily rely on physical properties or the T_2cutoff method combined with NMR logging data to construct the evaluation model. In this paper, the new method is compared with traditional methods, using the evaluation results of 21 sets of core samples for multi-method comparison. The mean absolute error (MAE) and mean relative error (MRE) of each method are calculated. Figure 18 shows the application effect of each method. Figure 18a shows the application result of the method proposed in this paper, with a goodness of fit between the predicted irreducible water saturation and the core irreducible water saturation reaching 0.943, an MAE of 2.37%, and an MRE of 8.46%. Figure 18b shows the application effect of the direct evaluation of irreducible water saturation using the porosity parameter [64]. Figure 18c shows the application effect of the evaluation of irreducible water saturation using the $\sqrt{{\displaystyle \raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$\phi $}\right.}}$ parameter [12]. Figure 18d shows the application effect of evaluating irreducible water saturation using the T_2cutoff method [20,21], and Figure 18e shows the application effect of the spectral coefficient method [29]. Comparing the method proposed in this paper with the other four classical methods, the accuracy of this method is the highest. The spectral coefficient method has the second-highest accuracy. Predicting irreducible water saturation directly using porosity parameters has the lowest accuracy, and the results of predicting irreducible water using the T_2cutoff method are significantly higher than the core irreducible water saturation. This demonstrates the higher accuracy and generalizability of the methods proposed in this paper.

The differences in the accuracy of each method are further discussed in this paper. The sorting coefficient and average pore throat radius can be considered a combination of the degree of mineral weathering, depositional environment, and transport distance. Core samples from the Mishrif Formation were used to obtain sorting coefficients and average pore throat radii from MICP data and were analyzed in conjunction with core irreducible water saturation. As the sorting coefficient changes from large to small, the irreducible water saturation increases (Figure 19a). With the sorting coefficient becoming smaller, the rock particle size tends to be more homogeneous, the specific surface area of the rock increases, and the film irreducible water increases. Additionally, a lower sorting coefficient corresponds to finer reservoir pore throats, and the fluid mobility deteriorates, increasing the capillary irreducible water (Figure 19b). Previous studies have shown that, in general, weaker sedimentary hydrodynamics result in a smaller sorting coefficient, stronger mechanical compaction and cementation, poorer pore throat connectivity and microscopic pore structures, and higher irreducible water saturation [31]. In other words, rock particles and pore radius directly affect irreducible water saturation. This explains why the previous parameters extracted based on the experimental data of mercury compaction to characterize pore throat size can be used to evaluate irreducible water. The T_2lm in this paper’s method is also proven to be highly correlated with the mode value, as both indicate the pore throat size of the reservoir.

The size of pore throats differs significantly from porosity in geological formations. While a larger porosity generally corresponds to a larger pore throat radii in homogeneous reservoirs, the Mishrif Formation studied here exhibits non-homogeneous characteristics. Figure 20a presents two cores from the Mishrif Formation, with pore throat size distributions extracted via Hg-pressure experiments. Despite similar porosities (19.2% vs. 19.3%), core samples M-107A and M-144A display distinct pore throat peaks: 1 μm and 0.466 μm, respectively, resulting in more than a fourfold difference in permeability. This discrepancy accounts for the low goodness of fit (0.184) observed between porosity and irreducible water saturation (Figure 20b). In contrast, the correlation between pore throat parameters and irreducible water saturation is notably stronger, as evidenced by a goodness of fit of 0.613 when correlating the average pore throat radius with irreducible water saturation (Figure 19). In reservoirs exhibiting significant non-homogeneity, the pore throat radius cannot be accurately inferred from porosity alone, which contributes to the highest average relative error (21.62%) observed in direct evaluations of irreducible water using porosity. While introducing permeability parameters improves accuracy to some extent, its effectiveness remains inferior to the method proposed in this study. Moreover, the complexity involved in assessing permeability further restricts the accuracy and applicability of this approach compared to the proposed method.

The T_2cutoff method is commonly employed for assessing irreducible water saturation using NMR logging data. Analysis of actual core samples reveals variability in T_2cutoff values (Figure 21a), ranging from 31.6 ms to 82 ms. This variability complicates the establishment of a uniform T_2cutoff for accurate irreducible water saturation evaluation, despite 92 ms often being used as a standard cut-off value. However, applying this cut-off frequently results in calculated irreducible water saturation values higher than those observed in core measurements. To address this discrepancy, this study integrates analysis from ground nuclear magnetic experiments. Traditionally, fluid relaxation processes in pore throats are assumed to be independent and non-interfering. Yet, recent research has uncovered a “diffusion coupling” phenomenon in carbonate reservoirs. In such formations, significant variation in pore scale leads to interconnected water content across different pore sizes. This diffusion among hydrogen-containing fluids in varying pore sizes complicates the accurate determination of relaxation time distributions [27,40]. NMR data from carbonate reservoirs in the Middle East (Figure 21b) demonstrate that after centrifugation, the long and short relaxation components of T₂ spectra do not correspond to pre-centrifugation readings. This indicates a notable “diffusion coupling” effect, where fluids in different pore throat radii intermix due to diffusion. Ramakrishnan, using the Monte Carlo random walk model, suggests that the surface relaxation rate plays a crucial role in accurately reflecting pore size distributions [65]. Experimental data from the Mishrif Formation in the study area indicate surface relaxation rates ranging from 0 to 5 μm/s, further complicating accurate reservoir irreducible water saturation assessment via T_2cutoff predictions. Consequently, the T_2cutoff method exhibits significant error in evaluating irreducible water saturation. Moreover, its limited applicability is exacerbated by the fact that most production wells do not gather NMR data, thereby restricting its generalizability.

Coates [29] proposed the spectral coefficient method as an alternative to the cut-off value approach for determining irreducible water saturation in carbonate rocks. This method assumes a consistent irreducible water content regardless of pore size, although this content decreases as pore size increases. Each T_2i signal reflects a specific irreducible water saturation due to its contribution from irreducible water at various T₂ time points. Comparative analysis shows that this method exhibits the lowest relative error among the four evaluated methods. Figure 22, based on experimental core data, demonstrates a strong correlation (R² = 0.73) between T_2lm and irreducible water saturation. This correlation is further supported by this study’s examination of the relationship between T_2lm and pore throat diameters. The significant association observed between T_2lm and irreducible water saturation, coupled with correlations to pore throat parameters, underscores the efficacy of the spectral coefficient method. This finding aligns with the perspective presented by Wang et al. [66], emphasizing the substantial correlation between irreducible water saturation and T_2lm in unconventional reservoirs, contrasting with the weaker correlation with porosity. Although Wang et al. did not specify reasons, this study provides empirical support for their observations.

In summary, the irreducible water saturation formula derived by the method in this paper considers the fractal dimension of the reservoir, porosity, and T_2lm, resulting in a higher accuracy. Additionally, this study combines the Thomeer Function with fractal theory and derives the specific expressions for the $p_d$ parameter and ${(B_v)}_{p_c\infty }$ parameter in the Thomeer Function.

A novel irreducible water saturation model was developed by integrating the T_2lm from NMR fractal permeability models. Validation with ground NMR and MICP data confirmed the correlation between pore throat diameter (Mode) and T_2lm values. Fractal theory was applied to derive numerical relationships among Thomeer Function parameters, elucidating connections between T_2lm and physical properties. Leveraging these insights, a robust predictive model was created that combines traditional logging curves with advanced deep learning techniques, facilitating accurate evaluation of irreducible water saturation even in the absence of NMR logging data. This method enhances the reliability of water saturation assessments and extends analytical capabilities when direct NMR measurements are unavailable.

6.2. Limitations and Errors of the Method

Additionally, this paper discusses the limitations of the methodology, noting that the Mishrif Formation has a very low clay content and is a pure greywacke reservoir. Previous studies have shown that clay mineral content affects the magnitude of irreducible water saturation. Experimental data from clay mineral-bearing cores in the Halfaya field show a positive correlation between clay mineral content and irreducible water saturation (Figure 23). As the clay mineral content increases, the specific surface area of the reservoir rock increases, enhancing its ability to adsorb formation water. The surface of clay minerals is generally negatively charged, which can directly adsorb electrically unbalanced polar water molecules and combine to form hydrated ions, indirectly attracting water molecules and increasing film irreducible water [67]. Additionally, clay minerals fill the pore space, strengthening the binding of pore fluid by capillary force and increasing capillary irreducible water.

Since the Mishrif Formation is almost free of clay minerals, the effect of clay mineral content is not reflected in the final form of the equation, which is a limitation of this method. When applying this method to other layer groups or reservoirs with different geological profiles, the form and process of evaluating irreducible water saturation can be followed. The effect of clay mineral content on irreducible water saturation should be considered in conjunction with actual core experimental data for clay-rich reservoirs.

Regarding the application error of this method, although the evaluation process of irreducible water saturation proposed in this paper accounts for the lack of NMR data from production wells, it cannot avoid the generation of carry-over error after inverting the T_2lm curves using the deep learning method and then evaluating the irreducible water saturation. This includes the evaluation error of porosity, which cannot be eliminated by constructing a separate error model. This issue is discussed in Section 5.2 of this paper. The error results discussed in Section 5.2 of this paper show that using the inverted T_2lm curve to evaluate irreducible water saturation increases the relative error. However, the overall evaluation accuracy can still provide effective data support for the formulation of subsequent production and development programs and the selection of perforated intervals.

7. Conclusions

This study introduces a novel method for predicting and evaluating irreducible water saturation by integrating actual core experimental data and practical applications, leading to the following conclusions:

(1)

The nuclear magnetic fractal permeability model effectively predicts irreducible water saturation.

(2)

A distinct numerical relationship exists between the modal parameter of pore throat diameter based on the Thomeer Function and T_2lm. Utilizing fractal theory, this relationship clarifies the connection between each parameter and the physical property parameter in the Thomeer Function, thereby establishing the numerical association between T_2lm and the Thomeer Function.

(3)

Employing deep learning, conventional logging curves, and derived parameter curves enables the effective inversion of the T_2lm curve for evaluating irreducible water saturation. While the inverted T_2lm curve exhibits a slightly higher relative error compared to that extracted from NMR logging data, it remains within an acceptable range, particularly valuable in the absence of NMR logging data. This method proves effective and feasible.

In summary, this paper presents a broadly applicable method for assessing irreducible water saturation. In wells lacking specialized logging data, a T_2lm curve can be constructed using conventional curves and a deep learning model, successfully applied in the Mishrif Formation within the Halfaya field, Middle East, yielding favorable outcomes.