Method for Measuring the Fractional Derivative of a Two-Dimensional Magnetic Field Based on Taylor–Riemann Series
Abstract
1. Introduction
2. Derivation of the Measurement Principle
2.1. Introduction to Fractional Derivative
2.2. Introduction to Taylor–Riemann Series
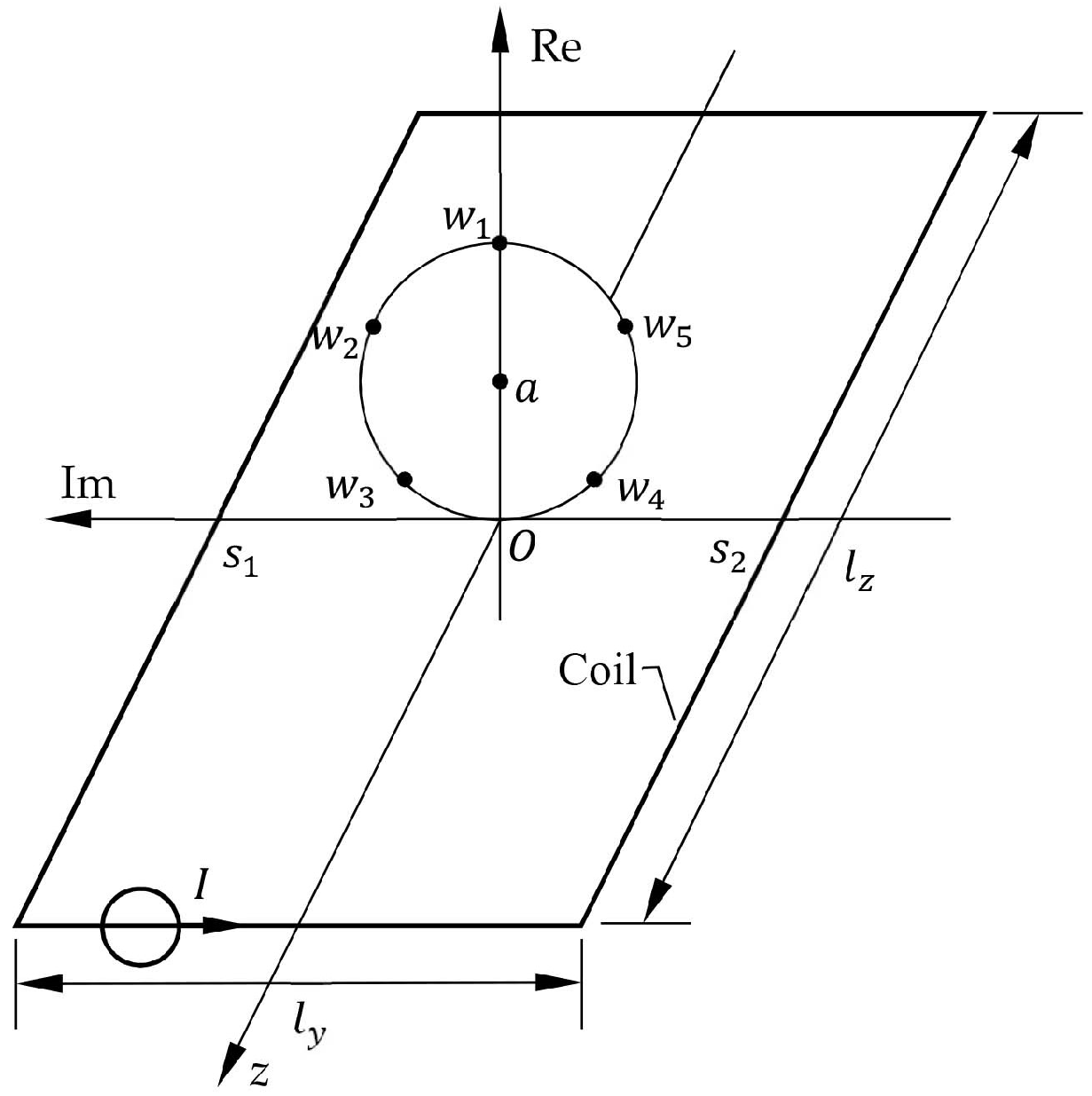
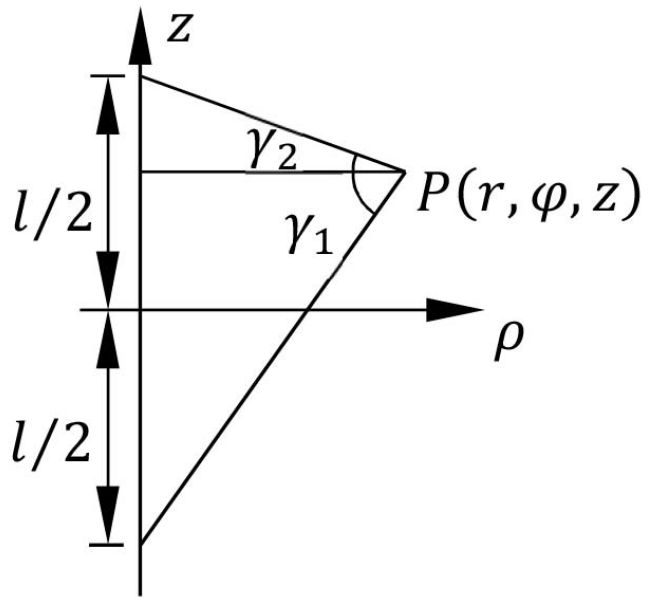
2.3. Implementation of the Measurement Principle
3. TR Method Simulation
3.1. Simulation Setup
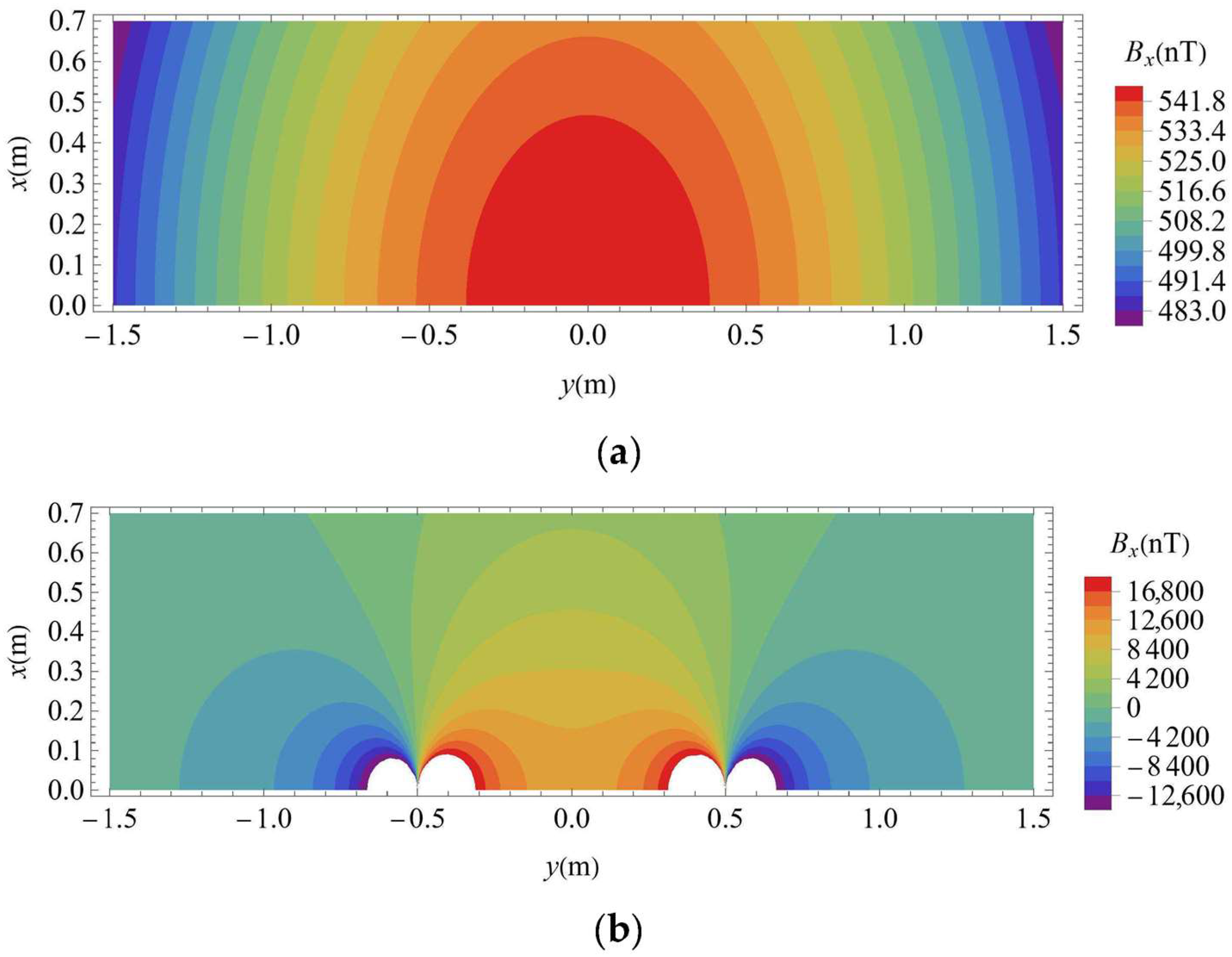
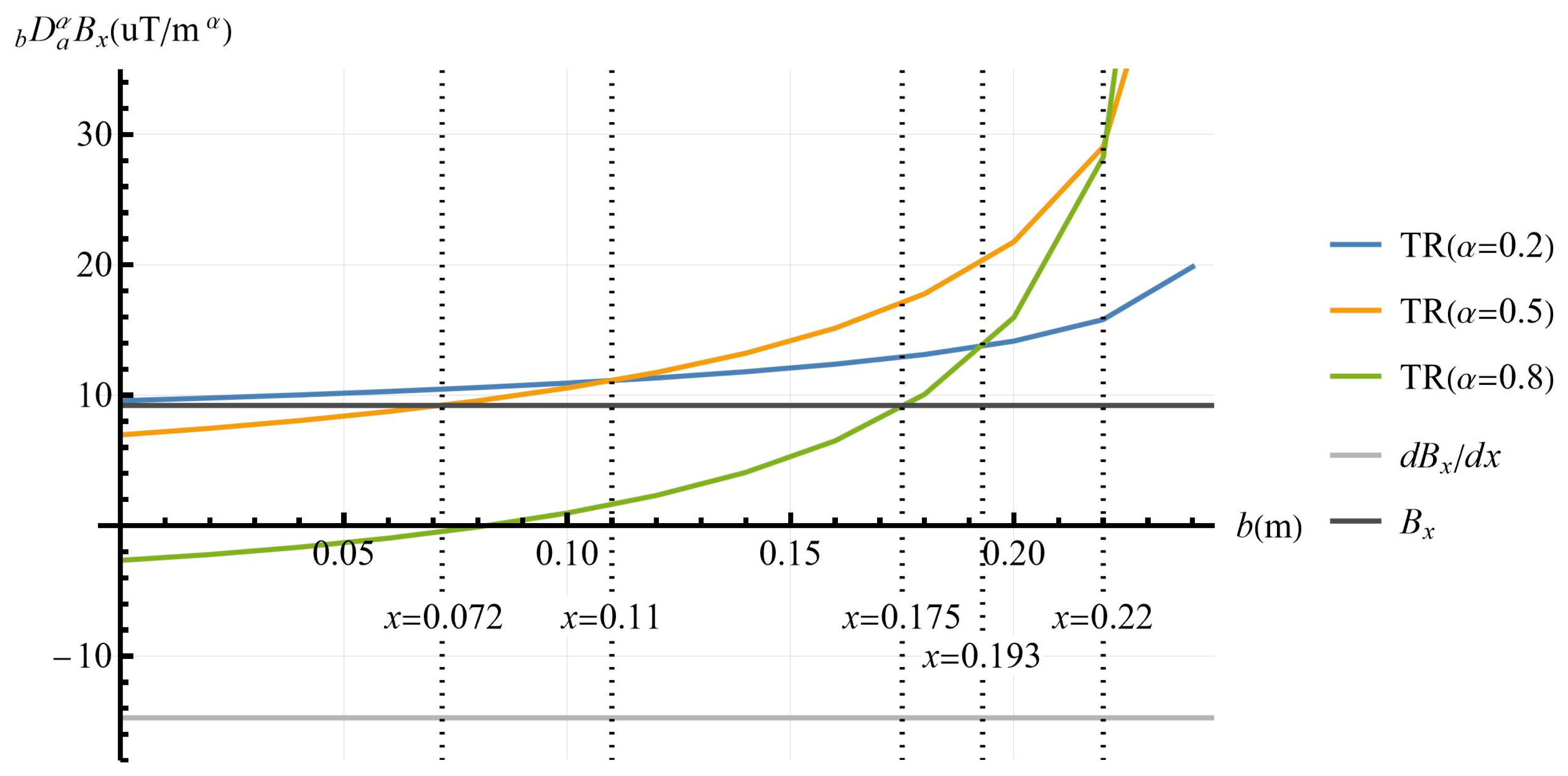
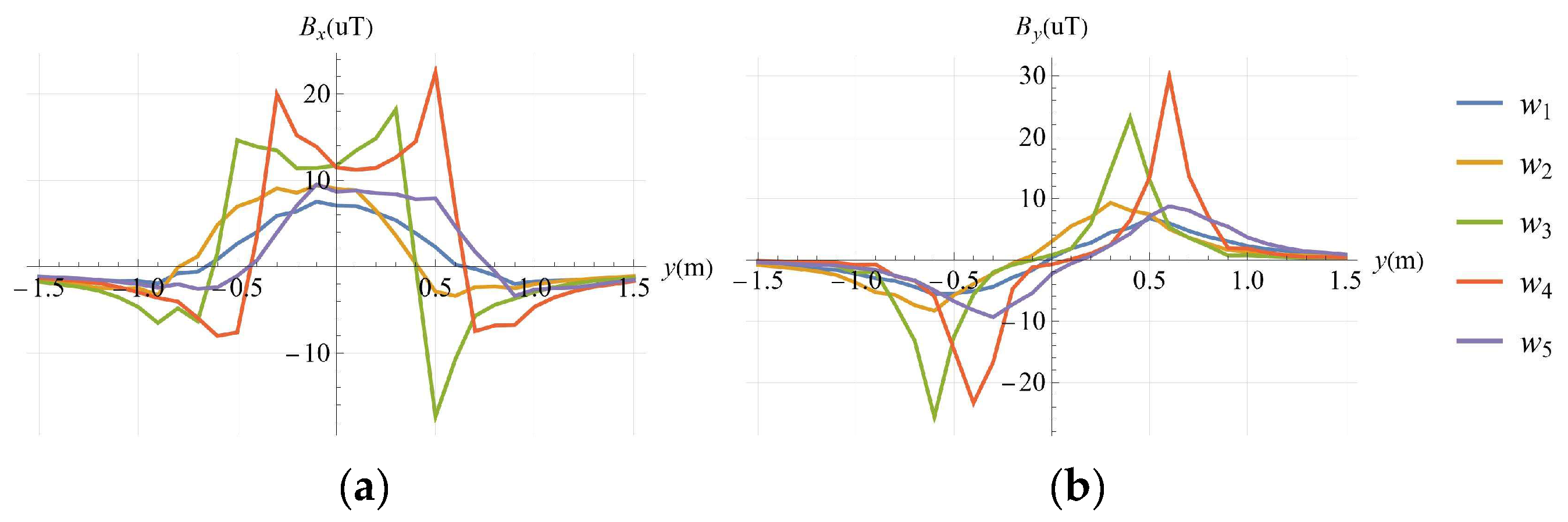
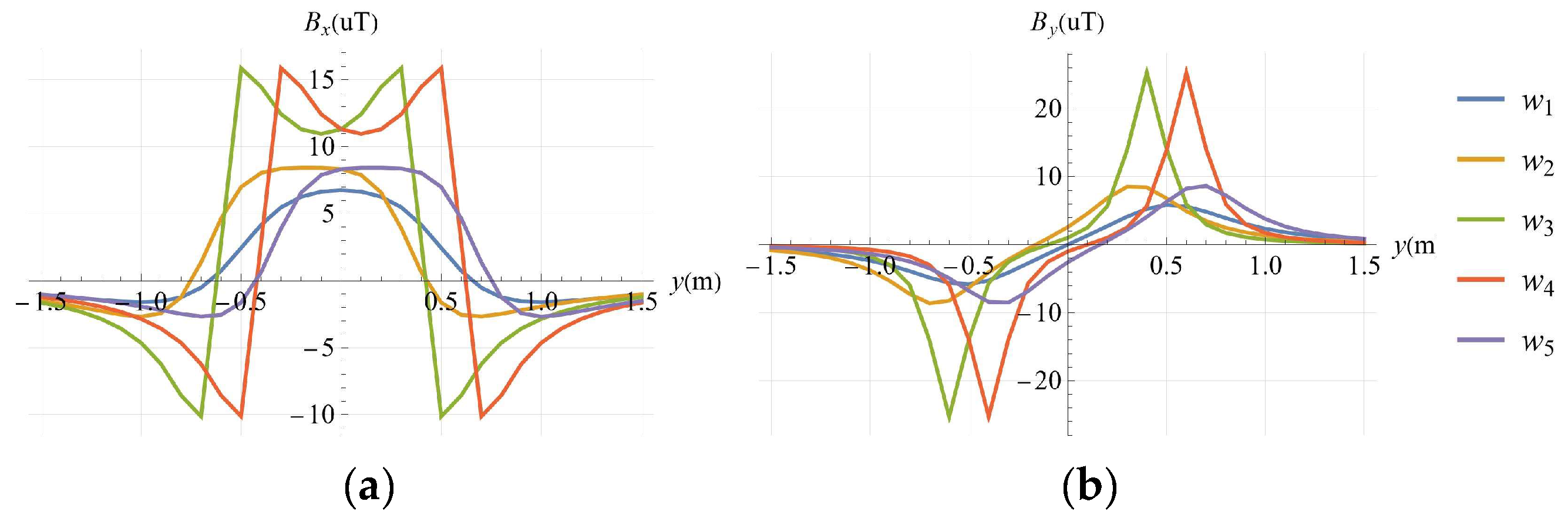
3.2. Single Point Simulation
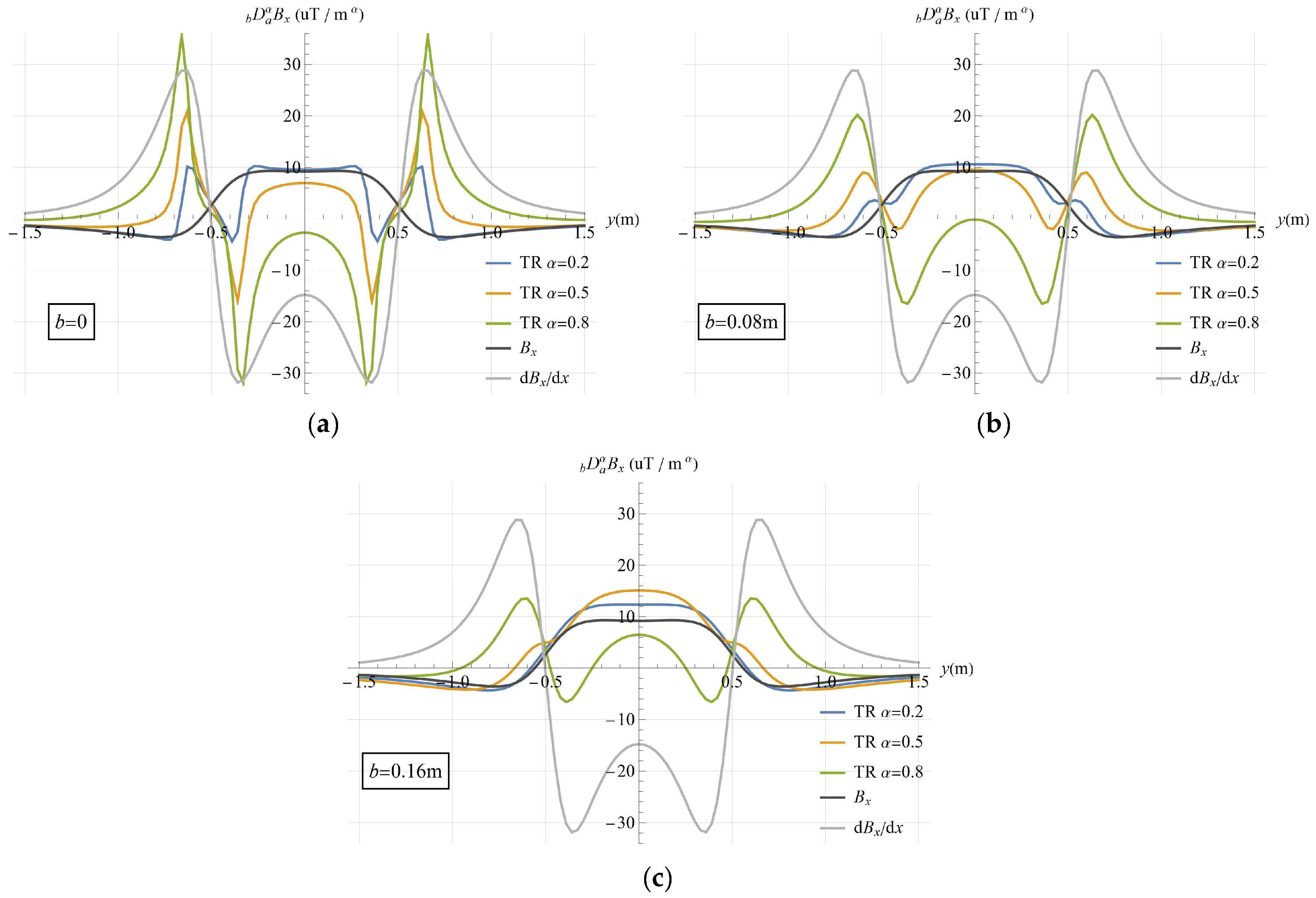
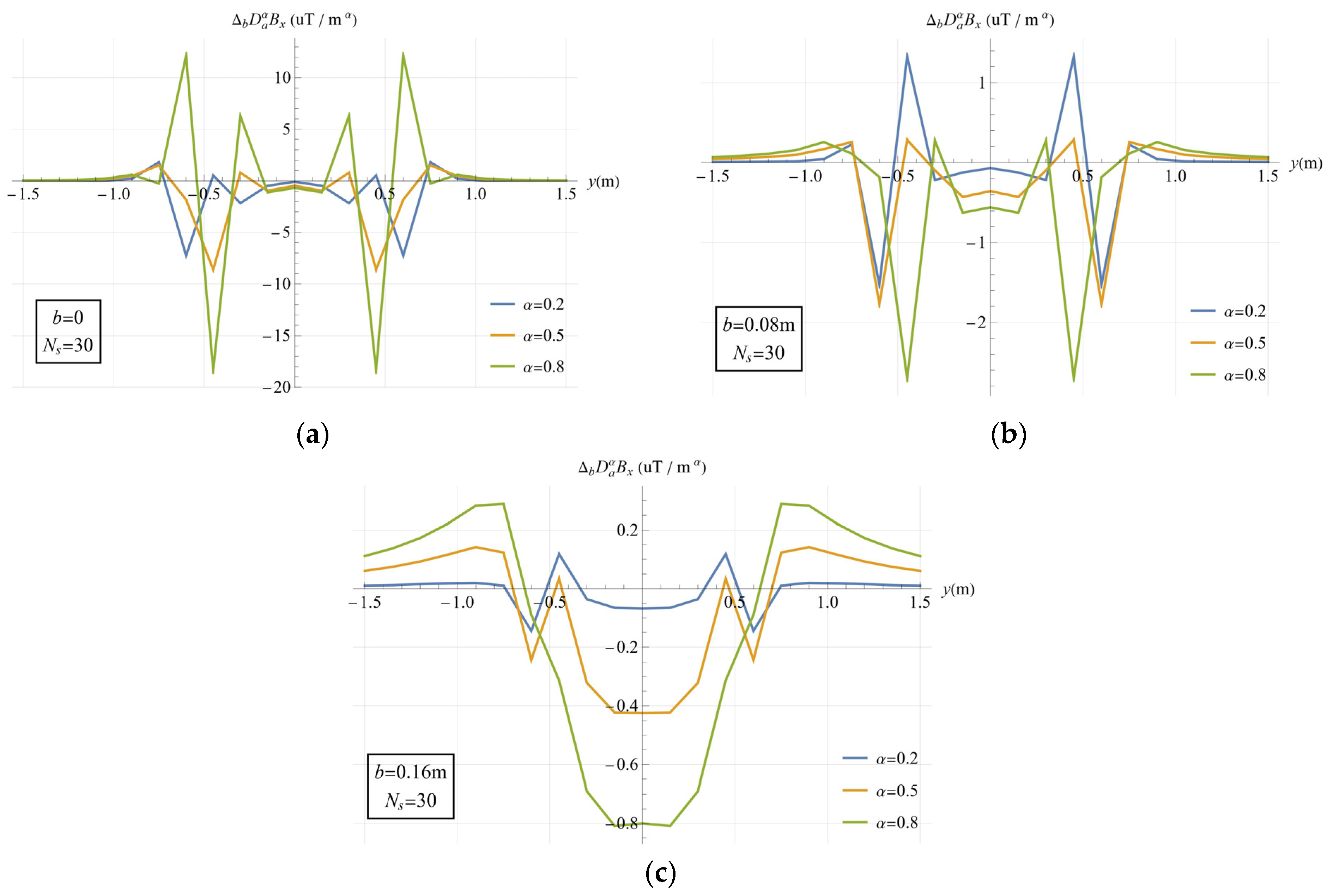
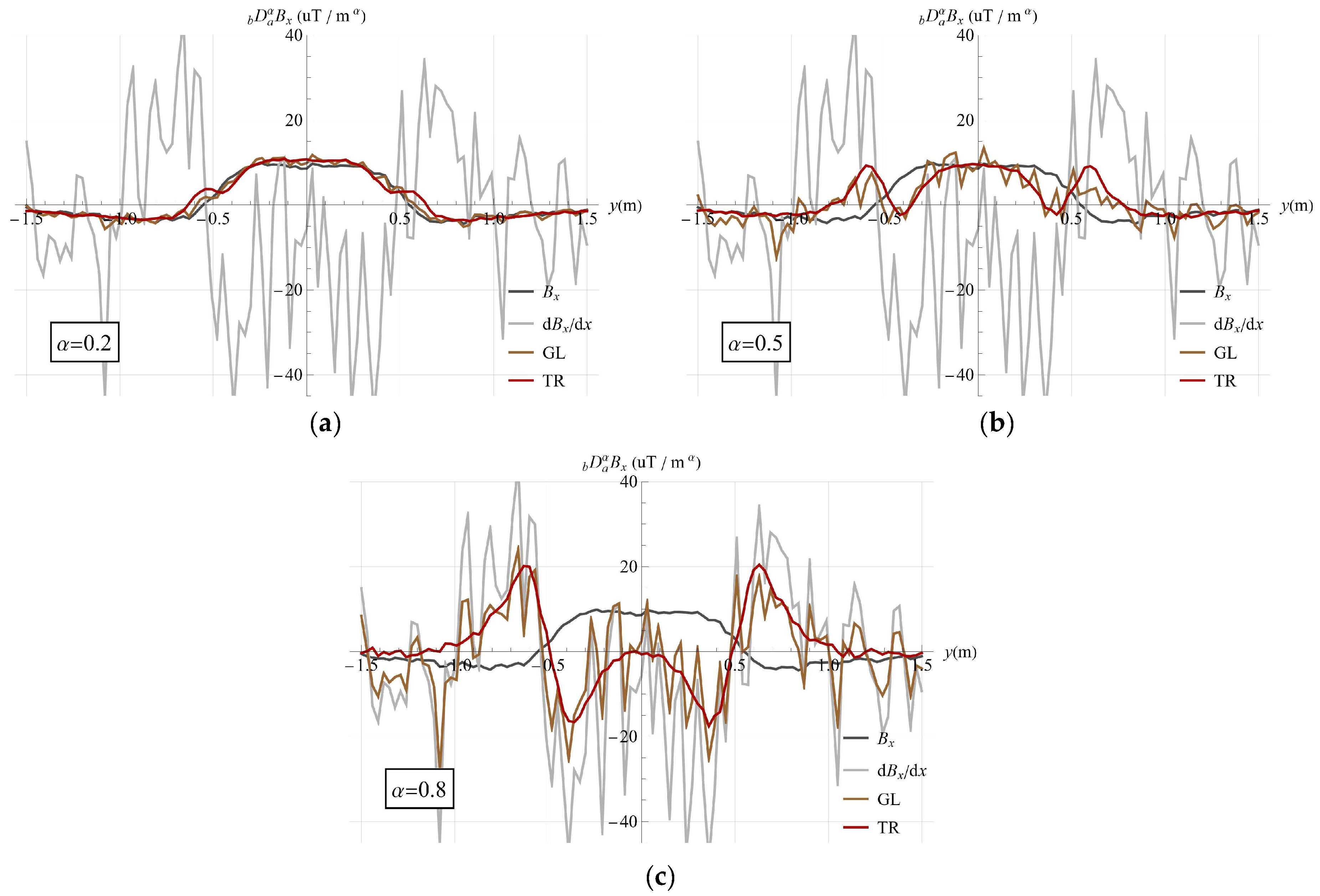
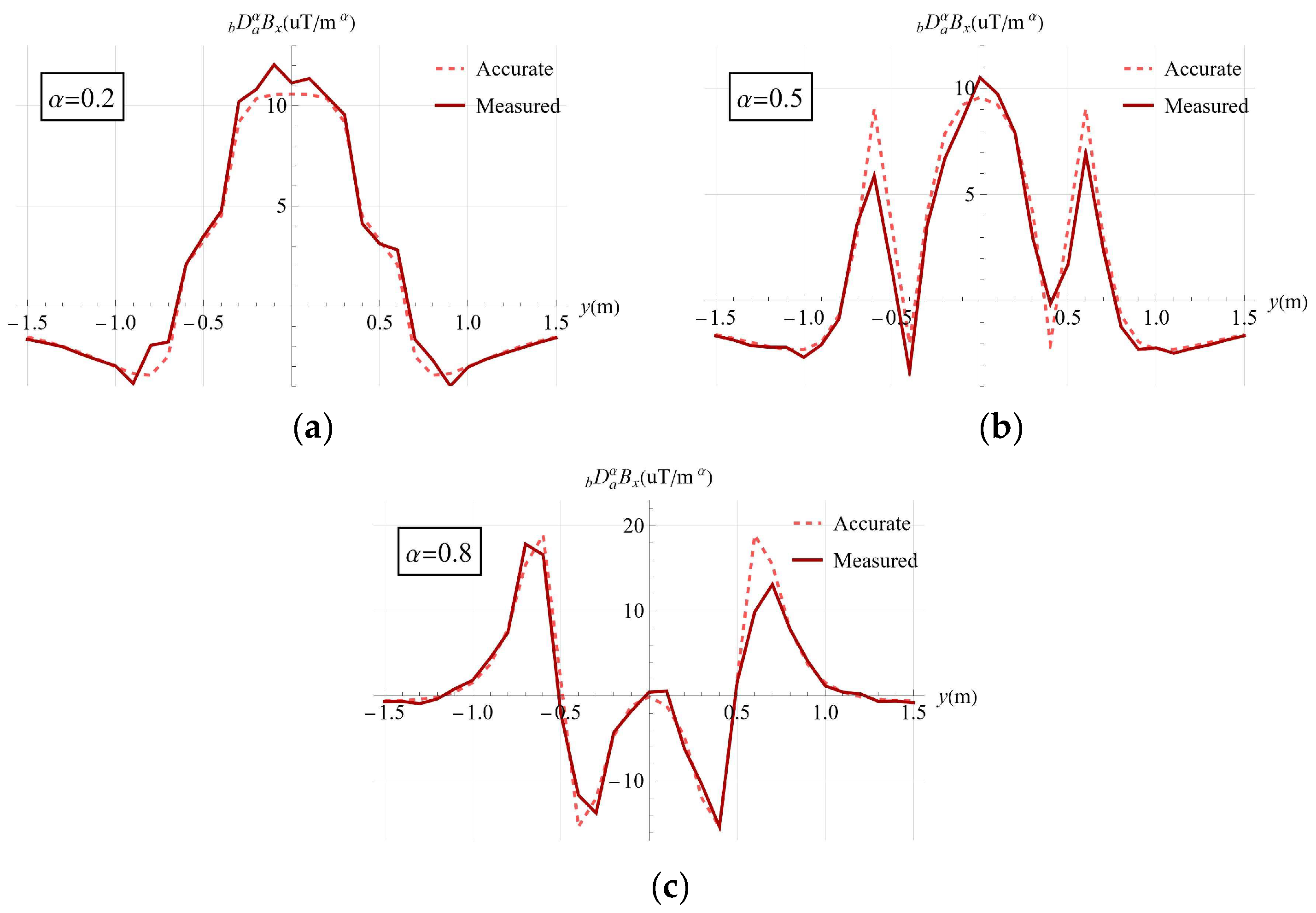
3.3. Survey Line Simulation
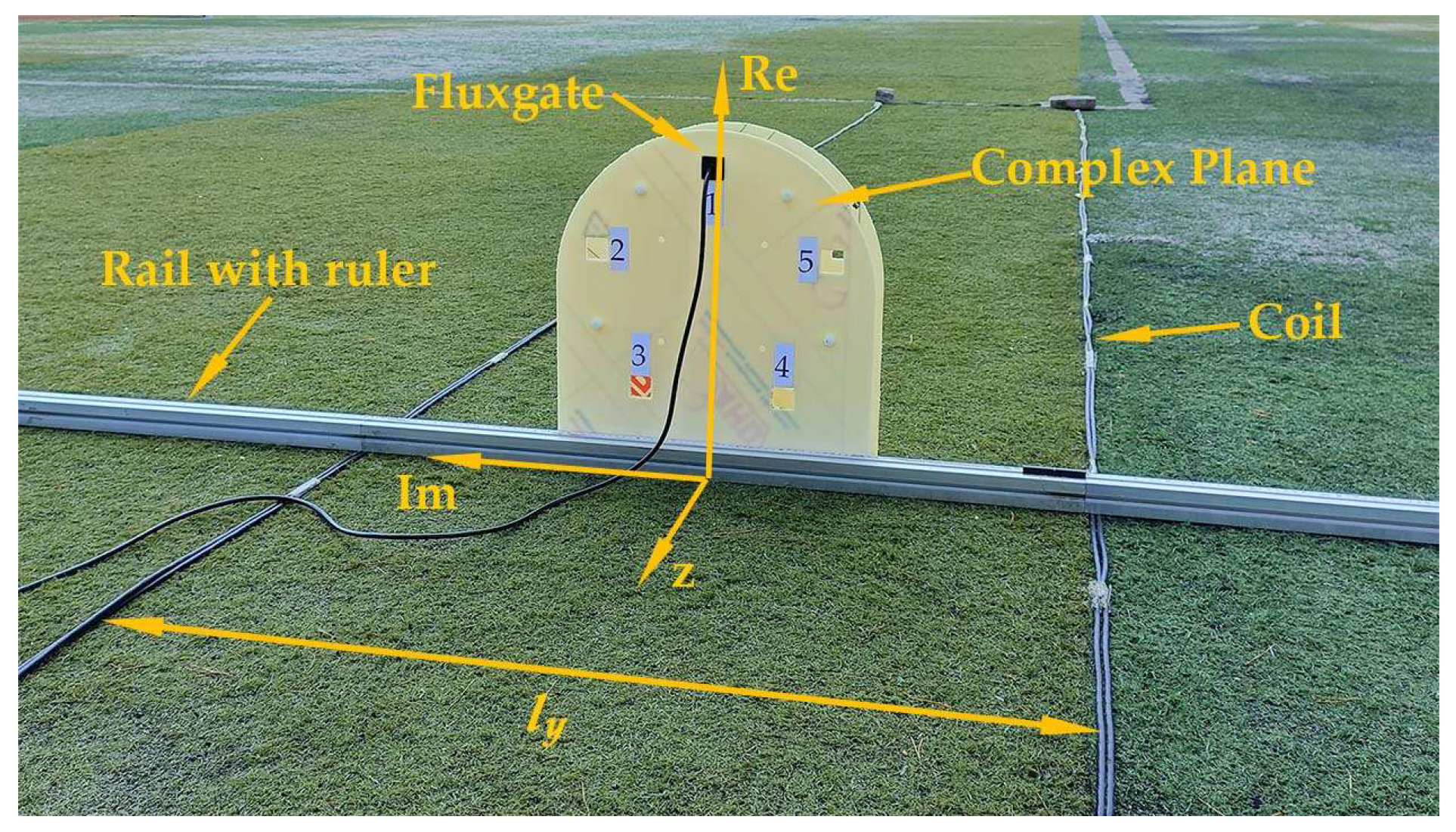
4. Experiment Implementation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993; pp. 1–3. [Google Scholar]
- Miah, B.A.; Sen, M.; Murugan, R.; Gupta, D. Developing Riemann–Liouville-Fractional Masks for Image Enhancement. Circ. Syst. Signal Process. 2024, 43, 3802–3831. [Google Scholar] [CrossRef]
- Hassan, S.K.; Ali Alazzawi, S.N.; Ibrahem, N.M.J. Some Results in Grunwald-Letnikov Fractional Derivative and its Best Approximation. J. Phys. Conf. Ser. 2021, 1818, 012020. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Atangana, A.; Gomez-Aguilar, J.F. Fractional derivatives with no-index law property: Application to chaos and statistics. Chaos Solit. Fract. 2018, 114, 516–535. [Google Scholar] [CrossRef]
- Atangana, A. Non-validity of index law in fractional calculus: A fractional differential operator with Markovian and non-Markovian properties. Physica A 2018, 505, 688–706. [Google Scholar] [CrossRef]
- Bouzeffour, F. Advancing Fractional Riesz Derivatives through Dunkl Operators. Mathematics 2023, 11, 4073. [Google Scholar] [CrossRef]
- Ho, K.P. Modular Hadamard, Riemann-Liouville and Weyl fractional integral. Mathematica 2023, 65, 263–274. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diago, CA, USA, 1999; p. 42. [Google Scholar]
- Lavoie, J.L.; Osler, T.J.; Tremblay, R. Fractional Derivatives and Special Functions. SIAM Rev. 1976, 18, 240–268. [Google Scholar] [CrossRef]
- Has, A.; Yılmaz, B. Effect of fractional analysis on magnetic curves. Rev. Mex. Fis. 2022, 68, 041401. [Google Scholar] [CrossRef]
- Weiss, C.J.; van Bloemen Waanders, B.G.; Antil, H. Fractional operators applied to geophysical electromagnetics. Geophys. J. Int. 2020, 220, 1242–1259. [Google Scholar] [CrossRef]
- Ge, J.; Everett, M.E.; Weiss, C.J. Fractional diffusion analysis of the electromagnetic field in fractured media—Part 2: 3D approach. Geophysics 2015, 80, E175–E185. [Google Scholar] [CrossRef]
- Podlubny, I. Geometric and Physical Interpretation of Fractional Integration and Fractional Differentiation. Fract. Calc. Appl. Anal. 2002, 5, 367–386. [Google Scholar]
- Bai, L.; Xue, D.Y. Geometric Meaning of a Special Riemann-Liouville Fractional-Order Integral. MIPAT 2020, 50, 234–239. [Google Scholar]
- Peters, L.J. The direct approach to magnetic interpretation and its practical application. Geophysics 1949, 14, 290–320. [Google Scholar] [CrossRef]
- Gunn, P.J. Linear transformations of gravity and magnetic fields. Geophys. Prospect. 1975, 23, 300–312. [Google Scholar] [CrossRef]
- Gunn, P.J.; Fitzgerald, D.; Yassi, N.; Dart, P. New algorithms for visually enhancing airborne geophysical data. Explor. Geophys. 1997, 28, 220–224. [Google Scholar] [CrossRef]
- Cooper, G.; Cowan, D. The application of fractional calculus to potential field data. Explor. Geophys. 2003, 34, 51–56. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: San Diego, CA, USA, 1974; pp. 48–51. [Google Scholar]
- Cooper, G.R.J.; Cowan, D.R. Sunshading geophysical data using fractional order horizontal gradients. TLE 2003, 22, 204–205. [Google Scholar] [CrossRef]
- Cowan, D.; Cooper, G. Separation filtering using fractional order derivatives. Explor. Geophys. 2005, 36, 393–396. [Google Scholar] [CrossRef]
- Arısoy, M.O.; Dikmen, U. Edge enhancement of magnetic data using fractional-order-derivative filters. Geophysics 2015, 80, J7–J17. [Google Scholar] [CrossRef]
- Hood, P. Gradient measurements in aeromagnetic surveying. Geophysics 1965, 30, 891–902. [Google Scholar] [CrossRef]
- Stolz, R.; Zakosarenko, V.; Schulz, M.; Chwala, A.; Fritzsch, L.; Meyer, H.G.; Köstlin, E.O. Magnetic full-tensor SQUID gradiometer system for geophysical applications. Lead. Edge 2006, 25, 178–180. [Google Scholar] [CrossRef]
- Pei, Y.H.; Yeo, H.G.; Kang, X.Y.; Pua, S.L.; Jhon, T. Magnetic gradiometer on an AUV for buried object detection. In OCEANS 2010 MTS/IEEE SEATTLE; IEEE: Seattle, WA, USA, 2010. [Google Scholar]
- Cocchi, L.; Carmisciano, C.; Palangio, P.; Gualdesi, L. S3MAG-Low Magnetic Noise AUV for Multipurpose Investigations Oceans; IEEE: Genova, Italy, 2015. [Google Scholar]
- Chen, J.F. Research on Method of Magnetic Anomaly Detection Based on Gradient Tensor. Ph.D. Thesis, National University of Defense Science and Technology, Changsha, China, 2012. [Google Scholar]
- Sunderland, A.; Ju, L.; Blair, D.G.; McRae, W.; Veryaskin, A.V. Optimizing a direct string magnetic gradiometer for geophysical exploration. Rev. Sci. Instrum. 2009, 80, 104705. [Google Scholar] [CrossRef]
- Tilbrook, D.L. Rotating magnetic tensor gradiometry and a superconducting implementation. Supercond. Sci. Technol. 2009, 22, 075002. [Google Scholar] [CrossRef]
- Munkhammar, J. Riemann-Liouville Fractional Derivatives and the Taylor-Riemann Series. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, June 2004. [Google Scholar]
- Xue, D.Y. Fractional Calculus and Fractional-Order Control; Science Press: Beijing, China, 2018; pp. 63–64. [Google Scholar]
- Hardy, G.H. Riemann’s form of Taylor’s series. J. Lond. Math. Soc. 1945, 20, 48–57. [Google Scholar] [CrossRef]
- Osler, T.J. Leibniz Rule, the Chain Rule, and Taylor’s Theorem for Fractional Derivatives. Ph.D. Thesis, New York University, New York, NY, USA, 1970. [Google Scholar]
- Lapidoth, A. A Foundation in Digital Communication, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017; pp. 314–340. [Google Scholar]




| Method | |||
|---|---|---|---|
| TR | * | ||
| GL |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Sui, Y. Method for Measuring the Fractional Derivative of a Two-Dimensional Magnetic Field Based on Taylor–Riemann Series. Fractal Fract. 2024, 8, 375. https://doi.org/10.3390/fractalfract8070375
Wang R, Sui Y. Method for Measuring the Fractional Derivative of a Two-Dimensional Magnetic Field Based on Taylor–Riemann Series. Fractal and Fractional. 2024; 8(7):375. https://doi.org/10.3390/fractalfract8070375
Chicago/Turabian StyleWang, Ruijian, and Yangyi Sui. 2024. "Method for Measuring the Fractional Derivative of a Two-Dimensional Magnetic Field Based on Taylor–Riemann Series" Fractal and Fractional 8, no. 7: 375. https://doi.org/10.3390/fractalfract8070375
APA StyleWang, R., & Sui, Y. (2024). Method for Measuring the Fractional Derivative of a Two-Dimensional Magnetic Field Based on Taylor–Riemann Series. Fractal and Fractional, 8(7), 375. https://doi.org/10.3390/fractalfract8070375







