An Efficient Numerical Solution of a Multi-Dimensional Two-Term Fractional Order PDE via a Hybrid Methodology: The Caputo–Lucas–Fibonacci Approach with Strang Splitting
Abstract
1. Introduction
Motivation
- The complex characteristics of fractional nonlinear PDEs make calculating analytical solutions challenging, driving ongoing research efforts to develop accurate and efficient numerical methodologies, with the two-term fractional order Sobolev model equation in both two and three dimensions holding significant importance across multiple scientific domains.
- This study aimed to introduce an efficient numerical framework specifically designed for solving PDEs with temporal fractions.
- The proposed methodology adopts a hybrid approach, integrating Fibonacci and Lucas polynomials with finite difference techniques, while also addressing the temporal direction through the utilization of the Liouville–Caputo fractional derivative in conjunction with a splitting mechanism.
- Lucas and Fibonacci polynomials, unlike orthogonal counterparts, like Chebyshev polynomials, are non-orthogonal, eliminating the need for interval transformations. Additionally, they facilitate the straightforward approximation of higher-order derivatives for unknown functions.
- Furthermore, the approach is characterized by its simplicity and ability to enhance the accuracy, even in scenarios involving fewer nodal points, with the aim to provide a robust and effective numerical solution to the intricate challenges posed by nonlinear PDEs.
2. Basic Concepts in Fractional Calculus and Polynomial Theory
2.1. Fibonacci and Lucas Polynomial Theory
- Fibonacci polynomials [49]:
- Lucas polynomials [49]:
2.2. Function Approximation
3. Suggested Methodology
3.1. Time Discretization
3.2. Spatial Discretization
3.3. Full Discretization
4. Analyzing Errors
Stability Analysis
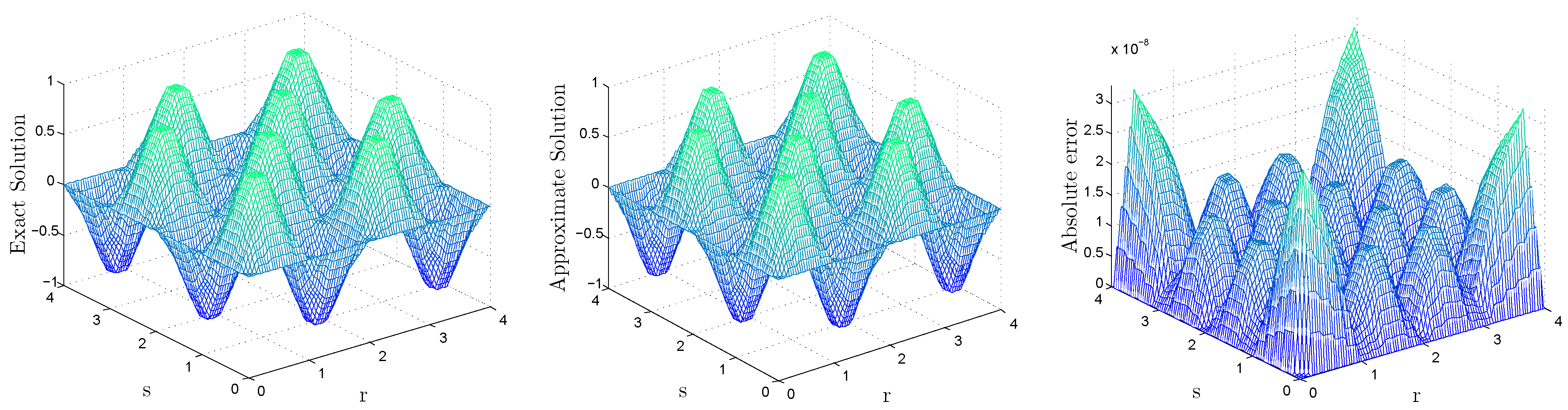
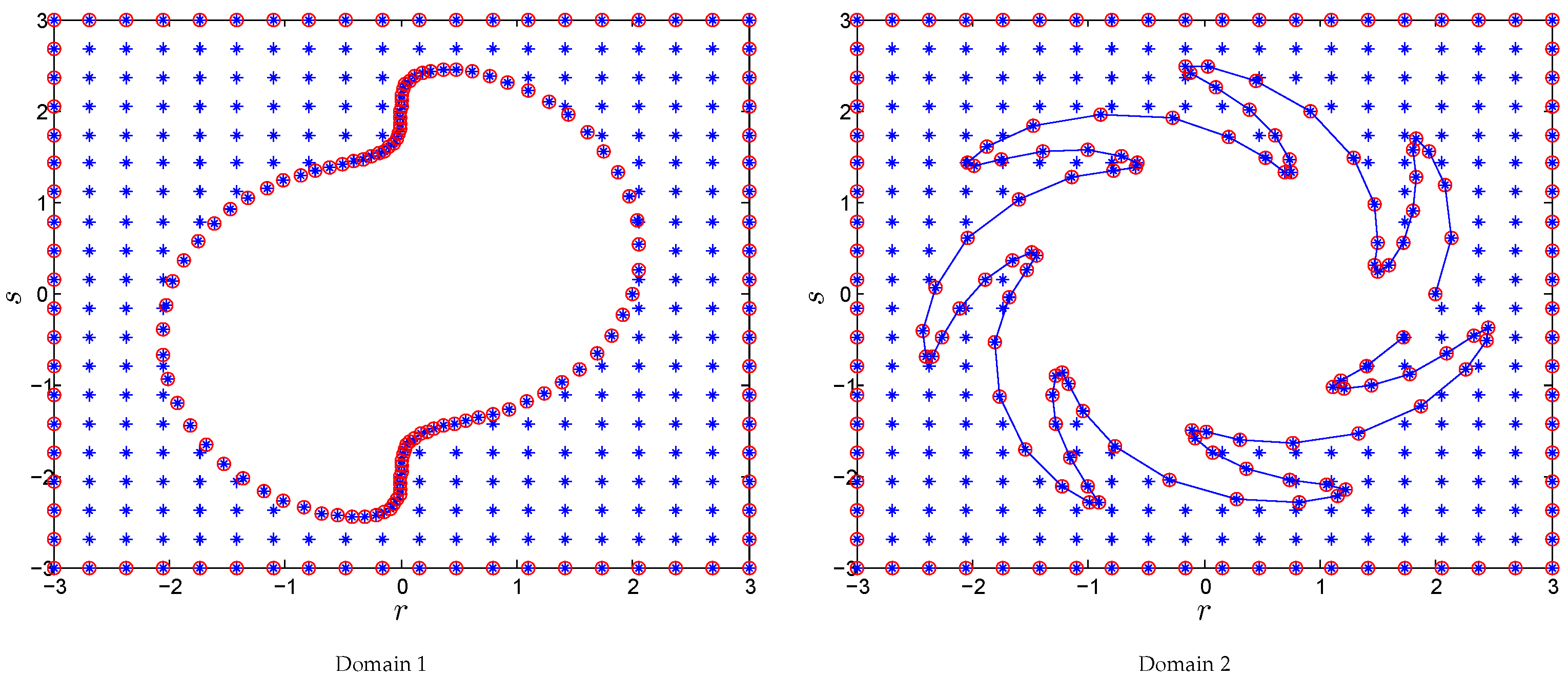
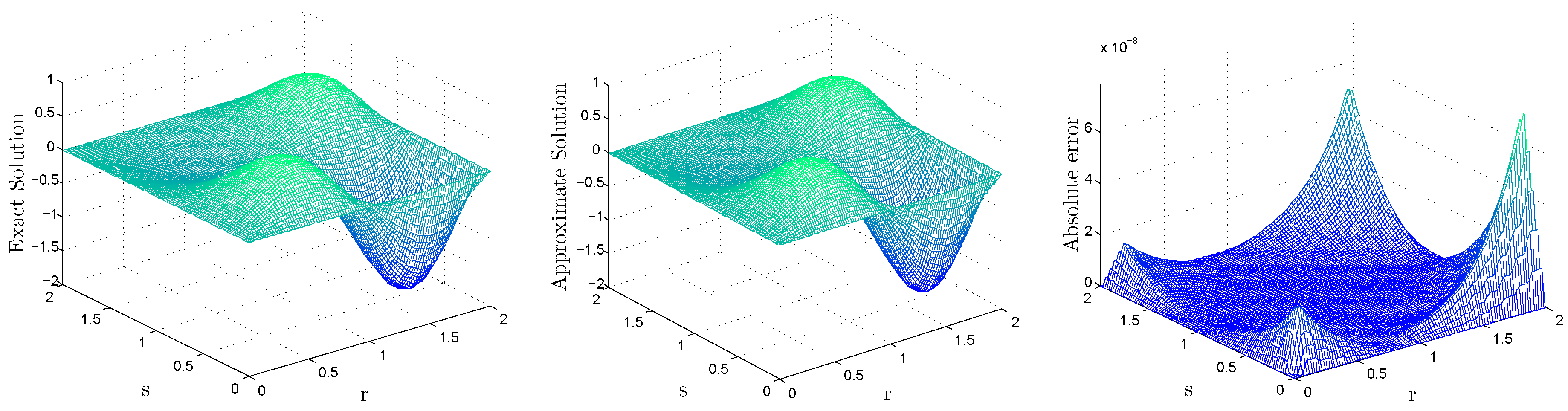
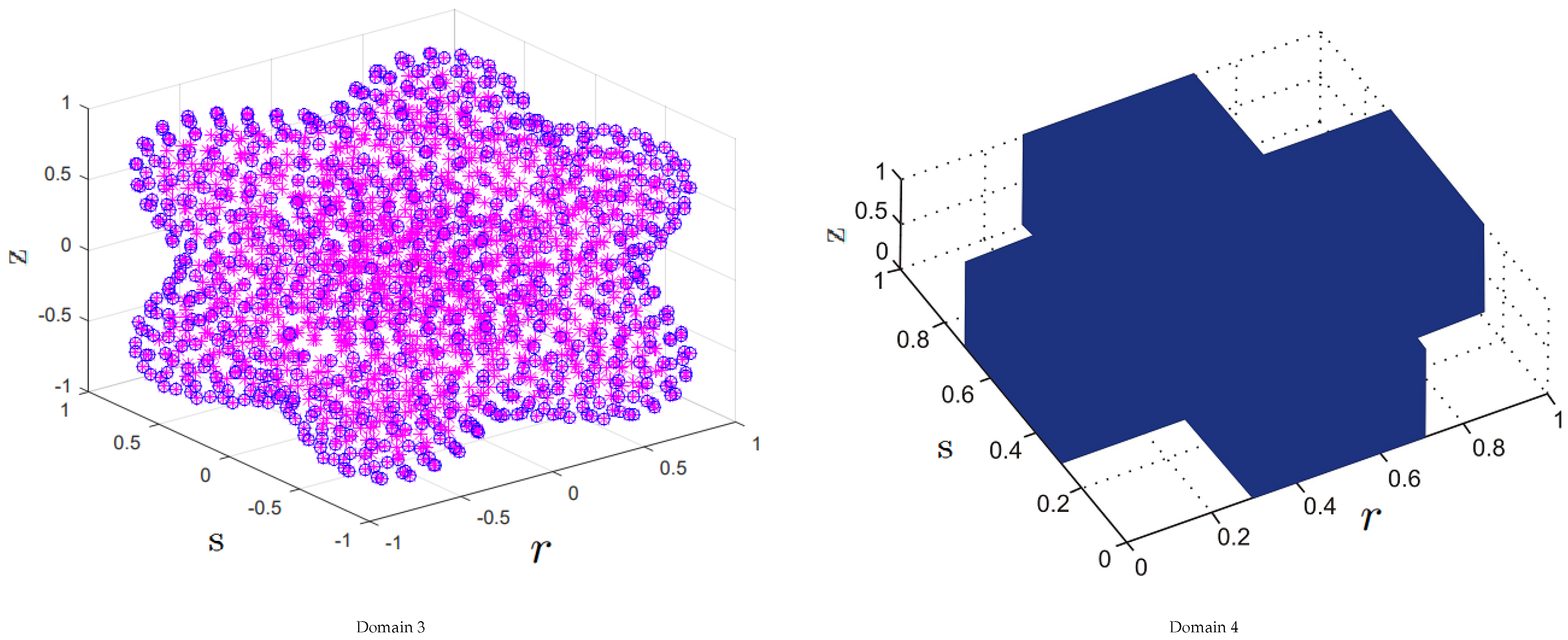
5. Discussion and Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jan, A.; Srivastava, H.M.; Khan, A.; Mohammed, P.O.; Jan, R.; Hamed, Y. In vivo HIV dynamics, modeling the interaction of HIV and immune system via non-integer derivatives. Fractal Fract. 2023, 7, 361. [Google Scholar] [CrossRef]
- Oderinu, R.A.; Owolabi, J.A.; Taiwo, M. Approximate solutions of linear time-fractional differential equations. J. Math. Comput. Sci. 2023, 29, 60–72. [Google Scholar] [CrossRef]
- Ahmad, I.; Ali, I.; Jan, R.; Idris, S.A.; Mousa, M. Solutions of a three-dimensional multi-term fractional anomalous solute transport model for contamination in groundwater. PLoS ONE 2023, 18, e0294348. [Google Scholar] [CrossRef] [PubMed]
- Siraj-ul-Islam; Ahmad, I. A comparative analysis of local meshless formulation for multi-asset option models. Eng. Anal. Bound. Elem. 2016, 65, 159–176. [Google Scholar] [CrossRef]
- Wang, K.L.; He, C.H. A remark on Wang’s fractal variational principle. Fractals 2019, 27, 1950134. [Google Scholar] [CrossRef]
- Anjum, N.; He, C.H.; He, J.H. Two-scale fractal theory for the population dynamics. Fractals 2021, 29, 2150182. [Google Scholar] [CrossRef]
- Zheltov, I.; Kochina, I.; Barenblatt, G. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks (strata). J. Appl. Math. Mech. 1960, 24, 852–864. [Google Scholar]
- Ting, T.W. A cooling process according to two-temperature theory of heat conduction. J. Math. Anal. Appl. 1974, 45, 23–31. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Afzal, I.; Ali, K. Chirped optical solitons for Triki–Biswas equation. Mod. Phys. Lett. B 2019, 33, 1950264. [Google Scholar] [CrossRef]
- Attia, R.A.; Lu, D.; MA Khater, M. Chaos and relativistic energy-momentum of the nonlinear time fractional Duffing equation. Math. Comput. Appl. 2019, 24, 10. [Google Scholar] [CrossRef]
- Kelly, J.F.; McGough, R.J.; Meerschaert, M.M. Analytical time-domain Green’s functions for power-law media. J. Acoust. Soc. Am. 2008, 124, 2861–2872. [Google Scholar] [CrossRef] [PubMed]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Showalter, R. Existence and representation theorems for a semilinear Sobolev equation in Banach space. SIAM J. Math. Anal. 1972, 3, 527–543. [Google Scholar] [CrossRef]
- Ewing, R.E. Numerical solution of Sobolev partial differential equations. SIAM J. Numer. Anal. 1975, 12, 345–363. [Google Scholar] [CrossRef]
- Wang, F.; Ahmad, I.; Ahmad, H.; Alsulami, M.; Alimgeer, K.; Cesarano, C.; Nofal, T.A. Meshless method based on RBFs for solving three-dimensional multi-term time fractional PDEs arising in engineering phenomenons. J. King Saud Univ.-Sci. 2021, 33, 101604. [Google Scholar] [CrossRef]
- Luo, Z.; Teng, F. A reduced-order extrapolated finite difference iterative scheme based on POD method for 2D Sobolev equation. Appl. Math. Comput. 2018, 329, 374–383. [Google Scholar] [CrossRef]
- Li, J.F.; Ahmad, I.; Ahmad, H.; Shah, D.; Chu, Y.M.; Thounthong, P.; Ayaz, M. Numerical solution of two-term time-fractional PDE models arising in mathematical physics using local meshless method. Open Phys. 2020, 18, 1063–1072. [Google Scholar] [CrossRef]
- Luo, Z.; Teng, F.; Chen, J. A POD-based reduced-order Crank–Nicolson finite volume element extrapolating algorithm for 2D Sobolev equations. Math. Comput. Simul. 2018, 146, 118–133. [Google Scholar] [CrossRef]
- Li, N.; Lin, P.; Gao, F. An expanded mixed finite element method for two-dimensional Sobolev equations. J. Comput. Appl. Math. 2019, 348, 342–355. [Google Scholar] [CrossRef]
- Heydari, M.; Rashid, S.; Jarad, F. A numerical method for distributed-order time fractional 2D Sobolev equation. Results Phys. 2023, 45, 106211. [Google Scholar] [CrossRef]
- Gao, F.; Qiu, J.; Zhang, Q. Local discontinuous Galerkin finite element method and error estimates for one class of Sobolev equation. J. Sci. Comput. 2009, 41, 436–460. [Google Scholar] [CrossRef]
- Gao, F.; Cui, J.; Zhao, G. Weak Galerkin finite element methods for Sobolev equation. J. Comput. Appl. Math. 2017, 317, 188–202. [Google Scholar] [CrossRef]
- Abu Arqub, O.; Alsulami, H.; Alhodaly, M. Numerical Hilbert space solution of fractional Sobolev equation in 1+1-dimensional space. Math. Sci. 2022, 18, 217–228. [Google Scholar] [CrossRef]
- Hussain, M.; Haq, S.; Ghafoor, A. Meshless RBFs method for numerical solutions of two-dimensional high order fractional Sobolev equations. Comput. Math. Appl. 2020, 79, 802–816. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahsan, M.; Elamin, A.E.A.; Abdel-Khalek, S.; Inc, M. Numerical simulation of 3-D Sobolev equation via local meshless method. Therm. Sci. 2022, 26, 457–462. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Guo, H.; Fu, H. A mass-conservative characteristic splitting mixed finite element method for convection-dominated Sobolev equation. Math. Comput. Simul. 2019, 160, 180–191. [Google Scholar] [CrossRef]
- Wang, K.L.; Yao, S.W.; Liu, Y.P.; Zhang, L.N. A fractal variational principle for the telegraph equation with fractal derivatives. Fractals 2020, 28, 2050058. [Google Scholar] [CrossRef]
- Wang, K.L.; Wang, K.J.; He, C.H. Physical insight of local fractional calculus and its application to fractional Kdv–Burgers–Kuramoto equation. Fractals 2019, 27, 1950122. [Google Scholar] [CrossRef]
- Dong, G.; Guo, Z.; Yao, W. Numerical methods for time-fractional convection-diffusion problems with high-order accuracy. Open Math. 2021, 19, 782–802. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- Salama, F.M.; Ali, N.H.M.; Abd Hamid, N.N. Fast O(N) hybrid Laplace transform-finite difference method in solving 2D time fractional diffusion equation. J. Math. Comput. Sci. 2021, 23, 110–123. [Google Scholar] [CrossRef]
- Wang, K.L. A novel variational approach to fractal Swift–Hohenberg model arising in fluid dynamics. Fractals 2022, 30, 2250156. [Google Scholar] [CrossRef]
- Wang, K. New variational theory for coupled nonlinear fractal Schrödinger system. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 589–597. [Google Scholar] [CrossRef]
- Deng, W. Finite element method for the space and time fractional Fokker–Planck equation. SIAM J. Numer. Anal. 2009, 47, 204–226. [Google Scholar] [CrossRef]
- Li, L.; Jiang, Z.; Yin, Z. Compact finite-difference method for 2D time-fractional convection–diffusion equation of groundwater pollution problems. Comput. Appl. Math. 2020, 39, 142. [Google Scholar] [CrossRef]
- Tansri, K.; Kittisopaporn, A.; Chansangiam, P. Numerical solutions of the space-time fractional diffusion equation via a gradient-descent iterative procedure. J. Math. Comput. Sci. 2023, 31, 353–366. [Google Scholar] [CrossRef]
- Dehghan, M.; Abbaszadeh, M.; Mohebbi, A. Legendre spectral element method for solving time fractional modified anomalous sub-diffusion equation. Appl. Math. Model. 2016, 40, 3635–3654. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Guo, T.; Nikan, O.; Avazzadeh, Z.; Qiu, W. Efficient alternating direction implicit numerical approaches for multi-dimensional distributed-order fractional integro differential problems. Comput. Appl. Math. 2022, 41, 236. [Google Scholar] [CrossRef]
- Qiao, H.; Cheng, A. A fast finite difference/RBF meshless approach for time fractional convection-diffusion equation with non-smooth solution. Eng. Anal. Bound. Elem. 2021, 125, 280–289. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Youssri, Y.H.; El-Sissi, N.; Sadek, M. New hypergeometric connection formulae between Fibonacci and Chebyshev polynomials. Ramanujan J. 2017, 42, 347–361. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.; Youssri, Y. Connection formulae between generalized Lucas polynomials and some Jacobi polynomials: Application to certain types of fourth-order BVPs. Int. J. Appl. Comput. Math. 2020, 6, 45. [Google Scholar] [CrossRef]
- Nadir, M. Lucas polynomials for solving linear integral equations. J. Theor. Appl. Comput. Sci. 2017, 11, 13–19. [Google Scholar]
- Çetin, M.; Sezer, M.; Güler, C. Lucas polynomial approach for system of high-order linear differential equations and residual error estimation. Math. Probl. Eng. 2015, 2015, 625984. [Google Scholar] [CrossRef]
- Mirzaee, F.; Hoseini, S.F. Application of Fibonacci collocation method for solving Volterra–Fredholm integral equations. Appl. Math. Comput. 2016, 273, 637–644. [Google Scholar] [CrossRef]
- Baykuş-Savaşaneril, N.; Sezer, M. Hybrid Taylor-Lucas collocation method for numerical solution of high-order Pantograph type delay differential equations with variables delays. Appl. Math. Inf. Sci. 2017, 11, 1795–1801. [Google Scholar]
- Oruç, Ö. A new algorithm based on Lucas polynomials for approximate solution of 1D and 2D nonlinear generalized Benjamin–Bona–Mahony–Burgers equation. Comput. Math. Appl. 2017, 74, 3042–3057. [Google Scholar] [CrossRef]
- Oruç, Ö. A new numerical treatment based on Lucas polynomials for 1D and 2D sinh-Gordon equation. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 14–25. [Google Scholar] [CrossRef]
- Ali, I.; Haq, S.; Nisar, K.S.; Baleanu, D. An efficient numerical scheme based on Lucas polynomials for the study of multidimensional Burgers-type equations. Adv. Differ. Equ. 2021, 2021, 43. [Google Scholar] [CrossRef]
- Ahmad, I.; Bakar, A.A.; Ali, I.; Haq, S.; Yussof, S.; Ali, A.H. Computational analysis of time-fractional models in energy infrastructure applications. Alex. Eng. J. 2023, 82, 426–436. [Google Scholar] [CrossRef]
- Jumarie, G. Stock exchange fractional dynamics defined as fractional exponential growth driven by (usual) Gaussian white noise. Application to fractional Black-Scholes equations. Insur. Math. Econ. 2008, 42, 271–287. [Google Scholar] [CrossRef]
- Jumarie, G. Derivation and solutions of some fractional Black-Scholes equations in coarse-grained space and time. Application to Merton’s optimal portfolio. Comput. Math. Appl. 2010, 59, 1142–1164. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and nonsingular kernel theory and application to heat transfer model. Therm. Sci. 2016, 20, 763. [Google Scholar] [CrossRef]
- He, J.H. A new fractal derivation. Therm. Sci. 2011, 15, 145–147. [Google Scholar] [CrossRef]
- Ali, I.; Haq, S.; Aldosary, S.F.; Nisar, K.S.; Ahmad, F. Numerical solution of one-and two-dimensional time-fractional Burgers’ equation via Lucas polynomials coupled with Finite difference method. Alex. Eng. J. 2022, 61, 6077–6087. [Google Scholar] [CrossRef]
- Hussain, M.; Haq, S.; Ghafoor, A.; Ali, I. Numerical solutions of time-fractional coupled viscous Burgers’ equations using meshfree spectral method. Comput. Appl. Math. 2020, 39, 6. [Google Scholar] [CrossRef]
- Marchuk, G.I. Some applicatons of splitting-up methods to the solution of problems in mathematical physics. Aplikace Matematiky 1968, 1, 103–132. [Google Scholar]
- Strang, G. On the construction and comparision of difference schemes. SIAM J. Numer. Anal. 1968, 5, 506–517. [Google Scholar] [CrossRef]
- Geiser, J.; Tanoglu, G.; Gucuyenenb, N. Higher order operator splitting methods via Zassenhaus product formula: Theory and applications. Comput. Math. Appl. 2011, 62, 1994–2015. [Google Scholar] [CrossRef][Green Version]
- Abd-Elhameed, W.; Youssri, Y. Spectral solutions for fractional differential equations via a novel Lucas operational matrix of fractional derivatives. Rom. J. Phys 2016, 61, 795–813. [Google Scholar]
- Ali, I.; Haq, S.; Nisar, K.S.; Arifeen, S.U. Numerical study of 1D and 2D advection-diffusion-reaction equations using Lucas and Fibonacci polynomials. Arab. J. Math. 2021, 10, 513–526. [Google Scholar] [CrossRef]
- Garmanjani, G.; Cavoretto, R.; Esmaeilbeigi, M. A RBF partition of unity collocation method based on finite difference for initial–boundary value problems. Comput. Math. Appl. 2018, 75, 4066–4090. [Google Scholar] [CrossRef]
- Lax, P.D. Weak solutions of nonlinear hyperbolic equations and their numerical computation. Commun. Pure Appl. Math. 1954, 7, 159–193. [Google Scholar] [CrossRef]


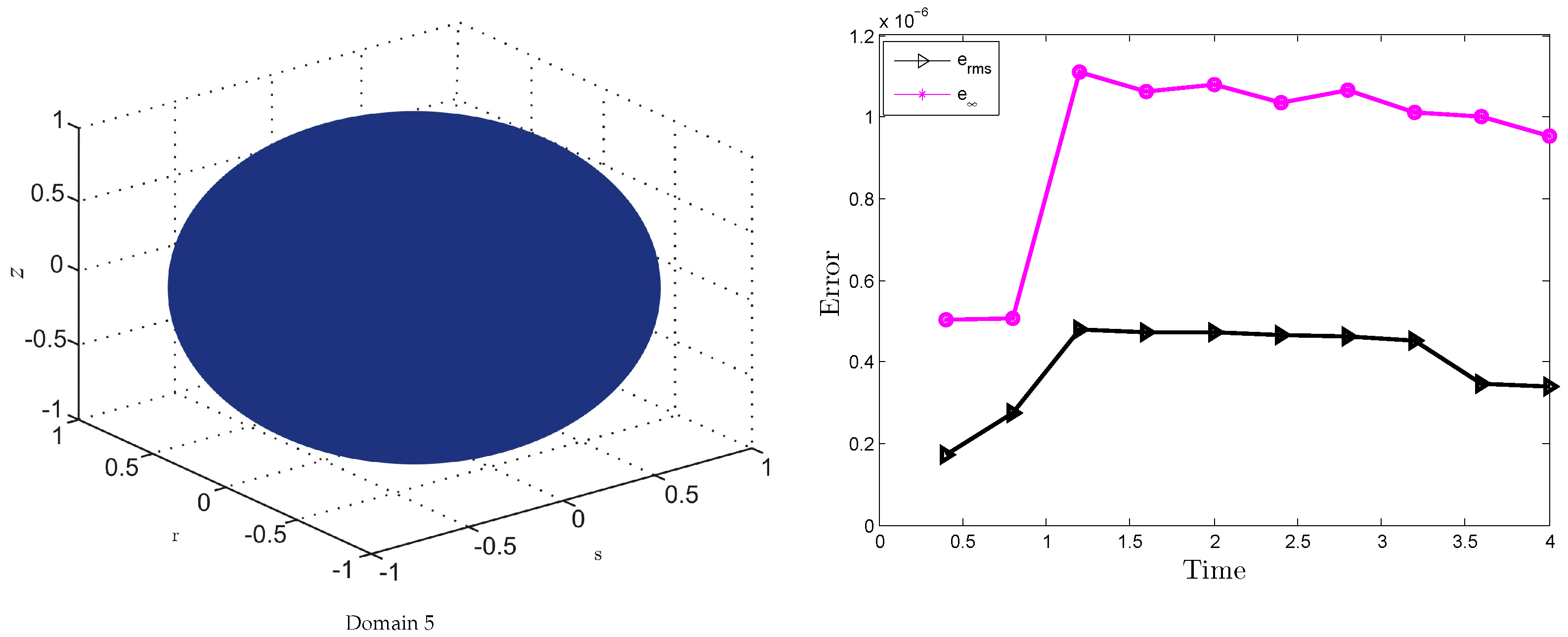

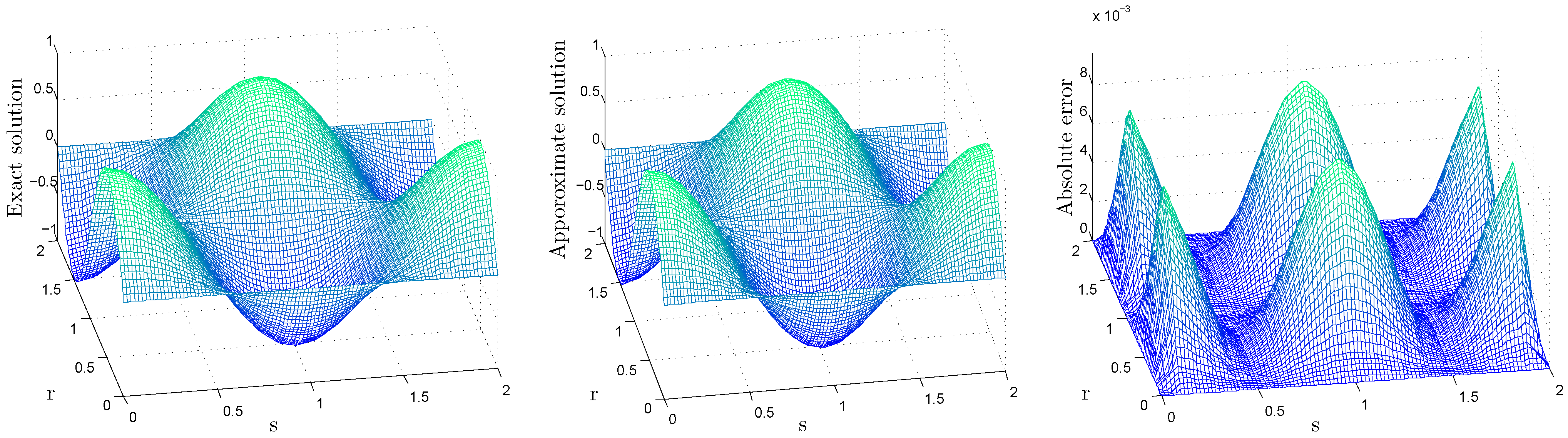
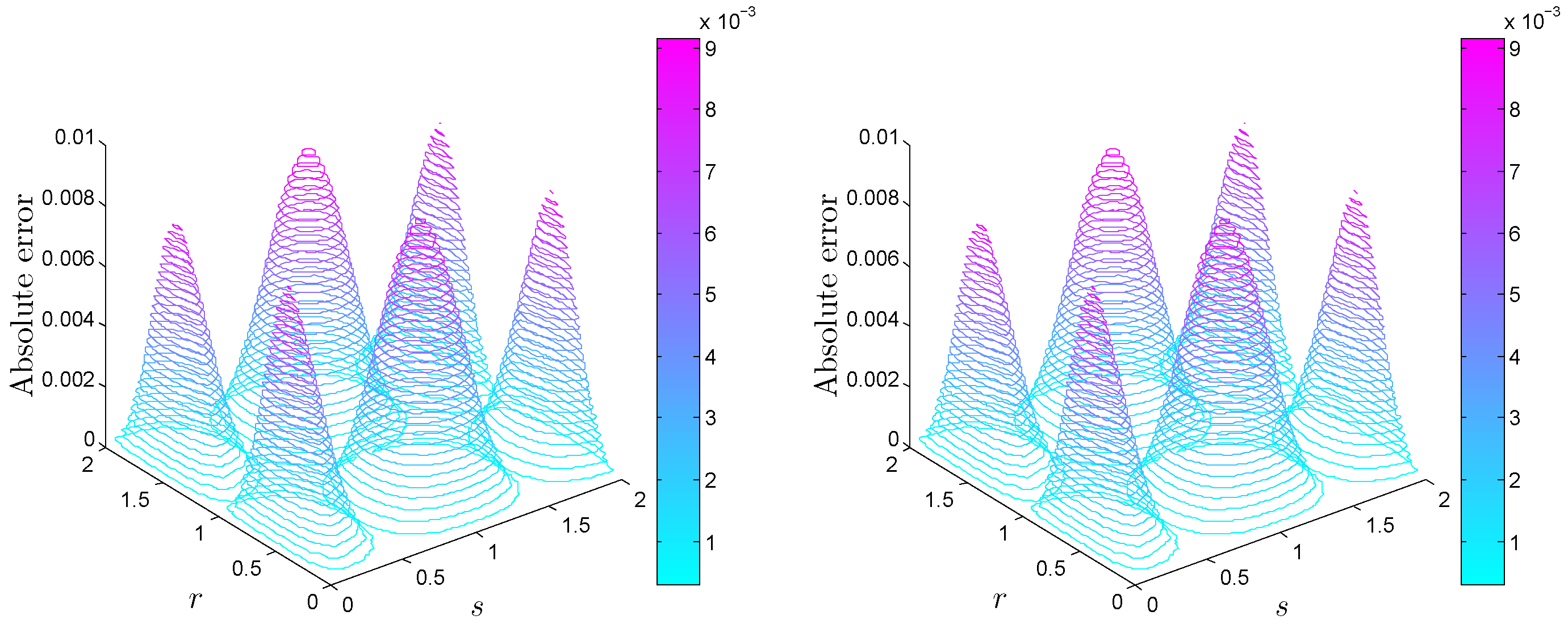
| Method | |||||
| [17] | HMM | [17] | HMM | ||
| Explicit | 0.1 | 1.8985 | 8.5002 | 1.5971 | 8.3765 |
| 0.05 | 9.2780 | 5.3215 | 8.2371 | 5.1759 | |
| 0.025 | 4.5880 | 1.0717 | 4.1804 | 1.0352 | |
| 0.0125 | 2.2815 | 9.0701 | 2.1057 | 9.0047 | |
| 0.00625 | 1.1377 | 8.0520 | 1.0567 | 8.6471 | |
| Implicit | 0.1 | 1.7500 | 8.3842 | 1.7904 | 8.5478 |
| 0.05 | 8.9133 | 5.2547 | 8.7217 | 5.5662 | |
| 0.025 | 4.4982 | 1.1406 | 4.3024 | 1.0639 | |
| 0.0125 | 2.2594 | 9.9320 | 2.1364 | 9.9331 | |
| 0.00625 | 1.1323 | 8.1481 | 1.0645 | 8.1101 | |
| Crank–Nicolson | 0.1 | 3.0659 | 9.0152 | 3.0957 | 8.3810 |
| 0.05 | 8.4249 | 1.2486 | 8.4718 | 1.1754 | |
| 0.025 | 2.4213 | 6.2692 | 2.3901 | 3.1455 | |
| 0.0125 | 7.1414 | 8.6427 | 6.8938 | 8.0157 | |
| 0.00625 | 2.1392 | 1.1503 | 2.0203 | 5.8023 | |
| CPU Time | |||||||
|---|---|---|---|---|---|---|---|
| 10 | 3.1204 | 2.7813 | 4.2101 | 3.7823 | 5.9105 | 3.7930 | 15.64 |
| 20 | 2.6534 | 2.6591 | 3.6587 | 3.6901 | 3.8257 | 3.7133 | 18.89 |
| 25 | 2.0673 | 2.2873 | 3.2510 | 3.1246 | 3.2780 | 3.3854 | 19.05 |
| Time | Error Norm | Domain 1 | Domain 2 | Domain 2 | Domain 2 | Domain 2 |
|---|---|---|---|---|---|---|
| HMM | HMM | IQ [17] | MQ [17] | IMQ [17] | ||
| t = 1 | 7.0321 | 8.1482 | 2.8503 | 1.0762 | 1.6486 | |
| 6.2456 | 8.2453 | 5.3969 | 1.2498 | 1.6465 | ||
| 6.2710 | 9.3608 | 5.8179 | 1.3473 | 1.7749 | ||
| t = 2 | 3.1438 | 4.1930 | 6.9177 | 7.4827 | 1.2021 | |
| 4.4711 | 5.591 | 1.1019 | 8.9038 | 1.2001 | ||
| 5.5379 | 5.6283 | 1.1879 | 9.5983 | 1.2937 | ||
| t = 3 | 9.3510 | 1.8646 | 1.9053 | 3.9556 | 6.5942 | |
| 1.0392 | 2.8366 | 2.6854 | 4.8116 | 6.5818 | ||
| 2.0406 | 2.9815 | 2.8949 | 5.1869 | 7.0953 |
| t = 1 | t = 1 | t = 2 | t = 2 | ||
| Method | HMM | [17] | HMM | [17] | |
| Explicit | 0.1 | 2.0148 | 5.1872 | 1.3867 | 3.7523 |
| 0.05 | 9.5461 | 2.5444 | 8.4984 | 1.8637 | |
| 0.025 | 8.3610 | 1.2612 | 5.5718 | 9.2941 | |
| 0.125 | 3.4513 | 6.2822 | 1.9845 | 4.6433 | |
| 0.00625 | 9.3719 | 3.1364 | 8.3805 | 2.3216 | |
| Implicit | 0.1 | 1.3584 | 4.8894 | 9.7926 | 3.7120 |
| 0.05 | 9.4241 | 2.4862 | 7.3200 | 1.8657 | |
| 0.025 | 7.3721 | 1.2528 | 5.7313 | 9.3447 | |
| 0.0125 | 2.6219 | 6.2845 | 9.9378 | 4.6732 | |
| 0.00125 | 8.9866 | 3.1458 | 7.5566 | 2.3357 | |
| Crank–Nicolson | 0.1 | 4.3021 | 3.5095 | 1.5380 | 2.5348 |
| 0.05 | 7.6320 | 9.2813 | 7.3817 | 7.1868 | |
| 0.025 | 9.8431 | 4.9749 | 8.0116 | 3.8280 | |
| 0.0125 | 4.9669 | 2.4637 | 2.0167 | 1.8688 | |
| 0.00625 | 7.3499 | 1.0941 | 7.9173 | 8.2362 | |
| [15] | [15] | CPU Time of HMM | |||
|---|---|---|---|---|---|
| 0.1 | 7.7488 | 3.7354 | 2.9285 | 9.2558 | 1.39 |
| 0.05 | 2.6377 | 8.5621 | 7.3125 | 2.3112 | 1.54 |
| 0.01 | 6.7313 | 3.5478 | 2.9195 | 9.2271 | 2.60 |
| 0.005 | 2.4307 | 8.5271 | 7.2896 | 2.3039 | 3.96 |
| 0.001 | 8.1268 | 3.2773 | 2.9007 | 9.1677 | 17.73 |
| 0.0005 | 2.4501 | 9.9388 | 7.2236 | 2.2830 | 42.14 |
| [15] | [15] | [15] | [15] | |||||
|---|---|---|---|---|---|---|---|---|
| 0.2 | 8.69430 | 5.3992 | 7.3170 | 2.3126 | 7.9456 | 3.9267 | 5.3832 | 1.7014 |
| 0.4 | 9.65010 | 6.5001 | 7.3053 | 2.3089 | 8.1655 | 4.9126 | 5.3746 | 1.6987 |
| 0.6 | 9.27650 | 8.4952 | 7.2584 | 2.2940 | 7.8037 | 5.7601 | 5.3402 | 1.6878 |
| 0.8 | 8.72000 | 7.3528 | 7.0765 | 2.2364 | 7.6584 | 3.9773 | 5.2065 | 1.6455 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, I.; Alshammari, A.O.; Jan, R.; Razak, N.N.A.; Idris, S.A. An Efficient Numerical Solution of a Multi-Dimensional Two-Term Fractional Order PDE via a Hybrid Methodology: The Caputo–Lucas–Fibonacci Approach with Strang Splitting. Fractal Fract. 2024, 8, 364. https://doi.org/10.3390/fractalfract8060364
Ahmad I, Alshammari AO, Jan R, Razak NNA, Idris SA. An Efficient Numerical Solution of a Multi-Dimensional Two-Term Fractional Order PDE via a Hybrid Methodology: The Caputo–Lucas–Fibonacci Approach with Strang Splitting. Fractal and Fractional. 2024; 8(6):364. https://doi.org/10.3390/fractalfract8060364
Chicago/Turabian StyleAhmad, Imtiaz, Abdulrahman Obaid Alshammari, Rashid Jan, Normy Norfiza Abdul Razak, and Sahar Ahmed Idris. 2024. "An Efficient Numerical Solution of a Multi-Dimensional Two-Term Fractional Order PDE via a Hybrid Methodology: The Caputo–Lucas–Fibonacci Approach with Strang Splitting" Fractal and Fractional 8, no. 6: 364. https://doi.org/10.3390/fractalfract8060364
APA StyleAhmad, I., Alshammari, A. O., Jan, R., Razak, N. N. A., & Idris, S. A. (2024). An Efficient Numerical Solution of a Multi-Dimensional Two-Term Fractional Order PDE via a Hybrid Methodology: The Caputo–Lucas–Fibonacci Approach with Strang Splitting. Fractal and Fractional, 8(6), 364. https://doi.org/10.3390/fractalfract8060364









