Prospective Analysis of Time-Fractional Emden–Fowler Model Using Elzaki Transform Homotopy Perturbation Method
Abstract
1. Introduction
2. Definitions and Fundamental Principles
3. Formulation of ET-HPM
4. Convergence Analysis
5. The Uniqueness Theorem
6. Numerical Applications
6.1. Problem 1
6.2. Problem 2
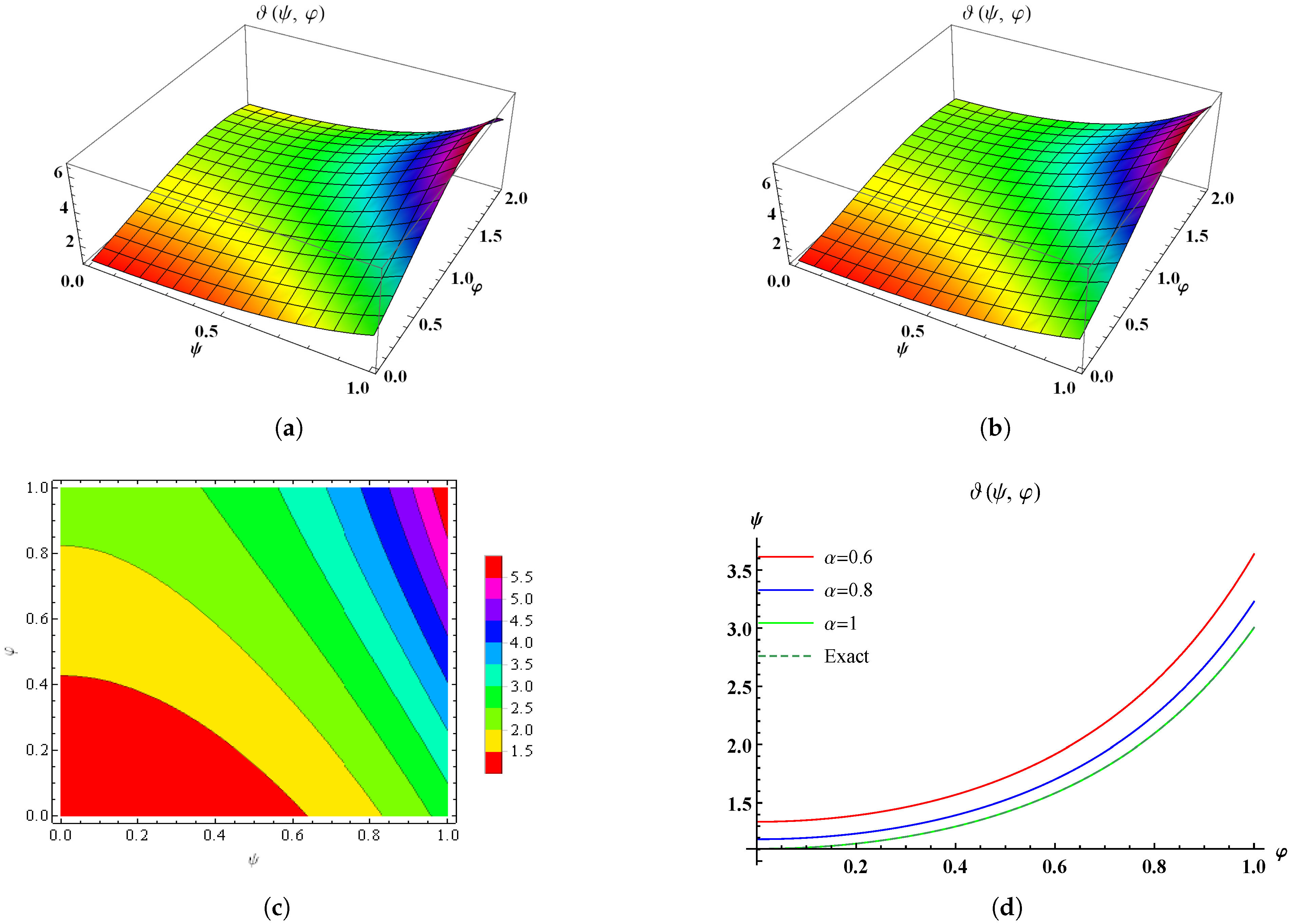
7. Numerical Findings and Analysis
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- AlBaidani, M.M.; Ganie, A.H.; Khan, A. Computational analysis of fractional-order KdV systems in the sense of the Caputo operator via a novel transform. Fractal Fract. 2023, 7, 812. [Google Scholar] [CrossRef]
- AlBaidani, M.M.; Aljuaydi, F.; Alharthi, N.; Khan, A.; Ganie, A.H. Study of fractional forced KdV equation with Caputo–Fabrizio and Atangana–Baleanu–Caputo differential operators. AIP Adv. 2024, 14, 015340. [Google Scholar] [CrossRef]
- Beghami, W.; Maayah, B.; Bushnaq, S.; Abu Arqub, O. The Laplace optimized decomposition method for solving systems of partial differential equations of fractional order. Int. J. Appl. Comput. Math. 2022, 8, 52. [Google Scholar] [CrossRef]
- Akram, M.; Ihsan, T.; Allahviranloo, T. Solving Pythagorean fuzzy fractional differential equations using Laplace transform. Granul. Comput. 2023, 8, 551–575. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; A Wiley: New York, NY, USA, 1993. [Google Scholar]
- Wu, G.C.; Shi, Y.G.; Wu, K.T. Adomian decomposition method and non-analytical solutions of fractional differential equations. Rom. J. Phys. 2011, 56, 873–880. [Google Scholar]
- Odibat, Z.; Momani, S.; Xu, H. A reliable algorithm of homotopy analysis method for solving nonlinear fractional differential equations. Appl. Math. Model. 2010, 34, 593–600. [Google Scholar] [CrossRef]
- Modanli, M.; Abdulazeez, S.T.; Husien, A.M. A residual power series method for solving pseudo hyperbolic partial differential equations with nonlocal conditions. Numer. Methods Partial. Differ. Equ. 2021, 37, 2235–2243. [Google Scholar] [CrossRef]
- Alomari, A. Homotopy-Sumudu transforms for solving system of fractional partial differential equations. Adv. Differ. Equ. 2020, 2020, 222. [Google Scholar] [CrossRef]
- Lane, H.J. On the theoretical temperature of the sun, under the hypothesis of a gaseous mass maintaining its volume by its internal heat, and depending on the laws of gases as known to terrestrial experiment. Am. J. Sci. 1870, 2, 57–74. [Google Scholar] [CrossRef]
- Mall, S.; Chakraverty, S. A novel Chebyshev neural network approach for solving singular arbitrary order Lane-Emden equation arising in astrophysics. Netw. Comput. Neural Syst. 2020, 31, 142–165. [Google Scholar] [CrossRef]
- Chowdhury, M.; Hashim, I. Solutions of Emden–Fowler equations by homotopy-perturbation method. Nonlinear Anal. Real World Appl. 2009, 10, 104–115. [Google Scholar] [CrossRef]
- Mall, S.; Chakraverty, S. Numerical solution of nonlinear singular initial value problems of Emden–Fowler type using Chebyshev Neural Network method. Neurocomputing 2015, 149, 975–982. [Google Scholar] [CrossRef]
- Syam, M.I. Analytical solution of the fractional initial Emden–Fowler equation using the fractional residual power series method. Int. J. Appl. Comput. Math. 2018, 4, 1–8. [Google Scholar] [CrossRef]
- Swati; Singh, K.; Verma, A.K.; Singh, M. Higher order Emden–Fowler type equations via uniform Haar Wavelet resolution technique. J. Comput. Appl. Math. 2020, 376, 112836. [Google Scholar] [CrossRef]
- Gul, H.; Ali, S.; Shah, K.; Muhammad, S.; Sitthiwirattham, T.; Chasreechai, S. Application of asymptotic homotopy perturbation method to fractional order partial differential equation. Symmetry 2021, 13, 2215. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O. Homotopy perturbation method with three expansions for Helmholtz-Fangzhu oscillator. Int. J. Mod. Phys. B 2021, 35, 2150244. [Google Scholar] [CrossRef]
- Kharrat, B.N.; Toma, G.A. Development of homotopy perturbation method for solving nonlinear algebraic equations. Int. J. Sci. Res. Math. Stat. Sci. 2020, 7, 47–50. [Google Scholar]
- Akter, M.T.; Chowdhury, M.M. Homotopy perturbation method for solving highly nonlinear reaction-diffusion-convection problem. Am. J. Math. Stat. 2019, 9, 136–141. [Google Scholar]
- Iqbal, S.; Javed, A. Application of optimal homotopy asymptotic method for the analytic solution of singular Lane–Emden type equation. Appl. Math. Comput. 2011, 217, 7753–7761. [Google Scholar] [CrossRef]
- He, J.H. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fractals 2005, 26, 695–700. [Google Scholar] [CrossRef]
- Yıldırım, A.; Momani, S. Series solutions of a fractional oscillator by means of the homotopy perturbation method. Int. J. Comput. Math. 2010, 87, 1072–1082. [Google Scholar] [CrossRef]
- Ghoreishi, M.; Md, A.I.B.; Ismail. The homotopy perturbation method (HPM) for nonlinear parabolic equation with nonlocal boundary conditions. Appl. Math. Sci. 2011, 5, 113–123. [Google Scholar]
- Javeed, S.; Baleanu, D.; Waheed, A.; Shaukat Khan, M.; Affan, H. Analysis of homotopy perturbation method for solving fractional order differential equations. Mathematics 2019, 7, 40. [Google Scholar] [CrossRef]
- Khader, M. Introducing an efficient modification of the homotopy perturbation method by using Chebyshev polynomials. Arab J. Math. Sci. 2012, 18, 61–71. [Google Scholar] [CrossRef]
- Elzaki, T.M. The new integral transform Elzaki transform. Glob. J. Pure Appl. Math. 2011, 7, 57–64. [Google Scholar]
- Aggarwal, S.; Bhatnagar, K.; Dua, A. Dualities between Elzaki transform and some useful integral transforms. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 4312–4318. [Google Scholar] [CrossRef]
- Jassim, H.K.; Shareef, M. On approximate solutions for fractional system of differential equations with Caputo-Fabrizio fractional operator. J. Math. Comput. Sci. 2021, 23, 58–66. [Google Scholar] [CrossRef]
- Mohamed, M.Z.; Yousif, M.; Hamza, A.E. Solving nonlinear fractional partial differential equations using the Elzaki transform method and the homotopy perturbation method. Abstr. Appl. Anal. 2022, 2022, 4743234. [Google Scholar] [CrossRef]
- Sedeeg, A.K.H. A coupling Elzaki transform and homotopy perturbation method for solving nonlinear fractional heat-like equations. Am. J. Math. Comput. Model. 2016, 1, 15–20. [Google Scholar]
- Liu, F.; Yang, L.; Nadeem, M. A new fractal transform for the approximate solution of Drinfeld–Sokolov–Wilson model with fractal derivatives. Fractals 2023, 31, 2350007. [Google Scholar] [CrossRef]

| ET-HPM | ET-HPM | ET-HPM | ET-HPM | Exact Results | Error Analysis | |
|---|---|---|---|---|---|---|
| (0.25, 0.01) | 1.28334 | 1.14351 | 1.09367 | 1.07519 | 1.07519 | 00000 |
| (0.50, 0.01) | 1.54801 | 1.37933 | 1.31922 | 1.29693 | 1.29693 | 00000 |
| (0.75, 0.01) | 2.11588 | 1.88533 | 1.80316 | 1.77269 | 1.77269 | 00000 |
| (1.00, 0.01) | 3.27713 | 2.92005 | 2.79279 | 2.74560 | 2.7456 | 00000 |
| (0.25, 0.03) | 1.4286 | 1.22415 | 1.13634 | 1.09690 | 1.09690 | 00000 |
| (0.50, 0.03) | 1.72322 | 1.4766 | 1.37069 | 1.32312 | 1.32312 | 00000 |
| (0.75, 0.03) | 2.35536 | 2.01828 | 1.87351 | 1.80849 | 1.8085 | 0.00001 |
| (1.00, 0.03) | 3.64806 | 3.12597 | 2.90175 | 2.80104 | 2.80105 | 0.00001 |
| (0.25, 0.05) | 1.5301 | 1.28832 | 1.17646 | 1.11903 | 1.11905 | 0.00002 |
| (0.50, 0.05) | 1.84565 | 1.55401 | 1.41689 | 1.34980 | 1.34983 | 0.00003 |
| (0.75, 0.05) | 2.52271 | 2.12407 | 1.93666 | 1.84496 | 1.84500 | 0.00004 |
| (1.00, 0.05) | 3.90725 | 3.28983 | 2.99956 | 2.85753 | 2.85759 | 0.00004 |
| ET-HPM | ET-HPM | ET-HPM | ET-HPM | Exact Results | Error Analysis | |
|---|---|---|---|---|---|---|
| (0.1, 0.01) | 1.00940 | 1.00118 | 1.00005 | 0.99991 | 0.99990 | 0.00001 |
| (0.2, 0.01) | 1.03743 | 1.00415 | 0.99979 | 0.99938 | 0.99960 | 0.00022 |
| (0.3, 0.01) | 1.07548 | 1.00293 | 0.99525 | 0.99594 | 0.99910 | 0.00316 |
| (0.4, 0.01) | 1.08962 | 0.97375 | 0.97084 | 0.97988 | 0.98840 | 0.00852 |
| (0.1, 0.03) | 1.01852 | 1.00388 | 1.00052 | 0.99984 | 0.99970 | 0.00014 |
| (0.2, 0.03) | 1.08700 | 1.01700 | 1.00200 | 0.99917 | 0.99880 | 0.00037 |
| (0.3, 0.03) | 1.19268 | 1.03293 | 1.00050 | 0.99557 | 0.99730 | 0.00173 |
| (0.4, 0.03) | 1.30197 | 1.02824 | 0.98064 | 0.97945 | 0.99520 | 0.01575 |
| (0.1, 0.05) | 1.01562 | 1.00498 | 1.00097 | 0.99984 | 0.99950 | 0.00034 |
| (0.2, 0.05) | 1.11876 | 1.02982 | 1.00535 | 0.99945 | 0.99800 | 0.00145 |
| (0.3, 0.05) | 1.28216 | 1.06541 | 1.00882 | 0.99639 | 0.99550 | 0.00089 |
| (0.4, 0.05) | 1.47214 | 1.08852 | 0.99616 | 0.98119 | 0.99200 | 0.01081 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nadeem, M.; Iambor, L.F. Prospective Analysis of Time-Fractional Emden–Fowler Model Using Elzaki Transform Homotopy Perturbation Method. Fractal Fract. 2024, 8, 363. https://doi.org/10.3390/fractalfract8060363
Nadeem M, Iambor LF. Prospective Analysis of Time-Fractional Emden–Fowler Model Using Elzaki Transform Homotopy Perturbation Method. Fractal and Fractional. 2024; 8(6):363. https://doi.org/10.3390/fractalfract8060363
Chicago/Turabian StyleNadeem, Muhammad, and Loredana Florentina Iambor. 2024. "Prospective Analysis of Time-Fractional Emden–Fowler Model Using Elzaki Transform Homotopy Perturbation Method" Fractal and Fractional 8, no. 6: 363. https://doi.org/10.3390/fractalfract8060363
APA StyleNadeem, M., & Iambor, L. F. (2024). Prospective Analysis of Time-Fractional Emden–Fowler Model Using Elzaki Transform Homotopy Perturbation Method. Fractal and Fractional, 8(6), 363. https://doi.org/10.3390/fractalfract8060363







