Dynamic Behavior and Optical Soliton for the M-Truncated Fractional Paraxial Wave Equation Arising in a Liquid Crystal Model

Abstract

The main purpose of this article is to investigate the dynamic behavior and optical soliton for the M-truncated fractional paraxial wave equation arising in a liquid crystal model, which is usually used to design camera lenses for high-quality photography. The traveling wave transformation is applied to the M-truncated fractional paraxial wave equation. Moreover, a two-dimensional dynamical system and its disturbance system are obtained. The phase portraits of the two-dimensional dynamic system and Poincaré sections and a bifurcation portrait of its perturbation system are drawn. The obtained three-dimensional graphs of soliton solutions, two-dimensional graphs of soliton solutions, and contour graphs of the M-truncated fractional paraxial wave equation arising in a liquid crystal model are drawn.

1. Introduction

Fractional partial differential equations (FPDEs) are partial differential equations [1,2] that involve fractional derivatives and are commonly used to describe complex systems with memory effects. FPDEs have wide applications in fluid mechanics, biology, signal processing, and financial mathematics [3]. In general, due to the widespread application of fractional derivatives in multiple fields [4,5,6,7,8], many researchers have proposed many different fractional derivatives from different perspectives. For example, the Riemann–Liouville fractional derivative, the conformable fractional derivative, the Caputo fractional derivative, and the Grünwald–Letnikov fractional derivative. Therefore, with the continuous development of fractional derivative theory, researchers have also delved deeper into the theory of fractional derivatives. Additionally, many different types of FPDEs have been proposed. Due to the complexity and diversity of fractional derivatives, on the one hand, many experts use the finite element method, the spectral method, and the finite difference method to solve the numerical solutions of these equations. On the other hand, many researchers use mathematical analysis methods to construct exact solutions [9,10] to these equations. The main purpose of this article is to study the dynamic behavior and soliton solutions of a very important class of FPDEs.

In this study, the M-truncated fractional paraxial wave equation arising in a liquid crystal model is presented as follows [11]:

$$i\frac{\partial \psi }{\partial y}+{\frac{a_1}{2}}_{\kappa }{\mathbb{D}}_{M,t}^{2\alpha ,d}\psi +\frac{a_2}{2}\frac{{\partial }^2\psi }{\partial x^2}+a_3{\left|\psi \right|}^2\psi =0,$$

(1)

where $a_1$, $a_2$, $a_3$ are real constants, which represent the coefficients of the dispersal effect, the Kerr nonlinearity effect, and the diffraction effect, respectively. ${ }_{\kappa }{\mathbb{D}}_{M,t}^{2\alpha ,d}$ stands for the M-fractional derivative, which was proposed by Oliveira and Sousa [12]. $\psi =\psi (x,y,t)$, where the variables $x,y,t$ represent the transverse, longitudinal, and temporal propagation, respectively. In [13,14], Hamood, et al. used the ${\varphi }^6$ model expansion technique and the Sardar subequation method to study the optical solitons of the paraxial wave model, respectively. In [11], Mannaf et al. studied the optical soliton solutions of Equation (1) by using the extended tanh method and the modified extended tanh method, respectively. However, despite our best efforts, there is still an insufficient body of literature on the dynamic behavior and soliton solutions of Equation (1). Solitons are a special wave phenomenon that occurs in nonlinear physics. Solitons were first proposed in the study of shallow water waves, but were later widely applied in fields such as optics, acoustics, and quantum physics. The optical soliton solution is usually used to describe the mathematical solution of the propagation of optical solitons under specific conditions, for example, the solution to the Schrödinger equation. This article will conduct research from two aspects. On the one hand, by using the method of planar dynamical systems, the dynamic behavior of two-dimensional dynamical systems and their disturbance systems are studied. On the other hand, the optical soliton solution of Equation (1) is constructed using the planar dynamical system method.

The remaining part of this article is arranged as follows: In Section 2, the phase portrait of the two-dimensional dynamical system and its perturbed system are discussed. In Section 3, the optical soliton solutions of Equation (1) are constructed. Finally, a brief conclusion is given.

2. Bifurcation and Chaotic Behaviors

2.1. Preliminary

Definition 1

(M-truncated fractional derivative [15]). For $\alpha \in (0,1]$, the M-truncated fractional derivative of $f:[0,+\infty )\to (-\infty ,+\infty )$ is defined as

$${ }_{\kappa }{\mathbb{D}}_{M,t}^{2\alpha ,d}(f)=\underset{h\to 0}{lim}\frac{f(t_{\kappa }{E}_d(h{t}^{\alpha }))-f(t)}{h},0<\alpha <1,d>0.$$

In Definition 1, $E_d(z)$ represents the truncated Mittag-Leffler function of one parameter, which is defined as

$${ }_{\kappa }{E}_d(z)=\sum _{j=0}^{\kappa }\frac{z^j}{\Gamma (dj+1)},z\in [0,+\infty ).$$

M-truncated fractional derivative has very important properties, and relevant conclusions can be referenced in reference [15].

2.2. Mathematical Derivation

Firstly, let us introduce the the wave transformation

$$\begin{array}{c}\hfill \psi (x,y,t)=\Psi (\xi )e^{i\eta },\xi =m_{1}x+m_{2}y+\frac{\Gamma (d+1)}{\alpha }\omega t^{\alpha },\eta =r_{1}x+r_{2}y+\frac{\Gamma (d+1)}{\alpha }\tau t^{\alpha }+\delta .\end{array}$$

(2)

Inserting Equation (2) into Equation (1), we obtain the real and imaginary components of the resultant expression

$$\left\{\begin{array}{c}(a_1{\omega }^2+a_2{m}_1^2){\Psi }^{{ }^{″}}(\xi )-2a_3{\Psi }^3(\xi )-(a_1{\tau }^2+a_2{r}_1^2+2r_2)\Psi (\xi )=0,\hfill \\ (2a_1\tau \omega +2a_2{m}_1{r}_1+2m_2){\Psi }^{{ }^{\prime }}(\xi )=0,\hfill \end{array}\right.$$

(3)

where ${\Psi }^{{ }^{\prime }}(\xi )\ne 0$.

From the second equation of Equation (3), we have

$$m_2=-(a_1\tau \omega +a_2{m}_1{r}_1).$$

(4)

In order to further analyze the dynamic behavior and soliton solutions of Equation (1), under the conditions satisfied by Equation (3), we can transform the first equation of Equation (3) into the following ordinary differential equation:

$${\Psi }^{{ }^{″}}-{\Im }_1{\Psi }^3-{\Im }_2\Psi =0,$$

(5)

Here, ${\Im }_1=\frac{2a_3}{a_1{\omega }^2+a_2{m}_1^2}$ and ${\Im }_2=\frac{a_1{\tau }^2+a_2{r}_1^2+2r_2}{a_1{\omega }^2+a_2{m}_1^2}$, where $a_1{\omega }^2+a_2{m}_1^2\ne 0$.

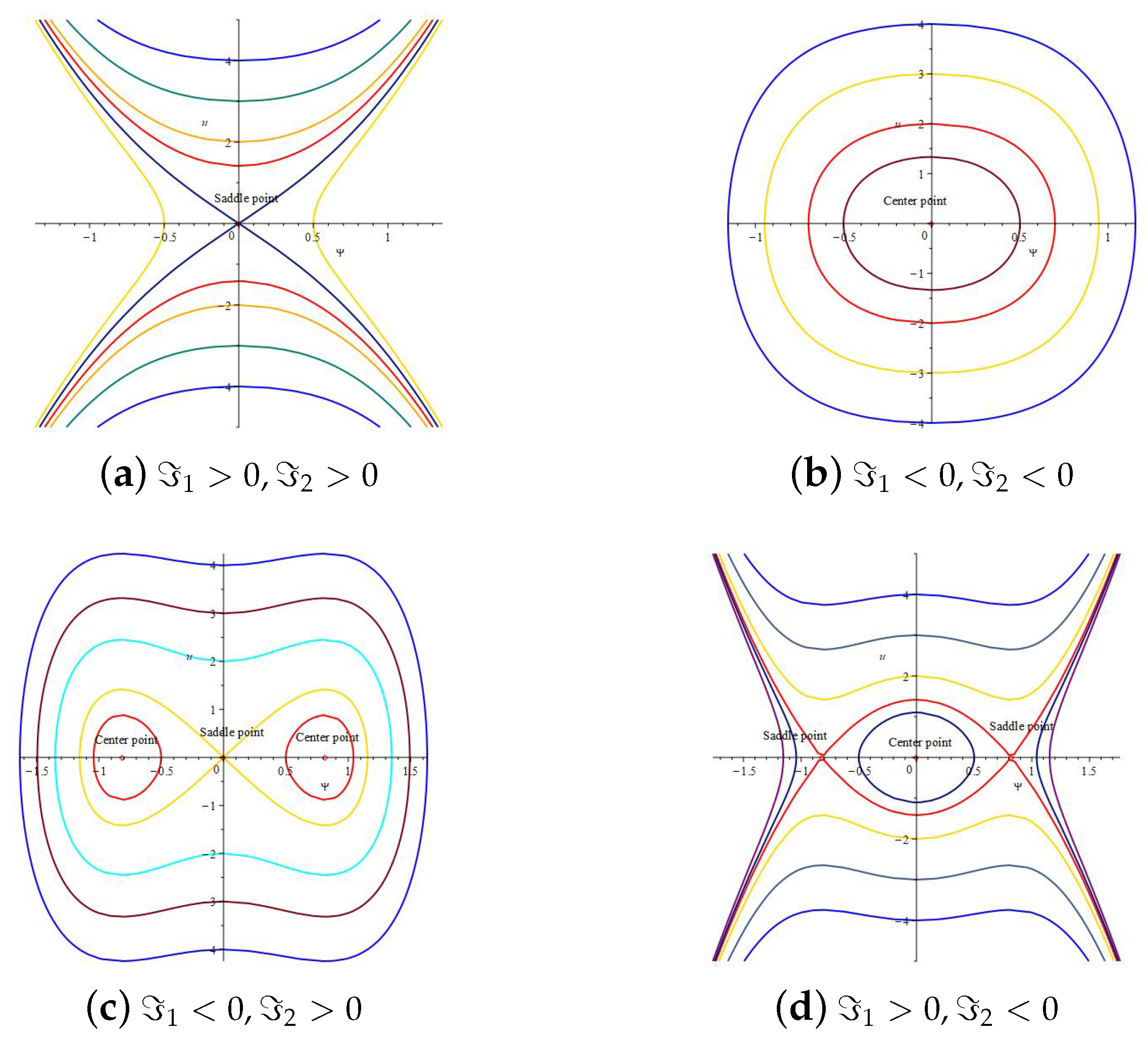
2.3. Qualitative Analysis

The two-dimensional dynamic system of Equation (5) can be described as follows:

$$\left\{\begin{array}{c}\frac{d\Psi }{d\xi }=u,\hfill \\ \frac{du}{d\xi }={\Im }_1{\Psi }^3+{\Im }_2\Psi ,\hfill \end{array}\right.$$

(6)

with its first integral

$$H(\Psi ,u)=\frac{1}{2}{u}^2-\frac{{\Im }_1}{4}{\Psi }^4-\frac{{\Im }_2}{2}{\Psi }^2=h.$$

(7)

Let $F({\Psi }_j)=0$ ( $j=0,1,2$) be the abscissa of the equilibrium point, where $F({\Psi }_j)={\Im }_1{\Psi }_j^3+{\Im }_2{\Psi }_j$. Assume that $\mathbf{M}({\Psi }_j,0)=\left(\begin{array}{cc}0& 1\\ 3{\Im }_1{\Psi }_j^2+{\Im }_2& 0\end{array}\right)$ is the coefficient matrix of (6) at the equilibrium point. Then, we obtain

$$\mathbf{det}(\mathbf{M}({\Psi }_j,0))=-F^{\prime }({\Psi }_j),j=0,1,2.$$

(8)

If ${\Im }_1{\Im }_2>0$, system (6) has one equilibrium point $(0,0)$ (see Figure 1a,b). If ${\Im }_1{\Im }_2<0$, the system (6) has three equilibrium points: $(0,0)$, $(\sqrt{-\frac{{\Im }_2}{{\Im }_1}},0)$, and $(-\sqrt{-\frac{{\Im }_2}{{\Im }_1}},0)$ (see Figure 1c,d).

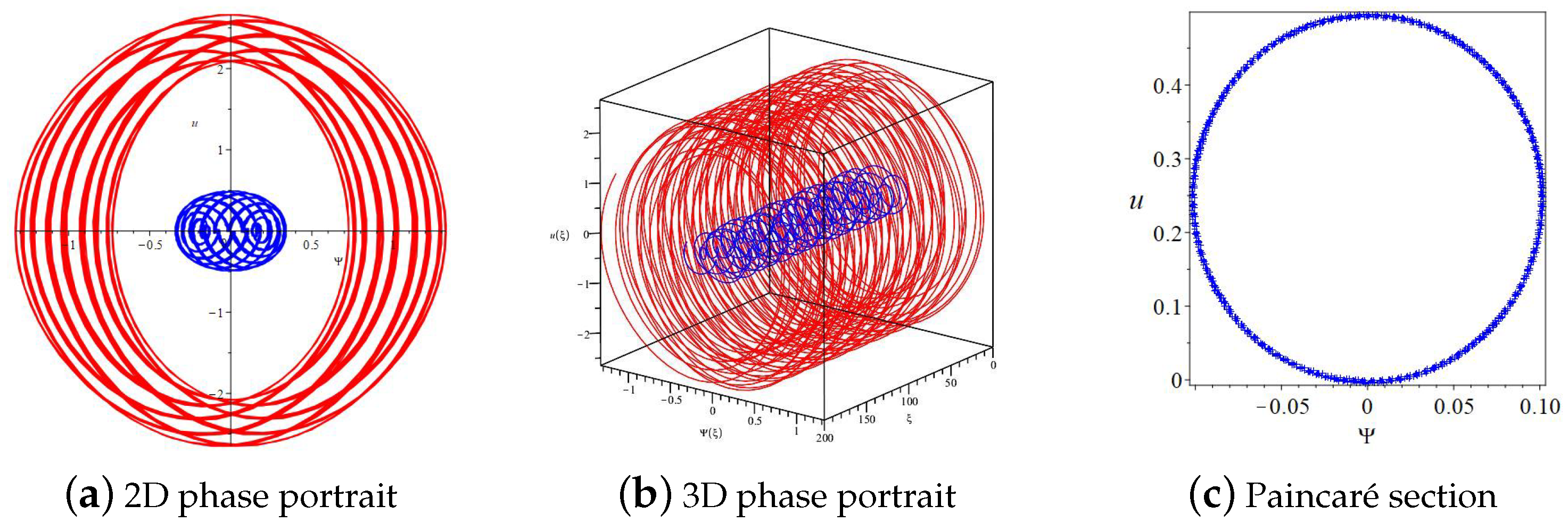
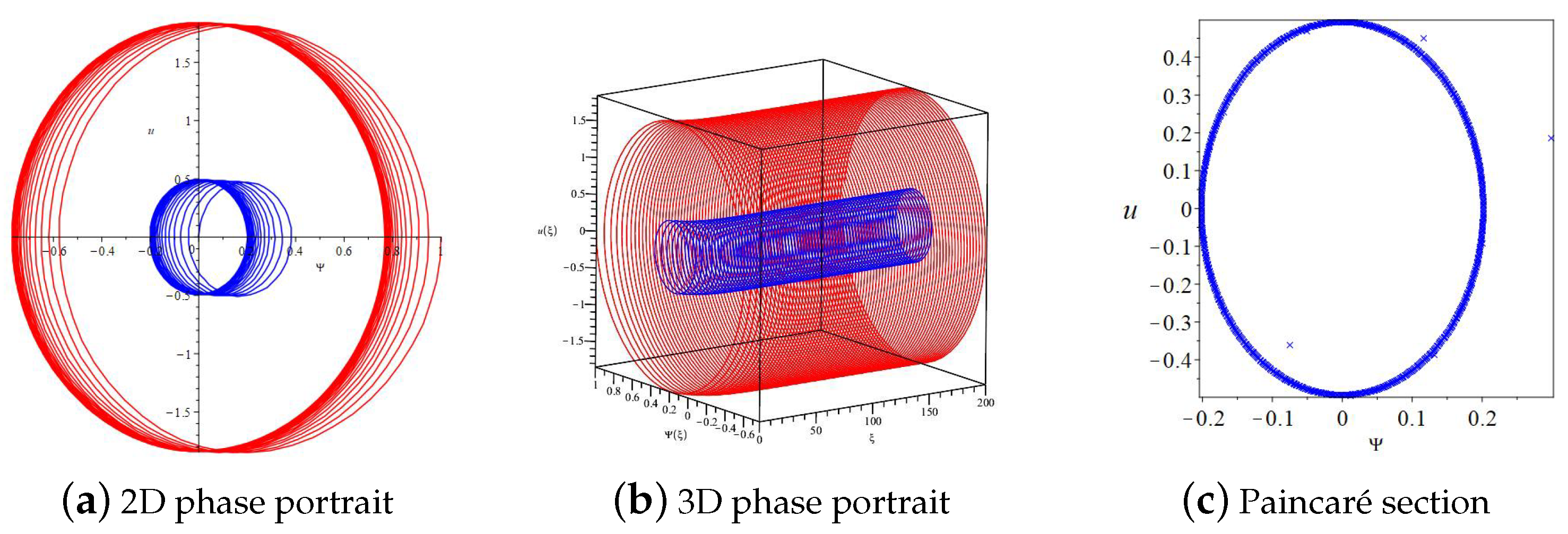
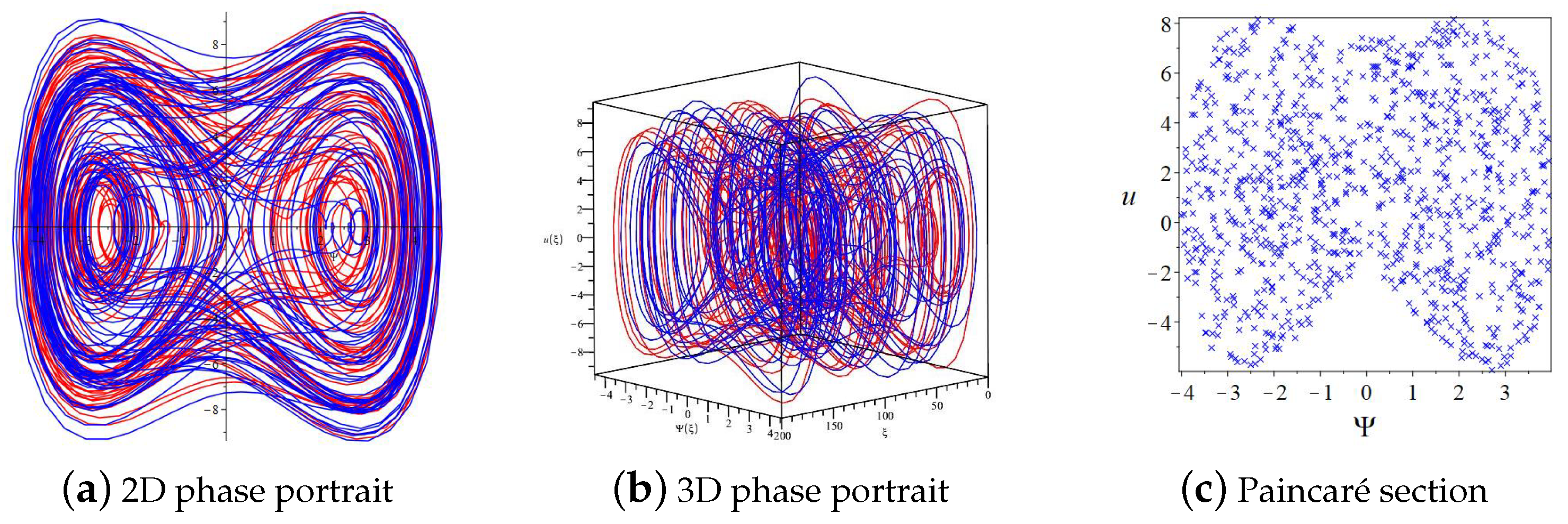
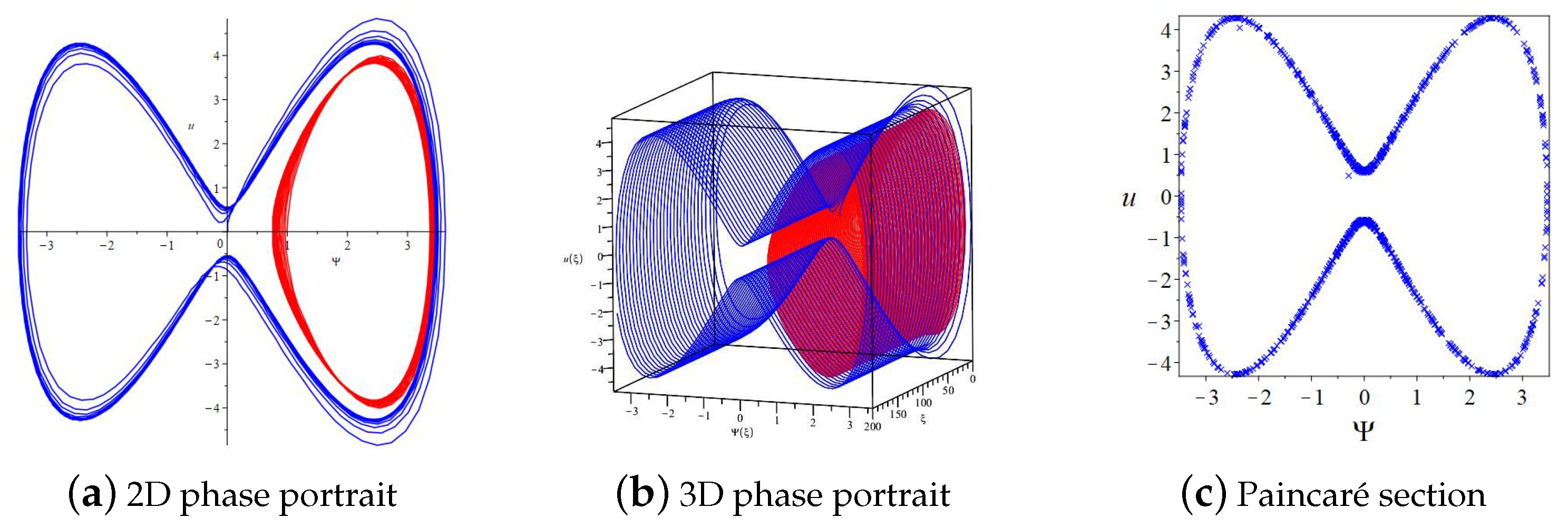
2.4. Qualitative Analysis with Perturbation Term

In this section, we add the following small perturbation term to system (6):

$$\left\{\begin{array}{c}\frac{d\Psi }{d\xi }=u,\hfill \\ \frac{du}{d\xi }={\Im }_1{\Psi }^3+{\Im }_2\Psi +f(\xi ),\hfill \end{array}\right.$$

(9)

where $f(\xi )=Asin(\varpi \xi )$ and $f(\xi )=A{e}^{-0.05\xi }$ are the perturbed terms. A stands for the amplitude of system (9). $\varpi$ is the frequency of system (9).

By fixing the parameters ${\Im }_1,{\Im }_2,A,\varpi$, we have drawn the two-dimensional, three-dimensional, and Paincaré section diagrams of system (9), as shown in Figure 2, Figure 3, Figure 4 and Figure 5. Specifically, when drawing two-dimensional and three-dimensional phase diagrams, we consider the graphs under different initial values. In Figure 6, we plotted the branch phase diagram of system (9) when $\varpi$ takes different values. Obviously, it can be seen from Figure 6 that when A reaches a critical point, the phase diagram of system (9) exhibits chaotic behavior.

3. Optical Soliton Solution of Equation (1)

Let be $h_0=H(0,0)=0$, $h_1=H(\pm \sqrt{-\frac{{\Im }_2}{{\Im }_1}},0)=\frac{{\Im }_2^2}{4{\Im }_1}$.

3.1. ${\Im }_1>0$, ${\Im }_2<0$, $0<h<\frac{{\Im }_2^2}{4{\Im }_1}$

Then, system (7) becomes

$$u^2=\frac{{\Im }_1}{2}({\Psi }^4+\frac{2{\Im }_2}{{\Im }_1}{\Psi }^2+\frac{4h}{{\Im }_1})=\frac{{\Im }_1}{2}({\varrho }_{1h}^2-{\Psi }^2)({\varrho }_{2h}^2-{\Psi }^2),$$

(10)

where ${\varrho }_{1h}^2=\frac{-{\Im }_2+\sqrt{{\Im }_2^2-4{\Im }_{1}h}}{{\Im }_1}$ and ${\varrho }_{2h}^2=\frac{-{\Im }_2-\sqrt{{\Im }_2^2-4{\Im }_{1}h}}{{\Im }_1}$.

Substituting (10) into $\frac{d\Phi }{d\xi }=u$ and integrating it, we can present the Jacobian function solutions

$$\begin{array}{c}\hfill {\psi }_1(x,y,t)=\pm {\varrho }_{1h}\mathbf{sn}({\varrho }_{2h}\sqrt{\frac{{\Im }_1}{2}}(m_{1}x+m_{2}y+\frac{\Gamma (d+1)}{\alpha }\omega t^{\alpha }),\frac{{\varrho }_{1h}}{{\varrho }_{2h}}){\mathbf{e}}^{i(r_{1}x+r_{2}y+\frac{\Gamma (d+1)}{\alpha }\tau t^{\alpha }+\delta )}.\end{array}$$

(11)

3.2. ${\Im }_1>0$, ${\Im }_2<0$, $h=\frac{{\Im }_2^2}{4{\Im }_1}$

When ${\varrho }_{1h}^2={\varrho }_{2h}^2=-\frac{{\Im }_2}{{\Im }_1}$, we can obtain the soliton solution of (1)

$$\begin{array}{c}\hfill {\psi }_2(x,y,t)=\pm \sqrt{-\frac{{\Im }_2}{{\Im }_1}}\mathbf{tanh}(\sqrt{-\frac{{\Im }_2}{2}}(m_{1}x+m_{2}y+\frac{\Gamma (d+1)}{\alpha }\omega t^{\alpha })){\mathbf{e}}^{i(r_{1}x+r_{2}y+\frac{\Gamma (d+1)}{\alpha }\tau t^{\alpha }+\delta )}.\end{array}$$

(12)

3.3. ${\Im }_1<0$, ${\Im }_2>0$, $-\frac{{\Im }_2^2}{4{\Im }_1}<h<0$

Then, system (7) becomes

$$u^2=-\frac{{\Im }_1}{2}(-{\Psi }^4-\frac{2{\Im }_2}{{\Im }_1}{\Psi }^2-\frac{4h}{{\Im }_1})=-\frac{{\Im }_1}{2}({\Psi }^2-{\varrho }_{3h}^2)({\varrho }_{4h}^2-{\Psi }^2),$$

(13)

where ${\varrho }_{3h}^2=\frac{-{\Im }_2+\sqrt{{\Im }_2^2-4{\Im }_{1}h}}{{\Im }_1}$ and ${\varrho }_{4h}^2=\frac{-{\Im }_2-\sqrt{{\Im }_2^2-4{\Im }_{1}h}}{{\Im }_1}$.

Substituting (13) into $\frac{d\Phi }{d\xi }=u$ and integrating it, we can present the Jacobian function solutions

$$\begin{array}{c}\hfill {\psi }_3(x,y,t)=\pm {\varrho }_{4h}\mathbf{dn}({\varrho }_{4h}\sqrt{-\frac{{\Im }_1}{2}}(m_{1}x+m_{2}y+\frac{\Gamma (d+1)}{\alpha }\omega t^{\alpha }),\frac{\sqrt{{\varrho }_{4h}^2-{\varrho }_{3h}^2}}{{\varrho }_{4h}})\\ \hfill {\mathbf{e}}^{i(r_{1}x+r_{2}y+\frac{\Gamma (d+1)}{\alpha }\tau t^{\alpha }+\delta )}.\end{array}$$

(14)

3.4. ${\Im }_1<0$, ${\Im }_2>0$, $h=0$

When ${\varrho }_{3h}^2=0,{\varrho }_{4h}^2==-\frac{2{\Im }_2}{{\Im }_1}$, we can obtain the soliton solution of (1)

$$\begin{array}{c}\hfill {\psi }_4(x,y,t)=\pm \sqrt{-\frac{2{\Im }_2}{{\Im }_1}}\mathbf{sech}(\sqrt{{\Im }_2}(m_{1}x+m_{2}y+\frac{\Gamma (d+1)}{\alpha }\omega t^{\alpha })){\mathbf{e}}^{i(r_{1}x+r_{2}y+\frac{\Gamma (d+1)}{\alpha }\tau t^{\alpha }+\delta )}.\end{array}$$

(15)

3.5. ${\Im }_1<0$, ${\Im }_2>0$, $h>0$

Then, system (7) becomes

$$u^2=-\frac{{\Im }_1}{2}(-{\Psi }^4-\frac{2{\Im }_2}{{\Im }_1}{\Psi }^2-\frac{4h}{{\Im }_1})=-\frac{{\Im }_1}{2}({\varrho }_{5h}^2+{\Psi }^2)({\varrho }_{6h}^2-{\Psi }^2),$$

(16)

where ${\varrho }_{5h}^2=\frac{{\Im }_2-\sqrt{{\Im }_2^2-4{\Im }_{1}h}}{{\Im }_1}$ and ${\varrho }_{6h}^2=\frac{-{\Im }_2-\sqrt{{\Im }_2^2-4{\Im }_{1}h}}{{\Im }_1}$.

Substituting (16) into $\frac{d\Phi }{d\xi }=u$ and integrating it, we can present the Jacobian function solutions

$$\begin{array}{c}\hfill {\psi }_5(x,y,t)=\pm {\varrho }_{6h}\mathbf{cn}(\sqrt{-\frac{{\Im }_1({\varrho }_{5h}^2+{\varrho }_{6h}^2)}{2}}(m_{1}x+m_{2}y+\frac{\Gamma (d+1)}{\alpha }\omega t^{\alpha }),\frac{{\varrho }_{6h}}{\sqrt{{\varrho }_{5h}^2+{\varrho }_{6h}^2}})\\ \hfill {\mathbf{e}}^{i(r_{1}x+r_{2}y+\frac{\Gamma (d+1)}{\alpha }\tau t^{\alpha }+\delta )}.\end{array}$$

(17)

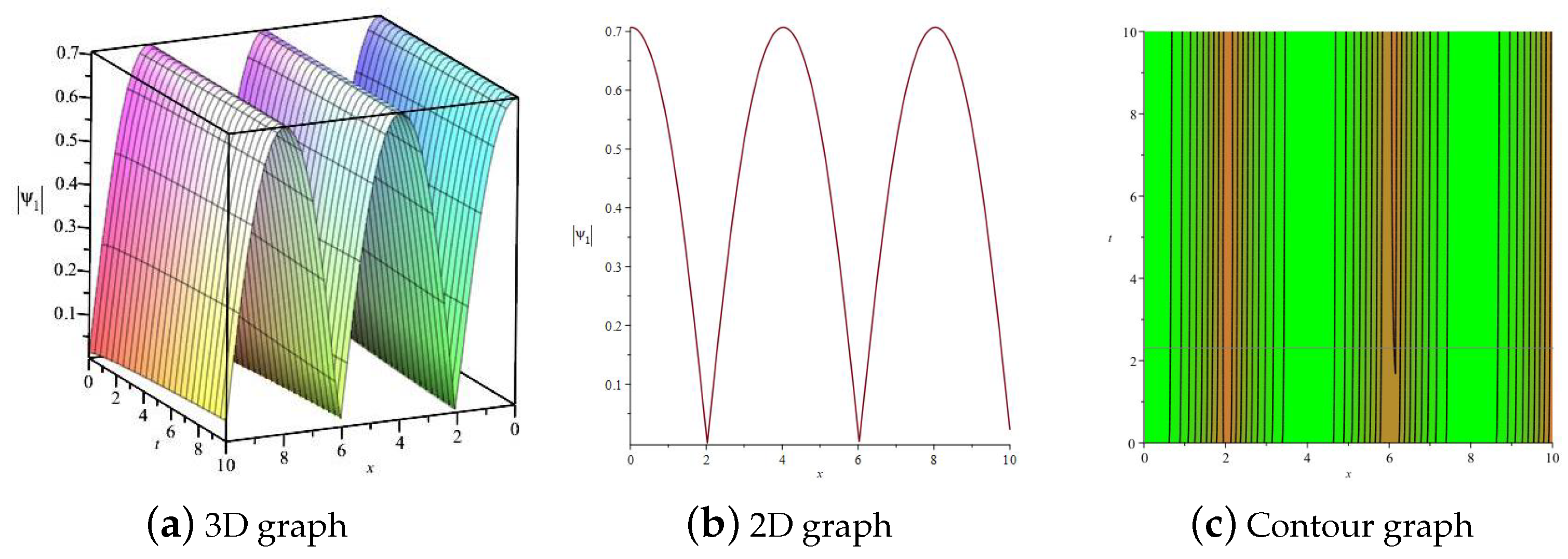
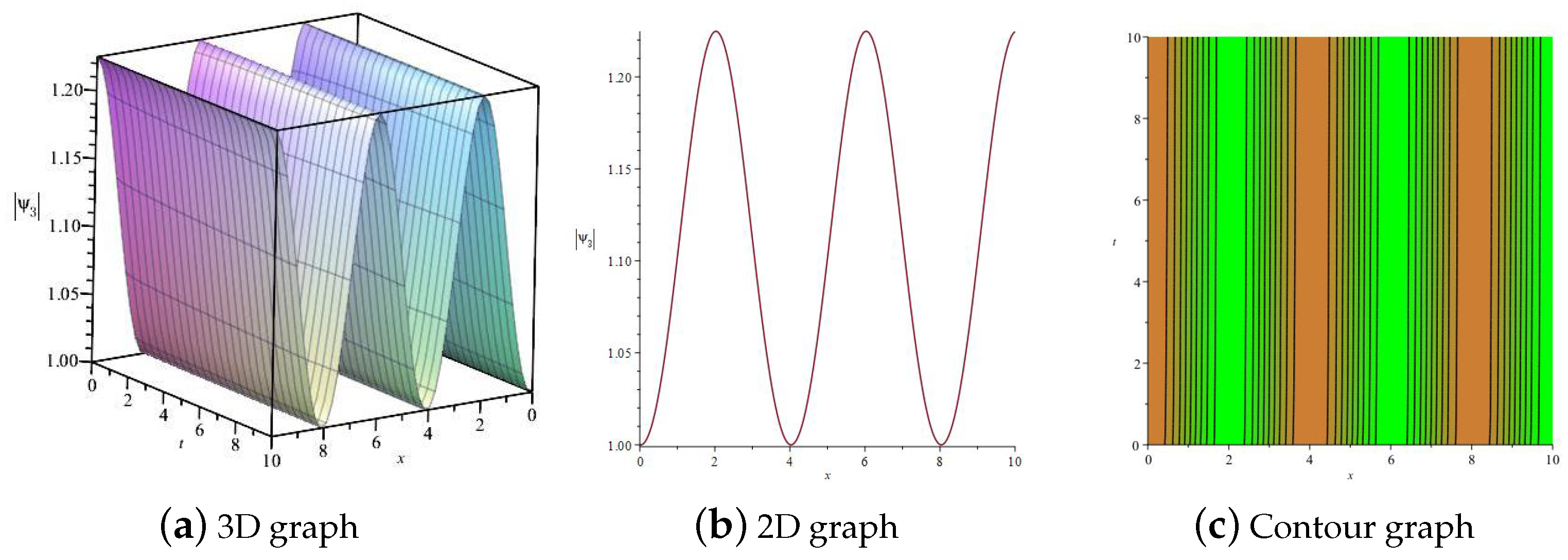
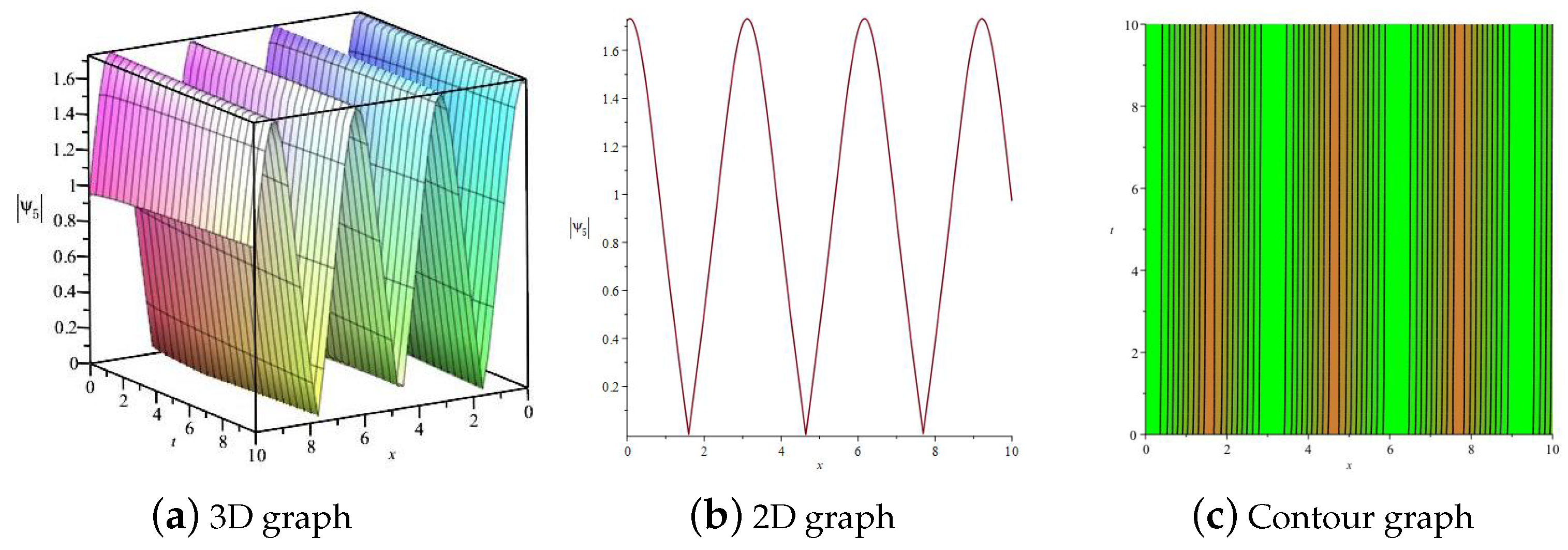
3.6. Numerical Simulations

In this section, we plotted the solutions ${\psi }_1(x,y,t)$, including the three-dimensional graph, two-dimensional graph, and counter graph, when $a_1=1,a_2=1,\omega =1,m_1=1,m_2=6,\tau =-7,r_1=1,r_2=-\frac{3}{2},\alpha =\frac{1}{2},d=1,h=\frac{3}{16}$ as shown in Figure 7. Obviously, the solution ${\psi }_1(x,y,t)$ of Equation (1) is a periodic function solution. We plotted the solutions ${\psi }_2(x,y,t)$, including the three-dimensional graph, two-dimensional graph, and counter graph, when $a_1=1,a_2=1,\omega =1,m_1=1,m_2=6,\tau =-7,r_1=1,r_2=1,\alpha =\frac{1}{2}$, as shown in Figure 8. Obviously, the solution ${\psi }_2(x,y,t)$ of Equation (1) is a kink-like soliton. Moreover, we also plot solutions ${\psi }_3(x,y,t)$, ${\psi }_4(x,y,t)$, and ${\psi }_5(x,y,t)$ of Equation (1), as shown in Figure 9, Figure 10 and Figure 11.

4. Conclusions

In this article, we use the theory of dynamical systems to study the dynamic behavior and optical soliton for Equation (1) in a liquid crystal model. Furthermore, we used mathematical software to draw a planar phase diagram of a two-dimensional dynamical system, and we can easily obtain the characteristics of some equilibrium points of the planar dynamical system from the planar phase diagram. And by adding small perturbations, the dynamic behavior of the two-dimensional system is analyzed. Based on different initial values, we have drawn planar phase diagrams using red and blue colors in the same coordinate system. From the perspective of plane dynamics theory, we have drawn a bifurcation phase diagram and Poincaré sections of a disturbance system. And we separately considered the dynamic behavior under periodic and small disturbances. In future research, we will consider the dynamic behavior and optical soliton solutions of more complex FPDEs.