Abstract
Intelligent control methodologies and artificial intelligence (AI) are essential components for the efficient management of energy storage modern systems, specifically those utilizing superconducting magnetic energy storage (SMES). Through the implementation of AI algorithms, SMES units are able to optimize their operations in real time, thereby maximizing energy efficiency. To have a more advanced understanding of this issue, DynamoMan is presented in this paper. For use with SMES systems, DynamoMan, an Artificial Neural Network (ANN)-tuned Fractional Order PID Brain Emotional Learning-Based Intelligent Controller (ANN-FOPID-BELBIC), has been developed. ANN tuning is employed to optimize the key settings of the reward/penalty generator of a BELBIC, which are important for its overall efficacy. Following this, DynamoMan is integrated into the SMES control system and compared to scenarios in which a BELBIC, PID, PI, and P are utilized. The findings indicate that DynamoMan performs considerably better than other models, demonstrating robust and control attributes alongside a considerably reduced period of settling time, especially when incorporated with the power grid.
1. Introduction
During a time characterized by growing energy demands and a swift shift towards renewable energy sources, it is crucial to employ intelligent control techniques and precise adjustments in energy storage systems. SMES is a promising solution due to its ability to efficiently store large amounts of energy with low losses. The intricate interplay between tuning parameters and control algorithms in SMES systems ensures seamless integration with existing power infrastructures while also enhancing the overall performance, dependability, and resilience of the system. To advance the development of renewable energy, it is essential to enhance intelligent control techniques and tunings in SMES technologies.
From our literature review, we found that modern electrical grids are expected to benefit from energy storage systems (ESSs), particularly when it comes to integrating renewable energy sources (RESs) [1]. A number of control schemes have been developed to maximize the use of ESSs for duties including voltage and frequency control. With an emphasis on SMES systems specifically, an overview of recent developments in ESS technology and control methodologies have been presented. SMES’s high efficiency and quick reaction times make it an appealing choice for effective energy storage [2,3]. SMES stores energy as a magnetic field, as compared to conventional battery-based storage devices, which minimizes losses during bidirectional power transfer. SMES is also advantageous for applications that need rapid power correction because of its quick response times and long operating lives [4]. Numerous investigations have focused on the utilization of SMES in diverse situations related to power systems. For example, SMES has been studied for frequency regulation tasks, where it manifests a field for maintaining grid stability and adaptable capacities [5]. SMES is also used in voltage control, particularly in grid-forming power inverters, where smart control strategies provide resilience to disturbances and parameter changes [6].
Control strategies are important in optimizing the performance of SMES systems. Recent research has focused on intelligent control schemes based on artificial intelligence techniques such as BEL [7]. These controllers present advantages such as adaptability to uncertain operating conditions and model-free operation, enhancing the resilience and efficiency of SMES systems. Moreover, the integration of SMES into power systems requires addressing technical challenges such as coil design, power electronics converters, and control system design [8,9]. Efforts have been made to develop cost-effective coil designs and efficient power electronic converters to maximize the benefits of SMES in power applications [10]. The research conducted in [11,12] integrated SMES with power compensation techniques to enhance the dynamic performance of power distribution networks. By deploying SMES alongside, for example, Distribution Static Synchronous Compensator (DSTATCOM), these studies aim to extend the range of compensation capabilities while reducing DC link voltage. The incorporation of advanced control algorithms, such as deep Q-learning (DQL) and Deep Bayesian Active Learning (DBAL), enables efficient operation under various loading scenarios, leading to improved power factors, load balancing, and harmonic elimination. Simulation studies validate the effectiveness of these approaches in enhancing power quality and meeting regulatory standards.
By examining the correlation between permanent magnets and high-temperature superconducting (HTS) coils for effective energy storage without the need for power electronic converters, the work conducted in [13] presents an alternative strategy to SMES. There are possible benefits to this idea in terms of ease of use, reliability, and energy economy. In [14], coupled with HESS, the power control method for distributed doubly fed induction generator (DFIG) systems is proposed in order to address the issues related to wind power integration. The plan efficiently controls power variations by coordinating the grid-side converter and HESS, maintaining grid compliance and reducing the impact of the inherent unpredictability in wind energy generation [15]. The SMH addressed the issues of grid variations and intermittency in wind power generation by using the special qualities of superconducting coils to achieve great efficiency and power density. Studies using analytical modeling and simulation show how SMH may improve the efficiency and reliability of wind thermal power systems.
An HTS flywheel ESS is presented in [16], including the development of a magnetic coupler with clutch functionality as a means of minimizing energy loss and self-discharge. The coupler reduces no-load losses by severing the flywheel from the generator/motor during energy retention phases, therefore increasing system efficiency. As manifested in [17], hybrid RESs will become significant in assisting the transition to sustainable energy sources. Through the integration of PV/wind hybrid systems with hybrid storage systems, the work intended to enhance system performance and energy quality under a range of operating situations.
In [18], there is emphasis on the critical role of advanced materials, particularly nanomaterials, in enhancing energy conversion and storage systems. Furthermore, ref. [19] emphasizes the benefits of HTS-SMES, including its quick response, high efficiency, and charge–discharge cycles. In order to boost the energy storage density and improve the utilization rate of HTS tapes, the work presents the idea of connected superconducting coils (CSCs). Nevertheless, new modular power conditioning systems (MPCSs) and decoupling control techniques are proposed to address issues with accurate power and current management in CSC systems. Analytical methods for calculating mutual inductance parameters between D-shaped coils used in large toroidal HTS-SMES magnets are taken into consideration by [20]. On the other hand, the research conducted in [21] analyzes the rising need for ESS technologies to satisfy customer demands and maintain a balance between the electricity supply/demand. ESS needs are expected to quadruple by 2030, necessitating the need for specialized systems and equipment to meet this need. An analysis was carried out in [22] that focused on the opportunities and difficulties associated with energy management in shipboard microgrids, with an emphasis on the function of energy storage systems in enhancing reliability and performance.
When SMES are outfitted with Voltage Source Converters (VSCs), a dispersed pattern of high-frequency PWM voltage is predicted [23]. The purpose of this work is to reduce the detrimental impacts of this uneven distribution on magnet insulation by proposing a revised control technique for the power conditioning system (PCS). Instead of high-frequency PWM voltage, the new approach makes sure that the magnet can tolerate continually varying DC voltage during SMES charging or discharging. The expanding significance of ESS in storing and supplying power, especially during peak hours, was discussed in [24]. The research presents a reliable energy retention system that generates power from solar and wind energy through the integration of batteries and supercapacitors. Furthermore, SMES’s potential was demonstrated in [25] through the improvement of grid power quality, due to its benefits including high power density, quick response times, and minimal energy loss. However, the conduction and switching losses of power devices may cause the energy stored in SMES to decrease. The developed work proposed a charging approach using constant duty cycle PWM to maintain the stored current in SMES at a rated level prior to grid-connected operation. Because of their inexpensive cost, high critical current density, low anisotropy, and critical temperature of roughly 40 K, MgB2 tapes and wires are the subject of much of the work conducted in [26]. The preparation process of MgB2, which is used to wind coils for the SMES system, is manifested.
The investigation conducted in [27] presents the development of a no-insulation (NI) REBCO coil system for use in SMES, and a limitation of SMES is anticipated. NI-REBCO coils, which are intended to achieve both high thermal stability and high current density, have been proposed as a solution to the poor energy density of SMES. This will allow for a larger storage density within SMES. Furthermore, ref. [28] illustrates the challenges faced in integrating RESs into the grid, notably with regard to operational adequacy, stability, and reliability. Integrating ESS into the power network is one way to handle erratic loads. In addition, ref. [29] discusses the challenges that conventional power systems have and provides microgrids as a solution for integrating microgeneration sources close to sites of consumption. FESS applications are reviewed in [30] for a variety of power system components, including as integrated energy systems, solar panels, wind turbine power plants, and coal-fired thermal power units. The researchers also look at hybrid energy storage systems and flywheel energy storage system arrays, addressing electric trading markets, configurations, and control methodologies.
In order to address the volatility of RES generation, energy storage technology (EST) is important [31]. Furthermore, the Dandelion Algorithm (DA) is used in [32] to integrate distributed BESS in order to improve the performance of an electrical distribution network (EDN). Using loss sensitivity factors (LSFs) to predetermine the search space for BES placements, the method uses the DA to find the best locations and sizes. Research on the effect of capacitor banks’ daily number of switches (NOS) on loss reduction in radial distribution systems is conducted in [33]. The study splits the day into several time intervals for capacitor size switching that correspond to the same NOS. Taking into account pertinent constraints, a Random Forest nonlinear programming model with discontinuous derivatives (DeepOptaCast) is developed.
Regarding the storage technologies in smart power systems, the challenges associated with distributed generating systems and RESs are explored in [34] regarding the market for electrical energy, especially with respect to frequency regulation. A new hybrid model called FARHAN is provided in [35], which has been developed to address the challenges associated with electrical load forecasting in smart grids. To effectively schedule smart grids, including renewable-integrated ones, FARHAN integrates descending neuron attention, long/short-term memory (LSTM), and Markov-simulated neural networks (MNNs) to maximize accuracy and analysis time for short-, mid-, and long-term smart grid planning decisions.
In order to increase the efficiency, this paper presents DynamoMan. It is an online intelligent adaptive model for optimizing SMES operations. By integrating ANN-based tuning techniques with the robust control capabilities of a BELBIC, precise energy storage and release are ensured concerning dynamic grid conditions and fluctuating energy demands.
2. Configuration of the Superconducting Magnetic Energy Storage
SMES technology is an important development in the area of energy storage. This innovation is driven by several aspects, including the universal transition towards renewable energy sources (RESs), the increasing use of electric cars for eco-friendly transportation, and the liberalization of power markets. These elements are making a considerable change in the electricity system. The functioning of power systems is being fundamentally transformed by these developments as renewable energy sources are affecting distribution networks, causing intermittent power supply and requiring the adoption of storage technologies to ensure stable operation. SMES, or superconducting magnetic energy storage, utilizes the unique characteristics of superconducting materials and magnetic fields to efficiently and rapidly store and release energy, distinguishing it from traditional batteries and capacitors. This technique has several benefits, such as a high energy density, quick response times, and almost limitless charge–discharge cycles. The SMES system’s concept and schematic design are illustrated in Figure 1, based on [36,37].
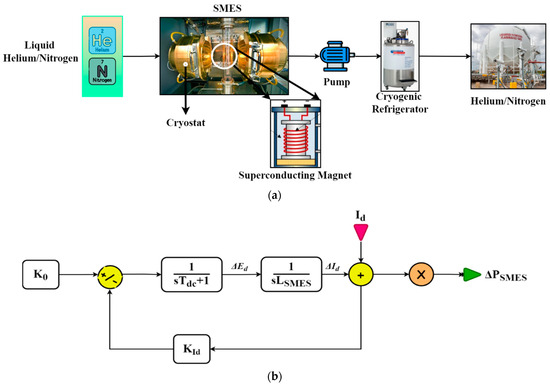
Figure 1.
(a) The schematic and (b) operating diagram of SMES.
The core of SMES systems consists of superconducting coils, as shown in Figure 1a, often manufactured from materials such as niobium–titanium (Nb-Ti) or niobium–tin (Nb-Sn). These substances demonstrate the property of superconductivity when they are cooled below their critical temperature. This enables the flow of electricity through the coils without any resistance. Applying an electric current to the coils produces a robust magnetic field, efficiently storing energy as magnetic potential. SMES has several significant benefits. The powerful magnetic fields generated by superconducting coils offer a high energy density, allowing for substantial energy storage in a compact area. This makes it particularly suitable for applications that have limited space, such as urban regions or vehicle integration. Furthermore, SMES exhibits quick response times, enabling the nearly immediate discharge of stored energy, which is essential for demanding applications like grid stability or electric car acceleration. Furthermore, SMES systems possess an extended operational lifespan as a result of the absence of deterioration observed in conventional batteries. This is made possible by the utilization of superconducting materials, which facilitate the passage of electric current without any resistance, hence reducing heat generation and prolonging the system’s functional duration. As a result, the expenses for maintenance are decreased, and the dependability is improved. Ongoing research is focused on addressing the challenges related to the scalability and affordability of superconducting materials and cryogenic cooling systems. The goal is to increase the performance and cost-effectiveness of these technologies. Figure 1b manifests the schematic transfer function model of SMES in Lapalace, which demonstrates how the firing angle of the bridge converter regulates the charging or discharging of the superconducting inductor coil. The output voltage of the bridge converter of SMES is mathematically formulated as [36]
where Ed, Eo, α, Id, and Rc are the inductor input voltage, open-circuit voltage of the converter, firing angle, inductor current, and equivalent commuting resistance. To adjust the voltage, Ed, the incremental change in frequency deviation is utilized. The generator rotor inertia initially supplies power to the system in the event of a sudden load disturbance. Consequently, the frequency deviation will become negative, which will compel the SMES to discharge simultaneously. Since the inductor’s current direction remains constant, the voltage of the SMES is negative. The incremental changes in superconducting coil voltage and current are implemented as [36]
In which the converter time constant and control loop gain are denoted by , in seconds, and , in [kV/Hz]. However, the system should be ensured by a fast current recovery. Consequently, the variation in inductor current must be detected and incorporated as a negative feedback signal into the SMES control loop, which makes the final equation [36]:
With , in [kV/kA], as the negative feedback gain of the system.
3. Proposed Control Strategy of DynamoMan
As with the developed controller in the robust regulation of SMESs, the ANN-FOPID-BELBIC controller is anticipated. Consequently, the controller is processed by two parts. In the first part, ANN fine-tunes the target parameters of the BELBIC; then, the fine-tuned BELBIC outputs the final control signal to control the signal. The greatest benefit of this work is that there is no need for user-based or offline tuning as the ANN performs online action. This feature causes the system to be robust and utilized in a wider range of applications.
3.1. Brain Emotional Learning-Based Intelligent Controller
The BELBIC is a control system, which was firstly introduced in [38], that takes inspiration from the emotional learning mechanisms discovered in the human brain [39], presenting a unique and innovative approach. A BELBIC, unlike traditional controllers that rely purely on mathematical models and algorithms, incorporates knowledge from neurology to enhance its ability to adapt and perform effectively in complex and changing contexts. The concept of a BELBIC is manifested in Figure 2.
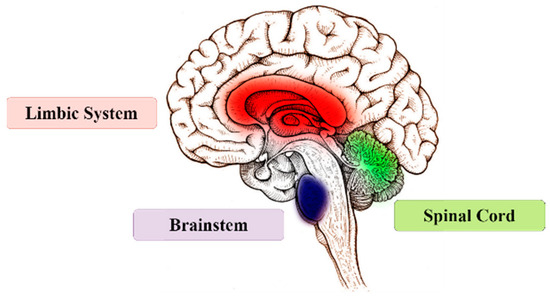
Figure 2.
The BELBIC main linking parts.
A BELBIC utilizes artificial neurons to replicate crucial emotional areas of the brain, such as the amygdala and prefrontal cortex, which are well-known for their involvement in decision-making and the regulation of behavior. By incorporating emotional input into the control loop, a BELBIC manages uncertainties, nonlinearities, and disturbances, similar to how humans respond to emotional inputs in real-life settings. Consequently, the red, green, and purple parts of the brain present the limbic system, brainstem, and the spinal cord, respectively. The limbic system, which encompasses the amygdala, hippocampus, and hypothalamus, is essential for the generation and regulation of emotions, the storage of emotional memories, and the connection between emotions and sensory experiences. The periaqueductal gray and the locus coeruleus regions of the medulla are responsible for the integration of these emotional signals and the regulation of physiological responses, including arousal and heart rate. At the same time, the spinal cord functions as a conduit, enabling the physical expression of emotions by transmitting sensory information from the body to the brain and motor commands from the brain to the body. Collectively, these regions facilitate the perception, processing, and expression of emotions, which in turn undergird intricate emotional learning and behavior. Moreover, the distinctive characteristic of a BELBIC is its ability to withstand and recover from challenges, adjust to different circumstances, and last for a long time. This makes it very suitable for use in robots, autonomous systems, and industrial processes, especially when traditional control methods may not be effective. Furthermore, BELBICs show potential for improving human–machine interaction by allowing computers to recognize and react to human emotions, thus promoting a more intuitive and adaptable system. Figure 3 and Figure 4 manifest the BELBIC used in this work.
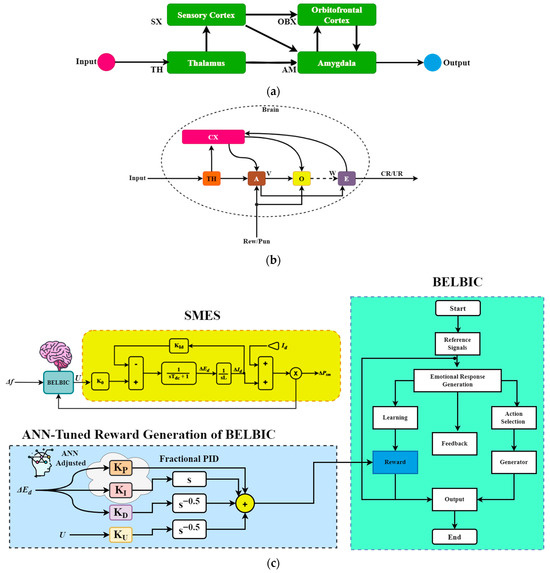
Figure 3.
The (a) overall, (b) detailed modeling and (c) flowchart of DynamoMan in SMES.
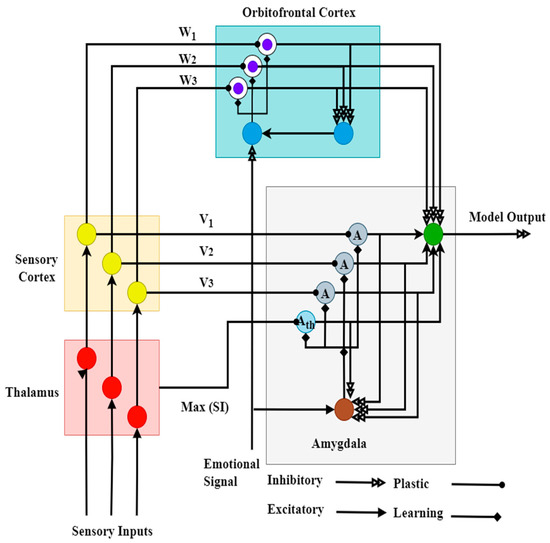
Figure 4.
The computational model of BELBIC.
Illustrated in Figure 3, the thalamus, an essential node, initiates response mechanisms in organisms by receiving sensory input. From that point, impulses divide into two branches, simultaneously reaching both the amygdala and the sensory cortex, thus preparing for additional cerebral processing. The cortical area, namely the CX region, plays a crucial function in examining the incoming signal, interpreting its importance, and considering its potential consequences. The sensory cortex has a crucial effect in controlling the distribution of signals between the amygdala and the orbitofrontal cortex, ensuring a precise balance of neuronal activity. After a complex series of neuronal signals, the sensory information in the CX changes and is then transmitted to the amygdala through route V. The relay mechanism plays a crucial role in the brain processing chain, enabling the conversion of sensory input into meaningful reactions and behaviors in animals. The process of the BELBIC begins with receiving input signals from the environment or the controlled system. These signals are then compared to a reference state to determine the intended goals. As a result, an emotional reaction is produced by comparing the current condition of the system with its emotional state. Subsequently, a reward generator generates reinforcement signals, which are then fed back into the system by a feedback mechanism. This loop modifies the controller’s behavior by incorporating earned rewards, allowing it to acquire knowledge and adjust its actions as time progresses. Consequently, the controller determines suitable actions by considering the emotional reaction, using previous encounters to enhance effectiveness and efficiently accomplish desired objectives. The model inner progress is illustrated in Figure 4, conceptualized from [40].
This function constitutes the major area for acquiring knowledge within this framework. The amygdala’s processing of rewards and punishments enhances the connection between the amygdala and the route. E’s brain will elicit an emotional response when exposed to a similar stimulus again. In contrast, the orbitofrontal cortex computes the disparity between the expected and real outcomes of a stimulus. The orbitofrontal cortex receives information about the perceived reward or punishment from the amygdala and sensory cortex. This information has been established in the brain through learning mechanisms over a period of time. Nevertheless, the organism’s reward or punishment is determined by the external environment and is a direct reflection of the most recent rewards or punishments it has encountered. By employing E, the resultant output remains consistent when these two pieces are properly aligned. On the other hand, the orbitofrontal cortex controls and manages emotional responses in order to support additional learning. Therefore, route W is only activated under these specific conditions. In this regard, BELBIC is conceptualized as [38]
where MO and i are the model output and number of inputs, respectively. The amygdala and orbitofrontal cortex outputs are defined by Ai and OCi, as in [41].
where Wi, and Vi are the orbitofrontal and amygdala gain parameters, respectively. SIi is the ith input, assumed by [41].
where are the amygdala and orbitofrontal cortex learning coefficients, respectively. Additionally, Ath is defined as [41]
in which Ath is the signal from thalamus to the amygdala. Also, are the initial value of the amygdala and stress generation, respectively. Now, by considering the SMES final characteristics (Equation (4)), the closed loop control signal of the system () is conducted as following:
Collectively, , and are the gains for the proportional, integral, and emotional components, respectively. of FOPID will be tuned by the ANN during the online process., As well, the error and emotional signals are symbolized by and . Accordingly, by combining Equations (4) and (11), the final characteristics function of the closed loop system is carried by
As a result of (12), the SMES and the load change can be controlled in a smooth way, utilizing the BELBIC. Also, the Kp, and Ki parameters are tuned by the ANN (Equation (18)). As the overall closed loop of the system determined, the neural implementations of the BELBIC can be performed to output the final control signal. Referring to (5–7) and (11):
Consequently, SI, and ES are updated to
In which [], and [] are the weighting coefficients for SI, and ES inputs, respectively. These mentioned coefficients are determined to make the BELBIC efficient in smoothly controlling the system with less overshoot, a reduced settling time, and a fast steady-state condition. As well, the whole process of SI and ES generation is manifested in Figure 5.
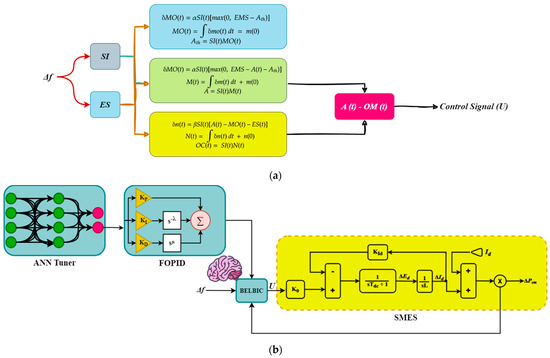
Figure 5.
Diagram of (a) the utilized BELBIC and (b) its implementation.
Based on the process and diagram of the BELBIC utilization, illustrated in Figure 5, N is the connection weight modulated as
In which the output of OC(t) is found by the multifaction of N(t) and SI(t).
3.2. Artificial Neural Network Parameter Tuner
Trial-and-error parameter optimization is an incredibly time-consuming procedure that necessitates a vast number of selections and numerous computer simulations. Utilizing concepts including fitness pressure, heredity, and diversity, evolutionary algorithms provide a more effective substitute for arbitrary trial-and-error approaches. Nevertheless, guaranteeing a positive reaction becomes a formidable task when the operational threshold experiences substantial alterations. To enhance the functionalities of the BELBIC, this work presents a methodology utilizing ANNs to optimize the values of controller parameters. The objective of this methodology is to improve the adaptability and responsiveness of the controller in chaotic environments.
Inspired by the structure and operation of biological neural networks in the human brain, an ANN is a computational model. It is composed of neuronal nodes that are interconnected and arranged in layers. An ANN generally consists of the following layers: input (one or more concealed) and output. Input signals are received by individual neurons, which compute a weighted sum of the sums, apply an activation function to the sum, and subsequently transmit the output to neurons in the following layer. By adjusting the weights of connections between neurons in response to labeled datasets (a process known as training), ANNs are able to recognize patterns, classify data, make predictions, and perform other tasks. ANNs have demonstrated exceptional proficiency in handling intricate, nonlinear associations within datasets. They have been implemented in a wide range of domains, including smart grids, forecasting, control systems, and optimization. ANNs provide notable benefits over conventional approaches in domains such as optimization tasks and control systems as they independently optimize parameter values with the goal of maximizing performance metrics. ANNs have the capability to effectively investigate the parameter space, detect optimal configurations, and adjust to dynamic environments by means of iterative training procedures. In addition, developments in deep learning architectures have augmented the capabilities of ANNs in solving nonlinear optimization problems and handling high-dimensional parameter spaces.
Particularly in this work, by dynamically adjusting the BELBIC’s parameters in real-time, the intelligent neural network increases the system’s resilience to a variety of uncertainties. The inclusion of this adaptive capability enhances the efficacy of the indicated approach in a more comprehensive spectrum of operational circumstances. Figure 6 depicts the schematic representation of the ANN supervisory control system utilized to optimize the calibration of BELBIC parameters. The primary objective of this architecture is to reduce the variation in the output of the SMES, represented by ΔE, and utilize its derivative as input for the ANN. The ANN generates suitable set points via this procedure; these set points are subsequently converted into modifications for reward/punishments of the BELBIC controller. Consequently, the control operation attains robustness and output stability.
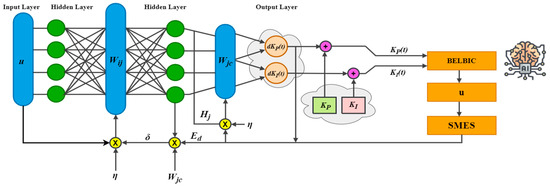
Figure 6.
The overall scheme of the ANN tuner implemented in the system.
Neurons are the processing units in an ANN that are inherently nonlinear. Three fundamental elements comprise each neuron, which includes weights an activation function , and a bias parameter . In an ANN, the activation function may be represented by the sign function, tangent sigmoid, or logarithmic sigmoid, among others. By employing the weighted input and bias, the hidden layer calculates its output, as mathematically represented, retrieved from [42], in (18):
where is the hidden layer number of nodes. Then, the output of the output layer (the outputs are the Kp, and Ki parameters) can be obtained as follows:
where is the output layer number of nodes. The learning procedure deals with the minimization of mean squared error as follows:
where is the number of samples and represents the reference input. The weights of the ANN are modified via supervised feedback, with the back-propagation algorithm being employed by the ANN coordinator during the learning process. The error value calculated in (20) is utilized as the foundation for revising the ANN weights in accordance with the methodology delineated subsequently.
It is noted that in Figure 6, the weight vector for the output layer is designated as W2, while the weight vector for the hidden layer is designated as W1. Ten linear neurons make up the input layer of the ANN in the suggested ANN-based fine-tuner structure, whereas forty nonlinear neurons make up the hidden layer. Moreover, the number of neurons in the ANN’s output layer must match the values of the control variables. In the output layer, the control variables are implemented as two linear neurons that represent the weights of the backstepping controller.
Determining the optimal weights for controller optimization through the tuning process poses a formidable obstacle. Conventional approaches to weight selection by trial and error are exceptionally laborious and time-intensive, necessitating a considerable quantity of iterations and comprehensive computer simulations. Evolutionary algorithms present a more advantageous option by capitalizing on fundamental principles including fitness pressure, heredity, and variety in order to efficiently traverse the weight space. Nevertheless, guaranteeing a positive reaction becomes especially arduous in situations where the operational threshold experiences substantial modifications. Regarding the tuning process of the model, it is an online process in which the system is not pre-tuned. The ANN in the model conducts online tuning during the process based on the reward/penalty function of the system inserted to the ANN. Consequently, this is an advantage of the model, which requires no pre-tuning and is tuned online for the system.
4. Conducted Simulation Results
In this section of the work, the DynamoMan controller, an ANN-tuned FOPID-BELBIC, is applied to the SMES, and the results are drawn. The parameters of DynamoMan are set to achieve optimal control, with α set to 0, β to 0.1, Vinitial to 40, Vth to −20, Winitial to −6, Ts at 0.01 s, derivative gain Kd to 50, control signal gain Ku to 120, proportional gain Kp to −0.003832, and Ki to 1.1611 × 10−6, as presented in Table 1. Also, it should be mentioned that DynamoMan was tested in two different scenarios of ANN-tuned FOPID-BELBIC, and ANN-tuned BELBIC. The simulation results are manifested by Figure 7, Figure 8 and Figure 9.

Table 1.
The final parameters of DynamoMan.
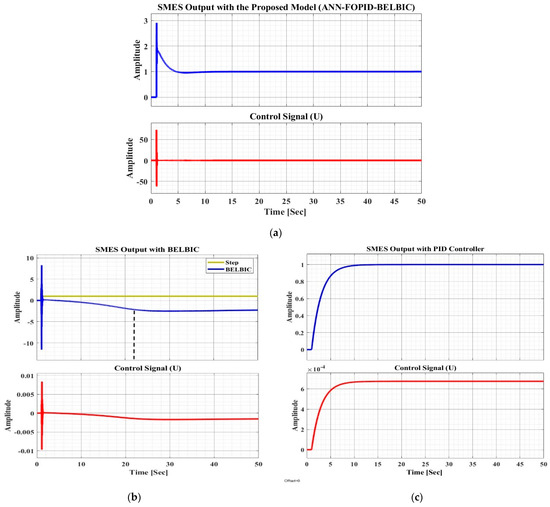
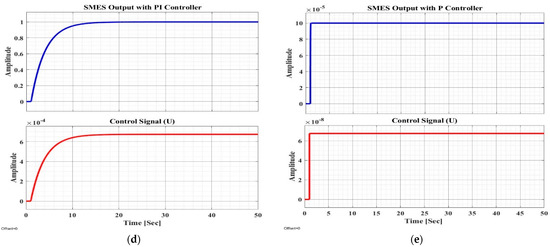
Figure 7.
The results of the system with (a) DynamoMan (ANN-FOPID-BELBIC), (b) BELBIC, (c) PID, (d) PI, and (e) P controller as the first scenario.
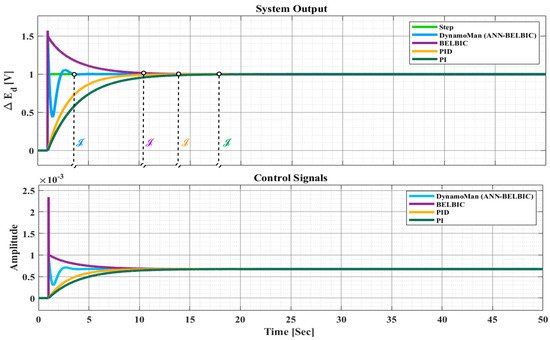
Figure 8.
The output and control signals of the system with/without DynamoMan.
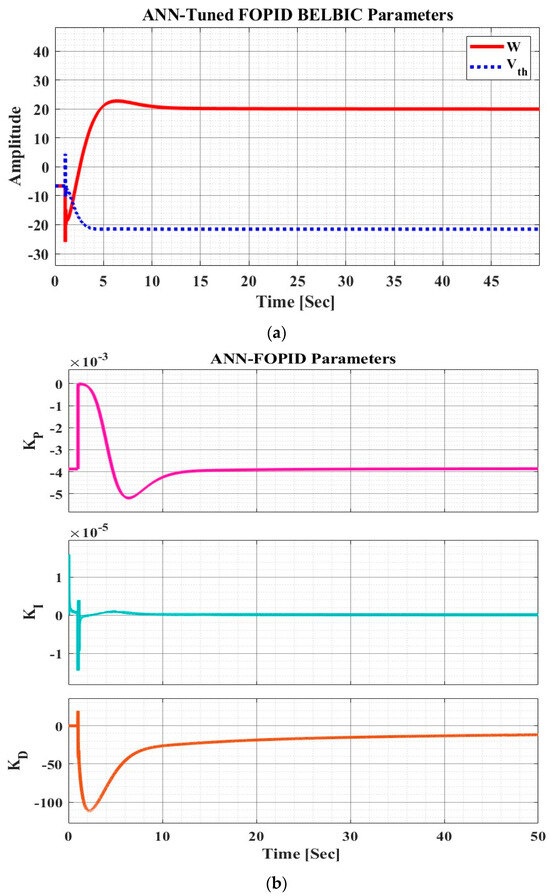
Figure 9.
(a) Controller parameters in both scenarios, and (b) ANN-tuned parameters in DynamoMan.
Manifested in Figure 7, the system is applied on different controllers of DynamoMan, PID, PI, P, and BELBIC. In order to evaluate the results, it is clear that settling time () is the main factor, since the frequency change should be controlled in the least time to make the system enter a steady state. is determined, and mirrored by a dashed line on the plots. Consequently, is around 1 [Sec] for the DynamoMan. Regarding the others, is near to 1.5 [Sec], higher than DynamoMan by about 0.5 [Sec], which is a considerable amount; this is when the utilizer makes sure to have the fastest stability over the system, after frequency change. Regarding the other scenario, the DynamoMan is an ANN-BELBIC, and the results are illustrated in Figure 8.
Regarding Figure 8, both scenarios are applied on the system. Consequently, both have overshoot at initial moments, which is originated from the dynamics, as well as the nature of the system when it interacts with the electricity grid. The overshoot at initial moments originates from the time that the storage charges the grid. Consequently, discharging occurs in the storage that causes deviation and change in frequency. So, this overshoot should be terminated at that moment, not proceeded further. However, has lower value in the first scenario than DynamoMan, an ANN-tuned FIPID-BELBIC. Concerning the , getting to the steady state, the scenario of DynamoMan has ab at nearly 3. However, is at 10, 14, and 17 for the BELBIC, PID, and PI, respectively. In the scenario implementing DynamoMan, there is considerably better performance. In this regard, the utilized parameters of the ANN-FIPID-BELBIC are anticipated in Figure 9.
As illustrated in Figure 9a, the system parameters of [W, V] for DynamoMan and BELBIC are presented. Regarding [W, Vth], the same theory of overshoot from the grid interactions and changes occurred; however, the performance of DynamoMan was overall better than the other scenario in relation to and other factors. Figure 9b conceptualizes the ANN-tuned parameters of DynamoMan in Ki, and Kp. In sequence, both parameters achieved a steady state considerably fast, and their effect is shown in the final output response of the system. In order to handle the overshoot, occurring at the initial moments of grid interactions, Ki raised to −1 × 10−6; conversely, Kp decreased to −5 × 10−3 at initial moments—this handles the overshoot caused by the changes in the grid interactions and makes the system perform smoothly in a reduced settling time and robust manner. As the BELBIC is working based on the reward/penalty performed by the feedback of the system output, Figure 10 depicts the reward/penalty profile of both scenarios.
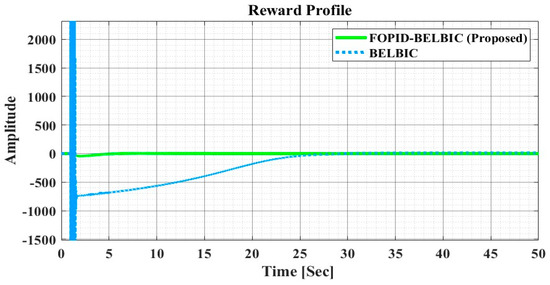
Figure 10.
Reward/penalty profile of both scenarios.
As shown in Figure 10, the generated profile for rewards and penalties indicates that DynamoMan obtained superior rewards in order to maintain stable and robust control of the grid, with the value ranging from 0 to 250. In contrast, it is incapable of handling changes in the system’s grid interaction in the second scenario, as it received a −3000 penalty for output performance at the outset, which conceptualizes the system’s harder-to-smooth control. As well, the comparison between the performance of different models is presented in Table 2, demonstrating that DynamoMan obtained better results than other models in a reduced settling time.

Table 2.
Settling Time Comparison Between Different Models.
5. Conclusions
As intelligent control methods are becoming considerably important in energy storage systems, as is their integration with grids, DynamoMan is investigated in this paper. By employing ANN tuning to optimize FOPID-BELBIC parameters, DynamoMan demonstrates superior performance in comparison to traditional BELBIC methodologies in smooth and robust control perspectives. The parameters of DynamoMan are tuned in order to maximize its efficiency: α is held constant at 0 and β is configured to 0.1. The Vth is defined as −20, while the Vinitial is set to 40. Additionally, the Ts is established at 0.01 s, and the Winitial is specified as −6. In addition, the controller features include a Ki of 1.1611 × 10−5, Kd of −50, and a Ku of 120. The Kp is −0.003832. It is noted that DynamoMan handles the overshoot that arises from the grid integration of the SMES. The performance of DynamoMan in SMES control applications in terms of settling time () contrasts with the other model—a single BELBIC attains comparable outcomes in 10 s, while DynamoMan exhibited a of 1 s. Future directions for the application of BELBIC and AI models in energy storage systems include the optimization of charge and discharge cycles, the enhancement of predictive maintenance, and the enhancement of defect detection. Energy storage systems can more accurately predict energy demand and supply, facilitate the integration of renewable energy sources, and assure grid stability by combining BELBICs with AI-driven predictive analytics. This combination has the potential to develop energy storage solutions that are more intelligent, autonomous, and resilient, thereby facilitating the transition to sustainable and decarbonized energy systems.
Author Contributions
A.S.—Conceptualization, idea, software, illustration, writing, review/editing. H.S.—Software, writing, review/editing. A.O. Review/editing, Supervision, Project Management, and Result Analytics. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the BMS-DC: Next Generation BMS Technology for Data Centers project, granted by Energy Cluster Denmark in 2024.
Data Availability Statement
The generated data can be made available upon a reasonable request to the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Oshnoei, A.; Oshnoei, S.; Jalilpoor, K.; Soudjani, S.; Blaabjerg, F. Grid Frequency Control Capability of Energy Storage Systems: Modeling, New Control Approach, and Real-time Validation. In Proceedings of the 8th IEEE Workshop on the Electronic Grid (eGRID), Karlsruhe, Germany, 16–18 October 2023; IEEE: Karlsruhe, Germany, 2023; pp. 1–6. [Google Scholar]
- Buckles, W.; Hassenzahl, W.V. Superconducting magnetic energy storage. IEEE Power Eng. Rev. 2000, 20, 16–20. [Google Scholar] [CrossRef]
- Vulusala, G.V.S.; Madichetty, S. Application of superconducting magnetic energy storage in electrical power and energy systems: A review. Int. J. Energy Res. 2018, 42, 358–368. [Google Scholar] [CrossRef]
- Fu, L.; Chen, Y.; Zhang, M.; Chen, X.; Shen, B. Multifunctional Superconducting Magnetic Energy Compensation for the Traction Power System of High-Speed Maglevs. Electronics 2024, 13, 979. [Google Scholar] [CrossRef]
- Oshnoei, A.; Sadeghian, O.; Anvari-Moghaddam, A. Intelligent power control of inverter air conditioners in power systems: A brain emotional learning-based approach. IEEE Trans. Power Syst. 2022, 38, 4054–4068. [Google Scholar] [CrossRef]
- Oshnoei, A.; Peyghami, S.; Blaabjerg, F. Intelligent Control Approach Applied for Grid-Forming Power Converters. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023; IEEE: Orlando, FL, USA, 2023; pp. 3013–3019. [Google Scholar]
- Yeganeh, M.S.; Oshnoei, A.; Mijatovic, N.; Dragicevic, T.; Blaabjerg, F. Intelligent secondary control of islanded AC microgrids: A brain emotional learning-based approach. IEEE Trans. Ind. Electron. 2022, 70, 6711–6723. [Google Scholar] [CrossRef]
- Adetokun, B.B.; Oghorada, O.; Abubakar, S.J. Superconducting magnetic energy storage systems: Prospects and challenges for renewable energy applications. J. Energy Storage 2022, 55, 105663. [Google Scholar] [CrossRef]
- Mukherjee, P.; Rao, V.V. Design and development of high temperature superconducting magnetic energy storage for power applications—A review. Phys. C Supercond. Appl. 2019, 563, 67–73. [Google Scholar] [CrossRef]
- Xue, X.D.; Cheng, K.W.; Sutanto, D. A study of the status and future of superconducting magnetic energy storage in power systems. Supercond. Sci. Technol. 2006, 19, R31. [Google Scholar] [CrossRef]
- Mangaraj, M.; Pilla, R.; Kumar, P.P.; Nuvvula, R.S.; Verma, A.; Ali, A.; Khan, B. Design and dynamic analysis of superconducting magnetic energy storage-based voltage source active power filter using deep Q-learning. Electr. Eng. 2024, 106, 1241–1250. [Google Scholar] [CrossRef]
- Mangaraj, M.; Nizami, T.K.; Babu, B.C.; Muyen, S.M. Realization of Superconducting-Magnetic Energy Storage Supported DSTATCOM Using DeepBayesian Active Learning. 2024; preprint. [Google Scholar]
- Li, G.; Li, C.; Han, B.; Li, B.; Li, W.; Yang, T.; Xin, Y. The Interaction between a High-Temperature Superconducting Coil and in-Series Permanent Magnets. IEEE Trans. Appl. Supercond. 2024, 34, 5700505. [Google Scholar] [CrossRef]
- Li, C.; Cao, Y.; Li, B.; Wang, S.; Chen, P. A novel power control scheme for distributed DFIG based on cooperation of hybrid energy storage system and grid-side converter. Int. J. Electr. Power Energy Syst. 2024, 157, 109801. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, C.; Liu, Z.; Wang, Y.; Liu, C. Application and analysis of superconducting magnetic eddy current heater used in wind thermal power generation system. IET Electr. Power Appl. 2024, 18, 668–680. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, G.; Wu, Y.; Zhang, D.; Jing, L. Study of Magnetic Coupler with Clutch for Superconducting Flywheel Energy Storage System. IEEE Trans. Appl. Supercond. 2024, 34, 5700805. [Google Scholar] [CrossRef]
- Jacques, B.J.; Armel, T.K.; Astrid, M.N.; René, T. Contribution to the improvement of the performances of PV/wind microgrids integrating a hybrid SMES/battery energy storage unit. J. Energy Storage 2024, 85, 111011. [Google Scholar] [CrossRef]
- Kulkarni, M.B.; Ayachit, N.H. Energy conversion and storage devices. In Green Nanomaterials in Energy Conversion and Storage Applications; Apple Academic Press: Palm Bay, FL, USA, 2024; pp. 75–93. [Google Scholar]
- Guo, W.; Hong, Y.; Lan, J.; Sang, W.; Liu, W.; Dai, S. Novel Multi-Modular Power Conditioning System and Decoupling Control Strategy for Smes with Coupled Superconducting Coil. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4692131 (accessed on 16 May 2024).
- Liu, W.; Dai, S.; Ma, T.; Shi, Y.; Song, M.; Li, L. Analytical Calculation of Mutual Inductance of D-shaped Coils Applied to High-Temperature Superconducting Magnet. IEEE Trans. Appl. Supercond. 2024, 34, 5700605. [Google Scholar] [CrossRef]
- Kumar, R.; Lee, D.; Ağbulut, Ü.; Kumar, S.; Thapa, S.; Thakur, A.; Jilte, R.D.; Saleel, C.A.; Shaik, S. Different energy storage techniques: Recent advancements, applications, limitations, and efficient utilization of sustainable energy. J. Therm. Anal. Calorim. 2024, 149, 1895–1933. [Google Scholar] [CrossRef]
- Nivolianiti, E.; Karnavas, Y.L.; Charpentier, J.F. Energy management of shipboard microgrids integrating energy storage systems: A review. Renew. Sustain. Energy Rev. 2024, 189, 114012. [Google Scholar] [CrossRef]
- Lin, D.; Shi, J.; Zhou, J.; Liu, Q.; Cheng, S.; Cheng, Q. A Novel PCS Control Strategy for SMES to Suppress Overvoltage of Magnet. IEEE Trans. Appl. Supercond. 2024, 34, 5701005. [Google Scholar] [CrossRef]
- Saikia, P.; Das, N.; Buragohain, M. Robust energy storage system for stable in wind and solar. Renew. Sustain. Energy Rev. 2024, 191, 114079. [Google Scholar] [CrossRef]
- Liu, L.; Sheng, J.; Wang, X.; Li, S.; Yang, K.; Jiang, J. Test of Charging and Grid Connected Process for SMES. IEEE Trans. Appl. Supercond. 2024, 34, 5700705. [Google Scholar] [CrossRef]
- Wang, M.; Guo, Q.; Zhu, Y.; Wu, B.; Wang, Q.; Feng, J.; Yan, G.; Liu, X.; Feng, Y.; Zhang, P. The Preparation of MgB 2 Conductors for Magnet Application of SMES in WST. IEEE Trans. Appl. Supercond. 2024, 34, 6200705. [Google Scholar] [CrossRef]
- Ogasawara, T.; Ishiyama, A. Evaluation of Effectiveness of Strand Transposition in Multi-Stacked Coils wound with No-Insulation Bundle REBCO Conductor for SMES. IEEE Trans. Appl. Supercond. 2024, 34, 5700905. [Google Scholar] [CrossRef]
- Emrani, A.; Berrada, A. A comprehensive review on techno-economic assessment of hybrid energy storage systems integrated with renewable energy. J. Energy Storage 2024, 84, 111010. [Google Scholar] [CrossRef]
- Suwi, O.; Justo, J.J. Comprehensive discussions on energy storage devices: Modeling, control, stability analysis with renewable energy resources in microgrid and virtual power plants. In Modelling and Control Dynamics in Microgrid Systems with Renewable Energy Resources; Academic Press: Cambridge, MA, USA, 2024; pp. 139–177. [Google Scholar]
- Ji, W.; Hong, F.; Zhao, Y.; Liang, L.; Du, H.; Hao, J.; Fang, F.; Liu, J. Applications of flywheel energy storage system on load frequency regulation combined with various power generations: A review. Renew. Energy 2024, 223, 119975. [Google Scholar] [CrossRef]
- Wang, D.; Liu, N.; Chen, F.; Wang, Y.; Mao, J. Progress and prospects of energy storage technology research: Based on multidimensional comparison. J. Energy Storage 2024, 75, 109710. [Google Scholar] [CrossRef]
- Patil, R.; Janamala, V. Dandelion Algorithm for Optimal Location and Sizing of Battery Energy Storage Systems in Electrical Distribution Networks. In Modern Approaches in Machine Learning and Cognitive Science: A Walkthrough; Springer International Publishing: Cham, Switzerland, 2024; Volume 4, pp. 315–323. [Google Scholar]
- Sadeghian, O.; Safari, A. Net saving improvement of capacitor banks in power distribution systems by increasing daily size switching number: A comparative result analysis by artificial intelligence. J. Eng. 2024, 2024, e12357. [Google Scholar] [CrossRef]
- Abriz, A.F.; Ghavifekr, A.A.; Soltaninejad, M.; Tavana, A.; Safari, A.; Ziamanesh, S. Modified Cuckoo Optimization Algorithm for Frequency Regulation of Microgrids. In Proceedings of the 2023 8th International Conference on Technology and Energy Management (ICTEM), Babol, Iran, 8–9 February 2023; pp. 1–5. [Google Scholar]
- Safari, A.; Kharrati, H.; Rahimi, A. Multi-Term Electrical Load Forecasting of Smart Cities Using a New Hybrid Highly Accurate Neural Network-Based Predictive Model. Smart Grids Sustain. Energy 2023, 9, 8. [Google Scholar] [CrossRef]
- Dekaraja, B.; Saikia, L.C. Impact of energy storage and flexible alternating current transmission devices in combined voltage and frequency regulation of multiarea Multisource Interconnected Power System. Energy Storage 2022, 4, e317. [Google Scholar] [CrossRef]
- Nadeem, F.; Hussain, S.S.; Tiwari, P.K.; Goswami, A.K.; Ustun, T.S. Comparative review of energy storage systems, their roles, and impacts on future power systems. IEEE Access 2018, 7, 4555–4585. [Google Scholar] [CrossRef]
- Lucas, C.; Shahmirzadi, D.; Sheikholeslami, N. Introducing BELBIC: Brain emotional learning based intelligent controller. Intell. Autom. Soft Comput. 2004, 10, 11–21. [Google Scholar] [CrossRef]
- Oshnoei, A.; Sorouri, H.; Teodorescu, R.; Blaabjerg, F. An intelligent synchronous power control for grid-forming inverters based on brain emotional learning. IEEE Trans. Power Electron. 2023, 38, 12401–12405. [Google Scholar] [CrossRef]
- Daryabeigi, E.; Zarchi, H.A.; Markadeh, G.R.; Rahman, M.A.; Lucas, C. Implementation of emotional controller (BELBIC) for synchronous reluctance motor drive. In Proceedings of the 2011 IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, ON, Canada, 15–18 May 2011; IEEE: Niagara Falls, ON, Canada, 2011; pp. 1088–1093. [Google Scholar]
- Giernacki, W. Minimum Energy Control of Quadrotor UAV: Synthesis and Performance Analysis of Control System with Neurobiologically Inspired Intelligent Controller (BELBIC). Energies 2022, 15, 7566. [Google Scholar] [CrossRef]
- Sorouri, H.; Sedighizadeh, M.; Oshnoei, A.; Khezri, R. An intelligent adaptive control of DC–DC power buck converters. Int. J. Electr. Power Energy Syst. 2022, 141, 108099. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).