Abstract
The main goal of the paper is to present and study models of multi-agent systems for which the dynamics of the agents are described by a Caputo fractional derivative of variable order and a kernel that depends on an increasing function. Also, the order of the fractional derivative changes at update times. We study a case for which the exchanged information between agents occurs only at initially given update times. Two types of linear variable-order Caputo fractional models are studied. We consider both multi-agent systems without a leader and multi-agent systems with a leader. In the case of multi-agent systems without a leader, two types of models are studied. The main difference between the models is the fractional derivative describing the dynamics of agents. In the first one, a Caputo fractional derivative with respect to another function and with a continuous variable order is applied. In the second one, the applied fractional derivative changes its constant order at each update time. Mittag–Leffler stability via impulsive control is defined, and sufficient conditions are obtained. In the case of the presence of a leader in the multi-agent system, the dynamic of the agents is described by a Caputo fractional derivative with respect to an increasing function and with a constant order that changes at each update time. The leader-following consensus via impulsive control is defined, and sufficient conditions are derived. The theoretical results are illustrated with examples. We show with an example the leader’s influence on the consensus.
Keywords:
multi-agent systems; leader; consensus; Caputo fractional derivative with respect to another function; fractional derivative of variable order; impulsive control MSC:
34A34; 34A08; 34D20
1. Introduction
Recently, the dynamics of multi-agent systems have been successfully modeled by fractional derivatives, and many theoretical results have been obtained (see, for example, ref. [1] for consensuses of linear systems, ref. [2] for consensuses of nonlinear multi-agent system via event-triggered control, refs. [3,4,5] for leader-following consensuses for fractional multi-agent systems, ref. [6] for consensuses under fixed topology, and ref. [7] for the output feedback containment control problem for multi-agent systems with missing measurements).
Usually, continuous control is used to study the behavior of the agents in the model. But practically, it is hard to achieve continuous communication among agents. This leads to reasonable study of model situations wherein the agents exchange information only at so-called update times. A good tool in this case is to use impulsive control for modeling the situation. This type of model was studied in [8,9] for integer-order systems, in [10,11] for fractional-order systems, in [12] for randomly occurring update times, and in [13] for models with generalized proportional Caputo fractional derivatives.
Fractional operators in which the order is a function of certain variables have attracted attention due to their applied significance in various research areas. Samko and Ross [14] first proposed the concept of variable-order diffintegrals as well as some basic properties. The basic definitions of variable-order fractional diffintegrals and numerical approximations were given in [15]. Variable-fractional calculations provide an effective mathematical tool for modeling complex dynamic problems (see, for example, [16,17,18,19,20]). In [21], the authors showed that variable-order fractional derivatives can capture the dynamics of some systems more accurately. The main practical advantage of the variable order in fractional operators is that the order of derivative in neural networks can vary as a function of time or the system’s state (see [22]). In [23], a brief overview of papers about some models of neural networks with fractional derivatives of different orders is presented.
Note that there are many generalizations of classical fractional integrals and derivatives. The base of the generalization of the classical definitions is the type of kernel considered. In the case when the kernel is of the type , the fractional diffintegrals with respect to another function are defined (see, for example, [24]). Some of the advantages of fractional diffintegrals with respect other functions are that they keep the main properties of classical fractional ones. Also, this type of derivative, as shown in [24] for population models, can more accurately model processes using different kernels for the fractional operator. This type of fractional derivative is applied to differential equations and has been studied by several authors (see, for example, ref. [24] for the existence and uniqueness of the problem with the Caputo fractional derivative and ref. [25] for the Hilfer-type fractional derivative).
In this paper, we consider multi-agent linear dynamic systems with the Caputo fractional derivative with respect to another function and variable order. We study a multi-agent system in which the agents interact and exchange information instantaneously and only at initially given update times, i.e., the so-called impulsive control protocol. We consider systems both without a leader and with a leader. In both cases, we set up the appropriate impulsive model, define stability by Mittag–Leffler functions, and study the system.
Note that impulsive control is a powerful control method: in particular when an agent exchanges information instantaneously at discrete times. It has been applied and studied by several authors for various types of multi-agent systems: for example, in [26], the scaled consensus is investigated by using impulsive controls; in [26], the impulsive approach is used to study the semi-global consensus; in [27], the impulsive average-consensus with time-delays is considered; in [28], the exponential consensus is investigated in the case for which the impulses are generated by an event-triggered mechanism and are subjected to actuation delays.
In [13], a multi-agent linear system via impulsive control is considered, and the consensus is studied. The applied fractional derivative is less general than the fractional derivative with respect to another function, which is applied in this paper. In the present paper, we keep the idea about the impulsive protocol, but we generalize the model of [13] in several ways. First, we consider variable order for the fractional derivative. This leads to qualitative changes in the study. For the model without a leader, we consider two cases: the case with a fractional derivative of variable order and the case of a fractional derivative with piecewise constant orders, i.e., we study the situation when, at the initially given impulsive points, the agents interact, and also, their behavior and dynamics are changed. In the case of a system with a leader, we study only piecewise constant orders of the fractional derivatives. This is required because of the more complex interactions between agents. Second, to be more general, we apply a fractional derivative with a kernel of the type with an increasing differentiable function with a range . Also, from our results, several partial cases, such as the dynamics described by the classical Caputo fractional derivative, could be obtained, which is not possible from the ones in [13]. In this way, in this paper, we study a model describing a more general situation compared to that of [13].
The main contributions of the article to the field of multi-agent systems, particularly in terms of consensus and formation control, can be summarized as follows:
- -
- We provide two models for a multi-agent system without a leader in which the interaction between agents occurs only at update times. The dynamics in the models are described by a variable-order Caputo fractional derivative with respect to another function.
- -
- We provide a model for a multi-agent system with a leader in which the interaction between any agent and the leader occurs only at update times. The dynamics are described by a Caputo fractional derivative with respect to another function, for which the order is changed at any update time.
- -
- We define and study impulsive Mittag–Leffler stability via impulsive protocol and leader-following consensus via impulsive protocol for the corresponding models.
- -
- All sufficient conditions depend significantly on the impulsive control.
- -
- We provide an example that shows the influence of the impulsive control on a system.
Our paper is structured as follows:
- -
- In Section 2, we give an overview of the Caputo fractional calculus with respect to another function. We give the basic results that will be used in subsequent parts of the paper. Also, we present the basic definitions and results for the variable-order Caputo fractional derivative and discuss its application for modeling multi-agent systems.
- -
- In Section 3, based on the main definitions from the previous section, we set up models for two basic cases: multi-agent systems both without a leader and with a leader. In the case without a leader, in the multi-agent system, we consider two different types of models: one with variable time order of the fractional derivative and one with a piecewise constant order. In the case of the presence of a leader in the system, we consider only a piecewise constant variable order of the corresponding fractional derivative.
- -
- In Section 4, we obtain our main results. In the case of a multi-agent system without a leader we define impulsive Mittag–Leffler stability and obtain sufficient conditions. In the case of the presence of a leader in the system, we study the leader-following consensus. All theoretical results are illustrated with examples.
- -
- To summarize, we finish the paper with a conclusion.
2. Preliminary Notes and Results
We recall the basic definitions of fractional operators with respect to another function , which are often called -fractional integrals and derivatives. Let the kernel be with (if ) and for all
2.1. -Fractional Diffintegrals of Constant Order
We start with the definitions of a constant fractional order of the fractional integral and derivative for scalar functions.
Definition 1
([29]). Let and . Then a η-fractional integral of order μ is
Definition 2
([29]). Let and . Then a η-Caputo fractional derivative of order μ is
In the vector case , Definitions 1 and 2 can be generalized component-wise.
We give some results that are known from the literature that will be used in our further study.
Lemma 1
(Theorems 1 and 2 [30]). For and , we have
and
Lemma 2
(Lemma 1 [30]). For and , we have
Lemma 3
(Lemma 2 [30]). The scalar linear η-Caputo fractional initial value problem
with , has a solution
where is the Mittag–Leffler function of one parameter.
Consider the following initial value problem (IVP) for a linear system of fractional differential equations:
where , A is a constant matrix, and .
Definition 3
([31]). The Mittag–Leffler matrix function with one parameter is
where A is a square matrix.
Lemma 4.
The solution to the IVP (6) is
Proof.
The claim follows from Lemma 2 for . Indeed, we have
□
2.2. -Fractional Diffintegrals of Variable Order
There are several different definitions of variable-order (VO) fractional diffintegrals (see, for example, [21,32]). Note that all of the defined VO fractional diffintegrals coincide if the VO is replaced with a constant order. We provide only one of them, which is the one used the most in the literature.
Now, we generalize the fractional integral with a constant order (see p. 461 [30]) to one with a variable order.
Definition 4.
Let the function . Then the variable-order η-fractional integral of type I is
We generalize Definition 1 [30] for a constant order of a Caputo fractional derivative to a variable order.
Definition 5.
Let . Then the variable-order η-Caputo fractional derivative of type I of a function is defined by
In the case of , Definitions 4 and 5 reduce to the variable-order fractional integrals and fractional Caputo derivative defined and used in [14,33].
Remark 1.
Similar to that mentioned in [14] about VO fractional integrals and VO Caputo fractional derivatives, the VO fractional operators and are not inverses of each other.
In [14], the Marchaud fractional derivative (Sections 5 and 13 [34]) is generalized to a variable order.
Definition 6
([14]). Let and the function . Then the variable-order η-Caputo fractional derivative of type II is
Lemma 5.
Let and . Then
Proof.
Lemma 6.
Let and . Then,
where is the one-parametric Mittag–Leffler function of variable order, which is defined by
Proof.
From Equation (16) and Lemma 5, we have
□
Corollary 1.
Let and . Then the IVP
has a unique solution .
Remark 2.
Note we could not generalize the scalar case (18) to a vector case and obtain a solution for the case of a system as is done in the case of constant order (see Lemma 4).
Remark 3.
Let and . Then
and Lemma 6 and Corollary 1 are not applicable to the derivative .
Therefore, in the scalar case, Definition 6 about variable-order fractional derivatives is more suitable than Definition 5.
Remark 4.
According to Remark 1, it is difficult to obtain an equivalent integral presentation of the solution of the corresponding differential equation with fractional derivatives defined in Definition 5. To avoid this, we can apply a piecewise constant variable order in fractional differential equations. Let points be given. Let the variable-order be given by
where are constants.
Then, instead of the IVP for the variable-order fractional differential equation
we can consider IVP for the system of constant-order fractional differential equations
, with a solution defined by
The main advantage of this approach is that we can use the results for fractional derivatives with constant orders.
In this paper, we use the Euclidean norm of .
For a matrix , we use the spectral norm
where are the eigenvalues of , and is the transpose of a matrix B. Then, we have
3. Statement of the Problem
Let the sequence of points be such that , , with and where is the initial time.
We denote
Consider a multi-agent system of N agents with a scalar variable , and initial value .
3.1. Multi-Agent System without a Leader
Consider the case for which the agents exchange information among themselves only at update times . The controller updates of each agent occur instantaneously at times , and the control input is called an impulsive control protocol.
Consider the set of the numbers of all agents that influence agent i at update time :
Thus, the impulsive control protocol of agent i at time , , based on the information it receives from its neighboring agents, can be written
where the weights are elements of the matrix
In the case without a leader, since the dynamic of any agent between two update times is described by a scalar equation, we can use the variable order of a fractional derivative given in Definition 6 and a piecewise constant order (see Remark 4).
3.1.1. Model of Fractional Derivative with Variable Order
We apply the -fractional derivative of variable-order given by Definition 6 and Equation (10).
Since between two update times and , any agent i has information only about its own state, then the dynamics of agent i are described by
where , .
At each time , agent i updates its state variable according to the impulsive control protocol defined by (22).
3.1.2. Model of Fractional Derivative with Piecewise Constant Order
We apply the -fractional derivative of variable order given in Definition 5.
Let the order of the fractional derivative be a piecewise constant function defined by
where are constants.
We assume the dynamics of each agent between two update times defined by the fractional derivative .
3.2. Multi-Agent System with a Leader
Consider a multi-agent system with fixed topology and a leader with state variable .
Consider the case of an impulsive control protocol, i.e., any agent and the leader interact instantaneously only at the update times described by
where the impulsive protocol is
Between two update times and , the leader has no interactions with other agents, and the dynamics of any agent i are based only on interactions between itself and other agents. In this case, we apply a piecewise constant order of the Caputo fractional derivative (see Remarks 2 and 3). Let the variable-order of the Caputo fractional derivative be defined by (25). Then, the dynamics of the agents and the leader between two update times is described by
where the constants present the weights. Note iff agent j does not influence agent i.
Remark 5.
From the equation of the leader in system (30), it follows inductively that for .
Note the components of the vector are deeply connected with the impulsive control protocol; they present the amount of the instantaneous interactions between the corresponding agent and the leader at the update time.
4. Main Results for the Models of Multi-Agent Systems with Impulsive Control Protocol
4.1. Multi-Agent System without a Leader
As mentioned in Section 3.1, we consider two different models. For both of them, we define and study impulsive Mittag–Leffler stability.
4.1.1. Model of Fractional Derivative with Variable Order
We study model (24) with a variable-order .
Definition 7.
Theorem 1.
Proof.
Let . According to Corollary 1 with , , and , the solution to (24) is
Let . Again, according to Corollary 1 with , , and , the solution to (24) is given by
On account of the second equation of (24) and (34) at the update time , we have
Using (36) in (35) implies
for any and all .
By induction with respect to intervals, we obtain
for and all , where .
Therefore, the system (26) is impulsively Mittag–Leffler stable with and . □
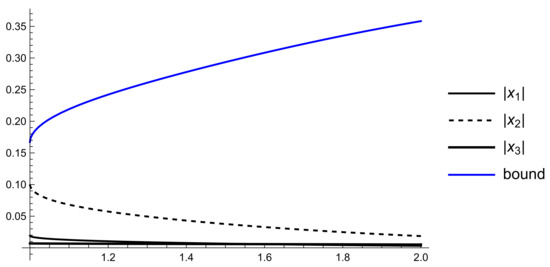
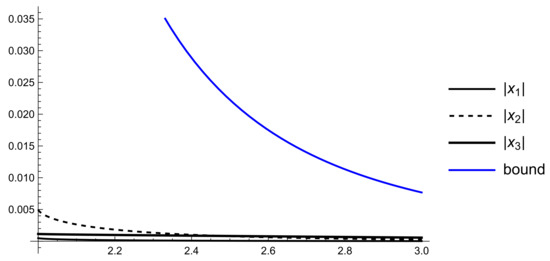
Example 1.
Consider the partial case of model (26) with i.e.,
The weighted connectivity matrix is
Then
i.e., and .
Then .
4.1.2. Model of Fractional Derivative with Piecewise Constant Order
We now define Mittag–Leffler-type stability in this case:
Definition 8.
Theorem 2.
Proof.
Let . According to Lemma 3 with , , and , the solution to (26) is given by
Let . Again, according to Lemma 3 with , , and , the solution to (26) is given by
On account of the second equation of (26) and (42) at the update time , we have
Using (44) in (43) implies
Apply induction and obtain
where .
Therefore, CFM (26) is impulsively Mittag–Leffler stable with and . □
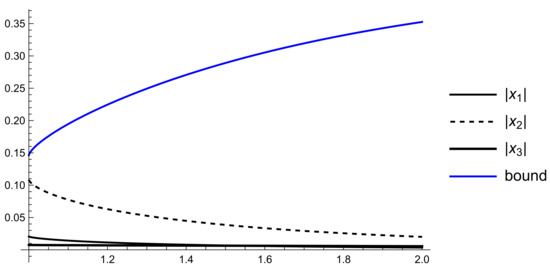
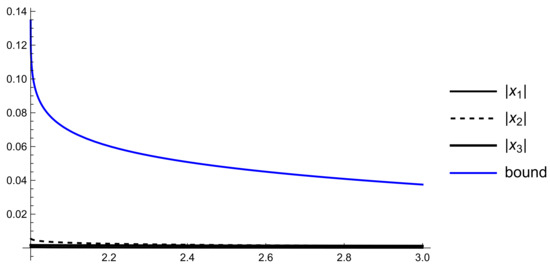
Example 2.
Consider the partial case of model (26) with , , i.e.,
The weighted connectivity matrix is
Then inequalities (39) hold, i.e., and .
Then .
According to Theorem 2, the model (47) is impulsively Mittag–Leffler stable, i.e.,
Remark 6.
Note that if a multi-agent model without a leader is impulsive Mittag–Leffler stable, then the norm of the state of any agent approaches zero over time.
Remark 7.
In the partial case and , the results of Theorems 1 and 2 coincide, and the result gives sufficient conditions for the model with a constant fractional derivative.
4.2. Multi-Agent System with a Leader
We obtain the explicit solution of the linear impulsive system (32).
Lemma 7.
Proof.
Let . By Lemma 4 with , , , we obtain
Therefore,
Let . Applying Lemma 4 with , , gives
By induction, applying Lemma 4 with , we get
□
Definition 9.
CFM (30) achieves leader-following consensus if for all .
Theorem 3.
Let the piecewise constant-order μ be defined by (25) and the number be such that the inequalities
hold, where
Then CFM (30) achieves the leader-following consensus.
Proof.
Example 3.
Let the piecewise constant order be given by
Consider the partial case of model (30) with
In this case , and
Then we get for all
According to Theorem 3, CFM (54) achieves a leader-following consensus, i.e.,
for .
Consider the case without impulsive control protocol, i.e., there is leader that interacts with the agents instantaneously at update times, i.e., consider the model
As a partial case of Lemma 7 with , the explicit solution to (55) is where . In this case, and we cannot apply Theorem 3 to conclude the consensus. Thus, the impulsive interaction of the leader can cause consensus in the multi-agent system.
Remark 8.
Note that in the partial case and or the studied models are reduced to the models with Caputo fractional derivatives, and the results of Theorems 1–3 give results for the classical fractional models.
5. Conclusions
Multi-agent systems are studied wherein the dynamics of the agents are modeled by fractional derivatives of Caputo type with variable order. To be more specific, we apply the Caputo fractional derivative with respect to another function. The main characteristic of the studied multi-agent systems is the impulsive control protocol, i.e., the information exchange between agents occurs instantaneously only at fixed update times. This leads to an impulsive model with a variable-order Caputo fractional derivative with respect to another function. We consider the case without a leader as well as the case with a leader. In the case without leader, we define impulsive Mittag–Leffler stability and study it. In the case with a leader in the system, we obtain sufficient conditions for leader-following consensus via impulsive control based on the leader’s influence. The theoretical results are illustrated with some examples. Note the obtained results for the considered fractional impulsive differential equations could be additionally applied to study different types of models.
Author Contributions
R.P.A., S.H. and D.O.; methodology, R.P.A., S.H. and D.O.; formal analysis, R.P.A., S.H. and D.O.; investigation, R.P.A., S.H. and D.O.; writing—original draft preparation, R.P.A., S.H. and D.O.; writing—review and editing, R.P.A., S.H. and D.O. All authors have read and agreed to the published version of the manuscript.
Funding
S.H. is partially supported by the Bulgarian National Science Fund under project KP-06-PN62/1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Song, C.; Cao, J. Consensus of fractional-order linear systems. In Proceedings of the 2013 9-th Asian Control Conference (ASCC), Istanbul, Turkey, 23–26 June 2013; pp. 1–4. [Google Scholar]
- Wang, F.; Yang, Y. On leaderless consensus of fractional-order nonlinear multi-agent systems via event-triggered control. Nonlinear Anal. Model. Control 2019, 24, 353–367. [Google Scholar] [CrossRef]
- Almeida, R.; Girejko, E.; Hristova, S.; Malinowska, A.B. Leader-following consensus for fractional mul-ti-agent systems. Adv. Differ. Equ. 2019, 2019, 301. [Google Scholar] [CrossRef]
- Ren, G.; Yu, Y.; Zhang, S. Leader-following consensus of fractional nonlinear multiagent systems. Math. Probl. Eng. 2015, 8, 919757. [Google Scholar] [CrossRef]
- Schmeidel, E. The existence of consensus of a leader-following problem with Caputo fractional derivative. Opusc. Math. 2019, 39, 77–89. [Google Scholar] [CrossRef]
- Yu, Z.; Jiang, H.; Hu, C. Leader-following consensus of fractional-order multi-agent systems under fixed topology. Neurocomputing 2015, 149, 613–620. [Google Scholar] [CrossRef]
- Parivallal, A.; Yun, S.; Jung, Y.M. Hybrid-Triggered Output Feedback Containment Control for Multi-Agent Systems with Missing Measurements. IEEE Trans. Signal Inf. Process. Netw. 2024, 10, 108–118. [Google Scholar] [CrossRef]
- Almeida, J.; Silvestre, C.; Pascoal, A.M. Continuous-time consensus with discrete-time communications. Syst. Control Lett. 2012, 61, 788–796. [Google Scholar] [CrossRef]
- Jiang, H.; Yu, J.; Zhou, C. Consensus of multi-agent linear dynamic systems via impulsive control protocols. Int. J. Syst. Sci. 2011, 42, 967–976. [Google Scholar] [CrossRef]
- Wang, F.; Yang, Y. Leader-following exponential consensus of fractional order nonlinear multi-agents system with hybrid time-varying delay: A heterogeneous impulsive method. Phys. A 2017, 482, 158–172. [Google Scholar] [CrossRef]
- Yu, Z.; Jiang, H.; Hu, C.; Yu, J. Necessary and sufficient condi tions for consensus of fractional-order multiagent systems via sampled-data control. IEEE Trans. Cybern. 2017, 47, 1892–1901. [Google Scholar] [CrossRef]
- Almeida, R.; Girejko, E.; Hristova, S.; Malinowska, A.B. On leader-following consensus in multi-agent systems with discrete updates at random times. Entropy 2020, 22, 650. [Google Scholar] [CrossRef] [PubMed]
- Bohner, M.; Hristova, S.; Malinowska, A.B.; Morgado, M.L.; Almeida, R. A generalized proportional Caputo fractional model of multi-agent linear dynamic systems via impulsive control protocol. Commun. Nonlinear Sci. Numer. Simul. 2022, 115, 106756. [Google Scholar] [CrossRef]
- Samko, S.G.; Ross, B. Integration and differentiation to a variable fractional order. Integral Transform. Spec. Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Tavares, D.; Almeida, R.; Torres, D.F.M. Caputo derivatives of fractional variable order: Numerical approximations. Commun. Nonlinear Sci. Numer. Simul. 2016, 35, 69–87. [Google Scholar] [CrossRef]
- Coimbra, C.F.M. Mechanics with variable-order differential operators. Ann. Phys. 2003, 12, 692–703. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, W.; Chen, Y.Q. Variable-order fractional differential operators in anomalous diffusion modeling. Phys. A 2009, 388, 4586–4592. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, W.; Wei, H.; Chen, Y.Q. A comparative study of constant order and variable-order fractional models in characterizing memory property of systems. Eur. Phys. J. Spec. 2011, 193, 185–192. [Google Scholar] [CrossRef]
- Alsaade, F.W.; Al-zahrani, M.S.; Yao, Q.; Jahanshahi, H.A. Model-free finite-time control technique for synchronization of variable-order fractional Hopfield-like neural network. Fractal Fract. 2023, 7, 349. [Google Scholar] [CrossRef]
- Din, A.; Li, Y.; Yusuf, A.; Liu, J.; Aly, A.A. Impact of information intervention on stochastic hepatitis B model and its variable-order fractional network. Eur. Phys. J. Spec. Top. 2022, 231, 1859–1873. [Google Scholar] [CrossRef]
- Sun, H.G.; Chang, A.; Zhang, Y.; Chen, W. A review of variable order fractional differential equations: Mathematical foundations, physical models, numerical methods and applications. Fract. Calc. Appl. Anal. 2019, 22, 27–59. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Nguyen, T.G.; Fathurrochman, I.; Sadat, R.; Ali, M.R. Applications of neural networks for the novel designed of nonlinear fractional seventh order singular system. Eur. Phys. J. Spéc. Top. 2022, 231, 1831–1845. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Castillo, O. Application of variable-order fractional calculus in neural net-works: Where do we stand? Eur. Phys. J. Spec. Top. 2022, 231, 1753–1756. [Google Scholar] [CrossRef]
- Almeida, R.; Malinowska, A.; Monteiro, M.T. Fractional differential equations with a Caputo derivative with respect to a kernel function and their applications. Math. Meth. Appl. Sci. 2018, 41, 336–352. [Google Scholar] [CrossRef]
- Kucche, K.D.; Mali, A.D.; Sousa, J.V. Theory of nonlinear Ψ-Hilfer fractional differential equations. arXiv 2018, arXiv:1808.01608. [Google Scholar]
- Donganont, M.; Liu, X. Scaled consensus problems of multi agent systems via impulsive protocols. Appl. Math. Modell. 2023, 116, 532–546. [Google Scholar] [CrossRef]
- Wei, L.; Chen, W.-H.; Luo, S.; Huang, G. Impulsive average-consensus of multi-agent systems with time-delays. J. Frankl. Inst. 2022, 359, 1544–1568. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, S. Exponential Consensus of Multi-Agent Systems under Event-Triggered Impulsive Control with Actuation Delays. Entropy 2023, 25, 877. [Google Scholar] [CrossRef]
- Almeida, R. Functional Differential Equations Involving the Ψ-Caputo Fractional Derivative. Fractal Fract. 2020, 4, 29. [Google Scholar] [CrossRef]
- Almeida, R. A Caputo fractional derivative of a function with respect to another function. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 460–481. [Google Scholar] [CrossRef]
- Miller, K.S.; Bertram, R. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Zhang, S.; Wang, J.; Hu, L. On definition of solution of initial value problem for fractional differential equation of variable order. AIMS Math. 2021, 6, 6845–6867. [Google Scholar] [CrossRef]
- Samko, S.G. Fractional integration and differentiation of variable order. Anal. Math. 1995, 21, 213–236. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives (Theory and Applications); Gordon & Breach Sci. Publ.: New York, NY, USA, 1992. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).