Constrained State Regulation Problem of Descriptor Fractional-Order Linear Continuous-Time Systems

Abstract

This paper deals with the constrained state regulation problem (CSRP) of descriptor fractional-order linear continuous-time systems (DFOLCS) with order $0<\alpha <1$. The objective is to establish the existence of conditions for a linear feedback control law within state constraints and to propose a method for solving the CSRP of DFOLCS. First, based on the decomposition and separation method and coordinate transformation, the DFOLCS can be transformed into an equivalent fractional-order reduced system; hence, the CSRP of the DFOLCS is equivalent to the CSRP of the reduced system. By means of positive invariant sets theory, Lyapunov stability theory, and some mathematical techniques, necessary and sufficient conditions for the polyhedral positive invariant set of the equivalent reduced system are presented. Models and corresponding algorithms for solving the CSRP of a linear feedback controller are also presented by the obtained conditions. Under the condition that the resulting closed system is positive, the given model of the CSRP in this paper for the DFOLCS is formulated as nonlinear programming with a linear objective function and quadratic mixed constraints. Two numerical examples illustrate the proposed method.

1. Introduction

Descriptor systems can be considered a powerful modeling tool since they can describe processes governed by differential and algebraic equations [1]. They play an important role in the field of system control theory because of their extensive practical background, such as in chemistry, robotics, and circuit systems [2,3,4]. CSRP is a basic problem in control systems in that there are always hard constraints on states and control inputs in practical engineering problems. When addressing constraints problems, an effective and generic approach relies on the invariance of polyhedral sets, an aspect thoroughly explored in [5,6,7,8,9]. In [10,11], the CSRP of descriptor integer order linear continuous-time systems has been discussed by reformulating the descriptor systems into equivalent state-space systems, and solutions are obtained by using the invariant sets methods.

Compared to integer-order differential equations, fractional-order differential equations can more accurately describe system behavior, especially in systems with memory effects and long-range dependencies. Due to the memory effects of fractional-order derivatives, they can better reflect the influence of the system’s historical states on its current state. Therefore, the theory and methods of fractional-order systems have wide applications in various fields such as control theory, signal processing, biomedical engineering, economics, physics, and more [12,13]. Researchers have conducted extensive studies on fractional-order systems, including stability [14], synchronization [15], and state estimation [16]. Moreover, in [17,18,19,20], the basic problems of stability and reachability of fractional-order positive systems are studied. Descriptor systems provide a more precise description of system non-linearity and complexity, thus offering better adaptability and performance in handling complex real-world problems. These advantages give descriptor systems an important position and promising prospects in scientific research and engineering applications. Hence, there are also many research results on descriptor fractional-order systems. The basic theory and application of the descriptor fractional-order system are studied in [21,22,23]. However, there are few studies on the CSRP of descriptor fractional-order systems. For example, in [24], a class of decentralized controllers for descriptor fractional-order positive systems stabilization is designed, and the solution of the controller gain matrix is given. However, state and control constraints were not considered in the above research. In practical engineering problems with state constraints, the stability of the system is a premise condition of the normal operation of the control system [25,26]. Because of the particularity of fractional calculus, methods of the integer order system cannot be directly applied to the fractional-order system with state constraints, which makes it necessary to study the constrained state regulation of DFOLCS.

Based on above reasons, the purpose of this work is to design the linear state feedback controller for the DFOLCS. We address the CSRP of DFOLCS by virtue of positively invariant set (PIS) theory in this paper. The necessary and sufficient conditions for the existence of a polyhedral PIS of the equivalent reduced system is presented, and models and corresponding algorithms for solving the CSRP of a linear feedback controller are also proposed by the obtained conditions. Under mild conditions where the resulting closed system is positive, the given model of the CSRP in this paper for the DFOLCS is formulated as nonlinear programming with a linear objective function and quadratic mixed constraints. Numerical examples illustrate the proposed method. The contributions highlighted in this paper are as follows:

(1) An equivalent fractional-order reduced system is obtained via the decomposition and separation method and coordinate transformation.

(2) A necessary and sufficient condition for the existence of polyhedral PIS in the equivalent reduced system is proposed based on PISs theory, Lyapunov stability theory, and some mathematical techniques.

(3) Two-controller design algorithm for the CSRP of generic DFOLCS is presented. Under the condition that the reduced system is positive, a nonlinear programming model is proposed, which is easily performed from a point of computational view.

The remainder of the paper is organized as following: Section 2 presents some preliminaries and formulation of the CSRP for the DFOLCS. In Section 3, an equivalent reduced system is derived by using coordinate transformation, the necessary and sufficient condition for the positive invariance of polyhedron for DFOLCS is proposed. Section 4 proposes two models and corresponding algorithms of CSRP. Section 5 concludes with illustrative examples. The paper ends with concluding remarks in Section 6.

Notations: $R^n$, $R_{+}^n$, and $R^{n\times n}$ represent the n dimensional space of real vectors, the n dimensional space of positive real vectors, and the space of $n\times n$ matrices with real entries, respectively. C is the complex number set and for any $z\in C$; $Re\left(z\right)$ denotes the real part of complex number z. $I_q$ and $I_{\left(i\right)}$ represent the $q\times q$ identity matrix and the $i^{th}$ row vector of the identity matrix $I_q$, respectively. $A_{\left(i\right)}$ denotes the $i^{th}$ row vector of matrix A. For $\sigma \in R_{+}^r$ means all components of $\sigma$ are nonnegative. $rank\left(E\right)$ is the rank of matrix E. $M_n$ is Metzler matrix with off-diagonal elements are nonnegative. $P\succ 0(P\prec 0)$ means that P is positive definite (negative definite).

2. Preliminaries and Problem Formulation

2.1. Descriptor Fractional-Order Linear Continuous-Time Systems

Consider the DFOLCS

$$\left\{\begin{array}{c}E{}_0{}^{c}D_t^{\alpha }\eta \left(t\right)=A\eta \left(t\right)+Bu\left(t\right),t>0,\hfill \\ \eta \left(t\right)={\eta }_0,-\infty <t\le 0,\hfill \end{array}\right.$$

(1)

and the standard fractional-order linear continuous-time systems (SFOLCS)

$$\left\{\begin{array}{c}{}_0{}^{c}D_t^{\alpha }\eta \left(t\right)=A\eta \left(t\right)+Bu\left(t\right),t>0,\hfill \\ \eta \left(t\right)={\eta }_0,-\infty <t\le 0,\hfill \end{array}\right.$$

(2)

where $0<\alpha <1$, $\eta \left(0\right)={\eta }_0$, $\eta \left(t\right)\in R^n$, $u\left(t\right)\in R^m$ is the state and control input, $E\in R^{n\times n}$ and $rank\left(E\right)=n_1<n$, i.e., E is a rank-deficient matri, $A\in R^{n\times n}$, $B\in R^{n\times m}$. The SFOLCS (2) (or DFOLCS (1)) is called (internally) positive if $\eta \left(t\right)\in R_{+}^n,t\ge 0$ for all initial conditions $\eta \left(0\right)\in R_{+}^n$ and every $u\left(t\right)\in R_{+}^m,t\ge 0$.

Definition 1

([27]). The Caputo fractional-order derivative ${}_0{}^{c}D_t^{\alpha }\eta \left(t\right)$ is defined as

$${}_0{}^{c}D_t^{\alpha }\eta \left(t\right)=\frac{1}{\Gamma (1-\alpha )}({\int }_0^t\frac{\frac{d\eta \left(\tau \right)}{d\tau }}{{(t-\tau )}^{\alpha }}d\tau ),$$

where $0<\alpha <1$ and

$$\Gamma \left(z\right)={\int }_0^{\infty }{e}^{-t}{t}^{z-1}dt,Re\left(z\right)\in R_{+}.$$

The initial information about $\eta \left(t\right)$ lacks adequacy for forecasting the system’s future behavior. Consequently, the depiction of Equation (2) does not precisely qualify as a state-space representation and is termed a “pseudo state-space”. Assuming $\eta \left(t\right)=\phi \left(t\right)$ for $t\in (-\infty ,0],$ the solution to system (2) is expressed as:

$$\eta \left(t\right)=-{\int }_0^t{e}_{\alpha }^{A(t-\tau )}\psi (\eta ,\alpha ,-\infty ,0,\tau )d\tau .$$

If system (2) with constant history, in other words, $\eta \left(t\right)={\eta }_0$ for $t\in (-\infty ,0]$, the initialization function is given by

$$\psi (\eta ,\alpha ,-\infty ,0,\tau )=-\frac{{\eta }_0{t}^{-\alpha }}{\Gamma (1-\alpha )},$$

thus, one has

$$\eta \left(t\right)=-{\int }_0^t{e}_{\alpha }^{A(t-\tau )}(-\frac{{\eta }_0{t}^{-\alpha }}{\Gamma (1-\alpha )})d\tau =E_{\alpha }\left(A{t}^{\alpha }\right){\eta }_0=\sum _{k=0}^{\infty }\frac{{\left(A{t}^{\alpha }\right)}^k}{\Gamma (k\alpha +1)}{\eta }_0,$$

where $E_{\alpha }(·)$ is the Mittag-Leffler function, which is defined as follows: $E_{\alpha }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (k\alpha +1)},\alpha \in R_{+},z\in C$.

Definition 2.

Set P is the PIS of the dynamical system (1) (or (2)) if and only if ${\eta }_0\in P⟹\eta (t;t_0,{\eta }_0)\in P,(t\ge t_0)$ where $\eta (t;t_0,{\eta }_0)$ is the trajectory of $(t_0,{\eta }_0).$

2.2. Problem Formulation

For DFOLCS (1), the state constraints polyhedral set is defined by

$$\Omega (G,\underline{\sigma },\overline{\sigma })=\left\{\eta \left(t\right)\in R_{+}^n:\underline{\sigma }\le G\eta \left(t\right)\le \overline{\sigma }\right\},$$

(3)

where $G\in R^{r\times n}$ with $rank\left(G\right)=r,$ and $\underline{\sigma }\in R_{+}^r,\overline{\sigma }\in R_{+}^r.$

The CSRP of DFOLCS (1) is to be studied. The objective is to find controller $u\left(t\right)=K\eta \left(t\right)$ such that for all initial states ${\eta }_0\in \Omega (G,\underline{\sigma },\overline{\sigma })$, the corresponding trajectory $\eta \left(t\right)$ will be asymptotically stable to the origin without violating the constraints (3).

3. Positively Invariant Conditions for Equivalent Reduced Systems

Motivated by the idea of the decomposition and separation method in integer order descriptor systems, we deal with the CSRP of DFOLCS (1) in the same way.

3.1. Equivalent Reduced System

Throughout the paper, we investigate DFOLCS (1) and have the following assumption:

(A): system (1) is regular, which means that there exists at least some $s\in C$ such that the determinant $det(sE-A)\ne 0$.

The regularity assumption (A) of system (1) guarantees the existence and uniqueness of the solution to system (1) [28].

Under the assumptions (A), for the DFOLCS (1), there must exist two nonsingular matrices $P_1\in R^{n\times n}$ and $P_2\in R^{n\times n}$ ($P_1$ and $P_2$ can be obtained by preforming the elementary row and column transformations on the identity matrix $I_n$) such that

$$P_{1}E{P}_2\left(P_2^{-1}{}_0{}^{c}D_t^{\alpha }\eta \left(t\right)\right)=P_{1}A{P}_2\left(P_2^{-1}\eta \left(t\right)\right)+P_{1}Bu\left(t\right),$$

(4)

where

$P_{1}E{P}_2=\left(\begin{array}{cc}{I}_{n_1}& 0\\ 0& 0\end{array}\right)$, $\tilde{A}=P_{1}A{P}_2=\left(\begin{array}{cc}{A}_1& A_2\\ A_3& A_4\end{array}\right)$, $\tilde{B}=P_{1}B=\left(\begin{array}{c}{\tilde{B}}_1\\ {\tilde{B}}_2\end{array}\right),$

${\tilde{B}}_1\in R^{n_1\times m},{\tilde{B}}_2\in R^{n_2\times m}$, $n_2=n-n_1.$

Define the new state vector $\tilde{\eta }\left(t\right)=P_2^{-1}\eta \left(t\right)=\left(\begin{array}{c}{\tilde{\eta }}_1\left(t\right)\\ {\tilde{\eta }}_2\left(t\right)\end{array}\right),{\tilde{\eta }}_1\left(t\right)\in R_{+}^{n_1},$

${\tilde{\eta }}_2\left(t\right)\in R_{+}^{n_2}.$ We have

$$\begin{array}{cc}\hfill {}_0{}^{c}D_t^{\alpha }{\tilde{\eta }}_1\left(t\right)& =A_1{\tilde{\eta }}_1\left(t\right)+A_2{\tilde{\eta }}_2\left(t\right)+{\tilde{B}}_{1}u\left(t\right),\hfill \\ \hfill 0& =A_3{\tilde{\eta }}_1\left(t\right)+A_4{\tilde{\eta }}_2\left(t\right)+{\tilde{B}}_{2}u\left(t\right).\hfill \end{array}$$

Since the DFOLCS (1) is not necessarily impulse-free, $A_4$ is not necessarily invertible. The impulse elimination algorithm based on dynamic decomposition is presented below.

Step 1: Perform decomposition procedure (4) for the DFOLCS (1).

Step 2: Find a matrix $K_{12}$ satisfying $det(A_4+{\tilde{B}}_2{K}_{12})\ne 0$, suppose $A_4+{\tilde{B}}_2{K}_{12}=I_{n-rank\left(E\right)}$. Under the assumption of impulse controllability, $rank\left[A_4{\tilde{B}}_2\right]=n-rank\left(E\right)$, such a $K_{12}$ is solvable.

Step 3: Find a $K_{11}\in R^{m\times n_1}$ makes $K_1=\left[K_{11}{K}_{12}\right].$

Remark 1.

The impulsive behavior that appears in the response of the DFOLCS is due to the singularity of matrix $A_4$. If the descriptor system is completely controllable (at its finite and infinite modes), the matrix $\left(A_4{\tilde{B}}_2\right)$ has a full row rank, and there exists a state feedback law such that the closed loop system does not exhibit impulsive modes and has pre-specified finite modes [10].

By the impulse elimination algorithm based on dynamic decomposition and Remark 1, system (1) is completely controllable if there exists a feedback control

$$u\left(t\right)=K\eta \left(t\right)=K_1\eta \left(t\right)+v\left(t\right)=K_1\eta \left(t\right)+K_2{\tilde{\eta }}_1\left(t\right),$$

(5)

where $K_1=\left[K_{11}{K}_{12}\right]$ such that the matrix $A_4+{\tilde{B}}_2{K}_{12}$ is invertible and $K_2{\tilde{\eta }}_1\left(t\right)$ is the feedback control law for the reduced system. The aim of this step is to separate the feedback control law of the reduced system. By substituting $u\left(t\right)$ in system (1) with (5), we have:

$$\begin{array}{ccc}E{}_0{}^{c}D_t^{\alpha }\eta \left(t\right)& =\hfill & (A+B{K}_1)\eta \left(t\right)+Bv\left(t\right)\hfill \\ & =\hfill & (A+B{K}_1)\eta \left(t\right)+B{K}_2{\tilde{\eta }}_1\left(t\right),\hfill \end{array}$$

(6)

from (4), there always exists two nonsingular matrices $P_1\in R^{n\times n}$ and $P_2\in R^{n\times n}$ such that

$$\begin{array}{c}{P}_{1}E{P}_2\left(P_2^{-1}{}_0{}^{c}D_t^{\alpha }\eta \left(t\right)\right)=P_1(A+B{K}_1)P_2\left(P_2^{-1}\eta \left(t\right)\right)+P_{1}B{K}_2{\tilde{\eta }}_1\left(t\right).\hfill \end{array}$$

(7)

Let $P_2^{-1}\eta \left(t\right)=\left(\begin{array}{c}{\tilde{\eta }}_1\left(t\right)\hfill \\ {\tilde{\eta }}_2\left(t\right)\hfill \end{array}\right),$ coordinate transformation

$$\eta \left(t\right)=P_2\left(\begin{array}{c}{\tilde{\eta }}_1\left(t\right)\hfill \\ {\tilde{\eta }}_2\left(t\right)\hfill \end{array}\right),{\tilde{\eta }}_1\left(t\right)\in R_{+}^{n_1},{\tilde{\eta }}_2\left(t\right)\in R_{+}^{n_2},$$

(8)

thus,

$$\begin{array}{cc}\hfill & P_{1}E{P}_2(P_2^{-1}{}_0{}^{c}D_t^{\alpha }{P}_2\left(\begin{array}{c}{\tilde{\eta }}_1\left(t\right)\hfill \\ {\tilde{\eta }}_2\left(t\right)\hfill \end{array}\right))\hfill \\ \hfill =& P_1(A+B{K}_1)P_2(P_2^{-1}{P}_2\left(\begin{array}{c}{\tilde{\eta }}_1\left(t\right)\hfill \\ {\tilde{\eta }}_2\left(t\right)\hfill \end{array}\right))+\left(\begin{array}{c}{\tilde{B}}_1\hfill \\ {\tilde{B}}_2\hfill \end{array}\right)K_2{\tilde{\eta }}_1\left(t\right)\hfill \\ \hfill =& P_1(A+B{K}_1)P_2\left(\begin{array}{c}{\tilde{\eta }}_1\left(t\right)\hfill \\ {\tilde{\eta }}_2\left(t\right)\hfill \end{array}\right)+\left(\begin{array}{c}{\tilde{B}}_1\hfill \\ {\tilde{B}}_2\hfill \end{array}\right)K_2{\tilde{\eta }}_1\left(t\right).\hfill \end{array}$$

(9)

From Remark 1 and assumptions A, system (6) is regular and does not exhibit impulsive modes if there exist two nonsingular matrices $P_1$ and $P_2$($P_1$ and $P_2$ can be obtained by performing the elementary row and column transformations on the identity matrix $I_n$), such that [28]:

$$\begin{array}{c}{P}_{1}E{P}_2=\left(\begin{array}{cc}{I}_{n_1}& 0\\ 0& 0\end{array}\right),P_1(A+B{K}_1)P_2=\left(\begin{array}{cc}{A}_1& 0\\ 0& I_{n_2}\end{array}\right),P_{1}B=\left(\begin{array}{c}{\tilde{B}}_1\\ {\tilde{B}}_2\end{array}\right),\hfill \end{array}$$

(10)

substituting (9) with (10), the system (6) is transformed into

$$\begin{array}{c}\left(\begin{array}{cc}{I}_{n_1}& 0\\ 0& 0\end{array}\right)\left(\begin{array}{c}{}_0{}^{c}D_t^{\alpha }{\tilde{\eta }}_1\left(t\right)\hfill \\ {}_0{}^{c}D_t^{\alpha }{\tilde{\eta }}_2\left(t\right)\hfill \end{array}\right)=\left(\begin{array}{cc}{A}_1& 0\\ 0& I_{n_2}\end{array}\right)\left(\begin{array}{c}{\tilde{\eta }}_1\left(t\right)\hfill \\ {\tilde{\eta }}_2\left(t\right)\hfill \end{array}\right)+\left(\begin{array}{c}{\tilde{B}}_1\hfill \\ {\tilde{B}}_2\hfill \end{array}\right)K_2{\tilde{\eta }}_1\left(t\right),\hfill \end{array}$$

(11)

the DFOLCS (1) is transformed into

$$\begin{array}{c}\hfill {}_0{}^{c}D_t^{\alpha }{\tilde{\eta }}_1\left(t\right)=A_1{\tilde{\eta }}_1\left(t\right)+{\tilde{B}}_1{K}_2{\tilde{\eta }}_1\left(t\right),\end{array}$$

(12)

$$\begin{array}{c}\hfill 0={\tilde{\eta }}_2\left(t\right)+{\tilde{B}}_2{K}_2{\tilde{\eta }}_1\left(t\right).\end{array}$$

(13)

By choosing the state feedback law $v\left(t\right)=K_2{\tilde{\eta }}_1$ with $K_2\in R^{m\times n_1}$, system (12) is an equivalent reduced system:

$${}_0{}^{c}D_t^{\alpha }{\tilde{\eta }}_1\left(t\right)=(A_1+{\tilde{B}}_1{K}_2){\tilde{\eta }}_1\left(t\right).$$

(14)

Lemma 1

([18]). The equivalent reduced system (14) is positive if and only if $(A_1+{\tilde{B}}_1{K}_2)\in M_{n_1}$.

Proof. 

(Sufficiency) Obviously, $\eta \left(t\right)>0$ when $A_1+{\tilde{B}}_1{K}_2$ is a Metzler matrix, and the solution of Equation (14), i.e., $\eta \left(t\right)={\displaystyle \sum _{k=0}^{\infty }}\frac{{\left[(A_1+{\tilde{B}}_1{K}_2)t^{\alpha }\right]}^k}{\Gamma (k\alpha +1)}{\eta }_0>0,$ for ${\eta }_0>0$. Thus, we obtain that system (14) is a positive matrix. □

(Necessity) For ${\eta }_0=e_i$ (the i-th column of the identity matrix $I_N$), the trajectory of the system does not leave the orthant $R_{+}^n$ only if ${\eta }_0^{\alpha }=(A_1+{\tilde{B}}_1{K}_2)e_i>0$, which implies ${(A_1+{\tilde{B}}_1{K}_2)}_{ij}>0$ for $i\ne j$. The matrix $A_1+{\tilde{B}}_1{K}_2$ has to be a Metzler matrix.

From (8), (3) can be rewritten as:

$$\begin{array}{c}\Omega (\overline{G},\underline{\sigma },\overline{\sigma })=\left\{\begin{array}{c}\left(\begin{array}{c}{\tilde{\eta }}_1\left(t\right)\hfill \\ {\tilde{\eta }}_2\left(t\right)\hfill \end{array}\right)\in R_{+}^n:\underline{\sigma }\le G{P}_2\left(\begin{array}{c}{\tilde{\eta }}_1\left(t\right)\hfill \\ {\tilde{\eta }}_2\left(t\right)\hfill \end{array}\right)\le \overline{\sigma }\hfill \end{array}\right\},\hfill \end{array}$$

(15)

from (13), ${\tilde{\eta }}_2\left(t\right)=-{\tilde{B}}_{2}v\left(t\right)$, by choosing the state feedback control $v\left(t\right)=K_2{\tilde{\eta }}_1\left(t\right)$ with $K_2=R^{m\times n_1},$ we have

$$\Omega (\overline{G},\underline{\sigma },\overline{\sigma })=\left\{\begin{array}{c}{\tilde{\eta }}_1\left(t\right):\underline{\sigma }\le G{P}_2\left(\begin{array}{c}{I}_{n_1}\\ -{\tilde{B}}_2{K}_2\end{array}\right){\tilde{\eta }}_1\left(t\right)\le \overline{\sigma }\hfill \\ {\tilde{\eta }}_2\left(t\right):{\tilde{\eta }}_2=-{\tilde{B}}_2{K}_2{\tilde{\eta }}_1\left(t\right)\hfill \end{array}\right\},$$

and $\overline{G}=G{P}_2\left(\begin{array}{c}{I}_{n_1}\\ -{\tilde{B}}_2{K}_2\end{array}\right)$, the polyhedral set (3) becomes the following form:

$$\Omega (\overline{G},\underline{\sigma },\overline{\sigma })=\left\{\begin{array}{c}{\tilde{\eta }}_1\left(t\right)\in R_{+}^{n_1}:\underline{\sigma }\le \overline{G}{\tilde{\eta }}_1\le \overline{\sigma }\hfill \\ {\tilde{\eta }}_2\left(t\right)\in R_{+}^{n_2}:{\tilde{\eta }}_2=-{\tilde{B}}_{2}v\left(t\right)\hfill \end{array}\right\},$$

(16)

Hence, a consequence of the above result is the following Proposition:

Proposition 1.

The polyhedral set $\Omega (G,\underline{\sigma },\overline{\sigma })$ is PIS of DFOLCS (1) if and only if the polyhedral set $\Omega (\overline{G},\underline{\sigma },\overline{\sigma })$ is PIS of the reduced system (14).

Proof. 

Assume that $\Omega (G,\underline{\sigma },\overline{\sigma })$ is PIS of DFOLCS (1); we have $\underline{\sigma }\le G{\eta }_0\le \overline{\sigma }⟹\underline{\sigma }\le G\eta \left(t\right)\le \overline{\sigma }$; the polyhedral set $\Omega (\overline{G},\underline{\sigma },\overline{\sigma })$ is PIS of the reduced system (14), and we have $\underline{\sigma }\le \overline{G}{\tilde{\eta }}_1\left(0\right)\le \overline{\sigma }⟹\underline{\sigma }\le \overline{G}{\tilde{\eta }}_1\left(t\right)\le \overline{\sigma }$. □

By lemma 1 in [10], $\underline{\sigma }\le G{\eta }_0\le \overline{\sigma }⟹\underline{\sigma }\le G\eta \left(t\right)\le \overline{\sigma }$ if and only if $\underline{\sigma }\le \overline{G}{\tilde{\eta }}_1\left(0\right)\le \overline{\sigma }⟹\underline{\sigma }\le \overline{G}{\tilde{\eta }}_1\left(t\right)\le \overline{\sigma }$.

Next, we provide the necessary and sufficient condition for the fractional-order polyhedral set to be a PIS.

3.2. Positive Invariance of Fractional Order Polyhedral Sets

Let $\overline{A}=A_1+{\tilde{B}}_1{K}_2,$ a condition that the polyhedron is PISs of the equivalent reduced system (14) will be discussed in the sequel.

Proposition 2

([29,30]). (P1): Hypothetical existence of Lyapunov function $V\left({\tilde{\eta }}_1\left(t\right)\right)$ and class-κ functions ${\beta }_i,i=1,2,3$ satisfy:

$$\left\{\begin{array}{c}{\beta }_1(\Vert {\tilde{\eta }}_1\left(t\right)\Vert )\le V\left({\tilde{\eta }}_1\left(t\right)\right)\le {\beta }_2(\Vert {\tilde{\eta }}_1\left(t\right)\Vert ),\hfill \\ {}_0{}^{c}D_t^{\alpha }V\left({\tilde{\eta }}_1\left(t\right)\right)\le -{\beta }_3(\Vert {\tilde{\eta }}_1\left(t\right)\Vert ),\hfill \end{array}\right.$$

(17)

where $\alpha \in (0,1),$ then system (14) is asymptotically stable.

(P2): system (14) is asymptotically stable if and only if

$$|arg\left({\lambda }_i\left(\overline{A}\right)\right)|>\frac{\alpha \pi }{2},i=1,2,\cdots ,n_1,$$

where ${\lambda }_i\left(\overline{A}\right)$ is the $i^{th}$ eigenvalue of matrix $\overline{A}$.

(P3): system (14) is asymptotically stable if there exist a matrix $P\succ 0$, $P\in R^{n_1\times n_1}$, such that

$${({\overline{A}}^{\frac{1}{\alpha }})}^{T}P+P({\overline{A}}^{\frac{1}{\alpha }})\prec 0.$$

Theorem 1.

The polyhedral set,

$$\Omega (\overline{G},\overline{\sigma })=\{{\tilde{\eta }}_1\left(t\right)\in R_{+}^{n_1}:\overline{G}{\tilde{\eta }}_1\left(t\right)\le \overline{\sigma }\},$$

with $\overline{G}\in R^{r\times n_1},\overline{\sigma }\in R_{+}^r$ is a PIS of system (14) if and only if

$$v({\tilde{\eta }}_1(t))=\underset{1,\cdots ,r}{max}\{max(\frac{{(\overline{G}{\tilde{\eta }}_1(t))}_1}{{\overline{\sigma }}_1},0),\cdots ,max(\frac{{(\overline{G}{\tilde{\eta }}_1(t))}_r}{{\overline{\sigma }}_r},0)\}$$

is not increasing along the trajectory of system (14).

Proof. 

If ${\tilde{\eta }}_1(t)\in \Omega (\overline{G},\overline{\sigma })$, $v({\tilde{\eta }}_1(t))=(\frac{{(\overline{G}{\tilde{\eta }}_1(t))}_i}{{\overline{\sigma }}_i})$, then $0\le v({\tilde{\eta }}_1(t))\le 1$ because $\Omega (\overline{G},\overline{\sigma })=\{{\tilde{\eta }}_1(t)\in R_{+}^{n_1}:\overline{G}{\tilde{\eta }}_1(t)\le \overline{\sigma }\}$ is a positively invariant. By Proposition 2, the ${}_0{}^{c}D_t^{\alpha }v({\tilde{\eta }}_1(t))$ is negative definite; hence,

$${}_0{}^{c}D_t^{\alpha }v({\tilde{\eta }}_1(t))=\frac{{\overline{G}}_{(i)}{}_0{}^{c}D_t^{\alpha }({\tilde{\eta }}_1(t))}{{\overline{\sigma }}_i}=\frac{{\overline{G}}_{(i)}\overline{A}{\tilde{\eta }}_1(t)}{{\overline{\sigma }}_i}<0.$$

(18)

Hence,

$$v({\tilde{\eta }}_1(t))=\underset{1,\cdots ,r}{max}\{max(\frac{{(\overline{G}{\tilde{\eta }}_1(t))}_1}{{\overline{\sigma }}_1},0),\cdots ,max(\frac{{(\overline{G}{\tilde{\eta }}_1(t))}_r}{{\overline{\sigma }}_r},0)\}$$

is not increasing along the trajectory of system (14). □

By $v\left({\tilde{\eta }}_1\left(t\right)\right)$, one has

$$\overline{G}{\tilde{\eta }}_1\left(t\right)\le v\left({\tilde{\eta }}_1\left(t\right)\right)\overline{\sigma },$$

the initial condition ${\tilde{\eta }}_1\left(0\right)$ satisfies $\overline{G}{\tilde{\eta }}_1\left(0\right)\le \overline{\sigma },$ then $v\left({\tilde{\eta }}_1\left(0\right)\right)=\frac{\overline{G}{\tilde{\eta }}_1\left(0\right)}{\overline{\sigma }}\le 1$ and $v\left({\tilde{\eta }}_1\left(t\right)\right)\le v\left({\tilde{\eta }}_1\left(0\right)\right),$ since $v\left({\tilde{\eta }}_1\left(t\right)\right)$ is not increasing along the trajectory of system (14). In the sequel,

$$\overline{G}{\tilde{\eta }}_1\left(t\right)\le v\left({\tilde{\eta }}_1\left(t\right)\right)\overline{\sigma }\le v\left({\tilde{\eta }}_1\left(0\right)\right)\overline{\sigma }\le \overline{\sigma },$$

so the polyhedral set $\Omega (\overline{G},\overline{\sigma })=\{{\tilde{\eta }}_1\left(t\right)\in R_{+}^{n_1}:\overline{G}{\tilde{\eta }}_1\left(t\right)\le \overline{\sigma }\}$ is a PIS of system (14).

It is known that for integer order systems, if $\overline{A}\in M_{n_1}$ and $\exists \overline{\sigma }>0,$ such that $\overline{A}\overline{\sigma }\le 0,$ then the equilibrium $\eta =0$ of system (14) is stable in the sense of Lyapunov [29]. In the following proposition, we will show that these conditions also imply the positive invariance of the set $\Omega (I_{n_1},\overline{\sigma })$ for the positive fractional-order system.

When the matrix $\overline{G}$ degenerates into the identity matrix $I_{n_1}$, we have the following proposition:

Proposition 3

([2]). The polyhedral set

$$\Omega (I_{n_1},\overline{\sigma })=\{{\tilde{\eta }}_1\left(t\right)\in R_{+}^{n_1}:{\tilde{\eta }}_1\left(t\right)\le \overline{\sigma }\},$$

is a PIS of system (14) if and only if

$$\overline{A}\in M_{n_1},$$

and

$$\overline{A}\overline{\sigma }\le 0.$$

To obtain the algebraic conditions for the polyhedral set $\Omega (\overline{G},\overline{\sigma })$ to be a PIS, the following propositions are proposed:

Proposition 4

([31]). Let $\overline{A}\in R^{n_1\times n_1}$ and $\alpha >0$. Then,

$$E_{\alpha }\left(\overline{A}{t}^{\alpha }\right)-I={\int }_0^t\overline{A}{e}_{\alpha }^{\overline{A}\tau }d\tau ,$$

where $e_{\alpha }^{\overline{A}t}=\sum _{k=0}^{\infty }\frac{{\overline{A}}^k{t}^{\alpha k}}{\Gamma (k\alpha +\alpha )}·t^{\alpha -1}.$

From Proposition 4, Proposition 5 can be obtained.

Proposition 5.

The polyhedral set $\Omega (\overline{G},\overline{\sigma })=\{{\tilde{\eta }}_1\left(t\right)\in R_{+}^{n_1}:\overline{G}{\tilde{\eta }}_1\left(t\right)\le \overline{\sigma }\}$ is a PIS of system (14), then,

$$\overline{G}{\tilde{\eta }}_1\left(t\right)=0⟹\overline{G}\overline{A}{\tilde{\eta }}_1\left(t\right)=0.$$

Proof. 

$\Omega (\overline{G},\overline{\sigma })$ is a PIS of system (14), by Theorem 1, $v({\overline{\eta }}_1(t))=\underset{1\le i\le r}{max}\{max(\frac{(\overline{G}{\tilde{\eta }}_1{(t)}_1}{{\overline{\sigma }}_1},0),\cdots ,max(\frac{(\overline{G}{\tilde{\eta }}_1{(t)}_r}{{\overline{\sigma }}_r},0)\}$ is not increasing along the trajectory of system (14). □

If $\overline{G}{\tilde{\eta }}_1(t_0)=0$, then $\forall t>t_0,v({\tilde{\eta }}_1(t;t_0,{\eta }_0))\le v({\tilde{\eta }}_1(t_0))=0,$ then

$$\underset{i}{max}\{max(\frac{{\left[\overline{G}{E}_{\alpha }(\overline{A}{(t-t_0)}^{\alpha }){\tilde{\eta }}_1(t_0)\right]}_i}{{\overline{\sigma }}_i},0)\}\le 0,$$

(19)

by Proposition 4, one has

$$\begin{array}{c}{\left[\overline{G}{E}_{\alpha }(\overline{A}{(t-t_0)}^{\alpha }){\tilde{\eta }}_1(t_0)\right]}_i={\left[\overline{G}(I+{\int }_{t_0}^t\overline{A}{e}_{\alpha }^{\overline{A}\tau }d\tau ){\tilde{\eta }}_1(t_0)\right]}_i\le 0.\hfill \end{array}$$

(20)

Since

$$\begin{array}{ccc}\hfill I+{\int }_{t_0}^t\overline{A}{e}_{\alpha }^{\overline{A}\tau }d\tau & =& I+{\int }_{t_0}^t\sum _{k=0}^{\infty }\frac{{(t-\tau )}^{(k+1)\alpha -1}}{\Gamma (k\alpha +\alpha )}·{\overline{A}}^{k+1}\hfill \\ & =& I+\sum _{k=1}^{\infty }{\overline{A}}^k\frac{{(t-t_0)}^{k\alpha }}{\Gamma (k\alpha +1)},\hfill \end{array}$$

(21)

then substitute (20) with (21), $\exists t>t_0,$$\overline{G}{\tilde{\eta }}_1\left(t_0\right)+\frac{{(t-t_0)}^{\alpha }}{\Gamma (\alpha +1)}·\overline{G}\overline{A}{\tilde{\eta }}_1\left(t_0\right)\le 0.$ Then $\overline{G}\overline{A}{\tilde{\eta }}_1\left(t_0\right)\le 0$, because $\frac{{(t-t_0)}^{\alpha }}{\Gamma (\alpha +1)}>0$ and $\overline{G}{\tilde{\eta }}_1\left(t_0\right)=0.$

For the initial state $-{\tilde{\eta }}_1\left(t_0\right),$$\overline{G}(-{\tilde{\eta }}_1\left(t_0\right))=0$ implies $\overline{G}\overline{A}\left({\tilde{\eta }}_1\left(t_0\right)\right)\ge 0.$ By the arbitrariness of ${\tilde{\eta }}_1\left(t_0\right)$, $\overline{G}{\tilde{\eta }}_1\left(t\right)=0⟹\overline{G}\overline{A}{\tilde{\eta }}_1\left(t\right)=0.$

The following result will also be used in the sequel.

Proposition 6

([5]). If $\overline{A}\in R^{n_1\times n_1},\overline{G}\in R^{r\times n_1},$$rank\left(\overline{G}\right)=r$ and $\overline{G}{\tilde{\eta }}_1\left(t\right)=0$ implies $\overline{G}\overline{A}{\tilde{\eta }}_1\left(t\right)=0$ for ${\tilde{\eta }}_1\left(t\right)\in R^{n_1},$ then there exists a matrix $H\in R^{r\times r},$ such that $\overline{G}\overline{A}-H\overline{G}=0.$

Proof. 

The row rectors ${\overline{G}}_{\left(i\right)}$ and $(\overline{G}$$\overline{A}{)}_{\left(i\right)}$ of the matrices $\overline{G}$ and $(\overline{G}$$\overline{A})$ belong to the same r-dimensional subspace of $R^{n_1}$ that is orthogonal to the $n_1-r$-dimensional null space of the matrix $\overline{G}$, according to lemma 2 in [5]; by $rank\left(\overline{G}\right)=r$, we obtain there exists a matrix $H\in R^{r\times r},$ such that $\overline{G}\overline{A}-H\overline{G}=0.$ □

An algebraic condition for a polyhedral set $\Omega (\overline{G},\overline{\sigma })$ to be a positive invariant for system (14) is presented in Theorem 2.

Theorem 2.

The polyhedral set,

$$\Omega (\overline{G},\overline{\sigma })=\{{\tilde{\eta }}_1\left(t\right)\in R_{+}^{n_1}:\overline{G}{\tilde{\eta }}_1\left(t\right)\le \overline{\sigma }\},$$

with $\overline{G}\in R^{r\times n_1},\overline{\sigma }\in R_{+}^r$ is a PIS of system (14) if and only if there exists a matrix $H\in M_r$ such that

$$\overline{G}\overline{A}-H\overline{G}=0,$$

(22)

and

$$H\overline{\sigma }\le 0.$$

(23)

Proof. Necessity.

$\Omega (\overline{G},\overline{\sigma })$ is a positively invariant, by Proposition 5, it yields

$$\overline{G}{\tilde{\eta }}_1\left(t\right)=0⟹\overline{G}\overline{A}{\tilde{\eta }}_1\left(t\right)=0,$$

from Proposition 6, one has

$$\exists H\in R^{r\times r},\overline{G}\overline{A}-H\overline{G}=0⟹\overline{G}\overline{A}=H\overline{G}.$$

Thus, one can obtain

$${}_0{}^{c}D_t^{\alpha }{\tilde{\eta }}_1\left(t\right)=\overline{A}{E}_{\alpha }\left(\overline{A}{t}^{\alpha }\right){\tilde{\eta }}_1\left(0\right)=\overline{A}{\tilde{\eta }}_1\left(t\right),$$

and

$${}_0{}^{c}D_t^{\alpha }\left(\overline{G}{\tilde{\eta }}_1\left(t\right)\right)=\overline{G}{}_0{}^{c}D_t^{\alpha }{\tilde{\eta }}_1\left(t\right)=\overline{G}\overline{A}{\tilde{\eta }}_1\left(t\right)=H\overline{G}{\tilde{\eta }}_1\left(t\right).$$

(24)

If $z\left(t\right)=\overline{G}{\tilde{\eta }}_1\left(t\right),$ then, from (24), it yields ${}_0{}^{c}D_t^{\alpha }z\left(t\right)=Hz\left(t\right).$ Hence,

$$z_0\le \overline{\sigma }⟹z(t;t_0,z_0)\le \overline{\sigma },$$

since $\overline{G}{\tilde{\eta }}_1\left(0\right)\le \overline{\sigma }⟹\overline{G}{\tilde{\eta }}_1(t;t_0,{\eta }_0)\le \overline{\sigma }.$

Therefore, the polyhedral set $\Omega (I_r,\overline{\sigma })=\{z\left(t\right)\in R_{+}^r:z\left(t\right)\le \overline{\sigma }\}$ is a PIS of system ${}_0{}^{c}D_t^{\alpha }\left(z\left(t\right)\right)=Hz\left(t\right).$ From Proposition 3, $H\in M_{r}andH\overline{\sigma }\le 0.$

Sufficiency. Because ${}_0{}^{c}D_t^{\alpha }{\tilde{\eta }}_1\left(t\right)=\overline{A}{\tilde{\eta }}_1\left(t\right),$ according to (22), if $z\left(t\right)=\overline{G}{\tilde{\eta }}_1\left(t\right),$ then,

$${}_0{}^{c}D_t^{\alpha }z\left(t\right)=\overline{G}{}_0{}^{c}D_t^{\alpha }{\tilde{\eta }}_1\left(t\right)=\overline{G}\overline{A}{\tilde{\eta }}_1\left(t\right)=H\overline{G}{\tilde{\eta }}_1\left(t\right)=Hz\left(t\right).$$

Thus, $H\in M_r$ and $H\overline{\sigma }\le 0,$ By Proposition 3, one can obtain

$$z_0\le \overline{\sigma }⟹z(t;t_0,z_0)\le \overline{\sigma },$$

one has $\overline{G}{\tilde{\eta }}_1\left(0\right)\le \overline{\sigma }⟹\overline{G}{\tilde{\eta }}_1(t;t_0,{\eta }_0)\le \overline{\sigma }.$

Hence, the polyhedral set $\Omega (\overline{G},\overline{\sigma })$ is a PIS of system (14).

Next, the polyhedral set $\Omega (\overline{G},\underline{\sigma },\overline{\sigma })$ is proven to be a PIS for system (14) in Theorem 3. □

Theorem 3.

The polyhedral set

$$\Omega (\overline{G},\underline{\sigma },\overline{\sigma })=\left\{{\tilde{\eta }}_1\left(t\right)\in R_{+}^{n_1}:\underline{\sigma }\le \overline{G}{\tilde{\eta }}_1\left(t\right)\le \overline{\sigma }\right\}$$

with $\overline{G}\in R^{r\times n_1},\underline{\sigma }\in R^r$, $\overline{\sigma }\in R_{+}^r$ is a PIS of system (14) if and only if there exists a matrix H such that

$$\overline{G}\overline{A}-H\overline{G}=0,$$

(25)

and

$$\widehat{H}\widehat{\sigma }\le 0.$$

(26)

with $\widehat{H}=\left(\begin{array}{cc}{H}^{+}& H^{-}\\ H^{-}& H^{+}\end{array}\right)$, $\widehat{\sigma }=\left(\begin{array}{c}\overline{\sigma }\\ -\underline{\sigma }\end{array}\right),$ and

$$\begin{array}{c}{H}_{ij}^{+}=\left\{\begin{array}{cc}{h}_{ij},fori=j,\hfill & \\ max(H_{ij},0),fori\ne j,\hfill \end{array}\right.\hfill \\ H_{ij}^{-}=\left\{\begin{array}{cc}0,fori=j,\hfill & \\ max(-H_{ij},0),fori\ne j.\hfill \end{array}\right.\hfill \end{array}$$

(27)

Proof. 

By (27), we have

$$H=H^{+}-H^{-}.$$

(28)

Substitute (25) with (28); it yields

$$\left(\begin{array}{c}\overline{G}\\ -\overline{G}\end{array}\right)\overline{A}=\left(\begin{array}{c}{H}^{+}{H}^{-}\\ H^{-}{H}^{+}\end{array}\right)\left(\begin{array}{c}\overline{G}\\ -\overline{G}\end{array}\right),$$

(29)

by (26), one has

$$\left(\begin{array}{c}{H}^{+}{H}^{-}\\ H^{-}{H}^{+}\end{array}\right)\left(\begin{array}{c}\overline{\sigma }\\ -\underline{\sigma }\end{array}\right)\le 0.$$

(30)

Let $\widehat{G}=\left(\begin{array}{c}\overline{G}\\ -\overline{G}\end{array}\right)$, $\widehat{\sigma }=\left(\begin{array}{c}\overline{\sigma }\\ -\underline{\sigma }\end{array}\right)$, and by (29) and (30), one can obtain

$$\widehat{G}\overline{A}=\widehat{H}\widehat{G},\widehat{H}\widehat{\sigma }\le 0,$$

by Theorem 2, the polyhedral set $\Omega (\widehat{G},\widehat{\sigma })=\{{\tilde{\eta }}_1\left(t\right)\in R_{+}^{n_1}:\widehat{G}{\tilde{\eta }}_1\left(t\right)\le \widehat{\sigma }\}$ is a PIS of system (14); thus, $\Omega (\overline{G},\underline{\sigma },\overline{\sigma })$ is a PIS of system (14). From (28) and (29), $\widehat{G}\overline{A}=\widehat{H}\widehat{G}$ if and only if $\overline{G}\overline{A}=H\overline{G}$; therefore, $\Omega (\overline{G},\underline{\sigma },\overline{\sigma })$ is a PIS of system (14) if and only if there exists a matrix $H,$ such that $\overline{G}\overline{A}-H\overline{G}=0$ and $\widehat{H}\widehat{\sigma }\le 0.$ □

If the reduced system (14) is a standard fractional-order positive linear continuous-time system, the following lemma gives the asymptotical stability conditions of the system (14).

Lemma 2

([18]). The system (14) remaining positive is asymptotically stable if there exists a vector $\lambda \in R^n,\lambda >0$ such that $\overline{A}\lambda <0.$

4. The Controller Design Algorithm

It is obvious that the control law $u\left(t\right)=K\eta \left(t\right)$ is a solution to the CSRP if and only if system (1) is completely controllable (that is does not exhibit impulsive modes) and for all initial states ${\eta }_0$, which satisfies inequalities (3), the corresponding trajectory asymptotically stable to the origin and without violating the constraints (3).

This condition can also be expressed by the following Theorem 4.

Theorem 4.

The control law $u\left(t\right)=K\eta \left(t\right)$ is a solution to the CSRP for system (1) if and only if the following conditions are satisfied:

(i) There exists an equivalent reduced system (14);

(ii) The equivalent reduced system (14) is asymptotically stable, and the polyhedral set $\Omega (\overline{G},\underline{\sigma },\overline{\sigma })$ is PIS of system (14).

Proof. 

The system (1) is completely controllable (that is does not exhibit impulsive modes) if and only if there exists an equivalent reduced system (14); all initial states ${\eta }_0$ which satisfying inequalities (3), the corresponding trajectory is asymptotically stable to the origin and without violating the constraints (3) if and only if the equivalence reduced system (14) asymptotically stable, and the polyhedral set $\Omega (\overline{G},\underline{\sigma },\overline{\sigma })$ is PIS of system (14). Thus, satisfying conditions (i) and (ii), the control law $u\left(t\right)=K\eta \left(t\right)$ is a solution to the CSRP for system (1). □

Case 1: If equivalent reduced system (14) is a SFOLCS. For system (1), from Theorems 3 and 4 and Proposition 2, the control law $u\left(t\right)=K\eta \left(t\right)$ is a solution of the CSRP, which can be solved by the following methods.

Step 1: Find an equivalent reduced system (14) of system (1).

Step 2: Establish the objective function

$$S(K_2,H,\epsilon )=\epsilon .$$

(31)

The constraints

$$\left\{\begin{array}{c}|arg\left({\lambda }_i\left(\overline{A}\right)\right)|>\frac{\alpha \pi }{2},i=1,2,\cdots ,n_1,\\ \overline{G}(A_1+{\tilde{B}}_1{K}_2)=H\overline{G},\\ \widehat{H}\widehat{\sigma }\le -\epsilon \widehat{\sigma },\end{array}\right.$$

(32)

or

$$\left\{\begin{array}{c}{({\overline{A}}^{\frac{1}{\alpha }})}^{T}P+P({\overline{A}}^{\frac{1}{\alpha }})\prec 0,\\ \overline{G}(A_1+{\tilde{B}}_1{K}_2)=H\overline{G},\\ \widehat{H}\widehat{\sigma }\le -\epsilon \widehat{\sigma },\end{array}\right.$$

(33)

where $\overline{G}=G{P}_2\left(\begin{array}{c}{I}_{n_1}\\ -{\tilde{B}}_2{K}_2\end{array}\right)$. The first inequalities in (32) and (33) ensure the asymptotical stability of system (14); the second and third equalities ensure the polyhedron $\Omega (\overline{G},\underline{\sigma },\overline{\sigma })$ is positively invariant to system (14); $\epsilon$ is the rate of convergence. But it is difficult to find a feasible solution of (32) because of the angle constraints. For (33), it can be formulated as a linear matrix inequality (LMI) problem, which can be solved by software such as Yalmip, CVX, and so on. But if the dimension is high, it is also not easy to find the solution.

Case 2: In Case 1, if the control law $v\left(t\right)=K_2{\tilde{\eta }}_1\left(t\right)$ make $A_1+{\tilde{B}}_1{K}_2\in M_{n_1}$, according to Lemma 1, the equivalent reduced system (14) is a fractional order positive linear continuous-time system, from Theorems 3 and 4 and Lemma 2, the control law $u\left(t\right)=K\eta \left(t\right)$ is a solution of the CSRP, which can be solved by the following nonlinear programming (35).

Step 1: Find an equivalent reduced system (14) of system (1).

Step 2: Establish the objective function

$$S(K_2,H,\epsilon )=\epsilon .$$

(34)

The constraints

$$\left\{\begin{array}{c}{(A_1+{\tilde{B}}_1{K}_2)}_{ij}>0,i\ne j,\\ (A_1+{\tilde{B}}_1{K}_2)\lambda <0,\\ \lambda >0,\\ \overline{G}(A_1+{\tilde{B}}_1{K}_2)=H\overline{G},\\ \widehat{H}\widehat{\sigma }\le -\epsilon \widehat{\sigma },\end{array}\right.$$

(35)

where $\overline{G}=G{P}_2\left(\begin{array}{c}{I}_{n_1}\\ -{\tilde{B}}_2{K}_2\end{array}\right)$. The first inequalities in (35) ensure the system (14) is positive; the second and third inequalities in (35) ensure asymptotic stability of system (14); and the fourth and fifth inequalities ensure the polyhedron $\Omega (\overline{G},\underline{\sigma },\overline{\sigma })$ is positively invariant to system (14). $\epsilon$ is the rate of convergence and maximizes of $\epsilon$ increases the rate of convergence to equilibrium.

Remark 2.

With fixed system parameters $A_1$ and ${\tilde{B}}_1$ as well as constraint parameters $\overline{G}$ and $\widehat{\sigma }$. It becomes evident from (35) that the parameter ε holds a significant correlation with the rate of convergence. Specifically, when $0<\epsilon <1$, the largest possible value of ε guarantees the fastest convergence rate towards the equilibrium.

5. Numerical Examples

We illustrate our method with the following examples.

Example 1.

Consider the descriptor fractional order linear continuous-time system

$$\left\{\begin{array}{cc}E{}_0{}^{c}D_t^{\alpha }{\eta }_1\left(t\right)=-2{\eta }_1\left(t\right)+{\eta }_2\left(t\right)-4{\eta }_3\left(t\right)+u_1\left(t\right),\hfill & \\ E{}_0{}^{c}D_t^{\alpha }{\eta }_2\left(t\right)=3{\eta }_1\left(t\right)-{\eta }_2\left(t\right)+2{\eta }_3\left(t\right)+{\eta }_4\left(t\right)+u_2\left(t\right),\hfill & \\ 0=-8{\eta }_1\left(t\right)+5{\eta }_2\left(t\right)+3u_1\left(t\right)+u_2\left(t\right),\hfill & \\ 0={\eta }_1\left(t\right)-3{\eta }_2\left(t\right)-u_1\left(t\right)+2u_2\left(t\right),\hfill & \\ \eta \left(0\right)={\eta }_0,\hfill \end{array}\right.$$

(36)

where $\alpha =0.7$, E, A and B are as follows

$$E=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right),A=\left(\begin{array}{cccc}-2& 1& -4& 0\\ 3& -1& 2& 1\\ -8& 5& 0& 0\\ 1& -3& 0& 0\end{array}\right),B=\left(\begin{array}{cc}1& 0\\ 0& 1\\ 3& 1\\ -1& 2\end{array}\right).$$

It is easy to verify that $det(sE-A)$ is not identically zero, so system (36) is regular.

The constraints on the state is given by (3) with

$$G=\left(\begin{array}{cccc}-0.9& -3.5& -11.9& -1.5\\ -2.7& -4.7& -1.5& -0.5\end{array}\right),\underline{\sigma }=\left(\begin{array}{c}1\\ 2\end{array}\right),\overline{\sigma }=\left(\begin{array}{c}2\\ 4\end{array}\right).$$

For system (36), from Theorems 3 and 4 and Lemma 2, the feedback control $u\left(t\right)=K\eta \left(t\right)$ is a solution to the CSRP, which can be solved by nonlinear programming.

Step 1: Find an equivalent reduced system.

By the impulse elimination algorithm based on dynamic decomposition, system (36) is impulse controllable if $rank\left[A_4{\tilde{B}}_2\right]=n-rank\left(E\right)=2$, according to $A_4+{\tilde{B}}_2{K}_{12}=I_2$; we obtain $K_{12}=\left(\begin{array}{cc}0.2857& -0.1429\\ 0.1429& 0.4286\end{array}\right)$; then the impulsive behavior can be eliminated, and the corresponding gain matrix is $K_1=\left[K_{11}{K}_{12}\right]$ with choose $K_{11}=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right)$ and $K_{12}=\left(\begin{array}{cc}0.2857& -0.1429\\ 0.1429& 0.4286\end{array}\right).$

$P_1$ and $P_2$ can be obtained by performing the elementary row and column transformations on the identity matrix $I_n$. From $P_1(A+B{K}_1)P_2=\left(\begin{array}{cc}{A}_1& 0\\ 0& I_2\end{array}\right),$ matrices $P_1$ and $P_2$ are given by:

$$P_1=\left(\begin{array}{cccc}1& 0& 3.714& 0.1429\\ 0& 1& -2.1429& -1.4286\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right),P_2=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 8& -5& 1& 0\\ -1& 3& 0& 1\end{array}\right),$$

then, from (10) and (11), the matrices $A_1$, ${\tilde{B}}_1$ and ${\tilde{B}}_2$ can be obtained

$$A_1=\left(\begin{array}{cc}-31.5714& 19.1429\\ 18.7143& -7.4286\end{array}\right),{\tilde{B}}_1=\left(\begin{array}{cc}12& 4\\ -5& -4\end{array}\right),{\tilde{B}}_2=\left(\begin{array}{cc}3& 1\\ -1& 2\end{array}\right).$$

by the controller $v\left(t\right)=K_2{\tilde{\eta }}_1\left(t\right)$ make the equivalent reduced system can be converted to

$$\begin{array}{ccc}\hfill {}_0{}^{c}D_t^{\alpha }{\tilde{\eta }}_1\left(t\right)& =& A_1{\tilde{\eta }}_1\left(t\right)+{\tilde{B}}_{1}v\left(t\right)\hfill \\ & =& \left[\left(\begin{array}{cc}-31.5714& 19.1429\\ 18.7143& -7.4286\end{array}\right)+\left(\begin{array}{cc}12& 4\\ -5& -4\end{array}\right)K_2\right]{\tilde{\eta }}_1\left(t\right),\hfill \end{array}$$

(37)

where ${\tilde{\eta }}_1\left(t\right)={\left(P_2^{-1}\eta \left(t\right)\right)}_1=\left(\begin{array}{c}{\tilde{\eta }}_{1_1}\left(t\right)\hfill \\ {\tilde{\eta }}_{1_2}\left(t\right)\hfill \end{array}\right)\in R^2.$

Step 2: Establish the objective function

$$S(K_2,H,\epsilon )=\epsilon .$$

Maximize the objective function with constraints

$$\left\{\begin{array}{c}{(A_1+{\tilde{B}}_1{K}_2)}_{ij}>0,i\ne j\\ (A_1+{\tilde{B}}_1{K}_2)\lambda <0,\\ \lambda >0,\\ \overline{G}(A_1+{\tilde{B}}_1{K}_2)=H\overline{G},\\ \widehat{H}\widehat{\sigma }\le -\epsilon \widehat{\sigma },\end{array}\right.$$

(38)

where $\overline{G}=G{P}_2\left(\begin{array}{c}{I}_{n_1}\\ -{\tilde{B}}_2{K}_2\end{array}\right).$ The third Equation in (38) is quadratic since $K_2$ in $\overline{G}$ is unknown, which makes (38) nonlinear.

The solution of (38) gives $\epsilon =1$,

$$K_2=\left(\begin{array}{cc}1.5678& -1.9511\\ 2.6130& 1.5214\end{array}\right),H=\left(\begin{array}{cc}-4.11& 0.43\\ 0.33& -1.96\end{array}\right),$$

and $\lambda =\left(\begin{array}{c}1.8938\hfill \\ 2.1707\hfill \end{array}\right)$ such that $(A_1+{\tilde{B}}_1{K}_2)\lambda =\left(\begin{array}{c}-0.4273\hfill \\ -7.3566\hfill \end{array}\right)<0.$

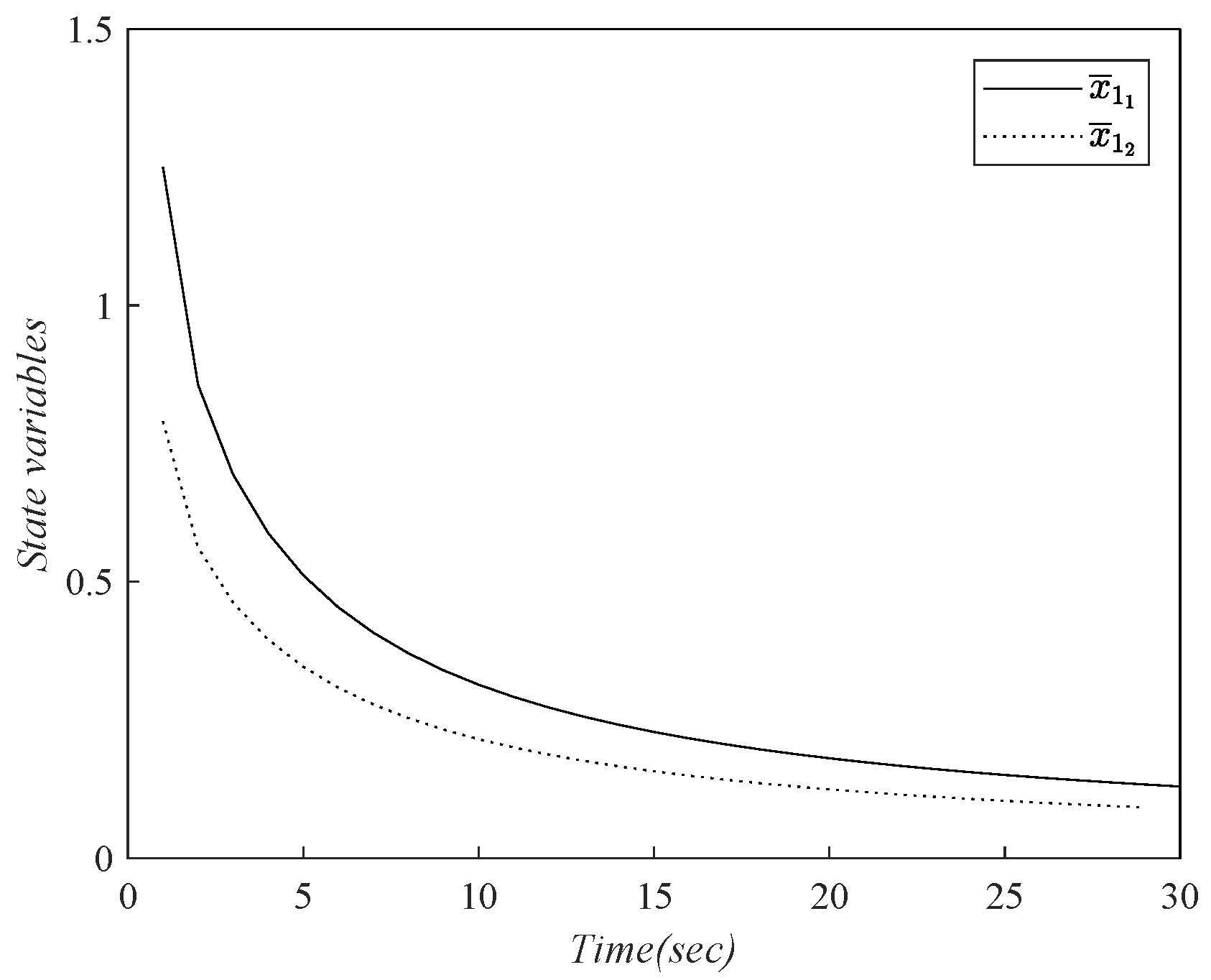
The result shows that there exists a linear state feedback controller $v\left(t\right)=K_2{\tilde{\eta }}_1\left(t\right),$ such that all initial states that satisfy state constraints $\{{\tilde{\eta }}_1\left(t\right)\in R_{+}^{n_1}:\underline{\sigma }\le \overline{G}{\tilde{\eta }}_1\left(t\right)\le \overline{\sigma }\}$ ($\overline{G}=\left(\begin{array}{cc}-2.051& 7.444\\ -1.255& -2.629\end{array}\right)$) and the corresponding trajectory of (37) is asymptotically stable and converges to the origin in the interval $t\in [0,30]$, 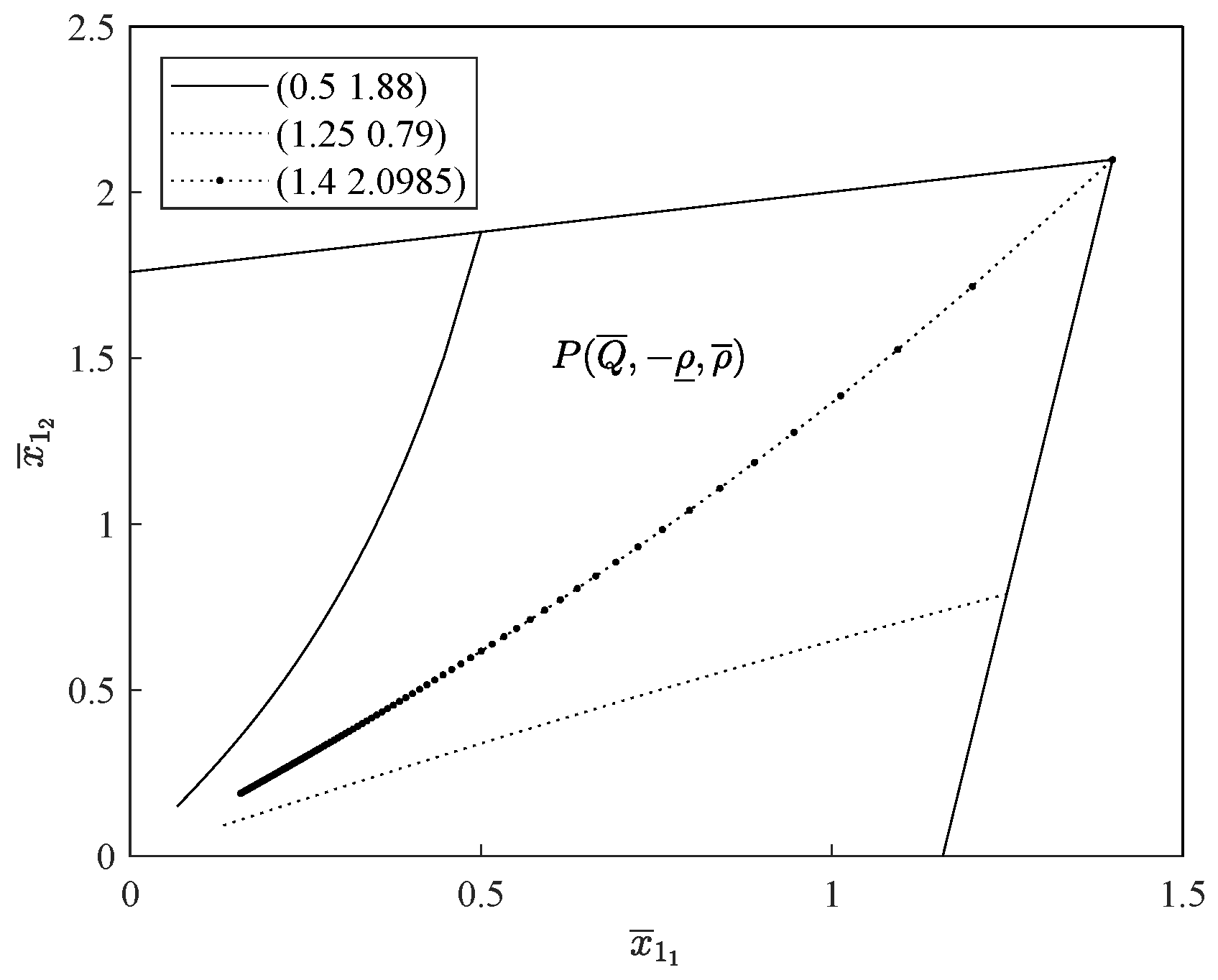which is shown in Figure 1.

In Figure 2, the trajectories originating from the initial state ${\tilde{\eta }}_1\left(0\right)={\left[0.60.3\right]}^T$ are depicted, all residing within the designated constraint region.

The above results also indicate that there exists an equivalent reduced system of (37), which is asymptotically stable, and the polyhedral $\Omega (\overline{G},\underline{\sigma },\overline{\sigma })$ is PIS of system (37), from Theorem 4 and (6), the control law

$$\begin{array}{ccc}\hfill u\left(t\right)& =& K\eta \left(t\right)=K_1\eta \left(t\right)+v\left(t\right)=K_1\eta \left(t\right)+K_2{\tilde{\eta }}_1\left(t\right)\hfill \\ & =& \left(\begin{array}{cccc}0& 0& 0.2857& -0.1429\\ 0& 0& 0.1429& 0.4286\end{array}\right)\eta \left(t\right)\hfill \\ & +& \left(\begin{array}{cc}1.5678& -1.9511\\ 2.6130& 1.5214\end{array}\right){\tilde{\eta }}_1\left(t\right)\hfill \\ & =& \left(\begin{array}{cccc}1.5678& -1.9511& 0.2857& -0.1429\\ 2.6130& 1.5214& 0.1429& 0.4286\end{array}\right)\eta \left(t\right),\hfill \end{array}$$

where ${\tilde{\eta }}_1\left(t\right)={\left(P_2^{-1}\eta \left(t\right)\right)}_1=\left(\begin{array}{c}{\tilde{\eta }}_{1_1}\left(t\right)\hfill \\ {\tilde{\eta }}_{1_2}\left(t\right)\hfill \end{array}\right)\in R^2.$

Hence, $K=\left(\begin{array}{cccc}1.5678& -1.9511& 0.2857& -0.1429\\ 2.6130& 1.5214& 0.1429& 0.4286\end{array}\right)$ is a solution to the CSRP of the DFOLCS (36).

Remark 3.

The reduced system (37) is not a positive system in that ${\tilde{B}}_1=\left(\begin{array}{cc}12& 4\\ -5& -4\end{array}\right)$ is not a nonnegative matrix, i.e., ${\tilde{B}}_1\notin R_{+}^{2\times 2}$, but by the controller $v\left(t\right)=K_2{\tilde{\eta }}_1\left(t\right)$, which makes $A_1+{\tilde{B}}_1{K}_2$ a Metzler matrix, the resulting system becomes positive system. By Lemma 1, we can guarantee the asymptotic stability and positivity of the closed loop from Lemma 2; hence, Theorem 4 is also valid.

Example 2.

We modify the state constraints in Example 1 with the state constraints in the form of (3) being given by

$$G=\left(\begin{array}{cccc}11& 0.2& 5& 3\\ 3& 2.6& 4& 1.6\end{array}\right),\underline{\sigma }=\left(\begin{array}{c}1\\ 2\end{array}\right),\overline{\sigma }=\left(\begin{array}{c}2\\ 4\end{array}\right).$$

For system (36), by Theorem 3, Theorem 4, and Lemma2, the feedback control $u=K\eta \left(t\right)$ is a solution to the CSRP, which can be obtained by the following algorithm that can be solved by nonlinear programming.

Step 1: Find an equivalent reduced system.

By the controller $v\left(t\right)=K_2{\tilde{\eta }}_1\left(t\right)$, the equivalent reduced system can be transformed into

$$\begin{array}{ccc}\hfill {}_0{}^{c}D_t^{\alpha }{\overline{\eta }}_1\left(t\right)& =& A_1{\overline{\eta }}_1\left(t\right)+{\tilde{B}}_{1}v\left(t\right)\hfill \\ & =& \left[\left(\begin{array}{cc}-31.5714& 19.1429\\ 18.7143& -7.4286\end{array}\right)+\left(\begin{array}{cc}12& 4\\ -5& -4\end{array}\right)K_2\right]{\tilde{\eta }}_1\left(t\right),\hfill \end{array}$$

(39)

where ${\tilde{\eta }}_1\left(t\right)={\left(P_2^{-1}\eta \left(t\right)\right)}_1=\left(\begin{array}{c}{\tilde{\eta }}_{1_1}\left(t\right)\hfill \\ {\tilde{\eta }}_{1_2}\left(t\right)\hfill \end{array}\right)\in R^2.$

Step 2: Establish the objective function

$$S(K_2,H,\epsilon )=\epsilon .$$

(40)

Maximize the object function with constraints

$$\left\{\begin{array}{c}{(A_1+{\tilde{B}}_1{K}_2)}_{ij}>0,i\ne j,\\ (A_1+{\tilde{B}}_1{K}_2)\lambda <0,\\ \lambda >0,\\ \overline{G}(A_1+{\tilde{B}}_1{K}_2)=H\overline{G},\\ \widehat{H}\widehat{\sigma }\le -\epsilon \widehat{\sigma },\end{array}\right.$$

(41)

where $\overline{G}=G{P}_2\left(\begin{array}{c}{I}_{n_1}\\ -{\tilde{B}}_2{K}_2\end{array}\right).$

The solution of (40) gives $\epsilon =0.7855,$

$$K_2=\left(\begin{array}{cc}1.7527& -1.8216\\ 2.4190& 0.7040\end{array}\right),H=\left(\begin{array}{cc}-1& 0.2\\ 0.23& -1\end{array}\right),$$

and $\lambda =\left(\begin{array}{c}0.7855\hfill \\ 1.2143\hfill \end{array}\right)$ such that $(A_1+{\tilde{B}}_1{K}_2)\lambda =\left(\begin{array}{c}-0.5574\hfill \\ -1.1640\hfill \end{array}\right)<0.$

The result in Figure 3 shows that there exists a linear state feedback controller $v\left(t\right)=K_2{\tilde{\eta }}_1\left(t\right)$ such that all initial states that satisfy state constraints $\{{\tilde{\eta }}_1\left(t\right)\in R_{+}^{n_1}:\underline{\sigma }\le \overline{G}{\tilde{\eta }}_1\left(t\right)\le \overline{\sigma }\}$$(\overline{G}=\left(\begin{array}{cc}0.2743& -1.6913\\ -2.1377& 1.2908\end{array}\right))$ are asymptotically stable and converge to the origin in the interval $t\in [0,30]$.

In Figure 4, trajectories emanating from the initial state ${\tilde{\eta }}_1\left(0\right)={\left[1.250.79\right]}^T$ are shown; they are also in the constraint region.

The above result indicates that there exists an equivalent reduced system of (39), which is asymptotically stable and converges to the equilibrium point with the polyhedral $\Omega (\overline{G},\underline{\sigma },\overline{\sigma })$ is a PIS of system (39), from Theorem 4 and (6), the control law

$$\begin{array}{ccc}\hfill u\left(t\right)& =& K\eta \left(t\right)=K_1\eta \left(t\right)+v\left(t\right)=K_1\eta \left(t\right)+K_2{\tilde{\eta }}_1\left(t\right)\hfill \\ & =& \left(\begin{array}{cccc}0& 0& 0.2857& -0.1429\\ 0& 0& 0.1429& 0.4286\end{array}\right)\eta \left(t\right)\hfill \\ & +& \left(\begin{array}{cc}1.5678& -1.9511\\ 2.6130& 1.5214\end{array}\right){\tilde{\eta }}_1\left(t\right)\hfill \\ & =& \left(\begin{array}{cccc}1.7527& -1.8216& 0.2857& -0.1429\\ 2.4190& 0.7040& 0.1429& 0.4286\end{array}\right)\eta \left(t\right),\hfill \end{array}$$

where ${\tilde{\eta }}_1\left(t\right)={\left(P_2^{-1}\eta \left(t\right)\right)}_1=\left(\begin{array}{c}{\tilde{\eta }}_{1_1}\left(t\right)\hfill \\ {\tilde{\eta }}_{1_2}\left(t\right)\hfill \end{array}\right)\in R^2.$

Hence, $K=\left(\begin{array}{cccc}1.7527& -1.8216& 0.2857& -0.1429\\ 2.4190& 0.7040& 0.1429& 0.4286\end{array}\right)$ is a solution to the CSRP of DFOLCS (36).

To demonstrate the universality of the controller design scheme, we will discuss an example where E is a full-row rank matrix, meaning that the scheme remains feasible even when the DFOLCS degenerates into the SFOLCS.

Example 3.

Consider SFOLCS with

$$A=\left[\begin{array}{cc}-2.5& 0.8\\ -0.85& 1.4\end{array}\right]andB=\left[\begin{array}{c}1\\ 0.5\end{array}\right]$$

and the state constraints in the form of (3) being given by

$$G=\left(\begin{array}{cc}0& 2\\ 1& 2\\ -0.5& 4\end{array}\right),\underline{\sigma }=\left(\begin{array}{c}0\\ 0\\ -1.8\end{array}\right),\overline{\sigma }=\left(\begin{array}{c}0.8\\ 2.4\\ 0\end{array}\right).$$

By Theorems 3 and 4 and Lemma 2, the feedback control $u=K\eta \left(t\right)$ is a solution to the CSRP, which can be obtained by the following algorithm that can be solved by nonlinear programming (34) and (35).

The solution of (40) gives $\epsilon =0.2,$$K=\left(\begin{array}{cc}1.5& -4\end{array}\right),$ and $\lambda =\left(\begin{array}{c}1.4\hfill \\ 0.2\hfill \end{array}\right)$ such that $(A+BK)\lambda =\left(\begin{array}{c}-2.04\hfill \\ -0.26\hfill \end{array}\right)<0.$

Obviously, there exists a linear state feedback controller $v\left(t\right)=K\eta \left(t\right)$ such that all initial states that satisfy state constraints $\{\eta \left(t\right)\in R_{+}^{n_1}:\underline{\sigma }\le \overline{G}\eta \left(t\right)\le \overline{\sigma }\}$ are asymptotically stable and converge to the origin. Hence, $u=1.5x_1-4x_2$ is a solution to the CSRP of SFOLCS.

Remark 4.

In practical engineering applications, state variables usually cannot be measured because of the varied and complicated work conditions, which makes state feedback impossible while dynamical output feedback can avoid the drawbacks [32,33], hence the output feedback of CSRP for DFOLCS will be an interesting topic in future research.

6. Conclusions

In this paper, the CSRP of DFOLCS is studied when $0<\alpha <1$. To obtain an equivalent reduced system, the decomposition and separation method and coordinate transformation are proposed. To find the necessary and sufficient conditions of positive invariance for the reduced system, the PISs theory, the Lyapunov stability theory, and some mathematical techniques are utilized. We also propose optimization models and a corresponding algorithm for finding the linear state feedback controller design of CSRP for DFOLCS. The CSRP is transformed into nonlinear programming with a linear objective function and quadratic mixed constraints. Our algorithm stands out for its ease of implementation compared to other methods. This is because the nonlinear optimization problem can be readily solved using any off-the-shelf mathematical software. Numerical examples further demonstrate the effectiveness of the proposed algorithm. An interesting question in this paper is the optimization problem (32). How to find the solution to (32) is our forthcoming research topic. The method proposed in this paper for solving CSRP is also attractive, and studying time delay and randomness helps us gain a deeper understanding of the behavior of complex systems, improve the performance and stability of systems, and optimize decision-making processes. Hence, another interesting research problem is to extend this method to delayed fractional order linear continuous-time systems and observer-based controller designs of stochastic systems [34].