Contributions to the Numerical Solutions of a Caputo Fractional Differential and Integro-Differential System

Abstract

The primary goal of this research is to offer an efficient approach to solve a certain type of fractional integro-differential and differential systems. In the Caputo meaning, the fractional derivative is examined. This system is essential for many scientific disciplines, including physics, astrophysics, electrostatics, control theories, and the natural sciences. An effective approach solves the problem by reducing it to a pair of algebraically separated equations via a successful transformation. The proposed strategy uses first-order shifted Chebyshev polynomials and a projection method. Using the provided technique, the primary system is converted into a set of algebraic equations that can be solved effectively. Some theorems are proved and used to obtain the upper error bound for this method. Furthermore, various examples are provided to demonstrate the efficiency of the proposed algorithm when compared to existing approaches in the literature. Finally, the key conclusions are given.

1. Introduction

Fractional analysis is a mathematical discipline concerned with examining the properties of integrals and derivatives of the non-integer order. Since two decades ago, this calculus has been the subject of research, attracting the attention of numerous academics around the globe. In addition, fractional calculus is gaining popularity in various fields, including materials science, water mechanics, potential theory, electricity, nature, mechanical engineering, and more. There has recently been an explosion of interest in fractional integro-differential and differential solutions. This theory has a wide range of applications, including thermodynamic modeling, viscoelasticity, astrophysics, and chaotic networks; see [1,2,3,4,5,6]. Fractional-order systems have also been widely used in information security, exploiting newly designed fractional-order 3D Lorenz chaotic systems and 2D discrete polynomial hyper-chaotic maps for high-performance multi-image encryption. Fractional-order chaotic systems exhibit more control factors and more sophisticated dynamical properties; see [7]. Under some conditions, those fractional integro-differential equations may have an exact solution determined. An effective approximation is required because solving integro-differential equations analytically is typically a problematic procedure. Indeed, various efficient approaches for examining fractional integro-differential and differential problems have been developed, including the matrix collocation method [8], finite integration method [9], dynamical analysis [10], reproducing kernel Hilbert space approximation [11], Euler wavelet approach [12], pseudo-operational matrix method [13], spline quasi-interpolants [14], Haar wavelet [15], homotopy analysis method [16], shifted Legendre projection method [17], airfoil collocation method and the iterated projection method [18]. In [19], the author proposed a collocation approach via the wavelet functions for weakly fractional integro-differential problems. In paper [20], the authors devised the sinc collocation strategy to deal with weakly fractional partial integro-differential problems. A polynomial approximation strategy was examined in [21] using a collocation method for the shifted Legendre polynomials. On the other hand, the authors of [22] presented a numerical method utilizing the Haar wavelet to address the following fractional coupled integral-differential system:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle {}^c\mathcal{J}_{0_{+}}^{\alpha }𝓁\left(\upsilon \right)+{𝓁}^{\prime }\left(\upsilon \right)+{\int }_0^{\upsilon }\lambda \left(\rho \right)d\rho =\sigma \left(\upsilon \right),0\le \upsilon \le 1,}\hfill \\ {}^c\mathcal{J}_{0_{+}}^{\beta }\lambda \left(\upsilon \right)+{\lambda }^{\prime }\left(\upsilon \right)+{\int }_0^{\upsilon }𝓁\left(\rho \right)d\rho =\varsigma \left(\upsilon \right),0\le \upsilon \le 1\hfill \end{array}\right.\end{array}$$

(1)

where $1\le \alpha ,\beta \le 2$, $0\le \upsilon \le 1$ and ${}^c\mathcal{J}_{0_{+}}^{\alpha }$ and ${}^c\mathcal{J}_{0_{+}}^{\beta }$ are the Caputo fractional derivatives. This system is currently the focus of extensive research because of its frequent occurrence in several engineering and scientific disciplines; see [22,23,24,25]. In [26], the authors considered some classes of stochastic fractional integro-differential equations of the type

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle {}_0{}^{\mathit{ABC}}D_t^{\alpha }X(t,\omega )=f(t,\omega )+{\lambda }_1{\int }_0^t{\varphi }_1(\tau ,X(\tau ,\omega ))d{\omega }_s+{\lambda }_2{\int }_0^t{\varphi }_2(\tau ,X(\tau ,\omega ))d{\omega }_{\tau },}\hfill \\ X(0,\omega )=X_0\left(\omega \right),0<\alpha \le 1,\hfill \end{array}\right.\end{array}$$

where X is the unknown stochastic process, $W_t$ is a Brownian motion. The fractional derivative was in the ABC sense introduced by Atangana and Baleanu. The authors approximated X using the Galerkin projection method based on the piecewise Chebyshev cardinal functions. The authors of [27,28,29] considered a linear fractional differential equation of the form

$${}^c\mathcal{J}_{0_{+}}^{\nu }𝓁(\upsilon )=-𝓁(\upsilon )+\sigma (\upsilon ).$$

(2)

Because of the memory effect of fractional derivatives, this fractional differential equation best describes physical processes having memory and hereditary features. In [30], the author suggested an implicit approach for the approximate solution of a significant class of fractional differential equations of the form

$${}^c\mathcal{J}_{0_{+}}^{\nu }\left[𝓁-{𝓁}_0\right]\left(\upsilon \right)=\beta 𝓁\left(\upsilon \right)+\sigma \left(\upsilon \right),𝓁\left(0\right)={\upsilon }_0.$$

(3)

It has been demonstrated that this equation serves as a suitable model for several physical phenomena, including diffusion processes and damping principles. The author developed the suggested process using a quadrature formula method. A few techniques for numerically solving these equations have been proposed; however, most of them lack error estimates. There are a few ways to solve the fractional differential equations of the above forms numerically. The aforementioned fractional systems are also the subject of much research because they are often used in engineering and science.

Chebyshev polynomials are an essential class of orthogonal polynomials; they have a significant impact in nearly every field of mathematical analysis, namely in interpolation and approximation theory, numerical integration, and spectral analysis. Refs. [31,32,33] are an excellent place to look for books on Chebyshev polynomials. The Chebyshev collocation scheme was widened in [34] for the following Volterra pantograph integro-differential problem:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\phi }^{\prime }\left(s\right)=& a_1\left(s\right)\phi \left(s\right)+a_2\left(s\right)\phi \left(qs\right)+b\left(s\right)\hfill \\ & +{\int }_0^s{k}_1(s,\varsigma )\phi \left(\varsigma \right)d\varsigma +{\int }_0^{qs}{k}_2(s,\varsigma )\phi \left(\varsigma \right)d\varsigma ,0<q<1,s\in [0,T].\hfill \end{array}\end{array}$$

(4)

The authors used Chebyshev polynomials to produce the pantograph operational matrices and their related derivatives. Furthermore, the information gathered from operational matrices was used to approximate the derivatives of unidentified functions. Furthermore, the weighted square norm allows for a thorough examination of convergence. The authors ran some numerical experiments to validate the high performance of the numerical technique. The results show that the computational technique is correct. The Chebyshev polynomials approach was used in [35] to examine a space-time fractional integro-differential problem of the form

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {}^{\mathit{CP}}\mathfrak{D}_{\mu \left(s\right)}[y(x,s)·w(x,s)]+\frac{\partial y(x,s)}{\partial s}\hfill \\ & =r(x,s)-{\int }_0^{s}y(x,T)·k(x,T)dT-{\int }_0^{t}y(x,T)dT,\hfill \end{array}\end{array}$$

(5)

$$\begin{array}{c}\hfill y(x,0)=w\left(x\right),x\in [0,1],y(0,s)=v\left(s\right),s\in [0,1].\end{array}$$

(6)

Applying operational matrices of Chebyshev polynomials derived from the Caputo–Prabhakar sense and appropriate collocation points would transform the variable fractional order integro-differential equation into a system of algebraic equations. Deriving four different kinds of Chebyshev polynomial operational matrices is the main objective of the Chebyshev polynomials approach. Such operational matrices convert an equation, which, when the variables are scattered, can also be viewed as a system of linear equations into the products of several dependent matrices. The authors of [36] established the concept of first and second kind Chebyshev derivations based on specific differential operators and the accompanying polynomial algebra. They then discovered the components of their kernels and established that each component of either kernel determines a polynomial identity for both forms of Chebyshev polynomials. They derived many polynomial identities for both forms of Chebyshev polynomials, the generalized hypergeometric function and a partial case of Jacobi polynomials.

Over the past 20 years, several approaches for solving compact operator equations with different projection methods have been produced. The primary objective of [37] is to improve and widen upon the findings of prior research utilizing the Kulkarni approach to approximate the solution of the following integro-differential equation:

$$\begin{array}{c}\hfill z^{\prime }\left(\lambda \right)+{\int }_{-1}^1\xi (\lambda ,\tau )z\left(\tau \right)d\tau =h\left(\lambda \right),-1\le \lambda \le 1.\end{array}$$

(7)

The above equation reads in the operator form as follows:

$$\begin{array}{c}\hfill Az-Tz=h,\end{array}$$

(8)

where

$$Az\left(\lambda \right):=z^{\prime }\left(\lambda \right),-1\le \lambda \le 1,$$

and

$$Tz\left(\lambda \right):=-{\int }_{-1}^1\xi (\lambda ,\tau )z\left(\tau \right)d\tau ,-1\le \lambda \le 1.$$

The approach equation is

$$\left[I-{\pi }_n\left(A^{-1}T\right)+\left(A^{-1}T\right){\pi }_n-{\pi }_n\left(A^{-1}T\right){\pi }_n\right]z_n=h.$$

(9)

Here, ${\left({\pi }_n\right)}_{n\ge 0}$ is the sequence of orthogonal projections defined via the corresponding normalized Legendre polynomials. In [38], the author worked on a different Legendre projection method for establishing the Cauchy integro-differential problems:

$${\phi }^{\prime }\left(\lambda \right)+{\oint }_{-1}^1\frac{\phi \left(t\right)}{t-\lambda }dt=h\left(\lambda \right),-1\le \lambda \le 1,$$

(10)

The approximate problem is finding ${\phi }_n$ such that

$${\phi }_n+A^{-1}C{\pi }_n{\phi }_n=A^{-1}h,$$

(11)

where

$$\left(Cz\right)\left(\lambda \right)={\oint }_{-1}^1\frac{z\left(t\right)}{t-\lambda }dt,-1\le \lambda \le 1,$$

(12)

Here, the approximate operator is $A^{-1}C{\pi }_n$. More recently, a projection approach was developed in [39] to solve the following system of second-kind Cauchy integral equations:

$$\begin{array}{cc}\hfill z\left(\lambda \right)-{\oint }_0^1\frac{y\left(t\right)}{t-\lambda }dt& =h_1\left(\lambda \right),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill y\left(\lambda \right)-{\oint }_0^1\frac{z\left(t\right)}{t-\lambda }dt& =h_2\left(\lambda \right).\hfill \end{array}$$

(14)

In contrast to earlier methodologies, the piecewise polynomial is employed, along with the development of the Galerkin approximation system characterized by the following form:

$$\begin{array}{cc}\hfill u_n^G-C_n^{\ast G}{u}_n^G& ={\pi }_n^P\xi ,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill v_n^G-C_n^G{v}_n^G& ={\pi }_n^P\zeta ,\hfill \end{array}$$

(16)

where $C_n^G:={\pi }_n^{P}C{\pi }_n^P$ and $C_n^{\ast G}:={\pi }_n^P{C}^{\ast }{\pi }_n^P$. Also, the author approached the Cauchy integral operator C on $[0,1]$ by the finite rank Kulkarni operator $C_n^K$ as follows:

$$\begin{array}{c}\hfill C_n^K:={\pi }_n^{P}C+C{\pi }_n^P-{\pi }_n^{P}C{\pi }_n^P.\end{array}$$

(17)

Motivated by the above researches, this study aims to introduce a different projection strategy for treating the following fractional integro-differential system:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle a{}^c\mathcal{J}_{0_{+}}^{\nu }𝓁\left(\upsilon \right)+b𝓁\left(\upsilon \right)+c{𝓁}^{\prime }\left(\upsilon \right)+d{\int }_0^1\psi \left(\upsilon ,\rho \right)\lambda \left(\rho \right)d\rho =\sigma \left(\upsilon \right),0\le \upsilon \le 1,}\hfill \\ a{}^c\mathcal{J}_{0_{+}}^{\nu }\lambda \left(\upsilon \right)+b\lambda \left(\upsilon \right)+c{\lambda }^{\prime }\left(\upsilon \right)+d{\int }_0^1\psi \left(\upsilon ,\rho \right)𝓁\left(\rho \right)d\rho =\varsigma \left(\upsilon \right),0\le \upsilon \le 1,\hfill \\ {\displaystyle \sum _{k=0}^{r-1}}\frac{{\upsilon }^k}{k!}{𝓁}^{\left(k\right)}\left(0\right)=0,{\displaystyle \sum _{k=0}^{r-1}}\frac{{\upsilon }^k}{k!}{\lambda }^{\left(k\right)}\left(0\right)=0,r-1<\nu <r.\hfill \end{array}\right.\end{array}$$

(18)

where ${}^c\mathcal{J}_{0_{+}}^{\nu }$ is the Caputo fractional derivative of order $0<\nu \le 2$. Here, $0_{+}$ for interval $[0,1]$ and c for the Caputo sense. This work generalizes such problems and improves some previously published results. In addition, Chebyshev polynomials of the first kind are employed as an alternative to both Legendre polynomials and piecewise polynomials. The corresponding approximate system is as follows:

$$\left\{\begin{array}{c}{\displaystyle a{\vartheta }_n+b{\mathfrak{R}}_{0_{+}}^{\nu }{\vartheta }_n+c{\mathfrak{R}}_{0_{+}}^{\nu -1}{\vartheta }_n+d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}{\vartheta }_n={\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\Psi ,}\hfill \\ a{\chi }_n+b{\mathfrak{R}}_{0_{+}}^{\nu }{\chi }_n+c{\mathfrak{R}}_{0_{+}}^{\nu -1}{\chi }_n+d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}{\chi }_n={\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\zeta .\hfill \end{array}\right.$$

(19)

It is important to highlight that the current issue, approximate operators, convergence order of the orthogonal projection, and derived systems are completely different from those described in the literature, namely in [37,38,39]. The introduction of computational approaches to approach the solution of coupled fractional integro-differential systems has garnered significant attention from mathematicians and researchers in the past years due to the frequent occurrence of these systems in various disciplines, including engineering and chemistry [40]. Consequently, numerical techniques have been devised to estimate the solutions of these systems. In recent years, systems of fractional integro-differential equations have been used in a variety of scientific and engineering disciplines, including physiological models, elasticity, technological mathematics, physics theory, economic mathematics, finance, electricity, fluid statics, dynamics, heat transfer, and movement theory. According to the literature study above, more research is needed on the method solution for a coupled Caputo integro-differential system. In response to this reality, this study conducts a numerical investigation of the Caputo fractional-order differential system mentioned previously. Following [41], the majority of the literature defines temporal fractional models according to the Caputo definition, which uses fractional differential equations or pseudo-state space descriptions. The Caputo formulation is well known because it allows for beginning conditions to be defined in terms of the integer derivatives of the derived functions in the models under consideration. Our research on the Caputo derivative is motivated by its importance as a common fractional operator, which is frequently used in a variety of fractional derivative applications. The present research intends to delve deeper into the characteristics and properties of this derivative, as well as incorporate realistic initial conditions widely used in physics. The projection method is crucial in approximation theory, and several authors have used Chebyshev polynomials to solve various functional equations using a variety of strategies, including the spectral collocation approach, the least-squares method, the operational matrix method, and the matrix collocation method. To tackle the presented problem for the first time, we use a projection strategy based on First-Kind Chebyshev Polynomials in this work. We use a different technique to address a distinct problem. Our strategy has two distinct advantages compared to other methods in the literature. The coupled system is converted into a fractional integro-differential system that can be solved separately using the current method. However, our algebraic system is considerably easier to solve than the one presented in the literature. Given specific requirements, this approach can be utilized in upcoming projects to address other categories of fractional partial differential systems. The present study aims to delineate several overall objectives:

• The numerical approach of a new class of fractional differential and integro-differential system is the subject of this research. This system is essential in many scientific fields, including science, finance, control theories, nature, and electrostatics;
• Chebyshev polynomials of the first kind are used to solve this problem;
• A suitable transformation reduces the number of equations that must be solved in a system of two independent equations;
• An error bound is established for the approach solution achieved by the suggested procedure;
• We present the existence of the approach solution to the system;
• We offer an application to solve a differential equation;
• We compare our results with those of alternative approaches.

We structure the remainder of this material as follows: Section 2 presents some fundamental concepts and properties of fractional calculus, as well as first-order shifted Chebyshev polynomials. In Section 3, we explore the fractional integro-differential system and transform it into two independent fractional integro-differential equations that may be studied using the method provided. Section 4 focuses on developing the projection method using shifted Chebyshev polynomials of the first order and we solve two algebraic problems. In Section 5, an error bound is established for the approximate solution achieved by the suggested method. Section 6 describes an application to a system of differential equations. Section 7 contains numerical test examples. Finally, in Section 8, the key conclusions are given.

2. Preliminaries

This section begins by examining the basic vocabulary and conceptual frameworks used in the field of fractional theory and shifted Chebyshev polynomials of the first kind.

2.1. Some Basic Concepts of Fractional Calculus

Definition 1

([42]). The gamma function, Γ, is described below:

$$\Gamma \left(\varsigma \right)=\underset{0}{\overset{+\infty }{\int }}{\mathrm{e}}^{-\tau }{\tau }^{\varsigma -1}d\tau ,\varsigma \in \mathbb{C},\mathit{Re}\left(\varsigma \right)>0.$$

(20)

Definition 2

([42]). The left-sided fractional Riemann–Liouville integral of order $\nu >0$ of integrable function $u:(0,\infty )\to \mathbb{R}$ is given as follows:

$${\mathfrak{R}}_{0_{+}}^{\nu }u\left(\upsilon \right):=\frac{1}{\Gamma \left(\nu \right)}{\int }_0^{\upsilon }\frac{u\left(\rho \right)}{{(\upsilon -\rho )}^{1-\nu }}d\rho ,\upsilon >0.$$

(21)

Definition 3

([42]). The left-sided fractional Riemann–Liouville derivative of order $\nu >0$ of integrable function $u:(0,\infty )\to \mathbb{R}$ is defined by

$${\mathcal{J}}_{0_{+}}^{\nu }u\left(\upsilon \right):=\frac{1}{\Gamma (1-\nu )}\frac{d}{d\upsilon }{\int }_0^{\upsilon }\frac{u\left(\rho \right)}{(\upsilon -\rho {)}^{\nu }}d\rho .$$

(22)

Definition 4

([42]). The Caputo fractional derivative of order $\nu >0$ for an absolutely continuous and integrable function $u:(0,\infty )\to \mathbb{R}$ is defined by

$${}^c\mathcal{J}_{0_{+}}^{\nu }u\left(\upsilon \right)={\mathfrak{R}}_{0_{+}}^{1-\nu }\frac{d}{d\upsilon }u\left(\upsilon \right)=\frac{1}{\Gamma (1-\nu )}{\int }_0^{\upsilon }{(\upsilon -\rho )}^{-\nu }{u}^{\prime }\left(\rho \right)d\rho .$$

(23)

Remark 1.

We have

$$\begin{array}{c}\hfill {}^c\mathcal{J}_{0_{+}}^{\nu }{\upsilon }^{\alpha }=\left\{\begin{array}{c}0,\mathit{for}\alpha \in \mathbb{N}\mathit{and}\alpha <\left[\nu \right],\hfill \\ \frac{\Gamma (\alpha +1)}{\Gamma (\alpha +1-\nu )}{\upsilon }^{\alpha -\nu },\mathit{for}\alpha \in \mathbb{N}\mathit{and}\alpha \ge \left[\nu \right]\mathit{or}\alpha \notin \mathbb{N}\mathit{and}\alpha >\left[\nu \right].\hfill \end{array}\right.\end{array}$$

(24)

Remark 2.

For $\nu >0$, we have

$${\mathcal{J}}_{0_{+}}^{\nu }u\left(\upsilon \right)=\frac{d}{d\upsilon }{\mathfrak{R}}_{0_{+}}^{1-\nu }u\left(\upsilon \right),$$

(25)

$${\mathfrak{R}}_{0_{+}}^{\nu }{\mathcal{J}}_{0_{+}}^{\nu }\left(u\left(\upsilon \right)-u\left(0\right)\right)=u\left(\upsilon \right)-u\left(0\right).$$

(26)

Remark 3.

For continuous function u, the relationship between the Caputo and Riemann–Liouville fractional derivatives is provided by

$${}^c\mathcal{J}_{0_{+}}^{\nu }u(\upsilon )={\mathcal{J}}_{0_{+}}^{\nu }(u(\upsilon )-u(0)),\nu >0.$$

(27)

In addition,

$${}^c\mathcal{J}_{0_{+}}^{\nu }u\left(\upsilon \right)={\mathcal{J}}_{0_{+}}^{\nu }\left(u\left(\upsilon \right)-\sum _{k=0}^{r-1}\frac{{\upsilon }^k}{k!}{u}^{\left(k\right)}\left(0\right)\right),\upsilon >0,r-1<\nu <r.$$

(28)

2.2. Shifted Chebyshev Polynomials of the First Kind

This subsection examines an important class of orthogonal polynomials. Through analytical formulas and recurrence relations, these polynomials can be combined to generate a new family of orthogonal polynomials referred as shifted Chebyshev polynomials.

Chebyshev polynomials ${\mathcal{E}}_n,n\in \mathbb{N}$ are described in the following manner:

$${\mathcal{E}}_n\left(\upsilon \right)=cos\left[narccos\left(\upsilon \right)\right],\mathrm{for} \mathrm{all}\upsilon \in [-1,1].$$

(29)

We can calculate ${\mathcal{E}}_n$ by using the explicit power series formula as follows:

$${\mathcal{E}}_n\left(\upsilon \right)=n\sum _{q=0}^{\lceil \frac{n}{2}\rceil }{(-1)}^q{2}^{n-2q-1}\frac{(n-q-1)!}{\left(q\right)!(n-2q)!}{\upsilon }^{n-2q},n=1,2,\dots .$$

(30)

Moreover, ${\mathcal{E}}_n$ are orthogonal polynomials with respect the following weight integral:

$$〈{\mathcal{E}}_m,{\mathcal{E}}_n〉={\int }_{-1}^1\frac{1}{\sqrt{1-{\upsilon }^2}}{\mathcal{E}}_m\left(\upsilon \right){\mathcal{E}}_n\left(\upsilon \right)d\upsilon =\left\{\begin{array}{cc}0,\hfill & n\ne m,\hfill \\ \frac{\pi }{2},\hfill & n=m\ne 0.\hfill \end{array}\right.$$

(31)

We let

$$\begin{array}{}\mathrm{(32)}& \hfill {\mathcal{E}}_n^{\mathcal{T}}\left(\upsilon \right)& =& {\mathcal{E}}_n(2\upsilon -1),n=0,2,3,\dots \hfill \mathrm{(33)}& & =& cos\left[narccos(2\upsilon -1)\right],\mathrm{for} \mathrm{all}\upsilon \in [0,1]\hfill \end{array}$$

indicate the corresponding orthogonal polynomials on $[0,1]$. We recall that

$$\begin{array}{ccc}\hfill {\mathcal{E}}_n^{\mathcal{T}}\left(\upsilon \right)& =& n\sum _{q=0}^n{(-1)}^{n-q}\frac{2^{2q}(n+q-1)!}{\left(2q\right)!(n-q)!}{\upsilon }^{q}n=1,2,3,\cdots \hfill \end{array}$$

(34)

Moreover,

$${〈{\mathcal{E}}_k^{\mathcal{T}},{\mathcal{E}}_j^{\mathcal{T}}〉}_{\omega }={\int }_0^1{\mathcal{E}}_k^{\mathcal{T}}\left(\upsilon \right){\mathcal{E}}_j^{\mathcal{T}}\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon =\left\{\begin{array}{cc}0,\hfill & k\ne j,\hfill \\ \pi ,\hfill & k=j=0,\hfill \\ \frac{\pi }{2},\hfill & k=j\ne 0.\hfill \end{array}\right.$$

(35)

Due to computational constraints, we employ the orthonormal basis of the shifted Chebyshev polynomials instead of the usual shifted Chebyshev polynomials. To this end, we introduce the following orthonormal basis of ${\mathcal{H}}_{\omega }$ as follows:

$${\mathcal{E}}_j^{\ast }:=\left\{\begin{array}{cc}\frac{{\mathcal{E}}_j^{\mathcal{T}}}{\sqrt{\pi }},\hfill & j=0,\hfill \\ \frac{\sqrt{2}{\mathcal{E}}_j^{\mathcal{T}}}{\sqrt{\pi }},\hfill & j\ne 0.\hfill \end{array}\right.$$

(36)

Thus,

$${\mathcal{E}}_j^{\ast }\left(\upsilon \right)=\left\{\begin{array}{cc}\frac{1}{\sqrt{\pi }},\hfill & j=0,\hfill \\ \frac{j\sqrt{2}}{\sqrt{\pi }}{\displaystyle \sum _{p=0}^j}{(-1)}^{j-p}\frac{2^{2p}(j+p-1)!}{\left(2p\right)!(j-p)!}{\upsilon }^p,\hfill & j\ne 0.\hfill \end{array}\right.$$

(37)

The first six terms of ${\mathcal{E}}_j^{\ast }$ are now explained:

$$\begin{array}{cc}\hfill {\mathcal{E}}_0^{\ast }\left(\upsilon \right)& =\frac{1}{\sqrt{\pi }},\hfill \\ \hfill {\mathcal{E}}_1^{\ast }\left(\upsilon \right)& =\frac{\sqrt{2}\left(2\upsilon -1\right)}{\sqrt{\pi }},\hfill \\ \hfill {\mathcal{E}}_2^{\ast }\left(\upsilon \right)& =\frac{\sqrt{2}\left(8{\upsilon }^2-8\upsilon +1\right)}{\sqrt{\pi }},\hfill \\ \hfill {\mathcal{E}}_3^{\ast }\left(\upsilon \right)& =\frac{\sqrt{2}\left(32{\upsilon }^3-48{\upsilon }^2+18\upsilon -1\right)}{\sqrt{\pi }},\hfill \\ \hfill {\mathcal{E}}_4^{\ast }\left(\upsilon \right)& =\frac{\sqrt{2}\left(128{\upsilon }^4-256{\upsilon }^3+160{\upsilon }^2-32\upsilon +1\right)}{\sqrt{\pi }},\hfill \\ \hfill {\mathcal{E}}_5^{\ast }\left(\upsilon \right)& =\frac{\sqrt{2}\left(512{\upsilon }^5-1280{\upsilon }^4+1120{\upsilon }^3-400{\upsilon }^2+50\upsilon -1\right)}{\sqrt{\pi }}.\hfill \end{array}$$

Chebyshev polynomials have received much attention because they are important in numerical analysis. This study emphasizes shifted Chebyshev polynomials, which are the first type. These polynomials have several intriguing and useful properties, including excellent approximation accuracy and the simplicity of numerical methods based on them.

3. Fractional Integro-Differential System

Let us consider the Lebesgue space of real-valued square integrable functions ${\mathcal{H}}_{\omega }:=L_{\omega }^2([0,1],\mathbb{R})$ on $[0,1]$, with respect to weight function

$$\omega \left(\upsilon \right):=\frac{1}{\sqrt{\upsilon -{\upsilon }^2}}.$$

Chebyshev polynomials of the first order are employed in this work to examine a projection approach for treating a system of fractional integro-differential equations of the form

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle a{}^c\mathcal{J}_{0_{+}}^{\nu }𝓁\left(\upsilon \right)+b𝓁\left(\upsilon \right)+c{𝓁}^{\prime }\left(\upsilon \right)+d{\int }_0^1\psi \left(\upsilon ,\rho \right)\lambda \left(\rho \right)d\rho =\sigma \left(\upsilon \right),0\le \upsilon \le 1,}\hfill \\ a{}^c\mathcal{J}_{0_{+}}^{\nu }\lambda \left(\upsilon \right)+b\lambda \left(\upsilon \right)+c{\lambda }^{\prime }\left(\upsilon \right)+d{\int }_0^1\psi \left(\upsilon ,\rho \right)𝓁\left(\rho \right)d\rho =\varsigma \left(\upsilon \right),0\le \upsilon \le 1,\hfill \\ {\displaystyle \sum _{k=0}^{r-1}}\frac{{\upsilon }^k}{k!}{𝓁}^{\left(k\right)}\left(0\right)=0,{\displaystyle \sum _{k=0}^{r-1}}\frac{{\upsilon }^k}{k!}{\lambda }^{\left(k\right)}\left(0\right)=0,r-1<\nu <r.\hfill \end{array}\right.\end{array}$$

(38)

According to [39], we examine the subsequent changing:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \chi :=\lambda -𝓁,\Psi :=\varsigma +\sigma ,}\hfill \\ \vartheta :=\lambda +𝓁,\zeta :=\varsigma -\sigma .\hfill \end{array}\right.\end{array}$$

(39)

The main goal of the four transformations is to turn coupled System (40) into a system of two separate fractional integro-differential equations, which can then be examined via the given method.

Lemma 1.

Problem (38) reads as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle a{}^c\mathcal{J}_{0_{+}}^{\nu }\vartheta +b\vartheta +c{\vartheta }^{\prime }+d{\int }_0^1\psi \left(.,\rho \right)\vartheta \left(\rho \right)d\rho =\Psi ,}\hfill \\ a{}^c\mathcal{J}_{0_{+}}^{\nu }\chi +b\chi +c{\chi }^{\prime }-d{\int }_0^1\psi \left(.,\rho \right)\chi \left(\rho \right)d\rho =\zeta .\hfill \end{array}\right.\end{array}$$

(40)

Proof. 

We have

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \lambda =\frac{\vartheta +\chi }{2},\sigma =\frac{\Psi -\zeta }{2},}\hfill \\ 𝓁=\frac{\vartheta -\chi }{2},\varsigma =\frac{\Psi +\zeta }{2}.\hfill \end{array}\right.\end{array}$$

(41)

By putting them into (38), we obtain

$$\begin{array}{cc}\hfill a{}^c\mathcal{J}_{0_{+}}^{\nu }(\vartheta -\chi )+b(\vartheta -\chi )+c{(\vartheta -\chi )}^{\prime }+d{\int }_0^1\psi (.,\rho )\lambda \left(\rho \right)d\rho & =\Psi -\zeta ,\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill a{}^c\mathcal{J}_{0_{+}}^{\nu }\left(\vartheta +\chi \right)+b\left(\vartheta +\chi \right)+c{\left(\vartheta +\chi \right)}^{\prime }+d{\int }_0^1\psi \left(.,\rho \right)\left(\vartheta -\chi \right)\left(\rho \right)d\rho & =\Psi +\zeta .\hfill \end{array}$$

(43)

Equations (42) and (43) are added together, and then (42) is subtracted from (43) to yield (40). □

Denoting by $\mathcal{B}$ the integral operator, i.e.,

$$\left(\mathcal{B}𝓁\right)\left(\upsilon \right):={\int }_0^1\psi \left(\upsilon ,\rho \right)𝓁\left(\rho \right)d\rho ,0\le \upsilon \le 1,$$

and setting

$$\mathcal{D}:=\left\{\lambda \in {\mathcal{H}}_{\omega }:{\lambda }^{\left(k\right)}\in {\mathcal{H}}_{\omega },\sum _{k=0}^{r-1}\frac{{\upsilon }^k}{k!}{\lambda }^{\left(k\right)}\left(0\right)=0,r-1<\nu <r\right\},$$

System (40) can be expressed in this way in the operator form:

$$\left\{\begin{array}{c}{\displaystyle a{}^c\mathcal{J}_{0_{+}}^{\nu }\vartheta +b\vartheta +c{\vartheta }^{\prime }+d\mathcal{B}\vartheta =\Psi ,}\hfill \\ a{}^c\mathcal{J}_{0_{+}}^{\nu }\chi +b\chi +c{\chi }^{\prime }-d\mathcal{B}\chi =\zeta .\hfill \end{array}\right.$$

(44)

It is important to remember that operator $\mathcal{B}$ is compact from ${\mathcal{H}}_{\omega }$ into itself.

Furthermore,

$${\mathfrak{R}}_{0_{+}}^{\nu }{}^c\mathcal{J}_{0_{+}}^{\nu }\lambda \left(\upsilon \right)=\lambda \left(\upsilon \right)-\sum _{k=0}^{r-1}\frac{{\upsilon }^k}{k!}{\lambda }^{\left(k\right)}\left(0\right),$$

(45)

and

$${\mathfrak{R}}_{0_{+}}^{\nu }{}^c\mathcal{J}_{0_{+}}^{\nu }\lambda (\upsilon )=\lambda (\upsilon ),\mathrm{for} \mathrm{all}\lambda \in \mathcal{D}.$$

(46)

Also, ${\mathfrak{R}}_{0_{+}}^{\nu }:{\mathcal{H}}_{\omega }\to \mathcal{D}$ is compact.

4. Development of the Method

By ${\mathfrak{P}}_n^{\mathcal{E}}$, the chain of bounded and finite rank orthogonal projections is denoted, outlined by

$${\mathfrak{P}}_n^{\mathcal{E}}\psi :=\sum _{j=0}^{n-1}{〈\psi ,{\mathcal{E}}_j^{\ast }〉}_{\omega }{\mathcal{E}}_j^{\ast },\mathrm{where}{〈\psi ,{\mathcal{E}}_j^{\ast }〉}_{\omega }:={\int }_0^1\omega \left(\sigma \right)\psi \left(\sigma \right){\mathcal{E}}_j^{\ast }\left(\sigma \right)d\sigma .$$

(47)

The corresponding norm on ${\mathcal{H}}_{\omega }$ is denoted by ${\parallel ·\parallel }_{\omega }$. Thus,

$$\underset{n\to \infty }{lim}{\parallel {\mathfrak{P}}_n^{\mathcal{F}}\vartheta -\vartheta \parallel }_{\omega }=0,\mathrm{for} \mathrm{all}\vartheta \in {\mathcal{H}}_{\omega }.$$

(48)

We let ${\mathcal{H}}_{\omega ,n}$ represent the space covered by the first n-orthonormal shifted Chebyshev polynomials of first kind. It is obvious that ${\mathfrak{R}}_{0_{+}}^{\nu }\left({\mathcal{H}}_{\omega ,n}\right)={\mathcal{H}}_{\omega ,n+1}$.

System (44) reads as follows:

$$\left\{\begin{array}{c}{\displaystyle a\vartheta +b{\mathfrak{R}}_{0_{+}}^{\nu }\vartheta +c{\mathfrak{R}}_{0_{+}}^{\nu -1}\vartheta +d\mathcal{B}{\mathfrak{R}}_{0_{+}}^{\nu }\vartheta ={\mathfrak{R}}_{0_{+}}^{\nu }\Psi ,}\hfill \\ a\chi +b{\mathfrak{R}}_{0_{+}}^{\nu }\chi +c{\mathfrak{R}}_{0_{+}}^{\nu -1}\chi -d\mathcal{B}{\mathfrak{R}}_{0_{+}}^{\nu }\chi ={\mathfrak{R}}_{0_{+}}^{\nu }\zeta .\hfill \end{array}\right.$$

(49)

The approximate solution of System (49) is denoted by $\left({\vartheta }_n,{\chi }_n\right)$. The corresponding approach system is as follows:

$$\left\{\begin{array}{c}{\displaystyle a{\vartheta }_n+b{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}{\vartheta }_n+c{\mathfrak{R}}_{0_{+}}^{\nu -1}{\mathfrak{P}}_n^{\mathcal{E}}{\vartheta }_n+d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}{\vartheta }_n={\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\Psi ,}\hfill \\ a{\chi }_n+b{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}{\chi }_n+c{\mathfrak{R}}_{0_{+}}^{\nu -1}{\mathfrak{P}}_n^{\mathcal{E}}{\chi }_n-d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}{\chi }_n={\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\zeta .\hfill \end{array}\right.$$

(50)

Alternatively,

$$\left\{\begin{array}{c}{\displaystyle a{\vartheta }_n+b{\mathfrak{R}}_{0_{+}}^{\nu }{\vartheta }_n+c{\mathfrak{R}}_{0_{+}}^{\nu -1}{\vartheta }_n+d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}{\vartheta }_n={\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\Psi ,}\hfill \\ a{\chi }_n+b{\mathfrak{R}}_{0_{+}}^{\nu }{\chi }_n+c{\mathfrak{R}}_{0_{+}}^{\nu -1}{\chi }_n-d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}{\chi }_n={\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\zeta .\hfill \end{array}\right.$$

(51)

We suppose that both operators $a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}+d{\mathfrak{R}}_{0_{+}}^{\nu }\mathcal{B}$ and $a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}-d{\mathfrak{R}}_{0_{+}}^{\nu }\mathcal{B}$ are invertible.

We know that ${\mathfrak{R}}_{0_{+}}^{\nu }$ is compact and

$$\underset{n\to \infty }{lim}\parallel \left({\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}-{\mathfrak{R}}_{0_{+}}^{\nu }\mathcal{B}\right){\mathfrak{R}}_{0_{+}}^{\nu }\mathcal{B}\parallel =0,\underset{n\to \infty }{lim}\parallel \left({\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}-{\mathfrak{R}}_{0_{+}}^{\nu }\mathcal{B}\right){\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}\parallel =0.$$

(52)

Writing

$$\left\{\begin{array}{c}{\displaystyle {\vartheta }_n=\sum _{k=0}^n{\beta }_{n,k}{\mathcal{E}}_k^{\ast },}\hfill \\ {\chi }_n={\displaystyle \sum _{k=0}^n}{\gamma }_{n,k}{\mathcal{E}}_k^{\ast },\hfill \end{array}\right.$$

(53)

we have

$$\begin{array}{c}\hfill {}^c\mathcal{J}_{0_{+}}^{\nu }\left({\mathcal{E}}_j^{\ast }\left(\upsilon \right)\right)=0,j=0,1,\dots ,\lceil \nu \rceil -1,\nu >0.\end{array}$$

(54)

Moreover, for $j=\lceil \nu \rceil ,\lceil \nu \rceil +1,\dots ,n-1,$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}^c\mathcal{J}_{0_{+}}^{\nu }{\mathcal{E}}_j^{\ast }\left(\upsilon \right)=& j\sum _{p=\lceil \nu \rceil }^j{(-1)}^{j-p}\frac{2^{2p}(j+p-1)!}{(j-p)!\left(2p\right)!}{}^c\mathcal{J}_{0_{+}}^{\nu }{\upsilon }^p\hfill \\ \hfill =& j\sum _{p=\lceil \nu \rceil }^j{(-1)}^{j-p}\frac{2^{2p}(j+p-1)!\Gamma (p+1)}{(j-p)!\left(2p\right)!\Gamma (p+1-\nu )}{\upsilon }^{p-\nu }.\hfill \end{array}\end{array}$$

Thus,

$$\begin{array}{ccc}\hfill {}^c\mathcal{J}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\psi \left(\upsilon \right)& =& \sum _{j=0}^{n-1}{〈\psi ,{\mathcal{E}}_j^{\ast }〉}_{\omega }{}^c\mathcal{J}_{0_{+}}^{\nu }{\mathcal{E}}_j^{\ast }\left(\upsilon \right)\hfill \\ & =& \sum _{j=\lceil \mu \rceil }^{n-1}\sum _{p=\lceil \mu \rceil }^i{〈\psi ,{\mathcal{E}}_j^{\ast }〉}_{\omega }{(-1)}^{j-p}\frac{2^{2p}j(j+p-1)!\Gamma (k+1)}{(j-p)!\left(2p\right)!\Gamma (p+1-\nu )}{\upsilon }^{p-\mu }.\hfill \end{array}$$

(55)

The following two independent linear systems can be solved to obtain $2n+2$ unknowns ${\beta }_{n,k}$ and ${\gamma }_{n,k}$:

$$\left\{\begin{array}{c}{\displaystyle \sum _{k=0}^n{\beta }_{n,k}\left[a{}^c\mathcal{J}_{0_{+}}^{\nu }+b{\mathcal{E}}_k^{\ast }+c{\left({\mathcal{E}}_k^{\ast }\right)}^{\prime }+d{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}{\mathcal{E}}_k^{\ast }\right]={\mathfrak{P}}_n^{\mathcal{E}}\Psi ,\mathrm{with}\sum _{k=0}^n{\beta }_{n,k}{\mathcal{E}}_k^{\ast }\left(0\right)=0,}\hfill \\ {\displaystyle \sum _{k=0}^n}{\gamma }_{n,k}\left[a{}^c\mathcal{J}_{0_{+}}^{\nu }+b{\mathcal{E}}_k^{\ast }+c{\left({\mathcal{E}}_k^{\ast }\right)}^{\prime }-d{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}{\mathcal{E}}_k^{\ast }\right]={\mathfrak{P}}_n^{\mathcal{E}}\zeta ,\mathrm{with}{\displaystyle \sum _{k=0}^n}{\gamma }_{n,k}{\mathcal{E}}_k^{\ast }\left(0\right)=0.\hfill \end{array}\right.$$

(56)

Consequently, two separate linear systems are produced:

$$\left\{\begin{array}{c}{\displaystyle b{\beta }_{n,k}+\sum _{m=0}^n{P}_n(k,m){\beta }_{n,m}=T_{n,k},k=0,\cdots ,n,}\hfill \\ b{\gamma }_{n,k}+{\displaystyle \sum _{m=0}^n}{\widehat{P}}_n(k,m){\gamma }_{n,m}={\widehat{T}}_{n,k},k=0,\cdots ,n,\hfill \end{array}\right.$$

(57)

where, for $k=0,\cdots ,n-1$ and $m=0,\cdots ,n$,

$$\begin{array}{ccc}\hfill P_n(k,m)& :=& a{\int }_0^1{}^c\mathcal{J}_{0_{+}}^{\nu }{\mathcal{E}}_m^{\ast }\left(\upsilon \right){\mathcal{E}}_k^{\ast }\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon +c{\int }_0^1{\left({\mathcal{E}}_m^{\ast }\right)}^{\prime }\left(\upsilon \right){\mathcal{E}}_k^{\ast }\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon \hfill \\ & +& d{\int }_0^1\left({\int }_0^1{\mathcal{E}}_m^{\ast }\left(\rho \right)\psi \left(\upsilon ,\rho \right)d\rho \right){\mathcal{E}}_k^{\ast }\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon ,\hfill \\ \hfill {\widehat{P}}_n(k,m)& :=& a{\int }_0^1{}^c\mathcal{J}_{0_{+}}^{\nu }{\mathcal{E}}_m^{\ast }\left(\upsilon \right){\mathcal{E}}_k^{\ast }\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon +c{\int }_0^1{\left({\mathcal{E}}_m^{\ast }\right)}^{\prime }\left(\upsilon \right){\mathcal{E}}_k^{\ast }\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon \hfill \\ & -& d{\int }_0^1\left({\int }_0^1{\mathcal{E}}_m^{\ast }\left(\rho \right)\psi \left(\upsilon ,\rho \right)d\rho \right){\mathcal{E}}_k^{\ast }\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon ,\hfill \\ \hfill P_n(n,m)& :=& {\mathcal{E}}_m^{\ast }\left(0\right),{\widehat{P}}_n(n,m):={\mathcal{E}}_m^{\ast }\left(0\right),\hfill \\ \hfill T_n\left(k\right)& :=& {\int }_0^1\Psi \left(\upsilon \right){\mathcal{E}}_k^{\ast }\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon ,{\widehat{T}}_n\left(k\right):={\int }_0^1\zeta \left(\upsilon \right){\mathcal{E}}_k^{\ast }\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon ,\hfill \\ \hfill T_n\left(n\right)& :=& 0,{\widehat{T}}_n\left(n\right):=0.\hfill \end{array}$$

For $k=0,1,\dots ,\lceil \nu \rceil -1$ and $m=0,1,\dots ,\lceil \nu \rceil -1,\nu >0$

$$\begin{array}{ccc}\hfill {\int }_0^1\left({\int }_0^1{\mathcal{E}}_m^{\ast }\left(\rho \right)\psi \left(\upsilon ,\rho \right)d\rho \right){\mathcal{E}}_k^{\ast }\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon & =& \frac{2km}{\pi }\sum _{p=0}^k\sum _{s=0}^m{A}_{p,s}{\int }_0^1\left({\int }_0^1\psi \left(\upsilon ,\rho \right){\rho }^{k}d\rho \right){\upsilon }^m\omega \left(\upsilon \right)d\upsilon ,\hfill \end{array}$$

where

$$A_{p,s}={(-1)}^{k-p+m-s}\frac{2^{2(p+s)}(k+p-1)!(m+s-1)!}{\left(2p\right)!\left(2s\right)!(k-p)!(m-s)!}.$$

Once the two systems are solved, the solutions are built as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle {\lambda }_n=\frac{1}{2}\sum _{k=0}^n\left[{\beta }_{n,k}+{\gamma }_{n,k}\right]{\mathcal{E}}_k^{\ast },}\hfill \\ {𝓁}_n=\frac{1}{2}{\displaystyle \sum _{k=0}^n}\left[{\beta }_{n,k}-{\gamma }_{n,k}\right]{\mathcal{E}}_k^{\ast }.\hfill \end{array}\right.\end{array}$$

(58)

In this method, a projection strategy for performing a system of fractional integro-differential equations of Form (38) is studied using Chebyshev polynomials of the first order. We first convert coupled System (40) into a system of two distinct fractional integro-differential equations. Next, we use the current method to investigate the produced equations. Two algebraic systems follow. In the end, we accomplish building the solutions of System (38).

5. Convergence Analysis

Now, we establish the convergence of the current method. To this end, let us introduce Sobolev space $H_{\varpi }^m([0,1],$$\mathbb{R})$ order $m\ge 0$ outfitted with the following norm:

$${∥\varphi ∥}_{\varpi ,m}^2=\sum _{k=0}^m{∥{\varphi }^{\left(k\right)}∥}_{\omega }^2.$$

(59)

Following [43], we have

$${∥(\mathcal{I}-{\mathfrak{P}}_n^{\ast })\gamma ∥}_{\varpi }\le \frac{G}{n^m},\mathrm{for} \mathrm{all}\gamma \in H_{\varpi }^m([0,1],\mathbb{R})\mathrm{and} \mathrm{for} \mathrm{some} \mathrm{constant}G>0.$$

(60)

Here, $\mathcal{I}$ denotes the identity operator. Since $b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}+d{\mathfrak{R}}_{0_{+}}^{\nu }\mathcal{B}$ and $b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}-d{\mathfrak{R}}_{0_{+}}^{\nu }\mathcal{B}$ are compact, operators ${(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}+d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B})}^{-1}$ and ${(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}-d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B})}^{-1}$ exist and are uniformly bounded with regard to n, for n large enough.

Theorem 1

([44]). If

$${\psi }_n=\sum _{j=0}^n{c}_j{\mathcal{E}}_j^{\ast },$$

(61)

then

$$\begin{array}{c}\hfill E_{{\mathcal{E}}^{\ast }}\left(n\right):=\mid \psi \left(\upsilon \right)-{\psi }_n\left(\upsilon \right)\mid \le \sum _{j=n+1}^{\infty }\mid c_j\mid ,\upsilon \in [0,1].\end{array}$$

(62)

Theorem 2.

Assume that $\varsigma ,\sigma ,\mathcal{B}\lambda ,\mathcal{B}𝓁\in H_{\varpi }^m([0,1],\mathbb{R})$. Then, there exist $G_1,G_2>0$ such that

$$\parallel {\vartheta }_n{-\vartheta \parallel }_{\varpi }\le \frac{G_1}{n^m},$$

(63)

and

$$\parallel {\chi }_n{-\chi \parallel }_{\varpi }\le \frac{G_2}{n^m}.$$

(64)

Proof. 

In fact,

$$\left\{\begin{array}{c}{\displaystyle a{\vartheta }_n+b{\mathfrak{R}}_{0_{+}}^{\nu }{\vartheta }_n+c{\mathfrak{R}}_{0_{+}}^{\nu -1}{\vartheta }_n+d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}{\vartheta }_n={\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\Psi ,}\hfill \\ a{\chi }_n+b{\mathfrak{R}}_{0_{+}}^{\nu }{\chi }_n+c{\mathfrak{R}}_{0_{+}}^{\nu -1}{\chi }_n-d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\mathcal{B}{\chi }_n={\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}\zeta .\hfill \end{array}\right.$$

(65)

Moreover,

$$\begin{array}{cc}\hfill \vartheta -{\vartheta }_n& ={\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}+d{\mathfrak{R}}_{0_{+}}^{\nu }\mathcal{B}\right)}^{-1}{\mathfrak{R}}_{0_{+}}^{\nu }\Psi \hfill \\ \hfill & -{\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}+d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B}\right)}^{-1}{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\Psi \hfill \\ \hfill & +{\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}+d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B}\right)}^{-1}{\mathfrak{R}}_{0_{+}}^{\nu }\Psi \hfill \\ \hfill & -{\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu }+d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B}\right)}^{-1}{\mathfrak{R}}_{0_{+}}^{\nu }\Psi \hfill \\ \hfill & ={\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}+d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B}\right)}^{-1}{\mathfrak{R}}_{0_{+}}^{\nu }\left[d\left({\mathfrak{P}}_n^{\ast }-\mathcal{I}\right)\mathcal{B}\vartheta +\left(\mathcal{I}-{\mathfrak{P}}_n^{\ast }\right)\Psi \right].\hfill \end{array}$$

In addition,

$$\begin{array}{cc}\hfill \chi -{\chi }_n& ={\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}-d{\mathfrak{R}}_{0_{+}}^{\nu }\mathcal{B}\right)}^{-1}{\mathfrak{R}}_{0_{+}}^{\nu }\zeta \hfill \\ \hfill & -{\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}-d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B}\right)}^{-1}{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\zeta \hfill \\ \hfill & +{\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}-d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B}\right)}^{-1}{\mathfrak{R}}_{0_{+}}^{\nu }\zeta \hfill \\ \hfill & -{\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu }-d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B}\right)}^{-1}{\mathfrak{R}}_{0_{+}}^{\nu }\zeta \hfill \\ \hfill & ={\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}-d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B}\right)}^{-1}{\mathfrak{R}}_{0_{+}}^{\nu }\left[d\left(\mathcal{I}-{\mathfrak{P}}_n^{\ast }\right)\mathcal{B}\chi +\left(\mathcal{I}-{\mathfrak{P}}_n^{\ast }\right)\Psi \right].\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill \vartheta -{\vartheta }_n& ={\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}+d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B}\right)}^{-1}{\mathfrak{R}}_{0_{+}}^{\nu }\left[d\left({\mathfrak{P}}_n^{\ast }-\mathcal{I}\right)\mathcal{B}(\lambda +𝓁)+\left(\mathcal{I}-{\mathfrak{P}}_n^{\ast }\right)(\varsigma +\sigma )\right].\hfill \end{array}$$

Also,

$$\begin{array}{cc}\hfill \chi -{\chi }_n& ={\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}-d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B}\right)}^{-1}{\mathfrak{R}}_{0_{+}}^{\nu }\left[d\left(\mathcal{I}-{\mathfrak{P}}_n^{\ast }\right)\mathcal{B}(\lambda -𝓁)+\left(\mathcal{I}-{\mathfrak{P}}_n^{\ast }\right)(\varsigma -\sigma )\right].\hfill \end{array}$$

Letting

$$\begin{array}{cc}\hfill Q_1& :=∥{\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}+d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B}\right)}^{-1}∥∥{\mathfrak{R}}_{0_{+}}^{\nu }∥,\hfill \\ \hfill Q_2& :=∥{\left(a\mathcal{I}+b{\mathfrak{R}}_{0_{+}}^{\nu }+c{\mathfrak{R}}_{0_{+}}^{\nu -1}-d{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\ast }\mathcal{B}\right)}^{-1}∥∥{\mathfrak{R}}_{0_{+}}^{\nu }∥,\hfill \end{array}$$

we obtain

$$\begin{array}{cc}\hfill {∥\vartheta -{\vartheta }_n∥}_{\varpi }& \le Q_1\left[d{∥\left(\mathcal{I}-{\mathfrak{P}}_n^{\ast }\right)\mathcal{B}(\lambda +𝓁)∥}_{\varpi }+{∥\left(\mathcal{I}-{\mathfrak{P}}_n^{\ast }\right)(\varsigma +h)∥}_{\varpi }\right]\hfill \\ \hfill & \le Q_1\left[\frac{G_3+G_4}{n^m}\right],\mathrm{for} \mathrm{some} \mathrm{constants}{G}_3,G_4>0.\hfill \end{array}$$

Moreover,

$$\begin{array}{cc}\hfill {∥\chi -{\chi }_n∥}_{\varpi }& \le Q_2\left[d{∥\left(I-{\mathfrak{P}}_n^{\ast }\right)\mathcal{B}(\lambda -𝓁)∥}_{\varpi }+{∥\left(I-{\mathfrak{P}}_n^{\ast }\right)(\varsigma -\sigma )∥}_{\varpi }\right]\hfill \\ \hfill & \le Q_2\left[\frac{G_5+G_6}{n^m}\right],\mathrm{for} \mathrm{some} \mathrm{constants}{G}_5,G_6>0\hfill \end{array}$$

Letting

$$G_1:=Q_{1}max\left\{G_3,G_4\right\}\mathrm{and}{G}_2:=Q_{2}max\left\{G_5,G_6\right\},$$

we accomplish the required outcomes. □

Proposition 1.

There exists $G>0$ such that

$$\parallel {\lambda }_n{-\lambda \parallel }_{\varpi }\le \frac{G}{2n^m},$$

(66)

and

$$\parallel {𝓁}_n{-𝓁\parallel }_{\varpi }\le \frac{G}{2n^m}.$$

(67)

Proof. 

In fact,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle {\lambda }_n=\frac{{\vartheta }_n+{\chi }_n}{2},}\hfill \\ {𝓁}_n=\frac{{\vartheta }_n-{\chi }_n}{2}.\hfill \end{array}\right.\end{array}$$

(68)

So,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \lambda -{\lambda }_n=\frac{\left(\vartheta -{\vartheta }_n\right)+\left(\chi -{\chi }_n\right)}{2},}\hfill \\ 𝓁-{𝓁}_n=\frac{\left(\vartheta -{\vartheta }_n\right)+\left({\chi }_n-\chi \right)}{2}.\hfill \end{array}\right.\end{array}$$

(69)

Thus,

$$\begin{array}{c}\hfill {∥\lambda -{\lambda }_n∥}_{\varpi }=\frac{{∥\vartheta -{\vartheta }_n∥}_{\varpi }+{∥\chi -{\chi }_n∥}_{\varpi }}{2},\end{array}$$

(70)

$$\begin{array}{c}\hfill {∥𝓁-{𝓁}_n∥}_{\varpi }=\frac{{∥\vartheta -{\vartheta }_n∥}_{\varpi }+{∥\chi -{\chi }_n∥}_{\varpi }}{2}.\end{array}$$

(71)

By applying Theorem 2, the intended outcomes are achieved, with $G:=G_1+G_2$. □

6. Applications to Differential Equation

The method described above can be easily examined in some important cases. We implement the present approach to a significant fractional differential problem in this part. We analyze this problem to demonstrate the efficacy of the present technique. This case is examined because it is a focal point of interest for numerous scholars across various scientific and technological fields. By employing fractional calculus, it is possible to model a physical phenomenon accurately that is influenced by the current time and its history.

Here, we consider the following differential problem:

$$a{}^c\mathcal{J}_{0_{+}}^{\nu }y\left(\upsilon \right)+\mathit{by}\left(\upsilon \right)+{\mathit{cy}}^{\prime }\left(\upsilon \right)=f\left(\upsilon \right),y\left(0\right)=0y^{\prime }\left(0\right)=00\le \upsilon \le 1.$$

(72)

In this case, Equation (72) reads as follows:

$$ay+b{\mathfrak{R}}_{0_{+}}^{\nu }y+c{\mathfrak{R}}_{0_{+}}^{\nu -1}y={\mathfrak{R}}_{0_{+}}^{\nu }f.$$

(73)

The corresponding approximate equation is as follows:

$$a{y}_n+b{\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}{y}_n+c{\mathfrak{R}}_{0_{+}}^{\nu -1}{\mathfrak{P}}_n^{\mathcal{E}}{y}_n={\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}f$$

(74)

or

$$a{y}_n+b{\mathfrak{R}}_{0_{+}}^{\nu }{y}_n+c{\mathfrak{R}}_{0_{+}}^{\nu -1}{y}_n={\mathfrak{R}}_{0_{+}}^{\nu }{\mathfrak{P}}_n^{\mathcal{E}}f.$$

(75)

Writing

$$y_n=\sum _{k=0}^n{c}_{n,k}{\mathcal{E}}_k^{\ast },$$

(76)

the following linear system can be solved to yield $n+1$ unknowns $c_{n,k}$:

$$\sum _{k=0}^n{c}_{n,k}\left[a{}^c\mathcal{J}_{0_{+}}^{\nu }+b{\mathcal{E}}_k^{\ast }+c{\left({\mathcal{E}}_k^{\ast }\right)}^{\prime }\right]={\mathfrak{P}}_n^{\mathcal{E}}f,\mathrm{with}\sum _{k=0}^n{\beta }_{n,k}{\mathcal{E}}_k^{\ast }\left(0\right)=0.$$

(77)

Consequently, the following linear system is produced,

$$b{c}_{n,k}+\sum _{m=0}^n{A}_n(k,m)c_{n,m}=b_{n,k},k=0,\cdots ,n.$$

(78)

Moreover, for $m=0,\cdots ,n$ and $k=0,\cdots ,n-1$,

$$\begin{array}{ccc}\hfill A_n(k,m)& :=& a{\int }_0^1{}^c\mathcal{J}_{0_{+}}^{\nu }{\mathcal{E}}_m^{\ast }\left(\upsilon \right){\mathcal{E}}_k^{\ast }\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon +c{\int }_0^1{\left({\mathcal{E}}_m^{\ast }\right)}^{\prime }\left(\upsilon \right){\mathcal{E}}_k^{\ast }\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon \hfill \\ \hfill A_n(n,m)& :=& {\mathcal{E}}_m^{\ast }\left(0\right),\hfill \\ \hfill b_n\left(k\right)& :=& {\int }_0^1\Psi \left(\upsilon \right){\mathcal{E}}_k^{\ast }\left(\upsilon \right)\omega \left(\upsilon \right)d\upsilon ,\hfill \\ \hfill b_n\left(n\right)& :=& 0.\hfill \end{array}$$

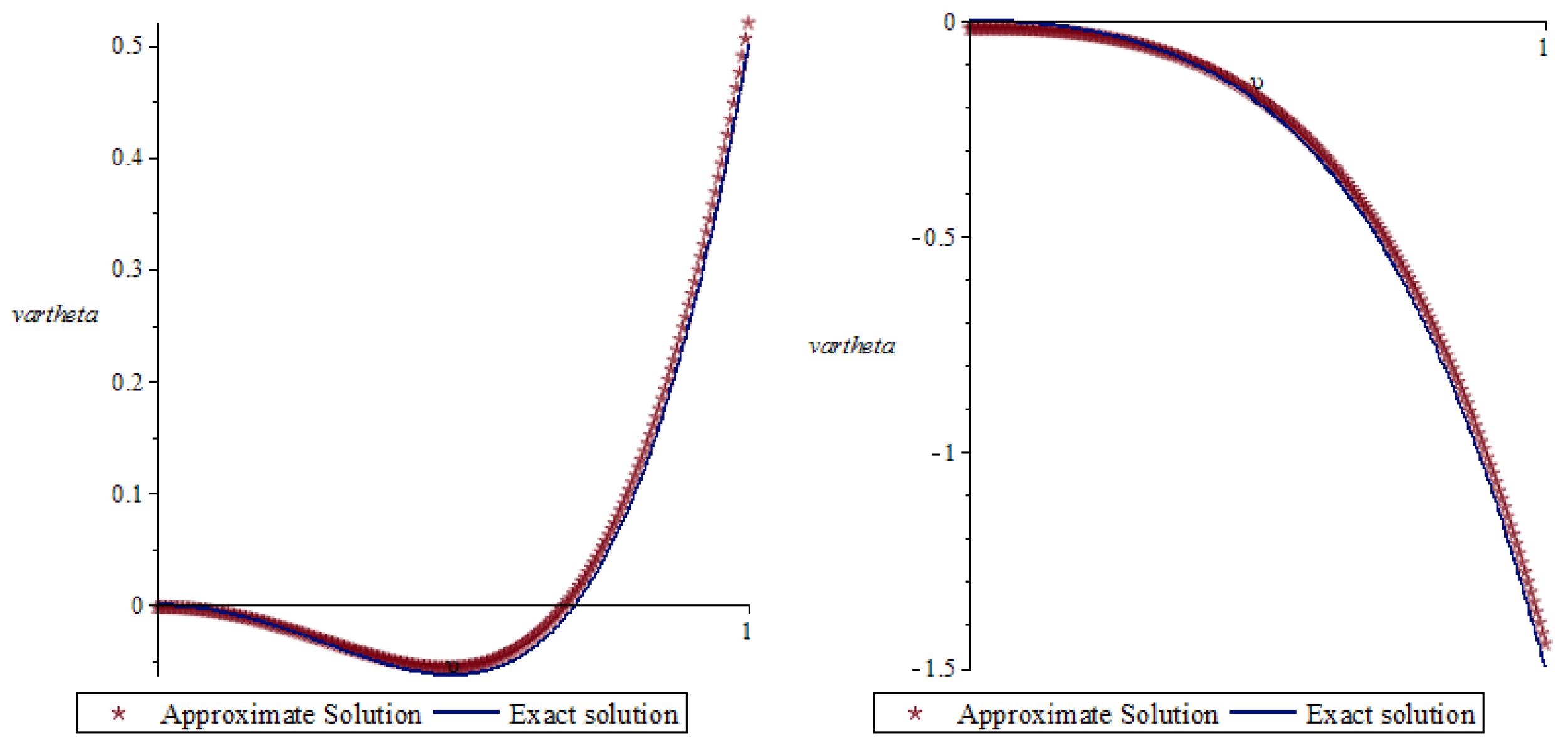
7. Numerical Simulations

This section includes some simulations to demonstrate prior results. These numerical evaluations were carried out using the Maple programming language.

Example 1.

In this first example, we illustrate fractional integro-differential System (38) that possesses the exact solutions shown below:

$$\begin{array}{c}\hfill 𝓁\left(\upsilon \right)=\frac{1}{2}\left({\upsilon }^5-{\upsilon }^7\right),\lambda \left(\upsilon \right)=\frac{1}{2}\left({\upsilon }^5+{\upsilon }^7\right),\nu =\frac{3}{4}.\end{array}$$

So,

$$\begin{array}{c}\hfill \vartheta \left(\upsilon \right)={\upsilon }^5,\chi \left(\upsilon \right)=-{\upsilon }^7,\end{array}$$

and

$$\begin{array}{ccc}\hfill \Psi \left(\upsilon \right)& =& \frac{{\upsilon }^2}{63\sqrt{\pi }}\left[63{\upsilon }^3\sqrt{\pi }+256{\upsilon }^{\frac{5}{2}}\pi +9\sqrt{\pi }\right].\hfill \end{array}$$

Also,

$$\begin{array}{c}\hfill \zeta \left(\upsilon \right)=-\frac{{\upsilon }^2}{1287\sqrt{\pi }}\left[1287{\upsilon }^5\sqrt{\pi }+6144{\upsilon }^{\frac{9}{2}}-143\sqrt{\pi }\right].\end{array}$$

We accomplish some simulations showing the efficacy of this instance. For example, for $n=7$, unknowns ${\beta }_{7,0}\cdots {\beta }_{7,7}$ are described as follows:

$$\begin{array}{ccc}\hfill {\beta }_{7,0}& =& 0.31823,{\beta }_{7,1}=0.52785,\hfill \\ \hfill {\beta }_{7,2}& =& 0.29802,{\beta }_{7,3}=0.11040,\hfill \\ \hfill {\beta }_{7,4}& =& 0.024445\times {10}^{-1},{\beta }_{7,5}=0.24568\times {10}^{-2},\hfill \\ \hfill {\beta }_{7,6}& =& -0.28004\times {10}^{-5},{\beta }_{7,7}=9.1014\times {10}^{-7}.\hfill \end{array}$$

Approximate solution ${\vartheta }_7$ is offered by

$$\begin{array}{ccc}\hfill {\vartheta }_7\left(\upsilon \right)& =& -0.27925\times {10}^{-3}\upsilon -0.47632\times {10}^{-1}{\upsilon }^4-0.25396\times {10}^{-1}{\upsilon }^6+0.59487\times {10}^{-2}{\upsilon }^7\hfill \\ & +& 1.0461{\upsilon }^5+0.35983\times {10}^{-1}{\upsilon }^3-0.12375\times {10}^{-4}-4+0.77152\times {10}^{-2}{\upsilon }^2.\hfill \end{array}$$

Moreover,

$$\begin{array}{ccc}\hfill {\gamma }_{7,0}& =& -0.25316,{\gamma }_{7,1}=-0.44638,\hfill \\ \hfill {\gamma }_{7,2}& =& -0.30230,{\gamma }_{7,3}=-0.15293,\hfill \\ \hfill {\gamma }_{7,4}& =& -0.055729,{\gamma }_{7,5}=-0.013917,\hfill \\ \hfill {\gamma }_{7,6}& =& -0.0021442,{\gamma }_{7,7}=-0.00015237.\hfill \end{array}$$

Approximate solution ${\chi }_7$ is presented by

$$\begin{array}{ccc}\hfill {\chi }_7\left(\upsilon \right)& =& -0.20744\times {10}^{-3}\upsilon -0.99588{\upsilon }^7+0.82657\times {10}^{-2}{\upsilon }^2+0.29487\times {10}^{-1}{\upsilon }^3\hfill \\ & -& 0.35584\times {10}^{-1}{\upsilon }^4+0.33095\times {10}^{-1}{\upsilon }^5-0.18006\times {10}^{-1}{\upsilon }^6+0.36837\times {10}^{-4}.\hfill \end{array}$$

Table 1. Outcomes for Example 1.

n	${∥\mathit{\vartheta }-{\mathit{\vartheta }}_{\mathit{n}}∥}_{\mathit{\varpi }}$	${∥\mathit{\chi }-{\mathit{\chi }}_{\mathit{n}}∥}_{\mathit{\varpi }}$
4	5.5421 × 10−4	8.5478 × 10−4
7	7.6542 × 10−5	5.6548 × 10−6
9	4.2356 × 10−7	6.4587 × 10−7
15	8.6548 × 10−14	7.4587 × 10−13
21	7.4528 × 10−17	6.9875 × 10−16

presents the numerical outcomes obtained for Example 1 using our suggested approach.

Figure 1 illustrates the numerical outcomes obtained for this Example via the present approximation.

Example 2.

In this example, we take $a=1,b=1,c=0,d=1.$ In this case, we investigate fractional integro-differential System (38) so that

$$\begin{array}{c}\hfill \Psi \left(\upsilon \right)=\frac{1}{840\sqrt{\pi }}\left[3072{\upsilon }^{7/2}+840{\upsilon }^4\sqrt{\pi }-420{\upsilon }^2\sqrt{\pi }-1120{\upsilon }^{3/2}\right],\nu =\frac{1}{2}.\end{array}$$

and

$$\begin{array}{c}\hfill \zeta \left(\upsilon \right)=-\frac{1}{840\sqrt{\pi }}\left[3072{\upsilon }^{7/2}+840{\upsilon }^4\sqrt{\pi }+420{\upsilon }^2\sqrt{\pi }+1120{\upsilon }^{3/2}-308\upsilon \sqrt{\pi }-245\sqrt{\pi }\right].\end{array}$$

Some numerical experiments are conducted in order to illustrate the efficacy of the current instance. For example, for $n=5$, unknowns ${\beta }_{5,0}\cdots {\beta }_{5,5}$ are described as follows:

$$\begin{array}{ccc}\hfill {\beta }_{5,0}& =& 0.11796,{\beta }_{5,1}=0.24900,{\beta }_{5,2}=0.19709,\hfill \\ \hfill {\beta }_{5,3}& =& 0.78087\times {10}^{-1},{\beta }_{5,4}=0.98708\times {10}^{-2},{\beta }_{5,5}=-0.24920\times {10}^{-4}.\hfill \end{array}$$

Approach solution ${\vartheta }_5$ is provided by

$$\begin{array}{ccc}\hfill {\vartheta }_5\left(\upsilon \right)& =& 0.77591\times {10}^{-2}\upsilon -0.44719\times {10}^{-1}{\upsilon }^3-0.44719{\upsilon }^2\hfill \\ & +& 1.0335{\upsilon }^4-0.10180\times {10}^{-1}{\upsilon }^5-0.17084\times {10}^{-2}.\hfill \end{array}$$

Moreover,

$$\begin{array}{ccc}\hfill {\gamma }_{5,0}& =& -0.55835,{\gamma }_{5,1}=-0.81377,{\gamma }_{5,2}=-0.34822,\hfill \\ \hfill {\gamma }_{5,3}& =& -0.079199,{\gamma }_{5,4}=-0.0095269,{\gamma }_{5,5}=-0.000084704.\hfill \end{array}$$

Approach solution ${\chi }_7$ is given by

$$\begin{array}{ccc}\hfill {\chi }_7\left(\upsilon \right)& =& 0.26600\times {10}^{-1}\upsilon -0.88641{\upsilon }^4-0.15186{\upsilon }^3+0.37873{\upsilon }^2\hfill \\ & -& 0.34602\times {10}^{-1}{\upsilon }^5-0.18385\times {10}^{-1}.\hfill \end{array}$$

Table 2. Numerical outcomes for Example 2.

n	${∥\mathit{\vartheta }-{\mathit{\vartheta }}_{\mathit{n}}∥}_{\mathit{\varpi }}$	${∥\mathit{\chi }-{\mathit{\chi }}_{\mathit{n}}∥}_{\mathit{\varpi }}$
6	3.7589 × 10−5	7.2546 × 10−5
8	6.2546 × 10−6	6.4548 × 10−5
10	3.2546 × 10−7	8.2746 × 10−6
14	6.2354 × 10−13	5.7854 × 10−11
20	5.2365 × 10−16	5.2546 × 10−15

illustrates the numerical results obtained for Example 1 using our proposed technique.

For this second example, let us take $a=1,b=1,c=0,d=1.$ The numerical findings acquired for this example using the present approach are depicted in Figure 2.

Example 3.

In this example, we take $a=1,b=0,c=1,d=1,$$\nu =1.75$, and

$$\begin{array}{c}\hfill \psi \left(\upsilon ,\rho \right)=\left\{\begin{array}{cc}1\hfill & \mathit{if}\rho \le \upsilon ,\hfill \\ 0\hfill & \mathit{otherwise},\hfill \end{array}\right.\end{array}$$

We obtain the coupled fractional system integral-differential equations given in Example 2 of [22]. The authors used a numerical approach based on the Haar wavelet. The primary problem is converted into a system of algebraic equations using the suggested method, which attempts to construct the fractional operational matrix integration. The present results are better than those obtained in [22]. Moreover, our algebraic system is significantly simpler to solve than the algebraic system of [22]. We present the numerical results for ${∥𝓁-{𝓁}_n∥}_2$ of Example 3 with comparison to [22] in

Table 3. Numerical outcomes for ${∥𝓁-{𝓁}_n∥}_2$ of Example 3.

n	[22]	The Present Approach ≤
16	3.478023 × 10−4	6.356487 × 10−14
32	6.371379 × 10−5	7.256987 × 10−18
64	9.371983 × 10−7	9.264875 × 10−23

. Also, we offer the numerical results for ${∥\lambda -{\lambda }_n∥}_2$ of this example with comparison to [22] in

Table 4. Numerical outcomes for ${∥\lambda -{\lambda }_n∥}_2$ of Example 3.

n	[22]	The Present Approach ≤
16	5.371897 × 10−4	7.954216 × 10−14
32	8.381098 × 10−5	6.574821 × 10−18
64	2.387639 × 10−6	8.739128 × 10−22

.

Example 4

([28]). We consider the following fractional differential equation:

$${}^c\mathcal{J}_{0_{+}}^{\nu }y(s)=-y(s)+f(s),y(0)=0,0<\nu <1,0\le s\le 1,$$

where

$$f\left(s\right)=s^2+\frac{2s^{2-\nu }}{\Gamma (3-\nu )}andy\left(s\right)=s^2.$$

The linear B-spline operational matrix method described in [29] and the wavelet collocation method are used in [28] to estimate the solutions to this problem. The absolute error of our method compared with the linear B-spline operational matrix approach presented in [29] for $J=8$ and the rapid wavelet collocation method for $L=0$; $J=5$ is shown in

Table 5. Numerical outcomes of Example 4.

${\mathit{s}}_{\mathit{i}}$	[22]	[22]	Our Method ≤
0.03125	0.059 × 10−12	0.043 × 10−4	2.252 × 10−17
0.09375	0.043 × 10−12	0.115 × 10−4	1.120 × 10−17
0.18750	0.053 × 10−12	0.134 × 10−4	3.700 × 10−17
0.28125	0.024 × 10−12	0.145 × 10−4	2.100 × 10−17
0.37500	0.003 × 10−12	0.153 × 10−4	2.000 × 10−17
0.46875	0.064 × 10−12	0.160 × 10−4	2.000 × 10−17
0.56250	0.054 × 10−12	0.165 × 10−4	1.000 × 10−17
0.65625	0.009 × 10−12	0.170 × 10−4	1.000 × 10−17
0.75000	0.017 × 10−12	0.173 × 10−4	3.000 × 10−17
0.84375	0.031 × 10−12	0.177 × 10−4	0.000 × 10−17
0.93750	0.201 × 10−12	0.180 × 10−4	0.000 × 10−17

.

8. Conclusions

We used shifted Chebyshev polynomials of the first kind and a projection method to solve a set of fractional integro-differential equations in this work. The present strategy involves transforming the given problem into two algebraic equations. The acquired systems are solved to obtain approximate solutions to the given problem. The integro-differential system under consideration exhibits clear significance in the realm of mathematical research, particularly about phenomena involving interactions within the field of physics. The impact of the fractional operator on the growth of numerical outcomes has been substantial. This approach can be employed to examine and resolve diverse fractional, integro-differential, and integral problems. Under certain circumstances, this approach may be used as a future project to solve the system of Cauchy fractional differential equations displayed in the ones that follow:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle a{}^c\mathcal{J}_{0_{+}}^{\nu }𝓁\left(\upsilon \right)+b𝓁\left(\upsilon \right)+c{𝓁}^{\prime }\left(\upsilon \right)+d{\int }_0^1\frac{\lambda \left(\rho \right)}{\upsilon -\rho }d\rho =\sigma \left(\upsilon \right),0\le \upsilon \le 1,}\hfill \\ a{}^c\mathcal{J}_{0_{+}}^{\nu }\lambda \left(\upsilon \right)+b\lambda \left(\upsilon \right)+c{\lambda }^{\prime }\left(\upsilon \right)+d{\int }_0^1\frac{𝓁\left(\rho \right)}{\upsilon -\rho }d\rho =\varsigma \left(\upsilon \right),0\le \upsilon \le 1.\hfill \end{array}\right.\end{array}$$

The study can be extended to the derivatives of Riemann–Liouville and Grünwald–Letnikov as future perspectives. As a result, these findings cast doubt on the accuracy of findings made in the field of time-fractional model analysis that involves beginning conditions.