Dynamical Behavior of the Fractional BBMB Equation on Unbounded Domain
Abstract
1. Introduction
2. Description of Method
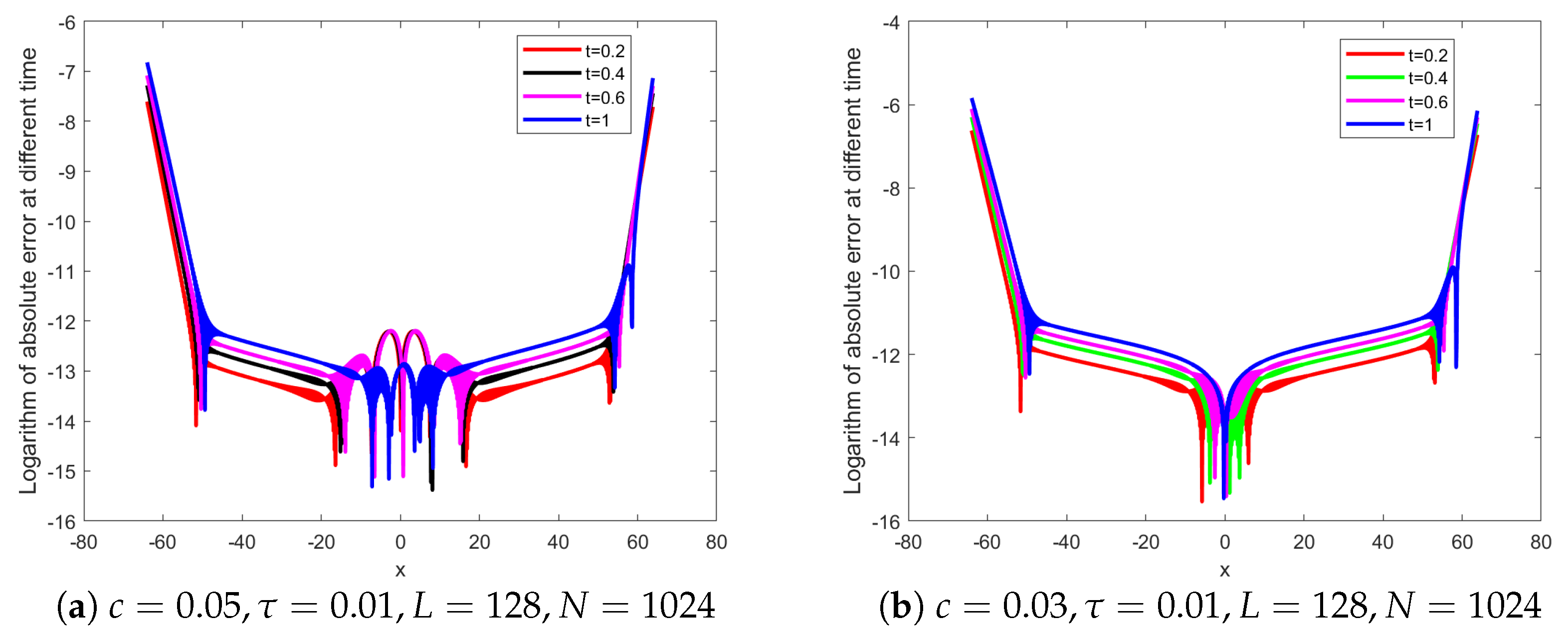
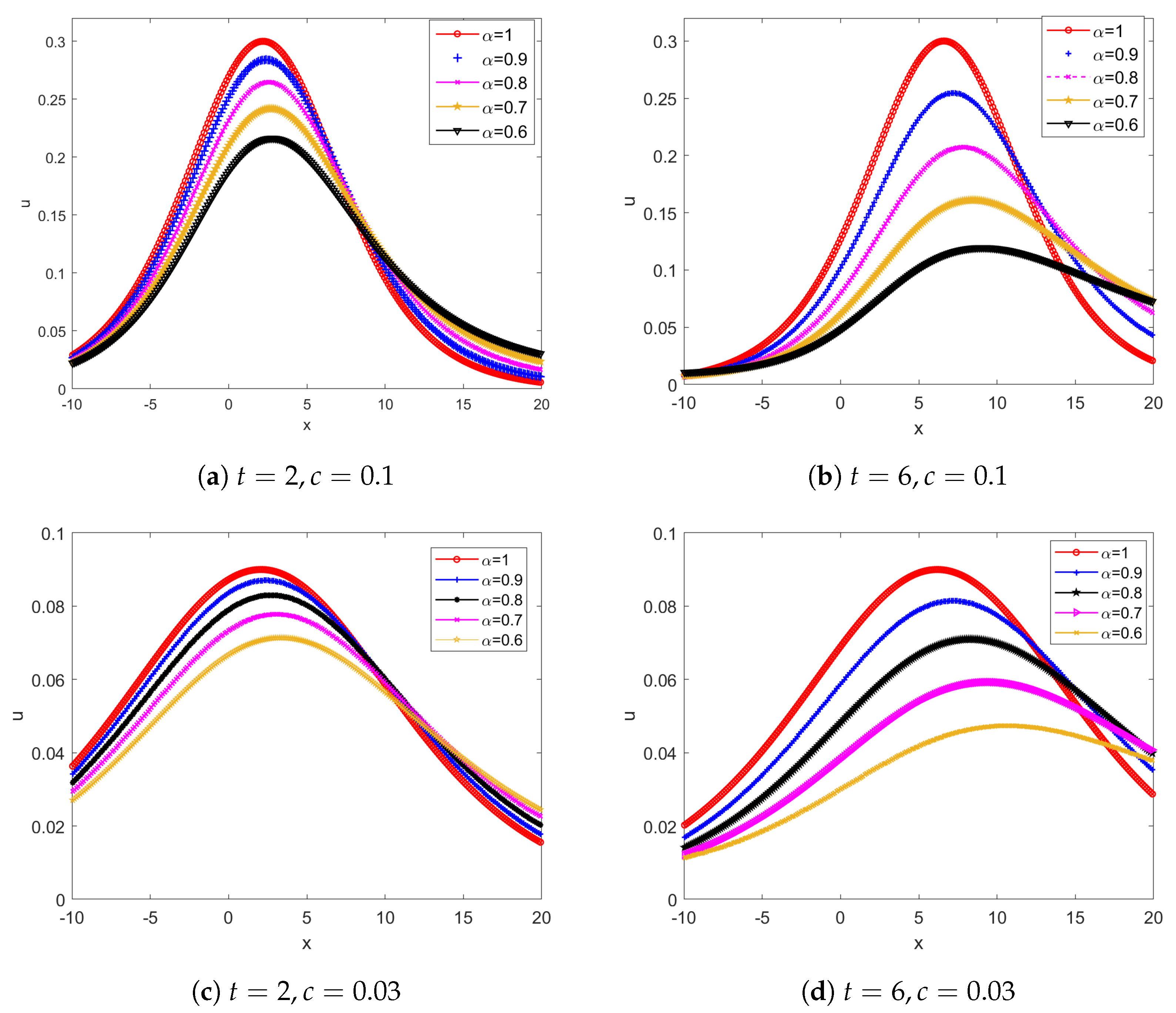
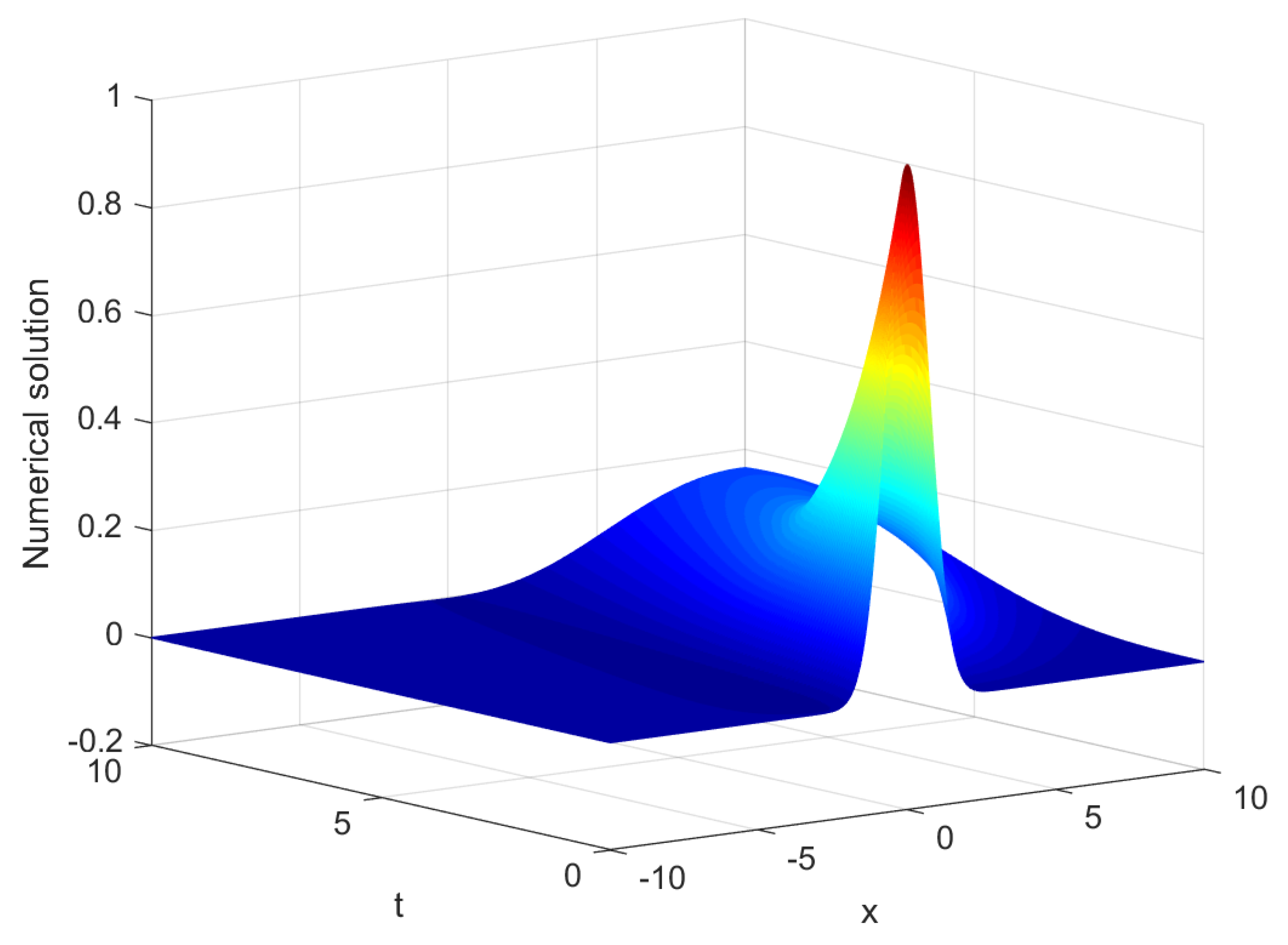
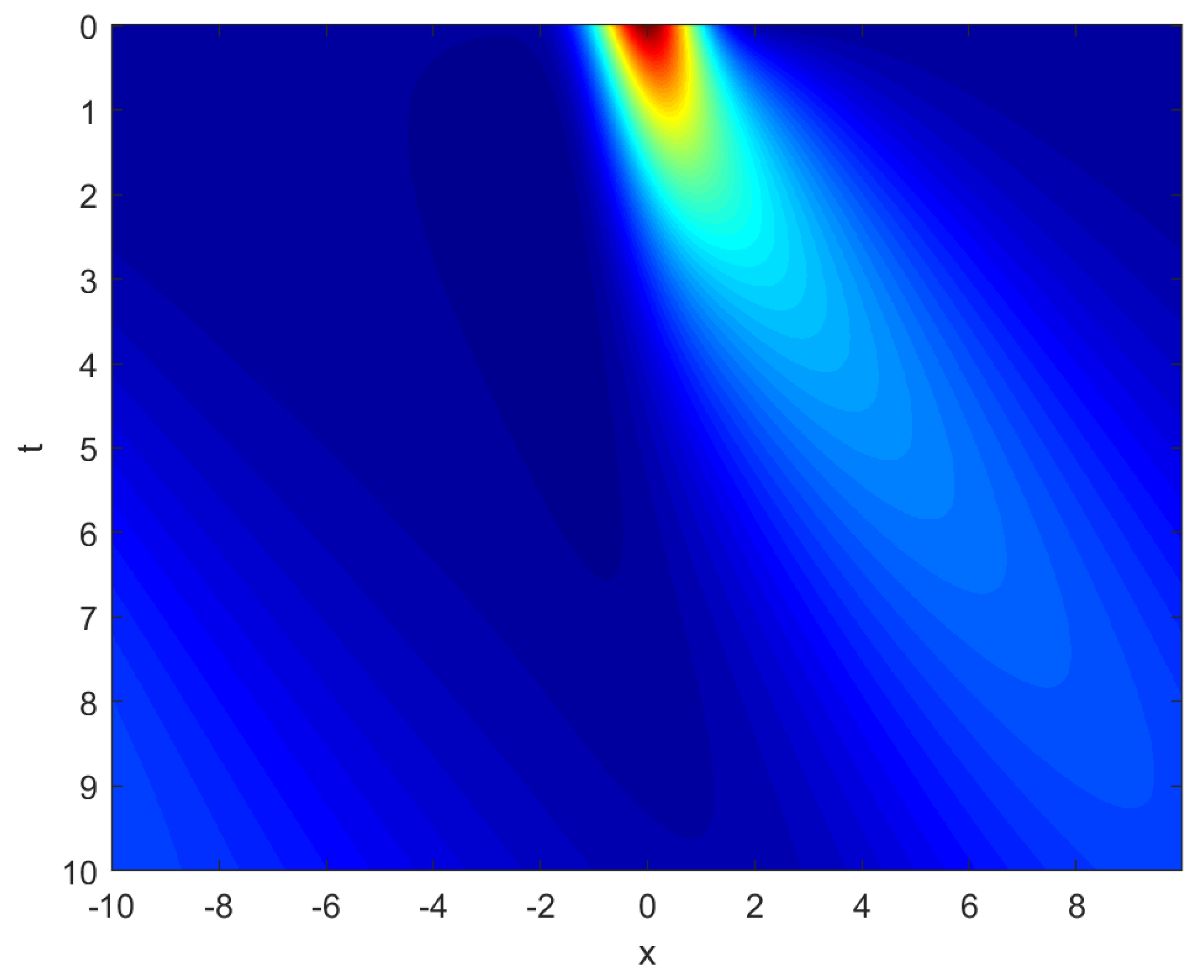
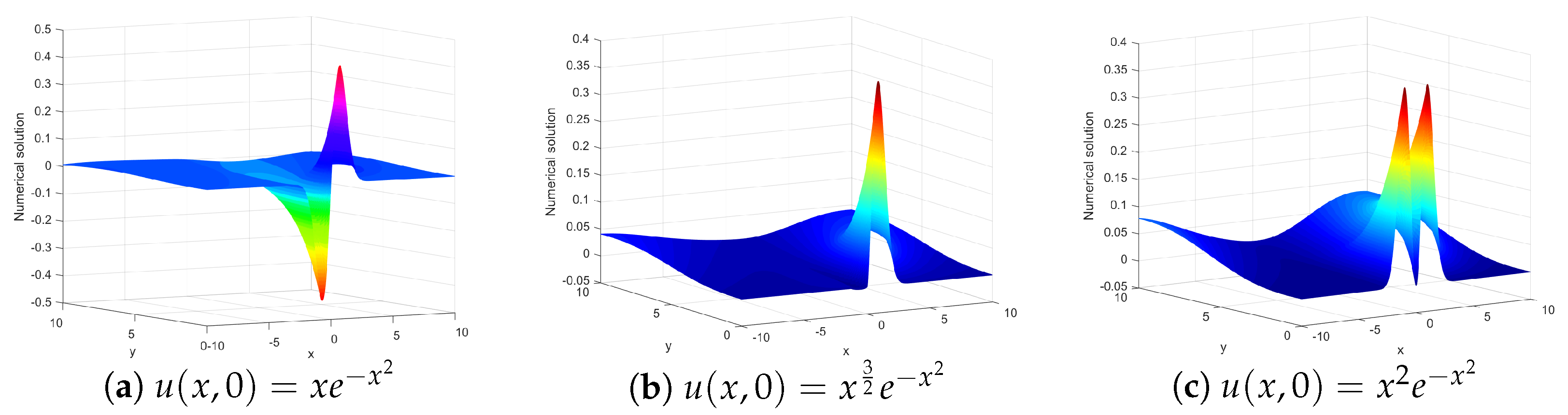
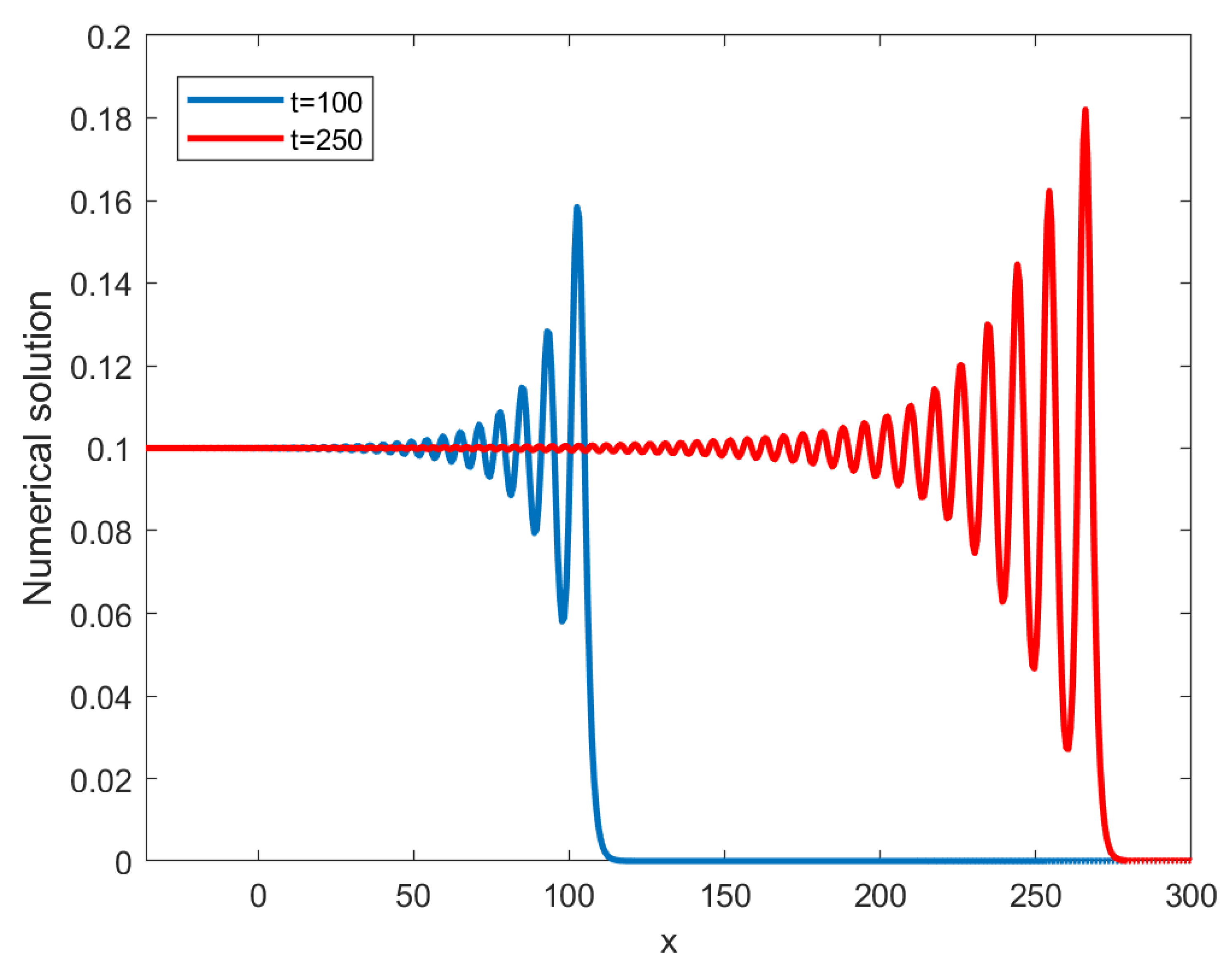
3. Numerical Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Daftardar-Gejji, V. (Ed.) Fractional Calculus and Fractional Differential Equations; Springer: Singapore, 2019. [Google Scholar]
- Li, Z.; Chen, Q.; Wang, Y.; Li, X. Solving two-sided fractional super-diffusive partial differential equations with variable coefficients in a class of new reproducing kernel spaces. Fractal Fract. 2022, 6, 492. [Google Scholar] [CrossRef]
- Li, C.P.; Li, Z.Q. The blow-up and global existence of solution to Caputo-Hadamard fractional partial differential equation with fractional Laplacian. J. Nonlinear Sci. 2021, 31, 80. [Google Scholar] [CrossRef]
- Kukreja, V.K. Numerical treatment of Benjamin-Bona-Mahony-Burgers equation with fourth-order improvised B-spline collocation method. J. Ocean Eng. Sci. 2022, 7, 99–111. [Google Scholar]
- Sagar, B.; Ray, S.S. Numerical and analytical investigation for solutions of fractional Oskolkov-Benjamin-Bona-Mahony-Burgers equation describing propagation of long surface waves. Int. J. Mod. Phys. B 2021, 35, 2150326. [Google Scholar] [CrossRef]
- Reetika, C.; Komal, D.; Devendra, K. A new numerical formulation for the generalized time-fractional Benjamin Bona Mohany Burgers’ equation. Int. J. Nonlinear Sci. Numer. Simul. 2022, 24, 883–898. [Google Scholar]
- Song, L.; Zhang, H. Solving the fractional BBM-Burgers equation using the homotopy analysis method. Chaos Solitons Fractals 2009, 40, 1616–1622. [Google Scholar] [CrossRef]
- He, J.H.; He, C.H.; Alsolami, A.A. A good initial guess for approximating nonlinear ossciliators by the homotopy perturbation method. Facta Univ.-Ser. Mech. Eng. 2023, 21, 21–29. [Google Scholar]
- He, J.H.; El-Dib, Y. The enhanced homotopy perturbation method for axial vibration of strings. Facta Univ.-Ser. Mech. Eng. 2021, 19, 735–750. [Google Scholar] [CrossRef]
- Heydari, M.H.; Razzaghi, M.; Avazzadeh, Z. Numerical investigation of variable-order fractional Benjamin-Bona-Mahony-Burgers equation using a pseudo-spectral method. Math. Methods Appl. Sci. 2021, 44, 8669–8683. [Google Scholar] [CrossRef]
- Majeed, A.; Kamran, M.; Abbas, M.; Bin Misro, M.Y. An efficient numerical scheme for the simulation of time-fractional nonhomogeneous Benjamin-Bona-Mahony-Burger model. Phys. Scr. 2021, 96, 084002. [Google Scholar] [CrossRef]
- Zhou, Y.T.; Li, C.; Stynes, M. A fast second-order predictor-corrector method for a nonlinear time-fractional Benjamin-Bona-Mahony-Burgers equation. Numer. Algorithms 2024, 95, 693–720. [Google Scholar] [CrossRef]
- Gao, X.L.; Zhang, H.L.; Wang, Y.L.; Li, Z.Y. Research on pattern dynamics behavior of a fractional vegetation-water model in arid flat environment. Fractal Fract. 2024, 8, 264. [Google Scholar] [CrossRef]
- Gao, X.L.; Wang, Y.L.; Li, Z.Y. Chaotic dynamic behavior of a fractional-order financial systems with constant inelastic demand. Int. J. Bifurc. Chaos 2024, 34, 2450111. [Google Scholar]
- Gao, X.L.; Zhang, H.L.; Li, X.Y. Research on pattern dynamics of a class of predator-prey model with interval biological coefficients for capture. AIMS Math. 2024, 9, 18506–18527. [Google Scholar] [CrossRef]
- Bona, J. Model equations for waves in nonlinear dispersive systems. Proc. Int. Congr. Math. 1978, 2, 887–894. [Google Scholar]
- Burgers, J.M. A Mathematical Model Illustrating the Theory of Turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar]
- Eslami, M.; Matinfar, M.; Asghari, Y.; Rezazadeh, H. Soliton solutions to the conformable time-fractional generalized Benjamin-Bona-Mahony equation using the functional variable method. Opt. Quantum Electron. 2024, 56, 1063. [Google Scholar] [CrossRef]
- Wang, K.J. Diverse wave structures to the modified Benjamin-Bona-Mahony equation in the optical illusions field. Mod. Phys. Lett. B 2023, 37, 2350012. [Google Scholar] [CrossRef]
- Zarebnia, M.; Parvaz, R. On the numerical treatment and analysis of Benjamin-Bona-Mahony-Burgers equation. Appl. Math. Comput. 2016, 284, 79–88. [Google Scholar] [CrossRef]
- Ning, J.; Wang, Y.L. Fourier spectral method for solving fractional-in-space variable coefficient KdV-Burgers equation. Indian J. Phys. 2024, 98, 1727–1744. [Google Scholar] [CrossRef]
- Han, C.; Wang, Y.L. Numerical solutions of variable-coefficient fractional-in-space KdV equation with the Caputo fractional derivative. Fractal Fract. 2022, 6, 207. [Google Scholar] [CrossRef]
- Korkmaz, A.; Dag, I. Numerical simulations of boundary-forced RLW equation with cubic b-spline-based differential quadrature methods. Arab. J. Sci. Eng. 2013, 38, 1151–1160. [Google Scholar] [CrossRef]
- Han, C.; Wang, Y.L.; Li, Z.Y. A high-precision numerical approach to solving space fractional Gray-Scott model. Appl. Math. Lett. 2022, 125, 107759. [Google Scholar] [CrossRef]
- Xu, Y.C.; Hu, J.S.; Hu, C.L. A new conservation finite difference scheme for generalized regularized long wave equation. J. Sichuan Univ. 2011, 48, 534–538. [Google Scholar]
- Wang, T.C.; Zhang, L.M. Conservative difference scheme for solving generalized regular long-wave equations. Chin. J. Appl. Math. 2006, 29, 8. [Google Scholar]
- Kutluay, S.; Esen, A. A finite difference solution of the regularized long-wave equation. Math. Probl. Eng. 2006, 2006, 39–62. [Google Scholar] [CrossRef]
- Li, C.P.; Wang, Z. The local discontinuous Galerkin fnite element methods for Caputo-type partial diferential equations: Numerical analysis. Appl. Numer. Math. 2019, 140, 1–22. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
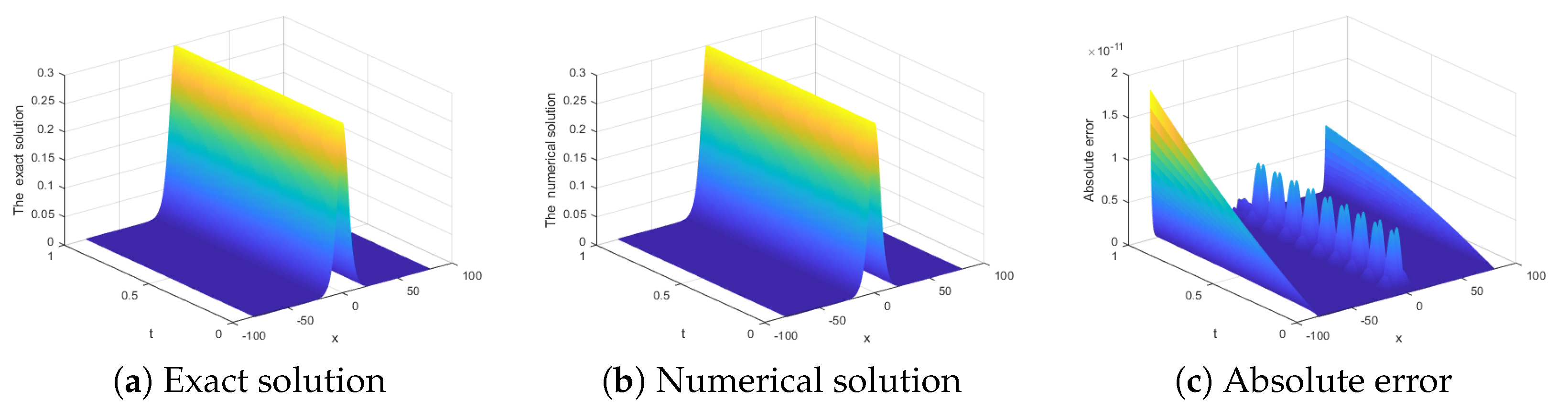
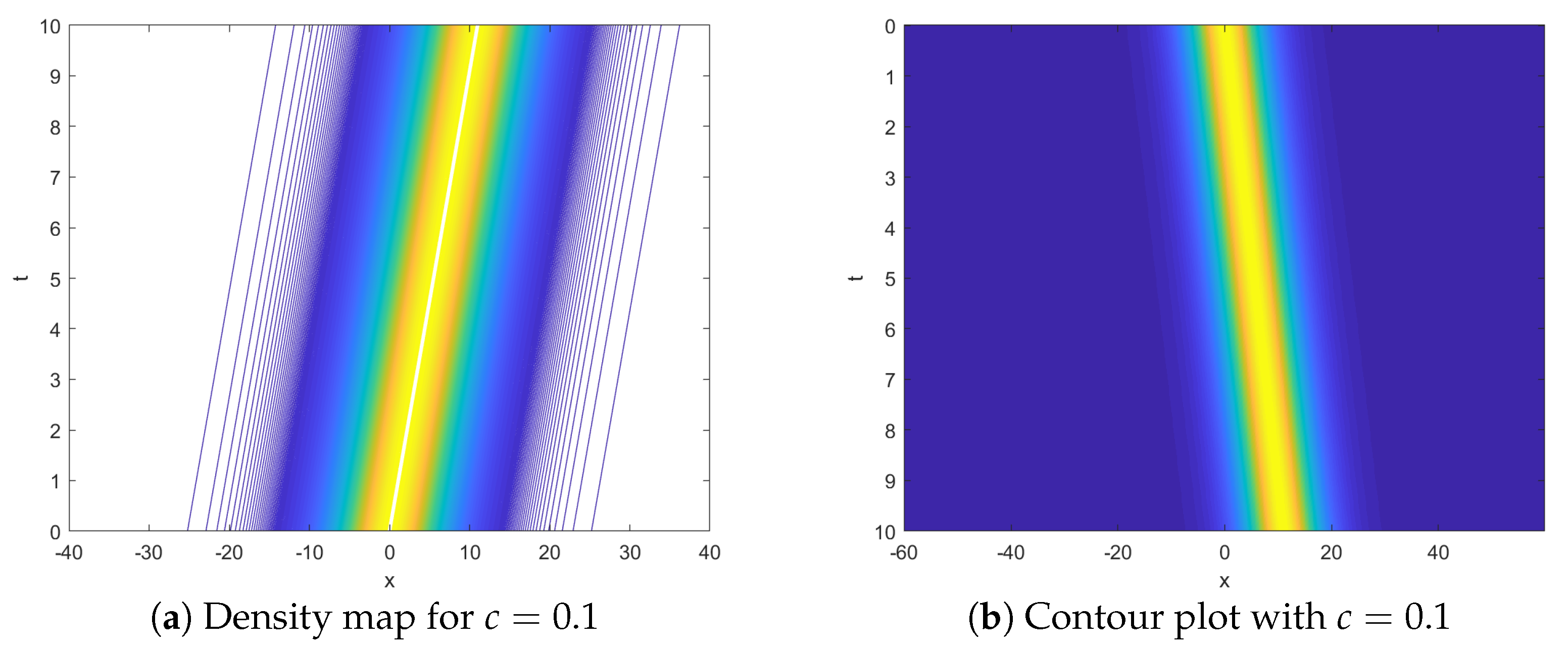
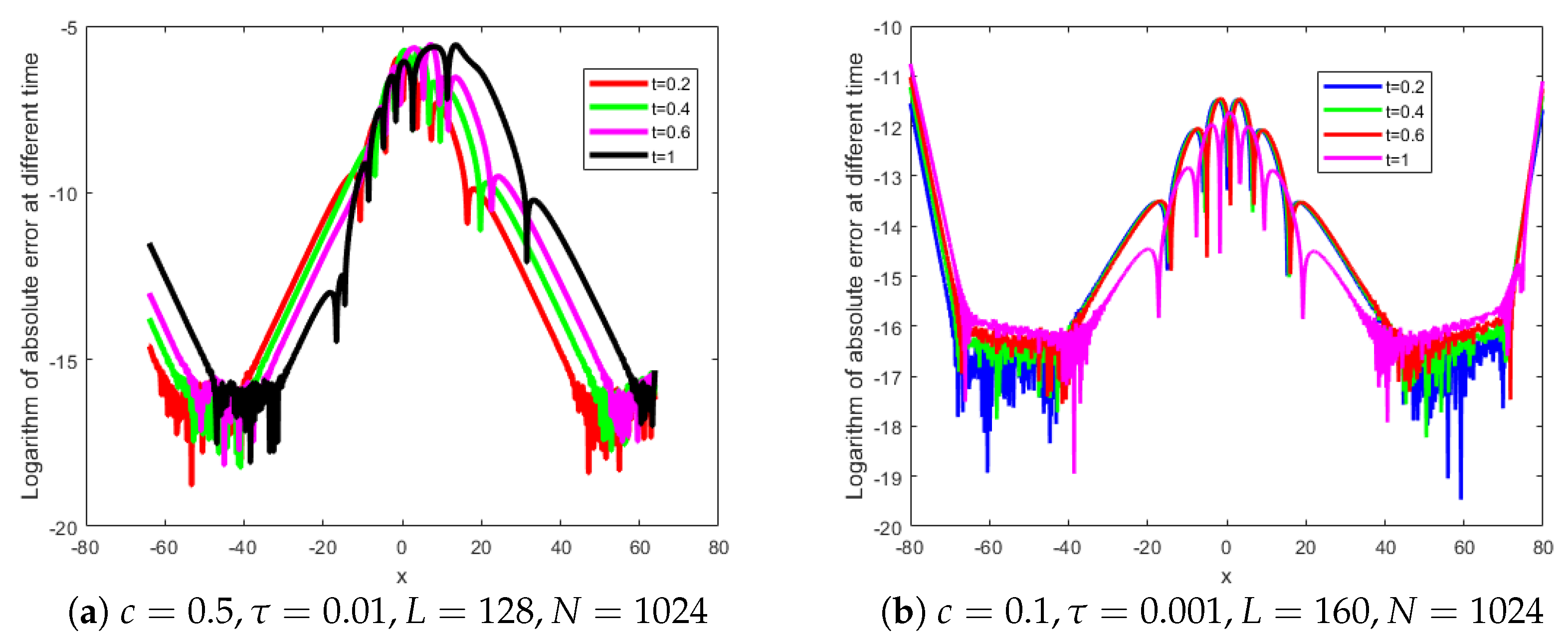
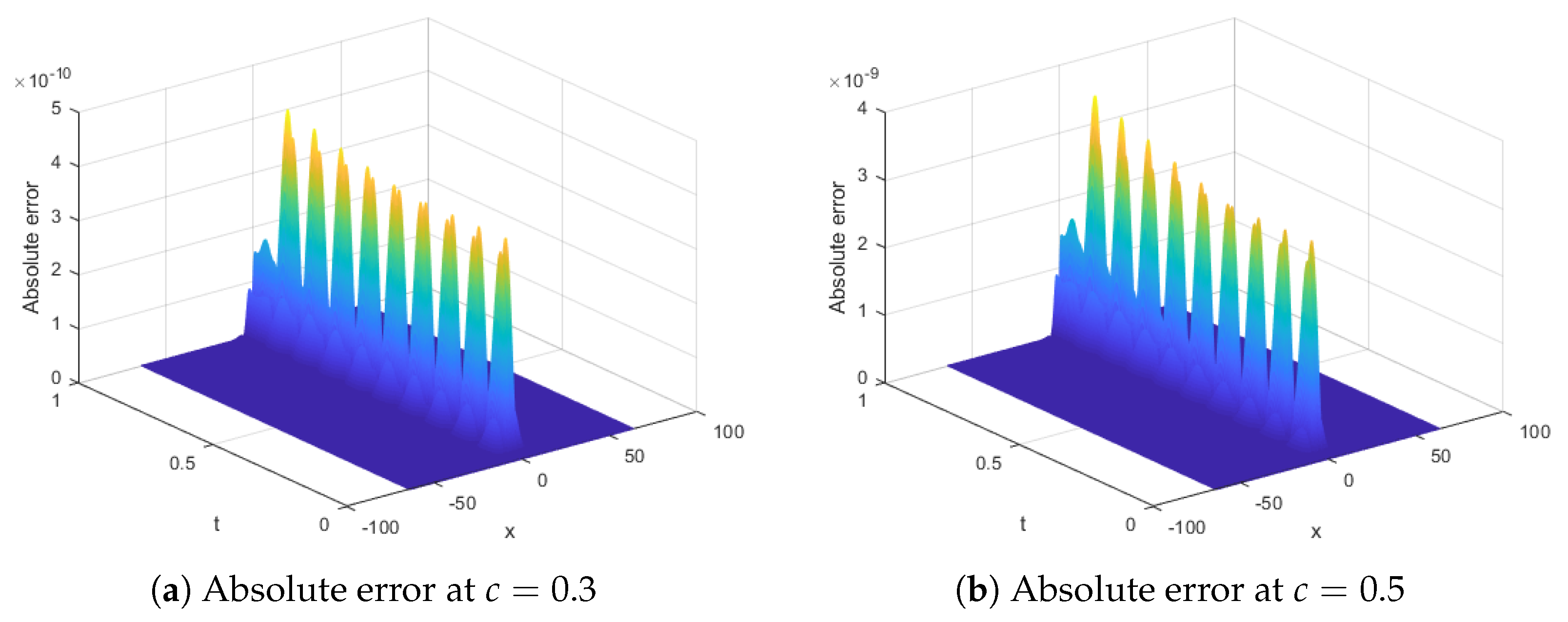









| t | Algorithm in [22] | Finite Element Method [22] | Cubic B-Spline Method [20] | Present Method |
|---|---|---|---|---|
| 2 | 6.8170 × 10−3 | 9.0000 × 10−6 | 3.5753 × 10−6 | 1.7367 × 10−7 |
| 4 | 1.3740 × 10−2 | 1.7000 × 10−5 | 5.9568 × 10−6 | 1.9645 × 10−7 |
| 6 | 2.0710 × 10−2 | 2.6000 × 10−5 | 8.4798 × 10−6 | 4.1904 × 10−7 |
| 8 | 2.7660 × 10−2 | 3.6000 × 10−5 | 1.0519 × 10−5 | 3.8485 × 10−7 |
| 10 | 3.4550 × 10−2 | 4.4000 × 10−5 | 1.2062 × 10−5 | 4.6152 × 10−7 |
| t | Algorithm in [22] | Finite Element Method [22] | Cubic B-Spline Method [20] | Present Method |
|---|---|---|---|---|
| 2 | 3.9200 × 10−4 | 2.7400 × 10−4 | 2.7430 × 10−4 | 6.9387 × 10−6 |
| 4 | 7.8600 × 10−4 | 2.3000 × 10−4 | 2.2998 × 10−4 | 1.8324 × 10−5 |
| 6 | 1.1830 × 10−3 | 2.2500 × 10−4 | 2.2498 × 10−4 | 3.3104 × 10−5 |
| 8 | 1.5820 × 10−3 | 2.2100 × 10−4 | 2.2103 × 10−4 | 5.0898 × 10−5 |
| 10 | 1.9830 × 10−3 | 2.1700 × 10−4 | 2.1676 × 10−4 | 7.3263 × 10−5 |
| Method | ||||
|---|---|---|---|---|
| Analytical | 3.9799497 | 0.81046249 | 2.579007 | |
| Present method | 0.01 | 3.9799497 | 0.81046249 | 2.579007 |
| Method I in [23] | 0.01 | 3.9799 | 0.8104 | 2.5790 |
| Method II in [23] | 0.01 | 3.9799 | 0.8104 | 2.5790 |
| Method in [24] | 0.01 | 3.97988 | 0.810453 | 2.57898 |
| p | x | Exact Solution | Numerical Solution | Absolute Error |
|---|---|---|---|---|
| 4 | −10 | 0.0094 | 0.0094 | 2.3306 × 10−12 |
| −5 | 0.1147 | 0.1147 | 7.3283 × 10−11 | |
| 0 | 0.9379 | 0.9379 | 1.5064 × 10−9 | |
| 5 | 0.1310 | 0.1310 | 1.8122 × 10−10 | |
| 10 | 0.0108 | 0.0108 | 3.5643 × 10−12 | |
| 8 | −10 | 0.0081 | 0.0081 | 2.5062 × 10−12 |
| −5 | 0.0992 | 0.0992 | 3.3017 × 10−10 | |
| 0 | 1.0515 | 1.0515 | 2.5424 × 10−9 | |
| 5 | 0.1133 | 0.1133 | 2.2898 × 10−10 | |
| 10 | 0.0093 | 0.0093 | 2.0325 × 10−12 |
| p | t | Finite Difference Scheme [25] | Finite Difference Scheme [26] | Present Method |
|---|---|---|---|---|
| 4 | 0.2 | 2.3111 × 10−3 | 2.4126 × 10−3 | 4.5129 × 10−9 |
| 0.4 | 4.7384 × 10−3 | 4.9448 × 10−3 | 4.9426 × 10−9 | |
| 0.6 | 7.1138 × 10−3 | 7.4230 × 10−3 | 5.9942 × 10−9 | |
| 0.8 | 9.2928 × 10−3 | 9.7015 × 10−3 | 6.9753 × 10−9 | |
| 1.0 | 1.1261 × 10−2 | 1.1760 × 10−2 | 5.6849 × 10−9 | |
| 8 | 0.2 | 1.1151 × 10−2 | 1.1290 × 10−2 | 7.5195 × 10−8 |
| 0.4 | 2.1295 × 10−2 | 2.2573 × 10−2 | 1.8036 × 10−7 | |
| 0.6 | 3.1416 × 10−2 | 3.2822 × 10−2 | 2.8450 × 10−7 | |
| 0.8 | 4.1946 × 10−2 | 4.2464 × 10−2 | 3.8517 × 10−7 | |
| 1.0 | 5.0220 × 10−2 | 5.1841 × 10−2 | 4.8838 × 10−7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Wang, H.; Zhang, H.; Li, Z.; Li, X. Dynamical Behavior of the Fractional BBMB Equation on Unbounded Domain. Fractal Fract. 2024, 8, 383. https://doi.org/10.3390/fractalfract8070383
Zhang W, Wang H, Zhang H, Li Z, Li X. Dynamical Behavior of the Fractional BBMB Equation on Unbounded Domain. Fractal and Fractional. 2024; 8(7):383. https://doi.org/10.3390/fractalfract8070383
Chicago/Turabian StyleZhang, Wei, Haijing Wang, Haolu Zhang, Zhiyuan Li, and Xiaoyu Li. 2024. "Dynamical Behavior of the Fractional BBMB Equation on Unbounded Domain" Fractal and Fractional 8, no. 7: 383. https://doi.org/10.3390/fractalfract8070383
APA StyleZhang, W., Wang, H., Zhang, H., Li, Z., & Li, X. (2024). Dynamical Behavior of the Fractional BBMB Equation on Unbounded Domain. Fractal and Fractional, 8(7), 383. https://doi.org/10.3390/fractalfract8070383






