Abstract
AI-driven mineral prospectivity mapping (MPM) is a valid and increasingly accepted tool for delineating the targets of mineral exploration, but it suffers from noisy and unrepresentative input features. In this study, a set of fractal and multifractal methods, including box-counting calculation, concentration–area fractal modeling, and multifractal analyses, were employed to excavate the underlying nonlinear mineralization-related information from geological features. Based on these methods, multiple feature selection criteria, namely prediction–area plot, K-means clustering, information gain, chi-square, and the Pearson correlation coefficient, were jointly applied to rank the relative importance of ore-related features and their fractal representations, so as to choose the optimal input feature dataset readily used for training predictive AI models. The results indicate that fault density, the multifractal spectrum width (∆α) of the Yanshanian intrusions, information dimension (D1) of magnetic anomalies, correlation dimension (D2) of iron-oxide alteration, and the D2 of argillic alteration serve as the most effective predictor features representative of the corresponding ore-controlling elements. The comparative results of the model assessment suggest that all the AI models trained by the fractal datasets outperform their counterparts trained by raw datasets, demonstrating a significant improvement in the predictive capability of fractal-trained AI models in terms of both classification accuracy and predictive efficiency. A Shapley additive explanation was employed to trace the contributions of these features and to explain the modeling results, which imply that fractal representations provide more discriminative and definitive feature values that enhance the cognitive capability of AI models trained by these data, thereby improving their predictive performance, especially for those indirect predictor features that show subtle correlations with mineralization in the raw dataset. In addition, fractal-trained models can benefit practical mineral exploration by outputting low-risk exploration targets that achieve higher capturing efficiency and by providing new mineralization clues extracted from remote sensing data. This study demonstrates that the fractal representations of geological features filtered by multi-criteria feature selection can provide a feasible and promising means of improving the predictive capability of AI-driven MPM.
1. Introduction
Mineral resources are a vital material foundation for economic and social development [1]. The exploration of new mineral prospects is urgently required to meet the ever-growing demand of mineral resources due to the progressive advancement of urbanization and industrialization [2]. Mineral prospectivity mapping (MPM) is a fundamental step in mineral exploration, aiming to quantify and map the probability of the presence of mineral deposits of the sought-after type that may be found by exploration in a given study area [3,4]. Essentially, MPM is a data mining procedure that mines information, knowledge, and insights from available multi-source exploratory data, which specifically includes obtaining mineralization-related information from evidential features, discovering knowledge of mineral systems based on multi-layer information, and gaining insights into mineral exploration strategies by integrating geo-knowledge [5,6,7,8]. Over the past two decades, artificial intelligence (AI) techniques, primarily machine learning algorithms, which are widely accepted to be excellent data mining techniques in both industry and academia, have proven to be promising tools for MPM [5,9]; e.g., artificial neural networks [10,11], random forest [12,13,14], logistic regression [15,16], and various deep learning algorithms [17,18,19].
Although AI algorithms have matured and proved to be valid for the outputting predictions of mineral prospectivity, the input data for AI models are not sound enough to objectively represent the target mineral systems [20], which degrades the effectiveness of AI models in practical exploration activities. This is mainly attributed to the intrinsically complex and noisy nature of geological features employed in the MPM task. Mineral deposits, as the targets of MPM, are end-products of the complex interplays between diverse ore-forming processes that leave behind their signatures in the form of various geological features [21,22], which are additionally overlaid by numerous temporal alterations and/or spatial deviations, resulting in nonlinear correlations between these features and mineral deposits that seem to be far too complex to be adequately handled by traditional prospectivity approaches that are mainly based on empirical judgement and qualitative analyses [18,23,24]. Therefore, two prerequisites for conducting an effective and efficient AI-driven MPM include (i) the construction of a sound input dataset that digs the underlying nonlinear ore-forming information from original features, and (ii) an exhaustive search for the optimal feature subset of the input dataset.
Fractal geometry provides an excellent solution for the first issue (i). The major attraction of fractal geometry stems from its ability for characterizing the irregular shapes of natural features that traditional Euclidean geometry fails to describe [25]. Diverse fractal and multifractal methods have been demonstrated to be powerful pattern recognition engines that can effectively reveal complex patterns in chaotic and irregular geological phenomena along with their underlying nonlinear dynamic processes [26,27,28,29,30]. Among the wide fractal applications in geoscience, great efforts have been made to probe the correlation between mineral deposits and ore-related evidential features via various fractal exponents [31,32,33,34]. The concentration–area (C–A) fractal model, proposed by Cheng et al. [35] and originally applied to identify mineralization-related geochemical anomalies [36,37], has been widely employed in MPM to separate geophysical anomalies [38,39,40], detect hydrothermal minerals from remote sensing data [25,41], discretize continuous values and classify mineral potential [31,42,43,44,45], and to outrank exploration layers [46]. On the other hand, multifractal analysis, taking into account fuzzy spatial distribution patterns as well as the irregular geometric shapes of geological features under multiple scaling rules [38], stands as an effective tool for portraying the overall complexity of mineralization systems [27,47,48,49]. All these fractal representations of geological features effectively recognize the inherent distribution patterns of mineralization-related features that can be used to trace the footprints of ore-related processes and are, thus, suitable to feed AI algorithms for training prospectivity models. Furthermore, fractal analyses yield the quantitative measurements of related features, which can be seamlessly integrated into the numeric input dataset and readily used for model training.
For the second issue (ii), feature selection is beneficial for improving model performance, elevating computational efficiency, and for decreasing the requirements of memory storage, given that exploratory data comprise a large number of irrelevant, redundant, and noisy features [50]. Feature selection can be broadly categorized into filter, wrapper, and embedded methods [50]. Since the wrapper and embedded methods evaluate the quality of selected features based on predefined machine learning algorithms before the implementation of specific AI algorithms, the problem of conditional independence among the judgement criteria of different AI algorithms may arise; therefore, filter methods, which are independent of any machine learning algorithms, are commonly used in AI-driven MPM. The filter methods focus on evaluating feature importance according to the inherent characteristics of geo-data and their contributions to final predictions. A set of evaluation criteria have been proposed and applied in MPM, such as information gain [18], Gini index [51], principal component analysis [52], and correlation [52]. Apart from these common criteria, several geologically constrained criteria, based on the principles of mineral prospectivity targeting and represented by the prediction–area (P–A) plot, have also been proposed and used to evaluate the ability of individual features to predict prospectivity in a practical MPM task [53,54,55]. Usually, in previous MPM studies, only one of these criteria has been utilized; however, given that geological features generally exhibit subtle correlations with mineralization in various complicated formats, the employment of multiple criteria is important as it is the only way that the different evaluation results of these complex features can be benchmarked and contrasted.
Although fractal and multifractal exponents are widely used in MPM studies and have proven to be an effectively nonlinear measurement, they commonly serve as global variables characterizing the distribution patterns of the whole study area. Few studies have employed them as direct predictor features that reflect the fine variation of local mineralization patterns due to the lack of implementation framework and the massive computation tasks. In this study, an elaborate scenario of multifractal calculation was carried out to obtain fractal representations of lithological, structural, geophysical, and remote sensing features related to mineralization in each predictive unit of the study area. Based on these, multiple evaluation criteria were employed to select the optimal combination of features used for training predictive AI models. The results demonstrate the effectiveness of the proposed framework in enhancing the predictive performance of AI-driven predictive models and contribute to delineating reliable targets for future exploration in the study area.
2. Study Area and Data Used
The Gannan ore district, located in the eastern segment of the famous Nanling metallogenic belt (Figure 1), was chosen as the case study area, since it is a matured tungsten mining area with an exploration history of more than a century. A large number of tungsten deposits have been well explored, and abundant geo-information are available, including geological, geophysical, geochemical and remote sensing data, which provide a data-rich foundation for this MPM study.
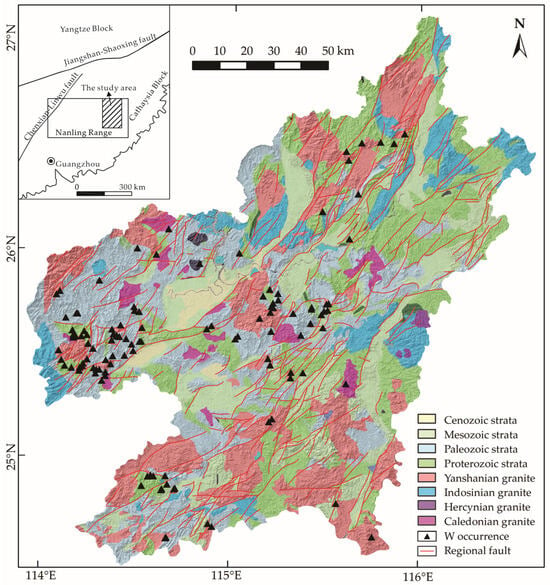
Figure 1.
Simplified geological map of Gannan district, modified from [56,57,58].
The sedimentary successions outcropped in this area consist mainly of Proterozoic lower greenschist facies clastic rocks and Paleozoic shallow marine carbonate and siliciclastic rocks, as well as Mesozoic volcaniclastics and terrigenous red-bed sandstone (Figure 1) [56]. Three groups of regional faults, trending approximately NE, NW, and EW, constitute the tectonic framework of this region (Figure 1). This area has experienced four episodes of granitic magmatism, namely Caledonian (Early-to-Middle Paleozoic), Hercynian (Late Paleozoic), Indosinian (Early Mesozoic), and Yanshanian (Late Mesozoic) [59,60]; of these, the Yanshanian tectono-magmatic activities are believed to be responsible for widespread tungsten mineralization in this region. More than 400 outcropped granitic intrusions, mainly biotite monzogranite, monzonite, and porphyritic monzogranite, have been identified in this region [60], which occupies an extensive area of approximately 14,000 km2 (Figure 1). The tungsten mineralization in this study is characterized by the quartz-vein type [59], containing eight large-scale, 18 moderate-scale, and considerable small-scale deposits with a total proved tungsten reserve of 1.7 Mt [60].
Eight features were originally selected from the multi-source spatial dataset. The geological and geophysical features, including Yanshanian intrusions, regional faults, and magnetic anomalies, were extracted from the Dataset of Geological Bureau of Mineral Resource of Ganzhou City, based on a regional geological survey, and were examined in the published literature [56,57,61]. The iron-oxide and argillic alterations were extracted from Landsat-8 remote sensing data with a spatial resolution of 15 m, based on an unpublished work conducted by our team. The geochemical anomalies of W, Mn, and Fe were selected from 39 elements as they are the basic constituents of wolframite ((Fe,Mn)WO4), which dominates the economic ores in this region. These anomalies were derived from the results of China’s National Geochemical Mapping Project with a sampling density of one sample per km2 [62,63].
A total of 118 tungsten occurrences, including historical mines, discovered deposits, and verified prospects, were employed as training samples. The study area was subdivided into 195,174 predictive units with a cell size of 450 m, following the rasterizing scenario of our previous work [18], based on the criterion proposed by Zuo and by Carranza [64,65]. The evidential features were transformed into raster maps in which each cell has a numerical representation of the features.
3. Methods
3.1. Proposed Framework
Numerous methods and procedures are involved in this study, including data preparation, fractal and multifractal analyses, feature selection, AI model training, model assessment, and interpretation. Figure 2 illustrates the flowchart of the proposed framework; the following sections describe in detail the key methods and processes used, i.e., fractal and multifractal methods, feature selection, and AI-driven models.
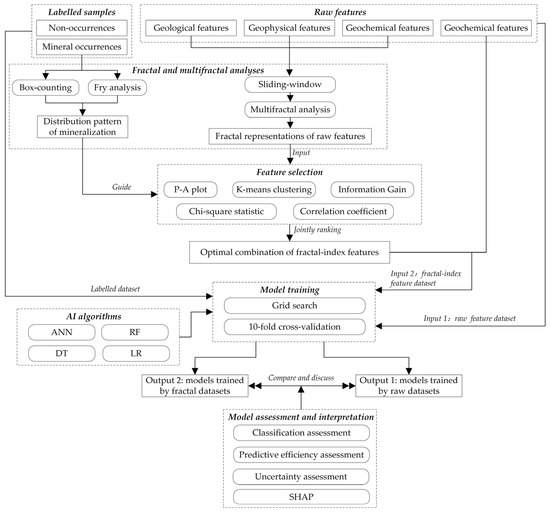
Figure 2.
Flowchart of the proposed framework of this study.
3.2. Fractal and Multifractal Methods
Fractal geometry provides a quantitative tool for portraying the complex distribution, connectivity, and self-similarity of a system [66]. In this paper, fractal geometry is used to dig the nonlinear information within the tungsten system in the study area. Specifically, the box-counting method is employed to depict the fractal characteristics of tungsten occurrences; the multifractal indices of ore-related features are measured using the moment method, with the aid of a sliding-window algorithm, which aims to capture sufficient data for a multifractal calculation.
The box-counting method is one of the most commonly used methods in fractal geometry. In this method, the evidential features are covered by a set of boxes with a side length of r. The number of non-empty boxes is denoted as N(r). The box-counting fractal dimension Db is defined as [28,67,68,69]:
In practical calculations, Db can be estimated from the slope of the fitting line on the double logarithmic plot of N(r) vs. r using the least square method [70]. In addition, Fry analysis is employed in this study to interpret the results of the fractal analyses, which helps in enhancing the subtle patterns of mineral occurrences and in delineating the spatial autocorrelations between these occurrences and geological features. This method is not elaborated here due to limited space. For detailed information of Fry analysis, readers are referred to [71,72,73,74,75,76].
Multifractal analysis, as an extension of monofractal analysis, has been extensively applied to quantify complex natural phenomena or to processes that exhibit similarity over a wide range of scales [47,66,77,78,79]. Before multifractal calculations, the sliding window algorithm is employed to assist in capturing sufficient local features within the massive predictive units in this study [80,81,82,83]. The sliding procedure can be described as follows (Figure 3a): (i) The feature under analysis is entirely covered by a series of grids. A window with a side length of m slides successively along the grids. The grid at the bottom left corner is set as the starting position. (ii) The window slides horizontally from left to right within a row. (iii) After crossing the row, the window moves upwards to the leftmost position of a new row and repeats step (ii). (iv) The window sliding procedure is finished when it reaches the end position at the upper right corner.
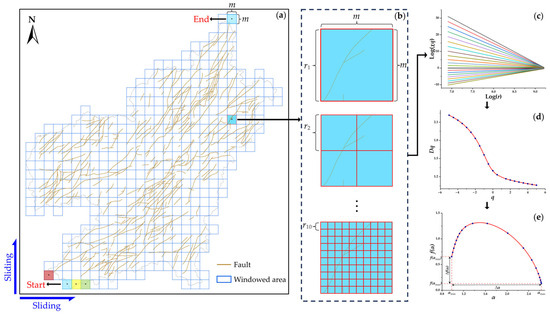
Figure 3.
Flowchart of multifractal analysis based on sliding window algorithm. (a) Sliding scenario across grids covering a map. (b) Scaling measure of windowed features. (c) The log–log plot of partition function χq(r) vs. scale r. (d) Spectrum of generalized fractal dimension Dq. (e) Multifractal spectrum curve.
After acquiring data via the sliding window procedure, the moment method, originally proposed by Halsey et al. [84], is used to estimate the multifractal spectrum. The captured features are covered by a defined number of boxes with a side length of r. This procedure is repeated 10 times with a varying r ranging from r1 to r10, as illustrated in Figure 3b. For a given r, the probability mass function of the ith box can be expressed as [28,84,85]:
where Ni(r) denotes the measurement of the targeting features, such as the length of the faults or the area of the intrusions, in the ith box at scale r, and Nt is the sum of the measurements of the targeting features across the entire window. The exponent indicates the singularity of a fractal structure in the targeting system.
The partition function χq(r) is the probability-weighted summation of each box, which is given by the following equation [28,84]:
where q represents the order of the statistical moment, and n is the total number of boxes in the window. There is an apparent relationship between χq(r) and r on the log–log plot (Figure 3c). The mass exponent τ(q) can be estimated from the slope of the fitting lines at a specific q, which can be formulized as [67,86]
The generalized fractal dimension Dq can be calculated using the following formula (Figure 3d) [67,87]:
In particular, when q equals 0, 1, and 2, D0, D1, and D2 refer to the capacity dimension, information dimension, and correlation dimension, respectively. As in Formula (5), D1 follows the L’Hôpital’s rule, which is defined as follows [88]:
The singularity exponent α and multifractal spectrum f(α) can be formulized as [67]
The plot of f(α) against α usually exhibits a bell-shaped unimodal curve (Figure 3e). On this plot, the width of the multifractal spectrum is denoted as Δα, which signifies the uniformity and singularity of the feature distribution throughout the measurement. The difference in spectrum height is represented by Δf(α), indicating the distribution discrepancy between high- and low-probability subsets.
The pseudo code for the implementation of multifractal calculations based on a sliding window is presented in Algorithm 1.
| Algorithm 1: Implementation of multifractal calculation based on sliding window |
| Input: Evidence layer L, center-of-mass coordinate set S, window length m, list of q values Q, list of r values R. |
| Output: Capacity dimension D0, information dimension D1, correlation dimension D2, spectral width ∆α, and spectral height ∆f(α) for the evidence layer. |
| Procedure: Window starts from the bottom-left corner of L. Slide right first, then slide up. Window ends at the upper-right corner of L. Calculate partition function χq, mass exponent τq, and generalized fractal dimension Dq. |
| for row in S do center_x = row [0] center_y = row [1] w_length = m w_position←[center_x, center_y] window←Create(w_length, w_position) a = Intersection_region(window, L) for r in R do p←number(element)/total_number(window) Save[P]←p χq←(P, Q), τq←(χq, R), Dq←(R, χq, Q) if q==0 then D0 = Dq=0 if q==1 then D1 = Dq=1 if q==2 then D2 = Dq=2 α(q) = dDq/dq, f(α) = qα − τq, Δα = αmax − αmin, Δf(α) = f(αmin) − f(αmax) Save[A]←(a: D0, D1, D2, ∆α, ∆f(α)) Output[A] end |
3.3. Criteria for Feature Selection
The criteria used for feature selection in this study include P–A plot, K-means clustering, information gain, chi-square, and the Pearson correlation coefficient. The former two criteria have some exclusive steps in MPM studies and, thus, are described in detail below.
Before the generation of the P–A plot, the logistic function is utilized to transform the values of evidential features into the same fuzzy space (Figure 4a) [53,89,90], which can be formulized as [55]
where fFd is the fuzzy score in the logistic space; Fd is the feature value assigned to each cell in an evidential map; and s and i are the slope and inflection point of the logistic function, respectively. The key parameters of s and i are determined via the data-driven method proposed by Yousefi and Nykänen [55], which is formulized as follows:
where Fdmax and Fdmin represent the maximum and minimum value of an evidential feature.
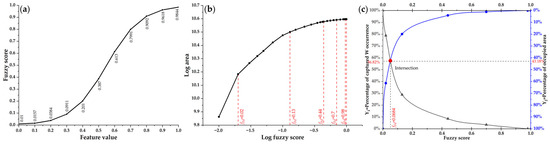
Figure 4.
Flowchart for generating P–A plot. (a) Transformation of feature value to fuzzy score using logistic function. (b) Classification of fuzzy scores by C–A fractal model. (c) Generation of P–A plot using thresholds identified by C–A model.
The transformed fuzzy scores can be categorized into different classes using the discriminative thresholds derived from a C–A model [35,43,55], which exhibits a power–law relationship between the fuzzy score fFd and the area , as given by [35,91]
where ν represents the threshold, and α1 and α2 correspond to different fractal dimensions. The thresholds of different classes are represented by the intersections of the fitting lines on a log-log plot of cumulative area vs. the corresponding fuzzy score (Figure 4b) [31,43].
The P–A plot is generated based on the above logistic transformation and C–A modeling. On a P–A plot, two curves, which show the cumulative percentage of known mineral occurrences predicted by different evidential classes and their corresponding cumulative percentage of area coverage, are plotted against the class thresholds [31,92,93]. The intersection point of these curves is recorded, while the percentage of predicted occurrences (Pr) and the percentage of occupied area (Oa) derived from the intersection points are used to define the normalized density (Nd) of a feature (Figure 4c), which is employed as a criterion for evaluating the relative importance of features [31,94]:
Nd provides a quantitative means to rank the priority of predictor features with respect to occurrence-capturing ability. If an intersection point has a high Nd, i.e., it has a relatively high Pr value and a low Oa value, this implies that the evidential feature identifies a large number of mineral occurrences within a limited area, indicating a strong predictive capability (Figure 4c).
K-means is a widely used unsupervised learning algorithm for partitioning samples in a dataset into K distinct clusters and ensuring high similarity among samples within the same cluster [95,96,97]. X = {xi, I = 1, 2, …, n} is taken as the dataset to be clustered, and K clusters C = {ck, k = 1, 2, …, K} are initially created. The K-means algorithm seeks to generate a partition such that the squared error between the empirical mean of a cluster and the data within that cluster is minimized [98], which is achieved by minimizing the following summation [98]:
where μk represents the center of the clusters. This objective function is minimized through multiple iterations in which the cluster centers are continuously updated until the cluster membership stabilizes [98,99].
Regular K-means clustering lacks effective ways of ranking feature importance when applied to MPM. To address this issue, we have proposed an improved K-means clustering, which focuses on the assessment of the capturing ability of target features. For each feature, five clusters (i.e., K = 5) are firstly generated by the K-means algorithm. Based on these clusters, two exponents are measured, namely (i) the percentage of the occurrences included in the cluster (Pk), and (ii) the percentage of the cells involved in the cluster (Ok). The measurement of a criterion (Nk) is defined by Pk/Ok for each cluster. In order to mitigate the random effect of this algorithm, a series of K values from K = 5 to K = 20 are adopted, resulting in 200 clusters by which to measure each feature. The highest value of Nk identified within 200 clusters serves as an index for estimating the importance of the corresponding feature.
Detailed descriptions of the other regular criteria for feature selections can be consulted in the corresponding references, e.g., [100,101] for information gain, [102] for the Pearson correlation coefficient, and [103,104] for chi-square statistic.
3.4. AI-Driven MPM
3.4.1. Machine Learning Algorithms
The main aim of this study is to evaluate and interpret the predictive performance of models trained by raw or fractal index datasets after the above-mentioned feature selections; therefore, some advanced but structurally complicated algorithms, such as deep learning and meta learning, are absent due to the difficulty of explaining their results. Instead, we employ a set of commonly used and easily interpretable machine learning algorithms, including artificial neural network (ANN), decision tree (DT), random forest (RF), and logistic regression (LR).
ANN, inspired by the structure of biological neurons [105], is one of the most widely used machine learning algorithms. A feed-forward neural network is adopted in this study due to its simple setup and strong robustness in executing MPM tasks [10,11,24]. In this model, neurons are the basic functional units for processing received information. The advantage of ANN lies in its ability to adjust the connections and weights between neurons [106,107,108]. A classic ANN includes an input layer, several hidden layers, and an output layer. The logistic function, also known as the sigmoid function in the ANN algorithm, is regarded as the transfer function between nodes in the hidden layer and output layer, which has a similar form to Formula (9):
where x is the input data. The neurons across different layers are fully connected. The communication of information begins at the input layer, passes through the hidden layers, and arrives at the output layer in a unidirectional process. Information propagation is facilitated by the weights assigned to the connections between neurons, which can be formulized as follows [12]:
where yi is the estimated value of neuron i; ωji represents the weight connecting neuron i in the previous layer to neuron j; bj denotes the bias term for neuron j; and f is the activation function. An optimizing procedure is implemented by updating the model parameters according to the loss calculation during the back-propagation process.
DT algorithm is a supervised learning algorithm used for both classification and regression. It constructs a tree-like model consisting of a root node, several branches, internal nodes, and leaf nodes [109,110,111,112]. The algorithm starts from the root node and progressively splits it into branches and leaf nodes. The main aim of DT is to make the best splits between nodes that optimally divide the feature dataset into the correct classes. To this end, information gain and Gini impurity are commonly used as decision criteria. The so-called “purity” in the DT algorithm is the degree to which all samples are correctly classified according to their true labels; therefore, Gini impurity quantifies the probability of misclassifying a randomly chosen sample from the dataset, which is formulized as [109]
where pi denotes the probability of a specific sample belonging to a specific class.
RF is a classic ensemble learning algorithm that integrates multiple decision trees [113,114,115]. This algorithm employs two random scenarios. Firstly, bootstrap sampling is performed to create training datasets by randomly selecting samples from the original dataset with replacement. Secondly, a subset of features is randomly selected for the splitting of the nodes in each decision tree. The introduction of randomness increases the diversity among the trees and mitigates the risk of overfitting [12,18]. Following these scenarios, multiple decision trees are constructed based on node splitting criteria such as information gain or Gini impurity. The final predictions are determined by a majority-voting mechanism that aggregates all the decision trees in the forest.
LR uses a maximum likelihood estimation to classify an input sample into a particular class [116,117,118,119]. In MPM applications, LR is used for binary classification, i.e., the predicted class is either 1 (mineral occurrence) or 0 (non-occurrence). In contrast to linear regression, the predictions of LR are transformed using the logistic function, which can be formulized as [120,121]
where p(x) denotes the predictive result; β0 is the intercept of the model; β1~βn represent the partial regression coefficients; and x1~xn represent the evidential feature variables.
3.4.2. Performance Metrics
A series of performance metrics are jointly employed in this study to comprehensively assess and interpret the predictive capability of AI models, including Accuracy, Kappa index, success rate curve, uncertainty, and the Shapley additive explanation (SHAP).
Accuracy and Kappa index, derived from the confusion matrix, are utilized to assess the classification accuracy of the trained model [122,123]:
In these formulas, the true positive (TP) denotes the number of samples with positive labels that have been correctly classified as positive; the true negative (TN) counts the times that negative samples are correctly classified as negative; the false positive (FP) records the number of negative samples that are incorrectly classified as positive; and the false negative (FN) refers to the number of positive samples that are incorrectly classified as negative.
The success rate curve measures predictive efficiency in a straightforward way [124,125,126,127]. It is generated by plotting success rate against area rate at varying thresholds. The success rate denotes the percentage of known mineral occurrences included in the prospective regions, and the area rate refers to the percentage of occupied area that the prospective regions cover. The slope of the fitting line denotes the ratio of the success rate on the Y-axis against the occupied area on the X-axis. A larger slope suggests a higher predictive efficiency that captures more occurrences within smaller delineated areas. The slope of the first fitting line measures the predictive efficiency of the cells with top prospectivity values, which is employed as an efficiency indicator.
There is an inevitable uncertainty in all the processes involved in MPM modeling due to the complexity of mineral systems, as well as to the inherent and stochastic errors brought about by model training. In order to quantify that uncertainty and to alleviate uncertainty-induced performance degradation, 10-iteration modeling procedures are conducted for each algorithm. The mean and standard deviation of the predictions at each cell are used to modulate the prospectivity value and quantitative uncertainty [101,128,129].
The SHAP algorithm, inspired by game theory, interprets machine learning models by evaluating the impact of predictor features on the model output [130,131,132]. This algorithm employs a linear additive feature method suitable for explaining linear or tree-like AI models, which can be formulized as [133]:
where g(α′) is the explanation function; ∅0 is the model output without any features; ∅j represents the SHAP value regarding the evidential feature j; and denotes the occupancy of the feature j. The SHAP plot elucidates the impact of each sample on model output with respect to a specific feature, whereas a higher SHAP value indicates stronger impact exerted by the sample.
3.5. Implementation of the Proposed Framework
The core steps of the proposed framework were implemented in Jupyter Notebook using Python. We wrote codes to perform the sliding-window-based multifractal analysis, Fry analysis, generation of the P–A plot, K-means clustering, and ANN predictive modeling. The DT, RF, and LR algorithms were implemented through calling code packages of scikit-learn. The source codes are included in the Supplementary Materials. The SHAP analysis was conducted using the SHAP package. Information gain, the Pearson correlation coefficient, and chi-square statistic were calculated with the aid of RapidMiner Studio 9.10.
The sliding-window-based multifractal analysis was time-consuming due to the elaborate scenario of region splitting and moment calculating conducted on each of the 195,174 predictive units for a single exponent within a specific feature map. It took approximately 300 h to obtain five multifractal representations, i.e., D0, D1, D2, ∆α, and ∆f(α), for all the available predictor features, using a computer with Intel Core i9-10920X CPU@3.50 GHz, NVIDIA RTX A4000.
The scenario of the machine learning prediction is described below.
(i) Dataset. The dataset included a labelled dataset used for model training and an unseen dataset used for prediction. The labelled samples were derived from our previous study, conducted in the same area [101], which comprised 118 known tungsten occurrences (positive samples) and 346 non-occurrences (negative samples). The negative samples were randomly selected according to the criteria proposed by Carranza and by Zuo [64,134]. Ten training datasets were then generated from the labelled dataset, and each training dataset included 118 positive samples and 118 negative samples that were randomly selected from 346 non-occurrences. These training datasets were then used for training 10 independent models for each AI algorithm. We implemented this step for two reasons. Firstly, the negative samples were randomly selected. Although the widely used selection criteria have been verified to be robust, including 10 independent model training processes is beneficial in alleviating the effect of randomness. Secondly, fluctuations in predictions can be observed across 10 independent models, so as to assess the predictive uncertainty mentioned above. The unseen dataset contains 195,174 predictive units with numerical feature values. The unseen dataset was input to the trained models to yield predictions. All the labelled datasets, training datasets, and the unseen dataset have two sets of representations, namely raw datasets with original feature values and fractal datasets with fractal representations of raw features. All these datasets are included in the Supplementary Materials, along with a detailed explanatory document (File S1: AlgorithmDetails.docx).
(ii) Model training. Each AI model was trained according to the grid-search strategy, i.e., the parameters of the models were determined by a trial-and-error procedure that tested all possible combinations of parameters within a reasonable range [135]. A description of the model parameters and their possible ranges is listed in Table S1. The training performance was evaluated via a stratified 10-fold cross-validation. In this procedure, the input training dataset was subdivided into 10 subsets with equal sizes and balanced labels, among which a single subset was retained as the validation dataset and the other nine were used for training models. This process was repeated 10 times until each subset had been used as the validation dataset once. The stratified cross-validation was chosen over a simple cross-validation, since previous studies have proved that MPM models trained by balanced datasets tend to be more stable [136]. The stratified 10-fold cross-validation was executed using the StratifiedKFold function in the code packages of scikit-learn.
(iii) Model assessment. The model performance was comprehensively assessed in terms of classification and prediction. The classification performance, including Accuracy and Kappa, was directly evaluated by the 10-fold cross-validation. For a given AI algorithm, the prediction of each cell was obtained by averaging the output of 10 models trained using different training datasets. Based on this prediction, the success rate curve was drawn to evaluate predictive efficiency.
4. Results
4.1. Fractal Representations of Mineralization-Related Features
The distribution pattern of mineral occurrences, which is an intrinsic feature of the mineral system, can be revealed and effectively portrayed using fractal analysis. The box-counting fractal calculation indicates that the distribution of tungsten occurrences exhibits a tri-fractal pattern, i.e., the log–log plot of the counted boxes N vs. the box size r can be fitted by three regression lines (Figure 5). From a fractal perspective, a single power–law (fractal) relationship implies an independent scale-invariant pattern that results from a specific pattern-forming mechanism. In this regard, the multi-line fractal model indicates that the tungsten mineralization in this area is subject to three different ore-controlling mechanisms operating at different scales, which can be identified by the intersections of the neighboring fitting lines in Figure 5, namely a camp scale ranging from 0 to 1703 m and a local scale between 1703 m and 4638 m, as well as a regional scale beyond 4638 m (Figure 5).
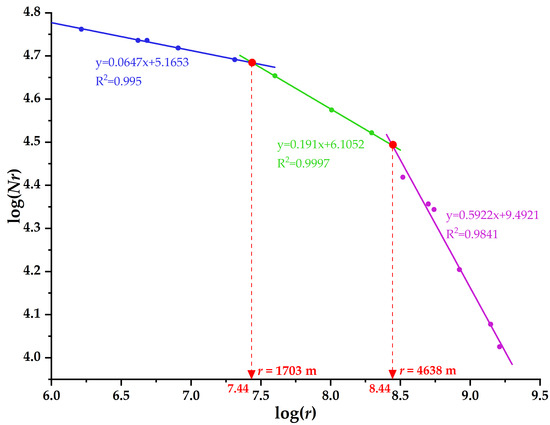
Figure 5.
Result of box-counting fractal analysis of tungsten occurrences.
A Fry analysis was conducted to further investigate the multi-scale ore-controlling mechanisms revealed by the above fractal results. As shown in Figure 6a, 13,806 Fry points were generated from 118 tungsten occurrences. Based on this, rose diagrams were drawn to unveil the preferential trends of plausible ore-related controls at various scales. The results indicate that the Fry points illustrate evident NE and EW trends at the local and regional scales, respectively (Figure 6c,d); however, the rose diagram shows no obvious dominant trend at the camp scale (Figure 6b). This suggests that tungsten mineralization is controlled by fundamental NE- and EW-trending features, which are mostly likely linked to the NE- and EW-trending faults in the study area. The NW-trending faults exhibit subtle controls in the rose diagrams at all scales, which implies that these faults were either inactive during the ore-forming periods or were formed after mineralization events, thus exerting subtle control on mineralization. Such an inference is consistent with the results of a previous study that performed a distance distribution analysis in this region, which also emphasized the controls of NE- and EW-trending faults on tungsten mineralization [33].
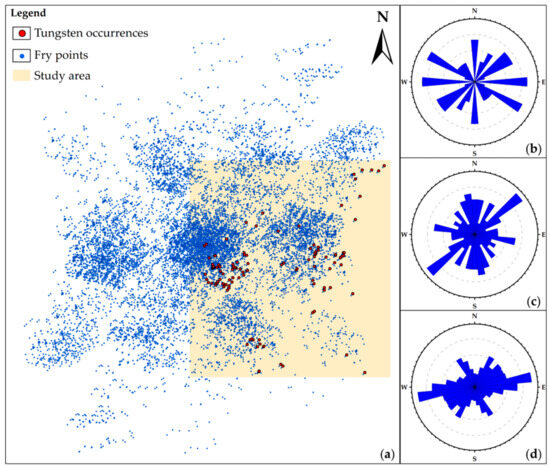
Figure 6.
Results of Fry analysis of mineral occurrences (a) showing dominant ore-controlling trends at camp scale (b), local scale (c), and regional scale (d).
Activated faults commonly serve as pathways for transporting ore-forming components (e.g., metals, fluids, and ligands) from deep-source regions to shallow trap zones. The NE- and EW-trending faults are believed to play such a role in the Gannan district due to the Fry analytical results and, thus, can be considered as effective predictor features closely related to mineralization. In order to dig the nonlinear information from these features, multifractal indices, including D0, D1, D2, ∆α, and ∆f(α), were calculated using the framework described in Section 3.2. Figure 7 depicts the contour maps of these indices, together with a density map of the faults that serves as a numerical representation of the raw fault data.
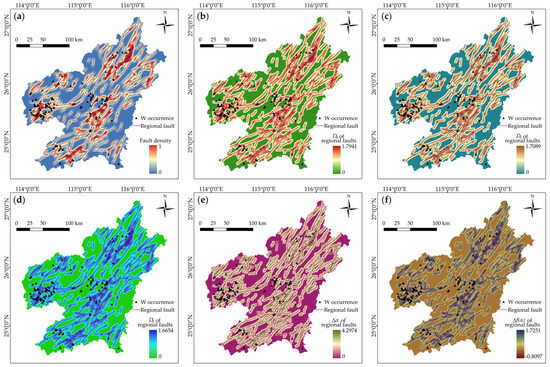
Figure 7.
Feature representations of regional faults. (a) Fault density. (b) D0 of regional faults. (c) D1 of regional faults. (d) D2 of regional faults. (e) ∆α of regional faults. (f) ∆f(α) of regional faults.
The Yanshanian granitic intrusions are interpreted as providing the metals and fluids required for ore formation, since many previous studies have proven that the tungsten mineralization in the study area is temporally, spatially, and genetically associated with Yanshanian intrusions [137,138,139]. Proximity to outcropped Yanshanian intrusions was employed as a pathfinder for tungsten mineralization (Figure 8a). In addition, the occurrences of the Yanshanian intrusions can be further represented by their multifractal indices, as shown in Figure 8b–f. The magnetic anomalies were used to trace the buried intrusions, given that intrusive rocks in this region exhibit obvious magnetic susceptibility and sedimentary wall rocks have no magnetism [140]; therefore, magnetic anomalies and their multifractal representations were employed as spatial proxies of mineralization (Figure 9).
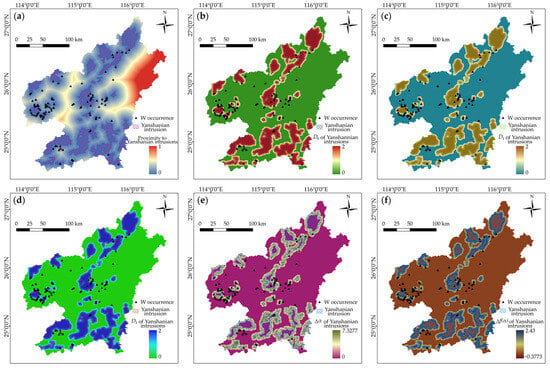
Figure 8.
Feature representations of Yanshanian intrusions. (a) Proximity to Yanshanian intrusions. (b) D0 of Yanshanian intrusions. (c) D1 of Yanshanian intrusions. (d) D2 of Yanshanian intrusions. (e) ∆α of Yanshanian intrusions. (f) ∆f(α) of Yanshanian intrusions.
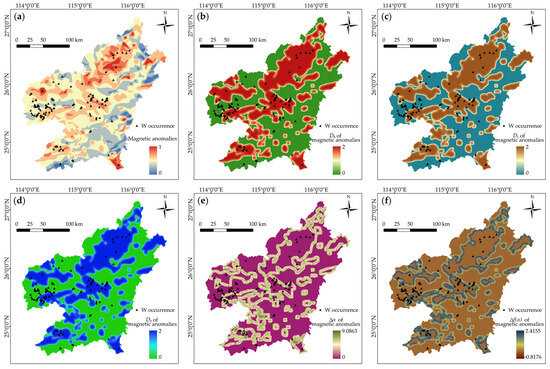
Figure 9.
Feature representations of magnetic anomalies. (a) Magnetic anomalies. (b) D0 of magnetic anomalies. (c) D1 of magnetic anomalies. (d) D2 of magnetic anomalies. (e) ∆α of magnetic anomalies. (f) ∆f(α) of magnetic anomalies.
Hydrothermal deposits are direct products of massive metal deposition; therefore, hydrothermal alterations and geochemical anomalies, which are footprints of ore-forming chemical deposition, were used as evidential features for MPM. Mappable alterations including iron-oxide and argillic alterations were extracted from Landsat-8 data after remote sensing processing (Figure 10a and Figure 11a). The multifractal quantifications of hydrothermal alterations were also calculated and presented in Figure 10 and Figure 11. Furthermore, W, Mn, and Fe anomalies were employed as geochemical evidence. However, multifractal representations of geochemical anomalies are absent in this study, because the original sampling data necessarily required for fractal calculation are confidential and inaccessible at present. Instead, we extracted anomaly information from the rasterized maps of W, Mn, and Fe anomalies as evidential layers for the subsequent MPM modeling (Figure 12).
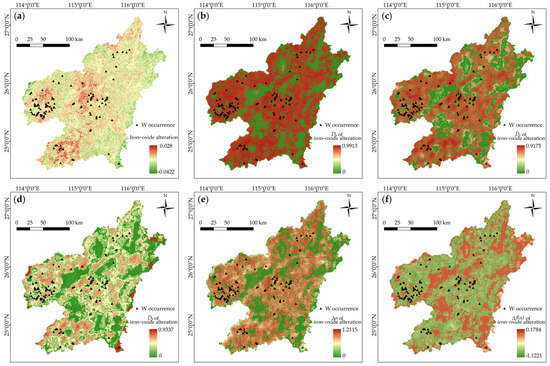
Figure 10.
Feature representations of iron-oxide alteration. (a) Iron-oxide alteration. (b) D0 of iron-oxide alteration. (c) D1 of iron-oxide alteration. (d) D2 of iron-oxide alteration. (e) ∆α of iron-oxide alteration. (f) ∆f(α) of iron-oxide alteration.
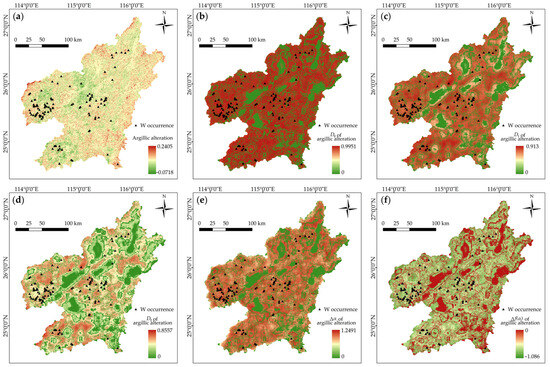
Figure 11.
Feature representations of argillic alteration. (a) Argillic alteration. (b) D0 of argillic alteration. (c) D1 of argillic alteration. (d) D2 of argillic alteration. (e) ∆α of argillic alteration. (f) ∆f(α) of argillic alteration.
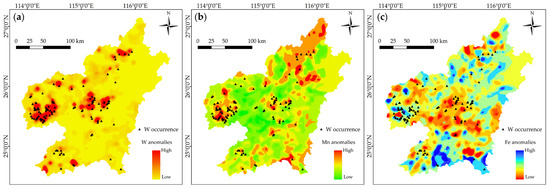
Figure 12.
Contour map of geochemical anomalies. (a) W anomalies. (b) Mn anomalies. (c) Fe anomalies.
The geological significance of the predictor features in MPM lies in their ability to recognize mineralization patterns. In this regard, fractal representations of the features are beneficial in providing discernible information favorable for identifying mineralization patterns, since various multifractal indices depict the different underlying ore-related patterns of the target features in terms of their irregularities and scaling characteristics. All the multifractal indices of faults and the raw data of fault density exhibit a similar distribution pattern that highlights NE-trending clustering of high index values. The tungsten occurrences are identified to be located in the intersection zones of NE-trending high-value zones with EW-trending highlighted zones (Figure 7). The multifractal representations of the Yanshanian intrusions have a similar pattern, which delineates the outcropped zones of the intrusions (Figure 8), except for the ∆α and ∆f(α) of intrusions that exhibit worm-shaped clusters of high-value cells (Figure 8e,f). The highlighted zones detect the inner and outer contact zones between outcropped intrusions and wall rocks, which are interpreted to be favorable locations for mineralization, as the known tungsten occurrences suit the range of the worm-shaped belts, especially for the western region, where 27 tungsten occurrences are situated around a ring-shaped zone (see the marked range shown in Figure 8e,f). The D0, D1, and D2 of magnetic anomalies outline the extensive areas of high magnetic susceptibility (Figure 9b–d). The ∆α and ∆f(α) of magnetic anomalies also show worm-shaped belts, but their correlation with mineralization is weak. Only the tungsten occurrences in the SW regions coincide with the highlighted zones, whereas most of the other occurrences fall beyond the range of high-value zones (Figure 9e,f). The original evidential maps of iron-oxide and argillic alterations have the highest spatial resolution of 15 m. They provide detailed information regarding altered minerals but, on the other hand, they may bring about unrelated or noisy information that impedes the recognition of mineralization patterns (Figure 10a and Figure 11a). The fractal representations of the alterations assist in extracting ore-related information and in reducing data dimension and volume, as shown in Figure 10b–f and Figure 11b–f. Among the multifractal indices, the D2 of the alterations provides distinguishable zonation that is favorable for recognizing mineralization. The tungsten occurrences can be clearly identified in the limited zones with moderate-to-high D2 values (Figure 10d and Figure 11d). In contrast, the other multifractal indices exhibit weaker recognition ability. For example, although most of the known occurrences are located in the high-value zones in the D0 maps (Figure 10b and Figure 11b), these zones occupy an excessively extensive area, which is not conducive for AI models in their creation of an efficient criterion to recognize mineralization.
4.2. Multi-Criteria Feature Selection of Fractal Index Evidential Layers
Five feature selection criteria were used in this study to evaluate the capability of individual evidential layers for predicting the prospectivity of tungsten mineralization (Table 1). Among these criteria, information gain, chi-square, and the Pearson correlation coefficient are regular and commonly used methods for general feature selection, while P–A plot and K-means clustering are more relevant to MPM and are endowed with an exploratory significance. The normalized density Nd can be used effectively as a quantitative index to measure the priority of predictor features in terms of their occurrence-capturing ability. For example, as shown in Table 1 and Figure 13, the ∆f(α) of the faults captures 57.49% of the known occurrences within 42.51% of the delimited area, yielding the highest Nd ratio on the P–A plots for fault-related features, followed by the D1, raw density, D0, D2, and ∆α of the fault distribution. Therefore, when judged by the criterion of P–A plot, the priority ranking for fault-related features is as follows: ∆f(α) > D1 > fault density > D0 > D2 > ∆α. The results of the K-means clustering also provide a ranking of the capturing efficiency of the evidential features. For example, the best cluster for evaluating the D2 of the Yanshanian granitic intrusions contains 1.71% of the cells, but captures 10.17% of tungsten occurrences, yielding the highest Nk ratio (5.9474) among the granite-related features, followed by D1, D0, ∆α, ∆f(α), and the raw granite feature.

Table 1.
Ranking of evidential features using multiple criteria.

Figure 13.
P–A plots of feature representations of evidential layers.
Compared to the above-mentioned criteria emphasizing the capturing efficiency of target predictor features, the regular criteria for feature selection, including information gain, chi-square, and correlation, weigh the relative importance of evidential features by evaluating their associations with tungsten occurrences from a data perspective. The resulting indices of these criteria and their ranks are listed in Table 1. Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 provide a visual summary of the ranking results normalized to a [0, 1] range. Finally, the average ranks of the five criteria were calculated (Table 1), and the first-ranked features, i.e., fault density, the ∆α of granite intrusions, D1 of magnetic anomalies, D2 of iron-oxide alteration, and the D2 of argillic alteration, were selected as the optimal features representative of the corresponding ore-related elements.
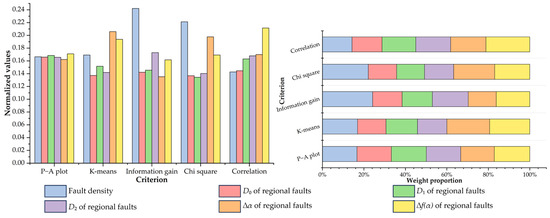
Figure 14.
Importance ranking of feature representations of regional fault.
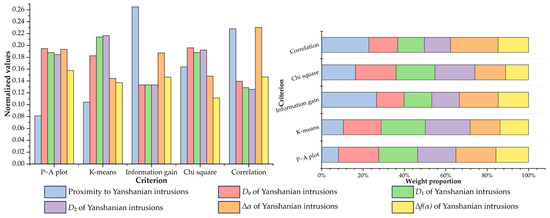
Figure 15.
Importance ranking of feature representations of Yanshanian intrusions.
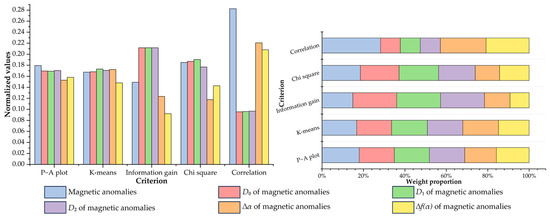
Figure 16.
Importance ranking of feature representations of magnetic anomalies.
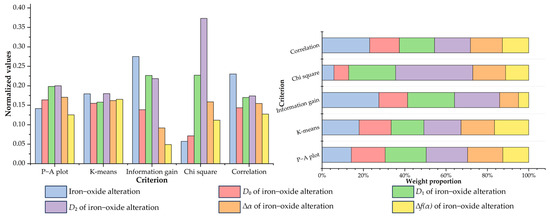
Figure 17.
Importance ranking of feature representations of iron-oxide alteration.
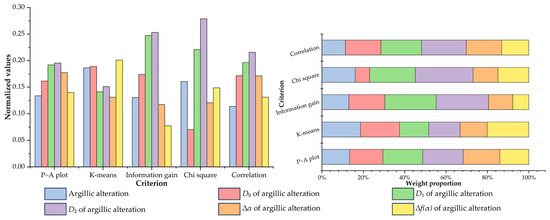
Figure 18.
Importance ranking of feature representations of argillic alteration.
4.3. Predictive Modeling
The selected features were employed as evidential input to AI models. Each model was trained 10 times to yield robust predictions. The model parameters and their optimal values derived from the 10-fold grid-search training process are listed in Tables S1–S5 in the Supplementary Materials.
A comprehensive comparative study of model performance was conducted on the four AI models trained by predictor features with different representations. The metrics for assessing model performance include classification accuracy and predictive efficiency (Figure 19). The former, measured by Accuracy and Kappa index, concerns classification precision from an algorithmic perspective, while the latter emphasizes the occurrence-capturing efficiency of mineral potential from an exploratory point of view. The success rate curve was employed to assess predictive efficiency, as shown in Figure 20. The ANN model trained by fractal representations yields the highest slope of 9.3785, which indicates that 78.81% of the known occurrences are successfully captured within 9% of the delineated area (Figure 20a), achieving the best predictive efficiency, followed by the fractal-trained RF model with a high slope value of 8.8983. Figure 19 illustrates the overall performance of the four algorithms trained by datasets with and without fractal representations. ANN and RF outperform the other two algorithms in classification precision with respect to their leading values of Accuracy and Kappa index, and they also perform better in predictive efficiency, except for the RF model trained by raw data, which falls behind the fractal-trained DT model. Regardless of the differences in model performance, it is noteworthy that, for a given AI algorithm, a model trained by fractal feature datasets always outperforms one trained by the raw data, demonstrated in the radar diagram (Figure 19), wherein each algorithm’s fractal-trained model (depicted in solid lines) encloses its counterpart (presented in dotted lines).
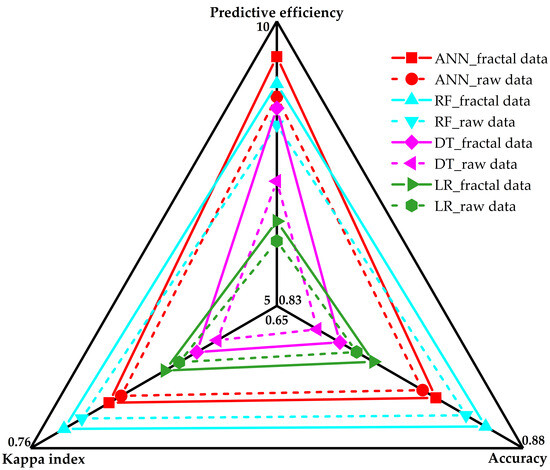
Figure 19.
Radar diagram showing comprehensive performance of AI models.
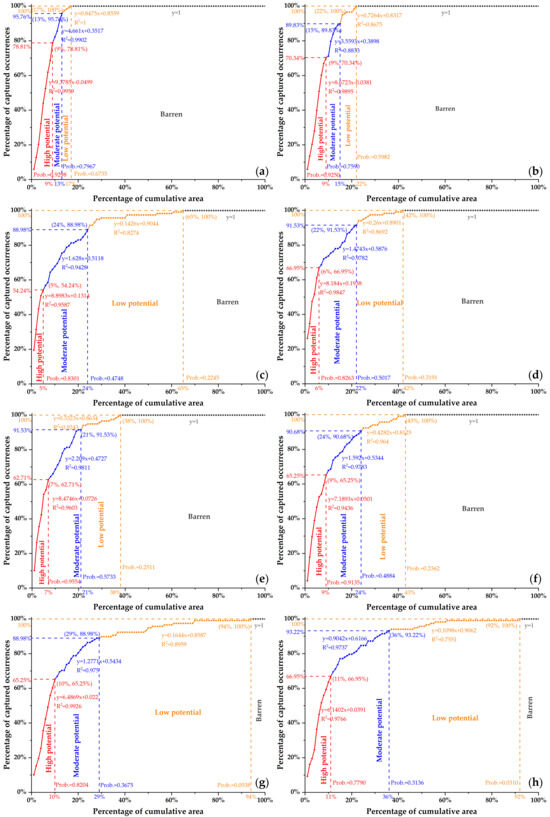
Figure 20.
Success rate curves of AI predictive models. (a) ANN model trained by fractal dataset. (b) ANN model trained by raw dataset. (c) RF model trained by fractal dataset. (d) RF model trained by raw dataset. (e) DT model trained by fractal dataset. (f) DT model trained by raw dataset. (g) LR model trained by fractal dataset. (h) LR model trained by raw dataset.
The predictions yielded by the AI models are illustrated in Figure 21. Four levels of mineral potential, including barren, low potential, moderate potential, and high potential, are distinguished based on thresholds derived from the intersections of different fitting lines on the success rate plots (Figure 20), and are delineated on the prospectivity maps (Figure 21).
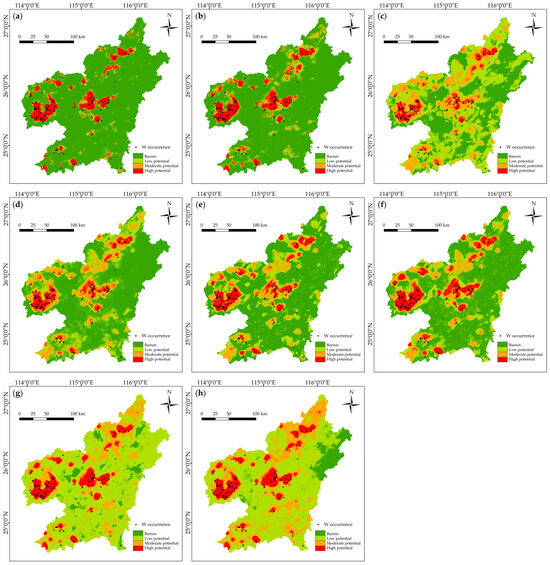
Figure 21.
Prospectivity maps generated by AI models. (a) ANN model trained by fractal dataset. (b) ANN model trained by raw dataset. (c) RF model trained by fractal dataset. (d) RF model trained by raw dataset. (e) DT model trained by fractal dataset. (f) DT model trained by raw dataset. (g) LR model trained by fractal dataset. (h) LR model trained by raw dataset.
5. Discussion
The comparative results of model performances reveal that, for each AI algorithm, the model trained by the fractal dataset outperforms its counterpart trained by the raw dataset. In this section, we discuss how the fractal index features improve the predictive performance of AI models, and how these models can benefit practical mineral exploration.
Machine learning algorithms have an inherent black-box effect, i.e., they are unable to offer transparent modeling processes suitable for explaining their predictions. In this study, the SHAP approach was employed to explain the output of ANN models which were found to be optimal models after model assessment, with a focus on their predictive performance when using four fractal index features (i.e., the ∆α of granite intrusions, D1 of magnetic anomalies, D2 of iron-oxide alteration, and the D2 of argillic alteration), compared to that when employing their raw data. As shown in Figure 22b, the points of the magnetic anomalies, iron-oxide, and argillic alterations are intertwined in their raw datasets. More specifically, the points with contrasting values cluster in the SHAP range of [−0.5~0.5] for the magnetic anomalies, [−0.6~0.3] for iron-oxide alteration, and [−0.1~0.2] for the argillic alteration, which indicates that both the high and low values of these features endow equally poor contributions to the model output. In contrast, the points derived from the fractal dataset for magnetic anomalies, iron-oxide, and argillic alteration are distinguishable in their value colors and positions on the SHAP-axis (Figure 22a). Most of the red points with high feature values are distributed on the positive SHAP-axis and clearly separated from the blue points with low feature values on the negative SHAP-axis. From a geological perspective, these anomaly-related features serve as indirect pathfinders for mineralization, and commonly have subtle correlations with mineralization, thus exhibiting less distinguishable patterns on the SHAP plots. The fractal representations of these anomalies significantly improve their contributions to the model output by extracting the underlying nonlinear ore-related information from the raw data. Yanshanian intrusions are widely recognized as the most prominent ore-controlling factor in this region and serve as a direct predictor of tungsten mineralization. They exhibit a clearly distinguishable point pattern on the SHAP plot of the raw data (Figure 22b). Since this feature is represented by proximity to Yanshanian intrusions, the blue points with low values, denoting closer distances to the intrusions, make greater contributions to the model output. The fractal representation (∆α) of the Yanshanian intrusions also has a strong impact on the model output, with almost all the red points clustered in a range of [0.1~1.3] on the positive SHAP-axis. In summary, for a given algorithm, fractal representations provide more discriminative and definitive feature values that enhance the cognitive capability of the AI model trained by these data, thereby improving its predictive performance, especially for those indirect predictor features that show subtle correlations with the mineralization in the raw dataset.
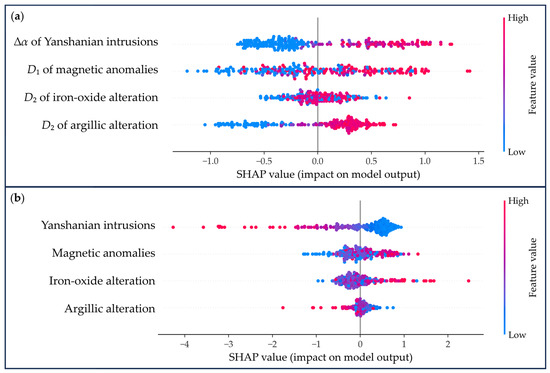
Figure 22.
SHAP plots for fractal representation (a) and raw data (b) of Yanshanian intrusions, magnetic anomalies, iron-oxide alteration, and argillic alteration.
The contribution of individual predictor features on each model can be illustrated in a more straightforward way when they are supported by information gain, as shown in Figure 23. The W and Mn anomalies, which serve as direct ore-forming elements, exert the most important influence on the predictive model in all the models. In the models trained by raw datasets, the Yanshanian intrusions also make a significant contribution, whereas other features contribute little to model output (Figure 23b). Such a pattern is coherent with the findings of our previous two studies [18,101]. The iron-oxide and argillic alteration, newly employed in this study, make very poor contributions to the raw datasets (Figure 23b). In the models trained by fractal datasets, the ∆α of the Yanshanian intrusions still make the third most significant contribution, while the D2 of iron-oxide alteration and D2 of argillic alteration make a strikingly important contribution to the predictive models, especially for the D2 of argillic alteration, which achieves an average weight comparable to the Yanshanian intrusions (Figure 23a). Such findings are beneficial to the practical prospecting work undertaken in this study. As a matured ore district, prominent ore-controlling factors such as Yanshanian intrusions have long been applied in mineral exploration, and the mineralization locations that are closely related to these factors and are easy to recognize have already been explored. The new mineralization clues are important but hard to find. Remote sensing alterations have been investigated but have proven to be ineffective due to high vegetation cover and to the complex distribution pattern of altered minerals. The findings of this study imply that the fractal representations of raw remote sensing data provide a surprisingly effective way to recognize mineralization patterns and, thus, contribute to mineral prospectivity. However, it should be noted that not all the fractal representations facilitate model prediction. Magnetic anomalies show the worst weight in the fractal-trained models (Figure 23a), whereas they make a moderate contribution to the models trained by raw data (Figure 23b). This may be attributed to the low resolution of the magnetic predictor map (Figure 9a), which may itself reflect a vague relationship with mineralization in the raw dataset; however, its fractal representations are not precise enough to extract nonlinear ore-related information.
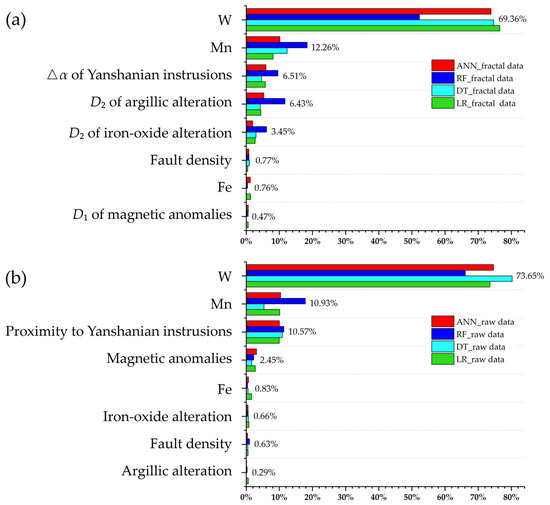
Figure 23.
Feature contributions of model prediction supported by information gain. (a) Fractal-trained models. (b) Models trained by the raw data. The numbers following the bars are the average contribution of specific features.
Mineral exploration is an expensive and high-risk activity; therefore, predictive efficiency and risk evaluation are essential for practical MPM, in addition to the common model assessment that focuses mainly on predictive precision. The success rate curve is employed in Section 4.3 to assess predictive efficiency. The calculation of uncertainty is further introduced here to evaluate the risk by 10-iteration predictive modeling. The uncertainty values and prospectivity values are illustrated in Figure 24. The probability–uncertainty diagrams for all the models show arch-shaped patterns to varying degrees. This pattern suggests that the cells with high or low prospectivity values have low uncertainty, while the cells with a moderate level of prospectivity have high uncertainty. This arch-shaped pattern is favorable for mineral exploration from an exploratory perspective, since the regions with the highest prospectivity values are the first-order regions of interest for future prospecting, and it is profitable to know that the high prospectivity values of these regions are verified to be certain and reliable. A scenario of prospectivity targeting that considers both predictive efficiency and exploration risk is presented in Figure 24. Different levels of mineral prospectivity are defined by the thresholds derived from the success rate curves (Figure 20), and an uncertainty threshold of 0.1 is determined to delineate low-risk zones, as the uncertainties of most cells containing known occurrences fall within this range. In this scenario, the final exploration targets are delineated by the overlapping regions of high-potential zones and low-risk cells (Figure 24). Targeting efficiency, which is similar to predictive efficiency and defined as the percentage of occurrences included (i.e., the number of occurrences within low-risk regions/total number of tungsten occurrences), divided by the percentage of cells involved (i.e., the number of low-risk cells/total number of cells), is used to quantitatively measure targeting performance (Table 2). This reveals that all the AI models benefit from the employment of fractal index feature datasets, with a 12.83%, 11.1%, 14.42%, and 4.2% improvement in targeting efficiency for the ANN, RF, DT, and LR models, respectively (Table 2).
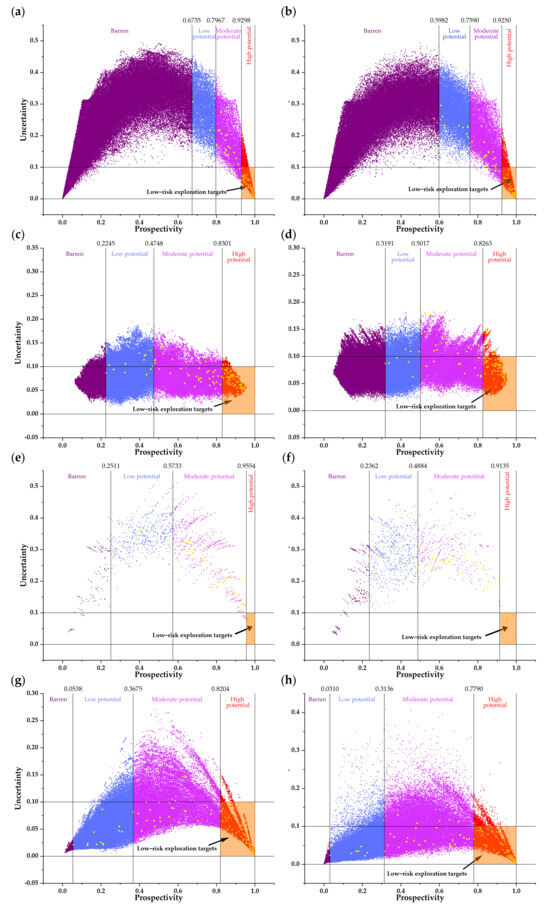
Figure 24.
Scatter plots showing prospectivity and uncertainty of AI models. (a) ANN model trained by fractal dataset. (b) ANN model trained by raw dataset. (c) RF model trained by fractal dataset. (d) RF model trained by raw dataset. (e) DT model trained by fractal dataset. (f) DT model trained by raw dataset. (g) LR model trained by fractal dataset. (h) LR model trained by raw dataset.

Table 2.
Targeting efficiency of the low-risk exploration targets delineated by AI models.
The work presented in this paper is the third MPM study undertaken in the Gannan district with the same labelled dataset. Compared to the previous two studies, which were characterized by the employment of a deep learning algorithm [18] and few-shot learning [101], this study contributes to the improvement of the predictive performance of regular AI models by enriching predictor feature sets rather than further introducing newly proposed machine learning algorithms with complex architecture. In this contribution, iron-oxide and argillic alteration extracted from remote sensing data were utilized as predictor features, which integrated the predictor feature set with all four multi-source data that are commonly used in MPM studies, including geological, geophysical, geochemical, and remote sensing information. Furthermore, and more importantly, the fractal representations of the raw dataset greatly enrich the available features used for model training. The results proved that, for a given machine learning algorithm, the enriched feature set is beneficial in improving classification accuracy (Figure 19), predictive performance (Figure 20), and targeting efficiency (Figure 24 and Table 2). The framework and findings of this paper can provide an alternative for any AI-driven MPM study troubled by scarce predictor features or the poor performance of available features.
6. Conclusions
AI models boost MPM tasks in a data-driven way, but they suffer from noisy and unrepresentative inputs. In this study, two attempts have been made to address this issue, namely (i) the introduction of fractal and multifractal analyses for digging and extracting the nonlinear ore-related information from the raw feature dataset, and (ii) the employment of multi-criteria feature selection to choose the optimal representations of the predictor features favorable for training AI models.
Eight multi-source evidential features, including NE- and EW-trending faults, Yanshanian granitic intrusions, magnetic anomalies, iron-oxide alteration, and argillic alteration, as well as W, Mn, and Fe anomalies, serve as predictor evidence based on box-counting fractal calculation, Fry analysis, and understanding of the mineral system. A set of multifractal indices including D0, D1, D2, ∆α, and ∆f(α) were calculated and assigned to each predictive unit, so as to represent different aspects of the target features regarding their irregularities and scaling characteristics. The P–A plot, K-means clustering, information gain, chi-square, and the Pearson correlation coefficient were jointly utilized for feature selection. The results indicate that fault density, the ∆α of Yanshanian intrusions, D1 of magnetic anomalies, D2 of iron-oxide alteration, and the D2 of argillic alteration averaged first rankings in the corresponding feature representations, and can be considered to be the optimal features used for training AI models.
The results of the model evaluation suggest that all the predictive models trained by the fractal index feature dataset outperform their counterparts trained by raw dataset in terms of Accuracy, Kappa index, and predictive efficiency. The SHAP analysis attributes the superior performance of the fractal-trained models to improvement in the cognitive capability of these AI models trained by fractal index features, which are more discriminative and definitive. This improvement is especially significant for the indirect predictor features that show subtle correlations with mineralization in the raw dataset. Furthermore, the fractal-trained models benefit practical mineral exploration by yielding exploration targets that achieve higher capturing efficiency and lower risk than the models trained by the raw dataset. In particular, the fractal representations of remote sensing alterations provide an effective way to recognize mineralization patterns and to contribute to mineral prospectivity.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/fractalfract8040224/s1, Source codes and used data: Table S1: Parameters used for training machine learning models; Table S2: Optimal parameters of ANN models derived from grid-search training process; Table S3: Optimal parameters of RF models derived from grid-search training process; Table S4: Optimal parameters of DT models derived from grid-search training process; Table S5: Optimal parameters of LR models derived from grid-search training process. File S1. Algorithm Details.
Author Contributions
Conceptualization, T.S.; methodology, M.F. and T.S.; software, M.F., Y.L. and Z.W.; validation, M.F., J.H. and L.M.; formal analysis, H.Z. and W.P.; investigation, M.F., W.P., H.Z. and Y.L.; resources, T.S., W.P. and F.C.; writing—original draft preparation, T.S. and M.F.; writing—review and editing, T.S. and M.F.; visualization, M.F. and T.S.; project administration, T.S. and F.C.; funding acquisition, T.S. and F.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant Nos. 42062021 and 42067042); Natural Science Foundation of Jiangxi Province for Distinguished Young Scholars (grant No. 20224ACB218003); China Postdoctoral Science Foundation (grant No. 2019M662267); Program of Qingjiang Excellent Young Talents, Jiangxi University of Science and Technology (grant No. JXUSTQJBJ2020001); Science and Technology Program of Ganzhou City (grant No. 202101095156); Ganpo Talent Support Program: Young Leading Talents in University (grant No. QN2023037); and Postgraduate Innovation Program of Jiangxi Province (grant No. YC2023-S682).
Data Availability Statement
Data are contained within the Supplementary Materials.
Acknowledgments
We are grateful to three anonymous reviewers for their constructive comments, which significantly improved the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhai, M.; Hu, R.; Wang, Y.; Jiang, S.; Wang, R.; Li, J.; Chen, H.; Yang, Z.; Lü, Q.; Qi, T.; et al. Mineral Resource Science in China: Review and perspective. Geogr. Sustain. 2021, 2, 107–114. [Google Scholar] [CrossRef]
- Okada, K. Breakthrough technologies for mineral exploration. Miner. Econ. 2022, 35, 429–454. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Developments in GIS-based mineral prospectivity mapping: An overview. In Proceedings of the Conference of Mineral Prospectivity, Orleans, France, 24–26 October 2017. [Google Scholar]
- Lou, Y.; Liu, Y. Mineral Prospectivity Mapping of Tungsten Polymetallic Deposits Using Machine Learning Algorithms and Comparison of Their Performance in the Gannan Region, China. Earth Space Sci. 2023, 10, e2022EA002596. [Google Scholar] [CrossRef]
- Yousefi, M.; Carranza, E.J.M.; Kreuzer, O.P.; Nykänen, V.; Hronsky, J.M.A.; Mihalasky, M.J. Data analysis methods for prospectivity modelling as applied to mineral exploration targeting: State-of-the-art and outlook. J. Geochem. Explor. 2021, 229, 106839. [Google Scholar] [CrossRef]
- Yousefi, M.; Kreuzer, O.P.; Nykänen, V.; Hronsky, J.M.A. Exploration information systems—A proposal for the future use of GIS in mineral exploration targeting. Ore Geol. Rev. 2019, 111, 103005. [Google Scholar] [CrossRef]
- Hu, X.; Li, X.; Yuan, F.; Jowitt, S.M.; Ord, A.; Ye, R.; Li, Y.; Dai, W.; Li, X.; Durance, P. 3D Numerical Simulation-Based Targeting of Skarn Type Mineralization within the Xuancheng-Magushan Orefield, Middle-Lower Yangtze Metallogenic Belt, China. Lithosphere 2020, 2020, 8351536. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, L. Quantitative 3D Association of Geological Factors and Geophysical Fields with Mineralization and Its Significance for Ore Prediction: An Example from Anqing Orefield, China. Minerals 2018, 8, 300. [Google Scholar] [CrossRef]
- Zuo, R.; Carranza, E.J.M. Machine Learning-Based Mapping for Mineral Exploration. Math. Geosci. 2023, 55, 891–895. [Google Scholar] [CrossRef]
- Tessema, A. Mineral Systems Analysis and Artificial Neural Network Modeling of Chromite Prospectivity in the Western Limb of the Bushveld Complex, South Africa. Nat. Resour. Res. 2017, 26, 465–488. [Google Scholar] [CrossRef]
- Maepa, F.; Smith, R.S.; Tessema, A. Support vector machine and artificial neural network modelling of orogenic gold prospectivity mapping in the Swayze greenstone belt, Ontario, Canada. Ore Geol. Rev. 2021, 130, 103968. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, L.; Wu, W. Machine Learning-Based 3D Modeling of Mineral Prospectivity Mapping in the Anqing Orefield, Eastern China. Nat. Resour. Res. 2021, 30, 3099–3120. [Google Scholar] [CrossRef]
- Li, T.; Xia, Q.; Zhao, M.; Gui, Z.; Leng, S. Prospectivity Mapping for Tungsten Polymetallic Mineral Resources, Nanling Metallogenic Belt, South China: Use of Random Forest Algorithm from a Perspective of Data Imbalance. Nat. Resour. Res. 2019, 29, 203–227. [Google Scholar] [CrossRef]
- Xiao, F.; Chen, W.; Wang, J.; Erten, O. A Hybrid Logistic Regression: Gene Expression Programming Model and Its Application to Mineral Prospectivity Mapping. Nat. Resour. Res. 2021, 31, 2041–2064. [Google Scholar] [CrossRef]
- Li, X.; Yuan, F.; Zhang, M.; Jia, C.; Jowitt, S.M.; Ord, A.; Zheng, T.; Hu, X.; Li, Y. Three-dimensional mineral prospectivity modeling for targeting of concealed mineralization within the Zhonggu iron orefield, Ningwu Basin, China. Ore Geol. Rev. 2015, 71, 633–654. [Google Scholar] [CrossRef]
- Zuo, R.; Xiong, Y.; Wang, J.; Carranza, E.J.M. Deep learning and its application in geochemical mapping. Earth-Sci. Rev. 2019, 192, 1–14. [Google Scholar] [CrossRef]
- Sun, T.; Li, H.; Wu, K.; Chen, F.; Zhu, Z.; Hu, Z. Data-driven predictive modelling of mineral prospectivity using machine learning and deep learning methods: A case study from southern Jiangxi Province, China. Minerals 2020, 10, 102. [Google Scholar] [CrossRef]
- Xiong, Y.; Zuo, R.; Carranza, E.J.M. Mapping mineral prospectivity through big data analytics and a deep learning algorithm. Ore Geol. Rev. 2018, 102, 811–817. [Google Scholar] [CrossRef]
- Roshanravan, B.; Kreuzer, O.P.; Bruce, M.; Davis, J.; Briggs, M. Modelling gold potential in the Granites-Tanami Orogen, NT, Australia: A comparative study using continuous and data-driven techniques. Ore Geol. Rev. 2020, 125, 103661. [Google Scholar] [CrossRef]
- Hu, X.; Chen, Y.; Liu, G.; Yang, H.; Luo, J.; Ren, K.; Yang, Y. Numerical modeling of formation of the Maoping Pb-Zn deposit within the Sichuan-Yunnan-Guizhou Metallogenic Province, Southwestern China: Implications for the spatial distribution of concealed Pb mineralization and its controlling factors. Ore Geol. Rev. 2022, 140, 104573. [Google Scholar] [CrossRef]
- Hu, X.; Liu, G.; Chen, Y.; Deng, Y.; Luo, J.; Wang, K.; Yang, Y.; Li, Y. Numerical simulation of ore formation within skarn-type Pb-Zn deposits: Implications for mineral exploration and the duration of ore-forming processes. Ore Geol. Rev. 2023, 163, 105768. [Google Scholar] [CrossRef]
- Thiergärtner, H. Theory and practice in mathematical geology—Introduction and discussion. Math. Geol. 2006, 38, 659–665. [Google Scholar] [CrossRef]
- Porwal, A.; Carranza, E.J.M.; Hale, M. Artificial neural networks for mineral-potential mapping: A case study from Aravalli Province, Western India. Nat. Resour. Res. 2003, 12, 155–171. [Google Scholar] [CrossRef]
- Forouzan, M.; Arfania, R. Integration of the bands of ASTER, OLI, MSI remote sensing sensors for detection of hydrothermal alterations in southwestern area of the Ardestan, Isfahan Province, Central Iran. Egypt. J. Remote Sens. Space Sci. 2020, 23, 145–157. [Google Scholar] [CrossRef]
- Cheng, Q. Fractal Derivatives and Singularity Analysis of Frequency—Depth Clusters of Earthquakes along Converging Plate Boundaries. Fractal Fract. 2023, 7, 721. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, T.; Wu, K.; Zhang, H.; Zhang, J.; Jiang, X.; Lin, Q.; Feng, M. Fractal-Based Pattern Quantification of Mineral Grains: A Case Study of Yichun Rare-Metal Granite. Fractal Fract. 2024, 8, 49. [Google Scholar] [CrossRef]
- Evertsz, C.J.; Mandelbrot, B.B. Multifractal measures. Chaos Fract. 1992, 473, 921–953. [Google Scholar]
- Zhang, Y.; He, G.; Xiao, F.; Yang, Y.; Wang, F.; Liu, Y. Geochemical Characteristics of Deep-Sea Sediments in Different Pacific Ocean Regions: Insights from Fractal Modeling. Fractal Fract. 2024, 8, 45. [Google Scholar] [CrossRef]
- Wang, W.; Pei, Y.; Cheng, Q.; Wang, W. Local Singularity Spectrum: An Innovative Graphical Approach for Analyzing Detrital Zircon Geochronology Data in Provenance Analysis. Fractal Fract. 2024, 8, 64. [Google Scholar] [CrossRef]
- Yousefi, M.; Carranza, E.J.M. Prediction–area (P–A) plot and C–A fractal analysis to classify and evaluate evidential maps for mineral prospectivity modeling. Comput. Geosci. 2015, 79, 69–81. [Google Scholar] [CrossRef]
- Wang, G.; Carranza, E.J.M.; Zuo, R.; Hao, Y.; Du, Y.; Pang, Z.; Sun, Y.; Qu, J. Mapping of district-scale potential targets using fractal models. J. Geochem. Explor. 2012, 122, 34–46. [Google Scholar] [CrossRef]
- Sun, T.; Wu, K.; Chen, L.; Liu, W.; Wang, Y.; Zhang, C. Joint Application of Fractal Analysis and Weights-of-Evidence Method for Revealing the Geological Controls on Regional-Scale Tungsten Mineralization in Southern Jiangxi Province, China. Minerals 2017, 7, 243. [Google Scholar] [CrossRef]
- Li, T.; Xia, Q.; Chang, L.; Wang, X.; Liu, Z.; Wang, S. Deposit density of tungsten polymetallic deposits in the eastern Nanling metallogenic belt, China. Ore Geol. Rev. 2018, 94, 73–92. [Google Scholar] [CrossRef]
- Cheng, Q.; Agterberg, F.P.; Ballantyne, S.B. The separation of geochemical anomalies from background by fractal methods. J. Geochem. Explor. 1994, 51, 109–130. [Google Scholar] [CrossRef]
- Zuo, R. Machine Learning of Mineralization-Related Geochemical Anomalies: A Review of Potential Methods. Nat. Resour. Res. 2017, 26, 457–464. [Google Scholar] [CrossRef]
- Ouchchen, M.; Boutaleb, S.; Abia, E.H.; El Azzab, D.; Miftah, A.; Dadi, B.; Echogdali, F.Z.; Mamouch, Y.; Pradhan, B.; Santosh, M.; et al. Exploration targeting of copper deposits using staged factor analysis, geochemical mineralization prospectivity index, and fractal model (Western Anti-Atlas, Morocco). Ore Geol. Rev. 2022, 143, 104762. [Google Scholar] [CrossRef]
- Akbari, S.; Ramazi, H.; Ghezelbash, R. Using fractal and multifractal methods to reveal geophysical anomalies in Sardouyeh District, Kerman, Iran. Earth Sci. Inform. 2023, 16, 2125–2142. [Google Scholar] [CrossRef]
- Ramezanali, A.A.; Mansouri, E.; Feizi, F. Integration of aeromagnetic geophysical data with other exploration data layers based on fuzzy AHP and C-A fractal model for Cu-porphyry potential mapping: A case study in the Fordo area, central Iran. Boll. Boll. Geofis. Teor. Appl. 2017, 58, 55–73. [Google Scholar]
- Ghezelbash, R.; Maghsoudi, A.; Carranza, E.J.M. Mapping of single- and multi-element geochemical indicators based on catchment basin analysis: Application of fractal method and unsupervised clustering models. J. Geochem. Explor. 2019, 199, 90–104. [Google Scholar] [CrossRef]
- Asl, R.A.; Afzal, P.; Adib, A.; Yasrebi, A.B. Application of multifractal modeling for the identification of alteration zones and major faults based on ETM+ multispectral data. Arab. J. Geosci. 2014, 8, 2997–3006. [Google Scholar] [CrossRef]
- Xue, B.; Zhang, M.; Browne, W.N.; Yao, X. A Survey on Evolutionary Computation Approaches to Feature Selection. IEEE Trans. Evol. Comput. 2016, 20, 606–626. [Google Scholar] [CrossRef]
- Forson, E.D.; Menyeh, A.; Wemegah, D.D.; Danuor, S.K.; Adjovu, I.; Appiah, I. Mesothermal gold prospectivity mapping of the southern Kibi-Winneba belt of Ghana based on Fuzzy analytical hierarchy process, concentration-area (C-A) fractal model and prediction-area (P-A) plot. J. Appl. Geophys. 2020, 174, 103971. [Google Scholar] [CrossRef]
- Behera, S.; Panigrahi, M.K.; Pradhan, A. Identification of geochemical anomaly and gold potential mapping in the Sonakhan Greenstone belt, Central India: An integrated concentration-area fractal and fuzzy AHP approach. Appl. Geochem. 2019, 107, 45–57. [Google Scholar] [CrossRef]
- Bai, H.; Cao, Y.; Zhang, H.; Zhang, C.; Hou, S.; Wang, W. Combining fuzzy analytic hierarchy process with concentration–area fractal for mineral prospectivity mapping: A case study involving Qinling orogenic belt in central China. Appl. Geochem. 2021, 126, 104894. [Google Scholar] [CrossRef]
- Ghaeminejad, H.; Abedi, M.; Afzal, P.; Zaynali, F.; Yousefi, M. A fractal-based outranking approach for integrating geochemical, geological, and geophysical data. Boll. Geofis. Teor. Appl. 2020, 61, 555–588. [Google Scholar]
- Zuo, R.; Wang, J. Fractal/multifractal modeling of geochemical data: A review. J. Geochem. Explor. 2016, 164, 33–41. [Google Scholar] [CrossRef]
- Behera, S.; Panigrahi, M.K. Mineral prospectivity modelling using singularity mapping and multifractal analysis of stream sediment geochemical data from the auriferous Hutti-Maski schist belt, S. India. Ore Geol. Rev. 2021, 131, 104029. [Google Scholar] [CrossRef]
- Li, X.; Yuan, F.; Zhou, T.; Deng, Y.; Zhang, D.Y.; Xu, C.; Zhang, R. Extraction of Multi-Fractal Geochemical Anomalies and Ore Genesis Prediction in the Tarbahatai-Sawuer Region, Xinjiang. Acta Petrol. Sin. 2015, 31, 426–434, (In Chinese with English abstract). [Google Scholar]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature Selection: A Data Perspective. ACM Comput. Surv. 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Wang, C.; Pan, Y.; Chen, J.; Ouyang, Y.; Rao, J.; Jiang, Q. Indicator element selection and geochemical anomaly mapping using recursive feature elimination and random forest methods in the Jingdezhen region of Jiangxi Province, South China. Appl. Geochem. 2020, 122, 104760. [Google Scholar] [CrossRef]
- Zekri, H.; Cohen, D.R.; Mokhtari, A.R.; Esmaeili, A. Geochemical Prospectivity Mapping Through a Feature Extraction–Selection Classification Scheme. Nat. Resour. Res. 2018, 28, 849–865. [Google Scholar] [CrossRef]
- Forson, E.D.; Wemegah, D.D.; Hagan, G.B.; Appiah, D.; Addo-Wuver, F.; Adjovu, I.; Otchere, F.O.; Mateso, S.; Menyeh, A.; Amponsah, T. Data-driven multi-index overlay gold prospectivity mapping using geophysical and remote sensing datasets. J. Afr. Earth Sci. 2022, 190, 104504. [Google Scholar] [CrossRef]
- Riahi, S.; Bahroudi, A.; Abedi, M.; Aslani, S. Hybrid outranking of geospatial data: Multi attributive ideal-real comparative analysis and combined compromise solution. Geochemistry 2022, 82, 125898. [Google Scholar] [CrossRef]
- Yousefi, M.; Nykänen, V. Data-driven logistic-based weighting of geochemical and geological evidence layers in mineral prospectivity mapping. J. Geochem. Explor. 2016, 164, 94–106. [Google Scholar] [CrossRef]
- Feng, C.; Zeng, Z.; Zhang, D.; Qu, W.; Du, A.; Li, D.; She, H. Shrimp zircon U–Pb and molybdenite Re–Os isotopic dating of the tungsten deposits in the Tianmenshan-Hongtaoling W–Sn orefield, southern Jiangxi Province, China, and geological implications. Ore Geol. Rev. 2011, 43, 8–25. [Google Scholar] [CrossRef]
- Fang, G.; Chen, Z.; Chen, Y.; Li, J.; Zhao, B.; Zhou, X.; Zeng, Z.; Zhang, Y. Geophysical investigations of the geology and structure of the Pangushan-Tieshanlong tungsten ore field, South Jiangxi, China—Evidence for site-selection of the 2000-m nanling scientific drilling project (SP-NLSD-2). J. Asian. Earth. Sci. 2015, 110, 10–18. [Google Scholar] [CrossRef]
- GeoCloud Database of China Geological Survey. Available online: http://geocloud.cgs.gov.cn (accessed on 5 February 2024).
- Mao, J.; Cheng, Y.; Chen, M.; Pirajno, F. Major types and time–space distribution of Mesozoic ore deposits in south China and their geodynamic settings. Miner. Depos. 2013, 48, 267–294. [Google Scholar]
- Feng, C.; Zhang, D.; Zeng, Z.; Wang, S. Chronology of the tungsten deposits in southern Jiangxi Province, and episodes and zonation of the regional W-Sn mineralization-evidence from high-precision zircon U-Pb, molybdenite Re-Os and muscovite Ar-Ar ages. Acta Geol. Sin. Engl. Ed. 2012, 86, 555–567. [Google Scholar]
- Jiangxi Bureau of Geology and Mineral Resources. Mineral Prospecting and Targeting of W-Sn-Pb-Zn Deposits in Southern Jiangxi Province; Jiangxi Bureau of Geology and Mineral Resources: Nanchang, China, 2002. (In Chinese) [Google Scholar]
- Xie, X.; Mu, X.; Ren, T. Geochemical mapping in China. J. Geochem. Explor. 1997, 60, 99–113. [Google Scholar]
- Chen, X.; Fu, J. Geochemical Maps of Nanling Range; China University of Geoscience Press: Wuhan, China, 2012. (In Chinese) [Google Scholar]
- Zuo, R.; Carranza, E.J.M. Support vector machine: A tool for mapping mineral prospectivity. Comput. Geosci. 2011, 37, 1967–1975. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Objective selection of suitable unit cell size in data-driven modeling of mineral prospectivity. Comput. Geosci. 2009, 35, 2032–2046. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance and Dimension; W.H. Freeman & Company: San Francisco, CA, USA, 1977. [Google Scholar]
- Chhabra, A.B.; Meneveau, C.; Jensen, R.V.; Sreenivasan, K.R. Direct determination of the f(α) singularity spectrum and its application to fully developed turbulence. Phys. Rev. Appl. 1989, 40, 5284–5294. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B.; Frame, M. Fractals, 1st ed.; Flammarion: Paris, France, 1997. [Google Scholar]
- Takayasu, H. Fractals in the Physical Sciences; Manchester University Press: Manchester, UK, 1990. [Google Scholar]
- Peternell, M.; Kruhl, J.H. Automation of pattern recognition and fractal-geometry-based pattern quantification, exemplified by mineral-phase distribution patterns in igneous rocks. Comput. Geosci. 2009, 35, 1415–1426. [Google Scholar] [CrossRef]
- Fry, N. Random point distributions and strain measurement in rocks. Tectonophysics 1979, 60, 89–105. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Controls on mineral deposit occurrence inferred from analysis of their spatial pattern and spatial association with geological features. Ore Geol. Rev. 2009, 35, 383–400. [Google Scholar] [CrossRef]
- Haddad-Martim, P.M.; Souza Filho, C.R.d.; Carranza, E.J.M. Spatial analysis of mineral deposit distribution: A review of methods and implications for structural controls on iron oxide-copper-gold mineralization in Carajás, Brazil. Ore Geol. Rev. 2017, 81, 230–244. [Google Scholar] [CrossRef]
- Vearncombe, J.; Vearncombe, S. The spatial distribution of mineralization; applications of Fry analysis. Econ. Geol. 1999, 94, 475–486. [Google Scholar] [CrossRef]
- Zuo, R.; Agterberg, F.P.; Cheng, Q.; Yao, L. Fractal characterization of the spatial distribution of geological point processes. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 394–402. [Google Scholar] [CrossRef]
- Parsa, M.; Maghsoudi, A.; Yousefi, M. Spatial analyses of exploration evidence data to model skarn-type copper prospectivity in the Varzaghan district, NW Iran. Ore Geol. Rev. 2018, 92, 97–112. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wheeler, J.A. The Fractal Geometry of Nature. Am. J. Phys. 1983, 51, 286–287. [Google Scholar] [CrossRef]
- Li, L.; Chang, L.; Le, S.; Huang, D. Multifractal analysis and lacunarity analysis: A promising method for the automated assessment of muskmelon (Cucumismelo, L.) epidermis netting. Comput. Electron. Agric. 2012, 88, 72–84. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Z.; Sun, Z.; Cai, J.; Wang, L. Investigation on the pore structure and multifractal characteristics of tight oil reservoirs using NMR measurements: Permian Lucaogou Formation in Jimusaer Sag, Junggar Basin. Mar. Pet. Geol. 2017, 86, 1067–1081. [Google Scholar] [CrossRef]
- Allain, C.; Cloitre, M. Characterizing the lacunarity of random and deterministic fractal sets. Phys. Rev. A 1991, 44, 3552–3558. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, E.P.; Barbosa, M.S.; Costa Lda, F. Self-referred approach to lacunarity. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 2005, 72, 016707. [Google Scholar] [CrossRef]
- Facon, J.; Menoti, D.; de Albuquerque Araújo, A. Lacunarity as a texture measure for address block segmentation. In Proceedings of the 10th Iberoamerican Congress on Pattern Recognition, CIARP 2005, Havana, Cuba, 15–18 November 2005. [Google Scholar]
- Cheng, Q. The gliding box method for multifractal modeling. Comput. Geosci. 1999, 25, 1073–1079. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A Gen. Phys. 1986, 33, 1141–1151. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, H.; Hu, Q.; Liu, L.; Jia, L.; Gao, S.; Wang, Y. Pore structure heterogeneity of Wufeng-Longmaxi shale, Sichuan Basin, China: Evidence from gas physisorption and multifractal geometries. J. Petrol. Sci. Eng. 2022, 208, 109313. [Google Scholar] [CrossRef]
- Atmanspacher, H.; Scheingraber, H.; Wiedenmann, G. Determination of f (α) for a limited random point set. Phys. Rev. Appl. 1989, 40, 3954. [Google Scholar] [CrossRef] [PubMed]
- Vázquez, E.V.; Ferreiro, J.P.; Miranda, J.G.V.; González, A.P. Multifractal Analysis of Pore Size Distributions as Affected by Simulated Rainfall. Vadose Zone J. 2008, 7, 500–511. [Google Scholar] [CrossRef]
- Ge, X.; Fan, Y.; Li, J.; Aleem Zahid, M. Pore structure characterization and classification using multifractal theory—An application in Santanghu basin of western China. J. Pet. Sci. Eng. 2015, 127, 297–304. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Yousefi, M.; Kamkar-Rouhani, A.; Carranza, E.J.M. Application of staged factor analysis and logistic function to create a fuzzy stream sediment geochemical evidence layer for mineral prospectivity mapping. Geochem. Explor. Environ. Anal. 2013, 14, 45–58. [Google Scholar] [CrossRef]
- Cheng, Q.; Agterberg, F.P. Multifractal modeling and spatial point processes. Math. Geol. 1995, 27, 831–845. [Google Scholar] [CrossRef]
- Yousefi, M.; Carranza, E.J.M. Data-Driven Index Overlay and Boolean Logic Mineral Prospectivity Modeling in Greenfields Exploration. Nat. Resour. Res. 2015, 25, 3–18. [Google Scholar] [CrossRef]
- Yousefi, M.; Carranza, E.J.M. Fuzzification of continuous-value spatial evidence for mineral prospectivity mapping. Comput. Geosci. 2015, 74, 97–109. [Google Scholar] [CrossRef]
- Mihalasky, M.J.; Bonham-Carter, G.F. Lithodiversity and its spatial association with metallic mineral sites, Great Basin of Nevada. Nat. Resour. Res. 2001, 10, 209–226. [Google Scholar] [CrossRef]
- Steinhaus, H. Sur la division des corp materiels en parties. Bull. Acad. Pol. Sci. 1956, 1, 801. [Google Scholar]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematics, Statistics and Probability, Berkeley, CA, USA, 27 December–7 January 1966; University of California Press: Berkeley, CA, USA, 1967. [Google Scholar]
- Lloyd, S.P. Least Squares Quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recogn. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Meilă, M. The uniqueness of a good optimum for k-means. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25 June 2006. [Google Scholar]
- Tien Bui, D.; Ho, T.-C.; Pradhan, B.; Pham, B.-T.; Nhu, V.-H.; Revhaug, I. GIS-based modeling of rainfall-induced landslides using data mining-based functional trees classifier with AdaBoost, Bagging, and MultiBoost ensemble frameworks. Environ. Earth Sci. 2016, 75, 1101. [Google Scholar] [CrossRef]
- Zhou, K.; Sun, T.; Liu, Y.; Feng, M.; Tang, J.; Mao, L.; Pu, W.; Huang, J. Prospectivity Mapping of Tungsten Mineralization in Southern Jiangxi Province Using Few-Shot Learning. Minerals 2023, 13, 669. [Google Scholar] [CrossRef]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Pearson, K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. In Breakthroughs in Statistics; Kotz, S., Johnson, N.L., Eds.; Springer: New York, NY, USA, 1992. [Google Scholar]
- Srivastava, R. Karl Pearson and “Applied” Statistics. Resonance 2023, 28, 183–189. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W.H. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Longbotham, N.; Chaapel, C.; Bleiler, L.; Padwick, C.; Emery, W.J.; Pacifici, F. Very High Resolution Multiangle Urban Classification Analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1155–1170. [Google Scholar] [CrossRef]
- Zaremotlagh, S.; Hezarkhani, A. The use of decision tree induction and artificial neural networks for recognizing the geochemical distribution patterns of LREE in the Choghart deposit, Central Iran. J. Afr. Earth Sci. 2017, 128, 37–46. [Google Scholar] [CrossRef]
- Panda, L.; Tripathy, S.K. Performance prediction of gravity concentrator by using artificial neural network—A case study. Int. J. Min. Sci. Technol. 2014, 24, 461–465. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman and Hall: New York, NY, USA, 1993. [Google Scholar]
- Quinlan, J.R. Introduction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Wu, X.; Kumar, V.; Ross Quinlan, J.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2007, 14, 1–37. [Google Scholar] [CrossRef]
- Chen, C.; He, B.; Zeng, Z. A method for mineral prospectivity mapping integrating C4.5 decision tree, weights-of-evidence and m-branch smoothing techniques: A case study in the eastern Kunlun Mountains, China. Earth Sci. Inform. 2013, 7, 13–24. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by random forest. R News 2002, 2, 18–22. [Google Scholar]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recogn. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Chung, C.F.; Agterberg, F.P. Regression models for estimating mineral resources from geological map data. Math. Geol. 1980, 12, 473–488. [Google Scholar] [CrossRef]
- Agterberg, F.P.; Bonham-Carter, G.F. Logistic regression and weights of evidence modeling in mineral exploration. In Proceedings of the 28th International Symposium on Application of Computer in the Mineral Industry (APCOM), Golden, CO, USA, 20–22 October 1999. [Google Scholar]
- Harris, J.R.; Sanborn-Barrie, M.; Panagapko, D.A.; Skulski, T.; Parker, J.R. Gold prospectivity maps of the Red Lake greenstone belt: Application of GIS technology. Can. J. Earth Sci. 2006, 43, 865–893. [Google Scholar] [CrossRef]
- Porwal, A.; González-Álvarez, I.; Markwitz, V.; McCuaig, T.C.; Mamuse, A. Weights-of-evidence and logistic regression modeling of magmatic nickel sulfide prospectivity in the Yilgarn Craton, Western Australia. Ore Geol. Rev. 2010, 38, 184–196. [Google Scholar] [CrossRef]
- Zhao, J.; Sui, Y.; Zhang, Z.; Zhou, M. Application of Logistic Regression and Weights of Evidence Methods for Mapping Volcanic-Type Uranium Prospectivity. Minerals 2023, 13, 608. [Google Scholar] [CrossRef]
- Yilmaz, I. Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison: A case study from Kat landslides (Tokat—Turkey). Comput. Geosci. 2009, 35, 1125–1138. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Zheng, X.; Wang, G.; Liu, D.; Cui, N. A Multi-Model Ensemble Approach for Gold Mineral Prospectivity Mapping: A Case Study on the Beishan Region, Western China. Minerals 2020, 10, 1126. [Google Scholar] [CrossRef]
- Fabbri, A.G.; Chung, C.J. On Blind Tests and Spatial Prediction Models. Nat. Resour. Res. 2008, 17, 107–118. [Google Scholar] [CrossRef]
- Zuo, R.; Cheng, Q.; Agterberg, F.P. Application of a hybrid method combining multilevel fuzzy comprehensive evaluation with asymmetric fuzzy relation analysis to mapping prospectivity. Ore Geol. Rev. 2009, 35, 101–108. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Chica-Olmo, M.; Chica-Rivas, M. Predictive modelling of gold potential with the integration of multisource information based on random forest: A case study on the Rodalquilar area, Southern Spain. Int. J. Geogr. Inf. Sci. 2014, 28, 1336–1354. [Google Scholar] [CrossRef]
- Zuo, R.; Zhang, Z.; Zhang, D.; Carranza, E.J.M.; Wang, H. Evaluation of uncertainty in mineral prospectivity mapping due to missing evidence: A case study with skarn-type Fe deposits in Southwestern Fujian Province, China. Ore Geol. Rev. 2015, 71, 502–515. [Google Scholar] [CrossRef]
- Parsa, M.; Carranza, E.J.M. Modulating the Impacts of Stochastic Uncertainties Linked to Deposit Locations in Data-Driven Predictive Mapping of Mineral Prospectivity. Nat. Resour. Res. 2021, 30, 3081–3097. [Google Scholar] [CrossRef]
- Parsa, M.; Lentz, D.R.; Walker, J.A. Predictive Modeling of Prospectivity for VHMS Mineral Deposits, Northeastern Bathurst Mining Camp, NB, Canada, Using an Ensemble Regularization Technique. Nat. Resour. Res. 2022, 32, 19–36. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4 December 2017. [Google Scholar]
- Marcilio, W.E.; Eler, D.M. From Explanations to Feature Selection: Assessing SHAP Values as feature Selection Mechanism. In Proceedings of the 33rd SIBGRAPI Conference on Graphics, Patterns and Images, Online, 7 November 2020. [Google Scholar]
- Luo, Z.; Zuo, R.; Xiong, Y.; Zhou, B. Metallogenic-Factor Variational Autoencoder for Geochemical Anomaly Detection by Ad-Hoc and Post-Hoc Interpretability Algorithms. Nat. Resour. Res. 2023, 32, 835–853. [Google Scholar] [CrossRef]
- Pradhan, B.; Jena, R.; Talukdar, D.; Mohanty, M.; Sahu, B.K.; Raul, A.K.; Abdul Maulud, K.N. A New Method to Evaluate Gold Mineralisation-Potential Mapping Using Deep Learning and an Explainable Artificial Intelligence (XAI) Model. Remote Sens. 2022, 14, 4486. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Hale, M.; Faassen, C. Selection of coherent deposit-type locations and their application in data-driven mineral prospectivity mapping. Ore Geol. Rev. 2008, 33, 536–558. [Google Scholar] [CrossRef]
- Sun, T.; Chen, F.; Zhong, L.; Liu, W.; Wang, Y. GIS-based mineral prospectivity mapping using machine learning methods: A case study from Tongling ore district, eastern China. Ore Geol. Rev. 2019, 109, 26–49. [Google Scholar] [CrossRef]
- Prado, E.M.G.; de Souza Filho, C.R.; Carranza, E.J.M.; Motta, J.G. Modeling of Cu-Au prospectivity in the Carajás mineral province (Brazil) through machine learning: Dealing with imbalanced training data. Ore Geol. Rev. 2020, 124, 103611. [Google Scholar] [CrossRef]
- Yang, J.; Kang, L.; Peng, J.; Zhong, H.; Gao, J.; Liu, L. In-situ elemental and isotopic compositions of apatite and zircon from the Shuikoushan and Xihuashan granitic plutons: Implication for Jurassic granitoid-related Cu-Pb-Zn and W mineralization in the Nanling Range, south China. Ore Geol. Rev. 2018, 93, 382–403. [Google Scholar] [CrossRef]
- Yang, J.; Kang, L.; Liu, L.; Peng, J.; Qi, Y. Tracing the origin of ore-forming fluids in the Piaotang tungsten deposit, south China: Constraints from in-situ analyses of wolframite and individual fluid inclusion. Ore Geol. Rev. 2019, 111, 102939. [Google Scholar] [CrossRef]
- Zhao, W.; Zhou, M.; Li, Y.; Zhao, Z.; Gao, J. Genetic types, mineralization styles, and geodynamic settings of Mesozoic tungsten deposits in south China. J. Asian Earth Sci. 2017, 137, 109–140. [Google Scholar] [CrossRef]
- Editorial Committee of China Mineral Geological Record. The Mineral Geological Records of China: Volume of Jiangxi Province; Geology Publishing House: Beijing, China, 2015. (In Chinese) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).