Discrete Element Method Analyses of Bond Degradation Evolutions for Cemented Soils

Abstract

The degradation of soil bonding, which can be described by the evolution of bond degradation variables, is essential in the constitutive modeling of cemented soils. A degradation variable with a value of 0/1.0 indicates that the applied stress is completely sustained by bonded particles/unbounded grains. The discrete element method (DEM) was used for cemented soils to analyze the bond degradation evolution and to evaluate the degradation variables at the contact scale. Numerical cemented soil samples with different bonding strengths were first prepared using an advanced contact model (CM). Constant stress ratio compression, one-dimensional compression, conventional triaxial tests (CTTs), and true triaxial tests (TTTs) were then implemented for the numerical samples. After that, the numerical results were adopted to investigate the evolution of the bond degradation variables B_N and B₀. In the triaxial tests, B₀ evolves to be near to or larger than B_N due to shearing, which indicates that shearing increases the bearing rate of bond contacts. Finally, an approximate stress-path-independent bond degradation variable B_σ was developed. The evolution of B_σ with the equivalent plastic strain can be effectively described by an exponential function and a hyperbolic function.

1. Introduction

Soil fabric and interparticle bonding together can be termed soil structure [1]. There are substantial distinctions in the mechanical properties between natural/artificially cemented soils (CSs) and uncemented soils (USs) ascribed to the interparticle bonding derived from cementation, as verified by experimental data [2,3]. Cemented soils exhibit structural yielding in isotropic compression and strain softening in triaxial tests. These characteristics are ascribed to the degradation evolutions of cementation bond contacts. Further, for silt-sized soils, fine particles can sustain themselves in a loose structure due to the van der Waals attraction force [4]. Loose cemented soils may undergo a considerable volume change under loading/wetting due to interparticle bond degradation and may cause engineering problems [5,6]. Accordingly, it is essential to quantify the bonding effect and to assess the bonding degradation evolution when carrying out constitutive modeling of cemented soil.

As a cemented soil is loaded, the interparticle bonds gradually break, and the cemented soil correspondingly performs towards the uncemented soil. A bond degradation variable represents the degree to which the soil bonding is damaged. Although it is complex to model the degree and degradation of interparticle bonding, a variety of formulations have been proposed and incorporated into constitutive models in recent decades. Some models have assumed a larger yield surface for cemented soil, which is progressively reduced during bond degradation. By comparing the yield surface size of cemented soil $p_{\mathrm{c}}$ and the corresponding uncemented soil $p_{\mathrm{c}0}$, the bonding effect can be assessed by evaluating the additional strength $\Delta p_{\mathrm{c}}=p_{\mathrm{c}}-p_{\mathrm{c}0}$ [7,8] or the strength ratio $R^{*}=p_{\mathrm{c}0}/p_{\mathrm{c}}$ [9,10,11]. Alternatively, in the disturbed state concept [12,13], cemented soil is modeled by a combination of material parts at relatively intact and fully adjusted states. The bonding effect can be quantified by the disturbance function D, which denotes the contribution ratio of fully adjusted states to material stress. In the damage model for cemented soils [14,15], a similar strategy is employed, and the bonding effect can be quantified by a bond degradation variable. However, owing to the difficulties in microscopic observations and the deficiency of the micromechanical basis, these bond degradation indicators that denote the debonding process are based on the macro mechanical differences between cemented and corresponding uncemented soils.

Since it is difficult to obtain insight into the debonding process at the particle and contact scales with current experimental technologies [16,17,18], the DEM [19] is a supplementary way to study microscopic behavior and analyze the bond degradation evolution of cemented soils. The DEM has been employed in microscopic investigations on various cemented soils, such as cemented sand, structural silt, methane hydrate-bearing soil, etc. [20,21,22,23,24,25]. The DEM has also been applied to correlate the macro- and micromechanical performances of geomaterials [15,26,27]. Thornton [26] relates the normal and tangential contact forces to the stress tensor, respectively. Jiang et al. [15] relates the forces at bonded contacts and the forces at unbonded contacts to the stress tensor, respectively, and developed micromechanical-based models for cemented soils.

In this study, a numerical sample is first produced using the particle flow code 3D (PFC3D) [28], whose contact model takes into account rolling and twisting resistances [29] and van der Waals forces [30,31] to sustain an open structure, followed by precompression and cementation bond generation. Subsequently, various loading paths, including constant stress ratio compression, one-dimensional compression, conventional triaxial, and true triaxial loading, are applied on cemented DEM assemblies with different bond strengths. After that, the evolution of two representative bond degradation variables versus plastic strain is micromechanically investigated. Finally, the bond degradation evolution of cemented soils not only depends on the plastic strain but also the stress path. Based on the DEM analyses of the bond degradation evolution, an approximate stress-path-independent bond degradation variable and its degradation evolution law are proposed.

2. Materials and Methods

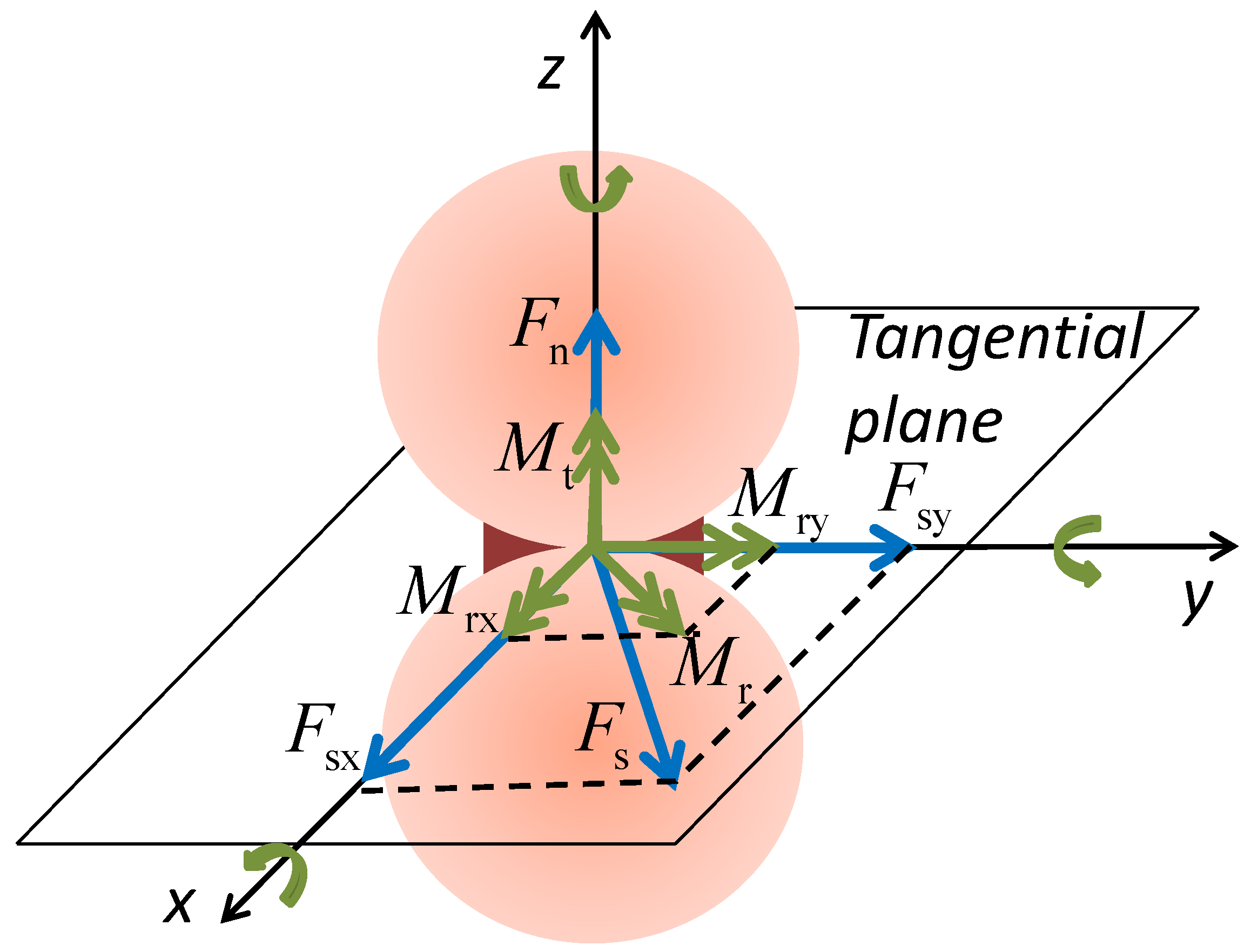
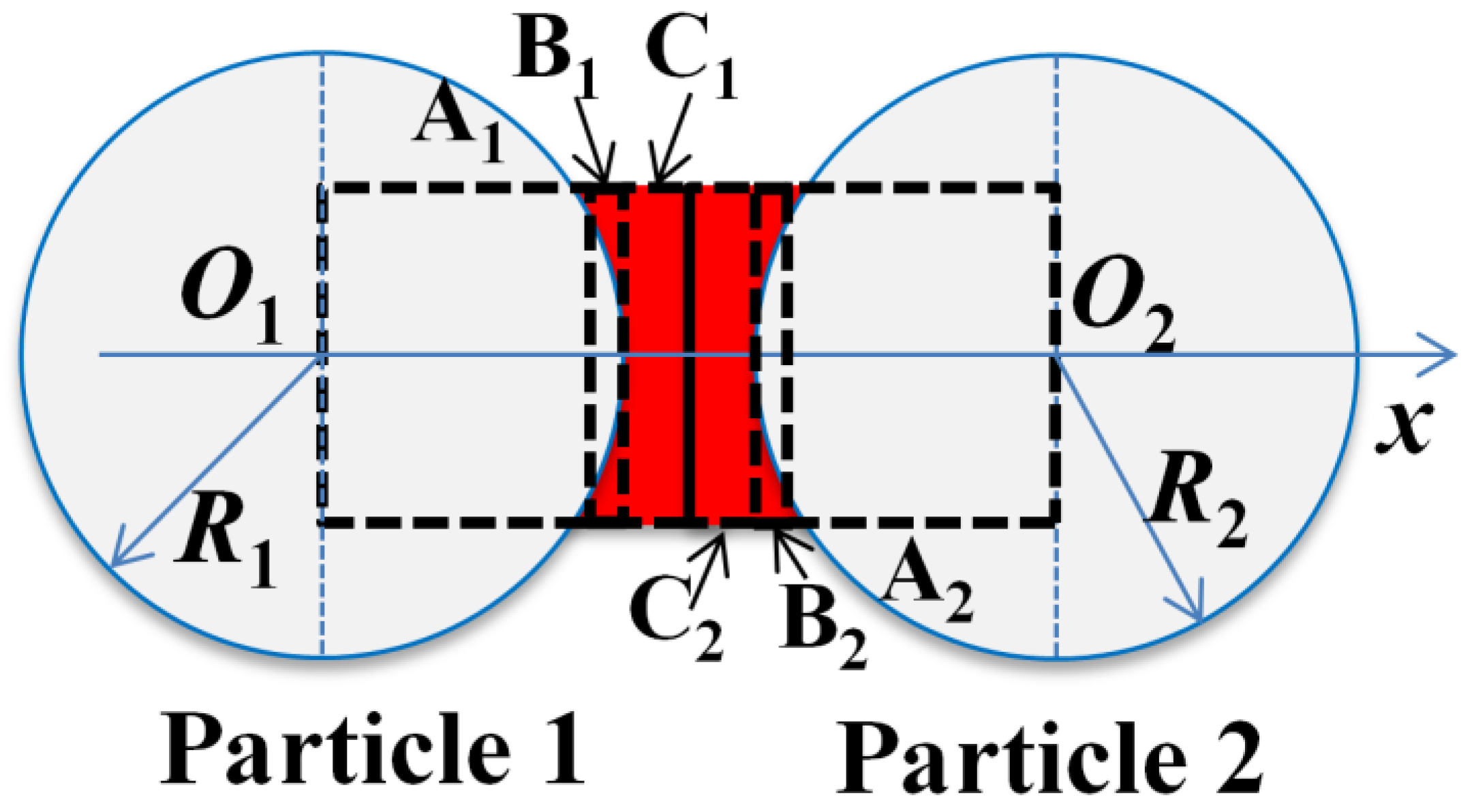
2.1. Bond Contact Model Framework

The force and moment at a contact point between particles are considered to be conveyed through both particle interactions and the bonding material in parallel. The total force (moment) vector is the sum of the force (moment) vector transmitted by the particle interaction and the force (moment) vector transmitted by the cementation bond. The schematic diagram (Figure 1) shows the forces and moments in four directions: normal, tangential, rolling, and twisting.

2.1.1. Particle Interaction

A three-dimensional contact model, which accounts for sliding, rolling and twisting resistances [28,29], was employed to account for the influence of particle shapes on sphere-based DEM simulations, and it was then further developed for soils with interparticle attraction forces, such as silt-sized soils with van der Waals forces [30].

The model posits that the interaction between two spheres occurs at the contact through a circular flat region with a specific radius $R_{\mathrm{c}}=\beta R$, where $\beta$ serves as the shape parameter governing the characteristics of rolling and twisting resistances, $R=2R_1{R}_2/(R_1+R_2)$ represents the shared radius of the particle pair, and R₁ and R₂ are their individual radii, respectively.

In the direction perpendicular to the surface, the normal force is computed by the following:

$$F_{\mathrm{n}}^{\mathrm{p}}=\left\{\begin{array}{c}{k}_{\mathrm{n}}{\delta }_{\mathrm{n}}-F_{\mathrm{v}} {\delta }_{\mathrm{n}}\ge 0\\ 0 {\delta }_{\mathrm{n}}<0\end{array}\right.$$

(1)

where k_n is the normal stiffness, δ_n is the normal overlap between a pair of particles with a negative value denoting separation, and F_v is the van der Waals force.

The tangential force, rolling moment, and twisting torque are determined through incremental calculations as follows:

$$F_{\mathrm{s}}^{\mathrm{p}}\leftarrow F_{\mathrm{s}}^{\mathrm{p}}-k_{\mathrm{s}}\Delta {\delta }_{\mathrm{s}}$$

(2)

$$M_{\mathrm{r}}^{\mathrm{p}}\leftarrow M_{\mathrm{r}}^{\mathrm{p}}-k_{\mathrm{r}}\Delta {\theta }_{\mathrm{r}}$$

(3)

$$M_{\mathrm{t}}^{\mathrm{p}}\leftarrow M_{\mathrm{t}}^{\mathrm{p}}-k_{\mathrm{t}}\Delta {\theta }_{\mathrm{t}}$$

(4)

where k_s, $k_{\mathrm{r}}=0.25k_{\mathrm{n}}{R}_{\mathrm{c}}{ }^2$, and $k_{\mathrm{t}}=0.5k_{\mathrm{s}}{R}_{\mathrm{c}}{ }^2$ denote the tangential, rolling, and twisting stiffnesses, respectively, and $\Delta {\delta }_{\mathrm{s}}$, $\Delta {\theta }_{\mathrm{r}}$, and $\Delta {\theta }_{\mathrm{t}}$ are the relative shear displacement increment, rotation increment, and twist increment, as introduced in the contact resolution in PFC^3D [28]. Tangential sliding is initiated and the contact transitions to the perfectly plastic stage once the tangential force reaches its limiting value, i.e., $‖F_{\mathrm{s}}^{\mathrm{p}}‖\le \mu (F_{\mathrm{n}}{ }^{\mathrm{p}}+F_{\mathrm{v}})$, where μ is the friction coefficient between the particles. Similarly, rolling is initiated when the rolling moment attains the limiting value, i.e., $‖M_{\mathrm{r}}^{\mathrm{p}}‖\le 0.25{\zeta }_{\mathrm{c}}{R}_{\mathrm{c}}(F_{\mathrm{n}}{ }^{\mathrm{p}}+F_{\mathrm{v}})$, where the local crushing parameter ${\zeta }_{\mathrm{c}}$ is 2.1. Plastic twisting is triggered when the torque reaches its limiting value, i.e., $M_{\mathrm{t}}^{\mathrm{p}}\le 0.65\mu R_{\mathrm{c}}(F_{\mathrm{n}}{ }^{\mathrm{p}}+F_{\mathrm{v}})$.

The normal and tangential stiffnesses can be calculated in a simple way to consider the effect of particle radii [28]:

$$k_{\mathrm{n}}=\pi R^2{E}^{*}/(R_1+R_2)$$

(5)

$$k_{\mathrm{s}}=k_{\mathrm{n}}/{\kappa }^{*}$$

(6)

where $E^{*}$ represents the effective modulus between particles, and ${\kappa }^{*}$ denotes the ratio of normal stiffness to shear stiffness.

2.1.2. Prefailure Behavior of the Cementation Bond

The connection between two spheres can be conceptualized as a short cylinder with concave spherical ends. The behavior of the cementation bond is proposed based on both contact tests and theoretical analyses. The bond cylinder radius is calculated by $R_{\mathrm{b}}={\lambda }_{\mathrm{b}}R$ [28], where ${\lambda }_{\mathrm{b}}$ is the bond radius multiplier. Before a bond breaks, the bond force and moment can be updated as follows [28,32]:

$$F_{\mathrm{n}}^{\mathrm{b}}\leftarrow F_{\mathrm{n}}^{\mathrm{b}}-k_{\mathrm{n}}^{\mathrm{b}}\Delta {\delta }_{\mathrm{n}}$$

(7)

$$F_{\mathrm{s}}^{\mathrm{b}}\leftarrow F_{\mathrm{s}}^{\mathrm{b}}-k_{\mathrm{s}}^{\mathrm{b}}\Delta {\delta }_{\mathrm{s}}$$

(8)

$$M_{\mathrm{r}}^{\mathrm{b}}\leftarrow M_{\mathrm{r}}^{\mathrm{b}}-k_{\mathrm{r}}^{\mathrm{b}}\Delta {\theta }_{\mathrm{r}}$$

(9)

$$M_{\mathrm{t}}^{\mathrm{b}}\leftarrow M_{\mathrm{t}}^{\mathrm{b}}-k_{\mathrm{t}}^{\mathrm{b}}\Delta {\theta }_{\mathrm{t}}$$

(10)

where $F_{\mathrm{n}}^{\mathrm{b}}$, $F_{\mathrm{s}}^{\mathrm{b}}$, $M_{\mathrm{r}}^{\mathrm{b}}$, and $M_{\mathrm{t}}^{\mathrm{b}}$ denote the transmission of normal force, tangential force, rolling moment, and twisting torque through the bond material, respectively. $k_{\mathrm{n}}^{\mathrm{b}}$, $k_{\mathrm{s}}^{\mathrm{b}}$, $k_{\mathrm{r}}^{\mathrm{b}}=0.25k_{\mathrm{n}}^{\mathrm{b}}{R}_{\mathrm{b}}{ }^2$, and $k_{\mathrm{t}}^{\mathrm{b}}=0.5k_{\mathrm{s}}^{\mathrm{b}}{R}_{\mathrm{b}}{ }^2$ are the normal stiffness, tangential stiffness, rolling stiffness, and twisting stiffness, respectively. $\Delta {\delta }_{\mathrm{n}}$ is the relative normal displacement increment.

The transmission of bond force and moment is assumed to occur through different components or sections, namely A₁, B₁, C₁, C₂, B₂, and A₂ in series, as shown in Figure 2. Hence, the bond normal stiffness can be calculated as follows [33]:

$$k_{\mathrm{n}}^{\mathrm{b}}=1/({\delta }_{\mathrm{A}1}+{\delta }_{\mathrm{A}2}+{\delta }_{\mathrm{B}1}+{\delta }_{\mathrm{B}2}+{\delta }_{\mathrm{C}1}+{\delta }_{\mathrm{C}2})$$

(11)

$${\delta }_{\mathrm{A}1}=\frac{R_1{\xi }_E}{\pi {\overline{E}}^{*}{R}_{\mathrm{b}}{ }^2}$$

$${\delta }_{\mathrm{B}1}=\left\{\begin{array}{c}\frac{1}{2\pi {\overline{E}}^{*}(1-{\eta }_E)R_1{\Lambda }_E}\left(\ln (\frac{{\Lambda }_E+1}{{\Lambda }_E-1})-\ln (\frac{{\Lambda }_E+{\xi }_E}{{\Lambda }_E-{\xi }_E})\right) (\mathrm{when} {\eta }_E<1)\\ \frac{R_1(1-{\xi }_E)}{\pi {\overline{E}}^{*}{R}_{\mathrm{b}}{ }^2} (\mathrm{when} {\eta }_E=1)\end{array}\right.$$

$${\delta }_{\mathrm{C}1}=\frac{h_0^{\mathrm{b}}/2}{{\eta }_E\pi {\overline{E}}^{*}{R}_{\mathrm{b}}^2}$$

where ${\delta }_{\mathrm{A}1}$, ${\delta }_{\mathrm{B}1}$, and ${\delta }_{\mathrm{C}1}$ are calculated by integration along the force-transmitting path, while ${\delta }_{\mathrm{A}2}$, ${\delta }_{\mathrm{B}2}$, and ${\delta }_{\mathrm{C}2}$ can be obtained similarly. ${\xi }_E=\sqrt{1-{(R_{\mathrm{b}}/R_1)}^2}$ and ${\Lambda }_E=\sqrt{1+\frac{{\eta }_E}{1-{\eta }_E}{(R_{\mathrm{b}}/R_1)}^2}$ are intermediate variables. $h_0^{\mathrm{b}}$ is the bond thickness, and $h_0^{\mathrm{b}}=0$ for a thin bond, which forms after the two particles have been in physical contact. ${\overline{E}}^{*}{ }_{ }$ is the bond effective modulus. Since the modulus of the bond material is smaller than that of the particles, the modulus reduction factor ${\eta }_E$ is incorporated. The stiffness will be reduced to the parallel bond [32] when ${\eta }_E=1$ and $h_0^{\mathrm{b}}=0$.

The bond tangential stiffness can be computed as follows [28]:

$$k_{\mathrm{s}}^{\mathrm{b}}=k_{\mathrm{n}}^{\mathrm{b}}/{\overline{\kappa }}^{*}$$

(12)

where ${\overline{\kappa }}^{*}$ represents the ratio of normal stiffness to shear stiffness in the bond.

2.1.3. Bond Failure Criterion

Upon reaching the failure criterion, the bond undergoes breakage, resulting in abrupt reductions in force and moment in the contact to their residual values. A bond failure criterion proposed in Shen et al. [34] is simplified [33] and applied in the simulations. This bond failure criterion considers the bond size effect and the coupled effect of the normal force, tangential force, rolling moment, and twisting torque on the bond failure. The criterion will be briefly introduced below.

The bond compressive and tensile strengths, denoted by $R_{\mathrm{nc}}^{\mathrm{b}}$ and $R_{\mathrm{nt}}^{\mathrm{b}}$, respectively, are expressed as follows [34]:

$$R_{\mathrm{nc}}^{\mathrm{b}}={\chi }_{\mathrm{c}}{\sigma }_{\mathrm{c}}^{\mathrm{b}}{A}_{\mathrm{b}}, {\chi }_{\mathrm{c}}=\frac{c_1}{{\lambda }_{\mathrm{b}}{ }^{c_3}}\exp (\frac{c_2{h}_0^{\mathrm{b}}}{2R_{\mathrm{b}}})$$

(13)

$$R_{\mathrm{nt}}^{\mathrm{b}}={\chi }_{\mathrm{t}}{\sigma }_{\mathrm{t}}^{\mathrm{b}}{A}_{\mathrm{b}}, {\chi }_{\mathrm{t}}=1$$

(14)

where $A_{\mathrm{b}}=\pi R_{\mathrm{b}}{ }^2$ represents the cross-sectional area of the bond cylinder. ${\sigma }_{\mathrm{c}}^{\mathrm{b}}$ represents the compressive strength, and ${\sigma }_{\mathrm{t}}^{\mathrm{b}}$ signifies the tensile strength of the bond material. ${\sigma }_{\mathrm{t}}^{\mathrm{b}}={\eta }_{\sigma }{\sigma }_{\mathrm{c}}^{\mathrm{b}}$, where ${\eta }_{\sigma }$ represents the ratio of tensile strength to compressive strength. ${\chi }_{\mathrm{c}}$ and ${\chi }_{\mathrm{t}}$ are two factors considering the bond size effect, for which $c_1=1.45$, $c_2=-0.7$, and $c_3=1/6$ were used.

The shearing, rolling, and twisting strengths, namely $R_{\mathrm{s}}^{\mathrm{b}}=S_{\mathrm{s}}^{\mathrm{b}}(R_{\mathrm{nc}}^{\mathrm{b}}+R_{\mathrm{nt}}^{\mathrm{b}})$, $R_{\mathrm{r}}^{\mathrm{b}}=S_{\mathrm{r}}^{\mathrm{b}}(R_{\mathrm{nc}}^{\mathrm{b}}+R_{\mathrm{nt}}^{\mathrm{b}})R_{\mathrm{b}}$, and $R_{\mathrm{t}}^{\mathrm{b}}=S_{\mathrm{t}}^{\mathrm{b}}(R_{\mathrm{nc}}^{\mathrm{b}}+R_{\mathrm{nt}}^{\mathrm{b}})R_{\mathrm{b}}$, of the bond depend on the compressive strength $R_{\mathrm{nc}}^{\mathrm{b}}$, the tensile strength $R_{\mathrm{nt}}^{\mathrm{b}}$, and the bond size [34], where $S_i^{\mathrm{b}}$ (I = s, r, and t, denoting shearing, rolling, and twisting, respectively) captures the impact of the normal force on the shearing, rolling, and twisting strengths. A simplified form of $S_i^{\mathrm{b}}$ can be expressed as follows [33,34]:

$$S_i^{\mathrm{b}}=m_i{f}_{\mathrm{n}}^{\mathrm{b}}{[\ln (1/f_{\mathrm{n}}^{\mathrm{b}})]}^{3/5}$$

(15)

where $f_{\mathrm{n}}^{\mathrm{b}}=(F_{\mathrm{n}}^{\mathrm{b}}+R_{\mathrm{nt}}^{\mathrm{b}})/(R_{\mathrm{nc}}^{\mathrm{b}}+R_{\mathrm{nt}}^{\mathrm{b}})$ is a dimensionless normal force, and the strength envelope shape parameters $m_{\mathrm{s}}=0.5$, $m_{\mathrm{r}}=0.3$, and $m_{\mathrm{t}}=0.36$ are adopted according to the data obtained by Shen et al. [34].

In general, a bond may be subjected to the normal and shear forces, rolling moment, and torque. A unified failure criterion can be characterized as follows [34]:

$${\left(\frac{‖F_{\mathrm{s}}^{\mathrm{b}}‖}{R_{\mathrm{s}}^{\mathrm{b}}}\right)}^2+{\left(\frac{‖M_{\mathrm{r}}^{\mathrm{b}}‖}{R_{\mathrm{r}}^{\mathrm{b}}}\right)}^2+{\left(\frac{M_{\mathrm{t}}^{\mathrm{b}}}{R_{\mathrm{t}}^{\mathrm{b}}}\right)}^2=1$$

(16)

2.2. DEM Simulations

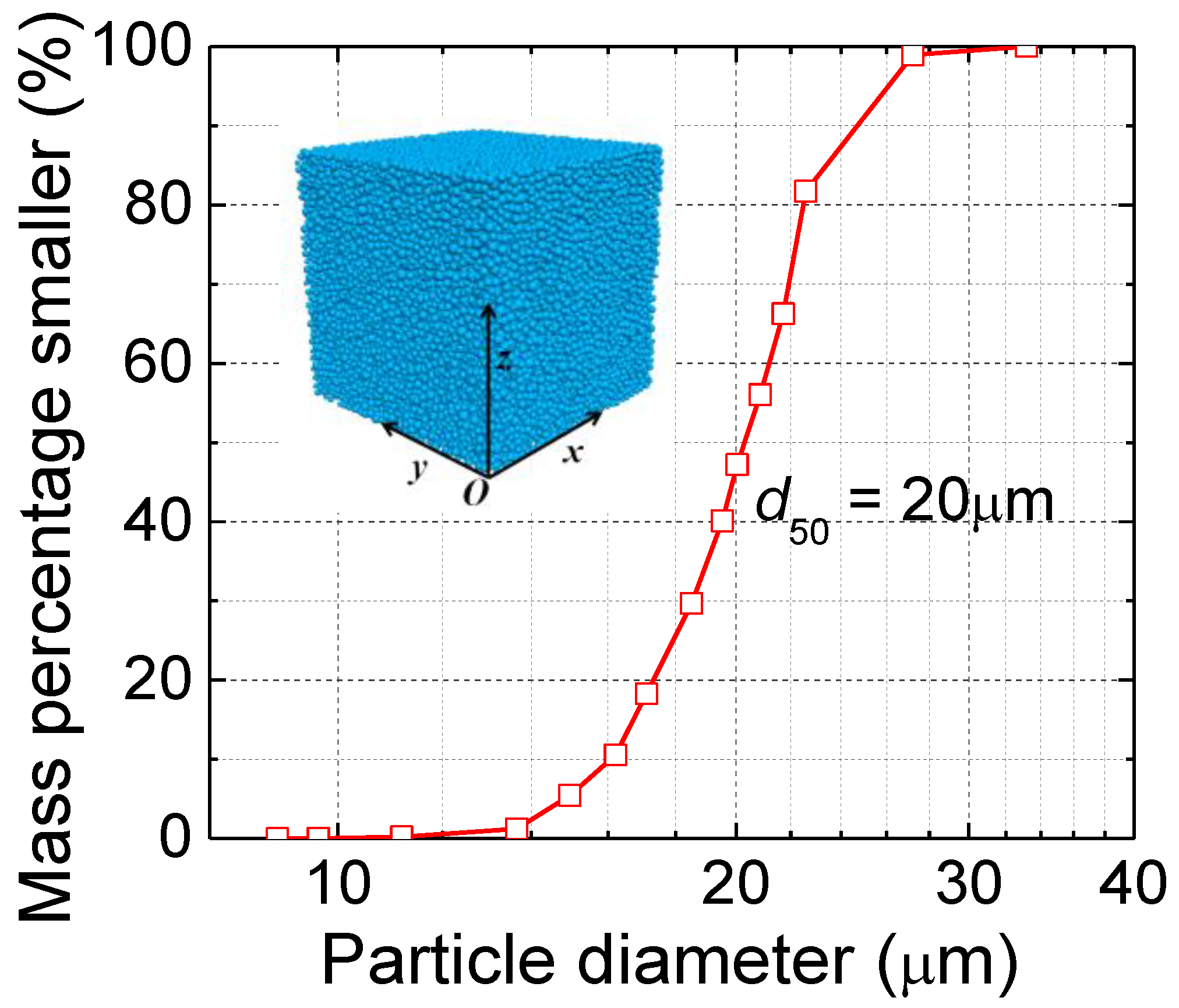
2.2.1. Sample Preparation

The particle and particle interaction parameters that are used to prepare the uncemented sample are the same as those of the saturated sample in the work of Li et al. [30] and are shown in

Table 1. DEM simulation parameters.

Parameters	Values
Particle
Particle density/kg·m−3	2710
Local damping coefficient	0.7
Particle interaction
Effective modulus $E^{*}$/MPa	800
Normal-to-shear stiffness ratio ${\kappa }^{*}$	1.5
Friction coefficient μ	0.5
Shape parameter β	0.21
Van der Waals force Fv/N	1.6 × 10−6
Bond contact
Bond effective modulus ${\overline{E}}^{*}{ }_{ }$/MPa	200
Bond modulus reduction factor ${\eta }_E$	0.2
Bond normal-to-shear stiffness ratio ${\overline{\kappa }}^{*}$	2.0
Compressive strength of the bond material ${\sigma }_{\mathrm{c}}^{\mathrm{b}}$/MPa	5; 25
Bond tension-to-compression strength ratio ${\eta }_{\sigma }$	0.1
Bond radius multiplier ${\lambda }_{\mathrm{b}}$	0.35
Bond thickness threshold $g_{\mathrm{c}}$	0.1

. In particular, at the ball–wall contacts, both the friction coefficient and the shape parameter are zero. A van der Waals force of 1.6 × 10⁻⁶ N is applied to each ball–ball contact because it cannot be neglected for silt-sized soils [4]. Figure 3 shows the grain size distribution curve of the DEM sample with a median grain size of 20 µm. An assembly is compacted in five layers via the multi-layer under-compaction method (UCM) [35]. The cubic sample is composed of 42,180 particles with a side length of 0.67 mm. When using the UCM method, the accumulated layers of the particles are compacted to an intermediate void ratio that is slightly higher than the target void ratio, 0.945, to obtain a homogenous DEM sample. Then, a vertical pressure of 12.5 kPa is applied to the top and bottom walls with the sidewalls kept stationary to reproduce an in situ K₀ stress state.

After sample preparation, the bonds were then installed at neighboring particles with a gap of less than $g_{\mathrm{c}}{R}_{\mathrm{b}}$, where $g_{\mathrm{c}}$ is the bond thickness threshold. Table 1 lists the bond parameters that were empirically set to study cemented silts in general [33]. The compressive and tensile strengths are significant parameters that control the shear strength of a cemented soil. Two representative compressive strengths, 5 MPa for weak bonds and 25 MPa for strong bonds, were analyzed in this study. Given that the experimental results indicate a significantly lower tensile strength compared to the compressive strength, the tension-to-compression strength ratio was assumed to be 0.1.

2.2.2. Simulation Execution

The mean stress p, deviator stress q, volumetric strain ${\epsilon }_{\mathrm{v}}$, and deviator strain ${\epsilon }_{\mathrm{s}}$ are expressed as follows:

$$p=\frac{1}{3}({\sigma }_1+{\sigma }_2+{\sigma }_3)$$

(17)

$$q=\frac{\sqrt{2}}{2}\sqrt{{({\sigma }_1-{\sigma }_2)}^2+{({\sigma }_2-{\sigma }_3)}^2+{({\sigma }_3-{\sigma }_1)}^2}$$

(18)

$${\epsilon }_{\mathrm{v}}={\epsilon }_1+{\epsilon }_2+{\epsilon }_3$$

(19)

$${\epsilon }_{\mathrm{s}}=\frac{\sqrt{2}}{3}\sqrt{{({\epsilon }_1-{\epsilon }_2)}^2+{({\epsilon }_2-{\epsilon }_3)}^2+{({\epsilon }_3-{\epsilon }_1)}^2}$$

(20)

where ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$ are the principal stresses of the stress tensor, and ${\epsilon }_1$, ${\epsilon }_2$, and ${\epsilon }_3$ are the principal strains of the stain tensor.

Following the installation of bonds, numerical samples underwent a series of tests, including constant stress ratio compression, one-dimensional compression (1D compression), conventional triaxial tests, and true triaxial tests. Figure 4 shows the stress paths in the DEM simulations. During one-dimensional compression, incremental loads were imposed on the top and bottom walls while keeping the sidewalls in a stationary position. In constant stress ratio compression (CSR compression), incremental loads were applied to the top and bottom walls, and the sidewalls were servo-controlled to maintain a constant principal stress ratio $CSR={\sigma }_3/{\sigma }_1$.

In triaxial tests, following the isotropic compression of samples to various confining stresses, continuous deviator loading was initiated by downward and upward movement of the top and bottom walls. Simultaneously, the sidewalls were servo-controlled to sustain a constant horizontal stress in the conventional triaxial tests and to align the horizontal stresses with their designated target values in the true triaxial tests (constant p). The target values are determined through the following calculation:

$${\sigma }_2=\frac{(3-3b)p-(1-2b){\sigma }_1}{2-b}$$

(21)

$${\sigma }_3=\frac{3p-(1+b){\sigma }_1}{2-b}$$

(22)

where the coefficient b = (σ₂ − σ₃)/(σ₁ − σ₃).

3. Results

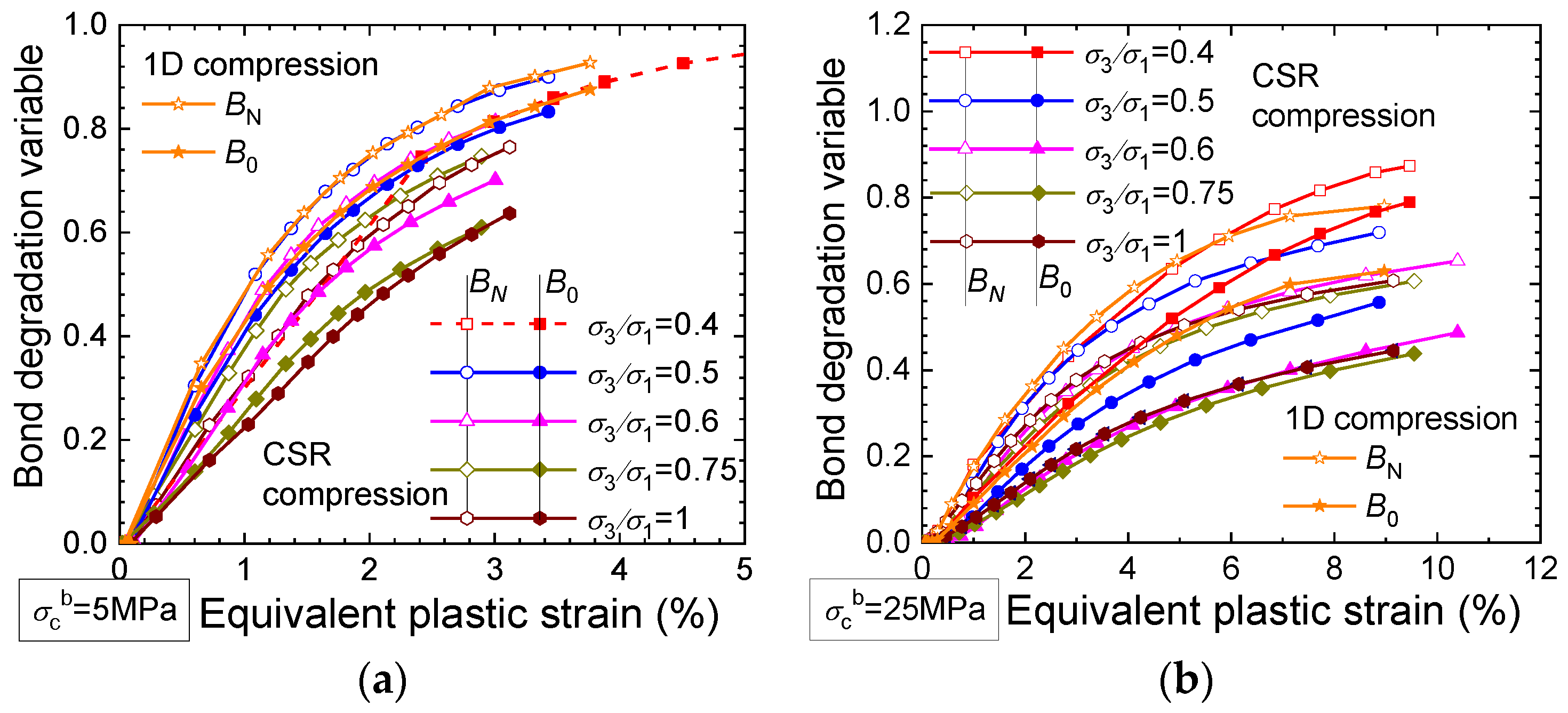
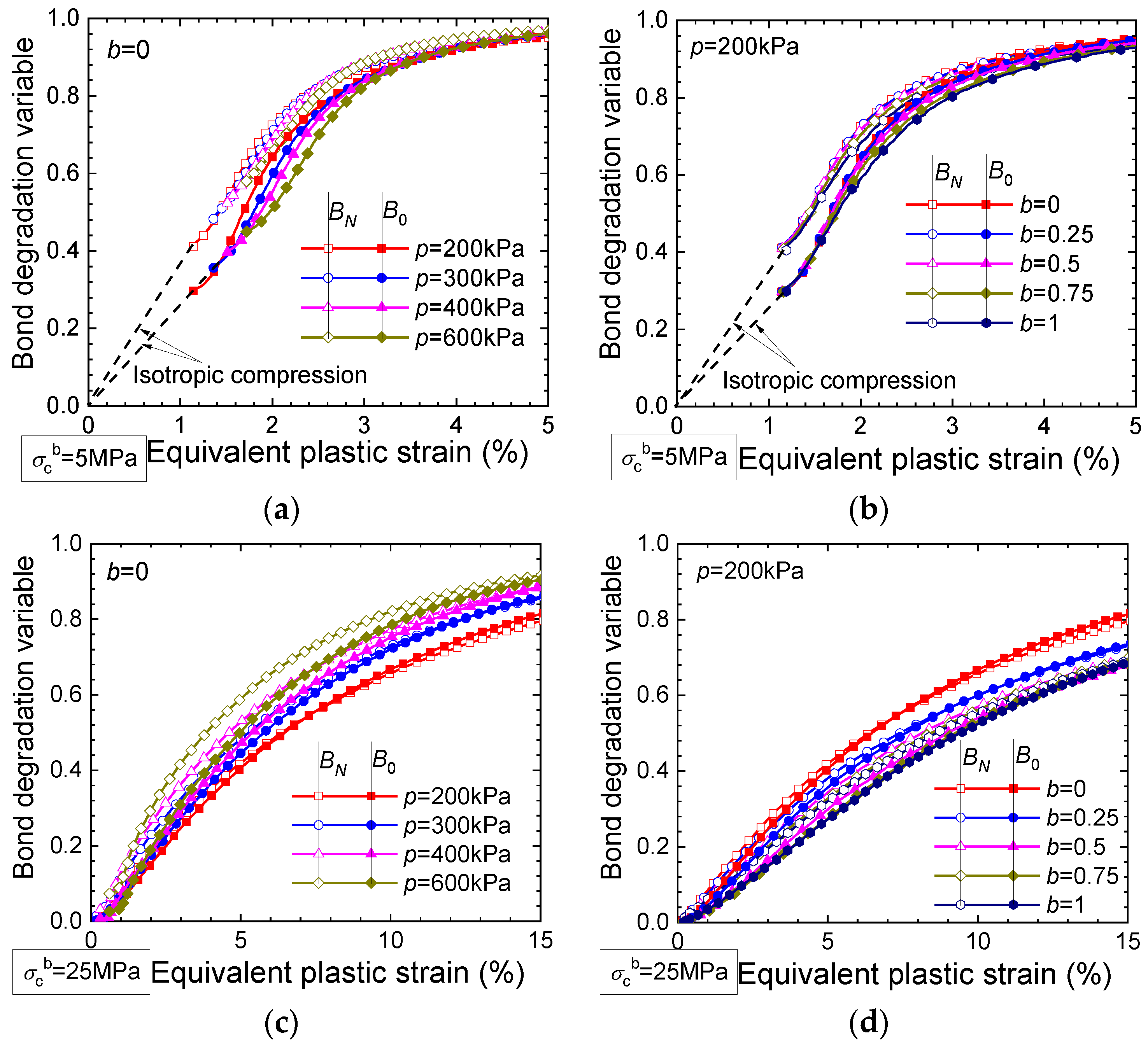
3.1. Bond Degradation Evolutions

The stress and strain of a granular material depend on the interparticle forces at the contacts. The average stress of a representative volume element (RVE) can be expressed as follows [36]:

$${\overline{\sigma }}_{ij}^{ }=\frac{1}{V^{ }}{\displaystyle \sum _{k=1}^{N^{ }}{F}_i^k}{l}_j^k$$

(23)

where V and N are the volume and the number of contacts of the RVE, respectively; $F_i^k$ is the contact force at contact k; and $l_j^k$ is the branch vector connecting the centers of the two particles.

In the disturbed state concept and damage mechanics [37] regarding cemented granular materials, it is assumed that cemented soils generally consist of bonded aggregates and unbonded grains. To evaluate the bond degradation in cemented soils subjected to external loading, a primary bond degradation variable can be defined as the ratio of the unbonded contact number to the total contact number as follows:

$$B_N=\frac{N^{\mathrm{d}}}{N}$$

(24)

where $N^{\mathrm{d}}$ is the number of unbonded contacts.

By assuming that the applied loading is independently sustained by bonded aggregates and unbonded grains, the second bond degradation variable can be defined as the ratio of the stress sustained by the unbonded contacts to the total stress as follows:

$$B_0=\frac{{\displaystyle \sum _{k=1}^{N^{\mathrm{d}}}{F}_i^k}{l}_j^k}{{\displaystyle \sum _{k=1}^N{F}_i^k}{l}_j^k}$$

(25)

Under external loading, the bonded aggregates in the cemented soil gradually break and transform into unbonded grains due to the breakage of bonded contacts. The bond degradation variables B_N and B₀ represent the degree to which the soil bonding is damaged. When the bond degradation variable equals zero, the applied loading is completely sustained by the bonded aggregates, indicating that the soil bonding is intact. The bond degradation variable of the soil increases as more bonded contacts break. When the value of the bond degradation variable reaches 1.0, the soil bonding is fully disturbed; the applied stress is completely sustained by the unbonded grains.

The bond degradation is commonly assumed to vary with the plastic strain. The bond degradation mainly evolves with the volumetric plastic strain in compression tests, while it primarily develops with the deviator plastic strain in triaxial tests. Hence, an equivalent plastic strain must be introduced to consider both the volumetric and deviator plastic strains. A simple equivalent plastic strain can be defined as ${\epsilon }_{\mathrm{d}}^{\mathrm{p}}=\sqrt{{({\epsilon }_{\mathrm{v}}^{\mathrm{p}})}^2+{({\epsilon }_{\mathrm{s}}^{\mathrm{p}})}^2}$, where ${\epsilon }_{\mathrm{v}}^{\mathrm{p}}$ is the volumetric plastic strain and ${\epsilon }_{\mathrm{s}}^{\mathrm{p}}$ is the deviator plastic strain.

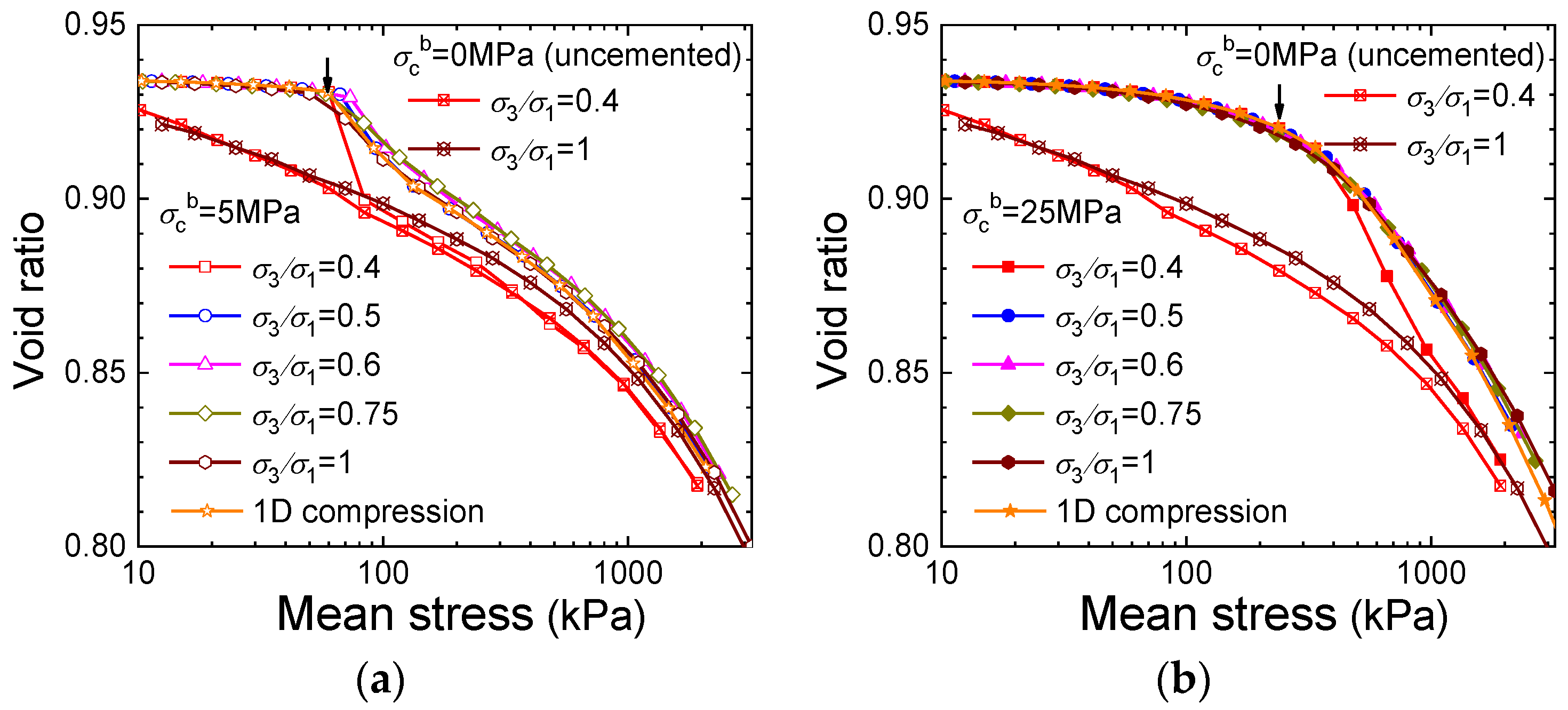
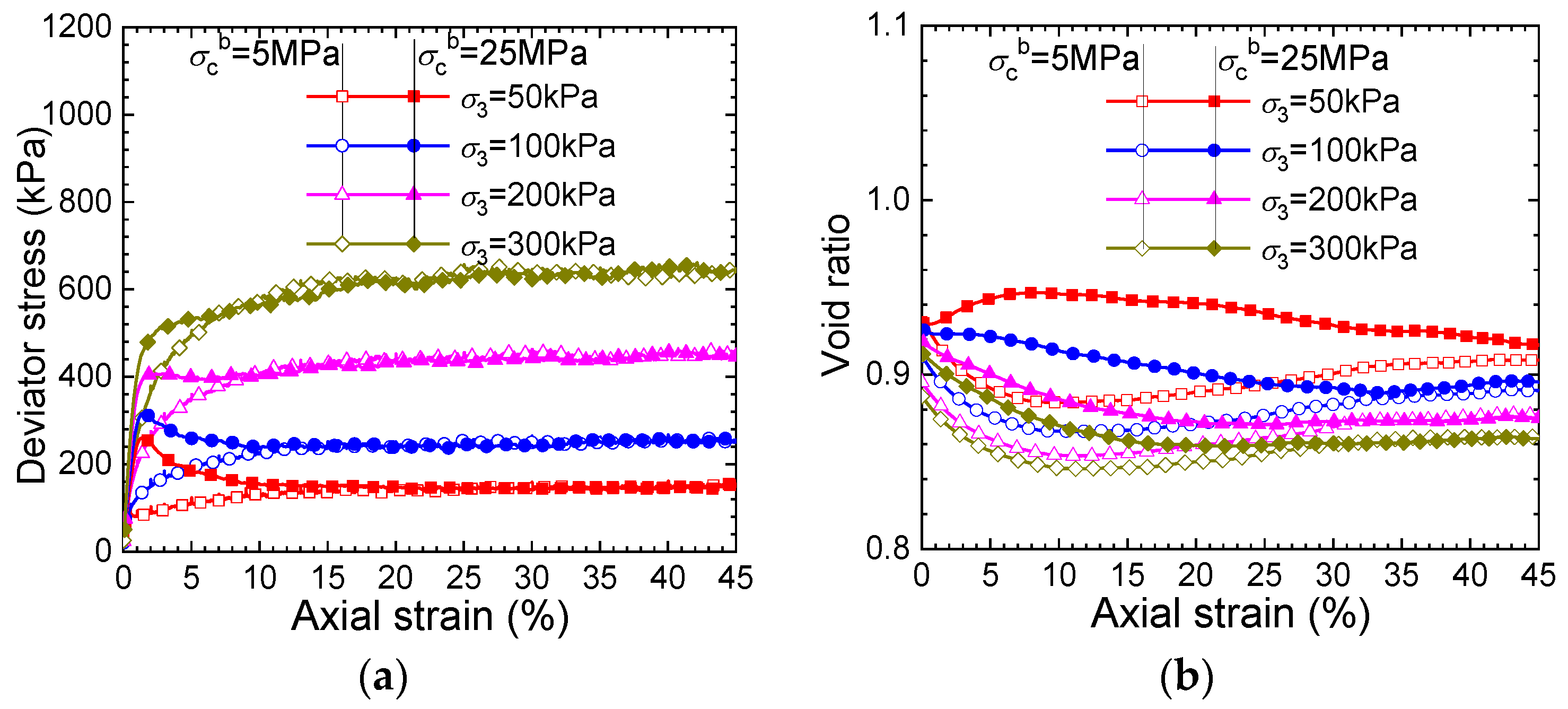
3.2. Compression Tests

Figure 5 shows the compression curves of the numerical samples under constant stress ratio compression with different principal stress ratios as well as the one-dimensional compression tests. For the numerical sample with weak bonds (${\sigma }_{\mathrm{c}}^{\mathrm{b}}=5\mathrm{MPa}$, sample I), the void ratio first gradually decreases and then accelerates after an obvious distinguishing point, namely the “structural yield stress” point, which agrees with the experimental results [38]. In contrast, the slopes of the compression curves vary relatively gradually for the numerical sample with strong bonds (${\sigma }_{\mathrm{c}}^{\mathrm{b}}=25\mathrm{MPa}$, sample II).

All of the specimens with different principal stress ratios are fairly coincident with each other except for the specimen with a principal stress ratio of ${\sigma }_3/{\sigma }_1=0.4$. Both the experimental [38,39] and DEM results illustrate that the compression curve with a small principal stress ratio is separated from the coincident curve, which is probably because the stress state approaches the sample strength envelope. The compression curve with ${\sigma }_3/{\sigma }_1=0.4$ is separated from the coincident curves at a mean stress of approximately 65 kPa for sample I, while it separates at approximately 400 kPa for sample II due to the different bond strengths.

Figure 6 shows the evolution of the bond degradation variables B_N and B₀ with the equivalent plastic strain under compression tests. Both variables increase at a decreasing rate with the equivalent plastic strain until they reach 1.0 under different principal stress ratios. There is a small threshold strain, especially for sample II, with strong bonds.

Both the principal stress ratio and the bond strength affect the evolution of the bond degradation variables. The effect of the principal stress ratio in sample II with strong bonds is more considerable than that in sample I. The bond degradation variables generally decrease as the principal stress ratio increases between 0.4 and 1.0. Except for ${\sigma }_3/{\sigma }_1=0.4$ in sample I, B₀ is smaller than the corresponding B_N, demonstrating the priority of the bonded contacts to sustain the applied loading throughout the compression tests.

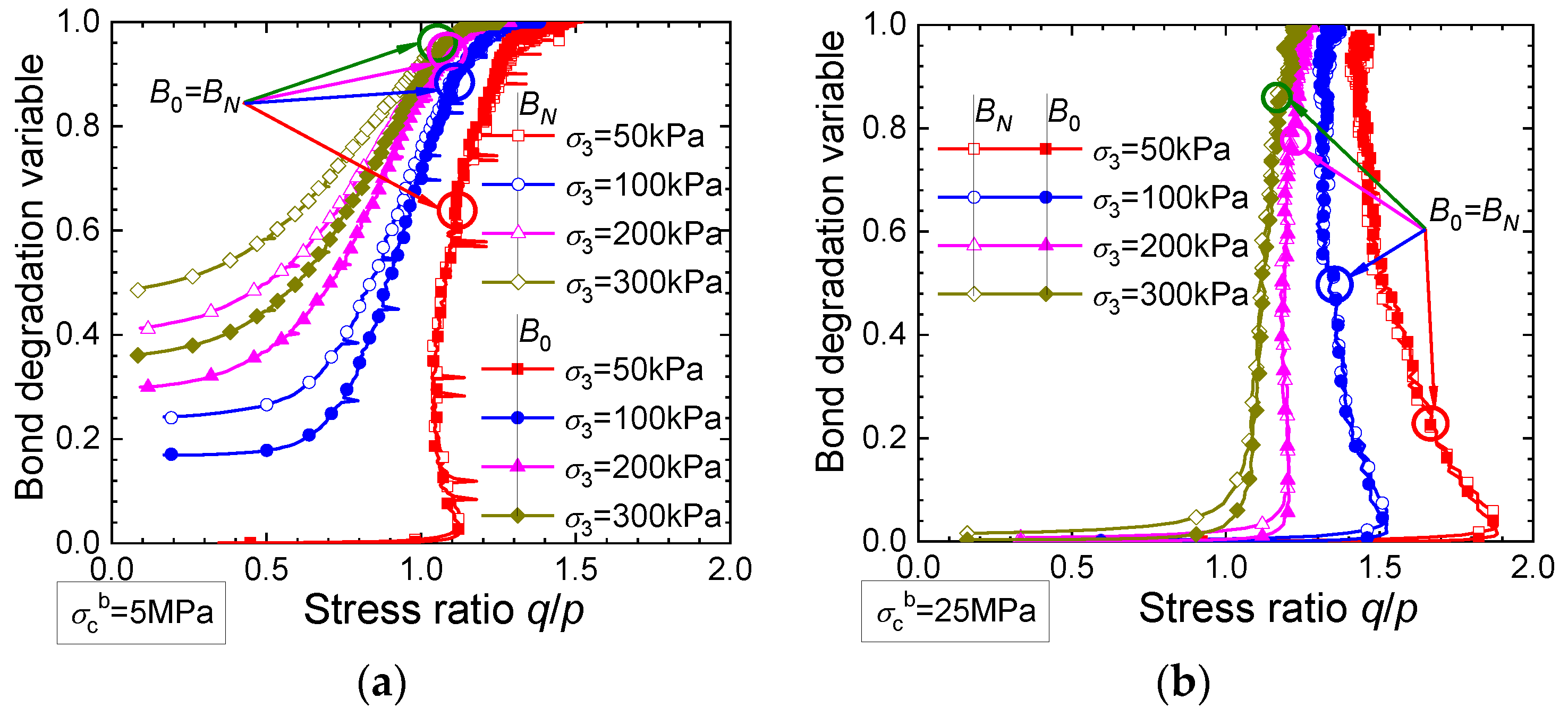
3.3. Conventional Triaxial Tests

Figure 7 shows the relationships between the deviator stress/void ratio and axial strain observed in the conventional triaxial tests. The DEM simulation reproduces the typical behavior of cemented soils [2,40]. The deviator stress increases, and the void ratio decreases with the increase in confining stress. The strain-softening behavior increases, and the tendency for the specimens to expand increases under shearing as the bond strength increases. The deviator stresses and void ratios are almost the same for samples I and II at the critical state, which demonstrates a similar critical state for samples with different bond strengths.

Figure 8 shows the evolution of the bond degradation variables B_N and B₀ in conventional triaxial tests. There are initial equivalent plastic strains and initial bond degradation variables at the beginning of shearing for sample I under confining stresses larger than 50 kPa, which is ascribed to isotropic compression before shearing. However, the initial degradation variables are almost zero after isotropic compression for sample II on account of the large bond strength.

The evolution of the bond degradation variables in sample I with weak bonds is slightly influenced by the confining stress; some curves form a rough “S” shape under shearing. The degradation variables of the robust bonds in Sample II show an upward trend with an increasing confining stress. The degradation variable B0 is smaller than BN at the intermediate stage of shearing, similar to the conclusion in the compression tests, while B₀ varies near or higher than B_N at the end of shearing when the stress state develops close to the strength envelope, as illustrated by the circles in Figure 8 and Figure 9.

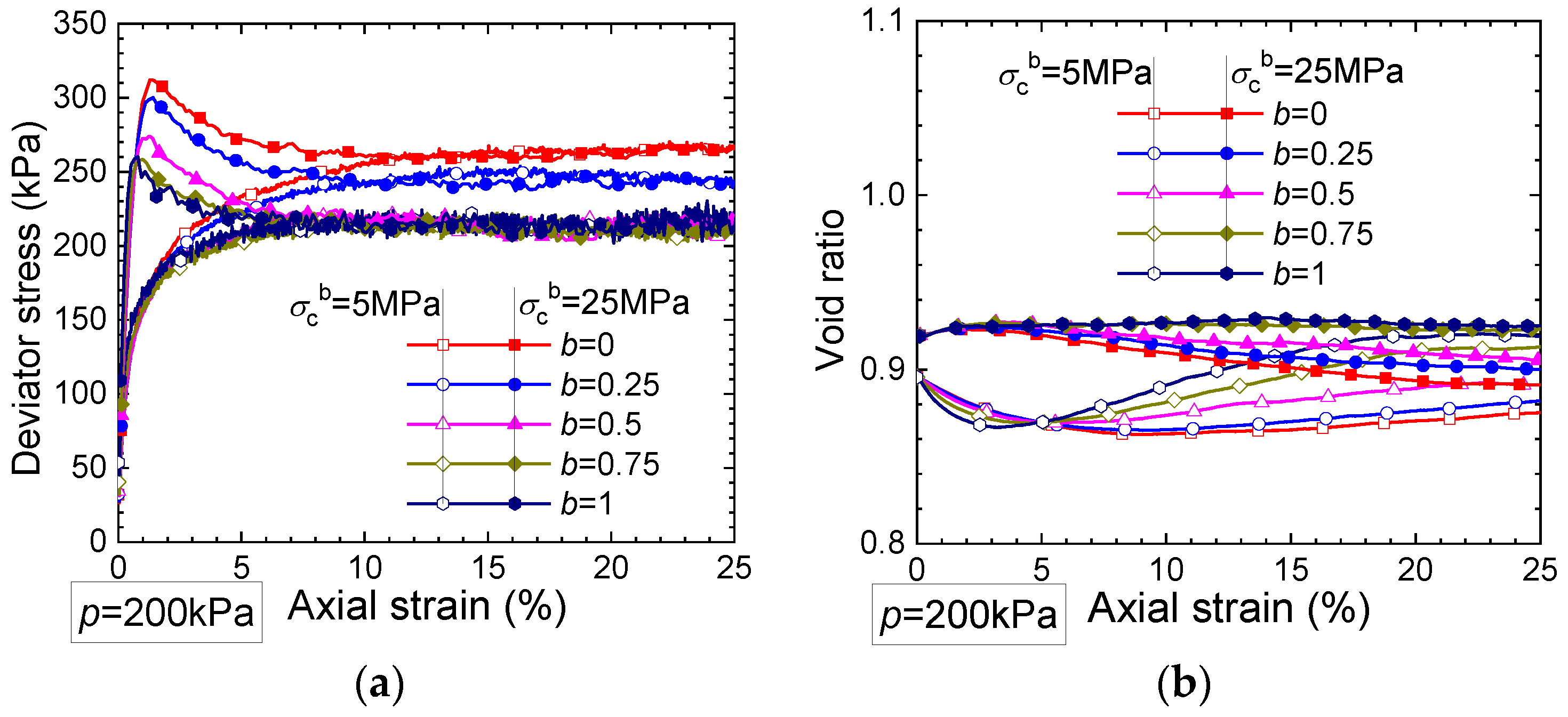
3.4. True Triaxial Tests

Figure 10 represents the macroscopic behavior of the numerical specimens in true triaxial tests (constant p). Parallel to the findings in conventional triaxial tests, there is an augmentation in the strain-softening behavior and an expanding tendency as the bond strength rises. In laboratory tests [41], it is noted that the deviator stress declines, and the void ratio increases with the growing coefficient b = (σ₂ − σ₃)/(σ₁ − σ₃).

Figure 11 shows the evolution of the bond degradation variables B_N and B₀ in the true triaxial tests. The degradation variables increase with the equivalent plastic strain, forming a rough “S” shape for sample I with weak bonds, and increase at a decreasing rate for sample II with strong bonds. The bond degradation variables are slightly influenced by the coefficient b for sample I, while they decrease considerably as the coefficient b increases for sample II. The degradation variable B₀ tends to be near or higher than B_N at the end of shearing, especially for the samples with a small confining stress and small coefficient b.

4. Discussion

The evolution of the bond degradation variables B_N and B₀ with the equivalent plastic strain appears to be affected by the ratio of principal stresses, confining stress, and coefficient b, especially for samples with strong bonds. Hence, there is a defect in using a general bond degradation evolution law, e.g., $B_N \mathrm{or} B_0=f({\epsilon }_{\mathrm{d}}^{\mathrm{p}})$, in constitutive modeling since the parameters in the formula are dependent on the stress path. It is necessary to further develop a stress-path-independent bond degradation variable.

The stress ratio and strength potential are incorporated into B₀ to derive a bond degradation variable B_σ that considers their effect on the bond degradation evolution as follows:

$$B_{\sigma }=\frac{2B_0}{1+{(\eta /{\eta }_{\mathrm{f}})}^2}$$

(26)

where $\eta =q/p$ is the stress ratio, ${\eta }_{\mathrm{f}}=q_{\mathrm{f}}/p$ is the strength potential, and $q_{\mathrm{f}}$ is the deviator stress at failure. ${\eta }_{\mathrm{f}}$ can be expressed by an extended elliptical envelope:

$${\eta }_{\mathrm{f}}=\max (M(\frac{p+p_{\mathrm{t}}}{p}){(\frac{p_{\mathrm{c}}}{p+p_{\mathrm{t}}}-1)}^{1/n},M)$$

(27)

The envelope, in which the parameters are determined using conventional triaxial tests, is shown in Figure 4 for both samples I and II. In the expression of B_σ, $\eta /{\eta }_{\mathrm{f}}$ is incorporated to accommodate the bond degradation rate.

Figure 12 shows the collective evolution of the bond degradation variables B₀ and B_σ with the equivalent plastic strain under all of the above stress paths. The impact of the stress path on the evolution of the bond degradation variable B_σ seems to be less pronounced compared to that on B₀. The collective data of B_σ can be effectively fitted using the following exponential formulation and hyperbolic formulation:

$$B_{\sigma }=1-\exp [-c_{\mathrm{a}}{({\epsilon }_{\mathrm{d}}^{\mathrm{p}})}^{c_{\mathrm{b}}}]$$

(28)

$$B_{\sigma }=\frac{{\epsilon }_{\mathrm{d}}^{\mathrm{p}}}{h_{\mathrm{a}}+h_{\mathrm{b}}{\epsilon }_{\mathrm{d}}^{\mathrm{p}}}$$

(29)

where $c_{\mathrm{a}}$ represents the increasing rate of B_σ, and $c_{\mathrm{b}}$ is an index. $1/h_{\mathrm{a}}$ controls the increasing rate of B_σ, and $1/h_{\mathrm{b}}$ represents the ultimate value of B_σ. Figure 12c,d show the fitting curves of both formulations.

In constitutive modeling, one-dimensional compression and conventional triaxial tests are recommended to determine the parameters in the evolution law of the bond degradation variable B_σ for simplicity.

5. Conclusions

This paper investigates the bond degradation evolution of cemented soils at the particle and contact scales. Numerical compression and triaxial tests reproduced the primary experimental mechanical behavior. Then, the simulation results were used to investigate the evolution of the bond degradation variables B_N and B₀. A stress-path-independent bond degradation variable B_σ was developed based on B_0, and its evolution law was formulated accordingly. The conclusions are as follows:

(1)

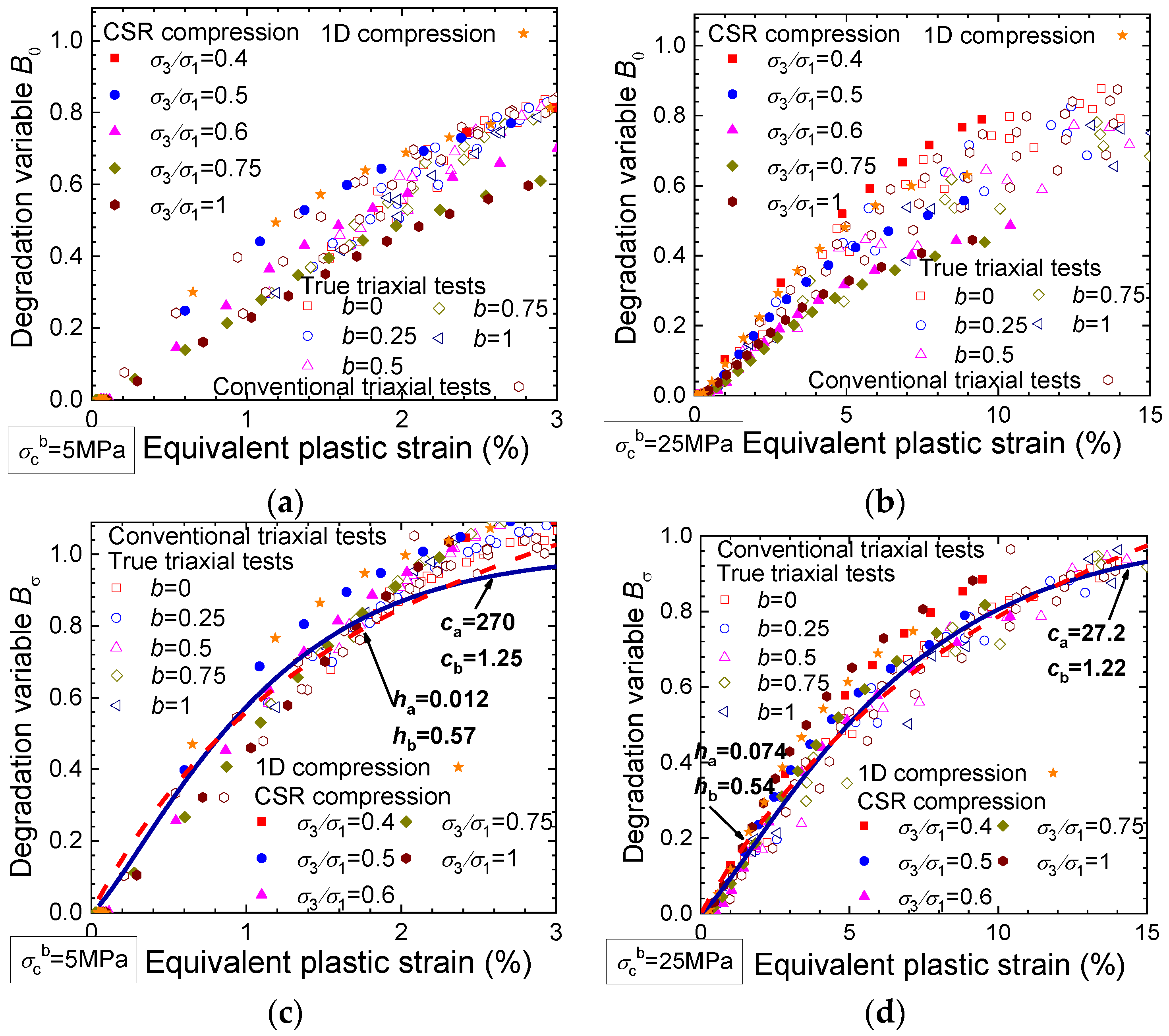
The bond degradation variables B_N, B₀, and B_σ represent the extent to which the soil bonding is damaged. A degradation variable of 0/1.0 indicates that the applied stress is completely sustained by the bonded aggregates/unbounded grains.

(2)

The bond degradation variables B_N and B₀ increase with the equivalent plastic strain until they reach 1.0 under varying stress paths. The evolutions of both variables are influenced by the principal stress ratio, confining stress, and coefficient b, especially for the sample with strong bonds.

(3)

In compression tests with principal stress ratios higher than 0.4, B₀ is smaller than the corresponding B_N, indicating the priority of the bonded contacts to sustain the applied loads. In triaxial tests, B₀ is smaller than B_N before the intermediate stage of shearing, and then B₀ evolves to be near or larger than B_N at the end of shearing when the stress state approaches the strength envelope.

(4)

The evolutions of the further developed bond degradation variable B_σ under different stress paths are approximately coincident with each other. The collective data of B_σ can be effectively fitted by an exponential or a hyperbolic evolution law.

In the future, the evolution of the bond degradation variables for unsaturated structured soils will be studied by taking capillary forces into account. A micromechanical-based constitutive model for cemented soils can be developed by incorporating the evolution law of the bond degradation variable.