1. Introduction
Fractional calculus is a branch of mathematical analysis that applies the concepts of integration and differentiation to orders that are not integers. Fractional calculus, in contrast to classical calculus, which deals with derivatives and integrals of integer order, involves derivatives and integrals of orders that are not integers since they are fractional. This field, which has found applications in a variety of scientific and engineering-related fields, has provided a more realistic framework for describing complicated processes that involve memory effects and long-range interactions [
1].
The discipline of fractional calculus remains a vibrant area of study, with continuous investigation into its various applications in domains such as physics, engineering, biology, economics, signal processing, and others. Fractional calculus is employed to mathematically represent and study intricate physical systems that encompass phenomena such as diffusion, heat conduction, wave propagation, viscoelasticity, electrochemistry, and control systems [
1]. It offers a more precise depiction of materials exhibiting memory effects, non-local behavior, and anomalous diffusion, characterized by non-random particle propagation [
2]. Biological systems, including medication administration, bioelectricity, enzyme kinetics, and brain networks, may be effectively modeled using fractional calculus. It aids in capturing the intricate dynamics and enduring memory exhibited in biological systems [
3]. Fractional calculus is employed in the development and examination of control systems that exhibit fractional dynamics. It facilitates the regulation of systems with memory and long-range interactions, resulting in enhanced system efficiency and stability. Fractional differential and integration are used in the analysis of viscoelastic materials, where the relationship between stress and strain is described by fractional differential equations; they are also used to simulate heat transfer in materials that exhibit memory effects and non-local interactions [
4].
The presence of singular kernels in certain locations and the absence of singular kernels in other locations have significantly contributed to the growing importance and ongoing research in the field of fractional calculus [
5,
6]. The presence of these obstacles has stimulated extensive research endeavors and ignited enthusiasm for the advancement of novel methodologies and techniques in the realm of fractional calculus. The issue of locality occurs when employing singular kernels, such as the conventional Riemann–Liouville or Caputo derivatives. These derivatives are local operators, implying that the derivative’s value at a certain place is only determined by the function’s values at that point and its immediate vicinity [
7]. Nevertheless, in several practical scenarios, especially those pertaining to intricate systems or substances, non-local behavior is evident, and the impact of remote sites becomes substantial. The conventional fractional derivatives are insufficient for accurately capturing this non-local behavior [
8,
9].
Caputo and Fabrizio [
10] were the first to attempt to develop the notion of fractional calculus in this particular situation. They achieved this by presenting a non-singular integral (kernel) based on a smooth exponential function that decreases. Indeed, they did not verify the presence of a single kernel in the fractional derivative operator based on the obtained data. Conversely, they asserted that the utilization of the fractional derivative factor is suitable for a multitude of physical phenomena. In order to enhance this approach, Atanagana-Baleanu introduced a method in [
11,
12] that substitutes a smooth exponential function with the extended Mittag–Leffler function, which is characterized by a single parameter.
In the field of mathematical physics, general fractional-order derivatives have been utilized to investigate mathematical models. These derivatives involve the use of non-singular kernels, which include functions such as exponential, Mittag–Leffler–Gauss, Kohlrausch–Williams–Watts, Miller–Ross, Lorenzo–Hartley, Gorenflo–Mainardi, Bessel, Mittag–Leffler, Wiman, and Prabhakar that are not singular [
13,
14]. In the realm of fractional calculus, there is a mathematical function that is considered the Rabotnov fractional–exponential function [
15]. This function is also known as the Rabotnov function. It was presented in the context of viscoelasticity and creep deformation by Nikolai Rabotnov, a Russian engineer and scientist. To describe the time-dependent behavior of viscoelastic materials, the Rabotnov function is frequently utilized. This is especially true when considering creep deformation. Both viscous (time-dependent) and elastic (time-independent) behaviors can be observed in viscoelastic materials [
16]. Creep is a term that describes the slow and time-dependent deformation of a material that occurs when it is subjected to continual tension. Several other fields have discovered uses for the Rabotnov function, such as material science, engineering, and biomechanics. With its help, we can model and study how materials creep, as well as predict how they will change shape over time when loaded continuously and describe the viscoelastic properties of living tissues [
17]. Engineers and scientists may be able to better understand and predict how viscoelastic materials will behave over time by adding the Rabotnov function to mathematical models. This, in turn, facilitates the enhancement of the design and investigation of structures, gadgets, and biological systems [
18].
There are two new fractional derivatives that were created by Yang et al. [
19] and Yang et al. [
20]. They are based on the Rabotnov fractional exponential function and the non-singular kernel with normalized sinc function. These derivatives are addressed. Because they are defined with the assistance of the normalized sinc function and the Rabotnov exponential function, both of which do not have a singular kernel, these fractional operators are quite fascinating. According to Cattani’s study [
21], the applications of the new FCs as well as some intriguing results may be found in the publication. In order to account for the fractal structure of the constructed material, Shymanskyi et al. [
22] provided mathematical models for the issue of thermal conductivity in clay block construction. The fractal structure of the material was taken into consideration using a fractional-order integrative discriminator.
Classical thermoelasticity is a branch of continuum mechanics that combines the ideas of elasticity and heat conduction to explain how materials react to both mechanical and thermal stresses. This paradigm facilitates the analysis of the relationship between temperature and mechanical deformation in solids. An essential premise of classical thermoelasticity is the notion that the velocity of thermal disturbances is infinitely fast. This assumption suggests that every instantaneous change in temperature at a specific spot has an immediate impact on the entire material.
Hyperbolic thermoelasticity is a modified version of conventional thermoelasticity that allows for a finite thermal propagation speed instead of assuming an infinite pace. It considers the limited velocity at which thermal disruptions spread within the material. This change enables more precise simulation of processes that involve fast heat transfer or high-frequency thermal waves. In the field of hyperbolic thermoelasticity, the conventional heat transfer equation is substituted with a hyperbolic partial differential equation, commonly known as the wave equation. This equation adds a limited thermal wave speed, referred to as the speed of heat or thermal wave velocity. The wave equation incorporates the temporal lag in the spread of thermal disruptions and enables the examination of momentary thermal impacts [
23].
In the context of generalized hyperbolic thermoelasticity, several extended models have been introduced in order to further improve the theory and address physical inconsistencies. Both Lord and Shulman [
24] (LS) and Green and Lindsay [
25] (GL) are credited with the development of the first and second generalized thermoelastic theories, respectively. Green and Naghdi [
26,
27] provided the most pertinent generalization of thermoelasticity, which was based on the law of entropy balance for thermal elasticity. Their idea was broken up into three distinct sections, which they referred to as GN-I, GN-II, and GN-III. Additionally, the linearized form of the GN-I theory is identical to the conventional heat transfer theory. The GN-II theory provides a fixed speed for heat propagation and does not have any energy dissipation. On the other hand, the GN-III theory allows thermal signals to propagate at both limited and unlimited velocities. Tzou [
28,
29] examined a constitutive equation in order to describe the logging behavior of heat transfer in materials. Tzou applied two-phase delays to both the heat flux vector and the temperature gradient, respectively. As the time of relaxation for the quick transient impacts is caused by thermal inertia, the phase lag of the heat flux vector is used as an interpretation. A delay time that is induced by the interactions between the microstructures is understood as the other phase lag of the temperature gradient.
Chen and Gurtin [
30] and Chen et al. [
31,
32] proposed a heat transfer framework for deformable materials that incorporates two temperatures: conduction temperature and thermodynamic temperature. The difference between these two temperatures is directly related to the heat source in conditions that do not change over time. In the absence of any heat supply, the two temperatures are equal. Quintanilla [
33] investigated the resolution potential, structural stability, and spatial patterns related to the concept of two temperatures (2TT). The concept of the thermoelasticity theory has been the focus of numerous research publications over the past 20 years, leading to the development of what is today referred to as extended thermodynamics [
34,
35,
36,
37].
In recent years, there have been notable breakthroughs in the study of thermoelasticity, namely in the utilization of fractional calculus to model and evaluate heat transfer processes. Conventional heat transfer models that rely on single kernel operators have restrictions on accurately representing non-local behavior and memory influences. Furthermore, fractional calculus is used to explain anomalous diffusion in materials, which happens when temperature changes do not spread in a way that follows the rules of classical diffusion. This is especially important to keep in mind when dealing with materials that have inconsistencies or complicated structures.
This work introduces an innovative method in the realm of thermoelasticity by suggesting a comprehensive fractional heat conduction model with two temperatures. By using the non-singular kernel of the Rabotnov fraction and the Liouville–Caputo-type exponential function, we hope to make fractional operators more useful in the heat conduction equation. The proposed model considers the intricate dynamics of heat transfer in materials exhibiting memory effects, non-local behavior, and anomalous diffusion. To address the limitations of single kernel-based fractional heat conduction models, we employ the non-singular kernel of the sinc function and Rabotnov fractional–exponential function. This enables us to simulate the long-distance interactions and memory-dependent processes that occur in the actual world. Moreover, using the exponential function in the Liouville–Caputo framework enables a more precise characterization of the time-varying thermal response.
Different models of generalized thermoelasticity theories with different fractional derivative operators and constitutive equations have been used. In order to unify and clarify the relationships between different theoretical models of thermoelasticity, it is necessary to generalize and compare these frameworks. For this reason, the current study aimed to discover common characteristics, examine basic assumptions, and investigate links between different theoretical perspectives. This technique enables a more in-depth understanding of the fundamental principles that regulate partial thermal coupling and supports the establishment of reliable and comprehensive models.
This work examined the thermomagnetic reactions of a circular solid cylinder when placed in a constant axial magnetic field as a way to apply the derived model. The cylinder border is traction-free, whereas the surrounding space is subjected to a heat flow with a constant velocity. The method of the Laplace transform was utilized to solve the linked governing equations. This method makes it possible to solve the converted problem analytically while also simplifying equations. To make the numerical results easier to understand, graphs were used to show how different fields affected the simple medium and how it was different from the non-simple medium and fractional operators.
Using a fractional exponential function, like the Rabotnov function, as a kernel function for predicting thermal diffusion is very helpful, especially when it comes to figuring out the inverse Laplace transform of the fractional derivative. Optimizing and calculating fractional-order operators and parameters simplifies the modeling of thermoelasticity. Several studies have shown and explored the use of the fractional derivative with the exponential Rabotnov kernel in real-world situations [
20,
38]. Research has demonstrated the utility of using this fractional component in simulating various physical and other processes. Additionally, the fractional derivative with the exponential Rabotnov kernel abides by the conventional rule for the derivative of a constant function, which is zero.
Following a logical sequence, this article begins with the derivation of the model, then moves on to investigate special instances, then presents the solution methodologies, and finally concludes with a discussion of the findings after providing the numerical results. Through the use of this structure, it is possible to obtain a full grasp of the suggested model and the applications it has in thermoelasticity.
3. Applicable Problem Formulation
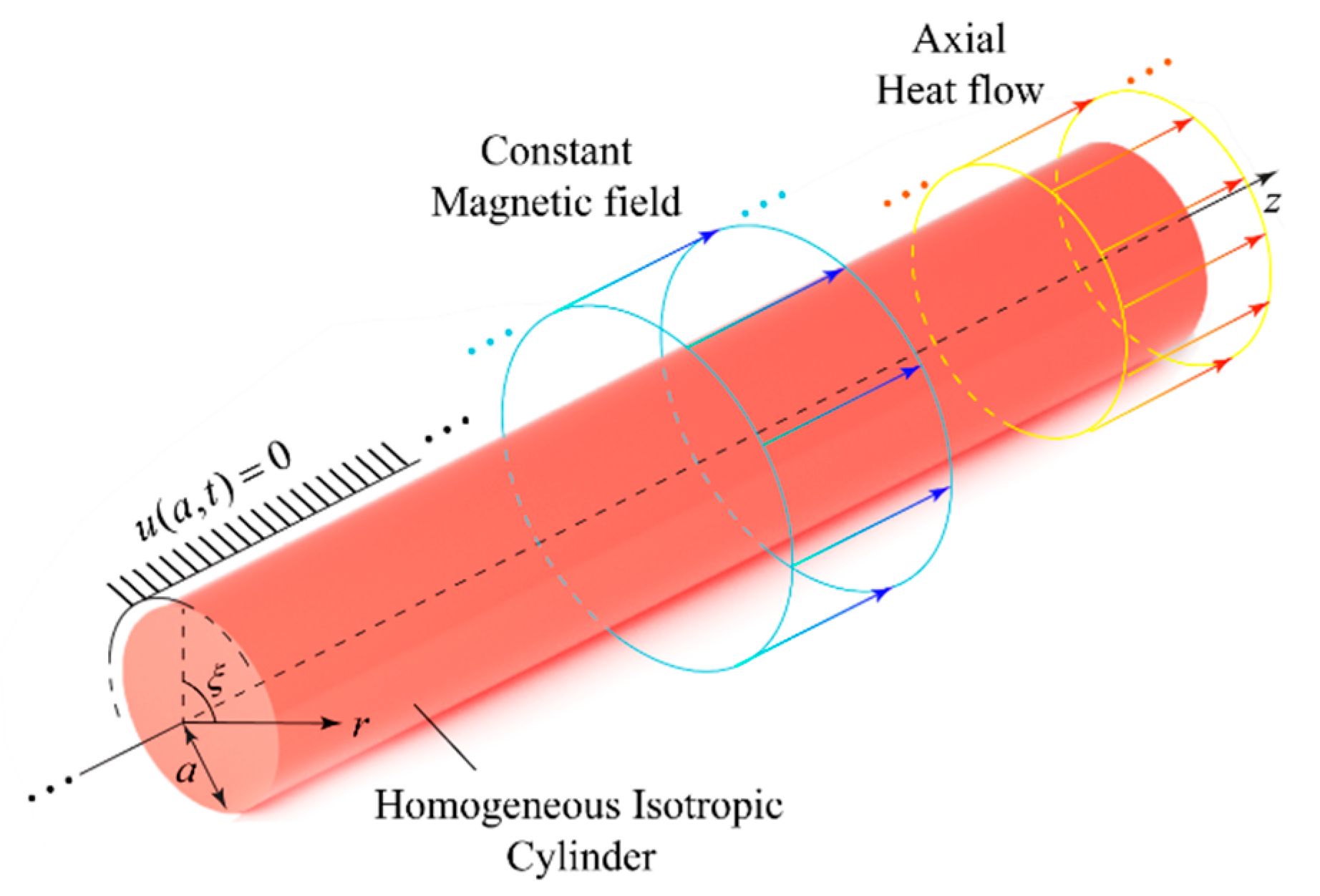
In the context of the proposed fractional thermoelasticity model, the problem of a long isotropic solid cylinder with radius
will be considered. The presence of a homogeneous axial magnetic field, denoted by
, which penetrates the cylindrical elastic medium, is taken into account. An axial heat flux was applied to the periphery of the solid cylinder. For the purpose of analysis and the nature of the problem, a cylindrical coordinate system
was used (see
Figure 1). The coordinate origin is fixed at the center of the cylinder, and the
axis is aligned with the cylinder axis. Since the problem is based on the assumption that the thermoelastic interactions are symmetric about the
axis, the functions involved depend only on the radial coordinate
and the time variable
. A consideration was given to the regularity requirement, which indicates that the solutions of the fields are restricted when r tends to zero.
In light of this, the equations that control a problem with one dimension may be expressed as
An induced magnetic field (
) is produced due to the interaction between the material characteristics of the cylinder and the external magnetic field surrounding it. Since it is assumed that the initial applied magnetic field
is axial and acts parallel to the
axis, the induced magnetic field
takes the same direction. Hence, from Equation (17), the electric current density
and the induced electric field
will each have a single component in the direction of the
orientation. As a result, we have the following relationships:
Substituting Equation (26) into Equations (18) and (19), the radial Lorentz force
and the stress Maxwell
components will have the following forms:
Matters deform and behave differently depending on their surface temperature, which is also important for several mechanical and thermal processes. The distribution of temperatures within an object affects its thermal and mechanical characteristics, which are crucial for thermoelastic material analysis and prediction.
This study assumes that the relationship between the change in temperature
, the specific heat capacity of the material
, and the thermal conductivity
is a linear proportional relationship. Based on the assumption of direct proportionality between the temperature change
, heat capacity
, and thermal conductivity
, they either rise or fall linearly when the temperature changes. Regardless of the fluctuation in density
and constant thermal expansion, we will assume the following [
44,
45]:
In this case, the reference values for specific heat capacity and thermal conductivity at a reference temperature are denoted by and , respectively. The rate at which these characteristics vary with temperature is determined by a constant called .
In general, the dependence of the coefficient of the specific heat capacity of the material and thermal conductivity on temperature is not always a linear function. It can display a variety of behaviors depending on the material and the temperature range it is exposed to. It is essential to keep in mind that the temperature dependence of K can vary greatly from one material to another, and even within the same material, it might display non-linear, stepwise, or other complicated behaviors to a certain extent. It is for this reason that the assumption of a linear connection between K and temperature can result in considerable inaccuracies in thermal prediction. Measurements taken in the laboratory or models that are already well known for a particular material are often utilized in order to precisely determine how the value of K varies with temperature and to incorporate its non-linear behavior into thermoelasticity models.
By utilizing Equations (9) and (28), it is possible to determine the thermal conductivity and specific heat of materials as a function of the conductive temperature as follows:
It is possible to apply the Kirchhoff transform, shown below, as a means of finding solutions:
Upon applying the operator
to both sides of Equation (30), we are able to derive the following
:Again, by applying the div operator (
) to Equation (31), we can obtain the following:
On the basis of the differentiation of Equation (30) with regard to time
, we can derive
As a result of inserting Equations (31) and (32) into Equation (13), the modified linear thermal conductivity equation with fractional order and two temperatures can be obtained as follows:
The parameter signifies the diffusivity of the material. Material composition, microstructure, and temperature variation are a few examples of the physical parameters that affect the thermal diffusion coefficient . Due to the requirement of Equation (28), we will assume that the thermal diffusion coefficient is constant for the purposes of this study.
On the basis of the assumption of linearity and the substitution of Equations (31) and (32) into Equation (27), as well as the execution of a number of mathematical operations, we are able to approximate Equation (9) to obtain the following formula:
After applying Equations (22) and (23), the equation of motion (25) may be expressed as follows:
By incorporating Equation (31) into Equation (36), we can obtain the following:
where
and
.
After neglecting the non-linear elements in the preceding equation and making the assumption that
, we are able to obtain the final result:
By introducing non-dimensional field variables, we can simplify the governing equations into non-dimensional forms. To do this, the original variables are divided by their corresponding reference values. The following non-dimensional variables can be defined as follows:
By inserting these definitions into the governing equations and correctly measuring the other quantities involved, we may derive the non-dimensional versions of the equations as follows:
where
In order to solve the aforementioned system of differential equations, it is possible to incorporate a new function
related to the radial displacement component
, commonly referred to as the potential function, in the following manner:
Upon substituting the suggested function
into Equations (40) and (42), the following results are obtained:
The initial conditions are imposed as follows at time
:
Additionally, we will take into account that for regularity requirements, the studied variables and are constrained when . This condition of regularity means that the different fields are finite when the radial distance approaches zero and do not show singularity or divergence.
A common occurrence in many manufacturing processes is the moving heat flow, a type of heat source utilized or created in machining. Thus, there are a variety of technical techniques that may be used to solve heat conduction issues with a moving heat flow, including metal cutting, welding, flame or laser hardening of metals, discharging a bullet in a rifle barrel, and more [
46]. Furthermore, the relative sliding of two bodies with heat created at the contact zone is a common feature of tribological applications and industrial processes. Moving heat flow analyzers have made it possible to characterize the temperatures produced during these operations in great detail [
47].
It will be assumed that the surrounding plane of the cylinder,
, undergoes a moving heat flux denoted by
. According to the following, the fractional-order-modified Fourier law (11) will be taken into account, and we thus have the following:
Using Equation (31) thereafter, we obtain
By taking into consideration the fact that the heat flow
flows at a constant speed
in the direction of the radial axis of the cylinder and decays exponentially with time, the following formula will be taken into consideration:
Given that the coefficients
and
are considered to be constants, the Dirac delta is denoted by the symbol
. Through the utilization of the Dirac delta function
, it is guaranteed that the heat flux is concentrated in a particular region
. We obtain the following result when we make use of the dimensionless variables (39) and then substitute them into (53):
In addition to the above, we will assume that mechanical constraints ensure the restriction of surface displacement and can be expressed mathematically by the following formula:
The condition sets a restriction on the mechanical response of the cylinder, ensuring that there is no displacement or distortion at the outside border. The situation can be understood as the outer surface of the cylinder being clamped or fixed, thus preventing any displacement or movement. The term usually used to describe this condition is the Dirichlet displacement boundary condition.
4. The Solution to the Problem
Due to its ability to streamline the mathematical formulation of differential equations and expedite frequency-domain solution methods, the Laplace transform is a valuable tool for differential equation analysis and solving. Differentiation, integration, and convolution may all be carried out more readily by turning the differential equations into algebraic equations in the Laplace domain. The function
is transformed using the Laplace transform, resulting in the function
. The variable
is a complex number with a positive real portion (
). The Laplace transform is computed by utilizing the following integral:
If we consider the initial conditions (50), then applying Laplace to the fundamental equations yields the following equations:
where
with
When the function
is eliminated from Equations (57)–(59), we obtain
where
When we introduce the parameters
, where
, 2, into Equation (65), we obtain the following formulas:
The coefficients
and
represent two solutions of the equation:
The solutions for
and
can be derived by solving Equation (68) as follows:
The general answer to Equation (67) under the regularity condition can be expressed as follows:
where
, (
, 2, 3), represents the integral parameters and
represents the first class of modified Bessel functions with zero order. The following may be deduced from Equations (47) and (71):
The differentiation of Equation (72) yields the following result:
When entering Equation (70) into Equation (59), the function
is obtained as follows:
If Equation (28) is substituted into Equation (30) and then integration is performed, the following conclusion may be obtained in the field of the Laplace transform:
The solutions to the aforementioned equations allow us to determine
and
as
Consequently, the following expressions may be used to determine the thermal stresses:
Moreover, Maxwell’s stress
has a solution that is provided by
In the transformed domain, the boundary conditions (54) and (55) are expressed as follows:
Using Equations (70) and (72), and the boundary conditions (82) and (83), we are able to achieve the following:
In order to obtain the parameters , (, 2), it is necessary to solve the system of Equations (84) and (85). As a result, the issue has been resolved successfully inside the Laplace transform field.
6. Results and Discussion
This section analyzes the behavior of an endlessly elastic copper cylinder submerged in a magnetic field and subjected to a moving heat source, focusing on the numerical findings and discussion. The objective of this study is to validate the novel thermoelasticity model for the heat transfer equation, which relies on fractional operators of fractional order.
Copper is a highly adaptable metal with a diverse set of mechanical characteristics that render it appropriate for a multitude of uses. Copper is a malleable metal, allowing it to be readily molded and fashioned into many shapes and dimensions. Due to this characteristic, it is often favored for the production of wires, tubes, and sheets. Copper possesses exceptional thermal conductivity, making it a very suitable substance for deployment in heat exchangers, condensers, and several other heat transfer applications. For the purposes of numerical calculations and comparisons, the physical properties of copper that can be used are as follows [
41]:
Some physical field variables were found numerically, including Maxwell stress , radial and hoop thermal stresses ( and ), deformation , dynamic temperature , and conductive temperature . These variables were found by using mathematics on copper material. Calculations were performed while varying the distance within the range from 0 to 1, with a fixed time . In addition, the size of the heat source was set to 1, and the frequency remained constant (). The numerical algorithm represented in Equation (86) was used to obtain the values of field variables under the influence of a number of different factors.
The main goal of this section is to assess the efficacy of modified fractional operators, classic fractional operators, and conventional derivatives in representing a physical phenomenon. The modified fractional operators under consideration are the Yang–Gao–Tenreiro Machado–Baleanu (YGTB) operator [
19] and the Yang–Abdel–Aty–Cattani (YAC) operator [
20]. Additionally, the conventional fractional operator being evaluated is the Riemann–Liouville (RL) operator. A comparison of results was performed to ascertain the advantages and disadvantages associated with each operator. The results of the proposed model will be consistent with the non-fractional two-temperature thermoelastic theory with phase delay and (2T-DPL) when the fractional order
.
A comparison of the fractional operators and the conventional derivative is being conducted with the intention of determining whether the fractional derivative is most likely to converge to the classical derivative as the order of differentiation becomes closer to 1. The proposed model allows us to observe the natural behavior of various physical domains by adjusting the fractional order
to appropriate values. The main difference between the bounded non-local fractional operators (YGTB and YAC) and the usual fractional model (RL) is evident when the numerical results with different fractional parameter values are considered.
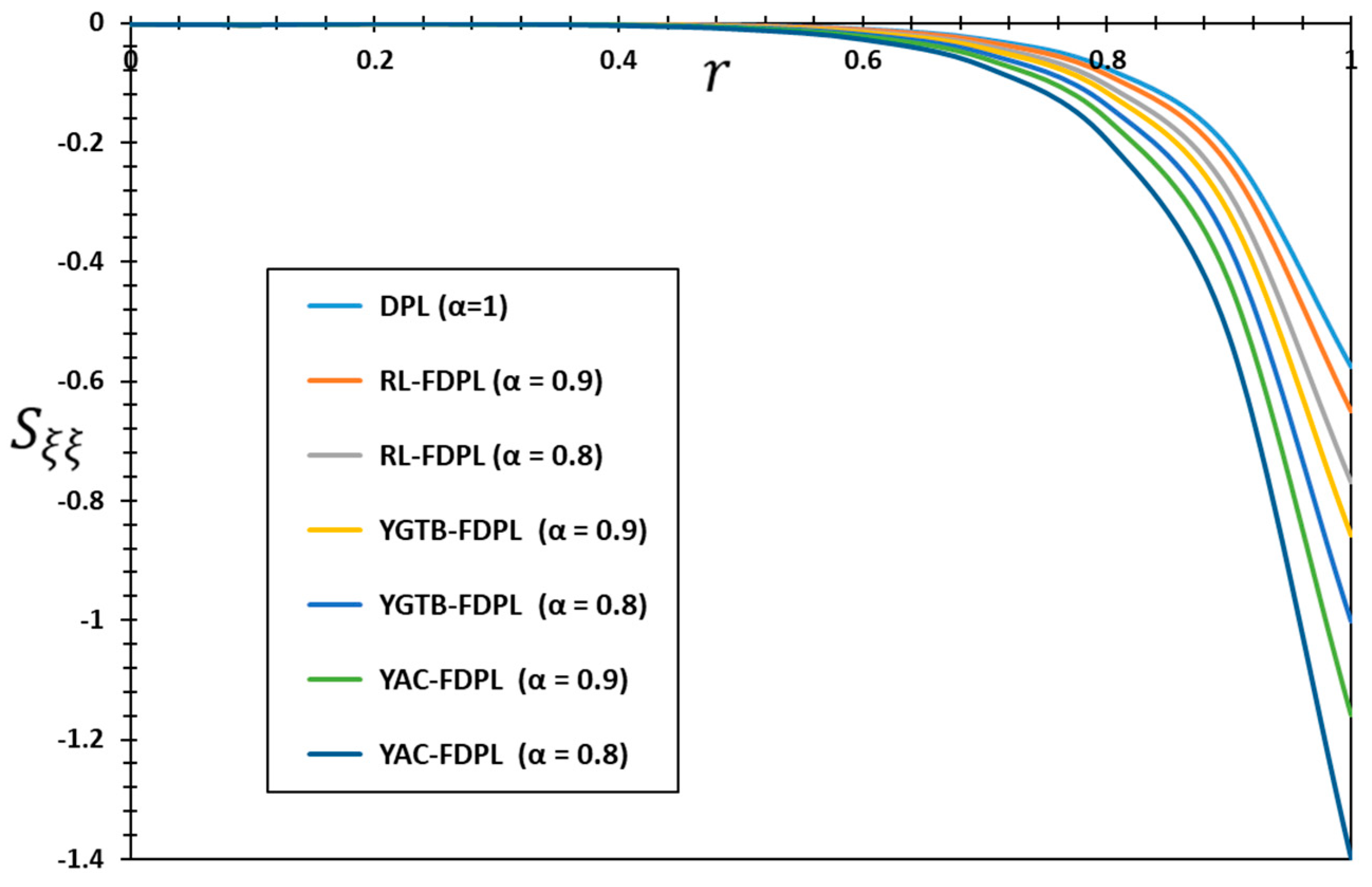
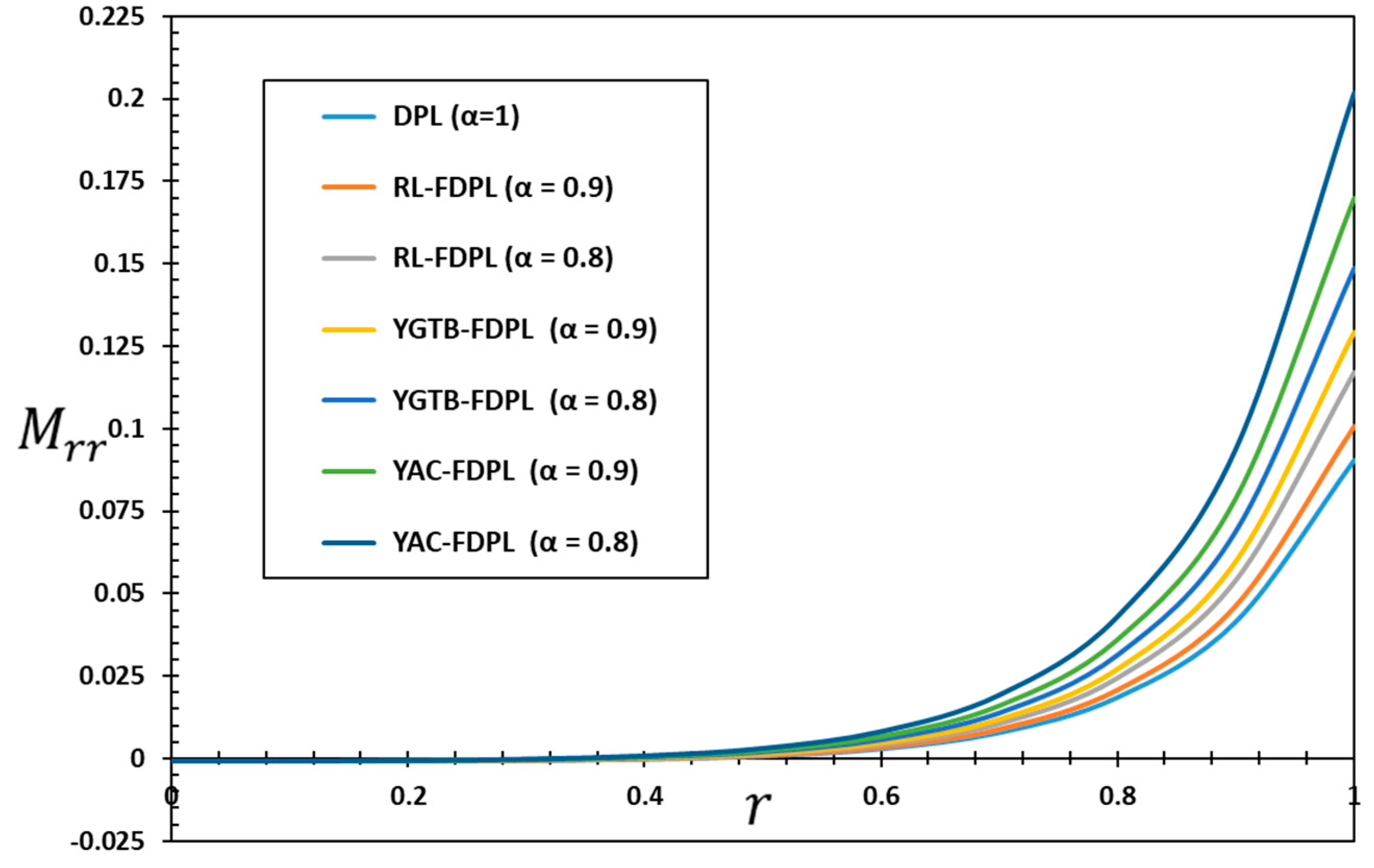
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6 and
Figure 7 offer a quantitative depiction that highlights the disparities between fractional and conventional thermoelastic models, facilitating comprehension and comparison of their behavior. In this scenario, the values
,
,
,
, and
are considered.
It is worth noting that based on the results and curves of different shapes, it is clear that the results obtained with the fractional derivative operator included in the thermal equation differ significantly from those obtained without it in terms of temperature, displacement, and thermal stress distributions. Thus, fractional differential operators can greatly influence the pattern and distribution of thermophysical fields in elastic materials. Fractional-order values and the type of fractional operator can affect the stability and steady state of thermal and mechanical waves. The reason for this is as follows:
Fractional differential operators create non-local and memory-dependent effects, resulting in different behaviors from traditional integer-order differential operators.
Utilizing fractional derivative operators enables the representation of non-singular diffusion, non-local transport processes, and memory effects in diverse physical systems, such as thermal and mechanical waves in elastic materials.
Increasing the fractional order can decrease the speed at which heat waves propagate inside the medium by affecting heat flow, as demonstrated by several figures and consistent with experimental findings. The waves decay faster as they move deeper into the elastic body when the fractional-order value is decreased. The fractional order can influence the speed of wave propagation and the decay rate. This phenomenon has numerous significant applications in various domains such as thermoelasticity, viscoelasticity, and control theory. Furthermore, the fractional heat transfer wave models are capable of accurately predicting the finite velocities of heat propagation owing to the hyperbolic nature of their mathematical form.
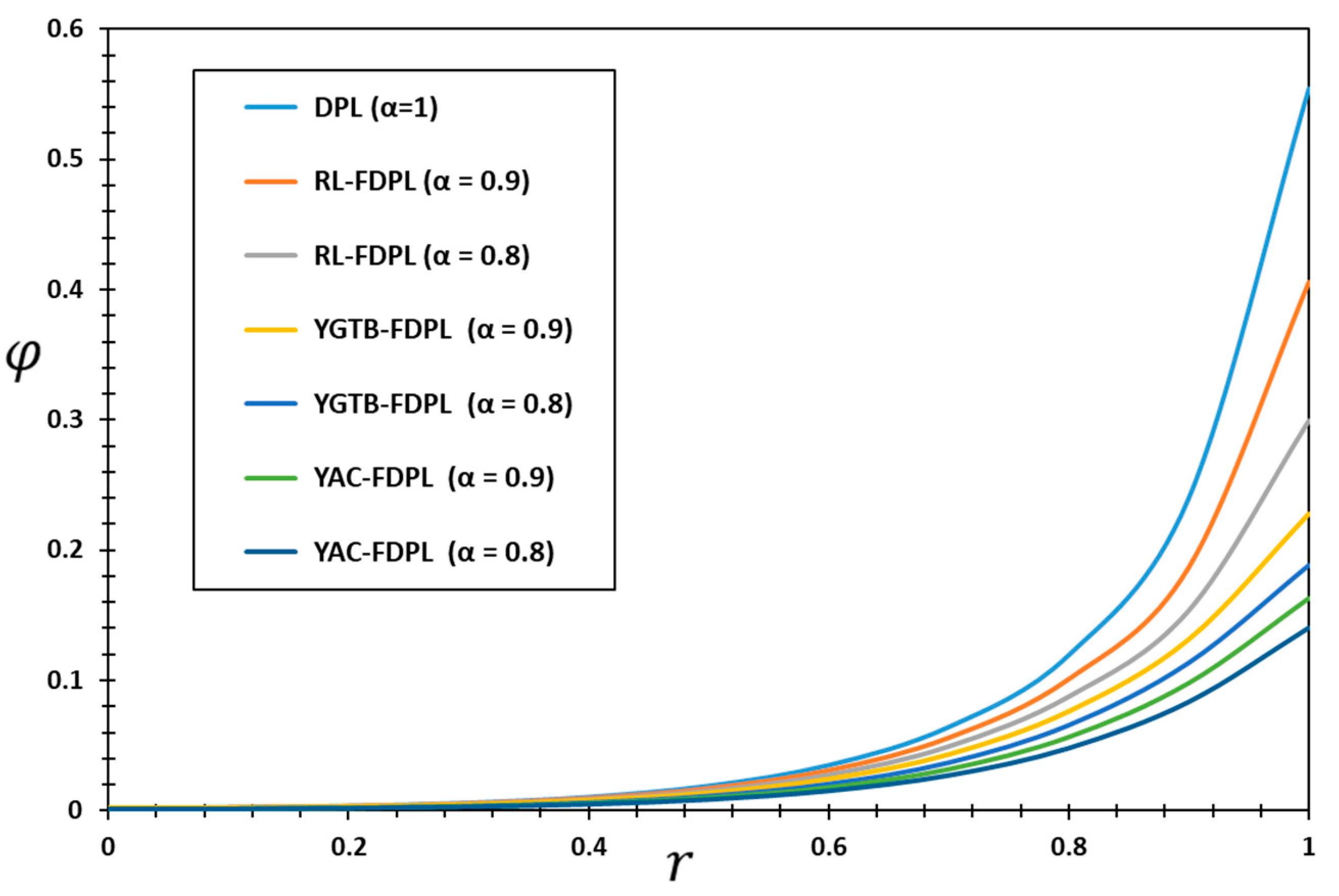
It is evident from
Figure 2 and
Figure 3 that the type of differential operator
and the values of the fractional order
have a significant impact on the thermodynamic and conductivity temperatures (
and
). It is also clear that the surface of the cylinder (
) experiences the largest values of the two temperatures, which then gradually decrease as they penetrate the body. The reason for this phenomenon is the constraint imposed by the fractal order
and delay phase times (
and
) on the finite speed of heat wave propagation. On the contrary, the heat transfer equations in the case of conventional models that do not use fractional differentiation may provide an impractical result for infinite speeds of heat wave propagation. Researchers often ignore this. However, this may lead to inaccurate or impractical predictions of thermal performance in actual systems.
The figures clearly indicate that the temperature values produced using the RL operator are greater than those obtained using the fractional YGTB and YAC operators. The use of fractional differential operators (YGTB and YAC) in heat transfer models can address this limitation by providing a finite rate of heat wave propagation, which is dictated by the fractional order
. Ultimately, this could lead to enhanced accuracy and authenticity when predicting thermodynamics in complex systems, such as those in biological tissues and other materials that exhibit memory properties, such as viscous materials [
52].
As a result of their ability to circumvent the singularity issues that are typically associated with conventional fractional derivative definitions, non-singular kernels are an essential component in the study of fractional calculus. Two examples of non-singular kernels that have been utilized in the study of fractional differential equations are the sinc function and the Rabotnov fractional–exponential function [
53].
As shown in
Figure 2,
Figure 3 and
Figure 4, the existence of a heat source inhibits the zeroing of all fields under consideration, except for displacement, as distance increases. When a heat source is absent, all physical fields within a bounded region of space have non-zero values. However, beyond this region, the fields vanish indistinguishably, illustrating the finite speed of the propagation phenomenon.
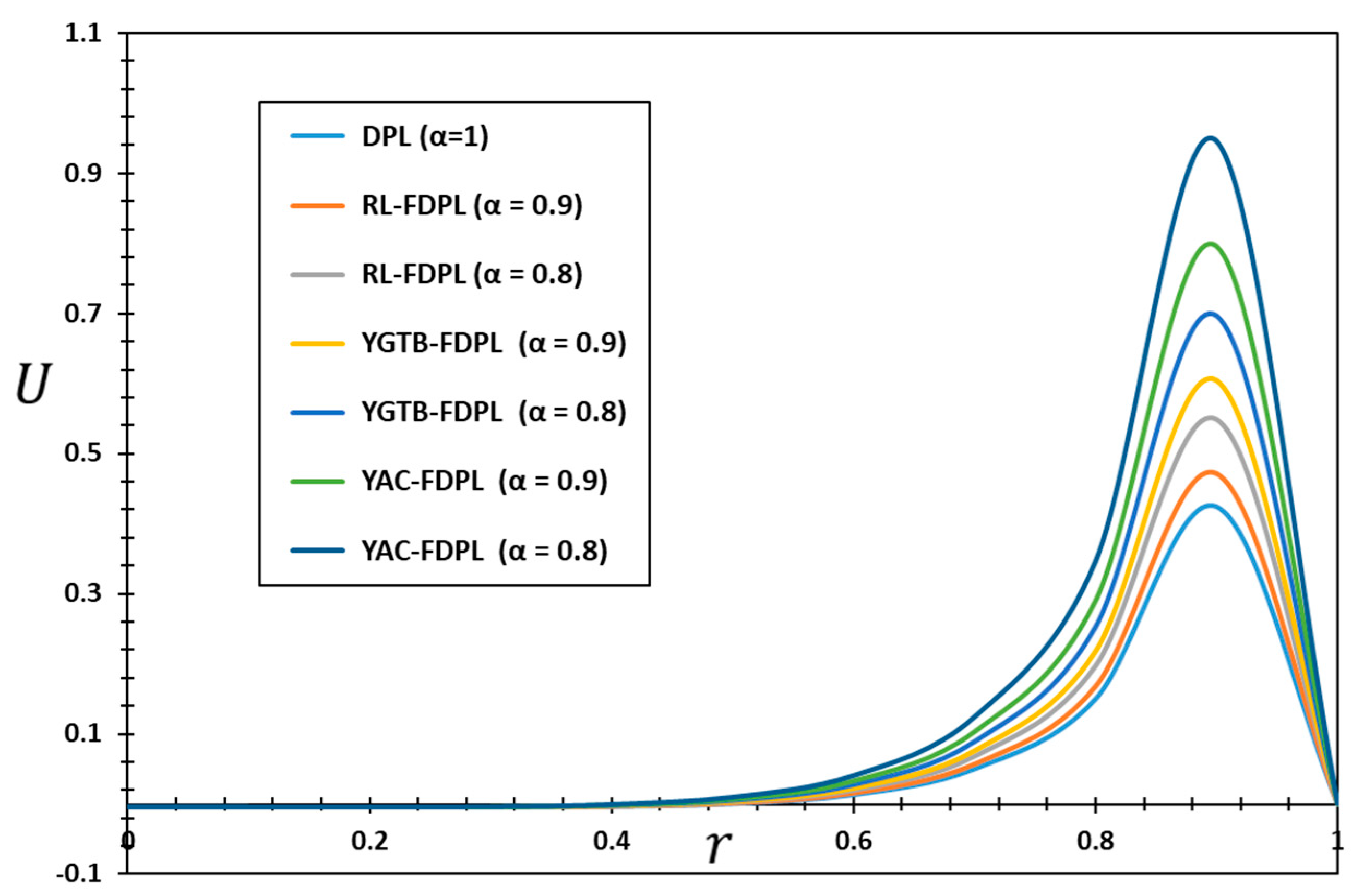
Figure 4 illustrates the impact of the fractional differential parameter
on the distribution of displacement
. As the distance between the two locations within the cylinder grows, the numerical values of
progressively drop until they hit zero. The figure demonstrates that increasing the values of
results in a corresponding rise in the displacement values. This correlation may be attributed to the periodic variations in the heat source throughout time. The displacement values
on the cylinder surface are always recorded as zero where the boundary condition is met, which confirms the reliability and accuracy of the numerical results and the computational technique used.
Figure 2 demonstrates that the fractional YAC thermoelastic model yields the smallest absolute displacement values, whereas the standard fractional RL thermoelastic model yields the largest absolute displacement values. These findings indicate that the fractional YAC thermoelastic model is better suited for accurately representing the system’s behavior since it yields more realistic and meaningful outcomes. Nevertheless, further examination and juxtaposition with empirical data are imperative to validate the superiority of the fractional YAC thermoelastic model in relation to other fractional models.
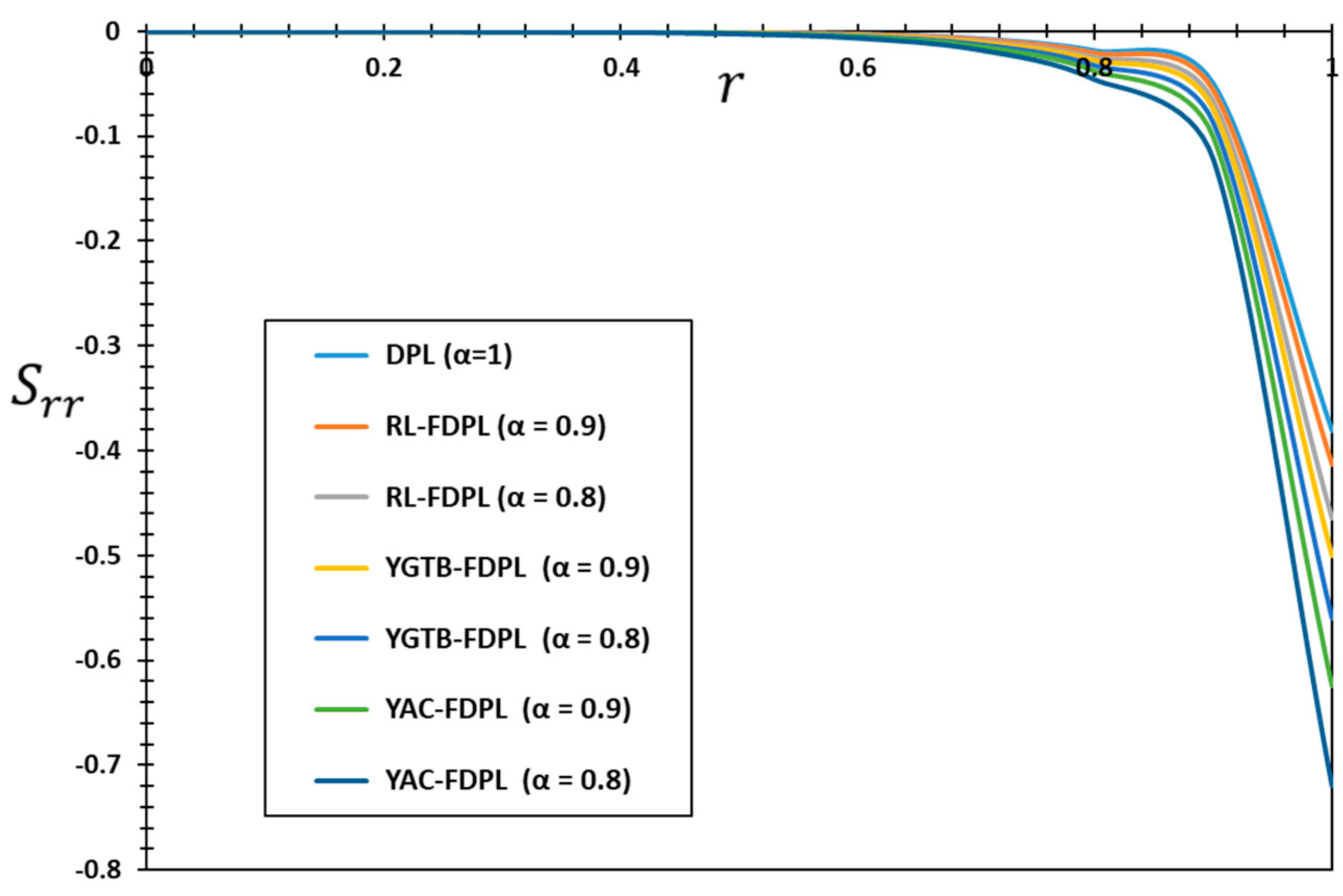
The numerical values in
Figure 5 and
Figure 6 show that the fractional differentiation parameter
and different fractional operators (RL, YGTB, and YAC) have a significant influence on how the radial stress
and hoop stress
propagate. The numerical values in the figures show how differences in the values of the fractional-order parameters affect the magnitudes of the thermal stresses (
and
). Depending on the type of fractional torch, pressures are likely to decrease in volume or grow in volume. The numerical results also show that large pressure values occur near the cylinder surface in the turbulent region. These pressures rapidly increase in magnitude away from the surface of the cylinder and then gradually decrease again until they completely disappear inside the elastic body.
It is also observed that thermal stresses always behave in a compressive manner near the cylinder surface in the turbulence region. In addition, it can be concluded that if fractional differentiation is included in the thermal conduction equation, the propagation of mechanical waves is reduced, consistent with physical evidence. This may be because fractional differentiation allows for the introduction of memory and genetic influences, both of which have an impact on the geographical and temporal distribution of thermal stresses. As values of the order of the fractional differential decrease, mechanical waves travel at a slower rate and may have a shorter wavelength as a result, leading to a decrease in the propagation of mechanical waves.
The effect of the parameter and fractional operators
on the fluctuation in Maxwell stress
is shown in
Figure 7 with the change in position inside the cylinder. The figure shows that the tension decreases rapidly as the distance between them increases and shows that the action of the magnetic field is immediate and limited. Furthermore, the figure provides evidence that the fractional parameter
affects the Maxwell stress in a relatively small way. In addition, comparing the appearance and absence of fractional operators reveals the numerical values of Maxwell stresses that grow and decrease, as well as the behavior of these values. This study shows that fractional factors (
) have a significant impact on how the Maxwell stress is distributed, especially near the cylinder surface, where the variable heat source flows.
Since they can more precisely measure fractional exchanges such as thermoelasticity, fluidity, etc., new fractional derivatives can be very useful for studying the large-scale behavior of many different types of elastic materials, both simple and non-simple. This work also makes a significant contribution to the study of the finite-time propagation of thermal waves because it has implications for modern aerodynamic engineering, which uses thermoplastic cylinders. Fractional derivations are a unique technique that can help better understand the behavior of heat waves in real-world applications. The modified heat conduction equation in the suggested model can accomplish this by incorporating phase delays [
54,
55]. In the field of aerospace engineering, this can have major implications for the design and optimization of thermo- and viscoelastic cylinders, as well as other materials. In general, the results of this research work can provide a great addition to the topic of fractional calculus and applications of this type in the fields of engineering design and physics.
When studying fractional calculus, non-singular kernels are very important because they help avoid the problems that arise with singularities that happen with standard definitions of fractional derivatives. Various diverse non-singular kernels have been employed to investigate fractional thermophysical models. Two instances include the sinc function and the Rabotnov fractional–exponential function
. We think that the YGTB- and YAC-modified fractional operators could be a good alternative to regular fractional operators and derivatives when it comes to modeling complex physical problems. This is because they are able to simulate the behavior of the problem. These fractional operators are intriguing as they are defined using the normalized sinc function and the Rabotnov exponential function, both of which do not have a singular kernel [
56]. On the other hand, further study is required in order to gain a comprehensive understanding of the benefits and drawbacks associated with these operators and to ascertain the most appropriate strategy for certain applications.