Abstract
In this article, we analyzed the time fractional higher-dimensional nonlinear modified model of wave propagation, namely the (3 + 1)-dimensional Benjamin–Bona–Mahony-type equation. The fractional sense was defined by the classical Riemann–Liouville fractional derivative. We derived firstly the existence of symmetry of the time fractional higher-dimensional equation. Next, we constructed the one-dimensional optimal system to the time fractional higher-dimensional nonlinear modified model of wave propagation. Subsequently, it was reduced into the lower-dimensional fractional differential equation. Meanwhile, on the basis of the reduced equation, we obtained its similarity solution. Through a series of analyses of the time fractional high-dimensional model and the results of the above obtained, we can gain a further understanding of its essence.
1. Introduction
It is known that differential equations originated from the real natural life, such as the RLC circuit model [1], population model [2], realistic ecological model [3], KdV model [4], diffusion type model [5], etc. By analyzing these models, we can better understand, comprehend, and utilize them. Meanwhile, since the higher-dimensional nonlinear models contain more spatial dimensions and z, they contain more information for the natural world. As a result, the nonlinear higher-dimensional models is one of the important topics in the field of mathematical physics. On the basis of the above idea, A.M. Wazwaz [6] derived five categories of Benjamin–Bona–Mahony-type equations of wave propagation and fluids, and obtained their exact solutions, such as the soliton, kink, and periodic solutions. At the same time, there is another type of fractional derivative that appears at the same time as integer order. We known that the fractional derivative is used to describe the complex nonlinear mechanism. There exist many different fractional derivative definitions, such as the Riemann–Liouville fractional derivative [7,8], Caputo fractional derivative [7,8], general fractional derivative [9], He’s fractional derivative [10], etc. They have been widely used in diffusion processes in solids, biological media, and fractal media [11]. Here, we considered one of the five categories of the following form:
where:
is the Riemann–Liouville fractional derivative. A.R. Seadawy et al. [12] obtained the periodic wave and kink wave of Equation (1). Liu et al. [13] studied the dynamical behavior of the traveling systems and deep neural network. S. Muhammad et al. [14] derived the diversity of soliton solutions of Equation (1). B. Muhammad et al. [15,16] found many solitary waves solutions by using the analytical method.
Due to the more detailed characterization of real life by fractional derivatives and the fact that high-dimensional nonlinear models contain more information, the main motivation of this paper is to explore the mechanism of water wave propagation by studying the high-dimensional model. The research results will fill the gap in the water wave theory in this regard. The aims of this article are to apply the symmetry scheme to investigate the time fractional higher-dimensional nonlinear modified equation of wave propagation (1). As a direct result, a series of new results were obtained. The fractional symmetry analysis scheme is an effective tool to deal with fractional differential equations, specifically the higher-dimensional nonlinear models [17,18,19,20,21,22,23,24]. For example, Adeyemo et al. [17] studied the time fractional (3 + 1)-dimensional generalized Zakharov-Kuznetsov equation type I, Liu et al. [18,19,20,21] researched the higher-dimensional KdV-type equation, dissipation Burgers equation, and diffusion equation, Sahoo et al. [22] discussed the (3 + 1)-dimensional time-fractional mKdV-ZK equation, and Zhuo et al. [23] analyzed the generalized (4 + 1)-dimensional time-fractional Fokas equation, Zhu et al. [24] considered the time-fractional (2 + 1)-dimensional Hirota-Satsuma-Ito equations. Therefore, we hope to find more novel results through this effective tool, laying the foundation for our deeper understanding of this model.
The compositions of this article as follows: the symmetries of Equation (1) through the symmetry scheme are derived in Section 2. In Section 3 and Section 4, we discuss, respectively, the one-dimensional optimal system and one-parameter Lie transformation group of Equation (1). With the help of the Erdélyi–Kober fractional operators, Equation (1) is reduced into the lower fractional differential equation in Section 5. Then, the similarity solution of the reduced equation is found. The conclusions and discussions of the entire text and future prospects are presented in Section 6.
2. Symmetry Scheme of Equation (1)
In the first place, the symmetries of the time fractional higher-dimensional nonlinear modified equation of wave propagation (1) were obtained. As a direct conclusion, we have Theorem 1.
Theorem 1.
The time fractional higher-dimensional nonlinear modified equation of wave propagation (1) has the infinitesimal generators of the forms:
Proof.
It is assumed that Equation (1) is invariant under a one-parameter Lie transformation group as follows:
where is an infinitesimal parameter.
In detail:
where , and are total derivatives [25,26].
At the same time, it is supposed that Equation (1) has the following general infinitesimal generator:
Utilizing the infinitesimal invariance criterion [11,12,13,14,15,16,17,18,19,20], one has:
where is the prolongation of X and:
For Equation (1), it can be written as:
Applying the invariance condition (4) to Equation (1), we can obtain the symmetry determining equation as follows:
where the -extended infinitesimal [17,18,19,20,21,22,23,24] is:
with:
Inserting the Equations (7) and (2) into Equation (6) and collecting the coefficients of different powers of u to zero, we have:
where are arbitrary parameters.
In addition, the constraint condition to hold the Riemann–Liouville fractional derivative structure. We get .
It can be spanned by the following four vector fields:
This concludes the proof. □
The above four vector fields (10) can construct a closed Lie algebra. Their commutation relationships can be found in Table 1.

Table 1.
The commutation table of Lie algebra.
3. Optimal System of Equation (1)
In order to reduce the original equation as much as possible and construct the exact solutions, we need to find the one-dimensional optimal system of Equation (1). With the help of the Lie series [25,26], the action of the adjoint operator can given by:
where is Lie bracket and is a constant.
Specifically:
The adjoint actions of the infinitesimal generators (10) are seen as Table 2.

Table 2.
The adjoint representation of infinitesimal generators (10).
Hence, we have the following result of the one-dimensional optimal system of Equation (1).
Theorem 2.
An optimal system of one-dimensional Lie subalgebras operators (10) to Equation (1) can be spanned by:
where are not all zero.
The simple proof process of this Theorem 2 can be found in references [25,26]. Here, we omit it.
Remark 1.
If making linear operator , then the Killing form is It can be seen that the value is conform to Equation (1) of integer order for the Killing form . That is to say, fractional differential equations have a wider research domain.
4. One-Parameter Lie Transformation Group of Equation (1)
In this subsection, we derived the one-parameter Lie transformation group [25,26] of Equation (1). It keep the solution set unchanged or transform the solution into a solution to differential equations. Hence, we may obtain new solutions from the known ones of this considered model.
In addition to constructing the one-parameter Lie transformation group, we solved the following initial problems [25,26]:
where is a small parameter.
Solving the above system (13) with vector fields (10), we can obtain the one-parameter Lie transformation groups of the forms:
As a result, we obtained Theorem 3.
Theorem 3.
If is an exact solution of the time fractional higher-dimensional nonlinear modified equation of wave propagation (1), then:
are also solutions to Equation (1).
Remark 2.
It is can be seen that the Lie transformation group , , and are invariant on spaces x, y, and z. The well known scaling symmetry action is .
5. Similarity Reduction and Similarity Solution of Equation (1)
In this section, we reduce Equation (1) into the lower dimensional fractional differential equation with the Erdélyi–Kober fractional operators [27]. In addition, we obtained the similarity solution of the reduced equation.
5.1. Similarity Reduction of Equation (1)
Case 1.
From , Equation (1) was reduced into the following form.
Theorem 4.
The similarity variables and group invariant solution were used to reduce Equation (1) into the following result:
where the represents the three parameters Erdélyi–Kober fractional differential operator [27]
where:
is the three parameters Erdélyi–Kober fractional integral operator [27].
Proof.
For , it has the characteristic equation of the form:
Solving characteristic Equation (16), we obtained, respectively, the similarity variables and group invariant solution:
and
Next, for the Riemann–Liouville fractional derivative definition, we have:
If considering , then expression (19) becomes:
Meanwhile, we note the following fact:
Hence, Equation (20) can be further reduced into the following form:
In summary, Equation (1) was reduced into the following form:
Proving the theorem. □
Case 2.
Similar to Case 1, Equation (1) easily was reduced into the following expression:
For Equation (24), the infinitesimal generators can be obtained through the fractional Lie group scheme:
Similarity, the infinitesimal generators (25) were used to reduce Equation (24) as Theorem 4 processes. Here, we ignore it.
Case 3.
Similar to Case 1, Equation (1) can be reduced into the following form:
If Theorem 1 processes are performed, then the infinitesimal generators are as follows:
Similarly, the infinitesimal generators (27) were used to reduce Equation (26). Here, we ignore it.
Case 4.
Similar to Case 1, Equation (1) can be reduced into the following form
If perform Theorem 1 processes, then we have
Similarity, the infinitesimal generators (29) were used to reduce Equation (27) as Theorem 4 processes. Here we ignore it.
Case 5.
In a similar way, Equation (1) was reduced into the following form:
It is easy to find an exact solution as follows:
where c is a free constant.
Taking the values , , , and into rational solution (31), Figure 1 was plotted.
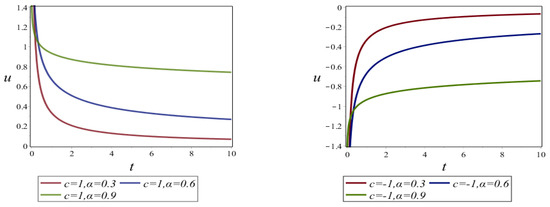
Figure 1.
Plots of evolution of rational solution (31) with the above parameter values.
Case 6.
Case 7.
In a similar way, Equation (1) was reduced into the following form:
This is known as the one-dimensional linear Burger equation.
Case 8.
5.2. Similarity Solution of Equation (24)
In this subsection, we proved firstly the reduced Equation (24) existence the similarity solution. Then, we presented specific expressions of similar solution.
It is supposed that Equation (24) is invariant under the following scaling transformation:
where p and q are arbitrary parameters to be determined later.
Inserting transformations (33) into Equation (24), we have:
which implies that:
has similarity solution.
We can use the following to find traveling wave similarity solution for Equation (24).
Let the similarity transformation be as follows:
where p, q, and c are arbitrary parameters to be determined later.
According to the definition of the Riemann–Liouville, one has:
Let , then Equation (37) becomes:
Furthermore:
Thereby, Equation (40) becomes the following ordinary differential equation of fractional order:
Now, we consider that Equation (42) has the special solutions of the following form:
Inserting the comparison expressions (45) and (41) into Equation (44), we have:
Conversely:
Therefore, we obtained the traveling wave similarity solution of Equation (24) of the form:
6. Conclusions and Discussion
In this paper, we studied the time fractional higher-dimensional nonlinear modified equation of wave propagation. As a result of obtaining novelty, the symmetries, one-dimensional optimal system, and one-parameter Lie transformation group of this considered model were derived. Next, the original Equation (1) carried out the similarity reduction of the lower differential equation. On the basis of the reduced equation, we constructed a similarity solution. Although the similarity solutions have been obtained for the reduced model, it is still difficult to seek other types of exact solutions, such as the soliton solutions, rational solutions, and Kink solutions. Therefore, how to obtain the exact solutions of the reduced equation is one of our future key tasks. Finally, these beautiful results can help us discover more evolutionary mechanisms of this considered model.
Author Contributions
Methodology, J.-G.L. formal analysis, J.-G.L. and Y.-Y.F.; writing original draft preparation, J.-G.L.; writing review and editing, J.-G.L. and Y.-Y.F.; funding acquisition, J.-G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (No. 11971475), the Natural Science Foundation of Jiangsu Province (No. BK20230708), and the Natural Science Foundation for the Universities in Jiangsu Province (No. 23KJB110003).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors are grateful to the anonymous referees for their useful comments and suggestions.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Atangana, A.; Nieto, J.J. Numerical solution for the model of RLC circuit via the fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7, 1687814015613758. [Google Scholar] [CrossRef]
- Schaub, M.; Abadi, F. Integrated population models: A novel analysis framework for deeper insights into population dynamics. J. Ornithol. 2011, 152, 227–237. [Google Scholar] [CrossRef]
- Letellier, C.; Aziz-Alaoui, M.A. Analysis of the dynamics of a realistic ecological model. Chaos Solitons Fractals 2002, 13, 95–107. [Google Scholar] [CrossRef]
- Lax, P.D. Periodic solutions of the KdV equation. Commun. Pure Appl. Math. 1975, 28, 141–188. [Google Scholar] [CrossRef]
- Caraballo Garrido, T.; Ngoc, T.B.; Thach, T.N.; Tuan, N.H. On initial value and terminal value problems for subdiffusive stochastic Rayleigh-Stokes equation. Discret. Contin. Dyn. Syst. Ser. B 2020, 26, 4299–4323. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. Exact soliton and kink solutions for new (3 + 1)-dimensional nonlinear modified equations of wave propagation. Open Eng. 2017, 7, 169–174. [Google Scholar] [CrossRef]
- Samko, S.; Kilbas, A.A.; Marichev, O. Fractional Integral and Derivatives: Theory and Applications; Gordon and Breach Science: Yverdon, Switzerland, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Yang, X.J. General Fractional Derivatives: Theory, Methods and Applications; CRC Press: New York, NY, USA, 2019. [Google Scholar]
- Wang, K.-J. A fractal modification of the unsteady Korteweg–de Vries model and its generalized fractal variational principle and diverse exact solutions. Fractals 2022, 30, 2250192. [Google Scholar] [CrossRef]
- Henry, B.I.; Langlands, T.A.; Straka, P. An introduction to fractional diffusion. Complex Phys. Biophys. Econophys. Syst. 2010, 9, 37–89. [Google Scholar]
- Seadawy, A.R.; Ali, K.K.; Nuruddeen, R.I. Avariety of soliton solutions for the fractional Wazwaz-Benjamin-Bona-Mahony equations. Results Phys. 2019, 12, 2234–2241. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, Y.; Li, K.; Zhang, S. Application of the dynamical system method and the deep learning method to solve the new (3 + 1)-dimensional fractional modified Benjamin-Bona-Mahony equation. Nonlinear Dyn. 2022, 110, 3737–3750. [Google Scholar] [CrossRef]
- Shakeel, M.; Turki, N.B.; Shah, N.A.; Tag, S.M. Diversity of Soliton Solutions to the (3 + 1)-Dimensional Wazwaz-Benjamin-Bona-Mahony Equations Arising in Mathematical Physics. Results Phys. 2023, 51, 106624. [Google Scholar] [CrossRef]
- Bilal, M.; Younas, U.; Baskonus, H.M.; Younis, M. Investigation of shallow water waves and solitary waves to the conformable 3D-WBBM model by an analytical method. Phys. Lett. A 2021, 403, 127388. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Inc, M.; Baleanu, D. New solitary wave solutions for variants of (3 + 1)-dimensional Wazwaz-Benjamin-Bona-Mahony equations. Front. Phys. 2020, 8, 332. [Google Scholar] [CrossRef]
- Adeyemo, O.D.; Zhang, L.; Khalique, C.M. Optimal solutions of Lie subalgebra, dynamical system, travelling wave solutions and conserved currents of (3 + 1)-dimensional generalized Zakharov-Kuznetsov equation type I. Eur. Phys. J. Plus 2022, 137, 954. [Google Scholar] [CrossRef]
- Liu, J.-G.; Zhang, Y.-F.; Wang, J.-J. Investigation of the time fractional generalized (2 + 1)-dimensional Zakharov-Kuznetsov equation with single-power law nonlinearity. Fractals 2023, 31, 2350033. [Google Scholar] [CrossRef]
- Liu, J.-G.; Yang, X.-J.; Feng, Y.-Y.; Cui, P.; Geng, L.-L. On integrability of the higher-dimensional time fractional KdV-type equation. J. Geom. Phys. 2021, 160, 104000. [Google Scholar] [CrossRef]
- Liu, J.-G.; Yang, X.-J.; Geng, L.-L.; Yu, X.-J. On fractional symmetry group scheme to the higher dimensional space and time fractional dissipative Burgers equation. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250173. [Google Scholar] [CrossRef]
- Liu, J.-G.; Geng, F.-Z.; Li, X. Supplement a high-dimensional time fractional diffusion equation. Alex. Eng. J. 2023, 15, 459–464. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S. Analysis of Lie symmetries with conservation laws for the (3+1) dimensional time-fractional mKdV-ZK equation in ion-acoustic waves. Nonlinear Dyn. 2017, 90, 1105–1113. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, Z.G.; Li, J.J.; Yang, H.W. Analysis of Lie symmetries with conservation laws and solutions of generalized (4 + 1)-dimensional time-fractional Fokas equation. Fractal Fract. 2022, 6, 108. [Google Scholar] [CrossRef]
- Zhu, H.-M.; Zhang, Z.-Y.; Zheng, J. The time-fractional (2 + 1)-dimensional Hirota-Satsuma-Ito equations: Lie symmetries, power series solutions and conservation laws. Commun. Nonlinear Sci. Numer. Simul. 2022, 115, 106724. [Google Scholar] [CrossRef]
- Bluman, G.W.; Anco, S. Symmetry and Integration Methods for Differential Equations; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Kiryakova, V.S. Generalized Fractional Calculus and Applications; Longman Scientific & Technical, Longman Group: Harlow, UK, 1994. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).