Analysis of Pore Characterization and Energy Evolution of Granite by Microwave Radiation
Abstract
1. Introduction
2. Experimental Equipment
3. Analysis of Results
4. Based on NMR Porosity Analysis
4.1. Effect of Microwaves on Granite Porosity
4.2. Porosity Fractal Characterization
4.3. Microwave Deterioration Damage Model
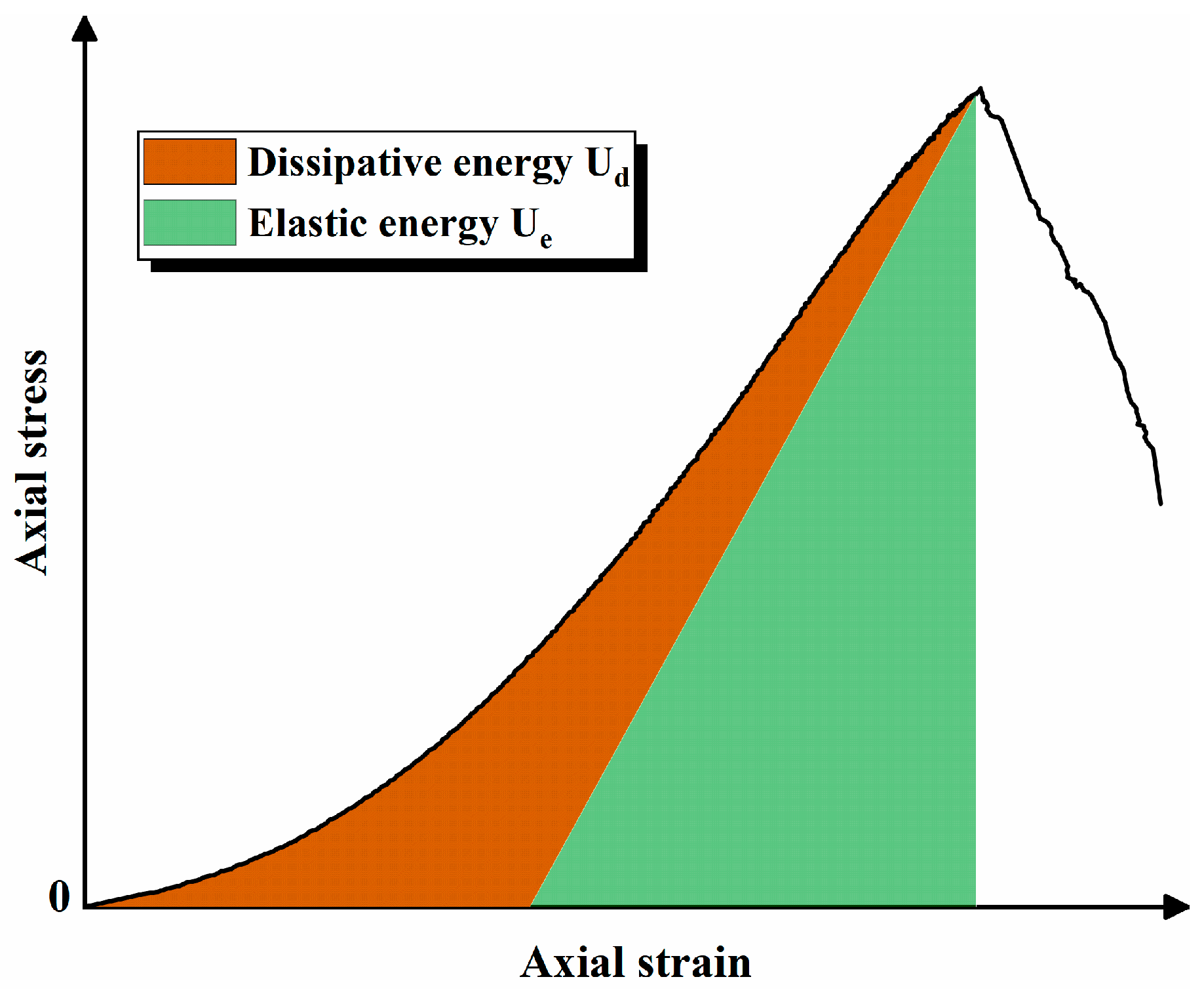
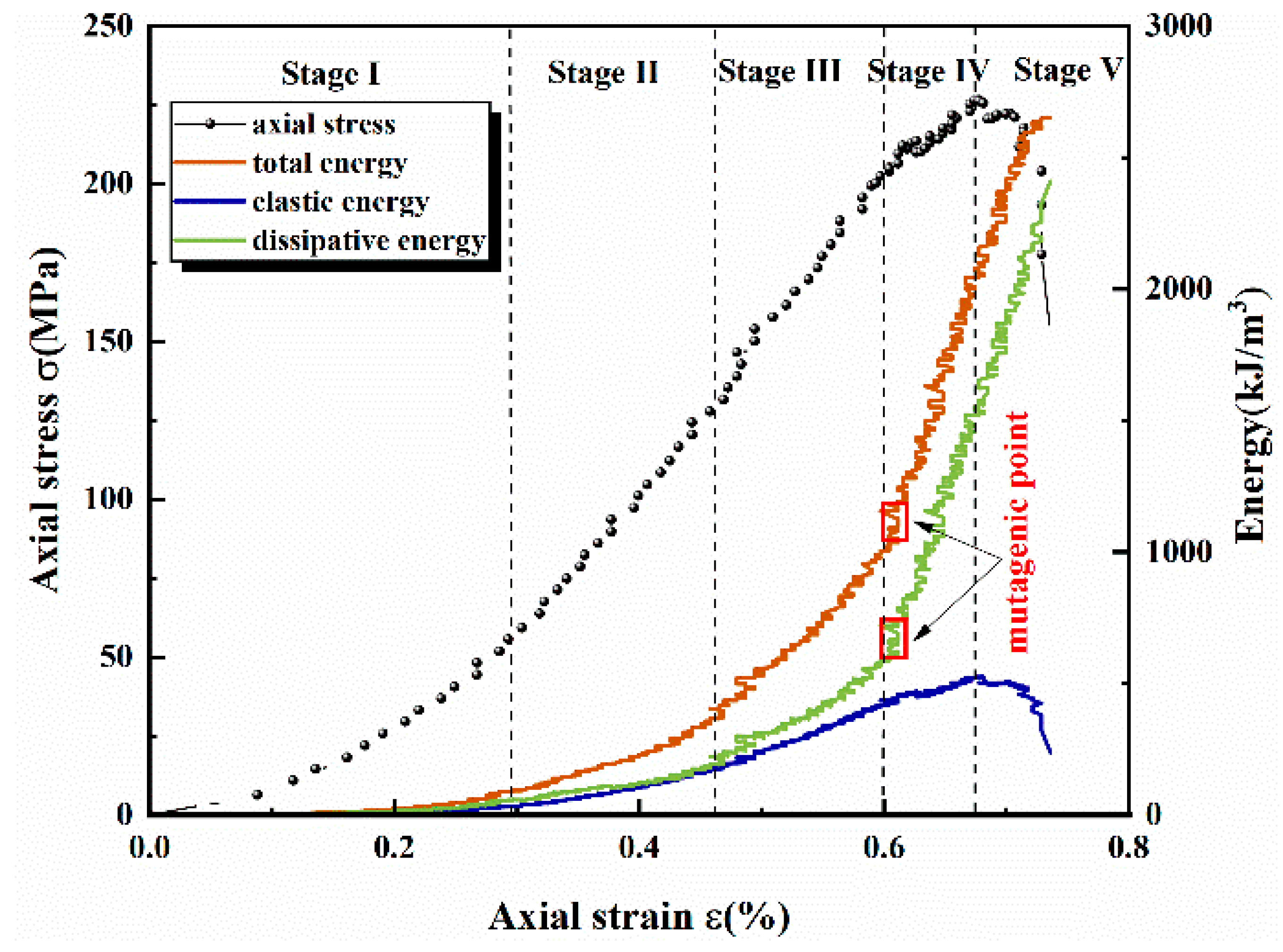
5. Energy Evolution Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.C.; Jiang, F.X.; Meng, X.J.; Wang, X.Y.; Zhu, S.T.; Feng, Y. Mechanism of Rock Burst Occurrence in Specially Thick Coal Seam with Rock Parting. Rock Mech. Rock Eng. 2016, 49, 1953–1965. [Google Scholar] [CrossRef]
- Lu, G.M.; Li, Y.H.; Hassani, F.; Zhang, X.W. Review of theoretical and experimental studies on mechanical rock fragmentation using microwave-assisted approach. Chin. J. Geotech. Eng. 2016, 38, 1497–1506. [Google Scholar]
- Yang, C.; Hassani, F.; Zhou, K.P.; Zhang, Q.; Wang, F.M.; Gao, F.; Topa, A. Numerical investigation of TBM disc cutter cutting on microwave-treated basalt with an unrelieved model. Arch. Civ. Mech. Eng. 2020, 22, 147. [Google Scholar] [CrossRef]
- Yang, C.; Hassani, F.; Zhou, K.P.; Xiong, X.; Wang, F.M.; Shao, Y. Effect of microwave treatment on the thermal properties and dynamic splitting behavior of red sandstone. Can. Geotech. J. 2022, 59, 1231–1242. [Google Scholar] [CrossRef]
- Yang, C.; Hassani, F.; Zhou, K.P.; Gao, F.; Topa, A. SPH-FEM simulations of microwave-treated basalt strength. Trans. Nonferrous Met. Soc. China. 2022, 32, 2003–2018. [Google Scholar] [CrossRef]
- Ma, Z.J.; Zheng, Y.L.; Zhao, X.B.; Li, J.C. Microwave-assisted hard rock breakage by impact hammers: Heating, fracturing and mechanical breakage. Bull. Assoc. Int. Geol. Ing. Environ. 2022, 81, 308. [Google Scholar] [CrossRef]
- Feng, X.T.; Li, S.P.; Yang, C.X.; Lin, F.; Tong, T.Y.; Su, X.X.; Zhang, J.Y. The Influence of the Rotary Speed of a Microwave Applicator on Hard-Rock Fracturing Effect. Rock Mech. Rock Eng. 2022, 55, 6963–6979. [Google Scholar] [CrossRef]
- Zou, C.J.; Quan, X.; Ma, Z.J.; Zheng, Y.L.; Zhao, X.B.; Li, J.C.; Zhao, J. Dynamic Strength and Indentation Hardness of a Hard Rock Treated by Microwave and the Influence on Excavation Rate. Rock Mech. Rock Eng. 2023, 56, 4535–4555. [Google Scholar] [CrossRef]
- Zhao, Q.H.; Zhao, X.B.; Zheng, Y.L.; Li, J.C.; He, L.; Zou, C.J. Microwave fracturing of water-bearing sandstones: Heating characteristics and bursting. Int. J. Rock Mech. Min. Sci. 2021, 136, 104495. [Google Scholar] [CrossRef]
- Zhao, Q.H.; Zhao, X.B.; Zheng, Y.L.; Li, J.C.; He, L.; Zou, C.J. Heating characteristics of igneous rock-forming minerals under microwave irradiation. Int. J. Rock Mech. Min. Sci. 2020, 135, 104519. [Google Scholar] [CrossRef]
- Gao, F.; He, Y.D.; Xiong, X.; Zhou, K.P.; Yang, C. Effect of strong dielectric substances on the damage characteristics of rocks exposed to microwave radiation: Insight from experiments and mechanisms. Int. J. Damage Mech. 2023, 32, 849–871. [Google Scholar] [CrossRef]
- Cheng, S.T. Study on the Influence of Heating Method on Thermal Induced Damage of Granite; Beijing University of Technology: Beijing, China, 2020. [Google Scholar]
- Gao, F.; Shao, Y.; Xiong, X.; Zhou, K.P.; Cao, S.P. Rising characteristics of internal and external temperatures of rock specimens under different microwave irradiation modes. Chin. J. Geotech. Eng. 2020, 42, 650–657. [Google Scholar]
- Xu, S.L. Experimental Research on Damage Characteristics of Basalt by Microwave Cyclic Irradiation; Xi’an University of Science and Technology: Xi’an, China, 2019. [Google Scholar]
- Yang, J.M.; Liu, J.T.; Guo, H.C.; Li, Q.M.; Wang, W. Effect of microwave heating on the mechanical properties and energy dissipation characteristics of hard rock. Environ. Earth Sci. 2022, 81, 415. [Google Scholar] [CrossRef]
- Tang, M.Y.; Gao, M.Z.; Li, S.W.; Yang, B.G.; Tang, R.F.; Li, F.; Liu, J.J. Failure behavior and energy evolution characteristics of deep roadway sandstone under different microwave irradiation modes. J. Cent. South Univ. 2023, 30, 214–226. [Google Scholar] [CrossRef]
- Hassani, F.; Shadi, A.; Rafezi, H.; Sasmito, A.P.; Ghoreishi-Madiseh, S.A. Energy analysis of the effectiveness of microwave-assisted fragmentation. Miner. Eng. 2020, 159, 106642. [Google Scholar] [CrossRef]
- Pressacco, M.; Kangas, J.J.; Saksala, T. Numerical Modelling of Microwave Heating Assisted Rock Fracture. Rock Mech. Rock Eng. 2022, 55, 481–503. [Google Scholar] [CrossRef]
- Pressacco, M.; Kangas, J.J.; Saksala, T. Numerical modelling of microwave irradiated rock fracture. Miner. Eng. 2023, 203, 108318. [Google Scholar] [CrossRef]
- Zhao, X.B.; Zhao, Q.H.; Zheng, Y.L.; He, L.; He, J.L.; Zhao, G.F.; Li, H. Cracking Behavior and Mechanism of Igneous Rocks Under Open-Ended Microwave Irradiation. Rock Mech. Rock Eng. 2022, 55, 6151–6169. [Google Scholar] [CrossRef]
- Rui, F.X.; Zhao, G.F.; Zhang, Y.L.; Fan, L.F.; Zhao, X.B. Study on the Mechanism of Rock Damage Under Microwave and Laser Irradiation Through Multiscale and Multiphysics Numerical Modelling. Rock Mech. Rock Eng. 2023, 57, 1079–1102. [Google Scholar] [CrossRef]
- Lu, G.M.; Li, Y.H.; Hassani, F.; Zhang, X.W. The influence of microwave irradiation on thermal properties of main rock-forming minerals. Appl. Therm. Eng. 2017, 112, 1523–1532. [Google Scholar] [CrossRef]
- Tian, J.; Lu, G.M.; Feng, X.T.; Li, Y.H.; Zhang, X.W. Experimental study of the microwave sensitivity of main rock-forming mineral. Rock Soil Mech. 2019, 40, 2066–2074. [Google Scholar]
- Hartlieb, P.; Toifl, M.; Kuchar, F.; Meisels, R.; Antretter, T. Thermo-physical properties of selected hard rocks and their relation to microwave-assisted comminution. Miner. Eng. 2016, 91, 34–41. [Google Scholar] [CrossRef]
- Lu, G.M.; Feng, X.T.; Li, Y.H.; Hassani, F.; Zhang, X.W. Experimental Investigation on the Effects of Microwave Treatment on Basalt Heating, Mechanical Strength, and Fragmentation. Rock Mech. Rock Eng. 2019, 52, 2535–2549. [Google Scholar] [CrossRef]
- Wang, H.C.; Rezaee, R.; Saeedi, A. Preliminary study of improving reservoir quality of tight gas sands in the near wellbore region by microwave heating. J. Nat. Gas Sci. Eng. 2016, 32, 395–406. [Google Scholar] [CrossRef]
- Bilali, L.; Benchanaa, A.; El, H.K.; Mokhlisse, A.; Outzourhit, A. A detailed study of the microwave pyrolysis of the Moroccan (Youssoufia) rock phosphate. J. Anal. Appl. Pyrolysis 2005, 73, 1–15. [Google Scholar] [CrossRef]
- Yao, J.H.; Tao, M.; Zhao, R.; Hashemi, S.S.; Wamg, Y.Q. Effect of microwave treatment on thermal properties and structural degradation of red sandstone in rock excavation. Miner. Eng. 2021, 162, 106730. [Google Scholar] [CrossRef]
- Li, X.B.; Wu, Y.C.; Li, Q.; Yin, T.B.; Huang, L.Q. Quantification of thermal damage and dynamic tensile behaviors of hard rock under microwave irradiation: An experimental investigation. Bull. Eng. Geol. Environ. 2022, 81, 461. [Google Scholar] [CrossRef]
- Ding, R.; Sun, Q.; Geng, J.S.; Luo, T.; Yuan, S.H. Porosity and mechanical strength of microwave-heated gabbro. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 196. [Google Scholar] [CrossRef]
- Li, J.L.; Zhu, L.Y.; Zhou, K.P.; Liu, H.W.; Cao, S.P. Damage characteristics of sandstone pore structure under freeze-cycles. Rock Soil Mech. 2019, 40, 3524–3532. [Google Scholar]
- Pan, Z.; Zhou, K.P.; Gao, R.G.; Jiang, Z.; Yang, C.; Gao, F. Research on the Pore Evolution of Sandstone in Cold Regions under Freeze-Thaw Weathering Cycles Based on NMR. Geofluids 2020, 2020, 884944. [Google Scholar] [CrossRef]
- Yan, J.P.; Wen, D.N.; Li, Z.Z.; Geng, B.; Cai, J.G.; Ling, Q.; Yun, Y. The Quantitative evaluation method of low permeable sandstone pore structure based on nuclear magnetic resonance(NMR) logging. Chin. J. Geophys. 2016, 59, 1543–1552. [Google Scholar]
- Jiang, Z.; He, H.; Tian, G.L.; Guo, W.Z.; Li, Y.Z.; Pan, Z. Pore Structure Quantification and Fractal Characterization of MSA Mortar Based on 1H Low-Field NMR. Fractal Fract. 2024, 8, 42. [Google Scholar] [CrossRef]
- Pan, Z.; Zhou, K.; Wang, Y.; Lin, Y.; Saleem, F. Comparative Analysis of Strength and Deformation Behavior of Cemented Tailings Backfill under Curing Temperature Effect. Materials 2022, 15, 3491. [Google Scholar] [CrossRef]
- Rui, F.X.; Zhao, G.F. Experimental and numerical investigation of laserinduced rock damage and the implications for laser-assisted rock cutting. Int. J. Rock. Mech. Min. Sci. 2021, 139, 104653. [Google Scholar] [CrossRef]
- Hu, G.Z.; Zhu, J.Q.; Sun, C.; Yang, N.; Qin, W. Fracturing effect and damage behaviors for microstructure in shale under microwave irradiation. J. China Coal Soc. 2020, 45, 3471–3479. [Google Scholar]
- Zhang, W.Q. Study on the Microscopic Mechanism of Rock Thermal Damage and the Evolution Characteristics of Macroscopic Physical and Mechanical Properties; China University of Mining and Technology: Xuzhou, China, 2017. [Google Scholar]
- Gao, M.Z.; Xie, J.; Yang, B.G.; Tang, R.F.; Deng, H.C.; Liu, Y.T.; Ye, S.Q.; Zhou, X.M.; Wang, S.L. Characteristics and mechanism of rock 3D volume fracturing in microwave field. J. China Coal Soc. 2022, 47, 1122–1137. [Google Scholar]
- Li, J.L.; Kaunda, R.B.; Rrora, S.; Hartlieb, P.; Nelson, P.P. Fully-coupled simulations of thermally-induced cracking in pegmatite due to microwave irradiation. J. Rock Mech. Geotech. Eng. 2019, 11, 242–250. [Google Scholar] [CrossRef]
- Liu, G.M.; Feng, X.T.; Li, Y.H.; Zhang, X.W. Influence of microwave treatment on mechanical behaviour of compact basalts under different confining pressures. J. Rock Mech. Geotech. Eng. 2020, 12, 213–222. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Liu, T.Y.; Jiang, C.; Zhao, C.; Chen, Z.; Zhou, K.P.; Chen, L.J. The Freeze-Thaw Strength Evolution of Fiber-Reinforced Cement Mortar Based on NMR and Fractal Theory: Considering Porosity and Pore Distribution. Materials 2022, 15, 7316. [Google Scholar] [CrossRef]
- Porteneuve, C.; Korb, J.P.; Petit, D.; Zanni, H. Structure–texture correlation in ultra-high-performance concrete: A nuclear magnetic resonance study. Cem. Concr. Res. 2002, 32, 97–101. [Google Scholar] [CrossRef]
- Gao, F.; Xiong, X.; Zhou, K.P.; Li, J.L.; Shi, W.C. Strength deterioration model of saturated sandstone under freeze-thaw cycles. Rock Soil Mech. 2019, 40, 926–932. [Google Scholar]
- Gao, F.; Cao, S.P.; Zhou, K.P.; Lin, Y.; Zhu, L.Y. Damage characteristics and energy-dissipation mechanism of frozen–thawed sandstone subjected to loading. Cold Reg. Sci. Technol. 2020, 169, 102920. [Google Scholar] [CrossRef]
- Gong, F.Q.; Zhang, P.L.; Xu, L. Damage constitutive model of brittle rock under uniaxial compression based on linear energy dissipation law. Int. J. Rock Mech. Min. Sci. 2022, 160, 105273. [Google Scholar] [CrossRef]
- Gong, F.Q.; Zhang, P.L.; Luo, S.; Li, J.C.; Huang, D. Theoretical damage characterisation and damage evolution process of intact rocks based on linear energy dissipation law under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2021, 146, 104858. [Google Scholar] [CrossRef]
- Yan, J.Y.; Gong, F.Q.; Luo, S. Effects of length-to-diameter ratio on energy storage characteristics of rock materials under uniaxial compression. Bull. Eng. Geol. Environ. 2022, 81, 508. [Google Scholar] [CrossRef]
- Wang, Z.L.; Li, S.Y.; Wang, J.G.; Xiong, F.; Xie, L.X. Mechanical behavior, mesoscopic properties and energy evolution of deeply buried marble during triaxial loading. Int. J. Damage Mech. 2022, 31, 1592–1612. [Google Scholar] [CrossRef]
- Dong, Y.X. Study on Rock Deformation and Strength Characteristics under Loading and Unloading after High Temperature; China University of Mining and Technology: Xuzhou, China, 2020. [Google Scholar]
- Luo, Y.; Gong, H.L.; Xu, K.; Pei, C.H.; Wei, X.Q.; Li, X.P. Progressive failure characteristic and energy accumulation of granite with a pre-fabricated fracture during conventional triaxial loading. Theor. Appl. Fract. Mech. 2022, 118, 103219. [Google Scholar] [CrossRef]
- Li, C.; Mo, P.Q.; Li, S.C. Stability analysis of energy dissipation mechanisms in rocks surrounding circular opening. Appl. Math. Model. 2024, 127, 327–342. [Google Scholar] [CrossRef]
- Zhu, X.H.; Liu, W.J. The rock fragmentation mechanism and plastic energy dissipation analysis of rock indentation. Geomech. Eng. 2018, 16, 195–204. [Google Scholar]

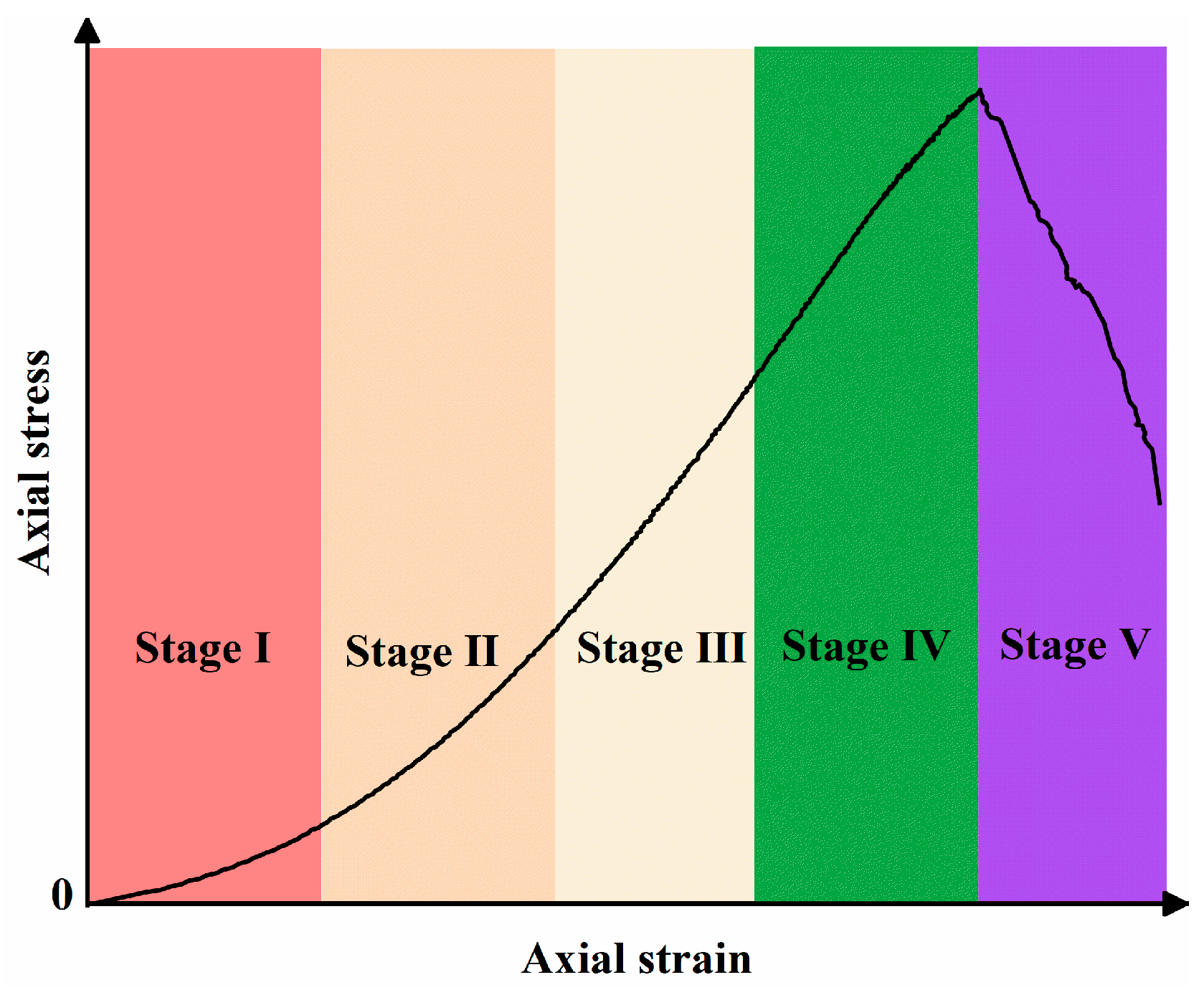
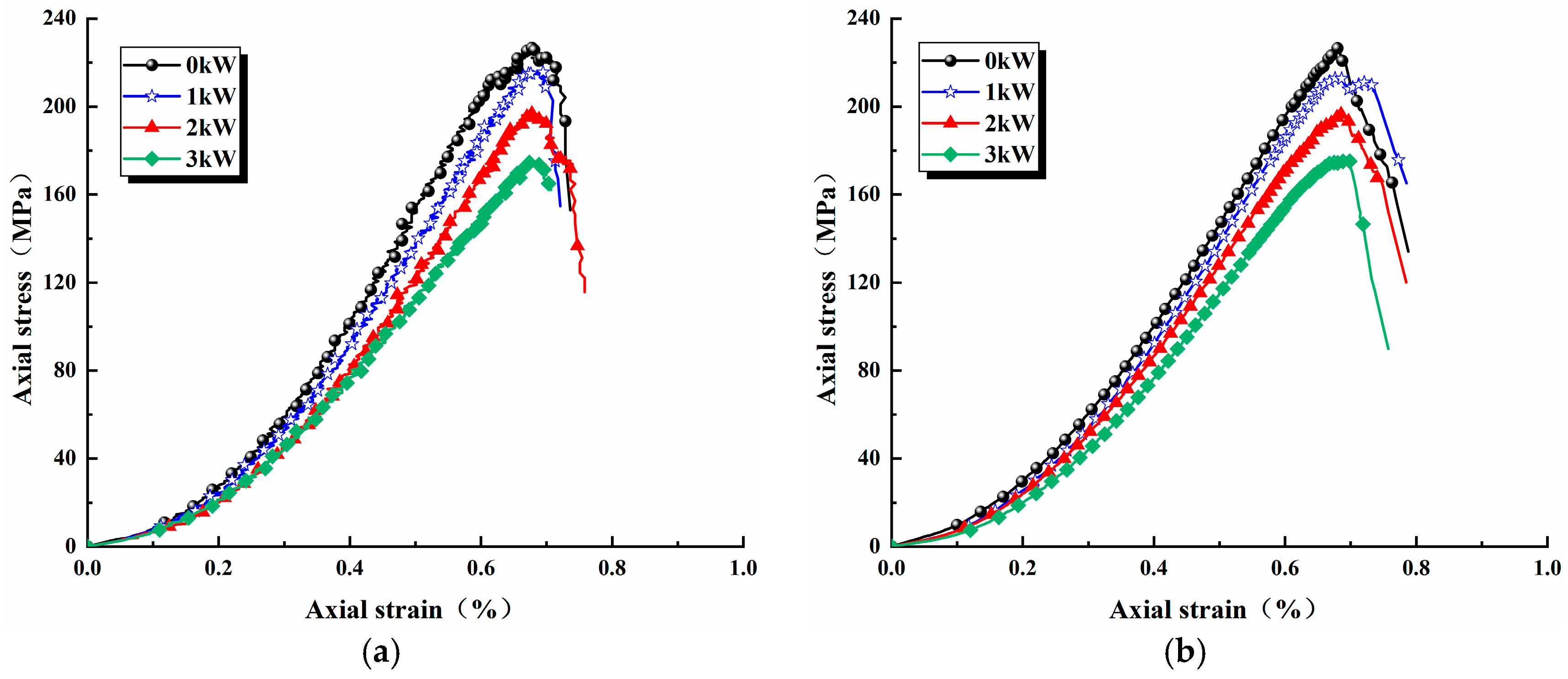
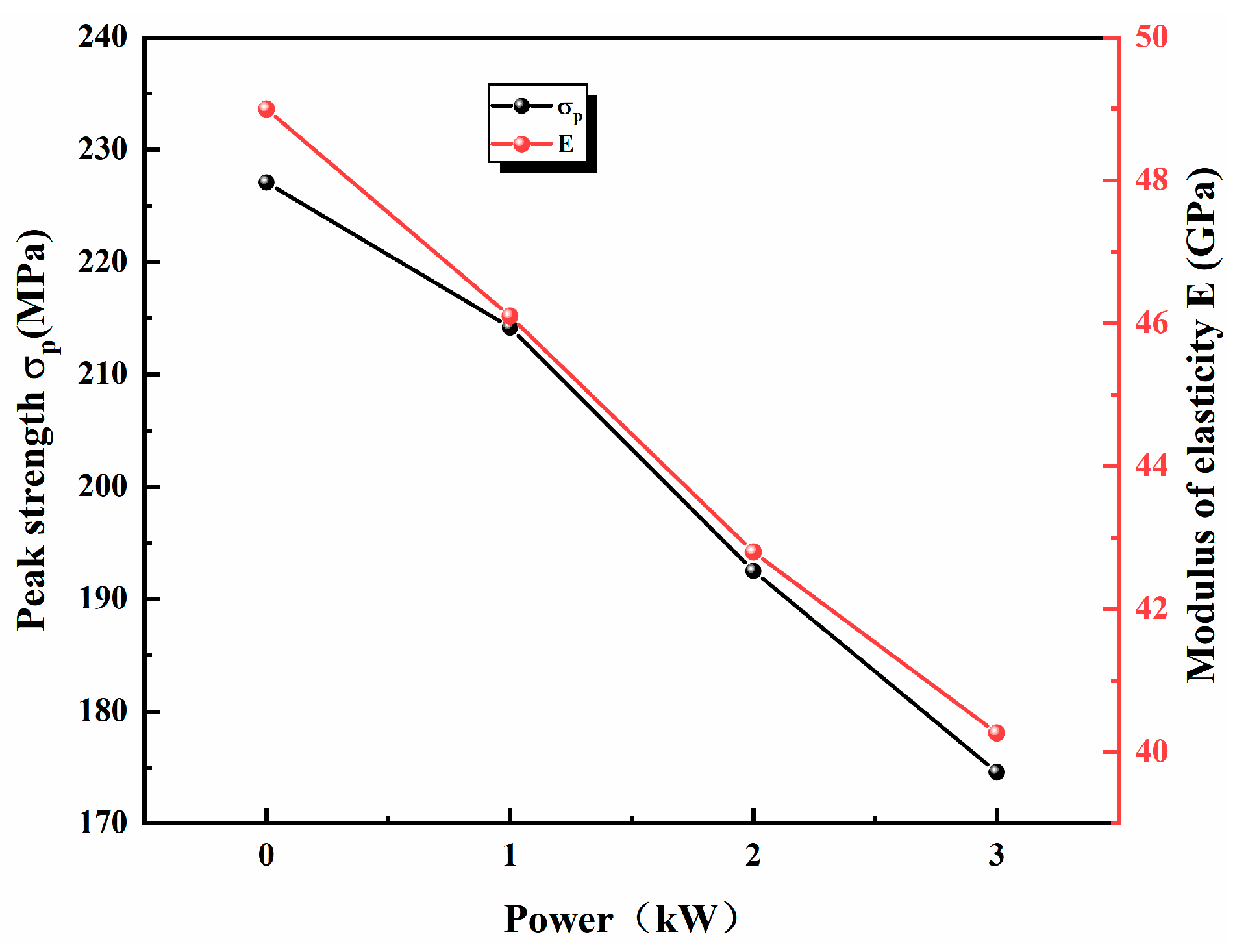

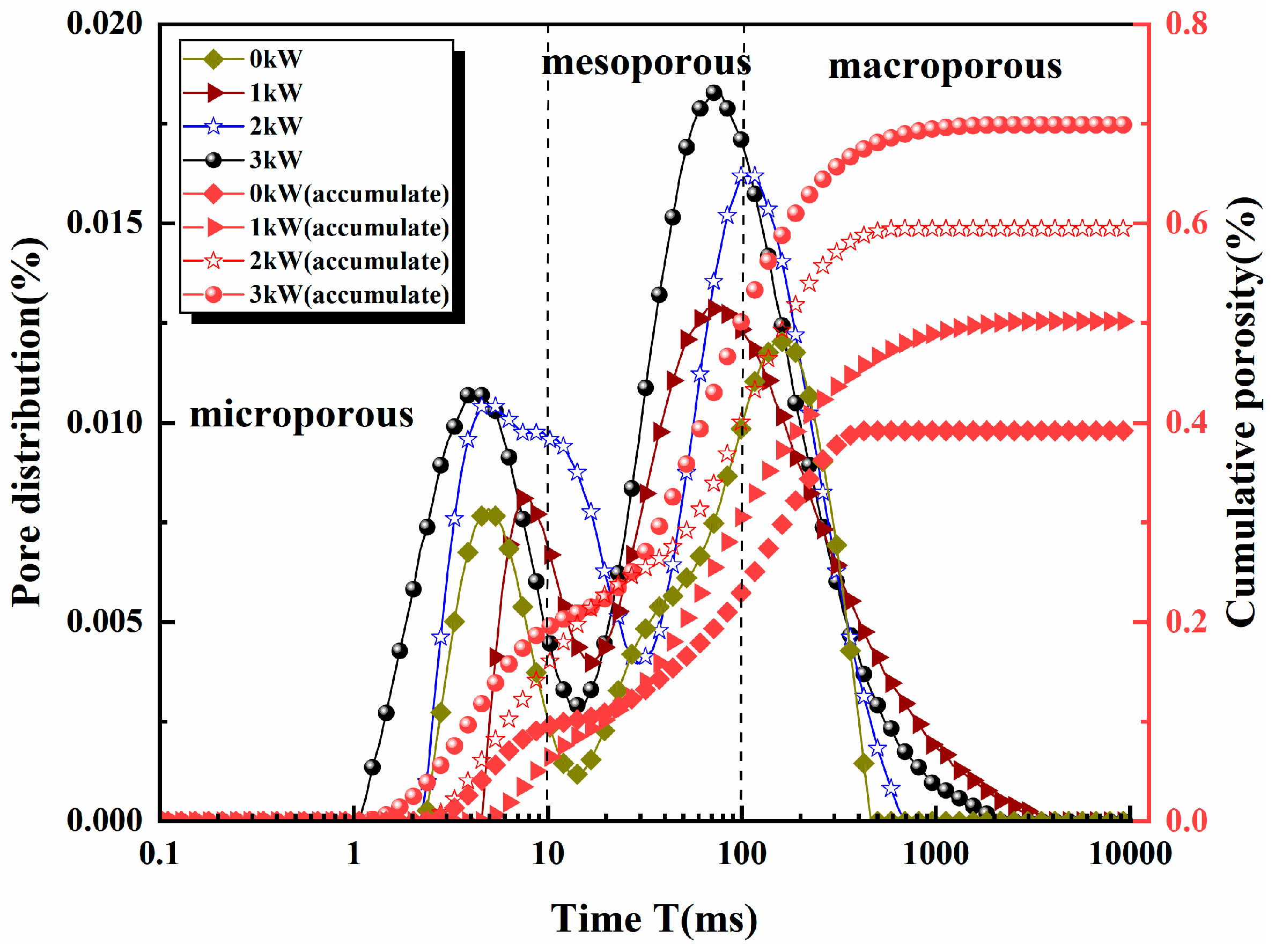

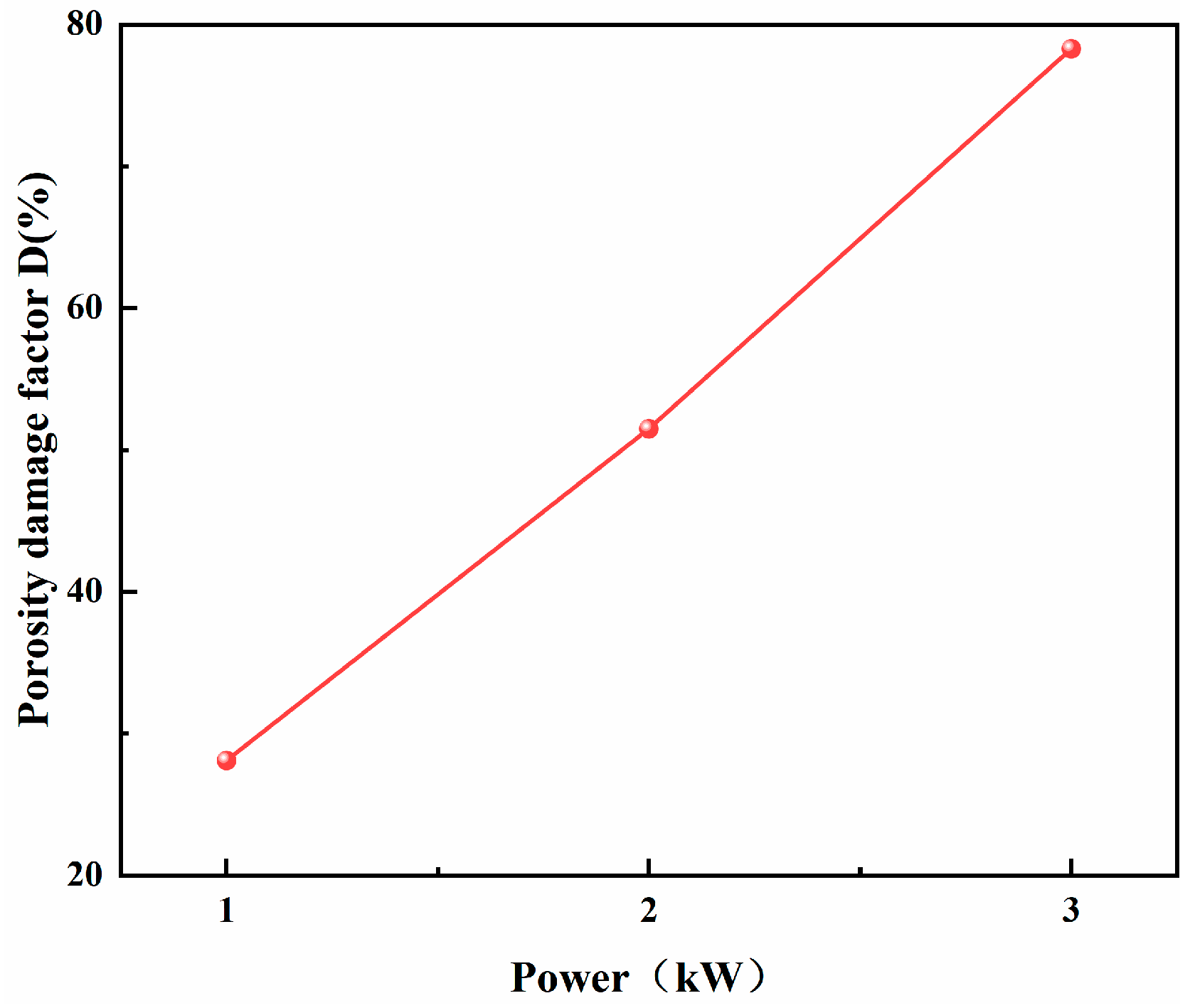
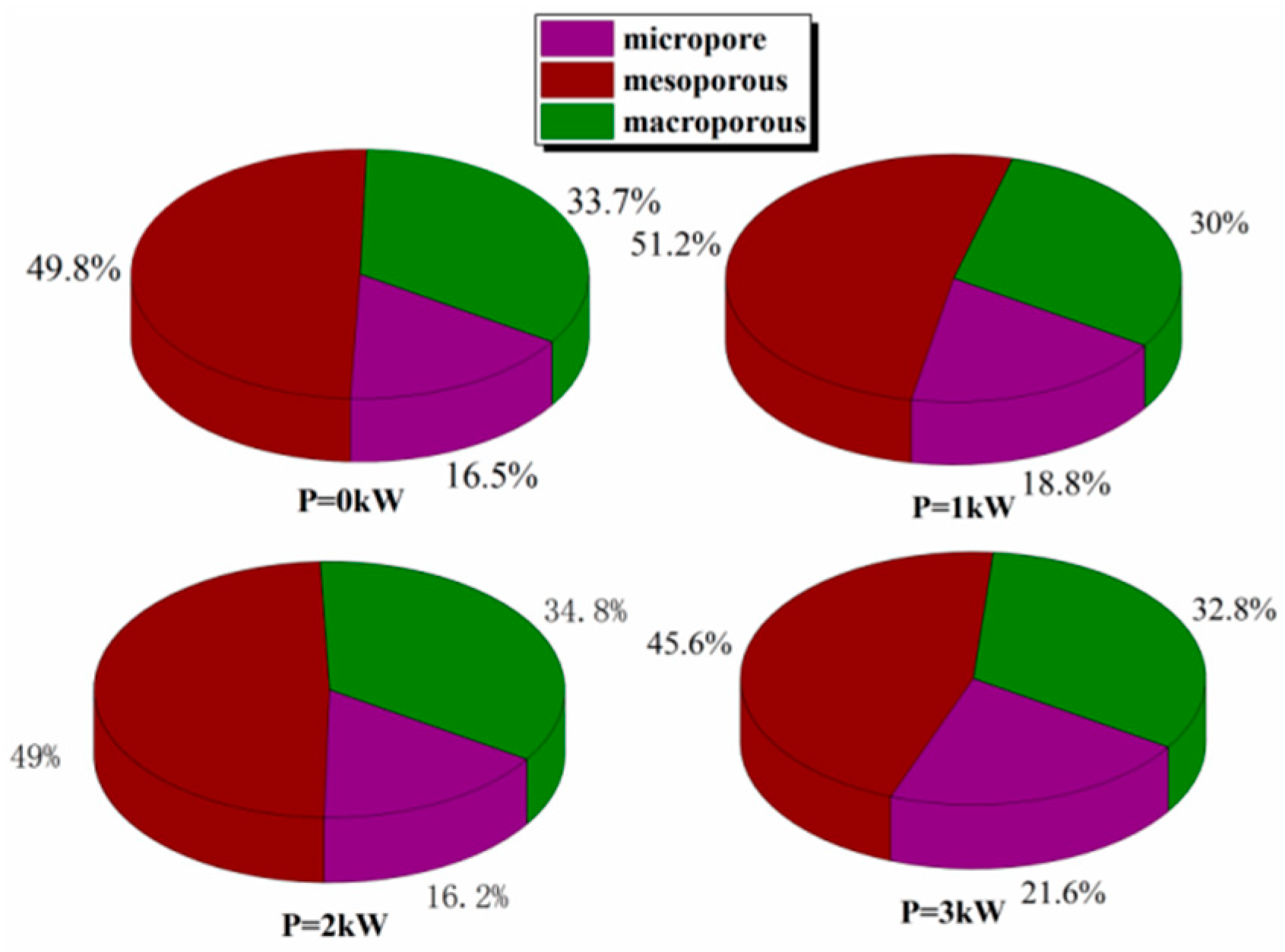
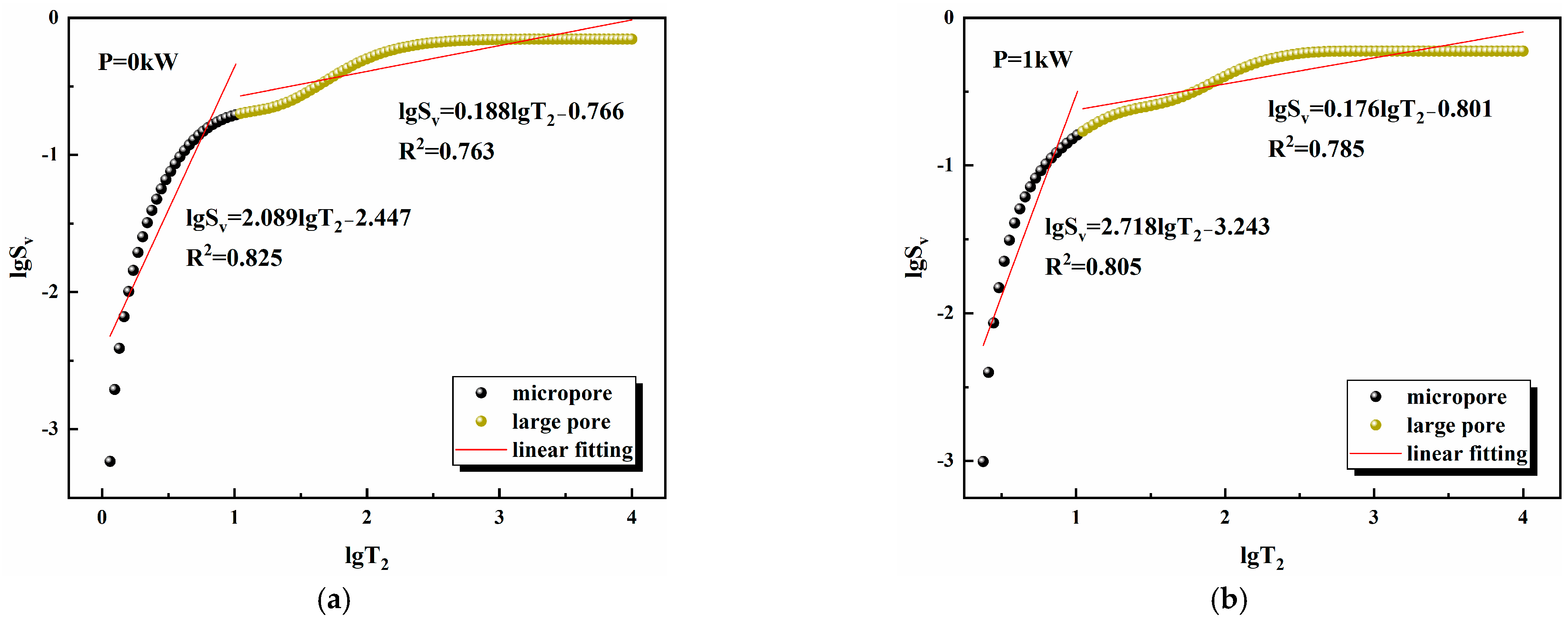
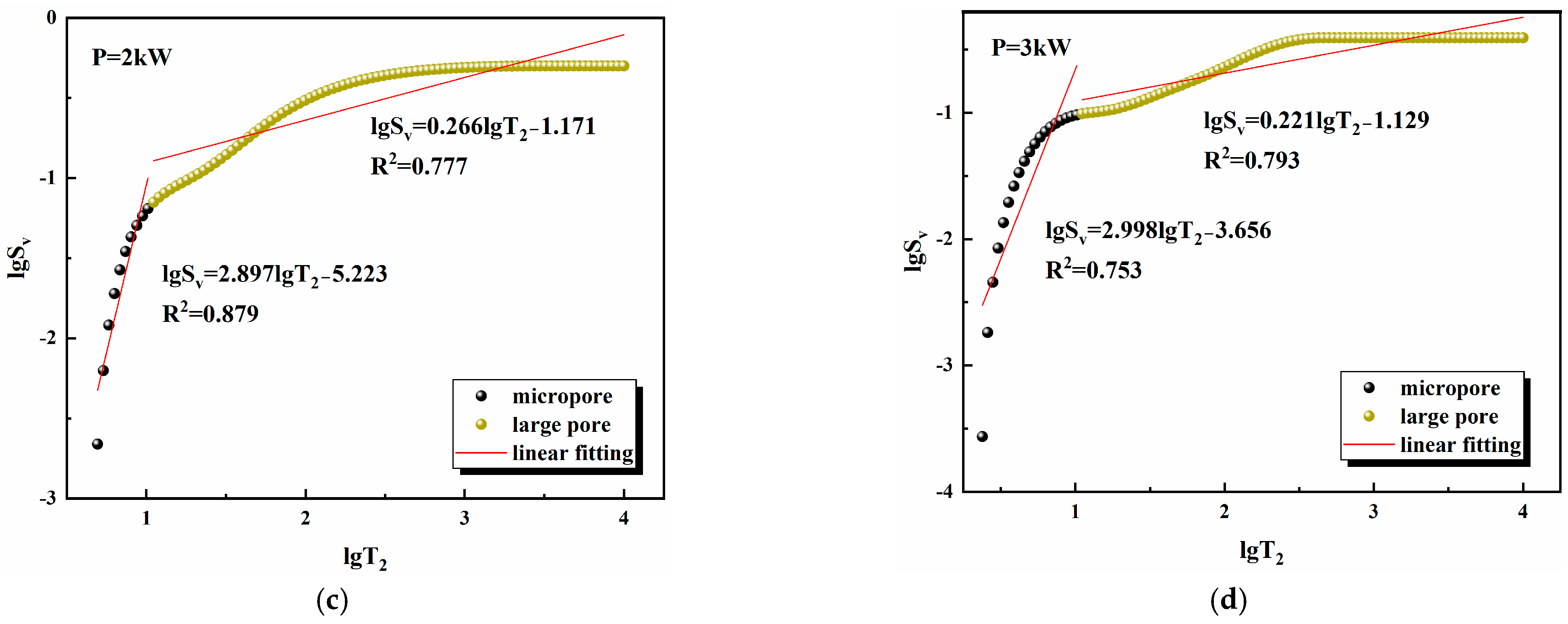
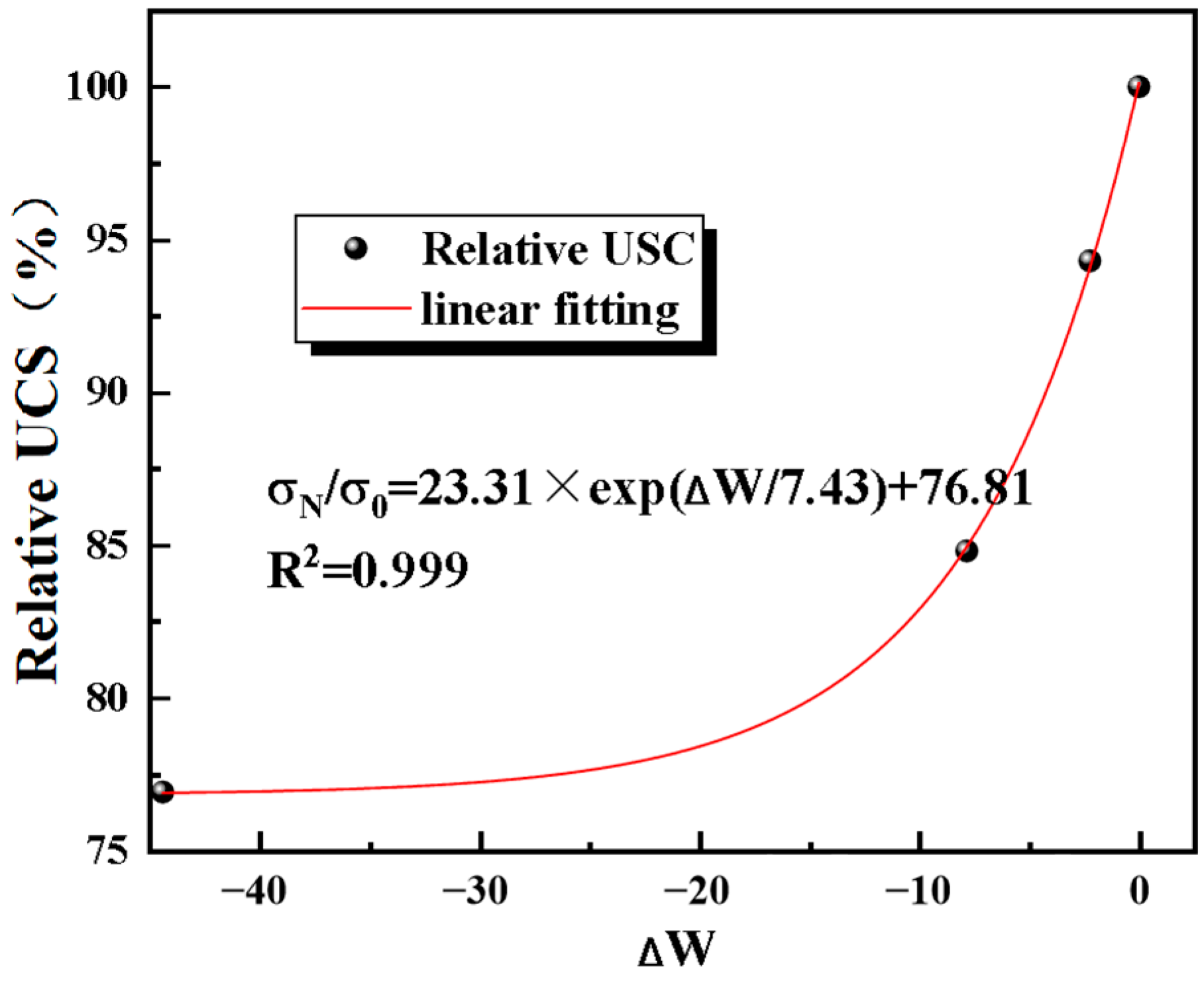
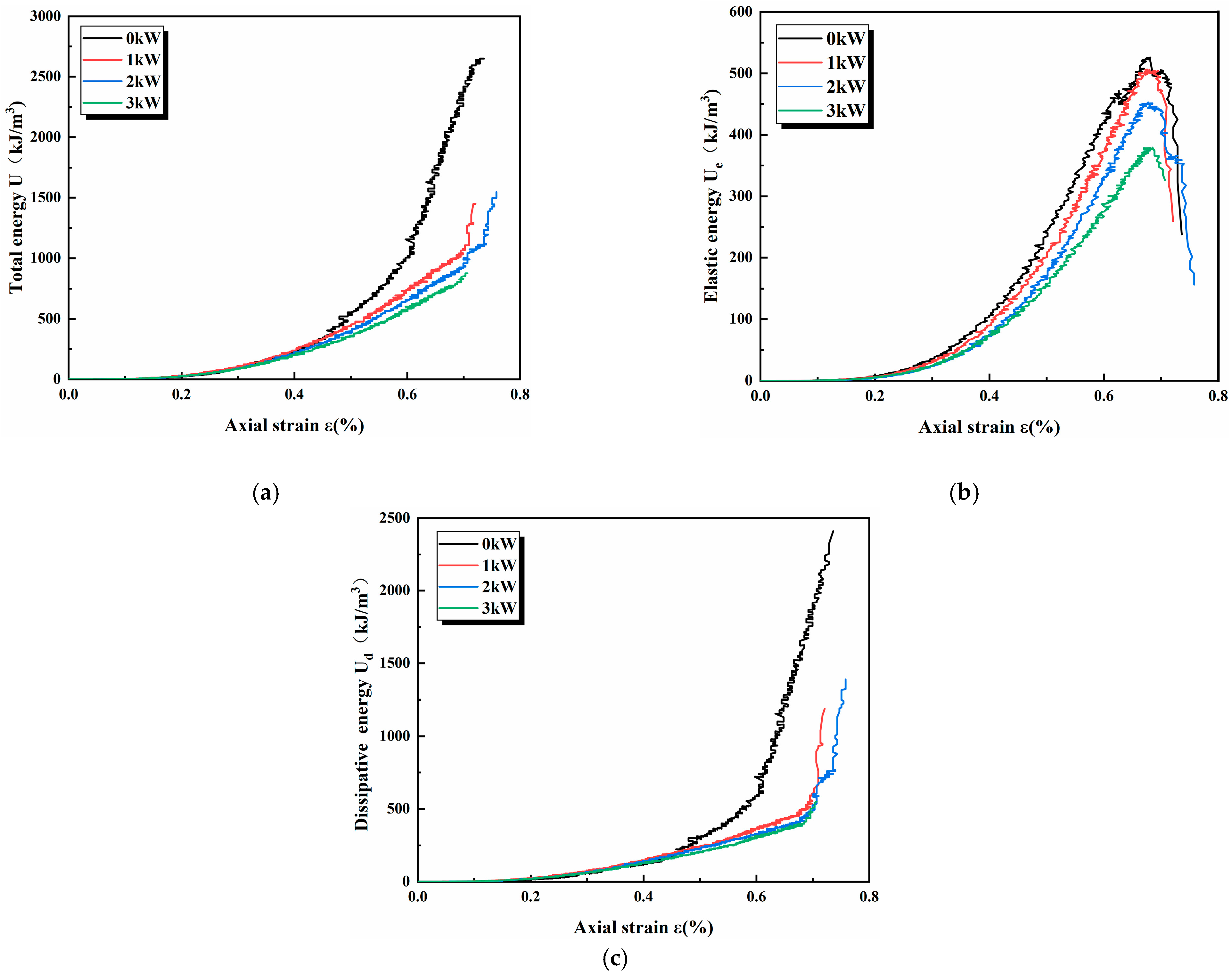
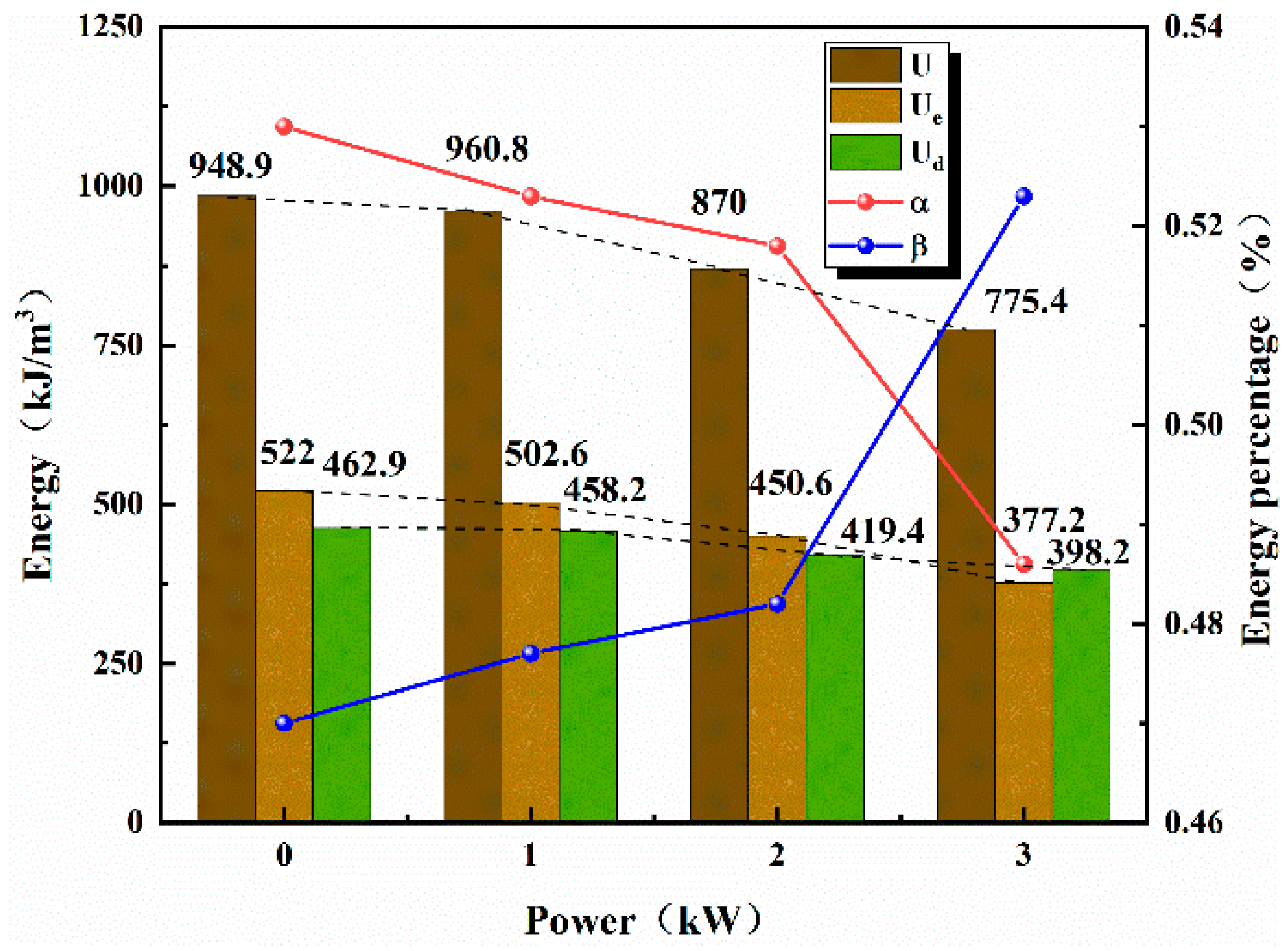
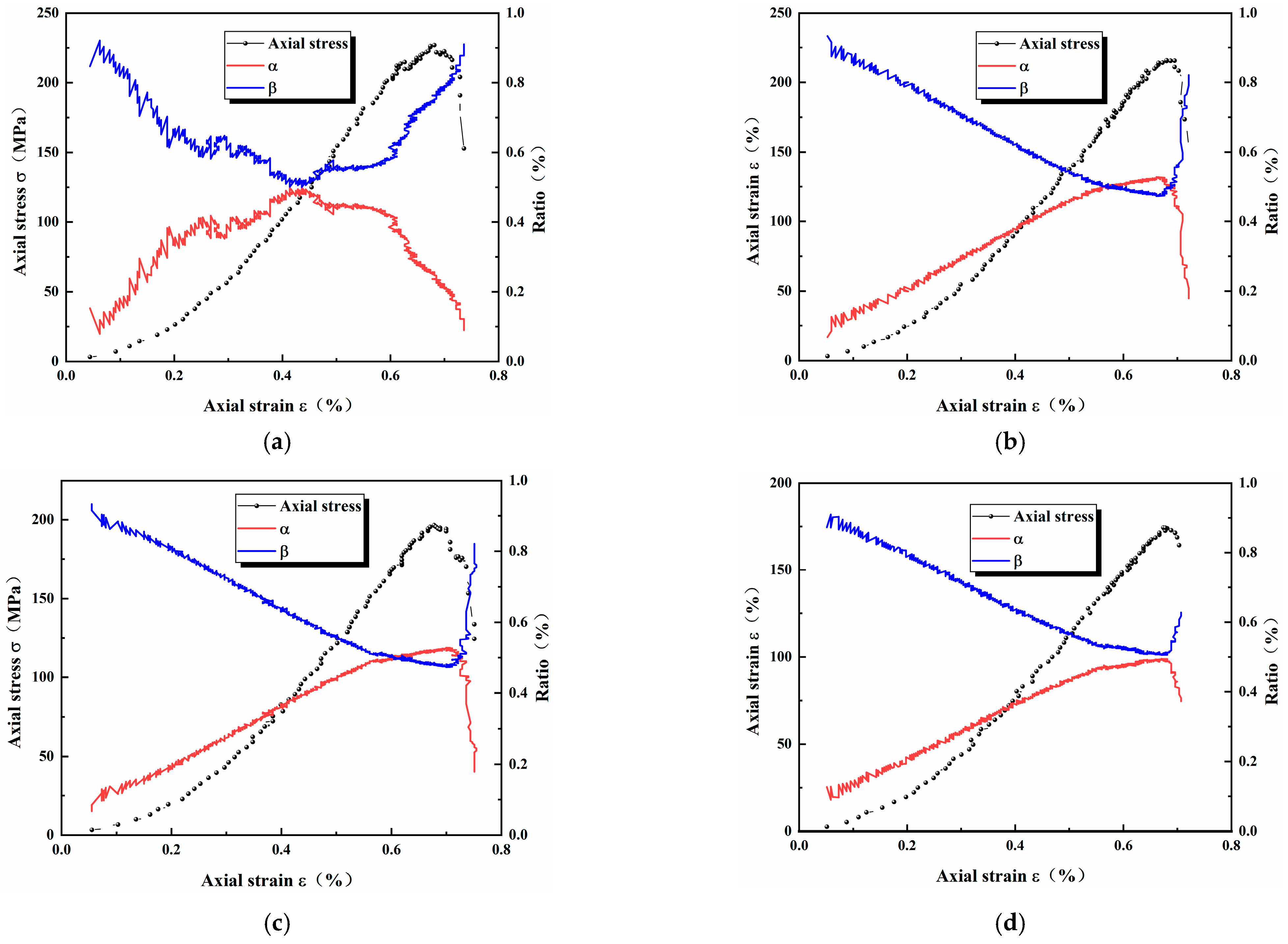
| Power (kW) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Total porosity (%) | 0.392 | 0.502 | 0.594 | 0.699 |
| Microporous (%) | 0.094 | 0.065 | 0.161 | 0.193 |
| Mesoporous (%) | 0.229 | 0.305 | 0.401 | 0.501 |
| Macroporous (%) | 0.069 | 0.132 | 0.032 | 0.002 |
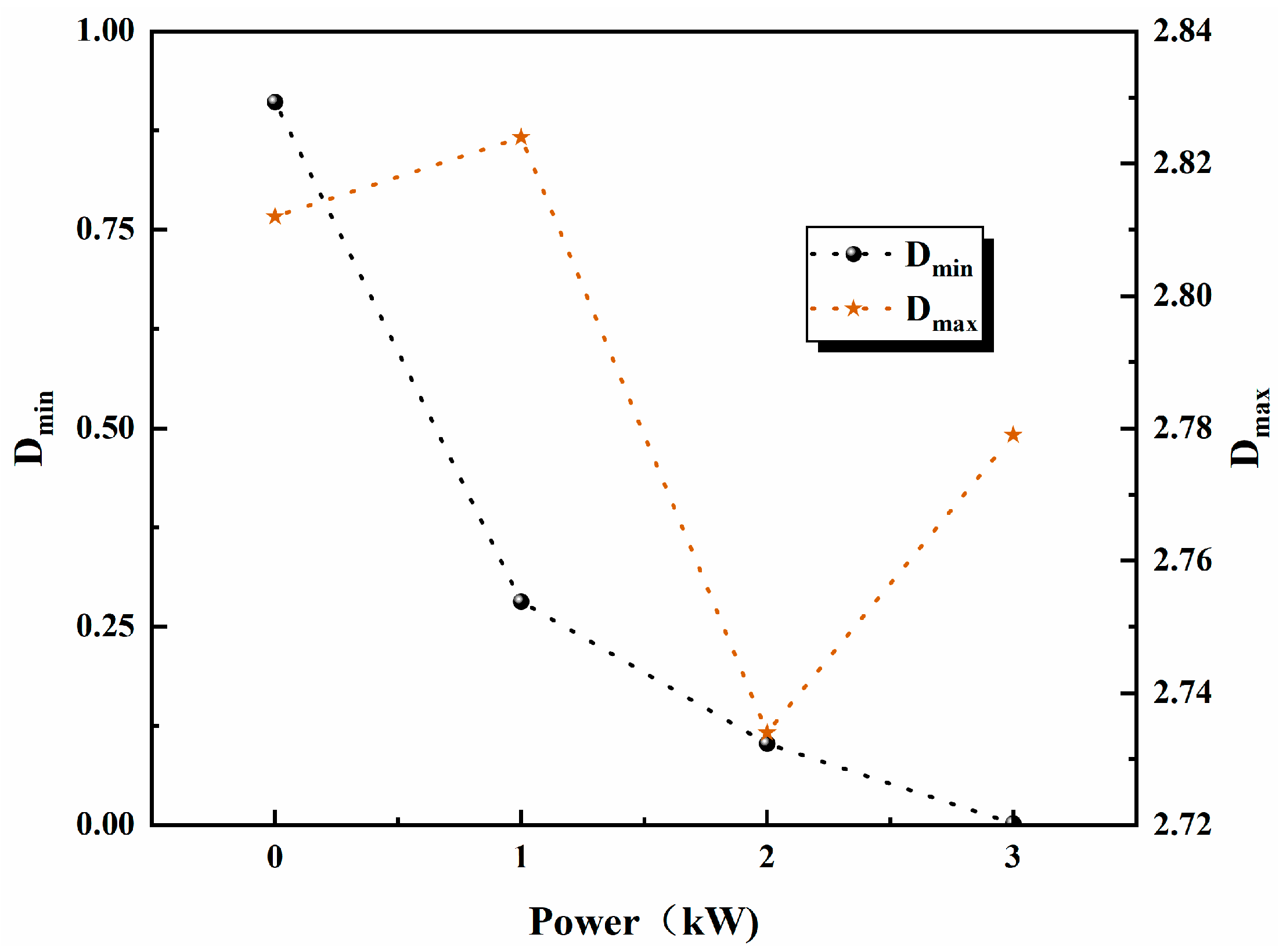
| Fractal Dimensions | Power (kW) | |||
|---|---|---|---|---|
| 0 | 1 | 2 | 3 | |
| 0.911 | 0.282 | 0.103 | 0.02 | |
| 2.812 | 2.824 | 2.734 | 2.779 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, K.; Zhang, Y.; Yang, C.; Yang, N.; Pan, Z. Analysis of Pore Characterization and Energy Evolution of Granite by Microwave Radiation. Fractal Fract. 2024, 8, 161. https://doi.org/10.3390/fractalfract8030161
Zhou K, Zhang Y, Yang C, Yang N, Pan Z. Analysis of Pore Characterization and Energy Evolution of Granite by Microwave Radiation. Fractal and Fractional. 2024; 8(3):161. https://doi.org/10.3390/fractalfract8030161
Chicago/Turabian StyleZhou, Keping, Yifan Zhang, Chun Yang, Niange Yang, and Zheng Pan. 2024. "Analysis of Pore Characterization and Energy Evolution of Granite by Microwave Radiation" Fractal and Fractional 8, no. 3: 161. https://doi.org/10.3390/fractalfract8030161
APA StyleZhou, K., Zhang, Y., Yang, C., Yang, N., & Pan, Z. (2024). Analysis of Pore Characterization and Energy Evolution of Granite by Microwave Radiation. Fractal and Fractional, 8(3), 161. https://doi.org/10.3390/fractalfract8030161








