Event-Triggered Adaptive Fuzzy Control for Strict-Feedback Nonlinear FOSs Subjected to Finite-Time Full-State Constraints

Abstract

In this article, an event-triggered adaptive fuzzy finite-time dynamic surface control (DSC) is presented for a class of strict-feedback nonlinear fractional-order systems (FOSs) with full-state constraints. The fuzzy logic systems (FLSs) are employed to approximate uncertain nonlinear functions in the backstepping process, the dynamic surface method is applied to overcome the inherent computational complexity from the virtual controller and its fractional-order derivative, and the barrier Lyapunov function (BLF) is used to handle the full-state constraints. By introducing the finite-time stability criteria from fractional-order Lyapunov method, it is verified that the tracking error converges to a small neighborhood near the zero and the full-state constraints are satisfied within a predetermined finite time. Moreover, reducing the communication burden can be guaranteed without the occurrence of Zeno behavior, and the example is given to demonstrate the effectiveness of the proposed controller.

1. Introduction

The fractional-order systems (FOSs) with infinite memory and genetic characteristics can describe the more nonclassic phenomenon in the physical systems [1,2], which have been applied in a lot of different areas such as secret communication [3,4], vehicle [5,6], circuit [7,8], finance [9,10], image [11,12,13], etc.

Many nonlinear controller results for FOSs have been presented including adaptive backstepping control, dynamic surface control (DSC), and so on. Among them, the adaptive backstepping control technology can settle the tracking control problem of FOSs with mismatched conditions, in which the approximation performance of neural networks (NNs) or fuzzy logic systems (FLSs) [14,15,16,17,18,19] are always used to handle unknown nonlinear functions in the FOSs, and the stability of the closed-loop system is accomplished. For example, the authors in [20] consider nonlinear FOSs under actuator faults and come up with a NN backstepping control scheme by using the property of NNs. An adaptive fuzzy control strategy for nonstrict-feedback nonlinear large-scale FOSs is designed and analyzed in [21]. Liu et al. [22] investigate the adaptive DSC for a class of parametric uncertain FOSs by utilizing backstepping mechanism. Despite many literatures and achievements have been obtained and published, output or state constraints are ignored and not considered there.

In fact, state constraints or output constraint are the most important factor restricting system performance, and generally widespread in plentiful physical systems. Once violate these constraints at some point of the operation, the control systems are unable to work normally and cause extreme harm. To address the constraint issue to guarantee the steady-state and transient behavior of the FOSs, the barrier Lyapunov function (BLF) by employing the relevant error constraints is the prevalent method to indirectly restrict system states, and a number of the constraint control strategies for FOSs has been achieved. The authors in [23] develop an adaptive NN constraint control strategy for uncertain nonlinear nonstrict-feedback FOSs under full-state constraints, and all the states remain in their constraint bounds by introducing the BLF. In [24], a bipartite consensus of multiple nonlinear FOSs with output constraints is assessed, and a distributed backstepping control method is developed, in which the BLFs are applied to restrict the output of followers into the preset range. To achieve the performance of the FOSs under asymmetric time-varying state constraints and input nonlinearities [25], a neural adaptive DSC is proposed by using asymmetric BLFs to refrain from the transgression of the pseudo-state constraints. The uncertain nonstrict-feedback incommensurate FOSs under output constraints is addressed in [26], and an adaptive NN controller based on the observer is proposed to guarantees the tracking error satisfying the constraints. In these traditional time-trigger schemes, the communication is performed periodically, leading to the waste of resources from the communications burden and vast data transmission.

Different from time-driven periodic sampling mechanism with fixed frequency, the frequency of event-driven control (ETC) is determined according to state error, which can save communication resources and computing resources of the system, and event-triggered control for FOSs have been proposed in some outstanding works. In [27], the ETC strategy for the FOSs has been designed to ensure the stability of the closed-loop system. For fractional-order multiagent networks in [28], a distributed ETC is designed to address the limitations of communication resources. In [29], an adaptive NN ETC for FOSs with unmodeled dynamics is proposed by using Mittag-Leffler input-to-state practical stability Lyapunov function. The authors in [30] research the state estimation of the fractional-order complex networked systems with randomly occurring nonlinearities, and an adaptive nonfragile state estimation method with event-triggered mechanism is designed. For nonlinear FOSs with uncertainty and disturbance in [31], the adaptive event-triggered fuzzy DSC strategy is investigated to reduce the transmission of control signals. In [32], the adaptive NN backstepping ETC algorithm for the nonlinear double-integrator FOSs with unknown dynamics and disturbances is presented. For nonstrict-feedback uncertain multi-input multi-output time-delay FOSs with actuator faults, the observer-based adaptive hybrid fuzzy controller via dynamic surface method and event-triggered mechanism is proposed in [33]. To our best knowledge, there is a lack of research on the finite-time state constrained ETC strategy for nonlinear FOSs.

In this article, the event-triggered finite-time adaptive control method for nonlinear FOSs with actuator saturation and full-state constraints is proposed, and the major innovations are given as follows:

(1)

Compared with state constrained controller [23,25,27,34] or finite-time controller for nonlinear FOSs [35,36,37,38], an event-triggered adaptive fuzzy finite-time DSC approach for strict-feedback uncertain nonlinear FOSs with actuator saturation and full-state constraints is proposed, in which the fuzzy logic systems are employed to approximate uncertain nonlinear functions in the backstepping process and the dynamic surface method is applied to overcome the inherent computational complexity from the virtual controller.

(2)

Compared with the results in [39,40], the event-triggered mechanism is designed together with finite-time full-state constrained adaptive controller, and the finite-time stability of the closed-loop systems is proved based on fractional-order Lyapunov criterion, which reduces the consumption of network resources to make the proposed controller more general for application.

2. Problem Formulations and Preliminary

2.1. Systems Dynamics and Some Basic Assumptions

The following strict-feedback nonlinear FOSs with actuator saturation are considered:

$$\left\{\begin{array}{c}{D}^{\alpha }{x}_i=f_i\left({\underline{x}}_i\right)+g_i\left({\underline{x}}_i\right)x_{i+1},i=1,2,\dots ,n-1\hfill \\ D^{\alpha }{x}_n=f_n\left(x\right)+g_n\left(x\right)u\left(\nu \right)\hfill \\ y=x_1\hfill \end{array}\right.$$

(1)

where ${\underline{x}}_i={\left(\begin{array}{cccc}{x}_1& x_2& \dots & x_i\end{array}\right)}^{\mathrm{T}}\in R^i\left(i=1,2,\dots ,n-1\right)$ and $x={\left(\begin{array}{cccc}{x}_1& x_2& \dots & x_n\end{array}\right)}^{\mathrm{T}}\in R^n$ are state vectors, $y\in R$ is output, $f_i\left(·\right)$ is unknown function, and $g_i\left(·\right)$ is known function, $i=1,2,\dots ,n$. $\alpha$ is fractional order, and ${\alpha }^{th}$ is the Caputo fractional derivative of continuous function $\xi \left(t\right)$, which is defined as [41,42]:

$${\displaystyle D_{t_0}^{\alpha }}\xi \left(t\right)=\frac{1}{\Gamma \left(n-\alpha \right)}{\displaystyle {\int }_{t_0}^t}{\left(t-\tau \right)}^{n-\alpha -1}{\xi }^{\left(n\right)}\left(\tau \right)d\tau$$

(2)

where $\Gamma \left(\alpha \right)={\displaystyle {\int }_0^{\infty }}{e}^{-t}{t}^{\alpha -1}dt$, $n-1<\alpha <n,n\in Z^{+}$. ${\displaystyle D_{t_0}^{\alpha }}$ is denoted as $D^{\alpha }$, when $t_0=0$.

Define an open set as ${\Omega }_i=\left\{\left.x_i\left(t\right)\in R\right|\left|x_i\right|<k_{c_i},k_{c_i}>0\right\}$, then each system state $x_i$ is constrained in ${\Omega }_i$. v is the control input, and $u\left(v\right)$ is the saturation input defined as:

$$u\left(\nu \right)=\left\{\begin{array}{cc}{u}_{max},\hfill & \nu \ge u_{max}\\ \nu ,\hfill & u_{min}<\nu <u_{max}\\ u_{min},\hfill & \nu \le u_{min}\end{array}\right.$$

(3)

where $u_{max}>0$ and $u_{min}<0$. Saturation (3) can be described as the smooth function as follow [43,44]:

$$u\left(\nu \right)=h\left(\nu \right)+\Delta \left(\nu \right)$$

(4)

where

$$h\left(\nu \right)=\left\{\begin{array}{cc}{u}_{max}·\frac{e^{\frac{\nu }{u_{max}}}-e^{-\frac{\nu }{u_{max}}}}{e^{\frac{\nu }{u_{max}}}+e^{-\frac{\nu }{u_{max}}}},& \nu \ge 0\\ u_{min}·\frac{e^{\frac{\nu }{u_{min}}}-e^{-\frac{\nu }{u_{min}}}}{e^{\frac{\nu }{u_{min}}}+e^{-\frac{\nu }{u_{min}}}},& \nu <0\end{array}\right.$$

(5)

and $\Delta \left(\nu \right)=u\left(\nu \right)-h\left(\nu \right)$ satisfying $\left|\Delta \left(\nu \right)\right|\le max\left\{u_{max}\left(1-tanh\left(1\right)\right),u_{min}\left(tanh\left(1\right)-1\right)\right\}=D$. Then, there is a constant $\mu ,0<\mu <1$, and one can get $h\left(\nu \right)=h_{{\nu }_{\mu }}\nu$ when selecting ${\nu }_0=0$. One can get

$$u\left(\nu \right)=h_{{\nu }_{\mu }}\nu +\Delta \left(\nu \right)$$

(6)

In this article, the event-triggered adaptive fuzzy finite-time controller for FOSs (1) will be constructed, so that:

(1)

output y follows desired $y_r\left(t\right)$, and the tracking error ${\vartheta }_1=y-y_r\left(t\right)$ converges to a small neighborhood of the origin in finite time;

(2)

the full-state constraints are satisfied no later than the predetermined finite time;

(3)

all the signals in the closed-loop system remain boundedness and the Zeno behavior is avoided to occur.

To complete the control objective, the following assumptions are made.

Assumption 1.

For $\forall k_{c_1}>0$, there exist positive constants  $A_0$, $A_1$, and $A_2$, such that $\left|y_r\right|\le A_0<k_{c_1}$,  $\left|D^{\alpha }{\displaystyle y_r^{ }}\left(t\right)\right|\le A_1$, and  $\left|D^{2\alpha }{\displaystyle y_r^{ }}\left(t\right)\right|\le A_2$. In addition, there exists a compact ${\Omega }_{y_r}=\left\{\left.{\left(\begin{array}{ccc}{y}_r& D^{\alpha }{y}_r& D^{2\alpha }{y}_r\end{array}\right)}^{\mathrm{T}}\right|{\displaystyle y_r^2}+{\left(D^{\alpha }{y}_r\right)}^2+{\left(D^{2\alpha }{y}_r\right)}^2\le {\delta }_{y_r},{\delta }_{y_r}>0\right\}$, such that  ${\left(\begin{array}{ccc}{y}_r& D^{\alpha }{y}_r& D^{2\alpha }{y}_r\end{array}\right)}^{\mathrm{T}}\in {\Omega }_{y_r}$.

Assumption 2.

There exist unknown constants  $0<g_{imin}\le g_{imax}$, such that  $0<g_{imin}\le \left|g_i\left({\underline{x}}_i\right)\right|\le g_{imax}$,  $i=1,2,\dots ,n$. Without loss of generality, it is further assumed that $0<g_{imin}\le g_i\left({\underline{x}}_i\right)\le g_{imax}$.

2.2. Necessary Preparations

Lemma 1

([45]). For $\forall q_1,q_2$ and $\forall s_1,s_2,s_3>0$, one can obtain:

$${\left|q_1\right|}^{s_1}{\left|q_2\right|}^{s_2}\le \frac{s_1}{s_1+s_2}{s}_3{\left|q_1\right|}^{s_1+s_2}+\frac{s_2}{s_1+s_2}{\displaystyle s_3^{-\frac{s_1}{s_2}}}{\left|q_2\right|}^{s_1+s_2}$$

(7)

Lemma 2

([46,47]). If $\varsigma \left(t\right)$ satisfy $\left|\varsigma \left(t\right)\right|\le {\displaystyle k_{b_0}^{ }}$ for $\forall {\displaystyle k_{b_0}^{ }}>0$, one can have

$$ln\frac{{\displaystyle k_{b_0}^2}}{{\displaystyle k_{b_0}^2}-{\varsigma }^2\left(t\right)}\le \frac{{\varsigma }^2\left(t\right)}{{\displaystyle k_{b_0}^2}-{\varsigma }^2\left(t\right)}$$

(8)

Lemma 3

([48]). Let $f\left(x\right)\in R$ is an unknown function, then there is FLS and a $\forall \epsilon >0$ such that

$$\underset{x\in \Omega }{sup}\left|f\left(x\right)-W^{\mathrm{T}}\Psi \left(x\right)\right|<\epsilon$$

(9)

where $\Psi \left(x\right)\in R^r$ denotes the basis function vector, and $W\in R^r$ represents the ideal constant weight vector.

Lemma 4

([49,50]). Let $x\left(t\right)\in R^n$, and $D^{\alpha }\left(x^{\mathrm{T}}\left(t\right)Px\left(t\right)\right)\le 2x^{\mathrm{T}}\left(t\right)P{D}^{\alpha }\left(x\left(t\right)\right)$ holds for $\forall t\ge t_0$ and $\alpha \in \left(0,1\right]$, $P=P^{\mathrm{T}}>0$.

Lemma 5

([51]). Let $h_1\left(·\right),h_2\left(·\right)\in R$. Assume that the function $h_1\left(h_2\right)$ is convex (i.e., ${\partial }^2{h}_1\left(h_2\right)/\phantom{{\partial }^2{h}_1\left(h_2\right)\partial {\displaystyle h_2^2}}\partial {\displaystyle h_2^2}\ge 0$), then, for $\forall t\ge 0$ and $\alpha \in \left(0,1\right]$, inequality $D^{\alpha }{h}_1\left(h_2\right)\le \partial h_1\left(h_2\right)/\phantom{D^{\alpha }{h}_1\left(h_2\right)\le \partial h_1\left(h_2\right)\partial h_2}\partial h_2· D^{\alpha }{h}_2$ holds.

Lemma 6

([52]). Let $f(t)\in C^1\left(\left(0,+\infty \right],R\right)$, then

$$D^{\alpha }{f}^{\beta }\left(t\right)=\frac{\Gamma \left(1+\beta \right)\Gamma \left(2-\alpha \right)}{\Gamma \left(1+\beta -\alpha \right)}{f}^{\beta -1}\left(t\right)D^{\alpha }f\left(t\right)$$

(10)

where $\alpha \in \left(0,1\right]$, and $\beta \in \left[1,\infty \right)$.

Lemma 7

([53]). For $\forall {\epsilon }^{\ast }>0$ and $z\in R$, it holds that

$$\left|z\right|-ztanh\left(\frac{z}{{\epsilon }^{\ast }}\right)\le 0.2785{\epsilon }^{\ast }$$

(11)

3. Main Results

3.1. Design of Adaptive Event-Triggered Controller

To adopt the backstepping technology with the DSC technology, the following coordinate transformations are considered:

$$\begin{array}{c}{\vartheta }_1=y-y_r\left(t\right)\hfill \\ {\vartheta }_i=x_i-{\mathsf{{\rm Y}}}_{i.l}\hfill \\ {\zeta }_i={\mathsf{{\rm Y}}}_{i.l}-{\mathsf{{\rm Y}}}_{i-1}\hfill \\ i=2,3,\dots ,n\hfill \end{array}$$

(12)

where ${\vartheta }_1$ is the tracking error, ${\vartheta }_i$ is the dynamic surface error, ${\zeta }_i$ is the filter output error, ${\mathsf{{\rm Y}}}_{i-1}$ is the virtual controller, and ${\mathsf{{\rm Y}}}_{i.l}$ is the filter output defined as:

$$\begin{array}{c}{\kappa }_i{D}^{\alpha }{\mathsf{{\rm Y}}}_{i.l}=-{\mathsf{{\rm Y}}}_{i.l}+{\mathsf{{\rm Y}}}_{i-1}\hfill \\ {\mathsf{{\rm Y}}}_{i.l}\left(0\right)={\mathsf{{\rm Y}}}_{i-1}\left(0\right),i=2,3,\dots ,n.\hfill \end{array}$$

(13)

where ${\kappa }_i$ is a constant.

For $t\in \left[t_k,t_{k+1}\right)$, the virtual control laws and actual control law are designed as follows:

$$\begin{array}{c}{\displaystyle {\mathsf{{\rm Y}}}_1=\frac{1}{g_1\left(x_1\right)}\left(-\frac{c_1{\displaystyle {\vartheta }_1^{2\rho -1}}}{{\left({\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}\right)}^{\rho -1}}\right.}\hfill \\ {\displaystyle \begin{array}{cc} & \end{array}\left.-\left(\frac{g_{1min}}{2{\displaystyle b_1^2}}{\theta }_1{∥{\Psi }_1\left(Z_1\right)∥}^2+\frac{1+{\displaystyle g_{1max}^2}}{2}{\displaystyle d_1^2}\right)\frac{{\vartheta }_1}{{\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}}\right)}\hfill \end{array}$$

(14)

$$\begin{array}{c}{\displaystyle {\mathsf{{\rm Y}}}_i=\frac{1}{g_i\left({\underline{x}}_i\right)}\left(-\left(\frac{1}{2{\displaystyle b_i^2}}{\theta }_i{g}_{imin}{∥{\Psi }_i\left({\underline{x}}_i\right)∥}^2+\frac{1+{\displaystyle g_{imax}^2}}{2}{\displaystyle d_i^2}\right)\frac{{\vartheta }_i}{{\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}}\right.}\hfill \\ {\displaystyle \begin{array}{cc} & \end{array}\left.+D^{\alpha }{\mathsf{{\rm Y}}}_{i.l}-\frac{c_i{\displaystyle {\vartheta }_i^{2\rho -1}}}{{\left({\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}\right)}^{\rho -1}}-\frac{g_{i-1}\left({\underline{x}}_{i-1}\right){\vartheta }_{i-1}\left({\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}\right)}{{\displaystyle k_{b_{i-1}}^2}-{\displaystyle {\vartheta }_{i-1}^2}}\right)}\hfill \\ i=2,\dots ,n-1\hfill \end{array}$$

(15)

$$\begin{array}{c}{\displaystyle {\mathsf{{\rm Y}}}_n=\frac{1}{g_n\left(x\right)h_{{\nu }_{\mu }}}\left(-\left(\frac{1}{2{\displaystyle b_n^2}}{\theta }_n{g}_{nmin}{∥{\Psi }_n\left(x\right)∥}^2+\frac{1+{\displaystyle g_{nmax}^2}}{2}{\displaystyle d_n^2}\right)\frac{{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}\right.}\hfill \\ {\displaystyle \begin{array}{cc} & \end{array}\left.+D^{\alpha }{\mathsf{{\rm Y}}}_{n.l}-\frac{c_n{\displaystyle {\vartheta }_n^{2\rho -1}}}{{\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}^{\rho -1}}-\frac{g_{n-1}\left({\underline{x}}_{n-1}\right){\vartheta }_{n-1}\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}{{\displaystyle k_{b_{n-1}}^2}-{\displaystyle {\vartheta }_{n-1}^2}}\right)}\hfill \end{array}$$

(16)

$$\Theta \left(t\right)=-\left(1+{\displaystyle {\lambda }_1^{\ast }}\right)\left({\mathsf{{\rm Y}}}_{n}tanh\left(\frac{{\mathsf{{\rm Y}}}_n{\vartheta }_n}{{\kappa }^{\ast }\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}\right)+{\displaystyle {\overline{\lambda }}_2^{\ast }}tanh\left(\frac{{\displaystyle {\overline{\lambda }}_2^{\ast }}{\vartheta }_n}{{\kappa }^{\ast }\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}\right)\right)$$

(17)

$$v\left(t\right)=\Theta \left(t_k\right), \forall t\in \left[t_k,t_{k+1}\right)$$

(18)

where $t_k$ is the controller update time, $k\in Z^{+}$. $b_i,c_i,d_i>0$ and ${\kappa }^{\ast }>0$ are the design parameters. ${\displaystyle k_{b_i}^{ }}>0$ will be given later, $i=1,2,\dots ,n$. ${\Psi }_i\left(·\right)$ is the basis function vector and will be specified later, ${\theta }_i$ is the estimate parameter of ${\displaystyle {\theta }_i^{\ast }}=\frac{1}{g_{imin}}{∥{\displaystyle W_i^{\ast }}∥}^2$, and ${\displaystyle W_i^{\ast }}$ is the optimal fuzzy weight in step i. ${\displaystyle {\overline{\lambda }}_2^{\ast }}>\frac{{\displaystyle {\lambda }_2^{\ast }}}{1-{\displaystyle {\lambda }_1^{\ast }}},{\displaystyle {\lambda }_1^{\ast }}\in \left(0,1\right)$ and ${\displaystyle {\lambda }_2^{\ast }}>0$ are the design parameters.

The parameter adaptive laws are designed as follows:

$$D^{\alpha }{\theta }_1=\frac{{\gamma }_1}{2{\displaystyle b_1^2}}\frac{{\displaystyle {\vartheta }_1^2}}{{\left({\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}\right)}^2}{∥{\Psi }_1\left(Z_1\right)∥}^2-{\varsigma }_1{\theta }_1$$

(19)

$$D^{\alpha }{\theta }_i=\frac{{\gamma }_i}{2{\displaystyle b_i^2}}\frac{{\displaystyle {\vartheta }_i^2}}{{\left({\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}\right)}^2}{∥{\Psi }_i\left({\underline{x}}_i\right)∥}^2-{\varsigma }_i{\theta }_i,i=2,\dots ,n$$

(20)

where ${\gamma }_1>0$, ${\varsigma }_1>0$,${\gamma }_i>0$ and ${\varsigma }_i>0$ are the design parameters.

The event sampling error is designed as

$$\mathsf{{\rm Y}}\left(t\right)=\Theta \left(t\right)-\Theta \left(t_k\right), \forall t\in \left[t_k,t_{k+1}\right)$$

(21)

Then the sampling instants from (18) are determined by the following triggering condition

$$t_{k+1}=inf\left\{\left.t\in R\right|\left|\mathsf{{\rm Y}}\left(t\right)\right|\ge {\displaystyle {\lambda }_1^{\ast }}\left|v\left(t\right)\right|+{\displaystyle {\lambda }_2^{\ast }}\right\}$$

(22)

3.2. Stability Analysis

The details of the proposed control scheme are given by using the backstepping technique, which involves n recursive steps.

Step 1: From (1) and (12), the derivative of ${\vartheta }_1$ is

$$\begin{array}{c}{D}^{\alpha }{\vartheta }_1=D^{\alpha }y-D^{\alpha }{y}_r\left(t\right)\hfill \\ =f_1\left(x_1\right)+g_1\left(x_1\right)x_2-D^{\alpha }{y}_r\left(t\right)\hfill \\ ={\displaystyle W_1^{\ast \mathrm{T}}}{\Psi }_1\left(Z_1\right)+{\epsilon }_1+g_1\left(x_1\right)\left({\vartheta }_2+{\zeta }_2+{\mathsf{{\rm Y}}}_1\right)\hfill \end{array}$$

(23)

where $F_1\left(Z_1\right)=F_1\left(x_1,D^{\alpha }{y}_r\left(t\right)\right)=f_1\left(x_1\right)-D^{\alpha }{y}_r\left(t\right)$ is approximated via the fuzzy system ${\displaystyle W_1^{\ast \mathrm{T}}}{\Psi }_1\left(Z_1\right)$ according to Lemma 3, and satisfies $F_1\left(Z_1\right)={\displaystyle W_1^{\ast \mathrm{T}}}{\Psi }_1\left(Z_1\right)+{\epsilon }_1$. Assume that there exists ${\overline{\epsilon }}_1>0$ such that ${\epsilon }_1\le {\overline{\epsilon }}_1$.

Construct the Lyapunov function candidate as

$$V_1=\frac{1}{2}ln\frac{{\displaystyle k_{b_1}^2}}{{\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}}+\frac{g_{1min}}{2{\gamma }_1}{\displaystyle {\tilde{\theta }}_1^2}$$

(24)

where ${\tilde{\theta }}_1={\displaystyle {\theta }_1^{\ast }}-{\theta }_1$.

Based on Lemmas 4 and 5, the $\alpha \mathrm{th}$ Caputo fractional derivative of $V_1$ on each time interval $\left[t_k,t_{k+1}\right)$ is

$$\begin{array}{c}{\displaystyle D^{\alpha }{V}_1=\frac{{\vartheta }_1}{{\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}}{D}^{\alpha }{\vartheta }_1-\frac{g_{1min}}{{\gamma }_1}{\tilde{\theta }}_1{D}^{\alpha }{\theta }_1}\hfill \\ {\displaystyle =\frac{{\vartheta }_1}{{\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}}{\displaystyle W_1^{\ast \mathrm{T}}}{\Psi }_1\left(Z_1\right)+\frac{{\vartheta }_1}{{\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}}\left({\epsilon }_1+g_1\left(x_1\right)\left({\vartheta }_2+{\zeta }_2+{\mathsf{{\rm Y}}}_1\right)\right)}\hfill \\ {\displaystyle -\frac{g_{1min}}{{\gamma }_1}{\tilde{\theta }}_1{D}^{\alpha }{\theta }_1}\hfill \end{array}$$

(25)

The Young’s inequality and Assumption 1 are applied and yields:

$$\frac{{\vartheta }_1}{{\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}}{\displaystyle W_1^{\ast \mathrm{T}}}{\Psi }_1\left(Z_1\right)\le \frac{1}{2{\displaystyle b_1^2}}\frac{{\displaystyle {\vartheta }_1^2}}{{\left({\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}\right)}^2}{\displaystyle {\theta }_1^{\ast }}{g}_{1min}{∥{\Psi }_1\left(Z_1\right)∥}^2+\frac{1}{2}{\displaystyle b_1^2}$$

(26)

$$\frac{{\vartheta }_1\left({\epsilon }_1+g_1\left(x_1\right){\zeta }_2\right)}{{\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}}\le \frac{{\displaystyle d_1^2}\left(1+{\displaystyle g_{1max}^2}\right){\displaystyle {\vartheta }_1^2}}{2{\left({\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}\right)}^2}+\frac{1}{2}{\displaystyle d_1^2}{\displaystyle {\overline{\epsilon }}_1^2}+\frac{1}{2}{\displaystyle d_1^2}{\displaystyle {\zeta }_2^2}$$

(27)

Substituting (26) and (27) into (25), one can get

$$\begin{array}{c}{\displaystyle D^{\alpha }V\le g_1\left(x_1\right)\frac{{\vartheta }_1{\vartheta }_2}{{\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}}+\frac{1}{2}{\displaystyle b_1^2}+\frac{1}{2}{\displaystyle d_1^2}{\displaystyle {\overline{\epsilon }}_1^2}+\frac{1}{2}{\displaystyle d_1^2}{\displaystyle {\zeta }_2^2}}\hfill \\ {\displaystyle -g_{1min}{\tilde{\theta }}_1\left(\frac{1}{{\gamma }_1}{D}^{\alpha }{\theta }_1-\frac{1}{2{\displaystyle b_1^2}}\frac{{\displaystyle {\vartheta }_1^2}}{{\left({\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}\right)}^2}{∥{\Psi }_1\left(Z_1\right)∥}^2\right)}\hfill \\ {\displaystyle +\left(\frac{g_{1min}}{2{\displaystyle b_1^2}}{\theta }_1{∥{\Psi }_1\left(Z_1\right)∥}^2+\frac{1+{\displaystyle g_{1max}^2}}{2}{\displaystyle d_1^2}\right)\frac{{\displaystyle {\vartheta }_1^2}}{{\left({\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}\right)}^2}}\hfill \\ {\displaystyle +g_1\left(x_1\right){\mathsf{{\rm Y}}}_1\frac{{\vartheta }_1}{{\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}}}\hfill \end{array}$$

(28)

Substituting (14) and (19) into (28), $D^{\alpha }{V}_1$ is presented as:

$$\begin{array}{c}{\displaystyle D^{\alpha }{V}_1\le -\frac{c_1{\displaystyle {\vartheta }_1^{2\rho }}}{{\left({\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}\right)}^{\rho }}+g_1\left(x_1\right)\frac{{\vartheta }_1{\vartheta }_2}{{\displaystyle k_{b_1}^2}-{\displaystyle {\vartheta }_1^2}}}\hfill \\ {\displaystyle \begin{array}{cc} & \end{array}+\frac{1}{2}{\displaystyle b_1^2}+\frac{1}{2}{\displaystyle d_1^2}{\displaystyle {\overline{\epsilon }}_1^2}+\frac{1}{2}{\displaystyle d_1^2}{\displaystyle {\zeta }_2^2}+\frac{g_{1min}{\varsigma }_1}{{\gamma }_1}{\tilde{\theta }}_1{\theta }_1}\hfill \end{array}$$

(29)

Step $i\left(i=2,3,\dots ,n-1\right)$: The derivative of ${\vartheta }_i$ is presented as:

$$\begin{array}{c}{\displaystyle D^{\alpha }{\vartheta }_i=D^{\alpha }{x}_i-D^{\alpha }{\mathsf{{\rm Y}}}_{i.l}}\hfill \\ {\displaystyle =f_i\left({\underline{x}}_i\right)+g_i\left({\underline{x}}_i\right)x_{i+1}-D^{\alpha }{\mathsf{{\rm Y}}}_{i.l}}\hfill \\ {\displaystyle ={\displaystyle W_i^{\ast \mathrm{T}}}{\Psi }_i\left({\underline{x}}_i\right)+{\epsilon }_i+g_i\left({\underline{x}}_i\right)\left({\vartheta }_{i+1}+{\zeta }_{i+1}+{\mathsf{{\rm Y}}}_i\right)-D^{\alpha }{\mathsf{{\rm Y}}}_{i.l}}\hfill \end{array}$$

(30)

where $f_i\left({\underline{x}}_i\right)$ is approximated by ${\displaystyle W_i^{\ast \mathrm{T}}}{\Psi }_i\left({\underline{x}}_i\right)$ such that $f_i\left({\underline{x}}_i\right)={\displaystyle W_i^{\ast \mathrm{T}}}{\Psi }_i\left({\underline{x}}_i\right)+{\epsilon }_i$, and there exists constant ${\overline{\epsilon }}_i>0$ satisfying ${\epsilon }_i\le {\overline{\epsilon }}_i$.

The Lyapunov candidate function is selected as

$$V_i=V_{i-1}+\frac{1}{2}ln\frac{{\displaystyle k_{b_i}^2}}{{\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}}+\frac{g_{imin}}{2{\gamma }_i}{\displaystyle {\tilde{\theta }}_i^2}+\frac{1}{2}{\displaystyle {\zeta }_i^2}$$

(31)

where ${\tilde{\theta }}_i={\displaystyle {\theta }_i^{\ast }}-{\theta }_i$ denotes the estimation error.

The $\alpha \mathrm{th}$ Caputo fractional derivative of $V_i$ is

$$\begin{array}{c}{\displaystyle D^{\alpha }{V}_i=D^{\alpha }{V}_{i-1}+\frac{{\vartheta }_i}{{\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}}{\displaystyle W_i^{\ast \mathrm{T}}}{\Psi }_i\left({\underline{x}}_i\right)}\hfill \\ {\displaystyle +\frac{{\vartheta }_i}{{\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}}\left({\epsilon }_i+g_i\left({\underline{x}}_i\right)\left({\vartheta }_{i+1}+{\zeta }_{i+1}+{\mathsf{{\rm Y}}}_i\right)-D^{\alpha }{\mathsf{{\rm Y}}}_{i.l}\right)}\hfill \\ {\displaystyle -\frac{g_{imin}}{{\gamma }_i}{\tilde{\theta }}_i{D}^{\alpha }{\theta }_i+{\zeta }_i{D}^{\alpha }{\zeta }_i}\hfill \end{array}$$

(32)

According to the Young’s inequality, the following inequality can be obtained:

$$\frac{{\vartheta }_i}{{\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}}{\displaystyle W_i^{\ast \mathrm{T}}}{\Psi }_i\left({\underline{x}}_i\right)\le \frac{1}{2{\displaystyle b_i^2}}\frac{{\displaystyle {\vartheta }_i^2}}{{\left({\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}\right)}^2}{\displaystyle {\theta }_i^{\ast }}{g}_{imin}{∥{\Psi }_i\left({\underline{x}}_i\right)∥}^2+\frac{1}{2}{\displaystyle b_i^2}$$

(33)

$$\frac{{\vartheta }_i\left({\epsilon }_i+g_i\left({\underline{x}}_i\right){\zeta }_{i+1}\right)}{{\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}}\le \frac{{\displaystyle d_i^2}\left(1+{\displaystyle g_{imax}^2}\right){\displaystyle {\vartheta }_i^2}}{2{\left({\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}\right)}^2}+\frac{1}{2}{\displaystyle d_i^2}{\displaystyle {\overline{\epsilon }}_i^2}+\frac{1}{2}{\displaystyle d_i^2}{\displaystyle {\zeta }_{i+1}^2}$$

(34)

Substituting (33) and (34) into (32), yields

$$\begin{array}{c}{\displaystyle D^{\alpha }{V}_i\le D^{\alpha }{V}_{i-1}+\frac{1}{2{\displaystyle b_i^2}}\frac{{\displaystyle {\vartheta }_i^2}}{{\left({\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}\right)}^2}{\displaystyle {\theta }_i^{\ast }}{g}_{imin}{∥{\Psi }_i\left({\underline{x}}_i\right)∥}^2+\frac{1}{2}{\displaystyle b_i^2}}\hfill \\ {\displaystyle -\frac{g_{imin}}{{\gamma }_i}{\tilde{\theta }}_i{D}^{\alpha }{\theta }_i+{\zeta }_i{D}^{\alpha }{\zeta }_i+\frac{\left(1+{\displaystyle g_{imax}^2}\right){\displaystyle {\vartheta }_i^2}}{2{\left({\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}\right)}^2}+\frac{1}{2}{\displaystyle d_i^2}{\displaystyle {\overline{\epsilon }}_i^2}+\frac{1}{2}{\displaystyle d_i^2}{\displaystyle {\zeta }_{i+1}^2}}\hfill \\ {\displaystyle +\frac{{\vartheta }_i}{{\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}}\left(g_i\left({\underline{x}}_i\right)\left({\vartheta }_{i+1}+{\mathsf{{\rm Y}}}_i\right)-D^{\alpha }{\mathsf{{\rm Y}}}_{i.l}\right)}\hfill \end{array}$$

(35)

Based on Lemma 5, formulas (12), (13), and DSC technology, one can get

$$D^{\alpha }{\zeta }_i=D^{\alpha }{\mathsf{{\rm Y}}}_{i.l}-D^{\alpha }{\mathsf{{\rm Y}}}_{i-1}=-\frac{{\zeta }_i}{{\kappa }_i}+H_i\left(·\right)$$

(36)

where

$$H_i\left(·\right)=-{\displaystyle \sum _{j=1}^{i-1}}\frac{\partial {\mathsf{{\rm Y}}}_{i-1}}{\partial x_j}{D}^{\alpha }{x}_j-\frac{\partial {\mathsf{{\rm Y}}}_{i-1}}{\partial {\theta }_{i-1}}{D}^{\alpha }{\theta }_{i-1}-\frac{\partial {\mathsf{{\rm Y}}}_{i-1}}{\partial {\mathsf{{\rm Y}}}_{i-1.l}}{D}^{\alpha }{\mathsf{{\rm Y}}}_{i-1.l}$$

(37)

Substituting (15), (19) and (36) into (35), the $D^{\alpha }{V}_i$ can be rewritten as

$$\begin{array}{c}{\displaystyle D^{\alpha }{V}_i\le D^{\alpha }{V}_{i-1}+\frac{g_i\left({\underline{x}}_i\right){\vartheta }_i{\vartheta }_{i+1}}{{\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}}}\hfill \\ {\displaystyle -\frac{c_i{\displaystyle {\vartheta }_i^{2\rho }}}{{\left({\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}\right)}^{\rho }}-\frac{g_{i-1}\left({\underline{x}}_{i-1}\right){\vartheta }_{i-1}{\vartheta }_i}{\left({\displaystyle k_{b_{i-1}}^2}-{\displaystyle {\vartheta }_{i-1}^2}\right)}}\hfill \\ {\displaystyle +\frac{g_{imin}{\varsigma }_i}{{\gamma }_i}{\tilde{\theta }}_i{\theta }_i+{\zeta }_i{D}^{\alpha }{\zeta }_i+\frac{1}{2}{\displaystyle d_i^2}{\displaystyle {\overline{\epsilon }}_i^2}+\frac{1}{2}{\displaystyle d_i^2}{\displaystyle {\zeta }_{i+1}^2}+\frac{1}{2}{\displaystyle b_i^2}}\hfill \\ {\displaystyle \le -{\displaystyle \sum _{j=1}^{i-1}}\frac{c_j{\displaystyle {\vartheta }_j^{2\rho }}}{{\left({\displaystyle k_{b_j}^2}-{\displaystyle {\vartheta }_j^2}\right)}^{\rho }}+{\displaystyle \sum _{j=1}^{i-1}}\frac{g_{jmin}{\varsigma }_j}{{\gamma }_j}{\tilde{\theta }}_j{\theta }_j}\hfill \\ {\displaystyle +{\displaystyle \sum _{j=1}^{i-1}}\frac{1}{2}{\displaystyle d_j^2}{\displaystyle {\overline{\epsilon }}_j^2}+{\displaystyle \sum _{j=1}^{i-1}}\frac{1}{2}{\displaystyle d_j^2}{\displaystyle {\zeta }_{j+1}^2}+{\displaystyle \sum _{j=1}^{i-1}}\frac{1}{2}{\displaystyle b_j^2}}\hfill \\ {\displaystyle +\frac{g_{i-1}\left({\underline{x}}_{i-1}\right){\vartheta }_{i-1}{\vartheta }_i}{{\displaystyle k_{b_{i-1}}^2}-{\displaystyle {\vartheta }_{i-1}^2}}+{\displaystyle \sum _{j=1}^{i-2}}{\zeta }_{j+1}{D}^{\alpha }{\zeta }_{j+1}}\hfill \\ {\displaystyle +\frac{g_i\left({\underline{x}}_i\right){\vartheta }_i{\vartheta }_{i+1}}{{\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}}-\frac{c_i{\displaystyle {\vartheta }_i^{2\rho }}}{{\left({\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}\right)}^{\rho }}-\frac{g_{i-1}\left({\underline{x}}_{i-1}\right){\vartheta }_{i-1}{\vartheta }_i}{\left({\displaystyle k_{b_{i-1}}^2}-{\displaystyle {\vartheta }_{i-1}^2}\right)}}\hfill \\ {\displaystyle +\frac{g_{imin}{\varsigma }_i}{{\gamma }_i}{\tilde{\theta }}_i{\theta }_i+{\zeta }_i{D}^{\alpha }{\zeta }_i+\frac{1}{2}{\displaystyle {\overline{\epsilon }}_i^2}+\frac{1}{2}{\displaystyle {\zeta }_{i+1}^2}+\frac{1}{2}{\displaystyle b_i^2}}\hfill \\ {\displaystyle \le -{\displaystyle \sum _{j=1}^i}\frac{c_j{\displaystyle {\vartheta }_j^{2\rho }}}{{\left({\displaystyle k_{b_j}^2}-{\displaystyle {\vartheta }_j^2}\right)}^{\rho }}+{\displaystyle \sum _{j=1}^i}\frac{g_{jmin}{\varsigma }_j}{{\gamma }_j}{\tilde{\theta }}_j{\theta }_j}\hfill \\ {\displaystyle +{\displaystyle \sum _{j=1}^i}\frac{1}{2}{\displaystyle d_j^2}{\displaystyle {\overline{\epsilon }}_j^2}+{\displaystyle \sum _{j=1}^i}\frac{1}{2}{\displaystyle d_j^2}{\displaystyle {\zeta }_{j+1}^2}+{\displaystyle \sum _{j=1}^i}\frac{1}{2}{\displaystyle b_j^2}}\hfill \\ {\displaystyle -{\displaystyle \sum _{j=1}^{i-1}}\frac{{\displaystyle {\zeta }_{j+1}^2}}{{\kappa }_{j+1}}+{\displaystyle \sum _{j=1}^{i-1}}\left|{\zeta }_{j+1}{H}_{j+1}\left(·\right)\right|+\frac{g_i\left({\underline{x}}_i\right){\vartheta }_i{\vartheta }_{i+1}}{{\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}}}\hfill \end{array}$$

(38)

Step n: From (6) and (12), one can get

$$\begin{array}{c}{D}^{\alpha }{\vartheta }_n=D^{\alpha }{x}_n-D^{\alpha }{\mathsf{{\rm Y}}}_{n.l}\hfill \\ =f_n\left(x\right)+g_n\left(x\right)\left(h_{{\nu }_{\mu }}\nu +\Delta \left(\nu \right)\right)-D^{\alpha }{\mathsf{{\rm Y}}}_{n.l}\hfill \\ ={\displaystyle W_n^{\ast \mathrm{T}}}{\Psi }_n\left(x\right)+{\epsilon }_n+g_n\left(x\right)h_{{\nu }_{\mu }}\nu +g_n\left(x\right)\Delta \left(\nu \right)-D^{\alpha }{\mathsf{{\rm Y}}}_{n.l}\hfill \end{array}$$

(39)

where $f_n\left(x\right)={\displaystyle W_n^{\ast \mathrm{T}}}{\Psi }_n\left(x\right)+{\epsilon }_n$, and ${\epsilon }_n\le {\overline{\epsilon }}_n,{\overline{\epsilon }}_n>0$.

The Lyapunov function candidate is as following

$$V_n=V_{n-1}+\frac{1}{2}ln\frac{{\displaystyle k_{b_n}^2}}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}+\frac{g_{nmin}}{2{\gamma }_n}{\displaystyle {\tilde{\theta }}_n^2}+\frac{1}{2}{\displaystyle {\zeta }_n^2}$$

(40)

where ${\tilde{\theta }}_n={\displaystyle {\theta }_n^{\ast }}-{\theta }_n$.

Then, one can have

$$\begin{array}{c}{\displaystyle D^{\alpha }{V}_n=D^{\alpha }{V}_{n-1}+\frac{{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}{\displaystyle W_n^{\ast \mathrm{T}}}{\Psi }_n\left(x\right)}\hfill \\ {\displaystyle +\frac{{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}\left({\epsilon }_n+g_n\left(x\right)h_{{\nu }_{\mu }}\nu +g_n\left(x\right)\Delta \left(\nu \right)-D^{\alpha }{\mathsf{{\rm Y}}}_{n.l}\right)}\hfill \\ {\displaystyle -\frac{g_{nmin}}{{\gamma }_n}{\displaystyle {\tilde{\theta }}_n^{ }}{D}^{\alpha }{\theta }_n+{\zeta }_n{D}^{\alpha }{\zeta }_n}\hfill \end{array}$$

(41)

It is true that

$$\frac{{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}{\displaystyle W_n^{\ast \mathrm{T}}}{\Psi }_n\left(x\right)\le \frac{1}{2{\displaystyle b_n^2}}\frac{{\displaystyle {\vartheta }_n^2}}{{\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}^2}{\displaystyle {\theta }_n^{\ast }}{g}_{nmin}{∥{\Psi }_n\left(x\right)∥}^2+\frac{1}{2}{\displaystyle b_n^2}$$

(42)

$$\frac{{\vartheta }_n\left({\epsilon }_n+g_n\left(x\right)\Delta \left(\nu \right)\right)}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}\le \frac{{\displaystyle d_n^2}\left(1+{\displaystyle g_{nmax}^2}\right){\displaystyle {\vartheta }_n^2}}{2{\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}^2}+\frac{1}{2}{\displaystyle d_n^2}{\displaystyle {\overline{\epsilon }}_n^2}+\frac{1}{2}{\displaystyle d_n^2}{D}^2$$

(43)

and

$$D^{\alpha }{\zeta }_n=D^{\alpha }{\mathsf{{\rm Y}}}_{n.l}-D^{\alpha }{\mathsf{{\rm Y}}}_{n-1}=-\frac{{\zeta }_n}{{\kappa }_n}+H_n\left(·\right)$$

(44)

where

$$H_n\left(·\right)=-{\displaystyle \sum _{j=1}^n}\frac{\partial {\mathsf{{\rm Y}}}_{n-1}}{\partial x_j}{D}^{\alpha }{x}_j-\frac{\partial {\mathsf{{\rm Y}}}_{n-1}}{\partial {\theta }_{n-1}}{D}^{\alpha }{\theta }_{n-1}-\frac{\partial {\mathsf{{\rm Y}}}_{n-1}}{\partial {\mathsf{{\rm Y}}}_{n-1.l}}{D}^{\alpha }{\mathsf{{\rm Y}}}_{n-1.l}$$

(45)

From Assumption 1 and the boundedness of one $V_n$ are compact, there exists a constant ${\Xi }_i>0$, such that $\left|H_i\right|\le {\Xi }_i$. Then the following inequality holds:

$$\left|{\zeta }_i{H}_i\right|\le \frac{{\displaystyle {\zeta }_i^2}{\displaystyle {\Xi }_i^2}}{2{\stackrel{⌢}{q}}_i}+\frac{{\stackrel{⌢}{q}}_i}{2}$$

(46)

where ${\stackrel{⌢}{q}}_i>0$, $i=1,2,\dots ,n$.

Substitute (42)–(46), (16) and (20) into (41) yields

$$\begin{array}{c}{\displaystyle D^{\alpha }{V}_n\le D^{\alpha }{V}_{n-1}+\frac{1}{2{\displaystyle b_n^2}}\frac{{\displaystyle {\vartheta }_n^2}}{{\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}^2}{\displaystyle {\theta }_n^{\ast }}{g}_{nmin}{∥{\Psi }_n\left(x\right)∥}^2}\hfill \\ {\displaystyle +\frac{1}{2}{\displaystyle b_n^2}+\frac{{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}\left(g_n\left(x\right)h_{{\nu }_{\mu }}\nu -D^{\alpha }{\mathsf{{\rm Y}}}_{n.l}\right)}\hfill \\ {\displaystyle +\frac{{\displaystyle d_n^2}\left(1+{\displaystyle g_{nmax}^2}\right){\displaystyle {\vartheta }_n^2}}{2{\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}^2}+\frac{1}{2}{\displaystyle d_n^2}{\displaystyle {\overline{\epsilon }}_n^2}+\frac{1}{2}{\displaystyle d_n^2}{D}^2}\hfill \\ {\displaystyle -\frac{g_{nmin}}{{\gamma }_n}{\displaystyle {\tilde{\theta }}_n^{ }}{D}^{\alpha }{\theta }_n-\frac{{\displaystyle {\zeta }_n^2}}{{\kappa }_n}+\left|{\zeta }_n{H}_n\left(·\right)\right|}\hfill \\ {\displaystyle \le D^{\alpha }{V}_{n-1}-\frac{{\displaystyle {\zeta }_n^2}}{{\kappa }_n}+\frac{{\displaystyle {\zeta }_n^2}{\displaystyle {\Xi }_n^2}}{2{\stackrel{⌢}{q}}_n}+\frac{{\stackrel{⌢}{q}}_n}{2}+\frac{1}{2}{\displaystyle d_n^2}{\displaystyle {\overline{\epsilon }}_n^2}}\hfill \\ {\displaystyle +\frac{1}{2}{\displaystyle d_n^2}{D}^2+\frac{1}{2}{\displaystyle b_n^2}+\frac{{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}\left(g_n\left(x\right)h_{{\nu }_{\mu }}\nu -D^{\alpha }{\mathsf{{\rm Y}}}_{n.l}\right)}\hfill \\ {\displaystyle +\left(\frac{1}{2{\displaystyle b_n^2}}{\theta }_n{g}_{nmin}{∥{\Psi }_n\left(x\right)∥}^2+\frac{1+{\displaystyle g_{nmax}^2}}{2}{\displaystyle d_n^2}\right)\frac{{\displaystyle {\vartheta }_n^2}}{{\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}^2}}\hfill \\ {\displaystyle -\frac{g_{nmin}}{{\gamma }_n}{\displaystyle {\tilde{\theta }}_n^{ }}\left(D^{\alpha }{\theta }_n-\frac{{\gamma }_n}{2{\displaystyle b_n^2}}\frac{{\displaystyle {\vartheta }_n^2}}{{\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}^2}{∥{\Psi }_n\left(x\right)∥}^2\right)}\hfill \end{array}$$

(47)

Theorem 1.

Consider the nonlinear FOSs (1) with the Assumptions 1 and 2. If the initial conditions satisfy $x_i\left(0\right)\in {\Omega }_x=\left\{\left.x_i\right|\left|x_i\left(0\right)\right|<k_{c_i}\right\}$, the actual controller (18) with virtual controllers (14)–(16), and parameter adaptive laws (19) and (20) can confirm that all the signals in the closed-loop system are bounded, all the states $x\left(t\right)$ do not transgress the pregiven sets, and the Zeno behavior is excluded. Moreover, for  $\forall t\ge T$, the closed-loop error signal  ${\displaystyle {\vartheta }_i^{ }}$ will stay around the compact set

$${\Omega }_{{\vartheta }_i}=\left\{\left.{\vartheta }_i\right|\left|{\vartheta }_i\right|\le {\displaystyle k_{b_i}^{ }}\sqrt{1-e^{-2{\left(\mathrm{M}/\phantom{\mathrm{M}\left(\sigma \left(1-\vartheta \right)\right)}\left(\sigma \left(1-\vartheta \right)\right)\right)}^{1/\phantom{1\rho }\rho }}}\right\},i=1,2,\dots ,n$$

(48)

 where 

$$\begin{array}{c}{\displaystyle T={\left(\frac{\Gamma \left(\frac{2-\rho }{1-\rho }\right)\Gamma \left(2-\alpha \right)\Gamma \left(\alpha +1\right)}{\sigma \vartheta \Gamma \left(\frac{2-\rho }{1-\rho }-\alpha \right)}\left({\displaystyle V_n^{1-\rho }}\left(0\right)-{\left(\frac{\mathrm{M}}{\sigma \left(1-\vartheta \right)}\right)}^{\frac{1}{\rho }}\right)\right)}^{\frac{1}{\alpha }}}\hfill \\ \vartheta \in \left(0,1\right)\hfill \end{array}$$

(49)

Proof. 

From the definition $\Delta \left(t\right)=\Theta \left(t\right)-u\left(t\right)$ and (22), one can have

$$\Theta \left(t\right)=\left(1+{\displaystyle {\lambda }_1^{\ast }}{\lambda }_1\left(t\right)\right)u\left(t\right)+{\displaystyle {\lambda }_2^{\ast }}{\lambda }_2\left(t\right)$$

(50)

where $\left|{\lambda }_1\left(t\right)\right|\le 1$ and $\left|{\lambda }_2\left(t\right)\right|\le 1$. Accordingly, one can obtain

$$\nu \left(t\right)=\frac{\Theta \left(t\right)-{\displaystyle {\lambda }_2^{\ast }}{\lambda }_2\left(t\right)}{1+{\displaystyle {\lambda }_1^{\ast }}{\lambda }_1\left(t\right)}$$

(51)

According to (16), (18), (19) and (51), inequality (47) can be rewritten as

$$\begin{array}{c}{\displaystyle D^{\alpha }{V}_n\le D^{\alpha }{V}_{n-1}+\frac{g_n\left(x\right)h_{{\nu }_{\mu }}{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}\frac{\Theta \left(t\right)-{\displaystyle {\lambda }_2^{\ast }}{\lambda }_2\left(t\right)}{1+{\displaystyle {\lambda }_1^{\ast }}{\lambda }_1\left(t\right)}}\hfill \\ {\displaystyle -\frac{c_n{\displaystyle {\vartheta }_n^{2\rho }}}{{\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}^{\rho }}-\frac{g_{n-1}\left({\underline{x}}_{n-1}\right){\vartheta }_{n-1}{\vartheta }_n}{{\displaystyle k_{b_{n-1}}^2}-{\displaystyle {\vartheta }_{n-1}^2}}}\hfill \\ {\displaystyle -g_n\left(x\right)h_{{\nu }_{\mu }}\frac{{\mathsf{{\rm Y}}}_n{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}+\frac{g_{nmin}}{{\gamma }_n}{\varsigma }_n{\displaystyle {\tilde{\theta }}_n^{ }}{\theta }_n}\hfill \\ {\displaystyle -\frac{{\displaystyle {\zeta }_n^2}}{{\kappa }_n}+\frac{{\displaystyle {\zeta }_n^2}{\displaystyle {\Xi }_n^2}}{2{\stackrel{⌢}{q}}_n}+\frac{{\stackrel{⌢}{q}}_n}{2}+\frac{1}{2}{\displaystyle d_n^2}{\displaystyle {\overline{\epsilon }}_n^2}+\frac{1}{2}{\displaystyle d_n^2}{D}^2+\frac{1}{2}{\displaystyle b_n^2}}\hfill \end{array}$$

(52)

In view of $\left|{\lambda }_1\left(t\right)\right|\le 1$ and $\left|{\lambda }_2\left(t\right)\right|\le 1$, one can have

$$\begin{array}{c}{\displaystyle \frac{\Theta \left(t\right){\vartheta }_n}{1+{\displaystyle {\lambda }_1^{\ast }}{\lambda }_1\left(t\right)}\le \frac{\Theta \left(t\right){\vartheta }_n}{1+{\displaystyle {\lambda }_1^{\ast }}}}\hfill \\ {\displaystyle \frac{{\displaystyle {\lambda }_2^{\ast }}{\lambda }_2\left(t\right)}{1+{\displaystyle {\lambda }_1^{\ast }}{\lambda }_1\left(t\right)}\le \left|\frac{{\displaystyle {\lambda }_2^{\ast }}}{1-{\displaystyle {\lambda }_1^{\ast }}}\right|}\hfill \end{array}$$

(53)

Using Lemma 7, it follows that

$$\begin{array}{c}{D}^{\alpha }{V}_n⩽D^{\alpha }{V}_{n-1}+\frac{g_{nmin}}{{\gamma }_n}{\varsigma }_n{\displaystyle {\tilde{\theta }}_n^{ }}{\theta }_n-\frac{c_n{\displaystyle {\vartheta }_n^{2\rho }}}{{\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}^{\rho }}\hfill \\ -\frac{g_n\left(x\right)h_{{\nu }_{\mu }}{\mathsf{{\rm Y}}}_n{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}-\frac{{\mathsf{{\rm Y}}}_n{\vartheta }_n{g}_n\left(x\right)}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}tanh\left(\frac{{\mathsf{{\rm Y}}}_n{\vartheta }_n}{{\kappa }^{\ast }\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}\right)\hfill \\ -\frac{g_n\left(x\right)h_{{\nu }_{\mu }}{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}\frac{{\displaystyle {\lambda }_2^{\ast }}{\lambda }_2\left(t\right)}{1+{\displaystyle {\lambda }_1^{\ast }}{\lambda }_1\left(t\right)}+\frac{{\displaystyle {\overline{\lambda }}_2^{\ast }}{\vartheta }_n{g}_n\left(x\right)}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}tanh\left(\frac{{\displaystyle {\overline{\lambda }}_2^{\ast }}{\vartheta }_n}{{\kappa }^{\ast }\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}\right)\hfill \\ -\frac{g_{n-1}\left({\underset{-}{x}}_{n-1}\right){\vartheta }_{n-1}{\vartheta }_n}{{\displaystyle k_{b_{n-1}}^2}-{\displaystyle {\vartheta }_{n-1}^2}}-\frac{{\displaystyle {\zeta }_n^2}}{{\kappa }_n}+\frac{{\displaystyle {\zeta }_n^2}{\displaystyle {\Xi }_n^2}}{2{\stackrel{⌢}{q}}_n}+\frac{{\stackrel{⌢}{q}}_n}{2}+\frac{1}{2}{\displaystyle d_n^2}{\displaystyle {\overline{\epsilon }}_n^2}+\frac{1}{2}{\displaystyle d_n^2}{D}^2+\frac{1}{2}{\displaystyle b_n^2}\hfill \\ ⩽D^{\alpha }{V}_{n-1}+\frac{g_{nmin}}{{\gamma }_n}{\varsigma }_n{\displaystyle {\tilde{\theta }}_n^{ }}{\theta }_n-\frac{c_n{\displaystyle {\vartheta }_n^{2\rho }}}{{\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}^{\rho }}\hfill \\ +h_{{\nu }_{\mu }}{g}_n\left(x\right)\left(\left|\frac{{\displaystyle {\overline{\lambda }}_2^{\ast }}{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}\right|-\frac{{\displaystyle {\overline{\lambda }}_2^{\ast }}{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}tanh\left(\frac{{\displaystyle {\overline{\lambda }}_2^{\ast }}{\vartheta }_n}{{\kappa }^{\ast }\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}\right)\right)\hfill \\ +h_{{\nu }_{\mu }}{g}_n\left(x\right)\left(\left|\frac{{\mathsf{{\rm Y}}}_n{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}\right|-\frac{{\mathsf{{\rm Y}}}_n{\vartheta }_n}{{\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}}tanh\left(\frac{{\mathsf{{\rm Y}}}_n{\vartheta }_n}{{\kappa }^{\ast }\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}\right)\right)\hfill \\ -\frac{g_{n-1}\left({\underset{-}{x}}_{n-1}\right){\vartheta }_{n-1}{\vartheta }_n}{{\displaystyle k_{b_{n-1}}^2}-{\displaystyle {\vartheta }_{n-1}^2}}-\frac{{\displaystyle {\zeta }_n^2}}{{\kappa }_n}+\frac{{\displaystyle {\zeta }_n^2}{\displaystyle {\Xi }_n^2}}{2{\stackrel{⌢}{q}}_n}+\frac{{\stackrel{⌢}{q}}_n}{2}+\frac{1}{2}{\displaystyle d_n^2}{\displaystyle {\overline{\epsilon }}_n^2}+\frac{1}{2}{\displaystyle d_n^2}{D}^2+\frac{1}{2}{\displaystyle b_n^2}\hfill \\ ⩽D^{\alpha }{V}_{n-1}-\frac{c_n{\displaystyle {\vartheta }_n^{2\rho }}}{{\left({\displaystyle k_{b_n}^2}-{\displaystyle {\vartheta }_n^2}\right)}^{\rho }}-\frac{g_{n-1}\left({\underset{-}{x}}_{n-1}\right){\vartheta }_{n-1}{\vartheta }_n}{{\displaystyle k_{b_{n-1}}^2}-{\displaystyle {\vartheta }_{n-1}^2}}-\frac{g_{nmin}}{{\gamma }_n}{\varsigma }_n{\displaystyle {\tilde{\theta }}_n^{ }}{\theta }_n\hfill \\ -\frac{{\displaystyle {\zeta }_n^2}}{{\kappa }_n}+\frac{{\displaystyle {\zeta }_n^2}{\displaystyle {\Xi }_n^2}}{2{\stackrel{⌢}{q}}_n}+\frac{{\stackrel{⌢}{q}}_n}{2}+\frac{1}{2}{\displaystyle d_n^2}{\displaystyle {\overline{\epsilon }}_n^2}+\frac{1}{2}{\displaystyle d_n^2}{D}^2+\frac{1}{2}{\displaystyle b_n^2}+0.557{\kappa }^{\ast }{g}_{nmax}{h}_{{\nu }_{\mu }}\hfill \\ ⩽-{\displaystyle \sum _{j=1}^n}\frac{c_j{\displaystyle {\vartheta }_j^{2\rho }}}{{\left({\displaystyle k_{b_j}^2}-{\displaystyle {\vartheta }_j^2}\right)}^{\rho }}+{\displaystyle \sum _{j=1}^n}\frac{g_{jmin}{\varsigma }_j}{{\gamma }_j}{\tilde{\theta }}_j{\theta }_j\hfill \\ +{\displaystyle \sum _{j=1}^{n-1}}\frac{1}{2}{\displaystyle d_j^2}{\displaystyle {\zeta }_{j+1}^2}-{\displaystyle \sum _{j=1}^{n-1}}\frac{{\displaystyle {\zeta }_{j+1}^2}}{{\kappa }_{j+1}}+{\displaystyle \sum _{j=1}^{n-1}}\frac{{\displaystyle {\zeta }_{j+1}^2}{\displaystyle {\Xi }_{j+1}^2}}{2{\stackrel{⌢}{q}}_{j+1}}+{\displaystyle \sum _{j=1}^{n-1}}\frac{{\stackrel{⌢}{q}}_{j+1}}{2}\hfill \\ +{\displaystyle \sum _{j=1}^n}\frac{1}{2}{\displaystyle d_j^2}{\displaystyle {\overline{\epsilon }}_j^2}+{\displaystyle \sum _{j=1}^n}\frac{1}{2}{\displaystyle b_j^2}+\frac{1}{2}{\displaystyle d_n^2}{D}^2+0.557{\kappa }^{\ast }{g}_{nmax}{h}_{{\nu }_{\mu }}\hfill \end{array}$$

(54)

Based on the estimation error ${\tilde{\theta }}_j={\displaystyle {\theta }_j^{\ast }}-{\theta }_j$, the following inequality holds:

$${\displaystyle {\tilde{\theta }}_j^{ }}{\theta }_j\le \frac{1}{2}{\displaystyle {\theta }_j^{\ast 2}}-\frac{1}{2}{\displaystyle {\tilde{\theta }}_j^2}$$

(55)

Then, one can obtain

$${\displaystyle \sum _{j=1}^n}\frac{g_{jmin}{\varsigma }_j}{{\gamma }_j}{\tilde{\theta }}_j{\theta }_j\le {\displaystyle \sum _{j=1}^n}\frac{g_{jmin}{\varsigma }_j}{2{\gamma }_j}{\displaystyle {\theta }_i^{\ast 2}}-{\displaystyle \sum _{j=1}^n}\frac{g_{jmin}{\varsigma }_j}{2{\gamma }_j}{\displaystyle {\tilde{\theta }}_i^2}$$

(56)

From (56), (54) can be rewritten as

$$\begin{array}{c}{\displaystyle D^{\alpha }{V}_n\le -{\displaystyle \sum _{j=1}^n}\frac{c_j{\displaystyle {\vartheta }_j^{2\rho }}}{{\left({\displaystyle k_{b_j}^2}-{\displaystyle {\vartheta }_j^2}\right)}^{\rho }}+{\displaystyle \sum _{j=1}^n}\frac{g_{jmin}{\varsigma }_j}{2{\gamma }_j}{\displaystyle {\theta }_i^{\ast 2}}-{\displaystyle \sum _{j=1}^n}\frac{g_{jmin}{\varsigma }_j}{2{\gamma }_j}{\displaystyle {\tilde{\theta }}_i^2}}\hfill \\ {\displaystyle +{\displaystyle \sum _{j=1}^n}\frac{1}{2}{\displaystyle d_j^2}{\displaystyle {\overline{\epsilon }}_j^2}+{\displaystyle \sum _{j=1}^{n-1}}\frac{1}{2}{\displaystyle d_j^2}{\displaystyle {\zeta }_{j+1}^2}-{\displaystyle \sum _{j=1}^{n-1}}\frac{{\displaystyle {\zeta }_{j+1}^2}}{{\kappa }_{j+1}}+{\displaystyle \sum _{j=1}^{n-1}}\frac{{\displaystyle {\zeta }_{j+1}^2}{\displaystyle {\Xi }_{j+1}^2}}{2{\stackrel{⌢}{q}}_{j+1}}+{\displaystyle \sum _{j=1}^{n-1}}\frac{{\stackrel{⌢}{q}}_{j+1}}{2}}\hfill \\ {\displaystyle +{\displaystyle \sum _{j=1}^n}\frac{1}{2}{\displaystyle b_j^2}+\frac{1}{2}{\displaystyle d_n^2}{D}^2+0.557{\kappa }^{\ast }{g}_{nmax}{h}_{{\nu }_{\mu }}}\hfill \\ {\displaystyle \le -\sigma \left({{\displaystyle \sum _{j=1}^n}\left(\frac{{\displaystyle {\vartheta }_j^2}}{2\left({\displaystyle k_{b_j}^2}-{\displaystyle {\vartheta }_j^2}\right)}\right)}^{\rho }+{\displaystyle \sum _{j=1}^n}\frac{g_{jmin}}{2{\gamma }_j}{\displaystyle {\tilde{\theta }}_i^2}+{\displaystyle \sum _{j=1}^{n-1}}\frac{1}{2}{\displaystyle {\zeta }_{j+1}^2}\right)+\Theta }\hfill \end{array}$$

(57)

where

$$\begin{array}{c}\sigma =min\left\{2^{\rho }{c}_i,{\varsigma }_i,\frac{2}{{\kappa }_{j+1}}-{\displaystyle d_j^2}-\frac{{\displaystyle {\Xi }_{j+1}^2}}{{\stackrel{⌢}{q}}_{j+1}},i=1,\dots ,n;j=1,\dots ,n-1\right\}\hfill \\ \Theta ={\displaystyle \sum _{j=1}^n}\frac{1}{2}{\displaystyle d_j^2}{\displaystyle {\overline{\epsilon }}_j^2}+{\displaystyle \sum _{j=1}^n}\frac{1}{2}{\displaystyle b_j^2}+\frac{1}{2}{\displaystyle d_n^2}{D}^2+{\displaystyle \sum _{j=1}^n}\frac{g_{jmin}{\varsigma }_j}{2{\gamma }_j}{\displaystyle {\theta }_j^{\ast 2}}+{\displaystyle \sum _{j=1}^{n-1}}\frac{{\stackrel{⌢}{q}}_{j+1}}{2}\hfill \\ \begin{array}{cc} & \end{array}+0.557{\kappa }^{\ast }{g}_{nmax}{h}_{{\nu }_{\mu }}\hfill \end{array}$$

(58)

According to Lemma 1, choose $q_1=1, q_2={\displaystyle \sum _{j=1}^n}\frac{g_{jmin}}{2{\gamma }_j}{\displaystyle {\tilde{\theta }}_j^2}, s_1=1-\rho , s_2=\rho$ and $s_3={\rho }^{\frac{\rho }{1-\rho }}$, then one can obtain

$${\left({\displaystyle \sum _{j=1}^n}\frac{g_{jmin}}{2{\gamma }_j}{\displaystyle {\tilde{\theta }}_j^2}\right)}^{\rho }\le \left(1-\rho \right)s_3+{\displaystyle \sum _{j=1}^n}\frac{g_{jmin}}{2{\gamma }_j}{\displaystyle {\tilde{\theta }}_j^2}$$

(59)

$${\left({\displaystyle \sum _{j=1}^{n-1}}\frac{1}{2}{\displaystyle {\zeta }_{j+1}^2}\right)}^{\rho }\le \left(1-\rho \right)s_3+{\displaystyle \sum _{j=1}^{n-1}}\frac{1}{2}{\displaystyle {\zeta }_{j+1}^2}$$

(60)

Based on (59) and (60), (57) can be rewritten as

$$\begin{array}{c}{\displaystyle D^{\alpha }{V}_n\le -\sigma {\displaystyle \sum _{j=1}^n}{\left(\frac{{\displaystyle {\vartheta }_j^2}}{2\left({\displaystyle k_{b_j}^2}-{\displaystyle {\vartheta }_j^2}\right)}\right)}^{\rho }}\hfill \\ {\displaystyle \begin{array}{cc} & \end{array}\begin{array}{cc} & \end{array}-\sigma {\left({\displaystyle \sum _{j=1}^n}\frac{g_{jmin}}{2{\gamma }_j}{\displaystyle {\tilde{\theta }}_j^2}\right)}^{\rho }-\sigma {\left({\displaystyle \sum _{j=1}^{n-1}}\frac{1}{2}{\displaystyle {\zeta }_{j+1}^2}\right)}^{\rho }+\mathrm{M}}\hfill \end{array}$$

(61)

where $\mathrm{M}=2\sigma \left(1-\rho \right)s_3+\Theta$.

From Lemma 2, (61) can be described as

$$D^{\alpha }{V}_n\le -\sigma {\displaystyle V_n^{\rho }}+\mathrm{M}$$

(62)

For $\forall \vartheta \in \left(0,1\right)$, (2) can be rewritten as $D^{\alpha }{V}_n\le -\sigma \vartheta {\displaystyle V_n^{\rho }}-\sigma \left(1-\vartheta \right){\displaystyle V_n^{\rho }}+\mathrm{M}$. If $V_n>{\left(\mathrm{M}/\phantom{\mathrm{M}\left(\sigma \left(1-\vartheta \right)\right)}\left(\sigma \left(1-\vartheta \right)\right)\right)}^{\frac{1}{\rho }}$, one can obtain

$$D^{\alpha }{V}_n\le -\sigma \vartheta {\displaystyle V_n^{\rho }}$$

(63)

Let $V={\displaystyle V_n^{1-\rho }}$, then $D^{\alpha }{V}^{\frac{1}{1-\rho }}\le -\sigma \vartheta {\displaystyle V_{ }^{\frac{\rho }{1-\rho }}}$. From Lemma 6, one can get

$$D^{\alpha }{V}^{\frac{1}{1-\rho }}=\frac{\Gamma \left(\frac{2-\rho }{1-\rho }\right)\Gamma \left(2-\alpha \right)}{\Gamma \left(\frac{2-\rho }{1-\rho }-\alpha \right)}{V}^{\frac{\rho }{1-\rho }}{D}^{\alpha }V$$

(64)

Then

$${\displaystyle D^{\alpha }V\le -\sigma \vartheta \frac{\Gamma \left(\frac{2-\rho }{1-\rho }-\alpha \right)}{\Gamma \left(\frac{2-\rho }{1-\rho }\right)\Gamma \left(2-\alpha \right)}}$$

(65)

From $V={\displaystyle V_n^{1-\rho }}$, one get

$${\displaystyle V_n^{1-\rho }}\left(t\right)-{\displaystyle V_n^{1-\rho }}\left(0\right)\le -\sigma \vartheta \frac{\Gamma \left(\frac{2-\rho }{1-\rho }-\alpha \right)}{\Gamma \left(\frac{2-\rho }{1-\rho }\right)\Gamma \left(2-\alpha \right)}\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}$$

(66)

From (66), the finite time T can be designed as (49), and one can get

$$V_n\le {\left(\mathrm{M}/\phantom{\mathrm{M}\left(\sigma \left(1-\vartheta \right)\right)}\left(\sigma \left(1-\vartheta \right)\right)\right)}^{\frac{1}{\rho }},\forall t\ge T$$

(67)

Furthermore, based on the definition of $V_n$, one can obtain

$$\frac{1}{2}ln\frac{{\displaystyle k_{b_i}^2}}{{\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}}\le {\left(\mathrm{M}/\phantom{\mathrm{M}\left(\sigma \left(1-\vartheta \right)\right)}\left(\sigma \left(1-\vartheta \right)\right)\right)}^{\frac{1}{\rho }},\forall t\ge T$$

(68)

This implies that

$$\left|{\vartheta }_i\right|\le {\displaystyle k_{b_i}^{ }}\sqrt{1-e^{-2{\left(\mathrm{M}/\phantom{\mathrm{M}\left(\sigma \left(1-\vartheta \right)\right)}\left(\sigma \left(1-\vartheta \right)\right)\right)}^{1/\phantom{1\rho }\rho }}},\forall t\ge T$$

(69)

Then, after the finite time T, the tracking error converges to ${\Omega }_{{\vartheta }_i}$.

The boundedness of $ln\frac{{\displaystyle k_{b_k}^2}}{{\displaystyle k_{b_i}^2}-{\displaystyle {\vartheta }_i^2}}$ can be obtained according to (67), thus $\left|{\displaystyle {\vartheta }_i^{ }}\right|$ remains in the set $\left|{\displaystyle {\vartheta }_i^{ }}\right|<{\displaystyle k_{b_i}^{ }}$. Also, it holds that ${\tilde{\theta }}_i$ and ${\displaystyle {\zeta }_{i+1}^{ }}$ are bounded. As ${\vartheta }_1$ and $y_r\left(t\right)$ are bounded, then $x_1$ is bounded. From (14), ${\mathsf{{\rm Y}}}_1$ is a function of ${\vartheta }_1$ and ${\displaystyle {\theta }_1^{ }}$. Then, ${\mathsf{{\rm Y}}}_1$ is bounded and satisfies $\left|{\mathsf{{\rm Y}}}_1\right|<{\overline{\mathsf{{\rm Y}}}}_1,{\overline{\mathsf{{\rm Y}}}}_1>0$. Using ${\vartheta }_2=x_2-{\mathsf{{\rm Y}}}_{2.l}$ and ${\zeta }_2={\mathsf{{\rm Y}}}_{2.l}-{\mathsf{{\rm Y}}}_1$, one can get that ${\mathsf{{\rm Y}}}_{2.l}$ and $x_2$ are bounded. Similarly, the boundedness of states $x_i,i=3,\dots ,n$, virtual controllers ${\mathsf{{\rm Y}}}_i,i=2,\dots ,n-1$, and controller $\nu$ are all obtained. From $x_1={\vartheta }_1+y_r\left(t\right)$ and $\left|y_r\left(t\right)\right|\le A_0$ according to Assumption 1, one can have $\left|x_1\right|\le \left|{\vartheta }_1\right|+\left|y_r\left(t\right)\right|<k_{b_1}+A_0$. Define $k_{b_1}=k_{c_1}-A_0$, one obtain $\left|{\zeta }_2\right|\le \sqrt{2}{\left(\mathrm{M}/\phantom{\mathrm{M}\left(\sigma \left(1-\vartheta \right)\right)}\left(\sigma \left(1-\vartheta \right)\right)\right)}^{\frac{1}{2\rho }}={\Delta }_2$, for $\forall t\ge T$, yielding $\left|x_2\right|\le \left|{\vartheta }_2\right|+\left|{\zeta }_2\right|+\left|a_1\right|<k_{b_2}+{\Delta }_2+{\overline{a}}_1$. Let $k_{b_2}=k_{c_2}-{\Delta }_2-{\overline{a}}_1$, one can get $\left|x_2\right|<k_{c_2}$. Similarly, one can in turn obtain $\left|x_i\right|<k_{c_i}$, $i=3,\dots ,n$. Thus, the condition of the full-state constraints is accomplished.

Now we will show that the proposed strategy can avoid the Zeno behavior, i.e., one can always find a positive $a^{\ast }>0$ such that $t_{k+1}-t_k\ge a^{\ast },\forall k\in Z^{+}$. From the sampling error (21), one can get $D^{\alpha }\left|\mathsf{{\rm Y}}\left(t\right)\right|=sign\left(\mathsf{{\rm Y}}\left(t\right)\right)D^{\alpha }\mathsf{{\rm Y}}\left(t\right)\le \left|D^{\alpha }\Theta \left(t\right)\right|$. Due to (17), $D^{\alpha }\Theta \left(t\right)$ is bounded and $\exists \zeta >0$ satisfying $\left|D^{\alpha }\Theta \left(t\right)\right|<\zeta$. According to $\mathsf{{\rm Y}}\left(t_k\right) = 0$ and $\underset{t\to t_{k+1}}{lim}\mathsf{{\rm Y}}\left(t\right)={\displaystyle {\lambda }_2^{\ast }}$, one gets $t_{k+1}-t_k\ge \frac{{\displaystyle {\lambda }_2^{\ast }}}{\zeta }$, which avoids the Zeno phenomenon. This completes the proof. □

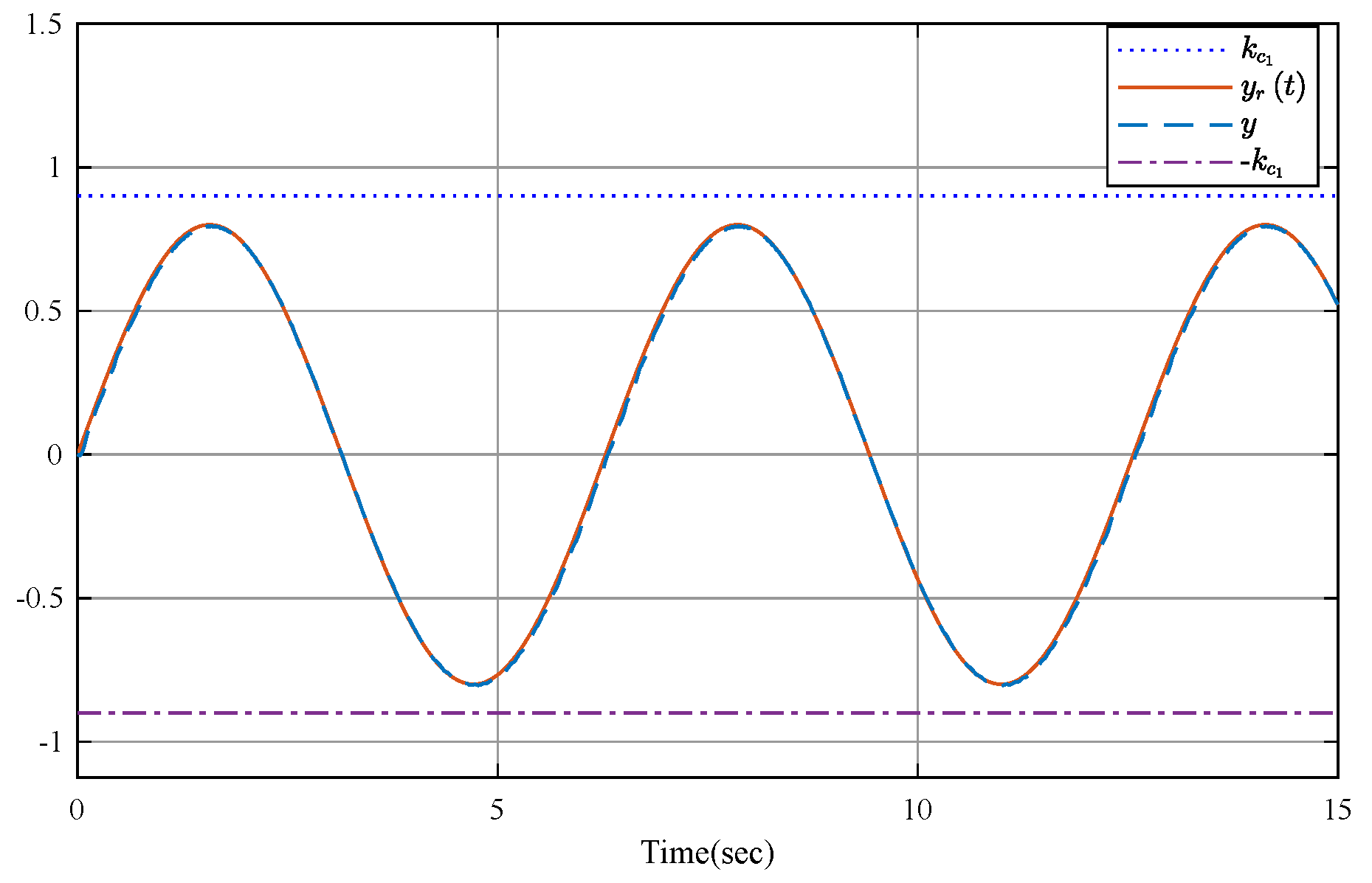
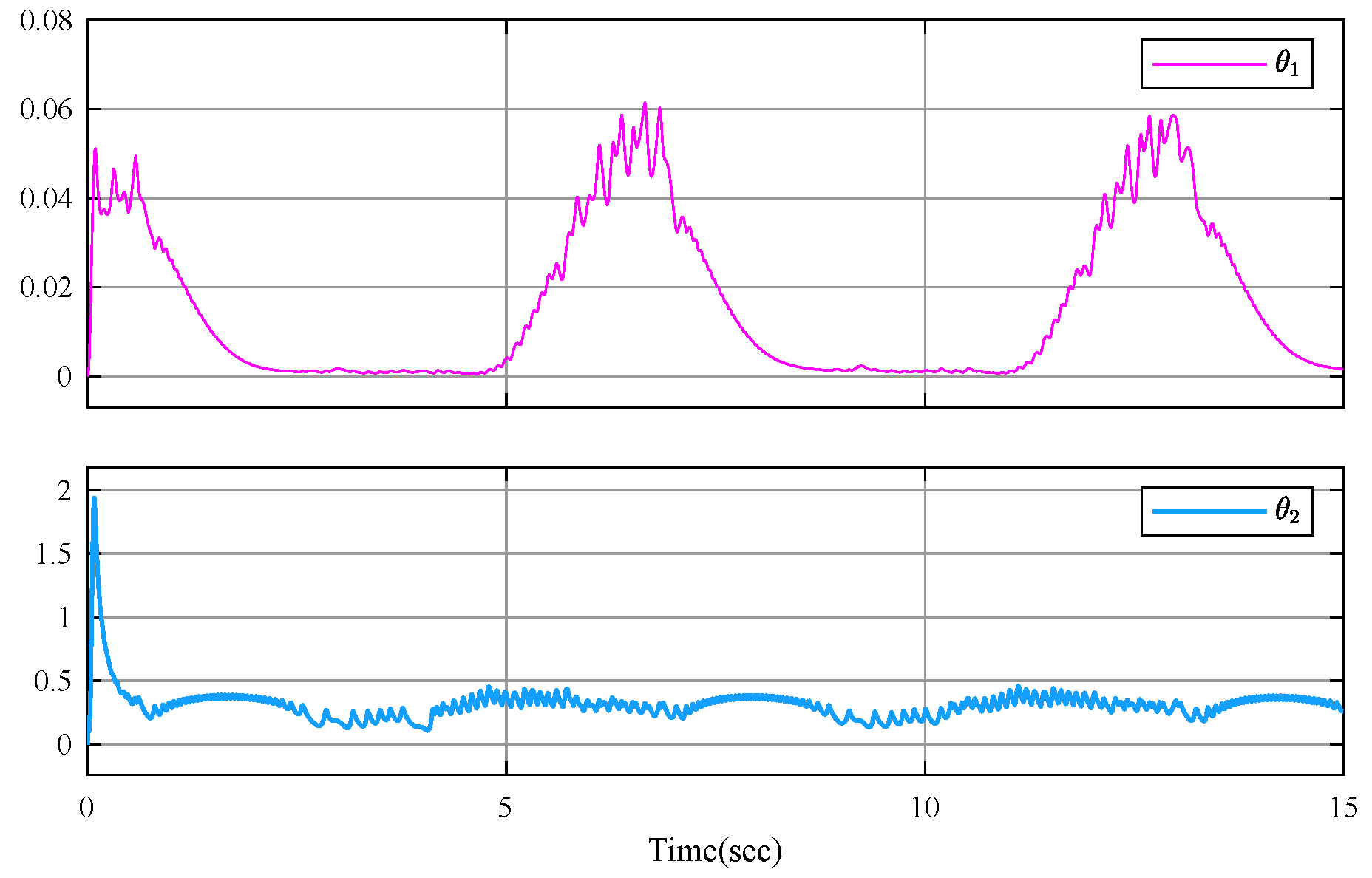
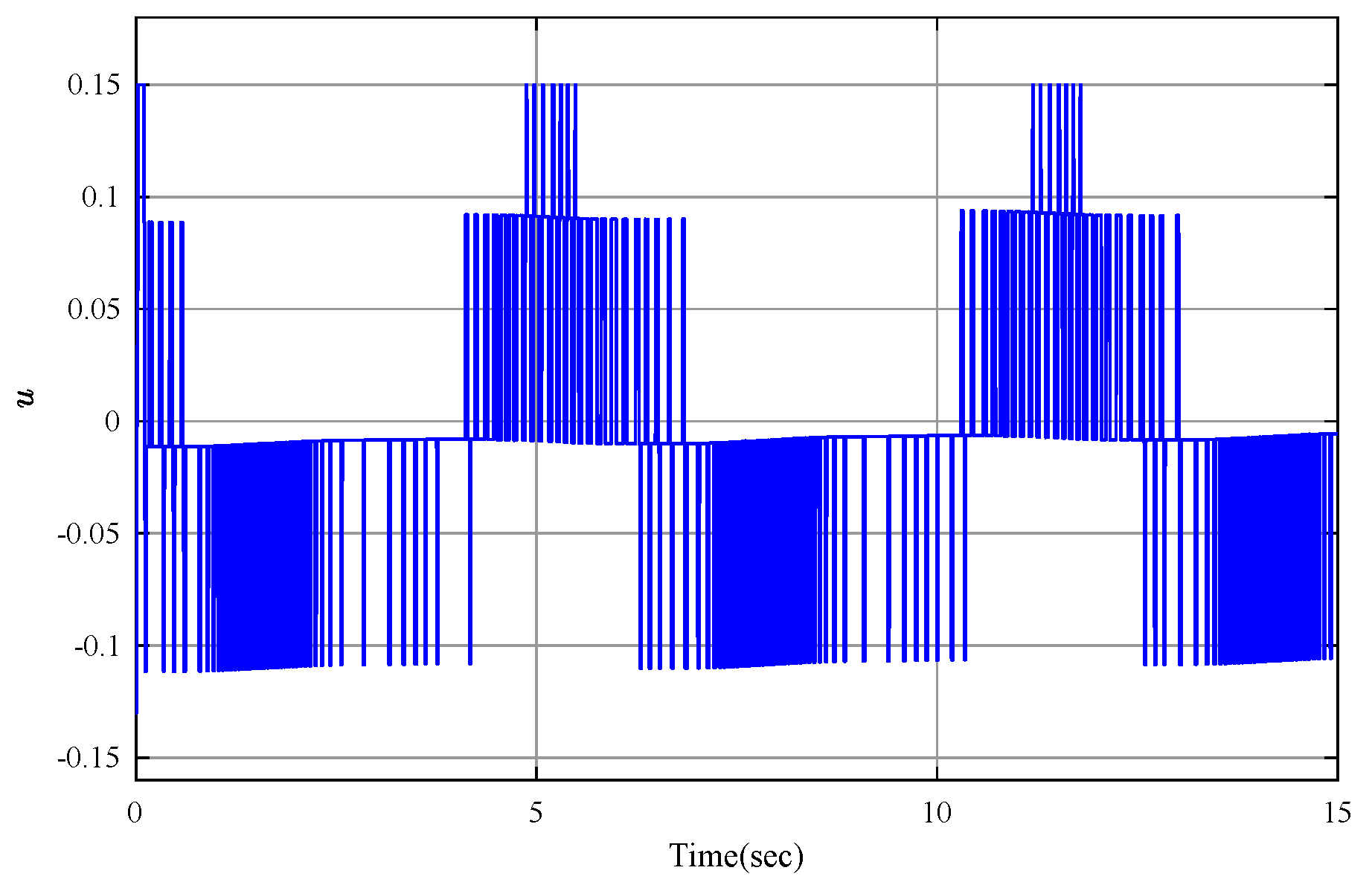
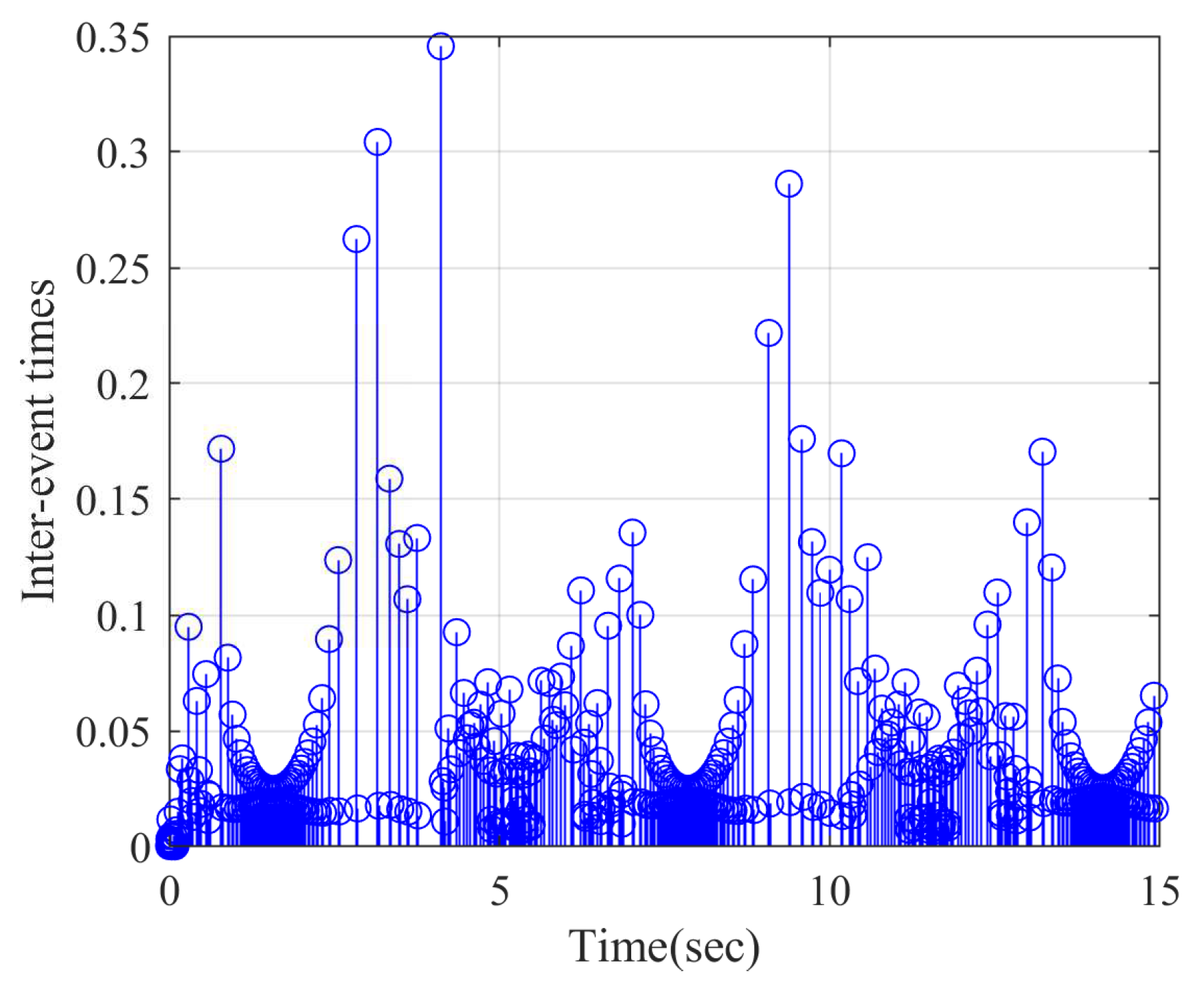
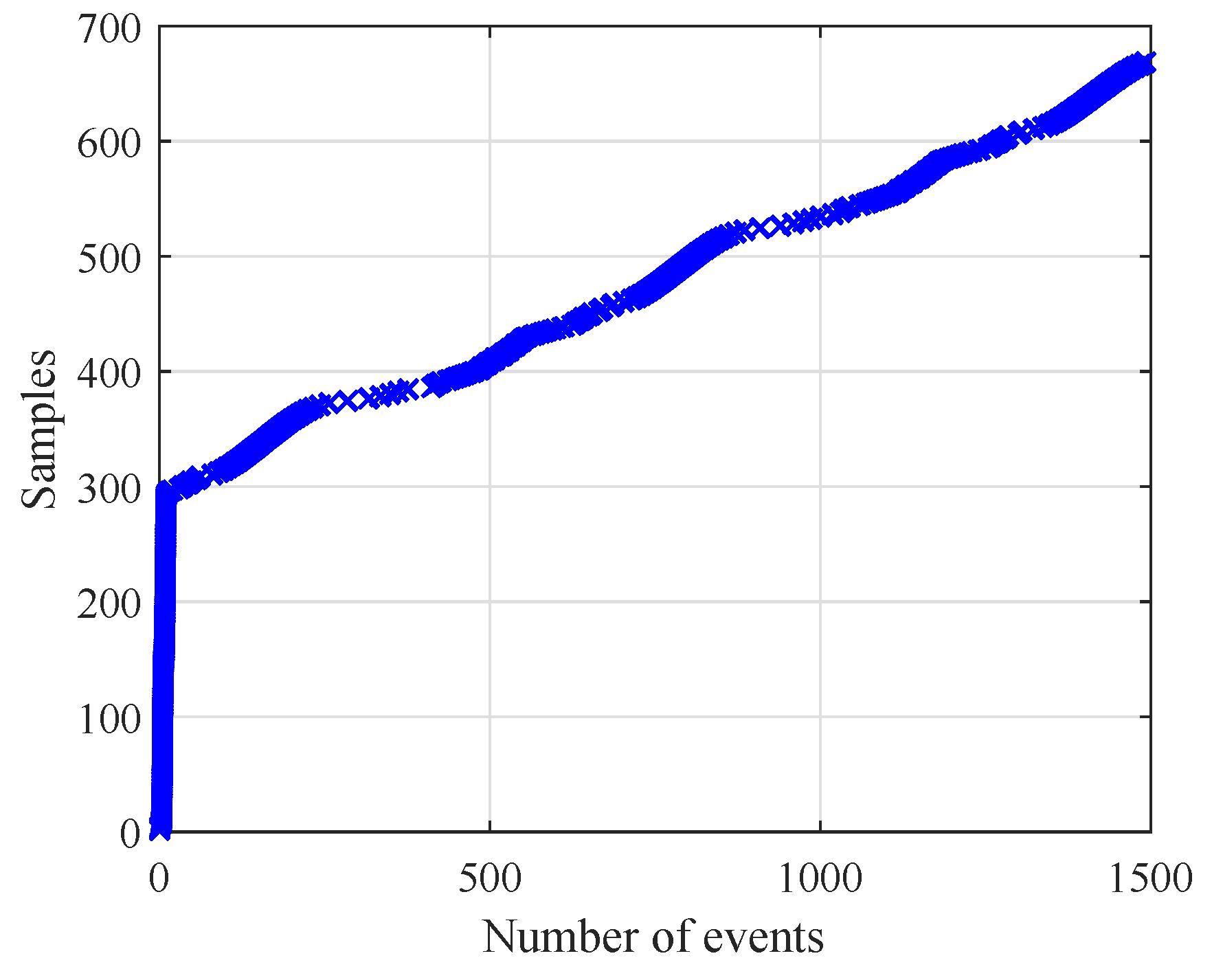
4. Simulation

Consider the following nonlinear FOSs:

$$\left\{\begin{array}{c}{D}^{0.8}{x}_1=0.8{\displaystyle x_1^2}+\left(6+3sin\left(x_1\right)\right)x_2\hfill \\ D^{0.8}{x}_2=0.5{\displaystyle x_1^3}cos\left(x_2\right)\hfill \\ \begin{array}{cc}\begin{array}{cc} & \end{array}& \end{array}+\left(5+sin\left({\displaystyle x_1^2}\right)+cos\left(x_1{\displaystyle x_2^2}\right)\right)u\left(\upsilon \right)\hfill \end{array}\right.$$

(70)

where $f_1\left(x_1\right)=0.8{\displaystyle x_1^2}$ and $f_2\left(x_2\right)=0.5{\displaystyle x_1^3}cos\left(x_2\right)$ are the unknown function, $g_1\left(x_1\right)=6+3sin\left(x_1\right)$ and $g_2\left(x_2\right)=5+sin\left({\displaystyle x_1^2}\right)+cos\left(x_1{\displaystyle x_2^2}\right)$ are the known function. The saturation parameters are $u_{max}=0.15$ and $u_{min}=-0.13$. The state constraints are given as $k_{c_1}=0.9$ and $k_{c_2}=0.65$. The reference signal is chosen as $y_r\left(t\right)=0.8sin\left(t\right)$.

The parameters are given as $b_1=b_2=0.1,c_1=1,c_2=0.8,d_1=1,d_2=0.5, {\kappa }_2=0.01,{\kappa }^{\ast }=1.1,\rho =0.5,{\gamma }_1=6,{\gamma }_2=0.05,{\varsigma }_1=0.1,{\varsigma }_2=0.01,{\displaystyle {\lambda }_1^{\ast }}=0.001$ and ${\displaystyle {\lambda }_2^{\ast }}=0.1$. The initial values are chosen as $x_1\left(0\right)=x_2\left(0\right)=0$, ${\theta }_1\left(0\right)=0$ and ${\theta }_2\left(0\right)=0$.

To deal with the unknown nonlinear $f_1\left(x_1\right)=0.8{\displaystyle x_1^2}$ and $f_2\left(x_2\right)=0.5{\displaystyle x_1^3}cos\left(x_2\right)$, the membership functions of FLS are designed as follows:

$$\begin{array}{c}\Psi \left(x_1\right)=exp\left(-\frac{{\left(x_1-x_{k_1}\right)}^2}{{\displaystyle {\delta }_1^2}}\right)\hfill \\ \Psi \left({\overline{x}}_2\right)=exp\left(-\frac{{\left(x_1-x_{k_1}\right)}^2}{{\displaystyle {\delta }_1^2}}-\frac{{\left(x_2-x_{k_2}\right)}^2}{{\displaystyle {\delta }_2^2}}\right)\hfill \\ x_{k_1}\in \left\{\left.0.2k_1-1\right|k_1=1,2,\dots ,9\right\}\hfill \\ x_{k_2}\in \left\{\left.0.25k_2-1\right|k_2=1,2,\dots ,6\right\}\hfill \\ {\delta }_1=0.15,{\delta }_2=0.15\hfill \end{array}$$

(71)

Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 show the simulation results by the proposed finite-time ECT controller. The trajectories of the tracking error and the system state are shown in Figure 1 and Figure 2. It can be found that the transient response of output y is reasonable in both magnitude and frequency content, state $x_1$ satisfies $\left|x_1\right|⩽k_{c_1}=0.9$ and state $x_2$ satisfies $\left|x_2\right|⩽k_{c_2}=0.65$, which are not to violate their constraint bound. Figure 3 illustrates the trajectories of parameters estimation, and the controller input u is depicted in Figure 4, which are all bounded. Figure 5 and Figure 6 list the sequence of steps of event-triggered sampling and the number of accumulated events. It demonstrates that the frequency of event-driven controller is not fixed, which is determined by the state error and can save communication resources and computing resources. It is clear that the tracking objective and stability of the closed-loop system in finite time can be achieved, and the communication burden can be reduced effectively.

5. Conclusions

An event-triggered adaptive fuzzy finite-time DSC approach for strict-feedback uncertain nonlinear FOSs with actuator saturation and full-state constraints has been proposed. The dynamic surface method is applied to overcome the difficulty of inherent computational complexity. By employing the BLFs and fractional-order Lyapunov method, the constraints are not violated, the closed-loop system is bounded, and the tracking error converges to a small region around the origin in finite time. Meanwhile, the Zeno behavior can be avoided and the simulation results verify the effectiveness. In the future, we will extend the results of this paper to switched fractional-order nonlinear systems, and apply the theoretical results to practical engineering applications.