Optimum Fractional Tilt Based Cascaded Frequency Stabilization with MLC Algorithm for Multi-Microgrid Assimilating Electric Vehicles
Abstract
1. Introduction
- •
- A new improved fractional order methodology is proposed in the paper for controlling frequency in multi-area RES-EV-based microgrid systems. The modified controller presents two cascaded inner and outer control loops based on 1+TD and FOTIDF, respectively, forming the proposed 1+TD/FOTIDF controller. Also, the proposed 1+TD/FOTIDF coordinates and controls EV batteries’ participation in the frequency regulation process.
- •
- A new modified liver cancer optimization algorithm (MLCA) is proposed to overcome the limitations of the conventional strategy of Liver cancer optimization algorithm (LCA). The proposed MLCA can avoid the early concourse to local optima and the debility of its exploration process. The proposed MLCA is based on three improvement mechanisms, including chaotic mutation (CM), quasi-oppositional based learning (QOBL), and the fitness distance balance (FDB).
- •
- The proposed MLCA is applied to optimally determine the parameters of the proposed 1+TD/FOTIDF controller. The obtained results show a better response and mitigation of different step generation/loading changes compared to other optimization methods and/or conventional controllers.
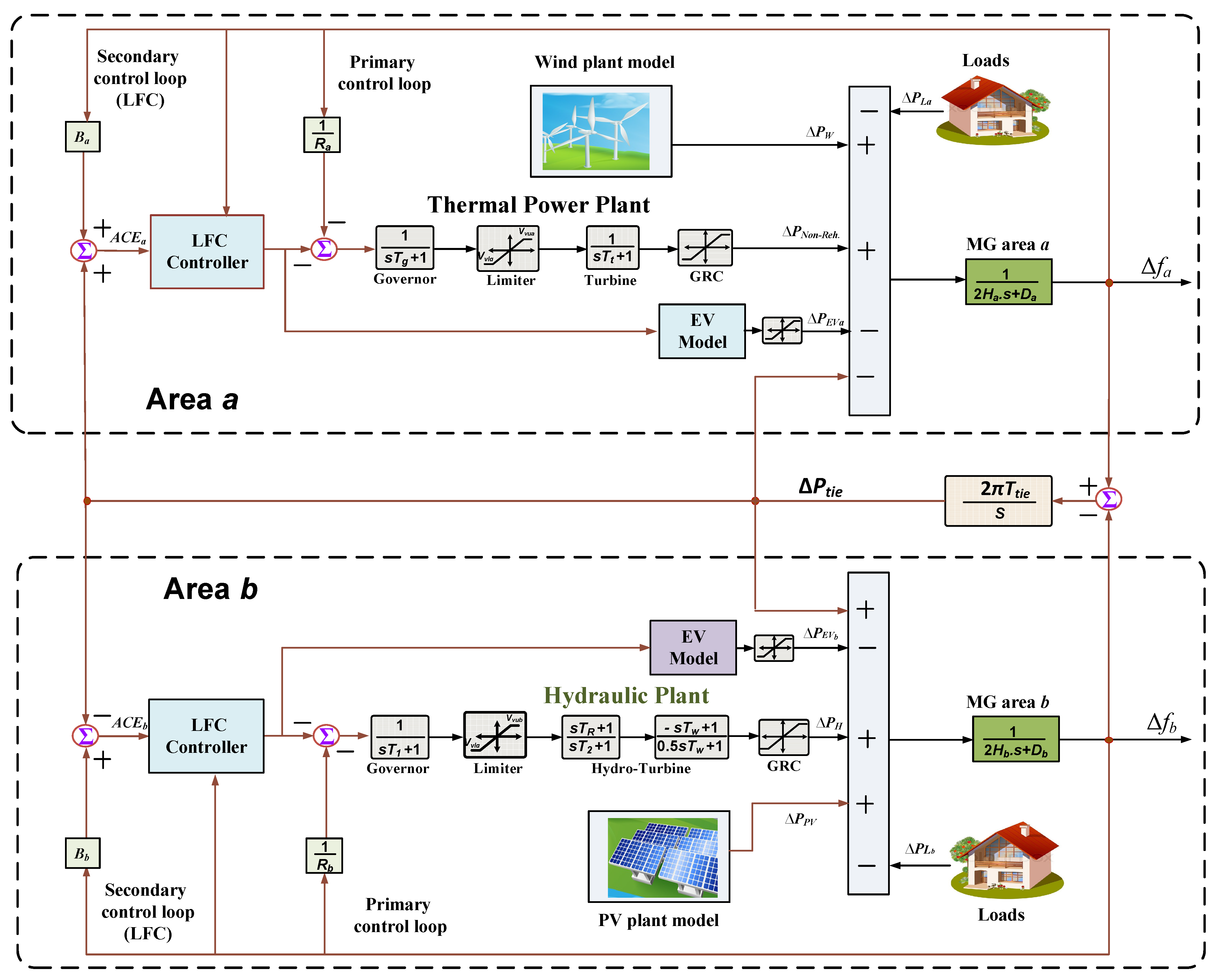
2. MG Model and Description
2.1. MGs’ Construction
2.2. Modeling of Thermal and Hydraulic Generators
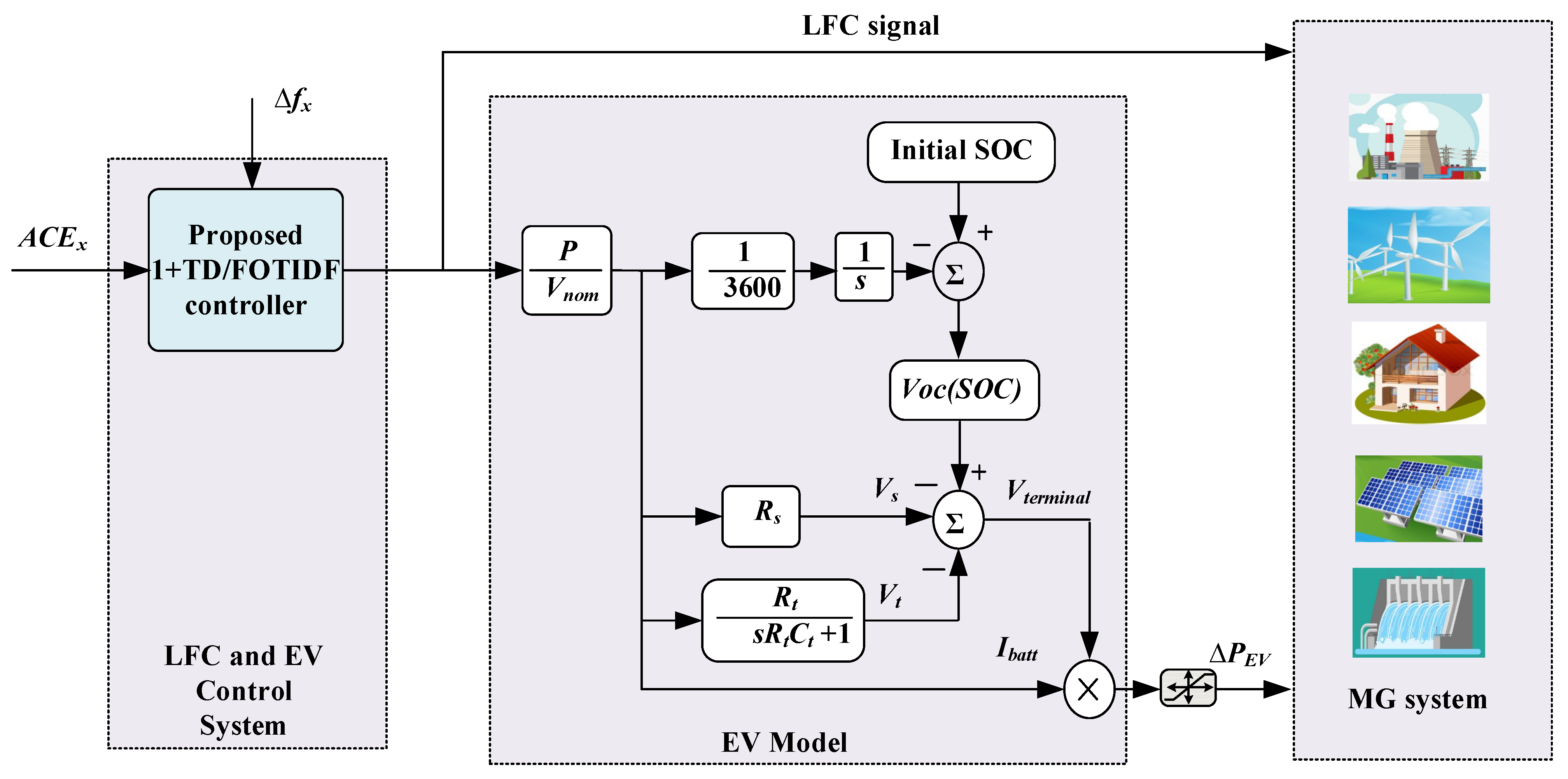
2.3. Modeling EVs’ BESSs
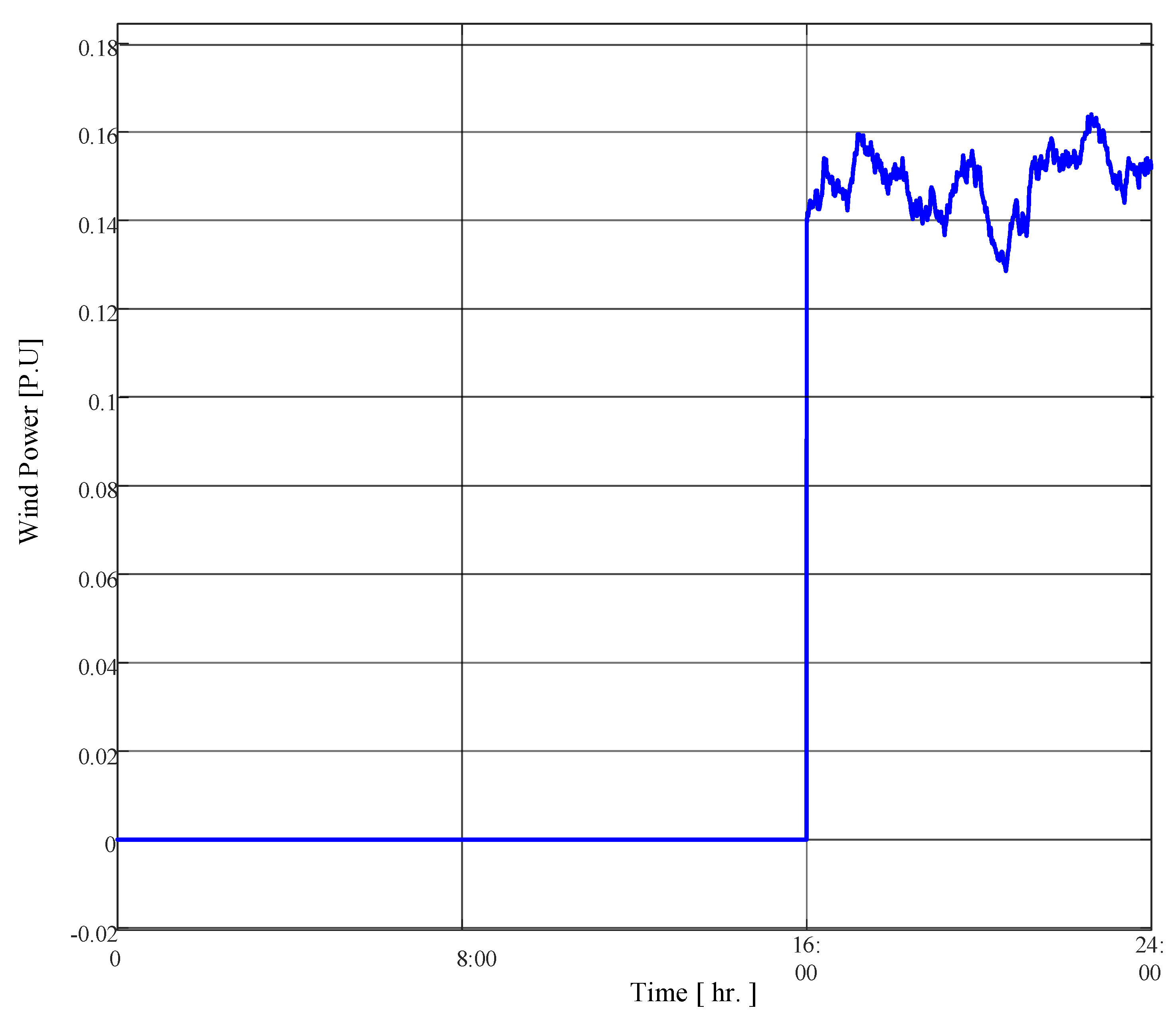
2.4. Wind Plant’s Model
2.5. Modeling of PV Power Plants
2.6. MG’s Complete Model
3. Overview of LFC and FO Operators
3.1. LFC Schemes in Literature
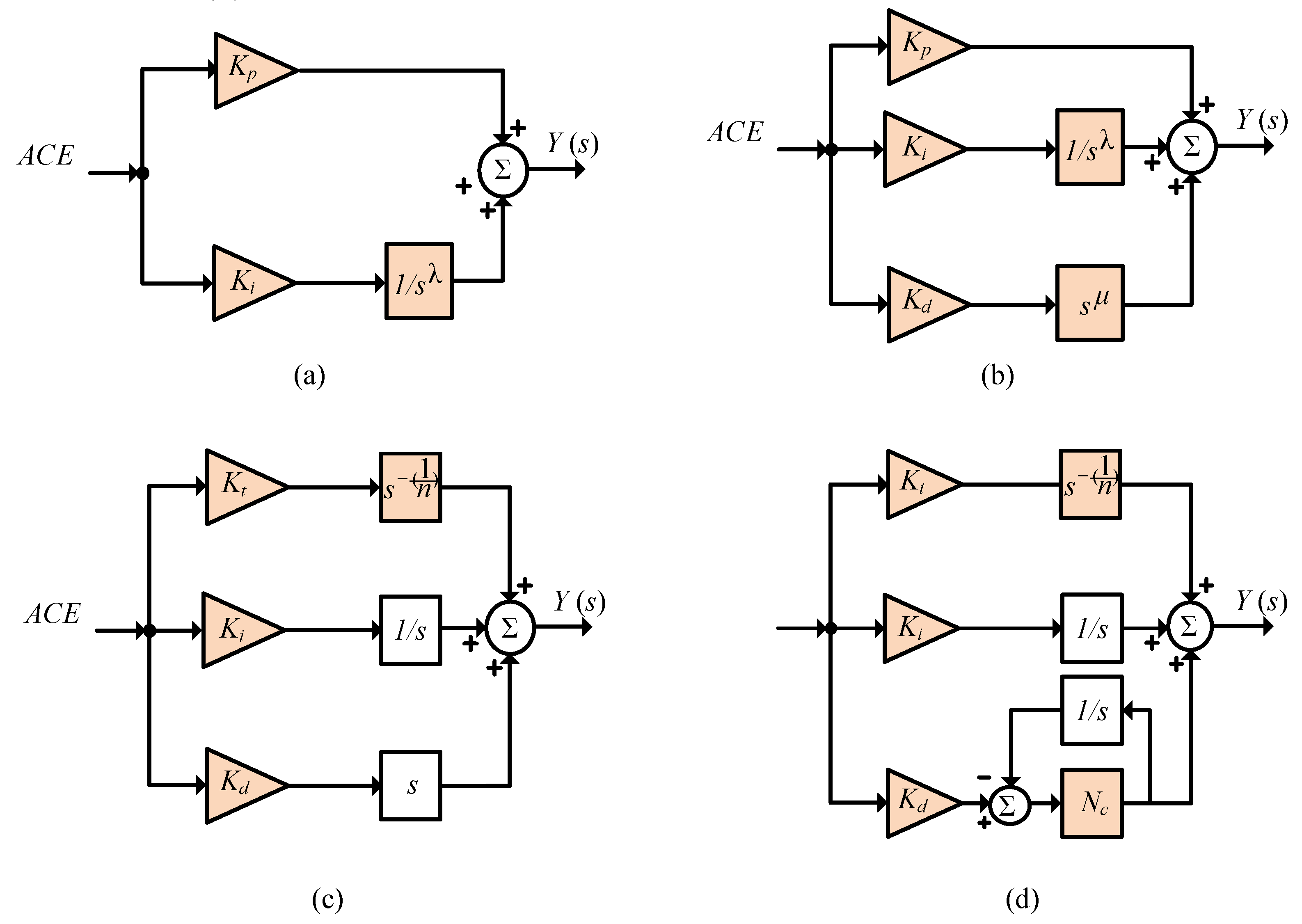
3.2. FO Operators Representation
3.3. Proposed 1+TD/FOTIDF LFC
4. The Proposed Modified Liver Cancer Optimization Algorithm and Its Performance Verification
4.1. Liver Cancer Optimization Algorithm
4.1.1. Tumor Size Estimation
4.1.2. Tumor Replication
4.1.3. Tumor Spreading
4.2. The Proposed Modified Liver Cancer Algorithm
4.2.1. The FDB Method
4.2.2. The QOBL Method
4.2.3. The Chaotic Mutation
4.3. MLCA Verification and Results Discussion
4.3.1. Application 1: Evaluation of the MLAC in Benchmark Functions
4.3.2. Statistical Analysis
4.3.3. Convergence Analysis
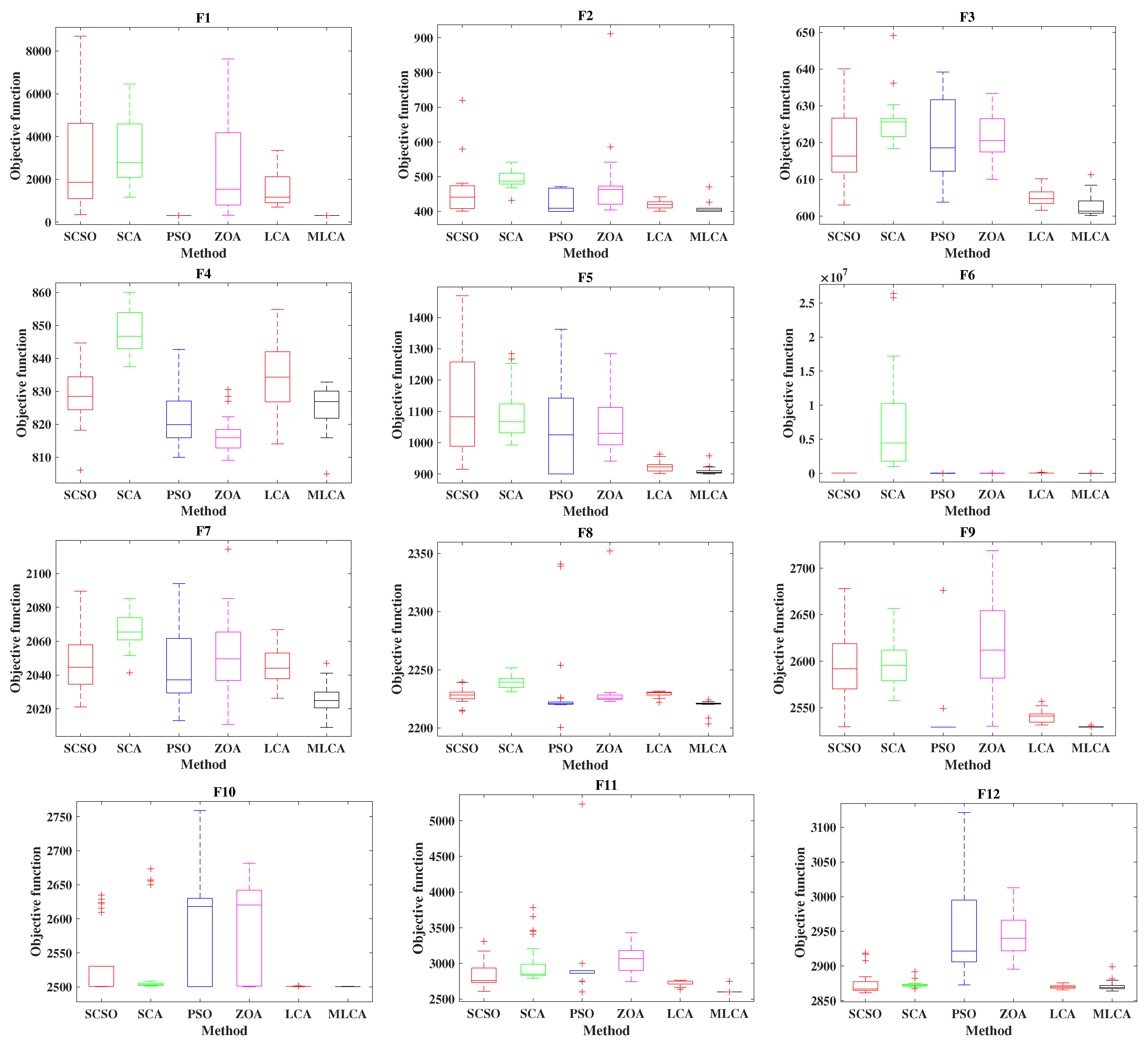
4.3.4. Boxplot Analysis
4.3.5. Wilcoxon and Fredman Tests
4.4. The Proposed MLCA-Based Control Parameters Optimization Process
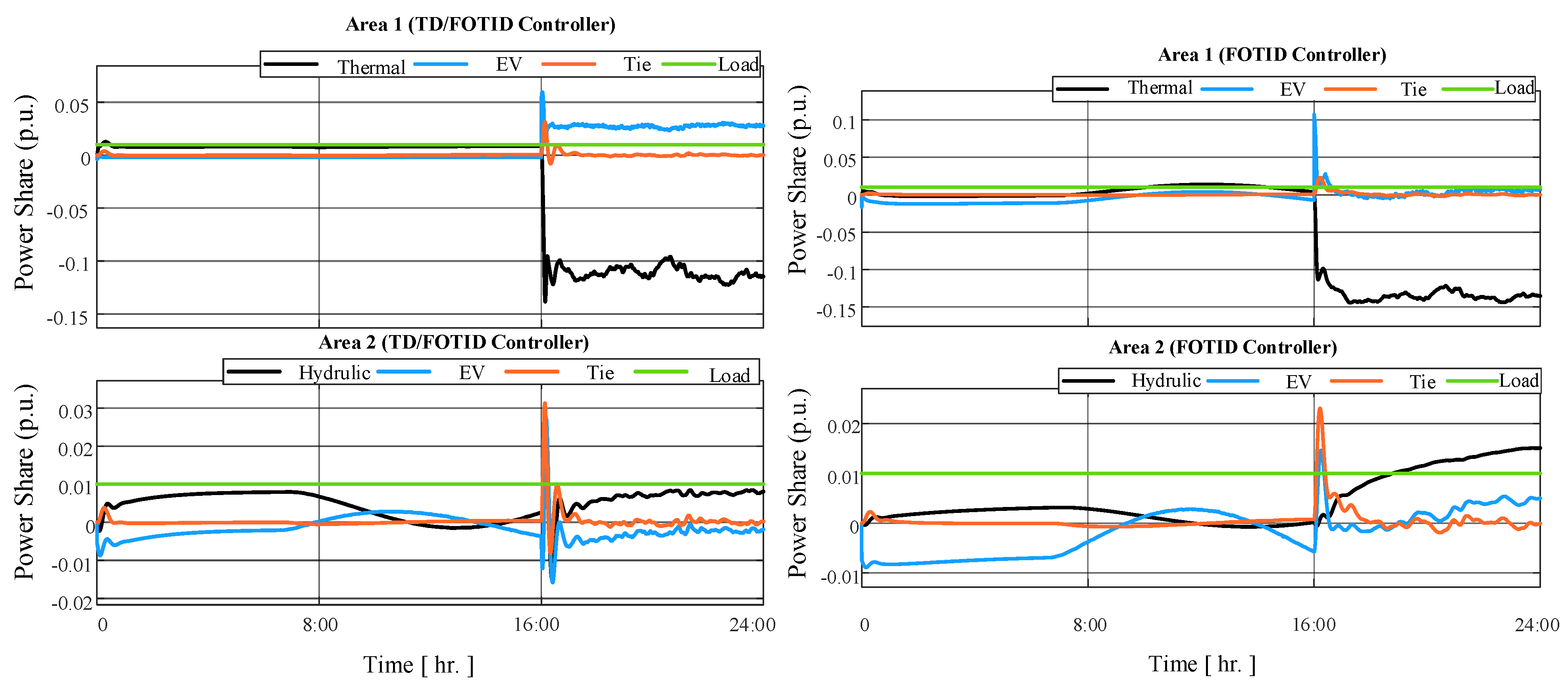
5. Results and Discussions
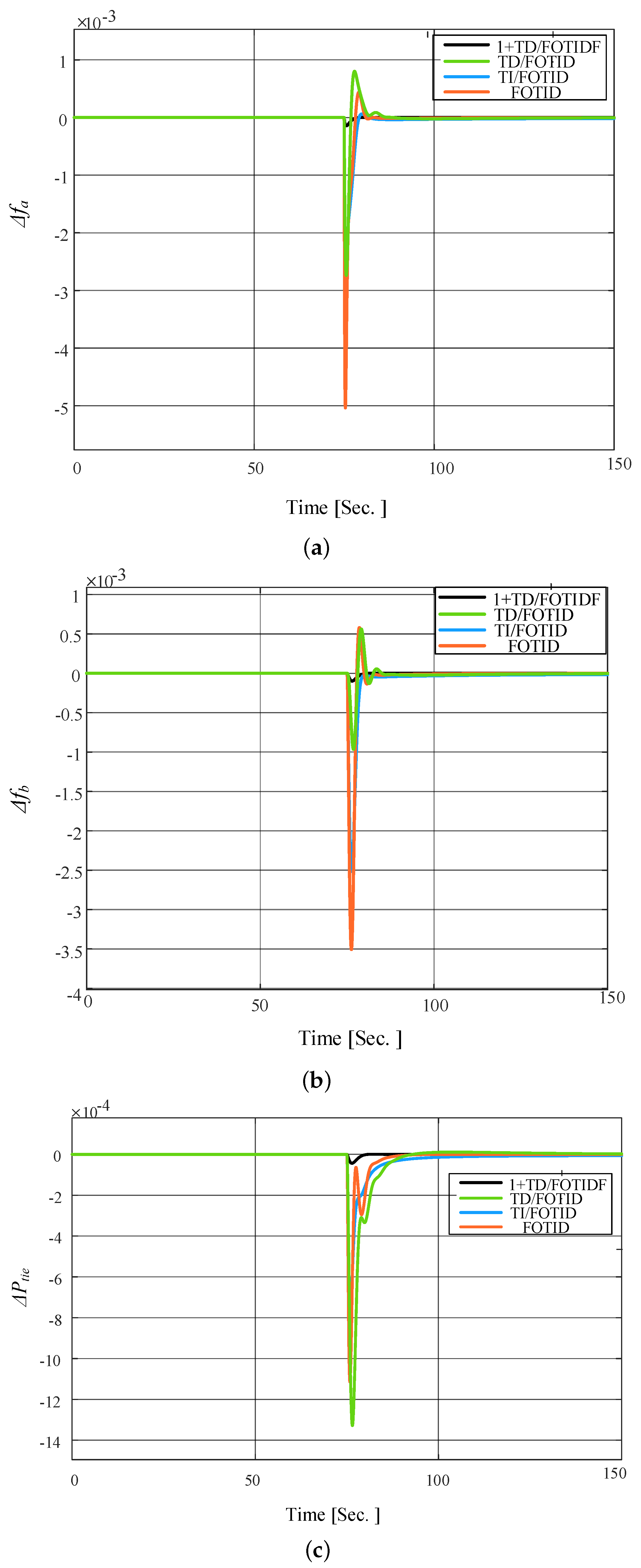
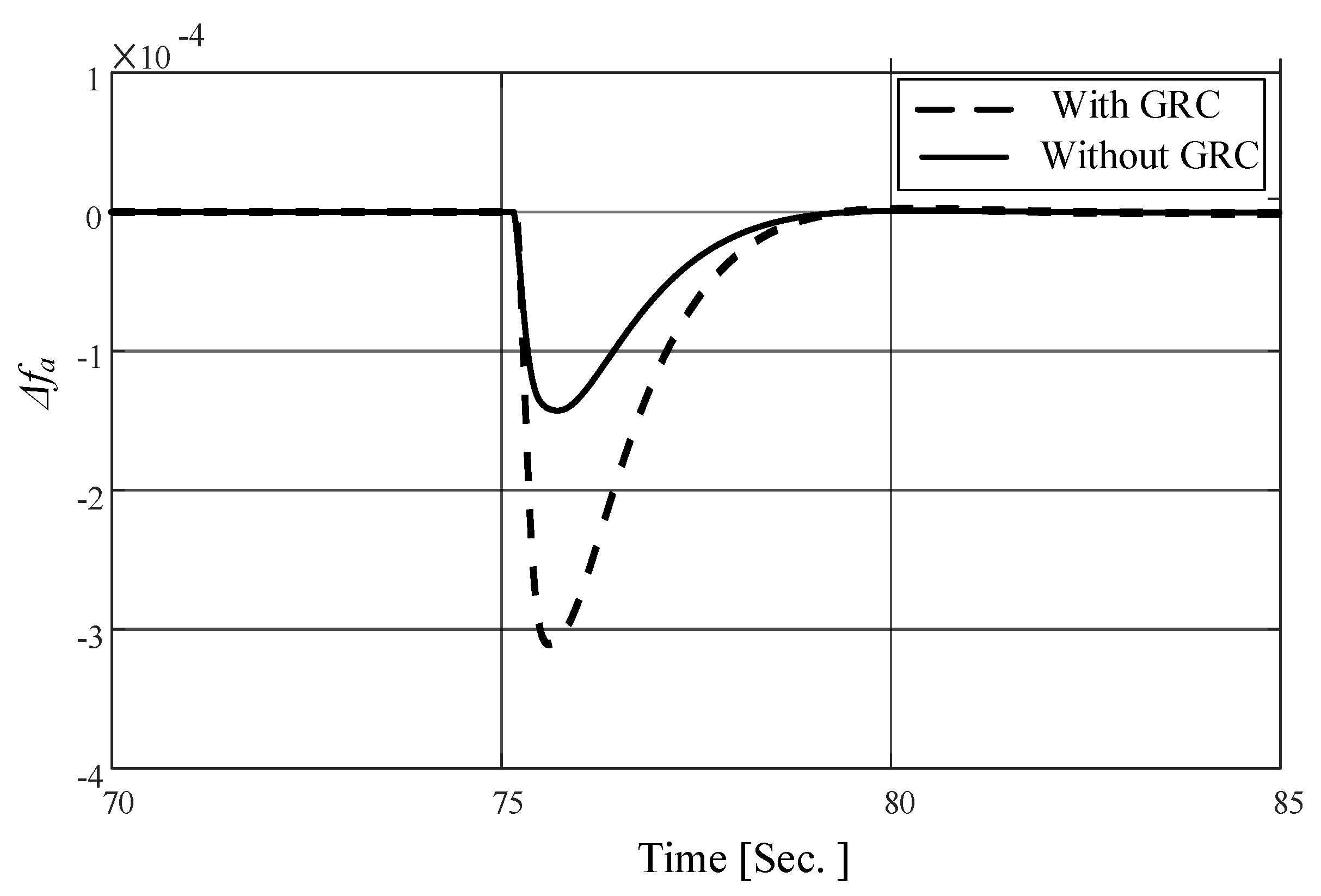
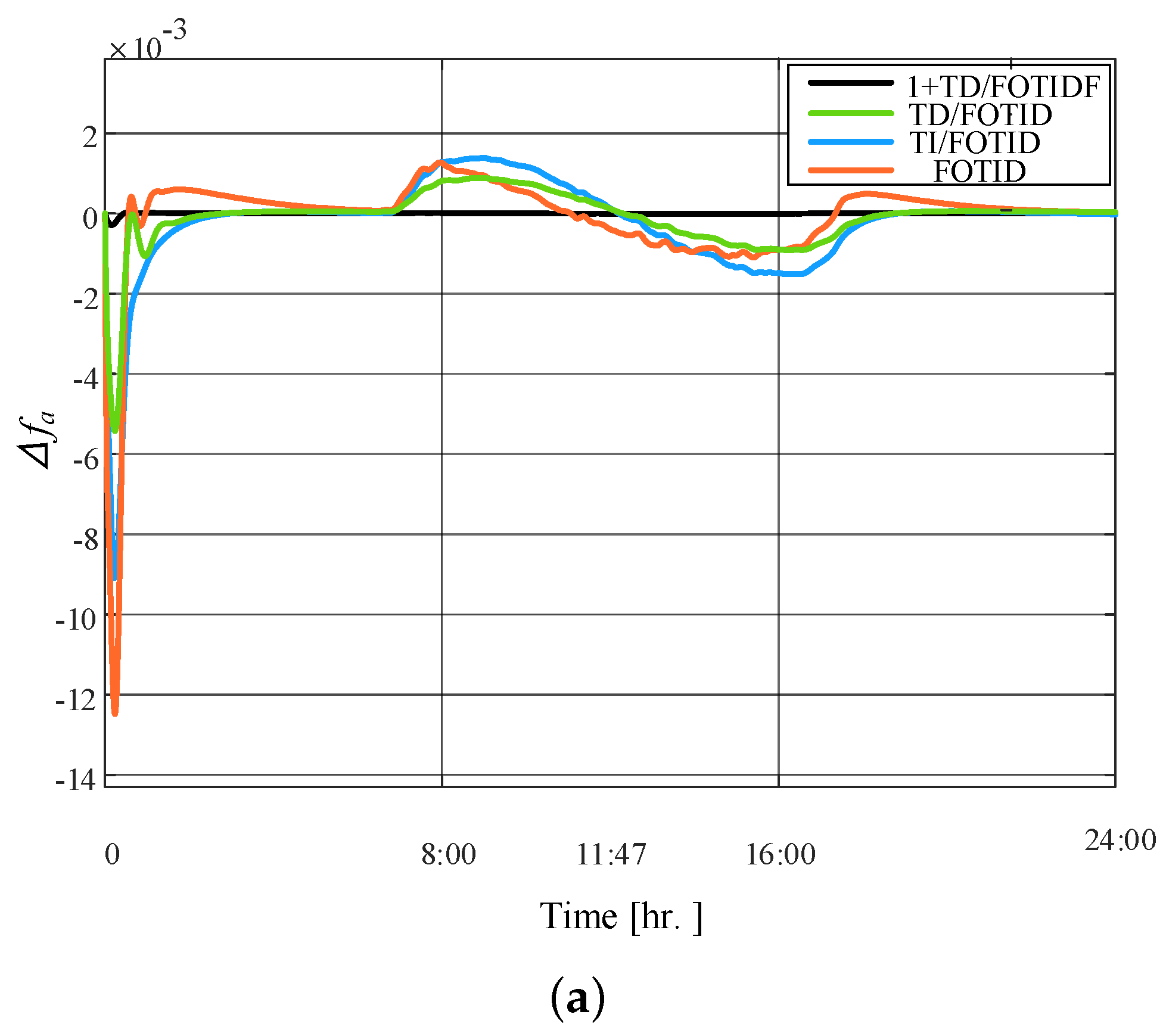
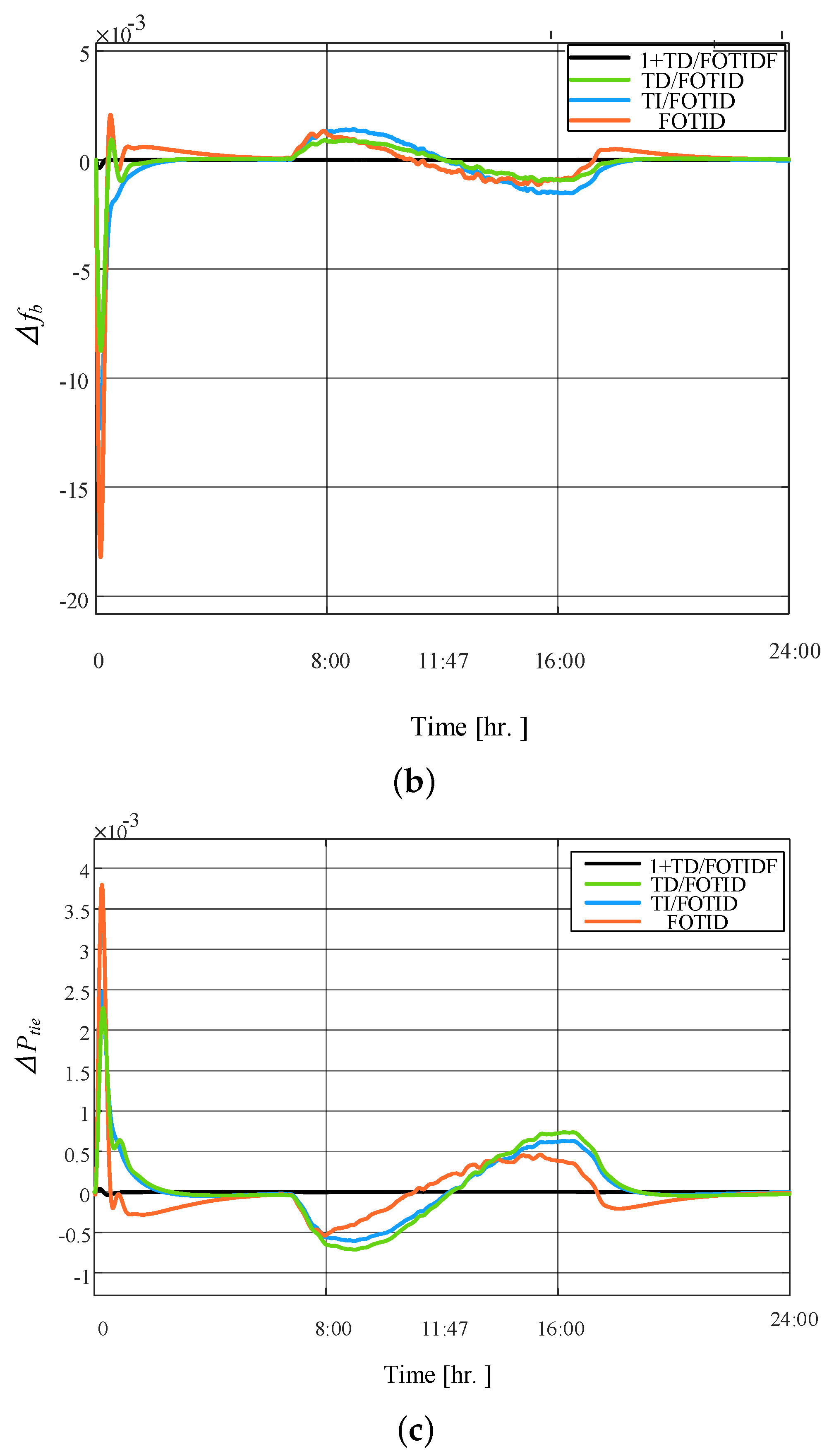
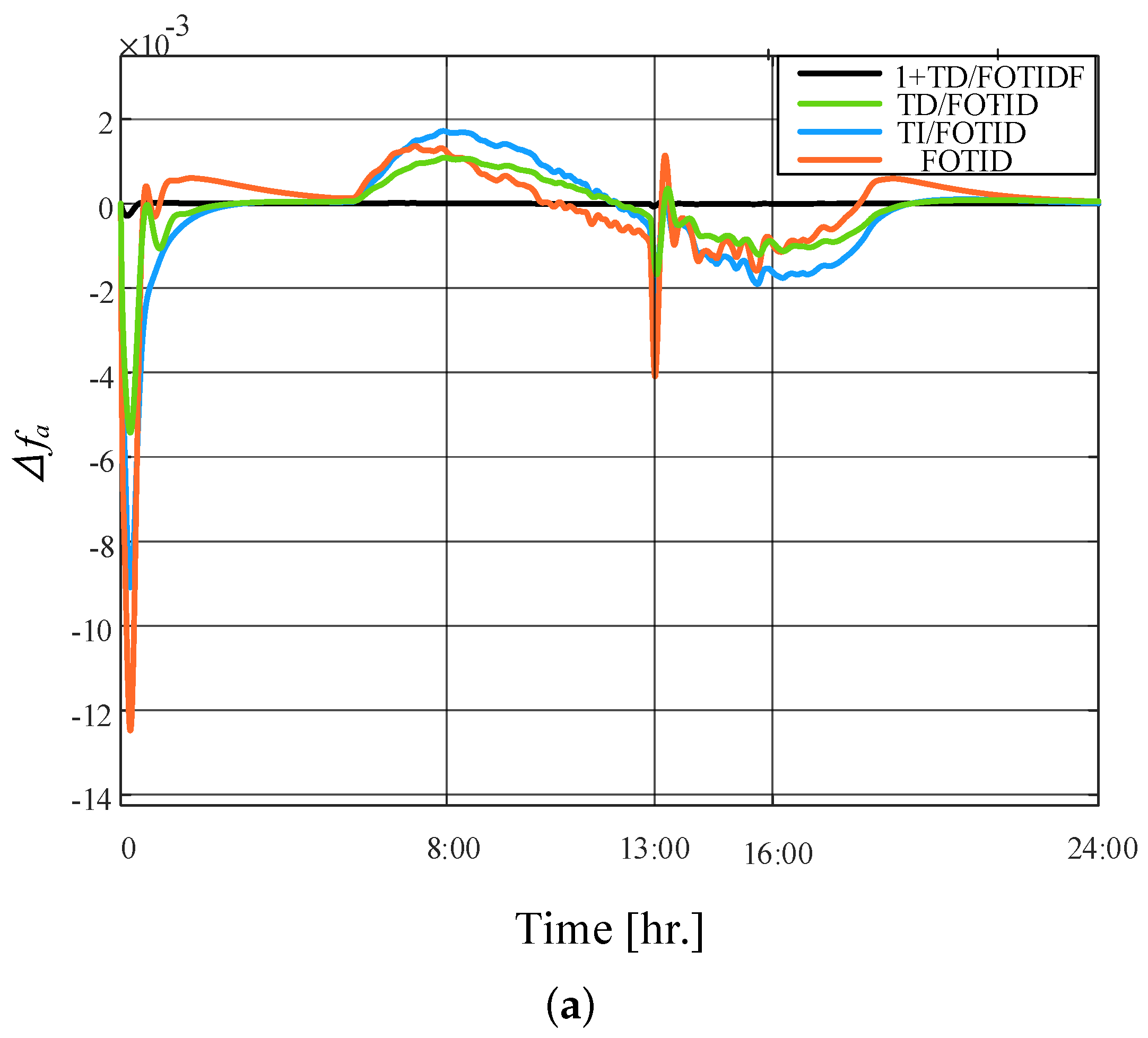
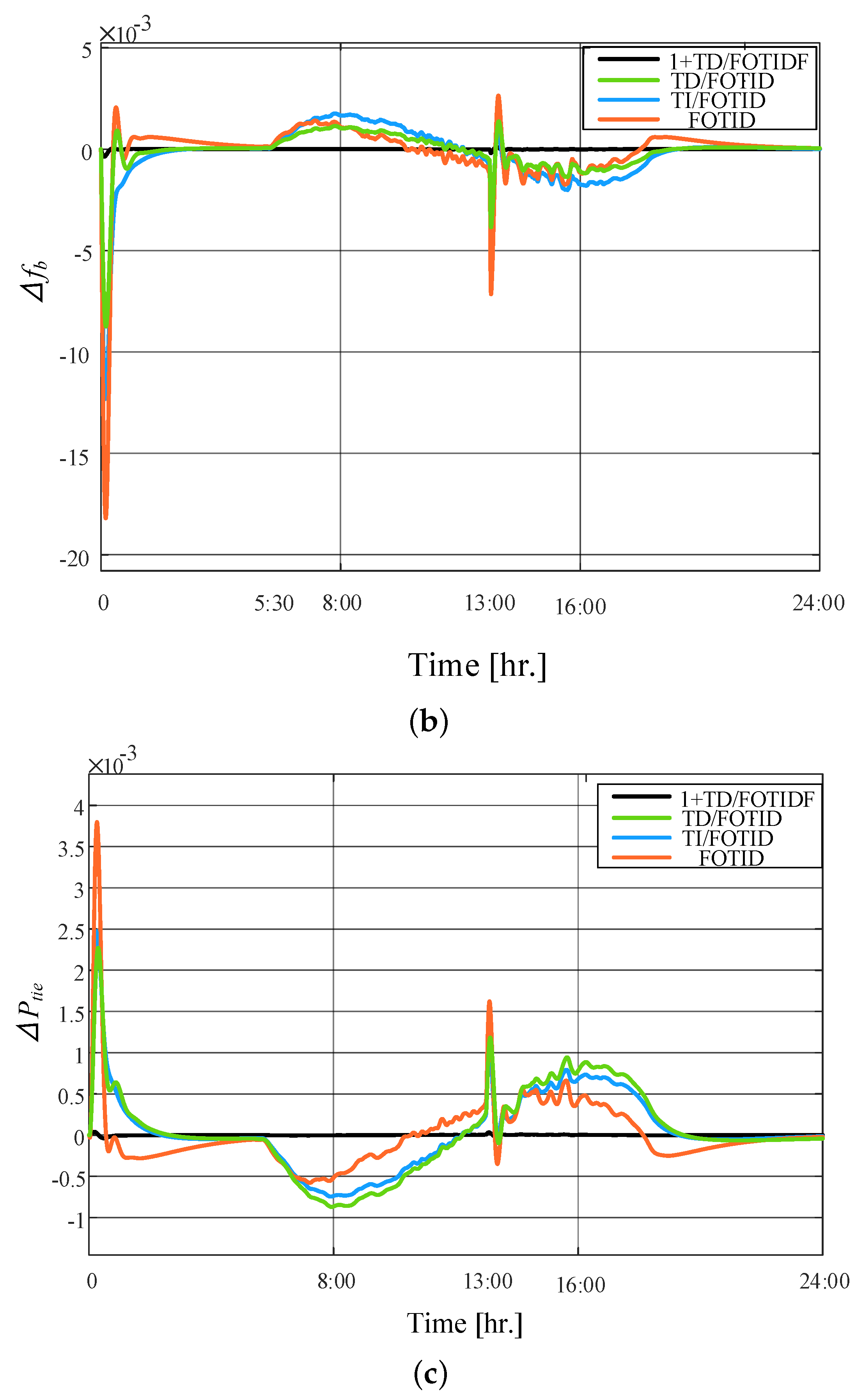
5.1. Scenario 1: 2% Step Load Change (SLC)
5.2. Scenario 2: SLC with PV Irradiation Case A
5.3. Scenario 3: SLC with PV Irradiation Case B
5.4. Scenario 4: SLC with sever PV Irradiation Case C
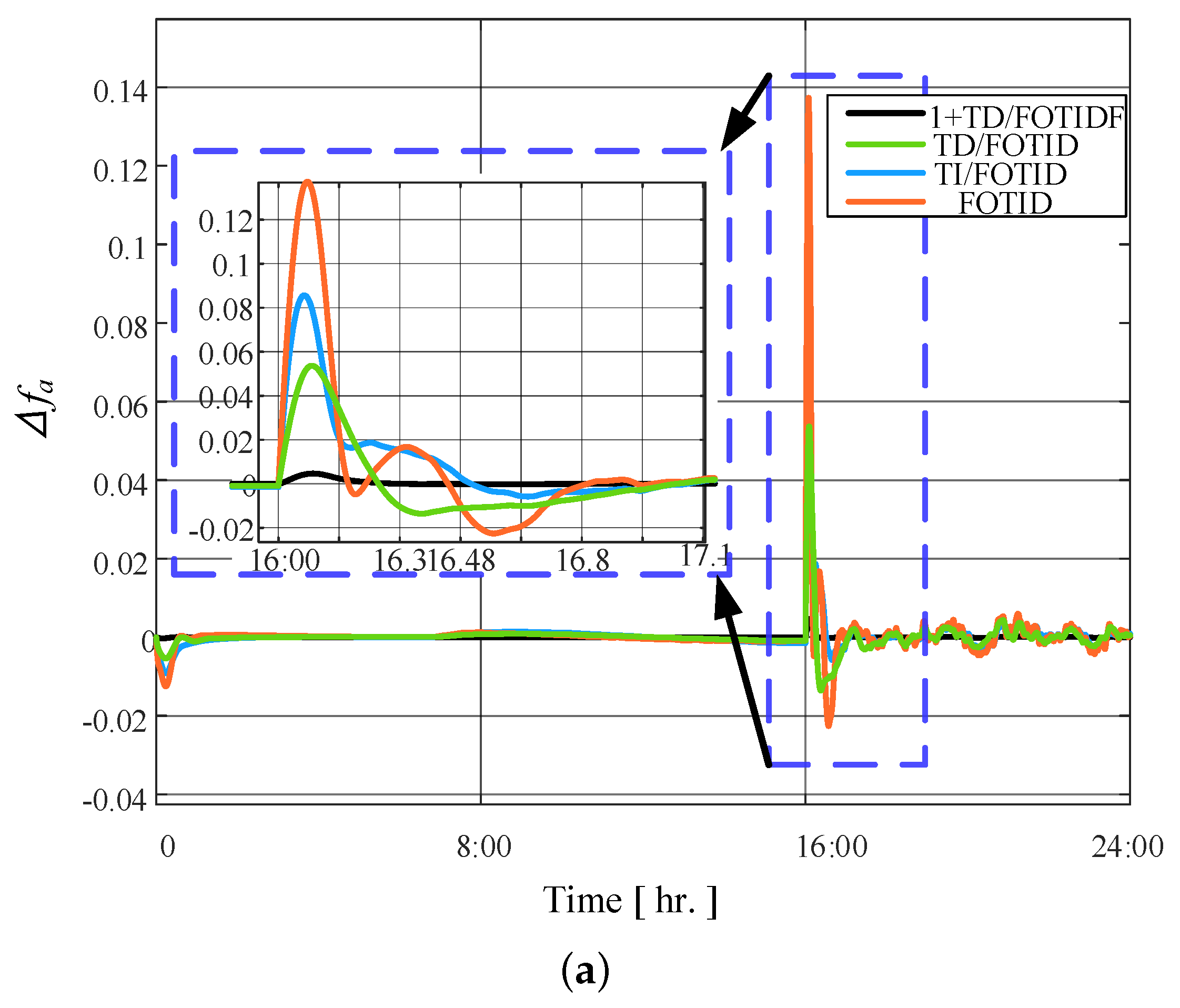
5.5. Scenario 5: High RESs of PV and Wind Generation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Ozkop, E.; Altas, I.H.; Sharaf, A.M. Load Frequency Control in Four Area Power Systems Using Fuzzy Logic PI Controller. In Proceedings of the 16th National Power Systems Conference, Hyderabad, India, 15–17 December 2010. [Google Scholar]
- Khodabakhshian, A.; Hooshmand, R. A new PID controller design for automatic generation control of hydro power systems. Int. J. Electr. Power Energy Syst. 2010, 32, 375–382. [Google Scholar] [CrossRef]
- Ibraheem.; Kumar, P.; Kothari, D. Recent Philosophies of Automatic Generation Control Strategies in Power Systems. IEEE Trans. Power Syst. 2005, 20, 346–357. [Google Scholar] [CrossRef]
- Morsali, J.; Zare, K.; Tarafdar Hagh, M. MGSO optimised TID-based GCSC damping controller in coordination with AGC for diverse-GENCOs multi-DISCOs power system with considering GDB and GRC non-linearity effects. IET Gener. Transm. Distrib. 2017, 11, 193–208. [Google Scholar] [CrossRef]
- Khooban, M.H.; Niknam, T. A new intelligent online fuzzy tuning approach for multi-area load frequency control: Self Adaptive Modified Bat Algorithm. Int. J. Electr. Power Energy Syst. 2015, 71, 254–261. [Google Scholar] [CrossRef]
- Lal, D.K.; Barisal, A. Comparative performances evaluation of FACTS devices on AGC with diverse sources of energy generation and SMES. Cogent Eng. 2017, 4, 1318466. [Google Scholar] [CrossRef]
- Tasnin, W.; Saikia, L.C. Performance comparison of several energy storage devices in deregulated AGC of a multi-area system incorporating geothermal power plant. IET Renew. Power Gener. 2018, 12, 761–772. [Google Scholar] [CrossRef]
- Rajbongshi, R.; Saikia, L.C. Combined control of voltage and frequency of multi-area multisource system incorporating solar thermal power plant using LSA optimised classical controllers. IET Gener. Transm. Distrib. 2017, 11, 2489–2498. [Google Scholar] [CrossRef]
- Tasnin, W.; Saikia, L.C. Maiden application of an sine–cosine algorithm optimised FO cascade controller in automatic generation control of multi-area thermal system incorporating dish-Stirling solar and geothermal power plants. IET Renew. Power Gener. 2018, 12, 585–597. [Google Scholar] [CrossRef]
- Ghasemi-Marzbali, A. Multi-area multi-source automatic generation control in deregulated power system. Energy 2020, 201, 117667. [Google Scholar] [CrossRef]
- Nosratabadi, S.M.; Bornapour, M.; Gharaei, M.A. Grasshopper optimization algorithm for optimal load frequency control considering Predictive Functional Modified PID controller in restructured multi-resource multi-area power system with Redox Flow Battery units. Control Eng. Pract. 2019, 89, 204–227. [Google Scholar] [CrossRef]
- Zhu, Q.; Jiang, L.; Yao, W.; Zhang, C.K.; Luo, C. Robust Load Frequency Control with Dynamic Demand Response for Deregulated Power Systems Considering Communication Delays. Electr. Power Compon. Syst. 2016, 45, 75–87. [Google Scholar] [CrossRef]
- Naveed, A.; Sonmez, S.; Ayasun, S. Stability Regions in the Parameter Space of PI Controller for LFC System with EVs Aggregator and Incommensurate Time Delays. In Proceedings of the 2019 1st Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Turkey, 12–15 June 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Elgerd, O.; Fosha, C. Optimum Megawatt-Frequency Control of Multiarea Electric Energy Systems. IEEE Trans. Power Appar. Syst. 1970, PAS-89, 556–563. [Google Scholar] [CrossRef]
- Linton, T. Automatic Generation Control of Electric Energy Systems—A Simulation Study. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 403–405. [Google Scholar] [CrossRef]
- Elgerd, O.I. Electric Energy Systems Theory, 2nd ed.; McGraw Hill Higher Education: Maidenhead, UK, 1983. [Google Scholar]
- Saha, D.; Saikia, L.C. Performance of FACTS and energy storage devices in a multi area wind-hydro-thermal system employed with SFS optimized I-PDF controller. J. Renew. Sustain. Energy 2017, 9, 024103. [Google Scholar] [CrossRef]
- Raju, M.; Saikia, L.C.; Sinha, N. Load frequency control of a multi-area system incorporating distributed generation resources, gate controlled series capacitor along with high-voltage direct current link using hybrid ALO-pattern search optimised fractional order controller. IET Renew. Power Gener. 2018, 13, 330–341. [Google Scholar] [CrossRef]
- Mohanty, B.; Panda, S.; Hota, P. Controller parameters tuning of differential evolution algorithm and its application to load frequency control of multi-source power system. Int. J. Electr. Power Energy Syst. 2014, 54, 77–85. [Google Scholar] [CrossRef]
- Kumari, S.; Shankar, G. Maiden application of cascade tilt-integral-derivative controller in load frequency control of deregulated power system. Int. Trans. Electr. Energy Syst. 2019, 30, e12257. [Google Scholar] [CrossRef]
- Dutta, A.; Debbarma, S. Frequency Regulation in Deregulated Market Using Vehicle-to-Grid Services in Residential Distribution Network. IEEE Syst. J. 2018, 12, 2812–2820. [Google Scholar] [CrossRef]
- Prasad, S.; Purwar, S.; Kishor, N. Load frequency regulation using observer based non-linear sliding mode control. Int. J. Electr. Power Energy Syst. 2019, 104, 178–193. [Google Scholar] [CrossRef]
- Saha, A.; Saikia, L.C. Utilisation of ultra-capacitor in load frequency control under restructured STPP-thermal power systems using WOA optimised PIDN-FOPD controller. IET Gener. Transm. Distrib. 2017, 11, 3318–3331. [Google Scholar] [CrossRef]
- Saha, A.; Saikia, L.C. Combined application of redox flow battery and DC link in restructured AGC system in the presence of WTS and DSTS in distributed generation unit. IET Gener. Transm. Distrib. 2018, 12, 2072–2085. [Google Scholar] [CrossRef]
- Ram Babu, N.; Saikia, L.C. AGC of a multiarea system incorporating accurate HVDC and precise wind turbine systems. Int. Trans. Electr. Energy Syst. 2019, 30, e12277. [Google Scholar] [CrossRef]
- Zare, K.; Hagh, M.T.; Morsali, J. Effective oscillation damping of an interconnected multi-source power system with automatic generation control and TCSC. Int. J. Electr. Power Energy Syst. 2015, 65, 220–230. [Google Scholar] [CrossRef]
- Tasnin, W.; Saikia, L.C.; Raju, M. Deregulated AGC of multi-area system incorporating dish-Stirling solar thermal and geothermal power plants using fractional order cascade controller. Int. J. Electr. Power Energy Syst. 2018, 101, 60–74. [Google Scholar] [CrossRef]
- Verma, Y.P.; Kumar, A. Load frequency control in deregulated power system with wind integrated system using fuzzy controller. Front. Energy 2012, 7, 245–254. [Google Scholar] [CrossRef]
- Shiva, C.K.; Mukherjee, V. A novel quasi-oppositional harmony search algorithm for AGC optimization of three-area multi-unit power system after deregulation. Eng. Sci. Technol. Int. J. 2016, 19, 395–420. [Google Scholar] [CrossRef]
- Gondaliya, S.; Arora, M.K. Automatic Generation Control of Multi Area Power Plants with the Help of Advanced Controller. Int. J. Eng. Res. Technol. 2015, V4, 470–474. [Google Scholar] [CrossRef]
- Haes Alhelou, H.; Hamedani Golshan, M.E.; Hajiakbari Fini, M. Wind Driven Optimization Algorithm Application to Load Frequency Control in Interconnected Power Systems Considering GRC and GDB Nonlinearities. Electr. Power Compon. Syst. 2018, 46, 1223–1238. [Google Scholar] [CrossRef]
- Gulzar, M.M.; Iqbal, M.; Shahzad, S.; Muqeet, H.A.; Shahzad, M.; Hussain, M.M. Load Frequency Control (LFC) Strategies in Renewable Energy-Based Hybrid Power Systems: A Review. Energies 2022, 15, 3488. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Symbiotic organism search algorithm applied to load frequency control of multi-area power system. Energy Syst. 2017, 9, 439–468. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Application of backtracking search algorithm in load frequency control of multi-area interconnected power system. Ain Shams Eng. J. 2018, 9, 257–276. [Google Scholar] [CrossRef]
- Safi, S.J.; Tezcan, S.S.; Eke, I.; Farhad, Z. Gravitational Search Algorithm (GSA) based PID Controller Design for Two Area Multi-Source Power System Load Frequency Control (LFC). Gazi Univ. J. Sci. 2018, 31, 139–153. [Google Scholar]
- Arora, K.; Kumar, A.; Kamboj, V.K.; Prashar, D.; Shrestha, B.; Joshi, G.P. Impact of Renewable Energy Sources into Multi Area Multi-Source Load Frequency Control of Interrelated Power System. Mathematics 2021, 9, 186. [Google Scholar] [CrossRef]
- Saxena, A.; Shankar, R. Improved load frequency control considering dynamic demand regulated power system integrating renewable sources and hybrid energy storage system. Sustain. Energy Technol. Assess. 2022, 52, 102245. [Google Scholar] [CrossRef]
- Xu, C.; Ou, W.; Pang, Y.; Cui, Q.; Rahman, M.u.; Farman, M.; Ahmad, S.; Zeb, A. Hopf Bifurcation Control of a Fractional-Order Delayed Turbidostat Model via a Novel Extended Hybrid Controller. Match Commun. Math. Comput. Chem. 2023, 91, 367–413. [Google Scholar] [CrossRef]
- Eshaghi, S.; Khoshsiar Ghaziani, R.; Ansari, A. Hopf bifurcation, chaos control and synchronization of a chaotic fractional-order system with chaos entanglement function. Math. Comput. Simul. 2020, 172, 321–340. [Google Scholar] [CrossRef]
- Kaslik, E.; Rădulescu, I.R. Stability and bifurcations in fractional-order gene regulatory networks. Appl. Math. Comput. 2022, 421, 126916. [Google Scholar] [CrossRef]
- Irudayaraj, A.X.R.; Wahab, N.I.A.; Premkumar, M.; Radzi, M.A.M.; Sulaiman, N.B.; Veerasamy, V.; Farade, R.A.; Islam, M.Z. Renewable sources-based automatic load frequency control of interconnected systems using chaotic atom search optimization. Appl. Soft Comput. 2022, 119, 108574. [Google Scholar] [CrossRef]
- Kong, F.; Li, J.; Yang, D. Multi-Area Load Frequency Control of Hydro-Thermal-Wind Power Based on Improved Grey Wolf Optimization Algorithm. Elektron. Elektrotechnika 2020, 26, 32–39. [Google Scholar] [CrossRef]
- Khadanga, R.K.; Kumar, A.; Panda, S. A modified Grey Wolf Optimization with Cuckoo Search Algorithm for load frequency controller design of hybrid power system. Appl. Soft Comput. 2022, 124, 109011. [Google Scholar] [CrossRef]
- Soliman, A.M.A.; Bahaa, M.; Mehanna, M.A. PSO tuned interval type-2 fuzzy logic for load frequency control of two-area multi-source interconnected power system. Sci. Rep. 2023, 13, 8724. [Google Scholar] [CrossRef]
- Kumar, R.; Sikander, A. A novel load frequency control of multi area non-reheated thermal power plant using fuzzy PID cascade controller. Sādhanā 2023, 48, 25. [Google Scholar] [CrossRef]
- Yousef, M.Y.; Mosa, M.A.; Ali, A.; Ghany, A.; Ghany, M. Load frequency control for power system considering parameters variation using parallel distributed compensator based on Takagi-Sugino fuzzy. Electr. Power Syst. Res. 2023, 220, 109352. [Google Scholar] [CrossRef]
- Saikia, N.; Das, N.K. Load Frequency Control of a Two Area Multi-source Power System with Electric Vehicle. J. Control. Autom. Electr. Syst. 2022, 34, 394–406. [Google Scholar] [CrossRef]
- El-Sehiemy, R.; Shaheen, A.; Ginidi, A.; Al-Gahtani, S.F. Proportional-Integral-Derivative Controller Based-Artificial Rabbits Algorithm for Load Frequency Control in Multi-Area Power Systems. Fractal Fract. 2023, 7, 97. [Google Scholar] [CrossRef]
- Kumari, N.; Gill, A.; Singh, M. Two-Area Power System Load Frequency Regulation Using ANFIS and Genetic Algorithm. In Proceedings of the 2023 4th International Conference for Emerging Technology (INCET), Belgaum, India, 26–28 May 2023; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar] [CrossRef]
- Halmous, A.; Oubbati, Y.; Lahdeb, M.; Arif, S. Design a new cascade controller PD-P-PID optimized by marine predators algorithm for load frequency control. Soft Comput. 2023, 27, 9551–9564. [Google Scholar] [CrossRef]
- Alhejji, A.; Ahmed, N.; Ebeed, M.; Sayed, K.; Refai, A. A Robust Cascaded Controller for Load Frequency Control in Renewable Energy Integrated Microgrid Containing PEV. Int. J. Renew. Energy Res. 2023, 13, 423–433. [Google Scholar] [CrossRef]
- Gulzar, M.M.; Sibtain, D.; Khalid, M. Cascaded Fractional Model Predictive Controller for Load Frequency Control in Multiarea Hybrid Renewable Energy System with Uncertainties. Int. J. Energy Res. 2023, 2023, 5999997. [Google Scholar] [CrossRef]
- Duman, S.; Balci, Y. Improvement of Load Frequency Control for Two-Area Modern Power Systems Involving Renewable Energy Sources Using a Novel Cascade Controller. 2023. Available online: https://www.researchsquare.com/article/rs-3215487/v1 (accessed on 15 January 2024).
- El-Sousy, F.F.M.; Aly, M.; Alqahtani, M.H.; Aljumah, A.S.; Almutairi, S.Z.; Mohamed, E.A. New Cascaded 1+PII2D/FOPID Load Frequency Controller for Modern Power Grids including Superconducting Magnetic Energy Storage and Renewable Energy. Fractal Fract. 2023, 7, 672. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Mohamed, E.A.; Selim, A.; Aly, M.; Alsadi, A.; Alhosaini, W.; Alnuman, H.; Ramadan, H.A. Improving load frequency control performance in interconnected power systems with a new optimal high degree of freedom cascaded FOTPID-TIDF controller. Ain Shams Eng. J. 2023, 14, 102207. [Google Scholar] [CrossRef]
- Hassan, A.; Aly, M.M.; Alharbi, M.A.; Selim, A.; Alamri, B.; Aly, M.; Elmelegi, A.; Khamies, M.; Mohamed, E.A. Optimized Multiloop Fractional-Order Controller for Regulating Frequency in Diverse-Sourced Vehicle-to-Grid Power Systems. Fractal Fract. 2023, 7, 864. [Google Scholar] [CrossRef]
- Elkasem, A.H.; Khamies, M.; Hassan, M.H.; Nasrat, L.; Kamel, S. Utilizing controlled plug-in electric vehicles to improve hybrid power grid frequency regulation considering high renewable energy penetration. Int. J. Electr. Power Energy Syst. 2023, 152, 109251. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Modeling and circuit-based simulation of photovoltaic arrays. In Proceedings of the 2009 Brazilian Power Electronics Conference, Bonito-Mato Grosso do Sul, Brazil, 27 September–1 October 2009; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Walker, G.R. Evaluating MPPT Converter Topologies Using a Matlab PV Model. J. Electr. Electron. Eng. Aust. 2001, 21, 49–55. [Google Scholar]
- Arya, Y. Impact of ultra-capacitor on automatic generation control of electric energy systems using an optimal FFOID controller. Int. J. Energy Res. 2019, 43, 8765–8778. [Google Scholar] [CrossRef]
- Micev, M.; Ćalasan, M.; Oliva, D. Fractional Order PID Controller Design for an AVR System Using Chaotic Yellow Saddle Goatfish Algorithm. Mathematics 2020, 8, 1182. [Google Scholar] [CrossRef]
- Dulf, E.H. Simplified Fractional Order Controller Design Algorithm. Mathematics 2019, 7, 1166. [Google Scholar] [CrossRef]
- Motorga, R.; Mureșan, V.; Ungureșan, M.L.; Abrudean, M.; Vălean, H.; Clitan, I. Artificial Intelligence in Fractional-Order Systems Approximation with High Performances: Application in Modelling of an Isotopic Separation Process. Mathematics 2022, 10, 1459. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Zellouma, D.; Bizon, N.; Colak, I. A new PI(1 +PI) controller to mitigate power ripples of a variable-speed dual-rotor wind power system using direct power control. Energy Rep. 2023, 10, 3580–3598. [Google Scholar] [CrossRef]
- Choudhary, R.; Rai, J.; Arya, Y. FOPTID+1 controller with capacitive energy storage for AGC performance enrichment of multi-source electric power systems. Electr. Power Syst. Res. 2023, 221, 109450. [Google Scholar] [CrossRef]
- Houssein, E.H.; Oliva, D.; Samee, N.A.; Mahmoud, N.F.; Emam, M.M. Liver Cancer Algorithm: A novel bio-inspired optimizer. Comput. Biol. Med. 2023, 165, 107389. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Aras, S.; Gedikli, E. Fitness-distance balance (FDB): A new selection method for meta-heuristic search algorithms. Knowl.-Based Syst. 2020, 190, 105169. [Google Scholar] [CrossRef]
- Hachemi, A.T.; Sadaoui, F.; Arif, S.; Saim, A.; Ebeed, M.; Kamel, S.; Jurado, F.; Mohamed, E.A. Modified reptile search algorithm for optimal integration of renewable energy sources in distribution networks. Energy Sci. Eng. 2023, 11, 4635–4665. [Google Scholar] [CrossRef]
- Adhikari, A.; Jurado, F.; Naetiladdanon, S.; Sangswang, A.; Kamel, S.; Ebeed, M. Stochastic optimal power flow analysis of power system with renewable energy sources using Adaptive Lightning Attachment Procedure Optimizer. Int. J. Electr. Power Energy Syst. 2023, 153, 109314. [Google Scholar] [CrossRef]
- Ebeed, M.; Mostafa, A.; Aly, M.M.; Jurado, F.; Kamel, S. Stochastic optimal power flow analysis of power systems with wind/PV/ TCSC using a developed Runge Kutta optimizer. Int. J. Electr. Power Energy Syst. 2023, 152, 109250. [Google Scholar] [CrossRef]
- Guvenc, U.; Duman, S.; Kahraman, H.T.; Aras, S.; Katı, M. Fitness–Distance Balance based adaptive guided differential evolution algorithm for security-constrained optimal power flow problem incorporating renewable energy sources. Appl. Soft Comput. 2021, 108, 107421. [Google Scholar] [CrossRef]
- Sharifi, M.R.; Akbarifard, S.; Qaderi, K.; Madadi, M.R. Developing MSA Algorithm by New Fitness-Distance-Balance Selection Method to Optimize Cascade Hydropower Reservoirs Operation. Water Resour. Manag. 2021, 35, 385–406. [Google Scholar] [CrossRef]
- Xia, J.; Zhang, H.; Li, R.; Wang, Z.; Cai, Z.; Gu, Z.; Chen, H.; Pan, Z. Adaptive Barebones Salp Swarm Algorithm with Quasi-oppositional Learning for Medical Diagnosis Systems: A Comprehensive Analysis. J. Bionic Eng. 2022, 19, 240–256. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Sahu, T.P. Multi-objective feature selection based on quasi-oppositional based Jaya algorithm for microarray data. Knowl.-Based Syst. 2022, 236, 107804. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Nadimi-Shahraki, M.H.; Barshandeh, S.; Abdollahzadeh, B.; Zamani, H. CQFFA: A Chaotic Quasi-oppositional Farmland Fertility Algorithm for Solving Engineering Optimization Problems. J. Bionic Eng. 2022, 20, 158–183. [Google Scholar] [CrossRef]
- Kandan, M.; Krishnamurthy, A.; Selvi, S.A.M.; Sikkandar, M.Y.; Aboamer, M.A.; Tamilvizhi, T. Quasi oppositional Aquila optimizer-based task scheduling approach in an IoT enabled cloud environment. J. Supercomput. 2022, 78, 10176–10190. [Google Scholar] [CrossRef]
- Latchoumi, T.P.; Parthiban, L. Quasi Oppositional Dragonfly Algorithm for Load Balancing in Cloud Computing Environment. Wirel. Pers. Commun. 2021, 122, 2639–2656. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Quasi-oppositional JAYA optimized 2-degree-of-freedom PID controller for load-frequency control of interconnected power systems. Int. J. Model. Simul. 2020, 42, 63–85. [Google Scholar] [CrossRef]
- Marzouk, R.; Alzahrani, J.S.; Alrowais, F.; Al-Wesabi, F.N.; Hamza, M.A. Quasi-oppositional wild horse optimization based multi-agent path finding scheme for real time IoT systems. Expert Syst. 2022, 39, e13112. [Google Scholar] [CrossRef]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M. Opposition versus randomness in soft computing techniques. Appl. Soft Comput. 2008, 8, 906–918. [Google Scholar] [CrossRef]
- Kapitaniak, T. Continuous control and synchronization in chaotic systems. Chaos Solitons Fractals 1995, 6, 237–244. [Google Scholar] [CrossRef]
- Sayed, G.I.; Khoriba, G.; Haggag, M.H. A novel chaotic salp swarm algorithm for global optimization and feature selection. Appl. Intell. 2018, 48, 3462–3481. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Jameel, M.; Abouhawwash, M. Exponential distribution optimizer (EDO): A novel math-inspired algorithm for global optimization and engineering problems. Artif. Intell. Rev. 2023, 56, 9329–9400. [Google Scholar] [CrossRef]
- Trojovska, E.; Dehghani, M.; Trojovsky, P. Zebra Optimization Algorithm: A New Bio-Inspired Optimization Algorithm for Solving Optimization Algorithm. IEEE Access 2022, 10, 49445–49473. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2022, 39, 2627–2651. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; MHS-95. IEEE: Piscataway, NJ, USA, 1995. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Wood, J. CCTV Ergonomics: Case Studies and Practical Guidance. In Meeting Diversity in Ergonomics; Elsevier: Amsterdam, The Netherlands, 2007; pp. 271–287. [Google Scholar] [CrossRef]


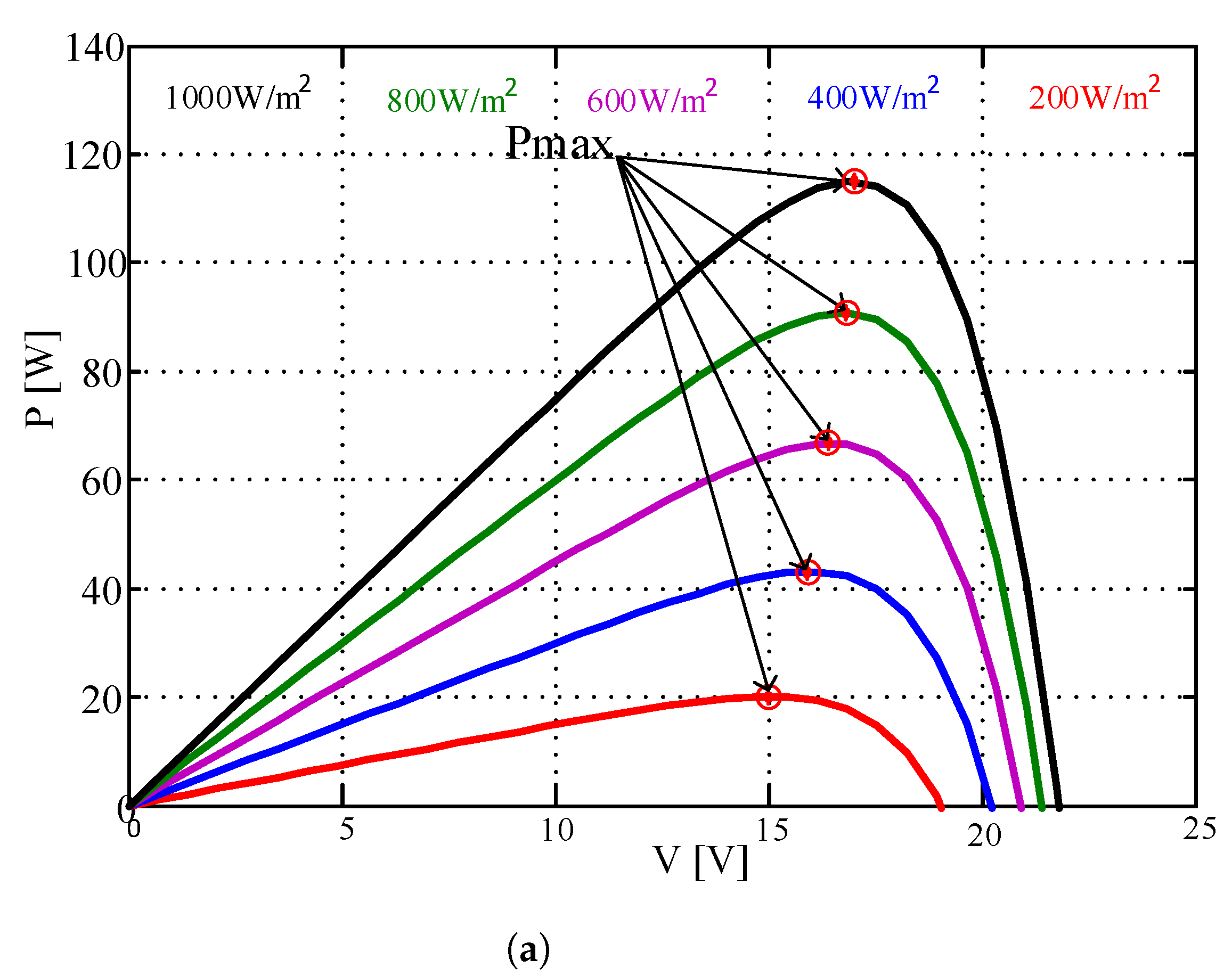









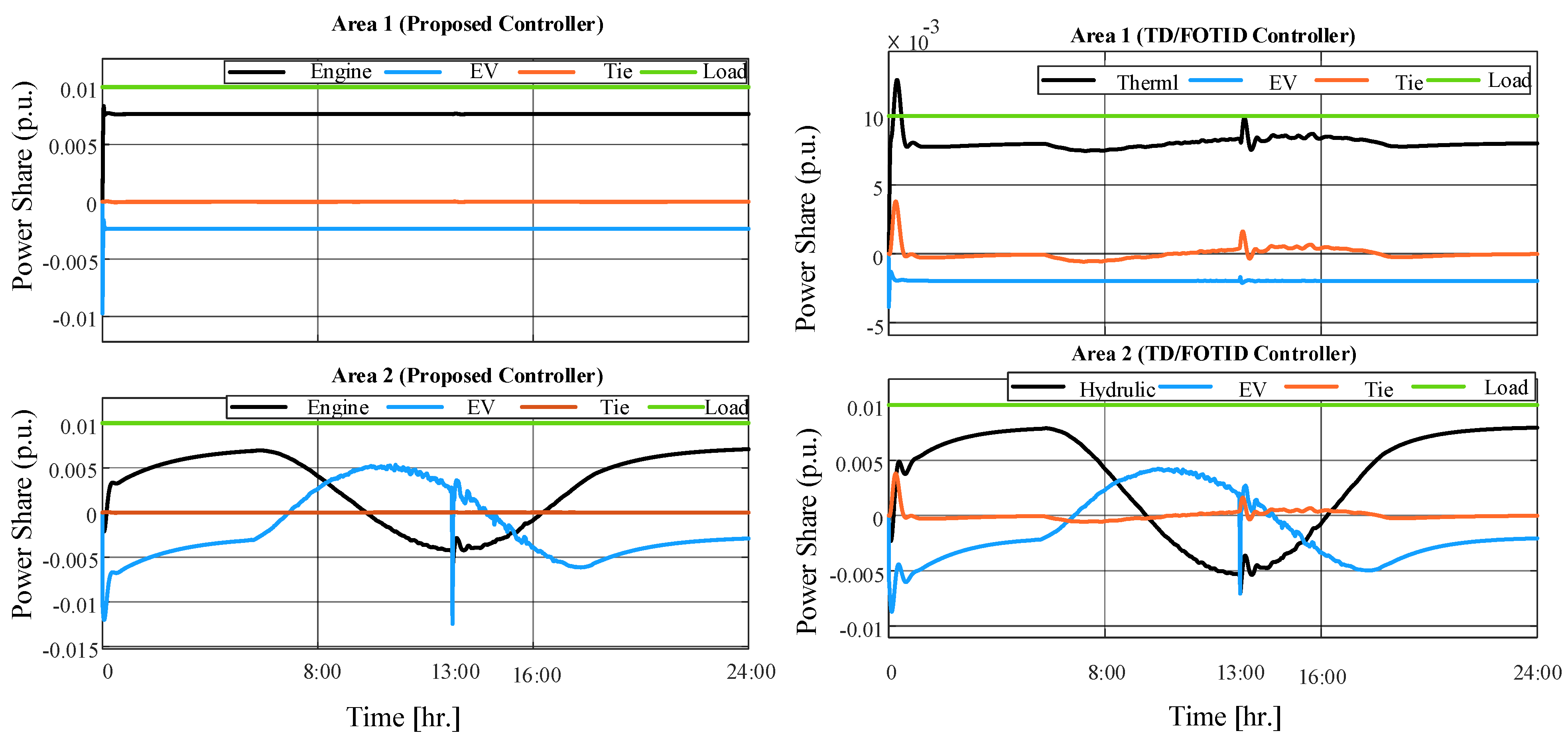
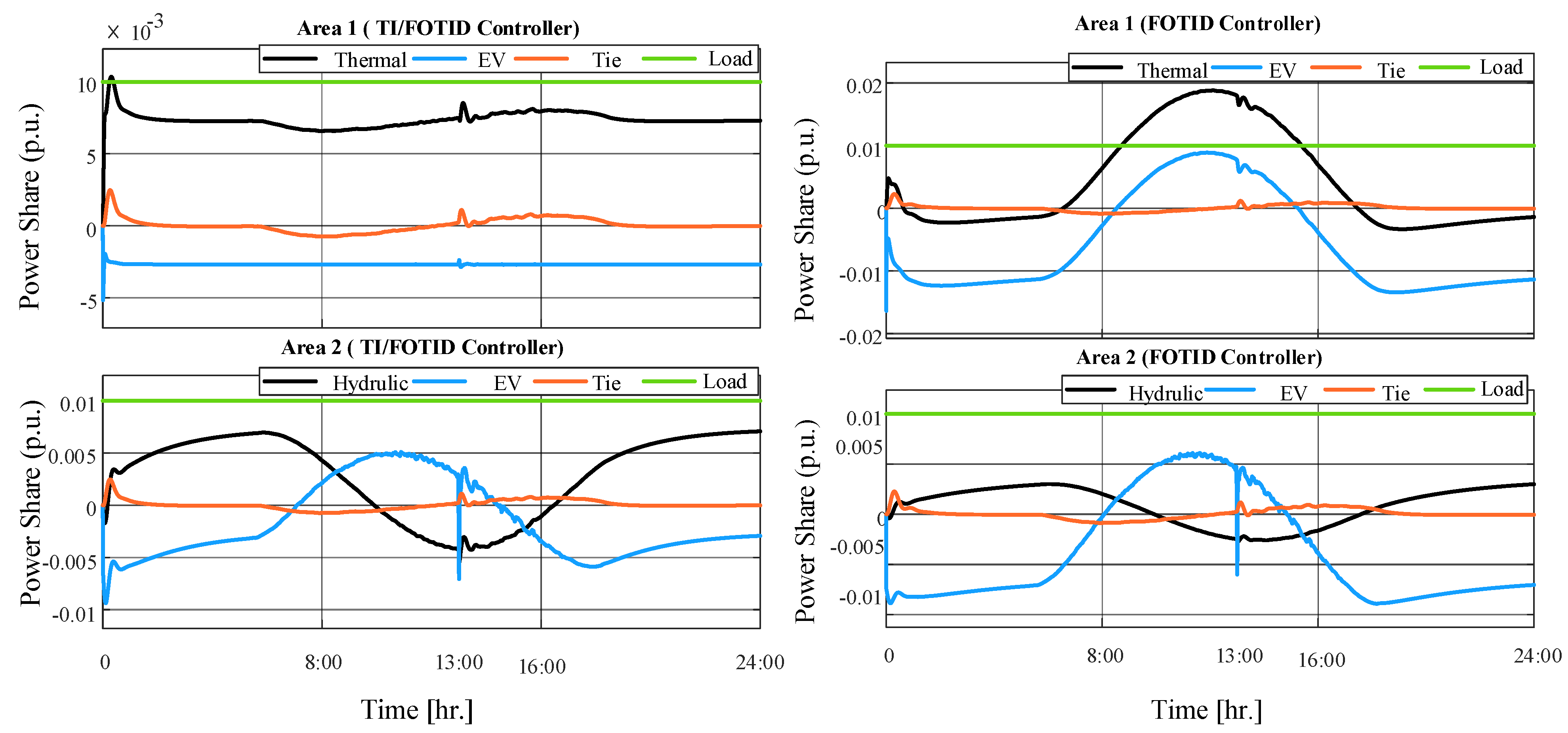

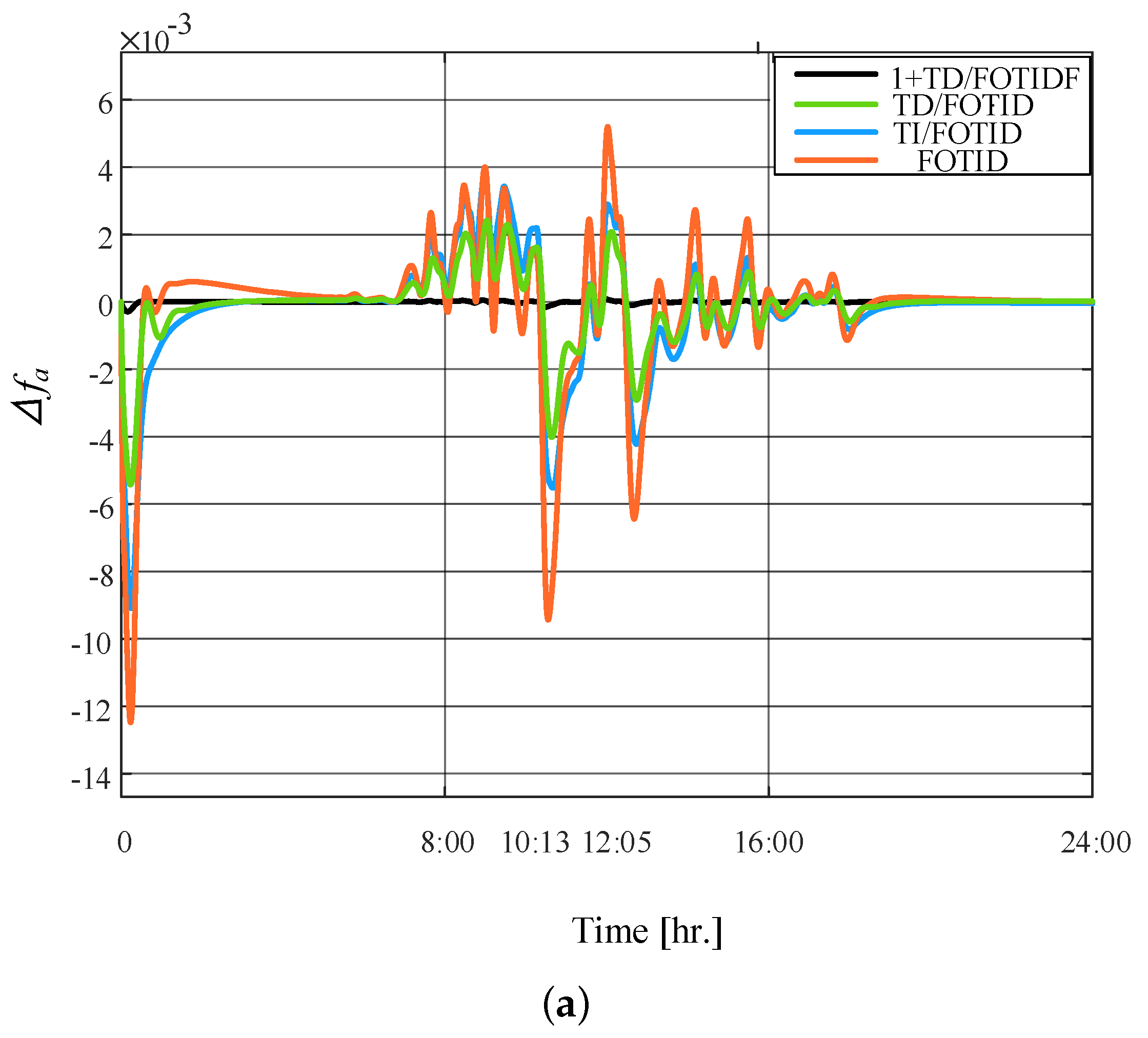
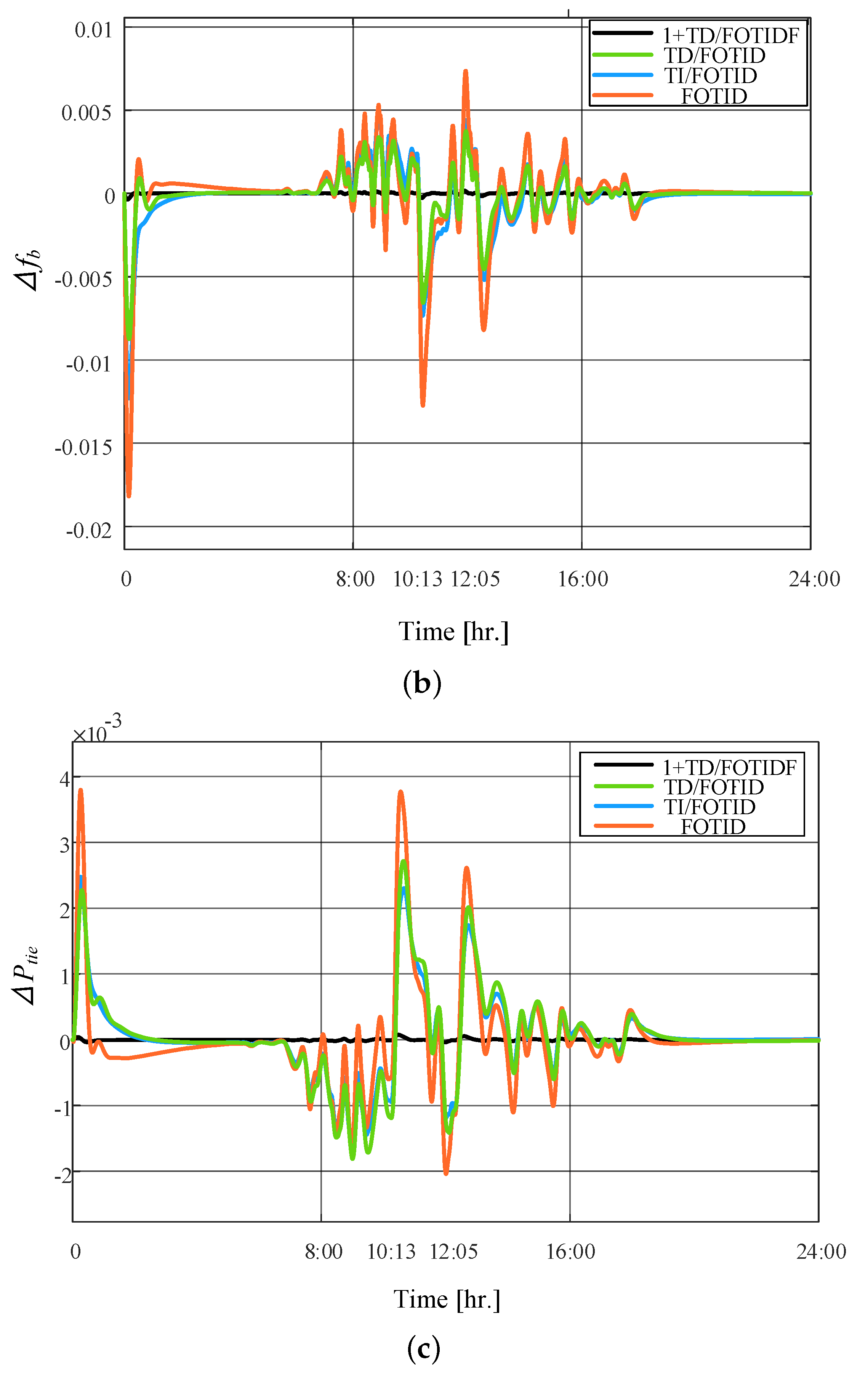


| Parameter | Value |
|---|---|
| Maximum Power value () | 115 W |
| Voltage at Maximum Power value () | 17.1 V |
| Current at Maximum Power value () | 6.7 A |
| Voltage value at Open-Circuit () | 21.8 V |
| Current value at Short -Circuit () | 7.5 A |
| Parameters | Symbols | Value | |
|---|---|---|---|
| Area | Area | ||
| Rated MGs’ capacity | (MW) | 1200 | 1200 |
| Droops constant | (Hz/MW) | 2.4 | 2.4 |
| Frequency bias values | (MW/Hz) | 0.4249 | 0.4249 |
| Valve gate limiting value (minimum) | (p.u.MW) | −0.5 | −0.5 |
| Valve gate limiting value (maximum) | (p.u.MW) | 0.5 | 0.5 |
| Time constant for thermal governor | (s) | 0.08 | - |
| Thermal turbines’ (time constant) | (s) | 0.3 | - |
| Governor of hydraulic generator (time constant) | (s) | - | 41.6 |
| Transient droops time constant for hydraulic governor | (s) | - | 0.513 |
| Governor of hydraulic generator resetting time | (s) | - | 5 |
| Hydraulic turbines’ water starting time | (s) | - | 1 |
| Inertia’s constants | (p.u.s) | 0.0833 | 0.0833 |
| Damping coefficient | (p.u./Hz) | 0.00833 | 0.00833 |
| PV generations time constant | (s) | - | 1.3 |
| PV generations’ gains | (s) | - | 1 |
| Wind generations’ time constants | (s) | 1.5 | - |
| Wind generations’ gains | (s) | 1 | - |
| EV BESSs’ models | |||
| Penetration level | - | 10% | 10% |
| BESS voltages (nominal) | (V) | 364.8 | 364.8 |
| BESS capacity | (Ah) | 66.2 | 66.2 |
| Series resistances | (ohms) | 0.074 | 0.074 |
| Transient resistance | (ohms) | 0.047 | 0.047 |
| Transient capacitances | (farad) | 703.6 | 703.6 |
| Constants value | 0.02612 | 0.02612 | |
| BESS’s SOC (maximum) | % | 95 | 95 |
| BESS’s energy capacity | (kWh) | 24.15 | 24.15 |
| Function | Type | Fmin | Boundaries | Description |
|---|---|---|---|---|
| F1 | Unimodal function | 300 | [−100, 100] | Shifted and full rotated Zakharov function |
| F2 | Basic functions | 400 | [−100, 100] | Shifted and full rotated Rosenbrock’s function |
| F3 | 600 | [−100, 100] | Shifted and full rotated expanded Schaffer’s F6 function | |
| F4 | 800 | [−100, 100] | Shifted and full rotated non-continuous Rastrigin’s function | |
| F5 | 900 | [−100, 100] | Shifted and rotated Levy function | |
| F6 | Hybrid functions | 1800 | [−100, 100] | Hybrid function 1 (N = 3) |
| F7 | 2000 | [−100, 100] | Hybrid function 2 (N = 6) | |
| F8 | 2200 | [−100, 100] | Hybrid function 3 (N = 5) | |
| F9 | Composition functions | 2300 | [−100, 100] | Composite function 1 (N = 5) |
| F10 | 2400 | [−100, 100] | Composite function 2 (N = 4 | |
| F11 | 2600 | [−100, 100] | Composite function 3 (N = 5) | |
| F12 | 2700 | [−100, 100] | Composite function 3 (N = 5) |
| Algorithm | Parameter | Value |
|---|---|---|
| PSO | , , , , | 300, 30, 2,2, 0.7 |
| SCSC | , , Sensitivity range (), Phases control range (R) | 300, 30, [2 - 0], [−2rg, 2rg] |
| SCA | , , b | 300, 30, [2 - 0] |
| ZOA | , , R | 300, 30, 0.01 |
| LCA | , | 300, 30 |
| MLCA | , , | 300, 30, 4 |
| Function No. | Optimizer | Average | Best | Worst | SD |
|---|---|---|---|---|---|
| F1 | SCSO | 3093.775 | 349.1486 | 8691.832 | 2493.022 |
| SCA | 3458.404 | 1164.057 | 6460.631 | 1667.455 | |
| PSO | 300.0105 | 300.0001 | 300.1228 | 0.024964 | |
| ZOA | 2406.967 | 323.1252 | 7635.127 | 2195.524 | |
| LCA | 1447.707 | 700.4051 | 3349.518 | 711.4054 | |
| MLCA | 300 | 300 | 300.001 | 0.000205 | |
| F2 | SCSO | 455.7817 | 401.0632 | 720.0985 | 68.29365 |
| SCA | 494.0413 | 432.2709 | 542.0408 | 25.87232 | |
| PSO | 424.9348 | 400 | 471.3437 | 30.60353 | |
| ZOA | 476.7607 | 404.1804 | 910.9457 | 99.36141 | |
| LCA | 420.9453 | 401.0094 | 442.2129 | 12.7182 | |
| MLCA | 409.3691 | 400 | 470.8066 | 19.38046 | |
| F3 | SCSO | 619.4869 | 603.0549 | 640.0254 | 10.06907 |
| SCA | 625.8878 | 618.392 | 649.0927 | 6.258529 | |
| PSO | 620.3777 | 603.8081 | 639.1443 | 10.40486 | |
| ZOA | 621.8001 | 610.0043 | 633.3335 | 5.858331 | |
| LCA | 605.1606 | 601.5796 | 610.2001 | 2.407723 | |
| MLCA | 603.0268 | 600.2005 | 611.2571 | 3.185232 | |
| F4 | SCSO | 829.3113 | 806.1021 | 844.7062 | 8.741245 |
| SCA | 848.0268 | 837.5241 | 860.1306 | 6.503605 | |
| PSO | 821.6901 | 809.9496 | 842.7831 | 7.669336 | |
| ZOA | 816.5859 | 809.1074 | 830.5366 | 5.63061 | |
| LCA | 834.6409 | 814.102 | 854.8532 | 10.1297 | |
| MLCA | 825.3515 | 804.9748 | 832.8336 | 6.299992 | |
| F5 | SCSO | 1141.826 | 915.4967 | 1469.342 | 171.9704 |
| SCA | 1083.895 | 992.3169 | 1283.928 | 80.46401 | |
| PSO | 1054.136 | 900 | 1362.665 | 153.0541 | |
| ZOA | 1061.449 | 940.9945 | 1283.71 | 96.35584 | |
| LCA | 923.2255 | 901.7043 | 963.4934 | 16.85943 | |
| MLCA | 909.5508 | 900.6334 | 957.7695 | 12.00111 | |
| F6 | SCSO | 4481.64 | 2187.17 | 8161.352 | 1751.289 |
| SCA | 7439635 | 963067.3 | 26425791 | 7135852 | |
| PSO | 3052.999 | 1860.679 | 8084.839 | 1582.306 | |
| ZOA | 3100.627 | 1881.875 | 7298.885 | 1587.5 | |
| LCA | 21954.04 | 2048.434 | 136689.1 | 32740.4 | |
| MLCA | 1923.427 | 1828.147 | 2521.161 | 141.062 | |
| F7 | SCSO | 2048.494 | 2021.093 | 2089.621 | 18.7493 |
| SCA | 2066.766 | 2041.341 | 2085.259 | 10.09232 | |
| PSO | 2044.901 | 2012.969 | 2094.026 | 21.58967 | |
| ZOA | 2053.452 | 2010.803 | 2114.428 | 22.98909 | |
| LCA | 2046.143 | 2026.291 | 2066.935 | 11.5397 | |
| MLCA | 2025.324 | 2008.956 | 2046.95 | 8.875774 | |
| F8 | SCSO | 2227.988 | 2214.531 | 2239.62 | 6.081599 |
| SCA | 2239.191 | 2231.123 | 2251.613 | 5.328733 | |
| PSO | 2235.924 | 2200.537 | 2341.024 | 39.94917 | |
| ZOA | 2231.259 | 2222.731 | 2352.093 | 25.27378 | |
| LCA | 2229.289 | 2222.178 | 2231.57 | 2.287831 | |
| MLCA | 2219.969 | 2203.455 | 2224.124 | 4.350484 | |
| F9 | SCSO | 2594.81 | 2529.458 | 2678.021 | 35.10836 |
| SCA | 2598.177 | 2557.816 | 2656.696 | 27.8627 | |
| PSO | 2541.842 | 2529.284 | 2676.216 | 40.64008 | |
| ZOA | 2614.066 | 2530.239 | 2718.711 | 45.68827 | |
| LCA | 2539.873 | 2531.308 | 2556.745 | 6.301353 | |
| MLCA | 2529.411 | 2529.284 | 2531.277 | 0.397224 | |
| F10 | SCSO | 2530.18 | 2500.426 | 2635.02 | 53.1725 |
| SCA | 2528.239 | 2501.45 | 2673.45 | 58.37221 | |
| PSO | 2596.806 | 2500.387 | 2759.12 | 68.34379 | |
| ZOA | 2578.921 | 2500.553 | 2681.633 | 71.62236 | |
| LCA | 2500.802 | 2500.463 | 2501.487 | 0.222178 | |
| MLCA | 2500.435 | 2500.276 | 2500.703 | 0.1111 | |
| F11 | SCSO | 2831.009 | 2609.066 | 3309.952 | 170.1567 |
| SCA | 3004.421 | 2793.088 | 3783.863 | 297.7186 | |
| PSO | 2953.419 | 2600.001 | 5230.808 | 485.1794 | |
| ZOA | 3053.657 | 2745.179 | 3430.171 | 182.3106 | |
| LCA | 2731.127 | 2636.21 | 2764.63 | 34.56173 | |
| MLCA | 2624.072 | 2600 | 2750.473 | 56.29244 | |
| F12 | SCSO | 2874.063 | 2861.454 | 2918.708 | 16.46731 |
| SCA | 2873.296 | 2867.157 | 2891.819 | 4.697798 | |
| PSO | 2951.277 | 2872.847 | 3121.534 | 69.80949 | |
| ZOA | 2943.05 | 2895.543 | 3012.8 | 31.04917 | |
| LCA | 2869.805 | 2865.583 | 2875.687 | 2.388877 | |
| MLCA | 2871.416 | 2864.046 | 2898.943 | 7.599243 |
| MLCA vs. | SCSO | SCA | PSO | FOX | LCA |
|---|---|---|---|---|---|
| F1 | 1.4157 × 10−9 | 1.4157 × 10−9 | 5.2120 × 10−9 | 1.4157 × 10−9 | 1.4157 × 10−9 |
| F2 | 9.6957 × 10−6 | 3.6690 × 10−9 | 1.1159 × 10−1 | 3.3440 × 10−7 | 8.1897 × 10−5 |
| F3 | 9.2880 × 10−9 | 1.4157 × 10−9 | 1.3079 × 10−8 | 1.5967 × 10−9 | 1.6708 × 10−3 |
| F4 | 8.7677 × 10−2 | 1.4055 × 10−9 | 1.8376 × 10−2 | 2.1373 × 10−5 | 9.6989 × 10−4 |
| F5 | 2.2857 × 10−9 | 1.4157 × 10−9 | 2.9771 × 10−2 | 1.8002 × 10−9 | 3.3128 × 10−4 |
| F6 | 2.5742 × 10−9 | 1.4157 × 10−9 | 3.2928 × 10−5 | 2.6597 × 10−6 | 2.0288 × 10−9 |
| F7 | 1.6471 × 10−6 | 1.5967 × 10−9 | 1.1285 × 10−4 | 6.7951 × 10−7 | 1.0585 × 10−7 |
| F8 | 3.7045 × 10−7 | 1.4157 × 10−9 | 8.0086 × 10−1 | 1.8002 × 10−9 | 2.0288 × 10−9 |
| F9 | 1.8002 × 10−9 | 1.4157 × 10−9 | 1.5288 × 10−6 | 1.5967 × 10−9 | 1.4157 × 10−9 |
| F10 | 2.5677 × 10−8 | 1.4157 × 10−9 | 2.4184 × 10−6 | 2.0288 × 10−9 | 1.6401 × 10−8 |
| F11 | 1.3090 × 10−7 | 1.4157 × 10−9 | 8.2805 × 10−9 | 2.2857 × 10−9 | 3.0175 × 10−7 |
| F12 | 1.8064 × 10−1 | 3.3915 × 10−3 | 1.0414 × 10−8 | 1.5967 × 10−9 | 5.7365 × 10−1 |
| Controller | Area | Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FOTID | a | 2.245 | 1.987 | 1.713 | 2.234 | ― | ― | ― | ― | 0.622 | 0.574 | ― |
| b | 2.956 | 2.016 | 0.895 | 2.923 | ― | ― | ― | ― | 0.714 | 0.882 | ― | |
| TI/FOTID | a | 3.155 | 2.019 | ― | 2.862 | 2.868 | 3.036 | 1.156 | 3.634 | 0.882 | 0.857 | ― |
| b | 2.738 | 1.583 | ― | 3.235 | 2.365 | 2.678 | 1.344 | 3.69 | 0.566 | 0.843 | ― | |
| TD/FOTID | a | 3.928 | ― | 1.037 | 3.555 | 4.018 | 3.346 | 2.147 | 3.944 | 0.788 | 0.948 | ― |
| b | 3.748 | ― | 1.164 | 4.022 | 3.571 | 3.176 | 2.291 | 3.891 | 0.758 | 0.788 | ― | |
| 1+TD/FOTIDF | a | 4.525 | ― | 3.851 | 4.576 | 4.864 | 3.865 | 3.998 | 4.977 | 0.948 | 0.877 | 151.36 |
| b | 4.118 | ― | 4.073 | 4.281 | 3.954 | 4.279 | 3.092 | 4.583 | 0.882 | 0.915 | 189.5 | |
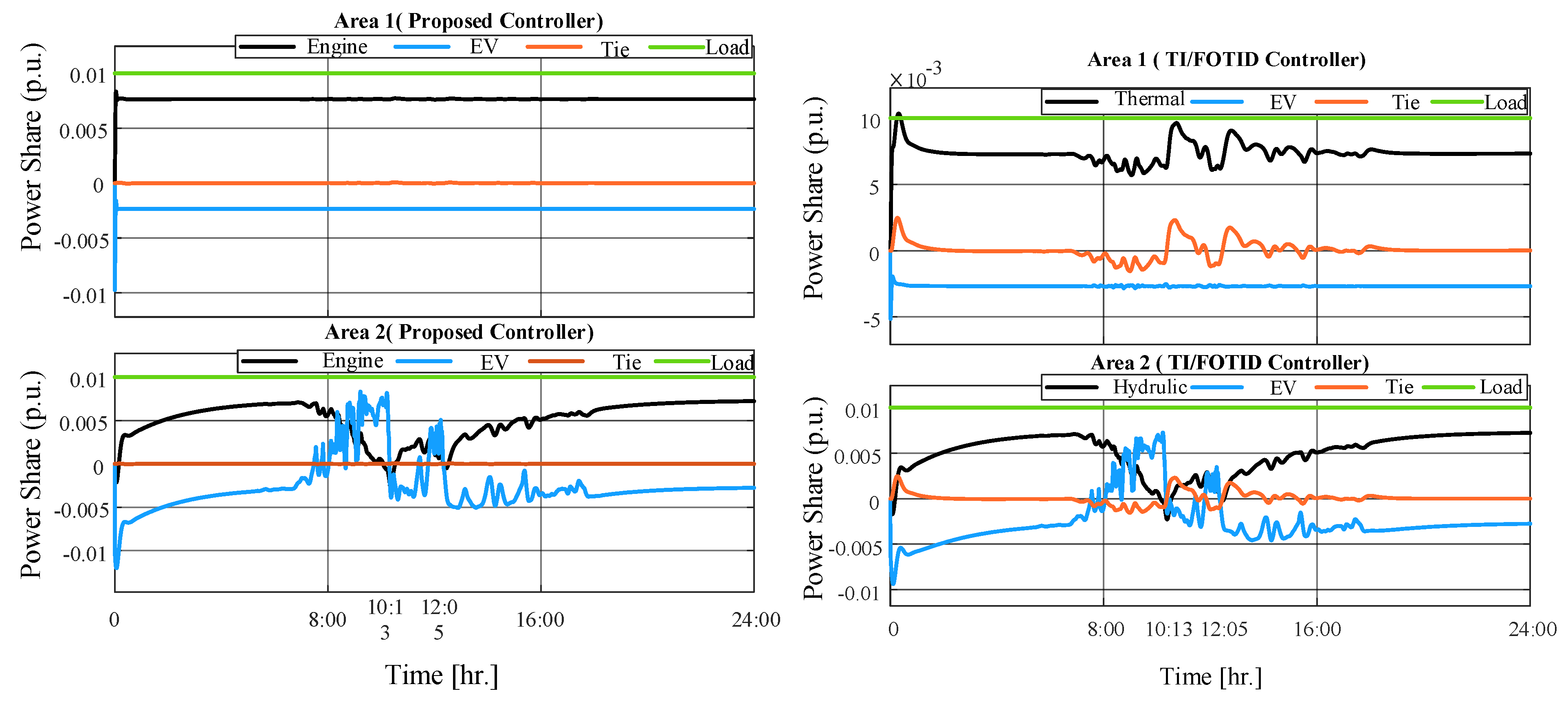
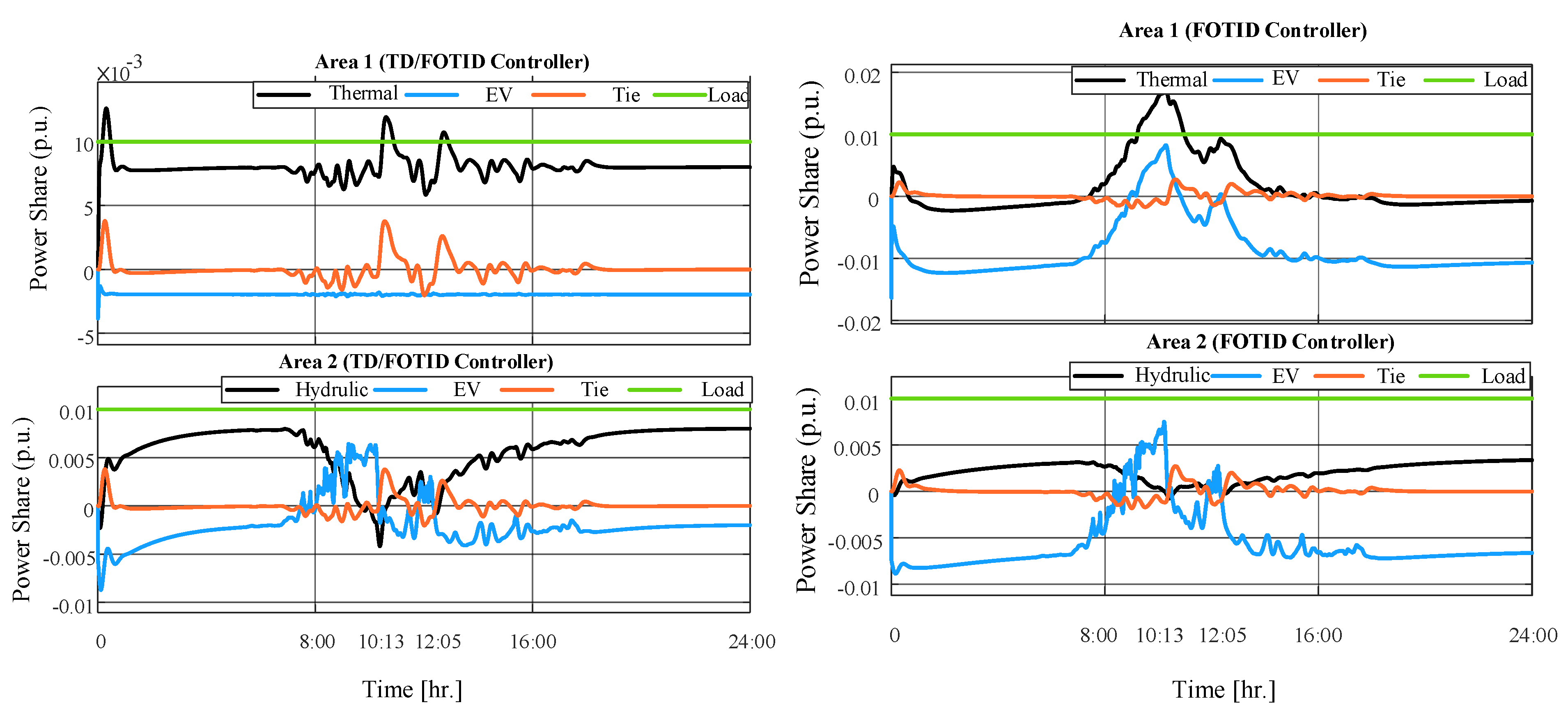
| Scenario | Controller | (P.U) | (P.U) | (P.U) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PO | PU | ST (s) | PO | PU | ST (s) | PO | PU | ST (s) | ||
| No.1 at 75 s | FOTID | 0.0019 | 0.0115 | 17 | 0.0021 | 0.0082 | 16 | 0.0005 | 0.0028 | 22 |
| TI/FOTID | 0.0002 | 0.0079 | 9 | 0.0016 | 0.0058 | 20 | 0.0001 | 0.0024 | 18 | |
| TD/FOTID | 0.0017 | 0.0058 | 15 | 0.0001 | 0.0023 | 10 | 0.0002 | 0.0016 | 10 | |
| 1+TD/FOTIDF | - | 0.0001 | 4 | - | 0.0005 | 5 | - | 8.4 × 10−5 | 6 | |
| No.2 at 8:00 AM. | FOTID | 0.0016 | 0.0012 | FU | 0.0017 | 0.0011 | FU | 0.0004 | 0.0005 | FU |
| TI/FOTID | 0.0017 | 0.0018 | FU | 0.0019 | 0.0015 | FU | 0.0006 | 0.0007 | FU | |
| TD/FOTID | 0.0008 | 0.0009 | FU | 0.0005 | 0.0007 | FU | 0.0007 | 0.0009 | FU | |
| 1+TD/FOTIDF | 1 × 10−6 | 1 × 10−5 | FU | 1.1 × 10−6 | 1.01 × 10−5 | FU | 1 × 10−6 | 1.1 × 10−6 | FU | |
| No.3 at 13:00 PM. | FOTID | 0.0012 | 0.0042 | FU | 0.0025 | 0.0073 | FU | 0.0016 | 0.0004 | FU |
| TI/FOTID | 0.0011 | 0.0023 | FU | 0.0019 | 0.0041 | FU | 0.0011 | 0.0003 | FU | |
| TD/FOTID | 0.0001 | 0.0021 | FU | 0.0014 | 0.0037 | FU | 0.0009 | 0.0001 | FU | |
| 1+TD/FOTIDF | 1 × 10−5 | 1 × 10−5 | FU | 0.9 × 10−5 | 1 × 10−6 | FU | 1 × 10−4 | 1 × 10−6 | FU | |
| No.4 at 10:00 AM. | FOTID | 0.0057 | 0.0099 | FU | 0.0072 | 0.0133 | FU | 0.0039 | 0.0021 | FU |
| TI/FOTID | 0.0028 | 0.0058 | FU | 0.0041 | 0.0033 | FU | 0.0022 | 0.0013 | FU | |
| TD/FOTID | 0.002 | 0.004 | FU | 0.0036 | 0.0031 | FU | 0.0021 | 0.0011 | FU | |
| 1+TD/FOTIDF | 0.0001 | 0.0004 | FU | 0.0001 | 0.0001 | FU | 1 × 10−4 | 1 × 10−5 | FU | |
| No.5 at 16:00 PM. | FOTID | 0.141 | 0.022 | FU | 0.123 | 0.0392 | FU | 0.033 | 0.0067 | FU |
| TI/FOTID | 0.0826 | 0.0018 | FU | 0.0524 | 0.0141 | FU | 0.0192 | 0.0031 | FU | |
| TD/FOTID | 0.0522 | 0.0151 | FU | 0.0198 | 0.011 | FU | 0.022 | 0.0023 | FU | |
| 1+TD/FOTIDF | 0.004 | - | 120 | 0.001 | - | 110 | 0.0013 | - | 180 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noman, A.M.; Aly, M.; Alqahtani, M.H.; Almutairi, S.Z.; Aljumah, A.S.; Ebeed, M.; Mohamed, E.A. Optimum Fractional Tilt Based Cascaded Frequency Stabilization with MLC Algorithm for Multi-Microgrid Assimilating Electric Vehicles. Fractal Fract. 2024, 8, 132. https://doi.org/10.3390/fractalfract8030132
Noman AM, Aly M, Alqahtani MH, Almutairi SZ, Aljumah AS, Ebeed M, Mohamed EA. Optimum Fractional Tilt Based Cascaded Frequency Stabilization with MLC Algorithm for Multi-Microgrid Assimilating Electric Vehicles. Fractal and Fractional. 2024; 8(3):132. https://doi.org/10.3390/fractalfract8030132
Chicago/Turabian StyleNoman, Abdullah M., Mokhtar Aly, Mohammed H. Alqahtani, Sulaiman Z. Almutairi, Ali S. Aljumah, Mohamed Ebeed, and Emad A. Mohamed. 2024. "Optimum Fractional Tilt Based Cascaded Frequency Stabilization with MLC Algorithm for Multi-Microgrid Assimilating Electric Vehicles" Fractal and Fractional 8, no. 3: 132. https://doi.org/10.3390/fractalfract8030132
APA StyleNoman, A. M., Aly, M., Alqahtani, M. H., Almutairi, S. Z., Aljumah, A. S., Ebeed, M., & Mohamed, E. A. (2024). Optimum Fractional Tilt Based Cascaded Frequency Stabilization with MLC Algorithm for Multi-Microgrid Assimilating Electric Vehicles. Fractal and Fractional, 8(3), 132. https://doi.org/10.3390/fractalfract8030132










