Abstract
In this paper, a discrete-time fractional flocking control algorithm of multi-agent systems is put forward to address the slow convergence issue of multi-agent systems. Firstly, by introducing Grünwald-Letnikov (G-L) fractional derivatives, the algorithm allows agents to utilize historical information when updating their states. Secondly, based on the Lyapunov stability theory, the convergence of the algorithm is proven. Finally, simulations are conducted to verify the effectiveness of the proposed algorithm. Comparisons are made between the proposed algorithm and other methods. The results show that the proposed algorithm can effectively improve the convergence speed of multi-agent systems.
MSC:
93A16
1. Introduction
A multi-agent system (MAS) consists of multiple autonomous and perceptually-abled agents that interact, communicate, and compete with each other based on specific rules to solve complex problems and accomplish tasks collectively. MASs span various domains, including robotics, network science, sociology, and economics, and have been widely applied in practical scenarios such as consensus control [1], logistics management, and decision support [2].
Flocking control of multi-agent systems has become a research hotspot in recent years. It refers to emergent collective behaviors in a swarm system where agents interact locally and achieve stability, order, and other specific goals [3]. Flocking control originates from the study of natural biological swarms which exhibit intelligent characteristics, such as fish schools, bird flocks, and insect colonies [4,5,6]. In 1987, Reynolds [7] introduced the Boids model, a discrete-time and space-based multi-agent system used to describe the behavioral interaction in bird-like animal swarms, such as seagulls or flocks of pigeons. The Boids model proposes three basic principles for agent behavior, separation, alignment, and cohesion, which enable collective synergy. On the basis of the Boids model, Vicsek et al. [8] focused only on the alignment principle and proposed the well-known Vicsek model. In this model, each particle adjusts its movement direction by perceiving and responding to the positions and orientations of surrounding particles.
Based on these models, flocking control in multi-agent systems has been extensively studied. Olfati et al. formulated the theoretical framework for swarm control in multi-agent systems based on Reynolds’ three principles, providing a theoretical analysis of the flocking phenomenon from the perspective of nonlinear control theory [9]. In 2019, Jia et al. [10] introduced a hierarchical mechanism to the classical Vicsek model, proposing a hierarchical flocking model to explain the collaborative behaviors of specific agents. It is worth noting that the existing research on swarm control in multi-agent systems mainly focuses on integer-order dynamics, such as first-order dynamics [11,12] and second-order dynamics [13,14], while studies based on fractional-order dynamics are relatively scarce. Fractional calculus has been widely applied in natural sciences and engineering fields, such as linear and nonlinear dynamics, intelligent algorithm optimization, and characterizing the internal structures of complex functions. Fractional calculus is a good approach for modeling complex physical systems [15,16] and improving system convergence rates [17,18]. Due to the “memory” property of fractional calculus, many complex phenomena in nature that integer-order dynamics cannot explain can be naturally described by the cooperative behaviors of agents with fractional-order dynamics, such as the foraging of microorganisms and the collective movement of bacteria [19]. Therefore, it is meaningful to investigate flocking control in multi-agent systems based on fractional-order dynamics. In addition, discrete-time systems are suitable to investigate this, since in continuous systems, in order to execute an implementation, the systems have to be discretized because there are no exact formulas of the solutions.
Inspired by the above results, this paper discusses the flocking control of discrete-time multi-agent systems with fractional dynamics. The main contributions are summarized as follows.
- A discrete-time multi-agent flocking control algorithm was derived based on Grünwald-Letnikov (G-L) fractional derivatives. Compared with existing flocking methods where only integer-order dynamics are considered, our algorithm allows agents to use historical information, which means that the current states of the agents depend on both recent and historical values. Thus, our method conforms more with the reality that individuals always exhibit a time-dependent memory effect in nature;
- Compared with existing research [18] where only the leaderless condition is taken into account, this paper investigates the fractional-order flocking control of multi-agent systems under the leader-following strategy. Based on the Lyapunov stability theory, the convergence of this algorithm is proven. Experimental results demonstrate that the proposed algorithm achieves consensus among agents and effectively improves the convergence rate.
This paper is organized as follows. In Section 2, some notations and basic definitions are given. In Section 3, the model formulation for the discrete-time flocking control algorithm of multi-agent systems is proposed, and the convergence of which is proven. In Section 4, simulations are given to verify our results. Finally, some conclusions are presented in Section 5.
2. Preliminaries
In this section, basin graph theory and definitions of the G-L fractional derivative are given.
2.1. Graph Theory
Let , and be the position vector, velocity vector and control input of agent i at time t, respectively. The topology of agents is described as an undirected graph , where denotes n agents and indicates that there is a communication link between agent i and agent j. is the set of neighbors of agent i at time t. Let r denote the communication radius, then . denotes the adjacency matrix with if and otherwise. The Laplacian matrix of graph G is defined as with and for .
In order to avoid the collision among agents, the agents need to keep a distance between the safety distance and communication radius r; therefore, the expected distance between every two agents is defined as
Equation (1) is called the -lattices system [9]. However, due to the interaction between individuals, the system cannot reach the ideal system and eventually evolves into the -lattices-like system with error , which is shown in Figure 1.
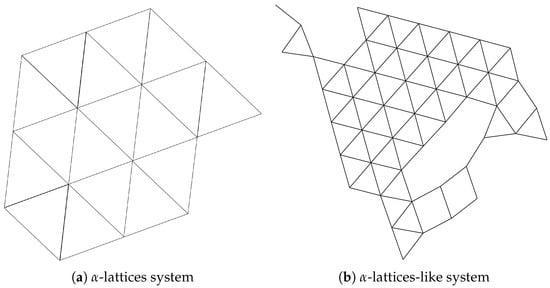
Figure 1.
The -lattices system and -lattices-like system.
2.2. Fractional Derivative
Fractions calculus, as a branch of mathematics, has evolved over several centuries, resulting in varying definitions. In this paper, we employ the Grunwald-Letnikov fractional derivative, which is defined as follows [20]:
where h is a positive real number and is an integer. is the fractional order and is the Gamma function with . is called the G-L fractional derivative of with order .
In discrete-time implementation, Equation (2) is given by
where , e is a positive integer, T is the sampling period and m is the truncation order.
Remark 1.
Equations (2) and (3) demonstrate a vital characteristic of fractional differentiation: it comprises an infinite series of terms, unlike integer differentiation, which consists of a finite series. Consequently, integer differentiation is referred to as a local operator, as it solely relies on the function’s value at a single point in time and its finite derivative. In contrast, fractional differentiation incorporates historical information throughout the evolutionary process, metaphorically representing the “memory” of all past events. It can be recognized as a non-local operator with memory effects. This particular property is crucial in accurately depicting the dynamic behavior observed in numerous natural, physical, and engineering systems.
Remark 2.
where e is a positive integer is applied for all the following equations. Thus all the time t is in the discrete-time domain in the rest of this paper.
3. The Proposed Flocking Control Method
In the current section, the proposed flocking control of multi-agent systems based on the G-L fractional derivative is given. Furthermore, the convergence of the algorithm is analyzed by using the Lyapunov stability theory.
3.1. Dynamics Model of Multi-Agent Systems
We consider that there are N agents in two-dimensional Euclidean space. In the general flocking control models [21,22,23], agents always update their states by integer-order dynamics, that is
where T is the time step. Now, let us see the updating speed of the agents. can be written as
Equation (5) is equivalent to
The above equation suggests that in the traditional integer-order flocking control, only current information is used to update the agents’ states. To apply the historical information to boost the performance of swarm flocking, we replace the plain derivative with the G-L fractional-order derivative with fractional order , as defined in Section 2.2, then we obtain the following relation:
where denotes the first-order derivative of . Without loss of generality, the first four terms of the fractional derivative, as given by Equation (3), are considered, then we obtain
Equation (8) reveals that the speed of the agents, based on fractional-order dynamics at time t, is a comprehensive result of historical information from the previous four moments. This contrasts integer-order flocking control, which relies solely on the information of the current state. Importantly, when , the fractional-order flocking control algorithm regresses to the traditional integer-order flocking control.
In order to make all agents move in the desired direction, a virtual leader is added, and the dynamics of which are designed as
where and represent the position vector and speed vector of the virtual leader at time t.
3.2. Control Protocol of the Agents
Now, we consider the control protocol of the agents. Assume that the control input of agent i at time t is
where is the relative distance control term, which is used to achieve aggression and separation. The definition of is
where with parameter , and
where the parameters a, b and c satisfy and . The gradient of -norm is . The term is used to control the agents to achieve speed alignment, which is expressed as
is used for the agents to follow the virtual leader, which is defined as
where and are positive real numbers, representing the feedback parameters.
Assumption 1.
The initial states of the multi-agent systems are connected, which means that the undirected graph is connected.
Assumption 2.
There are no collisions between agents in the initial state of the system.
Assumption 3.
All the agents can simultaneously receive instructions from the virtual leader.
Theorem 1.
Consider that Assumptions 1–3 are valid. For the multi-agent system described in Equations (8) and (9) with the control input in (10), if the sampling period is small enough such that , then we can obtain
- 1.
- The system will be asymptotic stable, and the agents’ positions will eventually tend to lattices;
- 2.
- The speed of all agents will tend towards the virtual leader;
- 3.
- There will be no collisions among the agents.
Proof of Theorem 1.
Here, we use the same technique as described in the stability analysis of flocking in [9,24] to prove the stability of our proposed model. Let , ; hence, it is obviously that , where . The total energy of a multi-agent system is composed of the total potential energy and the relative kinetic energy. According to Equations (10)–(14), the total energy of the system at time t is
where is the total potential energy at time t [24]
where . For simplicity, let , then we have
The energy function can be written as
Then we obtain
From the definition of , invoking Equations (10)–(14),
where , is the Laplacian matrix of the system at time t, and ⊗ denotes the Kronecker product. Since is a positive semi-definite matrix, is a positive matrix. Then we obtain , which means is decreasing. Therefore, for any , and the system will be asymptotically stable.
Assume that agents i and j collide during . Then and will increase, which contradicts that is decreasing. Therefore, the agents will not collide. Using the same method, the agents will not collide at each period . This completes the proof. □
3.3. Flow Chart of Our Proposed Algorithm
Figure 2 illustrates the procedure of the discrete-time fractional-order flocking control algorithm of multi-agent systems. First, the agent’s speed and position are set up. Next, the interaction force on the agent is calculated using Equations (10)–(14). After this, the agent updates its fractional speed based on the interaction force and Equation (8). Finally, the agent’s position is updated using Equation (8).
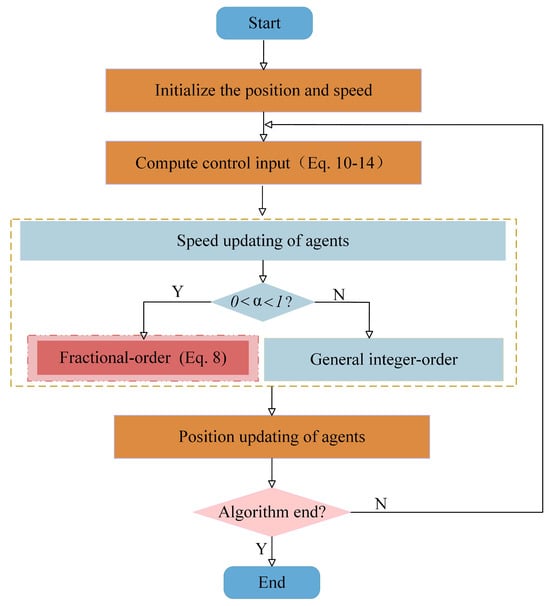
Figure 2.
Flow chart of our proposed flocking algorithm.
4. Simulation Results
In this section, some numerical simulations based on MATLAB are provided to illustrate the effectiveness of our proposed fractional-order flocking control algorithm.
4.1. Tests of the Fractional-Order Flocking Control Algorithm
The current simulation investigates the speed and position changes of agents based on G-L fractional-order dynamics. The multi-agent system is composed of 100 agents, and the initial location and direction angle are randomly generated in a area and , respectively, which is shown in Figure 3a. The red arrow represents the direction of the agents. Consider the communication radius , the subsequent expected distance between every two agents is , and besides and , the sampling period . The initial position of the virtual leader is , and the speed of it is constant (0.5, 0.5). The fractional order is .
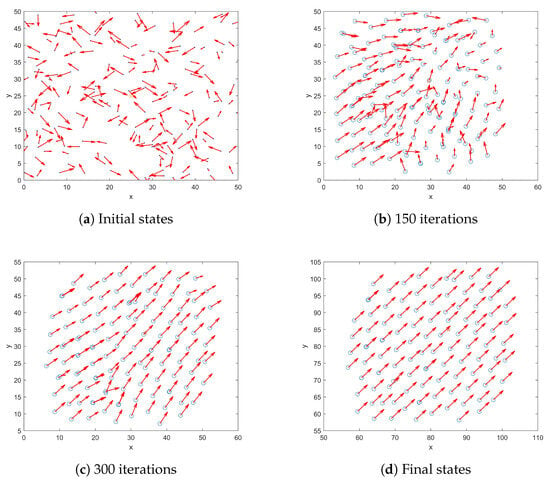
Figure 3.
The status of the agents.
Figure 3 illustrates the status of the multi-agent system based on our method at different time intervals. Figure 3a shows the initial states of the system, which are complete disorder. Figure 3b,c present the agents’ states after 150 and 300 iterations, respectively. Observably, with increasing iterations, the system transitions from disorder to order, and the speed of the agents gradually approach that of the virtual leader. The system’s final state is shown in Figure 3d, where all agents converge to a uniform state, exhibiting a lattice-like structure (verifying the first condition in Theorem 1).
The motion trajectories of the agents are shown in Figure 4. It can be seen that, at first, the whole system is disordered. With an increase in iterations, the degree of order of the system is improved through interactions between agents; in the end, the system reaches convergence, and all the agents move towards the upper-right direction.
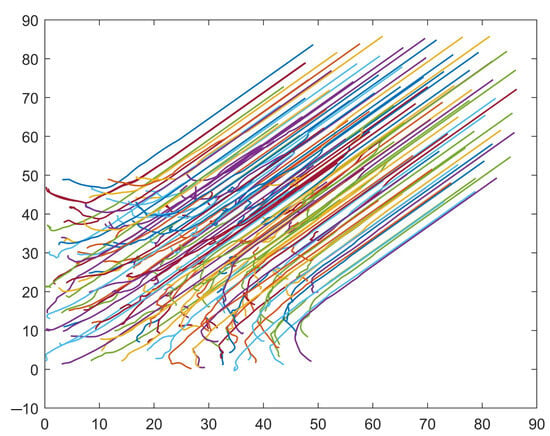
Figure 4.
The trajectories of the agents.
We define the speed error between agents and the virtual leader as
where and are the speed error in the direction of X-axis and Y-axis at time t, respectively. , and , are the speed components in the direction of X-axis and Y-axis at time t, respectively. Then, the global error between the agents and the virtual leader can be expressed as . The speed error between the agents and the virtual leader based on fractional-order flocking control is shown in Figure 5. Figure 5a is the speed error in the direction of the X-axis, and Figure 5b is the speed error in the direction of the Y-axis. Figure 5c shows the global error between the agents and the virtual leader. We can see that in the initial time, the speed error between the agents and the virtual leader is significant because the initial speed of the agents is random. Under the control of the fractional-order flocking algorithm, the agent’s speed gradually approaches the leader’s speed, and finally the speed error tends to 0. At this time, the speed of the agents and the virtual leader is consistent (verifying the second condition in Theorem 1).
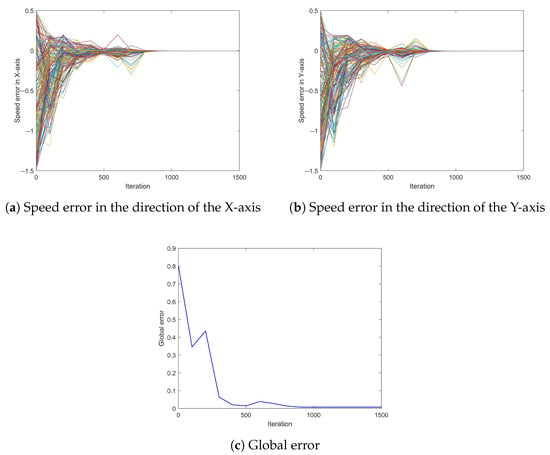
Figure 5.
The speed error between the agents and the virtual leader.
Above all, the multi-agent systems based on the fractional-order flocking control algorithm proposed in this paper can achieve flocking effectively. The speed of all agents gradually tends to that of the virtual leader over time. In addition, the distance between agents is always greater than 0, and thus Theorem 1 is verified.
4.2. Performance Test
In order to further illustrate the advantages of the proposed fractional-order flocking control method in this paper, comparisons were made among this method and two other commonly used flocking control algorithm, which are flocking control based on integer-order dynamics [9] and betweenness centrality with the influence degree (BCID) [25]. The selected system consists of 200 agents in a area. To avoid randomness and to obtain general results, 50 simulations are conducted, each with a maximum of 300 iterations. Other parameters were the same as those in Section 4.1. The states of the agents can be quantitatively expressed by the velocity direction order parameter , which is defined as
describes the degree of order of the agents’ movements. When , all agents in the system move in random directions and the system is completely disordered. When , all agents move in the same direction, and the system is ultimately ordered. It was found that the system will show apparent order when [26].
The results are shown in Figure 6. The initial state of the system is strongly disordered; therefore, the degree of order for all three methods is poor in the beginning. With the increase in iterations, the speed of the agents tend towards the virtual leader’s speed, and consequently the system gradually becomes ordered. Note that when there are fewer than 120 iterations, the convergence rate of our proposed fractional-order flocking control algorithm is no better than the other two algorithms. This is because the agents with fractional-order dynamics utilize the historical information to update their states; however, the order of the system at each moment in this period (less than 120 iterations) is relatively poor, and the use of such poor information will reduce the order of the system. However, as the order of the system gradually increases, "high-quality" historical information (the degree of order is relatively high) will accelerate the convergence rate of the system. Therefore, when the number of iterations reaches 120, the convergence rate of the multi-agent system based on the fractional-order flocking control algorithm is significantly higher than that of the integer-order method and BCID method, and the consistency of the system is eventually realized much faster.
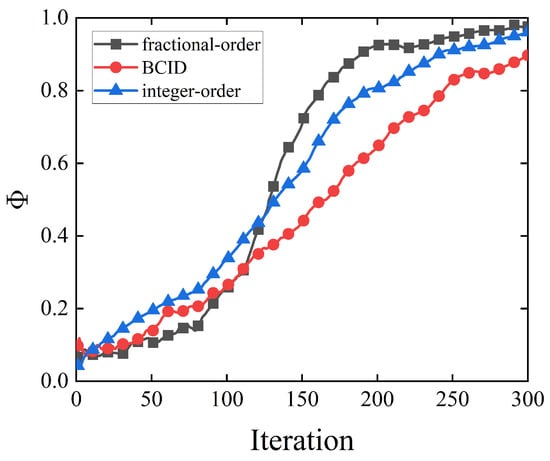
Figure 6.
The convergence rate comparison of the algorithms.
5. Conclusions
A discrete-time flocking control algorithm for multi-agent systems was proposed by introducing a G-L fractional derivative to the speed updating process of agents, which enables agents to utilize historical information. The convergence of this algorithm is proven. The simulation results demonstrate that multi-agent systems can achieve flocking based on this algorithm. Furthermore, our proposed algorithm can effectively improve the convergence rate of multi-agent systems. In future work, we will focus on applying this algorithm to multi-vehicle and multi-robot systems.
Author Contributions
Conceptualization, H.C. and M.H.; methodology, H.C. and W.H.; software, H.C.; validation, S.L. and C.W.; formal analysis, W.H.; investigation, M.H.; resources, H.C.; data curation, H.C.; writing—original draft preparation, H.C.; writing—review and editing, M.H. and W.H.; visualization, S.L. and C.W.; supervision, M.H.; project administration, M.H.; funding acquisition, M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, No. 62273356; National Talent Project of China, No. 2022-JCJQ-ZQ-001; Provincial Primary Research and Development Plan of Jiangsu, China, No. BE2021729; High-level Talents Innovation Project, China, No. KYZYJQJY2101.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Parivallal, A.; Sakthivel, R.; Amsaveni, R.; Alzahrani, F.; Alshomrani, A.S. Observer-based memory consensus for nonlinear multi-agent systems with output quantization and Markov switching topologies. Phys. A 2020, 551, 123949. [Google Scholar] [CrossRef]
- Amirkhani, A.; Barshooi, A.H. Consensus in multi-agent systems: A review. Artif. Intell. Rev. 2022, 55, 3897–3935. [Google Scholar] [CrossRef]
- Beaver, L.E.; Malikopoulos, A.A. An overview on optimal flocking. Annu. Rev. Control. 2021, 51, 88–99. [Google Scholar] [CrossRef]
- Berlinger, F.; Gauci, M.; Nagpal, R. Implicit coordination for 3D underwater collective behaviors in a fish-inspired robot swarm. Sci. Robot. 2021, 6, eabd8668. [Google Scholar] [CrossRef] [PubMed]
- Ling, H.J.; Mclvor, G.E.; Westley, J.; van der Vaart, K.; Vaughan, R.T.; Thornton, A.; Ouellette, N.T. Behavioural plasticity and the transition to order in jackdaw flocks. Nat. Commun. 2019, 10, 5174. [Google Scholar] [CrossRef] [PubMed]
- Mayor, R.; Etienne-Manneville, S. The front and rear of collective cell migration. Nat. Rev. Mol. Cell Biol. 2016, 17, 97–109. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirok, A.; Benjacob, E.; Cohen, I.; Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 1995, 75, 1226–1229. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control. 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Jia, Y.N.; Vicsek, T. Modelling hierarchical flocking. New J. Phys. 2019, 21, 093048. [Google Scholar] [CrossRef]
- Zou, Y.; An, Q.; Miao, S.X.; Chen, S.M.; Wang, X.M.; Su, H.S. Flocking of uncertain nonlinear multi-agent systems via distributed adaptive event-triggered control. Neurocomputing 2021, 465, 503–513. [Google Scholar] [CrossRef]
- Yan, T.R.; Xu, X.; Li, Z.Y.; Li, E.R. Flocking of multi-agent systems with unknown nonlinear dynamics and heterogeneous virtual leader. Int. J. Control Autom. Syst. 2021, 19, 2931–2939. [Google Scholar] [CrossRef]
- Carrillo, J.A.; Kalise, D.; Rossi, F.; Trelat, E. Controlling swarms towards flocks and mills. SIAM J. Control Optim. 2022, 60, 1863–1891. [Google Scholar] [CrossRef]
- Wang, X.M.; Sun, J.S.; Wu, Z.X.; Li, Z.T. Robust integral of sign of error-based distributed flocking control of double-integrator multi-agent systems with a varying virtual leader. Int. J. Robust Nonlinear Control. 2022, 32, 286–303. [Google Scholar] [CrossRef]
- Chen, W.; Hu, S.; Cai, W. A causal fractional derivative model for acoustic wave propagation in lossy media. Arch. Appl. Mech. 2016, 86, 529–539. [Google Scholar] [CrossRef]
- Pandey, V.; Holm, S. Connecting the grain-shearing mechanism of wave propagation in marine sediments to fractional order wave equations. J. Acoust. Soc. Am. 2016, 140, 4225–4236. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.B.; Hu, W.; Rahmani, A. Fractional-order artificial bee colony algorithm with application in robot path planning. Eur. J. Oper. Res. 2023, 306, 47–64. [Google Scholar] [CrossRef]
- Chen, H.T.; He, M.; Liu, J.T.; Xu, P.; Cao, X.H.; Han, W.; Yuan, G.D. A novel fractional-order flocking algorithm for large-scale UAV swarms. Complex Intell. Syst. 2023, 9, 6831–6844. [Google Scholar] [CrossRef]
- Kozlovsky, Y.; Cohen, I.; Golding, I.; Ben-Jacob, E. Lubricating bacteria model for branching growth of bacterial colonies. Phys. Rev. E 1999, 59, 7025–7035. [Google Scholar] [CrossRef]
- Teodoro, G.S.; Machado, J.A.T.; de Oliveira, E.C. A review of definitions of fractional derivatives and other operators. J. Comput. Phys. 2019, 388, 195–208. [Google Scholar] [CrossRef]
- Wu, J.H.; Yu, Y.Z.; Ma, J.; Wu, J.S.; Han, G.J.; Shi, J.L.; Gao, L.J. Autonomous cooperative flocking for heterogeneous unmanned aerial vehicle group. IEEE Trans. Veh. Technol. 2021, 70, 12477–12490. [Google Scholar] [CrossRef]
- Fu, X.W.; Pan, J.; Wang, H.X.; Gao, X.G. A formation maintenance and reconstruction method of UAV swarm based on distributed control. Aerosp. Sci. Technol. 2020, 104, 105981. [Google Scholar] [CrossRef]
- Zohdi, T.I. Multiple UAVs for mapping: A review of basic modeling, simulation, and applications. Annu. Rev. Environ. Resour. 2018, 43, 523–543. [Google Scholar] [CrossRef]
- Su, H.S.; Wang, X.F.; Lin, Z.L. Flocking of multi-agents with a virtual leader. IEEE Trans. Autom. Control. 2009, 54, 293–307. [Google Scholar] [CrossRef]
- Liu, J.T.; Wu, Z.H.; Xin, Q.; Yu, M.G.; Liu, L.L. Topology uniformity pinning control for multi-agent flocking. Complex Intell. Syst. 2023. Available online: https://link.springer.com/article/10.1007/s40747-023-01253-7 (accessed on 19 October 2023). [CrossRef]
- Cavagna, A.; Giardina, I. Bird flocks as condensed matter. Annu. Rev. Condens. Matter Phys. 2014, 5, 183–207. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).