Adaptive Fuzzy Fault-Tolerant Control of Uncertain Fractional-Order Nonlinear Systems with Sensor and Actuator Faults
Abstract
:1. Introduction
- (1)
- This paper addresses the FTC issue of FO nonlinear systems with simultaneous actuator faults and sensor faults. It should be mentioned that unlike this paper, the authors in [28,29,30,31,32] considered the adaptive fault-tolerant control issue for fractional-order nonlinear systems with actuator faults. However, in the actual control system, the sensor is more prone to failure than the actuator, and the performance of the system is also heavily dependent on the output signal of the sensor, so even if the sensor undergoes a small fault, the feedback control and stability of the closed-loop system will be greatly affected. It is obvious that the previous actuator faults compensation schemes are invalid for sensor faults compensation control problem, not to mention the case with both actuator and sensor faults. This makes the research of this work more difficult and challenging.
- (2)
- A nonlinear filtering-based DSC strategy is established by introducing auxiliary functions, which not only effectively solves the issue of computational burden existing in traditional FO nonlinear strict feedback systems, but also improves the control performance in contrast to the traditional linear filters-based DSC results [36,37]. Different from nonlinear filtering results [38,39], this paper compensates the effects of lumped uncertainties caused by actuator faults and sensor faults by designing a quadratic Lyapunov function which includes the lower bound of actuator and sensor faults coefficients.
- (3)
- The proposed fault compensation mechanism can erase the limitation condition that the unknown functions dependent on state variable must satisfy the monotonically increasing property, by use of the characteristics of fuzzy basis functions.
2. Preliminaries and Problem Formulation
2.1. Preliminaries
2.2. Problem Formulation
3. Nonlinear Filter-Based Adaptive Controller Design and Stability Analysis
3.1. Novel Nonlinear Filter Design
3.2. Adaptive Controller Design
3.3. Stability Analysis
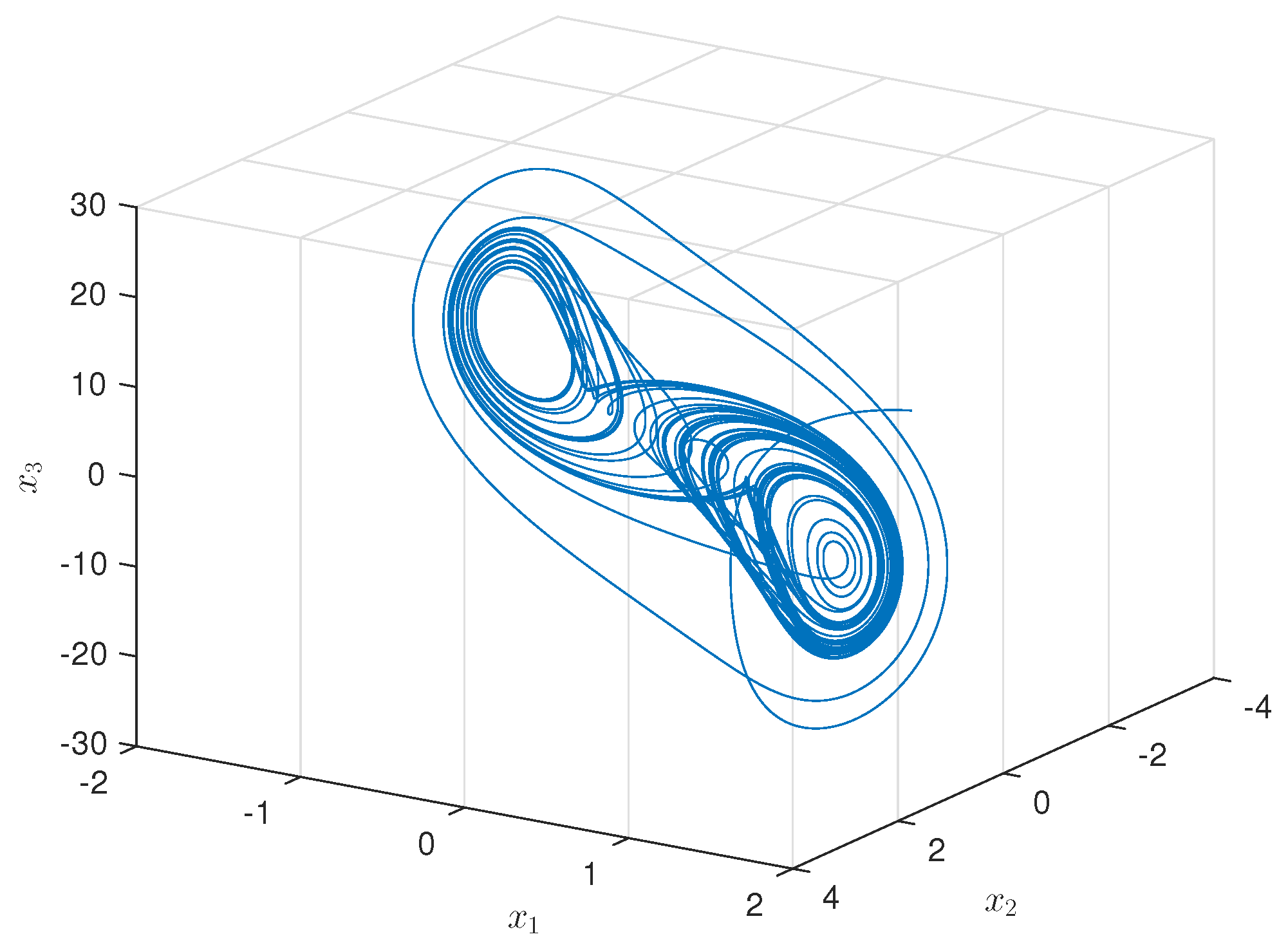
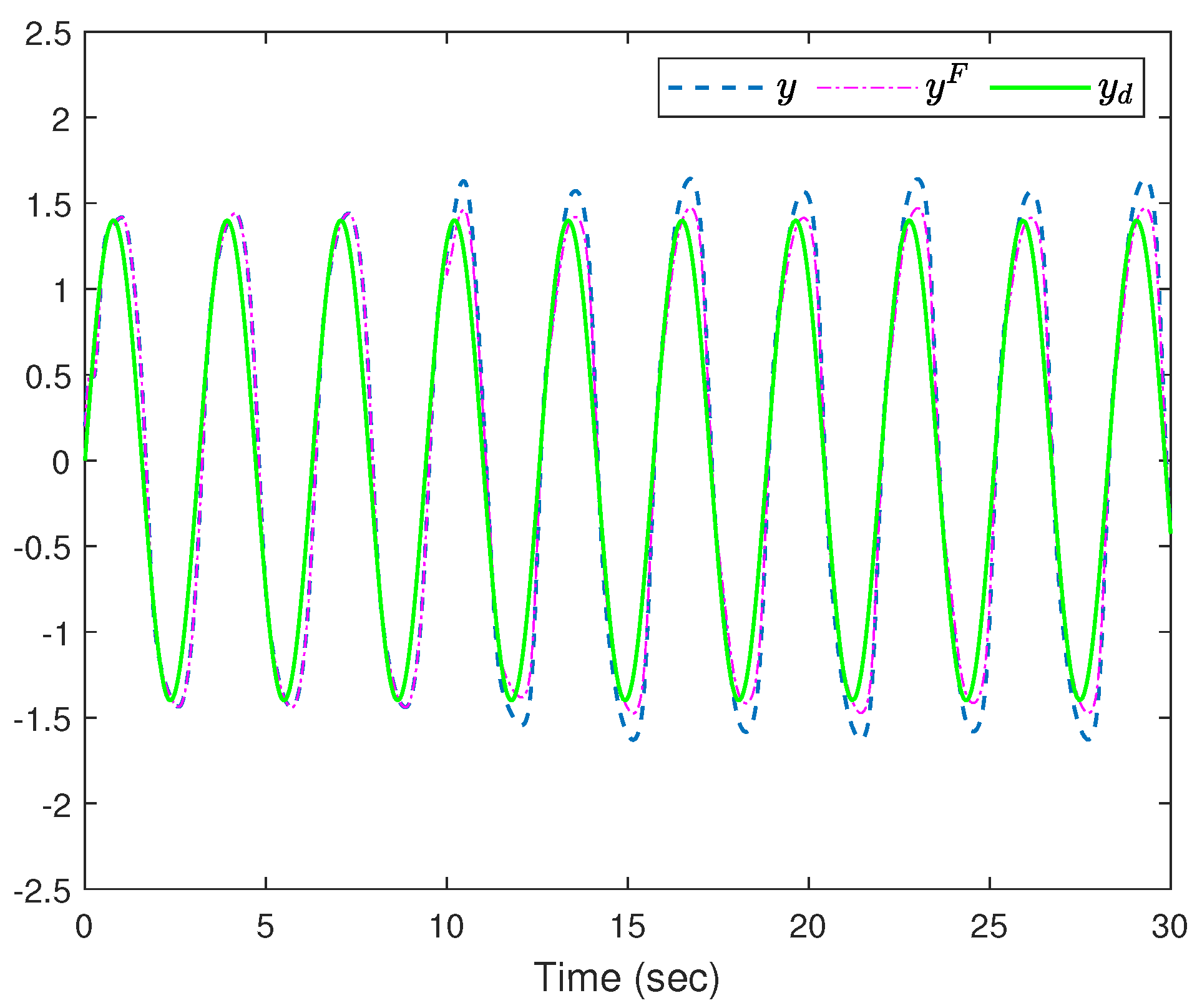
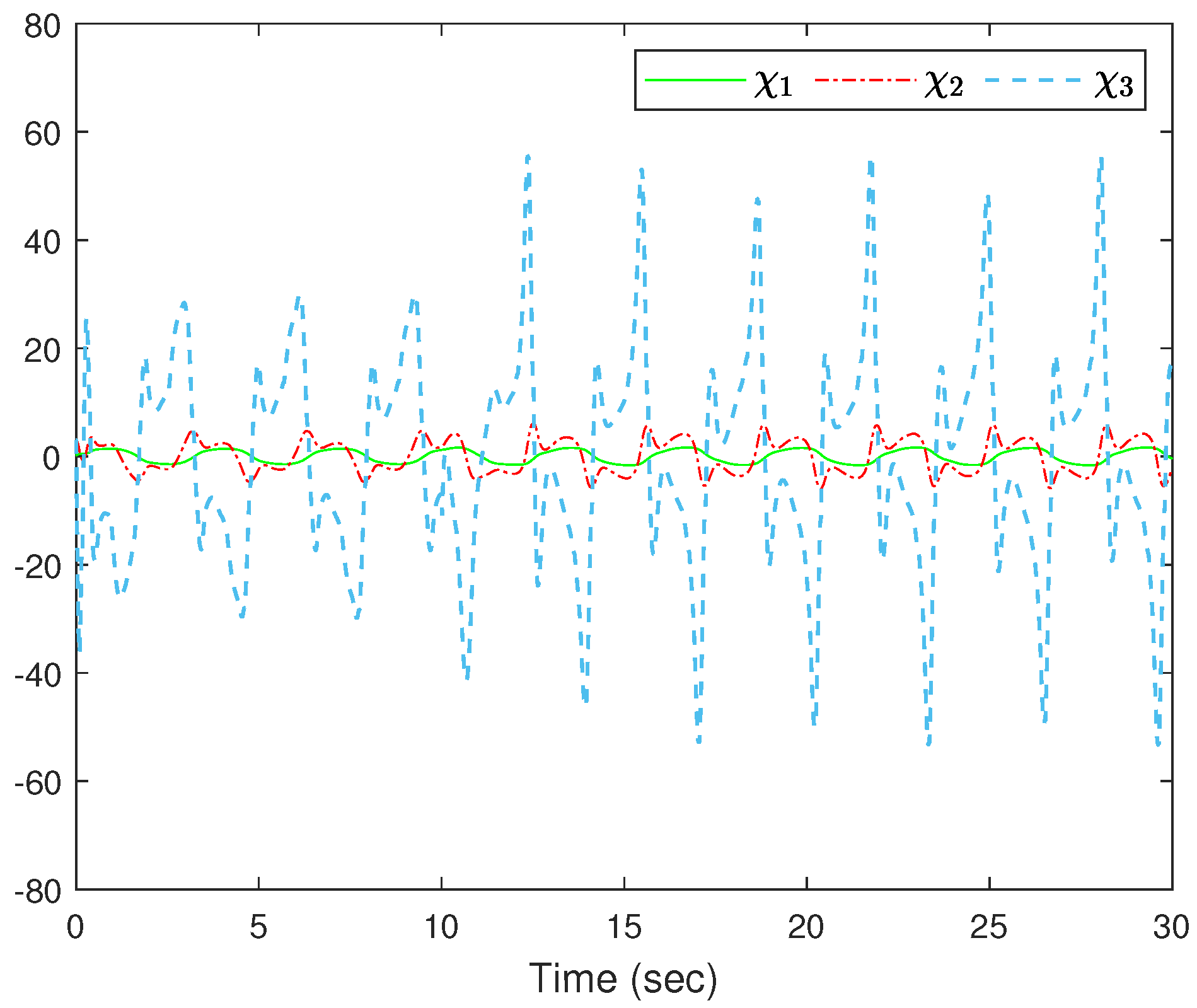
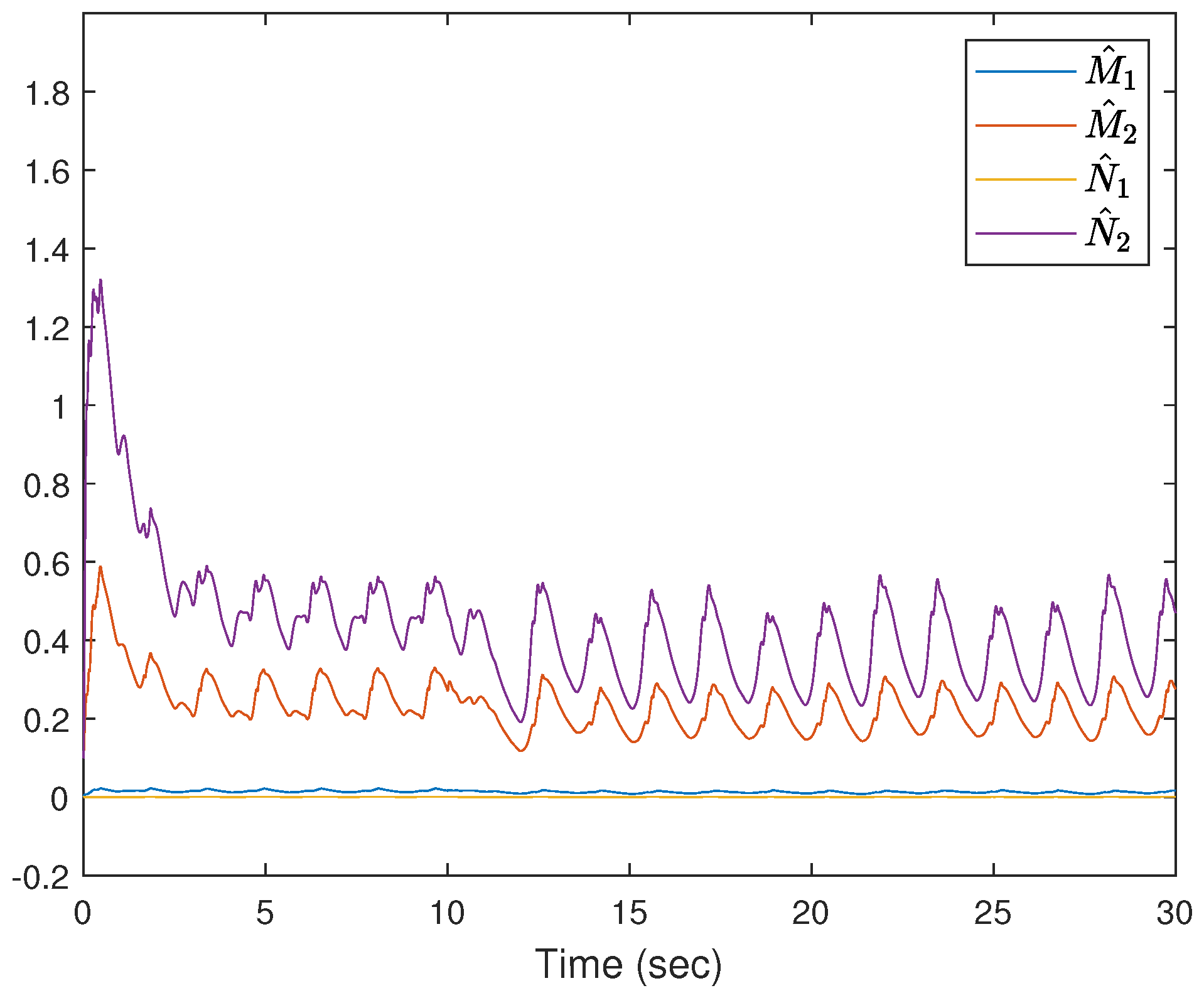
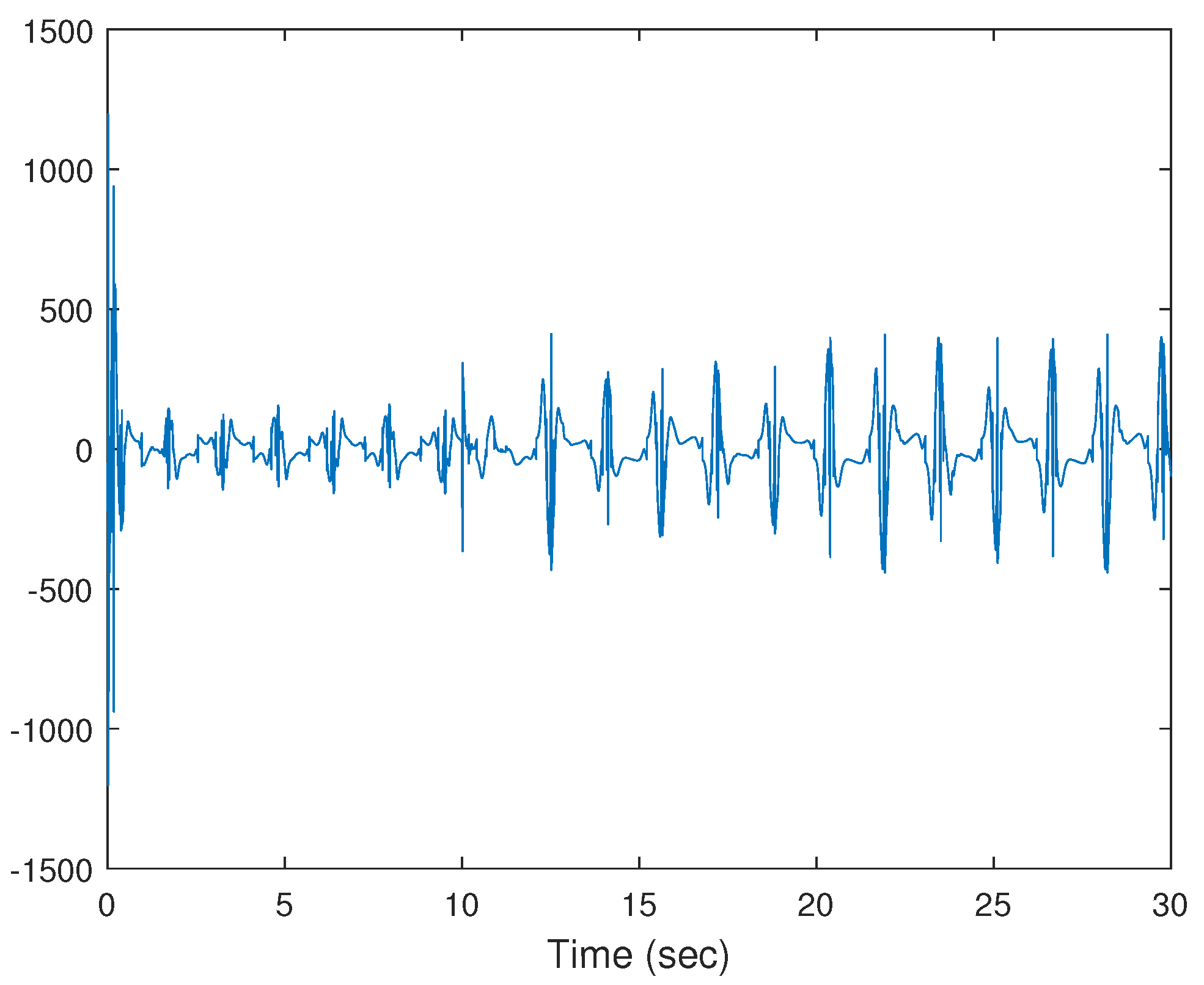
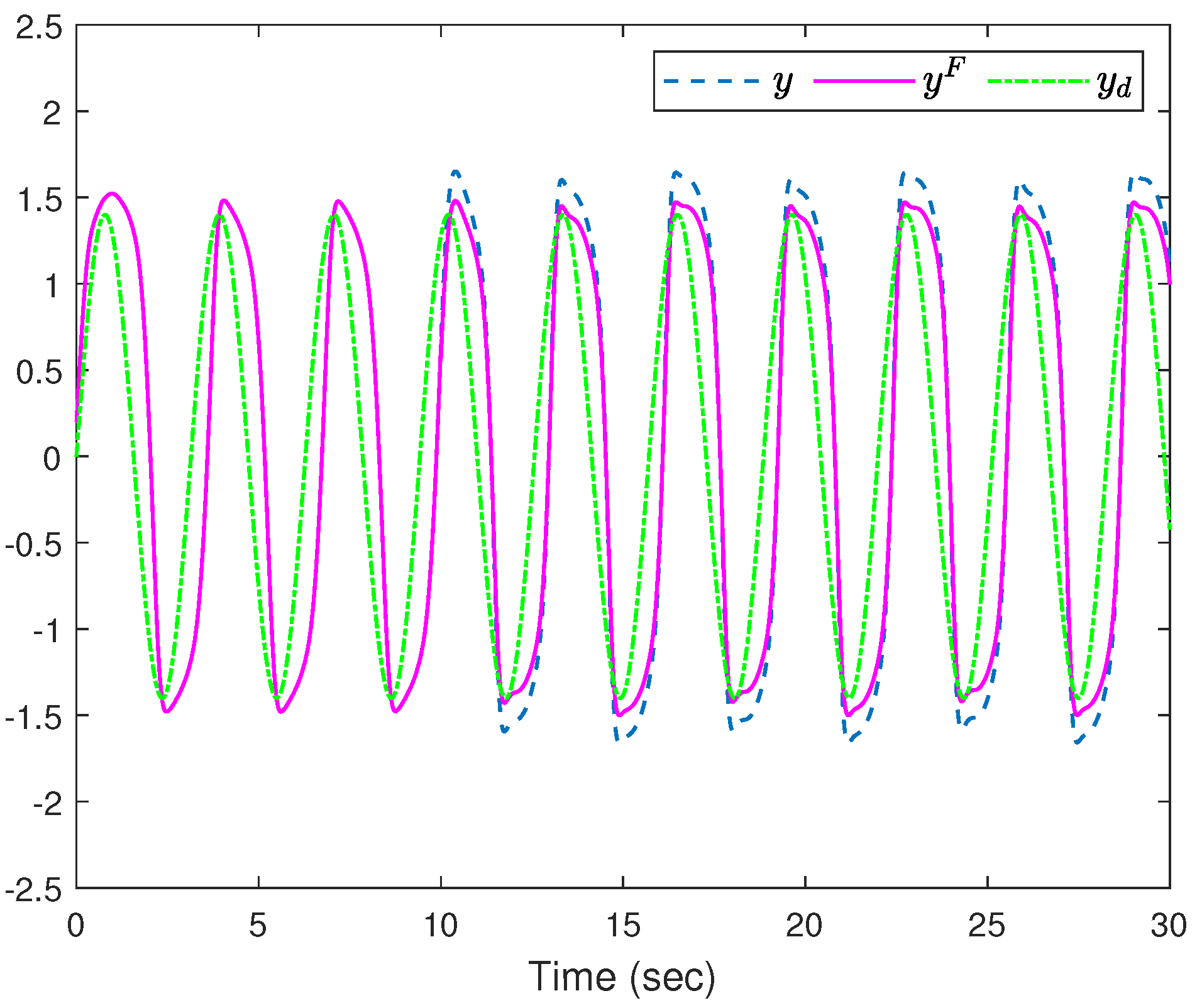
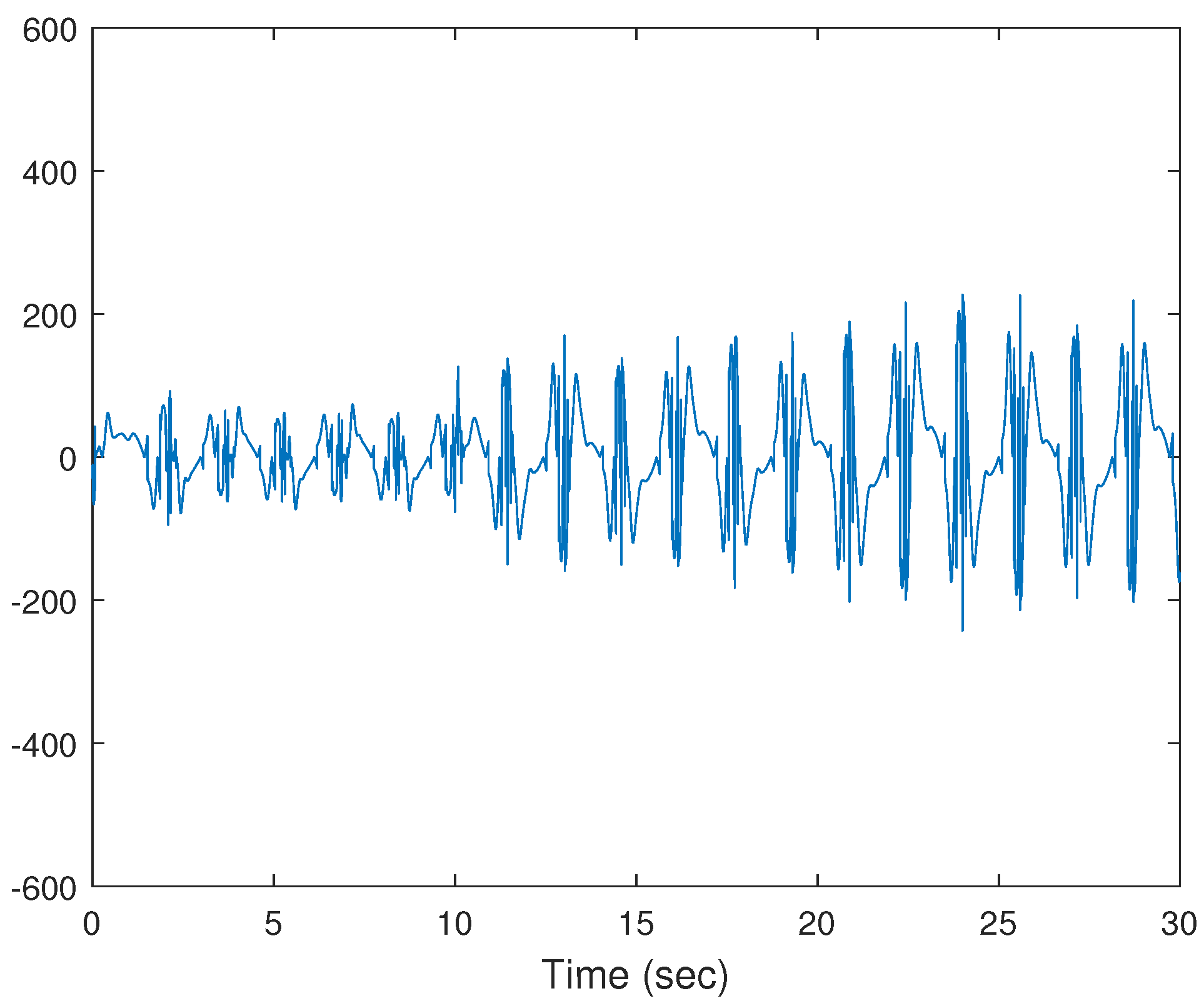
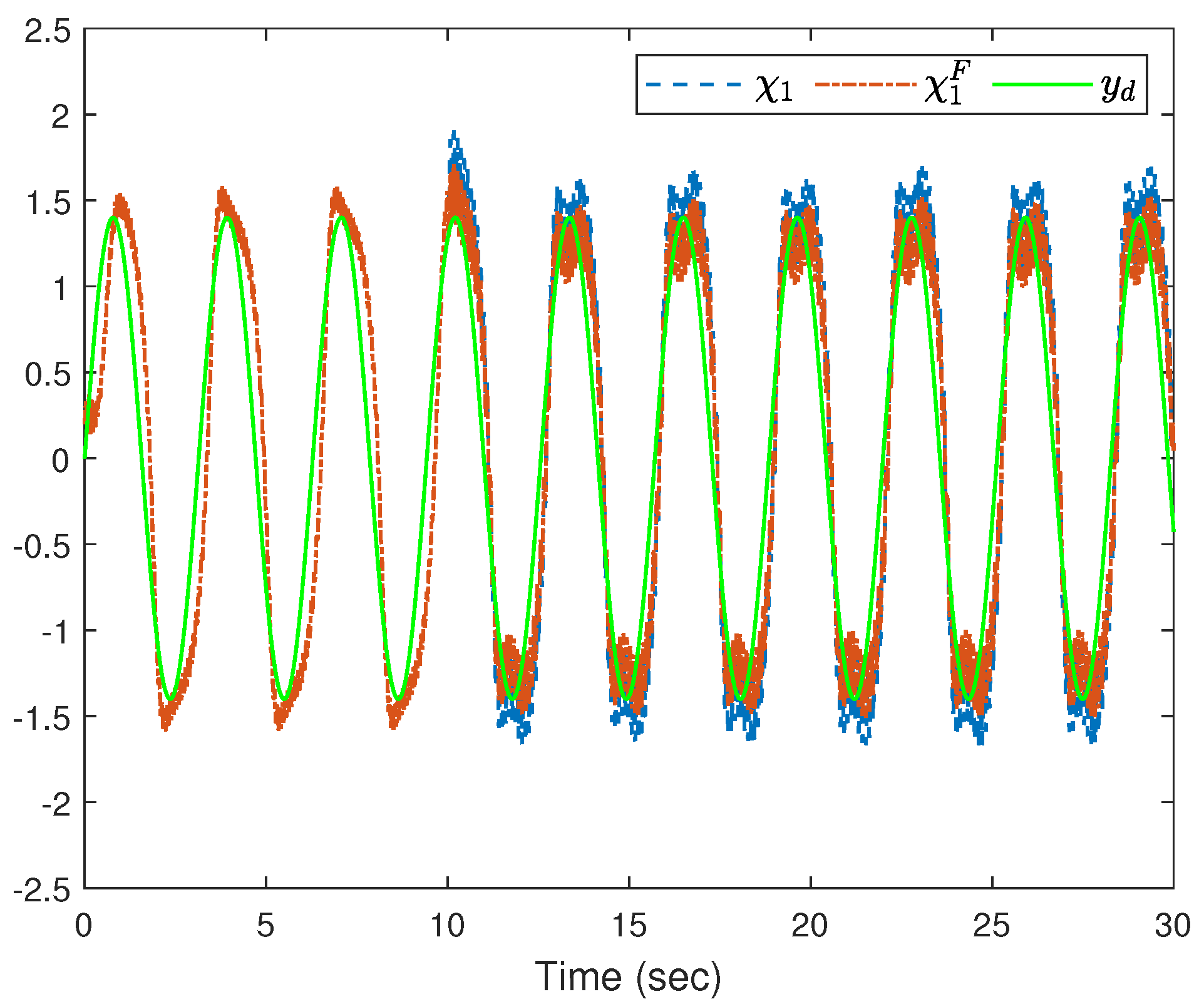
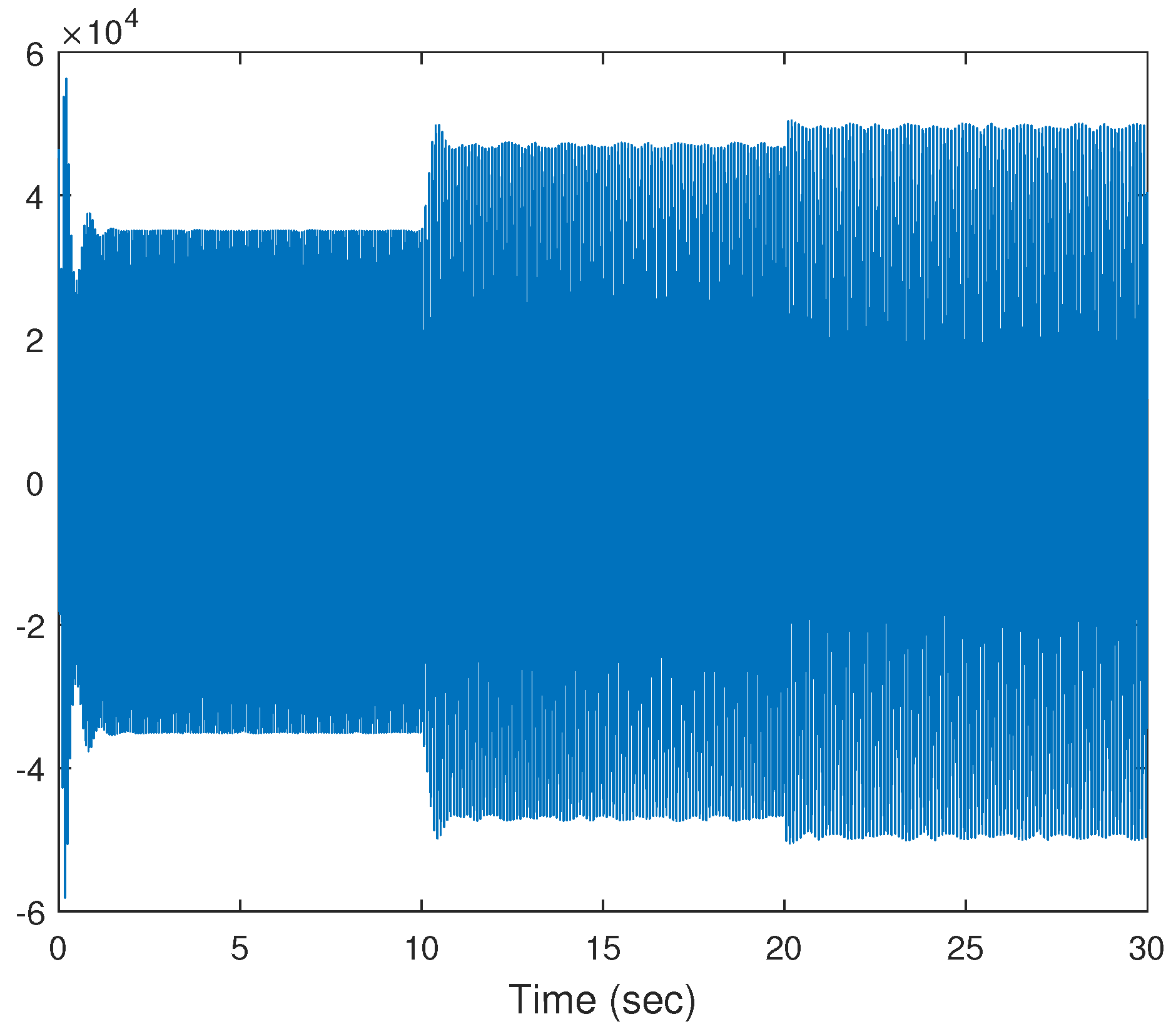
4. Simulation Study
- (i)
- (ii)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, J.G.; Chen, G. Robust stability and stabilization of fractional-order interval systems: An LMI approach. IEEE Trans. Autom. Control. 2009, 54, 1294–1299. [Google Scholar]
- Lan, Y.H.; Zhou, Y. LMI-based robust control of fractional-order uncertain linear systems. Comput. Math. Appl. 2011, 62, 1460–1471. [Google Scholar] [CrossRef]
- Wei, Y.H.; Peter, W.T.; Yao, Z.; Wang, Y. The output feedback control synthesis for a class of singular fractional order systems. ISA Trans. 2017, 69, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Djennoune, S.; Bettayeb, M. Optimal synergetic control for fractional-order systems. Automatica 2013, 49, 2243–2249. [Google Scholar] [CrossRef]
- Wang, B.; Ding, J.L.; Wu, F.J.; Zhu, D.L. Robust finite-time control of fractional-order nonlinear systems via frequency distributed model. Nonlinear Dyn. 2016, 85, 2133–2142. [Google Scholar] [CrossRef]
- Lan, Y.H.; Zhou, Y. Non-fragile observer-based robust control for a class of fractional-order nonlinear systems. Syst. Control. Lett. 2013, 62, 1143–1150. [Google Scholar] [CrossRef]
- Gong, P. Distributed tracking of heterogeneous nonlinear fractional-order multi-agent systems with an unknown leader. J. Frankl. Inst. 2017, 354, 2226–2244. [Google Scholar] [CrossRef]
- Chen, K.; Tang, R.N.; Li, C.; Wei, T.N. Robust adaptive fractional-order observer for a class of fractional-order nonlinear systems with unknown parameters. Nonlinear Dyn. 2018, 94, 415–427. [Google Scholar] [CrossRef]
- Ding, D.S.; Qi, D.L.; Wang, Q. Non-linear Mittag–Leffler stabilisation of commensurate fractional-order non-linear systems. IET Control. Theory Appl. 2015, 9, 681–690. [Google Scholar] [CrossRef]
- Hua, C.C.; Zhang, T.; Li, Y.F.; Guan, X.P. Robust output feedback control for fractional order nonlinear systems with time-varying delays. IEEE/CAA J. Autom. Sin. 2016, 3, 477–482. [Google Scholar]
- Wei, Y.H.; Chen, Y.Q.; Liang, S.; Wang, Y. A novel algorithm on adaptive backstepping control of fractional order systems. Neurocomputing 2015, 165, 395–402. [Google Scholar] [CrossRef]
- Wei, Y.H.; Tse, P.W.; Yao, Z.; Wang, Y. Adaptive backstepping output feedback control for a class of nonlinear fractional order systems. Nonlinear Dyn. 2016, 86, 1047–1056. [Google Scholar] [CrossRef]
- Liu, H.; Pan, Y.; Li, S.; Chen, Y. Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2209–2217. [Google Scholar] [CrossRef]
- Song, S.; Zhang, B.; Xia, J.; Zhang, Z. Adaptive backstepping hybrid fuzzy sliding mode control for uncertain fractional-order nonlinear systems based on finite-time scheme. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 1559–1569. [Google Scholar] [CrossRef]
- Li, Y.X.; Wei, M.; Tong, S.C. Event-triggered adaptive neural control for fractional-order nonlinear systems based on finite-time scheme. IEEE Trans. Cybern. 2022, 52, 9481–9489. [Google Scholar] [CrossRef] [PubMed]
- Sui, S.; Chen, C.L.P.; Tong, S.C. Neural-network-based adaptive DSC design for switched fractional-order nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4703–4712. [Google Scholar] [CrossRef] [PubMed]
- Gong, P.; Lan, W.Y. Adaptive robust tracking control for multiple unknown fractional-order nonlinear systems. IEEE Trans. Cybern. 2018, 49, 1365–1376. [Google Scholar] [CrossRef]
- Gong, P.; Lan, W.Y. Adaptive robust tracking control for uncertain nonlinear fractional-order multi-agent systems with directed topologies. Automatica 2018, 92, 92–99. [Google Scholar] [CrossRef]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Frasca, M. Control of imperfect dynamical systems. Nonlinear Dyn. 2019, 98, 2989–2999. [Google Scholar] [CrossRef]
- Gong, P.; Lan, W.Y.; Han, Q.L. Robust adaptive fault-tolerant consensus control for uncertain nonlinear fractional-order multi-agent systems with directed topologies. Automatica 2020, 117, 109011. [Google Scholar] [CrossRef]
- Chen, S.H.; Tao, G.; Joshi, S.M. On matching conditions for adaptive state tracking control of systems with actuator failures. IEEE Trans. Autom. Control. 2002, 47, 473–478. [Google Scholar] [CrossRef]
- Yang, G.-H.; Ye, D. Reliable H∞ control of linear systems with adaptive mechanism. IEEE Trans. Autom. Control. 2010, 55, 242–247. [Google Scholar] [CrossRef]
- Wang, W.; Wen, C. Adaptive actuator failure compensation control of uncertain nonlinear systems with guaranteed transient performance. Automatica 2010, 46, 2082–2091. [Google Scholar] [CrossRef]
- Li, X.J.; Yang, G.-H. Adaptive fault-tolerant synchronization control of a class of complex dynamical networks with general input distribution matrices and actuator faults. IEEE Trans. Neural Netw. Learn. Syst. 2015, 28, 559–569. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.M.; Ma, Z.Y.; Tong, S.C. Adaptive fuzzy output-constrained fault-tolerant control of nonlinear stochastic large-scale systems with actuator faults. IEEE Trans. Cybern. 2017, 47, 2362–2376. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.L.; Yang, G.-H. Fault-estimation-based output-feedback adaptive FTC for uncertain nonlinear systems with actuator faults. IEEE Trans. Ind. Electron. 2020, 67, 3065–3075. [Google Scholar] [CrossRef]
- Wu, L.-B.; Park, J.H. Adaptive fault-tolerant control of uncertain switched nonaffine nonlinear systems with actuator faults and time delays. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3470–3480. [Google Scholar] [CrossRef]
- Liu, H.; Wang, H.; Cao, J.; Alsaedi, A.; Hayat, T. Composite learning adaptive sliding mode control of fractional-order nonlinear systems with actuator faults. J. Frankl. Inst. 2019, 356, 9580–9599. [Google Scholar] [CrossRef]
- Xue, G.; Lin, F.; Li, S.; Liu, H. Adaptive fuzzy finite-time backstepping control of fractional-order nonlinear systems with actuator faults via command-filtering and sliding mode technique. Inf. Sci. 2022, 600, 189–208. [Google Scholar] [CrossRef]
- Liu, H.; Pan, Y.; Cao, J.; Wang, H.; Zhou, Y. Adaptive neural network backstepping control of fractional-order nonlinear systems with actuator saults. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5166–5177. [Google Scholar] [CrossRef]
- Lin, F.; Xue, G.; Li, S.; Pan, Y.; Cao, J. Finite-time sliding mode fault-tolerant neural network control for nonstrict-feedback nonlinear systems. Nonlinear Dyn. 2023, 111, 17205–17227. [Google Scholar] [CrossRef]
- Li, Y.X.; Wang, Q.Y.; Tong, S.C. Fuzzy adaptive fault-tolerant control of fractional-order nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1372–1379. [Google Scholar] [CrossRef]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Autom. Control. 2000, 45, 1893–1899. [Google Scholar] [CrossRef]
- Pan, Y.; Yu, H. Composite learning from adaptive dynamic surface control. IEEE Trans. Autom. Control. 2016, 61, 2603–2609. [Google Scholar] [CrossRef]
- Li, K.W.; Li, Y.M. Adaptive neural network finite-time dynamic surface control for nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5688–5697. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Pan, Y.; Cao, J. Composite learning adaptive dynamic surface control of fractional-order nonlinear systems. IEEE Trans. Cybern. 2019, 50, 2557–2567. [Google Scholar] [CrossRef]
- Song, S.; Park, J.H.; Zhang, B.; Song, X.; Zhang, Z. Adaptive command filtered neuro-fuzzy control design for fractional-order nonlinear systems with unknown control directions and input quantization. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 7238–7249. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Ma, H.J. Adaptive fuzzy backstepping dynamic surface control of strict-feedback fractional-order uncertain nonlinear systems. IEEE Trans. Fuzzy Syst. 2019, 28, 122–133. [Google Scholar] [CrossRef]
- Song, S.; Park, J.H.; Zhang, B.; Song, X.; Zhang, Z. Neuro-fuzzy-based adaptive dynamic surface control for fractional-order nonlinear strict-feedback systems with input constraint. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 3575–3586. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Tong, S.C.; Min, X.; Li, Y.X. Observer-based adaptive fuzzy tracking control for strict-feedback nonlinear systems with unknown control gain functions. IEEE Trans. Cybern. 2020, 50, 3903–3913. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.H.; Wang, T.; Gao, H.J. Adaptive neural fault-tolerant control for a class of strict-feedback nonlinear systems with actuator and sensor faults. Neurocomputing 2020, 380, 87–94. [Google Scholar] [CrossRef]
- Ma, Z.; Sun, K. Nonlinear filter-based adaptive output-feedback control for uncertain fractional-order nonlinear systems with unknown external disturbance. Fractal Fract. 2023, 7, 694. [Google Scholar] [CrossRef]
- Li, B.; Liu, Y.; Zhao, X. Robust H∞ control for fractional order systems with order α (0 < α < 1). Fractal Fract. 2022, 6, 86. [Google Scholar]
- Wang, X.; Xu, B.; Shi, P.; Li, S. Efficient learning control of uncertain fractional-order chaotic systems with disturbance. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 445–450. [Google Scholar] [CrossRef]
- Polycarpou, M.M. Stable adaptive neural control scheme for nonlinear systems. IEEE Trans. Autom. Control. 1996, 41, 447–451. [Google Scholar] [CrossRef]
- Li, Y.-X. Command filter adaptive asymptotic tracking of uncertain nonlinear systems with time-varying parameters and disturbances. IEEE Trans. Autom. Control. 2022, 67, 2973–2980. [Google Scholar] [CrossRef]
- Petráš, I. A note on the fractional-order Chua’s system. Chaos Solitons Fractals 2008, 38, 140–147. [Google Scholar] [CrossRef]


| & | & | & | |
|---|---|---|---|
| Fault-free | 1 | 1 | 0 |
| Partial loss of effectiveness fault | >0 | <1 | 0 |
| Bias | 1 | 1 | |
| Total loss of effectiveness (TLOE) fault | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, K.; Ma, Z.; Dong, G.; Gong, P. Adaptive Fuzzy Fault-Tolerant Control of Uncertain Fractional-Order Nonlinear Systems with Sensor and Actuator Faults. Fractal Fract. 2023, 7, 862. https://doi.org/10.3390/fractalfract7120862
Sun K, Ma Z, Dong G, Gong P. Adaptive Fuzzy Fault-Tolerant Control of Uncertain Fractional-Order Nonlinear Systems with Sensor and Actuator Faults. Fractal and Fractional. 2023; 7(12):862. https://doi.org/10.3390/fractalfract7120862
Chicago/Turabian StyleSun, Ke, Zhiyao Ma, Guowei Dong, and Ping Gong. 2023. "Adaptive Fuzzy Fault-Tolerant Control of Uncertain Fractional-Order Nonlinear Systems with Sensor and Actuator Faults" Fractal and Fractional 7, no. 12: 862. https://doi.org/10.3390/fractalfract7120862
APA StyleSun, K., Ma, Z., Dong, G., & Gong, P. (2023). Adaptive Fuzzy Fault-Tolerant Control of Uncertain Fractional-Order Nonlinear Systems with Sensor and Actuator Faults. Fractal and Fractional, 7(12), 862. https://doi.org/10.3390/fractalfract7120862






