An Improved Rock Resistivity Model Based on Multi-Fractal Characterization Method for Sandstone Micro-Pore Structure Using Capillary Pressure
Abstract
1. Introduction
2. Mathematical Derivations of a Resistivity Model Based on Multi-Fractal Characterization Method for Sandstone Micro-Pore Structure Using Capillary Pressure
2.1. Multi-Fractal Characterization Method for Sandstone Micro-Pore Structure Using Capillary Pressure
2.2. An Improved Rock Resistivity Model Considering Pore Structure
3. Model Validation
3.1. Multi Fractal Characterization of Pore Structure Using Capillary Pressure
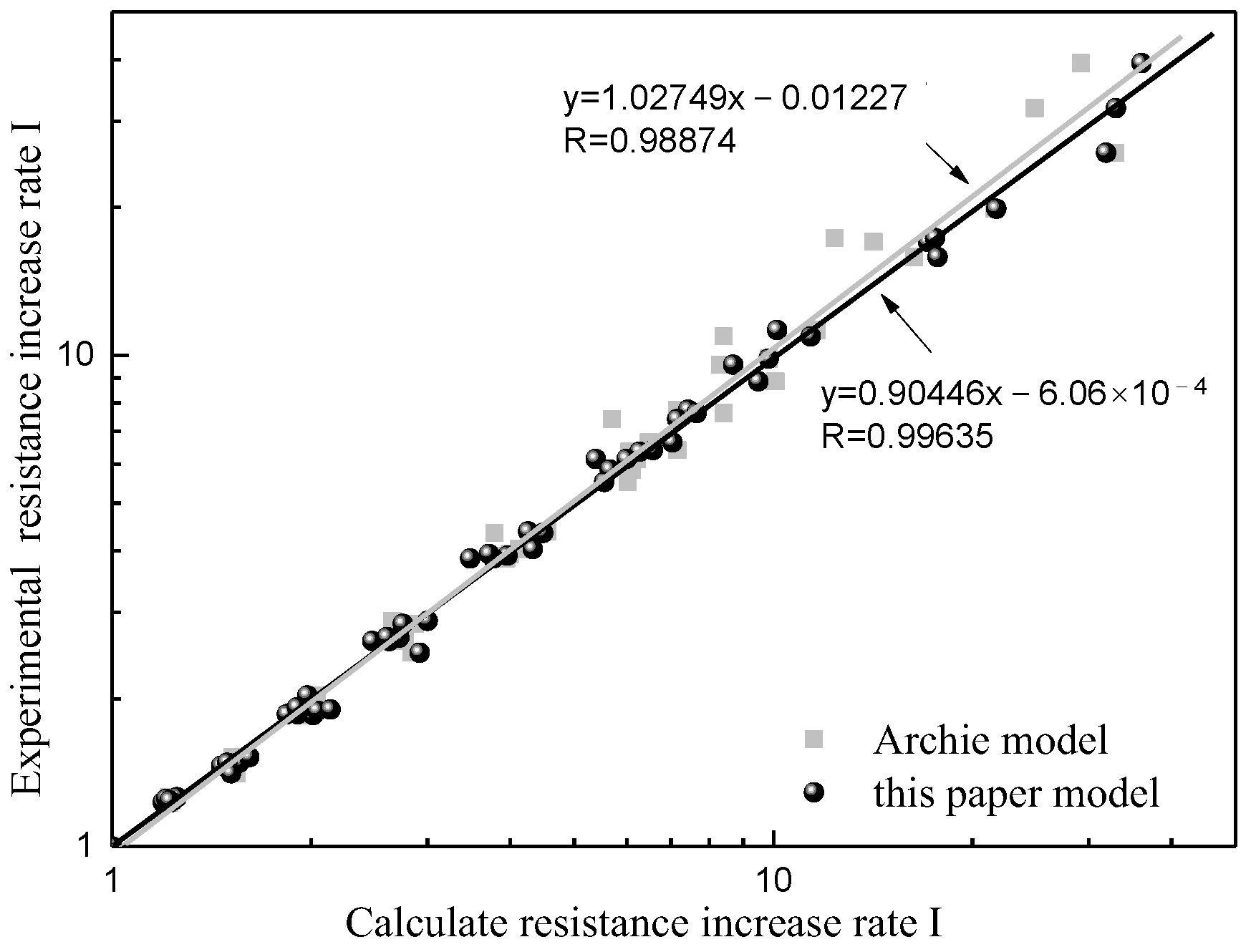
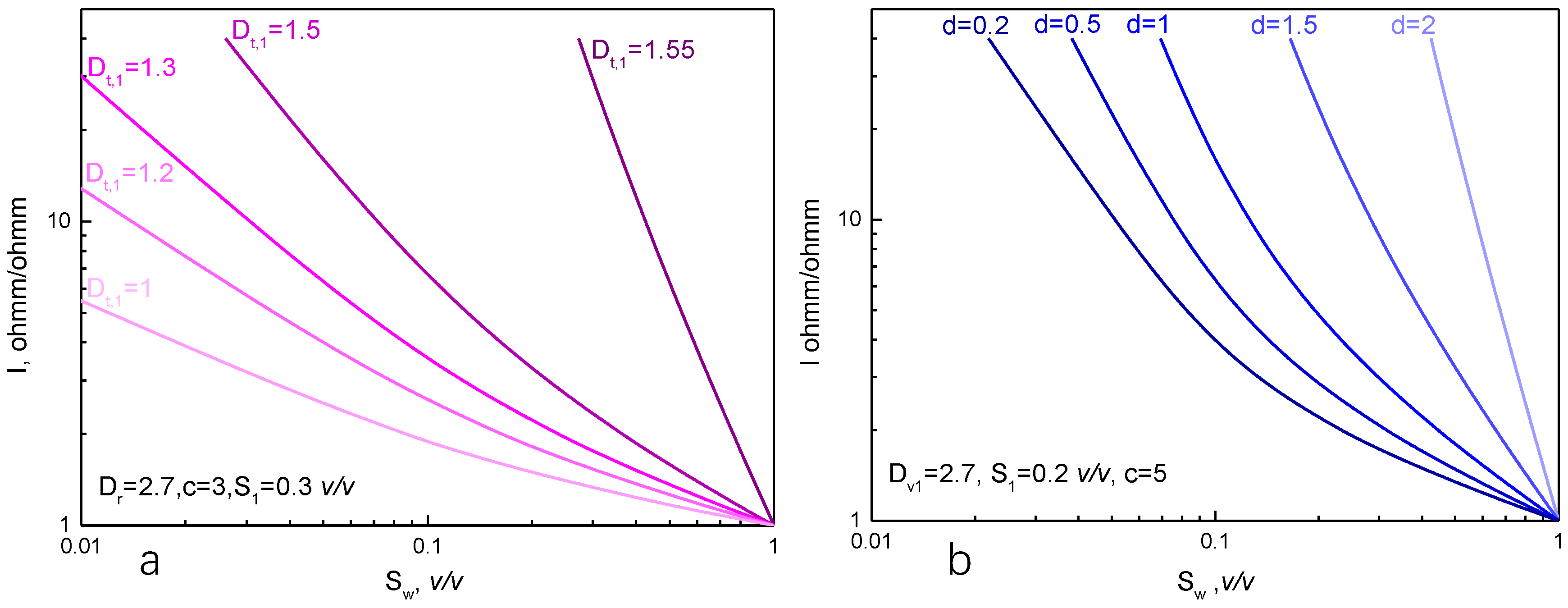
3.2. An Improved Rock Resistivity Model Considering Pore Structure
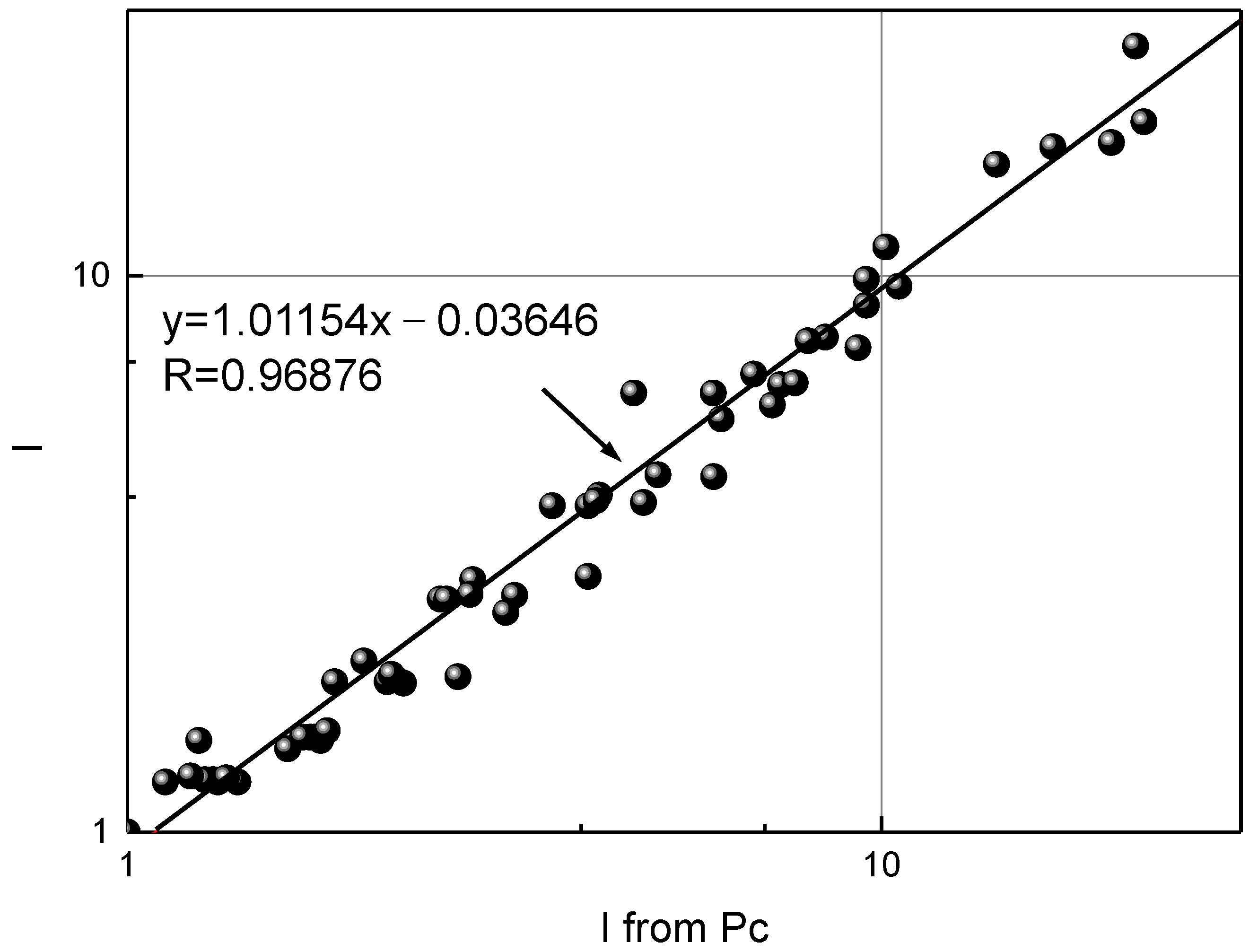
3.3. The Relationship between Capillary Pressure Curve and Resistivity Index Curve Based on Fractal Theory
4. Discussion and Future Work
4.1. Multi-Fractal Based Modeling of Capillary Pressure Curves
- (1)
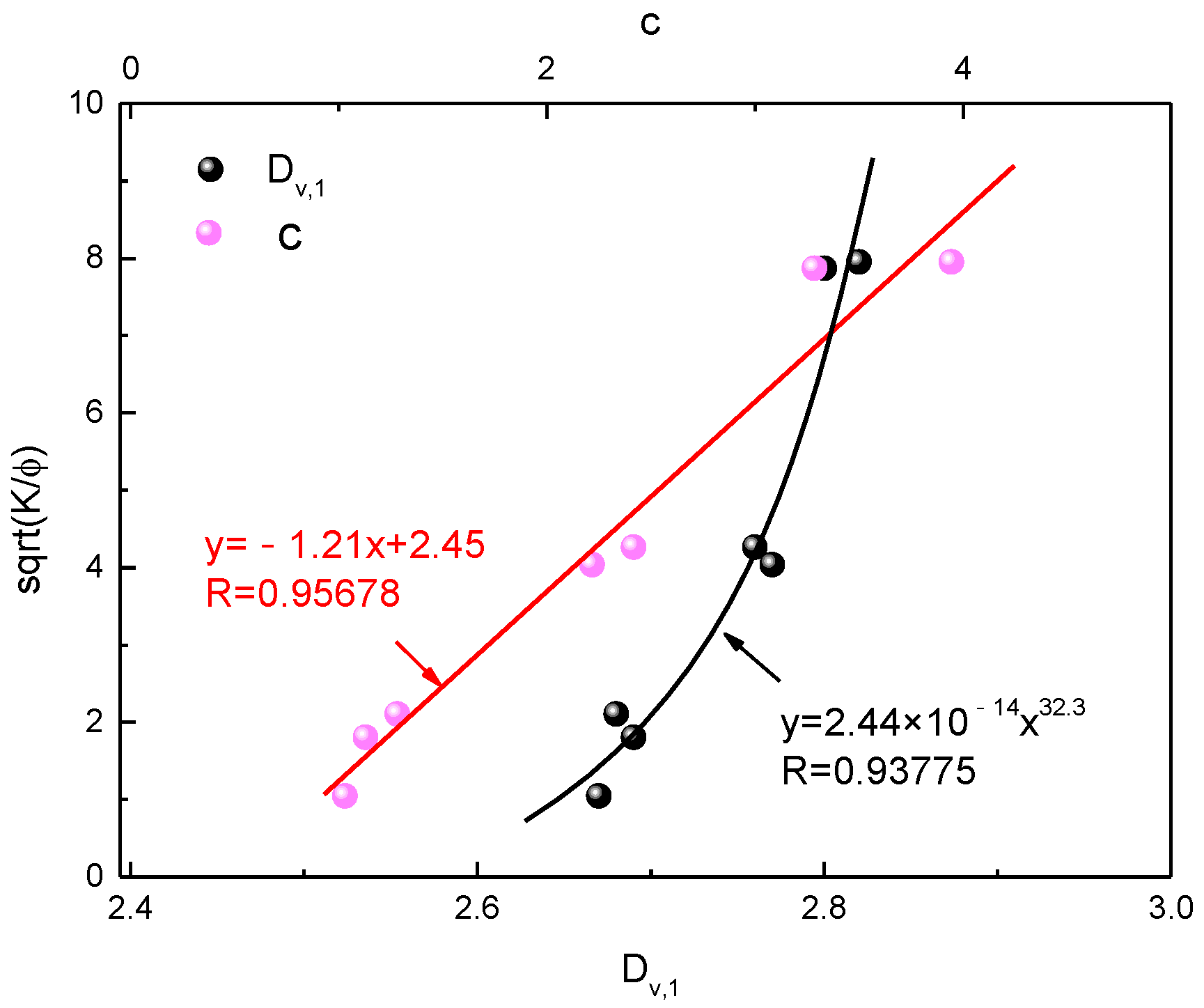
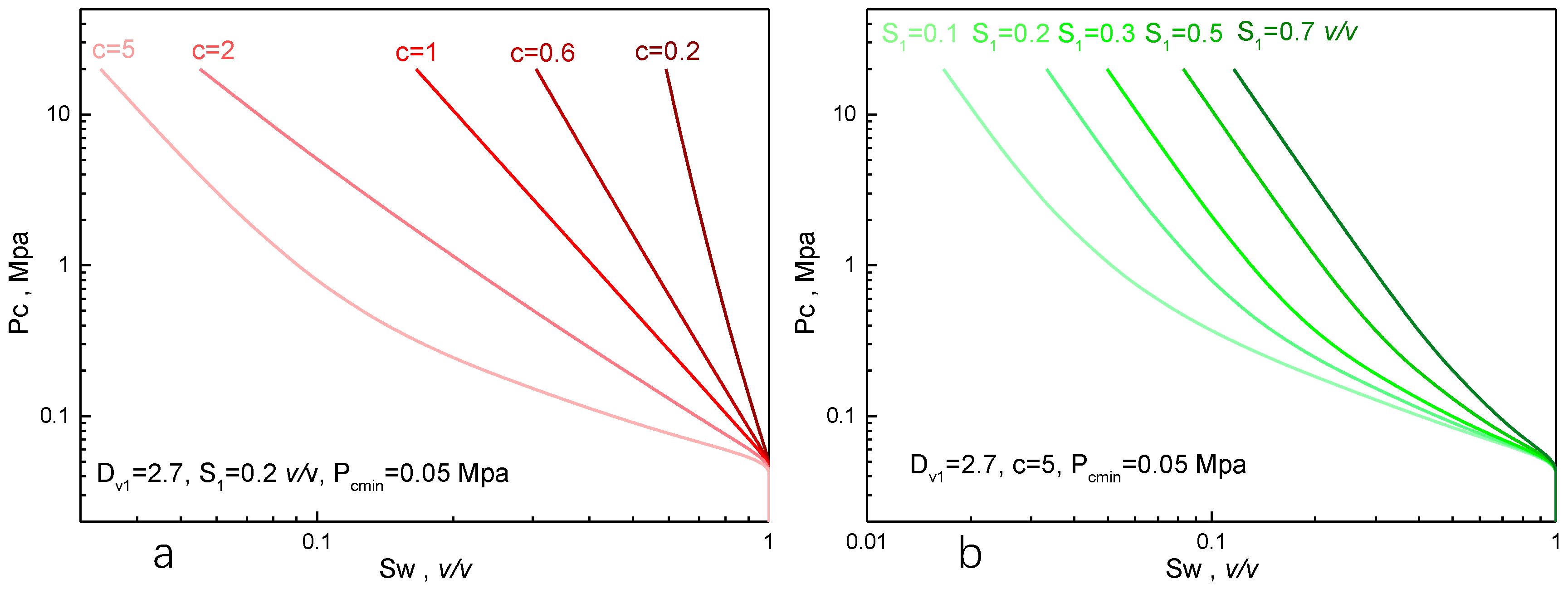
- According to Equation (6), the fractal and parameter c can be calculated from permeability and porosity measured in actual formation evaluation. Further, pore structure can be classified according to the fractals , , and parameter c, capillary pressure curve and pore structure characterization can be achieved.
- (2)
- Figure 11 analyzes the affection of , , c, and on capillary pressure curves according to Equation (6). The simulated capillary pressure curves with different c () and fixed , v/v, Mpa is depicted in Figure 11a. The result shows that as c increases ( decreases), under specific water saturation decreases, which is an indication of pore structure improvement, it is identical with that c has a positive correlation with . In addition, the capillary pressure curve exhibits non-power function features (power function exhibits linear feature in a logarithmic coordinate system). The simulated capillary pressure curves with different and fixed , , Mpa is depicted in Figure 11b. The result shows that as increases at large c value, under specific water saturation increases, it indicates that the pore structure gets poor.
4.2. Multi-Fractal Based Modeling of Resistivity Index Curves
4.3. Multi-Fractal Features of Pore Structure
4.4. Future Work
- The capillary pressure curve supplies fundamental data for pore structure characterization methods [43]. According to Equation (6), the pore structure characterization accuracy is improved for porous rock with complex pore structure, for instance, tight rock and shales.
- Reservoir flow unit division research based on capillary pressure curves is an important way for reservoir pattern studies [44]. According to Equation (6), more accurate reservoir flow unit division can be achieved.
- Resistivity models are crucial for oil and gas saturation calculation in practical applications [45]. In this paper, the accuracy of Equation (15) is improved than the Archie model. Equation (15) can be further utilized for reservoir estimation and shale organic carbon assessments.
- Equation (16) describes the relationship between the capillary pressure curve and rock resistivity based on multi-fractal theory. It provides a new idea and an effective way for studying the effect of pore structure on rock resistivity [46], especially for rocks with complex micro-pore structures, such as rock within fractures, shale, and carbonate rocks.
- As the heterogeneity of pore size and morphology of the study areas increases, single-dimension fractal theory is unable to meet the accuracy requirements. Multi-fractal theory can provide an effective way for pore structure characterization [47], which will be a research focus.
5. Conclusions
- (1)
- Based on multi-fractal theory, a multi-fractal characterization method for sandstone micro-pore structure using capillary pressure is developed, and its accuracy is improved than the commonly used power function model for the fitting of experimental capillary pressure curves. Based on the multi-fractal characterization method for sandstone micro-pore structure using capillary pressure, a rock resistivity model considering pore structure is developed. The new model is proven to have higher accuracy than the Archie model; it can accurately describe the rock conductivity characteristics and calculate the oil saturation of complex pore structure reservoirs.
- (2)
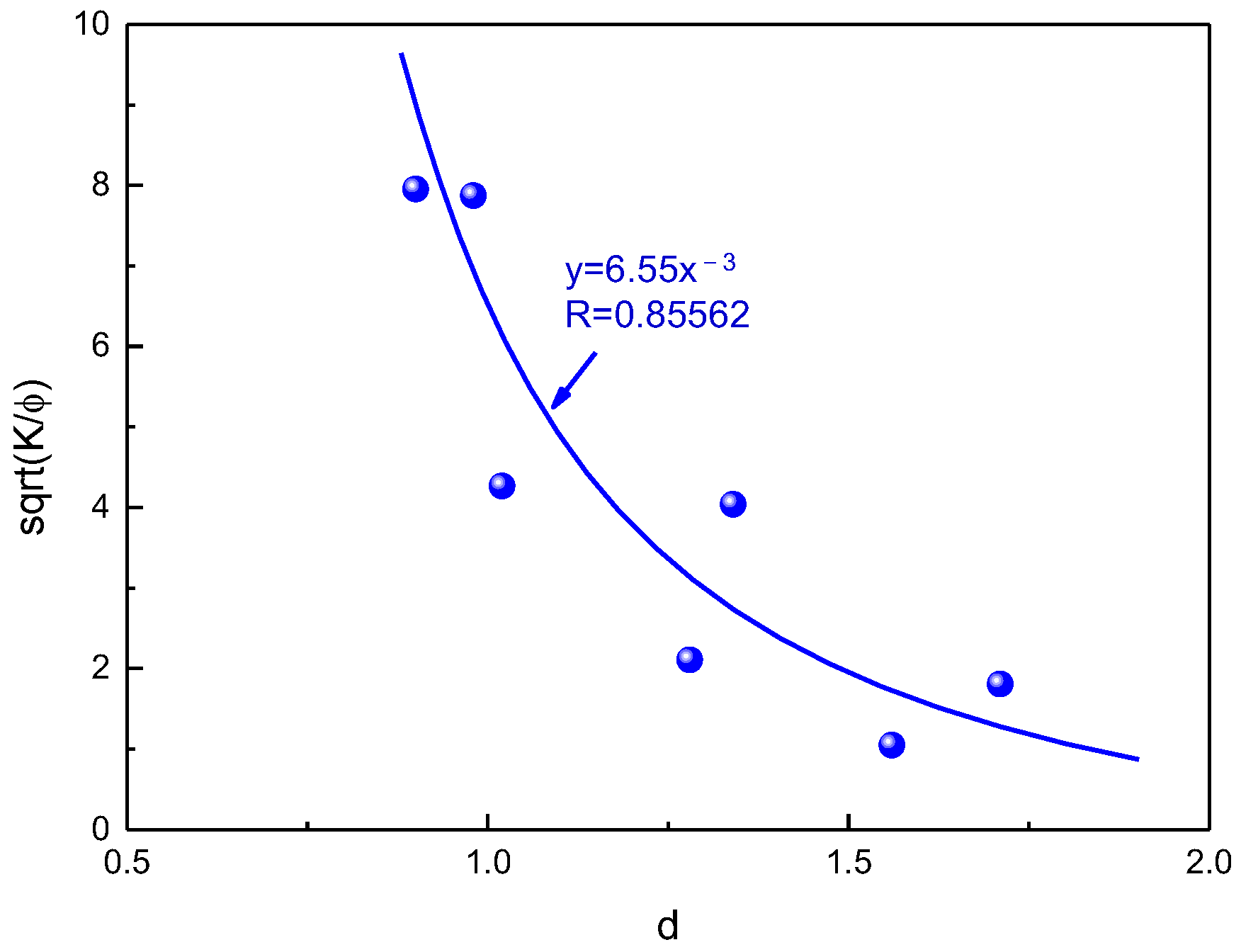
- A distinct interrelationship between fractal dimensions of capillary pressure curves () and resistivity index curves ( and ) is obtained. The capillary pressure curve can be directly converted to the resistivity index when d is determined. The fractal feature parameters , , c strongly depend on pore structure properties. Parameters c, d, and have a good relationship with , the pore structure typing result by and c is accordance with that according to the morphology of capillary pressure curve.
- (3)
- According to the multi-fractal-based analysis of capillary pressure curves and resistivity increase rate, the multi-fractal feature of pore structure is the main reason for non-Archie resistivity and non-power function capillary pressure relationships. As the difference between the two types of pores becomes stronger, non-Archie and non-power function features become obvious. Therefore, the multi-fractal method can improve the accuracy of pore structure characterization when rock pore structure complexity increases.
- (4)
- This study provides new ideas to improve the accuracy of pore structure characterization and oil saturation calculation; it has good application prospects and guiding significance in reservoir evaluation and rock physical characteristics research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cai, J.; Wei, W.; Hu, X.; Wood, D.A. Electrical conductivity models in saturated porous media: A review. Earth-Sci. Rev. 2017, 171, 419–433. [Google Scholar] [CrossRef]
- Zhu, L.; Wu, S.; Zhang, C.; Misra, S.; Zhou, X.; Cai, J. Characterization of pore electrical conductivity in porous media by weakly conductive and nonconductive pores. Surv. Geophys. 2023, 44, 877–923. [Google Scholar] [CrossRef]
- Jin, Y.; Li, S.; Yang, D. Experimental and theoretical quantification of the relationship between electrical resistivity and hydrate saturation in porous media. Fuel 2020, 269, 117378. [Google Scholar] [CrossRef]
- Adebayo, A.R.; Isah, A.; Mahmoud, M.; Al-Shehri, D. Effects of foam microbubbles on electrical resistivity and capillary pressure of partially saturated porous media. Molecules 2020, 25, 3385. [Google Scholar] [CrossRef]
- Iravani, M.A.; Deparis, J.; Davarzani, H.; Colombano, S.; Guérin, R.; Maineult, A. The influence of temperature on the dielectric permittivity and complex electrical resistivity of porous media saturated with DNAPLs: A laboratory study. J. Appl. Geophys. 2020, 172, 103921. [Google Scholar] [CrossRef]
- Sun, Z.; Mehmani, A.; Torres-Verdín, C. Pore-scale investigation of the electrical resistivity of saturated porous media: Flow patterns and porosity efficiency. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022608. [Google Scholar] [CrossRef]
- Tian, J.; Wang, L.; Sima, L.; Fang, S.; Liu, H. Characterization of reservoir properties and pore structure based on micro-resistivity imaging logging: Porosity spectrum, permeability spectrum, and equivalent capillary pressure curve. Pet. Explor. Dev. 2023, 50, 628–637. [Google Scholar] [CrossRef]
- Saafan, M.; Ganat, T. Inferring capillary pressure curve from 2D rock images based on fractal theory in low-permeability sandstone: A new integrated approach. Fractals 2021, 29, 2150149. [Google Scholar] [CrossRef]
- Schmitt, M.; Fernandes, C.P.; da Cunha Neto, J.A.; Wolf, F.G.; dos Santos, V.S. Characterization of pore systems in seal rocks using nitrogen gas adsorption combined with mercury injection capillary pressure techniques. Mar. Pet. Geol. 2013, 39, 138–149. [Google Scholar] [CrossRef]
- Hu, Y.; Yu, X.; Chen, G.; Li, S. Classification of the average capillary pressure function and its application in calculating fluid saturation. Pet. Explor. Dev. 2012, 39, 778–784. [Google Scholar] [CrossRef]
- Thomeer, J.H.M. Introduction of a pore geometrical factor defined by the capillary pressure curve. J. Pet. Technol. 1960, 12, 73–77. [Google Scholar] [CrossRef]
- Xu, W.S.; Luo, P.Y.; Sun, L.; Lin, N. A prediction model of the capillary pressure J-function. PLoS ONE 2016, 11, e0162123. [Google Scholar] [CrossRef][Green Version]
- Corey, A.T. The interrelation between gas and oil relative permeabilities. Prod. Mon. 1954, 19, 38–41. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Properties of porous media affecting fluid flow. J. Irrig. Drain. Div. 1966, 92, 61–88. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Wang, F.; Yang, K.; Cai, J. Fractal characterization of tight oil reservoir pore structure using nuclear magnetic resonance and mercury intrusion porosimetry. Fractals 2018, 26, 1840017. [Google Scholar] [CrossRef]
- Miao, T.; Yu, B.; Duan, Y.; Fang, Q. A fractal analysis of permeability for fractured rocks. Int. J. Heat Mass Transf. 2015, 81, 75–80. [Google Scholar] [CrossRef]
- Jafari, A.; Babadagli, T. Estimation of equivalent fracture network permeability using fractal and statistical network properties. J. Petrol. Sci. Eng. 2012, 92, 110–123. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, Z.; Lin, W.; Xiong, S.; Luo, Y.; Liu, X.; Xia, D. Fractal study on pore structure of tight sandstone based on full-scale map. Int. J. Oil Gas Coal Technol. 2019, 22, 123–139. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, F.; Zhang, C.; Song, Z.; Mo, W. Study on the Pore Structure and Fractal Dimension of Tight Sandstone in Coal Measures. Energy Fuels 2021, 35, 3887–3898. [Google Scholar] [CrossRef]
- Xie, W.; Yin, Q.; Wang, G.; Yu, Z. Variable dimension fractal-based conversion method between the nuclear magnetic resonance T2 spectrum and capillary pressure curve. Energy Fuels 2020, 35, 351–357. [Google Scholar] [CrossRef]
- Gao, H.; Yu, B.; Duan, Y.; Fang, Q. Fractal analysis of dimensionless capillary pressure function. Int. J. Heat Mass Transf. 2014, 69, 26–33. [Google Scholar] [CrossRef]
- Liu, P.; Yuan, Z.; Li, K. An improved capillary pressure model using fractal geometry for coal rock. J. Pet. Sci. Eng. 2016, 145, 473–481. [Google Scholar] [CrossRef]
- Li, K. Analytical derivation of Brooks–Corey type capillary pressure models using fractal geometry and evaluation of rock heterogeneity. J. Pet. Sci. Eng. 2010, 73, 20–26. [Google Scholar] [CrossRef]
- Li, B.; Liu, R.; Jiang, Y. A multiple fractal model for estimating permeability of dual-porosity media. J. Hydrol. 2016, 540, 659–669. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Yue, W. Pore-scale explanation of the archie’s cementation exponent: Microstructure, electrical anisotropy, and numerical experiments. Geophys. Res. Lett. 2019, 46, 5799–5807. [Google Scholar] [CrossRef]
- Xiao, L.; Zou, C.C.; Mao, Z.Q.; Shi, Y.J.; Jin, Y.; Guo, H.P.; Hu, X.X. Estimation of water saturation from nuclear magnetic resonance(NMR) and conventional logs in low permeability sandstone reservoirs. J. Petroleum Sci. Eng. 2013, 108, 40–51. [Google Scholar] [CrossRef]
- Shang, B.Z.; Hamman, J.G.; Caldwell, D.H. A Physical Model to Explain the First Archie Re1ationship and Beyond. In Proceedings of the SPE Annual Technical Conference and ExhIbition, Denver, CO, USA, 5–8 October 2004. [Google Scholar]
- Nigmatullin, R.R.; Dissado, L.A.; Soutougin, N.N. A fractal pore model for Archie’s law in sedimentary rocks. J. Phys. D Appl. Phys. 1992, 25, 32. [Google Scholar] [CrossRef]
- Wright, H.M.N.; Cashman, K.V.; Gottesfeld, E.H.; Roberts, J.J. Pore structure of volcanic clasts: Measurements of permeability and electrical conductivity. Earth Planet. Sci. Lett. 2009, 280, 93–104. [Google Scholar] [CrossRef]
- Rembert, F.; Jougnot, D.; Guarracino, L. A fractal model for the electrical conductivity of water-saturated porous media during mineral precipitation-dissolution processes. Adv. Water Resour. 2020, 145, 103742. [Google Scholar] [CrossRef]
- Feng, C.; Han, C.; Duan, W.; Wang, W.; Zhong, Y.; Feng, Z.; Zhang, N. Estimation of the Resistivity Index via Nuclear Magnetic Resonance Log Data Based on Fractal Theory. Geofluids 2020, 2020, 8871096. [Google Scholar] [CrossRef]
- Shi, Y.; Meng, H.; Liu, T.; Zhang, H.; Wang, C. Evaluation of Relative Permeability From Resistivity Data for Fractal Porous Media. Petrophysics-SPWLA J. Form. Eval. Reserv. Descr. 2020, 61, 303–317. [Google Scholar] [CrossRef]
- Luo, H.; Jougnot, D.; Jost, A.; Teng, J.; Thanh, L.D. A capillary bundle model for the electrical conductivity of saturated frozen porous media. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025254. [Google Scholar] [CrossRef]
- Hu, S.; Zhou, C.; Li, X.; Li, C.; Zhang, S. A tight sandstone trapezoidal pore oil saturation model. Pet. Explor. Dev. 2017, 44, 827–836. [Google Scholar] [CrossRef]
- Cai, R.J.; Tang, S.W.; He, Z. The modeling of electrical property in porous media based on fractal leaf vein network. Int. J. Eng. Sci. 2018, 123, 143–157. [Google Scholar] [CrossRef]
- Wei, W.; Cai, J.; Hu, X.; Han, Q. An electrical conductivity model for fractal porous media. Geophys. Res. Lett. 2015, 42, 4833–4840. [Google Scholar] [CrossRef]
- Wang, F.; Cai, J. Characterization of petrophysical properties in tight sandstone reservoirs. In Petrophysical Characterization and Fluids Transport in Unconventional Reservoirs; Elsevier: Amsterdam, The Netherlands, 2019; pp. 37–59. [Google Scholar]
- Guo, X.; Huang, Z.; Zhao, L.; Han, W.; Ding, C.; Sun, X.; Yan, R.; Zhang, T.; Yang, X.; Wang, R. Pore structure and multi-fractal analysis of tight sandstone using MIP, NMR and NMRC methods: A case study from the Kuqa depression, China. J. Pet. Sci. Eng. 2019, 178, 544–558. [Google Scholar] [CrossRef]
- Xie, W.; Yin, Q.; Zeng, J.; Wang, G.; Feng, C.; Zhang, P. Fractal-Based Approaches to Pore Structure Investigation and Water Saturation Prediction from NMR Measurements: A Case Study of the Gas-Bearing Tight Sandstone Reservoir in Nanpu Sag. Fractal Fract. 2023, 7, 273. [Google Scholar] [CrossRef]
- Ge, X.M.; Fan, Y.R.; Deng, S.G.; Du, Q.J. Research on correlation between capillary pressure and resistivity index based on fractal theory. J. China Univ. Pet. Ed. Nat. Sci. 2012, 36, 72–76, (In Chinese abstract). [Google Scholar]
- Zhou, J.; Liu, B.; Shao, M.; Song, Y.; Ostadhassan, M.; Yin, C.; Liu, J.; Jiang, Y. Pore structure analysis and classification of pyroclastic reservoirs in the Dehui fault depression based on experimental and well-logging data. Geoenergy Sci. Eng. 2023, 224, 211620. [Google Scholar] [CrossRef]
- Khurpade, P.D.; Kshirsagar, L.K.; Nandi, S. Characterization of heterogeneous petroleum reservoir of indian sub-continent: An integrated approach of hydraulic flow unit—Mercury intrusion capillary pressure—Fractal model. J. Pet. Sci. Eng. 2021, 205, 108788. [Google Scholar] [CrossRef]
- Zhang, G.; Li, H.; Hu, X.; Gao, Y. Study of the method portrayed by a river by calculating the tooth rate of the logging curve. J. Nat. Gas Geosci. 2019, 4, 63–70. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Sahimi, M. Electrical conductivity of partially saturated packings of particles. Transp. Porous Media 2017, 118, 1–16. [Google Scholar] [CrossRef]
- Song, Z.; Liu, G.; Yang, W.; Zou, H.; Sun, M.; Wang, X. Multi-fractal distribution analysis for pore structure characterization of tight sandstone—A case study of the Upper Paleozoic tight formations in the Longdong District, Ordos Basin. Mar. Pet. Geol. 2018, 92, 842–854. [Google Scholar] [CrossRef]


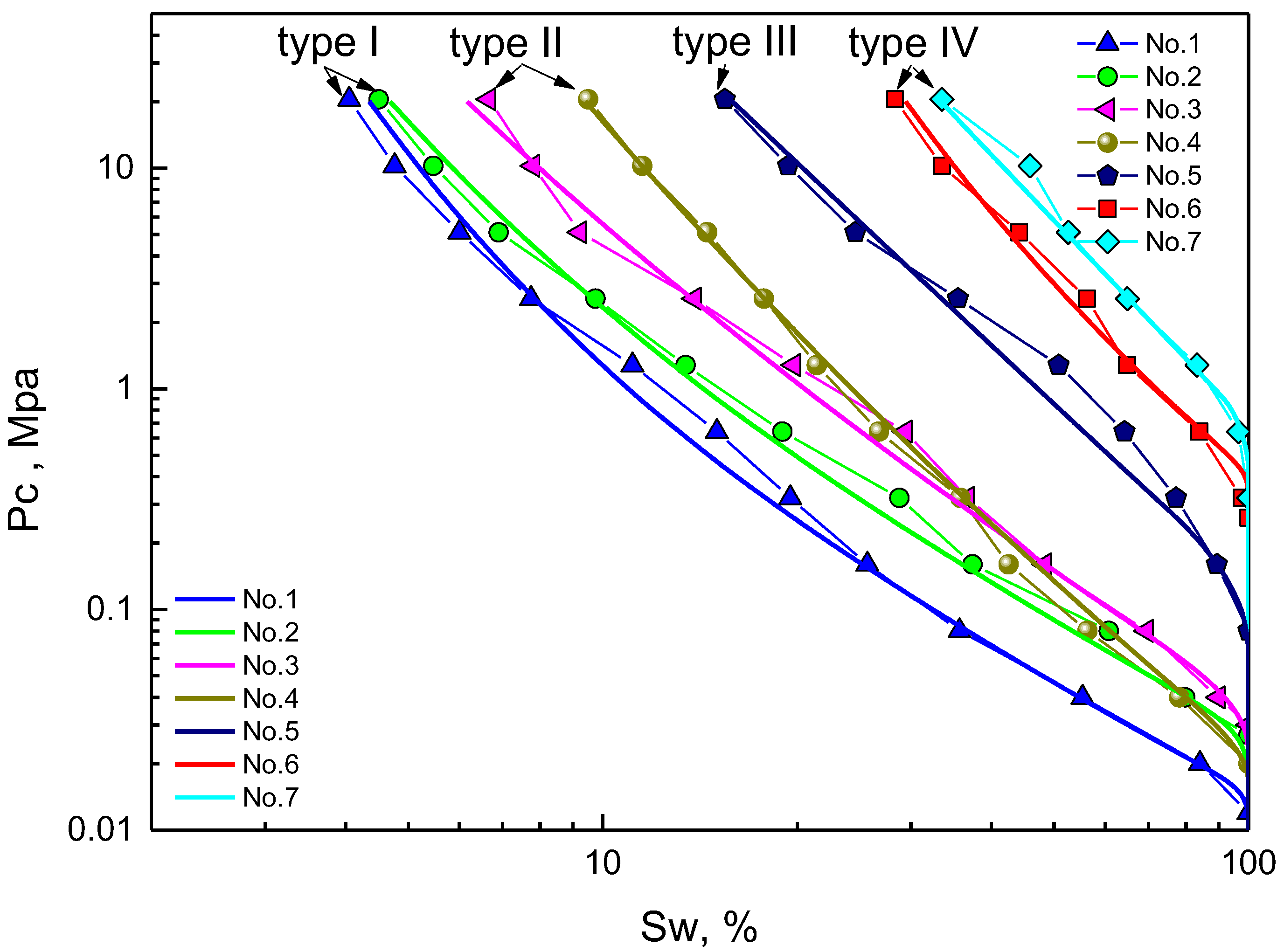

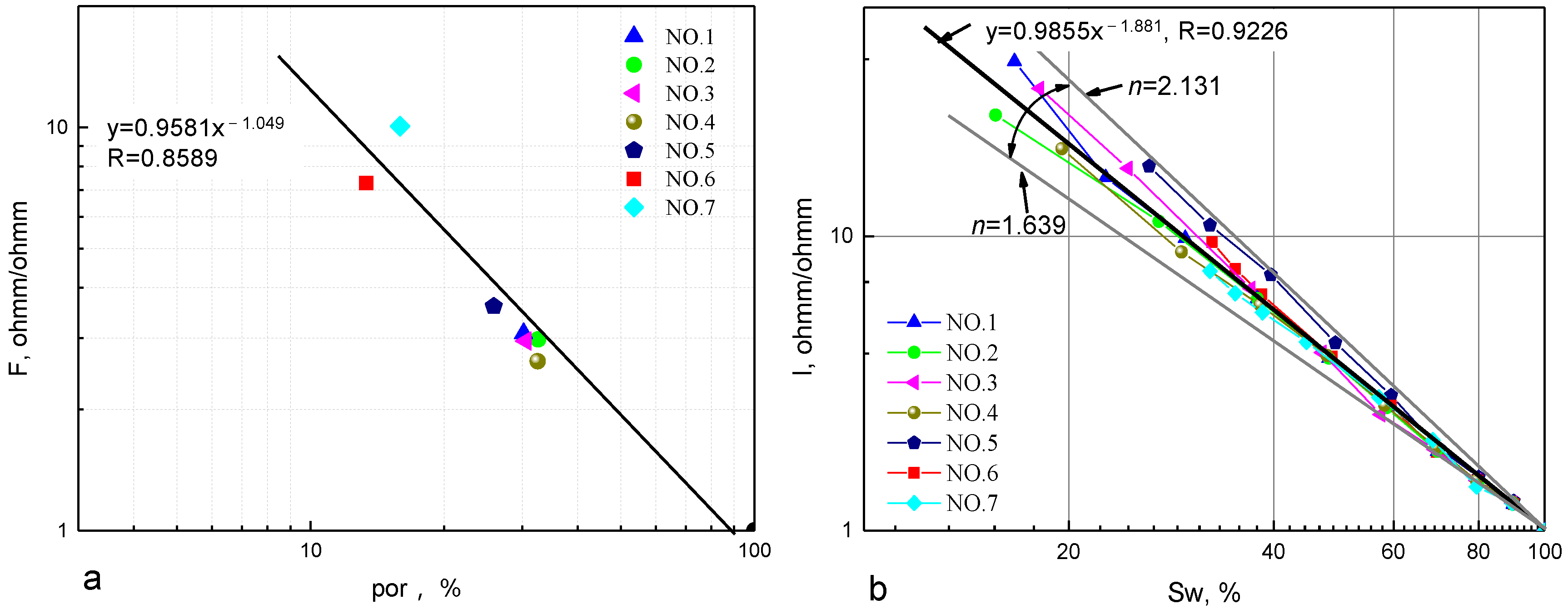
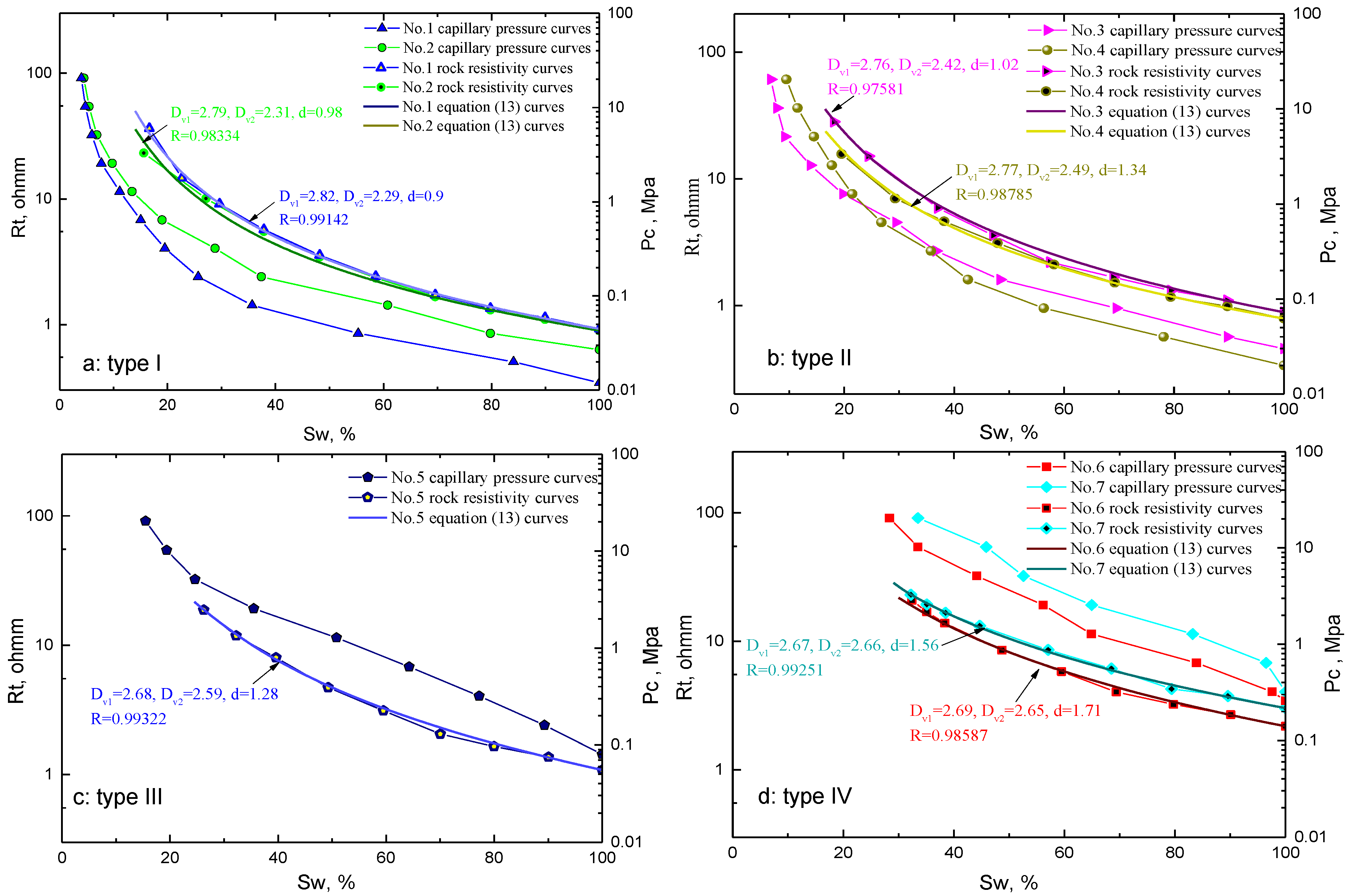
| Type | No. | Depth m | Porosity % | Permeability md | F | n | Dv1 | Dv2 | S1 | Pcmin | c | d |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 1 | 317.46 | 30.2 | 1910 | 3.08 | 1.889 | 2.82 | 2.29 | 0.14 | 0.015 | 3.95 | 0.9 |
| 2 | 316.82 | 32.59 | 2020 | 2.98 | 1.869 | 2.79 | 2.31 | 0.15 | 0.028 | 3.285 | 0.98 | |
| II | 3 | 319.23 | 30.55 | 556 | 2.95 | 1.981 | 2.76 | 2.42 | 0.18 | 0.038 | 2.42 | 1.02 |
| 4 | 321.55 | 32.5 | 530 | 2.63 | 1.841 | 2.77 | 2.49 | 0.27 | 0.023 | 2.22 | 1.34 | |
| III | 5 | 322.69 | 25.86 | 115 | 3.6 | 2.149 | 2.68 | 2.59 | 0.44 | 0.13 | 1.28 | 1.28 |
| IV | 6 | 314.55 | 13.35 | 14.7 | 7.27 | 1.932 | 2.67 | 2.66 | 0.5 | 0.41 | 1.03 | 1.56 |
| 7 | 318.77 | 15.91 | 52 | 10.07 | 1.746 | 2.69 | 2.65 | 0.59 | 0.69 | 1.13 | 1.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, W.; Yin, Q.; Zeng, J.; Yang, F.; Zhang, P.; Yan, B. An Improved Rock Resistivity Model Based on Multi-Fractal Characterization Method for Sandstone Micro-Pore Structure Using Capillary Pressure. Fractal Fract. 2024, 8, 118. https://doi.org/10.3390/fractalfract8020118
Xie W, Yin Q, Zeng J, Yang F, Zhang P, Yan B. An Improved Rock Resistivity Model Based on Multi-Fractal Characterization Method for Sandstone Micro-Pore Structure Using Capillary Pressure. Fractal and Fractional. 2024; 8(2):118. https://doi.org/10.3390/fractalfract8020118
Chicago/Turabian StyleXie, Weibiao, Qiuli Yin, Jingbo Zeng, Fan Yang, Pan Zhang, and Binpeng Yan. 2024. "An Improved Rock Resistivity Model Based on Multi-Fractal Characterization Method for Sandstone Micro-Pore Structure Using Capillary Pressure" Fractal and Fractional 8, no. 2: 118. https://doi.org/10.3390/fractalfract8020118
APA StyleXie, W., Yin, Q., Zeng, J., Yang, F., Zhang, P., & Yan, B. (2024). An Improved Rock Resistivity Model Based on Multi-Fractal Characterization Method for Sandstone Micro-Pore Structure Using Capillary Pressure. Fractal and Fractional, 8(2), 118. https://doi.org/10.3390/fractalfract8020118








