Local Singularity Spectrum: An Innovative Graphical Approach for Analyzing Detrital Zircon Geochronology Data in Provenance Analysis
Abstract
1. Introduction
2. Potential Biases in Detrital Zircon Geochronological Data Analysis
2.1. Sampling and Data Analysis
2.2. Geological Mechanism
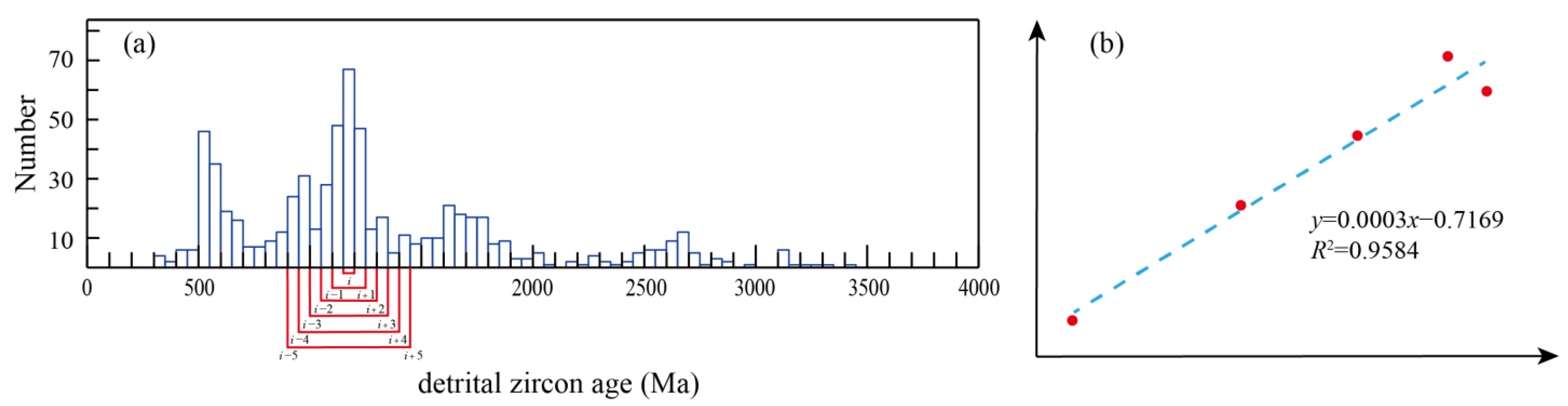
3. Local Singularity Analysis
4. Case Study
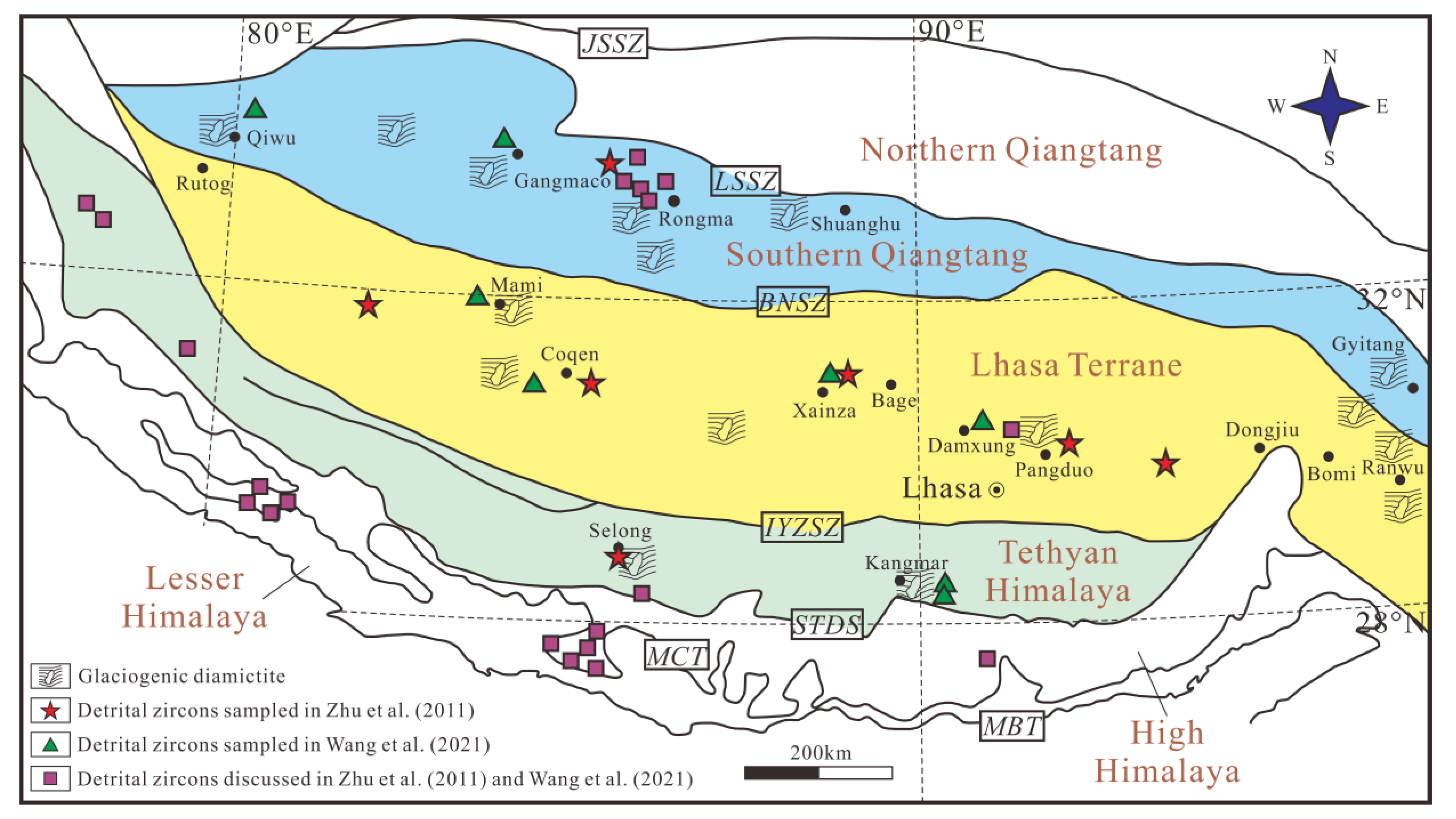
4.1. Study Area
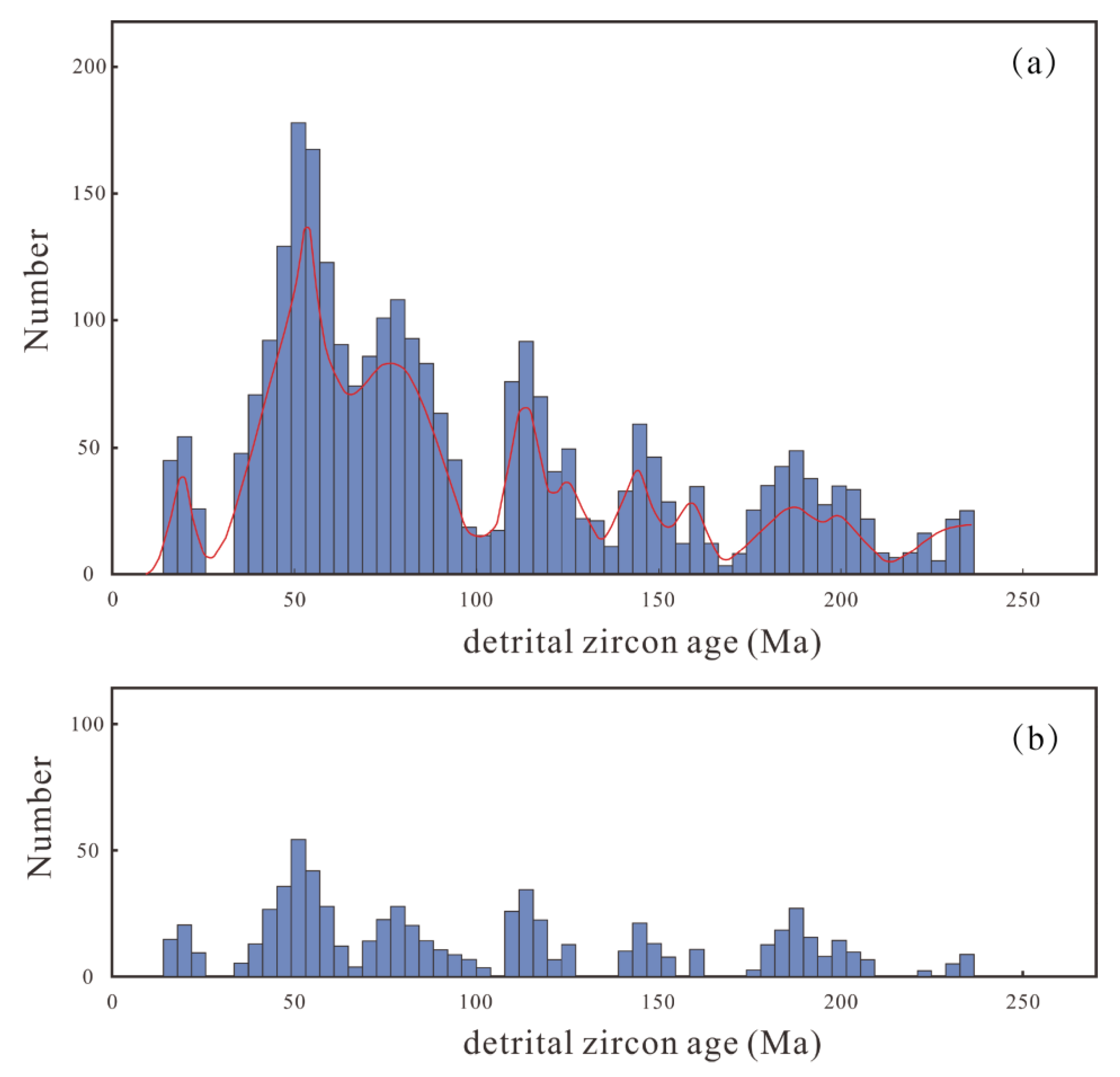
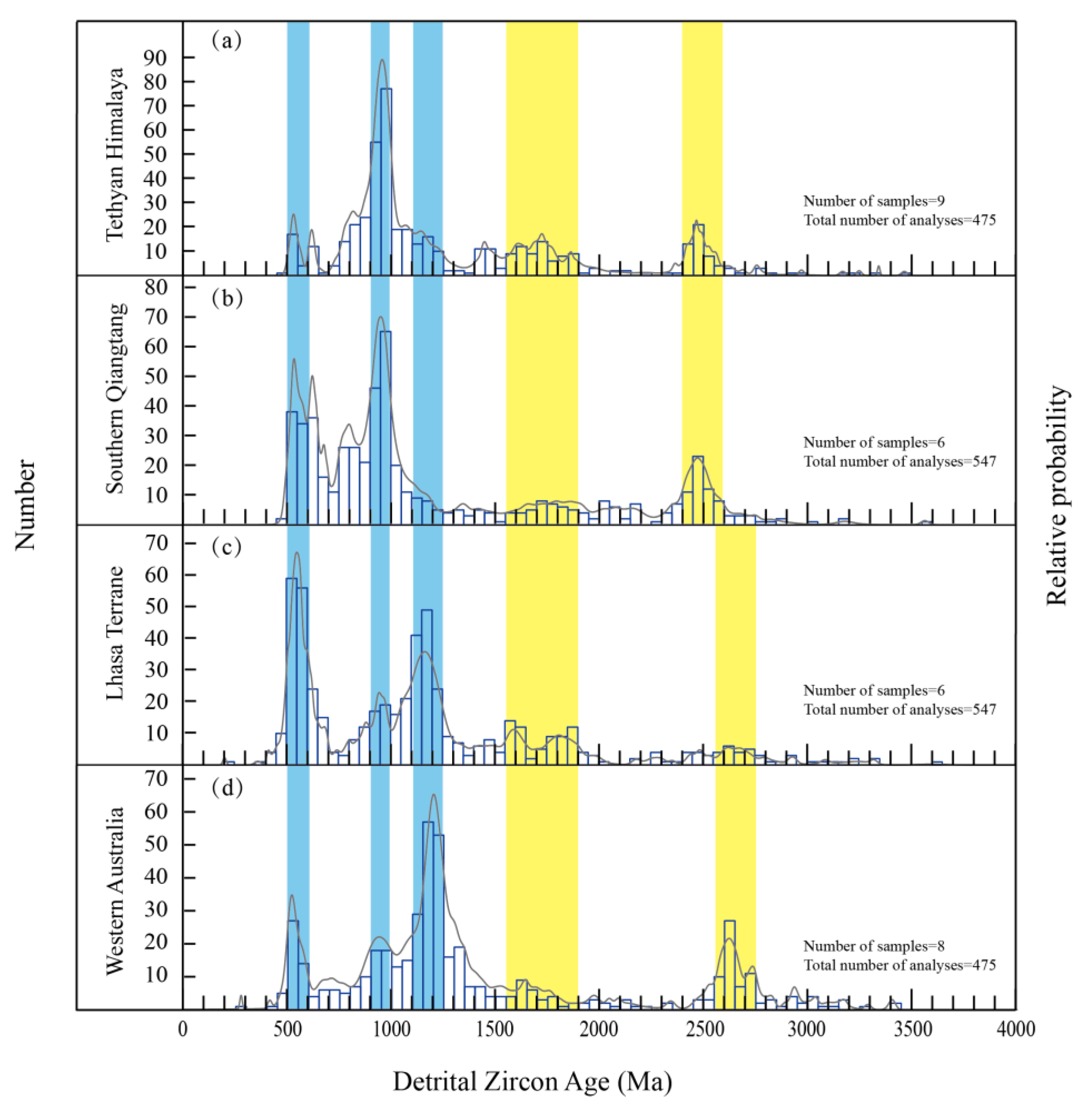
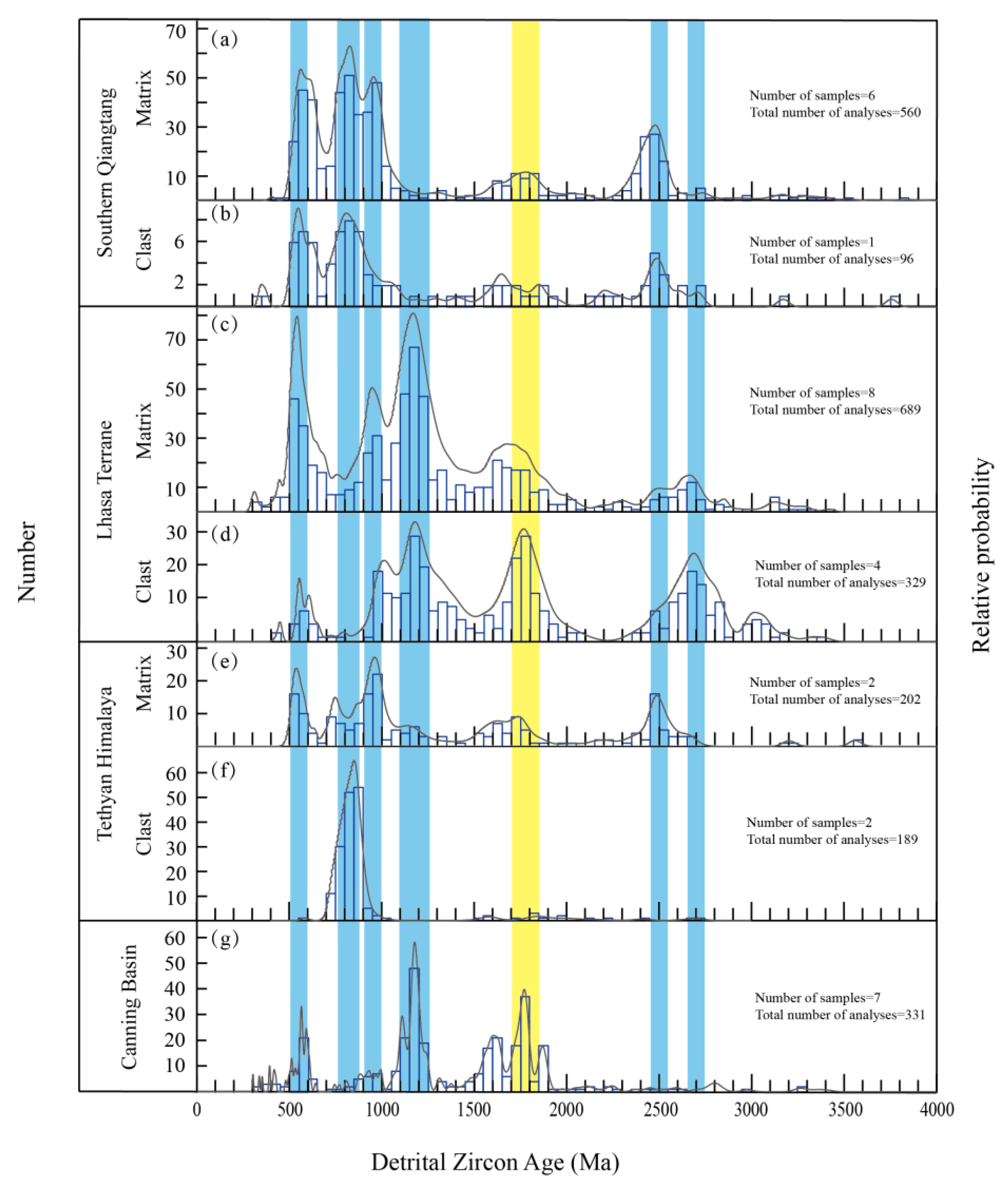
4.2. Datasets and Graphical Visualization
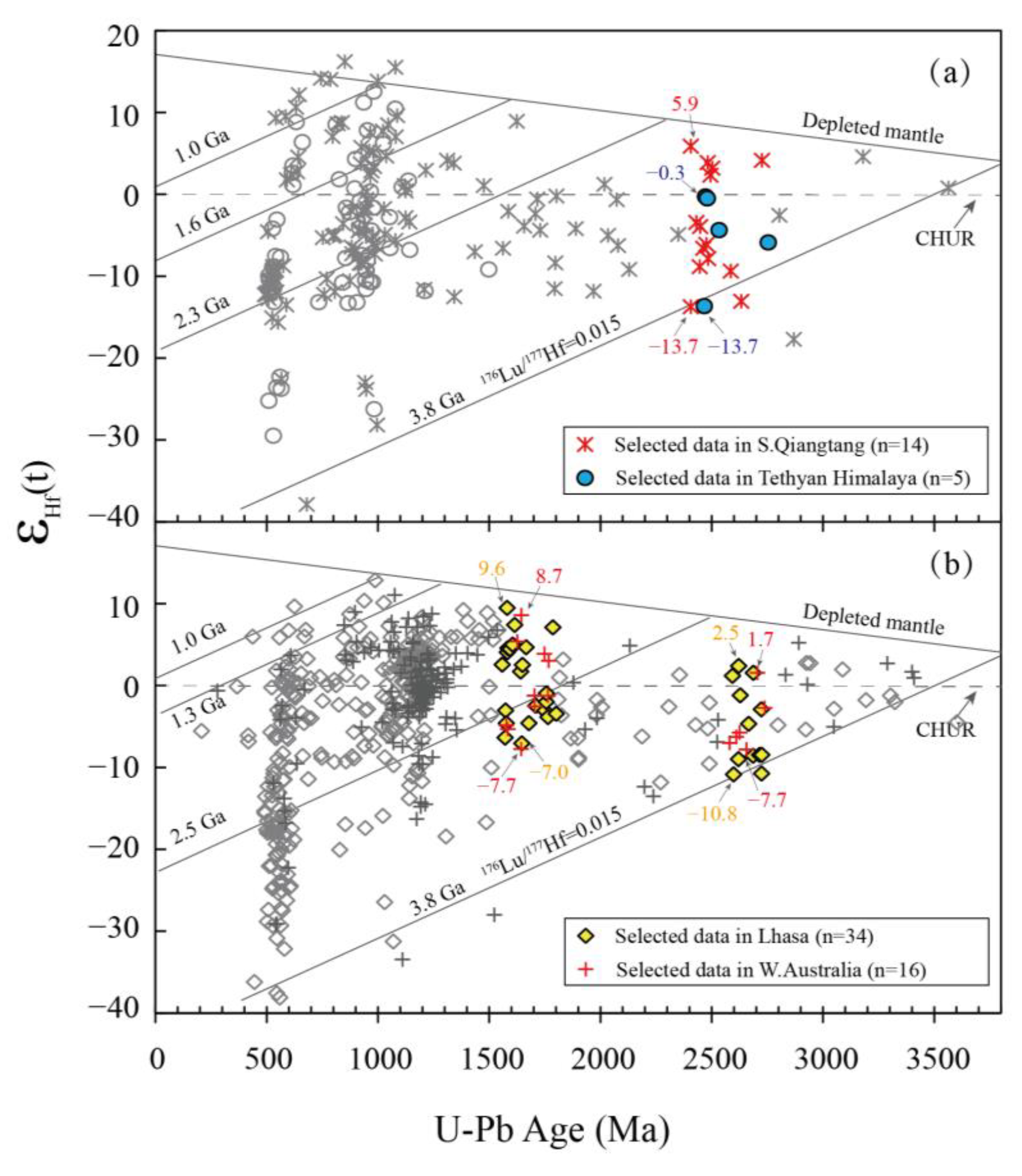
4.3. Singularity Analysis of U-Pb Age Data
5. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blatt, H.; Jones, R.L. Proportions of Exposed Igneous, Metamorphic, and Sedimentary Rocks. GSA Bull. 1975, 86, 1085–1088. [Google Scholar] [CrossRef]
- Link, P.K.; Fanning, C.M.; Beranek, L.P. Reliability and Longitudinal Change of Detrital-Zircon Age Spectra in the Snake River System, Idaho and Wyoming: An Example of Reproducing the Bumpy Barcode. Sediment. Geol. 2005, 182, 101–142. [Google Scholar] [CrossRef]
- Thomas, W.A.; Becker, T.P.; Samson, S.D.; Hamilton, M.A. Detrital Zircon Evidence of a Recycled Orogenic Foreland Provenance for Alleghanian Clastic-wedge Sandstones. J. Geol. 2004, 112, 23–37. [Google Scholar] [CrossRef]
- Dickinson, W.R.; Gehrels, G.E. Use of U-Pb Ages of Detrital Zircons to Infer Maximum Depositional Ages of Strata: A Test against a Colorado Plateau Mesozoic Database. Earth Planet. Sci. Lett. 2009, 288, 115–125. [Google Scholar] [CrossRef]
- Weltje, G.J.; von Eynatten, H. Quantitative Provenance Analysis of Sediments: Review and Outlook. Sediment. Geol. 2004, 171, 1–11. [Google Scholar] [CrossRef]
- Gehrels, G.E.; Blakey, R.; Karlstrom, K.E.; Timmons, J.M.; Dickinson, B.; Pecha, M. Detrital Zircon U-Pb Geochronology of Paleozoic Strata in the Grand Canyon, Arizona. Lithosphere 2011, 3, 183–200. [Google Scholar] [CrossRef]
- Scherer, E.E.; Whitehouse, M.J.; Münker, C. Zircon as a Monitor of Crustal Growth. Elements 2007, 3, 19–24. [Google Scholar] [CrossRef]
- Gehrels, G. Detrital Zircon U-Pb Geochronology: Current Methods and New Opportunities. In Tectonics of Sedimentary Basins; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; pp. 45–62. ISBN 978-1-4443-4716-6. [Google Scholar]
- Finch, M.A.; Weinberg, R.F.; Barrote, V.R.; Cawood, P.A. Hf Isotopic Ratios in Zircon Reveal Processes of Anatexis and Pluton Construction. Earth Planet. Sci. Lett. 2021, 576, 117215. [Google Scholar] [CrossRef]
- Fasulo, C.R.; Ridgway, K.D. Detrital Zircon Geochronology of Modern River Sediment in South-Central Alaska: Provenance, Magmatic, and Tectonic Insights into the Mesozoic and Cenozoic Development of the Southern Alaska Convergent Margin. Geosphere 2021, 17, 1248–1267. [Google Scholar] [CrossRef]
- Puetz, S.J.; Ganade, C.E.; Zimmermann, U.; Borchardt, G. Statistical Analyses of Global U-Pb Database 2017. Geosci. Front. 2018, 9, 121–145. [Google Scholar] [CrossRef]
- Amidon, W.H.; Burbank, D.W.; Gehrels, G.E. Construction of Detrital Mineral Populations: Insights from Mixing of U-Pb Zircon Ages in Himalayan Rivers. Basin Res. 2005, 17, 463–485. [Google Scholar] [CrossRef]
- Jacobson, C.E.; Grove, M.; Pedrick, J.N.; Barth, A.P.; Marsaglia, K.M.; Gehrels, G.E.; Nourse, J.A. Late Cretaceous–Early Cenozoic Tectonic Evolution of the Southern California Margin Inferred from Provenance of Trench and Forearc Sediments. GSA Bull. 2011, 123, 485–506. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Schertl, H.-P.; Wang, J.L.; Shen, K.; Liou, J.G. Source of Coesite Inclusions within Inherited Magmatic Zircon from Sulu UHP Rocks, Eastern China, and Their Bearing for Fluid–Rock Interaction and SHRIMP Dating. J. Metamorph. Geol. 2009, 27, 317–333. [Google Scholar] [CrossRef]
- Wernicke, B. The California River and Its Role in Carving Grand Canyon. GSA Bull. 2011, 123, 1288–1316. [Google Scholar] [CrossRef]
- Cheng, Q.M. Singularity Analysis of Global Zircon U-Pb Age Series and Implication of Continental Crust Evolution. Gondwana Res. 2017, 51, 51–63. [Google Scholar] [CrossRef]
- Parman, S.W. Helium Isotopic Evidence for Episodic Mantle Melting and Crustal Growth. Nature 2007, 446, 900–903. [Google Scholar] [CrossRef]
- Hawkesworth, C.; Cawood, P.; Kemp, T.; Storey, C.; Dhuime, B. A Matter of Preservation. Science 2009, 323, 49–50. [Google Scholar] [CrossRef] [PubMed]
- Vermeesch, P. How Many Grains Are Needed for a Provenance Study? Earth Planet. Sci. Lett. 2004, 224, 441–451. [Google Scholar] [CrossRef]
- Thomas, W.A. Detrital-Zircon Geochronology and Sedimentary Provenance. Lithosphere 2011, 3, 304–308. [Google Scholar] [CrossRef]
- Sircombe, K.N. Quantitative Comparison of Large Sets of Geochronological Data Using Multivariate Analysis: A Provenance Study Example from Australia. Geochim. Cosmochim. Acta 2000, 64, 1593–1616. [Google Scholar] [CrossRef]
- Hietpas, J.; Samson, S.; Moecher, D.; Chakraborty, S. Enhancing Tectonic and Provenance Information from Detrital Zircon Studies: Assessing Terrane-Scale Sampling and Grain-Scale Characterization. J. Geol. Soc. 2011, 168, 309–318. [Google Scholar] [CrossRef]
- Zimmermann, U.; Andersen, T.; Madland, M.V.; Larsen, I.S. The Role of U-Pb Ages of Detrital Zircons in Sedimentology—An Alarming Case Study for the Impact of Sampling for Provenance Interpretation. Sediment. Geol. 2015, 320, 38–50. [Google Scholar] [CrossRef]
- Lawrence, R.L.; Cox, R.; Mapes, R.W.; Coleman, D.S. Hydrodynamic Fractionation of Zircon Age Populations. GSA Bull. 2011, 123, 295–305. [Google Scholar] [CrossRef]
- Dodson, M.H.; Compston, W.; Williams, I.S.; Wilson, J.F. A Search for Ancient Detrital Zircons in Zimbabwean Sediments. J. Geol. Soc. 1988, 145, 977–983. [Google Scholar] [CrossRef]
- Andersen, T. Correction of Common Lead in U-Pb Analyses That Do Not Report 204 Pb. Chem. Geol. 2002, 192, 59–79. [Google Scholar] [CrossRef]
- Tucker, R.T.; Roberts, E.M.; Hu, Y.; Kemp, A.I.S.; Salisbury, S.W. Detrital Zircon Age Constraints for the Winton Formation, Queensland: Contextualizing Australia’s Late Cretaceous Dinosaur Faunas. Gondwana Res. 2013, 24, 767–779. [Google Scholar] [CrossRef]
- Schaltegger, U.; Schmitt, A.K.; Horstwood, M.S.A. U-Th-Pb Zircon Geochronology by ID-TIMS, SIMS, and Laser Ablation ICP-MS: Recipes, Interpretations, and Opportunities. Chem. Geol. 2015, 402, 89–110. [Google Scholar] [CrossRef]
- Andersen, T.; Kristoffersen, M.; Elburg, M.A. Visualizing, Interpreting and Comparing Detrital Zircon Age and Hf Isotope Data in Basin Analysis—A Graphical Approach. Basin Res. 2018, 30, 132–147. [Google Scholar] [CrossRef]
- Sircombe, K.N.; Hazelton, M.L. Comparison of Detrital Zircon Age Distributions by Kernel Functional Estimation. Sediment. Geol. 2004, 171, 91–111. [Google Scholar] [CrossRef]
- Cawood, P.A.; Hawkesworth, C.J.; Dhuime, B. Detrital Zircon Record and Tectonic Setting. Geology 2012, 40, 875–878. [Google Scholar] [CrossRef]
- Moecher, D.P.; Samson, S.D. Differential Zircon Fertility of Source Terranes and Natural Bias in the Detrital Zircon Record: Implications for Sedimentary Provenance Analysis. Earth Planet. Sci. Lett. 2006, 247, 252–266. [Google Scholar] [CrossRef]
- Condie, K.C.; Arndt, N.; Davaille, A.; Puetz, S.J. Zircon Age Peaks: Production or Preservation of Continental Crust? Geosphere 2017, 13, 227–234. [Google Scholar] [CrossRef]
- Stewart, J.H.; Gehrels, G.E.; Barth, A.P.; Link, P.K.; Christie-Blick, N.; Wrucke, C.T. Detrital Zircon Provenance of Mesoproterozoic to Cambrian Arenites in the Western United States and Northwestern Mexico. GSA Bull. 2001, 113, 1343–1356. [Google Scholar] [CrossRef]
- Dickinson, W.R. Impact of Differential Zircon Fertility of Granitoid Basement Rocks in North America on Age Populations of Detrital Zircons and Implications for Granite Petrogenesis. Earth Planet. Sci. Lett. 2008, 275, 80–92. [Google Scholar] [CrossRef]
- Cawood, P.A.; Nemchin, A.A. Provenance Record of a Rift Basin: U/Pb Ages of Detrital Zircons from the Perth Basin, Western Australia. Sediment. Geol. 2000, 134, 209–234. [Google Scholar] [CrossRef]
- Wang, W.L.; Zhao, J.; Cheng, Q.M. Nonlinearity. In Encyclopedia of Mathematical Geosciences; Daya Sagar, B.S., Cheng, Q.M., McKinley, J., Agterberg, F., Eds.; Encyclopedia of Earth Sciences Series; Springer International Publishing: Cham, Switzerland, 2021; pp. 1–6. ISBN 978-3-030-26050-7. [Google Scholar]
- Flinders, J.; Clemens, J.D. Non-Linear Dynamics, Chaos, Complexity and Enclaves in Granitoid Magmas. Earth Environ. Sci. Trans. R. Soc. Edinb. 1996, 87, 217–223. [Google Scholar] [CrossRef]
- Ghil, M. A Century of Nonlinearity in the Geosciences. Earth Space Sci. 2019, 6, 1007–1042. [Google Scholar] [CrossRef]
- Zhu, P.P.; Cheng, Q.M. Singularity Analysis of Volcanic Ages and Implications for Tectonic Setting in the Mesozoic, Great Xing’an Range, Northeast China. Minerals 2019, 9, 419. [Google Scholar] [CrossRef]
- Zhou, Y.Z.; Cheng, Q.M.; Liu, Y.; Zhu, P.P.; Wu, G.P.; Zhang, Z.J.; Yang, J. Singularity Analysis of Igneous Zircon U-Pb Age and Hf Isotopic Record in the Zhongdian Arc, Northwest Yunnan, China: Implications for Indosinian Magmatic Flare-up and the Formation of Porphyry Copper Deposits. Ore Geol. Rev. 2021, 139, 104476. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Kusky, T.; Yang, X.K.; Cheng, Q.M. A Paradigm Shift in Precambrian Research Driven by Big Data. Precambrian Res. 2023, 399, 107235. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Kusky, T.; Gao, M.; Cheng, Q.M. Spatio-Temporal Analysis of Big Data Sets of Detrital Zircon U-Pb Geochronology and Hf Isotope Data: Tests of Tectonic Models for the Precambrian Evolution of the North China Craton. Earth-Sci. Rev. 2023, 239, 104372. [Google Scholar] [CrossRef]
- Cheng, Q.M. Singularity Analysis of Magmatic Flare-Ups Caused by India—Asia Collisions. J. Geochem. Explor. 2018, 189, 25–31. [Google Scholar] [CrossRef]
- Cheng, Q.M. Extrapolations of Secular Trends in Magmatic Intensity and Mantle Cooling: Implications for Future Evolution of Plate Tectonics. Gondwana Res. 2018, 63, 268–273. [Google Scholar] [CrossRef]
- Chen, G.X.; Kusky, T.; Luo, L.; Li, Q.K.; Cheng, Q.M. Hadean Tectonics: Insights from Machine Learning. Geology 2023, 51, 718–722. [Google Scholar] [CrossRef]
- Chen, G.X.; Cheng, Q.M.; Lyons, T.W.; Shen, J.; Agterberg, F.; Huang, N.; Zhao, M.L. Reconstructing Earth’s Atmospheric Oxygenation History Using Machine Learning. Nat. Commun. 2022, 13, 5862. [Google Scholar] [CrossRef]
- Allégre, C.J.; Courtillot, V.; Tapponnier, P.; Hirn, A.; Mattauer, M.; Coulon, C.; Jaeger, J.J.; Achache, J.; Schärer, U.; Marcoux, J.; et al. Structure and Evolution of the Himalaya–Tibet Orogenic Belt. Nature 1984, 307, 17–22. [Google Scholar] [CrossRef]
- Yin, A.; Harrison, T.M. Geologic Evolution of the Himalayan-Tibetan Orogen. Annu. Rev. Earth Planet. Sci. 2000, 28, 211–280. [Google Scholar] [CrossRef]
- Xu, Z.Q.; Ji, S.C.; Cai, Z.H.; Zeng, L.S.; Geng, Q.R.; Cao, H. Kinematics and Dynamics of the Namche Barwa Syntaxis, Eastern Himalaya: Constraints from Deformation, Fabrics and Geochronology. Gondwana Res. 2012, 21, 19–36. [Google Scholar] [CrossRef]
- Audley-Charles, M.G. Reconstruction of Eastern Gondwanaland. Nature 1983, 306, 48–50. [Google Scholar] [CrossRef]
- Audley-Charles, M.G. Cold Gondwana, Warm Tethys and the Tibetan Lhasa Block. Nature 1984, 310, 165. [Google Scholar] [CrossRef]
- Audley-Charles, M.G. Evolution of the Southern Margin of Tethys (North Australian Region) from Early Permian to Late Cretaceous. Geol. Soc. Lond. Spec. Publ. 1988, 37, 79–100. [Google Scholar] [CrossRef]
- Metcalfe, I. Late Palaeozoic and Mesozoic Tectonic and Palaeogeographical Evolution of SE Asia. Geol. Soc. Lond. Spec. Publ. 2009, 315, 7–23. [Google Scholar] [CrossRef]
- Zhu, D.C.; Zhao, Z.D.; Niu, Y.L.; Mo, X.X.; Chung, S.L.; Hou, Z.Q.; Wang, L.Q.; Wu, F.Y. The Lhasa Terrane: Record of a Microcontinent and Its Histories of Drift and Growth. Earth Planet. Sci. Lett. 2011, 301, 241–255. [Google Scholar] [CrossRef]
- Sengör, A.M.C. Tectonics of the Tethysides: Orogenic Collage Development in a Collisional Setting. Annu. Rev. Earth Planet. Sci. 1987, 15, 213–244. [Google Scholar] [CrossRef]
- Sengör, A.M.C.; Cin, A.; Rowley, D.B.; Nie, S.Y. Space-Time Patterns of Magmatism along the Tethysides: A Preliminary Study. J. Geol. 1993, 101, 51–84. [Google Scholar] [CrossRef]
- Zhu, D.C.; Zhao, Z.D.; Niu, Y.L.; Dilek, Y.; Mo, X.X. Lhasa Terrane in Southern Tibet Came from Australia. Geology 2011, 39, 727–730. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, D.C.; Cawood, P.A.; Chung, S.L.; Zhao, Z.D. Resolving the Paleogeographic Puzzle of the Lhasa Terrane in Southern Tibet. Geophys. Res. Lett. 2021, 48, e2021GL094236. [Google Scholar] [CrossRef]
- Sengör, A.M.C.; Atayman, S. The Permian Extinction and the Tethys: An Exercise in Global Geology. In The Permian Extinction and the Tethys: An Exercise in Global Geology; Sengör, A.M.C., Atayman, S., Eds.; Geological Society of America: Boulder, CO, USA, 2009; Volume 448, ISBN 978-0-8137-2448-5. [Google Scholar]
- Leier, A.L.; Kapp, P.; Gehrels, G.E.; DeCelles, P.G. Detrital Zircon Geochronology of Carboniferous–Cretaceous Strata in the Lhasa Terrane, Southern Tibet. Basin Res. 2007, 19, 361–378. [Google Scholar] [CrossRef]
- Myrow, P.M.; Hughes, N.C.; Goodge, J.W.; Fanning, C.M.; Williams, I.S.; Peng, S.; Bhargava, O.N.; Parcha, S.K.; Pogue, K.R. Extraordinary Transport and Mixing of Sediment across Himalayan Central Gondwana during the Cambrian–Ordovician. GSA Bull. 2010, 122, 1660–1670. [Google Scholar] [CrossRef]
- Myrow, P.M.; Hughes, N.C.; Searle, M.P.; Almeida, C.M.; Peng, S.C.; Parcha, S.K. Stratigraphic Correlation of Cambrian–Ordovician Deposits along the Himalaya: Implications for the Age and Nature of Rocks in the Mount Everest Region. GSA Bull. 2009, 121, 323–332. [Google Scholar] [CrossRef]
- Dong, C.Y.; Li, C.; Wan, Y.S.; Wang, W.; Wu, Y.W.; Xie, H.Q.; Liu, D.Y. Detrital Zircon Age Model of Ordovician Wenquan Quartzite South of Lungmuco-Shuanghu Suture in the Qiangtang Area, Tibet: Constraint on Tectonic Affinity and Source Regions. Sci. China Earth Sci. 2011, 54, 1034–1042. [Google Scholar] [CrossRef]
- Pullen, A.; Kapp, P.; Gehrels, G.E.; Vervoort, J.D.; Ding, L. Triassic Continental Subduction in Central Tibet and Mediterranean-Style Closure of the Paleo-Tethys Ocean. Geology 2008, 36, 351–354. [Google Scholar] [CrossRef]
- Gehrels, G.E.; DeCelles, P.G.; Ojha, T.P.; Upreti, B.N. Geologic and U-Pb Geochronologic Evidence for Early Paleozoic Tectonism in the Dadeldhura Thrust Sheet, Far-West Nepal Himalaya. J. Asian Earth Sci. 2006, 28, 385–408. [Google Scholar] [CrossRef]
- Gehrels, G.E.; DeCelles, P.G.; Ojha, T.P.; Upreti, B.N. Geologic and U-Th-Pb Geochronologic Evidence for Early Paleozoic Tectonism in the Kathmandu Thrust Sheet, Central Nepal Himalaya. GSA Bull. 2006, 118, 185–198. [Google Scholar] [CrossRef]
- Veevers, J.J.; Saeed, A.; Belousova, E.A.; Griffin, W.L. U-Pb Ages and Source Composition by Hf-Isotope and Trace-Element Analysis of Detrital Zircons in Permian Sandstone and Modern Sand from Southwestern Australia and a Review of the Paleogeographical and Denudational History of the Yilgarn Craton. Earth-Sci. Rev. 2005, 68, 245–279. [Google Scholar] [CrossRef]
- Morón, S.; Cawood, P.A.; Haines, P.W.; Gallagher, S.J.; Zahirovic, S.; Lewis, C.J.; Moresi, L. Long-Lived Transcontinental Sediment Transport Pathways of East Gondwana. Geology 2019, 47, 513–516. [Google Scholar] [CrossRef]
- Clark, D.J.; Hensen, B.J.; Kinny, P.D. Geochronological Constraints for a Two-Stage History of the Albany–Fraser Orogen, Western Australia. Precambrian Res. 2000, 102, 155–183. [Google Scholar] [CrossRef]
- Sircombe, K.N.; Freeman, M.J. Provenance of Detrital Zircons on the Western Australia Coastline—Implications for the Geologic History of the Perth Basin and Denudation of the Yilgarn Craton. Geology 1999, 27, 879–882. [Google Scholar] [CrossRef]
- Dillinger, A.; George, A.D.; Parra-Avila, L.A. Early Permian Sediment Provenance and Paleogeographic Reconstructions in Southeastern Gondwana Using Detrital Zircon Geochronology (Northern Perth Basin, Western Australia). Gondwana Res. 2018, 59, 57–75. [Google Scholar] [CrossRef]
- Haines, P.W.; Kirkland, C.L.; Wingate, M.T.D.; Allen, H.; Belousova, E.A.; Gréau, Y. Tracking Sediment Dispersal during Orogenesis: A Zircon Age and Hf Isotope Study from the Western Amadeus Basin, Australia. Gondwana Res. 2016, 37, 324–347. [Google Scholar] [CrossRef]
- Kirkland, C.L.; Smithies, R.H.; Woodhouse, A.J.; Howard, H.M.; Wingate, M.T.D.; Belousova, E.A.; Cliff, J.B.; Murphy, R.C.; Spaggiari, C.V. Constraints and Deception in the Isotopic Record; the Crustal Evolution of the West Musgrave Province, Central Australia. Gondwana Res. 2013, 23, 759–781. [Google Scholar] [CrossRef]
- Ameen, S.M.M.; Wilde, S.A. Multiple Sources for Archean Granitoids in the Yalgoo Area, Yilgarn Craton, Western Australia: Geochemical and Isotopic Evidence. Precambrian Res. 2018, 314, 76–110. [Google Scholar] [CrossRef]
- Ivanic, T.J.; Van Kranendonk, M.J.; Kirkland, C.L.; Wyche, S.; Wingate, M.T.D.; Belousova, E.A. Zircon Lu–Hf Isotopes and Granite Geochemistry of the Murchison Domain of the Yilgarn Craton: Evidence for Reworking of Eoarchean Crust during Meso-Neoarchean Plume-Driven Magmatism. Lithos 2012, 148, 112–127. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Pei, Y.; Cheng, Q.; Wang, W. Local Singularity Spectrum: An Innovative Graphical Approach for Analyzing Detrital Zircon Geochronology Data in Provenance Analysis. Fractal Fract. 2024, 8, 64. https://doi.org/10.3390/fractalfract8010064
Wang W, Pei Y, Cheng Q, Wang W. Local Singularity Spectrum: An Innovative Graphical Approach for Analyzing Detrital Zircon Geochronology Data in Provenance Analysis. Fractal and Fractional. 2024; 8(1):64. https://doi.org/10.3390/fractalfract8010064
Chicago/Turabian StyleWang, Wenlei, Yingru Pei, Qiuming Cheng, and Wenjun Wang. 2024. "Local Singularity Spectrum: An Innovative Graphical Approach for Analyzing Detrital Zircon Geochronology Data in Provenance Analysis" Fractal and Fractional 8, no. 1: 64. https://doi.org/10.3390/fractalfract8010064
APA StyleWang, W., Pei, Y., Cheng, Q., & Wang, W. (2024). Local Singularity Spectrum: An Innovative Graphical Approach for Analyzing Detrital Zircon Geochronology Data in Provenance Analysis. Fractal and Fractional, 8(1), 64. https://doi.org/10.3390/fractalfract8010064







