Escape Criteria Using Hybrid Picard S-Iteration Leading to a Comparative Analysis of Fractal Mandelbrot Sets Generated with S-Iteration
Abstract
1. Introduction
2. Basic Definitions and Preliminaries
3. Escape Criterion
4. Rich and Exquisite Patterns of the Fractal Mandelbrot Sets
| Algorithm 1: Creation of the Mandelbrot sets using the hybrid Picard S-orbit |
 |
| Algorithm 2: Creation of the Mandelbrot sets using the S-orbit |
 |
4.1. Rich and Exquisite Patterns of the Mandelbrot Sets Using Hybrid Picard S-Iteration vs. S-Iteration and Quadratic Functions
4.2. Rich and Exquisite Patterns of the Mandelbrot Sets Using Hybrid Picard S-Iteration vs. S-Iteration and Cubic Functions
5. Conclusions and Discussion
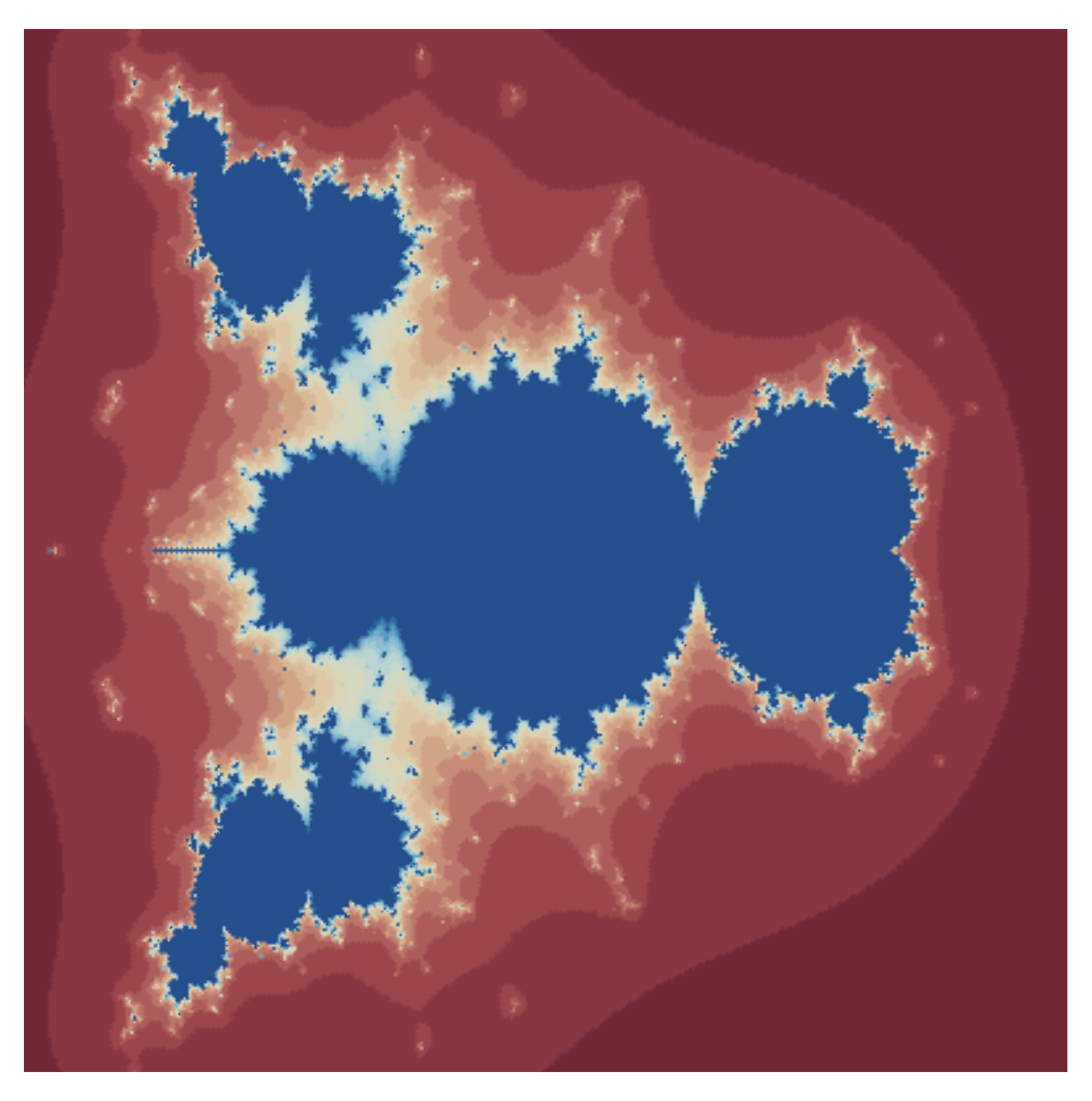
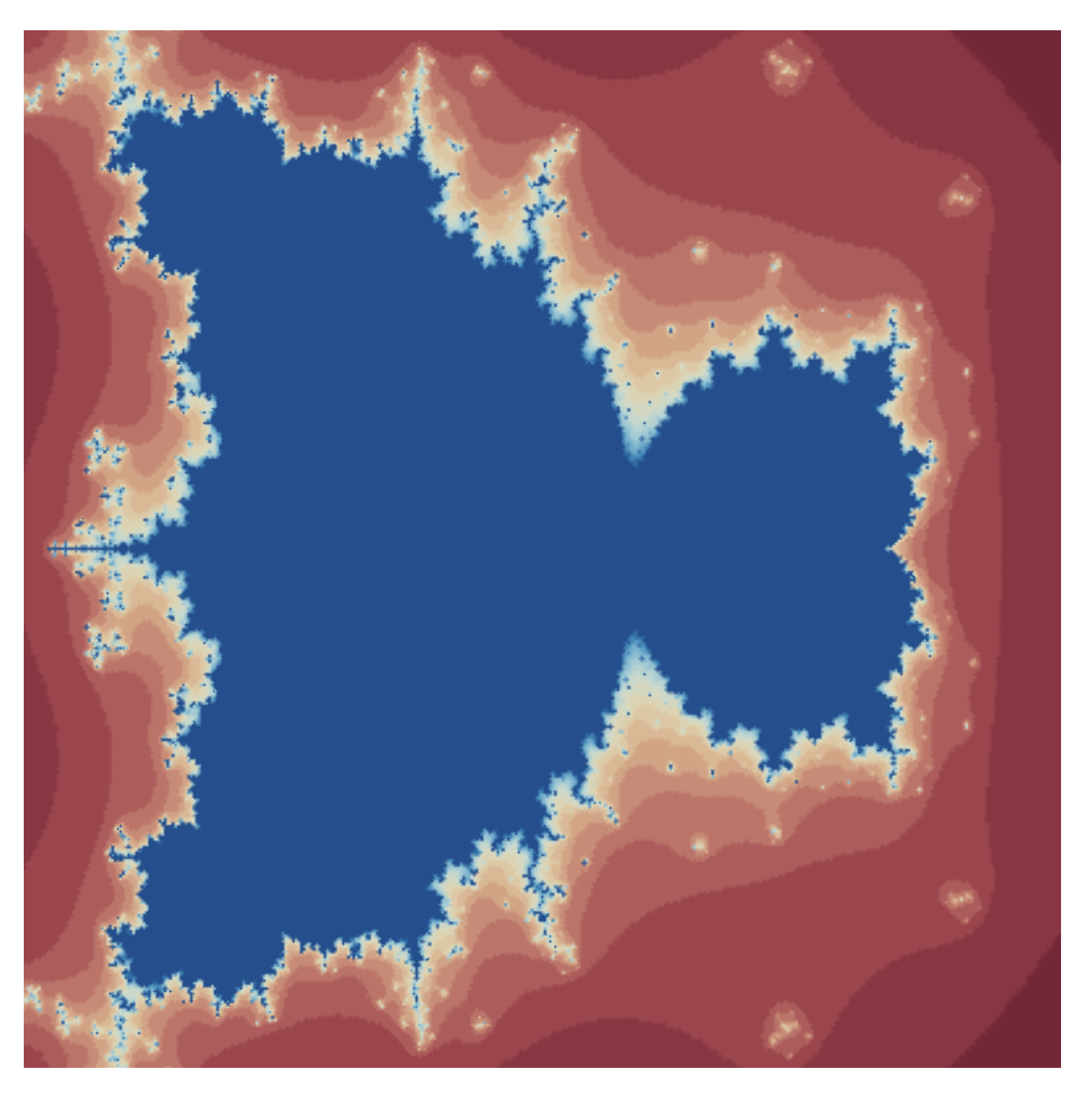
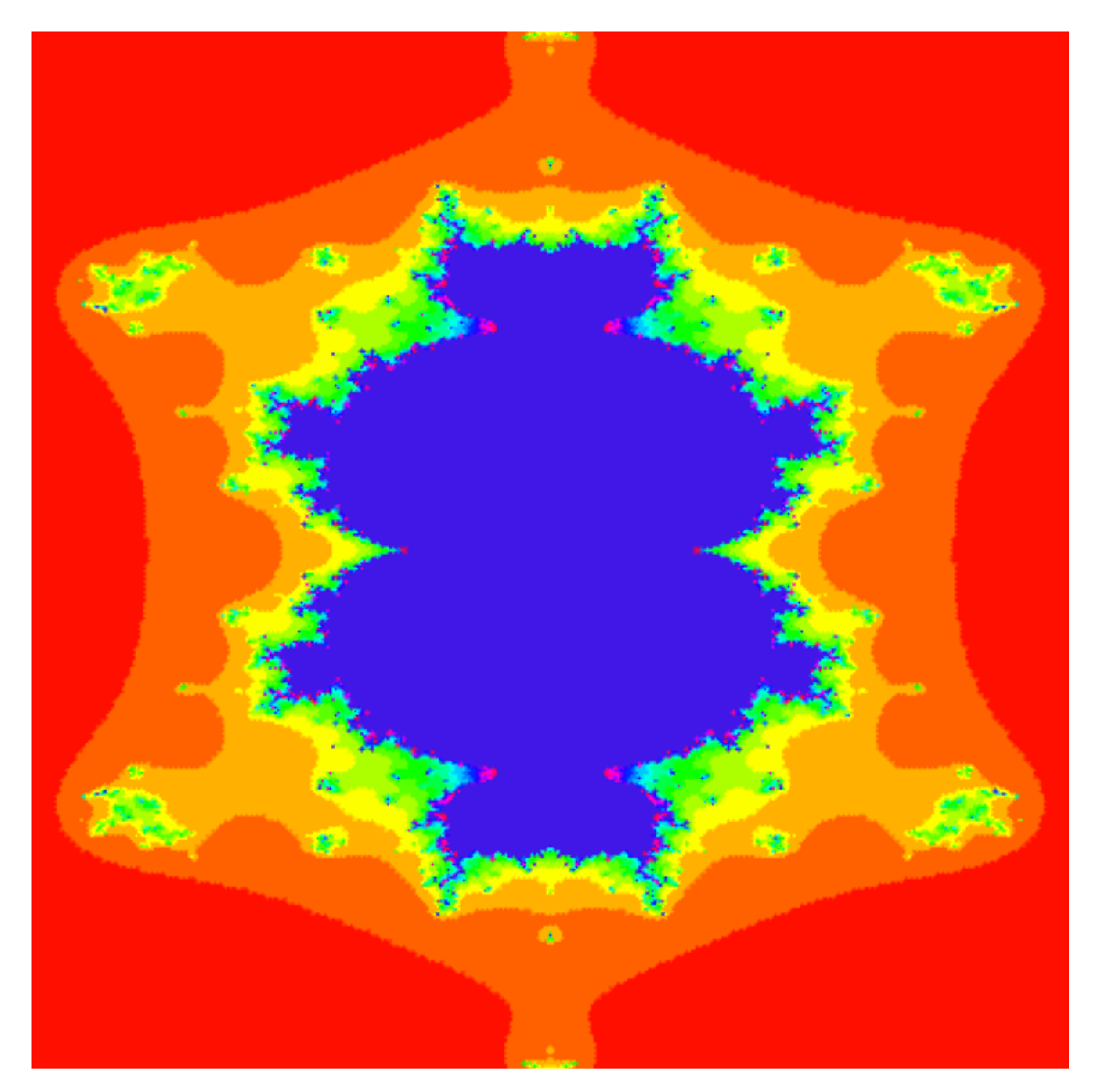
- Similarly in Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23, we fixed parameter and varied parameter to obtain quadratic Mandelbrot sets. Mandelbrot sets created using the hybrid Picard S-iteration procedure are quite spontaneous from those created via S-iteration.
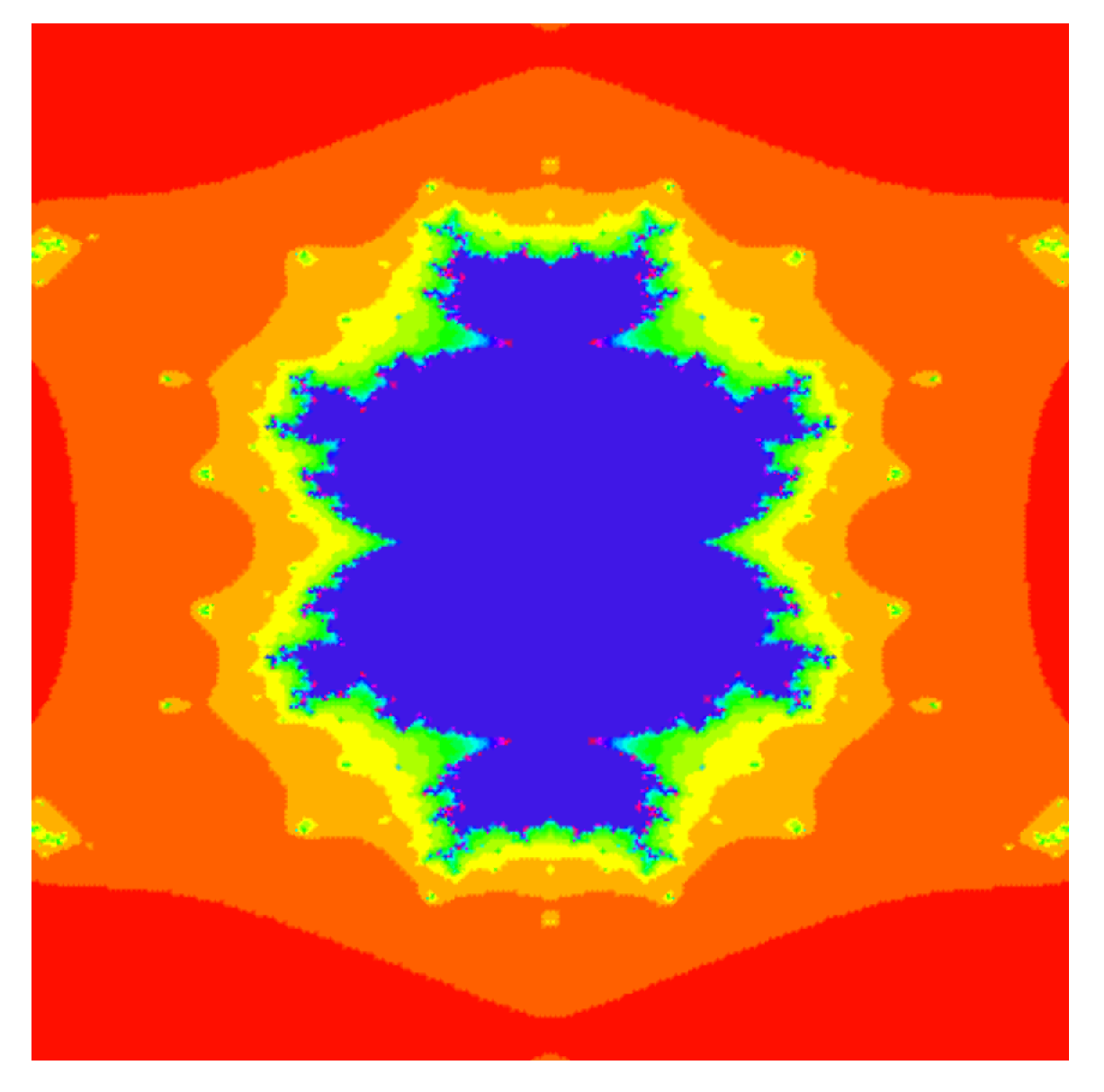
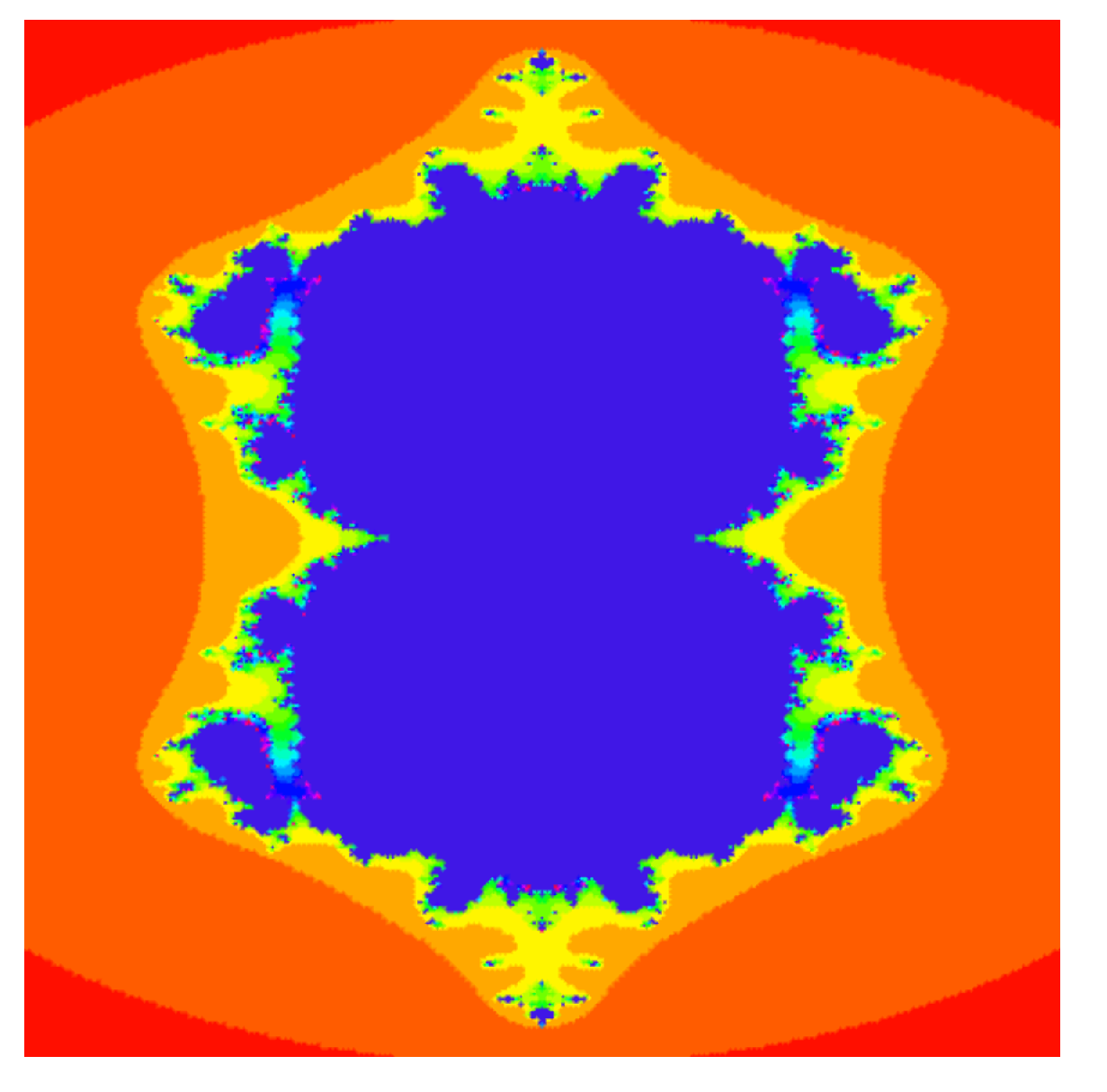
- The cubic Mandelbrot sets created in the hybrid Picard S-orbit and S-orbit with fixed parameter also have an obvious variation in figures for varying parameter .
- Quadratic Mandelbrot sets are symmetrical along the x-axis whereas cubic Mandelbrot sets are symmetrical along both the x-axis and y-axis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MS | Mandelbrot set |
| MSs | Mandelbrot sets |
| SO | S Orbit |
| PSO | Picard S-Orbit |
| PSIP | Picard S-Iteration Process |
References
- Diao, K.; Butler, D.; Ulanicki, B. Fractality in water distribution networks: Application to criticality analysis and optimal rehabilitation. Urban Water J. 2021, 18, 885–895. [Google Scholar] [CrossRef]
- Beata, K.E.H.; Dariusz, K. Fractal-heuristic method of water quality sensor locations in water supply network. Water 2020, 12, 832. [Google Scholar] [CrossRef]
- Wang, S.; Ji, H.; Zhan, Y.; Li, H.; Li, P. Research on the Model Improvement of a DLA Fractal River Network. IEEE Access 2020, 8, 100702–100711. [Google Scholar] [CrossRef]
- Liu, S.-A.; Bai, W.-L.; Liu, G.-C.; Li, W.-H.; Srivastava, H.M. Parallel fractal compression method for big video data. Complexity 2018, 2018, 2016976. [Google Scholar] [CrossRef]
- Martinez, F.; Manriquez, H.; Ojeda, A.; Olea, G. Organization Patterns of Complex River Networks in Chile: A Fractal Morphology. Mathematics 2022, 10, 1806. [Google Scholar] [CrossRef]
- Tehrani, D.H.T.; Solaimani, M. Persistent currents and electronic properties of Mandelbrot quantum rings. Sci. Rep. 2023, 13, 5710. [Google Scholar] [CrossRef]
- Taylor, R.; Spehar, B.; Hagerhall, C.; Van Donkelaar, P. Perceptual and Physiological Responses to Jackson Pollock’s Fractals. Front. Hum. Neurosci. 2011, 5, 10034. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH freeman New York: New York, NY, USA, 1982; Volume 2. [Google Scholar]
- Burger, E.B.; Starbird, M. The Heart of Mathematics: An Invitation to Effective Thinking; Springer Science Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Holtzman, S.R. Digital Mantras: The Languages of Abstract and Virtual Worlds; Mit Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Mitchell, K. The Fractal Art Manifesto. Online. Disponível em. 1999. Available online: https://www.fractalus.com/info/manifesto.htm (accessed on 8 December 2023).
- Li, D.; Shahid, A.A.; Tassaddiq, A.; Khan, A.; Guo, X.; Ahmad, M. CR iteration in the generation of antifractals with s-convexity. IEEE Access 2020, 8, 77214. [Google Scholar] [CrossRef]
- Dhurandhar, S.V.; Bhavsar, V.C.; Gujar, U.G. Analysis of z-plane fractal images from z→zα + cforα < 0. Comput. Graph. 1993, 17, 89–94. [Google Scholar]
- Lakhtakia, A.; Varadan, V.; Messier, R.; Varadan, V. On the symmetries of the Julia sets for the process z→zα + c. J. Phys. A Math. Gen. 1987, 20, 3533–3535. [Google Scholar] [CrossRef]
- Crowe, W.D.; Hasson, R.; Rippon, P.J.; Strain-Clark, P.E.D. On the structure of the mandelbar set. Nonlinearity 1989, 2, 541–553. [Google Scholar] [CrossRef]
- Domínguez, P.; Fagella, N. Residual Julia sets of rational and transcendental functions. In Transcendental Dynamics and Complex Analysis; Cambridge University Press: Cambridge, UK, 2010; pp. 138–164. [Google Scholar]
- Peherstorfer, F.; Stroh, C. Connectedness of Julia sets of rational functions. Comput. Methods Funct. Theory 2001, 1, 61–79. [Google Scholar] [CrossRef]
- Koss, L. Elliptic functions with disconnected Julia sets. Int. Bifurc. Chaos 2016, 26, 1650095. [Google Scholar] [CrossRef]
- Liu, S.-A.; Xu, X.-Y.; Srivastava, G.; Srivastava, H.M. Fractal properties of the generalized Mandelbrot set with complex exponent. Fractals 2023. [Google Scholar] [CrossRef]
- Katunin, A. Analysis of 4D hypercomplex generalization of Julia sets. In Computer Vision and Graphics: International Conference, ICCVG 2016, Warsaw, Poland, 19–21 September 2016; Proceedings 8; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 627–635. [Google Scholar]
- Dang, Y.; Kauffman, L.; Sandin, D. Hypercomplex Iterations: Distance Estimation and Higher Dimensional Fractals; World Scientific: Singapore, 2002. [Google Scholar]
- Griffin, C.; Joshi, G. Octonionic Julia sets. Chaos Solitons Fractals 1992, 2, 11–24. [Google Scholar] [CrossRef]
- Gdawiec, K. Inversion fractals and iteration processes in the generation of aesthetic patterns. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2017; Volume 36, pp. 35–45. [Google Scholar]
- Singh, S.L.; Mishra, S.; Sinkala, W. A new iterative approach to fractal models. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 521–529. [Google Scholar] [CrossRef]
- Prasad, B.; Katiyar, K. Fractals via Ishikawa iteration. In Proceedings of the International Conference on Logic, Information, Control and Computation, Gandhigram, India, 25–27 February 2011; pp. 197–203. [Google Scholar]
- Gdawiec, K.; Kotarski, W.; Lisowska, A. Biomorphs via modified iterations. J. Nonlinear Sci. Appl. 2016, 9, 2305–2315. [Google Scholar] [CrossRef]
- Kittiratanawasin, L.; Yambangwai, D.; Chairatsiripong, C.; Thianwan, T. An Efficient Iterative Algorithm for Solving the Split Feasibility Problem in Hilbert Spaces Applicable in Image Deblurring. Signal Recover. Polynomiography J. Math. 2023, 2023, 15. [Google Scholar] [CrossRef]
- Rani, M.; Kumar, V. Superior Julia set. J. Korea Soc. Math. Educ. Ser. D Res. Math. Educ. 2004, 8, 261–277. [Google Scholar]
- Rani, M.; Kumar, V. Superior mandelbrot set. Res. Math. Educ. 2004, 8, 279–291. [Google Scholar]
- Rana, R.; Chauhan, Y.S.; Negi, A. Non linear dynamics of ishikawa iteration. Int. J. Comput. Appl. 2010, 7, 43–49. [Google Scholar] [CrossRef]
- Chauhan, Y.S.; Rana, R.; Negi, A. New julia sets of ishikawa iterates. Int. J. Comput. Appl. 2010, 7, 34–42. [Google Scholar] [CrossRef]
- Kang, S.M.; Rafiq, A.; Latif, A.; Shahid, A.A.; Kwun, Y.C. Tricorns and Multi-corns of S-iteration scheme. J. Funct. Spaces 2015, 2015, 1–7. [Google Scholar]
- Ashish, M.R.; Chugh, R. Julia sets and mandelbrot sets in Noor orbit. Appl. Math. Comput. 2014, 228, 615–631. [Google Scholar] [CrossRef]
- Li, D.; Tanveer, M.; Nazeer, W.; Guo, X. Boundaries of filled Julia sets in generalized Jungck-Mann orbit. IEEE Access 2019, 7, 76859–76867. [Google Scholar] [CrossRef]
- Kwun, Y.C.; Tanveer, M.; Nazeer, W.; Gdawiec, K.; Kang, S.M. Mandelbrot and Julia sets via Jungck-CR iteration with s-convexity. IEEE Access 2019, 7, 12167–12176. [Google Scholar] [CrossRef]
- Kwun, Y.C.; Tanveer, M.; Nazeer, W.; Abbas, M.; Kang, S.M. Fractal generation in modified Jungck–S orbit. IEEE Access 2019, 7, 35060–35071. [Google Scholar] [CrossRef]
- Gdawie, K.; Shahid, A.A. Fixed point results for the complex fractal generation in the s-iteration orbit with s-convexity. Open J. Math. Sci. 2018, 2, 56–72. [Google Scholar] [CrossRef]
- Nazeer, W.; Kang, S.M.; Tanveer, M.; Shahid, A.A. Fixed point results in the generation of julia and mandelbrot sets. J. Equal. Appl. 2015, 2015, 298. [Google Scholar] [CrossRef]
- Cho, S.Y.; Shahid, A.A.; Nazeer, W.; Kang, S.M. Fixed Point Results for Fractal Generation in Noor Orbit and S-Convexity; SpringerPlus: Berlin/Heidelberg, Germany, 2016; Volume 5, p. 1843. [Google Scholar]
- Zou, C.; Shahid, A.; Tassaddiq, A.; Khan, A.; Ahmad, M. Mandelbrot sets and Julia sets in Picard–Mann orbit. IEEE Access 2020, 8, 64411–64421. [Google Scholar] [CrossRef]
- Prajapati, D.J.; Rawat, S.; Tomar, A.; Sajid, M.; Dimri, R.C. A Brief Study on Julia Sets in the Dynamics of Entire Transcendental Function Using Mann Iterative Scheme. Fractal Fract. 2022, 6, 397. [Google Scholar] [CrossRef]
- Tomar, A.; Kumar, V.; Rana, U.S.; Sajid, M. Fractals as Julia and Mandelbrot Sets of Complex Cosine Functions via Fixed Point Iterations. Symmetry 2023, 15, 478. [Google Scholar] [CrossRef]
- Tanveer, M.; Nazeer, W.; Gdawiec, K. On the Mandelbrot set of zp + logct via the Mann and Picard–Mann iterations. Math. Comput. Simul. 2023, 209, 184–204. [Google Scholar] [CrossRef]
- Devaney, R. A First Course in Chaotic Dynamical Systems: Theory and Experiment; Addison-Wesley: New York, NY, USA, 1982; Volume 2. [Google Scholar]
- Mann, W.R. Mean value methods in iteration. Proc. Am. Math. Soc. 1953, 4, 506–510. [Google Scholar] [CrossRef]
- Ishikawa, S. Fixed points by a new iteration method. Proc. Am. Math. Soc. 1974, 44, 147–150. [Google Scholar] [CrossRef]
- Agarwal, R.; Regan, D.O.; Sahu, D. Iterative construction of fixed points of nearly asymptotically nonexpansive mappings. J. Nonlinear Convex Anal. 2007, 8, 61. [Google Scholar]
- Gursoy, F. A picard-s iterative method for approximating fixed point of weak-contraction mappings. Filomat 2016, 30, 2829–2845. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Tanveer, M.; Azhar, M.; Arshad, M.; Lakhani, F. Escape Criteria for Generating Fractals of Complex Functions Using DK-Iterative Scheme. Fractal Fract. 2023, 7, 76. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Tanveer, M.; Azhar, M.; Nazeer, W.; Qureshi, S. A Four Step Feedback Iteration and Its Applications in Fractals. Fractal Fract. 2022, 6, 662. [Google Scholar] [CrossRef]
- Tassaddiq, A. General escape criteria for the generation of fractals in extended Jungck—Noor orbit. Math. Comput. Simul. 2022, 196, 1–14. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Tanveer, M.; Israr, K.; Arshad, M.; Shehzad, K.; Srivastava, R. Multicorn Sets of zk + cm via S-Iteration with h-Convexity. Fractal Fract. 2023, 7, 486. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M.; Hamanah, W.M. Certain New Models of the Multi-Space Fractal-Fractional Kuramoto-Sivashinsky and Korteweg-de Vries Equations. Mathematics 2022, 10, 1089. [Google Scholar] [CrossRef]
- Okeke, G.A. Convergence analysis of the Picard–Ishikawa hybrid iterative process with applications. Afr. Mat. 2019, 30, 817–835. [Google Scholar] [CrossRef]










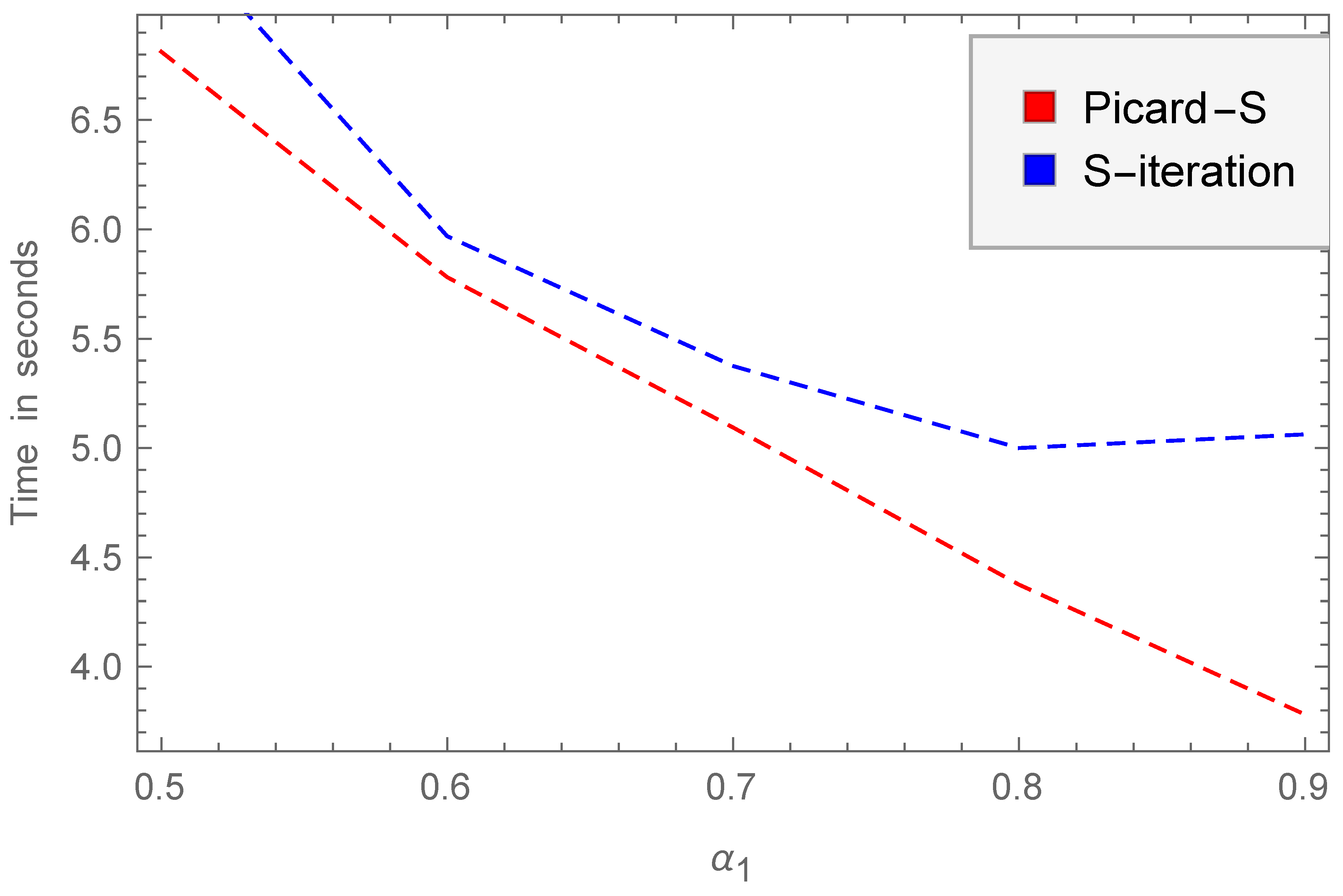






















| Time for the Hybrid Picard S-Iteration | Time for S-Iteration | |
|---|---|---|
| Time for the Hybrid Picard S-Iteration | Time for S-Iteration | |
|---|---|---|
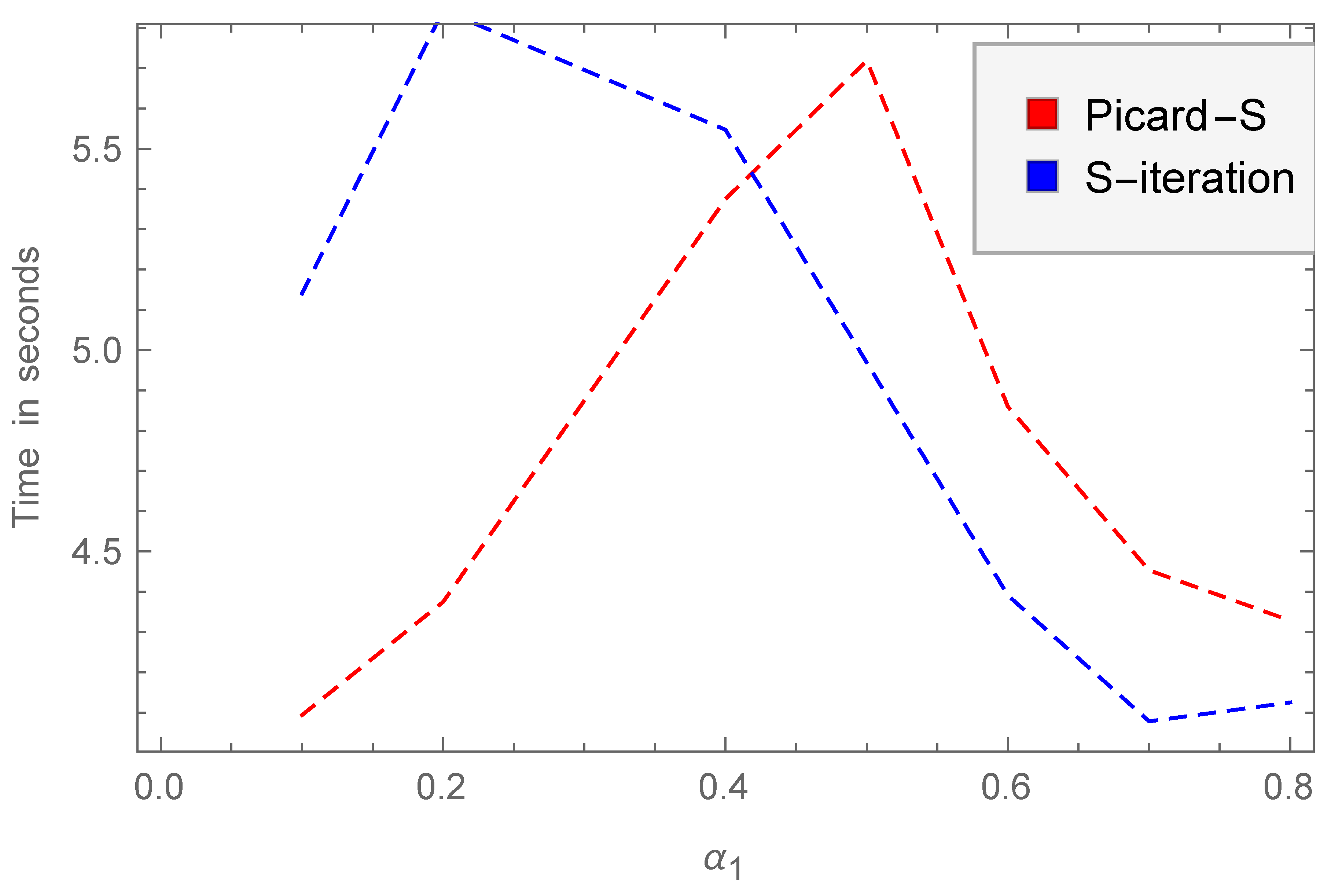
| Time for Picard S-Iteration | Time for S-Iteration | |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastava, R.; Tassaddiq, A.; Kasmani, R.M. Escape Criteria Using Hybrid Picard S-Iteration Leading to a Comparative Analysis of Fractal Mandelbrot Sets Generated with S-Iteration. Fractal Fract. 2024, 8, 116. https://doi.org/10.3390/fractalfract8020116
Srivastava R, Tassaddiq A, Kasmani RM. Escape Criteria Using Hybrid Picard S-Iteration Leading to a Comparative Analysis of Fractal Mandelbrot Sets Generated with S-Iteration. Fractal and Fractional. 2024; 8(2):116. https://doi.org/10.3390/fractalfract8020116
Chicago/Turabian StyleSrivastava, Rekha, Asifa Tassaddiq, and Ruhaila Md Kasmani. 2024. "Escape Criteria Using Hybrid Picard S-Iteration Leading to a Comparative Analysis of Fractal Mandelbrot Sets Generated with S-Iteration" Fractal and Fractional 8, no. 2: 116. https://doi.org/10.3390/fractalfract8020116
APA StyleSrivastava, R., Tassaddiq, A., & Kasmani, R. M. (2024). Escape Criteria Using Hybrid Picard S-Iteration Leading to a Comparative Analysis of Fractal Mandelbrot Sets Generated with S-Iteration. Fractal and Fractional, 8(2), 116. https://doi.org/10.3390/fractalfract8020116








